库伦土压力与朗肯土压力计算理论
(整理)土主动、被动土压力概念及计算公式

主动土压力挡土墙向前移离填土,随着墙的位移量的逐渐增大,土体作用于墙上的土压力逐渐减小,当墙后土体达到主动极限平衡状态并出现滑动面时,这时作用于墙上的土压力减至最小,称为主动土压力P a 。
被动土压力挡土墙在外力作用下移向填土,随着墙位移量的逐渐增大,土体作用于墙上的土压力逐渐增大,当墙后土体达到被动极限平衡状态并出现滑动面时,这时作用于墙上的土压力增至最大,称为被动土压力P p 。
上述三种土压力的移动情况和它们在相同条件下的数值比较,可用图6-2来表示。
由图可知P p >P o >P a 。
朗肯基本理论朗肯土压力理论是英国学者朗肯(Rankin )1857年根据均质的半无限土体的应力状态和土处于极限平衡状态的应力条件提出的。
在其理论推导中,首先作出以下基本假定。
(1)挡土墙是刚性的墙背垂直; (2)挡土墙的墙后填土表面水平;(3)挡土墙的墙背光滑,不考虑墙背与填土之间的摩擦力。
把土体当作半无限空间的弹性体,而墙背可假想为半无限土体内部的铅直平面,根据土体处于极限平衡状态的条件,求出挡土墙上的土压力。
如果挡土墙向填土方向移动压缩土体,σz 仍保持不变,但σx 将不断增大并超过σz 值,当土墙挤压土体使σx 增大到使土体达到被动极限平衡状态时,如图6-4的应力园O 3,σz 变为小主应力,σx 变为大主应力,即为朗肯被动土压力(p p )。
土体中产生的两组破裂面与水平面的夹角为245ϕ-︒。
朗肯主动土压力的计算根据土的极限平衡条件方程式σ1=σ3tg 2(45°+2ϕ)+2c ·tg(45°+2ϕ) σ3=σ1tg 2(45°-ϕ)-2c ·tg(45°-ϕ)当z=H 时p a =γHK a -2cK a在图中,压力为零的深度z 0,可由p a =0的条件代入式(6-3)求得a0K c 2z γ=(6-4)在z 0深度范围内p a 为负值,但土与墙之间不可能产生拉应力,说明在z 0深度范围内,填土对挡土墙不产生土压力。
土层地下结构水、土压力的计算
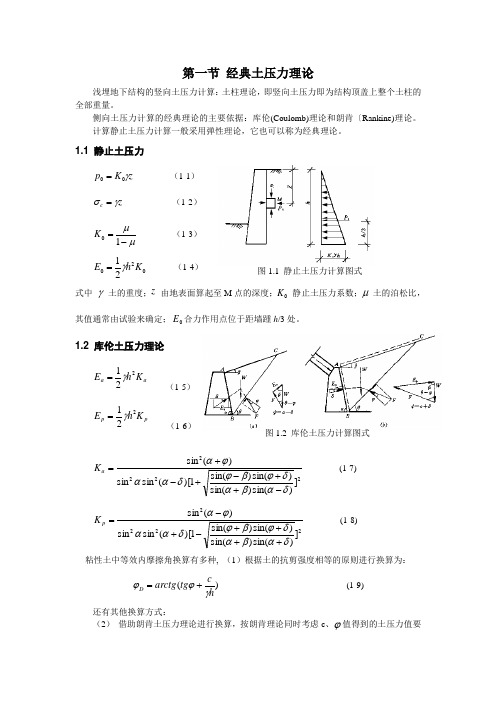
第一节 经典土压力理论浅埋地下结构的竖向土压力计算:土柱理论,即竖向土压力即为结构顶盖上整个土柱的全部重量。
侧向土压力计算的经典理论的主要依据:库伦(Coulomb)理论和朗肯〔Rankine)理论。
计算静止土压力计算一般采用弹性理论,它也可以称为经典理论。
1.1 静止土压力z K p γ00= (1-1)z c γσ= (1-2)μμ-=10K (1-3)02021K h E γ= (1-4)式中 γ-土的重度;z -由地表面算起至M 点的深度;0K -静止土压力系数;μ-土的泊松比,其值通常由试验来确定;0E 合力作用点位于距墙踵h /3处。
1.2 库伦土压力理论aa K h E 221γ= (1-5) p p K h E 221γ=(1-6)2222])sin()sin()sin()sin(1)[(sin sin )(sin δαβαδϕβϕδααϕα-++-+-+=a K (1-7) 2222])sin()sin()sin()sin(1)[(sin sin )(sin δαβαδϕβϕδααϕα++++-+-=p K (1-8) 粘性土中等效内摩擦角换算有多种, (1)根据土的抗剪强度相等的原则进行换算为:)(hctg arctg D γϕϕ+= (1-9) 还有其他换算方式:(2) 借助朗肯土压力理论进行换算,按朗肯理论同时考虑c 、ϕ值得到的土压力值要图1.1 静止土压力计算图式图1.2 库伦土压力计算图式和已换算成等效内摩擦角D ϕ后得到的土压力值相等,推算得到等效内摩擦角D ϕ。
(3)采用《建筑地基基础设计规范》计算。
1.3 朗肯土压力理论z z γσ= (1-10)z K x γσ0= (1-11)a a a K c zK p 2-=γ (1-12) P P P K c zK p 2+=γ (1-13)式中:)245(2ϕ-=tg K a ,)245(2ϕ+=tg K pγγ222221c K ch K h E a a a +-= (1-14) 图1.3 朗肯极限平衡状态第二节 地下结构的土层压力中南大学资源与安全学院 赵建平2.1 浅埋地下结构的竖向土层压力在软土地层中当地下结构物采用明挖法施工,埋置深度较浅(顶盖离地表面距离较近时),称为浅埋地下结构。
土主动被动土压力概念及计算公式

主动土压力挡土墙向前移离填土,随着墙的位移量的逐渐增大,土体作用于墙上的土压力逐渐减小,当墙后土体达到主动极限平衡状态并出现滑动面时,这时作用于墙上的土压力减至最小,称为主动土压力P a 。
被动土压力挡土墙在外力作用下移向填土,随着墙位移量的逐渐增大,土体作用于墙上的土压力逐渐增大,当墙后土体达到被动极限平衡状态并出现滑动面时,这时作用于墙上的土压力增至最大,称为被动土压力P p 。
上述三种土压力的移动情况和它们在相同条件下的数值比较,可用图6-2来表示。
由图可知P p >P o >P a 。
朗肯基本理论朗肯土压力理论是英国学者朗肯(Rankin )1857年根据均质的半无限土体的应力状态和土处于极限平衡状态的应力条件提出的。
在其理论推导中,首先作出以下基本假定。
(1)挡土墙是刚性的墙背垂直; (2)挡土墙的墙后填土表面水平;(3)挡土墙的墙背光滑,不考虑墙背与填土之间的摩擦力。
把土体当作半无限空间的弹性体,而墙背可假想为半无限土体内部的铅直平面,根据土体处于极限平衡状态的条件,求出挡土墙上的土压力。
如果挡土墙向填土方向移动压缩土体,σz 仍保持不变,但σx 将不断增大并超过σz 值,当土墙挤压土体使σx 增大到使土体达到被动极限平衡状态时,如图6-4的应力园O 3,σz 变为小主应力,σx 变为大主应力,即为朗肯被动土压力(p p )。
土体中产生的两组破裂面与水平面的夹角为245ϕ-︒。
朗肯主动土压力的计算根据土的极限平衡条件方程式σ1=σ3tg 2(45°+2ϕ)+2c ·tg(45°+2ϕ) σ3=σ1tg 2(45°-ϕ)-2c ·tg(45°-ϕ)a0K c 2z γ=(6-4)在z 0深度范围内p a 为负值,但土与墙之间不可能产生拉应力,说明在z 0深度范围内,填土对挡土墙不产生土压力。
墙背所受总主动土压力为P a ,其值为土压力分布图中的阴影部分面积,即γ+-γ=--γ=22c 2K cH 2K H 21)z H )(K c 2HK (21P a a 0a a a (6-5)2)填土为无粘性土(砂土)时根据极限平衡条件关系方程式,主动土压力为a a zK )245(ztg p 2γ=ϕ-︒γ= (6-6)上式说明主动土压力P a 沿墙高呈直线分布,即土压力为三角形分布,如图6-6所示。
土体主动、主动土压力概念及计算公式

[ 指南] 土体主动、主动土压力概念及计算公式主动土压力挡土墙向前移离填土,随着墙的位移量的逐渐增大,土体作用于墙上的土压力逐渐减小,当墙后土体达到主动极限平衡状态并出现滑动面时,这时作用于墙上的土压力减至最小,称为主动土压力P。
a被动土压力挡土墙在外力作用下移向填土,随着墙位移量的逐渐增大,土体作用于墙上的土压力逐渐增大,当墙后土体达到被动极限平衡状态并出现滑动面时,这时作用于墙上的土压力增至最大,称为被动土压力P。
上述三种土压力的移动情况和它们在相同条件下的数值比较,p可用图6-2 来表示。
由图可知P,P,P。
poa朗肯基本理论朗肯土压力理论是英国学者朗肯(Rankin)1857 年根据均质的半无限土体的应力状态和土处于极限平衡状态的应力条件提出的。
在其理论推导中, 首先作出以下基本假定。
(1) 挡土墙是刚性的墙背垂直;(2) 挡土墙的墙后填土表面水平;(3) 挡土墙的墙背光滑,不考虑墙背与填土之间的摩擦力。
把土体当作半无限空间的弹性体,而墙背可假想为半无限土体内部的铅直平面,根据土体处于极限平衡状态的条件,求出挡土墙上的土压力。
如果挡土墙向填土方向移动压缩土体,ζ仍保持不变,但ζ将不断增大并超过Z 值,ZXZ当土墙挤压土体使Z增大到使土体达到被动极限平衡状态时,如图6-4的应力园O, Z x3z变为小主应力,Z变为大主应力,即为朗肯被动土压力(p) 。
土体中产生的两组破裂面与xp,45:, 水平面的夹角为。
2 朗肯主动土压力的计算根据土的极限平衡条件方程式,,2 Z =Z tg(45?+)+2c?tg(45?+) 1322,,2 Z =Z tg(45?-)-2c?tg(45?-) 3122土体处于主动极限平衡状态时,Z = Z = Y Z, Z = Z =p,代入上式得1z3xa1) 填土为粘性土时填土为粘性土时的朗肯主动土压力计算公式为,,2,ap= γztg(45?-)-2c?tg(45?-)= γzK-2c (6-3) aa22由公式(6-3) ,可知,主动土压力p 沿深度Z 呈直线分布,如图6-5 所示。
郎肯土压力和库仑土压力的区别

朗肯土压力理论是根据半空间体的应力状态和土的极限平衡理论得出的土压力计算理论。
朗肯将上述原理应用于挡土墙土压力计算时。
假设墙背直立、光滑,墙后填土面水平。
这时,墙背与填土压力土界面上的剪应力为零。
不改变右边土体中的应力状态。
当挡土墙的变位符合上述主动或被动极限平衡条件时,作用在挡土墙墙背上的土压力即为朗肯主动土压力或朗肯被动土压力。
朗肯土压力理论是根据半空间的应力状态和土单元体的极限平衡条件而得出的土压力古典理论之一。
而库伦土压力理论是以整个滑动土体上力系的平衡条件来求解主动土压力,被动土压力计算的理论公式
朗肯土压力的使用范围:假设墙背光滑,直立,填土面水平。
库伦土压力的使用范围:墙后填土是理想的散粒体,滑动破坏面为一平面,滑动土楔体视为刚体。
库伦土压力与朗肯土压力计算理论

2.1 土压力理论土压力是指挡土墙后的填土因自重或外荷载作用对墙背产生的侧向压力。
土压力的计算是个比较复杂的问题。
它随挡土墙可能位移的方向分为主动土压力、被动土压力和静止土压力。
土压力的大小还与墙后填土的性质、墙背倾斜方向等因素有关。
2.1.1 库伦土压力[22]1773年著名的法国学者库伦(C.A.Coulomb)提出了一种计算土压力的理论。
这种理论是根据墙后所形成的滑动楔体静力平衡条件建立起来的,这种理论具有计算简单,适用范围广泛,且计算结果接近实际等优点,至今仍然被广泛使用于工程实践之中。
其基本假定如下:(l)墙后填土为理想散粒体(无粘聚力);(2)墙后填土产生主动土压力或被动土压力时,填土形成滑动楔体,且滑动面为通过墙踵的平面;(3)滑动楔体为刚体,不考虑滑动楔体内部的应力和变形条件1、主动土压力公式:212a a E H K γ=2a K = 式中:α—为墙背与铅直线夹角,逆时针为正值;K a —库仑主动土压力系数;β—填土表面与水平面所成坡角;δ—墙后填土与墙背的摩擦角,由试验或规范确定。
2、被动土压力公式212p p E H K γ=2p K =式中:K p —为库仑被动土压力系数。
2.1.2 朗肯土压力[23]朗肯土压力是英国学者朗肯在1857 年提出的一种经典的土压力理论,这种土压力理论是根据半空间体的应力状态和土的极限平衡理论得出的土压力计算理论之一。
这种土压力理论的计算方法比较简单,计算结果比较接近实际,至今仍然被广泛用于工程实践之中。
其基本假定如下:1).墙本身是刚性的,不考虑墙身的变形;2).墙后填土面水平且填土延伸到无限远处;3).墙背直立、光滑。
1、主动土压力公式无粘性土: 2(45-)2a Ztg ϕσγ=。
粘性土: 2(45-)2(45-)22a Ztg Ctg ϕϕσγ=-。
式中:C 一为土的粘聚力,Z —计算点距离填土面的深度(m);φ一内摩擦角σa 一为主动土压力γ—填土的重度a b c图2-1 朗肯土压力计算图无粘性土:主动土压力强度与深度z 成正比,土压力分布图呈三角形(图2-1b )。
【基坑工程课程作业】经典土压力理论与实际工作状态土压力的差异
经典土压力理论与实际工作状态土压力的差异1 经典土压力理论在土压力计算方法中,有两个著名的古典土压力理论,分别是朗肯土压力理论和库伦土压力理论。
这两种土压力理论都是极限平衡状态下作用在挡土墙上的土压力,都属于极限平衡理论。
不同点是朗肯土压力理论是从一点的应力状态出发,先求出土压力强度,再求总土压力,属于极限应力法;而库伦考虑整个滑动楔体静力平衡,直接求出总土压力,需要时在求解土压力强度,属于滑动楔体法。
1.1 朗肯土压力理论朗肯土压力理论由于概念明确,方法简单,至今仍被广泛使用。
朗肯土压力理论基于以下三个基本假设:①对象为弹性半空间土体;②不考虑挡土墙及回填土的施工因素;③挡土墙墙背竖直、光滑、填土面水平,无超载。
(1)主动土压力分布粘性土的土压力由二部分组成,一部分为由土的自重引起的土压力γzKa ,随深度z呈三角形变化;另一部分为由粘聚力c引起的土压力,为一负值,不随深度变化。
叠加的结果如图6-5c所示。
图中ade部分为负侧压力。
由于墙面光滑,土对墙面产生的拉力会使土脱离墙,出现深度为z0的裂隙。
因此,略去这部分土压力后,实际土压力分布为abc部分。
(2)被动土压力分布无粘性土被动土压力分布呈三角形(图6-6b),粘性土的土压力的分布为梯形(图6-6c)。
1.2 库伦土压力理论库伦土压力理论基于的基本假设:①墙后填土为均匀的无粘性土(c=0),填土表面倾斜(β>0);②挡土墙是刚性的,墙背倾斜,倾角为ε;③墙面粗糙,墙背与土本之间存在摩擦力(δ>0);④滑动破裂面为通过墙踵的平面。
(1)主动土压力分布主动土压力强度沿墙高呈三角形分布,主动土压力沿墙高的分布图形如图所示。
主动土压力合力作用点在离墙底的H/3高度处,作用方向与墙面的法线成δ角,与水平面成δ+ε角。
2 基坑支护结构实际工作状态时的土压力分布目前,基坑土压力计算的有关理论主要就是朗肯土压力理论和库伦土压力理论。
二者都是假设支护结构的滑动土为绝对刚性的,并且滑动面定为平面,没有考虑流场的变化、土体的蠕动改变、时空效应和沉降固结等因素,计算的结果较为偏激,不能真实准确地反映基坑土压力变化。
土力学与地基基础任务11 土压力及挡土墙设计
一、 概述 二、 土压力的分类 三、 郎肯土压力理论 四、 库仑土压力理论
学习目标:
1. 理解三种土压力的概念。 2. 掌握朗肯土压力理论; 3. 理解库伦土压力理论及其与朗肯土压力理论的比较; 4. 掌握常见情况下土压力的计算。
一、 概述
(一)挡土墙的应用
挡土墙——防止土体坍 塌的构筑物。
2,2
1H1K 1H1
(1H1 2H
下层应为 ', ' ,可近
似认为
h1Ka 'h2Ka wh2
三、朗肯土压力理论(Rankine,1857)
【例题7.1】某挡土墙,高度为5m,墙背垂直光滑,填土面水 平。填土为粘性土,其物理力学性质指标如下:c 8kPa , 18 , 18kN / m3。试计算该挡土墙主动土压力及其作用点位 置,并绘出主动土压力强度分布图。
(4)主动土压力 主动土压力强度分布如图7.7
所示。
总主动土压力
Ea
35.89 5 1.223 1
2
67.78kN / m
主动土压力作用点距墙底的距离为
(h z0 ) 5 1.223 1.26m
3
3
作业
1、某挡土墙,高度为5m,墙背垂直光滑,填 土面水平。填土为粘性土,其物理力学性质指 标如下:c 8kPa ,
2
三、朗肯土压力理论(Rankine,1857)
假定条件:墙背光滑(满足剪应力为零的边界条件)、直
立、填土面水平。当挡墙偏离土体时, x逐渐减小到 a时达到
朗肯主动极限平衡状态,主动土压力强度 a为:
粘性土:
a
z
tan
2
45
2
2c
土力学-第8章土压力
2. 主动土压力(Ea)
当挡土墙在墙后填土压力作用下离开填土移动,土 压力逐渐减小,墙后的填土达到极限平衡状态(或破坏) 时,作用在墙上的土压力称为主动土压力。
主动土压力强度σa(KPa)表示。
主动
EA 滑
动
面
13
3. 被动土压力(EP)
当挡土墙在外力作用下向填土挤压,土压力逐渐增 大,墙后填土达到极限平衡状态,作用在墙上的土压 力称为被动土压力。
8.3.2 主动土压力
f
极限平衡条件
31tan2 45 2 2ctan 45 2
Kav K0v v
大主应力 σ1 = σv=γz
小主应力
σ3 = σx
主动土压力强度 σa = σ3
主动土压力系数
Ka tan245 2
主动土压力强度
8.1 概述 8.2 挡土墙侧的土压力 8.3 朗肯土压力理论 8.4 库仑土压力理论 8.5 朗肯理论与库伦理论的比较
1
8.1 概述
挡土墙或挡土结构物
挡土墙
填土 建筑物
地下室 外墙 地下室
桥台
道路
挡土墙
2
3
混凝土挡土墙及复合排水管 完工 完工
4
建成后的坡间挡土墙
5
垮塌的重力式挡墙
6
7
8
26
8.3 朗肯土压力理论
小结:朗肯土压力理论
• 墙背垂直光滑,土面水平 • 主动和被动 • 极限平衡条件 • 砂土和粘性土
45+f/2
45-f/2
13 31
3f K0v v=z
1f
27
8.3 朗肯土压力理论
粘性土的主动土压力
ch6-3.4朗肯、库仑土压力计算解读
z
pp z K p
K p tg 2 (45 f / 2)
-朗肯被动土压力系数
Ep K p H 2 / 2
1 H 3
总被动土压力(大小、作用点)
1 E p K pH 2 2
p p K pH
6.3 朗肯土压力理论 •朗肯被动土压力计算-填土为粘性土
于是:被动土压力强度
p p h 1 z tg 2 (45 f / 2)
K0 v v=z
pp=1f
6.3 朗肯土压力理论 •朗肯被动土压力计算-填土为无粘性土(砂土) 被动土压力强度
p p z tg (45 f / 2)
2
3
pp=1
pa=3
45+f/2
1
z
-朗肯主动土压力系数
Ea Ka H 2 / 2
1 H 3
总主动土压力(大小、作用点)
1 E a K a H 2 2
pa K aH
6.3 朗肯土压力理论
•朗肯主动土压力计算-填土为粘性土
竖向应力为大主应力
1 v z
水平向应力为小主应力
6.3 朗肯土压力理论 •朗肯主动土压力计算-填土为粘性土 主动土压力强度
负号
-
z0
pa z K a 2c K a
Ka tg 2 (45 f / 2)
-朗肯主动土压力系数
z0
2c z0 K a -拉力区深度
z< 3 1tg (45 f / 2)
2
K0 v
v=z
6.3 朗肯土压力理论 •朗肯主动土压力计算-填土为无粘性土(砂土) 主动土压力强度
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.1 土压力理论
土压力是指挡土墙后的填土因自重或外荷载作用对墙背产生的侧向压力。
土压力的计算是个比较复杂的问题。
它随挡土墙可能位移的方向分为主动土压力、被动土压力和静止土压力。
土压力的大小还与墙后填土的性质、墙背倾斜方向等因素有关。
2.1.1 库伦土压力[22]
1773年著名的法国学者库伦(C.A.Coulomb)提出了一种计算土压力的理论。
这种理论是根据墙后所形成的滑动楔体静力平衡条件建立起来的,这种理论具有计算简单,适用范围广泛,且计算结果接近实际等优点,至今仍然被广泛使用于工程实践之中。
其基本假定如下:
(l)墙后填土为理想散粒体(无粘聚力);
(2)墙后填土产生主动土压力或被动土压力时,填土形成滑动楔体,且滑动面为通过墙踵的平面;
(3)滑动楔体为刚体,不考虑滑动楔体内部的应力和变形条件 1、主动土压力公式:
21
2
a a
E H K γ=
2a K =
式中:α—为墙背与铅直线夹角,逆时针为正值; K a —库仑主动土压力系数; β—填土表面与水平面所成坡角;
δ—墙后填土与墙背的摩擦角,由试验或规范确定。
2、被动土压力公式
21
2
p p E H K γ=
2p K =式中:K p —为库仑被动土压力系数。
2.1.2 朗肯土压力[23]
朗肯土压力是英国学者朗肯在1857 年提出的一种经典的土压力理论,这种土压力理论是根据半空间体的应力状态和土的极限平衡理论得出的土压力计算理论之一。
这种土压力理论的计算方法比较简单,计算结果比较接近实际,至今仍然被广泛用于工程实践之中。
其基本假定如下:
1).墙本身是刚性的,不考虑墙身的变形; 2).墙后填土面水平且填土延伸到无限远处; 3).墙背直立、光滑。
1、主动土压力公式
无粘性土:
2(45-)2
a Ztg ϕ
σγ=。
粘性土:
2
(45-)2(45-)2
2
a Ztg Ctg ϕ
ϕ
σγ=-。
式中:C 一为土的粘聚力,
Z —计算点距离填土面的深度(m);
φ一内摩擦角 σa 一为主动土压力 γ—填土的重度
a b c
图2-1 朗肯土压力计算图
无粘性土:主动土压力强度与深度z 成正比,土压力分布图呈三角形(图2-1b )。
据此可以求出墙单位长度总主动土压力为:
2a 1
2a E K H γ=
20a (45)2
K tg ϕ
=-
式中:K a -主动土压力系数 作用点位置在墙高的H/3处
粘性土:土压力分布图呈三角形(图2-1c ),粘性土的土压力强度由二部分组成,一部分为由土的自重引起的土压力γzK a ,随深度z 呈三角形变化;另一部分为由粘聚力c 引起的土压力
,为一负值,不随深度变化。
叠加的
结果如图2-1c 所示。
由于墙面光滑,土对墙面产生的拉力会使土脱离墙,出现深度为z 0的裂隙。
因此,略去这部分土压力后,实际土压力分布为三角形部分:
22
a 12-22a a C E K H CH K γγ
=+
作用点位置在墙高的(H-Z 0)/3处
其中a 点至填土表面的高度z 0称为临界深度: 由p a =0,求的
a
a
Z K γ=
2、被动土压力 无粘性土:
P P ZK σγ=
粘性土:
2P P P
ZK C K σγ=+
a b c
图2-2 朗肯被动土压力计算图
无粘性土:被动土压力强度与深度z 成正比,土压力分布图呈三角形,墙单位长度总被动土压力
21
2
R P E H K γ=
2
(45)2
P K tg ϕ
=+
式中:K p -被动土压力系数 σp -被动土压力 作用点位置在墙高的H/3处
粘性土:土压力分布图呈梯形(图2-2c ),粘性土的土压力强度由二部分组
成,一部分为由土的自重引起的土压力γzK a ,随深度z 呈三角形变化;另一部分为由粘聚力c 引起的土压力
,为正值,不随深度变化。
叠加的结果如
图2-2c 所示。
土压力分布为梯形面积:
21
22
P P P
E H K CH K γ=+
作用点位置在梯形面积重心
2.1.3 规范土压力计算
按照规程JGJ120—99[24],在计算及参数取值上采用直观、简单及偏于安全的方法,对于碎石土及砂土采用水土分算的形式,对于粉土及粘性土采用水土合算的形式,土的抗剪强度指标统一取为固结快剪指标且不考虑有效值的影响。
图2-3 水平荷载标准值计算简图
1、水平荷载标准值的计算
支护结构荷载标准值e ajk 应按当地可靠经验确定,当无经验时可按下列规定计算: (1)对于碎石土及砂土: 当计算点位于地下水位以上时:
e ajk =σ
ajk
K ajk —2c ik
ai K
当计算点位于地下水位以下时:
ajk e =ajk σK ai —2ik
c ai K +[(i z —wa h )—(m j —h wa )wa ηK ai ]
w γ
式中:K ai —第i 层的主动土压力系数;
ajk σ—作用于深度z j 处的竖应力标准值;
ik c —三轴试验(当有可靠经验时可采用直接剪切试验)确定第i 层
固结不排水(快)剪粘聚力标准值; j z —计算点深度;
j m —计算参数,当h z j <时,取j z ,j z >h 时,取h ; wa h —基坑外侧水位深度;
wa η—计算系数,当wa h =h 时,取1,当wa h >h 时,取零; w γ—水的深度。
(2)对于粉土及粘性土:
ajk e =ajk σai K —2ik
c ai K
(3)以上规定计算的基坑开挖面水平荷载标准值不小于零。
2、水平抗力标准值的计算
图2-4 水平抗力标准计算图
(1)对于碎石土及砂土,基坑内侧抗力标准值按下列规定计算:
pjk e =pi pjk K σ+2pi
K ik
c +(z j —h wa )(1—K pi )w γ
式中:σpjk —作用于基坑地面以下深度z j 处的竖向应力标准值; Kpi —第i 层土的被动土压力系数,
(2)对于粉土及粘性土,基坑内侧水平抗力标准值宜按如下式计算:
pjk e =pjk σpi K +2ik
c pi K。
