宁夏中卫市2021届新高考数学一模试卷含解析
2021年宁夏中卫市高考数学一模试卷(文科)(附答案详解)
2021年宁夏中卫市高考数学一模试卷（文科）学校:___________姓名：___________班级：___________考号：___________一、单选题（本大题共12小题，共60.0分）1.已知集合A={x|x2−x−6≤0}，B={x|x−1<0}，则A∪B=()A. (−∞,3]B. (−∞,2]C. (−∞,1)D. [−2,1)2.已知复数z=2+3i3−2i，则z−=()A. −iB. iC. 1+iD. 1−i3.“a2+b2ab≥2”是“a>0且b>0”的()A. 充要条件B. 充分不必要条件C. 必要不充分条件D. 既不充分也不必要条件4.等差数列{a n}前n项和为S n，a1+a9+a11=12，则S13=()A. 32B. 42C. 52D. 625.已知α∈(0,π)，且3cos2α−8cosα=5，则sinα=()A. √53B. 23C. 13D. √596.国防部新闻发言人在2020年9月24日举行的例行记者会上指出：“台湾是中国不可分割的一部分，解放军在台海地区组织实兵演练，展现的是捍卫国家主权和领土完整的决心和能力”，如图为我空军战机在海面上空绕台巡航已知海面上的大气压强是760mmHg，大气压强p(单位：mmHg)和高度ℎ(单位：m)之间的关系为p= 760e−ℎk(e是自然对数的底数，k是常数)，根据实验知500m高空处的大气压强是700mmHg，则我战机在1000m高空处的大气压强约是(结果保留整数)()A. 645mmHgB. 646mmHgC. 647mmHgD. 648mmHg7.某几何体的三视图如图所示，则该几何体的体积为()A. 3πB. 9πC. 12πD. 36π8. 函数y =1−ln|x|1+ln|x|⋅sinx 的部分图象大致为( )A.B.C.D.9. 已知m 为空间的一条直线，α，β为两个不同的平面，则下列说法正确的是( )A. 若m//α，α//β，则m//βB. 若α⊥β，m ⊥α，则m//βC. 若m//α，α⊥β，则m ⊥βD. 若m ⊥α，α//β，则m ⊥β10. 平面向量a ⃗ 与b ⃗ 的夹角为60°，a ⃗ =(2,0)，|a ⃗ +2b ⃗ |=2√3，则|b ⃗ |=( )A. √3B. 1C. 2D. √3−111. 已知斜率为k 1(k 1≠0)的直线l 与椭圆x 2+y 29=1交于A ，B 两点，线段AB 的中点为C ，直线OC(O 为坐标原点)的斜率为k 2，则k 1⋅k 2=( )A. −3B. −13C. −19D. −912. 已知定义在(0,+∞)上的函数f(x)的导函数为f′(x)，且满足(1−x)f(x)+xf′(x)>0，则关于x 不等式：2x−1x+2f(2x −1)−e x−3f(x +2)<0的解集为( )A. (12,3)B. (3,+∞)C. (1,3)D. (12,+∞)二、单空题（本大题共3小题，共15.0分）13. 曲线y =x 2−3lnx 在(1,f(1))处的切线方程为______ ．14. 已知实数x ，y 满足不等式组{x −y +2≥0x +y −3≤0y ≥1，则目标函数z =x −2y 的最大值为______ ．15. 如图，已知圆的半径为10，其内接三角形ABC 的内角A ，B分别为60°和45°，现向圆内随机撒一粒豆子，则豆子落在三角形ABC 内的概率为______ ．三、多空题（本大题共1小题，共5.0分）16.已知直线l：mx+y+3m−√3=0与圆x2+y2=12交于A，B两点，过A，B分别作l的垂线与x轴交于C，D两点，若|AB|=2√3，则m=(1)，|CD|=(2)．四、解答题（本大题共7小题，共82.0分）17.全国文明城市是中国所有城市品牌中含金量最高、创建难度最大的一个，是反映城市整体文明水平的综合性荣誉称号，是目前国内城市综合类评比中的最高荣誉，也是最具价值的城市品牌，作为普通市民，既是城市文明的最大受益者，更是文明城市的主要创造者，皖北某市为提高市民对文明城市创建的认识，举办了“创建文明城市”知识竞赛，从所有答卷中随机抽取400份试卷作为样本，将样本的成绩(满分100分，成绩均为不低于40分的整数)分成六段：[40,50)，[50,60)，…，[90,100]后得到如图所示的频率分布直方图．(Ⅰ)求样本的平均数；(Ⅱ)现从该样本成绩在[40,50)与[90,100]两个分数段内的市民中按分层抽样选取6人，求从这6人中随机选取2人，且2人的竞赛成绩之差的绝对值大于20的概率．18.已知公差不为0的等差数列{a n}中，a1=2，且a2+1，a4+1，a8+1成等比数列．(1)求数列{a n}通项公式；(2)设数列{b n}满足b n=3a n ，求适合方程b1b2+b2b3+⋯+b n b n+1=4532的正整数n的值．19.等腰直角三角形ABC中，∠BAC=90°，D为AC的中点，正方形BCC1B1与三角形ABC所在的平面互相垂直．(1)求证：AB1//平面DBC1；(2)若AB=2，求点D到平面ABC1的距离．20.已知椭圆E：x2a2+y2b2=1(a>b>0)过点Q(√22,√32)，椭圆上的动点P与其短轴两端点连线斜率乘积为−12．(1)求椭圆E的方程；(2)设F1，F2分别为E的左、右焦点，直线l过点F1且与E相交于A，B两点，当F2A⃗⃗⃗⃗⃗⃗⃗ ⋅F2B⃗⃗⃗⃗⃗⃗⃗ =2时，求△ABF2的面积．21. 已知函数f(x)=axlnx −bx 2−ax ．(Ⅰ)曲线y =f(x)在点(1,f(1))处的切线方程为x +y +12=0，求a ，b 的值； (Ⅱ)若a ≤0，b =12时，∀x 1，x 2∈(1,e)，都有|f(x 1)−f(x 2)||x 1−x 2|<3，求a 的取值范围．22. 在直角坐标系xOy 中，直线l 1的方程为y =√3x ，曲线C 的参数方程为{x =1+√3cosφy =√3sinφ(φ是参数，0≤φ≤π).以O 为极点，x 轴的非负半轴为极轴建立极坐标系．(1)分别写出直线l 1与曲线C 的极坐标方程；(2)若直线l 2：2ρsin(θ+π3)+3√3=0，直线l 1与曲线C 的交点为A ，直线l 1与l 2的交点为B ，求|AB|．23.已知函数f(x)=13|x−a|，(a∈R)(1)当a=2时，解不等式|x−13|+f(x)≥1；(2)设不等式|x−13|+f(x)≤x的解集为M，若[13,12]⊆M，求实数a的取值范围．答案和解析1.【答案】A【解析】解：∵集合A={x|x2−x−6≤0}={x|−2≤x≤3}，B={x|x−1<0}={x|x<1}，∴A∪B={x|x≤3}=(−∞,3]．故选：A．求出集合A，B，由此能求出A∪B．本题考查并集的求法，考查并集定义等基础知识，考查运算求解能力，是基础题．2.【答案】A【解析】解：∵z=2+3i3−2i =(2+3i)(3+2i)(3−2i)(3+2i)=13i13=i，∴z−=−i．故选：A．利用复数代数形式的乘除运算化简，再由共轭复数的概念得答案．本题考查复数代数形式的乘除运算，考查复数的基本概念，是基础题．3.【答案】C【解析】解：当a>0，b>0时，由基本不等式的性质得：a2+b2ab ≥2abab=2，故由a>0且b>0可推出a2+b2ab≥2，当a=−1，b=−1时，a2+b2ab =(−1)2+(−1)2−1⋅−1=2≥2，故由a2+b2ab≥2不能推出a>0且b>0，综上“a2+b2ab≥2”是“a>0且b>0”的必要不充分条件，故选：C．根据充分条件和必要条件的定义进行判断即可．本题主要考查了充分条件和必要条件的判断，根据充分条件和必要条件的定义是解决本题的关键，属于基础题．4.【答案】C【解析】解：设数列{a n }的公差为d ，由a 1+a 9+a 11=12可得：a 1+a 1+8d +a 1+10d =3(a 1+6d)=12，即a 7=4， ∴S 13=13(a 1+a 13)2=13a 7=52，故选：C ．先由题设条件求得a 7，再利用等差数列的性质和前n 项和公式求得结果即可． 本题主要考查等差数列的性质及基本量的计算，属于基础题．5.【答案】A【解析】 【分析】本题考查三角函数的化简求值，考查同角三角函数基本关系式与二倍角公式的应用，是基础题．利用二倍角的余弦把已知等式变形，化为关于cosα的一元二次方程，求解后再由同角三角函数基本关系式求得sinα的值． 【解答】解：由3cos2α−8cosα=5，得3(2cos 2α−1)−8cosα−5=0， 即3cos 2α−4cosα−4=0，解得cosα=2(舍去)，或cosα=−23． ∵α∈(0,π)，∴α∈(π2,π)，则sinα=√1−cos 2α=√1−(−23)2=√53．故选：A ．6.【答案】A【解析】解：∵500m 高空处的大气压强是700mmHg ， ∴700=760e −500k ，即e −500k =7076，当ℎ=1000m 时，有p =760e −1000k =760⋅(e −500k )2=760×(7076)2≈645． 故选：A ．由题意知，700=760e −500k ，求出e −500k 的值，再代入p =760e −1000k 中，求得p 的值，即可．本题考查函数的实际应用，熟练掌握指数的运算法则是解题的关键，考查学生的运算求解能力，属于基础题．7.【答案】A【解析】解：由三视图还原原几何体如图，该几何体为一个圆锥的四分之一，其中圆锥的底面半径为3，高为4．∴该几何体的体积为14×13π×32×4=3π．故选：A．由三视图还原原几何体，可知该几何体为一个圆锥的四分之一，其中圆锥的底面半径为3，高为4，再由圆锥体积公式求解．本题考查由三视图求面积、体积，关键是由三视图还原原几何体，是中档题．8.【答案】A【解析】解：函数y=1−ln|x|1+ln|x|⋅sinx是奇函数，排除D，当x=e−2时，y=−13sin1e2<0，x=1时，y=sin1>0，只有选项A满足题意．故选：A．利用函数的奇偶性排除选项，然后利用特殊值判断即可．本题考查函数的图象的判断，函数的奇偶性以及函数值的应用，考查分析问题解决问题的能力．9.【答案】D【解析】解：由m为空间的一条直线，α，β为两个不同的平面，知：对于A，若m//α，α//β，则m//β或m⊂β，故A错误；对于B，若α⊥β，m⊥α，则m//β或m⊂β，故B错误；对于C，若m//α，α⊥β，则m与β相交、平行或m⊂β，故C错误；对于D，若m⊥α，α//β，则由线面垂直的判定定理得m⊥β，故D正确．故选：D．对于A，推导出m//β或m⊂β；对于B，m//β或m⊂β；对于C，m与β相交、平行或m⊂β；对于D，由线面垂直的判定定理得m⊥β．本题考查命题真假的判断，考查空间中线线、线面、面面间的位置关系等基础知识，是基础题．10.【答案】B【解析】【试题解析】【分析】本题考查两个向量的数量积的定义，向量的模的求法，数量积公式的应用．利用两个向量的数量积的定义，|a⃗+2b⃗ |2=a⃗2+4a⃗⋅b⃗ +4b⃗ 2=4+4×2×|b⃗ |×cos60°+4|b⃗ |2=12解出|b⃗ |的值．【解答】解：由已知|a⃗|=2,|a⃗+2b⃗ |2=a⃗2+4a⃗⋅b⃗ +4b⃗ 2=4+4×2×|b⃗ |×cos60°+4|b⃗ |2=12，|b⃗ |=1，故选：B．11.【答案】D【解析】解：设点A(x1,y1)，B(x2,y2)，则C(x1+x22,y1+y22)，∴x12+y129=1，x22+y229=1，∴y12−y22x12−x22=−9，又k1=y1−y2x1−x2，k2=y1+y22−0x1+x22−0=y1+y2x1+x2，∴k1k2=y12−y22x12−x22=−9，故选：D．设出点A，B的坐标，表示出直线AB的斜率，直线OC的斜率，即可得出结果．本题考查了椭圆的定义，设而不求的方法处理直线与椭圆相交问题，属于基础题．12.【答案】A【解析】解：因为(1−x)f(x)+xf′(x)>0，所以[xf(x)e x]′=(1−x)f(x)+xf′(x)e x>0，令g(x)=xf(x)e x，x ∈(0,+∞)，则g′(x)>0，即g(x)在(0,+∞)上单调递增，不等式2x−1x+2f(2x −1)−e x−3f(x +2)<0⇔(2x−1)f(2x−1)e 2x−1<(x+2)f(x+2)e x+2⇔g(2x −1)<g(x +2)，于是有{2x −1<x +22x −1>0x +2>0，解得12<x <3，故选：A ．先将不等式2x−1x+2f(2x −1)−e x−3f(x +2)<0转化为(2x−1)f(2x−1)e 2x−1<(x+2)f(x+2)e x+2，进而考虑令g(x)=xf(x)e x，再结合函数单调性即可求解．本题主要考查了利用导数判断函数的单调性，分析出所要构造的新函数g(x)是解题的关键，属于中档题．13.【答案】x +y −2=0【解析】解：函数y =x 2−3lnx 的导数为f′(x)=2x −3x ， 即有f(x)在x =1处切线的斜率为k =2−3=−1，f(1)=1， 切点为(1,1)，则f(x)在x =1处切线的方程为y −1=−x +1， 故答案为：x +y −2=0．求出函数的导数，求得切线的斜率和切点，由斜截式方程可得切线的方程．本题考查导数的运用：求切线方程，正确求导和运用直线方程的形式是解题的关键，是基础题．14.【答案】0【解析】解：由约束条件作出可行域如图，联立{x +y −3=0y =1，解得A(2,1)，由z =x −2y ，得y =x2−z2，由图可知，当直线y =x2−z2过A 时， 直线在y 轴上的截距最小，z 有最大值为2−1×2=0． 故答案为：0．由约束条件作出可行域，化目标函数为直线方程的斜截式，数形结合得到最优解，把最优解的坐标代入目标函数得答案．本题考查简单的线性规划，考查数形结合思想，是中档题．15.【答案】3+√34π【解析】解：在△ABC 内，由正弦定理可得BCsinA =ACsinB =2R ，即BCsin60∘=ACsin45∘=20， 解得BC =10√3，AC =10√2，故sinC =sin(A +B)=sin(60°+45°)=sin60°cos45°+cos60°sin45°=√6+√24，所以S △ABC =12⋅AC ⋅BC ⋅sinC ==12×10√2×10√3×√6+√24=25(√3+3)，又S 圆=π⋅102=100π，故豆子落在三角形ABC 内的概率为S △ABC S 圆=25(√3+3)100π=3+√34π．故答案为：3+√34π．先利用正弦定理求出AC 和BC ，然后利用两角和的正弦公式求出sin C ，求出△ABC 的面积和圆的面积，由几何概型的计算公式求解即可．本题考查了几何概型问题的求解，涉及了正弦定理以及两角和差公式的应用，三角形面积公式的应用，考查了推理能力与化简计算能力，属于中档题．16.【答案】−√334【解析】解：|AB|=2√3，则圆心O(0,0)到直线l 的距离d =√12−(√3)2=3， 则有√3|√m 2+1=3，解得m =−√33， 直线l 的方程为：(−√33)x +y −2√3=0，则其倾斜角为30°，∵过A ，B 分别作l 的垂线与x 轴交于C ，D 两点，则|CD|=2√3cos30°=√3√32=4．故答案为：−√33，4．根据题意，由点到直线的距离求出m，可得直线l的倾斜角为30°，再利用直角三角形中的三角函数求出|CD|即可．本题考查直线与圆的位置关系，训练了利用垂径定理求弦长，是基础题．17.【答案】解：(Ⅰ)因为(0.005+0.010+0.020+a+0.025+0.010)×10=1所以a=0.03，从而样本平均数为[(45×0.005+55×0.010+65×0.020+75×0.030+85×0.025+95×0.010)×10=74．(Ⅱ)根据分层抽样，在[40,50)内选取2人，记为A，B，在[90,100]内选取4人，记为a，b，c，d．从这6人中选取2人的所有选取方法：AB，Aa，Ab，Ac，Ad，Ba，Bb，Bc，Bd，ab，ac，ad，bc，bd，cd，共15种，2人成绩之差的绝对值大于20的选取方法：Aa，Ab，Ac，Ad，Ba，Bb，Bc，Bd共8种．所以从这6人中随机选取2人，且2人的竞赛成绩之差的绝对值大于20的概率为815．【解析】(Ⅰ)由频率分布直方图列出方程能求出a，从而能求出样本平均数．(Ⅱ)根据分层抽样，在[40,50)内选取2人，记为A，B，在[90,100]内选取4人，记为a，b，c，d.从这6人中选取2人，利用列举法能求出2人的竞赛成绩之差的绝对值大于20的概率．本题考查平均数、概率的求法，考查频率分布直方图、古典概型、列举法等基础知识，考查运算求解能力，是基础题．18.【答案】解：(1)设公差为为d，a1=2，且a2+1，a4+1，a8+1成等比数列，∴(a4+1)2=(a2+1)(a8+1)，∴(3d+3)2=(3+d)(3+7d)，解得d=3，∴a n=a1+(n−1)d=2+3(n−1)=3n−1；(2)∵数列{b n}满足b n=3a n，∴b n=33n−1，∴b n b n+1=33n−1⋅33n+2=3(13n−1−13n+2)∴b1b2+b2b3+⋯+b n b n+1=3(12−15+15−18+⋅⋅+13n−1−13n+2)=3(12−13n+2)=4532，即13n+2=132，解得n=10，故正整数n的值为10．【解析】(1)由a2+1，a4+1，a8+1成等比数列，建立关于d的方程，解出d，即可求数列{a n}的通项公式；(2)表示出b n，利用裂项相消法求出b1b2+b2b3+⋯+b n b n+1，建立关于n的方程，求解即可本题考查等比数列和等差数列的概念与性质，以及裂项相消法求和，属于中档题19.【答案】解：(1)证明：连结B1C，设B1C∩BC1=O，连结OD，如图，∵O是B1C的中点，D为AC的中点，∴OD//AB1，∵OD⊂面BDC1，AB1⊄面BDC1，∴AB1//平面DBC1．(2)解：∵等腰直角三角形ABC中，∠BAC=90°，∴BA⊥AC，∵BA⊥CC1，∴BA⊥平面ACC1，∴BA⊥AC1，设点D到平面ABC1的距离为h，由V D−ABC1=V C1−ABD，代入可得：1 3×2√3×ℎ=13×12×2×1×2√2，解得点D到平面ABC1的距离为√63．【解析】(1)连结B1C，设B1C∩BC1=O，连结OD，推导出OD//AB1，由此能证明AB1//平面DBC1．(2)推导出BA⊥AC，BA⊥CC1，从而BA⊥平面ACC1，进而BA⊥AC1，由V D−ABC1=V C1−ABD，能求出点D到平面ABC1的距离．本题考查线面垂直的证明，考查点到平面的距离的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查推理能力与计算能力，属于中档题．20.【答案】解：(1)设B1(0,b)，B2(0,−b)，P(x,y)，则x 2a 2+y 2b 2=1(a >b >0)，由k PB 1⋅k PB 2=y−b x⋅y+b x=y 2−b 2x 2=−b 2a2=−12， ∴a 2=2b 2，①又Q 在E 上22a 2+34b 2=1，②， 由①②解得a 2=2，b 2=1， ∴椭圆E 的方程为x 22+y 2=1．(2)设直线l 的方程为x =my −1，代入到x 22+y 2=1可得(m 2+2)y 2−2my −1=0，③设A(x 1,y 1)，B(x 2,y 2)， ∴y 1+y 2=2m m 2+2，y 1y 2=−1m 2+2，④∴F 2A ⃗⃗⃗⃗⃗⃗⃗ ⋅F 2B ⃗⃗⃗⃗⃗⃗⃗ =(x 1−1,y 1)(x 2−1,y 2)=(my 1−2,y 1)(my 2−2,y 2)=(m 2+1)y 1y 2−2m(y 1+y 2)+4，⑤，把④代入⑤得F 2A ⃗⃗⃗⃗⃗⃗⃗ ⋅F 2B ⃗⃗⃗⃗⃗⃗⃗ =7−m2m 2+2=2，解得m =±1， 由对称性，不妨取m =1，则③变为3y 2−2y −1=0，解得y 1=−13，y 2=1 则△ABF 2的面积S =12×2(y 1−y 2)=1+13=43．【解析】(1)根据椭圆上的动点P 与其短轴两端点连线斜率乘积为−12，以及过点Q(√22,√32)，即可得到a 2=2b 2，22a 2+34b 2=1，解得即可， (2)设直线l 的方程为x =my −1，代入到x 22+y 2=1可得(m 2+2)y 2−2my −1=0，根据韦达定理和向量的运算即可求出m 的值，求出三角形的面积即可．本题考查椭圆的定义，考查直线与椭圆的位置关系，考查三角形面积的计算，考查学生分析解决问题的能力，属于中档题．21.【答案】解：(Ⅰ)由题意，f′(x)=a(1+lnx)−2bx −a =alnx −2bx ，由f′(1)=−2b =−1，得b =12，又f(1)=−b −a =−32，∴a =1． 即a =1，b =12；(Ⅱ)当a ≤0，b =12时，f′(x)=alnx −x <0， f(x)在(1,e)上单调递减，不妨设x 1<x 2，则f(x 1)>f(x 2)，原不等式即为f(x 1)−f(x 2)x 2−x 1<3．即f(x 1)−f(x 2)<3x 2−3x 1，即f(x 1)+3x 1<f(x 2)+3x 2． 令g(x)=f(x)+3x ，则g(x)在(1,e)上为单调增函数， ∴有g′(x)=f′(x)+3=alnx −x +3≥0在(1,e)上恒成立． 即a ≥x−3lnx，x ∈(1,e)，令ℎ(x)=x−3lnx，x ∈(1,e)，ℎ′(x)=lnx+3x−1(lnx)2， 令t(x)=lnx +3x −1，t′(x)=1x −3x 2=x−3x 2<0．∴t(x)在(1,e)上单调递减，t(x)>t(e)=3e ， 则ℎ′(x)>0，ℎ(x)在(1,e)上为单调增函数， ∴ℎ(x)<ℎ(e)=e −3，即a ≥e −3． 综上，e −3≤a ≤0．【解析】(Ⅰ)求出原函数的导函数，利用f′(1)=−2b =−1，求得b ，再由f(1)=−b −a =−32求解a ；(Ⅱ)当a ≤0，b =12时，f′(x)=alnx −x <0，f(x)在(1,e)上单调递减，不妨设x 1<x 2，则f(x 1)>f(x 2)，原不等式即为f(x 1)−f(x 2)x 2−x 1<3，即f(x 1)+3x 1<f(x 2)+3x 2，构造函数g(x)=f(x)+3x ，得到g′(x)=f′(x)+3=alnx −x +3≥0在(1,e)上恒成立，分离参数a ，得到a ≥x−3lnx，x ∈(1,e)，再由导数求函数ℎ(x)=x−3lnx，x ∈(1,e)的最值，可得a 的取值范围．本题考查利用导数研究过曲线上某点处的切线方程，考查利用导数求最值，考查化归与转化思想方法，属难题．22.【答案】解：(1)直线l 1的方程为y =√3x ，可得：tanθ=yx =√3， ∴直线l 1的极坐标方程为ρ=π3．曲线C 的普通方程为(x −1)2+y 2=3， 又∵x =ρcosθ，y =ρsinθ，所以曲线C 的极坐标方程为ρ2−2ρcosθ−2=0(0≤θ≤π)，(2)由题意，设A(ρ1,θ1)，则有{ρ2−2ρcosθ−2=0θ=π3，解得：ρ1=2,θ1=π3，设B(ρ2,θ2)，则有{2ρsin(θ+π3)+3√3=0θ=π3，解得：ρ2=−3,θ2=π3故得|AB|=|ρ1−ρ2|=5．【解析】本题主要考查了参数方程，极坐标方程的转换，以及利用极坐标的几何意义求解长度问题．属于基础题．(1)根据tanθ=yx可得直线l1极坐标．利用x=ρcosθ，y=ρsinθ带入可得曲线C的极坐标方程．(2)由题意，设A(ρ1,θ1)，联立方程组求解，同理，设利用直线的极坐标的几何意义求解即可．23.【答案】解：(1)a=2时，f(x)=13|x−2|，问题转化为解不等式|x−13|+13|x−2|≥1，①x≥2时，x−13+13(x−2)≥1，x−13+13x−23≥1，解得：x≥32，故x≥2；②13<x<2时，x−13+13(2−x)≥1，解得：x≥1，故1≤x<2；③x≤13时，13−x+13(2−x)≥1，解得：x≤0，综上，不等式的解集是：{x|x≤0或x≥1}；(2)|x−13|+13|x−a|≤x的解集包含[13,12]，∴x−13+13|x−a|≤x，|x−a|≤1，故−1≤x−a≤1，解得：−1+a≤x≤1+a，故{−1+a ≤131+a ≥12，解得：−12≤a ≤43．【解析】本题考查了解绝对值不等式问题，考查分类讨论思想，是一道中档题． (1)通过讨论x 的范围，去掉绝对值，解各个区间上的x 的范围，取并集即可； (2)问题转化为x −13+13|x −a|≤x ，求出x 的范围，得到关于a 的不等式组，解出即可．。
2021年全国新高考Ⅰ卷数学真题试卷(含答案及解析)
C. 乙与丙相互独立D. 丙与丁相互独立
【答案】B
【解析】
【分析】根据独立事件概率关系逐一判断
【详解】 ，
故选：B
【点睛】判断事件 是否独立，先计算对应概率，再判断 是否成立
二､选择题：本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，部分选对的得2分，有选错的得0分.
故选：AC
11.已知点 在圆 上，点 、 ，则（）
A.点 到直线 的距离小于
B.点 到直线 的距离大于
C.当 最小时，
D.当 最大时，
【答案】ACD
【解析】
【分析】计算出圆心到直线 的距离，可得出点 到直线 的距离的取值范围，可判断AB选项的正误；分析可知，当 最大或最小时， 与圆 相切，利用勾股定理可判断CD选项的正误.
（1）若小明先回答A类问题，记 为小明的累计得分，求 的分布列；
（2）为使累计得分 期望最大，小明应选择先回答哪类问题？并说明理由.
19.记 是内角 ， ， 的对边分别为 ， ， .已知 ，点 在边 上， .
（1）证明： ；
（2）若 ，求 .
20.如图，在三棱锥 中，平面 平面 ， ， 为 的中点.
15.函数 的最小值为______.
【答案】1
【解析】
【分析】由解析式知 定义域为 ，讨论 、 、 ，并结合导数研究的单调性，即可求 最小值.
【详解】A： 且 ，故平均数不相同，错误；
B：若第一组中位数为 ，则第二组的中位数为 ，显然不相同，错误；
C： ，故方差相同，正确；
D：由极差的定义知：若第一组的极差为 ，则第二组的极差为 ，故极差相同，正确；
2021年宁夏中卫市高考数学第一次联考试卷(理科)
2021年宁夏中卫市高考数学第一次联考试卷（理科）一、单选题（本大题共12小题，共60.0分）1. 已知集合A ={x|x >a}，B ={x|log 2x >1}，若A ∩B =A ，则a 的取值范围为( )A. (2,+∞)B. [2,+∞)C. (−∞,2)D. (−∞,2]2. 设复数z 满足z+1z−1=i ，则z =( )A. iB. 1+iC. −iD. 1−i3. 若a ∈(−π2,0)，且sinα+cosα=0，则sin3α=( )A. −√22B. √22C. −√32D. 124. 某学校为落实学生掌握社会主义核心价值观的情况，用系统抽样的方法从全校2400名学生中抽取30人进行调查．现将2400名学生随机地从1～2400编号，按编号顺序平均分成30组(1～80号，81～160号，…，2321−2400号)，若第3组抽出的号码为176，则第6组抽到的号码是( )A. 416B. 432C. 448D. 4645. 某市政府决定派遣8名干部分成两个小组，到该市甲、乙两个县去检查扶贫工作，若要求每组至少3人，则不同的派遣方案共有( ) A. 320种 B. 252种 C. 182种 D. 120种 6. 一百零八塔，位于宁夏吴忠青铜峡市，是始建于西夏时期的喇嘛式实心塔群，是中国现存最大且排列最整齐的喇嘛塔群之一，一百零八塔，因塔群的塔数而得名，塔群随山势凿石分阶而建，由下而上逐层增高，依山势自上而下各层的塔数分别为1，3，3，5，5，7，…，该数列从第5项开始成等差数列，则该塔群最下面三层的塔数之和为( ) A. 39 B. 45 C. 48 D. 517. 已知直线y =−x 被圆M ：x 2+y 2+Ey =0(E <0)截得的弦长为2√2，且圆N 的方程为x 2+y 2−2x −2y +1=0，则圆M 与圆N 的位置关系为( ) A. 相交 B. 外切 C. 相离 D. 内切 8. 直线y =a 与函数f(x)=tan(ωx +π4)(ω>0)的图象的相邻两个交点的距离为2π，若f(x)在(−m,m)(m >0)上是增函数，则m 的取值范围是( )A. (0,π4]B. (0,π2]C. (0,3π4]D. (0,3π2]9. 设数列{a n }的前n 项和为S n ，若2S n =3a n −2(n ∈N ∗)，则2S 10a6−2=( )A. 243B. 244C. 245D. 24610. 已知函数f(x)=∑|2i=0x −2i +1x−2i |，下列四个判断一定正确的是( )A. 函数f(x)为偶函数B. 函数f(x)最小值为6C. 函数y =f(x)的图象关于直线x =2对称D. 关于x 的方程[f(x)]2−m =0(m >0)的解集可能为{−2,0，3，6}11. 农历五月初五是端午节，民间有吃粽子的习惯，粽子又称粽籺，俗称“粽子”，古称“角黍”，是端午节大家都会品尝的食品，传说这是为了纪念战国时期楚国大臣、爱国主义诗人屈原.小明在和家人一起包粽子时，想将一丸子(近似为球)包入其中，如图，将粽叶展开后得到由六个边长为4的等边三角形所构成的平行四边形，将粽叶沿虚线折起来，可以得到如图所示的粽子形状的六面体，则放入丸子的体积最大值为()A. 512√6729π B. 16√23π C. 32√627π D. 128√281π12.已知函f(x)=e x−aln(ax−a)+a(a>0)，若关于x的不等式f(x)>0恒成立，则实数a的取值范围为()A. (0,e2]B. (0,e2)C. [1,e2]D. (1,e2)二、单空题（本大题共4小题，共20.0分）13.已知向量a⃗=(1,−2)，b⃗ =(k,1)且a⃗⊥(a⃗+b⃗ )，则k=______ ．14.已知一组数据4，a，3+a，5，7的平均数为5，则这组数据的方差为______ ．15.设α、β、r为平面，m、n、l为直线，以下四组条件：①α⊥β，α∩β=l，m⊥l；②α∩r=m，α⊥r，β⊥r；③α⊥r，β⊥r，m⊥α；④n⊥α，n⊥β，m⊥α；可以作为m⊥β的一个充分条件是______ ．16.已知F1，F2是双曲线C1：x2a2−y2b2=1(a>0,b>0)与椭圆C2：x225+y29=1的公共焦点，点P，Q分别是曲线C1，C2在第一、第三象限的交点，四边形PF1QF2的面积为6√6，设双曲线C1与椭圆C2的离心率依次为e1，e2，则e1+e2=______ ．三、解答题（本大题共7小题，共82.0分）17.在△ABC中，已知角A，B，C所对的边分别是a，b，c，a=√5，b=3，sinA+√5sinB=2√2．(1)求角A的值；(2)求△ABC的面积．18.已知抛物线C：y2=2x，过点(1,0)的直线l与抛物线C交于A，B两点，O为坐标原点．(1)若|AB|=2√2，求△AOB外接圆的方程；(2)若点A关于x轴的对称点是A′(A′与B不重合)，证明：直线A′B经过定点．19.我国脱贫攻坚战取得全面胜利，现行标准下农村贫困人口全部脱贫，消除了绝对贫困.为了解脱贫家庭人均年纯收入情况，某扶贫工作组对A，B两个地区2019年脱贫家庭进行简单随机抽样，共抽取500A地区B地区2019年人均年纯收入超过10000元100户150户2019年人均年纯收入未超过10000元200户50户假设所有脱贫家庭的人均年纯收入是否超过元相互独立．(Ⅰ)从A地区2019年脱贫家庭中随机抽取1户，估计该家庭2019年人均年纯收入超过10000元的概率；(Ⅱ)在样本中，分别从A地区和B地区2019年脱贫家庭中各随机抽取1户，记X为这2户家庭中2019年人均年纯收入超过10000元的户数，求X的分布列和数学期望；(Ⅲ)从样本中A地区的300户脱贫家庭中随机抽取4户，发现这4户家庭2020年人均年纯收入都超过10000元.根据这个结果，能否认为样本中A地区2020年人均年纯收入超过10000元的户数相比2019年有变化？请说明理由．20.如图，四边形ABCD中，AD//BC，∠BAD=90°，AB=BC=√2，AD=2√2，E，F分别是线段AD，CD的中点.以EF为折痕把△DEF折起，使点D到达点P的位置，G为线段PB的中点．(1)证明：平面GAC//平面PEF；(2)若平面PEF⊥平面ABCFE，求直线AG与平面PAC所成角的正弦值．21.已知函数f(x)=ke x−1−x．(1)讨论f(x)的单调性；(2)若函数g(x)=lnx−x+f(x)有三个极值点x1，x2，x3(x1<x2<x3)，求g(x1)+g(x2)+g(x3)的取x值范围．22. 在平面直角坐标系xOy 中，曲线C 的参数方程为{x =√3cosαy =sinα(α为参数)，以原点O 为极点，x 轴的正半轴为极轴建立极坐标系，直线l 的极坐标方程为ρsin(θ−π4)=√22．(1)求曲线C 的普通方程和直线l 的直角坐标方程；(2)若点M 的坐标为(1,2)，直线l 与曲线C 交于A 、B 两点，求1|MA|+1|MB|的值．23. 已知函数f(x)=|2x +a|，g(x)=|x −b|．(1)若a =1，b =3，解不等式f(x)+g(x)≥4；(2)当a >0，b >0时，f(x)−2g(x)的最大值是3，证明：a 2+4b 2≥92．答案和解析1.【答案】B【解析】解：∵A∩B=A，∴A⊆B，∵A={x|x>a}，B={x|x>2}，∴a≥2，∴a的取值范围为：[2,+∞)．故选：B．根据A∩B=A可得出A⊆B，然后求出B={x|x>2}，从而可得出a的取值范围．本题考查了描述法和区间的定义，对数函数的单调性，交集及其运算，考查了计算能力，属于基础题．2.【答案】C【解析】解：因为z+1z−1=i，所以z=1+ii−1=−1+i1−i=−(1+i)2(1−i)(1+i)=−i．故选：C．由已知等式等式求出z，然后由复数的除法运算求解即可．本题考查了复数的除法运算，解题的关键是掌握复数除法的运算法则，考查了化简运算能力，属于基础题．3.【答案】A【解析】解：因为sinα+cosα=0，所以tanα=sinαcosα=−1，又因为a∈(−π2,0)，所以α=−π4，则sin3α=sin(−3π4)=−sin3π4=−√22．故选：A．先利用同角三角函数关系得到tanα的值，然后利用特殊角的三角函数求出α，利用诱导公式求解sin3α即可．本题考查了三角函数的求值问题，主要考查了同角三角函数关系以及诱导公式的应用，解题的关键是利用特殊角的三角函数求出α，属于基础题．4.【答案】A【解析】解：样本间隔为2400÷30=80，设首个号码为x，则第三个号码为x+160，则x+160=176，解得x=16，则第6组抽到的号码为16+80×5=400+16=416，故选：A．先求出样本间隔，设出首个号码x，建立方程组求出x，利用系统抽样的定义进行求解即可．本题主要考查系统抽样的应用，根据样本间隔，结合条件求出首个号码是解决本题的关键．5.【答案】C【解析】解：因为若要求每组至少3人，所以有3，5和4，4两种，若人数为3，5，则有C 83A 22=112种；人数为4，4，则有C 84=70种； 共有112+70=182， 故选：C ．根据题意可得将8人分3，5和4，4两种，再分配两个县即可． 本题考查了分组分配问题，关键是分组，属于基础题． 6.【答案】D【解析】解：设该数列为{a n }，由题意得，a 5，a 6，…成等差数列，公差d =2，a 5=5， 设塔群共有n 层，则1+3+3+5+5(n −1)+(n−4)(n−5)2×2=108，解得，n =12，故最下面三层的塔数之和为a 10+a 11+a 12=3a 11=3(5+2×6)=51． 故选：D ．设该数列为{a n }，由题意得，a 5，a 6，…成等差数列，公差d =2，a 5=5，然后结合等差数列的求和公式可求n ，进而可求．本题主要考查了等差数列的求和公式及性质，属于基础题． 7.【答案】A【解析】解：根据题意，{y =−xx 2+y 2+Ey =0，则有2y 2+Ey =0， 解可得：y 1=0或y 2=−E2，又由y =−x ，则x 1=0或x 2=E2，即直线y =−x 与圆M ：x 2+y 2+Ey =0的交点为(0,0)和(E2,−E2)； 又由直线y =−x 被圆M ：x 2+y 2+Ey =0(E <0)截得的弦长为2√2，则有E 24+E 24=8，解可得E =±4，又由E <0，则E =−4，则圆M 的方程为x 2+y 2−4y =0，其圆心为(0,2)，半径r =2，圆N 的方程为x 2+y 2−2x −2y +1=0，即(x −1)2+(y −1)2=1，其圆心为(1,1)，半径R =1； 两圆圆心距|MN|=√1+1=√2，则有r −R <|MN|<R +r ，则两圆相交； 故选：A ．根据题意，联立直线y =−x 与圆M 的方程，计算可得交点的坐标，进而由直线y =−x 被圆M 截得的弦长为2√2，可得E 24+E 24=8，解可得E 的值，即可得M 的方程，分析圆M 、圆N 的圆心半径，分析可得答案．本题考查圆与圆的位置关系，涉及直线与圆的位置关系的判断，属于基础题． 8.【答案】B【解析】解：直线y =a 与函数f(x)=tan(ωx +π4)图象的相邻两个交点的距离为一个周期，则T =2π， 所以ω=πT =12，所以f(x)=tan(12x +π4)，由kπ−π2<12x+π4<kπ+π2，解得2kπ−3π2<x<2kπ+π2，(k∈Z)；所以函数f(x)在(−3π2,π2)上是单调增函数；又f(x)在(−m,m)上是单调增函数，即(−m,m)⊆(−3π2,π2 )，解得0<m≤π2；所以m的取值范围是(0,π2].故选：B．根据直线y=a与函数f(x)图象的相邻两个交点距离为一个周期，求出ω的值，写出f(x)的解析式，求出它的单调增区间，再求m的取值范围．本题考查了正切函数的图象与性质的应用问题，是基础题．9.【答案】B【解析】解：∵2S n=3a n−2=3(S n−S n−1)−2，∴S n+1=3(S n−1+1)(n≥2)，由2a1=3a1−2⇒a1=2⇒a1+1=3，∴数列{S n+1}是首项与公比均为3的等比数列，∴S n+1=3n，∴a6=S6−S5=36−35=2×35=2×243=486，∴2S10a6−2=2×(310−1)486−2=(35+1)(35−1)242=(243+1)(243−1)242=244，故选：B．由2S n=3a n−2可得数列{S n+1}是首项与公比均为3的等比数列，从而可求得S10及a6−2的值，于是可得答案．本题考查数列递推式，考查等比数列的判定及其通项公式的应用，考查数学运算能力，属于中档题．10.【答案】C【解析】解：f(x)=|x+1x |+|x−2+1x−2|+|x−4+1x−4|，则x≠0且x≠2且x≠4，则定义域关于原点不对称，则f(x)不可能是偶函数，故A错误，|x+1x |=)=|x|+|1x|≥2，当且仅当x=1x，即x=±1时，取等号，|x−2+1x−2|=|x−2|+|1x−2|≥2，当且仅当x−2=1x−2|，即x=3或x=1时，取等号，|x−4+1x−4|=|x−4|+|1x−4|≥2，当且仅当x−4=1x−4，即x=3或x=5时，取等号，则f(x)≥2+2+2=6，但三个不等式等号成立的条件不相同，故等号不能同时取，则最小值不是6，故B 错误，f(4−x)=)=|4−x +14−x|+|4−x −2+14−x−2|+|4−x −4+14−x−4|=|x −4+1x−4|+|x −2+1x−2|+|x +1x|=f(x)，则函数关于x =2对称，故C 正确，由[f(x)]2−m =0(m >0)得[f(x)]2=m ，(m >0)，则f(x)=±√m ， 若方程有解，则根关于x =2对称，−2，6关于x =2对称，但0，3关于x =2不对称，故D 错误， 故选：C ．分别根据函数的奇偶性，最值性质，对称性进行判断即可．本题主要考查命题的真假判断，利用函数的奇偶性，对称性和单调性的性质进行判断是解决本题的关键，是中档题． 11.【答案】A【解析】解：由题意可得每个三角形面积为S =12×4×2√3=4√3，由对称性可知该六面体是由两个正四面体合成的，可得该四面体的高为(4√33)=4√63，故四面体的体积为13×4√3×4√63=16√23， ∵该六面体的体积是正四面体的2倍， ∴六面体的体积是32√23， 由图形的对称性得，内部的丸子要是体积最大，就是丸子要和六个面相切，连接球心和五个顶点，把六面体分成了六个三棱锥， 设丸子的半径为R ，则32√23=6×13×4√3×R ，解得R =4√69， ∴丸子的体积的最大值为V max =4π3R 3=4π3×(4√69)3=512√6729π．故选：A ．先根据题意求得正四面体的体积，进而得到六面体的体积，再由图形的对称性得，内部的丸子要是体积最大，就是丸子要和六个面相切，设丸子的半径为R ，则32√23=6×13×4√3×R ，由此求得R ，进而得到答案． 本题考查空间几何体的体积，考查运算求解能力，推理论证能力和空间想象能力，考查直观想象、逻辑推理与数学运算等核心素养，属于中档题． 12.【答案】B【解析】解：∵f(x)=e x −aln(ax −a)+a >0(a >0)恒成立， ∴e x a>ln(x −1)+lna −1，∴e x−lna +x −lna >ln(x −1)+x −1， ∴e x−lna +x −lna >e ln(x−1)+ln(x −1)．令g(x)=e x +x ，易得g(x)在(1,+∞)上单调递增， ∴x −lna >ln(x −1)，∴−lna >ln(x −1)−x ． ∵ln(x −1)−x ≤x −2−x =−2，∴−lna>−2，∴0<a<e2，∴实数a的取值范围为(0,e2).故选：B．根据f(x)>0恒成立可得e x−lna+x−lna>e ln(x−1)+ln(x−1)，构造函数g(x)=e x+x，由g(x)的单调性可得x−lna>ln(x−1)，用放缩法求出ln(x−1)−x的最大值，从而得到a的取值范围．本题考查了函数恒成立问题和放缩法的应用，考查了转化思想和计算能力，属难题．13.【答案】−3【解析】解：根据题意，向量a⃗=(1,−2)，b⃗ =(k,1)，则a⃗+b⃗ =(1+k,−1)，若a⃗⊥(a⃗+b⃗ )，则a⃗⋅(a⃗+b⃗ )=(k+1)+2=0，解可得k=−3，故答案为：−3根据题意，求出a⃗+b⃗ 的坐标，由向量垂直的判断方法可得a⃗⋅(a⃗+b⃗ )=(k+1)+2=0，解可得k的值，即可得答案．本题考查向量数量积的计算，涉及向量的坐标计算，属于基础题．14.【答案】2【解析】解：因为这组数据的平均数为5，所以4+a+3+a+5+7=25，解得a=3，则这组数为3，4，5，6，7，[(3−5)2+(4−5)2+(5−5)2+(6−5)2+(7−5)2]=2．故方差s2=15故答案为：2．先利用平均数的计算公式求出a的值，从而得到这一组的数据，然后利用方差的计算公式求解即可．本题考查了平均数公式的应用，方差公式的应用，属于基础题．15.【答案】④【解析】解：①记面AD1为α，面AC为β，则AD为l，若视AB为m，m⊥l，但m在面β内，故①不满足条件；②若α、β、γ两两垂直，则可以得到m⊥β，但该条件中没有α⊥β，故反例只可能存在于此处，记面AD1为α，面BB1D1D为β，面AC为γ，则AD为m，但m与β成45°角，故②不满足条件；③注意到m⊥α，只要α、β不平行，就得不到m⊥β，记面AD1为α，面BB1D1D为β，面AC为γ，视AB为m，但m与β成45°角，故③不满足条件；④由n⊥α，n⊥β得α//β，再由m⊥α得m⊥β；故只有④满足条件故答案为：④题中线面关系既复杂又抽象，注意到其中包含大量的垂直关系，故可以在正方体内观察，结合线面垂直，面面垂直，线线垂直的判定及性质定理，逐一对已知中的四个结论进行判断即可得到答案．本题考查的知识点是直线与平面垂直的判定，在判断空间线面的关系，常常把他们放在空间几何体中来直观的分析，在判断线与面的平行与垂直关系时，正方体是最常用的空间模型，大家一定要熟练掌握这种方法．另外熟练掌握线线、线面、面面平行(或垂直)的判定及性质定理是解决此类问题的基础．16.【答案】2√10+45【解析】【分析】本题考查双曲线和椭圆的方程与性质，考查方程思想和运算能力，属于中档题．由题意可得a 2+b 2=16，根据双曲线C 1与椭圆C 2的对称性可得△PF 1F 2的面积为3√6，设P(x 0,y 0)，(x 0,y 0>0)，运用三角形的面积公式和点P 满足椭圆方程，解方程可得P 的坐标，再代入双曲线方程，结合a ，b 的关系，解方程可得a ，求得双曲线和椭圆的离心率，即可得到所求和． 【解答】解：由题意可得a 2+b 2=16，根据双曲线C 1与椭圆C 2的对称性可得△PF 1F 2的面积为3√6， 设P(x 0,y 0)，(x 0,y 0>0)，则{12⋅8⋅y 0=3√6x 0225+y 029=1，解得x 0=5√104，y 0=3√64， 代入双曲线的方程结合b 2=16−a 2，可得a 4−35a 2+250=0，结合0<a <c =4，解得a =√10， 双曲线的离心率为e 1=c a=4√10=2√105， 而椭圆的离心率e 2=45， ∴e 1+e 2=2√10+45． 故答案为：2√10+45．17.【答案】解：(1)因为a =√5，b =3，由正弦定理得asinA =bsinB =2R ， 所以sinA =√52R ，sinB =32R ，因为sinA +√5sinB =2√2， 所以√52R+3√52R=2√2，故R =√102，sinA =√52R =√22，因为a <b ，所以A 为锐角，A =π4； (2)由余弦定理得cosA =√22=b 2+c 2−a 22bc=9+c 2−56c，整理得c 2−3√2c +4=0， 解得c =2√2或c =√2当c =2√2时，S △ABC =12bcsinA =12×3×2√2×√22=3，当c =√2时，S △ABC =12bcsinA =12×3×√2×√22=32．【解析】(1)先由正弦定理表示出sinA =√52R ，sinB =32R ，然后结合已知可求R ，可求sin A ，进而可求A ； (2)由(1)结合余弦定理可求c ，然后结合三角形的面积公式即可求解．本题主要考查了正弦定理，余弦定理，三角形的面积公式在求解三角形中的应用，属于中档题． 18.【答案】解：(1)设直线l 的方程为x =ty +1，联立{x =ty +1y 2=2x，得y 2−2ty −2=0， 所以|AB|=√1+t 2√4t 2+8=2√(t 2+1)(t 2+2)，由|AB|=2√2，解得t =0，所以A ，B 的坐标为(1,√2)，(1,−√2)，△AOB 外接圆的圆心在x 轴上，设圆心为(a,0)，由a 2=(a −1)2+(√2)2，解得a =32，所以△AOB 外接圆的方程为(x −32)2+y 2=94．(2)证明：设A(x 1,y 1)，B(x 2,y 2)，则A′(x 1,−y 1)，由(1)知，y 1+y 2=2t ，y 1y 2=−2，设直线A′B 的方程为x =my +n ，联立{x =my +n y 2=2x，得y 2−2my −2n =0， 则(−y 1)y 2=−2n ，所以2n =−2，即n =−1，所以直线A′B 过定点(−1,0)．【解析】本题考查了直线与抛物线的相交问题，解题中需要一定的计算能力，属于中档题．(1)设直线l 的方程为x =ty +1，联立直线l 与抛物线的方程，结合弦长公式可得|AB|=2√2，解得t ，进而可得A ，B 的坐标，知△AOB 外接圆的圆心在x 轴上，设圆心为(a,0)，列a 2=(a −1)2+(√2)2，解得a ，进而可得答案．(2)设A(x 1,y 1)，B(x 2,y 2)，则A′(x 1,−y 1)，由(1)知，y 1+y 2，y 1y 2，联立直线A′B 与抛物线的方程，结合韦达定理可得(−y 1)y 2=−2n ，解得n ，进而可得答案．19.【答案】解：(Ⅰ)设事件C ：从A 地区2019年脱贫家庭中随机抽取1户，该家庭2019年人均纯收入超过10000元，从表格数据可知，A 地区抽出的300户家庭中2019年人均年收入超过10000元的有100户，因此P(C)可以估计为100300=13；(Ⅱ)设事件A ：从样本中A 地区2019年脱贫家庭中随机抽取1户，该家庭2019年人均纯收入超过10000元， 设事件B ：从样本中B 地区2019年脱贫家庭中随机抽取1户，该家庭2019年人均纯收入超过10000元， 由题意可知，X 的可能取值为0，1，2，P(X =0)=P(A −B −)=P(A −)P(B −)=(1−13)×(1−34)=16，P(X =1)=P(A −B ∪AB −)=P(A −)P(B)+P(A)P(B −)=(1−13)×34+13×(1−34)=712，P(X =2)=P(AB)=P(A)P(B)=13×34=14， X X 0 1 2 P 16712 14 所以X 的数学期望为E(X)=0×16+1×712+2×14=1312；(Ⅲ)设事件E 为“从样本中A 地区的300户脱贫家庭中随机抽取4户，这4户家庭2020年人均年纯收入都超过10000元”，假设样本中A 地区2020年人均年纯收入超过10000元的户数相比2019年没有变化，则由2019年的样本数据可得P(E)=C 1004C 3004≈0.012． 答案示例1：可以认为有变化，理由如下：P(E)比较小，概率比较小的事件一般不容易发生，一旦发生，就有理由认为样本中A 地区2020年人均年纯收入超过10000元的户数相比2019年发生了变化，所以可以认为有变化．答案示例2：无法确定有没有变化，理由如下：事件E 是随机事件，P(E)比较小，一般不容易发生，但还是有可能发生的，所以无法确定有没有变化．【解析】(Ⅰ)利用概率公式求解即可；(Ⅱ)确定X 的取值，分别求解其概率，然后列出分布列求出数学期望即可；(Ⅲ)先通过2019年的样本数据可得P(E)=C 1004C 3004≈0.012，然后据此说明理由即可． 本题考查了离散型随机变量及其分布列以及离散型随机变量的期望，考查了逻辑推理能力与运算能力，属于中档题．20.【答案】(1)证明：连接CE ，由题意知，四边形ABCE 为正方形，连接BE 交AC 于O ，连接OG ，所以O 为BE 中点，又因为G 为PB 中点，所以OG//PE ，因为E ，F 分别为AD ，CD 中点，所以AC//EF ，因为OG ∩AC =O ，PE ∩EF =E ，AC ，OG ⊂平面ACG ，PE ∩EF ⊂平面PEF ，所以平面GAC//平面PEF ．(2)解：建立如图所示的空间直角坐标系，各点坐标如下：A(0,−√2,0)，C(√2,0，0)，B(√2,−√2,0)，P(√22,√22,1)， G(3√24,−√24,12)， AG ⃗⃗⃗⃗⃗ =(3√24,3√24,12)，AC ⃗⃗⃗⃗⃗ =(√2,√2,0)，AP ⃗⃗⃗⃗⃗ =(√22,3√22,1)， 设平面PAC 的法向量为n⃗ =(x,y ，z)，{AC ⃗⃗⃗⃗⃗ ⋅n ⃗ =√2x +√2y =0AP ⃗⃗⃗⃗⃗ ⋅n ⃗ =√22x +3√22y +z =0，令y =−1，n ⃗ =(1,−1,√2)，所以直线AG 与平面PAC 所成角的正弦值为|AG ⃗⃗⃗⃗⃗⃗ ⋅n ⃗⃗ ||AG ⃗⃗⃗⃗⃗⃗ |⋅|n ⃗⃗ |=√22√102⋅2=√510．【解析】(1)根据平面与平面平行的判定定理证明；(2)用向量数量积求直线与平面成角的正弦值． 本题考查了直线与平面的位置关系，考查了直线与平面成角问题，属于中档题．21.【答案】解：(1)f′(x)=ke x−1−1，当k ≤0时，f′(x)<0，f(x)在(−∞,+∞)上单调递减；当k >0时，令f′(x)=0，得x =1−lnk ，当x ∈(−∞,1−lnk)时，f′(x)<0；当x ∈(1−lnk,+∞)时，f′(x)>0．故f(x)在(−∞,1−lnk)上单调递减，在(1−lnk,+∞)上单调递增．(2)g(x)=lnx −x +f(x)x =lnx −x +ke x−1x −1， g′(x)=(x−1)(ke x−1−x)x 2，因为g(x)有三个极值点x 1，x 2，x 3，所以g′(x)=0有三个根x 1，x 2，x 3，假设x 1=1，x 2，x 3是ke x−1−x =0的两个根，结合(1)可知，当k >0时，满足条件，则f(1−lnk)=ke −lnk −1+lnk =lnk <0，解得0<k <1，所以f(1)=k −1<0，所以方程ke x−1−x =0的两个根中有一个小于1，一个大于1，又x 1<x 2<x 3，所以x 2=1，x 1，x 3是ke x−1−x =0的两个根，所以g(x 2)=ln1−1+k −1=k −2，g(x 1)=lnx 2−x 2，g(x 3)=lnx 3−x 3，所以g(x 1)+g(x 2)+g(x 3)=k −2+ln(x 1x 3)−(x 1+x 3)=k −2−(x 1+x 3)+ln(ke x 1−1⋅ke x 3−1)=k −2−(x 1+x 3)+lnk 2+x 1−1+x 3−1=k −4+2lnk ，令ℎ(k)=k −4+2lnk ，0<k <1， 则ℎ′(k)=1+2k >0，所以ℎ(k)在(0,1)上单调递增，k →0时，ℎ(k)→−∞，ℎ(1)=−3，所以ℎ(k)<−3，所以g(x 1)+g(x 2)+g(x 3)的取值范围是(−∞,−3)．【解析】(1)对f(x)求导，对k 进行讨论，求出即可；(2)对g(x)求导，可得g′(x)=0有三个根x 1，x 2，x 3，结合(1)可得k >0，则有f(1−lnk)<0，从而可求得0<k <1，则g(x 1)+g(x 2)+g(x 3)=k −4+2lnk ，令ℎ(k)=k −4+2lnk ，利用导数求出ℎ(k)的范围，从而可得结论．本题主要考查利用导数研究函数的单调性，极值与最值，考查分类讨论与转化思想，以及运算求解能力，属于难题．22.【答案】解：(1)曲线C 的参数方程为{x =√3cosαy =sinα(α为参数)，转换为普通方程为x 23+y 2=1；直线l 的极坐标方程为ρsin(θ−π4)=√22，根据{x =ρcosθy =ρsinθx 2+y 2=ρ2转换为直角坐标方程为y =x +1． (2)把直线l ：x −y +1=0代入x 23+y 2=1， 得到：2x 2+3x =0，解得{x =0y =1或{x =−32y =−12， 即A(0,1)，B(−32,−12)，所以|MA|=√2，|MB|=5√22， 所以1|MA|+1|MB|=√22+√25=7√210．【解析】(1)直接利用转换关系，在参数方程、极坐标方程和直角坐标方程之间进行转换．(2)利用直线和椭圆的位置关系的应用，两点间的距离公式求出结果．本题考查的知识要点：参数方程极、坐标方程和直角坐标方程之间的转换，直线和椭圆的位置关系的应用，两点间的距离公式，主要考查学生的运算能力和数学思维能力，属于基础题．23.【答案】(1)解：当a =1，b =3时，f(x)+g(x)=|2x +1|+|x −3|={2−3x,x ≤−12x +4,−12<x ≤33x −2,x >3，当x ≤−12时，由2−3x ≥4，解得x ≤−23；当−12<x ≤3时，x +4≥4，解得0≤x ≤3；当x >3时，由3x −2≥4，解得x >3，所以不等式f(x)+g(x)≥4的解集为(−∞,−23]∪[0,+∞)．(2)证明：当a >0，b >0时，由不等式的基本性质，得f(x)−2g(x)=|2x +a|−|2x −2b|≤|2x +a −2x +2b|=a +2b ，所以a +2b =3，因为a+2b 2≤√a2+4b 22，即3≤√a 2+4b 22，所以a 2+4b 2≥92． 另解：根据柯西不等式，得(12+12)[a 2+(2b)2]≥(a +2b)2=9，即a 2+4b 2≥92，当且仅当a =2b ，即a =32，b =34时取得等号．【解析】(1)通过去掉绝对值符号，对x 分类讨论，求解不等式即可；(2)由不等式的性质可求得f(x)的最大值，即可求得a +2b 的值，再利用基本不等式或柯西不等式即可得证． 本题考查绝对值不等式的解法，不等式的证明，考查转化思想，逻辑推理与运算求解能力，属于中档题．。
2021年新高考Ⅰ卷数学试题(含答案)
2021年新高考Ⅰ卷数学试题本试卷共4页，22小题，满分150分，考试用时120分钟。
注意事项：1.答卷前，考生务必将自己的姓名、考生号、考场号和座位号填写在答题卡上。
用2B铅笔将试卷类型（B)填涂在答题卡相应位置上，将条形码横贴在答题卡右上角“条形码粘贴处”。
2.作答选择题时，选出每小题答案后，用 28铅笔在答题卡上对应题目选项的答案信息点涂黑：如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试卷上，3.非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新答案：不准使用铅笔和涂改液。
不按以上要求作答无效。
4.考生必须保持答题卡的整洁，考试结束后，将试卷和答题卡一井交回。
一、选择题：本题共8小题，每小题5分，共40分。
在每小题给出的四个选项中，只有一项是符合题目要求的。
1. 设集合A= {x|-2<x<4}. B = {2,3,4,5},则A∩B=A.{2}B.{2,3}C.{3,4,}D.{2,3,4}2.已知z=2-i，则(=A.6-2iB.4-2iC.6+2iD.4+2i3.已知圆锥的底面半径为，其侧面展开图为一个半圆，则该圆锥的母线长为A.2B.2C.4D.44.下列区间中，函数f(x)=7sin()单调递增的区间是A.(0,)B.( ,)C.(,)D.(,)5.已知F1,F2是椭圆C：的两个焦点，点M在 C 上，则|MF1|·|MF2|的最大值为A.13B.12C.9D.66.若tan=-2,则 =A.B.C.D.7.若过点（a,b)可以作曲线y=e x的两条切线，则A. e b<aB. e a<bC. 0<a<e bD. 0<b<e a8.有6个相同的球，分别标有数字1,2,3,4,5,6,从中有放回的随机取两次,每次取1个球，甲表示事件“第一次取出的球的数字是1”，乙表示事件“第二次取出的球的数字是2”，丙表示事件“两次取出的球的数字之和是8”，丁表示事件“两次取出的球的数字之和是7”，则A.甲与丙相互独立B.甲与丁相互独立C.乙与丙相互独立D.丙与丁相互独立二、选择题：本题共4小题，每小题5分，共20分。
宁夏中卫市2021版高考数学模拟试卷(理科)(4月份)C卷
宁夏中卫市2021版高考数学模拟试卷（理科）（4月份）C卷姓名:________ 班级:________ 成绩:________一、选择题： (共12题；共24分)1. （2分） (2017高二下·榆社期中) 设全集U=R，集合A={x∈N|x2＜6x}，B={x∈N|3＜x＜8}，则如图阴影部分表示的集合是（）A . {1，2，3，4，5}B . {1，2，3}C . {3，4}D . {4，5，6，7}2. （2分） (2019高二上·河南月考) 记为等差数列的前项和，若，，则（）A . 8B . 9C . 16D . 153. （2分）若（为虚数单位），则等于（）A .B .C .D .4. （2分） (2018高二上·桂林期中) 如图，网格纸上小正方形的边长为l，粗实线画出的是某几何体的三视图，则该几何体的体积为（）A . 16B .C .D . 85. （2分） (2018高三上·镇海期中) 已知双曲线的左右焦点分别为，为双曲线上一点，为双曲线渐近线上一点，均位于第一象限，且，，则双曲线的离心率为（）A .B .C .D .6. （2分）(2018·商丘模拟) 高考结束后6名同学游览我市包括日月湖在内的6个景区，每名同学任选一个景区游览，则有且只有两名同学选择日月湖景区的方案有（）A . 种B . 种C . 种D . 种7. （2分）(2019·邵阳模拟) 执行如图所示的程序框图，若输入x的值为2，则输出的y值为（）A . 2B . 3C . 4D . 58. （2分）(2017·怀化模拟) 已知ω＞0，设x1 ， x2是方程sin（ωx+ ）= 的两个不同的实数根，且|x2﹣x1|的最小值为2，则ω等于（）A .B .C .D .9. （2分） (2017高二下·汪清期末) 下列说法正确的是（）A . 函数y＝2sin(2x－ )的图象的一条对称轴是直线T＝B . 若命题p：“存在x∈R，x2－x－1＞0”，则命题p的否定为：“对任意x∈R， x2－x－1≤0”C . 若x≠0，则x＋≥2D . “a＝1”是“直线x－ay＝0与直线x＋ay＝0互相垂直”的充要条件10. （2分） (2016高二上·黑龙江期中) 正方体ABCD﹣A1B1C1D1中，BB1与平面ACD1所成角的正弦值为（）A .B .C .D .11. （2分）(2017·甘肃模拟) 设抛物线K：x2=2py（p＞0），焦点为F，P是K上一点，K在点P处的切线为l，d为F到l的距离，则（）A . =pB . =pC . =2pD . =12. （2分）(2017·青州模拟) 已知P是△ABC所在平面内一点，，现将一粒黄豆随机撒在△ABC内，则黄豆落在△PBC内的概率是（）A .B .C .D .二、填空题： (共4题；共5分)13. （2分） (2019高三上·金华月考) 世纪中叶，中国数学家贾宪给出了直到六次幂的二项式系数表，如图所示是《杨辉详解九章算法》开方作法本原，其中第层即为展开式的系数．贾宪称整张数表为“开放作法本原”，今称“贾宪三角”但贾宪未给出二项式系数的一般公式，因而未能建立一般正整数次幂的二项式定理．贾宪的数学著作已失传，13世纪数学家杨辉在《详解九章算法》中引用了开放作法本原图，注明此图出“《释锁算数》，贾宪用此术”，因而流传至今．只是后人往往因此把它误称为“杨辉三角”．展开式中的系数为-160，①则实数的值为________，②展开式中各项系数之和为________．14. （1分）以下四个命题中：①某地市高三理科学生有15000名，在一次调研测试中，数学成绩服从正态分布，已知，若按成绩分层抽样的方式抽取100份试卷进行分析，则应从120分以上（包括120分）的试卷中抽取份；②已知命题，则：；③在上随机取一个数，能使函数在上有零点的概率为；④设，则“ ”是“ ”的充要条件.其中真命题的序号为________.15. （1分） (2017高三上·同心期中) 已知，删除数列中所有能被整除的数，剩下的数从小到大排成数列，则 ________.16. （1分）等比数列{an}中的a1 ， a2015是函数的极值点，则log2a1+log2a2+…+log2a2015=________．三、解答题： (共7题；共55分)17. （10分） (2019高三上·北京月考) 如图：的三个内角A ， B ， C对应的三条边长分别是a ，b ，c ，角B为钝角，，，，（1）求，边a和的值；（2）求CD的长，的面积．18. （10分） (2020高一下·吉林月考) 如图，从参加环保知识竞赛的1200名学生中抽出60名，将其成绩（均为整数）整理后画出的频率分布直方图如下：观察图形，回答下列问题：（1） 79.5—89.5这一组的频数、频率分别是多少？（2）估计这次环保知识竞赛的及格率.（60分及以上为及格）19. （5分） (2016高二下·金堂开学考) 如图1，在直角梯形ABCD中，AD∥BC，∠BAD= ，AB=BC=1，AD=2，E是AD的中点，O是AC与BE的交点．将△AB E沿BE折起到图2中△A1BE的位置，得到四棱锥A1﹣BCDE．（Ⅰ）证明：CD⊥平面A1OC；（Ⅱ）若平面A1BE⊥平面BCDE，求平面A1BC与平面A1CD夹角（锐角）的余弦值．20. （10分）(2019·太原模拟) 已知椭圆的左、右焦点分别是，是其左右顶点，点是椭圆上任一点，且的周长为6，若面积的最大值为 .（1）求椭圆的方程；（2）若过点且斜率不为0的直线交椭圆于两个不同点，证明：直线于的交点在一条定直线上.21. （5分） (2019高三上·东湖期中) 已知函数 .（Ⅰ）讨论的单调性；（Ⅱ）若有两个零点，求的取值范围.22. （5分）(2017·常德模拟) 直角坐标系xOy中，以O为极点，x轴正半轴为极轴建立极坐标系，曲线C1的极坐标方程为，直线l的参数方程为（t为参数），直线l与曲线C1交于A，B 两点．（Ⅰ）求|AB|的长度；（Ⅱ）若曲线C2的参数方程为（α为参数），P为曲线C2上的任意一点，求△PAB的面积的最小值．23. （10分）(2017·大连模拟) 设函数f（x）=|x+4|．（1）若y=f（2x+a）+f（2x﹣a）最小值为4，求a的值；（2）求不等式f（x）＞1﹣ x的解集．参考答案一、选择题： (共12题；共24分)答案：1-1、考点：解析：答案：2-1、考点：解析：答案：3-1、考点：解析：答案：4-1、考点：解析：答案：5-1、考点：解析：答案：6-1、考点：解析：答案：7-1、考点：解析：答案：8-1、考点：解析：答案：9-1、考点：解析：答案：10-1、考点：解析：答案：11-1、考点：解析：答案：12-1、考点：解析：二、填空题： (共4题；共5分)答案：13-1、考点：解析：答案：14-1、考点：解析：答案：15-1、考点：解析：答案：16-1、考点：解析：三、解答题： (共7题；共55分)答案：17-1、答案：17-2、考点：解析：答案：18-1、答案：18-2、考点：解析：考点：解析：答案：20-1、答案：20-2、考点：解析：答案：21-1、考点：解析：答案：22-1、考点：解析：答案：23-1、答案：23-2、考点：解析：。
宁夏中卫市2021届新高考数学最后模拟卷含解析
宁夏中卫市2021届新高考数学最后模拟卷一、选择题：本题共12小题，每小题5分，共60分。
在每小题给出的四个选项中，只有一项是符合题目要求的。
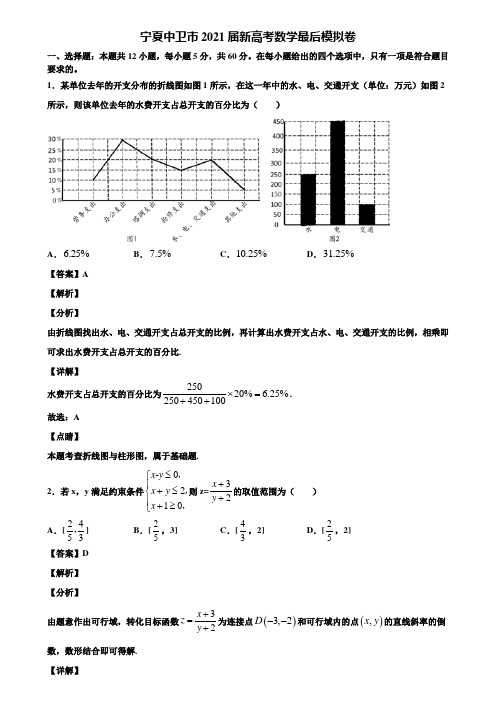
1．某单位去年的开支分布的折线图如图1所示，在这一年中的水、电、交通开支（单位：万元）如图2所示，则该单位去年的水费开支占总开支的百分比为（）A．6.25%B．7.5%C．10.25%D．31.25%【答案】A【解析】【分析】由折线图找出水、电、交通开支占总开支的比例，再计算出水费开支占水、电、交通开支的比例，相乘即可求出水费开支占总开支的百分比.【详解】水费开支占总开支的百分比为25020% 6.25% 250450100⨯=++.故选：A【点睛】本题考查折线图与柱形图，属于基础题.2．若x，y满足约束条件-0210x yx yx≤⎧⎪+≤⎨⎪+≥⎩，，，则z=32xy++的取值范围为（）A．[2453，] B．[25，3] C．[43，2] D．[25，2]【答案】D 【解析】【分析】由题意作出可行域，转化目标函数32xzy+=+为连接点()3,2D--和可行域内的点(),x y的直线斜率的倒数，数形结合即可得解. 【详解】由题意作出可行域，如图，目标函数32xzy+=+可表示连接点()3,2D--和可行域内的点(),x y的直线斜率的倒数，由图可知，直线DA的斜率最小，直线DB的斜率最大，由10x yx-=⎧⎨+=⎩可得()1,1A--，由210x yx+=⎧⎨+=⎩可得()1,3B-，所以121132DAk-+==-+，325132DBk+==-+，所以225z≤≤.故选：D.【点睛】本题考查了非线性规划的应用，属于基础题.3．设x，y满足约束条件2121x yx yx y+≤⎧⎪+≥-⎨⎪-≤⎩，若32z x y=-+的最大值为n，则2nxx⎛⎝的展开式中2x项的系数为( )A．60 B．80 C．90 D．120【答案】B【解析】【分析】画出可行域和目标函数，根据平移得到5n=，再利用二项式定理计算得到答案.【详解】如图所示：画出可行域和目标函数，32z x y=-+，即322zy x=+，故z表示直线与y截距的2倍，根据图像知：当1,1x y=-=时，32z x y=-+的最大值为5，故5n=.52xx⎛⎝展开式的通项为：()()35552155221rrr rr r rrT C x C xx---+⎛=⋅=⋅⋅-⋅⎝，取2r得到2x 项的系数为：()225252180C -⋅⋅-=.故选：B.【点睛】本题考查了线性规划求最值，二项式定理，意在考查学生的计算能力和综合应用能力.4．已知函数2()4ln f x ax ax x =--，则()f x 在(1,4)上不单调的一个充分不必要条件可以是（ ） A ．12a >-B ．1016a <<C ．116a >或102a -<< D ．116a >【答案】D 【解析】 【分析】先求函数在(1,4)上不单调的充要条件，即()0f x '=在(1,4)上有解，即可得出结论. 【详解】21241()24--'=--=ax ax f x ax a x x， 若()f x 在(1,4)上不单调，令2()241=--g x ax ax ，则函数2()241=--g x ax ax 对称轴方程为1x =在区间(1,4)上有零点（可以用二分法求得）. 当0a =时，显然不成立；当0a ≠时，只需0(1)210(4)1610a g a g a >⎧⎪=--<⎨⎪=->⎩或0(1)210(4)1610a g a g a <⎧⎪=-->⎨⎪=-<⎩，解得116a >或12a <-.故选:D. 【点睛】本题考查含参数的函数的单调性及充分不必要条件，要注意二次函数零点的求法，属于中档题. 5．已知3log 5a =，0.50.4b =，2log 5c =，则a ，b ，c 的大小关系为（ ） A ．c b a >> B ．b c a >>C ．a b c >>D ．c a b >>【答案】D 【解析】 【分析】与中间值1比较，,a c 可用换底公式化为同底数对数，再比较大小． 【详解】0.50.41<，3log 51>，又550log 2log 3<<，∴5511log 2log 3>，即23log 5log 5>， ∴c a b >>． 故选：D. 【点睛】本题考查幂和对数的大小比较，解题时能化为同底的化为同底数幂比较，或化为同底数对数比较，若是不同类型的数，可借助中间值如0，1等比较．6．i 为虚数单位,则32i 1i-的虚部为（ ）A ．i -B ．iC ．1-D ．1【答案】C 【解析】 【分析】利用复数的运算法则计算即可. 【详解】()()()()32122111111i i i ii i i i i i i -+-===-+=----+，故虚部为1-. 故选：C. 【点睛】本题考查复数的运算以及复数的概念，注意复数(),a bi a b R +∈的虚部为b ，不是bi ，本题为基础题，也是易错题.7．在ABC ∆中，30C =︒，2cos 3A =-，152AC =-，则AC 边上的高为（） A ．5 B ．2C ．5D ．15 【答案】C 【解析】 【分析】结合正弦定理、三角形的内角和定理、两角和的正弦公式，求得BC 边长，由此求得AC 边上的高. 【详解】过B 作BD CA ⊥，交CA 的延长线于D .由于2cos 3A =-，所以A 为钝角，且25sin 1cos 3A A =-=，所以()()sin sin sin CBA CBA A C π∠=-∠=+5321152sin cos cos sin 32A C A C -=+=⨯-⨯=.在三角形ABC 中，由正弦定理得sin sin a b A B=，即1525152-=-，所以25BC =.在Rt BCD ∆中有1sin 2552BD BC C ==⨯=，即AC 边上的高为5. 故选：C【点睛】本小题主要考查正弦定理解三角形，考查三角形的内角和定理、两角和的正弦公式，属于中档题. 8．设x ∈R ，则“|1|2x -< “是“2x x <”的（ ） A ．充分而不必要条件 B ．必要而不充分条件 C ．充要条件 D ．既不充分也不必条件【答案】B 【解析】 【分析】解出两个不等式的解集，根据充分条件和必要条件的定义，即可得到本题答案. 【详解】由|1|2x -<，得13x，又由2x x <，得01x <<，因为集合{|01}{|13}x x x x <<⊂-<<， 所以“|1|2x -<”是“2x x <”的必要不充分条件. 故选：B 【点睛】本题主要考查必要不充分条件的判断，其中涉及到绝对值不等式和一元二次不等式的解法.9．已知双曲线C 的一个焦点为()0,5，且与双曲线2214x y -=的渐近线相同，则双曲线C 的标准方程为( )A ．2214y x -=B ．221520y x -=C ．221205x y -=D ．2214x y -=【答案】B 【解析】 【分析】根据焦点所在坐标轴和渐近线方程设出双曲线的标准方程，结合焦点坐标求解. 【详解】∵双曲线C 与2214x y -=的渐近线相同，且焦点在y 轴上，∴可设双曲线C 的方程为2214y x k k-=，一个焦点为0,5，∴425k k +=，∴5k =，故C 的标准方程为221520y x -=.故选：B 【点睛】此题考查根据双曲线的渐近线和焦点求解双曲线的标准方程，易错点在于漏掉考虑焦点所在坐标轴导致方程形式出错.10．执行如图的程序框图，若输出的结果2y =，则输入的x 值为( )A ．3B ．2-C ．3或3-D ．3或2-【答案】D 【解析】 【分析】根据逆运算，倒推回求x 的值，根据x 的范围取舍即可得选项. 【详解】因为2y =,所以当()12+12x =，解得3>0x = ，所以3是输入的x 的值； 当122x --=时，解得20x =-<，所以2-是输入的x 的值， 所以输入的x 的值为2- 或3， 故选：D. 【点睛】本题考查了程序框图的简单应用，通过结果反求输入的值，属于基础题.11．据国家统计局发布的数据，2019年11月全国CPI （居民消费价格指数），同比上涨4.5%，CPI 上涨的主要因素是猪肉价格的上涨，猪肉加上其他畜肉影响CPI 上涨3.27个百分点．下图是2019年11月CPI 一篮子商品权重，根据该图，下列结论错误的是（ ）A ．CPI 一篮子商品中所占权重最大的是居住B ．CPI 一篮子商品中吃穿住所占权重超过50%C ．猪肉在CPI 一篮子商品中所占权重约为2.5%D ．猪肉与其他畜肉在CPI 一篮子商品中所占权重约为0.18% 【答案】D 【解析】 【分析】A.从第一个图观察居住占23%，与其他比较即可.B. CPI 一篮子商品中吃穿住所占23%+8%+19.9%=50.9%，再判断.C.食品占19.9%，再看第二个图，分清2.5%是在CPI 一篮子商品中，还是在食品中即可.D. 易知猪肉与其他畜肉在CPI 一篮子商品中所占权重约为2.1%+2.5%=4.6%. 【详解】A. CPI 一篮子商品中居住占23%，所占权重最大的，故正确.B. CPI 一篮子商品中吃穿住所占23%+8%+19.9%=50.9%，权重超过50%，故正确.C.食品占中19.9%，分解后后可知猪肉是占在CPI 一篮子商品中所占权重约为2.5%，故正确.D. 猪肉与其他畜肉在CPI 一篮子商品中所占权重约为2.1%+2.5%=4.6%，故错误. 故选：D 【点睛】本题主要考查统计图的识别与应用，还考查了理解辨析的能力，属于基础题. 12．函数()sin (0)f x x ωω=>的图象向右平移12π个单位得到函数()y g x =的图象，并且函数()g x 在区间[,]63ππ上单调递增，在区间[,]32ππ上单调递减，则实数ω的值为（ ） A ．74B ．32C ．2D ．54【答案】C 【解析】由函数()sin (0)f x x ωω=>的图象向右平移12π个单位得到[]1212g x sin x sin x πωπωω=-=-（）（）（），函数()g x 在区间,63ππ⎡⎤⎢⎥⎣⎦上单调递增，在区间,32ππ⎡⎤⎢⎥⎣⎦上单调递减，可得3x π=时，()g x 取得最大值，即23122k πωππωπ⨯-=+（），k Z ∈，0ω>，当0k =时，解得2ω=，故选C.点睛：本题主要考查了三角函数图象的平移变换和性质的灵活运用，属于基础题；据平移变换“左加右减，上加下减”的规律求解出()g x ，根据函数()g x 在区间,63ππ⎡⎤⎢⎥⎣⎦上单调递增，在区间,32ππ⎡⎤⎢⎥⎣⎦上单调递减可得3x π=时，()g x 取得最大值，求解可得实数ω的值.二、填空题：本题共4小题，每小题5分，共20分。
2021年宁夏回族自治区中卫市普通高校对口单招数学一模测试卷(含答案)
2021年宁夏回族自治区中卫市普通高校对口单招数学一模测试卷(含答案)一、单选题(20题)1.设则f(f(-2))=()A.-1B.1/4C.1/2D.3/22.若sinα与cosα同号，则α属于( )A.第一象限角B.第二象限角C.第一、二象限角D.第一、三象限角3.函数f(x)=的定义域是( )A.(0,+∞)B.[0,+∞)C.(0,2)D.R4.已知a=1.20.1，b=ln2，c=5-1/2，则a，b，c的大小关系是（）A.b＞a＞cB.a＞c＞bC.a＞b＞cD.c＞a＞b5.在等差数列{a n}中，如果a3+a4+a5+a6+a7+a8=30，则数列的前10项的和S10为（）A.30B.40C.50D.606.函数的定义域( )A.[3,6]B.[-9,1]C.(-∞,3]∪[6，+∞)D.(-∞，+∞)7.圆x2+y2-2x-8y+13=0的圆心到直线ax+y-1=0的距离为1，则a=()A.-4/3B.-3/4C.D.28.已知椭圆的一个焦点为F(0，1)，离心率e=1/2，则该椭圆的标准方程为（)A.x2/3+y2/4=1B.x2/4+y2/3=1C.x2/2+y2=1D.y2/2+x2=19.已知椭圆x2/25+y2/m2=1(m＞0)的左焦点为F1（-4,0)则m=()A.2B.3C.4D.910.以坐标轴为对称轴，离心率为，半长轴为3的椭圆方程是（）A.B.或C.D.或11.函数y=1/2x2-lnx的单调递减区间为（）.A.(-1,1]B.(0，1]C.[1，+∞)D.(0,+∞)12.己知，则这样的集合P有（）个数A.3B.2C.4D.513.复数z=2i/1+i的共轭复数是（)A.1+iB.1-iC.1/2+1/2iD.1/2-1/2i14.15.若a<b<0，则下列结论正确的是( )A.a2<b2B.a3<b<b3</bC.|a|<|b|D.a/b<116.A.-1B.-4C.4D.217.不等式-2x2+x+3<0的解集是（）A.{x|x＜-1}B.{x|x＞3/2}C.{x|-1＜x＜3/2}D.{x|x<-1或x＞3/2}18.椭圆9x2+16y2=144短轴长等于（）A.3B.4C.6D.819.已知直线L过点（0,7)，且与直线y=-4x+2平行，则直线L的方程为（）A.y=-4x-7B.y=4x—7C.y=-4x+7D.y=4x+720.A.B.C.D.二、填空题(20题)21.展开式中，x4的二项式系数是_____.22.正方体ABCD-A1B1C1D1中AC与AC1所成角的正弦值为。
2021年宁夏中卫市高考数学一模试卷(理科)(解析版)
2021年宁夏中卫市高考数学一模试卷（理科）一、选择题（共12小题）.1．已知全集U＝R，集合A＝{x|x2﹣4x+3＞0}，B＝{x|﹣1＜x＜2}，则（∁U A）∪B＝（）A．（﹣1，1]B．[1，2）C．[1，3]D．（﹣1，3]2．复数z＝，则z3＝（）A．﹣i B．i C．﹣1D．13．下列四个命题：①若a＞|b|，则a2＞b2②若a＞b，c＞d，则a﹣c＞b﹣d③若a＞b，c＞d，则ac＞bd④若a＞b＞0，c＜0，则其中正确命题的个数有（）A．1个B．2个C．3个D．4个4．为美化环境，某城市决定用鲜花装饰如图所示花柱，它的下面是一个直径为1m、高为3m的圆柱形物体，上面是一个半球形体，如果每平方米大约需要鲜花150朵，那么装饰一个这样的花柱大约需要鲜花朵数为（）（π≈3.1）A．1230B．1430C．1630D．18305．中心在原点的双曲线C的一条渐近线方程为x+y＝0，则C的离心率为（）A．2或B．或3C．2或D．或36．已知cos（θ﹣）＝，则sin2θ＝（）A．B．C．﹣D．﹣7．如图，在3×3的方格中，移动规则如下：每行均可左右移动，每列均可上下移动，每次仅能对某一行或某一列进行移动，其他行或列不变化．例如：若想移动成每行的数字相同，则最少需要移动（）次A．2B．3C．4D．58．将函数f（x）＝sin2x﹣1的图象向右平移个单位长度后得到函数g（x）的图象，则函数g（x）的单调递增区间是（）A．[﹣+kπ，+kπ]（k∈Z）B．[+kπ，+kπ]（k∈Z）C．[﹣+kπ，+kπ]（k∈Z）D．[﹣+kπ，+kπ]（k∈Z）9．已知抛物线C：y2＝2px（p＞0）的焦点为F，准线与x轴交于点K，过点K作圆的切线，切点分别为A，B．若，则p的值为（）A．1B．C．2D．310．已知符号函数，偶函数f（x）满足f（x+2）＝f（x），当x∈[0，1]时，f（x）＝x，则（）A．sgn（f（x））＞0B．C．sgn（f（2k））＝0（k∈Z）D．sgn（f（k））＝|sgnk|（k∈Z）11．如图，在正四棱柱ABCD﹣A1B1C1D1，E，F分别为AB，BC的中点，异面直线AB1与C1F所成角的余弦值为m，则（）A．直线A1E与直线C1F异面，且B．直线A1E与直线C1F共面，且C．直线A1E与直线C1F异面，且D．直线A1E与直线C1F共面，且12．已知函数f（x）＝x2﹣alnx﹣a（a＜2），若对于∀x1，x2∈[1，2]，x1≠x2，都有＞a恒成立，则实数a的取值范围为（）A．（﹣∞，）B．（﹣∞，]C．（﹣∞，1）D．（﹣∞，1]二、填空题（共4小题）.13．已知向量，满足＝（2，3），2﹣3＝（1，9），则的值为．14．已知实数x，y满足不等式组，则目标函数z＝x﹣2y的最大值为．15．的展开式中各项系数之和为2，则该展开式中x4的系数为．16．在△ABC中，记角A，B，C所对的边分别是a，b，c，面积为S，则的最大值为．三、解答题（本大题共5小题，满分60分．解答须写出文字说明，证明过程或演算步骤.）17．已知数列{a n}的前n项和是S n，且S n＝2a n﹣2，等差数列{b n}中，b1＝20，b3＝16．（1）求数列{a n}和{b n}的通项公式；（2）定义：a*b＝．记c n＝a n*b n，求数列{c n}的前10项的和T10．18．医学中判断男生的体重是否超标有一种简易方法，就是用一个人身高的厘米数减去105所得差值即为该人的标准体重．比如身高175cm的人，其标准体重为175﹣105＝70公斤，一个人实际体重超过了标准体重，我们就说该人体重超标了．已知某班共有30名男生，从这30名男生中随机选取6名，其身高和体重的数据如表所示：编号123456身高（cm）x165171160173178167体重（kg）y606362707158（1）从这6人中任选2人，求恰有1人体重超标的概率；（2）依据上述表格信息，用最小二乘法求出了体重y对身高x的线性回归方程：＝0.65x+，但在用回归方程预报其他同学的体重时，预报值与实际值吻合不好，需要对上述数据进行残差分析，按经验，对残差在区间[﹣3.5，3.5]之外的同学要重新采集数据．问上述随机抽取的编号为3，4，5，6的四人中，有哪几位同学要重新采集数据？参考公式：残差＝y i﹣x i﹣．19．如图，在平行四边形ABCD中，AB＝1，BC＝2，∠ACB＝，四边形ABEF为直角梯形，BE∥AF，∠BAF＝，BE＝2，AF＝3，平面ABCD⊥平面ABEF．（1）求证：AC⊥平面ABEF；（2）求平面ABCD与平面DEF所成锐二面角的余弦值．20．经过椭圆左焦点F1的直线l与圆相交于P，Q两点，M是线段PF2与C的公共点，且|MF1|＝|MP|．（1）求r；（2）l与C的交点为A，B，且A恰为线段PQ的中点，求△ABF2的面积．21．已知函数f（x）＝x2﹣ax+（a，b∈R）．（1）若a＞b＞0，证明f（a）＞f（b）；（2）若对任意x∈（0，+∞），b∈（﹣e，0），都有f（x）＞﹣e，求实数a的取值范围．选考题：（请考生在第22、23两道题中任选一题作答．如果多做，则按所做的第一题记分。
宁夏中卫市2021届新高考数学模拟试题(1)含解析
宁夏中卫市2021届新高考数学模拟试题（1）一、选择题：本题共12小题，每小题5分，共60分。
在每小题给出的四个选项中，只有一项是符合题目要求的。
1．已知双曲线()222210,0x y a b a b-=>>的左、右顶点分别是,A B ，双曲线的右焦点F 为()2,0，点P 在过F 且垂直于x 轴的直线l 上，当ABP ∆的外接圆面积达到最小时，点P 恰好在双曲线上，则该双曲线的方程为（ ）A ．22122x y -= B ．2213y x -= C ．2213x y -= D ．22144x y -= 【答案】A【解析】【分析】 点P 的坐标为()2,m ()0m >，()tan tan APB APF BPF ∠=∠-∠，展开利用均值不等式得到最值，将点代入双曲线计算得到答案.【详解】不妨设点P 的坐标为()2,m ()0m >，由于AB 为定值，由正弦定理可知当sin APB ∠取得最大值时，APB ∆的外接圆面积取得最小值，也等价于tan APB ∠取得最大值， 因为2tan a APF m +∠=，2tan a BPF m-∠=， 所以()2222tan tan 221a a a a m m APB APF BPF a a b b m m m m +--∠=∠-∠==≤=+-+⋅+， 当且仅当2b m m=()0m >，即当m b =时，等号成立， 此时APB ∠最大，此时APB 的外接圆面积取最小值，点P 的坐标为()2,b ，代入22221x y a b-=可得a =b == 所以双曲线的方程为22122x y -=． 故选：A【点睛】本题考查了求双曲线方程，意在考查学生的计算能力和应用能力.2．若集合{}(2)0A x x x =->，{}10B x x =->，则AB = A ．{}10x x x ><或 B ．{}12x x <<C ．{|2}x x >D ．{}1x x > 【答案】C【解析】【分析】解一元次二次不等式得{|2A x x =>或0}x <，利用集合的交集运算求得AB ={|2}x x >. 【详解】因为{|2A x x =>或0}x <，{}1B x x =>，所以AB ={|2}x x >，故选C. 【点睛】本题考查集合的交运算，属于容易题.3．将函数()sin(2)3f x x π=-()x R ∈的图象分别向右平移3π个单位长度与向左平移n (n >0)个单位长度，若所得到的两个图象重合，则n 的最小值为( )A ．3πB ．23πC ．2πD ．π【答案】B【解析】【分析】首先根据函数()f x 的图象分别向左与向右平移m,n 个单位长度后，所得的两个图像重合，那么m n k T +=⋅，利用()f x 的最小正周期为π，从而求得结果.【详解】()f x 的最小正周期为π， 那么3n k ππ+=(k ∈Z )， 于是3n k ππ=-，于是当1k =时，n 最小值为23π， 故选B.【点睛】 该题考查的是有关三角函数的周期与函数图象平移之间的关系，属于简单题目.4．已知函数()cos 221f x x x =++，则下列判断错误的是（ ）A ．()f x 的最小正周期为πB ．()f x 的值域为[1,3]-C ．()f x 的图象关于直线6x π=对称 D ．()f x 的图象关于点,04π⎛⎫- ⎪⎝⎭对称 【答案】D【解析】【分析】先将函数()cos 221f x x x =++化为()2sin 216f x x π⎛⎫=++ ⎪⎝⎭，再由三角函数的性质，逐项判断，即可得出结果.【详解】()cos 221f x x x =++可得1()2cos 2sin 212sin 21226f x x x x π⎛⎫⎛⎫=⋅++=++ ⎪ ⎪ ⎪⎝⎭⎝⎭对于A ，()f x 的最小正周期为22||2T πππω===,故A 正确； 对于B ，由1sin 216x π⎛⎫-≤+≤ ⎪⎝⎭，可得1()3f x -≤≤，故B 正确； 对于C ，正弦函数对称轴可得：()02,62x k k Z πππ+=+∈ 解得：()0,612x k k Z ππ=+∈， 当0k =，06x π=，故C 正确； 对于D ，正弦函数对称中心的横坐标为：()02,6x k k Z ππ+=∈ 解得：()01,212x k k Z ππ=+∈ 若图象关于点,04π⎛⎫-⎪⎝⎭对称，则12124k πππ+=- 解得：23k =-，故D 错误； 故选：D.【点睛】 本题考查三角恒等变换，三角函数的性质，熟记三角函数基本公式和基本性质，考查了分析能力和计算能力，属于基础题.5．某三棱锥的三视图如图所示，那么该三棱锥的表面中直角三角形的个数为（ ）A ．1B ．2C ．3D ．0【答案】C【解析】【分析】 由三视图还原原几何体，借助于正方体可得三棱锥的表面中直角三角形的个数.【详解】由三视图还原原几何体如图，其中ABC ∆，BCD ∆，ADC ∆为直角三角形.∴该三棱锥的表面中直角三角形的个数为3.故选：C.【点睛】本小题主要考查由三视图还原为原图，属于基础题.6．如图，抛物线M ：28y x =的焦点为F ，过点F 的直线l 与抛物线M 交于A ，B 两点，若直线l 与以F 为圆心，线段OF （O 为坐标原点）长为半径的圆交于C ，D 两点，则关于AC BD ⋅值的说法正确的是（ ）A ．等于4B ．大于4C ．小于4D ．不确定【答案】A利用F 的坐标为()2,0，设直线l 的方程为20x my --=，然后联立方程得282y x my x ⎧=⎨=-⎩，最后利用韦达定理求解即可【详解】据题意，得点F 的坐标为()2,0.设直线l 的方程为20x my --=，点A ，B 的坐标分别为()11,x y ，()22,x y .讨论：当0m =时，122x x ==；当0m ≠时，据282y x my x ⎧=⎨=-⎩，得()228440x m x -++=，所以124x x =，所以()()22AC BD AF BF ⋅=-⋅-()()121222224x x x x =+-⋅+-==.【点睛】本题考查直线与抛物线的相交问题，解题核心在于联立直线与抛物线的方程，属于基础题7．在复平面内，复数21(1)i i +-对应的点位于（ ） A ．第一象限B ．第二象限C ．第三象限D ．第四象限【答案】B【解析】【分析】化简复数为a bi +的形式，然后判断复数的对应点所在象限，即可求得答案.【详解】211(1)(1)22i i i i i i i i+++==---⋅ 111222i i -+==-+ ∴对应的点的坐标为11,22⎛⎫- ⎪⎝⎭在第二象限 故选：B.【点睛】本题主要考查了复数代数形式的乘除运算，考查了复数的代数表示法及其几何意义，属于基础题. 8．已知函数()log (|2|)(0a f x x a a =-->，且1a ≠)，则“()f x 在(3,)+∞上是单调函数”是“01a <<”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件 【答案】C先求出复合函数()f x 在(3,)+∞上是单调函数的充要条件，再看其和01a <<的包含关系，利用集合间包含关系与充要条件之间的关系，判断正确答案.【详解】()log (|2|)(0a f x x a a =-->，且1a ≠)， 由20x a -->得2x a <-或2x a >+，即()f x 的定义域为{2x x a <-或2}x a >+，（0,a >且1a ≠） 令2t x a =--，其在(,2)a -∞-单调递减，(2,)a ++∞单调递增，()f x 在(3,)+∞上是单调函数，其充要条件为2301a a a +≤⎧⎪>⎨⎪≠⎩即01a <<.故选：C.【点睛】本题考查了复合函数的单调性的判断问题，充要条件的判断，属于基础题.9．已知复数z 满足()1i +z =2i ，则z =（ ）AB ．1 C．2 D ．12【答案】A【解析】【分析】 根据复数的运算法则，可得z ，然后利用复数模的概念，可得结果.【详解】 由题可知：()()()22212221111i i i i i z i i i i --===++-- 由21i =-，所以1z i =+所以z ==故选：A【点睛】本题主要考查复数的运算，考验计算，属基础题.10．某四棱锥的三视图如图所示，则该四棱锥的表面积为（ ）A ．8B ．83C ．822+D ．842+【答案】D【解析】【分析】 根据三视图还原几何体为四棱锥，即可求出几何体的表面积．【详解】由三视图知几何体是四棱锥，如图，且四棱锥的一条侧棱与底面垂直，四棱锥的底面是正方形,边长为2,棱锥的高为2，所以1122222222284222S =⨯+⨯⨯⨯+⨯⨯⨯=+， 故选：D【点睛】本题主要考查了由三视图还原几何体，棱锥表面积的计算，考查了学生的运算能力，属于中档题. 11．已知a ，b 为两条不同直线，α，β，γ为三个不同平面，下列命题：①若//αβ，//αγ，则//βγ；②若//a α，//a β，则//αβ；③若αγ⊥，βγ⊥，则αβ⊥；④若a α⊥，b α⊥，则//a b .其中正确命题序号为( )A ．②③B ．②③④C ．①④D ．①②③ 【答案】C【解析】【分析】根据直线与平面，平面与平面的位置关系进行判断即可.【详解】根据面面平行的性质以及判定定理可得，若//αβ，//αγ，则//βγ，故①正确；若//a α，//a β，平面,αβ可能相交，故②错误；若αγ⊥，βγ⊥，则,αβ可能平行，故③错误；由线面垂直的性质可得，④正确；故选：C【点睛】本题主要考查了判断直线与平面，平面与平面的位置关系，属于中档题.12．设P ＝{y |y ＝－x 2＋1，x ∈R}，Q ＝{y |y ＝2x ，x ∈R}，则A ．P ⊆QB ．Q ⊆PC ．R C P ⊆QD ．Q ⊆R C P 【答案】C【解析】【分析】【详解】解：因为P ={y|y=-x 2+1，x ∈R}={y|y ≤1}，Q ={y| y=2x ，x ∈R }={y|y>0},因此选C二、填空题：本题共4小题，每小题5分，共20分。
2021年全国统一高考数学试卷(新高考Ⅰ卷)(含详细解析)
2021年全国统一高考数学试卷(新高考Ⅰ卷)(含详细解析)2021年全国统一高考数学试卷（新高考Ⅰ卷）注意事项：在答卷前，考生务必在答题卡上填写自己的姓名和准考证号。
回答选择题时，选出每小题的答案后，用铅笔在答题卡上对应题目的答案标号涂黑。
如需改动，用橡皮擦干净后，再选涂其他答案标号。
回答非选择题时，将答案写在答题卡上，写在本试卷上无效。
考试结束后，将本试卷和答题卡一并交回。
一、选择题：本题共8小题，每小题5分，共40分。
1.(5分) 设集合A={x|-2<x<4}，B={2,3,4,5}，则A∩B=（）A。
{2} B。
{2,3} C。
{3,4} D。
{2,3,4}2.(5分) 已知z=2-i，则|z-3i|=（）A。
6-2i B。
4-2i C。
6+2i D。
4+2i3.(5分) 已知圆锥的底面半径为2，其侧面展开图为一个半圆，则该圆锥的母线长为（）A。
2 B。
4 C。
4√2 D。
2√24.(5分) 下列区间中，函数f(x)=7sin(x)单调递增的区间是（）A。
(0,π/2) B。
(π/2,π) C。
(π,3π/2) D。
(3π/2,2π)5.(5分) 已知F1，F2是椭圆C的两个焦点，点M在C上，则|MF1|·|MF2|的最大值为（）A。
13 B。
12 C。
9 D。
66.(5分) 若tanθ=-2，则cos2θ=（）A。
-3/5 B。
-4/5 C。
-24/25 D。
-7/257.(5分) 若过点(a,b)可以作曲线y=ex的两条切线，则（）XXX<a B。
ea<b C。
0<a<eb D。
0<b<ea8.(5分) 有6个相同的球，分别标有数字1,2,3,4,5,6，从中有放回地随机取两次，每次取1个球，甲表示事件“两次取到的数字和为偶数”，乙表示事件“两次取到的数字都是奇数”，则P(甲∪乙)=（）A。
2/3 B。
5/9 C。
7/9 D。
宁夏中卫市高三数学下学期3月第一次模拟考试试题 理
学习资料宁夏中卫市2021届高三数学下学期3月第一次模拟考试试题 理本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分.第I 卷第22、23题为选考题，其他题为必考题。
考生做答时,将答案答在答题卡上，在本试卷上答题无效。
考试结束后,将本试卷和答题卡一并交回。
注意事项：1.答题前，考生先将自己的姓名、准考证号填写在答题卡上，认真核对条形码上的准考证号、姓名,并将条形码粘贴在指定位置上.2。
选择题答案使用2B 铅笔填涂,如需改动,用橡皮擦干净后，再选涂其他答案标号；非选择题答案使用0。
5毫米的黑色中性（签字)笔或炭素笔书写，字体工整、笔迹清楚。
3.请按照题号在各题的答题区域（黑色线框）内作答，超出答题区域书写的答案无效。
4.保持卡面清洁，不折叠，不破损.5.做选考题时，考生按照题目要求作答，并用2B 铅笔在答题卡上把所选题目对应的标号涂黑.第I 卷一、选择题（本大题共12个小题，每小题5分，共60分。
每小题给出的选项中，只有一项是符合题目要求的，请将正确的答案涂到答题卡上）1.全集U R =，集合{}2430A x x x =-+>，{}12B x x =-<<，则()U A B ⋃=( ）A 。
(]1,1-B 。
[)1,2C 。
[]1,3D.(]1,3-2.复数11i z i+=-，则3z =（ ） A.i -B 。
iC.-1D 。
13.下列四个命题:①若a b >，则22a b >；②若a b >，c d >，则a c b d ->-； ③若a b >，c d >,则ac bd >； ④若0a b >>，0c <，则c c a b> 其中正确命题的个数有（ ） A 。
1个B 。
2个C.3个D 。
4个4.为美化环境,某城市决定用鲜花装饰如图所示花柱，它的下面是一个直径为1m 、高为3m 的圆柱形物体，上面是一个半球形体，如果每平方米大约需要鲜花150朵，那么装饰一个这样的花柱大约需要鲜花朵数为()3.1π≈（ ）A.1230B.1430C 。
2021年新高考一卷数学试卷解析
2021年新高考一卷数学试卷解析
2021年全国新高考数学一卷是一份难度较高的试卷，以下是具体的解析：
1. 整体难度：该试卷整体难度较大，其中尤以最后两道大题为甚，很多考生在最后的时间里未能完成这些题目。
这需要考生在平时的学习和训练中，注重提高解题速度和准确度，同时也需要培养面对难题的应对策略。
2. 知识点覆盖面：该试卷对高中数学的主要知识点进行了全面的覆盖，包括代数、几何、概率统计等方面。
这有助于全面考察考生的数学知识储备和运用能力。
3. 题目类型：该试卷采用了多种类型的题目，如计算题、证明题、应用题等。
这有助于考察考生在不同题型下的解题能力和思维方式。
4. 创新性：与往年相比，该试卷在题目设计和知识点考察上具有一定的创新性。
例如，有些题目考察了考生对数学概念和方法的深度理解，而有些题目则考察了考生在解决实际问题方面的能力。
5. 考生反映：据考生反映，该试卷难度较大，部分题目较为新颖，需要考生具备较强的思维能力和应变能力。
同时，也有部分考生认为该试卷的题目设计较为合理，能够全面考察考生的数学能力和素质。
总的来说，2021年全国新高考数学一卷是一份难度较高、知识点覆盖面广、题目类型多样、具有创新性的试卷。
考生需要在平时的学习和训练中，注重提高解题速度和准确度，同时也需要培养面对难题的应对策略。
宁夏中卫市2021届新高考数学一月模拟试卷含解析
宁夏中卫市2021届新高考数学一月模拟试卷一、选择题：本题共12小题，每小题5分，共60分。
在每小题给出的四个选项中，只有一项是符合题目要求的。
1．过抛物线C 的焦点且与C 的对称轴垂直的直线l 与C 交于A ，B 两点，||4AB =，P 为C 的准线上的一点，则ABP ∆的面积为（ ） A ．1 B ．2 C ．4 D ．8【答案】C 【解析】 【分析】设抛物线的解析式22(0)y px p =>，得焦点为,02p F ⎛⎫⎪⎝⎭，对称轴为x 轴，准线为2p x =-，这样可设A点坐标为,22p ⎛⎫⎪⎝⎭，代入抛物线方程可求得p ，而P 到直线AB 的距离为p ，从而可求得三角形面积． 【详解】设抛物线的解析式22(0)y px p =>， 则焦点为,02p F ⎛⎫⎪⎝⎭，对称轴为x 轴，准线为2p x =-，∵ 直线l 经过抛物线的焦点，A ，B 是l 与C 的交点， 又AB x ⊥轴，∴可设A 点坐标为,22p ⎛⎫⎪⎝⎭， 代入22y px =，解得2p =，又∵点P 在准线上，设过点P 的AB 的垂线与AB 交于点D ，||222p pDP p =+-==， ∴11||||24422ABP S DP AB ∆=⋅=⨯⨯=. 故应选C. 【点睛】本题考查抛物线的性质，解题时只要设出抛物线的标准方程，就能得出A 点坐标，从而求得参数p 的值．本题难度一般．2．某三棱锥的三视图如图所示，则该三棱锥的体积为（ ）A ．113B ．4C ．133D ．5【答案】B 【解析】 【分析】还原几何体的直观图，可将此三棱锥1A CD E -放入长方体中, 利用体积分割求解即可. 【详解】如图，三棱锥的直观图为1A CD E -，体积11111111BB E A A CD E E AB A F A C E CC D E AD F D ADC C V V V V V V V ------=-----长方体 12121242222422222423232=⨯⨯-⨯⨯⨯-⨯⨯⨯⨯-⨯⨯⨯⨯=.故选:B.【点睛】本题主要考查了锥体的体积的求解,利用的体积分割的方法,考查了空间想象力及计算能力,属于中档题. 3．已知向量()1,3a =，b 是单位向量，若3a b -=，则,a b =（ ） A ．6π B ．4π C ．3π D ．23π 【答案】C 【解析】 【分析】设(,)b x y =，根据题意求出,x y 的值，代入向量夹角公式，即可得答案；设(,)b x y =，∴(1)a b x y -=-，b 是单位向量，∴221x y +=,3a b -=，∴22(1))3x y -+=，联立方程解得：1,2x y ⎧=-⎪⎪⎨⎪=⎪⎩或1,0,x y =⎧⎨=⎩当1,2x y ⎧=-⎪⎪⎨⎪=⎪⎩时，13122cos ,212a b -+<>==⨯；∴,3a b π<>= 当1,0,x y =⎧⎨=⎩时，11cos ,212a b <>==⨯；∴,3a b π<>= 综上所述：,3a b π<>=.故选：C. 【点睛】本题考查向量的模、夹角计算，考查函数与方程思想、转化与化归思想，考查逻辑推理能力、运算求解能力，求解时注意b 的两种情况.4．若数列{}n a 为等差数列，且满足5383a a a ++＝，n S 为数列{}n a 的前n 项和，则11S ＝（ ） A ．27 B ．33C ．39D ．44【答案】B 【解析】 【分析】利用等差数列性质，若m n p q ++＝，则m n p q a a a a ++＝ 求出63a ＝，再利用等差数列前n 项和公式得111116+)11(11332a a S a =＝＝【详解】解：因为 5383a a a ++＝，由等差数列性质，若m n p q ++＝，则m n p q a a a a ++＝得，63a ∴＝．n S 为数列{}n a 的前n 项和，则111116+)11(11332a a S a =＝＝．故选：B ．本题考查等差数列性质与等差数列前n 项和.(1)如果{}n a 为等差数列，若m n p q ++＝，则m n p q a a a a ++＝ ()*m n p q N ∈，，，． (2)要注意等差数列前n 项和公式的灵活应用，如21(21)n n S n a -=-. 5．下列函数中，值域为R 的偶函数是（ ）A ．21y x =+B ．x x y e e -=-C ．lg y x =D ．y =【答案】C 【解析】试题分析：A 中，函数为偶函数，但1y ≥，不满足条件；B 中，函数为奇函数，不满足条件；C 中，函数为偶函数且y R ∈，满足条件；D 中，函数为偶函数，但0y ≥，不满足条件，故选C ． 考点：1、函数的奇偶性；2、函数的值域．6． “2a =”是“直线210ax y +-=与(1)20x a y +-+=互相平行”的（ ） A ．充分不必要条件 B ．必要不充分条件 C ．充要条件 D ．既不充分也不必要条件【答案】A 【解析】 【分析】利用两条直线互相平行的条件进行判定 【详解】当2a =时，直线方程为2210x y +-=与20x y ++=，可得两直线平行；若直线210ax y +-=与()120x a y +-+=互相平行，则()12a a -=，解得12a =，21a =-，则“2a =”是“直线210ax y +-=与()120x a y +-+=互相平行”的充分不必要条件，故选A【点睛】本题主要考查了两直线平行的条件和性质，充分条件，必要条件的定义和判断方法，属于基础题． 7．若1tan 2α=，则cos2=α( ) A ．45-B ．35C ．45D ．35【答案】D 【解析】 【分析】直接利用二倍角余弦公式与弦化切即可得到结果． 【详解】∵1tan 2α=， ∴22222211cos sin 1tan 34cos21cos sin 1tan 514ααααααα---====+++， 故选D 【点睛】本题考查的知识要点：三角函数关系式的恒等变变换，同角三角函数关系式的应用，主要考查学生的运算能力和转化能力，属于基础题型．8．设双曲线()2222:10,0x y C a b a b-=>>的左右焦点分别为12,F F ，点()()0,0E t t >.已知动点P 在双曲线C 的右支上，且点2,,P E F 不共线.若2PEF ∆的周长的最小值为4b ，则双曲线C 的离心率e 的取值范围是（ ）A．3⎛⎫+∞ ⎪ ⎪⎝⎭B．1,3⎛ ⎝⎦C．)+∞D．(【答案】A 【解析】 【分析】依题意可得22221PEF C PE PF EF PE PF EF ∆=++=++1224PF a b ≥-= 即可得到()242a b a c +>+，从而求出双曲线的离心率的取值范围； 【详解】解：依题意可得如下图象，22221PEF C PE PF EF PE PF EF ∆=++=++112PE PF EF a =++- 1224PF a b ≥-=()12242PF a b a c ∴=+>+所以2b c > 则22244c a c -> 所以2234c a >所以22243c e a =>所以e >，即3e ⎛⎫∈+∞ ⎪ ⎪⎝⎭故选：A【点睛】本题考查双曲线的简单几何性质，属于中档题.9．某几何体的三视图如图所示，则该几何体的体积为（）A．83B．3 C．113D．4【答案】C【解析】【分析】首先把三视图转换为几何体，该几何体为由一个三棱柱体，切去一个三棱锥体，由柱体、椎体的体积公式进一步求出几何体的体积.【详解】解：根据几何体的三视图转换为几何体为：该几何体为由一个三棱柱体，切去一个三棱锥体，如图所示：故：111112*********V =⨯⨯⨯-⨯⨯⨯⨯=. 故选：C. 【点睛】本题考查了由三视图求几何体的体积、需熟记柱体、椎体的体积公式，考查了空间想象能力，属于基础题. 10．已知集合(){}lg 2A x y x ==-，集合1244x B x ⎧⎫=≤≤⎨⎬⎩⎭，则A B =（ ） A ．{}2x x >- B ．{}22x x -<<C ．{}22x x -≤<D ．{}2x x <【答案】C 【解析】 【分析】求出集合的等价条件,利用交集的定义进行求解即可. 【详解】解：∵{}2A x x =<,{}22B x x =-≤≤, ∴{}22A B x x ⋂=-≤<, 故选：C. 【点睛】本题主要考查了对数的定义域与指数不等式的求解以及集合的基本运算,属于基础题.11．已知定义在R 上的函数||()21x m f x -=-（m 为实数）为偶函数，记()0.5log 3a f =，()2log 5b f =，(2)c f m =+则a ，b ，c 的大小关系为( )A ．a b c <<B ．a c b <<C ．c a b <<D ．c b a <<【答案】B 【解析】 【分析】根据f （x ）为偶函数便可求出m ＝0，从而f （x ）＝2x ﹣1，根据此函数的奇偶性与单调性即可作出判断.【详解】解：∵f （x ）为偶函数； ∴f （﹣x ）＝f （x ）； ∴2x m --﹣1＝2x m -﹣1； ∴|﹣x ﹣m|＝|x ﹣m|； （﹣x ﹣m ）2＝（x ﹣m ）2； ∴mx ＝0； ∴m ＝0；∴f （x ）＝2x ﹣1；∴f （x ）在[0，+∞）上单调递增，并且a ＝f （|0.5log 3|）＝f （2log 3）， b ＝f （2log 5），c ＝f （2）； ∵0＜2log 3＜2＜2log 5； ∴a<c<b ． 故选B ． 【点睛】本题考查偶函数的定义，指数函数的单调性，对于偶函数比较函数值大小的方法就是将自变量的值变到区间[0，+∞）上，根据单调性去比较函数值大小．12．如果实数x y 、满足条件10{1010x y y x y -+≥+≥++≤，那么2x y -的最大值为（ ）A ．2B ．1C ．2-D ．3-【答案】B 【解析】 【分析】 【详解】解：当直线2x y z -=过点()0,1A -时，z 最大，故选B二、填空题：本题共4小题，每小题5分，共20分。
2021届宁夏中卫市高考数学教学质量检测试题
2019-2020学年高考数学模拟试卷一、选择题：本题共12小题，每小题5分，共60分。
在每小题给出的四个选项中，只有一项是符合题目要求的。
1．已知抛物线22(0)y px p =>上的点M 到其焦点F 的距离比点M 到y 轴的距离大12，则抛物线的标准方程为（ ） A ．2y x =B ．22y x =C ．24y x =D ．28y x =2．已知函数()32cos f x x x =+，若a f =，(2)b f =，2(log 7)c f =,则a ，b ，c 的大小关系是（ ）A ．a b c <<B ．c b a <<C ．b a c <<D ．b c a <<3．设双曲线221x y a b+=的一条渐近线为2y x =-，且一个焦点与抛物线24x y =的焦点相同，则此双曲线的方程为（ ）A ．225514x y -= B ．225514y x -= C ．225514y x -= D ．225514x y -= 4．若1tan 2α=，则cos2=α( )A ．45- B ．35C ．45D ．355．已知函数()5sin 12f x x π⎛⎫=+ ⎪⎝⎭，要得到函数()cos g x x =的图象，只需将()y f x =的图象( ) A ．向左平移12π个单位长度B ．向右平移12π个单位长度C ．向左平移512π个单位长度 D ．向右平移512π个单位长度 6．已知向量,a b 满足||1,||3a b ==,且a 与b 的夹角为6π,则()(2)a b a b +⋅-=( ) A ．12B ．32-C ．12-D ．327．已知3sin 2cos 1,(,)2παααπ-=∈，则1tan21tan 2αα-=+（ ） A ．12-B ．2-C ．12D ．28．赵爽是我国古代数学家、天文学家，大约在公元222年，赵爽为《周髀算经》一书作序时，介绍了“勾股圆方图”，亦称“赵爽弦图”（以弦为边长得到的正方形是由4个全等的直角三角形再加上中间的一个小正方形组成的）.类比“赵爽弦图”.可类似地构造如下图所示的图形，它是由3个全等的三角形与中间的一个小等边三角形拼成一个大等边三角形.设22DF AF ==，若在大等边三角形中随机取一点，则此点取自小等边三角形（阴影部分）的概率是（ ）A ．413B ．213C ．926D ．3139．当0a >时，函数()()2xf x x ax e =-的图象大致是（ ）A ．B ．C ．D ．10．已知函数2(0x y a a -=>且1a ≠的图象恒过定点P ，则函数1mx y x n+=+图象以点P 为对称中心的充要条件是( ) A ．1,2m n ==- B ．1,2m n =-= C ．1,2m n ==D ．1,2m n =-=-11．我国南北朝时的数学著作《张邱建算经》有一道题为：“今有十等人，每等一人，宫赐金以等次差降之，上三人先入，得金四斤，持出，下三人后入得金三斤，持出，中间四人未到者，亦依次更给，问各得金几何？”则在该问题中，等级较高的二等人所得黄金比等级较低的九等人所得黄金（ ） A ．多1斤B ．少1斤C ．多13斤 D ．少13斤 12．已知抛物线2:2(0)C y px p =>的焦点为F ，过点F 的直线l 与抛物线C 交于A ，B 两点（设点A 位于第一象限），过点A ，B 分别作抛物线C 的准线的垂线，垂足分别为点1A ，1B ，抛物线C 的准线交x 轴于点K ，若11||2||A KB K =，则直线l 的斜率为 A ．1B 2C ．22D 3二、填空题：本题共4小题，每小题5分，共20分。
2021年宁夏中卫市高考数学一模试卷(理科)
2021年宁夏中卫市高考数学一模试卷（理科）一、单选题（本大题共12小题，共60.0分）1.已知全集U=R，集合A={x|x2−4x+3>0}，B={x|−1<x<2}，则(∁U A)∪B=()A. (−1,1]B. [1,2)C. [1,3]D. (−1,3]2.复数z=1+i1−i，则z3=()A. −iB. iC. −1D. 13.下列四个命题：①若a>|b|，则a2>b2②若a>b，c>d，则a−c>b−d③若a>b，c>d，则ac>bd④若a>b>0，c<0，则ca >cb其中正确命题的个数有()A. 1个B. 2个C. 3个D. 4个4.为美化环境，某城市决定用鲜花装饰如图所示花柱，它的下面是一个直径为1m、高为3m的圆柱形物体，上面是一个半球形体，如果每平方米大约需要鲜花150朵，那么装饰一个这样的花柱大约需要鲜花朵数为()(π≈3.1)A. 1230B. 1430C. 1630D. 18305.中心在原点的双曲线C的一条渐近线方程为√3x+y=0，则C的离心率为()A. 2或√3B. √3或3C. 2或2√33D. 2√33或36.已知cos(θ−π4)=15，则sin2θ=()A. 225B. 2325C. −225D. −23257.如图，在3×3的方格中，移动规则如下：每行均可左右移动，每列均可上下移动，每次仅能对某一行或某一列进行移动，其他行或列不变化．例如：若想移动成每行的数字相同，则最少需要移动()次A. 2B. 3C. 4D. 58.将函数f(x)=sin2x−1的图象向右平移π6个单位长度后得到函数g(x)的图象，则函数g(x)的单调递增区间是()A. [−π3+kπ,π3+kπ](k ∈Z) B. [π4+kπ,π2+kπ](k ∈Z) C. [−π4+kπ,π4+kπ](k ∈Z)D. [−π12+kπ,5π12+kπ](k ∈Z)9. 已知抛物线C ：y 2=2px(p >0)的焦点为F ，准线与x 轴交于点K ，过点K 作圆(x −p 2)2+y 2=p 24的切线，切点分别为A ，B.若|AB|=√3，则p 的值为( ) A. 1 B. √3 C. 2D. 310. 已知符号函数sgnx ={1,x >00,x =0−1,x <0，偶函数f(x)满足f(x +2)=f(x)，当x ∈[0,1]时，f(x)=x ，则( )A. sgn(f(x))>0B. f(40412)=1C. sgn(f(2k))=0(k ∈Z)D. sgn(f(k))=|sgnk|(k ∈Z)11. 如图，在正四棱柱ABCD −A 1B 1C 1D 1,AB =√2AA 1，E ，F 分别为AB ，BC的中点，异面直线AB 1与C 1F 所成角的余弦值为m ，则( )A. 直线A 1E 与直线C 1F 异面，且m =√23B. 直线A 1E 与直线C 1F 共面，且m =√23C. 直线A 1E 与直线C 1F 异面，且m =√33D. 直线A 1E 与直线C 1F 共面，且m =√3312. 已知函数f(x)=x 2−alnx −a(a <2)，若对于∀x 1，x 2∈[1,2]，x 1≠x 2，都有|f(x 1)−f(x 2)||x 1−x 2|>a 恒成立，则实数a 的取值范围为( )A. (−∞,12)B. (−∞,12]C. (−∞,1)D. (−∞,1]二、单空题（本大题共4小题，共20.0分）13. 已知向量a ⃗ ，b ⃗ 满足a ⃗ =(2,3)，2a ⃗ −3b ⃗ =(1,9)，则a ⃗ ⋅b ⃗ 的值为______ ．14. 已知实数x ，y 满足不等式组{x −y +2≥0x +y −3≤0y ≥1，则目标函数z =x −2y 的最大值为______ ．15. (x +1x )(2x −ax )5的展开式中各项系数之和为2，则该展开式中x 4的系数为______．16. 在△ABC 中，记角A ，B ，C 所对的边分别是a ，b ，c ，面积为S ，则Sa 2+2bc 的最大值为______． 三、解答题（本大题共7小题，共82.0分）17. 已知数列{a n }的前n 项和是S n ，且S n =2a n −2，等差数列{b n }中，b 1=20，b 3=16．(1)求数列{a n }和{b n }的通项公式；(2)定义：a ∗b ={a,a ≤bb,a >b.记c n =a n ∗b n ，求数列{c n }的前10项的和T 10．18.医学中判断男生的体重是否超标有一种简易方法，就是用一个人身高的厘米数减去105所得差值即为该人的标准体重.比如身高175cm的人，其标准体重为175−105=70公斤，一个人实际体重超过了标准体重，我们就说该人体重超标了.已知某班共有30名男生，从这30名男生中随机选取6名，其身高和体重的数据如表所示：编号123456身高(cm)x165171160173178167体重(kg)y606362707158(2)依据上述表格信息，用最小二乘法求出了体重y对身高x的线性回归方程：ŷ=0.65x+â，但在用回归方程预报其他同学的体重时，预报值与实际值吻合不好，需要对上述数据进行残差分析，按经验，对残差在区间[−3.5,3.5]之外的同学要重新采集数据.问上述随机抽取的编号为3，4，5，6的四人中，有哪几位同学要重新采集数据？参考公式：残差êi =y i−b̂x i−â．19.如图，在平行四边形ABCD中，AB=1，BC=2，∠ACB=π6，四边形ABEF为直角梯形，BE//AF，∠BAF=π2，BE=2，AF=3，平面ABCD⊥平面ABEF．(1)求证：AC⊥平面ABEF；(2)求平面ABCD与平面DEF所成锐二面角的余弦值．20. 经过椭圆C ：x 22+y 2=1左焦点F 1的直线l 与圆F 2：(x −1)2+y 2=r 2(r >2)相交于P ，Q 两点，M 是线段PF 2与C 的公共点，且|MF 1|=|MP|． (1)求r ；(2)l 与C 的交点为A ，B ，且A 恰为线段PQ 的中点，求△ABF 2的面积．21. 已知函数f(x)=x 2−ax +blnx x(a,b ∈R)．(1)若a >b >0，证明f(a)>f(b)；(2)若对任意x ∈(0,+∞)，b ∈(−e,0)，都有f(x)>−e ，求实数a 的取值范围．22. 在直角坐标系xOy 中，直线l 1的方程为y =√3x ，曲线C 的参数方程为{x =1+√3cosφy =√3sinφ(φ是参数，0≤φ≤π).以O 为极点，x 轴的非负半轴为极轴建立极坐标系． (1)分别写出直线l 1与曲线C 的极坐标方程；(2)若直线l 2：2ρsin(θ+π3)+3√3=0，直线l 1与曲线C 的交点为A ，直线l 1与l 2的交点为B ，求|AB|．23. 已知函数f(x)=13|x −a|，(a ∈R)(1)当a =2时，解不等式|x −13|+f(x)≥1；(2)设不等式|x −13|+f(x)≤x 的解集为M ，若[13,12]⊆M ，求实数a 的取值范围．答案和解析1.【答案】D【解析】解：由x2−4x+3>0解得x<1或x>3，则A=(−∞,1)∪(3,+∞)，所以(∁U A)∪B=[1,3]∪(−1，2)=(−1，3]．故选：D．求出集合的等价条件，根据集合的基本运算进行求解即可．本题主要考査一元二次不等式的解法、补集与并集等基础知识；考查运算求解能力．2.【答案】A【解析】解：∵z=1+i1−i =(1+i)2(1−i)(1+i)=i，∴z3=i3=−i，故选：A．直接利用复数代数形式的乘除运算化简，然后利用i2=−1即可求出结果．本题考查了复数代数形式的乘除运算，是基础题．3.【答案】B【解析】解：①∵a>|b|，∴a2>b2，故正确；②∵a>b，c>d，∴a+c>b+d，因此a−c>b−d不正确；③取a=2，b=1，c=−2，d=−3，满足a>b，c>d，但是ac=−4<bd=−3，故不正确；④∵a>b>0，c<0，∴1b >1a>0，−c>0，∴−cb >−ca，∴ca>cb，故正确．综上可知：只有①④正确．故选：B．①由a>|b|，利用不等式的性质可得a2>b2；②由a>b，c>d，利用不等式的性质可得a+c>b+d，即可判断a−c>b−d是否正确；③取a=2，b=1，c=−2，d=−3，满足a>b，c>d，即可判断出；④由a>b>0，c<0，利用不等式的性质可得1b >1a>0，−c>0，于是−cb>−ca，因此ca>cb．本题考查了不等式的基本性质，属于基础题．4.【答案】C【解析】解：一个直径为1m、高为3m的圆柱形物体，上面是一个半球形体，∴这样的花柱的表面积为：S=2π⋅12⋅3+12⋅4π⋅(12)2≈10.85∵每平方米大约需要鲜花150朵，∴装饰一个这样的花柱大约需要鲜花朵数为：∖150×10.85=1627.5≈1630．故选：C．利用圆柱的表面积公式和球的表面积公式先求出这样的花柱的表面积，由此能求出装饰一个这样的花柱大约需要鲜花朵数．本题考查圆柱和球的表面积的求法，考查圆柱和球的表面积等基础知识，考查运算求解能力、应用意识等核心素养，是中档题．5.【答案】C【解析】解：如果焦点坐标在x轴，双曲线C的一条渐近线方程为√3x+y=0，则ba=√3，所以b=√3a，所以c=2a，此时e=2．如果双曲线的焦点坐标在y轴，双曲线C的一条渐近线方程为√3x+y=0，则：ab =√3，所以a=√3b，可得c=2√33a，所以e=2√33．故选：C．讨论双曲线的实轴实轴的轴，结合渐近线方程求解离心率即可．本题考查双曲线的简单性质的应用，判断双曲线的轴实轴的位置是解题的关键，是易错题．6.【答案】D【解析】解：因为cos(θ−π4)=15，所以cos2(θ−π4)=2cos2(θ−π4)−1=2×(15)2−1=−2325，又cos2(θ−π4)=cos(2θ−π2)=cos(π2−2θ)=sin2θ，所以sin2θ=−2325．故选：D．根据二倍角公式，求出cos2(θ−π4)，再根据诱导公式求出sin2θ．本题考查了三角函数求值问题，也考查了运算求解能力，是基础题．7.【答案】B【解析】解：易知最易达到的效果是第一行2，第二行1，第三行3，则需上下移动第三行，左右移动第二行．故变换过程为第三列上移1第二行左移1第三列上移1故选：B．易知最易达到的效果是第一行2，第二行1，第三行3，则需上下移动第三行，左右移动第二行．本题考查排合情推理的应用，注意理解题目中移动的规则，属于基础题．8.【答案】D【解析】解：将函数f(x)=sin2x−1的图象向右平移π6个单位长度后得到函数g(x)=sin2(x−π6)−1的图象，令2kπ−π2≤2x−π3≤2kπ+π2，求得kπ−π12≤x≤kπ+5π12，可得函数g(x)的单调递增区间为[−π12+kπ,5π12+kπ](k∈Z)，故选：D．由题意利用函数y=Asin(ωx+φ)的图象变换规律，正弦函数的单调性性，得出结论．本题主要考查函数y=Asin(ωx+φ)的图象变换规律，正弦函数的单调性，属于基础题．9.【答案】C【解析】解：连接FA，因为F就是圆(x−p2)2+y2=p24的圆心，所以FA⊥KA，且|FA|=p2．又|KF|=p，所以∠AKF=30°，那么∠AKB=60°，所以△AKB是等边三角形，所以|AB|=|AK|=√32p．又|AB|=√3，所以p=2．故选：C．连接FA，通过F是圆(x−p2)2+y2=p24的圆心，结合图形，FA⊥KA，通过求解△AKB是等边三角形，推出结果．考查抛物线的标准方程、焦点、准线以及圆有关的概念，考查数形结合的思维方法和考生对数量关系的分析能力．10.【答案】C【解析】解：依题意，由f(x+2)=f(x)，可知函数f(x)是以2为周期的周期函数．∵当x∈[0,1]时，f(x)=x，f(x)是偶函数，∴当x∈[−1,0]时，f(x)=−x．函数f(x)图象如下：根据图可得，0≤f(x)≤1，故sgn(f(x))≥0，选项A不正确；很明显，当x=2k，k∈Z时，f(x)=0，sgn(f(x))=0，选项C正确；f(40412)=f(2×1010+12)=f(12)=12，故选项B不正确；当k=2时，sgn(f(2))=sgn(0)=0，|sgn2|=1，故选项D不正确故选：C．本题先根据函数的周期性和奇偶性画出函数f(x)的图象，再根据符号函数的性质，以及函数的周期性，利用数形结合法可对四个选项逐个判断，可得正确选项．本题主要考查函数的周期性，奇偶性的应用，以及符号函数的性质应用．考查了数形结合法，转化和化归思想，排除法的应用．本题属中档题．11.【答案】B【解析】解：连结EF，A1C1，C1D，DF，∵E，F分别为AB，BC的中点，∴EF//A1C1，∴直线A1E与直线C1F共面，由题意得AB1//C1D，∴异面直线AB1与C1F所成角为∠DC1F，设AA1=√2，则AB=√2AA1=2，则DF=√5，C1F=√3，C1D=√6，由余弦定理得异面直线AB1与C1F所成角的余弦值：m=cos∠DC1F=2×√3×√6=√23．综上：直线A1E与直线C1F共面，且m=√23．故选：B．连结EF，A1C1，C1D，DF，推导出EF//A1C1，从而直线A1E与直线C1F共面，由题意得AB1//C1D，得异面直线AB1与C1F所成角为∠DC1F，由此能推导出直线A1E与直线C1F共面，且m=√23．本题考查两直线的位置关系的判断，考查异面直线所成角的余弦值的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查运算求解能力，是中档题．12.【答案】D【解析】解：f(x)=x2−alnx−a(a<2)，则f′(x)=2x−ax =2x2−ax>0，∴f(x)在[1,2]上为增函数，不妨设x1>x2，由函数f(x)的单调性可知，f(x1)>f(x2)，则|f(x 1)−f(x 2)||x 1−x 2|>a 等价于f(x 1)−ax 1>f(x 2)−ax 2，设ℎ(x)=f(x)−ax =x 2−alnx −ax −a ， 则函数ℎ(x)在[1,2]上为增函数，即ℎ′(x)=2x −ax −a ≥0在[1,2]上恒成立， 化简得a ≤2x 2x+1，x ∈[1,2]，设t =x +1，则a ≤2(t 2−2t+1)t=2(t +1t−2)，t ∈[2,3]，∵m(t)=2(t +1t −2)在[2,3]上单调递增， ∴m(t)min =m(2)=2×(2+12−2)=1，∴a ≤1． 故选：D ．分析可知，f(x)在[1,2]上为增函数，不妨设x 1>x 2，则f(x 1)−ax 1>f(x 2)−ax 2，构造函数ℎ(x)=f(x)−ax =x 2−alnx −ax −a ，则函数ℎ(x)在[1,2]上为增函数，再利用导数转化求解即可．本题考查利用导数研究函数的单调性，将所给式子适当变形，通过构造新函数利用导数求解是解决本题的关键，属于中档题． 13.【答案】−1【解析】解：因为a ⃗ =(2,3)，2a ⃗ −3b ⃗ =(1,9)，所以3b ⃗ =2(2,3)−(1,9)=(3,−3)， 所以b ⃗ =(1,−1)， 所以a ⃗ ⋅b ⃗ =2×1+3×(−1)=−1．故答案为：−1．由平面向量的线性坐标运算可先求出b ⃗ 的坐标，再根据平面向量数量积的坐标运算即可得解． 本题考查平面向量的线性和数量积的坐标运算，熟练掌握其运算法则是解题的关键，考查学生的运算能力，属于基础题． 14.【答案】0【解析】解：由约束条件作出可行域如图，联立{x +y −3=0y =1，解得A(2,1)，由z =x −2y ，得y =x2−z2，由图可知，当直线y =x2−z2过A 时，直线在y轴上的截距最小，z有最大值为2−1×2=0．故答案为：0．由约束条件作出可行域，化目标函数为直线方程的斜截式，数形结合得到最优解，把最优解的坐标代入目标函数得答案．本题考查简单的线性规划，考查数形结合思想，是中档题．15.【答案】−48【解析】【分析】由题意令x=1，则(1+1)×(2−a)5=2，解得a=1.再利用通项公式即可得出本题考查了二项式定理的应用、方程的解法，考查了推理能力与计算能力．【解答】解：由题意令x=1，则(1+1)×(2−a)5=2，解得a=1．∴(x+1x )(2x−ax)5即(x+1x)(2x−1x)5；(2x−1x )5的通项公式为：T r+1=C5r(2x)5−r(−1x)r=(−1)r25−r C5r x5−2r，分别令5−2r=3，5−2r=5，解得r=1，0．则展开式中x4的系数是：(−1)1×24C51+(−1)025C50=−48．故答案为：−4816.【答案】√312【解析】解：因为Sa2+2bc =12bcsinAb2+c2−2bccosA+2bc=12×sinAbc+cb+2−2cosA≤−14×sinAcosA−2，(当且仅当b=c时取得等号)，令sinA=y，cosA=x，故Sa2+2bc ≤−14×yx−2，因为x2+y2=1，且y>0，故可得点(x,y)表示的平面区域是半圆弧上的点，如下图所示：目标函数z=yx−2，表示圆弧上一点到点A(2,0)点的斜率，数形结合可知，当且仅当目标函数过点H(12,√32)，即A=60°时，取得最小值−√33；故可得z =y x−2∈[−√33,0), 又S a 2+2bc ≤−14×y x−2，故可得S a 2+2bc≤−14×(−√33)=√312，当且仅当A =60°，b =c ，也即三角形为等边三角形时，取得最大值． 故答案为：√312．由已知可得S a 2+2bc ≤−14×sinA cosA−2，令sinA =y ，cosA =x ，可得S a 2+2bc ≤−14×y x−2，数形结合可知z =y x−2∈[−√33,0)，又S a 2+2bc ≤−14×y x−2，可得Sa 2+2bc ≤−14×(−√33)=√312，当且仅当A =60°，b =c ，也即三角形为等边三角形时，取得最大值．本题考查三角形中边角互化、面积以及利用基本不等式求最值时，代数式的变形技巧，本题的难点一是不会建立已知条件与目标式之间的关系；二是式子结构较复杂不会变形，三角函数与基本不等式交汇一直是高考考查的热点，也是难点，属于难题．17.【答案】解：(1)对于数列{a n }，当n =1时，由S n =2a n −2得a 1=2；当n ≥2时，由S n =2a n −2，S n−1=2a n−1−2两式相减整理得a n =2a n−1，所以数列{a n }是首项为2，公比也为2的等比数列，所以数列{a n }的通项公式a n =2n ．设等差数列{b n }的公差为d ，则b 3−b 1=16−20=4=2d ，解得d =−2，所以数列{b n }的通项公式b n =22−2n ．综合以上知：a n =2n ，b n =22−2n ；(2)由(1)知：c n =a n ∗b n ={a n ,n ≤3b n ,n ≥4={2n ,n ≤322−2n,n ≥4， 所以T 10=a 1+a 2+a 3+b 4+b 5+b 6+⋯+b 10=a 1(1−q 3)1−q +7(b 4+b 10)2=2(1−23)1−2+7(14+2)2=24−2+56=70．【解析】(1)对于数列{a n }：当n =1时，由题设条件求出a 1，再由当n ≥2时，由S n =2a n −2，S n−1=2a n−1−2两式相减整理得a n =2a n−1，进而说明数列{a n }是首项为2，公比也为2的等比数列，从而求得a n ；对于数列{b n }：先设出等差数列{b n }的公差d ，再由题设条件求出d ，即可求得b n ．(2)先由(1)求得c n ，再求出T 10即可．本题主要考查等比数列和等差数列的概念、通项公式、前n 项和公式等基础知识，属于基础题． 18.【答案】解：(1)由图表可知，编号1的标准体重为165−105=60，编号2的标准体重为171−105=66，编号3的标准体重为160−105=55，编号4的标准体重为173−105=68，编号5的标准体重为178−105=73，编号6的标准体重为167−105=62．故编号3，4两人体重超标，故从6人中任取两人有C 62=15种取法，恰有一人体重超标共有C 21C 41=8种情况，故p =815；(2)x −=16(165+171+160+173+178+167)=169， y −=16(60+63+62+70+71+58)=64， 回归方程必过样本中心(169,64)，∴64=0.65×169+a ̂，解得a ̂=−45.85，则y ̂=0.65x −45.85，残差分析：ê3=62−0.65×160+45.85=3.85， ê4=70−0.65×173+45.85=3.4， ê5=71−0.65×178+45.85=1.15， ê6=58−0.65×167+45.85=−4.7． 故3号和6号需要重新采集数据．【解析】(1)求出6人中体重超标的人数，再由古典概型概率计算公式求解即可；(2)先根据回归方程必过样本中心求出a ̂=−45.85，再依次把预报值求出来，从而求出残差，进而判断出哪些同学要重新采集数据．本题考查的知识点为线性回归直线方程，相关系数和残差，考查的核心素养为逻辑推理，数学运算和数据分析，属于中档题．19.【答案】解：(1)证明：在△ABC 中，因为AB =1，BC =2，∠ACB =π6，由余弦定理可得AB 2=BC 2+AC 2−2BC ⋅AC ⋅cos∠ACB ，即1=4+AC 2−2×2⋅AC ⋅√32，解得AC =√3，所以AC 2+AB 2=BC 2，即AC ⊥AB ，又因为平面ABCD ⊥平面ABEF ，且平面ABCE ∩平面ABEF =AB ，AC ⊂平面ABCD ，所以AC ⊥平面ABEF ；(2)由平面ABCD ⊥平面ABEF ，平面ABCE ∩平面ABEF =AB ，∠BAF =π2，AF ⊂平面ABEF ，所以AF ⊥平面ABCD ，由(1)可知AF ⊥平面ABCD ，故建立空间直角坐标系如图所示，则A(0,0,0),B(1,0,0),C(0,0,√3),D(−1,0,√3),E(1,2,0),F(0,3,0)，所以DE ⃗⃗⃗⃗⃗⃗ =(2,2,−√3),DF ⃗⃗⃗⃗⃗ =(1,3,−√3)，设平面DEF 的一个法向量为n ⃗ =(x,y,z)，则有{n ⃗ ⋅DE ⃗⃗⃗⃗⃗⃗ =2x +2y −√3z =0n⃗ ⋅DF ⃗⃗⃗⃗⃗ =x +3y −√3z =0， 取z =4，则x =y =√3可得n ⃗ =(√3,√3,4)，又AF⃗⃗⃗⃗⃗ =(0,3,0)是平面ABCD 的一个法向量， 所以|cos <n ⃗ ,AF ⃗⃗⃗⃗⃗ >|=|n ⃗⃗ ⋅AF ⃗⃗⃗⃗⃗ ||n ⃗⃗ ||AF ⃗⃗⃗⃗⃗ |=3√3√3+3+16×3=√6622，所以平面ABCD 与平面DEF 所成锐二面角的余弦值为√6622． 【解析】(1)在△ABC 中，利用余弦定理求出AC ，然后由勾股定理可得AC ⊥AB ，结合面面垂直的性质定理证明即可；(2)利用面面垂直的性质定理证得AF ⊥平面ABCD ，又AF ⊥平面ABCD ，建立合适的空间直角坐标系，求出所需点的坐标和向量，利用待定系数法求出平面的法向量，然后利用向量的夹角公式求解即可．本题考查了立体几何的综合应用，涉及了面面垂直的性质定理，余弦定理，在求解空间角的时候，一般会建立合适的空间直角坐标系，将空间角问题转化为空间向量问题进行研究，属于中档题．20.【答案】解：(1)由C ：x22+y 2=1得长轴长2a =2√2，半焦距c =1，因为点M 在C 上，所以|MF 1|+|MF 2|=2a =2√2，因为|MF 1|=|MP|，所以r =|PF 2|=|MP|+|MF 2|=|MF 1|+|MF 2|=2√2；(2)设A(x 1,y 1)，B(x 2,y 2)，A 为线段PQ 的中点，则AF 1⊥AF 2，由F 1(−1,0)，F 2(1,0)，AF 1⃗⃗⃗⃗⃗⃗⃗ =(−1−x 1,−y 1)，AF 2⃗⃗⃗⃗⃗⃗⃗ =(1−x 1,=y 1)，所以AF 1⃗⃗⃗⃗⃗⃗⃗ ⋅AF 2⃗⃗⃗⃗⃗⃗⃗ =x 12+y 12−1=0，又x 122+y 12=1， 解得x 1=0，y 1=1或−1，若y 1=1，则A(0,1)，直线l 的方程为y =x +1，联立y =x +1和椭圆方程x 2+2y 2=2，可得B(−43,−13)，所以△ABF 2的面积S =12|F 1F 2|⋅|y 1−y 2|=12×2×43=43．若y 1=−1，同理可求得△ABF 2的面积S =43．综上，△ABF 2的面积为43．【解析】(1)求得椭圆的2a ，c ，运用椭圆的定义，结合圆的定义，可得圆的半径r ；(2)设A(x 1,y 1)，B(x 2,y 2)，运用圆的性质，结合向量垂直的条件，结合椭圆方程，求得A 的坐标，可得直线l 的方程，联立椭圆方程，可得B 的坐标，再由三角形的面积公式，计算可得所求值．本题考查椭圆和圆的方程和性质，考查直线和椭圆、直线和圆的位置关系，考查方程思想和运算能力，属于中档题．21.【答案】证明：(1)要证f(a)>f(b)，需证blna a >b 2−ab +lnb ， 即证lna a >b −a +lnbb， 即证a +lna a >b +lnbb ， 设g(x)=x +lnxx ，需证g(x)在(0,+∞)上单调递增， g′(x)=1+1−lnx x 2=x 2+1−lnxx 2，设ℎ(x)=x 2+1−lnx ，则ℎ′(x)=2x −1x=2x 2−1x ，令ℎ′(x)=0，得x =√22， 当x ∈(0,√22)时，ℎ′(x)<0，ℎ(x)单调递减；当x ∈(√22,+∞)时，ℎ′(x)>0，ℎ(x)单调递增． ∴ℎ(x)min =ℎ(√22)=3+ln22>0，即g′(x)>0在(0,+∞)上恒成立，∴g(x)在(0,+∞)上单调递增，故原问题得证；解：(2)由f(x)+e =x 2−ax +blnx x +e >0，得ax <x 2+blnx x +e ， ∵x >0，∴a <x +blnx x 2+e x ． 设F(x)=x +blnx x 2+e x ， 则F′(x)=1+b(1−2lnx)x 3−e x 2=x 2−e x 2+b(1−2lnx)x 3，∵b <0，∴当x ∈(0,√e)时，F′(x)<0，F(x)单调递减；当x ∈(√e,+∞)时，F′(x)>0，F(x)单调递增．∴F(x)min =F(√e)=2√e +b 2e ， ∴a <2√e +b 2e， 又a <2√e +b 2e 对任意b ∈(−e,0)都成立，∴a ≤2√e −12，即实数a 的取值范围是(−∞,2√e −12].【解析】(1)将有问题转化为函数的单调性问题，然后利用导数解决；(2)分离参数后构造函数，求得新函数的单调性及最值，进一步求解即可得答案．本题主要考查不等式恒成立问题，考查利用导数求最值，考查综合运用所学知识分析问题与解决问题的能力，属难题．22.【答案】解：(1)直线l 1的方程为y =√3x ，可得：tanθ=y x =√3，∴直线l 1的极坐标方程为ρ=π3．曲线C 的普通方程为(x −1)2+y 2=3，又∵x =ρcosθ，y =ρsinθ，所以曲线C 的极坐标方程为ρ2−2ρcosθ−2=0(0≤θ≤π)，(2)由题意，设A(ρ1,θ1)，则有{ρ2−2ρcosθ−2=0θ=π3，解得：ρ1=2,θ1=π3， 设B(ρ2,θ2)，则有{2ρsin(θ+π3)+3√3=0θ=π3，解得：ρ2=−3,θ2=π3故得|AB|=|ρ1−ρ2|=5．【解析】本题主要考查了参数方程，极坐标方程的转换，以及利用极坐标的几何意义求解长度问题．属于基础题．(1)根据tanθ=y x 可得直线l 1极坐标．利用x =ρcosθ，y =ρsinθ带入可得曲线C 的极坐标方程．(2)由题意，设A(ρ1,θ1)，联立方程组求解，同理，设利用直线的极坐标的几何意义求解即可． 23.【答案】解：(1)a =2时，f(x)=13|x −2|，问题转化为解不等式|x −13|+13|x −2|≥1，①x ≥2时，x −13+13(x −2)≥1， x −13+13x −23≥1， 解得：x ≥32，故x ≥2；②13<x <2时，x −13+13(2−x)≥1，解得：x ≥1，故1≤x <2；③x ≤13时，13−x +13(2−x)≥1，解得：x ≤0，综上，不等式的解集是：{x|x ≤0或x ≥1}；(2)|x −13|+13|x −a|≤x 的解集包含[13,12]， ∴x −13+13|x −a|≤x ，|x −a|≤1， 故−1≤x −a ≤1，解得：−1+a ≤x ≤1+a ，故{−1+a ≤131+a ≥12，解得：−12≤a ≤43．【解析】本题考查了解绝对值不等式问题，考查分类讨论思想，是一道中档题．(1)通过讨论x 的范围，去掉绝对值，解各个区间上的x 的范围，取并集即可；(2)问题转化为x −13+13|x −a|≤x ，求出x 的范围，得到关于a 的不等式组，解出即可．。
宁夏中卫市2021届新高考数学模拟试题(3)含解析
宁夏中卫市2021届新高考数学模拟试题（3）一、选择题：本题共12小题，每小题5分，共60分。
在每小题给出的四个选项中，只有一项是符合题目要求的。
1．等比数列{}n a 的各项均为正数，且384718a a a a +=，则3132310log log log a a a +++=( )A ．12B ．10C ．8D ．32log 5+【答案】B 【解析】 【分析】由等比数列的性质求得110a a ，再由对数运算法则可得结论． 【详解】∵数列{}n a 是等比数列，∴3847110218a a a a a a +==，1109a a =， ∴53132310312103110log log log log ()log ()a a a a a a a a +++==35log 910==．故选：B. 【点睛】本题考查等比数列的性质，考查对数的运算法则，掌握等比数列的性质是解题关键． 2．设F 为抛物线24x y =的焦点，A ，B ，C 为抛物线上三点，若0FA FB FC ++=，则|||||FA FB FC ++=（ ）.A ．9B ．6C ．38D ．316【答案】C 【解析】 【分析】设11(,)A x y ，22(,)B x y ，33(,)C x y ，由0FA FB FC ++=可得123316x x x ++=，利用定义将|||||FA FB FC ++用123,,x x x 表示即可.【详解】设11(,)A x y ，22(,)B x y ，33(,)C x y ，由0FA FB FC ++=及1(,0)16F ， 得111(,)16x y -+221(,)16x y -331(,)(0,0)16x y +-=，故123316x x x ++=， 所以123111|||||161616FA FB FC x x x ++=+++++=38. 故选：C. 【点睛】本题考查利用抛物线定义求焦半径的问题，考查学生等价转化的能力，是一道容易题.3．已知函数()2x f x x x ln a ⎛⎫=- ⎪⎝⎭，关于x 的方程f （x ）＝a 存在四个不同实数根，则实数a 的取值范围是（ ）A ．（0，1）∪（1，e ）B ．10e ⎛⎫ ⎪⎝⎭，C ．11e ⎛⎫ ⎪⎝⎭，D ．（0，1）【答案】D 【解析】 【分析】原问题转化为221x x a a =有四个不同的实根，换元处理令t =，对g （t）21lnt t t ⎫=--⎪⎭进行零点个数讨论. 【详解】由题意，a ＞2，令t =， 则f （x ）＝a ⇔2x x x ln a a ⎛⎫-= ⎪⎝⎭⇔221x x a a -=⇔221t -=⇔210lnt t t ⎫-=⎪⎭． 记g （t）21lnt t t ⎫=-⎪⎭．当t ＜2时，g （t ）＝2ln （﹣t）t 1t-）单调递减，且g （﹣2）＝2， 又g （2）＝2，∴只需g （t ）＝2在（2，+∞）上有两个不等于2的不等根．则210lnt t t ⎫--=⎪⎭221tlnt t =-， 记h （t ）221tlntt =-（t ＞2且t≠2）， 则h′（t ）()()()22222222212122141(1)(1)t t lnt lnt t t lnt t t t ⎛⎫-+- ⎪+--+⎝⎭==--．令φ（t ）2211t lnt t -=-+，则φ′（t ）()()2222222221211(1)(1)(1)t t t t t t t t t +---=-=-++＜2．∵φ（2）＝2，∴φ（t ）2211t lnt t -=-+在（2，2）大于2，在（2，+∞）上小于2．∴h′（t ）在（2，2）上大于2，在（2，+∞）上小于2， 则h （t ）在（2，2）上单调递增，在（2，+∞）上单调递减． 由211222112t t tlnt lnt limlim t →→+==-，可得1a ＜，即a ＜2．∴实数a 的取值范围是（2，2）． 故选：D ． 【点睛】此题考查方程的根与函数零点问题，关键在于等价转化，将问题转化为通过导函数讨论函数单调性解决问题.4．某几何体的三视图如图所示（单位：cm ），则该几何体的表面积是( )A ．28cmB ．212cmC ．()2452cmD ．()2454cm【答案】D 【解析】 【分析】根据三视图判断出几何体为正四棱锥，由此计算出几何体的表面积. 【详解】根据三视图可知，该几何体为正四棱锥.底面积为224⨯=.22215+1425452⨯⨯=所以该几何体的表面积是()2454cm .故选：D 【点睛】本小题主要考查由三视图判断原图，考查锥体表面积的计算，属于基础题. 5．已知平面向量()4,2a →=，(),3b x →=，//a b →→，则实数x 的值等于（ ）A ．6B ．1C ．32D ．32-【答案】A 【解析】 【分析】根据向量平行的坐标表示即可求解. 【详解】()4,2a →=，(),3b x →=，//a b →→，432x ∴⨯=，即6x =， 故选：A 【点睛】本题主要考查了向量平行的坐标运算，属于容易题.6．设1k >，则关于,x y 的方程()22211k x y k -+=-所表示的曲线是（ ）A ．长轴在y 轴上的椭圆B ．长轴在x 轴上的椭圆C ．实轴在y 轴上的双曲线D ．实轴在x 轴上的双曲线【答案】C 【解析】 【分析】根据条件，方程()22211k x y k -+=-．即222111y x k k -=-+，结合双曲线的标准方程的特征判断曲线的类型． 【详解】解：∵k ＞1，∴1+k>0，k 2-1＞0，方程()22211k x y k -+=-，即222111y x k k -=-+，表示实轴在y 轴上的双曲线，故选C ． 【点睛】本题考查双曲线的标准方程的特征，依据条件把已知的曲线方程化为222111y x k k -=-+是关键．7．已知命题p ：1m =“”是“直线0x my -=和直线0x my +=互相垂直”的充要条件；命题q ：对任意()2,∈=+a R f x x a 都有零点；则下列命题为真命题的是（ ）A ．()()p q ⌝∧⌝B ．()p q ∧⌝C ．p q ∨D ．p q ∧【答案】A 【解析】 【分析】先分别判断每一个命题的真假，再利用复合命题的真假判断确定答案即可. 【详解】当1m =时，直线0x my -=和直线0x my +=，即直线为0x y -=和直线0x y +=互相垂直， 所以“1m =”是直线0x my -=和直线0x my +=互相垂直“的充分条件， 当直线0x my -=和直线0x my +=互相垂直时，21m =，解得1m =±. 所以“1m =”是直线0x my -=和直线0x my +=互相垂直“的不必要条件.p ：“1m =”是直线0x my -=和直线0x my +=互相垂直“的充分不必要条件，故p 是假命题．当1a =时，2()1f x x =+没有零点，所以命题q 是假命题．所以()()p q ⌝∧⌝是真命题，()p q ∧⌝是假命题，p q ∨是假命题，p q ∧是假命题． 故选：A ． 【点睛】本题主要考查充要条件的判断和两直线的位置关系，考查二次函数的图象， 考查学生对这些知识的理解掌握水平.8．已知等边△ABC 内接于圆τ：x 2+ y 2=1，且P 是圆τ上一点，则()PA PB PC ⋅+的最大值是（ ）A B ．1C D ．2【答案】D 【解析】 【分析】如图所示建立直角坐标系，设()cos ,sin P θθ，则(1)cos PA PB PC θ⋅+=-，计算得到答案. 【详解】如图所示建立直角坐标系，则1,0A ，12⎛- ⎝⎭B ，1,2C ⎛- ⎝⎭，设()cos ,sin P θθ，则(1cos ,sin )(12cos ,2si (n ))PA PB PC θθθθ=--⋅--⋅+-222(1cos )(12cos )2sin 2cos cos 12sin 1cos 2θθθθθθθ=---+=--+=-≤.当θπ=-，即()1,0P -时等号成立. 故选：D .【点睛】本题考查了向量的计算，建立直角坐标系利用坐标计算是解题的关键. 9．已知三棱锥A BCD -的所有顶点都在球O 的球面上，AD ⊥平面,120ABC BAC ︒∠=，2AD =，若球O 的表面积为20π，则三棱锥A BCD -的体积的最大值为（ ） A ．33B ．23C ．3D ．23【答案】B 【解析】 【分析】由题意画出图形，设球0得半径为R ，AB=x, AC=y,由球0的表面积为20π，可得R 2=5，再求出三角形A BC 外接圆的半径,利用余弦定理及基本不等式求xy 的最大值，代入棱锥体积公式得答案. 【详解】设球O 的半径为R ，AB x =，AC y =， 由2420R ππ=，得25R =． 如图：设三角形ABC 的外心为G ，连接OG ，GA ，OA ， 可得112OG AD ==，则212AG R =-=． 在ABC ∆中，由正弦定理可得：24sin120BCAG ==︒，即23BC =，由余弦定理可得，222221122()32BC x y xy x y xy xy ==+-⨯-=++，4xy ∴．则三棱锥A BCD -的体积的最大值为11234sin120232⨯⨯⨯︒⨯=．故选：B ． 【点睛】本题考查三棱锥的外接球、三棱锥的侧面积、体积，基本不等式等基础知识，考查空间想象能力、逻辑思维能力、运算求解能力，考查数学转化思想方法与数形结合的解题思想方法，是中档题．10．一小商贩准备用50元钱在一批发市场购买甲、乙两种小商品，甲每件进价4元，乙每件进价7元，甲商品每卖出去1件可赚1元，乙商品每卖出去1件可赚1.8元.该商贩若想获取最大收益，则购买甲、乙两种商品的件数应分别为（ ） A ．甲7件，乙3件 B ．甲9件，乙2件C ．甲4件，乙5件D ．甲2件，乙6件【答案】D 【解析】 【分析】由题意列出约束条件和目标函数，数形结合即可解决. 【详解】设购买甲、乙两种商品的件数应分别x ，y 利润为z 元，由题意*4750,,,x y x y N +≤⎧⎨∈⎩ 1.8z x y =+， 画出可行域如图所示，显然当5599y x z =-+经过(2,6)A 时，z 最大.故选：D. 【点睛】本题考查线性目标函数的线性规划问题，解决此类问题要注意判断x ，y 是否是整数，是否是非负数，并准确的画出可行域，本题是一道基础题.11．已知命题300:2,80p x x ∃>->，那么p ⌝为（ ）A ．3002,80x x ∃>-≤ B ．32,80x x ∀>-≤ C ．3002,80x x ∃≤-≤ D ．32,80x x ∀≤-≤【答案】B 【解析】 【分析】利用特称命题的否定分析解答得解. 【详解】已知命题0:2p x ∃>，380x ->，那么p ⌝是32,80x x ∀>-≤. 故选：B ． 【点睛】本题主要考查特称命题的否定，意在考查学生对该知识的理解掌握水平，属于基础题.12．一个正方体被一个平面截去一部分后,剩余部分的三视图如下图,则截去部分体积与剩余部分体积的比值为（ ）A ．18B ．17C ．16D ．15【答案】D 【解析】 【分析】 【详解】试题分析：如图所示，截去部分是正方体的一个角,其体积是正方体体积的16,剩余部分体积是正方体体积的56,所以截去部分体积与剩余部分体积的比值为,故选D.考点：本题主要考查三视图及几何体体积的计算.二、填空题：本题共4小题，每小题5分，共20分。
宁夏中卫市2021届新高考数学三月模拟试卷含解析
宁夏中卫市2021届新高考数学三月模拟试卷一、选择题：本题共12小题，每小题5分，共60分。
在每小题给出的四个选项中，只有一项是符合题目要求的。
1．若函数32()3f x ax x b =++在1x =处取得极值2，则a b -=（ ） A ．-3 B ．3C ．-2D ．2【答案】A 【解析】 【分析】对函数()f x 求导,可得(1)0(1)2f f =⎧⎨='⎩,即可求出,a b ,进而可求出答案.【详解】因为32()3f x ax x b =++,所以2()36f x ax x '=+,则(1)360(1)32f a f a b '=+=⎧⎨=++=⎩,解得2,1a b =-=,则3a b -=-.故选:A. 【点睛】本题考查了函数的导数与极值,考查了学生的运算求解能力,属于基础题.2．已知函数3sin ()(1)()x x x xf x x m x e e-+=+-++为奇函数，则m =（ ） A ．12B ．1C ．2D ．3【答案】B 【解析】 【分析】根据()f x 整体的奇偶性和部分的奇偶性，判断出m 的值. 【详解】依题意()f x 是奇函数.而3sin y x x =+为奇函数，x xy e e -=+为偶函数，所以()()()1gx x m x =+-为偶函数，故()()0gx g x --=，也即()()()()110x m x x m x +---+=，化简得()220m x -=，所以1m =.故选：B 【点睛】本小题主要考查根据函数的奇偶性求参数值，属于基础题.3．已知角α的终边与单位圆221x y +=交于点01,3P y ⎛⎫ ⎪⎝⎭，则cos2α等于（ ） A ．19B ．79-C ．23-D ．13【答案】B 【解析】 【分析】先由三角函数的定义求出sin α，再由二倍角公式可求cos2α. 【详解】解：角α的终边与单位圆221x y +=交于点01,3P y ⎛⎫ ⎪⎝⎭1cos 3α=，2217cos 22cos 12139αα⎛⎫=-=⨯-=- ⎪⎝⎭，故选：B 【点睛】考查三角函数的定义和二倍角公式，是基础题.4．已知函数()()sin f x A x =+ωϕ（π0,0,2A >><ωϕ）的部分图象如图所示，且()()0f a x f a x ++-=，则a 的最小值为（ ）A ．π12B ．π6 C ．π3D ．5π12【答案】A 【解析】 【分析】a 是函数()f x 的零点，根据五点法求出图中零点及y 轴左边第一个零点可得．【详解】由题意3114126T ππ=-，T π=，∴函数()f x 在y 轴右边的第一个零点为56412πππ+=，在y 轴左边第一个零点是6412πππ-=-，∴a 的最小值是12π．故选：A. 【点睛】本题考查三角函数的周期性，考查函数的对称性．函数()sin()f x A x ωϕ=+的零点就是其图象对称中心的横坐标． 5．函数sin ln ||2y x x π⎛⎫=-⋅ ⎪⎝⎭图像可能是（ ） A ． B ．C ．D ．【答案】D 【解析】 【分析】先判断函数的奇偶性可排除选项A,C ，当0x +→时，可分析函数值为正，即可判断选项. 【详解】sin ln ||cos ln ||2y x x x x π⎛⎫=-⋅=- ⎪⎝⎭,cos()ln ||cos ln ||x x x x ∴---=-,即函数为偶函数， 故排除选项A,C ，当正数x 越来越小，趋近于0时，cos 0,ln ||0x x -<<， 所以函数sin ln ||02y x x π⎛⎫=-⋅> ⎪⎝⎭，故排除选项B,【点睛】本题主要考查了函数的奇偶性，识别函数的图象，属于中档题. 6．复数2(1)i i +的模为（ ）．A ．12B ．1C ．2D ．【答案】D 【解析】 【分析】利用复数代数形式的乘除运算化简，再由复数模的计算公式求解． 【详解】解：2(1)22i i i +=-+，∴复数2(1)i i +=故选：D ． 【点睛】本题主要考查复数代数形式的乘除运算，考查复数模的求法，属于基础题．7．给出下列四个命题：①若“p 且q ”为假命题，则p ﹑q 均为假命题；②三角形的内角是第一象限角或第二象限角；③若命题0:p x R ∃∈，200x ≥，则命题:p x R ⌝∀∈，20x <；④设集合{}1A x x =>，{}2B x x =>，则“x A ∈”是“x B ∈”的必要条件；其中正确命题的个数是（ ）A ．1B ．2C ．3D ．4【答案】B 【解析】 【分析】 ①利用p ∧q 真假表来判断，②考虑内角为90，③利用特称命题的否定是全称命题判断，④利用集合间的包含关系判断. 【详解】若“p 且q ”为假命题，则p ﹑q 中至少有一个是假命题，故①错误；当内角为90时，不是象限角，故②错误；由特称命题的否定是全称命题知③正确；因为B A ⊆，所以x B ∈⇒x A ∈，所以“x A ∈”是“x B ∈”的必要条件， 故④正确. 故选：B.本题考查命题真假的问题，涉及到“且”命题、特称命题的否定、象限角、必要条件等知识，是一道基础题. 8．运行如图所示的程序框图，若输出的值为300，则判断框中可以填（ ）A ．30i >?B ．40i >?C ．50i >?D ．60i >?【答案】B 【解析】 【分析】由30020010203040=++++，则输出为300，即可得出判断框的答案 【详解】由30020010203040=++++，则输出的值为300，401050i =+=，故判断框中应填40i >？ 故选：B ． 【点睛】本题考查了程序框图的应用问题，解题时应模拟程序框图的运行过程，以便得出正确的结论，是基础题．9．已知椭圆22221x y a b +=（a ＞b ＞0）与双曲线222212x y a b -=（a ＞0，b ＞0）的焦点相同，则双曲线渐近线方程为（ ） A ．3y x = B ．3y x =C ．2y x =D ．2y x =【答案】A 【解析】 【分析】由题意可得222222a b a b -=+，即223a b ，代入双曲线的渐近线方程可得答案.【详解】依题意椭圆22221(a b 0)x y a b +=>>与双曲线22221(a 0,b 0)2x y a b -=>>即22221(a 0,b 022)x y a b -=>>的焦点相同，可得：22221122a b a b -=+， 即223a b，∴3b a =3=,双曲线的渐近线方程为：3x y x =±=, 故选：A ． 【点睛】本题考查椭圆和双曲线的方程和性质，考查渐近线方程的求法，考查方程思想和运算能力，属于基础题． 10．已知α、,22ππβ⎛⎫∈- ⎪⎝⎭，αβ≠，则下列是等式sin sin 2αβαβ-=-成立的必要不充分条件的是（ ） A ．sin sin αβ> B ．sin sin αβ< C ．cos cos αβ> D ．cos cos αβ<【答案】D 【解析】 【分析】构造函数()sin h x x x =-，()sin 2f x x x =-，利用导数分析出这两个函数在区间,22ππ⎛⎫- ⎪⎝⎭上均为减函数，由sin sin 2αβαβ-=-得出sin sin 2ααββ-=-，分0α=、02πα-<<、02πα<<三种情况讨论，利用放缩法结合函数()y h x =的单调性推导出02παβ-<<<或02πβα<<<，再利用余弦函数的单调性可得出结论. 【详解】构造函数()sin h x x x =-，()sin 2f x x x =-， 则()cos 10h x x '=-<，()cos 20f x x '=-<，所以，函数()y f x =、()y h x =在区间,22ππ⎛⎫- ⎪⎝⎭上均为减函数，当02x π-<<时，则()()00h x h >=，()()00f x f >=；当02x π<<时，()0h x <，()0f x <.由sin sin 2αβαβ-=-得sin sin 2ααββ-=-. ①若0α=，则sin 20ββ-=，即()00f ββ=⇒=，不合乎题意；②若02πα-<<，则02πβ-<<，则()()sin sin 2sin h h αααβββββ=-=->-=，此时，02παβ-<<<，由于函数cos y x =在区间,02π⎛⎫- ⎪⎝⎭上单调递增，函数sin y x =在区间,02π⎛⎫- ⎪⎝⎭上单调递增，则sin sin αβ<，cos cos αβ<；③若02πα<<，则02πβ<<，则()()sin sin 2sin h h αααβββββ=-=-<-=，此时02πβα<<<，由于函数cos y x =在区间0,2π⎛⎫ ⎪⎝⎭上单调递减，函数sin y x =在区间0,2π⎛⎫ ⎪⎝⎭上单调递增，则sin sin αβ>，cos cos αβ<.综上所述，cos cos αβ<. 故选：D. 【点睛】本题考查函数单调性的应用，构造新函数是解本题的关键，解题时要注意对α的取值范围进行分类讨论，考查推理能力，属于中等题.11．若双曲线E ：221x y m n-=(0)mn >绕其对称中心旋转3π后可得某一函数的图象，则E 的离心率等于（ ）A ．3BC ．2或3D ．2【答案】C 【解析】 【分析】由双曲线的几何性质与函数的概念可知，此双曲线的两条渐近线的夹角为60，所以b a =，由离心率公式e =即可算出结果.【详解】由双曲线的几何性质与函数的概念可知，此双曲线的两条渐近线的夹角为60，又双曲线的焦点既可在x轴，又可在y 轴上，所以b a =3，2e ∴==或3. 故选：C 【点睛】本题主要考查了双曲线的简单几何性质，函数的概念，考查了分类讨论的数学思想. 12．某个命题与自然数n 有关，且已证得“假设()*n k k N =∈时该命题成立，则1n k =+时该命题也成立”．现已知当7n =时，该命题不成立，那么（ ） A ．当8n =时，该命题不成立 B ．当8n =时，该命题成立 C ．当6n =时，该命题不成立 D ．当6n =时，该命题成立【答案】C 【解析】 【分析】写出命题“假设()*n k k N=∈时该命题成立，则1n k =+时该命题也成立”的逆否命题，结合原命题与逆否命题的真假性一致进行判断. 【详解】由逆否命题可知，命题“假设()*n k k N =∈时该命题成立，则1n k =+时该命题也成立”的逆否命题为“假设当()1n k k N*=+∈时该命题不成立，则当n k =时该命题也不成立”，由于当7n =时，该命题不成立，则当6n =时，该命题也不成立，故选：C. 【点睛】本题考查逆否命题与原命题等价性的应用，解题时要写出原命题的逆否命题，结合逆否命题的等价性进行判断，考查逻辑推理能力，属于中等题.二、填空题：本题共4小题，每小题5分，共20分。
2021年宁夏中卫市高考数学一模试卷(理科)
2021年宁夏中卫市高考数学一模试卷（理科）一、选择题（本大题共12个小题，每小题5分，共60分，每小题给出的选项中，只有一项是符合题目要求的，请将正确的答案涂到答题卡上）1. 已知全集U＝R，集合A＝{x|x2−4x+3>0}，B＝{x|−1<x<2}，则(∁U A)∪B ＝（）A.(−1, 1]B.[1, 2)C.[1, 3]D.(−1, 3]【答案】D【考点】交、并、补集的混合运算【解析】求出集合的等价条件，根据集合的基本运算进行求解即可．【解答】由x2−4x+3>0解得x<1或x>3，则A＝(−∞, 1)∪(3, +∞)，所以(∁U A)∪B＝[1, 3]∪(−1, 2)＝(−1, 3]．2. 复数z＝，则z3＝（）A.−iB.iC.−1D.1【答案】A【考点】复数的运算【解析】直接利用复数代数形式的乘除运算化简，然后利用i2＝−1即可求出结果．【解答】∵z＝＝＝i，∴z3＝i3＝−i，3. 下列四个命题：①若a>|b|，则a2>b2②若a>b，c>d，则a−c>b−d③若a>b，c>d，则ac>bd④若a>b>0，c<0，则ca >cb其中正确命题的个数有（）A.1个B.2个C.3个D.4个【答案】B【考点】不等式的概念与应用【解析】①由a>|b|，利用不等式的性质可得a2>b2；②由a>b，c>d，利用不等式的性质可得a+c>b+d，即可判断a−c>b−d是否正确；③取a=2，b=1，c=−2，d=−3，满足a>b，c>d，即可判断出；④由a>b>0，c<0，利用不等式的性质可得1b >1a>0，−c>0，于是−cb>−ca，因此ca >cb．【解答】解：①∵a>|b|，∴a2>b2，故正确；②∵a>b，c>d，∴a+c>b+d，因此a−c>b−d不正确；③取a=2，b=1，c=−2，d=−3，满足a>b，c>d，但是ac=−4<bd=−3，故不正确；④∵a>b>0，c<0，∴1b >1a>0，−c>0，∴−cb >−ca，∴ca>cb，故正确．综上可知：只有①④正确．故选：B．4. 为美化环境，某城市决定用鲜花装饰如图所示花柱，它的下面是一个直径为1m、高为3m的圆柱形物体，上面是一个半球形体，如果每平方米大约需要鲜花150朵，那么装饰一个这样的花柱大约需要鲜花朵数为()(π≈3.1)A.1230B.1430C.1630D.1830【答案】C【考点】等可能事件的概率等可能事件【解析】利用圆柱的表面积公式和球的表面积公式先求出这样的花柱的表面积，由此能求出装饰一个这样的花柱大约需要鲜花朵数．【解答】一个直径为1m、高为3m的圆柱形物体，上面是一个半球形体，∴这样的花柱的表面积为：S＝≈10.85∵每平方米大约需要鲜花150朵，∴装饰一个这样的花柱大约需要鲜花朵数为：\150×10.85＝1627.5≈1630．5. 中心在原点的双曲线C的一条渐近线方程为x+y＝0，则C的离心率为（）A.2或B.或3C.2或D.或3【答案】C【考点】双曲线的离心率【解析】讨论双曲线的实轴实轴的轴，结合渐近线方程求解离心率即可．【解答】如果焦点坐标在x轴，双曲线C的一条渐近线方程为x+y＝0，则＝，所以b＝，所以c＝2a，此时e＝2．如果双曲线的焦点坐标在y轴，双曲线C的一条渐近线方程为x+y＝0，则：，所以a＝b，可得c＝a，所以e＝．6. 已知cos(θ−）＝，则sin2θ＝（）A. B. C.- D.-【答案】D【考点】二倍角的三角函数【解析】根据二倍角公式，求出cos2(θ−），再根据诱导公式求出sin2θ．【解答】因为cos(θ−）＝，所以cos2(θ−）＝2cos2(θ−）−1＝2×−1＝-，又cos2(θ−）＝cos(2θ−）＝cos（−2θ)＝sin2θ，所以sin2θ＝-．7. 如图，在3×3的方格中，移动规则如下：每行均可左右移动，每列均可上下移动，每次仅能对某一行或某一列进行移动，其他行或列不变化．例如：若想移动成每行的数字相同，则最少需要移动（）次A.2B.3C.4D.5【答案】B【考点】进行简单的合情推理【解析】易知最易达到的效果是第一行2，第二行1，第三行3，则需上下移动第三行，左右移动第二行．【解答】易知最易达到的效果是第一行2，第二行1，第三行3，则需上下移动第三行，左右移动第二行．故变换过程为第三列上移1第二行左移1第三列上移18. 将函数f(x)＝sin2x−1的图象向右平移个单位长度后得到函数g(x)的图象，则函数g(x)的单调递增区间是（）A.[-+kπ，+kπ](k∈Z)B.[+kπ，+kπ](k∈Z)C.[-+kπ，+kπ](k∈Z)D.[-+kπ，+kπ](k∈Z)【答案】D【考点】函数y=Asin（ωx+φ）的图象变换【解析】由题意利用函数y＝A sin(ωx+φ)的图象变换规律，正弦函数的单调性性，得出结论．【解答】将函数f(x)＝sin2x−1的图象向右平移个单位长度后得到函数g(x)＝sin2(x−）−1的图象，令2kπ−≤2x−≤2kπ+，求得kπ−≤x≤kπ+，可得函数g(x)的单调递增区间为[-+kπ，+kπ](k∈Z)，9. 已知抛物线C:y2＝2px(p>0)的焦点为F，准线与x轴交于点K，过点K作圆(x−p 2)2+y2=p24的切线，切点分别为A，B．若|AB|=√3，则p的值为（）A.1B.√3C.2D.3【答案】C【考点】圆与圆锥曲线的综合问题【解析】连接FA ，通过F 是圆(x −p2)2+y 2=p 24的圆心，结合图形，FA ⊥KA ，通过求解△AKB是等边三角形，推出结果． 【解答】连接FA ，因为F 就是圆(x −p2)2+y 2=p 24的圆心，所以FA ⊥KA ，且|FA|=p2．又|KF|＝p ，所以∠AKF ＝30∘，那么∠AKB ＝60∘， 所以△AKB 是等边三角形，所以|AB|=|AK|=√32p ． 又|AB|=√3，所以p ＝（2）10. 已知符号函数sgnx ={1,x >00,x =0−1,x <0 ，偶函数f(x)满足f(x +2)＝f(x)，当x ∈[0, 1]时，f(x)＝x ，则（ ） A.sgn （f(x)）>0 B.f(40412)=1C.sgn （f(2k)）＝0(k ∈Z)D.sgn （f(k)）＝|sgnk|(k ∈Z)【答案】 C【考点】 函数的周期性 【解析】本题先根据函数的周期性和奇偶性画出函数f(x)的图象，再根据符号函数的性质，以及函数的周期性，利用数形结合法可对四个选项逐个判断，可得正确选项． 【解答】很明显，当x ＝2k ，k ∈Z 时，f(x)＝0，sgn （f(x)）＝0，选项C 正确（1）f(40412)＝f(2×1010+12)＝f(12)=12，故选项B 不正确（2）当k ＝2时，sgn （f(2)）＝sgn(0)＝0，|sgn2|＝1，故选项D 不正确 故选：C ．11. 如图，在正四棱柱ABCD −A 1B 1C 1D 1，E ，F 分别为AB ，BC 的中点，异面直线AB 1与C 1F 所成角的余弦值为m ，则（ ）A.直线A1E与直线C1F异面，且B.直线A1E与直线C1F共面，且C.直线A1E与直线C1F异面，且D.直线A1E与直线C1F共面，且【答案】B【考点】异面直线及其所成的角【解析】连结EF，A1C1，C1D，DF，推导出EF // A1C1，从而直线A1E与直线C1F共面，由题意得AB1 // C1D，得异面直线AB1与C1F所成角为∠DC1F，由此能推导出直线A1E与直线C1F共面，且．【解答】连结EF，A1C1，C1D，DF，∵E，F分别为AB，BC的中点，∴EF // A1C1，∴直线A1E与直线C1F共面，由题意得AB1 // C1D，∴异面直线AB1与C1F所成角为∠DC1F，设AA1＝，则AB＝＝2，则DF＝，C1F＝，，由余弦定理得异面直线AB1与C1F所成角的余弦值：m＝cos∠DC1F＝＝．综上：直线A1E与直线C1F共面，且．12. 已知函数f(x)＝x2−a ln x−a(a<2)，若对于∀x1，x2∈[1, 2]，x1≠x2，都有>a恒成立，则实数a的取值范围为（）A.(−∞，）B.(−∞，]C.(−∞, 1)D.(−∞, 1]【答案】D【考点】利用导数研究函数的最值【解析】分析可知，f(x)在[1, 2]上为增函数，不妨设x1>x2，则f(x1)−ax1>f(x2)−ax2，构造函数ℎ(x)＝f(x)−ax＝x2−a ln x−ax−a，则函数ℎ(x)在[1, 2]上为增函数，再利用导数转化求解即可．【解答】f(x)＝x2−a ln x−a(a<2)，则f′(x)＝2x−＝>0，∴f(x)在[1, 2]上为增函数，不妨设x1>x2，由函数f(x)的单调性可知，f(x1)>f(x2)，则>a等价于f(x1)−ax1>f(x2)−ax2，设ℎ(x)＝f(x)−ax＝x2−a ln x−ax−a，则函数ℎ(x)在[1, 2]上为增函数，即ℎ′(x)＝2x−−a≥0在[1, 2]上恒成立，化简得a≤，x∈[1, 2]，设t＝x+1，则a≤＝2(t+−2)，t∈[2, 3]，∵m(t)＝2(t+−2)在[2, 3]上单调递增，∴m(t)min＝m(2)＝2×(2+−2)＝1，∴a≤1．二、填空题：（本大题共4小题，每小题5分，共20分.）已知向量，满足＝(2, 3)，2−3＝(1, 9)，则的值为________．【答案】−1【考点】平面向量数量积的性质及其运算【解析】由平面向量的线性坐标运算可先求出的坐标，再根据平面向量数量积的坐标运算即可得解．【解答】因为＝(2, 3)，2−3＝(1, 9)，所以3＝2(2, 3)−(1, 9)＝(3, −3)，所以＝(1, −1)，所以＝2×1+3×(−1)＝−1．已知实数x，y满足不等式组，则目标函数z＝x−2y的最大值为________．【答案】【考点】简单线性规划【解析】由约束条件作出可行域，化目标函数为直线方程的斜截式，数形结合得到最优解，把最优解的坐标代入目标函数得答案．【解答】由约束条件作出可行域如图，联立，解得A(2, 1)，由z＝x−2y，得y＝，由图可知，当直线y＝过A时，直线在y轴上的截距最小，z有最大值为2−1×2＝0．(x+1x )(2x−ax)5的展开式中各项系数之和为2，则该展开式中x4的系数为________．【答案】−48【考点】二项式定理及相关概念【解析】由题意令x＝1，则(1+1)×(2−a)5＝2，解得a＝1．再利用通项公式即可得出【解答】由题意令x＝1，则(1+1)×(2−a)5＝2，解得a＝1．∴(x+1x )(2x−ax)5即(x+1x)(2x−1x)5；(2x−1x )5的通项公式为：T r+1=∁5r(2x)5−r(−1x)r＝(−1)r 25−r∁5r x5−2r，分别令5−2r＝3，5−2r＝5，解得r＝1，0．则展开式中x4的系数是：(−1)1×24∁51+(−1)025∁50=−48．在△ABC中，记角A，B，C所对的边分别是a，b，c，面积为S，则的最大值为________．【答案】【考点】余弦定理【解析】由已知可得，令sin A＝y，cos A＝x，可得，数形结合可知，又，可得，当且仅当A＝30∘，b＝c，取得最大值．【解答】因为＝，（当且仅当b ＝c 时取得等号），令sin A ＝y ，cos A ＝x ，故，因为x 2+y 2＝1，且y >0，故可得点(x, y)表示的平面区域是半圆弧上的点，如下图所示：目标函数，表示圆弧上一点到点A(2, 0)点的斜率，数形结合可知，当且仅当目标函数过点，即A ＝30∘时，取得最小值；故可得，又，故可得，当且仅当A ＝30∘，b ＝c ，取得最大值．三、解答题（本大题共5小题，满分60分．解答须写出文字说明，证明过程或演算步骤.）已知数列{a n }的前n 项和是S n ，且S n ＝2a n −2，等差数列{b n }中，b 1＝20，b 3＝16． （1）求数列{a n }和{b n }的通项公式；（2）定义：a ∗b ={a,a ≤bb,a >b ．记c n ＝a n ∗b n ，求数列{c n }的前10项的和T 10．对于数列{a n }，当n ＝1时，由S n ＝2a n −2得a 1＝2；当n ≥2时，由S n ＝2a n −2，S n−1＝2a n−1−2两式相减整理得a n ＝2a n−1， 所以数列{a n }是首项为2，公比也为2的等比数列， 所以数列{a n }的通项公式a n =2n ．设等差数列{b n }的公差为d ，则b 3−b 1＝16−20＝4＝2d ，解得d ＝−2， 所以数列{b n }的通项公式b n ＝22−2n ． 综合以上知：a n ＝2n ，b n ＝22−2n ；由（1）知：c n ＝a n ∗b n ={a n ,n ≤3b n ,n ≥4 ={2n ,n ≤322−2n,n ≥4 ，所以T 10＝a 1+a 2+a 3+b 4+b 5+b 6+...+b 10=a 1(1−q 3)1−q+7(b 4+b 10)2=2(1−23)1−2+7(14+2)2=24−2+56=70．【考点】等比数列的通项公式 数列的求和【解析】（1）对于数列{a n }：当n ＝1时，由题设条件求出a 1，再由当n ≥2时，由S n ＝2a n −2，S n−1＝2a n−1−2两式相减整理得a n ＝2a n−1，进而说明数列{a n }是首项为2，公比也为2的等比数列，从而求得a n ；对于数列{b n }：先设出等差数列{b n }的公差d ，再由题设条件求出d ，即可求得b n ．（2）先由（1）求得c n ，再求出T 10即可． 【解答】对于数列{a n }，当n ＝1时，由S n ＝2a n −2得a 1＝2；当n ≥2时，由S n ＝2a n −2，S n−1＝2a n−1−2两式相减整理得a n ＝2a n−1， 所以数列{a n }是首项为2，公比也为2的等比数列， 所以数列{a n }的通项公式a n =2n ．设等差数列{b n }的公差为d ，则b 3−b 1＝16−20＝4＝2d ，解得d ＝−2， 所以数列{b n }的通项公式b n ＝22−2n ． 综合以上知：a n ＝2n ，b n ＝22−2n ；由（1）知：c n ＝a n ∗b n ={a n ,n ≤3b n ,n ≥4 ={2n ,n ≤322−2n,n ≥4 ，所以T 10＝a 1+a 2+a 3+b 4+b 5+b 6+...+b 10=a 1(1−q 3)1−q+7(b 4+b 10)2=2(1−23)1−2+7(14+2)2=24−2+56=70．医学中判断男生的体重是否超标有一种简易方法，就是用一个人身高的厘米数减去105所得差值即为该人的标准体重．比如身高175cm 的人，其标准体重为175−105＝70公斤，一个人实际体重超过了标准体重，我们就说该人体重超标了．已知某班共有30名男生，从这30名男生中随机选取6名，其身高和体重的数据如表所示：（1）从这6人中任选2人，求恰有1人体重超标的概率；（2）依据上述表格信息，用最小二乘法求出了体重y对身高x的线性回归方程：＝0.65x+，但在用回归方程预报其他同学的体重时，预报值与实际值吻合不好，需要对上述数据进行残差分析，按经验，对残差在区间[−3.5, 3.5]之外的同学要重新采集数据．问上述随机抽取的编号为3，4，5，6的四人中，有哪几位同学要重新采集数据？参考公式：残差＝y i−x i−．【答案】由图表可知，编号1的标准体重为165−105＝60，编号2的标准体重为171−105＝66，编号3的标准体重为160−105＝55，编号4的标准体重为173−105＝68，编号5的标准体重为178−105＝73，编号6的标准体重为167−105＝62．故编号3，4两人体重超标，故从6人中任取两人有种取法，恰有一人体重超标共有种情况，故p＝；＝(165+171+160+173+178+167)＝169，＝(60+63+62+70+71+58)＝64，回归方程必过样本中心(169, 64)，∴64＝0.65×169+，解得＝−45.85，则＝0.65x−45.85，残差分析：＝62−0.65×160+45.85＝3.85，＝58−0.65×167+45.85＝−4.7．故3号和6号需要重新采集数据．【考点】求解线性回归方程【解析】（1）求出6人中体重超标的人数，再由古典概型概率计算公式求解即可；（2）先根据回归方程必过样本中心求出＝−45.85，再依次把预报值求出来，从而求出残差，进而判断出哪些同学要重新采集数据．【解答】由图表可知，编号1的标准体重为165−105＝60，编号2的标准体重为171−105＝66，编号3的标准体重为160−105＝55，编号4的标准体重为173−105＝68，编号5的标准体重为178−105＝73，编号6的标准体重为167−105＝62．故编号3，4两人体重超标，故从6人中任取两人有种取法，恰有一人体重超标共有种情况，故p＝；＝(165+171+160+173+178+167)＝169，＝(60+63+62+70+71+58)＝64，回归方程必过样本中心(169, 64)，∴64＝0.65×169+，解得＝−45.85，则＝0.65x−45.85，残差分析：＝62−0.65×160+45.85＝3.85，＝70−0.65×173+45.85＝3.4，故3号和6号需要重新采集数据．如图，在平行四边形ABCD中，AB＝1，BC＝2，∠ACB＝，四边形ABEF为直角梯形，BE // AF，∠BAF＝，BE＝2，AF＝3，平面ABCD⊥平面ABEF．（1）求证：AC⊥平面ABEF；（2）求平面ABCD与平面DEF所成锐二面角的余弦值．【答案】证明：在△ABC中，因为AB＝1，BC＝2，∠ACB＝，由余弦定理可得AB2＝BC2+AC2−2BC⋅AC⋅cos∠ACB，即，解得，所以AC2+AB2＝BC2，即AC⊥AB，又因为平面ABCD⊥平面ABEF，且平面ABCE∩平面ABEF＝AB，AC⊂平面ABCD，所以AC⊥平面ABEF；由平面ABCD⊥平面ABEF，平面ABCE∩平面ABEF＝AB，∠BAF＝，AF⊂平面ABEF，所以AF⊥平面ABCD，由（1）可知AF⊥平面ABCD，故建立空间直角坐标系如图所示，则，所以，，取z＝4，则可得，又是平面ABCD的一个法向量，所以，所以平面ABCD与平面DEF所成锐二面角的余弦值为．【考点】直线与平面垂直二面角的平面角及求法【解析】（1）在△ABC中，利用余弦定理求出AC，然后由勾股定理可得AC⊥AB，结合面面垂直的性质定理证明即可；（2）利用面面垂直的性质定理证得AF⊥平面ABCD，又AF⊥平面ABCD，建立合适的空间直角坐标系，求出所需点的坐标和向量，利用待定系数法求出平面的法向量，然后利用向量的夹角公式求解即可．【解答】证明：在△ABC中，因为AB＝1，BC＝2，∠ACB＝，由余弦定理可得AB2＝BC2+AC2−2BC⋅AC⋅cos∠ACB，即，解得，所以AC2+AB2＝BC2，即AC⊥AB，又因为平面ABCD⊥平面ABEF，且平面ABCE∩平面ABEF＝AB，AC⊂平面ABCD，所以AC⊥平面ABEF；由平面ABCD⊥平面ABEF，平面ABCE∩平面ABEF＝AB，故建立空间直角坐标系如图所示，则，所以，设平面DEF的一个法向量为，则有，取z＝4，则可得，又是平面ABCD的一个法向量，所以，所以平面ABCD与平面DEF所成锐二面角的余弦值为．经过椭圆左焦点F1的直线l与圆相交于P，Q两点，M是线段PF2与C的公共点，且|MF1|＝|MP|．（1）求r；（2）l与C的交点为A，B，且A恰为线段PQ的中点，求△ABF2的面积．【答案】1；设A(x1, y1)，B(x2, y2)，A为线段PQ的中点，则AF1⊥AF2，由F1(−1, 0)，F2(1, 0)，＝(−1−x1, −y1)，＝(1−x1,＝y1)，所以，又，解得x1＝0，y1＝1或−1，若y1＝1，则A(0, 1)，直线l的方程为y＝x+1，联立y＝x+1和椭圆方程x2+2y2＝2，可得，所以△ABF2的面积．若y1＝−1，同理可求得△ABF2的面积．综上，△ABF2的面积为．【考点】圆与圆锥曲线的综合问题【解析】（1）求得椭圆的2a，c，运用椭圆的定义，结合圆的定义，可得圆的半径r；（2）设A(x1, y1)，B(x2, y2)，运用圆的性质，结合向量垂直的条件，结合椭圆方程，求得A的坐标，可得直线l的方程，联立椭圆方程，可得B的坐标，再由三角形的面积公式，计算可得所求值．【解答】1；设A(x1, y1)，B(x2, y2)，A为线段PQ的中点，则AF1⊥AF2，由F1(−1, 0)，F2(1, 0)，＝(−1−x1, −y1)，＝(1−x1,＝y1)，所以，又，解得x1＝0，y1＝1或−1，若y1＝1，则A(0, 1)，直线l的方程为y＝x+1，联立y＝x+1和椭圆方程x2+2y2＝2，可得，所以△ABF2的面积．若y1＝−1，同理可求得△ABF2的面积．综上，△ABF2的面积为．已知函数f(x)＝x2−ax+(a, b∈R)．（1）若a>b>0，证明f(a)>f(b)；（2）若对任意x∈(0, +∞)，b∈(−e, 0)，都有f(x)>−e，求实数a的取值范围．【答案】需证>b2−ab+ln b，即证，即证a+>，设g(x)＝x+，需证g(x)在(0, +∞)上单调递增，g′(x)＝1+，设ℎ(x)＝x2+1−ln x，则ℎ′(x)＝2x−，令ℎ′(x)＝0，得x＝，当x∈(0，）时，ℎ′(x)<0，ℎ(x)单调递减；当x∈（，+∞)时，ℎ′(x)>0，ℎ(x)单调递增．∴>0，即g′(x)>0在(0, +∞)上恒成立，∴g(x)在(0, +∞)上单调递增，故原问题得证；由f(x)+e＝>0，得ax<，∵x>0，∴a<x+．设F(x)＝x+，则F′(x)＝1+，∵b<0，∴当x∈(0，）时，F′(x)<0，F(x)单调递减；当x∈（）时，F′(x)>0，F(x)单调递增．∴，∴a<，又a<对任意b∈(−e, 0)都成立，∴a≤，即实数a的取值范围是(−∞，]．【考点】利用导数研究函数的最值【解析】（1）将有问题转化为函数的单调性问题，然后利用导数解决；（2）分离参数后构造函数，求得新函数的单调性及最值，进一步求解即可得答案．【解答】要证f(a)>f(b)，需证>b2−ab+ln b，即证，即证a+>，设g(x)＝x+，需证g(x)在(0, +∞)上单调递增，g′(x)＝1+，设ℎ(x)＝x2+1−ln x，则ℎ′(x)＝2x−，令ℎ′(x)＝0，得x＝，当x∈(0，）时，ℎ′(x)<0，ℎ(x)单调递减；当x∈（，+∞)时，ℎ′(x)>0，ℎ(x)单调递增．∴>0，即g′(x)>0在(0, +∞)上恒成立，∴g(x)在(0, +∞)上单调递增，故原问题得证；由f(x)+e＝>0，得ax<，∵x>0，∴a<x+．设F(x)＝x+，则F′(x)＝1+，∵b<0，∴当x∈(0，）时，F′(x)<0，F(x)单调递减；当x∈（）时，F′(x)>0，F(x)单调递增．∴，∴a<，又a<对任意b∈(−e, 0)都成立，∴a≤，即实数a的取值范围是(−∞，]．选考题：（请考生在第22、23两道题中任选一题作答．如果多做，则按所做的第一题记分。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
宁夏中卫市2021届新高考数学一模试卷一、选择题：本题共12小题，每小题5分，共60分。
在每小题给出的四个选项中，只有一项是符合题目要求的。
1．执行下面的程序框图，若输出的S 的值为63，则判断框中可以填入的关于i 的判断条件是（ ）A ．5i ≤B ．6i ≤C ．7i ≤D ．8i ≤【答案】B 【解析】 【分析】根据程序框图，逐步执行，直到S 的值为63，结束循环，即可得出判断条件. 【详解】 执行框图如下： 初始值：0,1S i ==，第一步：011,112S i =+==+=，此时不能输出，继续循环； 第二步：123,213S i =+==+=，此时不能输出，继续循环； 第三步：347,314S i =+==+=，此时不能输出，继续循环； 第四步：7815,415S i =+==+=，此时不能输出，继续循环； 第五步：151631,516S i =+==+=，此时不能输出，继续循环； 第六步：313263,617S i =+==+=，此时要输出，结束循环； 故，判断条件为6i ≤. 故选B 【点睛】本题主要考查完善程序框图，只需逐步执行框图，结合输出结果，即可确定判断条件，属于常考题型.2．地球上的风能取之不尽，用之不竭.风能是淸洁能源，也是可再生能源.世界各国致力于发展风力发电，近10年来，全球风力发电累计装机容量连年攀升，中国更是发展迅猛，2014年累计装机容量就突破了100GW，达到114.6GW，中国的风力发电技术也日臻成熟，在全球范围的能源升级换代行动中体现出大国的担当与决心.以下是近10年全球风力发电累计装机容量与中国新增装机容量图. 根据所给信息，正确的统计结论是（）A．截止到2015年中国累计装机容量达到峰值B．10年来全球新增装机容量连年攀升C．10年来中国新增装机容量平均超过20GWD．截止到2015年中国累计装机容量在全球累计装机容量中占比超过1 3【答案】D【解析】【分析】先列表分析近10年全球风力发电新增装机容量，再结合数据研究单调性、平均值以及占比，即可作出选择.【详解】年份2009 2010 2011 2012 2013 2014 2015 2016 2017 2018 累计装机容量158.1 197.2 237.8 282.9 318.7 370.5 434.3 489.2 542.7 594.1 新增装机容量39.1 40.6 45.1 35.8 51.8 63.8 54.9 53.5 51.4 中国累计装机装机容量逐年递增，A错误；全球新增装机容量在2015年之后呈现下降趋势，B错误；经计算，10年来中国新增装机容量平均每年为19.77GW，选项C错误；截止到2015年中国累计装机容量197.7GW，全球累计装机容量594.1158.1436GW-=，占比为45.34%，选项D正确.故选：D【点睛】本题考查条形图，考查基本分析求解能力，属基础题.3．下图为一个正四面体的侧面展开图，G为BF的中点，则在原正四面体中，直线EG与直线BC所成角的余弦值为（）A ．3 B ．6 C ．3 D ．33 【答案】C 【解析】 【分析】将正四面体的展开图还原为空间几何体，,,A D F 三点重合，记作D ，取DC 中点H ，连接,,EG EH GH ，EGH ∠即为EG 与直线BC 所成的角，表示出三角形EGH 的三条边长，用余弦定理即可求得cos EGH ∠.【详解】将展开的正四面体折叠，可得原正四面体如下图所示，其中,,A D F 三点重合，记作D ：则G 为BD 中点，取DC 中点H ，连接,,EG EH GH ，设正四面体的棱长均为a ， 由中位线定理可得//GH BC 且1122GH BC a ==， 所以EGH ∠即为EG 与直线BC 所成的角，221322EG EH a a a⎛⎫==-= ⎪⎝⎭， 由余弦定理可得222cos 2EG GH EH EGH EG GH+-∠=⋅222313a a a+-==，所以直线EG与直线BC，故选：C.【点睛】本题考查了空间几何体中异面直线的夹角，将展开图折叠成空间几何体，余弦定理解三角形的应用，属于中档题.4．函数()sin()(0)4f x A xπωω=+>的图象与x轴交点的横坐标构成一个公差为3π的等差数列，要得到函数()cosg x A xω=的图象，只需将()f x的图象（）A．向左平移12π个单位B．向右平移4π个单位C．向左平移4π个单位D．向右平移34π个单位【答案】A【解析】依题意有()f x的周期为()22ππ,3,sin334T f x A xπωω⎛⎫====+⎪⎝⎭.而()πππππsin3sin3sin3244124g x A x A x A x⎡⎤⎛⎫⎛⎫⎛⎫=+=++=++⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦，故应左移π12.5．将函数()sin6f x xπ⎛⎫=+⎪⎝⎭图象上每一点的横坐标变为原来的2倍，再将图像向左平移3π个单位长度，得到函数()y g x=的图象，则函数()y g x=图象的一个对称中心为（）A．,012π⎛⎫⎪⎝⎭B．,04π⎛⎫⎪⎝⎭C．(),0πD．4,03π⎛⎫⎪⎝⎭【答案】D【解析】【分析】根据函数图象的变换规律可得到()y g x=解析式，然后将四个选项代入逐一判断即可.【详解】解：()sin 6f x x π⎛⎫=+⎪⎝⎭图象上每一点的横坐标变为原来的2倍,得到1sin 26x π⎛⎫+⎪⎝⎭再将图像向左平移3π个单位长度，得到函数()1sin +236g x x ππ⎡⎤⎛⎫=+ ⎪⎢⎥⎝⎭⎣⎦的图象 ()1sin 23g x x π⎛⎫=+ ⎪⎝⎭，403g π⎛⎫=⎪⎝⎭故选：D 【点睛】考查三角函数图象的变换规律以及其有关性质，基础题.6．已知集合{}1,2,3,4,5,6U =，{}13,5A =,，{}2,3,4B =，则集合()UB A =( )A ．{}1,2,6B ．{}1,3,6C ．{}1,6D ．{}6【答案】D 【解析】 【分析】根据集合的混合运算，即可容易求得结果. 【详解】{}1,2,3,4,5A B ⋃=，故可得()UB A ={}6.故选：D. 【点睛】本题考查集合的混合运算，属基础题.7．已知等比数列{}n a 的前n 项和为n S ，若11a =，且公比为2，则n S 与n a 的关系正确的是（ ） A ．41n n S a =- B ．21n n S a =+ C ．21n n S a =- D ．43n n S a =-【答案】C 【解析】 【分析】在等比数列中，由11n n a a S qq-⋅=-即可表示之间的关系.【详解】由题可知，等比数列{}n a 中11a =，且公比为2，故11221112n nn n a a q a a q S -⋅-===---故选：C 【点睛】本题考查等比数列求和公式的应用，属于基础题.8．过圆224x y +=外一点(4,1)M -引圆的两条切线，则经过两切点的直线方程是（ ）． A ．440x y --= B ．440x y +-= C ．440x y ++= D ．440x y -+=【答案】A 【解析】过圆222x y r +=外一点(,)m n ，引圆的两条切线，则经过两切点的直线方程为20mx ny r +-=，故选A ．9．已知双曲线2222:1(0,0)x y C a b a b-=>>的左，右焦点分别为1F 、2F ，过1F 的直线l 交双曲线的右支于点P ，以双曲线的实轴为直径的圆与直线l 相切，切点为H ，若113F P F H =，则双曲线C 的离心率为（ ）A B ．C ．D 【答案】A 【解析】 【分析】在12PF F ∆中，由余弦定理，得到2||PF ，再利用12||||2PF PF a -=即可建立,,a b c 的方程. 【详解】由已知，1||HF b ===，在12PF F ∆中，由余弦定理，得2||PF ===1133PF HF b ==，12||||2PF PF a -=，所以32b a =，32b a ⇒=2e =∴=， 故选：A. 【点睛】本题考查双曲线离心率的计算问题，处理双曲线离心率问题的关键是建立,,a b c 三者间的关系，本题是一道中档题.10．设集合{}2560A x x x =--<，{}20B x x =-<，则AB =( )A ．{}32x x -<< B ．{}22x x -<< C ．{}62x x -<< D ．{}12x x -<<【答案】D 【解析】 【分析】利用一元二次不等式的解法和集合的交运算求解即可. 【详解】由题意知,集合}{16A x x =-<<,}{2B x x =<, 由集合的交运算可得,}{12A B x x ⋂=-<<. 故选:D 【点睛】本题考查一元二次不等式的解法和集合的交运算;考查运算求解能力;属于基础题. 11．已知函数21()(1)()2x f x ax x e a R =--∈若对区间[]01，内的任意实数123x x x 、、，都有123()()()f x f x f x +≥，则实数a 的取值范围是( ）A ．[]12， B ．[]e,4C ．[]14， D ．[)[]12,4e ⋃， 【答案】C 【解析】分析：先求导,再对a 分类讨论求函数的单调区间，再画图分析转化对区间[]01，内的任意实数123x x x 、、，都有()()()123f x f x f x +≥，得到关于a 的不等式组，再解不等式组得到实数a 的取值范围. 详解：由题得()[(1)]()xxxxf x ax e x e ax xe x a e =-+-=-=-'.当a ＜1时，()0f x '<，所以函数f （x ）在[]01，单调递减， 因为对区间[]01，内的任意实数123x x x 、、，都有()()()123f x f x f x +≥， 所以(1)(1)(0)f f f +≥， 所以111,22a a +≥ 故a≥1，与a ＜1矛盾，故a ＜1矛盾.当1≤a<e 时，函数f(x)在[0,lna]单调递增，在(lna,1]单调递减. 所以2max 1()(ln )ln ln ,2f x f a a a a a a ==-+ 因为对区间[]01，内的任意实数123x x x 、、，都有()()()123f x f x f x +≥，所以(0)(1)(ln )f f f a +≥，所以2111ln ln ,22a a a a a a +≥-+ 即211ln ln 1022a a a a a -+-≤令211()ln ln 1,(1)22g a a a a a a a e =-+-≤<，所以21()(ln 1)0,2g a a =-<'所以函数g(a)在（1，e ）上单调递减， 所以max 1()(1)02g a g ==-<， 所以当1≤a<e 时，满足题意.当a e ≥时，函数f(x)在(0,1)单调递增,因为对区间[]01，内的任意实数123x x x 、、，都有()()()123f x f x f x +≥， 所以(0)(0)(1)f f f +≥, 故1+112a ≥， 所以 4.a ≤ 故 4.e a ≤≤综上所述，a ∈[]14，. 故选C.点睛：本题的难点在于“对区间[]01，内的任意实数123x x x 、、，都有()()()123f x f x f x +≥”的转化.由于是函数的问题，所以我们要联想到利用函数的性质（单调性、奇偶性、周期性、对称性、最值、极值等）来分析解答问题.本题就是把这个条件和函数的单调性和最值联系起来，完成了数学问题的等价转化，找到了问题的突破口.12．数列{}n a 满足()*212n n n a a a n +++=∈N ，且1239a a a ++=，48a =，则5a =（ ）A ．212B ．9C ．172D ．7【答案】A 【解析】 【分析】先由题意可得数列{}n a 为等差数列，再根据1239a a a ++=，48a =，可求出公差，即可求出5a ． 【详解】数列{}n a 满足*212()n n n a a a n N +++=∈，则数列{}n a 为等差数列，1239a a a ++=，48a =， 1339a d ∴+=，138a d +=，52d ∴=， 54521822a a d ∴=+=+=， 故选：A ． 【点睛】本题主要考查了等差数列的性质和通项公式的求法，意在考查学生对这些知识的理解掌握水平，属于基础题．二、填空题：本题共4小题，每小题5分，共20分。