卡平方测验
第七章 卡平方测验

多个样本方差是否来自同一总体方差的统计测验
若总共有k个样本,第i个样本的样本方差si2来自总体方 差i2。想了解这k个总体方差之间是否有显著差异。
第二节 2在方差同质性测验中的应用
如果是大样本,计算出的2值可利用正态分布转为u 一个样本方差与已知总体方差的统计测验 值,直接与u比较,做出推断。即: 1.针对研究的问题提出一对统计假设。 u H : 2 = 2vvs 1 H : 2 ≠ 2 22 2 两尾测验时 0 0 A 0 (大端)一尾测验时 H0: 2 ≤ 02 vs HA: 2 > 02 (小端)一尾测验时 H0: 2 ≥ 02 vs HA: 2 < 02 2.利用试验数据计算一个统计量的值。 ( n 1) s 2 用df=n-1查2分布表。 2 计算统计量: 02 3.根据“小概率事件实际上不可能发生”原理作判断。
第二节 2在方差同质性测验中的应用
2 i 多个样本方差是否来自同一总体方差的统计测验 若总共有k个样本,第i个样本的样本方差si2来自总体方 5.077671 96.47574 1 160.4 19 3047.6 差i2。想了解这k个总体方差之间是否有显著差异。 4.782479 90.8671 2 119.4 19 2268.6 1.针对研究的问题提出一对统计假设。 2 vs 84.5662 3H0:85.72 =19 22 1628.3= 4.450853 A: 并非都相等 1 = … H k 用df=k-1查2分布表。 2.利用试验数据计算一个统计量的值。 4.837075 91.90443 4 126.1 19 2395.9 k 1 k 2 2 2 19.14808 ) 计算统计量: 9340.4 dfi ) ln s p (dfi ln si363.8135 76 (
第5章-卡平方测验

花色 F2代实际株数(O) 理论株数(E)
白色
192
187.5
黄皮
58
62.5
总数
250
250
O-E 4.5 -4.5
1.提出假设:观察次数与理论次数的差异由抽样误 差所引起,即H0:F2代南瓜果皮色泽分离符合 3:1比率,对备择假设HA:不符合3:1。
2.确定显著水平: 0.0,50.01
184
175
.3
1 2
50
41 .3
1
2
2
2
175 .3
41 .3
200
208 .7
1 2
2 4 .267
208 .7
当df=1时,(20.05,1) 3.84,(20.01,1) 6.63
由于 2 0 .0,1 5 3 .8 4 c 2 4 .2 62 0 7 .0,1 1 6 .63
效假设或否定无效假设。
第二节 适合性测验
一、适合性 2 测验的方法
适合性测验是指测验观察的实际次数与某种 理论或需要预期的理论次数是否相符合。
例1:某项试验观察淀粉质与非淀粉质玉米杂 交的F1代花粉粒,经碘处理后有3437粒呈 蓝色反映,3482粒呈非蓝色反映。如果属于 1对等位基因控制的遗传性状,F1代花粉粒 碘反映的理论比例应该是1:1,问其遗传性 状是否符合1对等位基因控制的遗传规律。
将本例数据代入上式
26200184504602 460
c2
2 76384210250
4.267
2. 2XC表的独立性测验
2XC表是指横行分为两组,纵列分为 C大于等于3组,因为df=(r-1)(c-1) ≥ 2,因此可以不做连续性的矫正。
五、卡平方测验

F2代红花与白花的理论比例为3:1
于是将各差数平方除以相应的理 论次数再相加,记为 论次数再相加,记为χ2,即:
(O − E ) 2 χ2 = ∑ E
故χ2是度量实际观察次数与理论次数 偏离程度的一个统计量, 越小, 偏离程度的一个统计量,χ2越小,表明实 际观察次数与理论次数越接近; χ2=0, 际观察次数与理论次数越接近 ; , 表示二者完全吻合; 越大, 表示二者完全吻合;χ2越大,表示二者相 差越大。 差越大。
各种自由度下右尾概率取α的临界
χα,df值列于附表4,供测验时查用。 值列于附表4 供测验时查用。
例如, 例如, df=10, α=0.05, , ,
χ20.05,10=18.31,表示 0.05, =18.31,
P( χ2 > 18.31)=0.05 图5.2)。 )=0.05(图 。 )=0.05
2×2表的独立性测验 × 表的独立性测验
H0:种子灭菌与散黑穗病发病无关, 种子灭菌与散黑穗病发病无关, 种子灭菌与散黑穗病发病无关 HA:种子灭菌与散黑穗病发病有关 种子灭菌与散黑穗病发病有关 显著水平 α=0.05 。
E11=460×(76/460)×(210/460)=34.7 × × 同理,O12=184相应的理论次数为 同理, 相应的理论次数为 E12=460×(384/460)×(210/460)=175.3 × × O21=50相应的理论次数为 相应的理论次数为 E21=460×(76/460)×(250/460)=41.3 × × O22=200相应的理论次数为 相应的理论次数为 E22=460×(384/460)×(250/460)=208.7 × ×
( x i − x ) 2 = ( n − 1) S 2
卡平方测验

根据处理及考察指标的多少分为不同的列联表:
宜宾学院
15
第四章 孟德尔遗传
检验程序
1、提出假设 H0:O-E=0;HA: O-E≠0 2、根据概率的乘法法则计算理论数:理论数的计算方法——
E ij
3、检验统计量:
i行总数 j列总数
总数
4、统计推断
宜宾学院
16
第四章 孟德尔遗传
[例] 表5.11为不同灌溉方式下水稻叶片衰老情况的调查资料。试
H0:稃尖和糯性性状在F2的分离符合9∶3∶3∶1; HA:不符合9∶3∶3∶1。
显著水平: 然后计算
表现型
=0.05。 值
稃尖有色非 糯 稃尖有色 糯稻 稃尖无色 非糯 稃尖无色 糯稻 总数
观察次数(O) 理论次数(E) O -E
宜宾学院
491 417.94 73.06
76 139.31 -63.31
4、依所得概率值的大小,接受或否定无效假设
在实际应用时,往往并不需要计算具体的概率值。 若实得 若实得 ≥ < 时,则H0发生的概率小于等于 时,则H0被接受。 , 属小概率事件,H0便被否定;
宜宾学院
8
第四章 孟德尔遗传
情况1:大豆花色一对等位基因的遗传研究如 下图:
P F1 F2 紫花 白花 紫花
稃尖有色 非糯 491 稃尖有色 糯稻 76 稃尖无色 非糯 90 稃尖无色 糯稻 86 总数 743
结果是否符合 9∶3∶3∶1的 理论比率?
宜宾学院
11
第四章 孟德尔遗传
二、 适合性检验
有一水稻遗传试验的适合性测验 按9∶3∶3∶1的理论比率算得各种ห้องสมุดไป่ตู้现型的理论次数E,
如稃尖有色非糯稻 E=743×(9/16)=417.94……
卡平方检验
观测值 Oi 4 36 129 188 211 176 142 80 30 4 1000
编码 Vi 0 1 2 3 4 5 6 7 8 9
V i2 0 1 4 9 16 564 844 880 852 560 240 36 4270
Oi*Vi2 0 36 516 1692 3376 4400 5112 3920 1920 324 21296
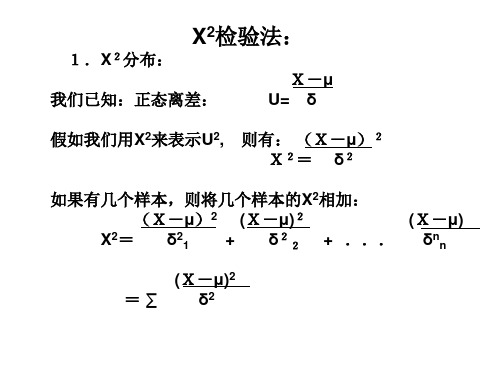
当样本的方差等于理论平均数时: 即 当样本的方差等于理论平均数时 (即: δ2 = µ) (X- 2 X-µ)2 X- U 则: X2= ∑ 由此可知: 由此可知: 1.X2分布是当样本的方差等于理论平均数时的一种特 殊形式的正态离差平方的分布. 殊形式的正态离差平方的分布. 其分布是连续的, 2.其分布是连续的,其值域的大小随着自由度的 增加 而增加。 而增加。 项数越多, 值越大)。 (即:项数越多,X2值越大)。 2、适合性检验: 、适合性检验: 已知:男女性别比例为: : 。调查某地100名新生 例:已知:男女性别比例为:1:1。调查某地 名新生 儿,得:男:58,女:42。 , 。 该地区新生儿是否符合1: 比例 比例? 问:该地区新生儿是否符合 :1比例? 假设: 符合1: 比例 比例)。 解:假设:H0:O-T=0(符合 :1比例)。 符合 HA:O-T≠0(不符合 :1比例)。 不符合1: 比例 比例)。 不符合
= = = = = =
2(|a-T|-1/2)2 + 2(|b-T|-1/2)2 n 分子分母同乘以2) (分子分母同乘以 ) 2[|a-(1/2a+1/2b)|-1/2]2+2[|b-(1/2a+1/2b)|-1/2]2 n 2[|a-1/2a-1/2b|-1/2]2 + 2[|b-1/2a-1/2b|-1/2]2 n 2[|1/2a-1/2b|-1/2]2 + 2[|1/2b-1/2a|-1/2]2 n 2×1/4[|a-b|-1]2 +2×1/4[|b-a|-1]2 × × n (|a-b|-1)2 n 一对基因 1:1分离 : 分离
卡平方χ2测验

第八章卡平方(X2 )测验知知识目标:•理解卡平方(X2)的概念;•掌握适合性测验的方法;•掌握独立性测验的方法;•了解卡平方(为2)的可加性和联合分析。
能力目标:•学会适合性测验的方法;“、,学会独立性测验的方法;前面介绍了数量性状资料的统计分析方法。
在生物和农业科学研究中,还有许多质量性状的资料,这样的资料可以转化为次数资料。
间断性变数的计数资料也可整理为次数资料。
凡是试验结果用次数表示的资料,皆称为次数资料。
次数资料的统计分析方法有二项分布的正态接近法和卡平方(%2)测验法等。
本章主要介绍卡平方测验。
第一节卡平方(X2)测验一、卡平方(X2)概念为了便于理解,现结合一实例说明X2统计量的意义。
菠菜雌雄株的性比为1:1,今观测200 株菠菜,其中有92棵雌株,108棵雄株。
按1:1的性比计算,雌、雄株均应为100株。
以。
表示实际观察次数,£表示理论次数,可将上述情况列成表8-1。
表8-1 菠菜雌雄株实际观测株数与理论株数的比较性别观测株数。
理论株数E 0-E (0-E)2/E雌92( 01) 100( E1) -80. 64雄108 (02) 100( E2) 80. 64合计20020001.28从表8-1看到,实际观察次数与理论次数存在一定的差异,这里雌、雄各相差8株。
这个差异是属于抽样误差,还是菠菜雌雄性比发生了实质性的变化?要回答这个问题,首先需要确定一个统计量用以表示实际观察次数与理论次数偏离的程度,然后判断这一偏离程度是否属于抽样误差,即进行显著性测验。
为了度量实际观察次数与理论次数偏离的程度,最简单的办法是求出实际观察次数与理论次数的差数。
从花-1看出:OjEr 8, O 2-E 2=8,由于这 两个差数之和为0,显然不能用这两个差数之和来表示实际观察次数与理论次数的偏离程度。
为了避免正、负抵消,可将两个差数O ]-E/O 2-E 2平方后再相加,即计算Z (O - E )2,其 值越大,实际观察次数与理论次数相差亦越大,反之则越小。
卡平方测验

0.05
(3)测验计算: : 在假设 H 0为正确的前题下, 则可得如下求理论值的比例式,求出理论值: 300∶100=231∶E1 300∶200=231∶E2 300∶100=69∶E3 300∶200=69∶E4 所以 E1=77 E2=154 E3=23 E4=46
健株 甲品种 乙品种 合 计 O 88 143 231 E 77(E1) 154(E2) 231 O 12 57 69
病株
E 23(E3) 100 46(E4) 200 69 300
合计
当 df r 1c 1 2 12 1 1时,
O E 0.5 2 2 E
77 154 2 2 2 2 2 2 2 .34 .5 6 . 63 4 0.5 9 12 23 0 57 46 0 . 5 0 . 01 , 1 88 77 0.5 143 154 0.5 12 23 54 23 46 77 154 2
注:卡方适合性测验还经常用来测验试验数据的次 数分布是否和某种理论分布(如二项分布、正态分布等) 相符,以推断实际的次数分布究竟属于哪一种曲线类型。
(即:拟合优度检验)
单向分组计数资料:将资料列成表格后,行数 R=1,列数C≥2的计数资料。 [例] 某地进行人口调查,共有人口378万人,其
中男、女人口分别为190、188(万人),即:
2 9.34 0 .05, 1 3.84
88 77 0.5
2
143 154 0.5
2
12 23
所以 p 0.05 。 (4)推断:否定H 0 ,接受 H A ,即发病率的高低与品 种有关。
卡平方测验公式

卡平方测验公式卡平方检验是一种常用的假设检验方法,用于检测两个变量之间是否存在统计学上的关联性。
其中,卡方分布是一种概率分布,常用于统计学分析中。
本文将从卡平方测验的定义、原理、公式、注意事项等方面进行详细介绍。
一、卡平方测验的定义卡平方测验(Chi-square test)是一种用于分析分类资料的统计方法,用来评估随机变量的频率分布与某种理论分布之间的偏离程度。
它通过比较实际观测值和理论值的差异,来判断这种差异是否显著。
二、卡平方测验的原理卡平方测验的原理是基于卡方分布的统计原理。
卡方分布是指自由度为n的卡方变量X2的概率分布,其概率密度函数为f(x) =x^(n/2-1)*e^(-x/2) / (2^(n/2)*Γ(n/2)) ,其中,Γ(n/2)为伽玛函数值。
卡方分布的特点是非对称的,取值范围为[0,+∞)。
卡平方测验的基本思路是:1.设定原假设和备择假设;2.收集样本数据;3.计算观测值的卡方值;4.确定自由度;5.查找卡方分布表,找到临界值;6.比较观测值的卡方值和临界值;7.根据比较结果,判断原假设是否成立。
三、卡平方测验的公式卡平方测验的公式如下:卡方值=Σ(观测值-理论值)²/理论值其中,Σ表示对所有分类统计量求和。
四、注意事项1.在进行卡平方测验时,样本数量应该尽可能大,否则可能会导致误差增大;2.进行卡平方测验时,要保证分类变量的独立性,即各分类变量之间应该互相独立;3.进行卡平方测验时,要注意设置显著性水平,一般取α=0.05或α=0.01;4.进行卡平方测验时,要选择合适的观测和理论值,否则可能会导致结果不准确;5.进行卡平方测验时,最好使用专业的卡平方测验软件或计算器,以提高效率和准确性。
五、总结卡平方测验是一种重要的假设检验方法,常用于分析分类数据和判断两个变量之间的关联性。
它基于卡方分布的统计原理,通过比较理论值和观测值的差异来判断原假设是否成立。
在进行卡平方测验时,需要注意样本数量的大小、分类变量的独立性、显著性水平的设置、观测和理论值的选择以及使用专业工具等因素。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
卡平方测验
实验目的
1.以提供的数据练习计算x2值,并测定其是否近似理论假设的期望比值。
2.依据相应自由度,检验计算所得x2值。
3.熟练掌握x2值的计算和利用x2值评估实验结果
实验原理
卡平方(x2)测验的目的是以吻合度断定所获得的资料与理论上期望的比值是否满足或近似,也就是x2测验可以测定所得数据是否偏离吻合概率。
显然,如果偏差小是因为偶然机会,偏差大则不是出于偶然机会。
卡平方x2测验试图为我们解决这个问题:“骗差小到何种程度才可以认为只是出于偶然机会。
”卡平方x2值的公式如下:
x2 =∑(O-E)2/E
这里的o是特定表现型个体的观察数目;E是这一表现型在理论上期望的数目;∑是各种表现型(O-E)2/E的累加值。
例如,高茎番茄和矮茎番茄杂交,F1全为高茎,F2有102株高茎和44株矮茎。
这些资料是否符合3:1的概率?回答这个问题必须计算x2值,把计算过程综合整理于表2-1。
2
计算所得的x值为2.0548,x值意味着什么呢?如果实际观察值(O)精确等于理论期望值(E),x2值为 0,是一个完满的好适度。
于是x2值小,表明观察结果接近期望比率;x2值大,表明观察结果与期望比率存在明显差异。
一般统计学家把P=1/20或P=0.05定为显著水平。
当两组变数自由度为1时,卡平方x2值为3.841的概率是0,05,观察值与期望值相抵触。
在刚才的实例中x2=2.0548,它小于允许最大值x2 =3.841,P>0.05。
因而可以认为偏差只是偶然机会,实验数据符合3:1的概率的假设。
