电磁场公式
电磁场公式总结
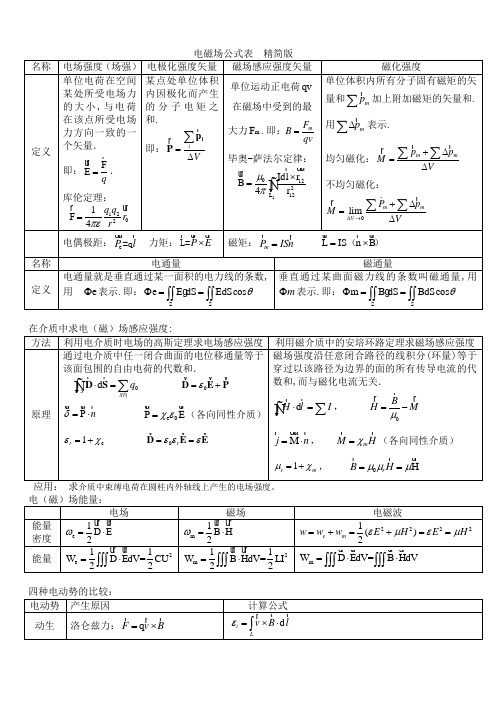
电磁场公式表 精简版 名称 电场强度(场强) 电极化强度矢量 磁场感应强度矢量 磁化强度定义 单位电荷在空间某处所受电场力的大小,与电荷在该点所受电场力方向一致的一个矢量. 即:F E q = . 库伦定理:12021F 4q q r rπε= 某点处单位体积内因极化而产生的分子电矩之和.即:i V =∆∑i p P 单位运动正电荷qv在磁场中受到的最大力m F .即:m F B qv = 毕奥-萨法尔定律: 1012212L Idl r B 4r μπ⨯=⎰ 单位体积内所有分子固有磁矩的矢量和m p ∑ 加上附加磁矩的矢量和.用m p ∆∑ 表示. 均匀磁化:m m p p M V +∆=∆∑∑ 不均匀磁化:0limm m V P p M V ∆→+∆=∆∑∑ 电偶极距:e P l =q 力矩:P E ⨯ L= 磁矩:m P ISn =L IS n B =⨯ () 名称电通量 磁通量定义 电通量就是垂直通过某一面积的电力线的条数,用 e Φ表示.即:SSe E dS EdScos θΦ==⎰⎰⎰⎰垂直通过某曲面磁力线的条数叫磁通量,用m Φ表示.即:SSm B dS BdScos θΦ==⎰⎰⎰⎰在介质中求电(磁)场感应强度:方法 利用电介质时电场的高斯定理求电场感应强度利用磁介质中的安培环路定理求磁场感应强度 原理 通过电介质中任一闭合曲面的电位移通量等于该面包围的自由电荷的代数和.0d SS q ⋅=∑⎰D S 内0ε=+D E PP n δ=⋅e 0P E χε=(各向同性介质)e 1r εχ=+ 0r εεε==D E E磁场强度沿任意闭合路径的线积分(环量)等于穿过以该路径为边界的面的所有传导电流的代数和,而与磁化电流无关.d H l I ⋅=∑⎰, 0B H M μ=-M j n =⋅ , m M H χ=(各向同性介质)1r m μχ=+, 0H r B H μμμ==应用: 求介质中束缚电荷在圆柱内外轴线上产生的电场强度。
大学物理电磁学公式

大学物理电磁学公式大学物理电磁学是物理学中的一个重要分支,研究电场和磁场以及它们之间的相互作用。
在学习和研究电磁学的过程中,我们经常会接触到一系列重要的公式。
以下是一些常见的大学物理电磁学公式的详细介绍。
1. 库仑定律(Coulomb's Law):库仑定律描述了两个点电荷之间相互作用力的大小和方向。
它的数学表达式为:F = k * |q1 * q2| / r²其中,F为两个电荷所受的力,k为库仑常数,q1和q2分别为两个电荷的大小,r为两个电荷之间的距离。
2. 电场强度(Electric Field Intensity):电场强度描述了电荷在某一点周围的电场的强弱。
对于一个点电荷,其电场强度的数学表达式为:E = k * |q| / r²其中,E为电场强度,k为库仑常数,q为电荷的大小,r为点电荷到被测点之间的距离。
3. 电势能(Electric Potential Energy):电势能描述了电荷由于存在于电场中而具有的能量。
对于一个点电荷,其电势能的数学表达式为:U = k * |q1 * q2| / r其中,U为电势能,k为库仑常数,q1和q2分别为两个电荷的大小,r为两个电荷之间的距离。
4. 电势差(Electric Potential Difference):电势差描述了电场中两个点之间的电势能的差异。
对于两个点电荷之间的电势差,其数学表达式为:ΔV = V2 - V1 = -∫(E · dl)其中,ΔV为电势差,V1和V2分别为两个点的电势,E为电场强度,dl为路径元素。
5. 电场线(Electric Field Lines):电场线用于可视化电场的分布情况。
电场线从正电荷流向负电荷,并且密集的电场线表示电场强度较大,稀疏的电场线表示电场强度较小。
6. 电场的高斯定律(Gauss's Law for Electric Fields):电场的高斯定律描述了电场通过一个闭合曲面的总通量与该闭合曲面内的电荷量之间的关系。
电磁场公式梳理

公式总结注:此文档仅梳理了相关公式,需掌握的概念、知识点请仔细研读课件。
第一章•三种正交坐标系长度元,面积元和体积元表达式•三种正交坐标系坐标单位矢量的转换•标量场图和矢量场图对应的方程•方向导数,梯度•面元矢量:•场量穿过面元的通量:0=⨯r d r A)(le G dldf ⋅=∴zfe yf e x f e f zy x ∂∂+∂∂+∂∂=∇ G f =∇dSeS d n =dSA S d A θcos =⋅AA div ⋅∇=y zx A A A divA A x y z∂∂∂=∇⋅=++∂∂∂⎰⎰⋅∇=⋅VSdVA S d A⎰⎰=⋅CCdlA l d A θcos环量散度高斯散度定理环量面密度n n e A rot A rot ⋅=旋度AA rot ⨯∇=斯托克斯定理Sd A l d A SC⋅⨯∇=⋅⎰⎰)(0=∇⨯∇φ0)(=⨯∇⋅∇AԦe x∂A z ∂y −∂A y ∂z +Ԧe y ∂A x ∂z −∂A z∂x +Ԧe z ∂A y ∂x −∂A x ∂y∇×ԦA =第二章()SI J r dS=⋅⎰v J Vρ=s N lI J e dl=⋅⎰PE D +=0εEP e χε0=0r D E Eεεε===⎰⨯=222C Bl d I F Bv q E q F ⨯+=在线性各向同性介质中在线性各向同性磁介质中m M Hχ=MBH -=μB Hμ=⋅=-=-⎰⎰S V dQ dJ d S dVdtdt ρ∂=+=+∂t d DJ J J J tS d t DJ l d H S l⋅∂∂+=⋅⎰⎰)(Sd B dt d l d E S l ⋅-=⋅⎰⎰0SB d S ⋅=⎰∑⎰⎰==⋅qdV S d D VV Sρt D J H ∂∂+=⨯∇t BE ∂∂-=⨯∇=⋅∇B vD ρ=⋅∇⎪⎪⎩⎪⎪⎨⎧=-=-=-=-ρn n n n t t SN t t D D B B E E J H H 1212121200⎪⎪⎩⎪⎪⎨⎧=-⋅=-⋅=-⨯=-⨯ρ)(0)(0)()(12121212D D e B B e E E e JH H e n n n n第三章22RdS R e S d d R θcos =∙=Ω⎰⋅=PA A ld Eφφ-∇=E⎰∙=-BA B A ld Eφφ⎪⎩⎪⎨⎧==∙∇=⨯∇EDD E ερ0''s n v P e Pρρ⎧=∙⎪⎨=-∇∙⎪⎩束缚面电荷:束缚体电荷:ερφv -=∇212φφ=1212sn nφφεερ∂∂-=∂∂R RV d E v v⎰''=341ρπε⎰=vv Rdvρπεφ041⎩⎨⎧=∙∇=⨯∇00J EJ E=γ1212n nφφγγ∂∂=∂∂12φφ=p J E=∙焦耳定理恒定电场()322121mJ E E D w e ε=∙= ⎰=V e dvW ρφ21⎰=V e dvE W 221ε电场能量密度电场能量H J B ⎧∇⨯=⎨∇⋅=⎩B H μ=B A=∇⨯024RCIdl e B Rμπ⨯=⎰V d RJ A V '=⎰'πμ40Sv n J MJ M e ⎧'=∇⨯⎨'=⨯⎩介质内部束缚体电流密度:介质表面束缚面电流密度:)(H IL 单位:亨ψ=1()2m VW H B dV=∙⎰221Hw m μ=AB⨯∇=φ-∇=∂∂+tA EtA ∂∂-=⋅∇φμε()m e S w w pt∂-∇⋅=++∂⎰⎰⎰++=⋅-V Vm m S pdv dv w w dt dS d S )((,)Re j t E r t E e ω∙⎡⎤=⎢⎥⎣⎦()()()()x xm y ym z zm E r e E r e E r e E r =++复矢量0ωωρH J j DE j B B D ⎧∇⨯=+⎪∇⨯=-⎪⎨∇=⎪⎪∇=⎩1(()())2c S E r H r *=⨯⎪⎪⎪⎩⎪⎪⎪⎨⎧><<<--100101022ωεγωεγωεγ良好导体:有损耗介质:良介质:100()()()()()()c c c j j j γγωγωεεωεωμμωμω'''=-'''=-'''=-()⎪⎪⎪⎩⎪⎪⎪⎨⎧=∙=∙∙-=∙∙+=∙⎰⎰⎰⎰⎰⎰⎰dv S d D S d B Sd B j l d E S d D j J l d H V CSSC SC ρωω 0ρω j J -=∙∇⎰⎰-=∙VSdv j S d J ρω EJ H B E Dγμε===⎥⎦⎤⎢⎣⎡⨯=*)()(Re r H r E S av 21第七章k ωμμηε==1z zH e E E H e ηη=⨯=⨯,k βωμε==22k ππλωμε==1p V fk ωλμε∴===avav e w S v ||=良介质12112,,,p c V j f γμαβωμεεμεμγμληεωεεμε⎧≈≈≈⎪⎪⎨⎛⎫⎪≈=+≈ ⎪⎪⎝⎭⎩良导体222222212,,()p c ff V j f ωμγωωπαβπμγβμγμγππωμλπηβωμγμγγ⎧≈≈==≈=⎪⎪⎨⎪=≈=≈+⎪⎩⎪⎩⎪⎨⎧====⋅-∙⋅-∙∙⋅-∙⋅-∙∙r k j r e jk rk j r e jk e H e H H e E eE E n n 0000沿任意方向传播的均匀平面波c cj K γεεωμεω=-=导电媒质引入复介电常数及复波速E =E 0•e −Γz =E 0•e −αz e −jβzn k e k=波矢量E =ηH ×Ԧe n ,H =1ηԦe n ×E极化的判别方法1、利用E x 和E y 的振幅和相位之间的关系判断x xm x y ym y E e E t kz e E t kz ωϕωϕ=-++-+cos()cos()线极化时,或当→±=-πϕϕ0x y 圆极化时,且当→±=-=2/,πϕϕx y xm xm E E )波传播的波为右旋(左旋,沿若)(z 2/z x y -+-=-πϕϕ椭圆极化其他一般情形,→)波传播的波为左旋(右旋,沿若)(z 2/z x y -++=-πϕϕ)波传播的波为右旋(左旋,沿若)(z z x y -+<-<-0ϕϕπ)波传播的波为左旋(右旋,沿若)(z z x y -+<-<πϕϕ02、利用复数形式判断)()(y x kz j ym y kz j xm x eE e e E e E ϕϕ+-+-∙+= y xj ym y j xm x eE e e E e z E ϕϕ +==∙)0()sin (cos )sin (cos y y ym y x x xm x j E e j E e ϕϕϕϕ+++=)sin sin ()cos cos (y ym y x xm x y ym y x xm x E e E e j E e E e ϕϕϕϕ+++=IR E j E +=线极化或或若:→==00//I R I R E E E E圆极化且若→=⊥||||I R I R E E E EI R I R E E E E 若、与波的传播方向符合右手螺旋关系,则为右旋波;若、与波的传播方向符合左手螺旋关系,则为左旋波。
电磁场强度计算

电磁场强度计算电磁场强度(或称电场强度和磁场强度)是描述电磁场中电磁力的物理量之一。
在本文中,我们将介绍计算电磁场强度的方法和公式,并说明其应用。
一、电磁场强度的定义和单位电磁场强度是指在一个给定点的电场或磁场中单位电荷或单位电流所受到的力的大小。
电场强度的单位是V/m,磁场强度的单位是T(特斯拉)。
二、电场强度的计算方法1. 对于具有轴对称分布的带电物体,可以使用库仑定律来计算电场强度。
根据库仑定律,电场强度(E)与电荷量(Q)之间的关系可以用以下公式表示:E = k * Q / r^2其中,k为库仑常数(k ≈ 8.99 × 10^9 N·m^2/C^2),Q为电荷量,r为距离。
2. 对于具有线对称分布的带电物体,可以使用电场环路定理来计算电场强度。
电场环路定理表明,通过一个闭合回路所包围的电场强度等于该回路上所有电荷量所贡献的电势之和。
因此,根据该定理,可以通过以下公式计算电场强度:E = Σ (k * Δq / r^2)其中,Σ表示对所有电荷量求和,Δq为每个电荷量,r为距离。
三、磁场强度的计算方法1. 对于具有轴对称分布的磁场,可以使用比奥-萨伐尔定律来计算磁场强度。
根据比奥-萨伐尔定律,磁场强度(B)与电流(I)之间的关系可以用以下公式表示:B = (μ0 / 4π) * (I / r)其中,μ0为真空中的磁导率(μ0 ≈ 4π × 10^-7 T·m/A),I为电流,r为距离。
2. 对于具有线对称分布的磁场,可以使用安培环路定理来计算磁场强度。
安培环路定理表明,在一个闭合回路上的磁场强度等于该回路上通过的电流所贡献的磁通量之和。
因此,根据该定理,可以通过以下公式计算磁场强度:B = Σ (μ0 * I / 2πr)其中,Σ表示对所有电流求和,I为电流,r为距离。
四、电磁场强度计算的应用1. 电磁场强度的计算在电磁学、电磁感应和电磁波等领域具有广泛的应用。
电磁场公式总结
1.磁感应强度是用来表示磁场的强弱和方向的物理量,是矢量,单位T),1T=1N/A•m
2.安培力F=BIL;(注:L⊥B) {B:磁感应强度(T),F:安培力(F),I:电流强度(A),L:导线长度(m)}
3.洛仑兹力f=qVB(注V⊥B);质谱仪〔见第二册P155〕 {f:洛仑兹力(N),q:带电粒子电量(C),V:带电粒子速度(m/s)}
8.电源总动率、电源输出功率、电源效率:P总=IE,P出=IU,η=P出/P总{I:电路总电流(A),E:电源电动势(V),U:路端电压(V),η:电源效率}
9.电路的串/并联 串联电路(P、U与R成正比) 并联电路(P、I与R成反比)
电阻关系(串同并反) R串=R1+R2+R3+…1/R并=1/R1+1/R2+1/R3+…
9.电势能:EA=qUA {EA:带电体在A点的电势能(J),q:电量(C),UA:A点的电势(V)}
10.电势能的变化ΔEAB=EB-EA {带电体在电场中从A位置到B位置时电势能的差值}
11.电场力做功与电势能变化ΔEAB=-WAB=-qUAB (电势能的增量等于电场力做功的负值)
12.电容C=Q/U(定义式,计算式) {C:电容(F),Q:电量(C),U:电压(两极板电势差)(V)}
接入被测电阻Rx后通过电表的电流为
Ix=E/(r+Rg+Ro+Rx)=E/(R中+Rx)
由于Ix与Rx对应,因此可指示被测电阻大小
(3)使用方法:机械调零、选择量程、欧姆调零、测量读数{注意挡位(倍率)}、拨off挡。
(4)注意:测量电阻时,要与原电路断开,选择量程使指针在中央附近,每次换挡要重新短接欧姆调零。
电磁感应的五个公式

电磁感应的五个公式
电磁感应是一种重要的物理现象,它是由于电磁场的存在而产生的。
电磁感应的五个公式是:
1. Faraday定律:电磁感应的强度与磁通率成反比,即B= -N∆Φ/∆t,其中B为磁感应强度,N为磁通率,Φ为磁通,t为时间。
2. 斯特林定律:电磁感应强度与磁通成正比,即B=μN,其中μ为磁导率。
3. 法拉第定律:电磁感应强度与电流成正比,即B=μI,其中I为电流。
4. 摩擦定律:电磁感应强度与电压成正比,即B=μV,其中V为电压。
5. 拉普拉斯定律:电磁感应强度与电场强度成反比,即B= -μ∇E,其中E为电场强度。
电磁感应是由于电磁场的存在而产生的,它是电磁学中最重要的现象之一。
电磁感应的五个公式是电磁学中最基本的公式,它们描述了电磁感应的强度与磁通率、磁导率、电流、电压和电场强度之间的关系。
电磁感应的公式可以用来计算电磁感应的强度,从而更好地理解电磁学中的现象。
电磁感应的公式不仅在电磁学中有重要的应用,而且在日常生活中也有广泛的应用。
例如,电磁感应的公式可以用来计算电机的功率,从而更好地控制电机的运行。
此外,电磁感应的公式还可以用来计算电磁波的传播速度,从而更好地控制电磁波的传播。
电磁感应的五个公式是电磁学中最基本的公式,它们描述了电磁感应的强度与磁通率、磁导率、电流、电压和电场强度之间的关系。
电磁感应的公式不仅在电磁学中有重要的应用,而且在日常生活中也有广泛的应用。
因此,学习和掌握电磁感应的五个公式对于理解电磁学中的现象和更好地应用电磁学都是非常重要的。
电磁场公式大全

电磁场公式大全电磁场是我们周围最为普遍的自然界现象之一,它会影响到我们大自然生态系统中的每一个角落。
有关电磁场的科学概念及其相关证据已经广泛运用于航空航天、电力技术和通信技术等各类技术领域,无论是工业应用还是实验室研究,都需要掌握一些常用的电磁场公式。
为了更好地了解电磁场的特性和应用,有必要先从“电磁场公式大全”入手,下面将介绍电磁场大全中的几个常用的公式:1、电磁场力:电磁场力F由电荷q、速度V及磁场B给出:F=qvXB;2、电磁势:电通量Φ∖电压U、电流I及磁通量B给出:U=Φ/BI;3、电偶极子:电偶极子表示两个带电粒子构成的电场,其公式:V=kq1q24/r;4、磁通量:磁通量表示电磁场中电流线圈的数量,由公式:B=μo1;5、磁密度:由公式表示,磁密度H=B/u;6、磁力线:磁力线表示一个磁场中的磁性物质的分布,由公式:m=H∕I;7、电磁功率:由公式表示,电磁功率P=UXI;8、电磁能量:磁场中的电磁能量由公式表示,W=U2∕2C;9、电磁感应强度:由公式表示,E=BXv;10、磁矩:磁矩由公式表示,M=BIA;上述九个公式中,前五个是电磁力学,后四个是电磁场的基本公式,它们是电磁理论研究的重要基础。
无论是在哪个领域进行电磁场研究,都要掌握和理解上述公式,这有利于更好地掌握电磁场的性质及运用。
现代电磁场理论的发展也使得上述的公式可以进行更加复杂的分析,包括电磁相位、电磁双极子、多维电磁场、电磁辐射以及强磁场等等,但是其基础公式仍然是上述九条。
由于电磁场是物理学中十分重要的领域,因此,要想真正理解它们,必须熟练掌握和掌握上述电磁场公式,以便在实际应用中正确使用它们。
当然,随着科学技术的发展,电磁场理论也不断发展,它们也将提供更多更强大的公式,以帮助我们更好地理解和使用电磁场的特性和运用。
电磁场基本规律-公式

1 109 8.854 1012 (F/m); 36
带电体 V ' 、带电曲面 S ' 、带电曲线 L ' 对 r 点处的点电荷 q 的作用力分别为:
1
q Fq 4 0
r' r r' r r' q V ' 3 dq ' 4 0 V ' 3 dv ' , r r' r r' S r ' r r ' q r r' q Fq ds ' , dq ' 3 4 0 S ' r r ' 3 4 0 S ' r r' l r ' r r ' q r r' q Fq dl ' ; dq ' 3 4 0 L ' r r ' 3 4 0 L ' r r'
电流强度: I t lim
L
电荷守恒定律与电流连续性方程:
r , t ( 形式) S J r, t ds t V r , t dv V t dv, r , t , (微分形式) J r , t = t
Idl I ' dl ' r r ' I ' dl ' r r ' Idl 0 Idl B r 3 L L' L L ' 3 L 4 r r' r r ' I ' dl ' r r ' I ' dl ' 0 磁感应强度 (磁通密度):B r 0 (T/ Wb/m2); 3 L ' L ' 4 4 r r' r r' 体积 V ' 中体电流、曲面 S ' 上的面电流在 r 点处产生的 B r 为: J r ' r r ' J r ' 0 0 B r dv ' dv ' , 3 V ' V ' 4 4 r r' r r' JS r ' r r ' JS r ' 0 0 B r ds ' ds ' , 3 4 S ' r r ' 4 S ' r r' FL ' L 0 4
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
电荷守恒定律:电荷既不能被创造,也不能被消灭,它们只能从一个物体转移到另一个物体,或从物体的
一部分转移到另一部分,在任何物理过程中电荷的代数和总是守恒的.
安培力 L
⎰式)
电场强度(场
电极化强度矢12
02
4q q r r
πε i V =∆ 12
2r ⎰ 均匀磁化:p M =
∑不均匀磁化:m m P p +∆∑m ISn = L IS n B =⨯() 就是一簇假想的曲线,其曲线上任一点的切线方向都与该点处的就是一簇假想的曲线,其曲线上任一点的切线方向与该点就是电势相等的点集
电位差(电压):单位正电荷的电位能差.即:
B AB AB
AB
A W A U Edl q q
===⎰.
P n δ=⋅
P E χε=(各向同性介质)e 1r εχ=+
0r εεε==D E E
H M μ=
-
M j n =⋅
1r m μχ=+
0H r B H μμμ==
(1)分析自由电荷分布的对称性求出磁场感应强度矢量
e δ.
D EdV=2⋅⎰⎰⎰
B HdV=2⋅⎰⎰⎰
d d S
⎰⎰d d I
L
t - 相互电流变化:
1d d I M t =- 12d I
ε
楞次定律:闭合回路中感应电流的方向,总是使得它所激发的磁场来阻止引起感应电流的磁通量的变化。
高斯定理和环路定理: 静电场 恒定磁场
t
⋅∂⎰⎰
⎰⎰∑=
⋅ε
q
dS E
x ∂d d L
H l I I t ⋅=+=⋅∂⎰
⎰⎰
z
H H ⎨∂∂⎪∂⎪∂d t -
⎰⎰E 和H 的振幅都正比于
电场和磁场的本质及内在联系:
静电场问题求解
基础问题
1.场的唯一性定理:
①已知V 内的自由电荷分布
②V 的边界面上的φ值或n ∂∂/φ值,
则V 内的电势分布,除了附加的常数外,由泊松方程
ερφ/2
-=∇
及在介质分界面上的边值关系
σφ
φεε
φφ-=∂∂-∂∂=)()(,n
n j i
j
i
唯一的确定。
两种静电问题的唯一性表述:
⑴给定空间的电荷分布,导体上的电势值及区域边界上的电势或电势梯度值→空间的电势分布和导体上的面电荷分布(将导体表面作为区域边界的一部分)
⑵给定空间的电荷分布,导体上的总电荷及区域边界上的电势或电势梯度值→空间的电势分布和导体上的面电荷分布(泊松方程及介质分界面上的边值关系)
2.静电场问题的分类:
分布性问题:场源分布E ⇔ρ电场分布
边值性问题:场域边界上电位或电位法向导数→电位分布和导体上电荷分布
3.求解边值性问题的三种方法:
电荷
电场 磁场
电流
变化 变化
运动
激
发
激发
分离变量法
①思想:根据泊松方程初步求解φ的表达式,再根据边值条件确定其系数
电像法
①思想:根据电荷与边值条件的等效转化,用镜像电荷代替导体面(或介质面)上的感应电荷(或极化电荷) 格林函数法
①思想:将任意边值条件转化为特定边值条件,根据单位点电荷来等价原来边界情况 静电场,恒流场,稳恒磁场的边界问题:
电磁场的认识规律
一.静电场的规律: 1.真空中的静电场; 电场强度E
dv
R R
z y x z y x E v
3
)',','(41),,(,
ρπε⎰
=
电场电势V 静电场的力F 静电场的能量
2.介质中的静电场; 电位移矢量D
0ε=+D E P
极化强度P
E
p
)(0εε-= e 0P E χε=(各向同性介质)
二.稳恒磁场与稳恒电流场 1.真空中的磁场强度B
31212110
4R R L d I u B c ⨯=⎰π dv R R r J u r B v 3
0)'(4)(
⨯=⎰π '43
,dV R R v B ⋅⨯=⎰Ω ρπ
μdq R R v v 304
⨯=⎰πμ30
4R R v q πμ ⨯= 2.真空中的电流密度J
t
j ∂∂-
=•∇ρ
荷密度
J ρν=⋅
3.磁场矢位A
')'(140dv r J R A v
⎰=πμ,A B
⨯∇=
4.介质中的磁场感应强度H
H B μ=
5.磁化强度M
H )1(
-=r u M (各向m
M H χ=同性介质)
6.磁场中的力F
7.磁场中的能量
三.麦克斯韦方程组与介质中的麦克斯韦方程组
实质:反映场与电荷及其运动形式(电流)的联系,揭示电场与磁场的相互转换关系 电荷:(自由电荷,极化电荷)
D ρ∇⋅= P ρρ∇⋅=-
电流:(传导电流,位移电流,磁化电流)
M J M ⨯∇=, t E t D J D ∂∂=∂∂= ε,0=∂∂+⋅∇t J ρ
麦克斯韦方程组与介质中的麦克斯韦方程组包含是各种矢量的散度与旋度运算,有微分,积分形式两种
⎪⎪⎪⎪⎩⎪⎪⎪
⎪⎨⎧
=⋅⋅=⋅⋅+=⋅-=⋅⎰⎰⎰⎰⎰⎰0s d B Q s d D s d D dt
d I l d H s d B dt
d l d E p s
s f u s u
(自由电荷)
⎪⎪⎪⎪⎩
⎪⎪
⎪⎪⎨
⎧=⋅∇=
⋅∇∂∂+=⨯∇∂∂-=⨯∇0B E t E J B t B E
ερε
μμ
四.三大定律: 欧姆定律
E J
σ=
焦耳定律 安倍定律
五.守恒定律: 电荷守恒 能量守恒
六.在边界条件下的电磁现象:
⎪⎪⎪⎩⎪⎪⎪⎨⎧=-⨯=-⨯=-⋅=-⋅=-⋅传导电流面密度)
自由电荷面密度),或()(0)(0)()(()(1212201212S S S J H H n E E n
B B n
E E n D D n
ερρ
七.静电场与稳恒磁场的比较:
八稳恒电流场与介质中静电场的比较:。
