物理竞赛光学试题整理版
高中物理竞赛几何光学测试题(含详细解析)

几何光学测试题1、如图(a )所示,一细长的圆柱形均匀玻璃棒,其一个端面是平面(垂直于轴线),另一个端面是球面,球心位于轴线上.现有一很细的光束沿平行于轴线方向且很靠近轴线人射.当光从平端面射人棒内时,光线从另一端面射出后与轴线的交点到球面的距离为a ;当光线从球形端面射人棒内时,光线在棒内与轴线的交点到球面的距离为b .试近似地求出玻璃的折射率n 。
2、内表面只反射而不吸收光的圆筒内有一半径为R 的黑球,距球心为2R 处有一点光源S ,球心O 和光源S 皆在圆筒轴线上,如图所示.若使点光源向右半边发出的光最后全被黑球吸收,则筒的内半径r 最大为多少?3、如图1中,三棱镜的顶角α为60︒,在三棱镜两侧对称位置上放置焦距均为 30.0cm f =的两个完全相同的凸透镜L 1和 L 2.若在L 1的前焦面上距主光轴下方14.3cm y =处放一单色点光源S ,已知其像S '与S 对该光学系统是左右对称的.试求该三棱镜的折射率.4、如图(a )所示,两平面镜A 和B 的镜面分别与纸面垂直,两镜面的交线过图中的O 点,两镜面间夹角为︒=15α,今自A 镜面上的C 点处沿与A 镜面夹角︒=30β的方向在纸面内射出一条光线,此光线在两镜面经多次反射后而不再与镜面相遇。
设两镜面足够大,1=CO m 。
试求:(1)上述光线的多次反射中,最后一次反射是发生在哪块镜面上? (2)光线自C 点出发至最后一次反射,共经历多长的时间?5、有一水平放置的平行平面玻璃板H ,厚3.0 cm ,折射率 1.5n =。
在其下表面下2.0 cm 处有一小物S ;在玻璃扳上方有一薄凸透镜L ,其焦距30cm f =,透镜的主轴与玻璃板面垂直;S 位于透镜的主轴上,如图(a )所示。
若透镜上方的观察者顺着主轴方向观察到S 的像就在S 处,问透镜与玻璃板上表面的距离为多少?6、望远镜的物镜直径D =250cm ,其焦距f =160m 。
全国中学生物理竞赛真题汇编---光学 参考答案
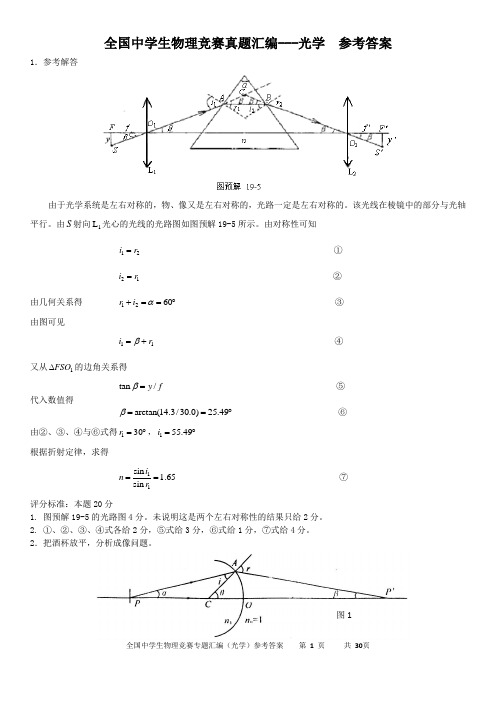
全国中学生物理竞赛真题汇编---光学 参考答案1.参考解答由于光学系统是左右对称的,物、像又是左右对称的,光路一定是左右对称的。
该光线在棱镜中的部分与光轴平行。
由S 射向1L 光心的光线的光路图如图预解19-5所示。
由对称性可知12i r = ①21i r = ②由几何关系得 1260r i α+==︒ ③ 由图可见11i r β=+ ④又从1FSO ∆的边角关系得tan /y f β= ⑤代入数值得arctan(14.3/30.0)25.49β==︒ ⑥由②、③、④与⑥式得130r =︒,155.49i =︒ 根据折射定律,求得11sin 1.65sin i n r == ⑦ 评分标准:本题20分1. 图预解19-5的光路图4分。
未说明这是两个左右对称性的结果只给2分。
2. ①、②、③、④式各给2分,⑤式给3分,⑥式给1分,⑦式给4分。
2.把酒杯放平,分析成像问题。
图11.未斟酒时,杯底凸球面的两侧介质的折射率分别为n 1和n 0=1。
在图1中,P 为画片中心,由P 发出经过球心C 的光线PO 经过顶点不变方向进入空气中;由P 发出的与PO 成α 角的另一光线PA 在A 处折射。
设A 处入射角为i ,折射角为r ,半径CA 与PO 的夹角为θ ,由折射定律和几何关系可得n 1sin i =n 0sin r (1) θ =i +α (2)在△PAC 中,由正弦定理,有sin sin R PCiα= (3) 考虑近轴光线成像,α、i 、r 都是小角度,则有1n r i n =(4) Ri PCα=(5) 由(2)、(4)、(5)式、n 0、n l 、R 的数值及 4.8PC PO CO =-=cm 可得θ =1.31i (6) r =1.56i (7)由(6)、(7)式有r >θ (8)由上式及图1可知,折射线将与PO 延长线相交于P ',P ' 即为P 点的实像.画面将成实像于P ' 处。
2023-2024全国初中物理竞赛试题精选精编第04讲光的反射及折射(解析版)

第04讲光的反射及折射(解析版)一、多选题1.(2023·山东青岛·九年级校考竞赛)如图所示,平面镜M与水平地面的夹角为60°,若把点光源S放在平面镜与水平面的角平分线上,且OS的距离为10cm,光源S的像S′(图中未画出)则()A.O与S′的连线为竖直方向B.S与像S′的距离为20cmC.若S以速率3m/s沿OS方向向外移动,则S′以速率3m/s沿SS′连线远离S运动D.若S以速率3m/s沿OS方向向外移动,则S′以速率6m/s沿SS′连线远离S运动【答案】AC【详解】AB.如下图所示,作S的像S',SS'关于镜面对称,依题意可知,∠MOS=30°,则∠SOM,∠S′OB=90°。
所以O与S′的连线为竖直方向;在直角三角形∠AOS中,依题意可知OS的距离为10cm,所以SA的距离为5cm,S与像S′的距离为10cm;故A 符合题意,B不符合题意;CD.若S以速率3m/s沿OS方向向外移动,由图可知,SS′等于OS,所以S′以速率3m/s 沿SS′连线远离S运动,故C符合题意,D不符合题意。
故选AC。
2.(2022秋·全国·八年级校联考竞赛)身高1.5m的小明沿直线匀速运动,路灯在行进线路的正上方,某时刻人影的长度为0.6m,前进4m后,影长变为1.4m,则路灯的高度可能为()设路灯的高度为'h ,如图b 所示,当小明向右运动时,根据三角形相似原理,则有''1.50.6h x ''1.5 1.4h x 联立③④解得:'3x m ,'9h m ,故AD 符合题意,故选AD 。
A .进入人眼的光是由蜡烛的像发出的B .如果将平面镜竖直上移,则像的位置不变C .如果将图中的平面镜截掉【分析】(1)平面镜成像是反射光线的反向延长线会聚形成的,而且平面镜成虚像;(2)根据平面镜成的像与物关于镜面对称的特点分析解答;(3)平面镜所成的像与物体大小相同;(4)平面镜成像时,物体经平面镜反射后,反射光线进入人的眼睛。
全国初中应用物理竞赛试题光学部分

全国初中应用物理竞赛试题光学专题第一部分:选择题1.汽车的观后镜是用来观察车后路面情况的装置,一般为凸面镜。
正常情况下,坐在驾驶员位置的人通过左侧观后镜应该看见如图1甲所示的效果。
在某次准备驾车外出前,坐在驾驶员位置的王师傅发现,从左侧观后镜中看到的是如图1乙所示的情景。
为确保行驶安全,左侧观后镜的镜面应适当完成图2中的哪种操作( )2.将一只点燃的蜡烛靠近家里的镜子,会发现镜子中出现了多个蜡烛的像,如图7所示。
对于这种现象,下列解释中正确的是 ( )A.镜子的质量不好,反射面不平整B.光经玻璃前表面和后表面发生多次反射后形成了多个虚像C.烛焰将附近的空气加热后,由于空气密度不均匀导致的折射形成了多个虚像D.火焰抖动的过程中,由于视觉暂留效应形成的错觉3.如图17所示为16mm电影放映机放电影,这种电影放映机使用宽度为16mm的电影胶片,电影中的声音以声音信号的方式刻录在电影胶片上,如图18所示。
电影放映机正常放映时,有关放映灯泡、放映机镜头(凸透镜)、电影胶片、反光镜(凸面镜或凹面镜)的种类及其相对位置关系,提出了如图19所示的几种猜想,其中可能正确的是( )4.有一次,电影刚开始放映时,小新发现银幕上的画面全部是倒立的。
在这种情况下,下列所述的观看效果中,不可能出现的场景是 ( )A.人退着向后走B.地上的碎陶片突然聚集起来,最后形成一只漂亮的陶罐C.听到的是正常的影片中的对白D.箭倒着飞向弓5.50年前华裔物理学家高锟在光导纤维通信领域取得突破性的进展并因此获得2009年的诺贝尔物理学奖。
光纤传播信息利用的原理是( )(A)光的全反射(B)光的折射(C)光的衍射(D)光的散射6.为了节能,商场安装了智能化的电动扶梯。
无人乘行时,扶梯运转得很慢;有人走近扶梯时,它会先慢慢加速,再匀速运转。
要实现这样的功能,需要安装传感器,则一般采用的传感器为( )(A)位移传感器(B)电压传感器(C)光电传感器(D)温度传感器7.一束复色光由空气射向玻璃,发生折射而分为a、b两束单色光,其传播方向如图所示。
物理竞赛光学专题40题刷题练习(带答案详解)

物理竞赛光学专题40题刷题练习(带答案详解)一、单选题1.有3种不同波长的光,每种光同时发出、同时中断,且光强都相同,总的光强为I,脉冲宽度(发光持续时间)为τ,光脉冲的光强I随时间t的变化如图所示。
该光脉冲正入射到一长为L的透明玻璃棒,不考虑光在玻璃棒中的传输损失和端面的反射损失。
在通过玻璃棒后光脉冲的光强I随时间t的变化最可能的图示是(虚线部分为入射前的总光强随时间变化示意图)( )A.B.C.D.【答案】D因为能量是没有损失的,所以通过玻璃棒后光脉冲的光强(图中实线总面积)应该与原来的光强(虚线面积)相同。
又因为是三种不同波长的光,所以在同种介质中传播的速度都不相同,所以到达玻璃棒右端点的时间都不同,故选项D符合题意,选项ABC不合题意。
2.埃及的古夫(Khufu)金字塔内有一条狭窄通道,尽头处被一块镶有两个铜制把手的石块堵住,如图所示.考古学家曾利用一台机器人来探测石块后面隐藏的秘密,该机器人上配备的探测设备有:(甲)超声波回声探测器、(乙)导电性传感器、(丙)可穿透石块的雷达.机器人沿着通道到达石块前,进行了以下探测工作:(1)两个铜把手在石块背面是否彼此连接;(2)石块是否能够移动;(3)在石块后面是否还有其他物体;(4)石块的厚度.针对上述各项探测工作,下表中哪一选项内所选的探测设备最合适?()A.AB.BC.CD.D【答案】C研究两个铜把手在石块背面是否彼此连接,可以用导电性传感器测试(乙),因铜导电而石块不导电,若两个铜把手连接,能形成通路,加上电源就能通电;即导电表示两个把手相连,不导电表示两个把手没有连接研究石块是否能够移动,可以用超声波回声探测器(甲),测量声波碰到石块反射回来的时间差就能获得石块的速度;研究在石块后面是否还有其他物体可以用可穿透石块的雷达(丙)分析.测量石块的厚度可以用超声波回声探测器(甲),利用前后表面反射波的路程差获得.A.乙丙乙甲与分析结果不相符;故A项不合题意.B.丙乙甲丙与分析结果相符;故B项不合题意.C. 乙甲丙甲与分析结果相符;故C项符合题意.D. 甲乙乙丙与分析结果不相符;故D项不合题意.3.根据光的薄膜干涉原理,可用下图甲的装置检查被检平面是否平整.如果被检平面是平整的,那么被检平面就与透明标准样板之问形成一层很薄的、横截面为三角形的空气层,此时若用平行的单色光按图甲所示的方式照射透明样板,便可看到彼此平行的、等间距的、明暗相间的条纹,如图乙所示.如果在某次检验中看到了如图丙所示的条纹,则据此可知,被检平面有缺陷处的缺陷类型属于()A.凸起B.凹下C.可能凸起,也可能凹下D.无法判断【答案】B薄膜干涉是等厚干涉,即明条纹处空气膜的厚度相同。
高二物理竞赛光学综合测试题(打印版)

高二物理竞赛光学综合测试题(历年真题检测)姓名______________ 分数_________________一、(12分)一台二氧化碳气体激光器发生的激光功率为P=1000W,出射的光束截面积为A=1.00mm2.试问:1.当该光束以i=30°的入射角入射到一物体表面上(可视为镜面),该表面对光的反射率为R=20%,试求该表面单位面积所受的光压和切向力。
2.这束光垂直射到温度T为273K,厚度d为2.00cm的铁板上,如果有80%的光束能量被激光照射到的那一部分铁板所吸收,并使其熔化成为与光束等截面积的直圆柱形孔,这需要多长时间?已知:铁的有关参数为:热容量C=26.6J/(mol·K),密度ρ=7.9×103kg/m3,熔点T m=1797K,熔解热L m=1.49×104J/mol,摩尔质量μ=56×10-3kg/mol。
二、(15分)一折射率为n,曲率半径为R1和R2的薄双凸透镜,放在折射率为n1和n2的介质之间,如图所示,请由球面折射公式成像公式求透镜的焦距和物像公式。
【国培4.08】三、(15分)如图所示,半径为R1得到平凸透镜平放在半径为R2的圆柱形玻璃体上,求相应的牛顿环形状。
四、(18分)如图所示,L1和L2为两个共轴的薄凸透镜,OO’为其主轴,L1的焦距f1=10cm,口径(直径)为d1=4.0cm,L2的焦距f2=5.0cm,口径(直径)为d2=2.0cm。
两镜相距a=30cm。
AB为一与透镜共轴的直径为d=2.0cm的均匀发光圆盘,它有清晰的边缘,把它放在L1左侧20 cm处,它在L2右侧垂直于OO’的光屏P 上成像。
1.求光屏应放在何处;2.现发现光屏上的像的中间部分较亮,边缘部分较暗。
为了使像的边缘部分也能和中间部分一样亮,但又不改变像的位置和大小,可以在OO’上插放一个共轴的薄透镜L3。
求L3应放在何处;口径(直径)至少要多大;焦距应是多少。
高中物理竞赛专题 光学
n0 n1 sin 1 nx sin x nA sin A
3
n0 n1 sin 1 nx sin x nA sin A
P点光线的方向由x 决定:
sin
x
n0 nx
1 1 4qx
Y
nx n0 1 4qx
a
P点光线的切线斜率 kp : k p tan x
1 4qx
并按照
n ny 渐n1变1, n2为2 y距2 轴线a处的折射率, 为
常数,包裹层折射率也为n2 。光纤置于空气中,取Ox轴沿光纤轴
线方向,O为光纤端点的中心。假设 一束单色光从O点以入射角θi
进入光纤,入射面为xOy :
(亚洲奥赛04年题)
1)求出光线在光纤里的轨迹方程 y=f(x);
2)求出光可以在光纤纤芯中传播的最大入射角θiM;
x a14
4) qi =qiM时光信号沿光纤的传输速度(= x1/τ)
c
pan12
n12 n22
1
sin 2 qi
2n12
x1 ap
n12 sin 2 q
n12 n22
y
sin qiM n12 n22
vM
2cn2 n12 n22
qi O
n2
a
x1
n1
x
15
二、几何光学成像
单球面折射成像公式--阿贝不变式:
✓ 第一个交点坐标
y
x1 ap
n12 sin 2 q
n12 n22
O
n0 n2
x1
ax n1
n2 12
✓通过一线段元 ds 时间为 dt ds n ds vc
线段元 ds dx2 dy2 1 y'2 dx
全国中学生物理竞赛集锦(光学)..
全国中学生物理竞赛集锦(光学)第29届预赛3•图中L 为一薄凸透镜,ab 为一发光圆面,二者共轴, S 为与L 平行放置的屏,已知这时 ab 可在屏上成清晰的像•现将透镜切除一半,只保留主轴以上的一半透镜,这时ab 在S 上的像(B )A •尺寸不变,亮度不变. SB •尺寸不变,亮度降低. |a A L c •只剩半个圆,亮度不变. tvD •只剩半个圆,亮度降低.第29届复赛七、(16分)图中乙为一薄凸透镜.0为髙等于2, 00cm 与光轴垂 直放置的线状物,已知Q 经厶成一实像,像距为40.0cm.现于妇 的右方依次放置薄凹透镜S 厶和薄凸透镜乂以及屏巴它们之间 的距离如图所示*所有的透镜都共轴,屏与光轴垂直,3、。
焦距 已知物Q 经上述四个透镜最后在屏上成倒立的实像,橡高为0.500cm.T 1 27,5cm —H1 2&0ctn 一H2,5cm5.0cmt 厶焦距的大小为 _______________ cm f h 焦距的大小为 ______________ cm.现保持Q 、血、人和尸位置不变,而沿光轴平移鸟和最后在屏上成倒立的实像,像髙为1- 82cm,此时&到乙的距离为 ___________________ cmt 為到“的距离为 _______________ cm.最后结果保留至小数点后一位.的大小均为15. Oem第28届预赛7. (10分)近年来,由于 微结构材料”的发展,研 制具有负折射率的人工材料的光学性质及其应用, 已受人们关注.对正常介质,光线从真空射人折射 率为n 的介质时,人射角和折射角满足折射定律公 式,人射光线和折射光线分布在界面法线的两侧; 若介质的折射率为负,即 n<0,这时人射角和折射角仍满足折射定律公式,但人射光线与折射光线分 布在界面法线的同一侧•现考虑由共轴的两个薄凸 透镜L !和L 2构成的光学系统,两透镜的光心分别为 很小夹角的光线人射到 有负折射率的介质平板 介质的折射率第28届复赛七、(20分)如图所示,L 是 一焦距为2R 的薄凸透镜,MN M ; ? 为其主光轴。
国中学生物理竞赛真题大全光学
国中学生物理竞赛真题大全光学TYYGROUP system office room 【TYYUA16H-TYY-TYYYUA8Q8-全国中学生物理竞赛真题汇编---光学1.(19Y5)五、(20分)图预19-5中,三棱镜的顶角α为60,在三棱镜两侧对称位置上放置焦距均为30.0cmf=的两个完全相同的凸透镜L1和 L2.若在L1的前焦面上距主光轴下方14.3cmy=处放一单色点光源S,已知其像S'与S对该光学系统是左右对称的.试求该三棱镜的折射率.2.(21Y6)六、(15分)有一种高脚酒杯,如图所示。
杯内底面为一凸起的球面,球心在顶点O下方玻璃中的C点,球面的半径R=,O到杯口平面的距离为。
在杯脚底中心处P点紧贴一张画片,P点距O点。
这种酒杯未斟酒时,若在杯口处向杯底方向观看,看不出画片上的景物,但如果斟了酒,再在杯口处向杯底方向观看,将看到画片上的景物。
已知玻璃的折射率n1=,酒的折射率n2=。
试通过分析计算与论证解释这一现象。
3.(22Y3)三、(18分)内表面只反射而不吸收光的圆筒内有一半径为尺的黑球,距球心为2R处有一点光源S,球心p和光源s.皆在圆筒轴线上,如图所示.若使点光源向右半边发出的光最后全被黑球吸收,则筒的内半径r最大为多少?4.(16F2)(25分)两个焦距分别是1f和2f的薄透镜1L和2L,相距为d,被共轴地安置在光具座上。
1. 若要求入射光线和与之对应的出射光线相互平行,问该入射光线应满足什么条件? 2. 根据所得结果,分别画出各种可能条件下的光路示意图。
5.(17F2)如图1所示,在真空中有一个折射率为n(n>n0,n0为真空的折射率),半径为r的质地均匀的小球,频率为ν的细激光束在真空中沿直线BC传播,直线BC与小球球心O 的距离为l(l<r),光束于小球体表面的点C经折射进入小球(小球成为光传播的介质),并于小球表面的点D又经折射进入真空.设激光束的频率在上述两次折射后保持不变.求在两次折射过程中激光束中一个光子对小球作用的平均力的大小.图16.(17F6)、普通光纤是一种可传输光的圆柱形细丝,由具有圆形截面的纤芯A和包层B组成,B的折射率小于A的折射率,光纤的端面和圆柱体的轴垂直,由一端面射入的光在很长的光纤中传播时,在纤芯A和包层B的分界面上发生多次全反射.现在利用普通光纤测量流体F的折射率.实验方法如下:让光纤的一端(出射端)浸在流体F中.令与光纤轴平行的单色平行光束经凸透镜折射后会聚光纤入射端面的中心O,经端面折射进入光纤,在光纤中传播.由点O出发的光束为圆锥形,已知其边缘光线和轴的夹角为α,如图3甲所示.最后光从另一端面出射进入流体F.在距出射端面h1处放置一垂直于光纤轴的毛玻璃屏D,在D上出现一圆形光斑,测出其直径为d1,然后移动光屏D至距光纤出射端面h2处,再测出圆形光斑的直径d2,如图3乙所示.图31.若已知A和B的折射率分别为nA与nB,求被测流体F 的折射率nF的表达式.2.若nA、nB和α0均为未知量,如何通过进一步的实验以测出nF的值?7.(18F1)(22分)有一放在空气中的玻璃棒,折射率 1.5n =,中心轴线长45cm L =,一端是半径为110cm R =的凸球面.1.要使玻璃棒的作用相当于一架理想的天文望远镜(使主光轴上无限远处物成像于主光轴上无限远处的望远系统),取中心轴线为主光轴,玻璃棒另一端应磨成什么样的球面?2.对于这个玻璃棒,由无限远物点射来的平行入射光柬与玻璃棒的主光轴成小角度1φ时,从棒射出的平行光束与主光轴成小角度,求21/φφ(此比值等于此玻璃棒望远系统的视角放大率).8.(19F5)(20分)薄凸透镜放在空气中,两侧焦点和透镜中心的距离相等。
(完整版)上海物理竞赛分类试题一声光学87-99
上海物理竞赛分类试题一:声光学(87-99)1.(87)如图2所示,两个相互垂直的平面镜,在其中任一位置放置光源S ,那么它所成的像共有A 1个。
B 2个。
C 3个。
D 4个。
.2.图5中光线由玻璃进入水中时,折射线只可能通过A A 点。
B B 点。
C C 点。
D D 点。
3. 某人从平面镜里看到台钟的钟面如图1所示,这表明当时的准确时间是 ( )A.6点55分;B.10点40分;C.5点05分;D.5点20分。
4.已知凸透镜的焦距为f ,那么符合成象规律的是(多选) ···································( )A.如果得到倒立的像,则物距u 必须大于焦距f 才有可能;B.如果得到正立的像,则物距u 必须小于焦距f 才有可能;C.如果在屏上得到缩小的像,则物距u 必须大于两倍焦距才有可能;D.如果得到与物同侧的缩小的像,则物距u 必须等于焦距f 才有可能。
5. 关于物体颜色的正确说法是(多选) ····························································( )A.白纸能反射各种单色光,而黑纸能吸收各种单色光;B.由红、橙、黄、绿、蓝、靛、紫等七种颜色混在一起就得到白颜料;C.白光是由各种单色光混合而成的;D.红色透明体只能吸收红色光。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二步:数学推导 EO区内E点光线的入射角 iE最大,同样FO区内F点的 光线的入射角iF最大; R
E
O iEBiblioteka P iFnF
r 如果 P 点在右半边,则有 iF > iE , P 点在左边,则反之; 求 F点光线的最大入射角
sin OFP sin iF r R
sin iE sin EOP r EP
X
n y n0 qy
n0 sin 0 n sin
由初始条件 求出0:
sin 30 n0 sin 90 0
o o
ymax
n0 n 1
2 0
4
11
q
例5、图示三棱镜的顶角 =60o,在三棱镜两侧对称位置放置焦距
R
n
1 ic arcsin n
发光区
O
4
第二步:反射光的几何性质 考察任意一点 A 发出的 光线在球面上任意一点P 反 射后的光线
P 点的法线沿 PO 方向
P’
P
A
O
B B’
反射线、折射线、法线三者共面 因此反射光线一定在 APO 平面内,与发光面交点 B 在 AO 延长线上,即AO所在的直径上 A点发出的其它光线反射后都与 AO所在的直径相交
A Y B X O
射定律求曲面法线方程的
方法,再结合已知条件, f n n’
C’
F
可求得CC’曲线方程。
用等光程原理求解本题更简单
2
选取一条入射光线AB
和一条沿 X 轴入射
的光线; 等光程:
A
Y
C
B ( x, y)
X
n AB n'BF n'OF
几何关系:
O n n’
2
f
F
AB x
例1、证明:入射到光纤一端的光线锥的最大夹角为 证明:
arcsin n n
2 1
2 2
两次折射关系:
2
i2 i1 n1 n2
sin n1 cos i1 n1 sin i1 n2 sin i2
角越大,i1 越小,
n2 i1 必须大于临界角 i1 ic arcsin n 1
n’ = 1 A
D
q
C
B
7
全反射条件:g arcsin 1 C n 只要 g 的最小值小于临界角, 则总会有光线出来 三角几何关系
sin n sin b
D
F
q
b
E
g
n E点和F点法线的夹角 = n’ = 1 DB和水平方向的夹角: A
g b
g 最小
2
q
b 最大
2
C
B
C点发出光线 CD的 最大
tan q
n 1 1
max
2
q
8
例3: 一块平行平板,其厚度为 d,光线 从O点垂直入射, 若平板折射率按 n0 1 4qx 变化,q 为常数,并在 A 点以 角出射,求 光线轨迹、A 点的位置和平板的厚度。 Y 解: 介质折射率连续变化,可将平 板沿 X 方向切成一系列薄片,对 每层薄片应用折射定律。 折射定律决定光线在每一点的 方向,从而确定光线的轨迹; 折射定律的级联形式:
o
例4、 一个透明光学材料,折射率在 y 方向向两侧对称地 n y n0 qy ,在xoy 平面内有一光线以入射角 降低: qo=30o 射向O点,求此光线能到达离 X 轴最远的距离。
解: 从上题可知,光线进入折射率非均匀介质后弯曲, 而且是倾向于向折射率大的方向偏折。
从图可知:光线 X 轴最远点 Y 为切线在水平方向时的切点处。 0 沿Y 方向分割成一系列薄层, O 应用折射定律。 q0
O X
bx
A
d
nx n0 1 4qx
n0 n1 sin b1 nx sin b x n A sin b A
9
n0 n1 sin b1 nx sin b x n A sin b A P点光线的方向由bx 决定: nx n0 1 4qx n0 1 Y sin b x nx 1 4qx
BF
OF f
CC’曲线方程:
2
f x
2 2
2
y
C’
n' n x
n'2 y 2 2n' n n' fx 0
椭圆方程
n’ = - n’ 时:
y 2 4 fx
抛物型反射镜
3
例1 有一半导体发光管,发光区为半径为 r 的圆盘,发 光面上覆盖一折射率为 n、半径为 R 的半球型介质,如 图所示。问:要使发光区发出的全部光线在球面上不发 生全反射,介质半球的半径 R 至少应多大?(第11届全 国中学生物理竞赛题) 解: 第一步:全反射条件
P点光线的切线斜率 kp : k p tan b x
1 4qx d
bx
P(x, y) A
曲线 y = f(x)与斜率 kp: k dy p dx x 2 光线轨迹方程:y q
O
X
n0 A点的条件:n A sin 90 b A sin 和 sin b A n A sin sin 2 2 2 d yA 结论: 和 xA n n sin 2 A 0 10 2n0 q 4n0 q
sin iF sin FOP sin EOP r FP FP
iF
max
r arcsin R
max
EP FP
不发生全反射: iF
1 ic arcsin n
R nr
6
例2 图示一个盛有折射率为 n 的一体的槽,槽中的中部 扣着一个对称屋脊形的薄璧透明罩ADB,顶角为2q,罩内 为空气,整个罩子浸没在液体中,槽底 AB 的中点有一亮 点 C。 试求出:位于液体上方图示平面内的眼睛从侧面观 察可看到亮点的条件(液槽有足够的宽度;罩璧极薄,可 不计它对光线产生折射的影响) (第13届全国中学生物理竞赛予赛题) 解: 在液面上折射时,所 有光线都发生全反射时 , 则光线出不来。 n
结果得证
1
例2、设曲面 S 是有曲线 CC’ 绕 X 轴旋转而成的。曲面两 侧的折射率分别为 n 和 n’,如果所有平行于X 轴的平行光 线经曲面折射后都相交于X 轴上一点 F,则曲面成为无像 差曲面,已知OF = f,求曲线所满足的方程。如果 n ’ = n ’ , C 结果如何? 解: 分析--解本题可用折
