MATLAB的血管三维重建源代码
matlab三维图代码
1.generate grid[x,y] = meshgrid(x, y);read excel dataz1 = xlsread('data.xls');z1(1 , :) = [];z1(: , 1) = [];z = z1;change the rowsa = 1 : 21;a1 = 21 : -1 : 1;z(a, :) = z(a1, :);% mesh the resultfigure(1)mesh(x,y,z)plot the contourfigure(2)contour(x,y,z)colorbar2clear;clf;X=[1200 1600 2000 2400 2800 3200 3600 4000]; Y=[3600 3200 2800 2400 2000 1600 1200];%[X,Y]=meshgrid(x,y);Z=[1480 1500 1550 1510 1430 1300 1200 980 1500 1550 1600 1550 1600 1600 1600 1550 1500 1200 1100 1550 1600 1550 1380 1070 1500 1200 1100 1350 1450 1200 1150 1010 1390 1500 1500 1400 900 1100 1060 9501320 1450 1420 1400 1300 700 900 8501130 1250 1280 1230 1040 900 500 700];figure(1)subplot(2,2,1)contour(X,Y,Z,16)title('等高线1')xlabel('x-axis')ylabel('y-axis')subplot(2,2,3)contour3(X,Y,Z,16)title('等高线2')xlabel('x-axis')ylabel('y-axis') zlabel('z-axis') subplot(2,2,2)surf(X,Y,Z)title('地貌图1') xlabel('x-axis') ylabel('y-axis') zlabel('z-axis') subplot(2,2,4) surfc(X,Y,Z)title('地貌图2') xlabel('x-axis') ylabel('y-axis') zlabel('z-axis') figure(2)subplot(2,2,1) contour(X,Y,Z,16) title('等高线1') xlabel('x-axis') ylabel('y-axis') rotate3dsubplot(2,2,3) contour3(X,Y,Z,16) title('等高线2') xlabel('x-axis') ylabel('y-axis') zlabel('z-axis') rotate3dsubplot(2,2,2)surf(X,Y,Z)title('地貌图') xlabel('x-axis') ylabel('y-axis') zlabel('z-axis') rotate3dsubplot(2,2,4) surfc(X,Y,Z)title('地貌图2') xlabel('x-axis') ylabel('y-axis') zlabel('z-axis') rotate3dfigure(3)subplot(2,2,1)surf(X,Y,Z) title('地貌图1') xlabel('x-axis') ylabel('y-axis') zlabel('z-axis') subplot(2,2,2) surfc(X,Y,Z) title('地貌图2') xlabel('x-axis') ylabel('y-axis') zlabel('z-axis') subplot(2,2,3) surfl(X,Y,Z) title('地貌图3') xlabel('x-axis') ylabel('y-axis') zlabel('z-axis') figure(4) subplot(2,2,1) surf(X,Y,Z) title('地貌图1') xlabel('x-axis') ylabel('y-axis') zlabel('z-axis') rotate3d subplot(2,2,2) surfc(X,Y,Z) title('地貌图2') xlabel('x-axis') ylabel('y-axis') zlabel('z-axis') rotate3d subplot(2,2,3) surfl(X,Y,Z) title('地貌图3') xlabel('x-axis') ylabel('y-axis') zlabel('z-axis') rotate3d3% 读取图象数据到矩阵[A, map] = imread('input.bmp');% 得到图象信息info = imfinfo('input.bmp');w = info.Width;h = info.Height;% 创建与图象大小相对应的网格[x,y] = meshgrid(1:w,1:h);z = x - y + y - x;i = 1;j = 1;% 用图象灰度值填充高度值while (i - 1) * w + j <= w * hz(i,j) = A(i,j);j = j + 1;if j > wj = 1;i = i + 1;endend;% 绘制三维图象meshc(x,y,z);% 绘制表面surf(x,y,z,'FaceColor','interp','EdgeColor','none','FaceLighting','phong')。
matlab画三维图像的示例代码（附demo）
matlab画三维图像的⽰例代码（附demo）当我们学习surface命令时，已经看到了三维作图的⼀些端倪。
在matlab中我么可以调⽤mesh(x,y,z)函数来产⽣三维图像。
⾸先，我们⽤z=cos(x)sin(y)在-2pi ≤x,y≤ 2pi内的图像来看看:[x,y] = meshgrid(-2*pi:0.1:2*pi);z = cos(x).*sin(y);mesh(x,y,z),xlabel('x'),ylabel('y'),zlabel('z')显⽰图像如下：同样⽤mesh命令产⽣z = ye-(x2+y2)的三维图像：[x,y] = meshgrid(-2:0.1:2);z = y.*exp(-x.^2-y.^2);mesh(x,y,z),xlabel('x'),ylabel('y'),zlabel('z')下⾯绘制表⾯带有渐变颜⾊的图像，可以通过 surf 和 surfc 命令实现，只要简单更改上⾯例⼦中的命令为：surf(x,y,z),xlabel('x'),ylabel('y'),zlabel('z')则图像如下所⽰，图像表⾯的颜⾊与⾼度是相称的:若使⽤surfc则会在图像中留下映像：surfc(x,y,z),xlabel('x'),ylabel('y'),zlabel('z')还可以调⽤surfl（命令中的'l'表⽰这是⼀个光照表⾯ lighted surface）命令显⽰三维光照物体的表⾯，可以使⽤这个命令产⽣没有线条的三维图像，图像还可以是彩⾊的或灰度的。
例如仍然产⽣函数z = ye-(x2+y2)的灰度图像，图像中的阴影可设置为flat、interp、faceted：surfl(x,y,z),xlabel('x'),ylabel('y'),zlabel('z')shading interp;colormap(gray);下⾯我们使⽤matlab内置函数来产⽣像球形或圆柱形这样的基本图像，例如：t = 0:pi/10:2*pi;[X,Y,Z] = cylinder(1+sin(t));surf(X,Y,Z),colormap('default');axis square会得到如下图像：试试另⼀个稍微有点不同的函数，阴影设置为faceted：t = 0:pi/10:2*pi;[X,Y,Z] = cylinder(1+cos(t));surf(X,Y,Z),shading faceted;axis square若将阴影设置为shading flat，则图像显⽰为：以上就是本⽂的全部内容，希望对⼤家的学习有所帮助，也希望⼤家多多⽀持。
三维血管重建优秀论文含源代码
三维血管重建优秀论文含源代码Prepared on 21 November 2021血管的三维重建摘要本文探讨血管的三维重建，由血管的相继100张平行切片图像计算血管的中轴线与半径，并绘制血管在三个坐标平面上的投影。
由于血管的表面是由球心沿着某一曲线（称为中轴线）的球滚动包络而成，由此我们得出结论：每个切片一定包含滚动球的大圆，并且它一定为切片的最大内切圆，而最大圆所对应的半径即为血管半径，所以求血管半径就转化为求每一个切片内部的点到切片外部轮廓的最大半径。
首先，读取100张血管切面图，把它们转换成Logical矩阵，从中提取切片截面轮廓点构成一个新的矩阵。
然后找到原图片矩阵中像素点的内点（切片图片中轮廓线中的点），从而得到内点到切片轮廓点的最小距离矩阵和最小距离中的最大值矩阵，最大值即为血管半径。
最后计算所有切片的血管半径，并对这些半径求平均值，得到平均血管半径为：μm。
由100张切片的最大内切圆圆心坐标拟合得出中轴线方程以及其在三个坐标平面内的投影曲线方程。
由中轴线得到血管的三维立体重建图，用平面)74=iiZ去截血,0(,=2449,,管的三维立体重建图，得到新的4张截面图。
把它们分别与题设中的对应截面进行内点个数对比。
我们定义两张切片所共同拥有的内点个数与原切片内点个数的比值为重合度。
计算得到平均重合度为：% 。
关键词：血管半径中轴线切片重建（来自作者：欢迎各界人士批评指正，。
文章作于2011年8月10日，陕西科技大学理学院实验室）1问题的重述断面可用于了解生物组织、器官等的形态。
例如，将样本染色后切成厚约1μm的切片，在显微镜下观察该横断面的组织形态结构。
如果用切片机连续不断地将样本切成数十、成百的平行切片，可依次逐片观察。
根据拍照并采样得到的平行切片数字图象，运用计算机可重建组织、器官等准确的三维形态。
假设某些血管可视为一类特殊的管道，该管道的表面是由球心沿着某一曲线（称为中轴线）的球滚动包络而成。
CT图像三维重建(附源码)
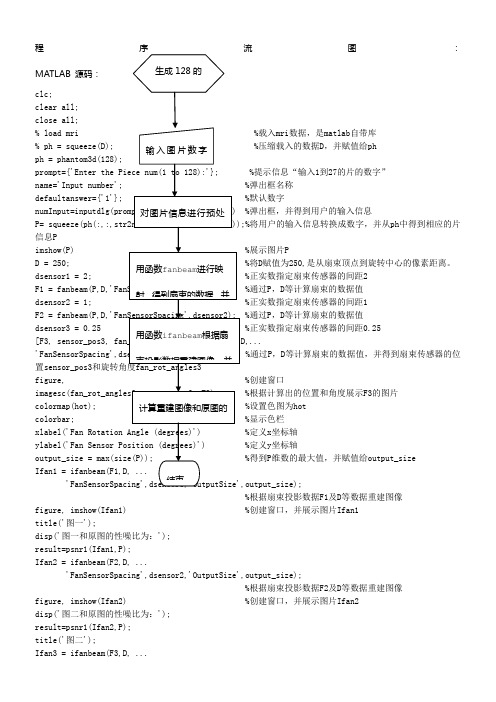
程序流图：MATLAB 源码： clc;clear all;close all;% load mri %载入mri 数据，是matlab 自带库% ph = squeeze(D); %压缩载入的数据D ，并赋值给ph ph = phantom3d(128);prompt={'Enter the Piece num(1 to 128):'}; %提示信息“输入1到27的片的数字”name='Input number'; %弹出框名称defaultanswer={'1'}; %默认数字numInput=inputdlg(prompt,name,1,defaultanswer) %弹出框，并得到用户的输入信息 P= squeeze(ph(:,:,str2num(cell2mat(numInput))));%将用户的输入信息转换成数字，并从ph 中得到相应的片信息Pimshow(P) %展示图片PD = 250; %将D 赋值为250,是从扇束顶点到旋转中心的像素距离。
dsensor1 = 2; %正实数指定扇束传感器的间距2F1 = fanbeam(P,D,'FanSensorSpacing',dsensor1); %通过P ，D 等计算扇束的数据值 dsensor2 = 1; %正实数指定扇束传感器的间距1F2 = fanbeam(P,D,'FanSensorSpacing',dsensor2); %通过P ，D 等计算扇束的数据值dsensor3 = 0.25 %正实数指定扇束传感器的间距0.25 [F3, sensor_pos3, fan_rot_angles3] = fanbeam(P,D,...'FanSensorSpacing',dsensor3); %通过P ，D 等计算扇束的数据值，并得到扇束传感器的位置sensor_pos3和旋转角度fan_rot_angles3figure, %创建窗口imagesc(fan_rot_angles3, sensor_pos3, F3) %根据计算出的位置和角度展示F3的图片colormap(hot); %设置色图为hot colorbar; %显示色栏xlabel('Fan Rotation Angle (degrees)') %定义x 坐标轴ylabel('Fan Sensor Position (degrees)') %定义y 坐标轴output_size = max(size(P)); %得到P 维数的最大值，并赋值给output_size Ifan1 = ifanbeam(F1,D, ... 'FanSensorSpacing',dsensor1,'OutputSize',output_size);%根据扇束投影数据F1及D 等数据重建图像figure, imshow(Ifan1) %创建窗口，并展示图片Ifan1title('图一');disp('图一和原图的性噪比为：');result=psnr1(Ifan1,P);Ifan2 = ifanbeam(F2,D, ...'FanSensorSpacing',dsensor2,'OutputSize',output_size);%根据扇束投影数据F2及D 等数据重建图像figure, imshow(Ifan2) %创建窗口，并展示图片Ifan2disp('图二和原图的性噪比为：');result=psnr1(Ifan2,P);title('图二');Ifan3 = ifanbeam(F3,D, ...生成128的输入图片数字对图片信息进行预处用函数fanbeam 进行映射，得到扇束的数据，并用函数ifanbeam 根据扇束投影数据重建图像，并计算重建图像和原图的结束'FanSensorSpacing',dsensor3,'OutputSize',output_size);%根据扇束投影数据F3及D等数据重建图像figure, imshow(Ifan3) %创建窗口，并展示图片Ifan3title('图三');disp('图三和原图的性噪比为：');result=psnr1(Ifan3,P);function [p,ellipse]=phantom3d(varargin)%PHANTOM3D Three-dimensional analogue of MATLAB Shepp-Logan phantom% P = PHANTOM3D(DEF,N) generates a 3D head phantom that can% be used to test 3-D reconstruction algorithms.%% DEF is a string that specifies the type of head phantom to generate.% Valid values are:%% 'Shepp-Logan' A test image used widely by researchers in% tomography% 'Modified Shepp-Logan' (default) A variant of the Shepp-Logan phantom% in which the contrast is improved for better% visual perception.%% N is a scalar that specifies the grid size of P.% If you omit the argument, N defaults to 64.%% P = PHANTOM3D(E,N) generates a user-defined phantom, where each row% of the matrix E specifies an ellipsoid in the image. E has ten columns,% with each column containing a different parameter for the ellipsoids:%% Column 1: A the additive intensity value of the ellipsoid% Column 2: a the length of the x semi-axis of the ellipsoid% Column 3: b the length of the y semi-axis of the ellipsoid% Column 4: c the length of the z semi-axis of the ellipsoid% Column 5: x0 the x-coordinate of the center of the ellipsoid% Column 6: y0 the y-coordinate of the center of the ellipsoid% Column 7: z0 the z-coordinate of the center of the ellipsoid% Column 8: phi phi Euler angle (in degrees) (rotation about z-axis)% Column 9: theta theta Euler angle (in degrees) (rotation about x-axis) % Column 10: psi psi Euler angle (in degrees) (rotation about z-axis)%% For purposes of generating the phantom, the domains for the x-, y-, and % z-axes span [-1,1]. Columns 2 through 7 must be specified in terms% of this range.%% [P,E] = PHANTOM3D(...) returns the matrix E used to generate the phantom. %% Class Support% -------------% All inputs must be of class double. All outputs are of class double.%% Remarks% -------% For any given voxel in the output image, the voxel's value is equal to the% sum of the additive intensity values of all ellipsoids that the voxel is a% part of. If a voxel is not part of any ellipsoid, its value is 0.%% The additive intensity value A for an ellipsoid can be positive or negative;% if it is negative, the ellipsoid will be darker than the surrounding pixels.% Note that, depending on the values of A, some voxels may have values outside % the range [0,1].%% Example% -------% ph = phantom3d(128);% figure, imshow(squeeze(ph(64,:,:)))%% Copyright 2005 Matthias Christian Schabel (matthias @ stanfordalumni . org) % University of Utah Department of Radiology% Utah Center for Advanced Imaging Research% 729 Arapeen Drive% Salt Lake City, UT 84108-1218%% This code is released under the Gnu Public License (GPL). For more information, % see : /copyleft/gpl.html%% Portions of this code are based on phantom.m, copyrighted by the Mathworks %[ellipse,n] = parse_inputs(varargin{:});p = zeros([n n n]);rng = ( (0:n-1)-(n-1)/2 ) / ((n-1)/2);[x,y,z] = meshgrid(rng,rng,rng);coord = [flatten(x); flatten(y); flatten(z)];p = flatten(p);for k = 1:size(ellipse,1)A = ellipse(k,1); % Amplitude change for this ellipsoidasq = ellipse(k,2)^2; % a^2bsq = ellipse(k,3)^2; % b^2csq = ellipse(k,4)^2; % c^2x0 = ellipse(k,5); % x offsety0 = ellipse(k,6); % y offsetz0 = ellipse(k,7); % z offsetphi = ellipse(k,8)*pi/180; % first Euler angle in radianstheta = ellipse(k,9)*pi/180; % second Euler angle in radianspsi = ellipse(k,10)*pi/180; % third Euler angle in radianscphi = cos(phi);sphi = sin(phi);ctheta = cos(theta);stheta = sin(theta);cpsi = cos(psi);spsi = sin(psi);% Euler rotation matrixalpha = [cpsi*cphi-ctheta*sphi*spsi cpsi*sphi+ctheta*cphi*spsi spsi*stheta;-spsi*cphi-ctheta*sphi*cpsi -spsi*sphi+ctheta*cphi*cpsi cpsi*stheta;stheta*sphi -stheta*cphi ctheta];% rotated ellipsoid coordinatescoordp = alpha*coord;idx = find((coordp(1,:)-x0).^2./asq + (coordp(2,:)-y0).^2./bsq + (coordp(3,:)-z0).^2./csq <= 1);p(idx) = p(idx) + A;endp = reshape(p,[n n n]);return;function out = flatten(in)out = reshape(in,[1 prod(size(in))]);return;function [e,n] = parse_inputs(varargin)% e is the m-by-10 array which defines ellipsoids% n is the size of the phantom brain imagen = 128; % The default sizee = [];defaults = {'shepp-logan', 'modified shepp-logan', 'yu-ye-wang'};for i=1:narginif ischar(varargin{i}) % Look for a default phantomdef = lower(varargin{i});idx = strmatch(def, defaults);if isempty(idx)eid = sprintf('Images:%s:unknownPhantom',mfilename);msg = 'Unknown default phantom selected.';error(eid,'%s',msg);endswitch defaults{idx}case 'shepp-logan'e = shepp_logan;case 'modified shepp-logan'e = modified_shepp_logan;case 'yu-ye-wang'e = yu_ye_wang;endelseif numel(varargin{i})==1n = varargin{i}; % a scalar is the image size elseif ndims(varargin{i})==2 && size(varargin{i},2)==10e = varargin{i}; % user specified phantomelseeid = sprintf('Images:%s:invalidInputArgs',mfilename);msg = 'Invalid input arguments.';error(eid,'%s',msg);endend% ellipse is not yet definedif isempty(e)e = modified_shepp_logan;endreturn;%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% Default head phantoms: % %%%%%%%%%%%%%%%%%%%%%%%%%%%%%function e = shepp_logane = modified_shepp_logan;e(:,1) = [1 -.98 -.02 -.02 .01 .01 .01 .01 .01 .01];return;function e = modified_shepp_logan%% This head phantom is the same as the Shepp-Logan except% the intensities are changed to yield higher contrast in% the image. Taken from Toft, 199-200.%% A a b c x0 y0 z0 phi theta psi% -----------------------------------------------------------------e = [ 1 .6900 .920 .810 0 0 0 0 0 0-.8 .6624 .874 .780 0 -.0184 0 0 0 0-.2 .1100 .310 .220 .22 0 0 -18 0 10-.2 .1600 .410 .280 -.22 0 0 18 0 10.1 .2100 .250 .410 0 .35 -.15 0 0 0.1 .0460 .046 .050 0 .1 .25 0 0 0.1 .0460 .046 .050 0 -.1 .25 0 0 0.1 .0460 .023 .050 -.08 -.605 0 0 0 0.1 .0230 .023 .020 0 -.606 0 0 0 0.1 .0230 .046 .020 .06 -.605 0 0 0 0 ];return;function e = yu_ye_wang%% Yu H, Ye Y, Wang G, Katsevich-Type Algorithms for Variable Radius Spiral Cone-Beam CT %% A a b c x0 y0 z0 phi theta psi% -----------------------------------------------------------------e = [ 1 .6900 .920 .900 0 0 0 0 0 0-.8 .6624 .874 .880 0 0 0 0 0 0-.2 .4100 .160 .210 -.22 0 -.25 108 0 0-.2 .3100 .110 .220 .22 0 -.25 72 0 0.2 .2100 .250 .500 0 .35 -.25 0 0 0.2 .0460 .046 .046 0 .1 -.25 0 0 0.1 .0460 .023 .020 -.08 -.65 -.25 0 0 0.1 .0460 .023 .020 .06 -.65 -.25 90 0 0.2 .0560 .040 .100 .06 -.105 .625 90 0 0-.2 .0560 .056 .100 0 .100 .625 0 0 0 ]; return;% func——计算两幅图像的psnr值function result=psnr1(in1,in2)z=mse(in1,in2);result=10*log10(255.^2/z)% plot(result)function z=mse(x,y)if ndims(x)==3x=rgb2gray(x);endif ndims(y)==3y=rgb2gray(y);endx=double(x);y=double(y);[m1,n1]=size(x);[m2,n2]=size(y);m=min(m1,m2);n=min(n1,n2);z=0;for i=1:mfor j=1:nz=z+(x(i,j)-y(i,j)).^2;endendz=z/(m*n);。
血管的三维重建论文(完结版)2
血管的三维重建摘要本文对于血管的三维重建问题，通过分析给定图片的像素数据，通过以下方法完成了血管的三维重建。
首先我们假定血管为等径管道，将血管看作半径不变的球沿着一条中轴线滚动形成。
根据题目中提供的100张BMP图片的像素点坐标数据，通过分析其几何特性，给出寻找其中轴线和半径的方法，由此找到每张图片中最大内切圆的圆心和半径，利用平均法，得到半径的平均值约为29.25 m.，即为管道半径。
接下来利用100个圆心的坐标利用最小二乘法拟合得到中轴线的方程：x t=7.9021t7−1.6321t6+0.1378t5−0.0056t4+0.0001t3y t=−2.9429t7+0.6330t6−0.0546t5+0.0023t4−0.0001t3z t=t通过对圆心坐标点绘制出的曲线与拟合后的曲线进行对比，发现拟合的曲线与得到的圆心坐标点非常吻合，从而更好的反映了中轴线上各点。
然后再用枚举法以得到的圆心坐标点为球心，画出100个球面上的点组成的还原图与100张切片的边界叠加成的还原图进行比对，形状相符，成功的还原了血管的三维图像。
关键词：血管；三维重建；像素；还原；最小二乘拟合；滚动法；枚举法1.问题的重述断面可用于了解生物组织、器官等的形态。
例如，将样本染色后切成厚约1 m的切片，在显微镜下可以观察该横断面的组织形态结构。
如果用切片机连续不断地将样本切成数十、成百的平行切片，可依次逐片观察。
根据拍照并采样得到的平行切片数字图象，运用计算机可重建组织、器官等准确的三维形态。
假设某些血管可视为一类特殊的管道，该管道的表面是由球心沿着某一曲线（称为中轴线）的球滚动包络而成。
例如圆柱就是这样一种管道，其中轴线为直线，由半径固定的球滚动包络形成。
现有某管道的相继100张平行切片图像，记录了管道与切片的交。
图像文件名依次为0.bmp、1.bmp、…、 99.bmp，格式均为BMP，宽、高均为512个像素（pixel）。
血管三维重建的数学模型
血管三维重建的数学模型刘俊健、吴友玲、徐勇哲[摘要]:本文探讨了血管的三维重建问题.我们首先利用数字图象处理的相关技术,从100张图中读取出相应数据,然后以定位所需的相关参数(包括中心轴线和半径)为目标,主要运用了包络面相关理论及几何拓扑网络中的相关知识得出了如下结论：切片一定包含一个滚动球的大圆,并且它恰好是切片内的最大圆.运用这些结论设计出有效的算法,利用数学软件(Matlab 及Maple)和计算机技术,对100个切片编程求解,找出切片所包含的最大圆,即得到中心轴线与100个切片交点的坐标及大圆半径.经过误差分析确定出管道半径为69849.29=r ,并给出了中心轴线上点的坐标,最后我们还绘制出中心轴线在zx yz xy ,,平面上的投影图.关键词：三维重建;最大圆;中轴线;有障碍物的最大空隙问题1 问题的提出生物组织连续切片的计算机三维重建技术是把一系列切片的图象，通过计算机进行处理,从而得到该生物组织立体结构的一种方法.在切片图象内部寻找定位结构,是此核技术的关键,同时也是目前国内外三维重建技术的共同难题.解决此难题的一个重要方向是通过提取切片中二维图象的数据信息,建立模型,以达到定位效果.假设某类血管表面可视为由球心沿着一曲线（称为中轴线）的球滚动包络而成.现有一此类血管相继100张平行切片图象,记录了管道与切片的交.图象格式为BMP,宽、高均为512个象素（pixel ）.假设管道中轴线与每张切片有且只有一个交点,球半径固定,切片间距以及图象象素的尺寸均为1.如果取坐标系的Z 轴垂直于切片,第1张切片为平面0=Z ,第100张切片为平面99=Z .z Z =切片图象中象素在文件中出现的前后次序为 （-256,-256,z ）,（-256,-255,z ）,…（-256,255,z ）, （-255,-256,z ）,（-255,-255,z ）,…（-255,255,z ）, ……（ 255,-256,z ）,（ 255,-255,z ）,…（255,255,z ）.试计算管道的中轴线与半径,给出具体的算法,并绘制中轴线在XY 、YZ 、ZX 平面的投影图.2 基本假设和符号说明1) 假设血管为实心体,其表面为一包络面；2) 假设管道中轴线与每张切片有且只有一个交点,滚动球的半径固定； 3) 假设切片间距以及图象的象素尺寸均为1； 4) m 表示中轴线,是一空间曲线； 5) r 表示滚动球的半径；6) S 表示球心沿中轴线滚动形成的包络面；7) V 表示由曲面S 与平面0=Z ,99=Z 所围成的管道体； 8) i F 表示管道体V 与平面i Z =的切片； 9) i e 表示i F 的边界.没有说明的符号在文中初次引用时均作出了说明.3 问题的分析与模型的建立首先分析题目中所给出的100张图片.对这100张黑白图片通过计算机图象处理,我们可以观察到其切片呈现一个旋转渐变的过程,如图（一）因此我们估计该血管的形状类似一条螺旋管.只要将这一百张切片在空间中定位,由于切片间距非常小（为一个象素）,所以就可以近似地还原出血管的三维结构.现先对每张图作出一些数据上的分析.针对BMP 图象的存储格式,我们将所给的图片转为二值图象处理.所谓二值图象,就是只有黑白两个灰度级,即象素灰度级非1即0.我们可以从每张图中读取出一个512阶的0-1矩阵.其中0表示象素为黑色.1表示象素为白色.我们可以给出矩阵元素的位置与题目中所定坐标系之间的坐标变换.即矩阵的第i 行,第j 列的元素坐标相应转化为)256,257(i j --.现在我们把问题转化为数学语言.在笛卡尔坐标系内,有一半径为r 的球,沿空间的某一曲线m （称为中轴线）,滚动包络形成空间曲面S ,现有100张平面图,99,,1,0===Z Z Z ,其中0Z ,99Z 与曲面S 围成一实心管道体,现题目就是要求我们求出该管道体的中轴线m 及滚动球的半径,并要给出中轴线m 在XY,YZ,ZX 平面上的内投影图.现设管道V 中轴线m 的方程为：⎪⎩⎪⎨⎧===)()()(t z z t y y t x x 其中99)(,0)(],,[990990==∈t Z t Z t t t 由于管道体中心轴线m 与每张切片有且只有一个交点,则不妨设中心轴m 与切片)990( =i F i 有且只有点)),(),((i t Y t X O i ,i Z 与1+i Z 的间距为1个象素,在如此小的间距下,我们可以用100个交点i O 近似地刻画中轴线.结论1：管道体V 与平面i Z =的切片i F 一定包含一个过滚动球球心,半径为r 的圆A . 现证明如下：以中心轴m 与平面i F 的唯一交点)),(),((i i Y t X O i 为球心（亦即包含一个滚动球的大圆）,r 为半径所作出的球A 与平面i Z =交于圆A ,其中圆A 的半径为r ,由于球A 在管道体V 内,所以球A 与平面i Z =的切片也在管道体与i Z =的切片内,亦即圆在i F 内,结论1得证.结论2：管道体V 与平面i Z =的切片i F 内的最大圆恰好是滚动球中过球心半径为r 的圆A ,并且最大圆唯一.现证明如下： 由中轴线m 的方程：⎪⎩⎪⎨⎧===)()()(t Z z t Y y t X x ],[990t t t = )1( 其中99)(,0)(990==t Z t Z . 有曲面S （即包络面）的方程来：⎩⎨⎧=-+-+-=-+-+-0)('))(()('))(()('))(())(())(())((2222t Z t Z z t Y t Y y t X t X x r t Z z t Y y t X x )2(现考虑i Z =,取't t =使得i t Z =)'(则⎩⎨⎧=-+-=-+-0)('))(()('))(())'(())'((0000222t Y t Y y t X t X x r t Y y t X x )3( （3）式的几何意义是,在切片i F 的边界曲线i S 上的点与中轴线和切片的交点的最近距离为r ,即可作以))'(),'((t Y t X 为圆心,半径为r 的圆.边界曲线i S 和中轴线m 与切片i F 的交点)),(),((i t Y t X O i 的距离达到最大值r .又由于每一个i 属于集合{}99,,1,0 ,i z =与中轴线⎪⎩⎪⎨⎧===)()()(t Z z t Y y t X x 只有唯一交点,故只有唯一点t 满足i t Z =)(,所以切片包含的最大圆唯一.结论2得证.至此,我们只要在每个切片上找出一个能被切片i F 包含的最大圆的圆心,即为该切片与中轴线的交点.就一般包络面而言,切片的最大圆应是唯一的,但由于数据存储误差,我们可能会找到多于一个的最大圆.所以我们需要一个能找出多人最大圆的可行算法.利用以上的分析和结论,我们试图求出管道体半径r 及每个切片与中轴线的100个交点,由于BMP 存储方式的限制,每个切片实际是由有限多个点组成.我们利用几何拓扑网络中的有障碍物的最大空隙问题解法,把障碍物视为半径为0的圆,因此我们可以在切片上作如下约束优化：222)()(R s.t.Rmax i i y y x x ---=其中,i i i i F y x S y x ∈∈),( ),(i F 为管道体切片,i S 为i F 的边界,且i F 、i S 均为限点集.上述模型可简化为如下：))()((22i i y y x x Min Max r -+-=其中i i i i F y x S y x ∈∈),( ),( i F 为管道体切片,i S 为i F 的边界,且i F ,i S 均为限点集,关于r 的求解和圆心坐标,算法及求解结果将于下部分给出.4 模型的求解与算法的实现我们根据上面的在切片上进行约束优化思想,利用计算机编程来寻找最优解.由于切片图象是用BMP格式存储的,因此它都有是由一些有限的点构成,我们用Matlab读入每张图,用一个512⨯512的0-1矩阵表示,其中0表示象素为黑色的点.去掉所有非零元素,并记下所有零元素在矩阵中出现的位置,再转化为题中的笛卡儿坐标系的坐标,这样,就可以用描点方法作出切片的用点集表示的图,如果我们对100个切片上的点都在空间中描出来,那么就可以大体反映出管道体的三维结构.受图片存储的精度所限,只能在表示切片的点集上寻找最大圆心.我们根据上节中所列出来的约束优化思想,再利用计算机编程的方法来寻找最大圆.首先我们要作出切片的边界.由于图上的点都是呈阵列排布的,只要依次取切片上的点,选出与1相邻的0点即为切片的边界.现在按如下算法寻找最大圆的圆心和半径:1．取出切片点集中的一个点,再算出该点与边界上各点的距离,找出最小值,记为h,这就是以该点为圆心所能作出的包含于切片的最大圆的半径.2．继续取点集中的下一个点,再算出该点与边界上各点的距离,再找出最小值与 h进行比较,若比h大则把值赋给h,若与h相等则把值赋给h并记下坐标,同时还把这个点都记起来,这样就保证若最大圆不唯一,也可把所有最大圆找出来.3．取遍切片点集上的所有点运行第二步,最后得出的h即为该切片中最大圆的半径,相应该点的坐标即为切片与中轴线交点的坐标.()．源程序见附录我们记每张切片上点的数目为n1,切片边界上点的数目为n2,显然n2远小于n1,我们要进行n1重循环,每一次循环作n2次比较,其复杂性不超过O()21n,所以,此算法为有效算法.我们用Matlab编程进行搜索,利用Matlab强大的矩阵运算功能,在编程时进行向量化,大大提高了程序的效率,对100张图分别算出如下半径和交点的坐标：注：上表中（X,Y,Z）表示与中轴线交点的笛卡儿坐标.R表示在切片上最大圆半径.由于图象精度问题及算法的误差.每张切片上算出的半径有微小差异,我们根据误差产生的原因进行分析（详细分析过程下节给出）,取出所有半径中最大值r=29.69849,即为题目所要求的半径,把所得的100个中轴线上的点在空间中描出来,得到结果如图（二）所示：图（二）为了不影响最终结果的客观性和全面性,我们对数据可以不作任何拟合,以图表的方式给出结果,以供有需要人士随时查阅.我们已经求出中轴线上100个紧密的点,因此中轴线在XY,YZ,ZX平面上的投影应该是一些紧密的点,为直观起见,我们把这些点用线段连接起来,得到的投影图如下：在XY平面的投影在XZ平面的投影在YZ平面的投影５ 结果分析由于BMP 图象是用点阵来表示的,用它读取出来的数据只能近似还原出原来的结构,因此得到的中轴线上的点必然有一定的误差,不过由于中轴线上的点非常密,作成的图表的效果也很不错.对于得到的100个半径的数据,我们取其中的最大值作为管道的半径,是基于如下的误差分析：由于程序算法可知,我们得到的最大圆的半径是切片点集中的所有点到边界点集的最短路距离中的最大值,所以由该点作出的圆不会超出切片的范围内,但由于我们找最大圆时,圆心都定在象素点上,而实际切片包含的最大圆的圆心可能不在象素点上,如图（三）所示：在正方形点集图上,每一个交点代表一个象素.我们取象素点为圆心找最大圆,只能找到半径为1的圆,其中中间的四个交点都可能是圆心,它实际包含的最大圆的半径应为1.5,圆心落在大正方形的中心点（非象素点）上.所以,当所得的大圆与切片只有一个切点时,大圆半径一定仍可以扩大,但所扩大的长度不会超过一个象素.而且有两段边界出现平行时,会出现不止一个最大圆圆心.而我们在程序中也考虑了进去,但并没有发现有出现这种情况.因此,只要提高图象的分辨率,便可减少误差.但由于点与点之间总有间隔.分辨率不可能无穷大,所以误差总是存在的.因此对于我们得出的100个半径值,我们取出其中最大值便是误差最小的,而我们这批数据找到的最大值为29.69849,最小值为28.86174,相差为0.83675,误差没有超过一个象素.CD图（三）６模型的改进与推广考虑到生物结构的完整性和连续性,我们当然希望得到的100个点能连成较为光滑的空间曲线,但实验数据在坐标平面上往往表现为一些离散的点.直接用这些观测点依序连结的折线来反映其变化情势常常过于粗糙.因此需要给出光滑的实验曲线,通常要求这条实验曲线与观测数据的残差平方和最小.对于本模型中的数据点,我们可作进一步的调整,从误差分析,我们可以知道许多切片上取得“最大圆”实质并非真正最大圆,但它必与已切片相切于一点,而与该点切线垂直的方向上的圆点,与切片的点相距应小于１个象素,所以其圆心可以适当向这个方向微调.经过调整修复后,我们还原出近似的三维血管图象如下：在误差分析时,我们发现误差很大程度上是由图象存储的精度决定的,只要数据足够精确,我们的模型将会得到更准确的结果,误差将会大大的减少.随着计算机技术的飞速发展和分辨电子显微学的发展,我们必能得出更为完善的结果.参考文献1.周培德、卢开澄. 计算几何. 北京：清华大学出版社.19992.夏良正.数学图象处理.南京：东南出版社. 1998.83.张宜华、史惠康.精通MA TLAB5. 北京：清华大学出版社.1999,６4.李世奇、杜梦琴.计算机代数系统应用程序设计.重庆：重庆大学生出版社.1999.45.数学手册编写组.数学手册.北京：高等教育出版社.19796.何昆等.生物组织细胞连续切三维重建的研究进展. 军事医学科学院刊. 2000年第24卷北京.2000.3 编辑:许智杰方创彬。
MATLAB血管源代码
附录1：图像二值矩阵的0-1互换的matlab程序代码（zhuanhua.m） function b0=zhuanhua(b0) %图像二值矩阵的0-1互换for i=1:512for j=1:512if b0(i,j)==1b0(i,j)=0;else b0(i,j)=1;endendend附录2：求各切片的最大内切圆的半径及圆心坐标matlab程序代码（ff.m） function [r, zhongxindian]=ff %输出各切片最大内切圆半径及圆心坐标a=zeros(512,512);b=zeros(512,512);for i=1:512for j=1:512a(i,j)=i-257; %横坐标的对应b(i,j)=j-257; %纵坐标的对应endend %图像在xyz面上的x轴、y轴坐标zhongxindian=zeros(100,2);r=zeros(100,1);for k=0:99t=strcat('f:/',int2str(i),'.bmp');b=imread(t);b=zhuanhua(b);%将01互换blunkuo=edge(b,'sobel');%提取轮廓bgujia=bwmorph(b,'skel',inf);%提取骨架%寻找内切圆[x0,y0,v0]=find(b0lunkuo);[a0,b0,c0]=find(b0gujia);m=length(a0);n=length(x0);juli=zeros(m,n);cunfang=zeros(m,2);for i=1:mfor j=1:np1=a0(i);q1=b0(i);p2=x0(j);q2=y0(j);juli(i,j)=sqrt((a(p1,q1)-a(p2,q2))^2+(b(p1,q1)-b(p2,q2))^2);%骨架上的各个点到轮廓的距离end[zx,zxxh]=min(juli(i,:));%骨架上一点到轮廓的最短距离即以骨架上各个点为圆心的内切园的半径cunfang(i,1)=zx;cunfang(i,2)=zxxh;end[zd,zdxh]=max(cunfang(:,1));%寻找半径中最大的半径和其对应的圆心坐标g=a0(zdxh);h=b0(zdxh);zhongxindian(k+1,1)=a(g,h);zhongxindian(k+1,2)=b(g,h);r(k+1)=zd;end附录3：通过计算不同次数多项式拟合的偏差平方和确定拟和次数的matlab程序代码（pczx.m）function j=pczx(z,t) %根据不同次数的多项式拟合与原图数据偏差平方和的大小来确定多项式拟和的次数delta=zeros(10,1);for k=1:10[p,s]=polyfit(z,t,k);delta(k)=s.normrend[i,j]=min(delta);附录4：根据轮廓画出血管的三维图像的matlab程序代码 for b=0:99 %提取原图的轮廓，根据轮廓画出血管的三维图像m1=imread([int2str(b),'.bmp']);m(:,:,b+1)=edge(m1,'sobel');endfor k=0:99for i=1:512for j=1:512if (m(i,j,k+1)==1)plot3(i,j,k+1,'r-.');hold onendendendendgrid ontitle('血管三维图')rotate3dhold off附录5：绘制中轴线及在各平面的投影图matlab程序代码 format longpx=polyfit(z,x,7);%x,z的7次多项式拟合x1=polyval(px,z);py=polyfit(z,y,5);%y,z的5次多项式拟合y1=polyval(py,z);figure(1); %画中心轴线图plot3(x1,y1,z)grid onxlabel('X轴');ylabel('Y轴');zlabel('Z轴');title('血管中轴线图');figure(2); %画中心轴线在xoz平面上的投影plot(z,x1,'-r')ylabel('Z轴');xlabel('X轴')title('血管中轴线XOZ平面投影图');grid onfigure(3);%画中心轴线在yoz平面上的投影plot(z,y1,'-b')xlabel('Z轴');ylabel('Y轴');title('血管中轴线YOZ平面投影图');grid onfigure(4);%画中心轴线在xoy平面上的投影plot(x1,y1,'-g')xlabel('X轴');ylabel('Y轴');title('血管中轴线XOY平面投影图');grid on附录6：求第pn张拟合图的轮廓的二值矩阵的matlab程序代码（dian.m） function pnjj=dian(px,py,pn) %输出pnjj，为第pn张拟合图片的轮廓二值矩阵a=zeros(991);b=zeros(991);q=zeros(991);w=zeros(991);r=zeros(1,2);s=zeros(1,2);k=1;for c=0:0.1:99a(k)=7*px(1)*c.^6+6*px(2)*c.^5+5*px(3)*c.^4+4*px(4)*c.^3+3*px(5)*c.^2+2*px(6)*c+px(7); b(k)=4*py(1)*c.^3+3*py(2)*c.^2+2*py(3)*c+py(4); %中心轴线方程关于z的导数即[a(k),b(k),1]为z在k处的切线的方向向量q(k)=px(1)*c.^7+px(2)*c.^6+px(3)*c.^5+px(4)*c.^4+px(5)*c.^3+px(6)*c.^2+px(7)*c+px(8);w(k)=py(1)*c.^5+py(2)*c.^4+py(3)*c.^3+py(4)*c.^2+py(5)*c; %中心轴线方程在z=k处的x,y值k=k+1;end%提取新的截痕u=[];v=[];syms x yk=1;for i=0:0.1:99m=a(k)*(x-q(k))+b(k)*(y-w(k))+(pn-i);n=(x-q(k))^2+(y-w(k))^2+(pn-i)^2-29.49^2;[g,h]=solve(m,n);r=double(g);s=double(h);if (abs(imag(r(1)))<0.01) %去除复数根u=[u;[real(r(1))+256 real(r(2))+256]];v=[v;[real(s(1))+256 real(s(2))+256]];endk=k+1;end%根据新的切平面的轮廓坐标得到新轮廓的图像矩阵plot(v(:,1),u(:,1),'r.',v(:,2),u(:,2),'r.')axis([0 512 0 512]);pnj=imread(strcat(int2str(pn),'.bmp'));lk=edge(pnj,'sobel');pnjj=zeros(512);u=round(u);v=round(v);for t=1:length(u(:,1))pnjj(u(t,1),v(t,1))=1;pnjj(u(t,2),v(t,2))=1;endfigure(1);%画原图轮廓imshow(lk)figure(2);%画新图轮廓imshow(pnjj)figure(3);%画原图与新图的轮廓图对比imshow(pnjj|lk)pnjj=zhuanhua(pnjj);附录7：求拟合图与原切片图的重合度的matlab程序代码（baifenbi1.m） function baifenbi=baifenbi1(pnjj,pn) %输出拟合图与原切片图的重合度%填充新图juzheng=pnjj; %pnjj为通过dian.m得到的轮廓边界二值矩阵%先填充左边界的右半部分for i=1:511for j=1:511if(pnjj(i,j)==0&pnjj(i,j+1)~=0)pnjj(i,j+1)=pnjj(i,j);endendendyou=pnjj;%再填充右边界的左半部分for i=1:512for j=512:-1:2if(juzheng(i,j)==0&juzheng(i,j-1)~=0)juzheng(i,j-1)=juzheng(i,j);endendendzuo=juzheng;shijijuzheng=you|zuo; %通过矩阵的或运算得到填充后的新图imshow(you|zuo)%原图的黑点的个数biaozhunjuzheng=imread(strcat(int2str(pn),'.bmp'));nbiao=0;for i=1:512for j=1:512if(biaozhunjuzheng(i,j)==0)nbiao=nbiao+1;endendend%新图与原图重合部分黑点的个数chonghegs=0;for i=1:512for j=1:512if(biaozhunjuzheng(i,j)==0&shijijuzheng(i,j)==0) chonghegs=chonghegs+1;endendend%求百分比baifenbi=chonghegs/nbiao;。
血管切片的三维重建
血管切片的三维重建
钱志刚;刘磊;王月娇
【期刊名称】《河北大学学报（自然科学版）》
【年(卷),期】2002(022)002
【摘要】为了利用血管切片图像重建血管的三维形态,首先用优化算法提取了图像信息,然后依据样条插值利用MATLAB建立了2个模型,进而重建了血管的三维形态,并对结果进行了分析与比较,验证了模型的正确性.
【总页数】6页(P118-123)
【作者】钱志刚;刘磊;王月娇
【作者单位】河北大学数学与计算机学院,河北,保定,071002;河北大学数学与计算机学院,河北,保定,071002;河北大学数学与计算机学院,河北,保定,071002
【正文语种】中文
【中图分类】O29
【相关文献】
1.血管连续切片图象的计算机三维重建 [J], 曹海峰;王晨光;孔亮;尹海东;孟军
2.基于切片图像的血管三维重建方法 [J], 韩西安;杨海涛;邱铭铭;赵东杰
3.血管切片的三维重建 [J], 柳海东;陈璐;江浩;卢钦和
4.利用切片的二维空间相关操作实现血管的三维重建 [J], 胡亦斌;向杰;程翔;王若鹏
5.基于切片二维图像的血管三维重建研究 [J], 靳瀛; 王敬前
因版权原因，仅展示原文概要，查看原文内容请购买。
基于matlab的医学影像后处理的代码
医学影像后处理是指对医学图像进行数字化处理和分析，以提取相关信息和改善图像质量的一系列技术和方法。
随着计算机技术的不断发展，基于matlab的医学影像后处理的代码已经成为医学影像处理领域的主流技术之一。
本文将探讨基于matlab的医学影像后处理的代码，包括其应用领域、相关算法和实现方法等内容。
一、应用领域基于matlab的医学影像后处理的代码被广泛应用于医学影像学及临床实践中。
具体包括但不限于以下几个方面：1. 医学图像的增强处理。
利用matlab编写的代码可以对医学图像进行增强处理，提高图像的对比度、清晰度和视觉效果，有利于医生准确诊断病情。
2. 医学图像的分割和识别。
基于matlab的代码可以对医学图像进行分割处理，将图像中的不同组织和器官进行识别和分离，有助于医生对病变区域进行精准定位和分析。
3. 医学图像的三维重建和可视化。
利用matlab编写的代码可以对医学图像进行三维重建和可视化，使医生能够更直观地了解病变的空间分布和形态结构，有助于手术规划和治疗方案的制定。
二、相关算法基于matlab的医学影像后处理的代码涉及多种算法和技术，主要包括但不限于以下几种：1. 图像的滤波算法。
常用的医学图像滤波算法包括均值滤波、中值滤波、高斯滤波等，可以有效去除噪声和增强图像的特征。
2. 区域生长算法。
该算法基于种子点，通过定义生长准则将相邻像素点进行合并，实现医学图像的分割和识别。
3. 边缘检测算法。
常用的边缘检测算法包括Sobel算子、Canny算子等，可以有效提取医学图像中的边缘信息，有助于病变区域的定位和分析。
4. 三维重建算法。
基于matlab的三维重建算法主要包括曲面重建、体绘制和渲染等技术，可以将医学图像转换为三维模型进行可视化和分析。
三、实现方法基于matlab的医学影像后处理的代码的实现方法主要包括以下几个步骤：1. 数据采集和预处理。
首先需要获取医学图像数据，并进行预处理，包括格式转换、去噪等操作，为后续处理做好准备。
血管的三维重建
血管的三维重建1 摘要序列图像的三维重建在各学科中都起到至关重要的作用，本次讨论的是血管的三维重建。
首先，假设该管道是由球心沿着某一曲面的球滚动包络而成，故本次的主要目的是求出中轴线坐标及半径。
现有100张平行切片图像，本次建立的模型可分为四步;第一步，采集图形边界点数据。
由于每张图片都是512*512的矩阵，故此数据很大，采用imread()函数将其读入矩阵A中。
第二步，最大内切圆寻找及半径的确定。
提出两种方案,分别是切线法和最大覆盖法; 从上述两种方法分析及考虑到我们所使用的工具和材料, 可以得出方法二更加直观, 计算机实现更容易, 计算复杂度更低, 所以我们采用后者。
根据以上算法, 我们抽取了所有的切片图进行半径的提取, 然后再求其平均值, 求其均值得到球的半径为29.6345。
第三步，轨迹的搜索。
在第二步中求出了血管的半径，轨迹的搜索就可以建立在半径确定的基础上, 当然我们也可以求出每一个切面图形的最大内切圆, 然后得到每个圆心的坐标, 即中轴线坐标, 但这样做计算机的运算量会很大, 同时由于最大内切圆搜索法的稳定性不高, 从而会造成搜索的不精确, 所以采用定半径搜索。
本文提出了三种方法, 分别为网格法、蒙特卡罗法和非线性规划法;本次采用非线性规划来实现。
第四步，绘制中轴线空间曲线图和在XOY、YOZ、XOZ 三个平面的投影图。
由定理1: 切片上血管截面图的头部顶点在XOY 平面上的投影点一定会落在中轴线在XOY 平面上的投影曲线上（在论文中以证明），并得出推论：切片上血管截面中中位线与中轴线在XOY 面上的投影重合。
最后可由中轴线和血管半径在作图软件中达到血管的三维重建，本次的模型还存在一定的不足，其假设为管道中轴线与每个切面有且只有一个交点，事实上还存在有多个交点的情况，但为了简化模型在此做了一定的假设，故会存在一定的误差。
关键词：三维重建内切圆半径轨迹（中轴线）注：求边界时采用了老师的思想和程序。
血管三维图像重建的数学方法
α文章编号:100127445(2003)0320206203血管三维图像重建的数学方法黄新民(广西大学数学与信息科学学院,广西南宁530004)摘要:使用M A TLAB 读出血管切片图的数据,算出其半径及中轴线方程,建立了血管曲面的参数方程,实现了图形的三维重建.关键词:血管;参数方程;三维重建中图分类号:O 24211 文献标识码:A2001年全国大学生数学建模竞赛中的A 题:血管的三维重建,要求学生从给定的100张平行切片图中,编程读出图像中的数据,并以此计算管道的中轴线与半径,给出具体算法,并绘制中轴线在X Y ,Y Z ,ZX 平面的投影图.该题的具体计算已经在文[1～6]中有许多详细而细致的讨论.但是所有这些文章都没有说明使用的计算机语言及相应的程序.按题目所附参考材料看,出题人建议的是使用C ++程序.事实上许多软件都可以处理图形图像,而且还比使用C ++编程更容易.本文使用M A TLAB 比较简单地完成题目所要求的计算.原竞赛题目中只要求给出图像的中轴线及其在三个坐标平面上的投影,实际上并没有真正实现血管的三维图像重建,本文将讨论实现图形三维重建的一个方法.要将图形数据读入,在M A TLAB 中只要使用命令i m read 即可实现.程序虽然简单,但数据量较大,因此要通过几次计算才能将所有数据读完,再用命令save 存储到硬盘上,以便下一步计算时使用.对于读出的每一张图,我们需要读出血管截面数据及其边界数据,以便下一步从中读出每张内切圆的圆心坐标与内切圆半径.M A TLAB 记录的图形数据是这样的:如果记录图形数据的是一个二维数组A (i ,j ),则第i 行第j 列上的数值为一个0到255的整数(占用一个字节的存储空间),这个值对应于一个有三列元素的长为256的颜色向量表中的一行,该行的三分量就分别对应于红、绿、兰颜色的颜色值.本题中由于只有黑白两色,所以数组中每个元素只有值为零及为1两个.在程序中我们用值为1记血管截面上的点,因此就用周围四个点的值和为4(因此每一个点的值都是1)来找出血管截面的内点,去掉内点后我们就得到了血管截面的边界点.不过我们得到的还不能算是真正的血管截面的边界.因为图形扫描成数据点时,血管截面中的每一个点实际代表了一小片面积的中心.我们不妨称这个边界为血管截面的内边界.而元素值为0的点(也就是血管截面外的点)的边界称为外边界.将内外边界求平均表示真正的边界才更准确.读出边界及所围的区域数据后,我们从区域中每取出一个点,计算其与边界的最小距离(这就是在这个点所作的与边界相切的圆半径),再从所有内切圆的半径中找出最大时的圆心坐标与半径,就得到小球在这个血管截面处时的球心坐标与球半径.求出所有各张图的球心坐标与球半径,就得到了中轴线坐标及球半径(严格地说球半径应该是一个常数,但是由于扫描与计算误差,因此只能取所有半径的平均值为球心半径).此程序的编写也不复杂.但实际使用时不难发现由于数据量大,需要计算很长时间(当然我们将程序运行后就可以静候结果),为加快计算速度可以使用各种办法.在本文中我们发现圆半径不小于29,第28卷第3期2003年9月广西大学学报(自然科学版)Journal of Guangxi U niversity (N at Sci Ed )V o l .28,N o.3 Sep t .,2003 α收稿日期:20021208;修订日期:20030810作者简介:黄新民(1945),男,广西贺州人,广西大学教授.因此将内点与边界点相同x 坐标的边界点比较其y 坐标,当两个点的坐标之差小于29时就将这个点从内点中排除.对坐标y 相同的点亦作同样处理.由于减法比计算距离的平方运算要快,因此这样做可以加快计算过程.算出中轴线坐标及球半径后,只要使用简单的二维作图命令p lo t 就可以画出中轴线向三个坐标平面的投影图,完成建模题的要求.但是这样做出的图形并没有实现图形的真正三维重建.血管的三维图像重建有多种方法,最简单的是将每张图的轮廓线按其高度在三维空间中复原.本文将介绍实现图像三维重建的另外一种方法.这种方法与学生在大学中所学的高等数学及线性代数的知识密切相关,而且重建的图像可以使用光照、颜色等加工,使图形显得十分美丽,值得介绍.设已求出中轴线方程:x =x (z ),y =y (z ),0≤z ≤99,下面我们求半径为r 的球沿此中轴线运动而得的包络面方程.设(X ,Y ,Z )是包络面上任意一点,则存在z 使得(X -x (z ))2+(Y -y (z ))2+(Z -z )2=r 2.(1)上式的z 为一个参数,当它从0运动到99时其轨迹就形成了管道.将(1)式两边对参数z 求导,则得第二个方程x ′(z )(X -x (z ))+y ′(z )(Y -y (z ))+(Z -z )=0.(2)将(2)式代入(1),化简后得(1+x ′(z )2)(X -x (z ))2+2x ′(z )y ′(z )(X -x (z ))(Y -y (z ))+(1+y ′(z )2)(Y -y (z ))2=r 2,(3)(3)式左方是一个二次型,容易求出其特征值分别是Κ1=1,Κ2=1+x ′(z )2+y ′(z )2,其相应的特征向量是p 1=-y ′(z )x ′(z ), p 2=x ′(z )y ′(z ).因此作变换X -x (z )=-y ′(z )u +x ′(z )v , Y -y (z )=x ′(z )u +y ′(z )v ,(4)之后,(3)式将化简为(x ′(z )2+y ′(z )2)(u 2+(1+x ′(z )2+y ′(z )2)v 2)=r 2,(5)因此,(u ,v )可建立参数式u =r co s (t )x ′(z )2+y ′(z )2, v =r sin (t )(x ′(z )2+y ′(z )2)(1+x ′(z )2+y ′(z )2).将上式代入(4)式,立即得到管道曲面的参数方程X =x (z )+-ry ′(z )co s (t )x ′(z )2+y ′(z )2+rx ′(z )sin (t )(x ′(z )2+y ′(z )2)(1+x ′(z )2+y ′(z )2),Y =y (z )+rx ′(z )co s (t )x ′(z )2+y ′(z )2+ry ′(z )sin (t )(x ′(z )2+y ′(z )2)(1+x ′(z )2+y ′(z )2),Z =z -x ′(z )2+y ′(z )21+x ′(z )2+y ′(z )2r sin (t ).其中0≤z ≤99,0≤t ≤2Π,在中轴线坐标及球半径r 求出来后,可以通过数据拟合得到中轴线的参数方程(由于数据是近似的,因此作数据拟合是合适的)x =x (z ), y =y (z ), 0≤z ≤99.然后就可以画出血管的三维图形了.通过选择观察点及颜色、光照等可以作出十分精致的三维图像.下面的程序即为作图程序(其中x (z ),y (z )是分别拟合成六次多项式).图1是此程序运行后得到的M A TLAB 作出的血管三维图.load cendata %调入中轴线坐标数据,假设存储在变量B 中,共100行,分别表示x ,y ,r 坐标x =B (:,1);%中轴线的x 坐标向量y =B (:,2);%中轴线的y 坐标向量r =sum (B (:,3)) 100;%内切圆半径平均值702第3期黄新民:血管三维图像重建的数学方法z =[0:99]’;%z 坐标向量p 1=po lyfit (z ,x ,6);%以z 为自变量将x 拟合成六次多项式p 2=po lyfit (z ,y ,6);%以z 为自变量将y 拟合成六次多项式zz =[0:0.4:99]’;%重新定义步长更小的高度坐标向量zz xx =po lyval (p 1,zz );%用拟合多项求对应于zz 的坐标xx yy =po lyval (p 2,zz );%用拟合多项求对应于zz 的坐标yy dx 1=po lyder (p 1);%对x 的多项式微分多项式dy 1=po lyder (p 2);%对y 的多项式微分多项式dx 2=po lydval (dx 1,zz );%求x’(z )dy 2=po lydval (dy 1,zz );%求y’(z)图1 用M A TLAB 作出 的血管三维图R 2=dx 2,^2+dy 2.^2;r 1=sqrt (R 2);r 2=r 1.3sqrt (1+R 2);t =linspace (0,23p i ,251);%定义角度s =size (t );X =xx 3ones (s )+r 3((-dy 2. r 1)3co s (t )+(dx 2. r 2)3sin (t ));Y =yy 3ones (s )+r 3((dx 2. r 1)3co s (t )+(dy 2. r 2)3sin (t ));Z =zz 3ones (s )-r 3(r 1. r 2)3sin (t );m esh (X ,Y ,Z ) %三维网线作图surface (X ,Y ,Z )%三维表面作图axis equal%按实际比例值作图axis off%不画坐标轴,使图形更逼真h idden off%消隐,去掉曲面上的网线,使图形更逼真view ([35,88])%选择观察角shading interp%使作图时片与片之平滑过渡co lo r m ap ho t%色彩处理(不一定恰当,请读者自己尝试)caxis ([-70,450])%重设颜色,使颜色接近红色cam ligh t (200,180)%指定光源位置,这些值为尝试值,不一定合适ligh ting gouraud %设置照明方式参考文献:[1] 廖武斌,邓俊晔,王 丹.管道切片的三维重建[J ].工程数学学报,2002,19(5):22228..[2] 胡亦斌,向 杰,程 翔.利用切片的二维空间相关操作实现血管的三维重建[J ].工程数学学报,2002,19(5):29234.[3] 徐 晋,刘雪峰,柏容刚.血管的三维重建[J ].工程数学学报,2002,19(5):35240.[4] 柳海东,陈 璐,江 浩.管道切片的三维重建[J ].工程数学学报,2002,19(5):41246.[5] 丁峰平,周立丰,李孝朋.血管管道的三维重建[J ].工程数学学报,2002,19(5):47253.[6] 汪国昭,陈凌钧.血管三维重建的问题[J ].工程数学学报,2002,19(5):54258.3D recon struction of blood vesselHU AN G X in 2m in(Co llege of M athem atics and Info r m ati on Science ,Guangxi U niversity ,N anning 530004,Ch ina )Abstract :M A TLAB is u sed to ob tain data of b lood vessel slices .T he radiu s of the b lood vessel is deter m ined and the axes cu rve has calcu lated .T he p aram etric equati on is ob tained and the 3D i m age of b lood vessel su rface is recon structed .Key words :b lood vessel ;param etric equati on ;3D recon structi on(责任编辑 刘海涛)802广西大学学报(自然科学版)第28卷 。
旧题新作——基于MATLAB的切片三维重建
旧题新作——基于MATLAB的切片三维重建切片三维重建可以被描述为一种通过利用二维横截面（切片）图像重新构建三维物体的技术。
这种技术广泛应用于医学影像、工程领域等多个领域。
本文将探讨如何使用MATLAB来进行简单的切片三维重建。
在开始之前，需要了解MATLAB的一些基本概念。
MATLAB是一种数学软件，常用于数学计算、数据分析和可视化，同时也有成熟的图像处理工具箱。
本文所涉及的代码和操作都可以在MATLAB中进行。
首先，需要准备三个不同方向的二维切片图像。
这些图像可以通过CT扫描、MRI等获得，并且需要通过DICOM格式进行导入。
在MATLAB中导入DICOM格式图像的方法如下：```A = dicomread('file.dcm');```其中，file.dcm是DICOM图像文件的名称。
然后，可以将三个不同方向的二维图像组合成一个三维矩阵。
如下所示：```V = cat(4, A1, A2, A3);```其中，A1、A2和A3分别是三个不同方向的二维图像，V为三维矩阵。
在创建完三维矩阵之后，可以使用isosurface函数进行三维表面绘制。
isosurface 函数的使用方法如下：其中，threshold是一个阈值，用于控制三维表面的显示，fv为三维表面上的三角形顶点。
接着，可以使用patch函数将三维表面绘制出来。
具体操作方法如下：如此一来，三维表面就可以显示出来了。
最后，可以使用光源来改善三维显示效果。
MATLAB提供了light函数，可以轻松设置光源。
使用方法如下：```light('Position', [x y z]);```其中，x、y和z是光源的坐标位置。
现在，就可以使用以上几步来实现一个简单的切片三维重建了。
代码如下：```% 导入DICOM格式图像A1 = dicomread('file1.dcm');A2 = dicomread('file2.dcm');A3 = dicomread('file3.dcm');% 使用patch函数将三维表面绘制出来p = patch(fv);% 设置坐标轴axis equal;xlabel('X');ylabel('Y');zlabel('Z');```以上代码将三个不同方向的二维图像组合成一个三维数据矩阵，使用isosurface函数得到三维表面，然后使用patch函数将其绘制出来，并设置光源和坐标轴。
血管的三维重建建模论文 推荐
血管的三维重建摘要本文以血管的三维重建为研究对象，对100张平行切片图像进行分析，利用这些宽、高均为512象素的切片，计算管道的半径和确定中轴线方程，并在此基础上画出重建后的血管三维图像，主要内容如下：对于问题一，计算管道的半径，由于血管表面是由球心沿着某一曲线（称为中轴线）的球滚动包络而成，可以得出结论：切片中包含的最大圆的半径即血管半径，所以问题转化为求每一切片上的最大内切圆的半径。
为了便于计算，运用Matlab imread 函数，将BMP 格式文件转化为0-1矩阵，然后运用edge bwmorph 、函数确定轮廓和骨架的位置，并求解骨架上每一点到边缘的最短距离。
这些最短距离中的最大值即为最大内切圆半径也就是血管半径。
最后对所有的半径取平均值，得出结果：100()1=29.41666100k k RR ==∑对于问题二，根据问题一中求出的100个圆心坐标及半径求解中轴线方程，运用Matlab 软件对圆心所形成的曲线进行n 阶多项式拟合。
为使中轴线较为光滑，在Matlab 拟合工具箱多次试验后，取最高阶次=7n 。
由于z 轴值是逐层单调递增的,为简化方程的计算,取t 为参变量，分别对其投影在YZ 、ZX 平面上进行多项式拟合，最后得到中轴线在平面投影上拟合的曲线方程如下：()()()-107-76-55432-107-86-55-3432-3.2310 1.16910-1.628100.00108-0.035260.5706-3.105+5.243=3.06110-9.62310+1.3610-0.640610+0.01912-0.298+1.89-1.63.3=y t t t t t t t t f x t t t t t t t t z t t ⎧=⨯+⨯⨯+⎪+⎪⎪=⨯⨯⨯⨯⎨⎪⎪⎪⎩最后根据方程画出中轴线图形，YZ YX ZX 、、平面的投影在拟合工具箱中可以直接得到。
对于问题三，根据问题一、二求出的中轴线的参数方程和100张切片的最大内切圆的半径，运用Matlab 软件画出血管的三维立体图。
基于MATLAB的血管三维重建源代码
附录1：图像二值矩阵的0-1互换的matlab程序代码（zhuanhua.m）function b0=zhuanhua(b0)%图像二值矩阵的0-1互换for i=1:512for j=1:512if b0(i,j)==1b0(i,j)=0;else b0(i,j)=1;endendend附录2：求各切片的最大内切圆的半径及圆心坐标matlab程序代码（ff.m）function[r,zhongxindian]=ff%输出各切片最大内切圆半径及圆心坐标a=zeros(512,512);b=zeros(512,512);for i=1:512for j=1:512a(i,j)=i-257;%横坐标的对应b(i,j)=j-257;%纵坐标的对应endend%图像在xyz面上的x轴、y轴坐标zhongxindian=zeros(100,2);r=zeros(100,1);for k=0:99t=strcat('f:/',int2str(i),'.bmp');b=imread(t);b=zhuanhua(b);%将01互换blunkuo=edge(b,'sobel');%提取轮廓bgujia=bwmorph(b,'skel',inf);%提取骨架%寻找内切圆[x0,y0,v0]=find(b0lunkuo);[a0,b0,c0]=find(b0gujia);m=length(a0);n=length(x0);juli=zeros(m,n);cunfang=zeros(m,2);for i=1:mfor j=1:np1=a0(i);q1=b0(i);p2=x0(j);q2=y0(j);juli(i,j)=sqrt((a(p1,q1)-a(p2,q2))^2+(b(p1,q1)-b(p2,q2))^2);%骨架上的各个点到轮廓的距离end[zx,zxxh]=min(juli(i,:));%骨架上一点到轮廓的最短距离即以骨架上各个点为圆心的内切园的半径cunfang(i,1)=zx;cunfang(i,2)=zxxh;end[zd,zdxh]=max(cunfang(:,1));%寻找半径中最大的半径和其对应的圆心坐标g=a0(zdxh);h=b0(zdxh);zhongxindian(k+1,1)=a(g,h);zhongxindian(k+1,2)=b(g,h);r(k+1)=zd;end附录3：通过计算不同次数多项式拟合的偏差平方和确定拟和次数的matlab程序代码（pczx.m）function j=pczx(z,t)%根据不同次数的多项式拟合与原图数据偏差平方和的大小来确定多项式拟和的次数delta=zeros(10,1);for k=1:10[p,s]=polyfit(z,t,k);delta(k)=s.normrend[i,j]=min(delta);附录4：根据轮廓画出血管的三维图像的matlab程序代码for b=0:99%提取原图的轮廓，根据轮廓画出血管的三维图像m1=imread([int2str(b),'.bmp']);m(:,:,b+1)=edge(m1,'sobel');endfor k=0:99for i=1:512for j=1:512if(m(i,j,k+1)==1)plot3(i,j,k+1,'r-.');hold onendendendendgrid ontitle('血管三维图')rotate3dhold off附录5：绘制中轴线及在各平面的投影图matlab程序代码format longpx=polyfit(z,x,7);%x,z的7次多项式拟合x1=polyval(px,z);py=polyfit(z,y,5);%y,z的5次多项式拟合y1=polyval(py,z);figure(1);%画中心轴线图plot3(x1,y1,z)grid onxlabel('X轴');ylabel('Y轴');zlabel('Z轴');title('血管中轴线图');figure(2);%画中心轴线在xoz平面上的投影plot(z,x1,'-r')ylabel('Z轴');xlabel('X轴')title('血管中轴线XOZ平面投影图');grid onfigure(3);%画中心轴线在yoz平面上的投影plot(z,y1,'-b')xlabel('Z轴');ylabel('Y轴');title('血管中轴线YOZ平面投影图');grid onfigure(4);%画中心轴线在xoy平面上的投影plot(x1,y1,'-g')xlabel('X轴');ylabel('Y轴');title('血管中轴线XOY平面投影图');grid on附录6：求第pn张拟合图的轮廓的二值矩阵的matlab程序代码（dian.m）function pnjj=dian(px,py,pn)%输出pnjj，为第pn张拟合图片的轮廓二值矩阵a=zeros(991);b=zeros(991);q=zeros(991);w=zeros(991);r=zeros(1,2);s=zeros(1,2);k=1;for c=0:0.1:99a(k)=7*px(1)*c.^6+6*px(2)*c.^5+5*px(3)*c.^4+4*px(4)*c.^3+3*px(5)*c.^2+2*px(6)*c+px(7); b(k)=4*py(1)*c.^3+3*py(2)*c.^2+2*py(3)*c+py(4);%中心轴线方程关于z的导数即[a(k),b(k),1]为z在k处的切线的方向向量q(k)=px(1)*c.^7+px(2)*c.^6+px(3)*c.^5+px(4)*c.^4+px(5)*c.^3+px(6)*c.^2+px(7)*c+px(8);w(k)=py(1)*c.^5+py(2)*c.^4+py(3)*c.^3+py(4)*c.^2+py(5)*c;%中心轴线方程在z=k处的x,y值k=k+1;end%提取新的截痕u=[];v=[];syms x yk=1;for i=0:0.1:99m=a(k)*(x-q(k))+b(k)*(y-w(k))+(pn-i);n=(x-q(k))^2+(y-w(k))^2+(pn-i)^2-29.49^2;[g,h]=solve(m,n);r=double(g);s=double(h);if(abs(imag(r(1)))<0.01)%去除复数根u=[u;[real(r(1))+256real(r(2))+256]];v=[v;[real(s(1))+256real(s(2))+256]];endk=k+1;end%根据新的切平面的轮廓坐标得到新轮廓的图像矩阵plot(v(:,1),u(:,1),'r.',v(:,2),u(:,2),'r.')axis([05120512]);pnj=imread(strcat(int2str(pn),'.bmp'));lk=edge(pnj,'sobel');pnjj=zeros(512);u=round(u);v=round(v);for t=1:length(u(:,1))pnjj(u(t,1),v(t,1))=1;pnjj(u(t,2),v(t,2))=1;endfigure(1);%画原图轮廓imshow(lk)figure(2);%画新图轮廓imshow(pnjj)figure(3);%画原图与新图的轮廓图对比imshow(pnjj|lk)pnjj=zhuanhua(pnjj);附录7：求拟合图与原切片图的重合度的matlab程序代码（baifenbi1.m）function baifenbi=baifenbi1(pnjj,pn)%输出拟合图与原切片图的重合度%填充新图juzheng=pnjj;%pnjj为通过dian.m得到的轮廓边界二值矩阵%先填充左边界的右半部分for i=1:511for j=1:511if(pnjj(i,j)==0&pnjj(i,j+1)~=0)pnjj(i,j+1)=pnjj(i,j);endendendyou=pnjj;%再填充右边界的左半部分for i=1:512for j=512:-1:2if(juzheng(i,j)==0&juzheng(i,j-1)~=0)juzheng(i,j-1)=juzheng(i,j);endendendzuo=juzheng;shijijuzheng=you|zuo;%通过矩阵的或运算得到填充后的新图imshow(you|zuo)%原图的黑点的个数biaozhunjuzheng=imread(strcat(int2str(pn),'.bmp'));nbiao=0;for i=1:512for j=1:512if(biaozhunjuzheng(i,j)==0)nbiao=nbiao+1;endendend%新图与原图重合部分黑点的个数chonghegs=0;for i=1:512for j=1:512if(biaozhunjuzheng(i,j)==0&shijijuzheng(i,j)==0)chonghegs=chonghegs+1;endendend%求百分比baifenbi=chonghegs/nbiao;。
matlab 三维重建代码
matlab 三维重建代码
三维重建在 Matlab 中可以通过多种方法实现，其中包括体素重建、点云重建和三角网格重建等。
以下是一个简单的示例代码，用于通过点云重建实现三维重建：
matlab.
% 生成示例点云数据。
x = randn(100,1);
y = randn(100,1);
z = x.^2 + y.^2;
% 使用点云数据进行三维重建。
ptCloud = pointCloud([x, y, z]);
mesh = pcfitmesh(ptCloud, 5); % 使用点云拟合三角网格。
% 可视化结果。
pcshow(mesh)。
上述代码首先生成了一个简单的示例点云数据，然后使用
`pcfitmesh` 函数对点云进行三角网格重建，最后通过 `pcshow` 函数可视化重建结果。
除了点云重建，还可以使用其他方法进行三维重建，比如体素重建可以使用 `vol3d` 函数进行体素化，然后通过体素数据进行三维重建。
需要根据具体的三维重建需求选择合适的方法和工具函数，以上仅是一个简单的示例代码。
希望这能帮到你。
【 数学建模竞赛】血管的三维重建模型g资料
血管的三维重建模型摘要：本文对血管三维重建中，中轴线及球的半径确定问题进行了讨论。
首先，根据问题及图象处理提取有效数据，给出两种可行算法，利用上述数据建立了最大最小方法和二次规划方法。
搜索中心点，并给出全局和局部搜索，得到各切片中心点坐标(见表1)，并通过插值方式得到中轴线图象及其各投影。
最后对模型给出检验方式。
一 、问题的重述假设某些血管可视为一类特殊的管道,该管道的表面是由球心沿着某一曲线 (称为中轴线)的球（命名为包络球）滚动包络而成。
现有某管道的相继100张平行切片图象,记录了管道与切片的交。
假设：管道中轴线与每张图片有且只有一个交点；球半径固定；切片间距以及图象象素的尺寸均为1.取坐标的Z 轴垂直于切片，第1张切片为平面0=Z ，第100张切片为平面99=Z . 计算管道的中轴线与半径，给出具体的算法，并绘制中轴线在XY 、YZ 、ZX 平面的投影图。
二、模型假设与符号说明1、 基本假设：（1） 该管道的表面为一定长半径的球沿一固定的曲线运动所得曲面族包络的光滑表面。
（2） 该管道的中轴线连续而且光滑。
（3） 该管道的中轴线与每个切面有且只有一个交点。
（4） 图象象素的尺寸为1. （5） 切片的间距尺寸为1.2、 符号说明：L 中轴线R 包络球的半径()z y x O i ,, 中轴线与第i 个切片的交点（定为此切片的中心）i S 第i 个切片切得的图形 i D 第i 个切片的图象数据矩阵三、问题分析及建模准备 问题分析：通常血管的表面可认为是连续且光滑的曲面，断面可用于了解其形态等特性。
本问题给出的是一些离散的切面，要求重建出原图中轴线和求出包络球半径。
因为每一个切面与中轴线L 有且只有一个交点i O ，如果找出所有i O ,就可以用插值或拟合的方式作出L 的近似图象，其在坐标平面上的投影就很容易画出。
问题的关健转变为求每个平面上的i O . 建模准备：1、 图象的读取由于切片图象中只有黑、白两种颜色的象素,而且所给的BMP 格式图象文 件是512×512象素的.因此,把图象读取为一个512×512的数字矩阵；用数字1表示黑色的象素，用数字0表示白色的象素。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
图片下载2001数学建模A题附录1：图像二值矩阵的0-1互换的matlab程序代码（zhuanhua.m）function b0=zhuanhua(b0) %图像二值矩阵的0-1互换for i=1:512for j=1:512if b0(i,j)==1b0(i,j)=0;else b0(i,j)=1;endendend附录2：求各切片的最大内切圆的半径及圆心坐标matlab程序代码（ff.m）function [r, zhongxindian]=ff %输出各切片最大内切圆半径及圆心坐标a=zeros(512,512);b=zeros(512,512);for i=1:512for j=1:512a(i,j)=i-257; %横坐标的对应b(i,j)=j-257; %纵坐标的对应endend %图像在xyz面上的x轴、y轴坐标zhongxindian=zeros(100,2);r=zeros(100,1);for k=0:99t=strcat('f:/',int2str(i),'.bmp');b=imread(t);b=zhuanhua(b);%将01互换blunkuo=edge(b,'sobel');%提取轮廓bgujia=bwmorph(b,'skel',inf);%提取骨架%寻找内切圆[x0,y0,v0]=find(b0lunkuo);[a0,b0,c0]=find(b0gujia);m=length(a0);n=length(x0);juli=zeros(m,n);cunfang=zeros(m,2);for i=1:mfor j=1:np1=a0(i);q1=b0(i);p2=x0(j);q2=y0(j);juli(i,j)=sqrt((a(p1,q1)-a(p2,q2))^2+(b(p1,q1)-b(p2,q2))^2);%骨架上的各个点到轮廓的距离end[zx,zxxh]=min(juli(i,:));%骨架上一点到轮廓的最短距离即以骨架上各个点为圆心的内切园的半径cunfang(i,1)=zx;cunfang(i,2)=zxxh;end[zd,zdxh]=max(cunfang(:,1));%寻找半径中最大的半径和其对应的圆心坐标g=a0(zdxh);h=b0(zdxh);zhongxindian(k+1,1)=a(g,h);zhongxindian(k+1,2)=b(g,h);r(k+1)=zd;end附录3：通过计算不同次数多项式拟合的偏差平方和确定拟和次数的matlab程序代码（pczx.m）function j=pczx(z,t) %根据不同次数的多项式拟合与原图数据偏差平方和的大小来确定多项式拟和的次数delta=zeros(10,1);for k=1:10[p,s]=polyfit(z,t,k);delta(k)=s.normrend[i,j]=min(delta);附录4：根据轮廓画出血管的三维图像的matlab程序代码for b=0:99 %提取原图的轮廓，根据轮廓画出血管的三维图像m1=imread([int2str(b),'.bmp']);m(:,:,b+1)=edge(m1,'sobel');endfor k=0:99for i=1:512for j=1:512if (m(i,j,k+1)==1)plot3(i,j,k+1,'r-.');hold onendendendendgrid ontitle('血管三维图')rotate3dhold off附录5：绘制中轴线及在各平面的投影图matlab程序代码format longpx=polyfit(z,x,7);%x,z的7次多项式拟合x1=polyval(px,z);py=polyfit(z,y,5);%y,z的5次多项式拟合y1=polyval(py,z);figure(1); %画中心轴线图plot3(x1,y1,z)grid onxlabel('X轴');ylabel('Y轴');zlabel('Z轴');title('血管中轴线图');figure(2); %画中心轴线在xoz平面上的投影plot(z,x1,'-r')ylabel('Z轴');xlabel('X轴')title('血管中轴线XOZ平面投影图');grid onfigure(3);%画中心轴线在yoz平面上的投影plot(z,y1,'-b')xlabel('Z轴');ylabel('Y轴');title('血管中轴线YOZ平面投影图');grid onfigure(4);%画中心轴线在xoy平面上的投影plot(x1,y1,'-g')xlabel('X轴');ylabel('Y轴');title('血管中轴线XOY平面投影图');grid on附录6：求第pn张拟合图的轮廓的二值矩阵的matlab程序代码（dian.m）function pnjj=dian(px,py,pn) %输出pnjj，为第pn张拟合图片的轮廓二值矩阵a=zeros(991);b=zeros(991);q=zeros(991);w=zeros(991);r=zeros(1,2);s=zeros(1,2);k=1;for c=0:0.1:99a(k)=7*px(1)*c.^6+6*px(2)*c.^5+5*px(3)*c.^4+4*px(4)*c.^3+3*px(5)*c.^2+2*px(6)*c+px(7);b(k)=4*py(1)*c.^3+3*py(2)*c.^2+2*py(3)*c+py(4); %中心轴线方程关于z的导数即[a(k),b(k),1]为z在k处的切线的方向向量q(k)=px(1)*c.^7+px(2)*c.^6+px(3)*c.^5+px(4)*c.^4+px(5)*c.^3+px(6)*c.^2+px(7)*c+px(8);w(k)=py(1)*c.^5+py(2)*c.^4+py(3)*c.^3+py(4)*c.^2+py(5)*c; %中心轴线方程在z=k处的x,y 值k=k+1;end%提取新的截痕u=[];v=[];syms x yk=1;for i=0:0.1:99m=a(k)*(x-q(k))+b(k)*(y-w(k))+(pn-i);n=(x-q(k))^2+(y-w(k))^2+(pn-i)^2-29.49^2;[g,h]=solve(m,n);r=double(g);s=double(h);if (abs(imag(r(1)))<0.01) %去除复数根u=[u;[real(r(1))+256 real(r(2))+256]];v=[v;[real(s(1))+256 real(s(2))+256]];endk=k+1;end%根据新的切平面的轮廓坐标得到新轮廓的图像矩阵plot(v(:,1),u(:,1),'r.',v(:,2),u(:,2),'r.')axis([0 512 0 512]);pnj=imread(strcat(int2str(pn),'.bmp'));lk=edge(pnj,'sobel');pnjj=zeros(512);u=round(u);v=round(v);for t=1:length(u(:,1))pnjj(u(t,1),v(t,1))=1;pnjj(u(t,2),v(t,2))=1;endfigure(1);%画原图轮廓imshow(lk)figure(2);%画新图轮廓imshow(pnjj)figure(3);%画原图与新图的轮廓图对比imshow(pnjj|lk)pnjj=zhuanhua(pnjj);附录7：求拟合图与原切片图的重合度的matlab程序代码（baifenbi1.m）function baifenbi=baifenbi1(pnjj,pn) %输出拟合图与原切片图的重合度%填充新图juzheng=pnjj; %pnjj为通过dian.m得到的轮廓边界二值矩阵%先填充左边界的右半部分for i=1:511for j=1:511if(pnjj(i,j)==0&pnjj(i,j+1)~=0)pnjj(i,j+1)=pnjj(i,j);endendendyou=pnjj;%再填充右边界的左半部分for i=1:512for j=512:-1:2if(juzheng(i,j)==0&juzheng(i,j-1)~=0)juzheng(i,j-1)=juzheng(i,j);endendendzuo=juzheng;shijijuzheng=you|zuo; %通过矩阵的或运算得到填充后的新图imshow(you|zuo)%原图的黑点的个数biaozhunjuzheng=imread(strcat(int2str(pn),'.bmp'));nbiao=0;for i=1:512for j=1:512if(biaozhunjuzheng(i,j)==0)nbiao=nbiao+1;endendend%新图与原图重合部分黑点的个数chonghegs=0;for i=1:512for j=1:512if(biaozhunjuzheng(i,j)==0&shijijuzheng(i,j)==0)chonghegs=chonghegs+1;endendend%求百分比baifenbi=chonghegs/nbiao;。