吉林省名校调研卷系列(省命题A)2020届九年级下学期第一次综合测试数学试题(word版,包含答案)
吉林省名校调研2020年中考数学一模试卷解析版
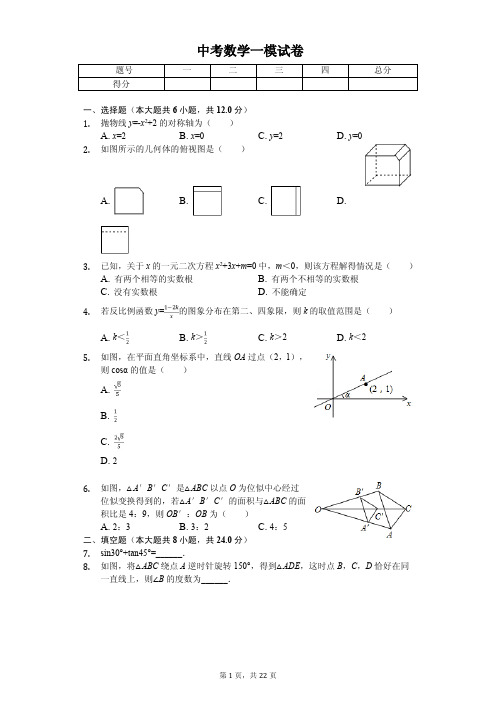
中考数学一模试卷题号一二三四总分得分一、选择题(本大题共6小题,共12.0分)1.抛物线y=-x2+2的对称轴为( )A. x=2B. x=0C. y=2D. y=02.如图所示的几何体的俯视图是( )A. B. C. D.3.已知,关于x的一元二次方程x2+3x+m=0中,m<0,则该方程解得情况是( )A. 有两个相等的实数根B. 有两个不相等的实数根C. 没有实数根D. 不能确定4.若反比例函数y=的图象分布在第二、四象限,则k的取值范围是( )A. k<B. k>C. k>2D. k<25.如图,在平面直角坐标系中,直线OA过点(2,1),则cosα的值是( )A.B.C.D. 26.如图,△A′B′C′是△ABC以点O为位似中心经过位似变换得到的,若△A′B′C′的面积与△ABC的面积比是4:9,则OB′:OB为( )A. 2:3B. 3:2C. 4:5D. 4:9二、填空题(本大题共8小题,共24.0分)7.sin30°+tan45°=______.8.如图,将△ABC绕点A逆时针旋转150°,得到△ADE,这时点B,C,D恰好在同一直线上,则∠B的度数为______.9.在正方形网格中,△ABC的位置如图所示,则sin B的值为______.10.如图,△ABC中,P为边AB上一点.且∠ACP=∠B,若AP=2,BP=3,则AC的长为______.11.如图,AB是⊙O的直径,点C、D在⊙O上,连结AD、BC、BD、DC,若BD=CD,∠DBC=20°,则∠ABC的度数为______.12.如图,铁道路口的栏杆短臂长1m,长臂长16m,当短臂端点下降0.5m时,长臂端点升高为______.(杆的宽度忽略不计)13.在平面直角坐标系中,点A和点C分别在y轴和x轴的正半轴上,以OA,OC为边分别作矩形OABC,双曲线y=(x>0)交AB于点E,AE:EB=1:3,则矩形的面积为______.14.二次函数y=2x2-4x+4的图象如图所示,其对称轴与它的图象交于点P,点N是其图象上异于点P的一点,若PM⊥y轴,MN⊥x轴,则=______.三、计算题(本大题共2小题,共14.0分)15.如图,为测量小岛A到公路BD的距离,先在点B处测得∠ABD=37°,再沿BD方向前进150m到达点C,测得∠ACD=45°,求小岛A到公路BD的距离.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)16.如图,⊙O是△ABC的外接圆,E是弦BC的中点,P是⊙O外一点且∠PBC=∠A,连接OE并延长交⊙O于点F,交BP于点D.(1)求证:BP是⊙O的切线;(2)若⊙O的半径为6,BD=8,求弦BC的长.四、解答题(本大题共10小题,共82.0分)17.解方程:x2+8x=9.18.已知y是x的反比例函数,且x=3时,y=8.(1)写出y与x之间的函数关系式;(2)如果自变量x的取值范围为3≤x≤4.求y的取值范围.19.如图,已知△ABC中,AB=AC=5,cos A=.求底边BC的长.20.2019年中国北京世园会开园期间,为了满足不同人群的游览需求,组委会倾情打造了四条趣玩路线,分别是“解密世园会”、“爱我家,爱园艺”、“园艺小清新之旅”和“快速车览之旅”小明一家想通过抽签的方法选择其中的两条路线进行游玩,于是他们制作了如下四张卡片,然后从四张卡片中随机抽取其中的两张若小明最钟爱的游玩路线是“园艺小清新之旅“,小明的爸爸和妈妈最钟爱的游玩路线是“解密世园会”,请用列表法或画树状图法求出:他们同时抽中“园艺小清新之旅”和“解密世园会”的概率是多少?21.已知半圆的直径CD=12cm,如图所示,弧DE所对的圆心角∠ECD=30°,求阴影部分的周长.22.图(a)、图(b)是两张形状,大小完全相同的8×8的方格纸,方格纸中的每个小正方形的边长均为1,请在图(a)、图(b)中分别画出符合要求的图形,要求:所画图形各顶点必须与方格纸中的小正方形顶点重合.(1)以AB为一边,画一个成中心对称的四边形ABCD,使其面积为12;(2)以EF为一边,画△EFP,使其面积为的轴对称图形.23.如图,已知一次函数y=kx+b的图象交反比例函数y=的图象于点A(2,-4)和点B(h,-2),交x轴于点C.(1)求这两个函数的解析式;(2)连接OA、OB.求△AOB的面积;(3)请直接写出不等式kx+b>的解集.24.如图1,在Rt△ABC中,∠BAC=90°,AB=AC,D,E两点分别在AC,BC上,且DE∥AB,将△CDE绕点C按顺时针方向旋转,记旋转角为α.(1)问题发现:当α=0°时,的值为______;(2)拓展探究:当0°≤α<360°时,若△EDC旋转到如图2的情况时,求出的值;(3)问题解决:当△EDC旋转至A,B,E三点共线时,若设CE=5,AC=4,直接写出线段BE的长______.25.如图,一条顶点坐标为(-1,)的抛物线与y轴交于点C(0,5),与x轴交于点A和点B,有一宽度为1,长度足够的矩形(阴影部分)沿x轴方向平移,与y 轴平行的一组对边交抛物线于点P和Q,交直线AC于点M和N,交x轴于点E 和F(1)求抛物线的解析式;(2)当点M和N都有在线段AC上时,连接MF,如果MF=AF,求点Q的坐标;(3)在矩形的平移过程中,当以点P,Q,M,N为顶点的四边形是平行四边形时,求点M的坐标.26.如图,在▱ABCD中,∠ABD=90°,AD=5,BD=3,点P从点A出发,沿折线AB一BC以每秒1个单位长度的速度向终点C运动(点P不与点A、B、C重合).在点P的运动过程中,过点P作AB所在直线的垂线,交边AD或边CD于点Q,以PQ为一边作矩形PQMN,且QM=2,MN与BD在PQ的同侧,设点P的运动时间为t(秒).(1)当t=5时,求线段CP的长;(2)求线段PQ的长(用含t的代数式表示);(3)当点M落在BD上时,求t的值;(4)当矩形PQMN与▱ABCD重叠部分图形为五边形时,直接写出t的取值范围.答案和解析1.【答案】B【解析】解:∵抛物线y=-x2+2,∴该抛物线的对称轴为直线x=0,故选:B.根据题目中的抛物线y=-x2+2,可以直接写出该抛物线的对称轴.本题考查二次函数的性质,解答本题的关键是明确题意,利用二次函数的性质解答.2.【答案】C【解析】解:从上边看是左右各一个矩形,左边的矩形大,故选:C.根据从上边看得到的图形是俯视图,可得答案.本题考查了简单组合体的三视图,从上边看得到的图形是俯视图.3.【答案】B【解析】解:△=9-4m,∵m<0,∴-4m>0,∴△=9-4m>0,故选:B.根据根的判别式即可求出答案.本题考查根的判别式,解题的关键是熟练运用根的判别式,本题属于基础题型.4.【答案】B【解析】解:∵反比例函数y=的图象分布在第二、四象限,∴1-2k<0,解得k>,故选:B.根据反比例函数的图象和性质,由1-2k<0即可解得答案.本题考查了反比例函数的图象和性质:①、当k>0时,图象分别位于第一、三象限;当k<0时,图象分别位于第二、四象限.②、当k>0时,在同一个象限内,y随x的增大而减小;当k<0时,在同一个象限,y随x的增大而增大.5.【答案】C【解析】解:如图,作AH⊥x轴于H.∵A(2,1),∴OH=2,AH=1,∴OA===,∴cosα===,故选:C.如图,作AH⊥x轴于H.利用勾股定理求出OA,根据三角函数的定义解决问题即可.本题考查解直角三角形,坐标由图形的性质等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题.6.【答案】A【解析】解:由位似变换的性质可知,A′B′∥AB,A′C′∥AC,∴△A′B′C′∽△ABC.∵△A'B'C'与△ABC的面积的比4:9,∴△A'B'C'与△ABC的相似比为2:3,∴=故选:A.先求出位似比,根据位似比等于相似比,再由相似三角形的面积比等于相似比的平方即可.本题考查的是位似变换的概念和性质,如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形,这个点叫做位似中心.7.【答案】【解析】解:原式=+1=.故答案为:.分别把各特殊角度的三角函数值代入进行计算即可.本题考查的是特殊角的三角函数值,熟记各特殊角度的三角函数值是解答此题的关键.8.【答案】15°【解析】解:∵将△ABC绕点A逆时针旋转150°,得到△ADE,∴∠BAD=150°,AD=AB,∵点B,C,D恰好在同一直线上,∴△BAD是顶角为150°的等腰三角形,∴∠B=∠BDA,∴∠B=(180°-∠BAD)=15°,故答案为:15°.先判断出∠BAD=150°,AD=AB,再判断出△BAD是等腰三角形,最后用三角形的内角和定理即可得出结论.此题主要考查了旋转的性质,等腰三角形的判定和性质,三角形的内角和定理,判断出三角形ABD是等腰三角形是解本题的关键.9.【答案】【解析】解:作AE⊥BC于E.在Rt△ABE中,∵AE=BE=4,∠AEB=90°,∴∠ABE=∠BAE=45°,∴sin B=sin45°=,故答案为.作AE⊥BC于E.利用等腰直角三角形的性质解决问题即可.本题考查解直角三角形,解题的关键是学会添加常用辅助线,构造直径三角形解决问题.10.【答案】【解析】解:AB=AP+BP=2+3=5,∵∠ACP=∠B,∠A=∠A,∴△ACP∽△ABC,∴=,∴AC2=AP•AB=2×5=10,∴AC=,故答案为:.AB=AP+BP=5,由∠ACP=∠B,∠A=∠A,得出△ACP∽△ABC,得出=,代入数值即可得出结果.本题考查了相似三角形的判定与性质,熟练掌握相似三角形的判定与性质是解题的关键.11.【答案】50°【解析】解:∵AB是⊙O的直径,∴∠ADB=90°,∵BD=CD,∠DBC=20°,∴∠C=∠DBC=20°,∴∠A=∠C=20°,∴∠ABD=90°-∠A=70°,∴∠ABC=∠ABD-∠DBC=70°-20°=50°故答案为50°先由直径所对的圆周角为90°,可得:∠ADB=90°,由BD=CD,∠DBC=20°,根据等腰三角形性质可得:∠C=20°,根据同弧所对的圆周角相等,即可求出∠A=20°,根据三角形内角和定理求得∠ABD=70°,进而即可求得∠ABC的度数.此题主要考查了圆周角定理,关键是掌握圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半,直径所对的圆周角为90°.12.【答案】8m【解析】解:如图,由题意知∠BAO=∠C=90°,∵∠AOB=∠COD,∴△ABO∽△CDO,∴,即=,解得:CD=8,故答案为:8m.由题意证△ABO∽△CDO,可得,即=,解之可得.本题主要考查相似三角形的应用,熟练掌握相似三角形的判定与性质是解题的关键.13.【答案】24【解析】解:设E点坐标为(t,),∵AE:EB=1:3,∴B点坐标为(4t,),∴矩形OABC的面积=4t•=24.故答案为:24.根据反比例函数图象上点的坐标特征设E点坐标为(t,),则利用AE:EB=1:3,B 点坐标可表示为(4t,),然后根据矩形面积公式计算.本题考查了反比例函数y=(k≠0)系数k的几何意义:从反比例函数y=(k≠0)图象上任意一点向x轴和y轴作垂线,垂线与坐标轴所围成的矩形面积为|k|.14.【答案】2【解析】解:∵二次函数y=2x2-4x+4=2(x-1)2+2,∴点P的坐标为(1,2),设点M的坐标为(a,2),则点N的坐标为(a,2a2-4a+4),∴===2,故答案为:2.根据题目中的函数解析式可得到点P的坐标,然后设出点M、点N的坐标,然后计算即可解答本题.本题考查二次函数的性质,解答本题的关键是明确题意,利用二次函数的性质解答.15.【答案】解:过A作AE⊥CD垂足为E,设AE=x米,在Rt△ABE中,tan B=,∴BE==x,在Rt△ABE中,tan∠ACD=,∴CE==x,∵BC=BE-CE,∴x-x=150,解得:x=450.答:小岛A到公路BD的距离为450米.【解析】过A作AE⊥CD垂足为E,设AE=x米,再利用锐角三角函数关系得出BE=x,CE=x,根据BC=BE-CE,得到关于x的方程,即可得出答案.此题主要考查了解直角三角形的应用,解一般三角形,求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.16.【答案】(1)证明:如图,连接OB,∵E是弦BC的中点,∴BE=CE,OE⊥BC,==,∴∠BOE=∠A,∠OBE+∠BOE=90°,∵∠PBC=∠A,∴∠BOE=∠PBC,∴∠OBE+∠PBC=90°.即BP⊥OB.∴BP是⊙O的切线(2)解:∵OB=6,BD=8,BD⊥OB.∴OD==10.∵△OBD的面积=OD•BE=OB•BD,∴BE==4.8.∴BC=2BE=9.6【解析】(1)连接OB,由垂径定理的推论得出BE=CE,OE⊥BC,=,由圆周角定理得出∠BOE=∠A,证出∠OBE+∠PBC=90°,得出∠OBD=90°即可;(2)由勾股定理求出OD,由△OBD的面积求出BE,即可得出弦BC的长.本题考查了切线的判定、垂径定理的推论、圆周角定理、勾股定理、三角形面积的计算;熟练掌握垂径定理的推论和圆周角定理是解决问题的关键.17.【答案】解:x2+8x=9,x2+8x-9=0,(x+9)(x-1)=0,x+9=0或x-1=0,解得x1=-9,x2=1.【解析】先把方程化为一般式,然后利用因式分解法解方程.本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).18.【答案】解:(1)设反比例函数是y=(k≠0),当x=3时,y=8,代入可解得k=24.所以y=.(2)当x=3时,y=8,当x=4时,y=6,∴自变量x的取值范围为3≤x≤4.y的取值范围为6≤y≤8.【解析】(1)根据反比例函数的定义设出表达式,再利用待定系数法解出系数则可;(2)分别代入x的值求得y值后即可求得y的取值范围;本题考查了反比例函数的性质及反比例函数的定义,能够利用待定系数法确定反比例函数的解析式是解答本题的关键,难度不大.19.【答案】解:过点B作BD⊥AC,垂足为点D,在Rt△ABD中,cos A=,∵cos A=,AB=5,∴AD=AB•cos A=5×=3,∴BD==4,∵AC=AB=5,∴DC=2,∴BC==2.【解析】过点B作BD⊥AC,垂足为点D,解直角三角形即可得到结论.本题考查了解直角三角形,勾股定理,等腰三角形的性质,正确的作出辅助线是解题的关键.20.【答案】解:设上述四张卡片从左到右依次用字母A,B,C,D表示,则抽取结果可以用如下树状图表示:从树状图可知,所有等可能结果有12种,其中能同时能抽中A和D的结果有2种,所以他们同时抽中“园艺小清新之旅”和“解密世园会”的概率是.【解析】首先根据题意画出树状图,然后由树状图求得所有等可能的结果与恰好抽中A 和D的情况,再利用概率公式即可求得答案.此题考查了树状图法与列表法求概率.用到的知识点为:概率=所求情况数与总情况数之比.21.【答案】解:CE交半圆于F,连接OF、DF,如图,∵弧DE所对的圆心角∠ECD=30°,∴的长为=2π,∵∠DOF=2∠ECD=60°,∴的长度为=2π,∵CD为直径,∴∠CFD=90°,∴DF=CD=6,CF=DF=6,∴EF=12-6,∴阴影部分的周长=2π+2π+12-6=4π+12-6.【解析】CE交半圆于F,连接OF、DF,如图,先利用弧长公式计算出的长为2π,再根据圆周角定理得到∠DOF=60°,∠CFD=90°,然后利用弧长公式计算出的长和EF=12-6,从而得到阴影部分的周长.本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了弧长公式.22.【答案】解:(1)如图所示:四边形ABCD是面积为12的平行四边形;(2)如图所示:△EFP是面积为的等腰三角形.【解析】(1)根据平行四边形的底边为4,高为3,进行画图;(2)根据等腰三角形的腰为5,腰上的高为3,进行画图.本题主要考查了利用图形的基本变换进行作图,作图时需要运用平行四边形的性质以及等腰三角形的性质进行计算.注意:平行四边形是中心对称图形,等腰三角形是轴对称图形.23.【答案】解:(1)把A(2,-4)的坐标代入y=得:m=-8,∴反比例函数的解析式是y=-;把B(h,-2)的坐标代入y=-得:-2=-,解得:n=4,∴B点坐标为(4,-2),把A(2,-4)、B(4,-2)的坐标代入y=kx+b,得:,解得:,∴一次函数解析式为y=x-6;(2)∵y=x-6,∴当y=0时,x=0+6=6,∴OC=6,∴△AOB的面积=△AOC的面积-三角形BOC的面积=×6×4-×6×2=12-6=6;(3)由图象知,kx+b>的解集为0<x<2或x>4.【解析】(1)先把点A的坐标代入y=,求出m的值得到反比例函数解析式,再求点B的坐标,然后代入反比例函数解析式求出点B的坐标,再将A、B两点的坐标代入y=kx+b,利用待定系数法求出一次函数的解析式;(2)先求出C点坐标,再根据△AOB的面积=△AOC的面积-三角形BOC的面积即可求解;(3)观察函数图象即可求出不等式kx+b>的解集.本题主要考查了反比例函数图象与一次函数图象的交点问题以及观察图象的能力,待定系数法求函数解析式,求出点B的坐标是解题的关键.24.【答案】 7或1【解析】解:(1)∵∠BAC=90°,AB=AC,∴△ABC为等腰直角三角形,∠B=45°,∵DE∥AB,∴∠DEC=∠B=45°,∠CDE=∠A=90°,∴△DEC为等腰直角三角形,∴cos∠C==,∵DE∥AB,∴==,故答案为:;(2)由(1)知,△BAC和△CDE均为等腰直角三角形,∴==,又∠BCE=∠ACD=α,∴△BCE∽△ACD,∴==,即=;(3)①如图3-1,当点E在线段BA的延长线上时,∵∠BAC=90°,∴∠CAE=90°,∴AE===3,∴BE=BA+AE=4+3=7;②如图3-2,当点E在线段BA上时,AE===3,∴BE=BA-AE=4-3=1,综上所述,BE的长为7或1,故答案为:7或1.(1)先证△DEC为等腰直角三角形,求出=,再通过平行线分线段成比例的性质可直接写出的值;(2)证△BCE∽△ACD,由相似三角形的性质可求出的值;(3)分两种情况讨论,一种是点E在线段BA的延长线上,一种是点E在线段BA上,可分别通过勾股定理求出AE的长,即可写出线段BE的长.本题考查了等腰直角三角形的性质,锐角三角函数,相似三角形的判定与性质等,解题关键是注意分类讨论思想在解题过程中的运用.25.【答案】解:(1)根据题意,抛物线顶点为,设抛物线为.抛物线过点C(0,5),∴,抛物线解析式为.(2)易得:A(-5,0),B(3,0).如图,作FD⊥AC于D,∵OA=5,OC=5,∴∠CAO=45°.设AF=m,则.在△MEF中,FM2=ME2+EF2,∴,解得(不符合题意,舍去).∴AF=2,∴点Q的横坐标为-3.又点Q在抛物线上,∴Q(-3,4),(3)设直线AC的解析式y=kx+n,由题意,得∴直线AC的解析式y=x+5.由已知,点Q,N,F及点P,M,E横坐标分别相同.设F(t,0),E(t+1,0),N(t,t+5),M(t+1,t+6),.在矩形平移过程中,以P,Q,N,M为顶点的平行四边形有两种情况:①点Q,P在直线AC同侧时,QN=PM.∴,解得:t=-3.∴M(-2,3).②点Q,P在直线AC异侧时,QN=MP.∴,解得∴.∴符合条件的点M是(-2,3),.【解析】(1)设抛物线为,把点(0,5)代入即可解决问题.(2)作FD⊥AC于D,设AF=m,则,列出方程求出m的值即可解决问题.(3)设F(t,0),E(t+1,0),N(t,t+5),M(t+1,t+6),.①当MN是对角线时,由QN=PM,列出方程即可解决问题.②点Q,P在直线AC异侧时,QN=MP,解方程即可.本题考查二次函数综合题、平行四边形的判定与性质、勾股定理等知识,解题的关键是学会待定系数法确定函数解析式,学会分类讨论,用方程的思想解决问题,属于中考压轴题.26.【答案】解:(1)如图1中,在Rt△ABD中,∵∠ABD=90°,AD=5,BD=3,∴AB==4,∵四边形ABCD是平行四边形,∴AD=BC=5,CD=AB=4,当t=5时,点P在BC上,PB=1,∴PC=4.(2)①如图2中,当0<t<4时,∵PQ∥BD,∴=,∴=,∴PQ=t.②如图3中,当5<t<10时,∵PQ∥BD,∴=,∴=,∴PQ=(9-t).(3)①如图4中,当点P在线段AB上时,点M在线段BD上,∵QM∥AB,∴=,∴=,∴DQ=,∴AQ=DQ,∵PQ∥BD,∴AP=PB=2,∴t=2.②如图5中,当点P在线段BC上,点M与D重合时,易知QM=QC=2,PB=PC=,此时t=4+=.(4)①如图6中,当点P在线段AB上,重叠部分是五边形PBKMQ时,2<t<4.②如图7中,当点P在线段BC上,重叠部分是五边形PQDKN时,4<t<6.5.【解析】(1)如图1中,利用勾股定理求出AB的长,t=5时,点P在线段BC上,易知PB=1,PC=4;(2)分两种情形求解即可①如图2中,当0<t<4时,②如图3中,当5<t<10时;(3)分两种情形求解即可①如图4中,当点P在线段AB上时,点M在线段BD上,求出AP.②如图5中,当点P在线段BC上,点M与D重合时;(4)分两种情形分别求解即可①如图6中,当点P在线段AB上,重叠部分是五边形PBKMQ时,2<t<4.②如图7中,当点P在线段BC上,重叠部分是五边形PQDKN 时,4<t<6.5;本题考查四边形综合题、平行四边形的性质、平行线分线段成比例定理、勾股定理等知识,解题的关键是学会用分类讨论的思想思考问题,学会利用平行线分线段成比例定理,构建方程解决问题,属于中考压轴题.。
吉林省名校调研卷系列(省命题A)2020年九年级下学期第一次模拟测试英语试题(word版)

吉林省名校调研卷系列(省命题A)2020届九年级下学期第一次模拟测试英语试题一、听力部分(共20分)I.情景反应根据你所听到的句子,选择恰当的应答语。
(5分)()1. A. Thank you. B. Good night. C. Just kidding.()2. A. Be active. B. Open your eyes. C. OK. I will speak slowly.()3. A. An engineer. B. You bet. C. Nothing.()4. A. Nice idea. B. Here it is. C.I will miss you.()5. A. Not far from here. B. About 10 stops. C. At the third crossing. II.对话问答根据你所听到的对话及问题,选择正确答案。
(5分)()6. A. Sunny. B. Cloudy. C. Rainy.()7. A. Twice a week. B. Twice a month. C. Every month.()8. A. At 9:30. B. At 10:00. C. At 10:30.()9. A. Her mother. B. Her brother. C. Her grandfather.()10. A. Because it's popular. B. Because it's relaxing. C. Because it s exciting.III.图片理解看图听描述,选择与你所听到的描述内容相符合的选项。
(下列图中有一幅图片与描述内容无关)(5分)11. 12. 13. 14. 15.D.短文理解根据你所听到的短文内容 ,判断下列各句正(T)、误(F)。
(5分)()16. David will leave school in June 2021.()17. David's school is big.()18. There are many subjects in David's school.()19. David's teachers are friendly to them.()20. They go to the hospital as helpers each term.二、基础知识(共15分)V.句意填词根据所给句子,填入一个适当的单词,使句意完整。
吉林省长春市名校调研2020-2021学年九年级下学期第一次月考数学试题

A.2B.3C.4D.5
二、填空题
9.比较大小: (填“>”、“=”或“<”).
10.如图,在5×5的正方形网格中,每个小正方形的边长均为1,点O、A、B都在格点上,则tan∠AOB的值为_____.
(1)求sinA的值.
(2)当x为何值时,点R落在BC上.
(3)当菱形APRQ与△ABC重叠部分的图形为四边形时,求y与x的函数关系式.
(4)直接写出当x为何值时,经过三角形顶点的直线同时将菱形、三角形的面积二等分.
23.如图,在平面直角坐标系中,直线y= +2分别交x轴、y轴于点A、B,抛物线y=﹣x2+bx+c经过点A、B.点P是x轴上一个动点,过点P作垂直于x轴的直线分别交抛物线和直线AB于点E和点F.设点P的横坐标为m.
17.如图,点A、B在⊙O上,CB为⊙O的切线,AC=BC,求证:AC为⊙O的切线.
18.如图,抛物线y=﹣ x2+ x+c经过点(﹣2,2),求c的值及函数的最大值.
19.如图,吊车在水平地面上吊起货物时,吊绳BC与地面保持垂直,吊臂AB与水平线的夹角为64°,吊臂底部A距地面1.5m.
(1)当吊臂底部A与货物的水平距离AC为5m时,求吊臂AB的长;
(1)点A的坐标为____.
(2)求这条抛物线所对应的函数表达式.
(3)点P在线段OA上时,若以B、E、F为顶点的三角形与△FPA相似,求m的值.
(4)若E、F、P三个点中恰有一点是其它两点所连线段的中点(三点重合除外),称E、F、P三点为“共谐点”.直接写出E、F、P三点成为“共谐点”时m的值.
2020年吉林省长春市名校调研中考数学一模试卷含答案

中考数学一模试卷题号一二三四总分得分一、选择题(本大题共8小题,共24.0分)1.如图,数轴上两点A,B表示的数互为相反数,则点B表示的数为()A. -6B. 6C. 0D. 无法确定2.下列标志是轴对称图形的是( )A. B. C. D.3.下列计算正确的是( )A. a2•a3=a6B. 3a2-a2=2C. a6÷a2=a3D. (-2a)2=4a24.如图,下列条件不能判定AB∥CD的是( )A. ∠GDH+∠DHE=180°B. ∠FEB+∠GCE=180°C. ∠BAD=∠ADGD. ∠GCE=∠AEF5.如图,Rt△ABC中,∠C=90°,AB=10,BC=8,将△ABC折叠,使B点与AC的中点D重合,折痕为EF,则线段BF的长是( )A.B. 2C.D.6.用白铁皮做罐头盒.每张铁皮可制盒身16个,或制盒底48个,一个盒身与两个盒底配成一套罐头盒.现有15张白铁皮,设有x张用于制盒身,y张用于制盒底,能使盒身和盒底配套,依题意可列的方程组及该方程组的解正确的是( )A. B.C. D.7.小明希望测量出电线杆AB的高度,于是在阳光明媚的一天,他在电线杆旁的点D处立一标杆CD,使标杆的影子DE与电线杆的影子BE部分重叠(即点E、C、A 在一条直线上),量得ED=2米,DB=4米,CD=1.5米,则电线杆AB长为( )A. 2米B. 3米C. 4.5米D. 5米8.如图,A(1,y1)、B(-2,y2)是双曲线y=上的两点,且y1+y2=1.若点C的坐标为(0,-1),则△ABC的面积为( )A. 1B. 2C. 3D. 4二、填空题(本大题共6小题,共18.0分)9.科学家在实验室中检测出某种微生物的直径约为0.0000035米,将0.0000035用科学记数法表示是______.10.计算:×=______.11.分解因式:2x2-4x=______.12.若关于x的一元二次方程x2-2x+m-3=0有两个相等的实数根,则m的值是______.13.如图,在⊙O中,=,∠AOB=40°,点D在⊙O上,连结CD,AD,则∠ADC的度数是______.14.如图,已知MA=MB,那么数轴上点A所表示的数是______.三、计算题(本大题共2小题,共15.0分)15.先化简,再求值:(x-2y)2-(x+y)(3x-y)-5y2,其中x=-2,y=1.16.2018年10月23日,港珠澳大桥正式开通,成为横亘在伶仃洋上一道靓丽的风景.大桥主体工程隧道的东、西两端各设置了一个海中人工岛,来衔接桥梁和海底隧道,西人工岛上的A点和东人工岛上的B点间的距离约为5.6千米,点C是与西人工岛相连的大桥上的一点,A,B,C在一条直线上.如图,一艘观光船沿与大桥段垂直的方向航行,到达P点时观测两个人工岛,分别测得与观光船航向的夹角∠DPA=18°,∠DPB=53°,求此时观光船到大桥AC段的距离PD的长.(参考数据:sin18°≈0.31,cos18°≈0.95,tan18°≈0.33,sin53°≈0.80,cos53°≈0.60,tan53°≈1.33.)四、解答题(本大题共8小题,共63.0分)17.京剧脸谱是京剧艺术独特的表现形式.京剧表演中,经常用脸谱象征人物的性格,品质,甚至角色和命运.如红脸代表忠心耿直,黑脸代表强悍勇猛.现有三张不透明的卡片,其中两张卡片的正面图案为“红脸”,另外一张卡片的正面图案为“黑脸”,卡片除正面图案不同外,其余均相同,将这三张卡片背面向上洗匀,从中随机抽取一张,记录图案后放回,重新洗匀后再从中随机抽取一张.请用画树状图或列表的方法,求抽出的两张卡片上的图案都是“红脸”的概率.(图案为“红脸”的两张卡片分别记为A1、A2,图案为“黑脸”的卡片记为B)18.学校广播站要招聘一名播音员,擅长诵读的小龙想去应聘,但是不知道是否符合应聘条件,于是在微信上向好朋友亮亮倾诉,如图是他们的部分对话内容.面对小龙的问题,亮亮也犯了难.聪明的你用所学方程知识帮小龙准确计算一下,他是否符合学校广播站应聘条件?19.如图,AB是⊙O的切线,A为切点,AC是⊙O的弦,过O作OH⊥AC于点H.若OH=3,AB=8,BO=10.求:(1)⊙O的半径;(2)弦AC的长(结果保留根号).20.学习成为现代城市人的时尚,我市图书馆吸引了大批读者,有关部门统计了2018年第一季度到市图书馆的读者的职业分布情况,统计图如下:(1)在统计的这段时间内,共有______万人到市图书馆阅读,其中商人所占百分比是______.(2)将条形统计图补充完整.(3)若今年4月到市图书馆的读者共28000名,估计其中约有多少名职工.21.如图1是甲、乙两个圆柱形水槽的轴截面示意图,乙槽中有一圆柱形铁块放其中(圆柱形铁块的下底面完全落在水槽底面上)现将甲槽中的水匀速注入乙槽,甲、乙两个水槽中水的深度y甲(厘米),y乙(厘米)与注水时间x(分钟)之间的关系如图2所示,根据图象提供的信息,解答下列问题:(1)图2中折线ABC表示______槽中的深度与注水时间之间的关系,线段DE表示______槽中的深度与注水时间之间的关系(以上两空选填“甲”或“乙”),点B的纵坐标表示的实际意义是______.(2)当0≤x≤4时,分别求出y甲和y乙与x之间的关系式;(3)注水多长时间时,甲、乙两个水槽中的水的深度相同?(4)若乙槽底面积为36平方厘米(壁厚不计),求乙槽中铁块的体积;(5)若乙槽中铁块的体积为112立方米(壁厚不计),求甲槽底面积______(直接写出结果).22.如图,在菱形四边形ABCD中,∠ABC=60°,AB=4,对角线AC、BD交于点O,点P为直线BD上的动点(不与点B重合),连接AP,将线段AP绕点P逆时针旋转60°得到线段PE,连接CE、BE.(1)问题发现如图1,当点E在直线BD上时,线段BP与CE的数量关系为______;∠ECB=______°.(2)拓展探究如图2,当点P在线段BO延长线上时,(1)的结论是否成立?若成立,请加以证明;若不成立,请说明理由;(3)问题解决当∠BEC=30°时,请直接写出线段AP的长度.23.如图,在平面直角坐标系中,直线y=x+n与抛物线y=ax2+bx+3相交子点A(-5,-7)、B(5,c),点C、D在直线AB上,且点D在点C的右侧,过点C、D分别作CF、DE平行于y轴交抛物线于点F、E,以点C、D、E、F为顶点的多边形记作图形M,其面积为S,设点C的横坐标为m,点D的横坐标为m+2,当-5<m<5时,解答下列问题:(1)求直线与抛物线所对应的函数关系式;(2)求s与m的函数关系式;(3)当M为中心对称图形时,求m的值;(4)将M沿直线AB翻折,E、F两点的对应点为E′、F′,请直接写出C、D、E、F四个点中有且只有两个点同时落在第四象限时m的取值范围.24.如图,平面直角坐标系中,直线y=x+4分别交x轴、y轴于点A、C,直线BC与直线AC关于y轴对称,动点D从点A出发,沿AC以每秒2个单位长度的速度向终点C运动,当点D出发后,过点D作DE∥BC交折线A-O-C于点E,以DE为边作等边△DEF,设△DEF与△ACO重叠部分图形的面积为S,点D运动的时间为t 秒.(1)写出坐标:点A(______),点B(______),点C(______);(2)当点E在线段AO上时,求S与t之间的函数关系式;(3)求出以点B、E、F为顶点的三角形是直角三角形时t的值;(4)直接写出点F运动的路程长为______.答案和解析1.【答案】B【解析】【分析】根据数轴上点的位置,利用相反数定义确定出B表示的数即可.此题考查了数轴,以及相反数,熟练掌握相反数的性质是解本题的关键.【解答】解:∵数轴上两点A,B表示的数互为相反数,点A表示的数为-6,∴点B表示的数为6,故选:B.2.【答案】B【解析】解:A、不是轴对称图形,故本选项错误;B、是轴对称图形,故本选项正确;C、不是轴对称图形,故本选项错误;D、不是轴对称图形,故本选项错误.故选:B.根据轴对称图形的概念求解.本题考查了轴对称图形的概念:轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合.3.【答案】D【解析】解:A、a2•a3=a5,故此选项错误;B、3a2-a2=2a2,故此选项错误;C、a6÷a2=a4,故此选项错误;D、(-2a)2=4a2,正确.故选:D.直接利用合并同类项法则以及同底数幂的乘除运算法则、积的乘方运算法则分别判断得出答案.此题主要考查了合并同类项以及同底数幂的乘除运算、积的乘方运算,正确掌握相关运算法则是解题关键.4.【答案】A【解析】解:根据∠GDH+∠DHE=180°,不能得到AB∥CD,故A选项不能判定;根据∠FEB+∠GCE=180°,∠FEB=∠AEC,可得∠AEC+∠GCE=180°,进而得到AB∥CD,故B选项能判定;根据∠BAD=∠ADG,可得AB∥CD,故C选项能判定;根据∠GCE=∠AEF,可得AB∥CD,故D选项能判定;故选:A.根据同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行,进行判断即可.本题主要考查了平行线的判定,解题时注意:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.5.【答案】D【解析】解:∵Rt△ABC中,∠C=90°,AB=10,BC=8∴AC=6∵D是AC中点∴AD=CD=3∵折叠∴DF=BF∴设BF=x,则CF=8-x在Rt△DCF中,DF2=CD2+CF2∴x2=9+(8-x)2∴x=∴BF=故选:D.根据题意可得:CD=3,在Rt△DCF中,根据勾股定理可列方程,解方程可得BF的长.本题考查了翻折问题,勾股定理的运用,关键是通过勾股定理列出方程.6.【答案】C【解析】[分析]设用制盒身的铁皮为x张,用制盒底的铁皮为y张,根据铁皮共15张且制作的盒底的数量为盒身数量的2倍,即可得出关于x,y的二元一次方程组,解之即可得出x的值,再将其代入16x中即可求出结论.[详解]解:设用制盒身的铁皮为x张,用制盒底的铁皮为y张,根据题意得:,解得:,所以盒身的铁皮为9张,用制盒底的铁皮为6张.故选:C.[点评]本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.7.【答案】C【解析】解:∵CD∥AB,∴△ECD∽△EAB,∴ED:EB=CD:AB,∴2:6=1.5:AB,∴AB=4.5米.答:电线杆AB长为4.5米.故选:C.根据题意求出△ECD∽△EBA,利用相似三角形的对应边成比例即可解答.本题主要考查了把实际问题抽象到相似三角形中,利用相似三角形的相似比,列出方程,通过解方程即可求出电线杆的高.8.【答案】C【解析】解:(1)∵A(1,y1)、B(-2,y2)是双曲线y=上的两点,∴y1=k,y2=-,∵y1+y2=1∴k-=1∴k=2∴双曲线的解析式:y=∵A(1,y1)、B(-2,y2)是双曲线y=上两点,∴点A(1,2),点B(-2,-1)∵点C(0,-1)∴BC∥x轴∴S△ABC=×2×3=3,故选:C.将点A,点B代入解析式,再根据y1+y2=1,可求双曲线y=的解析式,将点A,点B代入解析式,可求点A,点B坐标,则可得BC∥x轴,根据三角形面积公式可求△ABC的面积.本题考查了反比例函数的性质,用待定系数法求解析式,熟练掌握图象上点的坐标满足图象的解析式是本题的关键.9.【答案】3.5×10-6【解析】解:将0.0000035用科学记数法表示是3.5×10-6.故答案为:3.5×10-6.绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10-n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.本题考查用科学记数法表示较小的数,一般形式为a×10-n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.10.【答案】【解析】解:原式==.故答案为:.直接利用二次根式的乘法运算法则计算得出答案.此题主要考查了二次根式的乘法,正确掌握运算法则是解题关键.11.【答案】2x(x-2)【解析】解:2x2-4x=2x(x-2).故答案为:2x(x-2).首先找出多项式的公因式,然后提取公因式法因式分解即可.此题主要考查了提取公因式法因式分解,根据题意找出公因式是解决问题的关键.12.【答案】4【解析】解:∵关于x的一元二次方程x2-2x+m-3=0有两个相等的实数根,∴△=(-2)2-4×1×(m-3)=0,即4-m=0,解得m=4.故答案是:4.由于关于x的一元二次方程x2-2x+m-3=0有两个相等的实数根,可知其判别式为0,据此列出关于m的方程,解答即可.本题主要考查了根的判别式的知识,解答本题的关键是掌握一元二次方程有两个相等的实数根,则可得△=0,此题难度不大.13.【答案】20°【解析】解:连接OC.∵=,∴∠AOB=∠AOC=40°,∴∠ADC=∠AOC=20°,故答案为20°根据等弧所对的圆周角相等,求出∠AOC即可解决问题.本题考查圆周角定理,圆心角,弧,弦之间的关系等知识,解题的关键是学会添加常用辅助线,灵活运用所学知识解决问题.14.【答案】1-【解析】解:根据题意,由勾股定理得:MB==,∴MA=MB=,∴A到原点的距离是-1,∵A在原点左侧,∴点A所表示的数是1-.故答案为:1-.首先在直角三角形中,利用勾股定理可以求出线段MB的长度,得出MA的长度,求出点A与原点的距离,即可得出数轴上点A所表示的数.此题主要考查了实数与数轴之间的对应关系、勾股定理;熟练掌握勾股定理,并能进行推理计算是解决问题的关键.15.【答案】解:原式=x2-4xy+4y2-(3x2-xy+3xy-y2)-5y2=x2-4xy+4y2-3x2+xy-3xy+y2-5y2=-2x2-6xy,当x=-2,y=1时,原式=-2×(-2)2-6×(-2)×1=4.【解析】原式利用完全平方公式,多项式乘以多项式法则计算,去括号合并得到最简结果,把x与y的值代入计算即可求出值.此题考查了整式的混合运算-化简求值,熟练掌握运算法则是解本题的关键.16.【答案】解:在Rt△DPA中,∵tan∠DPA=,∴AD=PD•tan∠DPA,在Rt△DPB中,∵tan∠DPB=,∴BD=PD•tan∠DPB,∴AB=BD-AD=PD•(tan∠DPB-tan∠DPA),∵AB=5.6,∠DPB=53°,∠DPA=18°,即5.6=(tan53°-tan18°)•PD,∴PD==5.6,则此时观光船到大桥AC段的距离PD的长为5.6千米.【解析】在直角三角形DPA中,利用锐角三角函数定义表示出AD,在直角三角形DPB 中,利用锐角三角函数定义表示出BD,由DB-AD表示出AB,进而求出所求即可.此题考查了解直角三角形的应用,熟练掌握锐角三角函数定义是解本题的关键.17.【答案】解:画树状图为:由树状图可知,所有可能出现的结果共有9种,其中两次抽取的卡片上都是“红脸”的结果有4种,所以P(两张都是“红脸”)=,答:抽出的两张卡片上的图案都是“红脸”的概率是.【解析】根据题意画出树状图,求出所有的情况数和两次抽取的卡片上都是“红脸”的情况数,再根据概率公式计算即可.此题主要考查了概率的求法.用到的知识点为数状图和概率,概率=所求情况数与总情况数之比,关键是根据题意画出树状图.18.【答案】解:设小龙每分钟读x个字,小龙奶奶每分钟读(x-50)个字,根据题意,得:=,解得:x=260,经检验,x=260是所列方程的解,并且符合实际问题的意义.∵学校广播站招聘条件是每分钟250-270字,∴小龙符合学校广播站应聘条件.【解析】设小龙每分钟读x个字,小龙奶奶每分钟读(x-50)个字,根据奶奶读了1050个字和小龙读1300个字的时间相同,列出关系式即可得出答案.本题考查了分式方程的应用,解答本题的关键是读懂题意,找出等量关系,列方程求解.19.【答案】解:(1)∵AB是⊙O的切线,∴OA⊥AB,∴∠OAB=90°,OA===6,即圆的半径为6;(2)∵OH⊥AC,∴CH=AH,∴AC=2AH,∵AH===3,则:AC=6.【解析】(1)在Rt△OAB中,利用勾股定理,即可求解;(2)在Rt△OAH中,利用勾股定理求AH的长度,即可求解.本题利用了切线的性质和勾股定理解决问题,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.20.【答案】(1)16,12.5% ;(2)职工的人数为16-(4+2+4)=6(万人),补全条形图如下:(3)估计其中职工人数为28000×=10500(人).【解析】解:(1)这段时间,到图书馆阅读的总人数为4÷25%=16(万人),其中商人所占百分比为×100%=12.5%,故答案为:16,12.5%;(2)职工的人数为16-(4+2+4)=6(万人),补全条形图如下:(3)估计其中职工人数为28000×=10500(人).(1)用学生数除以其所占的百分比即可得到总人数,然后用商人数除以总人数即可得到商人所占的百分比;(2)根据各职业人数之和等于总人数可得职工的人数,据此可补全图形;(3)用总人数乘以职工占总人数的百分比即可得到职工人数.本题考查了条形统计图、扇形统计图及用样本估计总体的知识,解题的关键是从两种统计图中整理出进一步解题的有关信息.21.【答案】(1)乙,甲,乙槽中圆柱形铁块的高度是14厘米 60(cm2);(2)设线段AB、DE的解析式分别为:y甲=k1x+b1,y乙=k2x+b2,∵AB经过点(0,2)和(4,14),DE经过(0,12)和(6,0)∴,解得,,解得:,∴当0≤x≤4时,y乙和y甲与x之间的解析式分别为y乙=3x+2和y甲=-2x+12,(3)当y甲=y乙时,即3x+2=-2x+12,解得x=2,∴当2分钟时两个水槽水面一样高;(4)由图象知:当水槽中没有没过铁块时4分钟水面上升了12cm,即1分钟上升3cm ,当水面没过铁块时,2分钟上升了5cm,即1分钟上升2.5cm,设铁块的底面积为acm2,则乙水槽中不放铁块的体积分别为:2.5×36cm3,放了铁块的体积为3×(36-a)cm3,∴1×3×(36-a)=1×2.5×36,解得a=6,∴铁块的体积为:6×14=84(cm3).(5)60(cm2).【解析】解:(1)乙;甲;乙槽中圆柱形铁块的高度是14厘米;故答案为:乙,甲,乙槽中圆柱形铁块的高度是14厘米;(2)见答案;(3)见答案;(4)见答案;(5)∵铁块的体积为112cm3,∴铁块的底面积为112÷14=8(cm2),可设甲槽的底面积为m,乙槽的底面积为n,则根据前4分钟和后2分钟甲槽中流出的水的体积和乙槽中流入的水的体积分别相等列二元一次方程组,∵“匀速注水”,没过铁块前和没过铁块后注水速度未变,则总水体积不变∴,解得:m=60(cm2),故甲槽底面积为60(cm2).故答案为:60(cm2).【分析】(1)根据题目中甲槽向乙槽注水可以得到折线ABC是乙槽中水的深度与注水时间之间的关系,点B表示的实际意义是乙槽内液面恰好与圆柱形铁块顶端相平;(2)根据题意分别求出两个水槽中y与x的函数关系式即可;(3)令y相等即可得到水位相等的时间;(4)用水槽的体积减去水槽中水的体积即可得到铁块的体积;(5)根据题意列方程组即可得到结论.本题考查的是用一次函数解决实际问题,此类题是近年中考中的热点问题.注意利用一次函数求最值时,关键是应用一次函数的性质;即由函数y随x的变化,结合自变量的取值范围确定最值.22.【答案】(1)问题发现BP=CE,90;(2)拓展探究结论仍然成立,如图,连接AE,由(1)可知:△AEP,△ABC都是等边三角形,∴AE=AP,AB=AC,∠EAP=∠BAC=60°,∴∠EAC=∠BAP,且AE=AP,AB=AC,∴△AEC≌△APB(SAS).∴EC=BP,∠ABP=∠ACE=30°,∴∠ECB=∠ACE+∠ACB=90°.∴结论仍然成立;(3)问题解决如图,当点E在AC左侧时,∵∠BEC=30°,∠ECB=90°,∴∠EBC=60°,且∠ABC=60°,∴BE与AB重合,∵AB=BC=4,∠BEC=30°,∠ECB=90°,∴BE=2BC=8,∴AE=BE-AB=4,∴△APE是等边三角形,∴AP=AE=4(此时点P与点D重合),如图,若点E在AC右侧时,∵∠BEC=30°,∠ECB=90°,∴∠EBC=60°,∵∠DBC=30°,∴∠DBE=∠DBC+∠EBC=90°,∵BC=AB=4,∠EBC=90°,∠BEC=30°,∴BE=2BC=8,CE=BC=4,∵BP=CE,∴BP=4,在Rt△BEP中,EP==4,∵△APE是等边三角形,∴AP=PE=4,综上所述:AP的长为4或4.【解析】解:(1)问题发现如图,连接AE,∵四边形ABCD是菱形,∠ABC=60°,∴AC⊥BD,∠ABD=∠ABC=30°,AO=CO,∴BD垂直平分AC,∴AE=CE,∵旋转∴AP=EP,∠APD=60°,∴△AEP是等边三角形∴AP=AE,∠EAP=60°∵∠APD=∠ABD+∠PAB∴∠PAB=60°-30°=30°∴AP=PB∴AP=PB=AE=EC∵AB=BC,∠ABC=60°∴∠ACB=60°∵△AEP是等边三角形,AC⊥BD,∴∠EAO=30°,∵AE=EC∴∠ECO=∠EAO=30°,∵∠ECB=∠ECO+∠ACB∴∠ECB=90°故答案为:BP=EC,90°(2)见答案;(3)见答案.【分析】(1)问题发现连接AE,根据菱形的性质可得AC⊥BD,∠ABD=∠ABC=30°,AO=CO,根据线段垂直平分线的性质可得AE=EC,由旋转的性质可得△AEP是等边三角形,可得AP=AE,∠EAP=60°,根据三角形的外角的性质和等腰三角形的判定,可证AP=PB=AE=EC,由菱形的性质可得∠ACB=60°,根据等边三角形的性质和等腰三角形的性质可得∠ACE=30°,即可得∠ECB=90°;(2)拓展探究由等边三角形的性质可得AE=AP,AB=AC,∠EAP=∠BAC=60°,可得∠EAC=∠BAP,根据“SAS”可证△AEC≌△APB,可得EC=BP,∠ABP=∠ACE=30°,即可得∠ECB=90°;(3)问题解决分点E在AC左侧,点E在AC右侧两种情况讨论,根据直角三角形的性质和等边三角形的性质以及勾股定理可求点P的坐标.本题是四边形综合题,考查了菱形的性质,全等三角形的判定和性质,直角三角形的性质,等边三角形的性质,勾股定理等知识,灵活运用相关的性质定理、综合运用知识是解题的关键,注意分情况讨论思想的应用.23.【答案】解:(1)∵直线y=x+n经过点A(-5,-7),B(5,c),∴-7=-5+n,∴n=-2.∴c=5-2=3,∴直线解析式为y=x-2.把A(-5,-7),B(5,3)代入y=ax2+bx+3得到解得,∴抛物线解析式为y=-x2+x+3.(2)①当-5<m≤3时,∵点C横坐标为m,∴C(m,m-2),D(m+2,m),F(m,-m2+m+3),E[m+2,-(m+2)2+(m+2)+3],∴FC=-m2+m+3-(m-2)=-m2+5,ED=-(m+2)2+5,∴S=×2×[-m2+5-(m+2)2+5]=-m2-m+.②当3<m<5时,S=S=×2×[-m2+5+(m+2)2-5]=m+(3)①当-5<m≤3时,当M为平行四边形时,M为中心对称图形,∴CF=DE,∴-m2+5=-(m+2)2+5,解得m=-1.②当3<m<5时,可得-m2+5=(m+2)2-5,解得m=-1+2或-1-2(舍弃),综上所述,m=-1或-1+2.(4)如图1中,当点F′落在y轴上时,因为C(m,m-2),则F(m,-m2+m+3),∵CF=CF′,∴-m=-m2+m+3-(m-2),解得:m=或(舍弃),如图2中,当点D在y轴上时,m+2=0,m=-2,如图3中,当点D在x轴上时,m+2=2,m=0,如图4中,当点C在x轴上时,m=2,综上所述,当C、D、E′、F′四个点中有且只有两个点同时落在第四象限时m的取值范围为<m≤-2,或0<m<2.【解析】(1)由直线y=x+n经过点A(-5,-7),B(5,c),求出n,c,把A(-5,-7),B(5,3)代入y=ax2+bx+3解方程组即可.(2)分两种情形讨论:求出FC、ED,根据梯形的面积公式计算即可.(3)分两种情形讨论:当M为平行四边形时,M为中心对称图形,由CF=DE,列出方程计算即可.(4)分别求出当点F′落在y轴上时(如图1中),m的值;当点D在y轴上时(如图2中),m的值;当点D在x轴上时(如图3中),m的值;当点C在x轴上时(如图4中),m的值,由此即可解决问题.本题考查二次函数的综合题、翻折变换、一次函数.梯形的面积公式等知识,解题的关键是灵活应用待定系数法确定函数解析式,学会分类讨论,学会可以特殊位置考虑问题,找到问题的突破口,属于中考压轴题.24.【答案】(1)-4,0 ; 4,0; 0,4;(2)Rt△ACO中,tan∠CAO===,∴∠CAO=60°,∵AC=BC,∴∠ABC=∠CAO=60°,∵DE∥BC,∴∠AED=∠ABC=60°,∴△ADE是等边三角形,∴AD=AE=2t,当点F在OC上时,如图1,∵∠AED=∠DEF=60°,∴∠OEF=30°,∵∠EOF=90°,∵EF=DE=AD=2t,∴OE=EF=t,∵AO=AE+OE=2t+t=4,t=,①当0<t≤时,点E在线段OA上,△DEF与△ACO重叠部分图形是△DEF,如图2,S=•(2t)2=;(5分)②当<t≤2时,如图3,△DEF与△ACO重叠部分图形是四边形DEGH,∵AE=2t,OE=4-2t,Rt△EOG中,∠EGO=30°,∴OG=OE=(4-2t),∴GH=OH-OG=t-=3t-4,Rt△FHG中,∠HGF=30°,∴FH==3t-4,∴S=S△DEF-S△GHF,=-,=-t-8;(7分)(3)①如图4,当0<t≤2时,∠EFB=90°,∠FBE=30°,∴BE=2EF=2AD,则8-2t=4t,t=;(9分)②如图5,当2<t<4时,E在y轴上,∠FEB=90°,∠FBE=30°,∵∠ABC=60°,∴∠EBO=30°,∵OB=4,∴OE=,BE=,∴EF=,BF=,∵BF=AD,∴2t=,t=,(11分)综上,t的值是秒或秒;(4) 4+4 .【解析】解:(1)x=0时,y=4,∴C(0,4),当y=0时,x+4=0,x=-4,∴A(-4,0),∵直线BC与直线AC关于y轴对称,∴B(4,0),故答案为:-4,0;4,0;0,4;(3分)(2)Rt△ACO中,tan∠CAO===,∴∠CAO=60°,∵AC=BC,∴∠ABC=∠CAO=60°,∵DE∥BC,∴∠AED=∠ABC=60°,∴△ADE是等边三角形,∴AD=AE=2t,当点F在OC上时,如图1,∵∠AED=∠DEF=60°,∴∠OEF=30°,∵∠EOF=90°,∵EF=DE=AD=2t,∴OE=EF=t,∵AO=AE+OE=2t+t=4,t=,①当0<t≤时,点E在线段OA上,△DEF与△ACO 重叠部分图形是△DEF,如图2,S=•(2t)2=;(5分)②当<t≤2时,如图3,△DEF与△ACO重叠部分图形是四边形DEGH,∵AE=2t,OE=4-2t,Rt△EOG中,∠EGO=30°,∴OG=OE=(4-2t),∴GH=OH-OG=t-=3t-4,Rt△FHG中,∠HGF=30°,∴FH==3t-4,∴S=S△DEF-S△GHF,=-,=-t-8;(7分)(3)①如图4,当0<t≤2时,∠EFB=90°,∠FBE=30°,∴BE=2EF=2AD,则8-2t=4t,t=;(9分)②如图5,当2<t<4时,E在y轴上,∠FEB=90°,∠FBE=30°,∵∠ABC=60°,∴∠EBO=30°,∵OB=4,∴OE=,BE=,∴EF=,BF=,∵BF=AD,∴2t=,t=,(11分)综上,t的值是秒或秒;(4)动点D从点A出发,DE∥BC,点E在线段OA上时,如图6,点F的运动路径为等边△ACB中BC边上的高线AF,此时AF==4,当点E在线段OC上时,设BC的中点为P,如图7,点F的运动路径为PC的长,∵PC=BC=4,∴点F运动的路程长为:4+4,故答案为:4+4.(13分)(1)分别令x=0和y=0代入直线y=x+4中,可得A和C的坐标,根据对称性可得B的坐标;(2)根据三角函数特殊值求∠CAO=60°,得△ADE是等边三角形,表示AD=AE=2t,计算当点F在OC上时,如图1,根据AO=AE+OE=2t+t=4,列方程可得t的值,①当0<t≤时,点E在线段OA上,△DEF与△ACO重叠部分图形是等边△DEF,如图2,②当<t≤2时,如图3,△DEF与△ACO重叠部分图形是四边形DEGH,根据面积差可得结论;(3)①如图4,当0<t≤2时,∠EFB=90°,根据BE=2EF=2AD列式可得结论;②如图5,当2<t<4时,E在y轴上,根据BF=AD=2t,得t的值;(4)①点E在线段OA上时,如图6,点F的运动路径为等边△ACB中BC边上的高线AF ,②当点E在线段OC上时,设BC的中点为P,如图7,点F的运动路径为PC的长,相加可得结论.此题是一次函数的综合题,主要考查了:一次函数与x轴、y轴交点的求法、三角函数的定义、勾股定理及几何动点问题,此类题常运用方程的思想解决问题,解(2)和(3)的关键是:分两种情况进行讨论.。
吉林省东2020届九年级数学下学期第一次综合测试题

文档根源为 :从网络采集整理.word 版本可编写 .支持.吉林省东 2017 届九年级数学放学期第一次综合测试题(时间: 120 分钟;满分: 120 分)注意事项:1.答题前,考生务势必自己的姓名,准考据号填写在答题卡上,并将条形码正确粘贴在条形码地区内 .2.答题时,考生务必依据考试要求在答题卡上的指定地区内作答,在厕纸、试卷上答题无效.一、选择题(本大题共8 小题,每题 3 分,共 24 分)1. 在,,, 0 这四个数中,最小实数是()(A)( B)( C)( D)02. 图 1 和图 2 中全部的正方形都全相等,将图 1 的正方形放在图 2 中的①②③④某一地点成为 6 个正方形,所构成的图形不可以围成正方体的地点是()(A)①( B)②( C)③( D)④3. 成人的大脑皮质约含有14 000 000 000个神经元胞体,14 000 000 000这个数据用科学记数法表示为()(A)(B)(C)(D)4.如图,田亮同学用剪刀沿直线将一片平坦的树叶减掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解说这一现象的数学知识是()(A)垂线段最短(B)经过一点有无数条直线(C)经过两点,有且只有一条直线(D)两点之间,线段最短5. 如图,∥,均分∠交于点,若∠= 50°,则∠的大小为()(A) 65°( B) 115°( C) 125°( D)130°6. 互联网“微商”经营已成为大众创业新门路,某微信平台一件商品标价为200 元,按标价的五折销售,仍可赢利20 元,则这件商品的进价为()(A) 120 元(B)100 元(C)80 元( D)60 元7. 对于的一元二次方程有实数根,则的取值范围是()(A)( B)( C)( D)8. 如图,点是矩形的对称中心,= 3,= 3,动点从点出发,以每秒 2 个单位的速度,沿→→→向终点运动,连接、. 设△的面积为,点的运动时间为( s),在以下图像中,能正确反应与的函数关系式的是()文档根源为 :从网络采集整理.word 版本可编写 .支持.二、填空题(本大题共9.分解因式=6 小题,每题 3 分,共;18 分)10. 不等式组的解集是;11. 如图,正五边形放在某平面直角坐标系后,若极点、、、的坐标分别是,,,,则点的坐标为.12. 如图,以点为位似中心,将△减小后获得△,已知= 3 ,则△与△的面积比为。
吉林省名校调研卷系列(省命题A)2020届九年级下学期第一次模拟测试化学试题(word版)

吉林省名校调研卷系列(省命题A)2020届九年级下学期第一次模拟测试化学试题可能用到的相对原子质量:H-1 Cl-35.5一、单项选择题(每小题1分,共10分)1.下列物质的用途不正确的是()A.铜作导线B.金刚石裁玻璃C.小苏打制发酵粉D.补铁剂预防甲状腺肿大2.下列实验操作错误的是()A.倾倒液体B.读取液体体积C.点燃酒精灯D.滴加液体3.空气中体积分数最大的气体是()A.氮气B.氧气C.二氧化碳D.稀有气体4.下列说法正确的是()A.海水中最多的元素是钠B.地壳中含量最多的元素是氧C.人体中含量最多的元素是钙D.空气中含量最多的元素是碳5.钠在二氧化碳中燃烧生成炭黑和一种白色固体,它可能是()A.碳酸钠B.硫酸钠C.碳酸氢钠D.氢氧化钠6.保护环境,人人有责。
下列做法错误的是()A.生活购物时,用布袋代替塑料袋B.上班上学时,鼓励低碳出行C.农业生产中,禁止使用化肥D.工作学习中,提倡纸张双面使用7.化学与生产、生活息息相关,下列说法错误的是()A.油锅着火,可用锅盖盖灭B.洗洁精有乳化作用,可用来清洗油污C.港珠澳大桥使用的吊绳所含的聚乙烯纤维,属于有机合成材料D.为延长食品的保质期,可用福尔马林(甲醛的水溶液)作防腐剂8.我国西汉时期,在(淮南万毕术)中记载“曾青得铁则化为铜”.意思是可溶性的铜的化合物与铁发生反应得到单质铜,此为现代湿法冶金的先驱。
下列说法正确的是()A.该反应属于复分解反应B.该反应证明了铁的金属活动性比铜强C.若铁足量,溶液的颜色逐渐变为无色D.由该反应可推测出铜能与稀硫酸反应9.逻辑推理是学习化学常用的思维方法,下列推理正确的是()A.原子是不带电的粒子.所以不带电的粒子一定是原子B.单质只含一种元素,所以含一种元素的物质一定是单质C.溶液是均一、稳定的,所以均一、稳定的混合物一定是溶液D.碱中含有氢元素和氧元素.所以含有氢元素和氧元素的物质-定是碱10.物质的鉴别和除杂是重要的实验技能。
2020届初三中考数学一诊联考试卷含答案解析 (吉林)

2020届**市初三中考一诊联考试卷数学注意事项:1.答卷前,考生务必将自己的姓名、准考证填写在答题卡上。
2.回答客观题时,选出每小题答案后,用2B铅笔把答题卡上对应的答案标号涂黑。
如需改正,必须用橡皮擦擦涂干净,回答非客观题,将答案写在答题卡上,写在试卷上无效。
3.考试结束后,将本试卷和答题卡一并收回。
4.考试时间:120分钟。
一、单选题(共10题,每题3分,共30分,四个选项中只有一项符合题目要求)1.小明总结了以下结论:①a(b+c)=ab+ac;②a(b﹣c)=ab﹣ac;③(b﹣c)÷a=b÷a﹣c÷a(a≠0);④a÷(b+c)=a÷b+a÷c(a≠0);其中一定成立的个数是( )A.1 B.2 C.3 D.42.如图,正方形ABCD中,分别以B、D为圆心,以正方形的边长a为半径画弧,形成树叶形(阴影部分)图案,则树叶形图案的周长为A .a πB .2a πC .1a 2πD .3a π3.如图, AB 是⊙O 的直径,⊙O 的半径为5,⊙O 上有定点C 和动点P ,它们位于直径AB 的异侧, 过点C 作CP 的垂线,与PB 的延长线交于点Q,若tan ∠ABC=34,则线段CQ 的长度的最大值为( )A .10B .152C .403D .2034.“十一”国庆节期间,几名同学包租一辆面包车前去旅游,面包车的租价为180元,出发时又增力了两名同学,结果每个同学比原来少摊了3元钱车费.设参加旅游的同学共x 人,则所列方程为( )A .18018032x x -=+B .18018032x x -=+C .18018032x x -=-D .18018032x x-=- 5.下列四个立体图形中,从正面看到的图形与其他三个不同的是( ) A . B . C . D .6.如图,在△ABC中,AD平分∠BAC,按如下步骤作图:第一步,分别以点A、D为圆心,以大于12AD的长为半径在AD两侧作弧,交于两点M、N;第二步,连接MN,分别交AB、AC于点E、F;第三步,连接DE、DF.若BD=6,AF=4,CD=3,则BE的长是()A.2B.4C.6D.87.如图1,在矩形ABCD中,E是AD上的一点,点P从点B沿折线BE﹣ED ﹣DC,运动到点C时停止;点Q从点B沿BC运动到点C时停止,速度均为每秒1个单位长度,如果点P,Q同时开始运动,设运动时间为t,△BPQ的面积为y,已知y与t的函数图象如图2所示,以下结论:①BC=10;②cos∠ABE=35;③当t=12时,△BPQ是等腰三角形;④当14≤t≤20时,y=110﹣5t,其中正确的有()A.1个B.2个C.3个D.4个8.若一组数据a1,a2,a3的平均数为4,方差为3,那么数据a1+2,a2+2,a3+2的平均数和方差分别是()A.4,3B.6,3C.3,4D.6,59.如图,在平面直角坐标系中,⊙P的圆心是(2,a),半径为2,直线y=﹣x与⊙P相交于A、B两点,若弦AB的长为,则a的值是()A.﹣B.﹣C.﹣2D.﹣210.如图所示,已知 AB∥CD,下列结论正确的是()A.∠1=∠2B.∠2=∠3C.∠1=∠4D.∠3=∠4二、填空题(共4题,每题4分,共16分)11.如图,在矩形ABCD中,AB=6,BC=4,点E是边BC上一动点,把△DCE沿DE折叠得△DFE,射线DF交直线CB于点P,当△AFD为等腰三角形时,DP的长为_____.12.甲、乙二人在相同情况下,各射靶10次,两人命中环数的平均数都是7,方差2S甲=2.8,2S乙=1.5,则射击成绩较稳定的是______.(填“甲”或“乙”)13.如图,正比例函数y 1=k 1x 的图象与反比例函数y 2=2k x(x >0)的图象相交于点A B 是反比例函数图象上一点,它的横坐标是3,连接OB ,AB ,则△AOB 的面积是_____.14.2019年4月10日,人类首次看到黑洞,该黑洞的质量是太阳的65亿倍,距离地球大约55000000光年,将数据55000000用科学记数法表示为______.三、解答题(共6题,总分54分)15.“村村通公路政策,是近年来国家构建和谐社会,支持新农村建设的一项重大公共决策,是一项民心工程,惠民工程某镇政府准备向甲、乙两个工程队发包一段“村村通”工程建设项目,经调查:甲、乙两队单独完成该工程,乙队所需时间是甲队的2倍;甲、乙两队共同完成该工程需30天;若甲队每天所需劳务费用为2400元,乙队每天所需劳务费用为1500元,从节约资金的角度考虑,应选择哪个工程队更合算?16.如图,已知△ABC ,利用尺规完成下列作图(不写画法,保留作图痕迹).(1)作△ABC 的外接圆;(2)若△ABC 所在平面内有一点D ,满足∠CAB=∠CDB ,BC=BD ,求作点D .17.如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(-3,0)、(0,4),抛物线y=2 3 x2+bx+c经过点B,且顶点在直线x=52上.(1)求抛物线对应的函数关系式;(2)若把△ABO沿x轴向右平移得到△DCE,点A、B、O的对应点分别是D、C、E,当四边形ABCD是菱形时,试判断点C和点D是否在该抛物线上,并说明理由;(3)在(2)的条件下,连接BD,已知对称轴上存在一点P使得△PBD的周长最小,求出P点的坐标;(4)在(2)、(3)的条件下,若点M是线段OB上的一个动点(点M与点O、B不重合),过点M作∥BD交x轴于点N,连接PM、PN,设OM的长为t,△PMN的面积为S,求S和t的函数关系式,并写出自变量t的取值范围,S是否存在最大值?若存在,求出最大值和此时M点的坐标;若不存在,说明理由.。
2020年吉林省长春市名校调研中考数学一模试卷

中考数学一模试卷一、选择题(本大题共8小题,共24.0分)1.的相反数是()A. B. C. D.2.如图是由五个相同的小正方块搭成的几何体,其左视图是()A.B.C.D.3.不等式组的解集在数轴上表示为()A. B.C. D.4.如图,直尺经过一块三角板DCB的顶点B,∠C=30°,∠ABC=20°,则∠AEF的度数为()A. 150°B. 140°C. 130°D. 100°5.如图,等边△ABC的边长为1cm,D、E分别是AB、AC上的点,将△ADE沿直线DE折叠,点A落在点A′处,且点A′在△ABC外部,则阴影部分图形的周长为()A. 3cmB. 4cmC. 4.5cmD. 5cm6.某家具生产厂生产桌椅,已知每块板材可做桌子1张或椅子3把,现计划用100块这种板材生产一批桌椅(不考虑板材的损耗),设用x块板材做桌子,用y块板材做椅子,使得恰好配套(一张桌子两把椅子),则下列方程组正确的是()A. B. C. D.7.如图,双曲线y=(x>0)的图象经过正方形OCDF的对角线的交点A,则正方形OCDF的面积为()A. 6B. 12C. 24D. 488.小明在某次投篮中刚好把球打到篮板的点D处后进球,已知小明与篮筐底的距离BC=5米,眼睛与地面的距离AB=1.7米,视线AD与水平线的夹角为∠α,已知tanα=,则点D到地面的距离CD是()A. 2.7米B. 3.0米C. 3.2米D. 3.4米二、填空题(本大题共6小题,共18.0分)9.一根头发的直径约为0.0000715米,该数用科学记数法表示为______.10.分解因式:5x2-8x=______.11.计算-9的结果是______.12.如图,在▱ABCD中,AD>CD,按下列步骤作图:①分别以点A、C为圆心,大于AC的长为半径画弧,两弧的交点分别为点F、G;②过点F、G作直线FG,交边AD于点E,若△CDE的周长为11,则▱ABCD的周长为______.13.如图,身高1.6米的小丽在阳光下的影长为2米,在同一时刻,一棵大树的影长为8米,则这棵树的高度为______米.14.如图抛物线y=ax2+c与直线y=3相交于点A、B,与y轴交于点C(0,-1),若∠ACB为直角,则当ax2+c<0时自变量x的取值范围是______.三、解答题(本大题共10小题,共78.0分)15.先化简,再求值:(x-5)(x+1)+(x+2)2,其中x=-2.16.因课外活动的需要,鹏胜同学第一次在文具店买若干支笔芯,花了30元,第二次再去买该款笔芯时,发现每一盒(20支装)价钱升了2元,他这一次买该款笔芯的数量是第一次的2倍,花了68元,求他两次买的笔芯分别是多少支?17.甲、乙两人都握有分别标记为A、B、C的三张牌,两人做游戏,游戏规则是:每人各出一张牌,若两人出的牌相同,则为平局;若两人出的牌不同,则A胜B,B 胜C,C胜A.(1)用树状图或列表等方法,列出甲、乙两人一次游戏的所有可能的结果;(2)求出现平局的概率.18.已知在网格中每个小正方形的边长都是1,图1中的阴影图案是由一条对角线和以格点为圆心,半径为2的圆弧围成的弓形.(1)图1中阴影部分的面积是______(结果保留π);(2)请你在图2中以图1为基本图案,借助轴对称,平移或旋转设计一个轴对称的花边图案(要求至少含有两种图形变换).19.如图,在△ABC中,AB=AC,以AB为直径作⊙O交BC于点D.过点D作EF⊥AC,垂足为E,且交AB的延长线于点F.(1)求证:EF是⊙O的切线;(2)若AB=8,∠A=60°,求BD的长.20.某校为了了解七年级1000名学生的身体健康情况,从该年级随机抽取了若干名学生,将他们按体重(均为整数,单位:kg)分成五组(A:39.5-46.5;B:46.5-53.5;C:53.5-60.5;D:60.5-67.5;E:67.5-74.5),并依据统计数据绘制了如下两幅尚不完整的统计图.请解答下列问题:(1)这次随机抽取了______名学生调查,并补全频数分布直方图;(2)在抽取调查的若干名学生中体重在______组的人数最多,在扇形统计图中D 组的圆心角是______度;(3)请你估计该校七年级体重超过60kg的学生大约有多少名?21.周末,甲、乙两名大学生骑自行车去距学校6000米的净月潭公园,两人同时从学校出发,以a米/分的速度匀速行驶,出发4.5分钟时,甲同学发现忘记带学生证,以1.5a米/分的速度按原路返回学校,取完学生证(在学校取学生证所用时间忽略不计),继续以返回时的速度追赶乙,甲追上乙后,两人以相同的速度前往净月潭,乙骑自行车的速度始终不变,设甲,乙两名大学生距学校的路程为s(米),乙同学行驶的时间为t(分),s与t之间的函数图象如图所示.(1)求a,b的值;(2)求甲追上乙时,距学校的路程;(3)当两人相距500米时,直接写出t的值是______.22.如图,在矩形ABCD中,AB=6,BC=10,将矩形沿直线EF析折叠,使得点A恰好落在BC边上的点G处,且点E、F分别在边AB、AD上含端点),连结CF,(1)当B=3时,求AE的长;(2)当AF取得最小值时,求折痕EF的长;(3)连结CF,当△FCG是以CG为底的等腰三角形时,直接写出BG的长,23.如图,在平面直角坐标系中,把抛物线y=x2先向右平移1个单位长度,再向下平移4个单位长度,得到抛物线y=(x-h)2+k,所得抛物线与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,顶点为M.(1)写出h、k的值及点A、B的坐标;(2)判断△BCM的形状,并计算其面积;(3)点P是抛物线上的一动点,在y轴上存在点Q,使以点A、B、P、Q为顶点组成的四边形是平行四边形,求点P的坐标.24.如图,在Rt△ABC中,∠C=90°,AB=13,BC=12,四边形PDEF为矩形PD=4,PF=8.点P从点B出发,沿BC以每秒1个单位长度的速度向点C运动伴随点P的运动,矩形PDEF在射线BC上滑动:点Q从点P出发,沿折线PDDE以每秒1个单位长度的速度匀速运动,点P,Q同时出发,当点Q到达点E时,两点同时停止运动,连结QC,设点P的运动时间为t秒(t>0)(1)求线段PC的长.(用含t的代数式表示)(2)当点Q落在AB边上时,求r的值.(3)设△PQC的面积为S,求S与t之间的函数关系式.(4)当四边形PDEF与△ABC重叠部分图形为五边形时,直接写出使△PQC为直角三角形时t的取值范围.答案和解析1.【答案】A【解析】解:根据相反数的定义,得的相反数是.故选:A.理解相反数的定义:只有符号不同的两个数叫互为相反数,0的相反数是0.掌握求一个数的相反数的方法,即在这个数的前面加负号.2.【答案】A【解析】解:从左边看,从左往右小正方形的个数依次为:2,1.左视图如下:故选:A.细心观察图中几何体中正方体摆放的位置,根据左视图是从左面看到的图形判定则可.本题主要考查了几何体的三种视图和学生的空间想象能力,视图中每一个闭合的线框都表示物体上的一个平面,而相连的两个闭合线框常不在一个平面上.3.【答案】A【解析】解:由3x-2>1,解得x>1,3-2x≥-1,解得xx≤2,不等式组的解集为1<x≤2,在数轴上表示为:故选:A.先求出不等式组中每一个不等式的解集,再求出它们的公共部分,然后把不等式的解集表示在数轴上即可.本题考查了在数轴上表示不等式的解集,把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.4.【答案】C【解析】解:∵∠C=30°,∠ABC=20°,∴∠BAD=∠C+∠ABC=50°,∵EF∥AB,∴∠AEF=180°-∠BAD=130°,故选:C.依据三角形外角性质,即可得到∠BAD,再根据平行线的性质,即可得到∠AEF的度数.本题主要考查了平行线的性质,解题时注意:两直线平行,同旁内角互补.5.【答案】A【解析】解:由折叠可得AD=A′D;AE=A′E,∴阴影部分图形的周长为AB+BC+AC=3cm.故选:A.由折叠可得阴影部分图形的周长正好等于原等边三角形的周长.考查折叠的问题;用到的知识点为:折叠前后的线段相等.6.【答案】C【解析】解:设用x块板材做桌子,用y块板材做椅子,∵用100块这种板材生产一批桌椅,∴x+y=100 ①,生产了x张桌子,3y把椅子,∵使得恰好配套,一张桌子两把椅子,∴2x=3y②,①和②联立得:,故选:C.设用x块板材做桌子,用y块板材做椅子,根据“用100块这种板材生产一批桌椅”,即可列出一个二元一次方程,根据“每块板材可做桌子1张或椅子3把,使得恰好配套,一张桌子两把椅子”,列出另一个二元一次方程,即可得到答案.本题考查了由实际问题抽象出二元一次方程组,正确找出等量关系,列出二元一次方程组是解题的关键.7.【答案】C【解析】解:设A(a,a),C(2a,0),∵点A在反比例函数y=的图象上,∴a2=6,∴正方形OCDF的面积=2a•2a=4a2=4×6=24,故选:C.由于双曲线y=(x>0)的图象经过正方形OCDF的对角线的交点A,设A(a,a),进而根据正方形的性质表示出点C的坐标,然后根据正方形面积公式即可求得.本题考查了反比例函数图象上点的坐标特征:反比例函数y=(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.也考查了正方形的性质.8.【答案】C【解析】解:在直角△ADE中,∠DAE=α,AE=5米,tan,∴tanα===,∴DE=1.5米.又CE=AB=1.7米,∴CD=CE+DE=3.2米.故选:C.通过解直角△ADE得到DE的长度,然后由矩形ABCE的性质求得CE的长度,易得CD=CE+DE.考查了解直角三角形的应用,利用数学知识解决实际问题是中学数学的重要内容.解决此问题的关键在于正确理解题意的基础上建立数学模型,把实际问题转化为数学问题.9.【答案】7.15×10-5【解析】解:0.0000715=7.15×10-5;故答案为7.15×10-5.绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10-n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.本题考查用科学记数法表示较小的数,一般形式为a×10-n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.10.【答案】x(5x-8)【解析】解:5x2-8x=x(5x-8).故答案为:x(5x-8).直接找出公因式进而提取分解因式即可.此题主要考查了提取公因式法分解因式,正确找出公因式是解题关键.11.【答案】-【解析】解:原式=2-9×=2-3=-.故答案为:-.直接化简二次根式,进而合并求出答案.此题主要考查了二次根式的加减运算,正确化简二次根式是解题关键.12.【答案】22【解析】解:由作法得FG垂直平分AC,∴EA=EC,∵△CDE的周长为11,即CE+DE+CD=11,∴AE+DE+CD=11,即AD+CD=11,∵四边形ABCD为平行四边形,∴AD=BC,AB=CD,∴▱ABCD的周长=2(AD+CD)=2×11=22.故答案为22.利用基本作图得到FG垂直平分AC,则EA=EC,再利用等线段代换得到AD+CD=11,从而得到平行四边形的周长.本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了线段垂直平分线的性质.13.【答案】6.4【解析】解:∵同一时刻的两个物体,影子,经过物体顶部的太阳光线三者构成的两个直角三角形相似,=,∴=,∴BC=6.4米.故答案为6.4.在同一时刻物高和影长成正比,即在同一时刻的两个物体,影子,经过物体顶部的太阳光线三者构成的两个直角三角形相似.本题考查了相似三角形在测量高度时的应用,解题时关键是找出相似的三角形,然后根据对应边成比例列出方程,建立适当的数学模型来解决问题.14.【答案】-2<x<2【解析】【分析】此题主要考查了二次函数与不等式,正确得出函数与x轴交点是解题关键.直接利用抛物线的性质结合等腰直角三角形的性质得出B点坐标,进而求出抛物线解析式,得出图象与x轴交点进而得出答案.【解答】解:∵抛物线y=ax2+c与直线y=3相交于点A、B,与y轴交于点C(0,-1),∴DC=4,抛物线关于y轴对称,∴AC=CB,∵∠ACB为直角,∴△ACB是等腰直角三角形,∴AD=BD=DC=4,∴B(4,3),把B,C点坐标代入抛物线解析式可得:,解得:,故抛物线解析式为:y=x2-1,当y=0时,0=x2-1,解得:x1=-2,x2=2,故当ax2+c<0时自变量x的取值范围是:-2<x<2.故答案为:-2<x<2.15.【答案】解:(x-5)(x+1)+(x+2)2=x2+x-5x-5+x2+4x+4=2x2-1,当x=-2时,原式=8-1=7.【解析】先算乘法,再合并同类项,最后代入求出即可.本题考查了整式的混合运算和求值,能正确根据整式的运算法则进行化简是解此题的关键.16.【答案】解:设他第一次买的笔芯为x支,则第二次买的笔芯为2x支.由题意得方程:=,化简,得:,解得:x=40,2x=80,经检验,x=40是原分式方程的解.答:他两次买的笔芯分别是40支、80支.【解析】根据“第二次购买的单价-第一次购买的单价=每支的单价=”这一等量关系即可列出方程求解.此题考查了分式方程的应用,能根据单价列出相应的等量关系是解决本题的关键.17.【答案】解:(1)画树状图得:则共有9种等可能的结果;(2)∵出现平局的有3种情况,∴出现平局的概率为:=.【解析】此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.(1)首先根据题意画出树状图,然后由树状图求得所有等可能的结果;(2)由(1)可求得出现平局的情况,再利用概率公式求解即可求得答案.18.【答案】π-2【解析】解:(1)图中的阴影部分面积为:-×2×2=π-2;故答案为:π-2;(2)如图2所示:答案不唯一.(1)直接利用阴影部分所在扇形减去所在三角形面积即可得出答案;(2)利用基本图形结合轴对称以及旋转、平移得出符合题意的图形.此题主要考查了扇形面积求法以及利用轴对称设计图案、利用平移以及旋转设计图案,正确利用基本图形进行变换是解题关键.19.【答案】(1)证明:连接OD,AD,∵AB是⊙O的直径,∴AD⊥BC,∵AB=AC,∴BD=CD,∵OA=OB,∴OD∥AC,∵EF⊥AC,∴OD⊥EF,∴EF是⊙O的切线;(2)解:∵AB=AC,AD⊥BC,∴∠BAD=∠BAC=30°,∴BD=AB==4.【解析】(1)作辅助线,根据等腰三角形三线合一得BD=CD,根据三角形的中位线可得OD∥AC,所以得OD⊥EF,从而得结论;(2)根据等腰三角形三线合一的性质证得∠BAD=∠BAC=30°,由30°的直角三角形的性质即可求得BD.本题主要考查的是圆的综合应用,解答本题主要应用了圆周角定理、等腰三角形的性质,圆的切线的判定,30°的直角三角形的性质,掌握本题的辅助线的作法是解题的关键.20.【答案】解:(1)50(2)C,72(3)样本中体重超过60kg的学生是10+8=18人,估计该校七年级体重超过60kg的学生大约有×1000=360人.【解析】解:(1)这次抽样调查的样本容量是4÷8%=50,B组的频数=50-4-16-10-8=12,补全频数分布直方图,如图:故答案为:50;(2)在抽取调查的若干名学生中体重在C组的人数最多;D组的圆心角=×360°=72°,故答案为:C、72;(3)见答案.(1)根据A组的百分比和频数得出样本容量,并计算出B组的频数补全频数分布直方图即可;(2)由图表得出C组学生最多,并计算出D组的圆心角即可;(3)根据样本估计总体即可.此题考查频数分布直方图,关键是根据频数分布直方图得出信息进行计算.21.【答案】5.5分钟或17.5分钟【解析】解:(1)由题意a==200,b==30,∴a=200,b=30.(2)+4.5=7.5,设t分钟甲追上乙,由题意,300(t-7.5)=200t,解得t=22.5,22.5×200=4500,∴甲追上乙时,距学校的路程4500米.(3)两人相距500米是的时间为t分钟.由题意:1.5×200(t-4.5)+200(t-4.5)=500,解得t=5.5分钟,或300(t-7.5)+500=200t,解得t=17.5分钟,故答案为5.5分钟或17.5分钟.(1)根据速度=路程÷时间,即可解决问题.(2)首先求出甲返回用的时间,再列出方程即可解决问题.(3)分两种情形列出方程即可解决问题.本题考查一次函数的应用、速度、时间、路程之间的关系等知识,解题的关键是读懂图象信息,学会寻找等量关系列出方程解决问题,属于中考常考题型.22.【答案】解:(1)由折叠易知:AE=EG,设AE=EG=x,则有BE=6-x,在Rt△BEG中,由勾股定理得:(6-x)2+(3)2=x2,解得:x=,即:AE=;(2)由折叠易知:AF=FG,而当FG⊥BC时,FG的值最小,即此时AF能取得最小值,又∵当FG⊥BC时,点E与点B重合,如图1所示:此时四边形AEGF是正方形,∴折痕EF==6;(3)由△CFG是以CG为底的等腰三角形,则腰FG=FC,如图2所示:过F作FH⊥CG于H,则有:AF=FG=FC,CH=DF=GH,设AF=FG=FC=x,则DF=10-x=CH=GH,在Rt△CFH中,∵CF2=CH2+FH2∴x2=62+(10-x)2,解得:x=,∴DF=CH=GH=10-x=,∴BG=10-×2=.【解析】(1)根据折叠得出AE=EG,据此设AE=EG=x,则有BE=6-x,由勾股定理求解可得;(2)由FG⊥BC时FG的值最小,即此时AF能取得最小值,显然四边形AEGF是正方形,从而根据勾股定理可得答案;(3)由△CFG是以CG为底的等腰三角形,则腰FG=FC,过F作FH⊥CG于H,则有:AF=FG=FC,CH=DF=GH,设AF=FG=FC=x,则DF=10-x=CH=GH,在Rt△CFH中,由勾股定理得出方程,解方程即可.本题是四边形综合题目,考查了折叠变换的性质、矩形的性质、勾股定理、正方形的判定与性质、等腰三角形的性质等知识;本题综合性强,熟练掌握矩形的性质,由勾股定理得出方程是解题的关键.23.【答案】解:(1)抛物线y=x2先向右平移1个单位长度,再向下平移4个单位长度,得到抛物线y=(x-1)2-4,故h=1,k=-4,y=(x-1)2-4=x2-2x-3,令y=0,则x=3或-1,即点A、B的坐标分别为(-1,0)、(3,0);(2)点M的坐标为(1,-4),则BC=3,CM=,BM=,故MB2=BC2+CM2,故为直角三角形,其面积等于×CM×BC=3=3;(3)①当AB是平行四边形的一条边时,即PQ=AB=4,即x=±4,把x=±4代入函数表达式得:y=5或21,故点P(4,5)或(-4,21);②当AB是平行四边形的对角线时,设点P的横坐标为m,点Q的坐标为(0,n),则AB的中点即为PQ的中点,则m+0=3-1,解得:m=2,故点P(2,-3);综上,点P的坐标为P(4,5)或(-4,21)或(2,-3).【解析】解:(1)抛物线y=x2先向右平移1个单位长度,再向下平移4个单位长度,得到抛物线y=(x-1)2-4,故h=1,k=-4,y=(x-1)2-4=x2-2x-3,令y=0,则x=3或-1,即点A、B的坐标分别为(-1,0)、(3,0);(2)点M的坐标为(1,-4),则BC=3,CM=,BM=,故MB2=BC2+CM2,故为直角三角形,其面积等于×CM×BC=3=3;(3)①当AB是平行四边形的一条边时,即PQ=AB=4,即x=±4,把x=±4代入函数表达式得:y=5或21,故点P(4,5)或(-4,21);②当AB是平行四边形的对角线时,设点P的横坐标为m,点Q的坐标为(0,n),则AB的中点即为PQ的中点,则m+0=3-1,解得:m=2,故点P(2,-3);综上,点P的坐标为P(4,5)或(-4,21)或(2,-3).本题考查的是二次函数综合运用,涉及到平行四边形的性质、点的平移、中点的性质、面积的计算等,其中(3),要注意分类求解,避免遗漏.24.【答案】解:(1)PC=BC-PB=12-t(0<t<12);(2)如图1中,当Q落在AB边上时,DM+PM=4,∵PM=t,DM=(t-4),∴t+(t-4)=4,解得t=.(3)①当0<t≤4时,如图2中,S=•(12-t)•t=-t2+6t.②当4<t<12时,如图3中,S=•(12-t)•4=-2t+24.(4)如图4中,当点E在AB上时,∵EF∥AC,∴=,即=,∴BF=,BP=BF-8=,∴当<t≤4时,点Q在线段PD上,此时∠QPC=90°,△QPC是直角三角形;如图5中,当点Q在线段AC上时,∠QCP=90°,此时∠QCP是直角三角形.此时t+t-4=12,解得t=8,如图6中,当∠PQC=90°时,作QK⊥BC于K.∵△PQK∽△QCK,∴QK2=PK•KC,∴42=(t-4)(12-t-t+4),整理得t2-12t+40=0,△<0,此种情形不存在.综上所述,当<t≤4或t=8s时,△PQC是直角三角形.【解析】(1)根据PC=BC-PB计算即可;(2)当Q落在AB边上时,根据DM+PM=4,构建方程即可解决问题;(3)分两种情形①当0<t≤4时,如图2中;②当4<t<12时,如图3中,分别求解即可解决问题;(4)分三种情形分别讨论求解,①当<t≤4时,点Q在线段PD上,此时∠QPC=90°,△QPC是直角三角形;②如图5中,当点Q在线段AC上时,∠QCP=90°,此时∠QCP 是直角三角形.③如图6中,当∠PQC=90°时,作QK⊥BC于K;本题考查四边形综合题,矩形的性质、平移变换、平行线分线段成比例定理、相似三角形的判定和性质等知识,解题的关键是学会用分类讨论的思想思考问题,学会利用参数构建方程解决问题,属于中考压轴题.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
吉林省名校调研卷系列(省命题 A )2020 届九年级下学期第一次综合测试数学试题 一、选择题 (每小题 2分,共 12分)1.抛物线 y=-x 2 + 2 的对称轴为 ( )A. x=2B. x =0C. y= 2D. y= 02. 如图所示几何体的俯视图是 ( )3. 已知关于 x 的一元二次方程 x 2+3x+m= 0, 若 m < 0, 则该方程解的情况是 ( ) A. 有两个相等的实数根 B. 有两个不相等的实数根 C. 没有实数根 D.不能确定1A. k <2 1 B. k >2C. k > 2D. k < 25. 如图,在平面直角坐标系中 ,直线 OA 过点 A(2,1), 则 cos α的值是 ( ) √5 12 √5A. 5B. 2C. 5D.2(第 5题) (6.如图, △A'B'C 是△ ABC 以点O 为位似中心经过位似变换得到的 ,若△ A'B'C' 的面积与△ ABC 的面积比是 4:9, 则 OB' : OB 为( )A. 2: 3B. 3: 2C. 4: 5D. 4: 9二、填空题 (每小题 3分,共 24分)7. 计算 :sin30 °+ tan45 ° = 8.如图,将△ ABC 绕点 A 逆时针旋转 150°,得到△ ADE, 这时点 B 、C 、D 恰好在同一直线上4. 若反比例函数 1-2ky=的图象分布在第二、四象限,则 k 的取值范围是 ( )正面矩形 OABC 双, 曲线 y=6(x>0) 交 AB 于点 E,若 AE: EB= 1 : 3, 则矩形的面积为 ____x14. 二次函数 y=2x 2-4x +4 的图象如图所示 , 其对称轴与它的图象交于点 P, 点 N 是其图象上异 于点 P 的一点,若 PM ⊥y 轴,MN ⊥ x 轴,则 三、解答题 (每小题 5分,共 20分)215. 解方程 :x 2+8x= 9.16. 已知 y 是 x 的反比例函数,且 x=3 时, y=8. (1) 写出 y 与 x 之间的函数关系式 ; (2)当 3≤x ≤4时,直接写出 y 的取值范围。
(第 8题) ( 第9题) ( 第 10题) (9.在正方形网格中 , △ ABC 的位置如图所示 ,则 sinB = ____10.如图,在△ ABC 中,P 为边 AB 上一点,且∠ ACP=∠B,若 AP=2,BP=3,则 AC 的长为11. 如图,AB 是⊙O 的直径,点 C 、D 在⊙ O 上, 则, ∠ABC = ________12. 如图,铁道路口的栏杆短臂长 1m ,长臂长 ________ m (杆的宽度忽略不计 ).连接 AD 、BC 、BD 、DC,若 BD = CD,∠DBC= 20°,16m, 当短臂端点下降 0.5m 时,长臂端点升高MN PM2 =则∠ B 的度数为 _______第 11题 )( 第 14 题 ),点 A 和点 C 分别在 y 轴和工轴的正半轴上, 以 OA 、OC 为边作 13. 如图 , 在平面直角坐标系中18. 2019 年中国北京世园会开园期间,为了满足不同人群的游览需求 , 组委会倾情打造了四条趣玩路线 . 分别是“解密世园会” 、“爱我家,爱园艺” 、“快速车览之旅 " 和“园艺小清新之 旅" ,小明一家想通过抽签的方法选择其中的两条路线进行游玩 , 于是他们制作了如下四张卡片. 然后从四张卡片中随机抽取其中的两张 . 若小明最钟爱的游玩路线是 “园艺小清新之旅” 小明的爸爸和妈妈最钟爱的游玩路线是“解密世园会” ,请用列表或画树状图的方法求他们 同时抽中”园艺小清新之旅 " 和“解密世园会”的概率是多少 ?四、解答题 (每小题 7分,共 28分)19. 如图、为测量小岛 A 到公路 BD 的距离,先在点 B 处测得∠ ABD= 37°,再沿 BD 方向前进 150m 到达点 C,测得∠ ACD = 45 ° ,求小岛 A 到公路 BD 的距离 (参考数据 :sin37 °≈ 0.60,cos37 °≈ 0.80,tan37 °≈ 0.75)20. 如图,已知半圆 O 的直径 CD = 12, D ⌒E 所对的圆心角∠ ECD = 30°,求阴影部分的周长 (结果保留根号和 π )21. 图①、图②是两张形状 , 大小完全相同的 8X8 的方格纸, 方格纸中的每个小正方形的边长均为 1. 请在图①、图②中分别画出符合要求的图形,要求所画图形各顶点必须与方格纸中 的小正方形顶点重合。
(1) 在图①中 ,以 AB 为一边,画一个成中心对称的四边形 ABCD ,使其面积为 12; (2) 在图②中,以 EF 为一边,画△ EFP,使其是面积为 125 的轴对称图形22. 如图,⊙O是ABC的外接圆,E 是弦BC的中点,P是⊙ O外点. 且∠ PBC=∠A,连接OE并延长, 交⊙O于点F,交BP于点 D.(1) 求证:BP 是⊙ O 的切线:(2) 若⊙ O的半径为 6.BD = 8, 求弦BC的长.五、解答题(每小题8 分, 共16 分)23. 如图,已知一次函数y= kx +b的图象交反比例函数y=m x的图象于点A(2,-4) 和点B(h,-2), x交x 轴于点 C.(1) 求这两个函数的解析式;(2) 连接QA、OB.求△ AOB的面积;24. 如图① ,在Rt△ABC中, ∠BAC= 90°.AB = AC.D、E两点分别在AC、BC上,且DE ∥ AB. 将△ CDE绕点C按顺时针方向旋转,记旋转角为a.(1) 问题发现: 当a=0°时,B A E D的值为BE(3) 问题解决:当△ CDE旋转至A、B、E三点共线时,若设CE = 5.AC = 4. 直接写出线段BE 的长.m的解集.(2) 拓展探究:当0°≤ a < 360 时, 若△ CDE旋转到如图②的情况时求出A BE D的值六、解答题(每小题10 分,共20分)25. 如图,一条顶点坐标为(-1, 136)的抛物线与y轴交于点C(0,5). 与x轴交于点A和点B(点B在点A右侧) ,有一宽度为 1.长崖足够的矩形(阴影部分)沿x轴方向平移,与y轴平行的一组对边交抛物线于点P和点Q(点P在点Q右侧), 交直线AC于点M和点N(点M在点N右侧), 交x 轴于点E和点F(点E在点F右侧)(1) 求抛物线的解析式;(2) 当点M和点N都在线段AC上时,连接MF .如果MF = √2l0AF , 求点Q的坐标;(3) 在矩形平移的过程中,当以点P、Q、M、N 为顶点的四边形是平行四边形时,直接写出点M 的坐标。
|26. 如图,在? ABCD中, ∠ ABD=90°,AD= 5,BD=3 , 点P从点A出发,沿折线AB- BC 以每秒个单位长度的速度向终点C运动(点P不与点A、B.C重合). 在点P运动的过程中,过点P 作AB 所在直线的垂线. 交边AD或边CD于点Q,以PQ为一边作矩形PQMN且, QM=2.MN与BD 在PQ的同侧,设点P 的运动时间为t( 秒),(1) 当t= 5 时, 求线段CP的长;(2) 求线段PQ的长( 用含t 的代数式表示);(3) 当点M落在BD上时,求t 的值;(4) 当矩形POMN与?ABCD重叠部分圆形为五边形时,直接写出t 的取值范围。
名紳研E •席專恥数学g)6.AH 5Q 】2.8见別M.?(,ΛB 5 r AAJD 二 3,.∙.B D :S <■ ■ nr * P βBC = 2 ∙∕5∙° •八眾欢用字母AbC"农示,则曲树状图如禺肾示, 从拥扶13可加,折有叮仇姑果冇12种,丼中能同时抽中A 希D 的结呆宿2豺,历以 他们问眄4*中“园艺小⅛⅛⅛-M w 和乍冷世园会"的概半是春=右 四>19..H s ⅛Λ丄 CDd 足为 E,说/1E = 土 来,在 RtAABE 中 I UnB =BE∙'∙ EE=篇=彳工,程 RιΔΛCE 中.7 ZACD -45β,ΛCE =x,V BC ≈βE - Cy 鲁e—戈 m "O,解捋 X = 4$C e 冬■小岛A 列公路BD 的距;85为450札M 解准孩OF 、DF 「: 5&所对帕囿心•处^ECD -= 30°♦ Λ 6&的歩为辿_口_』* 180 2αr√.∙Z∞F ^乙口…匚二命的代度为驾評“制心为如, ""F? % •DF =*CD =6,CF = 6√3∙ΛFF = 12-6∙∕3,Λ PI 助部分 ⑵如艮瞬示■备烹不哦一rτrv∏-r:们⅛⅛Γ-J l H 2. C 3, H J-β 5 L斗冷8.15谱15 Z J 5. MIll =L 9∙JT ⅛ ≡ B2416∙M≡<1>>F = V ⑵6≤y≤8∙I?.解盘点B#丄AC ・”为血「「r ・vr ・r1 ■ 4L 一3 —心‘儿W — 2+、念山・5)也6) 7-尹一亍十4"仏=加上"3(—2 —联 *3 一∖f^)∙综上林符合条件的点叫*"),(-2+化;伫:(-276,_6). 26*(1)如图①,当/ =5时,7;*BC上,凹L 1幕PC-4.P 茯PQ^AP・-,.VTO--L⑵①如图②,当0VzV4Bt,∙.∙pQ 〃如J丽 AB tee 3 4 4PQ CP ・匹=LZi I .∙βPQ _ ②如田③•当4<∕V9时J∙∙PQ Z∕ED∙∙∙∙而3 5 3—(9 — 0. •■ ■, ・ QS(3)①如田④•当点P在线段AB上出点M在线段BD上,TI // 'I∙∙而=Z综,・・・# =学,・・・EQ =辛,∙∙.λQ = DQ・•;&〃扭,・•・册-PE = ?;=?.②如图⑤■当点P在线段BC上,点M与氏D吏今时,易知Q^ = Q G = 2, EB =PC一∙∣,此时< ≡ 4 + I _ 学.317. 如图, 在△ ABC中,AB= AC= 5.cosA= 3 * 5,求底边BC的长.5(4)①如图⑥,当点P农线^ABΛ.tl部分是五边形PBEMQ时,2<Z<4. ②如图⑦,当点P在线枚BC上,重金部分是五边形PQDFN时,4 </<6. 5.A B肉⑸田⑥CM DQB 图⑦1,。
