专题训练讲义--正方形
最新正方形的性质与判定讲义

正方形的性质及判定一、知识点归纳(一)正方形的概念:一组邻边相等的矩形叫做正方形。
(二)正方形的性质:1、 因为ABCD 是正方形⇒⎪⎩⎪⎨⎧.321分对角)对角线相等垂直且平(角都是直角;)四个边都相等,四个(有通性;)具有平行四边形的所( 正方形是轴对称图形,对称轴有4条,也是中心对称二、例题讲解考点 ①正方形与等腰三角形(等边三角形)结合1. 如图,E 是正方形ABCD 的对角线BD 上一点,且BE =BC ,则∠ACE =° 2. 如图,四边形ABCD 是正方形,延长CD 到E ,使CE =CB ,则∠DBE = °.3. 如图,正方形ABCD 中,点E 在BC 的延长线上,AE 平分∠DAC ,则下列结论:(1)∠E =22.5°; (2) ∠AFC =112.5°; (3) ∠ACE =135°;(4)AC =CE ;(5) AD ∶CE =1∶ 2.其中正确的有 ( )A .5个 B.4个 C.3个 D.2个4. 如图,等边△EDC 在正方形ABCD 内,连结EA 、EB ,则∠AEB = °;∠ACE = °.5. 已知正方形ABCD ,以CD 为边作等边△CDE ,则∠AED 的度数是 °.考点②正方形与旋转结合1. 如图1,四边形ABCD 是正方形,E 是边CD 上一点,若△AFB 经过逆时针旋转角θ后与△AED 重合,则θ的取值可能为 ( )A.90°B.60°C.45°D.30°2. 已知正方形ABCD 中,点E 在边DC 上,DE = 2,EC = 1(如图2所示) 把线段AE 绕点A 旋转,使点E 落在直线BC 上的点F 处,则F 、C 两点的距离为___________.3. 如图3,在正方形ABCD 中,点E ,F 分别为DC ,BC 边上的点,且满足∠EAF =45°,连接EF ,求证:DE +BF =EF .考点③正方形对角线的对称性1. 如图:正方形ABCD 中,AC =10,P 是AB 上任意一点,PE ⊥AC 于E ,PF ⊥BD 于F ,则PE +PF =.可以用一句话概括:正方形边上的任意一点到两对角线的距离之和等于 .思考:如若P 在AB 的延长线时,上述结论是否成立?若不成立,请写出你的结论,并加以说明.2.如图,点P 是正方形ABCD 的对角线BD 上一点,PE ⊥BC 于点E ,PF ⊥CD 于点F ,连接EF 给出下列五个结论:①AP =EF ;②AP ⊥EF ;③△APD 一定是等腰三角形;④∠PFE =∠BAP ;⑤PD = 2EC .其中正确结论的序号是 .思考:当点P 在DB 的长延长线上时,请将备用图补充完整,并思考(1)正确结论是否依旧成立?若成立,直接写出结论;若不成立,请写出相应的结论.考点④正方形的折叠1.如图1,将边长为8cm 的正方形纸片ABCD 折叠,使点D 落在BC 边中点E 处,点A 落在点F 处,折痕为MN ,则线段CN 的长是 .2. 如图2,四边形ABCD 是边长为9的正方形纸片,将其沿MN 折叠,使点B 落在CD 边上的B '处,点A 对应点为A ',且C B '=3,则AM 的长是 .3如图3,正方形ABCD 中,AB =6,点E 在边CD 上,且CD =3DE .将△ADE 沿AE 对折至△AFE ,延长EF 交边BC 于点G ,连结AG 、CF .下列结论:①△ABG ≌△AFG ;②BG =GC ;③AG ∥CF ;④S △FGC P=3.其中正确结论的个数是 .课后练习1、已知:如图,正方形ABCD 中,CM =CD ,MN ⊥AC ,连结CN ,则∠DCN =_____=____∠B ,∠MND =_______=_______∠B.2.在正方形ABCD 中,AB =12 cm ,对角线AC 、BD 相交于O ,则△ABO 的周长是( )A.12+122B.12+62C.12+2D.24+623.正方形的面积是31,则其对角线长是________. 4. 如图,在正方形ABCD 中,△PBC 、△QCD 是两个等边三角形,PB 与DQ 交于M ,BP 与CQ 交于E ,CP 与DQ 交于F .求证:PM = QM .5. 如图4,正方形ABCD 的对角线AC 、BD 相交于点O ,正方形A ′B ′C ′D ′的顶点A ′与点O 重合,A ′B ′交BC 于点E ,A ′D ′交CD 于点F ,若正方形A ′B ′C ′D ′绕点O 旋转某个角度后,OE =OF 吗?两正方形重合部分的面积怎样变化?为什么?6.如图,P 是边长为1的正方形ABCD 对角线AC 上一动点(P 与A 、C 不重合),点E 在射线BC 上,且PE=PB .试判断PE 与PB 的关系.7. 如图,正方形ABCD 的面积为12,△ADE 是等边三角形,点E 在正方形ABCD 内,在对角线AC 上有一点P ,使PB +PE 的和最小,则这个最小值为 .8.如图①,将边长为4cm 的正方形纸片ABCD 沿EF 折叠(点E 、F 分别在边AB 、CD 上),使点B 落在AD 边上的点M 处,点C 落在点N 处,MN 与CD 交于点P , 连接EP .(1)如图②,若M 为AD 边的中点,①△AEM 的周长=_____cm ;②求证:EP =AE +DP ;(2)随着落点M 在AD 边上取遍所有的位置(点M 不与A 、D重合),△PDM 的周长是否发生变化?请说明理由.(三)正方形的判定: ⎪⎭⎪⎬⎫++++一组邻边等矩形)(一个直角)菱形(一个直角一组邻边等)平行四边形(321⇒四边形ABCD 是正方形1、判断:(1)四条边都相等的四边形是正方形。
正方形的性质与判定讲义汇编

正方形的性质及判定一、知识点归纳(一)正方形的概念:一组邻边相等的矩形叫做正方形。
(二)正方形的性质:1、 因为ABCD 是正方形⇒⎪⎩⎪⎨⎧.321分对角)对角线相等垂直且平(角都是直角;)四个边都相等,四个(有通性;)具有平行四边形的所( 正方形是轴对称图形,对称轴有4条,也是中心对称二、例题讲解考点 ①正方形与等腰三角形(等边三角形)结合1. 如图,E 是正方形ABCD 的对角线BD 上一点,且BE =BC ,则∠ACE =°2. 如图,四边形ABCD 是正方形,延长CD 到E ,使CE =CB ,则∠DBE = °.3. 如图,正方形ABCD 中,点E 在BC 的延长线上,AE 平分∠DAC ,则下列结论:(1)∠E =22.5°; (2) ∠AFC =112.5°; (3) ∠ACE =135°;(4)AC =CE ;(5) AD ∶CE =1∶ 2.其中正确的有 ( )A .5个 B.4个 C.3个 D.2个4. 如图,等边△EDC 在正方形ABCD 内,连结EA 、EB ,则∠AEB = °;∠ACE = °.5. 已知正方形ABCD ,以CD 为边作等边△CDE ,则∠AED 的度数是 °.考点②正方形与旋转结合1. 如图1,四边形ABCD 是正方形,E 是边CD 上一点,若△AFB 经过逆时针旋转角θ后与△AED 重合,则θ的取值可能为 ( )A.90°B.60°C.45°D.30°2. 已知正方形ABCD 中,点E 在边DC 上,DE = 2,EC = 1(如图2所示) 把线段AE 绕点A 旋转,使点E 落在直线BC 上的点F 处,则F 、C 两点的距离为___________.3. 如图3,在正方形ABCD 中,点E ,F 分别为DC ,BC 边上的点,且满足∠EAF =45°,连接EF ,求证:DE +BF =EF .考点③正方形对角线的对称性1. 如图:正方形ABCD 中,AC =10,P 是AB 上任意一点,PE ⊥AC 于E ,PF ⊥BD 于F ,则PE +PF =.可以用一句话概括:正方形边上的任意一点到两对角线的距离之和等于 .思考:如若P 在AB 的延长线时,上述结论是否成立?若不成立,请写出你的结论,并加以说明.2.如图,点P 是正方形ABCD 的对角线BD 上一点,PE ⊥BC 于点E ,PF ⊥CD 于点F ,连接EF 给出下列五个结论:①AP =EF ;②AP ⊥EF ;③△APD 一定是等腰三角形;④∠PFE =∠BAP ;⑤PD = 2EC .其中正确结论的序号是 .思考:当点P 在DB 的长延长线上时,请将备用图补充完整,并思考(1)正确结论是否依旧成立?若成立,直接写出结论;若不成立,请写出相应的结论.考点④正方形的折叠1.如图1,将边长为8cm 的正方形纸片ABCD 折叠,使点D 落在BC 边中点E 处,点A 落在点F 处,折痕为MN ,则线段CN 的长是 .2. 如图2,四边形ABCD 是边长为9的正方形纸片,将其沿MN 折叠,使点B 落在CD 边上的B '处,点A 对应点为A ',且C B '=3,则AM 的长是 .3如图3,正方形ABCD 中,AB =6,点E 在边CD 上,且CD =3DE .将△ADE 沿AE 对折至△AFE ,延长EF 交边BC 于点G ,连结AG 、CF .下列结论:①△ABG ≌△AFG ;②BG =GC ;③AG ∥CF ;④S △FGC P=3.其中正确结论的个数是 .课后练习1、已知:如图,正方形ABCD 中,CM =CD ,MN ⊥AC ,连结CN ,则∠DCN =_____=____∠B ,∠MND =_______=_______∠B.2.在正方形ABCD 中,AB =12 cm ,对角线AC 、BD 相交于O ,则△ABO 的周长是( )A.12+122B.12+62C.12+2D.24+623.正方形的面积是31,则其对角线长是________. 4. 如图,在正方形ABCD 中,△PBC 、△QCD 是两个等边三角形,PB 与DQ 交于M ,BP 与CQ 交于E ,CP 与DQ 交于F .求证:PM = QM .5. 如图4,正方形ABCD 的对角线AC 、BD 相交于点O ,正方形A ′B ′C ′D ′的顶点A ′与点O 重合,A ′B ′交BC 于点E ,A ′D ′交CD 于点F ,若正方形A ′B ′C ′D ′绕点O 旋转某个角度后,OE =OF 吗?两正方形重合部分的面积怎样变化?为什么?6.如图,P 是边长为1的正方形ABCD 对角线AC 上一动点(P 与A 、C 不重合),点E 在射线BC 上,且PE=PB .试判断PE 与PB 的关系.7. 如图,正方形ABCD 的面积为12,△ADE 是等边三角形,点E 在正方形ABCD 内,在对角线AC 上有一点P ,使PB +PE 的和最小,则这个最小值为 .8.如图①,将边长为4cm 的正方形纸片ABCD 沿EF 折叠(点E 、F 分别在边AB 、CD 上),使点B 落在AD 边上的点M 处,点C 落在点N 处,MN 与CD 交于点P , 连接EP .(1)如图②,若M 为AD 边的中点,①△AEM 的周长=_____cm ;②求证:EP =AE +DP ;(2)随着落点M 在AD 边上取遍所有的位置(点M 不与A 、D重合),△PDM 的周长是否发生变化?请说明理由.(三)正方形的判定: ⎪⎭⎪⎬⎫++++一组邻边等矩形)(一个直角)菱形(一个直角一组邻边等)平行四边形(321⇒四边形ABCD 是正方形1、判断:(1)四条边都相等的四边形是正方形。
第05讲 正方形的性质与判定(原卷版)-初中数学暑假自学课讲义(9年级北师大版)
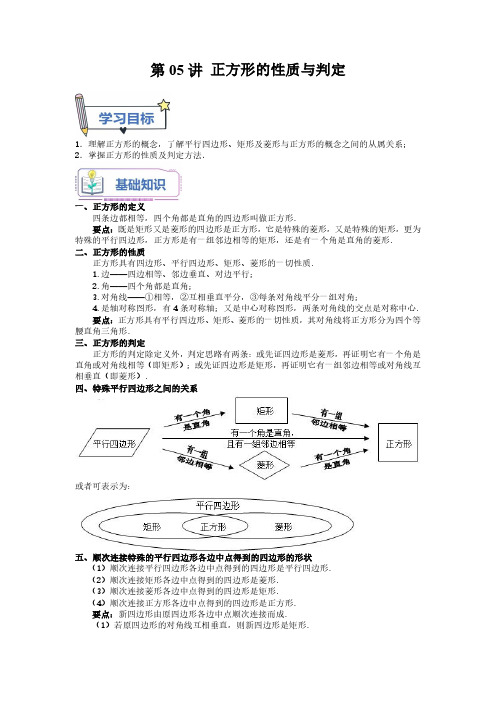
第05讲正方形的性质与判定1.理解正方形的概念,了解平行四边形、矩形及菱形与正方形的概念之间的从属关系;2.掌握正方形的性质及判定方法.一、正方形的定义四条边都相等,四个角都是直角的四边形叫做正方形.要点:既是矩形又是菱形的四边形是正方形,它是特殊的菱形,又是特殊的矩形,更为特殊的平行四边形,正方形是有一组邻边相等的矩形,还是有一个角是直角的菱形.二、正方形的性质正方形具有四边形、平行四边形、矩形、菱形的一切性质.1.边——四边相等、邻边垂直、对边平行;2.角——四个角都是直角;3.对角线——①相等,②互相垂直平分,③每条对角线平分一组对角;4.是轴对称图形,有4条对称轴;又是中心对称图形,两条对角线的交点是对称中心.要点:正方形具有平行四边形、矩形、菱形的一切性质,其对角线将正方形分为四个等腰直角三角形.三、正方形的判定正方形的判定除定义外,判定思路有两条:或先证四边形是菱形,再证明它有一个角是直角或对角线相等(即矩形);或先证四边形是矩形,再证明它有一组邻边相等或对角线互相垂直(即菱形).四、特殊平行四边形之间的关系或者可表示为:五、顺次连接特殊的平行四边形各边中点得到的四边形的形状(1)顺次连接平行四边形各边中点得到的四边形是平行四边形.(2)顺次连接矩形各边中点得到的四边形是菱形.(3)顺次连接菱形各边中点得到的四边形是矩形.(4)顺次连接正方形各边中点得到的四边形是正方形.要点:新四边形由原四边形各边中点顺次连接而成.(1)若原四边形的对角线互相垂直,则新四边形是矩形.(2)若原四边形的对角线相等,则新四边形是菱形.(3)若原四边形的对角线垂直且相等,则新四边形是正方形.考点1:正方形的性质例1.正方形、矩形、菱形都具有的特征是()A .对角线互相平分B .对角线相等C .对角线互相垂直D .对角线平分一组对角例2.正方形具有而菱形不一定有的性质是()A .对角线相等B .对角线互相垂直C .对角相等D .四条边相等考点2:利用正方形的性质求长度例3.正方形一条对角线长为22,则周长为()A .4B .42C .8D .82例4.如图,菱形ABCD 的面积为2120cm ,正方形AECF 的面积为250cm ,则菱形的边长是()A .13cm B .15cm C .17cm D .20cm例5.如图,在正方形ABCD 中,点E 是对角线AC 上一点,作EF AB ⊥于点F ,连接DE ,若114BC BF ==,,则DE 的长为()A .36B .62C .213D 65考点3:利用正方形的性质求角度例6.一个正方形和一个直角三角形的位置如图所示,若1∠=α,则2∠=()A .45α-︒B .90α-︒C .270α︒-D .180α︒-例7.如图,以正方形ABCD 的一边BC 向正方形外作等边EBC ,则AED ∠的度数是()A .30︒B .20︒C .15︒D .10︒例8.如图,已知正方形ABCD 中,DA DE =,CF AE ∥,则ECF ∠的度数是()A .30︒B .35︒C .40︒D .45︒考点4:利用正方形的性质求面积例9.如图,正方形ABCD 的边长为8,在各边上顺次截取6AE BF CG DH ====,则四边形EFGH 的面积是()A .34B .36C .40D .100例10.如图,在菱形ABCD 中,=60B ∠︒,4AB =,则正方形ACEF 的面积为()A .8B .12C .16D .20例11.如图,在ABC 中,90B Ð=°,2AB =,4BC =.四边形ADEC 是正方形,则正方形ADEC 的面积是()A .8B .12C .18D .20例12.如图将边长为a 的大正方形与边长为b 的小正方形放在一起(0,0)a b >>,则三角形AEG 的面积()A .与a 、b 大小都有关B .与a 、b 的大小都无关C .只与a 的大小有关D .只与b 的大小有关考点5:正方形的判定例13.如图,在矩形ABCD 中,对角线AC BD 、交于点O ,下列条件中,能使矩形ABCD 成为正方形的是()A .AC BC =B .60AOB ∠=︒C .OA AD =D .BC CD =例14.有下列四个条件:①90ABC ∠=︒;②AC BD ⊥;③AB BC =;④AC BD =;从中选两个作为补充条件,使平行四边形ABCD 为正方形,现有下列四种选法,你认为错误的是()A .①②B .①③C .②③D .②④考点6:中点四边形例15.连接菱形各边中点,可得到的“中点四边形”是矩形,主要是因为()A .菱形的四条边都相等B .菱形的对角线互相垂直C .菱形的对角线互相平分D .以上答案都不对例16.如图,AC 、BD 是四边形ABCD 的两条对角线,顺次连接四边形ABCD 各边中点得到四边形EFGH ,要使四边形EFGH 为矩形,应添加的条件是()A .AC ⊥BDB .AB =CDC .AB ∥CD D .AC =BD例17.若顺次联结一个四边形各边的中点得到的图形是矩形,则这个四边形的对角线()A .互相平分B .相等C .互相垂直D .互相垂直且平分考点7:正方形的判定与性质综合例18.如图,点E 是正方形对角线AC 上一点,过E 作EF AD ∥交CD 于F ,连接BE ,若5BE =,4DF =,则AC 的长为()A .42B .52C .62D .72例19.如图,正方形ABCD 的边长为1,E 为AD 边上一点(与点A 、D 不重合),连接CE ,交BD 于点F .当DEF 是等腰三角形时,则AE 的长为()A .12B .23C .21-D .22-例20.如图,正方形ABCD 边长为10,点M 在对角线AC 上运动,N 为DC 上一点,DN =2,则DM +MN 长的最小值为()A .8B .10C .241D .102例21.如图,ABCD 为正方形,O 为AC 、BD 的交点,△DCE 为Rt △,∠CED=90°,∠DCE=30°,若OE=,则正方形的面积为()A .5B .4C .3D .2例22.ABCD 是边长为1的正方形,BPC 是等边三角形,则BPD 的面积为()A .14B 314-C .18D .318考点8:正方形的判定与性质解答题例23.如图,若四边形ABCD 的对角线AC 与BD 相交于点O ,且2OA OB OC OD AB ===,则四边形ABCD 是正方形吗?例24.如图,M 、N 分别是正方形ABCD 的边AD CD 、的中点,CM 与BN 交于点P ,连结AP ,求证:AP AB =.例25.如图,在正方形ABCD 中,E 是AB 上一点,F 是AD 延长线上一点,且DF =BE .(1)求证:CE =CF ;(2)若点G 在AD 上,且∠GCE =45°,则GE =BE +GD 成立吗?为什么?例26.如图,E ,F 是正方形ABCD 的对角线BD 上的两点,且BE =DF .(1)≌△CDF ;(2)若AB =2,BE =2,求四边形AECF 的面积.例27.如图,正方形ABCD 中,AE BF =.(1)求证:BCE CDF ≌;(2)求证:CE DF ⊥;(3)若6CD =,且2241DG GE +=,则BE =_______.一、单选题1.(2022·湖南衡阳·统考中考真题)下列命题为假命题的是()A .对角线相等的平行四边形是矩形B .对角线互相垂直的平行四边形是菱形C .有一个内角是直角的平行四边形是正方形D .有一组邻边相等的矩形是正方形2.(2021·广西玉林·统考中考真题)一个四边形顺次添加下列中的三个条件便得到正方形:a .两组对边分别相等b .一组对边平行且相等c .一组邻边相等d .一个角是直角顺次添加的条件:①a→c→d ②b→d→c ③a→b→c则正确的是:()点F是边AB上一点,连接A.45︒B.侧作正方形APCD、正方形PBEF,A.2αB.90°﹣度数为()A.50°B.55°二、填空题、相交于点O,6.(2021·黑龙江·统考中考真题)如图,在矩形ABCD中,对角线AC BD在不添加任何辅助线的情况下,请你添加一个条件______,使矩形ABCD是正方形.7.(2015·广西南宁·中考真题)如图,在正方形ABCD外作等边ADE,则∠=___________︒.BED8.(2020·江苏镇江·统考中考真题)如图,点P 是正方形ABCD 内位于对角线AC 下方的一点,∠1=∠2,则∠BPC 的度数为_____°.三、解答题9.(2022·湖北恩施·统考中考真题)如图,已知四边形ABCD 是正方形,G 为线段AD 上任意一点,CE BG ⊥于点E ,DF CE ⊥于点F .求证:DF BE EF =+.10.(2019·四川内江·统考中考真题)如图,在正方形ABCD 中,点E 是BC 上的一点,点F 是CD 延长线上的一点,且BE DF =,连结,,AE AF EF .(1)求证:ABE ∆≌ADF ∆;(2)若5AE =,请求出EF 的长.11.(2021·山东泰安·统考中考真题)四边形ABCD 为矩形,E 是AB 延长线上的一点.(1)若AC EC =,如图1,求证:四边形BECD 为平行四边形;(2)若AB AD =,点F 是AB 上的点,AF BE =,EG AC ⊥于点G ,如图2,求证:DGF △是等腰直角三角形.12.(2020·黑龙江鹤岗·统考中考真题)以Rt ABC ∆的两边AB 、AC 为边,向外作正方形ABDE 和正方形ACFG ,连接EG ,过点A 作AM BC ⊥于M ,延长MA 交EG 于点N .(1)如图1,若90BAC ∠=︒,AB AC =,易证:EN GN =;(2)如图2,90BAC ∠=︒;如图3,90BAC ∠≠︒,(1)中结论,是否成立,若成立,选择一个图形进行证明;若不成立,写出你的结论,并说明理由.13.(2023·陕西·模拟预测)已知,四边形ABCD 是正方形,DEF 绕点D 旋转(DE AB <),90EDF ∠=︒,DE DF =,连接AE ,CF .(1)如图1,求证:ADE V ≌CDF ;(2)直线AE 与CF 相交于点G .①如图2,BM AG ⊥于点M ,⊥BN CF 于点N ,求证:四边形BMGN 是正方形;②如图3,连接BG ,若4AB =,2DE =,直接写出在DEF 旋转的过程中,线段BG 长度的最小值.一、单选题长为()A .5cm4.如图,四边形ABCDA.22.5°B 5.如图,正方形A.406.如图,在正方形若AB=4,则线段AE的长为(A.22B交CD于点G.若1AE=,A.2B.1 AF相交于点G,点A.3439.如图,在正方形接DE,F是DE的中点,连接CF的距离为()A .235B .435()A .①③二、填空题11.正方形是有一组邻边_______,并且有一个角是_______的平行四边形,因此它既是______又是________.12.若正方形的边长为a ,则它的对角线长为__________.13.已知矩形ABCD ,给出三个关系式:①;AB BC =②;AC BD =③,AC BD ⊥如果选择关系式__________作为条件(写出一个即可),那么可以判定矩形为正方形,理由是_______________________________.14.在正方形ABCD 中,E 是对角线AC 上一点,且AE =AB ,则∠EBC 的度数是___________.15.作正方形ABCD 中对角线AC 的平行线BF ,点E 在直线BF 上,且四边形AEFC 是菱形,贴EAB ∠=_______.16.如图,E 是正方形ABCD 的对角线BD 上一点,连接CE ,过点E 作EF AD ⊥,垂足为点F .若6AF =,10EC =,则正方形ABCD 的面积为___.17.如图,在正方形ABCD交AD于F.当∠18.如图,点P是正方形⑤PD=2EC,其中正确结论的序号是=+.求证:AF DF BE20.如图,若四边形ABCD则四边形21.如图,求证:22.如图,交AG23.如图,E ,F 是正方形(1)求证:△ABE ≌△CDF ;(2)若AB =32,BE =2,求四边形24.如图,正方形ABCD 中,EF ED ⊥,交AB 于点F ,以(1)求证:①EFB EBF ∠=∠②矩形DEFG 是正方形;(2)求AG AE +的值.25.已知,四边形ABCD 是正方形,连接AE ,CF(1)如图1,求证:ADE CDF V V ≌;(2)直线AE 与CF 相交于点G .①如图2,BM AG ⊥于点M ,⊥BN CF 点N ,证明矩形BMGN 是正方形②如图3,连接BG ,若4AB =,2DE =直接写出在DEF 旋转的过程中,线段最小值.。
八年级下学期正方形的性质和判定讲义

正方形知识精讲一、正方形的定义有一组邻边相等、一个内角是的平行四边形叫做正方形。
二。
正方形的性质1、正方形的四条边都相等,四个角都是直角;2、正方形既是矩形,又是菱形,它既有矩形的性质,又有菱形的性质、3、正方形是轴对称图形,对称轴有4条、三、正方形的判定1、有一组邻边相等的矩形是正方形;2、有一个角是直角的菱形是正方形;3、对角线互相垂直的矩形是正方形;4、对角线相等的菱形是正方形;5、对角线互相垂直、平分且相等的四边形是正方形;6、四条边相等且四个角是直角的四边形是正方形、四、弦图模型如图1,Rt△DCE≌Rt△CAF;如图2,Rt△BAE≌Rt△CBF、三点剖析一、考点:1。
正方形的性质;2、正方形的判定;3、弦图模型二、重难点:正方形性质的应用和判定;弦图模型、三。
易错点:正方形、矩形、菱形性质与判定的区别、例题讲解一:性质例2、1、1如图,在正方形ABCD中,点F为CD上一点,BF与AC交于点E、若∠CBF=20°,则∠AED等于度、【答案】65【解析】∵正方形ABCD,∴AB=AD,∠BAE=∠DAE,在△ABE与△ADE中,∴△ABE≌△ADE(SAS),∴∠AEB=∠AED,∠ABE=∠ADE,∵∠CBF=20°,∴∠ABE=70°,∴∠AED=∠AEB=180°﹣45°﹣70°=65°,例2。
1、2如图,正方形ABCD的对角线AC与BD相交于点O,∠ACB的角平分线分别交AB、BD于M、N两点,若AM=2,则正方形的边长为( )A、4B、3C、2+D、【答案】C【解析】过点M作MF⊥AC于点F,如图所示、∵MC平分∠ACB,四边形ABCD为正方形,∴∠CAB=45°,FM=BM。
在Rt△AFM中,∠AFM=90°,∠FAM=45°,AM=2,∴FM=AM•sin∠FAM=、AB=AM+MB=2+、例2、1。
2014年八年级数学下册同步讲义-18.4正方形

18.4 正方形例1.如图,正方形ABCD 中,点E 是BC 延长线上一点,且AC=CE ,AE 交CD 于点F ,求∠E 和∠AFC 的度数.例2.已知,如图,在正方形ABCD 中,点E 在对角线AC 上,求证:BE=DE.例3.如图,点E 是正方形ABCD 的边CD 上一点,点F 是CB 的延长线上一点,且DE=BF .求证:EA ⊥AF .例4.如图,E 、F 分别为正方形ABCD 的边BC 、CD 上的一点,AM ⊥EF 于M,AM=AB,求证:EF=BE+DE.例5.如图,在正方形ABCD 中,P 为对角线BD 上一点,PE ⊥BC,垂足为E,PF ⊥CD,垂足为F,求证:EF=AP.正方形定义:一个角是直角的菱形或邻边相等的矩形。
正方形的性质:四条边都相等,四个角都是直角。
正方形既是矩形,又是菱形。
课堂练习:1.正方形是轴对称图形,它的对称轴有( )A.1条B.2条C.4条D.无数条 2.平行四边形、矩形、菱形、正方形都具有的性质是( )A.对角线相等B.对角线互相平分C.对角线平分一组对角D.对角线互相垂直 3.下列结论中,正确的有( )①正方形具有平行四边形的一切性质;②正方形具有矩形的一切性质; ③正方形具有菱形的一切性质; ④正方形有两条对称轴; ⑤正方形有四条对称轴. A.1个B.2个C.3个D.4个4.某正方形园地是由边长为1的四个小正方形组成的,现在园地上建一个花园(即每个图中的阴影部分),使花坛面积是园地面积的一半,以下图中的设计不合要求的是( )5.如图,正方形ABCD 内有两条相交线段MN 、EF ,M 、N 、E 、F 分别在边AB 、CD 、AD 、BC 上,小明认为:若MN=EF ,则MN ⊥EF;小亮认为:若MN ⊥EF,则MN=EF .你认为( )A.仅小明对B.仅小亮对C.两人都对D.两人都不对 6.已知,在正方形网格中,每个小方格都是边上为1的正方形,A ,B 两点在小方格的顶点上,位置如图所示,点C 也在小方格的顶点上,且以A 、B 、C 为顶点的三角形的面积为1,则这样的点C 有( ) A. 3个 B. 4个 C. 5个 D.6个 7.正方形的面积是52,则它的对角线长是( ) A.552B.2C.54D.5108.若正方形的面积为4cm2,则它的边长为,对角线长为9.一个正方形的对角线长3cm,则它的面积为10.以线段AB的两个端点A、B为顶点作位置不同的正方形,一共可作个.11.边长为2的正方形中有一点P那么这个点P到四边的距离之和为_______12.已知正方形ABCD中,边长AB=4,E、F分别为CD和AD的中点,则△BEF的面积是________13.如图,P是正方形ABCD内一点,如果△ABP为等边三角形,DP的延长线交BC于C,那么∠PCD=14.如图,E是正方形ABCD内的一点,若△ABE是等边三角形,那么∠BCE=15.如图,延长正方形ABCD的边AB到E,使BE=AC,则∠E=16.如图所示,把25个边长为1的小正方形拼成一个大正方形,A、B、C、D都是小正方形的顶点,则四边形ABCD的面积为17.如图,正方形ABCD,以CD为边作等边三角形CDE,求∠CED的度数。
(完整)三年级长方形和正方形讲义.doc

长方形和正方形讲义知梳理:知点一:四形的特征四边形的特征:有()条直的边,有()个角,的封闭图形。
知点二:方形和正方形的特点(1)长方形对边(),四个角都是()角。
( 2)正方形四条都(),四个角都是()角。
知点三:周周的定:封形()的度,是它的周。
形按形状分:( 1)形,如方形,正方形⋯⋯(2)不形:如叶形状的形。
周的求法:(1)不形的周采用法;(2)形的周采用直尺量法。
知点四:方形和正方形的周1.理解意2.算方形的周长方形的周长=(长 +宽)× 2或= 长+宽 +长 +宽或= 长× 2+ 宽× 2长方形的长= 周长÷ 2—宽长方形的宽= 周长÷ 2—长3.算正方形的周正方形的周长=边长× 4或 =边长 +边长 +边长 +边长正方形的 =周÷ 4知点五:运用方形和正方形的周公式解决例题讲解:四边形的特征★例 1: 把四边形的涂一涂长方形和正方形的特征★例 2: 把下面的图形放到相应的横线上长方形 ______________正方形___________平行四边形__________★例 3:小画室·小红想画一个长 4 厘米、宽2厘米的长方形,你能帮她画完吗?·画一个与右图同样大的正方形。
★例 4:数一数______个正方形______ 个长方形______个平行四边形练习: 1、判断。
(1)正方形有四条边,只有对边相等。
()(2)对边相等的四边形一定是长方形。
()(3)由四条线段围成的图形中四边形。
()(4)四条边都相等的图形一定是正方形。
()(5)长方形和正方形的对边都相等。
()2、(如图)在上面的图形中任意选 2 个,拼成一个长方形或正方形。
选()和()拼成长方形选()和()拼成正方形周长的计算★例 5:( 1)计算下列图形的周长。
20m32dm18m5厘米6厘米2厘米10厘米( 2)一个正方形边长是8 分米,另一个正方形的边长是它的 2 倍,另一个正方形的周长是多少分米?(3)一块长方形菜地的长是 8 米,长是宽的 2 倍。
菱形、正方形讲义

判定①:有一组邻边相等的矩形是正方形. 判定②:有一个角是直角的菱形是正方形.
四边形小结
图形 性质
平行四边形
对边平行且相等
√
四条边都相等
对角相等
√
四个角都是直角
对角线互相平分
√
对角线互相垂直
对角线相等
每条对角线平分一
(1) 【习题4】 如图 1,在菱形 ABCD 中,∠ADC=120°,则 BD:AC 等于( ).
(A) 3 :2 (B) 3 :3 (C)1:2 (D) 3 :1
8/9
【习题5】 已知:如图,在正方形 ABCD 中,AE⊥BF,垂足为 P,AE 与 CD 交于点 E,•BF•与 AD 交于点 F,求证:AE=BF.
【习题2】 已知一个四边形的对角线互相垂直,•那么顺次连接这个四边形的四边中点所得的四边形 是( ).
(A)矩形 (B)菱形 (C)等腰梯形 (D)正方形
【习题3】 用两个全等的直角三角形拼下列图形:①矩形;②菱形;③正方形;④平行四边形;⑤等 腰三角形;⑥等腰梯形.其中一定能拼成的图形是( ).
(A)①②③ (B)①④⑤ (C)①②⑤ (D)②⑤⑥
新知学习
1.菱形 在平行四边形中,如果内角大小保持不变仅改变边的长度,能否得到一个特殊的平行四边形
平行四边行
临边相等
菱形
(1)菱形的定义
有一组邻边相等的平行四边形叫做菱形
(2)菱形的性质
菱形是特殊的平行四边形,它具有平行四边形的所有性质,•还具有自己独特的性质: ① 边的性质:对边平行且四边相等. ② 角的性质:邻角互补,对角相等. ③ 对角线性质:对角线互相垂直平分且每条对角线平分一组对角. ④ 对称性:菱形是中心对称图形,也是轴对称图形.
0901五年级思维班讲义3-正方形队列

广州市现代奥林匹克培训学校五年级思维班讲义(3)正方形队列学校班次姓名【典型例题】例1、有一个正方形池塘,四个角都栽一棵树。
如果每边栽6棵,四边一共要栽多少棵?提示:我们可不可以图示池塘四周的树呢?与你自己所想像的有没有差异?规律在哪里?例2、一个正方形草地四周等距离地种有菊花,一共80棵,四个角上都种有一棵,每一边种多少棵?提示:如果四个角上都没有种,那么一共就有多少棵?这样每一边又有多少棵?例3、三(1)班的学生进行队列训练,排成的正方形方阵,已知最外层每边有6个人,求这个班共有多少人?提示:方阵,每向里一层,每边数就少几?所有四边数就少2×4=8,外层的个数与相邻的内层的个数是不是有一个固定的差?【知识要点】正方形队列在日常生活中经常看到,如盛大的庆典活动时,各种大型团体操的表演,又如陆、海、空三军仪仗队都是方阵。
方阵还可以由棋子、树木、红旗等实物排成。
方阵分为实心方阵和空心方阵,解决这类问题要注意以下三点:1、据题意确实是实心方阵还是空心方阵问题,然后选用适当的方法解答。
2、对于较复杂的问题可画图帮助理解题意,分析思考找出解答方法。
3、分清每层总数和每边数之间的数量关系。
牢记相邻两边的个数相差2。
广州市现代奥林匹克培训学校奥数五年级思维班(3)《正方形队列》课堂练习学校班次姓名你会做吗?在正方形围墙四周等距离地装有96盏灯,四个角上都装有一盏,这样每边都有多少盏?你能做吗?小朋友做游戏排成两层空心方阵,外层每边有8人。
求做游戏的小朋友的人数。
你敢做吗?用围棋子排成三层空心方阵,最里层共有12颗,求这个方阵共有棋子多少颗?日期:月日整洁:( A B C )评分:教师签名:《正方形队列》课外作业学校班次姓名我会做!在大楼的正方形平顶四周等距离地装上彩灯,四个角上都装上一盏,每一边装有8盏,一共有多少盏彩灯?我能做!小朋友做游戏排成两层空心方阵,外层每边有8人。
求做游戏的小朋友的人数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十五讲专题训练讲义----正方形一.正方形的性质:【例1】如图12,B、C、E是同一直线上的三个点,四边形ABCD与四边形CEFG是都是正方形.连接BG、DE.(1)观察猜想BG与DE之间的大小关系,并证明你的结论.(2)在图中是否存在通过旋转能够互相重合的两个三角形?若存在,请指出,并说出旋转过程;若不存在,请说明理由.【例2】如图,E是正方形ABCD边BC延长线上一点,CE=AC,AE交CD于F,求∠AFC的度数。
【例3】如图4-60,正方形ABCD的对角线相交于O,EF∥AB,并且分别与OA,OB相交于E,F.若BE=3厘米,求CF的长.【练习1】如图所示,正方形中,点是边上一点,连接,交对角线于点,连接,则图中全等三角形共有()A.1对B.2对C.3对D.4对【练习2】如图,已知正方形ABCD的边长为3,E为CD边上一点,1DE=.以点A为中心,把△ADE顺时针旋转90︒,得△ABE',连接EE',则EE'的长等于.【练习3】如图,已知P是正方形ABCD对角线BD上一点,且BP= BC,则∠ACP度数是.【练习4】如图1,正方形ABCD的边CD在正方形ECGF的边CE上,连结BE、DG.(1)观察猜想BE与DC之间的大小关系,并说明你的结论; (2) 图中是否存在通过旋转能够互相重合的两个三角形? 若存在,请说出旋转过程; 若不存在,请说明理由.【练习5】如图5,在等腰Rt△ABC中,∠C=90°,正方形DEFG的顶点D在边AC上,点E、F在边AB上,点G在边BC上.(1)求证AE=BF;(2)若BC=cm,求正方形DEFG的边长.D Q CN B【练习6】在正方形ABCD 中,AC 为对角线,E 为AC 上一点,连接EB 、ED(1)求证:△BEC ≌△DEC ;(2)延长BE 交AD 于F ,当∠BED =120°时,求EFD ∠的度数.【练习7】如图,点P 是正方形ABCD 的对角线BD 上一点,PE ⊥BC 于点E ,PF ⊥CD 于点F ,连接EF 给出下列五个结论:①AP =EF ;②AP ⊥EF ;③△APD 一定是等腰三角形;④∠PFE =∠BAP ;⑤PD =2EC .其中正确结论的序号是 . 二.正方形的折纸:【例1】(08哈尔滨)如图,将边长为8cm 的正方形纸片ABCD 折叠,使点D 落在BC 边中点E 处,点A 落在点F 处,折痕为MN ,则线段CN 的( ).(A )3cm (B )4cm(C )5cm (D )6cm【练习】 (2006 荆门大纲)如图,有一张面积为1的正方形纸片ABCD ,M ,N 分别是AD ,BC 边的中点,将C 点折叠至MN 上,落在P 点的位置,折痕为BQ ,连结PQ ,则PQ = .三.正方形的面积:【练习1】正方形ABCD 、正方形BEFG 和正方形RKPF 的位置如图所示,点 G 在线段DK 上,正方形BEFG 的边长为4,则DEK ∆的面积为( )(A )10 (B )12 (C )14 (D )16【练习2】如图,正方形ABCD 中,边长为2,其中正方形A ’B ’C ’O 与正方形ABCD 全等,顶点O 在正方形ABCD 对角线交点O ,求阴影部分面积。
1. 边长为1的正方形ABCD 绕点A 逆时针旋转30°得到正方形AB ′C ′D ′,两图叠成一个“蝶形风筝”(如图所示阴影部分),则这个风筝的面积是( )。
A .2-33B .332C .2-43D .22. 将n 个边长都为lcm 的正方形按如图所示的方法摆放,点A 1,A 2,……,A n 分别是正方形的中心,则n 个这样的正方形重叠部分(阴影部分)的面积和为( )A .41cm 。
B .4n cm 2 C.(n -41)cm 2 D .(41)n cm 2 3. 如图,正方形ABCD 各边中点为E 、F 、G 、H ,设正方形ABCD 面积为S ,求图中LKMN 的面积。
4. 如图,四边形ABCD 是边长为a 的正方形,点G ,E 分别是边AB ,BC 的中点,∠AEF =90o ,且EF 交正方形外角的平分线CF 于点F .(1)证明:∠BAE =∠FEC ;(2)证明:△AGE ≌△ECF ;(3)求△AEF 的面积.四.正方形的判定:【例1】如图,正方形ABCD 中,DH CG BF AE ===.求证:四边形EFGH 是正方形.【练习1】已知:如图,△ABC 中,︒=∠90C ,CD 平分ACB ∠,BC DE ⊥,AC DF ⊥,垂足分别为E 、F .求证:四边形CFDE 是正方形.【练习2】如图,正方形ABCD 中,E 、F 、G 、H 分别为四边中点,连接AG 、BH 、CE 、DF 依次相交于M 、N 、P 、Q 。
求证:四边形MNPQ 是正方形五.正方形的有关计算:【例1】已知:如图,已知四边形ABCD 是正方形,︒=∠=35,MCE MN CE .求ANM ∠.【例2】如图,四边形ABCD 为正方形,以AB 为边向正方形外做等边三角形ABE ,交BD 于F ,求∠AFD 的度数。
【练习1】如图,P 是正方形ABCD 边AB 上任意一点,AC,BD 交于O,PM ⊥OA,PN ⊥OB 于N,若AB=10,则四边形PMON 的周长为____________.【练习2】在正方形ABCD 中,O 是对角线的交点,过O 作OE ⊥OF ,分别交AB 、BC 于E 、F ,若AE =4,CF =3,则EF = ;【练习4】在正方形ABCD 中,E 在BC 上,且BE=2,EC=1,点P 在BD 上,求PE+PC 的最小值;【练习5】如图,将边长为a 的正方形ABCD 沿直线l 按顺时针方向翻滚,当正方形翻滚一周时,正方形的中心O 所经过的路径长为____。
【练习7】(2006,福州)如图5,小正方形边长为1,连接小正方形的三个顶点,可得△ABC ,则AC 边上的高是( ); B ; C ; D .六.正方形的综合题:【例1】.如图,正方形ABCD中,MN⊥EF,求证:MN=EF【例2】如图,正方形形ABCD的边长为1、P、Q分别在AB、AD上,已知△APQ周长为2,求证:∠PCQ=450;【例3】已知正方形ABCD中,M是AB的中点,E是AB延长线上一点,MN⊥DM且交∠CBE的平分线于N,(如图甲)(1)求证:MD=MN;(2)若将上述条件中的“M为AB的中点”改为“M为AB上任意一点”,其余的条件不变,(如图乙),则结论MD=MN还成立吗?如果成立,请证明,若不成立,请说明理由;【练习1】如图所示,在正方形ABCD中,E为BD上一点,AE的延长线交BC的延长线于F,交CD于H,G 为FH中点,求证:EC⊥CG。
【练习2】在正方形ABCD中,AC与BD交于点O.M,N分别是OA,OB上的点,且MN//AB.求证(1)BM=CN; (2)BM⊥CN.【练习3】已知,如图,以△ABC的边AB、AC为边,分别向形外作一个正方形,中心分别为O1、O2,D为BC中点。
求证:O1D⊥O2D。
【练习6】如图,点E、F在正方形ABCD的边BC、CD上,BE=CF.(1)AE与BF相等吗?为什么?(2)AE与BF是否垂直?说明你的理由。
【练习7】如图,正方形ABCD中对角线AC、BD相交于O,E为AC上一点,AG⊥EB交EB于G,AG交BD 于F。
(1)说明OE=OF的道理;(2)在(1)中,若E为AC延长线上,AG⊥EB交EB的延长线于G,AG、BD的延长线交于F,其他条件不变,如图2,则结论:“OE=OF”还成立吗?请说明理由。
专题训练讲义---正方形一.正方形的性质:【例1】(2008湖北襄樊)如图12,B、C、E是同一直线上的三个点,四边形ABCD与四边形CEFG是都是正方形.连接BG、DE.(1)观察猜想BG与DE之间的大小关系,并证明你的结论.(2)在图中是否存在通过旋转能够互相重合的两个三角形?若存在,请指出,并说出旋转过程;若不存在,请说明理由.解:(1)BG=DE ∵四边形ABCD 和四边形CEFG 都是正方形,∴GC=CE ,BC=CD ,∠BCG=∠DCE=90°)∴△BCG ≌△DCE ∴BG=DE(2)存在. △BCG 和△DCE ;△BCG 绕点C 顺时针方向旋转90°与△DCE 重合【例2】如图,E 是正方形ABCD 边BC 延长线上一点,CE=AC ,AE 交CD 于F ,求∠AFC 的度数。
【例3】如图4-60,正方形ABCD 的对角线相交于O ,EF ∥AB ,并且分别与OA ,OB 相交于E ,F .若BE=3厘米,求CF 的长.【练习1】(2008年沈阳市)如图所示,正方形中,点是边上一点,连接,交对角线于点,连接,则图中全等三角形共有( C )A .1对B .2对C .3对D .4对 【练习2】(08沈阳)如图所示,正方形ABCD 中,点E 是CD 边上一点,连接AE ,交对角线BD 于点F ,连接CF ,则图中全等三角形共有( )A .1对B .2对C .3对D .4对 【练习3】(2008佛山12)如图,已知P 是正方形ABCD 对角线BD 上一点,且BP = BC ,则∠ACP 度数是 22.5 ° .【练习4】(2005山西) 如图1,正方形ABCD 的边CD 在正方形ECGF 的边CE 上,连结BE 、DG.(1) 观察猜想BE 与DC 之间的大小关系,并说明你的结论; (2) 图中是否存在通过旋转能够互相重合的两个三角形? 若存在,请说出旋转过程; 若不存在,请说明理由.【练习5】(2008广东肇庆市)如图5,在等腰Rt △ABC 中,∠C =90°,正方形DEFG 的顶点D 在边AC 上,点E 、F 在边AB 上,点G 在边BC 上.(1)求证AE =BF ; (2)若BC =cm ,求正方形DEFG 的边长.A D C E F 第8题图解:(1)∵ 等腰Rt △ABC 中,∠90°, ∴ ∠A =∠B ∵ 四边形DEFG 是正方形,∴ DE =GF ,∠DEA =∠GFB =90°∴ △ADE ≌△BGF ∴ AE =BF(2)∵ ∠DEA =90°,∠A=45°∴ ∠ADE =45°∴ AE =DE . 同理BF =GF∴ EF =AB===cm ∴ 正方形DEFG 的边长为【练习6】如图4-52,在正方形ABCD 外以CD 为边作等边△CDE .求AED ∠的度数.【练习7】如图所示,在正方形ABCD 中,P 是对角线BD 上一点,PE ⊥BC 于E ,PF ⊥CD 于F ,•连结AP ,EF ,求证:AP=EF .二.正方形的折纸:【例1】(08哈尔滨)如图,将边长为8cm 的正方形纸片ABCD 折叠,使点D 落在BC 边中点E 处,点A 落在点F 处,折痕为MN ,则线段CN 的( ). (A )3cm (B )4cm(C )5cm (D )6cm【练习】 如图,有一张面积为1的正方形纸片ABCD ,M ,N 分别是AD ,BC边的中点,将C 点折叠至MN 上,落在P 点的位置,折痕为BQ ,连结PQ ,则PQ =. 三.正方形的判定:【例1】如图,正方形ABCD 中,DH CG BF AE ===.求证:四边形EFGH 是正方形. 【例2】已知:如图,△ABC 中,︒=∠90C ,CD 平分ACB ∠,BC DE ⊥,AC DF ⊥,垂足分别为E 、F .求证:四边形CFDE 是正方形.四.正方形的有关计算:【例1】已知:如图4-57,已知四边形ABCD 是正方形,︒=∠=35,MCE MN CE .求ANM ∠.【例2】如图,四边形ABCD 为正方形,以AB 为边向正方形外做等边三角形ABE ,交BD 于F ,求∠AFD 的度数。
