简支梁例题
3节装配式钢筋混凝土简支梁设计例题

l 2 0 d
故按正截面承载能力计算所确定的截面尺寸满 足抗剪方面的构造要求。
9
(2)分析梁内是否需要配置剪力钢筋
跨中: 0.50×10-3ftdbh0=0.50×103×1.39×180×1381=172.76kN 支点: 0.50×103ftdbh0=0.50×103×1.39×180×1450.10=181.4kN 因 0V d ,l / 2 (135kN)(0.5103 ) fcdbh0 0Vd ,0 (707kN) 故可在梁跨中的某长度范围内按构造配置箍筋,其 余区段应按计算配置箍筋
0 M d f cd b 'f x(h0 )
2840 106 13.8 2200x(1365 x ) 2 x 2 2730x 187088 0
x 2
故属于第一类T型 截面
简化整理得:求解二次方程得 到合理解: X=70.3mm﹤hf’(=175mm) 将各已知值及X=70.3mm代入 公式,可得
21
22
23
现在按照同时满足梁跨间各正截面和斜截面抗弯要 求,确定弯起钢筋的弯起点位置。 钢筋弯起后相应各正截面抗弯承载能力
梁区段 截面纵筋 有效高度 H0(mm) 1450.1 T形截面类别 受压区高度 x(mm) 15 抗弯承载 能力 Mui(kN.m) 649.6
支座中心~ 1点
2 Ф32
第一类
1点~2点
2点~3点 3点~4点 4点~N1钢 筋截断处 N1钢筋截断 处~梁跨中
4 Ф32
b'f 3 b 2bh 12h'f 180 2 0 12175 2280 mm
故取受压翼板的有效宽度
(2)钢筋数量计算
力学(弯曲)例题
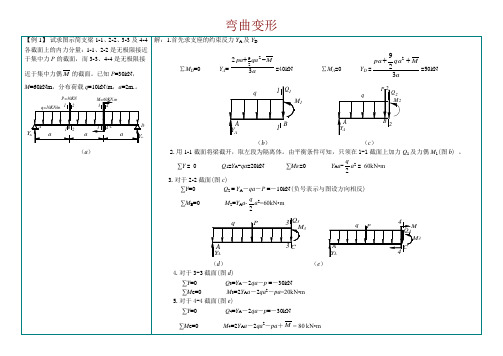
AB段:由键力图上查得Q=- qa<0,由 知,M图斜率为负值。
BC段:因q<0,由 知,Q图斜率为负值,在Q图上,随着x的增加,剪力由正值变为负值;因为 ,故M图的斜率由正值变为负值,当Q=0时,M取得最大值。
CD段:情况同AB段。
【例3】矩形截面松木梁两端搁在墙上,
承受由梁板传来的荷载作用如图所示。已知梁的间距a=1.2m,两墙的间距为L=5m,楼板承受均布荷载,起面集度为P=3KN/ ,松木的弯曲许用应力[σ]=10MPa。试选择梁的截面尺寸。设 。
(a)
解:此题可以采用下面四种不同方法求解。
解一:利用附录五上简支梁受集中载荷作用的解答。由查表可知,当简支梁上作用集中载荷P时,梁中点的挠度为
令梁在左半跨作用均布载荷,如图a所示,稍作变化即可得中点挠度
=-
解二:利用对称性求解。原题半跨均布载荷可分解为正对称载荷和反对称载荷两种情况的叠加(图b)。
解:梁计算简图如图所示荷载的线集中度为:q=
最大弯矩在跨中截面,其值
1.按正应力强度条件选择截面尺寸
h=1.5b,W =
b≥
取b=150mm,h=1.5b=225mm。
2.该梁为木梁,须校核剪应力强度。在邻近支座的截面上有
Q
矩形截面梁
剪切强度足够。故选定b=150mm,h=225mm。
【例4】简支梁在半个跨度上作用的均布载荷q,如图a所示,试求梁中点的挠度。
(d)(e)
4.对于3-3截面(图d)
∑Y=0Q3=YA-2qa-p=-30kN
∑MC=0M3=2YAa-2qa2-pa=20kN•m
5.对于4-4截面(图e)
∑Y=0Q4=YA-2qa-p=-30kN
节装配式钢筋混凝土简支梁设计例题

技术发展与改进
材料优化
随着材料科学的进步,钢筋和混凝土的性能得到不断提升,提高了 节装配式钢筋混凝土简支梁的承载能力和耐久性。
结构设计优化
通过改进结构设计,如采用新型节点连接方式和优化截面形式,提 高了节装配式钢筋混凝土简支梁的抗震性能和承载能力。
施工工艺改进
采用预制化生产方式,提高施工效率,减少现场作业时间,降低施工 成本。
预制构件的生产
模板制作
根据设计图纸,制作预制构件的模板, 确保尺寸和形状符合要求。
钢筋加工与绑扎
混凝土浇筑与养护
将搅拌好的混凝土浇筑入模板中,并 进行适当的养护,以确保混凝土的强 度和质量。
按照设计要求,对钢筋进行加工和绑 扎,确保钢筋的位置和间距准确。
预制构件的运输与堆放
运输方式选择
根据预制构件的大小和重量,选 择合适的运输方式,如平板车、
梁的配筋
纵向钢筋
纵向钢筋是梁的主要受力 钢筋,通常采用HRB400 级钢筋。
横向箍筋
横向箍筋用于固定纵向钢 筋的位置,并提高梁的抗 剪承载能力。
纵向预应力筋
纵向预应力筋通过施加预 应力来提高梁的承载能力 和抗裂性能。
梁的节点连接
焊接连接
通过焊接的方式将梁的节点连接 在ห้องสมุดไป่ตู้起,具有较高的承载能力和
刚度。
05
节装配式钢筋混凝土简 支梁的应用与发展
应用场景
桥梁工程
节装配式钢筋混凝土简支梁广泛应用于桥梁工程中,尤其在跨度 较大或特殊结构需求的桥梁设计中。
建筑结构
在建筑结构中,节装配式钢筋混凝土简支梁可作为楼面、屋面等承 重结构,满足建筑物的承载需求。
道路工程
在道路工程中,节装配式钢筋混凝土简支梁可作为道路桥梁的桥跨 结构,提高道路通行能力。
例题-简支梁内力计算

ql/2 -ql/2
剪力图
ql2/8
弯矩图
2
2、计算截面内力 距离A支座为x的任一截面上的弯矩和剪 力(内力)分别用Mx、Vx表示。
q R1 A R2 x
Mx Vx
由∑Fy=0,得到R2-Vx- qx=0பைடு நூலகம்
Vx= ql/2-qx
对x截面取矩,由∑Mx=0,得到Mx+ qx×x/2-R2×x=0
3、绘制内力图
Mx= qlx/2-qx2/2
横坐标表示x,纵坐标表示内力(弯矩或剪力,即为内力图。
线分布荷载q的合力为ql力臂合力点到a点的距离为l2荷载对a点的力矩为qlql2qx距离a支座为x的任一截面上的弯矩和剪力内力分别用m表示
简支梁内力计算
已知简支梁跨度为l、分布荷载q。求截面弯矩和剪力分布。
〖解〗
R1
1、求支座约束反力
A
三个约束反力分别用R1、R2、R3表示。 R2
q B
l
R3
由静力平衡条件:∑Fx=0 得到R1=0;
对A点取力矩,力矩等于力×力臂。反力R1、 R2 的力臂为0; 反力R3 的力臂为l,对A点的力矩为-R3 l;线分布荷载q的合力为ql
力臂(合力点到A点的距离)为l/2,荷载对A点的力矩为 ql2/2 。
由∑MA=0,0+0- R3 l+ ql2/2=0
得到R3=ql/2
1
∑Fy=0,得到R2= R3 = ql/2
简支梁计算例题

简支梁计算例题摘要:1.引言:简支梁的概述2.计算方法:简支梁的内力计算3.例题:简支梁计算的具体步骤4.总结:简支梁计算的重要性正文:一、引言:简支梁的概述简支梁是指在两端支承,中间自由悬挂的梁。
它是工程中常见的一种结构形式,广泛应用于房屋建筑、桥梁、输电线路等领域。
简支梁的计算主要包括内力计算和挠度计算。
本文主要介绍简支梁的内力计算方法,并通过一个例题来说明具体的计算步骤。
二、计算方法:简支梁的内力计算简支梁的内力计算主要包括弯矩和剪力。
在计算时,一般采用静力平衡法或力矩平衡法。
其中,静力平衡法适用于简支梁在均布荷载作用下的内力计算;力矩平衡法则适用于简支梁在集中荷载作用下的内力计算。
三、例题:简支梁计算的具体步骤假设有一简支梁,梁的长度为L,截面尺寸为b×h,材料为钢筋混凝土,弹性模量为Ec,截面惯性矩为I。
在梁的中心施加一个均布荷载q,求梁在荷载作用下的弯矩和剪力。
1.根据均布荷载求梁的弯矩:首先,根据均布荷载的定义,求得荷载对梁端弯矩的影响。
设梁的一端受到的弯矩为M,则有:M = ql/82.根据弯矩求梁的剪力:根据静力平衡原理,梁在弯矩作用下,梁的剪力V 可表示为:V = M/Ec * h3.计算梁的挠度:根据力矩平衡原理,梁在荷载作用下的挠度f 可表示为:f = V * L / (Ec * I)四、总结:简支梁计算的重要性简支梁计算在工程中有着重要的意义。
通过计算,可以了解梁在荷载作用下的内力分布情况,从而为梁的材料选择、截面尺寸设计以及梁的强度分析提供依据。
桥梁结构检算 题目

桥梁结构检算题目
以下是一个简单的桥梁结构检算题目:
题目:某桥梁主梁采用简支梁,跨度为10m,桥面宽度为,设计荷载为公路-Ⅱ级。
请对该桥梁进行结构检算。
解:
1. 计算跨度:L=10m
2. 桥面宽度:b==3m
3. 设计荷载:公路-Ⅱ级,即汽车总重为550kN,人群荷载为30kN/m2
4. 计算简支梁的弯矩和剪力,根据弯矩和剪力的计算公式,得到弯矩M和剪力V的值。
5. 根据桥梁规范和材料力学原理,进行桥梁的结构检算,包括正截面承载力检算、斜截面承载力检算、刚度检算等。
6. 根据计算结果,确定是否需要进行加固或改建。
此题仅为示例,具体解法需要根据实际工程背景和规范进行。
简支梁计算例题

简支梁计算例题设计任务:设计一个简支梁,已知梁的跨度L=6米,梁的截面尺寸为b×h=200×400毫米,承受均布荷载设计值q=70kN/m(包括自重),混凝土强度等级为C25,纵向受拉钢筋采用HRB400级钢筋,箍筋采用HPB300级钢筋。
1. 计算梁所受总弯矩M:M = qL²/ 8 = 70 ×6²/ 8 = 255 kN·m2. 计算梁的截面面积A:A = b ×h = 200 ×400 = 80000 mm²3. 计算梁的截面模量W:W = α×A ×fcm = 1.1 ×80000 ×30 = 2640000 N·mm4. 计算梁的抗弯承载力Mu:Mu = fcmw = 30 ×2640000 = 79200000 N·mm > M = 25500000 N·mm5. 计算梁的纵筋数量:由M/mho²+fyAs/s ≤fcd得出As ≥M/(mho²+ fy/s),其中fy为HRB400级钢筋的抗拉强度设计值,取值为360N/mm²。
通过计算得出As≥8176mm²,选用2Φ28的钢筋,As=12568mm²。
6. 计算箍筋数量:根据构造要求,选用Φ8@200的箍筋,每米长度内布置箍筋数量为n=1×100/200+1=2个。
7. 验算裂缝宽度:根据规范要求,裂缝宽度不应超过Wmax=0.3mm。
根据M/γfW≤Wmax,其中γf为受拉或受压区纵向普通钢筋的配筋率,取值为As/(bho),通过计算得出W≤Wmax。
8. 绘制施工图,标明梁的跨度、截面尺寸、纵向钢筋和箍筋的位置和规格。
结论:根据以上计算和验算,该简支梁的设计满足要求,可以用于实际工程中。
混凝土简支梁桥的计算-例题

485
1996
纵剖面
18
485
解:(1) 永久作用集度
主梁:
g [0.18 1.30 (0.08 0.14)(1.60 0.18)] 25.0 9.76 kN / m 2
横隔梁:边主梁横隔板:
14 8
100 130 100 130
8 14 130
g2
{[1.00
(0.08 2
附加剪力计算:
Q0q
(1
)
a 2
(m0
mc ) qk
y
1.296 1 (0.438 0.538) 7.875 0.916 2.29 kN
公路-II级作用下,边主梁支点的最大剪力为:
Q0q Q0' q Q0q 175.13 2.29 172.84 kN
18.73 kN
本章小结
要求同学们能熟练掌握运用以下知识点:
1、桥面板的有效工作宽度的确定; 2、桥面板内力计算的方法; 3、钢筋混凝土及预应力混凝土梁桥变形计算的原理; 4、杠杆原理的基本思路、计算方法及适用场合; 5、刚性横梁法的基本思路、计算方法及适用场合; 6、抗扭修正系数的含义。
钢筋混凝土简支梁桥主梁的永久作用效应 ,已知每侧的栏
杆及人行道构件的永久作用为 5 kN / m 。
沥青混凝土厚2cm 250号混凝土垫层(6~12cm)
75
700
75
i=1.5%
i=1.5%
158
14 8
100 130 100 130
8 14 130
2
160
160
160
160
横剖面
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
如图所示简支梁,截面尺寸 b ×h = 250×500,采用 C20 混凝土,纵向受拉钢筋采用Ⅱ级(HRB335)钢筋,箍筋用Ⅰ级(HPB235)钢筋,梁内配有纵向受拉钢筋 325,箍筋φ6@200,试确定该梁所能承受的均布荷载设计值(不包括梁自重)。
解:1、由抗弯确定得均布荷载设计值:
bh A s =
ρ=
=⨯465
25014730.01267, c
y f f 1αρξ=
==
⨯⨯
6
.90.130001267.00.396 < ξb = 0.55,适筋,
()()8
.164396.05.01396.04652506.90.15.012
2
01=⨯-⨯⨯⨯⨯⨯=-=ξξαbh f M c kN
·
m,
2
8l
M q =
=
=⨯⨯2
3
4260
10
8.164872.65 kN/m
扣去梁得自重后能承担的净荷载: 5.025.0252.1-72.65 q'⨯⨯⨯==68.9 kN/m 2、由抗剪确定得均布荷载设计值:
0025.17.0h s
nA f bh f V sv yv
t +===
⨯⨯⨯
⨯+⨯⨯⨯465200
3.221025.14652501.17.012
4.056 kN ,
=
⨯4260
2
.1240562
= q 58.24 kN/m
扣去梁得自重后能承担的净荷载: 5.025.0252.1-58.24 'q'⨯⨯⨯==54.49kN/m 最后承担的净荷载为54.49kN/m
钢筋混凝土矩形截面简支梁,b ×h = 200×500,L = 4.04 m ,支座 a = 240mm ,承受均布荷载设计值 80 kN/m (包括自重),混凝土强度等级为 C20,纵向受拉钢筋采用Ⅱ级(HRB335)钢筋,箍筋用Ⅰ级(HPB235)钢筋,求箍筋和弯起钢筋的数量。
解:1、求V : 04
.4802
121 V ⨯⨯=
=
ql =161.6 kN
2、验算截面尺寸:h o =h- a s = 465,hw / b < 4,
3、是否按计算配箍:4652001.17.07.00⨯⨯⨯=bh f t = 71.6 kN<V ,应按计算配箍。
4、求纵筋和抗弯钢筋:纵筋, =
⨯⨯=
2
04
.4808
1 M 163.
2 kN ·m ,
2
6
2
1465
2006.910
2.163⨯⨯⨯=
=
bh f M
c s αα=0.393
()()
73
.0393.02115.02115.0=⨯-+⨯=-+⨯=s s αγ,
465
73.030010
2.1636
⨯⨯⨯=
=
h f M As s y γ= 1602mm 2,选 422 (As = 1520mm 2)
若配箍筋又配弯起钢筋,可利用122以45度弯起则弯筋承担的剪力
488.6445sin 3003808.0sin 8.00
=⨯⨯⨯===s y b s b s f A V α kN ,
V cs =V-V sb =161.6-64.488=97.112kN, 选箍筋φ6@200
106.15 465200
28.322101.254652001.10.7 25.17.000=⨯⨯⨯
⨯+⨯⨯⨯=+=h s
nA f bh f V sv yv
t >97.112
kN
一钢筋混凝土矩形截面简支梁,截面尺寸 200×600,荷载如图所示,采用 C20 混凝土,箍筋用Ⅰ级(HPB235)钢筋。
要求配置箍筋
解:025.0bh f c c β=A
V 2712005652006.9125.0>=⨯⨯⨯⨯,V B =186250,截面尺寸符合要求.
AB 段,65.2565
15000
===h a λ
186250
V 59595.95652001.11
65.275.11
75
.10=<=⨯⨯⨯+=
+bh f t λ,
应按计算配箍筋,001
75
.1h s
nA f ftbh V V sv yv
cs A ++=
=λ,
067.1565
2100.19.595951862501
=⨯⨯-=
s
nA sv , 选φ
8@90, =
⨯=9050
21
s
nA sv 1.118>1.067(可以)
最小配箍率的验算
00125
.0210
1.124
.024
.0min ===yv
t sv f f ρ<00559.090
2003.502=⨯⨯=
=bs
A n
sv sv ρ(可以)
CD 段, 565
30000
==h a λ=5.3>3, 取λ=3,
53125
V 54381.25
5652001.14
75.11
75
.10=>=⨯⨯⨯=
+bh f t λ,仅需按构造配箍筋选φ8@250
DE 段, 35.3565
30000
>===h a λ, 取λ=3,
73125
543815652001.14
75.11
75
.10<=⨯⨯⨯=
+bh f t λ,
应按计算配箍筋,001
75
.1h s
nA f ftbh V V sv yv
cs E ++=
=λ,565
2100.154381731251
⨯⨯-=
s
nA sv =0.158, 选φ8@250,
0.1580.402250
3.5021
>=⨯=
s
nA sv (可以)
最小配箍率的验算
00125
.0210
1.124
.024
.0min ===yv
t sv f f ρ<002.0250
2003.502=⨯⨯=
=bs
A n
sv sv ρ(可以)
EB 段,65
.2565
15000
==
=
h a λ,
166250
V 59595.95652001.11
65.275.11
75
.10=<=⨯⨯⨯+=
+bh f t λ
应按计算配箍筋,00175.1h s nA f ftbh V V sv yv cs B ++==λ,899.0565
2100.19
.595951662501=⨯⨯-=s nA sv , 选φ
8@100,
0.8991.006100
3.5021
>=⨯=
s
nA sv (可以)
最小配箍率的验算
00125
.0210
1.124
.024
.0min ===yv
t sv f f ρ<00503.0100
2003.502=⨯⨯=
=bs
A n
sv sv ρ(可以)。
