函数线性相关与无关的判断方法
微分方程的线性无关判定

微分方程的线性无关判定线性无关是微分方程理论中一个非常重要的概念。
对于给定的微分方程组来说,我们希望找到一组解,使得它们能够覆盖整个解空间。
而这组解的线性无关性质决定了解空间的维度和基本解系的个数。
首先,我们需要明确什么是线性无关的概念。
对于给定的n个函数f1(x), f2(x), ..., fn(x),如果存在一组常数c1, c2, ..., cn,使得c1 f1(x) + c2 f2(x) + ... + cn fn(x) = 0对于所有的x成立当且仅当c1 = c2 = ... = cn = 0,则称这组函数是线性无关的。
也就是说,任何一个函数都不能表示为其他函数的线性组合。
接下来,我们来介绍微分方程的线性无关判定。
对于给定的n阶齐次线性微分方程:a_n(x)y^(n)+a_(n-1)(x)y^(n-1)+...+a_1(x)y'+a_0(x)y=0其中,a_i(x)为给定的已知函数,y是待求的未知函数。
如果存在n 个线性无关的解y1(x), y2(x), ..., yn(x),则它们构成方程的一个基本解系。
这意味着任何解都可以表示为这n个解的线性组合。
那么,如何判定一组解是否线性无关呢?下面是判定线性无关的两种典型方法:方法一:Wronskian判别式法给定n个函数f1(x), f2(x), ..., fn(x),计算它们的Wronskian 行列式:W(f1, f2, ..., fn) = , f1 f2 ... fnf1' f2' ... fn...........f1^(n-1) f2^(n-1) ... fn^(n-1如果W(f1, f2, ..., fn)(x0) ≠ 0,对于其中一个x0,则这组函数线性无关。
反之,如果W(f1, f2, ..., fn)(x) = 0,对于所有的x,则这组函数线性相关。
方法二:求解平凡齐次线性微分方程法给定n个函数f1(x), f2(x), ..., fn(x),假设存在一组常数c1, c2, ..., cn,满足c1 f1(x) + c2 f2(x) + ... + cn fn(x) = 0对于所有的x。
线性代数笔记

线性代数序章线性代数基础知识1.单位矩阵:对角线上均为1,其余元素都是0的n 阶方阵,记作I在矩阵多项式f(A) 中单位阵I 对应代数多项式 f(x) 中的 1,纯量阵kI 对应常数k 2.零矩阵:元素全为0的矩阵,记作O3.矩阵的p 阶子式:设},min{n m L =,指以)(L p a a pp ≤-11的p 个元素为主对角线构成的,含2p 个元素的p 阶方阵的行列式第一篇线性空间第一章向量和向量组1.1 线性组合1.向量组和矩阵的对应关系:一个向量组A 对应一个矩阵的列(或行)向量组A’2.线性表示:如果存在一组数{}i x 使向量∑==ni ii i ax b 1,那么称b 能被向量组A (或记{}i a )线性表示;也就是线性方程组Ax=b 有解(这也是求坐标表示的方法)3.等价:如果向量组B’中的任何向量b 都能被组A’线性表示,反之亦成立,称组B’和组A’等价; 也就是矩阵方程AX=B 和BX -1=A 都有解,即)()(B r A r = 行向量组等价与矩阵等价的关系:(1)向量组的等价(不要求两个组同向量数)和矩阵的等价(要求两个阵同型)是不同的概念 (2)当两个同型矩阵A ,B 的列向量组等价,A 与B 等价此时:方程Ax=0和Bx=0同解,r(A)=r(B)(3)当矩阵A 与B 等价,经行/列变换得到B ,则A 与B 的行/列向量组等价1.2 线性相关性和秩1.线性相关:对于向量n a a a ,...,,21,如果存在不全为零的实数n k k k ,...,,21使得01=∑=ni ii ak ,那么这些向量线性相关,也就是方程Ak=0有非零解线性无关:对于向量n a a a ,...,,21,如果当且仅当n k k k ,...,,21全为零时,才有01=∑=ni ii ak ,那么这些向量线性无关,也就是方程Ak=0只有零解2.判定方法:如果向量组A 对应的矩阵的秩<向量数,则组A 线性相关; 如果向量组A 对应的矩阵的秩 = 向量数,则组A 线性无关;3.向量组的秩定义:向量组A 中线性无关向量的最大个数,记为r ,A 中任意r+1个向量都线性相关4.向量组与矩阵的秩:矩阵的秩 = 行向量组的秩 = 列向量组的秩1.3 基、维数和坐标1.基:如果向量空间V 中任一向量都可被V 中一线性无关向量组A 线性表示,称组A 为V 的一个基 基变换:设A,B 为V 的两组基,记B A P 1-=为过渡矩阵,则A P B T=2.维数:基中的向量数r (也是基的秩)称为向量空间V 的维数,称V 为r 维向量空间3.坐标:如果向量空间V 中一向量∑==ni ii i ax b 1,且{}i a 是V 的基,则称{}i x 为b 在基A 中的坐标证明向量组A 是空间V 的基,就是要写出V 中任一向量{}i b 在基A 中的坐标表达式坐标变换:设A,B 为V 的两组基,对应坐标为x,y ,记B A P 1-=为过渡矩阵,则x P y 1-=1.4 范数、投影和正交性1.向量的范数:x x xx T ni i==∑=12,n 为向量维数2.广义的向量夹角:ba ba b a T = ,cos ;b 在a 上的投影:a a a b a p T T =3.向量的正交性:两个向量x,y 的点积(或y x T)为零,则两向量正交;零向量没有长度,和所有向量都正交正交和线性相关性:如果一组向量互正交,则它们线性无关4.规范正交基:两两正交的单位基向量组向量的坐标:设q 为规范正交基,若向量∑==n i i i q x b 1,则坐标b q x T i i =或写作b Q x T =5. 基向量的规范正交化:第二章向量空间2.1 向量空间和子空间1.向量空间:对加法和数乘封闭,包含所有n 维实向量的非空集合,记作nR 公理化定义:设V 是一非空集合,R 为实数域; Part1:运算的封闭性若对于任意两个元素V ∈βα,,总有唯一的元素V ∈γ 与之对应,称γ 为βα ,的和;若对于实数λ与任一元素V ∈α,总有唯一的元素V ∈δ与之对应,称δ 为λα,的积;Part2:运算的法则 八条运算律分别为:(1)加法交换律(2)加法结合律(3)加法元为0 (4)元素的负元素唯一 (5)乘法元为1 (6)乘法交换律(7)数乘结合律(8)乘法结合律若和与积运算具备封闭性且满足八条运算律,即称V 为实向量空间,V 中元素称为向量。
高中高中数学第二章统计2.3.1变量之间的相关关系2.3.2两个变量的线性相关课件新人教A版必修3

解:(1)画出散点图.
(2)判断变量x,y是否具有相关关系?如果具有相关关系,那么是正相关还是 负相关?
解:(2)具有相关关系.根据散点图,左下角到右上角的区域,变量x的值由小 变大时,另一个变量y的值也由小变大,所以它们具有正相关关系.
方法技巧 两个随机变量x和y是否具有相关关系的确定方法: (1)散点图法:通过散点图,观察它们的分布是否存在一定规律,直观地判断 (如本题); (2)表格、关系式法:结合表格或关系式进行判断; (3)经验法:借助积累的经验进行分析判断.
4
4
解:(2)由表中的数据得: xi yi =52.5, x =3.5, y =3.5, xi2 =54,
i 1
i 1
n
所以 b =
xi yi n x y
i 1
n
xi2
2Hale Waihona Puke nx=52.5 4 3.5 3.5 54 4 3.52
=0.7,
i 1
a = y - b x =3.5-0.7×3.5=1.05,
年份x
储蓄存款 y(千亿元)
2013 5
2014 6
2015 7
2016 8
2017 10
为了研究计算的方便,工作人员将上表的数据进行了处理,t=x-2 012,z=y-5 得到表2:
时间代号t
1
2
3
4
5
z
0
1
2
3
5
(1)求z关于t的线性回归方程;
5
5
解:(1) t =3, z =2.2, ti zi=45, ti2 =55,
知识探究
1.相关关系与函数关系不同 函数关系中的两个变量间是一种确定性关系,相关关系是一种不确定性关系. 2.正相关和负相关 (1)正相关 在散点图中,点散布在从左下角到右上角的区域,对于两个变量的这种相关 关系,我们就称它为正相关. (2)负相关 在散点图中,点散布在从左上角到右下角的区域,对于两个变量的这种相关 关系,我们就称它为负相关.
2020年高考数学一轮复习专题6.5相关系数及回归方程练习(含解析)

6.5 相关系数及回归方程两个变量间的相关关系:①有关概念:相关关系与函数关系不同.函数关系中的两个变量间是一种确定性关系.相关关系是一种非确定性关系,即相关关系是非随机变量与随机变量之间的关系.如果一个变量的值由小变大时另一个变量的值由小变大,这种相关称为正相关;如果一个变量的值由小变大时另一个变量的值由大变小,这种相关称为负相关;如果散点图中点的分布从整体上看大致在一条直线附近,就称这两个变量之间具有线性相关关系.②回归方程: 是两个具有线性相关关系的变量的一组数据的回归方程,其中是待定参数. 的计算公式.考向一 样本中心【例1-1】某种产品的广告费支出与销售额之间有如下对应数据(单位:百万元),根据下表求出关于的线性回归方程为,则表中的值为( )A. B. C. D.y bx a =+1122()()()n n x y x y x y ,,,,,,a b 、a b 、1122211()()()()nni i i ii i nni ii i x x y y x y nx yb x x xn x a y bx====⎧---⎪⎪==⎪⎨--⎪⎪=-⎪⎩∑∑∑∑x y y x 6.5175ˆ.yx =+a 505456.564【答案】B【解析】根据规律知道回归直线一定过样本中心,故得到,将坐标代入方程得到的值为.故答案为:B. 【例1-2】已知表中数据y 与x 有较好的线性关系,通过计算得到y 关于x 的线性回归方程为ˆˆ1.05yx a =+,则相应于下列各点的残差中绝对值最小的是( )A .(2,4)B .(4,6)C .(8,10)D .(10,12.5)【答案】D【解析】ˆˆˆ6,8.3,8.3 1.056,2, 1.052x y aa y x ==∴=⨯+∴=∴=+, 相应于点(2,4),(4,6),(8,10),(10,12.5)的残差分别为0.1,0.2,0.4,0---,故选D.【举一反三】1.“关注夕阳、爱老敬老”—某马拉松协会从2013年开始每年向敬老院捐赠物资和现金.下表记录了第x 年(2013年是第一年)与捐赠的现金y (万元)的对应数据,由此表中的数据得到了y 关于x 的线性回归方程.ˆ035ymx =+,则预测2019年捐赠的现金大约是( ) A .5万元B .5.2万元C .5.25万元D .5.5万元【答案】C5,196x y a ==+6.5175ˆ.yx =+a 54【解析】由已知得,29t =, 所以样本点的中心点的坐标为(4.5,3.5),代入.ˆ035ymx =+, 得3.5 4.50.35m =+,即0.7m =,所以0.7035ˆ.x y=+, 取7x =,得ˆ0.770.35 5.25y=⨯+=, 预测2019年捐赠的现金大约是5.25万元.2.某同学将收集到的6组数据对,制作成如图所示的散点图(各点旁的数据为该点坐标),并由这6组数据计算得到回归直线l :y bx a =+$$$和相关系数r .现给出以下3个结论:①0r >;②直线l 恰过点D ;③1b >. 其中正确结论的序号是( )A .①②B .①③C .②③D .①②③【答案】A【解析】由图像可得,从左到右各点是上升排列的,变量具有正相关性,所以0r >,①正确; 由题中数据可得: 1.5 2.4 3.54 5.8 6.846x +++++==, 2.1 2.8 3.3 3.5 4.35 3.56y +++++==,所以回归直线过点(4,3.5)D ,②正确;又61621()()10.360.514120.14()iii ii x x yy b x x ==--==≈<-∑∑,③错误.故选A 3.有一散点图如图所示,在5个(,)x y 数据中去掉(3,10)D 后,下列说法正确的是( )A .残差平方和变小B .相关系数r 变小C .相关指数2R 变小D .解释变量x 与预报变量y 的相关性变弱【答案】A【解析】∵从散点图可分析得出:只有D 点偏离直线远,去掉D 点,变量x 与变量y 的线性相关性变强, ∴相关系数变大,相关指数变大,残差的平方和变小,故选:A.考向二回归方程【例2】某人经营淡水池塘养草鱼,根据过去40期的养殖档案,该池塘的养殖重量X (百斤)都在20百斤以上,其中不足40百斤的有8期,不低于40百斤且不超过60百斤的有20期,超过60百斤的有12期.根据统计,该池塘的草鱼重量的增加量y (百斤)与使用某种饵料的质量x (百斤)之间的关系如图所示.(1)根据数据可知y 与x 具有线性相关关系,请建立y 关于x 的回归方程ˆˆˆybx a =+;如果此人设想使用某种饵料10百斤时,草鱼重量的增加量须多于5百斤,请根据回归方程计算,确定此方案是否可行?并说明理由.(2)养鱼的池塘对水质含氧量与新鲜度要求较高,某商家为该养殖户提供收费服务,即提供不超过3台增氧冲水机,每期养殖使用的冲水机运行台数与鱼塘的鱼重量X 有如下关系:若某台增氧冲水机运行,则商家每期可获利5千元;若某台冲水机未运行,则商家每期亏损2千元.视频率为概率,商家欲使每期冲水机总利润的均值达到最大,应提供几台增氧冲水机? 附:对于一组数据()()()1122,,,,n n x y x y x y ,其回归方程ˆˆˆybx a =+的斜率和截距的最小二乘估计公式分别为1221ˆni ii ni i x y nxy bx nx ==-=-∑∑()()()121,niii ni i x x y y x x ==--=-∑∑ˆˆay bx =- 【答案】(1)337y 1313x =+$当10x =时,此方案可行.(2)应提供2台增氧冲水机 【解析】(1)依题意,5,4,x y ==()()5126iii x x y x =--=∑()()()515213ˆ,13iii i i x x y y bx x ==--∴==-∑∑337ˆ451313a y bx =-=-⨯=$所以3371313y x =+$当10x =时,67ˆ513y=>,故此方案可行. (2)设盈利为Y ,安装1台时,盈利5000Y =, 安装2台时,12040,3000,5X Y p <<==;440,10000,5X Y p ==…. 14()300010000860055E Y ∴=⨯+⨯=安装3台时,12040,1000,5X Y p <<==; 4060,8000,X Y =剟3;5P =160,15000,5X Y P >==. 13()1000800055E Y ∴=⨯+⨯11500080005+⨯=.86008000>,故应提供2台增氧冲水机.【举一反三】1.李克强总理在2018年政府工作报告指出,要加快建设创新型国家,把握世界新一轮科技革命和产业变革大势,深入实施创新驱动发展战略,不断增强经济创新力和竞争力.某手机生产企业积极响应政府号召,大力研发新产品,争创世界名牌.为了对研发的一批最新款手机进行合理定价,将该款手机按事先拟定的价格进行试销,得到一组销售数据(),(1,2,,6)i i x y i =,如表所示:已知611606i i y y ===∑.(1)若变量,x y 具有线性相关关系,求产品销量y (百件)关于试销单价x (千元)的线性回归方程ˆˆˆy bx a =+;(2)用(1)中所求的线性回归方程得到与i x 对应的产品销量的估计值i y .当销售数据(),i i x y 对应的残差的绝对值ˆ1i i y y -≤时,则将销售数据(),i i x y 称为一个“好数据”.现从6个销售数据中任取3个子,求“好数据”个数ξ的分布列和数学期望()E ξ.(参考公式:线性回归方程中ˆˆ,ba 的估计值分别为1221ˆˆˆ,)ni ii nii x y nxyb ay bx xnx =-=-==--∑∑. 【答案】(1) ˆ482yx =-+ (2)见解析 【解析】(1)由611606i i y y ===∑,可求得48t =,故11910ni ii x y==∑,=1980nx y ,21199ni i x ==∑,2=181.5nx ,代入可得122119101980704199181.517.5ni ii ni i x y nx yb x nx==---====---∑∑,ˆˆ604 5.582ay bx =-=+⨯=, 所以所求的线性回归方程为ˆ482yx =-+. (2)利用(1)中所求的线性回归方程ˆ482yx =-+可得,当13x =时,170y =;当24x = 时,266y =;当35x =时,362y =;当46x =时,458y =;当57x =时,554y =;当68x =时,650y =.与销售数据对比可知满足||1(1,2,,6)i i y y i -≤=的共有4个“好数据”:(3,70)、(4,65)、(5,62)、(6,59) 于是ξ的所有可能取值为1,2,31242361(1)5C C P C ξ===,2142363(2)5C C P C ξ===,3042361(3)5C C P C ξ===, ∴ξ 的分布列为:所以1232555E ξ=⨯+⨯+⨯=.考向三 非线性回归【例3】近期,某公交公司分别推出支付宝和微信扫码支付乘车活动,活动设置了一段时间的推广期,由于推广期内优惠力度较大,吸引越来越多的人开始使用扫码支付.某线路公交车队统计了活动刚推出一周内每一天使用扫码支付的人次,用x 表示活动推出的天数,y 表示每天使用扫码支付的人次(单位:十人次),统计数据如表所示:根据以上数据,绘制了如图所示的散点图.(1)根据散点图判断,在推广期内,y a bx =+与(,xy c d c d =⋅均为大于零的常数)哪一个适宜作为扫码支付的人次y 关于活动推出天数x 的回归方程类型?(给出判断即可,不必说明理由);(2)根据(1)的判断结果及表l 中的数据,求y 关于x 的回归方程,并预测活动推出第8天使用扫码支付的人次;(3)推广期结束后,车队对乘客的支付方式进行统计,结果如表所示:已知该线路公交车票价为2元,使用现金支付的乘客无优惠,使用乘车卡支付的乘客享受8折优惠,扫码支付的乘客随机优惠,根据统计结果得知,使用扫码支付的乘客,享受7折优惠的概率为16,享受8折优惠的概率为13,享受9折优惠的概率为12.根据所给数据以事件发生的频率作为相应事件发生的概率,估计一名乘客一次乘车的平均费用. 参考数据:其中lg i i u y =,7117i i u u ==∑.【答案】(1)xy c d =⋅适宜作为扫码支付的人数y 关于活动推出天数x 的回归方程类型;(2)y 关于x 的回归方程式为:0.25ˆ 3.4710xy=⨯,第8天使用扫码支付的人次为347人次;(3)1.66元.【解析】(1)根据散点图判断,x y c d =⋅适宜作为扫码支付的人数y 关于活动推出天数x 的回归方程类型;(2)由(1)知回归方程为x y c d =⋅,两边同时取常用对数得:()lg lg lg lg xy c dc d x =⋅=+⋅,设lg y u =,lg lg u c d x ∴=+⋅,又4x =, 1.54u =,721140i i x ==∑,7172221750.1274 1.547lg 0.2514074287i ii i i x u xu d x x==--⨯⨯∴====-⨯-∑∑,把样本中心点()4,1.54代入lg lg u c d x =+⋅,即1.54lg 0.254c =+∙,解得:4ˆl 0.5gc=, 0.5405ˆ.2ux ∴=+, lg 0.540.25y x ∴=+,y ∴关于x 的回归方程式为:()0.540.250.540.250.2510101040ˆ 3.71xx x y +==⨯=⨯,把8x =代入上式得,23.4734ˆ107y=⨯=, 活动推出第8天使用扫码支付的人次为347人次;(3)记一名乘客乘车支付的费用为Z ,则Z 的取值可能为:2,1.8,1.6,1.4, 则()20.1P Z==,()11.80.30.152P Z ==⨯=, ()11.60.60.30.73P Z ==+⨯=,()11.40.30.056P Z ==⨯=; 分布列为:所以,一名乘客一次乘车的平均费用为:20.1 1.80.15 1.60.7 1.40.05 1.66⨯+⨯+⨯+⨯=(元). 【举一反三】1.为方便市民出行,倡导低碳出行.某市公交公司推出利用支付宝和微信扫码支付乘车活动,活动设置了一段时间的推广期,在推广期内采用随机优惠鼓励市民扫码支付乘车.该公司某线路公交车队统计了活动推广期第一周内使用扫码支付的情况,其中 (单位:天)表示活动推出的天次, (单位:十人次)表示当天使用扫码支付的人次,整理后得到如图所示的统计表1和散点图. 表1:(1)由散点图分析后,可用作为该线路公交车在活动推广期使用扫码支付的人次关于活动推出天次的回归方程,根据表2的数据,求此回归方程,并预报第8天使用扫码支付的人次(精确到整数).表2:表中,.(2)推广期结束后,该车队对此期间乘客的支付情况进行统计,结果如表3.表3:统计结果显示,扫码支付中享受5折支付的频率为,享受7折支付的频率为,享受9折支付的频率为.已知该线路公交车票价为1元,将上述频率作为相应事件发生的概率,记随机变量为在活动期间该线路公交车搭载乘客一次的收入(单位:元),求的分布列和期望.参考公式:对于一组数据,其回归直线的斜率和截距的最小二乘估计分别为参考数据:,,.【答案】(1) ,人次为2447 (2)见解析【解析】(1)由题意得,,,关于的线性回归方程为,关于的回归方程为,当时,,第8天使用扫码支付的人次为2447;(2)由题意得的所有取值为0.5,0.7,0.9,1,,,,,的分布列为:1.有下列说法:①若某商品的销售量y (件)关于销售价格x (元/件)的线性回归方程为5350y x =-+,当销售价格为10元时,销售量一定为300件;②线性回归直线y bx a =+$$$一定过样本点中心(,)x y ;③若两个随机变量的线性相关性越强,则相关系数r 的值越接近于1;④在残差图中,残差点比较均匀落在水平的带状区域中即可说明选用的模型比较合适,与带状区域的宽度无关;⑤在线性回归模型中,相关指数2R 表示解释变量对于预报变量变化的贡献率,2R 越接近于1,表示回归的效果越好;其中正确的结论有几个( ) A .1 B .2C .3D .4【答案】B【解析】①当销售价格为10时,销售量的预估值为300件,但预估值与实际值未必相同,①错误; ②由最小二乘法可知,回归直线必过(),x y ,②正确;③若两个随机变量为负相关,若线性相关性越强,相关系数r 越接近1-,③错误; ④残差图中,带状区域越窄,模型拟合度越高,④错误;⑤相关指数2R 越接近1,拟合度越高,则在线性回归模型中,回归效果越好,⑤正确. 可知正确的结论为:②⑤,共2个本题正确选项:B2.已知下表为x 与y 之间的一组数据,若y 与x 线性相关,则y 与x 的回归直线y bx a =+必过点( )A .(2,2)B .(1.5,0)C .(1,2)D .(1.5,4)【答案】D【解析】由题可得32x =,4y =, 22223333(0)(14)(1)(34)(2)(54)(3)(74)102222ˆ233335(0)(1)(2)(3)2222b --+--+--+--===-+-+-+-,3ˆ4212a=-⨯=,则回归方程为ˆ21yx =+,将A ,B ,C ,D 四项分别代入方程,只有(1.5,4)这个点在直线上,故选D 。
备战高考数学复习考点知识与题型讲解85---变量间的相关关系及回归模型

备战高考数学复习考点知识与题型讲解第85讲变量间的相关关系及回归模型考向预测核心素养两个变量线性相关的判断及应用,经验回归方程的求法及应用是高考考查的热点,各种题型均会出现.数据分析、数学运算一、知识梳理1.变量的相关关系(1)相关关系:两个变量有关系,但又没有确切到可由其中的一个去精确地决定另一个的程度,这种关系称为相关关系.(2)散点图每一个成对样本数据都可用直角坐标系中的点表示出来,由这些点组成了统计图.我们把这样的统计图叫做散点图.(3)相关关系的分类:正相关和负相关.(4)线性相关:一般地,如果两个变量的取值呈现正相关或负相关,而且散点落在一条直线附近,我们称这两个变量线性相关.2.样本相关系数(1)r=∑ni=1(x i-x)(y i-y)∑ni=1(x i-x)2∑ni=1(y i-x)2.(2)当r>0时,称成对样本数据正相关;当r<0时,称成对样本数据负相关.(3)|r|≤1;当|r|越接近1时,成对样本数据的线性相关程度越强;当|r|越接近0时,成对样本数据的线性相关程度越弱.3.一元线性回归模型参数的最小二乘估计(1)我们将y^=b^x+a^称为Y关于x的经验回归方程,其中⎩⎪⎨⎪⎧b ^=∑ni =1(x i-x )(y i-y )∑ni =1(x i-x )2,a ^=y -b ^x .(2)残差分析①对于响应变量Y ,通过观测得到的数据称为观测值,通过经验回归方程得到的y ^称为预测值,观测值减去预测值称为残差.残差是随机误差的估计结果,通过对残差的分析可以判断模型刻画数据的效果,以及判断原始数据中是否存在可疑数据等,这方面工作称为残差分析.②残差的散点图比较均匀地集中在以横轴为对称轴的水平带状区域内,则满足一元线性回归模型对随机误差的假设.在R 2表达式中,∑i =1 n (y i -y )2与经验回归方程无关,残差平方和∑i =1n(y i -y ^i )2与经验回归方程有关.因此R 2越大,意味着残差平方和越小,即模型的拟合效果越好;R 2越小,表示残差平方和越大,即模型的拟合效果越差.[提醒](1)经验回归直线过样本的中点(x ,y ).(2)回归分析和独立性检验都是基于成对样本观测数据进行估计或推断 ,得出的结论都可能犯错误.二、教材衍化1.(人A 选择性必修第三册P 103习题8.1T 1改编)下列四个散点图中,变量x 与y 之间具有负的线性相关关系的是( )解析:选D.观察题图可知,只有D选项的散点图表示的是变量x与y之间具有负的线性相关关系,故选D.2.(人A选择性必修第三册P138复习T1改编)已知变量x与y正相关,且由观测数据算得样本平均数x-=3,y-=3.5,则由该观测数据算得的经验回归方程可能是( )A.y^=0.4x+2.3B.y^=2x-2.4C.y^=-2x+9.5D.y^=-0.3x+4.4解析:选A.由题意,x与y正相关,故排除C,D,将(x-,y-)代入经验回归方程检验得A正确.3.(人A选择性必修第三册P120习题8.2T2(2)改编)已知x,y的对应取值如下表,可得到经验回归方程为y^=0.95x+a^,则a^=( )x 013 4y 2.2 4.3 4.8 6.7A.3.25B.2.6C.2.2D.0解析:选B.经验回归直线过点(2,4.5),所以4.5=0.95×2+a^,所以a^=2.6.4.(人A选择性必修第三册P120习题8.2T2(2)改编)某车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了5次试验.根据收集到的数据(如下表),由最小二乘法求得经验回归方程y^=0.67x+54.9.零件数x/个1020304050加工时间y/min62758189 现发现表中有一个数据看不清,请你推断出该数据的值为________.解析:由x=30,得y=0.67×30+54.9=75.设表中的“模糊数字”为a,则62+a+75+81+89=75×5,所以a=68.答案:68一、思考辨析判断正误(正确的打“√”,错误的打“×”)(1)利用样本点的散点图可以直观判断两个变量的关系是否可以用线性关系来表示.( )(2)经验回归直线y^=b^x+a^至少经过点(x1,y1),(x2,y2),…,(x n,y n)中的一个点.( )(3)任何一组数据都对应着一个经验回归方程.( )答案:(1)√(2)×(3)×二、易错纠偏1.(回归模型意义不明致误)一位母亲记录了自己儿子3~9岁的身高数据(略),由此建立的身高与年龄的一元线性回归模型为y^=7.19x+73.93,用这个模型预报这个孩子10岁时的身高,则正确的叙述是( )A.身高一定是145.83 cmB.身高在145.83 cm以上C.身高在145.83 cm左右D.身高在145.83 cm以下解析:选C.由一元线性回归模型可得y^=7.19×10+73.93=145.83,所以预报这个孩子10岁时的身高在145.83 cm左右.2.(忽视经验回归直线过样本点中心致误)已知变量x和y的统计数据如下表:x 34567y 2.534 4.5 6根据上表可得经验回归方程为y^=b^x-0.25,据此可以预测当x=8时,y^=( ) A.6.4 B.6.25C.6.55D.6.45解析:选 C.由题中图表可知,x-=5,y-=4,因为经验回归方程经过样本的中心(x-,y-),则4=5b^-0.25,得b^=0.85,则经验回归方程为y^=0.85x-0.25,再将x=8代入方程,得y^=6.55.3.(决定系数的意义及应用不清致误)x和y的散点图如图所示,在相关关系中,若用y=c1e c2x拟合时的决定系数为R21,用y^=b^x+a^拟合时的决定系数为R22,则R21,R22中较大的是________.解析:由题图知,用y=c1e c2x拟合的效果比y^=b^x+a^拟合的效果要好,所以R21>R22,故较大者为R21.答案:R21考点一成对数据的相关性判断(自主练透)复习指导:通过收集现实问题中的成对数据作出散点图,并利用散点图直观认识变量间的相关关系.1.对变量x,y有观测数据(x i,y i)(i=1,2,…,10),得散点图如图①,对变量u,v有观测数据(u,v i)(i=1,2,…,10),得散点图如图②.由这两个散点图可以判i断( )A.变量x与y正相关,u与v正相关B.变量x与y正相关,u与v负相关C.变量x与y负相关,u与v正相关D.变量x与y负相关,u与v负相关解析:选C.由题图可得两组数据均线性相关,且图①的经验回归方程斜率为负,图②的经验回归方程斜率为正,则由散点图可判断变量x与y负相关,u与v正相关.2.对四组数据进行统计,获得如图所示的散点图,关于其相关系数的比较,正确的是( )A.r2<r4<0<r3<r1B.r4<r2<0<r1<r3C.r4<r2<0<r3<r1D.r2<r4<0<r1<r3解析:选A.由题图知图①与图③是正相关,故r1>0,r3>0,图②与图④是负相关,故r2<0,r4<0,且图①与图②的样本点集中在一条直线附近,因此r2<r4<0<r3<r1,故选A.3.某公司在2020年上半年的月收入x(单位:万元)与月支出y(单位:万元)的统计资料如表所示:月份1月份2月份3月份4月份5月份6月份收入x 12.314.515.017.019.820.6支出y 5.63 5.75 5.82 5.89 6.11 6.18 根据统计资料,则( )A.月收入的中位数是15,x与y有正线性相关关系B.月收入的中位数是17,x与y有负线性相关关系C.月收入的中位数是16,x与y有正线性相关关系D.月收入的中位数是16,x与y有负线性相关关系解析:选C.月收入的中位数是15+172=16,收入增加,支出增加,故x 与y 有正线性相关关系.判定两个变量相关性的方法(1)画散点图:点的分布从左下角到右上角,两个变量正相关;点的分布从左上角到右下角,两个变量负相关.(2)相关系数:当r >0时,正相关;当r <0时,负相关;|r |越接近于1,相关性越强.(3)经验回归方程:当b ^>0时,正相关;当b ^<0时,负相关.考点二 一元线性回归模型(多维探究)复习指导:经历用不同估算方法描述两个变量线性相关的过程,知道最小二乘法的思想,能根据给出的一元线性回归模型系数公式建立经验回归方程,并进一步了解回归的基本思想、方法及初步应用.角度1 经验回归方程(2022·贵州凯里第一中学高二期中)某市2017至2021年农村居民家庭人均纯收入y (单位:千元)的数据如下表:年份 2017 2018 2019 2020 2021 年份代号t12 3 4 5 人均纯收入y 3.13.53.94.64.9从表可以看出,人均纯收入y 与年份代号t 线性相关,已知i =15t i y i =64.70.(1)求y 关于t 的经验回归方程y ^=b ^t +a ^;(2)预测2025年的人均纯收入为多少.(附:参考公式:【解】 (1)由题中表格知,n =5,t -=15(1+2+3+4+5)=3,y -=15(3.1+3.5+3.9+4.6+4.9)=4,i =15t 2i =12+22+32+42+52=55,则b ^==64.7-5×3×455-5×32=0.47,a ^=y --b ^t -=4-0.47×3=2.59,故经验回归方程为y ^=0.47t +2.59.(2)当年份为2025年时,对应的年份代码t =9, 所以y ^=0.47×9+2.59=6.82, 故2025年的人均纯收入约为6.82千元. 角度2 相关系数足球是世界普及率最高的运动,我国大力发展校园足球.为了解本地区足球特色学校的发展状况,社会调查小组得到如下统计数据:年份x 2016 2017 2018 2019 2020 足球特色学校y (百个)0.30 0.60 1.00 1.40 1.70根据上表数据,计算y 与x 的相关系数r ,并说明y 与x 的线性相关程度. (已知:0.75≤|r |≤1,则认为y 与x 线性相关程度很强;0.3≤|r |<0.75,则认为y 与x 线性相关程度一般;|r |≤0.25,则认为y 与x 线性相关程度较弱.参考公式和数据:r =∑ni =1(x i -x )(y i -y )∑ni =1(x i -x )2∑ni =1(y i -y )2,∑ni =1(x i -x )2=10,∑ni =1(y i -y )2=1.3,13≈3.605 6)【解】 由题得x =2 018,y =1,所以r=∑ni=1(x i-x)(y i-y)∑ni=1(x i-x)2∑ni=1(y i-y)2=3.610 × 1.3=3.63.605 6≈0.998>0.75,所以y与x的线性相关程度很强.一元线性回归模型应用要点(1)建立经验回归方程的步骤①计算出x,y,x21+x22+…+x2n,x1y1+x2y2+…+x n y n的值;②利用公式计算参数a^,b^;③写出经验回归方程y^=b^x+a^.(2)经验回归方程的拟合效果,可以利用相关系数判断,当|r|越接近于1时,两变量的线性相关程度越强.|跟踪训练|某公司为了准确地把握市场,做好产品生产计划,对过去四年的数据进行整理得到了第x年与年销售量y(单位:万件)之间的关系如下表:x 123 4y 12284256(1)在图中画出表中数据的散点图;(2)根据散点图选择合适的回归模型拟合y与x的关系(不必说明理由);(3)建立y 关于x 的经验回归方程,预测第5年的销售量.参考公式:经验回归方程y ^=b ^x +a ^的斜率和截距的最小二乘估计分别为b ^=∑ni =1 (x i -x )(y i -y )∑ni =1 (x i -x )2=∑ni =1x i y i -nx y ∑n i =1x 2i -n x 2,a ^=y -b ^x . 解:(1)作出的散点图如图:(2)根据散点图观察,可以用一元线性回归模型拟合y 与x 的关系. (3)观察(1)中散点图可知各点大致分布在一条直线附近,列出表格:i x i y i x 2i x i y i 1 1 12 1 12 2 2 28 4 56 3 3 42 9 126 4 4 56 16 224 ∑1013830418可得x =52,y =692,所以b ^=∑4i =1x i y i -4x y ∑4i =1x 2i -4x 2=418-4×52×69230-4×⎝ ⎛⎭⎪⎫522=735,a ^=y -b ^x =692-735×52=-2.故经验回归方程为y ^=735x -2.当x =5时,y ^=735×5-2=71.故预测第5年的销售量大约为71万件.考点三 非线性回归模型(综合研析)某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x (单位:千元)对年销售量y (单位:t)和年利润z (单位:千元)的影响,对近8年的年宣传费x i 和年销售量y i (i =1,2,…,8)数据作了初步处理,得到如图所示的散点图及一些统计量的值.x y w∑8i =1(x i -x )2∑8i =1(w i -w )2∑8i =1(x i -x )·(y i -y )∑8i =1(w i -w )·(y i -y ) 46.6 563 6.8 289.81.61469108.8表中w i =x i ,w =18∑8i =1w i .(1)根据散点图判断,y =a +bx 与y =c +d x 哪一个适宜作为年销售量y 关于年宣传费x 的回归方程类型;(给出判断即可,不必说明理由)(2)根据(1)的判断结果及表中数据,建立y 关于x 的回归方程;(3)已知这种产品的年利润z 与x ,y 的关系为z =0.2y -x .根据(2)的结果回答下列问题:①当年宣传费x =49千元时,年销售量及年利润的预报值是多少? ②年宣传费x 为何值时,年利润的预报值最大?附:对于一组数据(u1,v1),(u2,v2),…,(u n,v n),其回归直线v^=a^+b^u的斜率和截距的最小二乘估计分别为:b^=∑ni=1(u i-u)(v i-v)∑ni=1(u i-u)2,a^=v-b^u.【解】(1)由散点图可以判断y=c+d x适宜作为年销售量y关于年宣传费x的回归方程类型.(2)令w=x,先建立y关于w的经验回归方程,由d^=∑8i=1(w i-w)·(y i-y)∑8i=1(w i-w)2=108.81.6=68.得c^=y-d^w=563-68×6.8=100.6.所以y关于w的经验回归方程为y^=100.6+68w,因此y关于x的非线性经验回归方程为y^=100.6+68x.(3)①由(2)知,当x=49时,年销售量y的预报值y^=100.6+6849=576.6,年利润z的预报值z^=576.6×0.2-49=66.32.②根据(2)的结果知,年利润z的预报值z^=0.2(100.6+68x)-x=-x+13.6x +20.12.所以当x=13.62=6.8,即x=46.24时,z^取得最大值.故年宣传费为46.24千元时,年利润的预报值最大.非线性回归分析问题求解策略有些非线性回归分析问题并不给出经验公式,这时我们可以画出已知数据的散点图,把它与学过的各种函数(幂函数、指数函数、对数函数等)的图象进行比较,挑选一种跟这些散点拟合得最好的函数,用适当的变量进行变换,把问题化为线性回归分析问题,使之得到解决.其一般步骤为:|跟踪训练|中国是茶的故乡,也是茶文化的发源地.中国茶的发现和利用已有四千七百多年的历史,且长盛不衰,传遍全球.为了弘扬中国茶文化,某酒店推出特色茶食品“排骨茶”,为了解每壶“排骨茶”中所放茶叶量x(单位:克)与食客的满意率y的关系,通过调查研究发现可选择函数模型y=1100e kx+c来拟合y与x的关系,根据以下数据:茶叶量x/克1234 5ln(100y) 4.34 4.36 4.44 4.45 4.51 可求得y关于x的回归方程为( )A.y^=1100e0.043x+4.291B.y^=1100e0.043x-4.291C.y^=e0.043x+4.291D.y^=e0.043x-4.291解析:选 A.由表中数据可知x-=1+2+3+4+55=3,4.34+4.36+4.44+4.45+4.515=4.42.对于A,y^=1100e0.043x+4.291化简变形可得100y^=e0.043x+4.291,两边同时取对数可得ln(100y^)=0.043x+4.291,将x-=3代入可得ln(100y^)=0.043×3+4.291=4.42,与题中数据吻合,故选项A正确;对于B,y^=1100e0.043x-4.291化简变形可得100y^=e0.043x-4.291,两边同时取对数可得ln(100y^)=0.043x-4.291,将x-=3代入可得ln(100y^)=0.043×3-4.291=-4.162≠4.42,所以选项B错误;对于C,y^=e0.043x+4.291,两边同时取对数可得ln y^= 0.043x+4.291,而表中所给数据为ln(100y^)的相关量,所以C错误;对于D,y^=e0.043x-4.291,两边同时取对数可知ln y^=0.043x-4.291,而表中所给数据为ln(100y^)的相关量,所以D错误;故选A.[A 基础达标]1.对两个变量x,y进行线性回归分析,计算得到相关系数r=-0.996 2,则下列说法中正确的是( )A.x与y正相关B.x与y具有较强的线性相关关系C.x与y几乎不具有线性相关关系D.x与y的线性相关关系还需进一步确定解析:选B.因为相关系数r=-0.996 2,所以x与y负相关,因为|r|=0.996 2,非常接近1,所以相关性很强,故选B.2.(2022·四川省彭山一中高三入学考试)下列命题错误的是( )A.线性相关系数r越大,两个变量的线性相关性越强;反之,线性相关性越弱B.抛掷均匀硬币一次,出现正面的次数是随机变量C.将一组数据中的每个数据都乘以同一个非零常数a后,标准差也变为原来的a倍D.若回归直线的斜率估计值为0.25,x=2,y=3,则回归直线的方程为y=0.25x+2.5解析:选A.对于A,线性相关系数|r|越接近于1,则相关性越强,所以A错误;对于B,抛掷均匀硬币一次,出现正面的次数是随机变量,所以B正确;对于C,由标准差的定义可知将一组数据中的每个数据都乘以同一个非零常数a后,标准差也变为原来的a倍,所以C正确;对于D,因为回归直线的斜率估计值为0.25,x=2,y=3,所以b^=0.25,a^=y-b^x=3-2×0.25=2.5,则回归直线的方程为y=0.25x+2.5,所以D 正确.3.(多选)(2022·重庆巴蜀中学高三月考)为了建立茶水温度y随时间x变化的函数模型,小明每隔1分钟测量一次茶水温度,得到若干组数据(x1,y1),(x2,y2),…,(x n,y),绘制了如图所示的散点图.小明选择了如下2个函数模型来拟合茶水温度y随时间nx的变化情况,函数模型一:y=kx+b(k<0,x≥0);函数模型二:y=ka x+b(k>0,0<a<1,x≥0),下列说法正确的是( )A.变量y与x具有负的相关关系B.由于水温开始降得快,后面降得慢,最后趋于平缓,因此模型二能更好的拟合茶水温度随时间的变化情况C.若选择函数模型二,利用最小二乘法求得y=ka x+b的图象一定经过点(x-,y-)D.当x=5时,通过函数模型二计算得y=65.1,用温度计测得实际茶水温度为65.2,则残差为0.1解析:选ABD.观察散点图,变量x与y具有负的相关关系,A正确;由于函数模型二中的函数y=ka x+b(k>0,0<a<1,x≥0),在x≥0时,函数单调递减,可得B正确;若选择函数模型二,利用最小二乘法求出的回归方程一定经过(a x,y),C错误;由于残差=真实值-预测值,因此残差为65.2-65.1=0.1,故D正确.4.经调查某地若干户家庭的年收入x(万元)和年饮食支出y(万元)具有线性相关关系,并得到y关于x的经验回归方程:y^=0.245x+0.321,可知,家庭年收入每增加1万元,年饮食支出平均增加________万元.解析:x变为x+1,y^=0.245(x+1)+0.321=0.245x+0.321+0.245,因此家庭年收入每增加1万元,年饮食支出平均增加0.245万元.答案:0.2455.(2022·合肥检测)某公司一种型号的产品近期销售情况如下表:根据上表可得到经验回归方程y^=0.75x+a^,据此估计,该公司7月份这种型号产品的销售额为________万元.解析:由题意,x=2+3+4+5+65=4,y=15.1+16.3+17.0+17.2+18.45=16.8,经验回归直线y^=0.75x+a^过(x,y),可得a^=13.8,当x=7时,可得y^=0.75×7+13.8=19.05.答案:19.056.(2020·高考全国卷Ⅱ)某沙漠地区经过治理,生态系统得到很大改善,野生动物数量有所增加.为调查该地区某种野生动物的数量,将其分成面积相近的200个地块,从这些地块中用简单随机抽样的方法抽取20个作为样区,调查得到样本数据(x i,yi)(i=1,2,…,20),其中x i和y i分别表示第i个样区的植物覆盖面积(单位:公顷)和这种野生动物的数量,并计算得∑20i =1x i =60,∑20i =1y i =1 200,∑20i =1(x i -x )2=80,∑20i =1(y i -y )2=9 000,∑20i =1(x i -x )(y i -y )=800.(1)求该地区这种野生动物数量的估计值(这种野生动物数量的估计值等于样区这种野生动物数量的平均数乘以地块数);(2)求样本(x i ,y i )(i =1,2,…,20)的相关系数(精确到0.01);(3)根据现有统计资料,各地块间植物覆盖面积差异很大.为提高样本的代表性以获得该地区这种野生动物数量更准确的估计,请给出一种你认为更合理的抽样方法,并说明理由.附:相关系数r =∑ni =1(x i -x )(y i -y )∑ni =1 (x i -x )2∑ni =1(y i -y )2,2≈1.414.解:(1)由已知得样本平均数y =120∑20i =1y i =60,从而该地区这种野生动物数量的估计值为60×200=12 000.(2)样本(x i ,y i )(i =1,2,…,20)的相关系数r =∑20i =1(x i -x )(y i -y )∑20i =1 (x i -x )2∑20i =1(y i -y )2=80080×9 000=223≈0.94.(3)分层随机抽样:根据植物覆盖面积的大小对地块分层,再对200个地块进行分层随机抽样.理由如下:由(2)知各样区的这种野生动物数量与植物覆盖面积有很强的正相关.由于各地块间植物覆盖面积差异很大,从而各地块间这种野生动物数量差异也很大,采用分层随机抽样的方法较好地保持了样本结构与总体结构的一致性,提高了样本的代表性,从而可以获得该地区这种野生动物数量更准确的估计.7.某品牌手机厂商推出新款的旗舰机型,并在某地区跟踪调查得到这款手机上市时间(x 个月)和市场占有率(y %)的几组相关对应数据:(1)根据上表中的数据,用最小二乘法求出y 关于x 的经验回归方程;(2)根据上述经验回归方程,分析该款旗舰机型市场占有率的变化趋势,并预测自上市起经过多少个月,该款旗舰机型市场占有率能超过0.5%(精准到月).解:(1)根据表中数据,计算x -=15×(1+2+3+4+5)=3,y -=15×(0.02+0.05+0.1+0.15+0.18)=0.1,所以b ^=1×0.02+2×0.05+3×0.1+4×0.15+5×0.18-5×3×0.112+22+32+42+52-5×32=0.042,所以a ^=0.1-0.042×3=-0.026, 所以经验回归方程为y ^=0.042x -0.026.(2)由上面的经验回归方程可知,上市时间与市场占有率正相关, 即上市时间每增加1个月,市场占有率都增加0.042个百分点; 由y ^=0.042x -0.026>0.5, 解得x ≥13;预计上市13个月时,该款旗舰机型市场占有率能超过0.5%.[B 综合应用]8.(2022·河南省湘豫名校联盟高三联考)如下表,根据变量x 与y 之间的对应数据可求出y ^=-0.32x +b .其中y -=8.现从这5个样本点对应的残差中任取一个值,则残差不大于0的概率为( )A.15B.25C.35D.45解析:选C.由表中的数据可知,x =10+15+20+25+305=20,设y 的最后一个数据为n ,则y =11+10+8+6+n5=8,所以n =5,将x ,y 代入y ^=-0.32x +b 得b =14.4, 这5个样本点对应的残差分别为:y 1-y ^1=11-(-0.32×10+14.4)=-0.2, y 2-y ^2=10-(-0.32×15+14.4)=0.4, y 3-y ^3=8-(-0.32×20+14.4)=0, y 4-y ^4=6-(-0.32×25+14.4)=-0.4, y 5-y ^5=5-(-0.32×30+14.4)=0.2, 所以残差不大于0的概率为35.9.(多选)(2022·石家庄市藁城新冀明中学阶段性测试)某市对2016年至2020年这五年间全市烧烤店盈利店铺的个数进行了统计,具体统计数据如下表所示:根据所给数据,得出y 关于t 的经验回归方程为y ^=b ^t +273,则下列说法正确的是( )A .该市2016年至2020年全市烧烤店盈利店铺个数的平均数y =219B .y 关于t 的经验回归方程为y ^=-18t +273 C .估计该市2022年烧烤店盈利店铺的个数为147D .预测从2027年起,该市烧烤店盈利店铺的个数将不超过100解析:选ABC.由已知数据得t -=3,y -=219,故A 正确;因为y 关于t 的经验回归直线过点(3,219),所以219=3b ^+273,所以b ^=-18,所以y 关于t 的经验回归方程为y ^=-18t +273.故B 正确;2022年的年份代码为7,故2022年该市烧烤店盈利店铺的个数约为y ^=-18×7+273=147.故C 正确;令-18t +273≤100,由t ∈N *,得t ≥10,故从2025年起,该市烧烤店盈利店铺的个数将不超过100.故D 不正确,故选ABC.[C 素养提升]10.(2022·江苏省南通市高三教学质量监测)紫甘薯对环境温度要求较高,根据以往的经验,随着温度的升高,其死亡株数呈增长的趋势.下表给出了2019年种植的一批试验紫甘薯在温度升高时6组死亡的株数.经计算,x =16∑i =16 x i =26,y =16∑i =16y i =33,∑i =16 (x i -x )·(y i -y )=557,∑i =16(x i -x )2=84,∑i =16 (y i -y )2=3 930,∑i =16(y i -y ^i )2=236.64,e 8.060 5≈3 167,其中x i ,y i 分别为试验数据中的温度和死亡株数,i =1,2,3,4,5,6.(1)若用一元线性回归模型,求y 关于x 的经验回归方程y ^=b ^x +a ^(结果精确到0.1);(2)若用非线性回归模型求得y 关于x 的非线性经验回归方程y ^=0.06e 0.230 3x ,且决定系数为R 2=0.884 1.①试与(1)中的回归模型相比,用R2说明哪种模型的拟合效果更好;②用拟合效果好的模型预测温度为35 ℃时该批紫甘薯的死亡株数(结果取整数).解:(1)由题意,得b^=∑i=16(x i-x-)(y i-y-)∑i=16(x i-x-)2=55784≈6.6,所以a^=33-6.6×26=-138.6,所以y关于x的经验回归方程为y^=6.6x-138.6. (2)①经验回归方程y^=6.6x-138.6对应的决定系数为R2=1-∑i=16(y i-y^i)∑i=16(y i-y-)2=1-236.643 930≈0.939 8,因为0.939 8>0.884 1,所以经验回归方程y^=6.6x-138.6比非线性经验回归方程y^=0.06e0.230 3x的拟合效果更好.②当x=35时,y=6.6×35-138.6=92.4≈92,即当温度为35 ℃时,该批紫甘薯的死亡株数为92.21 / 21。
二次函数的线性关系与相关性

二次函数的线性关系与相关性二次函数是一类常见且重要的数学函数,其表达式为y = ax^2 + bx+ c,其中a、b、c为实数且a ≠ 0。
本文将探讨二次函数中的线性关系以及相关性。
一、线性关系与二次函数线性关系是指函数中的变量呈现出直线关系的特点。
在二次函数中,我们可以通过简单的变换找到与二次项无关的线性关系。
例如,考虑二次函数y = ax^2 + bx + c,当我们对x进行平移变换,令x - h = X,则问题可以转换为求关于X的二次函数,即y = a(X + h)^2 + b(X + h) + c= aX^2 + (2ah + b)X + (ah^2 + bh + c)此时,原函数y = ax^2 + bx + c与新函数y = aX^2 + (2ah + b)X + (ah^2 + bh + c)呈现出线性关系。
二、相关性与二次函数相关性是指变量之间的相互关系程度。
在二次函数中,我们可以通过对函数图像的观察来判断其相关性。
1. 当a > 0时,二次函数开口向上,形成一个U型曲线。
此时,随着x的增大,y也随之增大,二者呈正向相关。
反之,随着x的减小,y也随之减小。
即二次函数的相关性与自变量x的取值方向一致。
2. 当a < 0时,二次函数开口向下,形成一个倒U型曲线。
此时,随着x的增大,y反而减小,二者呈负向相关。
反之,随着x的减小,y反而增大。
即二次函数的相关性与自变量x的取值方向相反。
三、实例分析为了更好地理解二次函数的线性关系与相关性,我们以一个实例进行分析。
假设有一个二次函数y = 2x^2 - 3x + 1。
1. 线性关系:我们进行平移变换,令x - 1 = X,则函数变为y = 2(X + 1)^2 - 3(X + 1) + 1 = 2X^2 - 1,此时与原二次函数呈现出线性关系。
2. 相关性:由于a = 2 > 0,因此函数开口向上,与自变量x的取值方向一致,呈正向相关。
相关性、最小二乘估计、回归分析与独立性检验

【例1】关于人体的脂肪含量(百分比)和年龄关系的研究中, 得到如下一组数据:
年龄 23 27 39 41 45 49 50 51 脂肪 9.5 17.8 21.2 25.9 27.5 26.3 28.2 29.6 含量 判断它们是否有相关关系.
【解题指南】判断有无相关关系,一种常用的简便方法就是绘 制散点图. 【规范解答】本题涉及两个变量:年龄与脂肪含量,可以以年 龄为自变量,考查脂肪含量的变化趋势,分析相关关系通常借 助散点图.
高(x) 60
62 64 65
66 67
68
70 72 74
儿子身 63.6 65.2 66 65.5 66.9 67.1 67.4 68.3 70.1 70 高(y)
①画出散点图,说明变量y与x的相关性;
②如果y与x之间具有线性相关关系,求线性回归方程.
(已知:
2
x=66.8,y=67.01,x
【即时应用】
(1)由一组样本数据(x1,y1),(x2,y2),…,(xn,yn)得到回 归直线方程y=a+bx,判断下面说法是否正确.(请在括号内打
“√”或“×”)
①任何一组观测值都能得到具有代表意义的回归直线方程;
()
②直线y=a+bx至少经过点(x1,y1),(x2,y2),…,(xn,yn)
(2)x与y的增长速度之比即约为回归方程的斜率的倒数
1 10 5 . 4.4 44 22
答案:(1)①× ②× ③√ ④√ (2)
5
22
3.独立性检验
(1)2×2列联表
设A,B为两个变量,每一个变量都可以取两个值,变量A:A1,
A2= A1 ;变量B:B1,B2= B1,通过观察得到如表所示的数据:
【高考数学总复习】:回归性分析与独立性检验(知识点讲解+真题演练+详细解答)
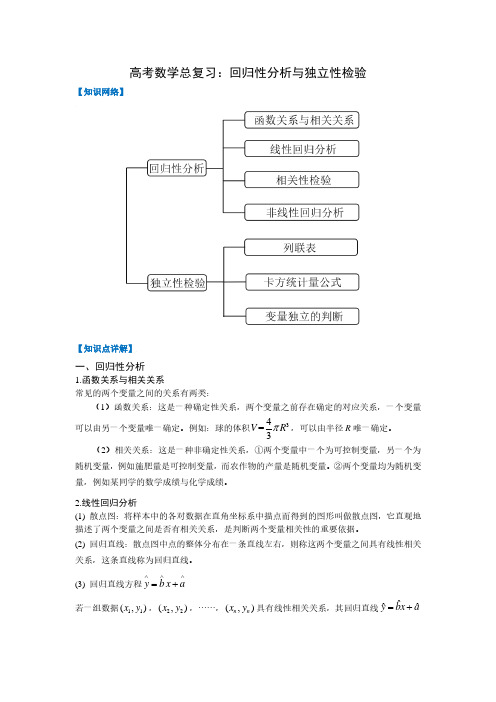
量,例如某同学的数学成绩与化学成绩。
2.线性回归分析 (1) 散点图:将样本中的各对数据在直角坐标系中描点而得到的图形叫做散点图,它直观地 描述了两个变量之间是否有相关关系,是判断两个变量相关性的重要依据。 (2) 回归直线:散点图中点的整体分布在一条直线左右,则称这两个变量之间具有线性相关
(a b)(c d)(a c)(b d )
通过对统计量 K2 的研究,一般情况下认为:
①当 K 2 ≤3.841 时,认为变量 X 与 Y 是无关的。
②当 K 2 >3.841 时,有 95%的把握说变量 X 与 Y 有关;
④ 当 K 2 >6.635 时,有 99%的把握说变量 X 与 Y 有关;
定在多大程度上可以认为“两个分类变量有关系”的方法称为两个分类变量的独立性检验。
2.分类变量的理解: 分类变量是说明事物类别的一个名称,其取值是分类数据。如“性别”就是一个分类变 量,其变量值为“男”或“女”;“行业”也是一个分类变量,其变量值可以为“零售 业”,说明 X 与 Y 无关的把握越小
6. 右表是对与喜欢足球与否的统计列联表依据表中的数据,得到( )
A. K 2 9.564 B. K 2 3.564 C. K 2 2.706 D. K 2 3.841
7. 对两个分类变量 A、B 的下列说法中正确的个数为( ). ①A 与 B 无关,即 A 与 B 互不影响;②A 与 B 关系越密切,则 K2 的值就越大;③K2
x yw
46.6 563 6.8
8
(xi x )2
i 1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
函数线性相关与无关的判断方法
判断函数集合中的函数是否线性相关或线性无关,可以使用以下方法:
1. 解线性方程组:对于给定的函数集合,可以将其表示为一个线性方程组,然后解该方程组,如果方程组存在非零解,则函数集合线性相关;反之,如果方程组只有零解,则函数集合线性无关。
2. 行列式判断法:对于一个函数集合,可以构造一个矩阵,将函数依次作为矩阵的行或列。
然后计算该矩阵的行列式,如果行列式的值不为零,则函数集合线性无关;反之,如果行列式的值为零,则函数集合线性相关。
3. 线性组合判断法:对于给定的函数集合,可以尝试找到一组不全为零的系数,使得函数集合中的函数的线性组合等于零函数。
如果能找到这样的系数,则函数集合线性相关;反之,如果不存在这样的系数,则函数集合线性无关。
4. 维数判断法:对于一个函数集合,在向量空间中可以将其表示为向量的形式。
如果该函数集合所生成的向量空间的维数等于函数集合中函数的个数,则函数集合线性无关;反之,如果向量空间的维数小于函数集合中函数的个数,则函数集合线性相关。
