大学物理3第10章习题分析与解答
大学物理3第11章习题分析与解答
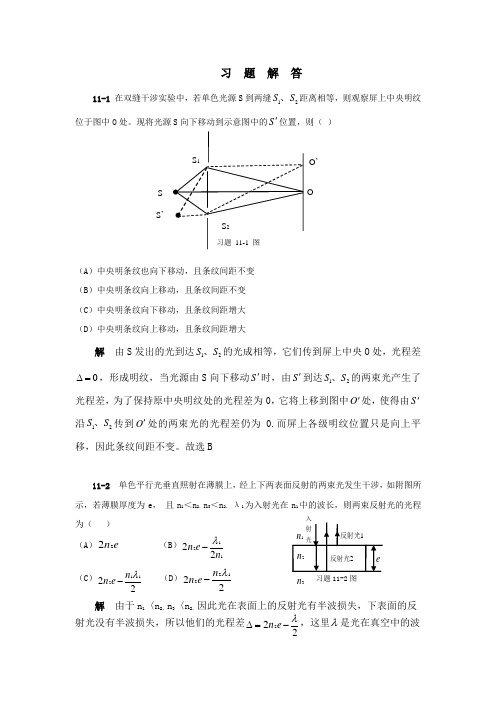
习 题 解 答11-1 在双缝干涉实验中,若单色光源S 到两缝21S S 、距离相等,则观察屏上中央明纹位于图中O 处。
现将光源S 向下移动到示意图中的S '位置,则( )(A )中央明条纹也向下移动,且条纹间距不变 (B )中央明条纹向上移动,且条纹间距不变 (C )中央明条纹向下移动,且条纹间距增大 (D )中央明条纹向上移动,且条纹间距增大解 由S 发出的光到达21S S 、的光成相等,它们传到屏上中央O 处,光程差0=∆,形成明纹,当光源由S 向下移动S '时,由S '到达21S S 、的两束光产生了光程差,为了保持原中央明纹处的光程差为0,它将上移到图中O '处,使得由S '沿21S S 、传到O '处的两束光的光程差仍为0.而屏上各级明纹位置只是向上平移,因此条纹间距不变。
故选B11-2 单色平行光垂直照射在薄膜上,经上下两表面反射的两束光发生干涉,如附图所示,若薄膜厚度为e , 且n 1<n 2,n 3<n 2, λ1为入射光在n 1中的波长,则两束反射光的光程为( )(A )e n 22 (B )11222n e n λ-(C )22112λn e n - (D )22122λn e n -习题11-2图解 由于n 1〈n 2,n 3〈n 2,因此光在表面上的反射光有半波损失,下表面的反射光没有半波损失,所以他们的光程差222λ-=∆e n ,这里λ是光在真空中的波3n S S ’OO ’长,与1λ的关系是11λλn =。
故选C11-3 如图所示,两平面玻璃板构成一空气劈尖,一平面单色光垂直入射到劈尖上,当A 板与B 板的夹角θ增大时,干涉图样将发生( )变化 (A )干涉条纹间距增大,并向O 方向移动 (B )干涉条纹间距减小,并向B 方向移动 (C )干涉条纹间距减小,并向O 方向移动 (D )干涉条纹间距增大,并向B 方向移动解 空气劈尖干涉条纹间距θλsin 2n l =∆,劈尖干涉又称为等厚干涉,即k相同的同一级条纹,无论是明纹还是暗纹,都出现在厚度相同的地方. 当A 板与B 板的夹角θ增大时,△l变小. 和原厚度相同的地方向顶角方向移动,所以干涉条纹向O 方向移动。
2016第十章 热力学习题课

第 九 章 气 体 动 理 论
m i 3 E RT 10 8.311 124.7( J ) M 2 2
Q E W 124.7 209 84.3(J )
31
普 通 物 理 教 程
第十章 热力学习题
6. 一定量的某种理想气体在等压过程中对外作 功为 200 J.若此种气体为单原子分子气体 ,则该过程中需吸热___________ J;若为 双原子分子气体,则需吸热___________ J. 【分析与解答】
第 九 章 气 体 动 理 论
1
普 通 物 理 教 程
第十章 热力学习题
【分析与解答】 m i 因为 QV R T
M 2
第 九 章 气 体 动 理 论
m pV = RT M
氧气和水蒸气的自由度不同,吸收热量相等 则温度升高不同,压强增加亦不同。 正确答案是B。
,
2
普 通 物 理 教 程
第十章 热力学习题
WN2 WHe
p(V2 V1 ) TN2 5 p(V2 V1 ) THe 7
正确答案是B。
10
普 通 物 理 教 程
第十章 热力学习题
6. 一定量的理想气体,由初态a经历a c b过程到达终态b(如 图10-19示),已知a、b两状态处于同一条绝热线上,则 ______. (A)内能增量为正,对外作功为正,系统吸热为正。 (B)内能增量为负,对外作功为正,系统吸热为正。 (C)内能增量为负,对外作功为正,系统吸热为负。 (D)不能判断。
内能增加了ΔE = | W2 |
E = ;
Q=
第 九 章 气 体 动 理 论
29
普 通 物 理 教 程
第十章 热力学习题
大学物理《普通物理学简明教程》振动、波动和光学习题精解概要

A1 φ0A2
π/4x
O
图10-17
解(1)如图10-17,两矢量间夹角为 ,所以合振动振幅
合振动初相
(2)合振动A再与第三个振动合成.根据振动叠加条件, 时合振动有极大值,即
(k=0,1,2…)
当 时合振动有极小值,即
(k=0,1,2…)
10-19当两个同方向的简谐振动合成为一个振动时,其振动表式为:
3应用同一直线上两个简谐振动的合成规律时,要特别注意它们的相位差和合成的振幅的关系;同向时,合振幅最大,反向时,合振幅最小。
10.4思考题选答
1弹簧振子的无阻尼自由振动是简谐振动,同一弹簧振子在简谐驱动力持续作用下的稳态受迫振动也是简谐振动,这两种简谐运动有什么区别?
答:弹簧振子的无阻尼自由振动是在“无阻尼”,包括没有空气等外界施加的阻力和弹簧内部的塑性因素引起的阻力的情况下发生的,是一种理想情况。由于外界不能输入能量,所以弹簧振子的机械能守恒。这时振动的频率由弹簧振子自身的因素( )决定。
解:(1)根据振动方程可知:振幅 ,角率 ,初相 ,周期 =1秒;(2)分析质点运动情况:从t=0时刻起, ;向 轴负方向运动,直到 ,即 为止;质点改变运动方向,向 轴正方向运动到位置P点。最短时间间隔为:
(3) 处的时刻。
第11章机械波基础
答:从质量的意义上来说,质量表示物体的惯性,弹簧本身的质量计入时,系统的质量增大,更不易改变运动状态。对不断地周期性改变运动状态的弹簧振
子的简谐运动来说,其进程一定要变慢。这就是说,考虑弹簧的质量时,弹簧振子的振动周期将变大。
10.5习题解答
10-1质量为10g的小球与轻弹簧组成的系统,按 的规律而振动,式中t以s为单位,试求:
式中t以s为单位。求各分振动的角频率和合振动的拍的周期。
大物习题解答-大学物理习题答案(许瑞珍_贾谊明)-第3章 刚体力学

第三章 刚体力学3-1 一通风机的转动部分以初角速度ω0绕其轴转动,空气的阻力矩与角速度成正比,比例系数C 为一常量。
若转动部分对其轴的转动惯量为J ,问:(1)经过多少时间后其转动角速度减少为初角速度的一半?(2)在此时间内共转过多少转? 解:(1)由题可知:阻力矩ωC M -=,又因为转动定理 dtd JJ M ωβ== dtd JC ωω=-∴ dt JC d t ⎰⎰-=∴00ωωωω t JC-=0lnωω t JCe-=0ωω当021ωω=时,2ln CJt =。
(2)角位移⎰=tdt 0ωθ⎰-=2ln 00C J t JC dt eωCJ 021ω=,所以,此时间内转过的圈数为CJ n πωπθ420==。
3-2 质量面密度为σ的均匀矩形板,试证其对与板面垂直的,通过几何中心的轴线的转动惯量为)(1222b a ab J +σ=。
其中a ,b 为矩形板的长,宽。
证明一:如图,在板上取一质元dxdy dm σ=,对与板面垂直的、通过几何中心的轴线的转动惯量为 dm r dJ ⎰=2dxdy y x a a b b σ⎰⎰--+=222222)()(1222b a ab +=σ证明二:如图,在板上取一细棒bdx dm σ=,对通过细棒中心与棒垂直的转动轴的转动惯量为2121b dm ⋅,根据平行轴定理,对与板面垂直的、通过几何中心的轴线的转动惯量为22)2(121x adm b dm dJ -+⋅=dx x ab dx b 23)2(121-+=σσ 33121121ba a b dJ J σσ+==∴⎰)(1222b a ab +=σ3-3 如图3-28所示,一轻绳跨过两个质量为m 、半径为r 的均匀圆盘状定滑轮,绳的两端分别挂着质量为m 2和m 的重物,绳与滑轮间无相对滑动,滑轮轴光滑,求重物的加速度和各段绳中的张力。
解:受力分析如图ma T mg 222=- (1) ma mg T =-1 (2) βJ r T T =-)(2 (3) βJ r T T =-)(1 (4)βr a =,221mr J =(5) 联立求出g a 41=, mg T 811=,mg T 451=,mg T 232=3-4 如图3-29所示,一均匀细杆长为L ,质量为m ,平放在摩擦系数为μ的水平桌面上,设开始时杆以角速度0ω绕过细杆中心的竖直轴转动,试求:(1)作用于杆的摩擦力矩;(2)经过多长时间杆才会停止转动。
10 热力学基础 习题分析与解答 第二版

第10章 热力学基础 习题解答(一). 选择题1. 1摩尔氧气和1摩尔水蒸气(均视为刚性分子理想气体),在体积不变的情况下吸收相等的热量,则它们的:(A )温度升高相同,压强增加相同。
(B )温度升高不同,压强增加不同。
(C )温度升高相同,压强增加不同。
(D )温度升高不同,压强增加相同 。
[ ] 【分析与解答】因为2V m iQ R T M =∆,p nkT=氧气和水蒸气的自由度不同,吸收热量相等,则温度升高不同,压强增加亦不同。
正确答案是B 。
2. 一定量理想气体,从状态A 开始,分别经历等压、等温、绝热三种过程(AB 、AC 、AD ),其容积由V1都膨胀到2V1,其中 。
(A) 气体内能增加的是等压过程,气体内能减少的的是等温过程。
(B) 气体内能增加的是绝热过程,气体内能减少的的是等压过程。
(C) 气体内能增加的是等压过程,气体内能减少的的是绝热过程。
(D) 气体内能增加的是绝热过程,气体内能减少的的是等温过程。
[ ] 【分析与解答】正确答案是C 。
3. 如图所示,一定量的理想气体,沿着图10-18中直线从状态a( 压强p1 = 4 atm ,体积V1=2 L )变到状态b ( 压强p2 =2 atm ,体积V2 =4 L ).则在此过程中: (A ) 气体对外做正功,向外界放出热量. (B ) 气体对外做正功,从外界吸热. (C ) 气体对外做负功,向外界放出热量. (D ) 气体对外做正功,内能减少. [ ]p (atm)P 图10-18 【分析与解答】 因为a ab b p V p V =,a b T T =,内能变化为零,吸热等于做功,而此过程为单向体积膨胀过程,系统对外做正功,从外界吸热。
正确答案是B 。
4. 若在某个过程中,一定量的理想气体的内能E 随压强p 的变化关系为一直线(其延长线过E -p 图10-19的原点),则该过程为:(A ) 等温过程 (B ) 等压过程 (C ) 等体过程 (D ) 绝热过程 [ ]图10-19【分析与解答】因为22m i iE RT pV M ==,p 与V 成线性关系,故为等体过程。
大学物理3第11章习题分析与解答

大学物理3第11章习题分析与解答-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN习 题 解 答11-1 在双缝干涉实验中,若单色光源S 到两缝21S S 、距离相等,则观察屏上中央明纹位于图中O 处。
现将光源S 向下移动到示意图中的S '位置,则( )(A )中央明条纹也向下移动,且条纹间距不变 (B )中央明条纹向上移动,且条纹间距不变 (C )中央明条纹向下移动,且条纹间距增大 (D )中央明条纹向上移动,且条纹间距增大解 由S 发出的光到达21S S 、的光成相等,它们传到屏上中央O 处,光程差0=∆,形成明纹,当光源由S 向下移动S '时,由S '到达21S S 、的两束光产生了光程差,为了保持原中央明纹处的光程差为0,它将上移到图中O '处,使得由S '沿21S S 、传到O '处的两束光的光程差仍为0.而屏上各级明纹位置只是向上平移,因此条纹间距不变。
故选B11-2 单色平行光垂直照射在薄膜上,经上下两表面反射的两束光发生干涉,如附图所示,若薄膜厚度为e , 且n 1<n 2,n 3<n 2, λ1为入射光在n 1中的波长,则两束反射光的光程为( )(A )e n 22 (B )11222n e n λ-3n S S ’OO ’(C )22112λn e n - (D )22122λn e n - 习题11-2图解 由于n 1〈n 2,n 3〈n 2,因此光在表面上的反射光有半波损失,下表面的反射光没有半波损失,所以他们的光程差222λ-=∆e n ,这里λ是光在真空中的波长,与1λ的关系是11λλn =。
故选C11-3 如图所示,两平面玻璃板构成一空气劈尖,一平面单色光垂直入射到劈尖上,当A 板与B 板的夹角θ增大时,干涉图样将发生( )变化(A )干涉条纹间距增大,并向O 方向移动 (B )干涉条纹间距减小,并向B 方向移动 (C )干涉条纹间距减小,并向O 方向移动 (D )干涉条纹间距增大,并向B 方向移动解 空气劈尖干涉条纹间距θλsin 2n l =∆,劈尖干涉又称为等厚干涉,即k相同的同一级条纹,无论是明纹还是暗纹,都出现在厚度相同的地方. 当A 板与B 板的夹角θ增大时,△l变小. 和原厚度相同的地方向顶角方向移动,所以干涉条纹向O 方向移动。
大学物理第3章习题解答

第三章 刚体的定轴转动3-1掷铁饼运动员手持铁饼转动1.25圈后松手,此刻铁饼的速度值达到125-⋅=s m v 。
设转动时铁饼沿半径为R=1.0 m 的圆周运动并且均匀加速。
求: (1)铁饼离手时的角速度; (2)铁饼的角加速度;(3)铁饼在手中加速的时间(把铁饼视为质点)。
解:(1)铁饼离手时的角速度为(rad/s)250125===.//R v ω(2)铁饼的角加速度为)(rad/s 83925122252222..=⨯⨯==πθωα(3)铁饼在手中加速的时间为(s)628025251222..=⨯⨯==πωθt3-2一汽车发动机的转速在7.0s 内由2001min -⋅r 均匀地增加到3001min -⋅r 。
(1)求在这段时间内的初角速度和末角速度以及角加速度; (2)求这段时间内转过的角度和圈数;(3)发动机轴上装有一半径为r=0.2m 的飞轮,求它的边缘上一点在第7.0s 末的切向加速度、法向加速度和总加速度。
解:(1)初角速度为(rad/s)9206020020./=⨯=πω末角速度为(rad/s)3146030002=⨯=/πω角加速度为)(rad/s 9410792031420...=-=-=tωωα(2)转过的角度为)186(rad 1017172314920230圈=⨯=⨯+=+=..t ωωθ(3)切向加速度为)(m/s 388209412t ...=⨯==R a α法向加速度为)(m /s 10971203142422n ⨯=⨯==..R a ω总加速度为)(m/s 10971)10971(378242422n 2t ⨯=⨯+=+=...a a a总加速度与切向的夹角为9589378101.97arctan arctan 4t n '︒=⨯==.a a θ3-3 如图所示,在边长为a 的六边形顶点上分别固定有质量都是m 的6个小球(小球的直径a d <<)。
大学物理习题分析与解答

大学物理1 习题分析与解答 第1章 质点运动学习题分析与解答1.1 云室为记录带电粒子轨迹的仪器。
当快速带电粒子射入云室时,在其经过的路径上产生离子,使过饱和蒸气以离子为核心凝结成液滴,从而可采用照相方法记录该带电粒子的轨迹。
若设作直线运动带电粒子的运动方程为: (SI 单位),12C C α、、均为常量,并在粒子进入云室时计时,试描述其运动情况.解:分析 本题为一维直线运动问题,为已知运动学方程求带电粒子其他物理量的问题,属于运动学第一类问题,该类问题可直接应用求导方法处理。
即由带电粒子运动学方程对时间t 求导得到带电粒子的速度、加速度,进一步得到其初、终状态的位置、速度、加速度等运动学信息。
作如图1.1所示一维坐标系,选择计时处为坐标原点,则有Ox图1.1 1.1题用图12222e d e d d e d t tt x C C xv C t v a C vtαααααα---=-∴====-=- (1.1.1) 故带电粒子的初始状态为 2012020200t x C C v C a C v ααα=⇒=-==-=-、、 (1.1.2) 带电粒子的最终状态为 100t x C v a ∞∞∞=∞⇒===、、 (1.1.3) 讨论:(1)由(1.1.1)式知,粒子进入云室后作减速运动,其加速度为速度的一次函数;(2)由(1.1.2)式得到粒子的初始位置、初始速度和初始加速度; (3)由(1.1.3)式得到粒子的终态位置、终态速度和终态加速度;(4)由(1.1.1)式的加速度、速度及初始条件,对时间t 积分可得速度和运动学方程,此类问题属于运动学第二类问题,一般可直接应用积分方法处理。
1.2 将牛顿管抽为真空且垂直于水平地面放置,如图1.2所示自管中O 点向上抛射小球又落至原处用时2t ,球向上运动经h 处又下落至 h 处用时1t 。
现测得1t 、2t 和 h ,试由此确定当地重力加速度的数值.解:分析 本题为匀加速直线运动问题,由该类问题的运动学方程出发即可求解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习 题 解 答10-1 把单摆摆球从平衡位置向位移正方向拉开,是摆线与竖直方向成一微小角度θ,然后由静止放手任其振动,从放手时开始计时.若用余弦函数表示其运动方程,则该单摆振动的初相为( )(A) 2π (B )π/2 (C)0 (D)θ解 由已知条件可知其初始时刻的位移正向最大。
利用旋转矢量图可知,初相相位是0.故选C10-2 如图所示,用余弦函数描述一简谐振动。
已知振幅为A ,周期为T ,初相3πϕ-=,则振动曲线为( )解 由已知条件可知初始时刻振动的位移是23co s AA y =⎪⎭⎫ ⎝⎛-=π,速度是()A t A v ωϕωω23sin =+-=,方向是向y 轴正方向,则振动曲线上0=t 时刻的斜率是正值。
故选A10-3 已知某简谐振动的振动曲线和旋转矢量图如附图(a )、(b )所示,位移的单位为厘米,时间单位为秒,则此简谐振动的振动方程为( ) (A )cm t x ⎪⎭⎫⎝⎛+=ππ3232cos 2 (B )cm t x ⎪⎭⎫ ⎝⎛-=ππ3232cos 2(C)cm t x ⎪⎭⎫ ⎝⎛-=ππ3234cos 2 (D )cm t x ⎪⎭⎫ ⎝⎛+=ππ3234cos 2习题10-3图习题 10-2 图解 由振动图像可知,初始时刻质点的位移是2A-,且向y 轴负方向运动,附图(b )是其对应的旋转矢量图,由图可知,其初相位是π32,振动曲线上给出了质点从2A -到A 的时间是s 1,其对应的相位从π32变化到π2,所以它的角速度1-s rad 32T 2⋅==ππω 简谐振动的振动方程为⎪⎭⎫ ⎝⎛+=ππ3234cos 2t x故选D10-4 弹簧振子做简谐振动,已知此振子势能的最大值为100J,当振子处于最大位移的一半时其动能为( )(A )25J (B )50J (C)75J (D)100J解 物体做简谐运动时,振子势能的表达式是221kx E P =,其动能和势能都随时间做周期性变化,物体通过平衡位置时,势能为零,动能达到最大值;位移最大时,势能达到最大值221kA E P =,动能为零,但其总机械能却保持不变.当振子处于最大位移的一半时其势能为2281)2(21'kA A k E p ==,所以此时的动能是J J J kA kA kA E k 754310043218121222=⨯=⨯=-=故选C10-5 一质点作简谐振动,速度最大值Vm=0.05m/s ,振幅A=2cm.若令速度具有正最大值的那一时刻为t=0,则振动表达式为 。
解 速度的最大值105.0-⋅==s m A v m ω,A =0.02m,所以)(5.202.005.01-⋅===s rad A v m ω 振动的一般表达式)cos(ϕω+=t A x ,现在只有初相位没确定,速度具有正最大值时位于原点处,由旋转矢量法可知2πϕ-=,振动的表达式为m t y )25.2cos(02.0π-=.10-6 已知一个谐振子的振动曲线如图(a)、对应的旋转矢量图(b )所示,求:a 、b 、c 、d 、e 各点状态的相位分别为 。
解 结合旋转矢量图附图(b),振动曲线上的a,b,c,d,e 对应旋转矢量图上的e d c b a '''''、、、、,所以其相位分别是3432230ππππ、、、、10-7 一简谐振动的旋转矢量如图所示,振幅矢量长2cm,则该简谐振动的初相为 ,振动方程为 。
解 振动方程的一般表达式是)cos(ϕω+=t A x ,ϕ是指t = 0时对应的相位,也是初相位,由图可知t=0时的角度是4π,所以该简谐振动的初相为4π.角速度是ππθω===ttt ,代入振动方程可得到)4cos(02.0ππ+=t x (m).10-8 质点的振动曲线如图所示。
试求: (1)振动表达式(2)点P 对应的相位(3)到达点P 对应位置所需时间。
解 (1)根据振动曲线对应的旋转振幅矢量可知,初相03πϕ=-,从t=0到t=1s 时间内相位差为5()236πππϕ∆=--=,所以角频率为56t ϕπω∆==∆ 可得振动表达式为50.06cos()63y t m ππ=-习题10-8图习题 10-6 图ω(2)P 点相对应的相位为0。
(3)到达P 点所需时间为0()'3'0.456t s πϕπω--∆∆=== 10-9 沿x 轴作简谐振动的小球,振幅A=0.04m ,速度的最大值10.06m v m s -=⋅。
若取速度为正的最大值时t=0。
试求:(1)振动频率;(2)加速度的最大值; (3)振动的表达式。
解 (1) 速度的最大值10.06m v A m s ω-==⋅,A=0.04m10.06 1.50.04m v rad s A ω-===⋅, 324Hz ωνππ==。
(2)加速度的最大值220.09m a A m s ω-==⋅。
(3)速度为正的最大值时t=0,由旋转矢量法可知:2πϕ=-振动的表达式为 30.04cos()22y t m π=-10-10 一物体质量为0.25 kg ,在弹性力作用下作谐振动,弹簧劲度系数为 25 N ・m -1,如果起始振动时具有势能0.06J 和动能0.02J ,求(1)振幅;(2)动能恰等于势能时的位移; (3)经过平衡位置时物体的速度。
解 物体做简谐振动时,振子势能的表达式是2p 12E kx =,动能表达式是2k 12E mv =。
其动能和势能都随时间做周期性变化,物体通过平衡位置时,势能为零,动能达到最大值;位移最大时,势能达到最大值2p 12E kA =,动能为零,但其总机械能却保持不变为212E kA =。
(1)由于振动过程总机械能却保持不变,210.060.02252A +=⨯⨯,A=0.08m 。
(2)动能恰等于势能时,也就是此时势能是总机械能的一半,22p 111'222E kx kA ==⨯,0.0572x A m =±=± (3)通过平衡位置时,势能为零,动能达到最大值,此时210.060.022mv +=⨯, 10.8v m s -=⋅.10-11 一质点作简谐振动,其振动方程为26.010cos()()34x t SI ππ-=⨯-。
求: (1)当x 值为多大时,系统的势能为总能量的一半?(2)质点从平衡位置移动到上述位置所需最短时间为多少秒?解 (1)系统的势能为总能量的一半时,有226.010 4.24102x m m --=±⨯⨯=±⨯ (2)质点从平衡位置移动到上述位置所需最短时间为60.7588T t s s ===10-12 一质点同时参与两个同方向的简谐振动,其振动方程分别为21510cos(4)()3x t SI π-=⨯+22310sin(4)()6x t SI π-=⨯-求合振动的振动方程。
解 22222310sin(4)310cos(4)310cos(4)6623x t t t ππππ---=⨯-=⨯--=⨯-作两振动的旋转矢量图,如图所示。
由图得合振动的振幅和初相分别为 A =(5-3)cm=2cm ,3πϕ=合振动方程为2210cos(4)()3x t m π-=⨯+10-13 火车在铁轨上行驶,每经过铁轨接缝处即受到一次振动,从而使装在弹簧上面的车厢上下振动。
设每段铁轨长12.5m,弹簧平均负重5.4×104N ,而弹簧每受9.8×103N 的力将压缩1.6mm 。
试问火车速度多大时,振动特别强?解 由题意可得弹簧劲度系数316139.810 6.125101.610k N m N m ---⨯=⋅=⨯⋅⨯1133222--⋅=⋅⨯=⋅=s m s m u ππωπλ系统的振动角频率1133.34s rad s ω--==⋅=⋅ 火车的固有周期22 3.140.1833.34T s s πω⨯=== 因此,当火车在接轨处受到振动周期等于固有周期时,振动将最强,于是1112.569.40.18L v m s m s T --==⋅=⋅时,振动将特别强烈。
10-14 一平面简谐波的波动方程为),)(3cos(1.0SI x t y πππ+-=0=t 时的波形曲线如附图所示,则((A )O 点的振幅为m 1.0-(B )波长为(C )b a 、两点间相位差为2/π(D )波速为9m/s解 波动方程的一般表达式是 ,对比所给的波动方 程可知:各质点的振幅都是0.1m,波长λ=2m ,角频率-1s rad 3⋅=πω 所以波速a,b 两点间距离差是对应的相位差是 故选C10-15 某平面简谐波在s t 25.0=时波形图如图所示,则该波的波函数为( )(A) (B) (C) (D) m x t y ]2)8(4cos[5.0ππ--=mx t y ]2)8(4cos[5.0ππ++=m x t y ]2)8(4cos[5.0ππ-+=m x t y ]2)8(4cos[5.0ππ+-=rad rad r 2422πλλπλπϕ=⨯=∆=∆4λ)2cos(ϕλπω+=x t A y .0解 波动方程的一般表达式为 ,由图可知cm 5.0=A ,s m u /8=,所以x 前的系数取负值。
当s t 25.0=时,0,000〈=υy ,此时的相位是将已知条件带入方程可得 所以波函数为 故选A10-16 一平面简谐波在弹性媒质中传播时,某一时刻在传播方向上介质中某质元在负的最大位移处,则它的能量( )(A )动能为零,势能最大 (B )动能为零,势能为零 (C )动能最大,势能最大 (D )动能最大,势能为零解 介质中某质元的动能表达式 )2(sin 21222ϕλπωωρ+-=x t dVA dW k ,质元的弹性势能)2(sin 21222ϕλπωωρ+-=x t dVA dW p ,所以在波动传播的介质中,任一体积元的动能、势能均随t x ,作周期性的变化,且变化是同相位的. 体积元在平衡位置时,动能、势能和总机械能均最大. 体积元的位移最大时,三者均为零. 故选B10-17 频率为Hz 100,传播速度为1300-⋅sm 的平面简谐波,波线上距离小于波长的两点振动的相位差为π,则此两点相距( )(A) m 5.1 (B) m 19.2 (C) m 5.0 (D) m 25.0解 相位差与波程差之间的关系是 ,本题中. 故选A10-18 两列相干波沿同一直线反向传播形成驻波,则相邻波节间各质点的振动( )(A) 振幅相同,相位相同 (B)振幅不全相等,相位相同 (C) 振幅相同,相位不同 (D)振幅不全相等,相位不同解 驻波方程为,因此根据其特点,两波节间 2π2πϕ-=m x t y ]2)8(4cos[5.0ππ--=])(cos[ϕω+±A =u xt y r ∆=∆λπϕ2mm v u s m u Hz v 3100300,300,1001===⋅==-λm m r 5.1232=⨯=∆=∆ππϕπλt x x y ωπcos 2cos2A =各点运动振幅不同,但相位相同,故选B 。
