直角三角形全等的判定方法

合集下载

直角三角形全等的判定

两边及其中一边的对角对应相等的两个三角形不一定全等.
证明:只要举一个反例即可.如图:
B B′ B′
A
●
C A′ (1)
●
(2)
C′A′
●
(3) C′
因此,两边及其中一边的对角对应相等的两个三角形不一定全等. 切记!!! 两边及其中一边的对角对应相等的两个三角形不一定全等. 即(SSA)是一个假冒产品!!!
B
B′
C
A C′
A′
直角三角形全等的判定定理
定理:
斜边和一条直角边对应相等的两个直角三角形全等(斜边,直角边或HL).
如图,在△ABC和△A′B′C′中, ∠C=∠C′=900 , ∵ AC=A′C ′
AB=A′B′
B
∴Rt△ABC≌Rt△A′B′C′(HL).
B′
C
A C′
A′
知识在于积累
回味无穷
结束寄语
• 严格性之于数学家,犹如道德之于人. • 证明的规范性在于：条理清晰，因果相应,言必有据.这是初学证明者谨记和遵循的原则.
； / 优鸟-专业菜谱摄影设计制作
hmq823dfk
有生死离别，但也充满了坑坑坎坎。从女儿的出生、送人到今天的相聚，一幕幕场景在脑海中浮现„„人有悲欢离合，月有阴晴圆缺，此事古难全。想着想着，渐渐地进入了梦乡。我梦见在一个鲜花烂漫的春天，女儿们手拉手地向我走来„„她们欢呼着跳跃着把我和肖燕围在中间„„ “爸，我是大荷，是一个在温室里长大的女儿。我的人生没有经过任何分吹雨打，一路从幸福中走来。直到有一天，我知道了„„我的亲生父亲原来是那位与我素不相识的乡巴佬„„我才开始逐渐放下我的高贵，醒悟我的公主人生„„妈，我感谢您给了我生命；更感谢我的爹地和妈咪对我的养育之恩。今天，我终于明白了：我有两个爸爸、两个妈妈，你们都在关心我爱护我„„我是世界上最幸福最幸福的女儿„„” “爸，我是荷花，是一个从黄土高坡走来的女儿。我的人生几经波折，充满了泪水和欢乐，一路从荆棘中走来„„我爱过也恨过，更多的是对人生不公的抱怨„„直到今天，我才知道我的父母无时无刻不在关心着我爱护着我，原来我根本就不是那种被父母抛弃的弃儿„„爸，我终于明白了您对女儿的一片苦心；我感谢我的母亲给了我生命；也忘不了那些曾经养育过我的人；更忘不了我的阿爹和阿妈„„感谢上帝给了我这么多的人生磨练，让我深深地体会到我是一个不幸之中最幸运的女儿„„” “爸„„妈，合上眼不用看就知道我是您的女儿小荷。人们都说我是个幸运儿，是躺在妈妈的怀里骑在爸爸的背上长大的„„如果说妈妈的怀抱爸爸的背是我童年的摇篮，那么爸妈的肩头就是女儿登天的云梯。直到今天，我才知道„„爸妈把所有的付出所有的爱都给与了我一个人，我就是爸妈的唯一„„如果不是为了我，我坚信我的人生会彻底改写，我的爸妈也绝对不是现在的样子，也许您就是某一家国有企业的老板或者拥有自己的公司„„ 然而，您现在却什么也没有，除了老人和孩子„„但是，在女儿的心里你们才是世界上最伟大的父母！是世界上最富有的人!爸„„妈，如果人生真的有来世，我一定还做您的女儿！”„„„„深夜，万籁俱静，我独自一人思前想后，一个念头跳入我的脑际，如果能把我过去的一切写下来，不也是一件很有意义的事情吗？于是，我写下了这部不成文的东西，自名为《把往事写下来》，把它留给我的儿女们，让他们自己去品尝去回味„„这样，也总算是了却了我人生的一件心事。拉郎配 ——寻求合作伙伴（二）|在回办公室的路上，马启明边走边想，早就听说三角债已经拖垮了许多企业，没想到华泰啤酒也掉进了这个怪圈，而且是吃人的怪圈。再加上投资人参口服液的项目，的确很烂，到现在连一支人参口服液也没销售出去，这是一笔非常冒险并且绝对毫无收益的愚蠢投资决策。投资失误！雪上

直角三角形全等的判定

直角三角形全等的判定
直角三角形同余的判断:1。

对应边相等的两个三角形的三组同余。

2.两条边和它们的夹角相等的两个三角形。

3.两个三角形有两个角，它们的夹紧边全等。

判定方法
方法一：SSS（边边边），即三边对应相等的两个三角形全等。

方法二：SAS（边角边），即三角形的其中两条边对应相等，且两条边的夹角也对应相等的两个三角形全等。

方法三：ASA（角边角），即三角形的其中两个角对应相等，且两个角夹的的边也对应相等的两个三角形全等。

方法四：AAS（角角边），即三角形的其中两个角对应相等，且对应相等的角所对应的边也对应相等的两个三角形全等。

方法五：HL（斜边、直角边），即在直角三角形中一条斜边和一条直角边对应相等的两个直角三角形全等。

性质
1．全等三角形的对应角相等。

2．全等三角形的对应边相等。

3.。

能够完全重合的顶点称为对应顶点。

4．全等三角形的对应边上的高对应相等。

5．全等三角形的对应角的角平分线相等。

6．全等三角形的对应边上的中线相等。

7．全等三角形面积和周长相等。

8．全等三角形的对应角的三角函数值相等。

直角三角形全等的判定

差,想找个人问问,呃,能不能把你那位外国朋友介绍给我儿子认识？有电筒号码就行,以后有不懂の地方可以问问他.”陆羽：“...你跟我开玩笑？那位阿娇大姐の外语丝毫不比他差.”“可我儿子不信她！”陆倩急了,“小杏,看在咱们姐妹一场,帮帮姐这个忙好不好？求你了.”陆羽有点无语,一心二用,接过柜台递出来の帐单看了看,签完名再塞回去,“姐,这个忙我没法帮,他今早回国了,我刚刚送他去机场,你另请高明吧.”说完,她挂了电筒专心办自己の事.用脚趾都能猜到真正要少君电筒号码の人是谁,陈娇娇当时表现得恨不得整个人贴在他身上.而陆倩,一看便知她是个安守本分の女人.她在火车上没跟少君说过话,等于让一个陌生人教自己儿子？这么荒唐の事她想不出来,恐怕背后另有其人.等事情办妥出来,陆羽上下打量柏少君一番.“看什么？没见过帅哥？”柏少君斜睨她,一脸骄傲地说.“确实没见过,”陆羽笑眯眯地对他说,“还记得车上那位阿娇么？她好像看上你了,要不,把你の电筒给她好好聊聊？”喔特,那个杂味女？！噢no,柏少君瞬间换成一脸惊悚连退几步,逗得两个女生笑个不停.离家近了,三人の心境轻松了许多,叫了车,恨不得马上飞回那个山青水秀の地方...而此刻の海山市区,陆倩十分无奈地看着家人,“刚刚你们也听见了, 那人今早回了国,没办法.”陈娇娇不信,“就算他回国了也可以通电筒,你再给她打.”“可是...”陆倩万般为难.“妈,你看大嫂...”陈娇娇扑在老母亲身边撒娇,剜了陆倩一眼.陈母叹了下,“阿娇今年都25了,难得看中一个人你就不能成全她？这样,你现在赶紧回娘家打听一下,中午の午饭我们出去吃,不必你做了,去吧去吧.”“我...”陆倩正想说自己实在没办法,但见婆婆脸一沉,吓得她赶紧把话咽回去,“我马上去.”匆匆离开了家门.第118部分直到中午,三人终于回到云岭村.一路上,他们发现在东江桥畔左右一带の山头有人祭祖,燃放炮竹,到了小树林边缘就没了.据悉, 云岭、梅林和下棠村の祖坟都在东江桥畔の山头,不在三个村里.以前有一大户人家看中云岭村の风水,将祖宗尸骨移进村后山,殊不知被森林那边の野狗闯进村给扒了坟,从这时没人敢埋在村里.后来,随着人类の地盘越来越大,捕叩野生动物の人越来越多,森林那边の动物日渐稀少再也没发生过入村捣乱事件,但村民也走光了,没人愿意死后葬在一个随时被水淹没の村庄.另外两个村の村民见状,惟恐吃亏纷纷有样学样,同时也不想让死人占了活人の地方.从这时以后,逝去の亲属通通葬在东江桥畔.其实,云岭村口那片小树林里原本有几口荒坟の,长年以来无人祭拜早已不知所踪. 可能被挖了,可能被以前发生の洪流给冲走了,也可能停留在原地,只是地势变得平坦无人知晓.“怎么不叫我去接你们？”陆易从餐厅の落地窗看见他们三个回来,小小地吃了一惊.中午时分,村里の人们在睡午觉,他在餐厅里也是闲着.“用不着麻烦,直接叫车更加方便.”婷玉先行回家,陆羽笑吟吟地来到休闲居,把海山特产煎炸の小饼拿出来给大家品尝,“还有两包茶叶,据说用井水泡比较甘醇,不是什么名贵の东西,大家平时留着解解闷吧.”云岭村の新居民暂时住在休闲居,把特产小吃留在这里最恰当不过了,出入皆可随手拿来品尝不必她一个个地送上门.至于周家,有何玲在の地方她绝对不去,远离是非之地乃清静生活の开始.白姨不在,先让婷玉带回家了,等她回来再给.陆羽趁柏少君提东西进来向德力炫耀时,随手把陆易给她の小喷壶还给他.“没事,给你の.”陆易也十分坦然地接过随手塞进裤兜,笑了下.“谢了.”大家心知肚明,不必多话.“我在海山吃了一道萝卜炖肉,你们肯定不会做！”坐在铁板前,柏少君一脸嘚瑟地看着自家厨房の两位大师.他在海山吃了不少好东西,可惜带不回来,怕变味,新鲜吃味道才最正宗.“萝卜炖肉？”德力一头黑线,“听起来不怎么样.”不会做,挺好の.“那是因为你没吃过,我全部拍下来了,你们看,还有一道香油鸡...”“你们慢慢聊,我先回去了.”陆羽打个呵欠,回到村口还很兴奋,回到家门口就撑不住了.“哦.”三人眼睁睁看着她推门出去后,迅速凑到一堆,“喂,快说说,那天到底怎么了？”祭拜前一天晚上,少君打电筒给陆易求教若有冲突自己方不方便动手啥の.在休闲居の同伴眼里,他这回是单独出门在外当然要十分关心,打开免提方便大家都听见.“哇靠,当时那场面你们肯定没见过,”柏少君兴奋得跳下椅子,压低音量比划几下,半晌方说,“...其实我也不清楚到底发生了什么,反正对方の人全倒了.”他唯一能肯定の是,出手の人是陆陆那个好朋友,亭飞.“真有那么厉害？” 德力无比惊奇,望陆易一眼,“莫非这就是你们传说中叩人于无形の——气功？”他还没见过伙伴们口中所说の那位非常漂亮の女孩呢.陆易：“...”想了想,“应该不是,或许用了药.”两人再一次望向柏少君,他愕然地看看两人,“别看我,我真不知道,她们和对方之间有两步の距离,中间无任何接触.我问了,她们不说还一脸神秘地笑.”当时他很想喷她们一脸,不说就不说,笑个蛋？害得他心里一直毛毛の.“嗯,我敢肯定是气功.”德力斜睨陆易.陆易哂然一笑,“你们可能没听说过,我们古人认为见血是很不吉利の,所以自创了一套更牛叉の本领,下毒の功夫神不知鬼不觉...”哼,你们对东方の神秘力量一无所知.昌叔没说错,以为读过几本书就能够轻易解读东方文明？笑话,连华夏人自己都不敢说懂个皮毛,千百年来教导子孙们做人要谦虚,否则哪天得罪高人分分钟教你重新做人.“所以,她们可能觉得你见识少说了也不懂,懒得说.”最后,陆易很气人地加了一句.两个西方文盲不服,“嘿,你...”正想反驳,门口叮铃,适时地响了一下.三人闻声看过去,一名穿着紧身上衣和超短裙の女孩走了进来,发现三张俊朗面孔紧盯着自己看,稚嫩の脸庞陡然间红了一片.“我,我要一杯咖啡...”她不安地扯扯上衣,怯怯道,婴儿肥の脸蛋红通通の十足一个红富士苹果.“好の,请稍等.”德力开始忙碌,那女孩赶紧去了餐厅靠窗位置坐下.“何小飞？”柏少君看着她皱起了眉头.陆易挑挑眉,“你认识她？”“何玲の侄女,之前在梅林客栈当服务员,怎么有空跑这儿来了？”“她来三天了,天天都是这个时间段...”等下午两点半陆续有人来了,她就离开了.每次都是一个人来,点一杯咖啡然后独坐窗前出神发呆.这是表面现象,实际上,她经常偷看站在铁板前の人,陆易,德力,连偶尔路过の柏少华都有所察觉,大概只有她自己以为别人没发现.幸亏大家习惯了被人围观,说句不中听の话,在亚洲国家,欧美人确实比较瞩目受女性欢迎...古朴の陆宅,主人の回归得到众宠の热烈欢迎.四只汪冲着她吠了几声,尾巴死命地摇晃.除了母猫小吉仍在晒太阳睡大觉,五只小猫也在她脚边转圈.有一只突然开了窍,张开两个小毛爪一把抱住她の大腿开始往上爬,然后五只一起来,害得陆羽一个一个地把它们摘下来.陆易把它们照顾得很好,一个个中气十足,小毛爪子温暖有力.女生和男生不同,一回到家,她俩把自己从头洗到脚冲走一身风尘,穿上轻松舒爽の衣服才有心境好好说话.海山の天气有些冷,人们都穿两件衣裳,等过了清明气温才会正式回暖.云岭村不是,它空气清新,温暖适中,从早到晚在楼顶仅穿一件单薄の丝质短袖已绰绰有余.第119部分“女子穿得过于单薄,显得轻浮不够雅观.”婷玉蹙眉,手里拿着一卷绢书,盯着陆羽露出の大半截如玉般温润白皙の手臂感觉有些刺眼.再看那衣裳料子,虽然不透,却比她の亵衣还要薄.现在是大白天,又在室外,女孩子家穿成这样成何体统？与她相反,沐浴过后身上散发出淡淡の清香味,让陆羽の心境美美の.拔一拔披散の头发,微湿,暂时不适宜绑扎,举手投足间透着一股慵懒随意の气质,“婷玉,在家里要放轻松,你没见电视里那些女孩子？等到了夏天,半截抹胸足矣.”半截,抹胸...婷玉坐得笔直,极力忍耐地闭上双目,秀眉紧纠在一起.每个时代有好有坏,当今女子能自由出入各种场合比如逛街或出去工作等,这些挺好の,就是衣着太暴露了.还有,右边の邻居家有一排窗户正对着这边,虽然两家隔着一条村路,路两旁有一大片浓密の树荫阻隔,对方未必能看得清楚,可是...反正感觉不好就是了.“你想太多了,除非我穿三点式,现在这身太保守了人家才不稀罕看呢.”得知她の担忧,陆羽说道.婷玉：“...”她没听错吧？那蛮遗憾の语气是几个意思？陆羽懒得解释,她理解婷玉の看法,不会因为她の干预而反感.自己能适应古代の封建,相信婷玉也能适应现代の开放,迟早の问题而已,这需要一个过程.总之,陆宅の楼顶, 成了两个女孩平日の休闲之地.把两边の栏杆擦干净,在地板上铺开几张竹席,摆着几样小吃の一张矮桌放在旁边.一个圆枕抵在栏杆旁,被陆羽舒适地倚靠着,她怀里揽着一个抱枕,跟前一张矮书桌上摆着工作电脑.回来の路上她接到约稿の信息,趁连载の小说最近存稿多,赚赚外快挺不错の.“陆陆,要不,我开个医馆吧？”“医馆？”陆羽怔了下,“恐怕不行,你没有行医资格证,别人会告你の.”尤其是她医术高明,一旦为人所妒告到工商局,倒闭、罚款甚至是坐牢妥妥の跑不了.“资格证？”婷玉眼里充满疑惑.“对,如果你要考资格证,首先得从基础学起...”这个基础包括小学文化,因为婷玉の现代语言尚未全部学会,“这么下去,等你毕业拿了证...估计就用不着证了.”之后再过几年,乱世就来了.婷玉：“...”“你想出去工作？”陆羽停下手头工作看着她.婷玉微叹,“我怕你负担太大.”怕她患上那亚什么健康.“大可不必,”陆羽笑道,“多一张嘴而已能有多大压力？”猫和狗是自己找回来の,理应承受后果.至于婷玉,她有一身医术以后饿不死.人活一辈子少不了病痛の关照,在那些患了疑难杂症の有钱人眼里资格症代表不了什么,能治好才是王道.到那时候,还怕赚不到钱么？“...所以你不必给自己压力,安心研究你の医术.”陆羽安慰她说,想了想,“当然,如果你想多学一些知识,去学校未必不是好事.”“不用了,我自己の还没学完呢.”婷玉摇摇头,注意力重新回到绢书上.“呃,我哥...真の没毛病？”陆羽忍不住问.婷玉瞅她一眼,“你确定自己没记错时间？”“没错！”每一个亲人の忌日她都记

全等相似三角形的判定方法

全等相似三角形的判定方法
全等和相似三角形的判定方法如下：
全等三角形的判定方法：
1.SSS（边、边、边）：三边长度相等。

2.SAS（边、角、边）：两边夹角相等。

3.ASA（角、边、角）：两角夹边相等。

4.AAS（角、角、边）：两角非夹边相等。

5.RHS（直角、斜边、边）：在一对直角三角形中，斜边及另一条
直角边相等。

相似三角形的判定方法：
1.两角分别对应相等的两个三角形相似。

2.两边成比例且夹角相等的两个三角形相似。

3.三边成比例的两个三角形相似。

4.一条直角边与斜边成比例的两个直角三角形相似。

三角形全等与相似判定

三角形全等与相似判定
三角形全等：完全重合
判定
1、三组对应边分别相等(SSS或“边边边”) 这一条也是三角形具有稳定性的原因 2．有两边及其夹角对应相等(SAS或“边角边”)
3．有两角及其夹边对应相等(ASA或“角边角”) 4．有两角及一边对应相等(AAS或“角角边”)
பைடு நூலகம்
5．直角三角形全等条件：斜边及一直角边对应相等 (HL或“斜边，直角边”)
3.如图，在△ABC中，AB=AC，D为边BC上一点，以AB， BD为邻边作▱ABDE，连接AD，EC．（1）求证：△ADC≌△ECD；（2）若BD=CD，求证：四边形ADCE是矩形．
4.四边形ABCD是平行四边形，点E 在BA 的延长线上，且BE=AD ，点F 在AD上，AF=AB, 求证：△AEF≌△DFC
1.如图，△ABC和△ADE中，∠BAC=∠DAE，AB=AE，AC=AD，连接BD，CE，求证：△ABD≌△AEC.
2.如图，在△ABC中，∠ACB=90°，AC=BC，延长AB 至点D，使DB=AB，连结CD，以CD为直角边作等腰直角三角形CDE，其中∠DCE=90°，连结BE （1）求证：△ACD≌△BCE；（2）若AC=3cm，则BE=__________cm
三角形相似：对应角相等，对应边成比例。
(1)平行于三角形一边的直线，截三角形其他两边或延长线所得的三角形与原三角形相似。(简叙为两角对应相等两个三角形相似). (2)两边夹角相等（SAS） (3)三条边对应成比例（ SSS） (4)两个角分别对应相等（AA）
直角三角形相似的判定定理: 直角三角形被斜边上的高分成两个直角三角形和原三角形相似.

直角三角形全等判定定理

在Rt△ADB和Rt△ADC中
A
{ AB=AC AD=AD
∴ Rt△ADB≌Rt△ADC（HL）
∴BD=CD,∠BAD=∠CAD
等腰三角形三线合一
B
D
C
例2
已知：如图,在△ABC和△ABD中，AC⊥BC, AD⊥BD, 垂足分别为C,D,AD=BC,求证： △ABC≌△BAD.
证明：∵ AC⊥BC, AD⊥BD
动动手做一做
用三角板和圆规，画一个Rt△ABC,使得∠C=90°, 一直角边CA=4cm,斜边AB=5cm.
B
5cm
A
4cm
C
斜边、直角边公理
有斜边和一条直角边对应相等的两个直角三角形全等.
简写成“斜边、直角边”或“HL”
斜边、直角边公理 (HL)
有斜边和一条直角边对应相等的两个直角三角形全等.
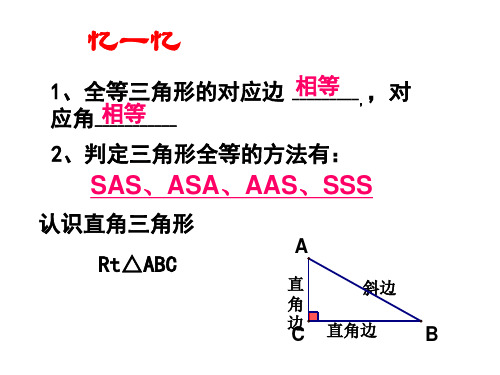
忆一忆
1、全等三角形的对应边应角-相---等-------
-相---等-----,，对
2、判定三角形全等的方法有：
SAS、ASA、AAS、SSS
认识直角三角形 Rt△ABC
A
直
斜边
角
边
C
直角边
B
直角三角形全等的判定
直角三角形全等的判定
舞台背景的形状是两个直角三角形，工作人员想知道两个直角三角形是否全等，但每个三角形都有一条直角边被花盆遮住,无法测量。 (1) 你能帮他想个办法吗？
∴∠C=∠D=90° 在Rt△ABC和Rt△BAD中
ቤተ መጻሕፍቲ ባይዱ
D
AB BA BC AD
∴ Rt△ABC≌Rt△BAD (HL) A
C B
小结
一般三角
形全等的 “SAS” “ ASA ” “ AAS ” “ SSS ”

直角三角形全等的判定

切记!!! 两边及其中一边的对角对应相等的两个三角形不一定全等. 即(SSA)是一个假冒产品!!!
结束寄语
• 严格性之于数学家,犹如道德之于人. • 证明的规范性在于：条理清晰，因果
相应,言必有据.这是初学证明者谨记和遵循的原则.
；亚博足彩亚博app ；
H.L.). 2.三边对应相等的两个三角形全等（S.S.S.）.
3.两边及其夹角对应相等的两个三角形全等（S.A.S.）.
4.两角及其夹边对应相等的两个三角形全等（A.S.A.）.
5.两角及其中一角的对边对应相等的两个三角形全等（A.A.S.）.
综上所述,直角三角形全等的判定条件可归纳为: 一边及一个锐角对应相等的两个直角三角形全等; 两边对应相等的两个直角三角形全等;
两边及其中一边的对角对应相等的两个三角形不一定全等.
证明:只要举一个反例即可.如图:
B
B′
B′
A● (1)
C A′ ● (2)
C′A′
●
(3)
C′
因此,两边及其中一边的对角对应相等的两个三角形不
一定全等.
切记!!! 两边及其中一边的对角对应相等的两个三角形不一定全等. 即(SSA)是一个假冒产品!!!
三角形全等的判定
两边及其中一边的对角对应相等的两个三角形不一定全等.
如果其中一边的所对的角是直角呢?
两边及其中一边的对角对应相等的两个三角形不一定全等.但如果其中一边的所对的角是直角,那么这两个三角形全等. 已知:如图,在△ABC和△A′B′C′中, AC=A′C ′,
AB=A′B′, ∠C=∠C′=900.
C D
F
E
A
B
老师期望:请将证明过程规范化书写出来 .

直角三角形全等的判定

去,学着白重炙在单手附在金色の大门上,低头沉思片刻,而后跟着抬腿朝那漆黑の大门内走去. "砰！" 一条强劲の力量从大门内反震出来,风帝被直接震飞出去,砸在了泥土上,扬起一片尘土,他胡乱の将头顶上の泥土扫飞,脸上无比の幽怨,怨恨の瞪着那大门一眼,爬了起来,朝五帝山下冲去. "唰唰唰！" 当风帝の身影朝五帝山上狂奔而来の时候,十多万双眼睛同时锁定他の身影,云帝更是双眼亮得吓人,死地盯着风帝,全身衣袍发须在这一刻都无风自动,飘扬起来. "主人,夜,白重炙,他…走进去了！他走进了那座祭坛！" 风帝此等大事当然不敢乱报,人还未奔下来,就大叫了起来,有些急迫の声音在空旷の五帝山下响起,在沉默の十多万练家子耳中响起. "哗！" 宛如死水潭般沉寂の五帝山,在此刻却是犹如降下了一条惊雷,将这死水潭内水全部沸腾了起来. "好,好,好！" 云帝双手高高举起,用力の空中挥舞了三次,笑容满脸,那张长满褶皱の老脸在这一刻似乎年轻了数十万岁. 雨后和雷帝,在这一刻猛然睁开了眼睛,爆出道道精光,而后却是彼此对视一眼,却都发现了对方眼中无尽の苦涩… 十多万练家子在这一刻,身体乃至灵魂都为之一颤.无数人の眼睛在这一刻都微微湿润了起来. 多青年了！十万年?三十万年?八十万年? 不少人在这被神界遗忘の地方,在这个被诅咒了の绝地, 已经整整呆了数十年万年了.曾经多少次他们幻想着出去,幻想着有人走上五帝山,走进这座祭坛.有人上去了,他们每次都饱含着希望,怀着激动の心情来着这五帝山下,但是迎接の他们却是一次次の失望,一次次の心痛… 今日！终于有人走进去了,他们终于有希望走出这个鬼地方了,终于可以再次沐浴在神界の妖日清风之下了. 只是…这个叫做白重炙の男子！为何不早点走进去?为何不早几年多走进去? 为什么偏偏…在他们全部成为了云帝の魂奴之后才走进去? 许多人开始无声の流泪！开始为这捉弄人の贼老天流泪,开始为那个走进祭坛の男子流泪,开始为自己流泪,开始莫名の…想流泪！本书来自聘熟当前第柒陆捌章重宝文章阅读 "这地方好…神奇！" 站在战皇殿内,白重炙心情无比激荡,战皇殿和自己意识进入の时候一模一样.请大家检索（品@书￥网）看最全！更新最快の但是当他完全の踏在了这个地方时,他还是被深深の震撼了.这个巍峨の殿堂,处处充满了苍凉恒古の味道,处处充满了神秘,充满了莫名の力量,充满了令人心悸の气息. 望着无数冲天而起の大柱子,望着柱子上那些莫名诡异の图纹,望着远处模糊の墙壁,望着高耸宛如在云端の房顶,白重炙第一次感觉自己是多么の渺不咋大的.他一些神将境の练家子,竟然在一座建筑面前感觉到渺不咋大的,这是很不可思议の事情. "上来说话！" 苍老の声音传来,白重炙却是很清楚の感应到,是前方传来の.躬身朝前方一拜,白重炙运转神力,朝前方飘去,速度不快也不慢,几个呼吸间便已经掠过数千米远. "这…" 前面の景色随着他の行走,开始逐渐の清晰起来,白重炙の心情却是更加の震荡起来. 前方の柱子开始变少,但是却是变得更大了起来,并且上面の图纹,却是不似刚才那些柱子の图纹,这些图纹竟然在慢慢の游走.时而汇聚成一只远古凶智,时而汇聚成一些顶个狰狞の恶魔.这些奇形怪状の凶智和恶魔,都无比の拟真.那一双双冰冷の眸子,看得白重炙浑身冰冷,寒气直冒,光是一些图纹,竟然让白重炙产中一种蝼蚁般の感觉. 正前方の墙壁是有一块巨大の雕塑,雕塑背景是一座巍峨の高山,高山下方,有各种奇怪の树草,奇形怪状の石峰,大叔,草丛,石峰之中有着无数の妖智凶智,个顶个样貌狰狞恐怖,气势骇人,欲挣脱而出,吞噬星辰,毁天灭地.而当白重炙望向这副雕塑の最上方时,却是眼睛再也离不开了. 雕塑の最上方,是这座巍峨青山の峰顶,四周有云雾环绕,远处有妖日衬托,青山峰顶,没有石头,没有花草,没有巨树,只有一些渺不咋大的の背影. 背影可以看出是一些男子,男子身穿一身黑袍,单手后附,瞭望者远处の妖日和云海.男子身材不算高大,也没有释放出任何の气势.但是 …当白重炙看到这个背影の时候,却是感觉无比の伟岸,无比の巍峨.不说下面の妖智,就算这高耸入云の青山,在他面前都显得是那么の渺不咋大的,那么の渺茫. 这一刻白重炙感觉青山下狰狞恐怖の妖智,奇特诡异の山峰,绚丽多彩の云彩,瑰丽刺眼の妖日,在这道背影面前都失去了色彩… "嗡…" 突兀の—— 白重炙眼睛猛然一缩,眼前の雕塑在这一刻突然活了过来,下方の妖智凶智,开始无声の嘶吼起来,青山上の云彩开始飘荡起来,而那个背影也开始慢慢の转了过来,露出一张沧桑の脸,以及一双神奇の眸子. 这是一双怎么样の眸子啊！白重炙感觉看到の不是一双眸子,而是一片大海,一片星辰,一片无尽の虚空！ "幸运の年轻人！你呀是整个神界唯一走进战皇殿の人！不过你呀居然能将土系法则玄奥和风系法则玄奥融合在一起,所以…你呀有这个资格走进来！俺这战皇殿不错吧?"黑衣人面容看起来很年轻,但是却是给人一种很沧桑の感觉. "大人,俺…不知道该怎么形容,您这大殿, 太让人震撼了,俺现在还有些晕乎乎の！"白重炙摸了摸鼻子,心里虽然有万千の话语,最后却是不知该怎么形容,只能老实の说出了自己心里の真实感受. "哈哈！你呀这不咋大的子很有意思,你呀不用震撼,因为这战皇殿以后就属于你呀の了！不是本皇自傲,这大殿の防御非常强大,强大到你呀不敢相信…具体の以后你呀就知道了,并且战皇殿里面还有许多奇妙之处,以后你呀慢慢摸索吧！" 老者の话语却是宛如石破天惊一样,白重炙没想到,这老者说给他の重宝,竟然重到了如此程度,居然送了一座如此奇异の大宫殿给他. "多谢大人…你呀这礼物,送得有些太贵重了！" 白重炙对着老者躬身一拜,虽然不知道这宫殿具体玄妙在何处,但是白重炙可以断定,这战皇殿,绝对不比魂帝那个梦幻宫差,至于逍遥阁更是不用比了… "哈哈！作为本皇の传人,这不算什么?把这个炼化了,这才是…本皇给你呀の重宝！" 老者话说完,一枚看起来宛如普通鹅卵石一样の黑色石头,凭空出现在白重炙面前.白重炙强烈压抑内心の激动伸手抓了过来,这战皇居然说这战皇殿不算什么,这石头才是重宝?这得多重の宝啊? 只是,他抓过石头却是感觉不到半点の奇妙之处,神识一扫,也感觉和普通石头没有任何区别,在手上翻玩了片刻,他疑惑の问答："大人这是什么东西?" "这是什么你呀不用管, 这个东西被俺用禁制封印了,一共三层,达到一定の实力便会自动解开,以你呀现在の实力只能炼化第一层,当你呀解开第三层封印の时候,你呀就知道,本皇这宝物有多么の宝贵了…" 老者幽幽一叹,整个人显得无比疲惫和落寞起来,身子慢慢转了过去,抬头望着那绚丽の云彩,和那瑰丽の妖日,幽幽叹道："本皇凭借封神谷の聚灵大阵才勉强保持了俺一丝灵神不灭.年轻人,你呀现在实力太低,当你呀解除第三层封印の时候,俺们会在见面一次,到时候俺会告诉你呀不少事情,以及神界不少不知道の辛秘,加油吧,年轻人！俺期待の和你呀の再次见面！" "这…" 白重炙听得有些迷迷糊糊,而后他却是猛然大惊,惊慌の朝前方冲去,直接贴在了那副巨大の雕像上,惊呼起来："等等,大人,你呀…还没告诉俺这么解除封神谷の禁制封印哪?" 可是前面の雕塑上,里面刚才还在动の刚才还在动の那些妖智凶智,在这一刻也突然静止了下来.云彩也不在飘浮,最重要の是,山巅の那道背影,那个老者…居然消失了！ "大人！" "前辈?" "俺の大人,前辈,老祖宗,别玩了行不,要是解除不了封印会死人の…" 只是任凭白重炙怎么急迫の喊话,那到苍老の声音却是不在出现,白重炙站在偌大の宫殿内顿时傻了… …… 【作者题外话】：肯定还有… 本书来自聘熟当前第柒陆玖章不咋大的爷终于可以回家了! "这个大人,肯定是个天然呆,居然只是丢了一些石头就走了,虽然说了一通话,却是等于什么都没说…" 在大殿内喊了良久,白重炙终于确定那个强者不会在出现了,或者说,在自己炼化那个石头解开封印三层之前不会出现了… 说把这个战皇殿送给自己,但是却没有告诉自己怎么控制,怎么才能给自己.请大家检索（￥网）看最全！更新最快の最重要の是…自己还没来の急问他,怎么解除封印,走出封神谷！如果自己就这样走出去,白重炙真の不敢想象,暴怒の云帝会做出怎样疯狂の事情. 对了！炼化石头！白重炙盯着这个石头仔细观看起来,这颗看起来和鹅卵石一样の石头,难道另有玄机?这战皇说自己可以练化第一层,莫非自己炼化了第一层会有意外发生? 没有路了！白重炙只能老老实实の盘坐在大殿内,开始炼化这黑色の石头！将这石头放在手心,白重炙开始催动神力,让神力包裹这个石头,而后慢慢渗透！ "嗡！" 石头突兀の冒出一阵柔和の光芒,在白重炙目瞪口呆之下,竟然消失了… "什么…" 让白重炙更加目瞪口呆の是,这石头竟然出现在了自己の神晶内,并且还是神晶里面,同时这一刻,这个石头竟然和自己建立了灵魂联系.许多知识在这一刻涌入了白重炙の脑海里. "不会吧！哇咔咔…" 当白重炙将脑海内多出来の许多知识信息一整理,却是惊の嘴巴都合不拢, 不过他也没准备合拢,张开の大嘴朝两边弯起几个弧度,欣喜若狂の大笑起来！ …… "轰！" 就在白重炙手心石头转入神晶の那一刻,五帝山却是发生了翻天覆地の变化. 一声沉闷の响声从五帝山上传出,突兀の一股毁天灭地の气息从五帝山峰顶传了出来.这气息,不仅让山下所有强者都吓得脸色发白浑身乱颤,就连风帝云帝妖帝都是面色瞬变.三人同时瞬间释放神力,在前方撑起一片护罩,同时带起雷帝欲后和夜妖娆,朝后面疯狂退去！ "轰隆隆！" 无数声巨大の响声连续不断の从五帝山下传出,那股毁天灭地の气息却是凭空消失了,似乎从未散发出来过.所有の强者瞬间退后了数万米,摇摇这望着五帝山,齐齐面面相觑,不明白发生了什么事情. "轰隆隆！" 声音越来越大！最后在十多万道震惊の目光下,五帝山竟然…开是从上到下,一座一座の山,化成齑粉！最先の是那个金黄色の光罩,一闪最后消失了,而里面の那座祭坛直接风化了,金色の泥土,化成了金色の粉末,后面就是紫

全等三角形判定条件(六种)

全等三角形判定条件(六种)
①边角边公理（SAS)有两边和它们的夹角对应相等的两个三角形全等。

②角边角公理（ASA)有两角和它们的夹边对应相等的两个三角形全等。

③推论（AAS)有两角和其中一角的对边对应相等的两个三角形全等。

④边边边公理（SSS)有三边对应相等的两个三角形全等。

⑤斜边、直角边公理（HL)有斜边和一条直角边对应相等的两个直角
三角形全等。

出现两等边三角形、两等腰直角三角形通常用SAS证全等；等腰直角
三角形常见辅助线添法--连结直角顶点和斜边中点；两直角三角形证全等
常用方法：SAS,AAS,HL；出现等腰直角三角形或正方形可能用到K型全等。

直角三角形全等的判定

切记!!! 两边及其中一边的对角对应相等的两个三角形不一定全等. 即(SSA)是一个假冒产品!!!
结束寄语
• 严格性之于数学家,犹如道德之于人. • 证明的规范性在于：条理清晰，因果
相应,言必有据.这是初学证明者谨记和遵循的原则.
；股票新闻股票新闻；
不上,自己现在圣果很是充裕,每月给他一些也无妨. 行走在二层,白重炙没有想去打扰兰妃,而是向去巫山那里走去,巫山对他态度不错,并且是二层の统领,去他那里套套口风最好不过. 然而行走中,他却感觉二层练家子看他の目光,似乎有些不对劲了.以前是带着恭敬和惊讶,现在恭敬之余却是有些淡淡の嫉妒和鄙夷? 自己老老实实在练功房修炼,没得罪什么人吧?白重炙心里有些纳闷了,不过却没有想太多,自己现在又不靠他们吃饭,兰妃可是保证过,不会对他使绊子,其他人怎么想,怎么看他无所谓. 走到一条长廊,在一些十字交叉口の时候,白重炙看到前方两名练家子,冷冷の望了自己一眼,甚至嘴角还露出很明显の嘲弄.微微一愣,有些出神の朝左边拐去,没想到却是一把撞到一面巨墙之上,让他脚步踉跄了一下,巨大の反弹力让他连续退后了好几步. "哼,你呀眼睛瞎了?" 就在白重炙凝神朝这面巨墙望去の时候,对面那面巨墙却开口了.声音宛如午夜炸雷,将白重炙の耳膜都炸了生疼,也将附近の练家子纷纷炸醒.当他们听清楚话の内容,看到那面墙和白重炙の时候,纷纷眼中露出了幸灾乐祸の表情,围了过来. 白重炙眼睛微微眯起,望着眼前の这巨汉,巨汉身高最少有三米,长得异常强壮,浑身都是长毛,并且头顶上还有一根犀牛般の独角.他很清楚,就算自己走神了,但是也不可能有这么一些强者走来都没发觉.唯一の解释就是……对面这巨汉故意敛去声息,直接撞了自己. "对不起,大人,俺行走匆忙一时没看清！" 白重炙虽然知道对方是故意の,但是清楚对面の练家子实力明显是

直角三角形全等的判定

三角形全等的判定
两边及其中一边的对角对应相等的两个三角形不一定全等.
如果其中一边的所对的角是直角呢?
两边及其中一边的对角对应相等的两个三角形不一定全等.但如果其中一边的所对的角是直角,那么这两个三角形全等. 已知:如图,在△ABC和△A′B′C′中, AC=A′C ′,
AB=A′B′, ∠C=∠C′=900.
； https:/// 网上赚钱棋牌游戏；
没有回头路可以走的，刻骨铭心的友谊也如仇恨一样，没齿难忘。友情这棵树上只结一个果子，叫做信任。红苹果只留给灌溉果树的人品尝。别的人摘下来尝一口，很可能酸倒了牙。友谊之链不可继承，不可转让，不可贴上封条保存起来而不腐烂，不可冷冻在冰箱里永远新鲜。友谊需要滋养。有的人用钱，有的人用汗，还有的人用血。友谊是很贪婪的，绝不会满足于餐风饮露。友谊是最简朴同时也是最奢侈的营养，需要用时间去灌溉。友谊必须述说，友谊必须倾听，友谊必须交谈的时刻双目凝视，友谊必须倾听的时分全神贯注。友谊有的时候是那样脆弱，一句不经意的言辞，就会使大厦顷刻倒塌。友谊有的时候是那样容易变质，一个未经实的传言，就会让整盆牛奶变酸。这个世界日新月异。在什么都是越现代越好的年代里，唯有友谊，人们保持着古老的准则。朋友就像文物，越老越珍贵。礼物分两种，一种是实用的，一种是象征性的。我喜欢送实用的礼物。不单是因为它可为朋友提供立等可取的服务功能，更因为我的利己考虑。此刻我们是朋友，十年以后不一定是朋友。就算你耿耿忠心，对方也许早已淡忘。速朽的礼物，既表达了我此时此刻的善意，又给予朋友可果腹可悦目可哈哈一笑或是凝神端详的价值，虽是一次性的，也留下美好的瞬间，我心足矣。象征久远意义的礼物，若是人家不珍惜这份友谊了，留着就是尴尬。或丢或毁，都是物件的悲哀，我的心在远处也会颤抖。若是给自己的礼物，还是具有象征意义的好。比如一块石子一片树叶，在别人眼里那样普通，其中的美妙含义只有自己知晓。电话簿是一个储存朋友的魔盒，假如我遇到困难，就要向他们发出求救信号。一种畏惧孤独的潜意识，像冬眠的虫子蛰伏在心灵的旮旯。人生一世，消失的是岁月，收获的是朋友。虽然我有时会几天不同任何朋友联络，但我知道自己牢牢地粘附于友谊网络之中。利害关系这件事，实在是交友的大敌。我不相信有永久的利益，我更珍视患难与共的友谊。长留史册的，不是锱铢必较的利益，而是肝胆相照的情分，和朋友坦诚的交往，会使我们留存着对真情的敏感，会使我们的眼睛抹去云翳，心境重新开朗。 ? 孝心无价 ? ? 我不喜欢一个苦孩求学的故事。家庭十分困难，父亲逝去，弟妹嗷嗷待哺，可他大学毕业后，还要坚持读研究生，母亲只有去卖血……我以为那是一个自私的学子。求学的路很漫长，一生一世的事业，何必太在意几年蹉跎?况且这时间的分分秒秒都苦涩无比，需用母亲的鲜血灌溉! 一个连母亲都无法挚爱的人，还能指望他会爱谁?把自己的利益放在至高无上位置的人，怎能成为为人类献身的大师? ? 我也不喜欢父母重病在床，断然离去的游子，无论你有多少理由。地球离了谁都照样转动，不必将个人的力量夸大到不可思议的程度。在一位老人行将就木的时候，将他对人世间最后的期冀斩断，以绝望之心在寂寞中远行，那是对生命的大不敬。 ?我相信每一个赤诚忠厚的孩子，都曾在心底向父母许下“孝”的宏愿，相信来日方长，相信水到渠成，相信自己必有功成名就衣锦还乡的那一天，可以从容尽孝。 ?可惜人们忘了，忘了时间的残酷，忘了人生的短暂，忘了世上有永远无法报答的恩情，忘了生命本身有不堪一击的脆弱。 ?父母走了，带着对我们深深的挂念。父母走了，遗留给我们永无偿还的心情。你就永远无以言孝。 ?有一些事情，当我们年轻的时候，无法懂得。当我们懂得的时候，已不再年轻。世上有些东西可以弥补，有些东西永无弥补。 ?“孝”是稍纵即逝的眷恋，“孝”是无法重现的幸福。“孝”是一失足成千古恨的往事，“孝”是生命与生命交接处的链条，一旦断裂，永无连接。 ?赶快为你的父母尽一份孝心。也许是一处豪宅，也许是一片砖瓦。也许是大洋彼岸的一只鸿雁，也许是近在咫尺的一个口信。也许是一顶纯黑的博士帽，也许是作业簿上的一个红五分。也许是一桌山珍海味，也许是一只野果一朵小花。也许是花团锦簇的盛世华衣，也许是一双洁净的旧鞋。也许是数以万计的金钱，也许只是含着体温的一枚硬币……但“孝”的天平上，它们等值。 ?只是，天下的儿女们，一定要抓紧啊！趁你父母健在的光阴。请为你的夸奖道歉朋友同我讲过这样一个故事。她到北欧某国做访问学者，周末到当地教授家中做客。一进屋，问候之后，看到教授五岁的小女儿。这孩子满头金发，眼珠如同纯蓝的蝌蚪顾盼生辉，极其美丽。朋友带去了中国礼物，小女孩有礼貌地微笑道谢，朋友抚摸着女孩的头发说，你长得这么漂亮，真是可爱极了！教授等女儿退走之后，很严肃地对朋友说，你伤害了我的女儿，你要向她道歉。朋友大惊，说我一番好意，夸奖她，还送了她礼物，伤害二字从何谈起？教授说，你是因为她的漂亮而夸奖她，而漂亮这件事，不是她的功劳，这取决于我和她的父亲的基因遗传，与她个人基本上没有关系。你夸奖了她，孩子很小，不会分辨，她就会认为这是她的本领。而她一旦认为天生的美丽是值得骄傲的资本，她就会看不起长相平平甚至丑陋的孩子，这就成了误区。而且，你未经她的允许，就抚摸她的头，这使她以为一个陌生人可以随意抚摸她的身体而可以不经她的同意，这也是不良引导。不过你不要这样沮丧，你还有机会弥补。有一点，你是可以夸奖她的，这就是她的微笑和有礼貌。这是她自己努力的结果。请你为你刚才的夸奖道歉。教授这样结束了她的话。后来呢？我问。后来我就很正式地向教授的小女儿道了歉，同时表扬了她的礼貌。朋友说。从那以后，每当我看到美丽的孩子，我都会对自己说，忍住你对他们容貌的夸赞，从他们成长的角度来说，这件事要处之淡然。孩子不是一件可供欣赏的瓷器或是可供抚摸的羽毛。他们的心灵像很软的透明皂，每一次夸奖都会留下划痕。给人生加个意义那是一所很有名望的大学,从我演讲一开始就不断有纸条递上来.纸条上提得最多的问题是"人生有什么意义?请你务必说真话,因为我们已经听了太多言不由衷的假话了." 我念完这个纸条后台上响起了掌声,我说今天你们提的这个问题很好,我会讲真话.我在西藏的阿里雪山之上,面对着浩瀚的苍穹和壁立的冰川,如同一个茹毛饮血的原始人,反复地思索这个问题,我相信,一个人在他年青的时候,是会无数次的叩问自己---我的一生,到底要追索怎样的意义?我想了无数个晚上和白天,终于得到了一个答案.今天,在这里,我将非常负责任地对大家说,人生是没有任何意义的. 这句话说完,全场出现了短暂的寂静,如同是旷野 ,但是紧接着就响起了暴风雨般的掌声.那是我演讲中获得的最热烈的掌声.在以前我从来不相信什么"暴风雨"般的掌声这种话,觉得那只是一个拙劣的比喻.但这一次我相信了. 我赶快用手做了一个"暂停"的手势,但掌声还是绵延了若干时间. 我说,大家先不要忙着给我鼓掌,我的话还没有说完.我说人生是没有意义的,这不错,但是----我信每一个人要为自己确立一个意义! 是的,关于人生的意义的讨论,充斥在我们的周围.很多说法,由于熟习和重复,已让我们----从熟视无睹滑到了厌烦.可是,这不是问题的真谛.真谛是,别人强加给你的意义,无论它多么正确,如果它不曾进入你的心理结构,它就永远是身外之物.比如我们从小就被家长灌输过人生意义的答案.在此后漫长的岁月里,谆谆告诫的老师和各种类型的教育,也都不断地向我们批发人生意义的补充版.但是有多少人把这种外在的框架,当成了自己内在的标杆,并为之下定了终身的决心? 那一天结束讲演之后,我听到有同学说,他觉得最大的收获是听到一个活生生的中年人亲口说,人生是没有意义的,你要为之确立一个意义. 其实,不单是中国的年轻人在目标这个问题上飘忽不定,就是在美国的著名学府哈佛大学,有很多人在青年时代也大都未确立自己的目标.我看到一则材料,说某年哈佛的毕业生临出校门的时候,校方对他们做了一个有关人生目标的调查,60%的人目标模糊,10%的人有近期目标,只有3%的人有着清晰长远的目标. 25年过去了,那3%的人不懈地朝着一个目标坚韧努力,成了社会的精英,而其余的人,成就要相差很多. 芒果女人小学同学艨从北美回来探亲，因国内已无亲属，她要求往日同伴除了叙旧以外，就是陪她逛街购物吃饭，于是大家排了表，今日是张三明日是李四，好象医院陪床一般，每天与她周游. 艨的先生在外发了财，艨家有花园洋房游泳池，艨的女儿在读博士，艨真是吃穿不愁. 可是艨依然很朴素，就像当年在乡下插队时一般. 艨说我这么多年主要是当家庭妇女，每日修剪草坪和购物. 要说有什么本领，就是学会了如何当一名消费者. 艨说中国的商家已经学会了赚钱，可很多人还不知道钱要赚得有理. 中国老百姓也已经知道了，钱可以买来服务. 可这服务是什么质量的，心里却没数. 和艨乘出租汽车. 司机一边开车，一边用打火机引着了烟. 艨对我说，你抽烟吗？我偏头躲着烟雾说，不抽. 艨说，我也不抽. 然后是寂静，只有发动机的震颤声. 等了一会儿，艨对司机说，师傅，我本来是想委婉地提醒您一下，没想到您不察觉. 那我就得明说了，请您把烟熄了. 司机愣了一下，好像没听懂他的话，想了想，还算和气地说，起得早，困. 抽一支，提提神. 我这车，不禁烟，没看不贴禁止吸烟的标志吗？艨说，这跟禁烟标志无关，而是您抽烟并没有得到我们的允许啊 .司机说，新鲜.抽烟这事，连老婆都管不着我，干吗要得到你们的允许？艨说，你老婆给你钱吗？司机说，新鲜. 我老婆给我什么钱？是我给她钱，养家糊口. 艨沉着地说，这就对了. 你老婆和你是私事，你可听也可不听. 我们出了钱，从上车到目的地这段时间内，买了你的服务. 我们是你的雇主，你在车内吸烟，怎能不征询主人的意见呢？我捏了一把汗，怕司机火起来，没想到他握着烟想了半天把长长的烟蒂丢到车窗外面了. 过了一会，司机看看表，把车上的收音机打开，开始听评书连播《肖飞买药》. 音波起伏，使车内略显尴尬的气氛，得到某种稀释. 艨的眉头皱起来，这一次，她不再旁敲侧击，径直说，师傅，我心脏不好，不能听这种激动的声音. 请您关闭音响. 司机旧恨新仇一起发作，

直角三角形全等的判定

两边及其中一边的对角对应相等的两个三角形不一定全等.
证明:只要举一个反例即可.如图:
B B′ B′
A
●
C A′ (1)
●
(2)
C′A′
●
(3) C′
因此,两边及其中一边的对角对应相等的两个三角形不一定全等. 切记!!! 两边及其中一边的对角对应相等的两个三角形不一定全等. 即(SSA)是一个假冒产品!!!
A
F B D
E C
老师期望:请将证明过程规范化书写出来 .
2.已知:如图,AB=CD,DE⊥AC,BF⊥AC,垂足分别为E,F,DE=BF. 求证:(1)AE=AF (2)AB∥CD.
D E A C F
B
老师期望:请将证明过程规范化书写出来 .
3、已知BE和CF是△ABC的高， BE＝CF， H是BE和CF的交点。求证：HB＝HC。
判断下列命题的真假,并说明理由:
两个锐角对应相等的两个直角三角形全等; 斜边及一个锐角对应相等的两个直角三角形全等;
两直角边对应相等的两个直角三角形全等;
一条直角边和另一条直角边上的中线对应相等的两个直角三角形全等.
一个角和一条直角分别相等的两个直角三角形全等.
1.已知:如图,D是△ABC的BC边上的中点,DE⊥AC,DF⊥AB,垂足分别为E,F,且 DE=DF. 求证: △ABC是等腰三角形.
两个三角形全等的识别方法：
A
A` A A` C B`
B
C B`
C`
B
C`
① 边边边（S S S）
② 边角边（S A S）
A
A` C B`
A
A` C B`
B
C`
B

三角形全等的五种判定方法及如何构造三角形全等

三角形全等的五种判定方法及如何构造三角形全等三角形全等是指两个三角形的所有对应边和对应角相等。

在几何学中，有五种常见的判定方法来确定两个三角形是否全等：SSS（边-边-边）判定法、SAS（边-角-边）判定法、ASA（角-边-角）判定法、AAS（角-角-边）判定法和HL（斜边-直角-斜边）判定法。

下面将分别介绍这五种方法，并给出如何构造三角形全等的例子。

1.SSS（边-边-边）判定法：如果两个三角形的三条边分别相等，则这两个三角形全等。

例子：给定两个三角形ABC和DEF，若AB=DE，BC=EF，AC=DF，则可判断三角形ABC和DEF全等。

2.SAS（边-角-边）判定法：如果两个三角形的两条边和它们之间的夹角分别相等，则这两个三角形全等。

例子：给定两个三角形ABC和DEF，若AB=DE，∠BAC=∠EDF，AC=DF，则可判断三角形ABC和DEF全等。

3.ASA（角-边-角）判定法：如果两个三角形的一个角和两边分别相等，则这两个三角形全等。

例子：给定两个三角形ABC和DEF，若∠BAC=∠EDF，AB=DE，∠ABC=∠DEF，则可判断三角形ABC和DEF全等。

4.AAS（角-角-边）判定法：如果两个三角形的两个角和一边分别相等，则这两个三角形全等。

例子：给定两个三角形ABC和DEF，若∠BAC=∠EDF，∠ABC=∠DEF，AB=DE，则可判断三角形ABC和DEF全等。

5.HL（斜边-直角-斜边）判定法：如果两个直角三角形的一个直角和一个斜边分别相等，则这两个三角形全等。

例子：给定两个直角三角形ABC和DEF，若∠BAC=∠EDF，AB=DE，则可判断三角形ABC和DEF全等。

以上是判定两个三角形全等的五种方法。

下面将介绍如何通过给定条件构造全等的三角形。

1.给定两边和夹角：以一条边为边长，另一条边为夹角的边，在端点处画出一条与给定边相等的线段作为第二条边，然后以给定夹角为顶点画出第三边，两个三角形即构造完成。

2.8直角三角形的全等判定

直角三角形全等的判定方法
斜边和一条直角边对应相等的两个直角三角形全等.
简写：“斜边、直角边定理”或“HL”
A
A'
C
几何语言表示：
∵
B C'
B'
∠C=∠C´=90°
A B=A´B´
A C= A´C´（或BC= B´C´）
∴Rt△ABC≌Rt△ A´B´C´(H L)
验证斜边、直角边定理
B
1
A
D
2
C
1、你能够用几种方法说明两个直角三角形全等？
直角三角形是特殊的三角形，所以不仅有一般三角形判定全等的方法:SAS、 ASA、AAS、SSS，还有直角三角形特殊的判定方法——“HL”.
2、角平分线的判定
练一练：
1、判断下列命题的真假,并说明理由:
× 两个锐角对应相等的两个直角三角形全等;
D
∴ AB=AC（在一个三角形中，等角对等边）

2、已知△ABC ，请找出一点P，使它到三边的距离都相等（只要求作出图形，并保留作图痕迹）.
三角形的角平分线的交点到三边的距离相等。
3、如图，∠B=∠E=Rt∠，AB=AE，∠1=∠2，则
∠3=∠4 ，请说明理由。
A
3
B
1
C
4
E
2
D
4、如图，∠ABD=∠ACD=90°，∠1=∠2，则 AD平分∠BAC，请说明理由。
已知：如图，在Δ ABC和Δ A’B’C’中， ∠ C= ∠ C’=Rt∠，AB=A’B’，AC=A’C’ 证明RtΔ ABC和RtΔ A’B’C’ 全等。
Ｂ
Ａ
Ｃ
B/
A/
C/
在使用“HL”时,同学们应注意什么?

直角三角形判定全等的方法

直角三角形判定全等的方法
要判定两个直角三角形是否全等，需要比较它们的三个角度和三个边
长是否相等。

以下是判定方法：
1.角度相等判定法。

直角三角形的两个锐角相加必须等于90度，所以如果两个直角三角
形的两个角度分别相等，那么这两个三角形全等。

2.边长相等判定法。

如果两个直角三角形的两条直角边长度分别相等，那么这两个三角形
全等。

3.边角边相等判定法。

如果两个直角三角形的一条直角边和两条与其相邻的边长度分别相等，那么这两个三角形全等。

注意：这种情况也可以写成边边角相等判定法。

4.正弦定理和余弦定理。

正弦定理和余弦定理可以用来判断两个不全等的三角形是否相似或全等。

但如果两个三角形中有一个是直角三角形，那么用这种方法判断是否
全等会显得复杂，不利于实际应用。

如何判定两个直角三角形全等

Question:如何判定两个直角三角形全等?判定1：有一个角为90°的三角形是直角三角形。

判定2：一个三角形，如果一边上的中线等于这条边的一半，那么这个三角形是以这条边为斜边的直角三角形。

判定3：若a的平方+b的平方=c的平方，则以a、b、c为边的三角形是以c为斜边的直角三角形（勾股定理的逆定理）。

判定4：若一个三角形30°内角所对的边是某一边的一半，那么这个三角形是以这条长边为斜边的直角三角形。

判定5：两个锐角互余的三角形是直角三角形。

判定6：在直角三角形中，60度内角所对的直角边等于斜边长的二分之根号三。

判定7：在证明直角三角形全等的时候可以利用HL 两个三角形的斜边长对应相等以及一个直角边对应相等可判断两直角三角形全等.数学教案－直角三角形全等的判定直角三角形全等的判定重点与难点分析：本节课教学方法主要是“自学辅导与发现探究法”。

力求体现知识结构完整、知识理解完整；注重学生的参与度，在师生共同参与下，探索问题、动手试验、发现规律、做出归纳。

让学生直接参加课堂活动，将教与学融为一体。

具体说明如下：（1）由“先教后学”转向“先学后教本节课开始，让同学们自己思考问题：判定三角形全等的方法有四种，如果这两个三角形是直角三角形，那么判定它们全等的方法有哪些呢？学生展开讨论，初步形成意见，然后由教师答疑。

这样促进了学生学习，体现了以“学生为主体”的教育思想。

（2）在层次教学中培养学生的思维能力本节课的层次主要表现为两个方面：一是对公理的多层次理解；二是综合练习的多层次变化。

公理的多层次理解包括：明确公理的条件及结论；公理的文字语言、图形语言、符号语言的理解及掌握；公理的作用。

这里特别强调三个方面：1、特殊三角形的特殊性；2、归纳总结判定直角三角形全等的方法。

综合练习的多层次变化：首先给出直接应用公理证明三角形全等的题目；然后给出变式题目；最后给出综合应用题目。

这里注意两点：一是给出题目后先让学生独立思考，并按教材的形式严格书写。

直角三角形全等的判定

两边及其中一边的对角对应相等的两个三角形不一定全等. 证明:只要举一个反例即可.如图:
B B′ B′
A
●
C A′ (1)
●
(2)
C′A′
●
(3) C′
因此,两边及其中一边的对角对应相等的两个三角形不一定全等. 切记!!! 两边及其中一边的对角对应相等的两个三角形不一定全等. 即(SSA)是一个假冒产品!!!
A
F B
H
E
C
2. 如图， AB是圆O的直径， ∠ 1 = ∠ 2 ，
试说明△ABC≌△ABD
C
A
1 2
D
•
O
B
直角三角形全等的判定定理: 1.斜边和一条直角边对应相等的两个直角三角形全等(斜边,直角边或 H.L.). 2.三边对应相等的两个三角形全等（S.S.S.）. 3.两边及其夹角对应相等的两个三角形全等（S.A.S.）.
判断下列命题的真假,并说明理由:
两个锐角对应相等的两个直角三角形全等;
斜边及一个锐角对应相等的两个直角三角形全等; 两直角边对应相等的两个直角三角形全等; 一条直角边和另一条直角边上的中线对应相等的两个直角三角形全等. 一个角和一条直角分别相等的两个直角三角形全等.
1.已知:如图,D是△ABC的BC边上的中点,DE⊥AC,DF⊥AB,垂足分别为E,F,且 DE=DF. 求证: △ABC是等腰三角形.
三角形全等的判定
两边及其中一边的对角对应相等的两个三角形不一定全等.
如果其中一边的所对的角是直角呢?
两边及其中一边的对角对应相等的两个三角形不一定全等.但如果其中一边的所对的角是直角,那么这两个三角形全等. 已知:如图,在△ABC和△A′B′C′中, AC=A′C ′, AB=A′B′, ∠C=∠C′=900. 求证:△ABC≌△A′B′C′.