电路分析与电子线路综合训练题(DOC43页)
电路分析模拟试题3套及答案doc资料

《电路理论》1一、填空题1.对称三相电路中,负载Y联接,已知电源相量︒∠=∙0380AB U (V ),负载相电流︒∠=∙305A I (A );则相电压=∙C U (V ),负载线电流=∙Bc I (A )。
2.若12-=ab i A ,则电流的实际方向为 ,参考方向与实际方向 。
3.若10-=ab i A ,则电流的实际方向为 ,参考方向与实际方向 。
4.元件在关联参考方向下,功率大于零,则元件 功率,元件在电路中相当于 。
5.回路电流法自动满足 定律,是 定律的体现6.一个元件为关联参考方向,其功率为―100W ,则该元件 功率,在电路中相当于 。
7.在电路中,电阻元件满足两大类约束关系,它们分别是 和 。
8.正弦交流电的三要素是 、 和 。
9.等效发电机原理包括 和 。
10.回路电流法中自阻是对应回路 ,回路电流法是 定律的体现。
11.某无源一端口网络其端口电压为)302sin(240)(︒+=t t u (V),流入其端口的电流为)602cos(260)(︒-=t t i (A),则该网络的有功功率 ,无功功率 ,该电路呈 性。
若端口电压电流用相量来表示,则其有效值相量=∙U ,=∙I 。
12.无源二端电路N 的等效阻抗Z=(10―j10) Ω,则此N 可用一个 元件和一个 元件串联组合来等效。
13 .LC 串联电路中,电感电压有效值V 10U L =,电容电压有效值V 10U C =,则LC 串联电路总电压有效值=U ,此时电路相当于 。
14.对称三相电路中,当负载△联接,已知线电流为72A ,当A 相负载开路时,流过B 和C 相的线电流分别为 和 。
若A 相电源断开,流过B 和C 相的线电流分别为 和 。
15.对称三相星形连接电路中,线电压超前相应相电压 度,线电压的模是相电压模的 倍。
16 .RLC 并联谐振电路中,谐振角频率0ω为 ,此时电路的阻抗最 。
17 .已知正弦量))(402sin()(1A t t i ︒+=,))(1102cos()(2A t t i ︒+-=,则从相位关系来看,∙1I ∙2I ,角度为 。
电工线路分析考试题及答案

电工线路分析考试题及答案一、选择题(每题2分,共20分)1. 电路的基本组成包括电源、负载和______。
A. 导线B. 开关C. 电阻D. 电容2. 在串联电路中,各电阻两端的电压之和等于______。
A. 电源电压B. 总电阻C. 电流D. 功率3. 欧姆定律表明,电流与电压的关系是______。
A. 正比B. 反比C. 无关D. 有时正比,有时反比4. 并联电路中,各支路的电流之和等于______。
A. 电源电流B. 总电压C. 总电阻D. 电源电压5. 电阻的单位是______。
A. 欧姆B. 安培C. 伏特D. 瓦特6. 电感元件的特点是______。
A. 阻碍电流变化B. 阻碍电压变化C. 阻碍电流和电压变化D. 不阻碍电流和电压变化7. 电容元件的特点是______。
A. 储存电荷B. 消耗电荷C. 阻碍电流D. 产生电流8. 交流电的频率是指______。
A. 每秒电流方向改变的次数B. 电流强度C. 电压大小D. 电流方向9. 三相交流电的相位差是______。
A. 0度B. 30度C. 60度D. 90度10. 功率因数是指______。
A. 有功功率与视在功率的比值B. 无功功率与视在功率的比值C. 有功功率与无功功率的比值D. 视在功率与无功功率的比值答案:1. A2. A3. A4. A5. A6. A7. A8. A9. C10. A二、填空题(每空2分,共20分)1. 电阻的公式为 R = ______ / I,其中 R 代表电阻,I 代表电流。
2. 在串联电路中,总电阻等于各部分电阻之 ______。
3. 电容器的单位是 ______,符号为μF。
4. 电流的国际单位是 ______,符号为 A。
5. 三相交流电的电压相量可以表示为 ______、Vb 和 Vc。
6. 功率因数的提高可以减少 ______ 的损耗。
7. 电路的功率计算公式为P = U × ______。
电路图分析专项训练(新)

电路图分析专项训练(新)1. 简介电路图分析是电子工程领域中的重要基础知识,对于电路设计、故障排除和维修具有重要意义。
本文档旨在提供一种专项训练,帮助研究者加强对电路图的理解与分析能力。
2. 训练目标- 加深对电路图符号和元件功能的理解。
- 学会分析电路图中的电流路径和电压变化。
- 掌握电路图分析的基本方法和步骤。
- 培养解决电路问题时的逻辑思维和问题诊断能力。
3. 训练内容3.1 电路图符号和元件功能- 研究电阻、电容、电感、开关等常见电路元件的符号和功能。
- 了解各种电子元件在电路中的作用和应用。
3.2 电流路径和电压变化分析- 分析电路图中各个路径的电流流向和大小。
- 观察并计算电路元件之间的电压变化。
3.3 电路图分析的基本方法和步骤- 研究如何根据电路图进行正确的分析和推理。
- 掌握基本的电路图分析技巧,如串联、并联、等效电路的转换等。
3.4 问题诊断和解决- 练分析具体电路图中的问题,并进行故障诊断。
- 学会运用所学的电路图分析方法解决实际的电路问题。
4. 训练建议- 从简单电路图开始,逐步深入研究和训练。
- 多进行实践,通过模拟电路环境来加强理论知识的应用能力。
- 参考相关教材和在线资源,扩充研究内容。
5. 结论电路图分析专项训练是提升电子工程技能的重要环节,通过系统的研究和实践,可以帮助研究者掌握电路图分析的基本技巧和解决问题的能力。
建议研究者持续努力,不断提升自己的电路图分析能力。
参考资料:- "电路分析与设计" 作者:张学工,清华大学出版社,2018年。
电路分析试题和答案(全套)

电路分析试题(Ⅰ)二. 填空(每题1分,共10分)1.KVL体现了电路中守恒的法则。
2.电路中,某元件开路,则流过它的电流必为。
3.若电路的支路数为b,节点数为n,则独立的KCL方程数为。
4.在线性电路叠加定理分析中,不作用的独立电压源应将其。
5.若一阶电路电容电压的完全响应为uc(t)= 8 - 3eV,则电容电压的零输入响应为。
7.若一个正弦电压的瞬时表达式为10cos(100πt+45°)V,则它的周期T 为。
8.正弦电压u(t)=220cos(10t+45°)V, u(t)=220sin(10t+120°)V,则相位差φ=。
9.若电感L=2H的电流i =2 cos(10t+30°)A (设u ,为关联参考方向),则它的电压u为。
三.求下图单口网络的诺顿等效电路,并画等效电路图。
(15分)a b四.用结点分析法,求各结点电位和电压源功率。
(15分)1 2五.一阶电路如图,t = 0开关断开,断开前电路为稳态,求t ≥ 0电感电流(t) ,并画出波形。
(15分)电路分析试题(Ⅱ)二. 填空(每题1分,共10分)1.电路的两类约束是。
2.一只100Ω,1w的电阻器,使用时电阻上的电压不得超过 V。
3.含U和I两直流电源的线性非时变电阻电路,若I单独作用时,R 上的电流为I′,当U单独作用时,R上的电流为I",(I′与I"参考方向相同),则当U和I共同作用时,R上的功率应为。
4.若电阻上电压u与电流i为非关联参考方向,则电导G的表达式为。
5.实际电压源与理想电压源的区别在于实际电压源的内阻。
6.电感元件能存储能。
9.正弦稳态电路中, 某电感两端电压有效值为20V,流过电流有效值为2A,正弦量周期T =πS , 则电感的电感量L=。
10.正弦稳态L,C串联电路中, 电容电压有效值为8V , 电感电压有效值为12V , 则总电压有效值为。
11.正弦稳态电路中, 一个无源单口网络的功率因数为0. 5 , 端口电压u(t) =10cos (100t +ψu) V,端口电流(t) = 3 cos(100t - 10°)A (u,i为关联参考方向),则电压的初相ψu为。
电子线路综合练习题三
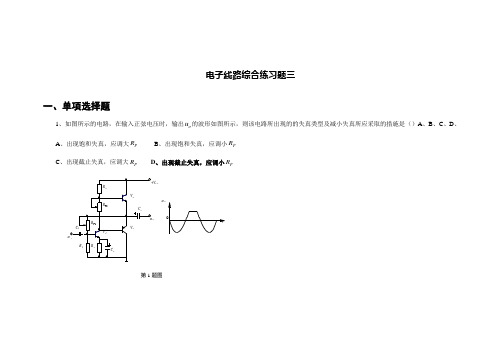
电子线路综合练习题三一、单项选择题1、如图所示的电路,在输入正弦电压时,输出o u 的波形如图所示,则该电路所出现的的失真类型及减小失真所应采取的措施是()A 、B 、C 、D 、 A 、出现饱和失真,应调大P R B 、出现饱和失真,应调小P R C 、出现截止失真,应调大P R D 、出现截止失真,应调小P RR R R R R 112233312C C C V V V +V ccu u ioP 1P2Ou ot第1题图+-u s+V cc+-u o123R R R fff fC C s2第2题图R R R R R 112233312P1P2C C C V V V +V c cu u ioOu ot第3题图2、如图所示的电路中,欲稳定电路的输出电压,应采用的方法是() A 、1与3连接B 、1与4连接C 、2与3连接D 、2与4连接3、如图所示的电路中,输入信号I u 为正弦波,输出o u 的波形如图所示,为减少失真应() A 、调大1P R B 、调小1P R C 、调大2P R D 、调小2P R∞u u io R p5KΩ10KΩ10KΩ第5题图CW7908∞C C IoR R R p 12R L++--U U I o第4题图4、如图所示,三端稳压器采用CW7908,输入 电压I U 足够大,1R =2R =400Ω,P R 的总阻值 也为400Ω,则输出电压Uo 的 可调范围是() A 、-2.67 ~ -5.53V B 、-12 ~ -24V C 、12 ~ 24V D 、2.67 ~ 5.53V5、如图所示的电路,P R 的总阻值也为10K Ω,则电路电压放大倍数IO u u uA 的可调范围是()A 、-1.5 ~ -3VB 、-0 ~ 3VC 、1.5 ~ 3VD 、1 ~ 2VR R R C C C L L 1112223+V c c第6题图第7题图6、如图电路所示,以下说法正确的是()A 、电路不满足振幅平衡条件,故不能自激振荡B 、电路不满足相位平衡条件,故不能自激振荡C 、电路不满足振幅及相位平衡条件,故不能自激振荡D 、电路满足相位平衡条件,且结构合理,故有可能自激振荡7、某组合逻辑电路的输出Y 与AB 的波形如图所示,则该电路的逻辑功能为 A 、与非B 、或非C 、异或D 、同或8、若误用万用表的电流表或电阻挡去测量电路的两点间的直流电压,则()A 、万用表的指针不动B 、万用表测量误差太大C 、万用表读数不稳定D 、可能损伤或烧毁表头9、测得某放大电路中三极管的三个电极对地电位分别是:V 1=-1.5V ,V 2 = -1.5V ,V 3 = -1.5V ,则三个电极的顺序和管型分别为A 、b c e PNP 型B 、b c e NPN 型C 、c b e PNP 型D 、c b eNPN 型 10、在N 型半导体中()A 、只有自由电子B 、只有空穴C 、有空穴也有自由电子D 、以上答案都不对 11、收音机搜索电台,利用的原理是( )A 、自激原理B 、调谐原理C 、蒸馏原理D 、稳压原理 12、场效晶体管是一种( )控制性电子元件 A 、电流B 、电压C 、光D 、磁&&&11ABY13、三端集成稳压器CW7812的输出电压为A 、-12VB 、-24VC 、24VD 、12V14、直接耦合放大器电路存在零点漂移的主要原因是( )A 、电阻阻值B 、参数受温度影响C 、三极管参数的分散性D 、电源电压不稳定15、引入负反馈后,放大器的状态为( ) A 、静态B 、动态C 、开环状态D 、闭环状态 16、LC 正弦波振荡器电路的振荡频率为A 、LCf 10=B 、LC f 10= C 、LCf π210= D 、LC f π210=17、下列逻辑式中,正确的逻辑公式( )A 、AB B A =+ B 、B A B A =+C 、B A B A +=+D 、以上都不对二、填空题1、在图3—3—14所示的电路中,当ωt =Cω1时,电路相当于_________状态。
电子线路试题及答案

电子线路试题及答案### 电子线路试题及答案#### 一、选择题(每题2分,共20分)1. 电阻串联时,总电阻值等于各电阻值之和。
这种说法是()。
- A. 正确- B. 错误2. 一个电路中的电流源可以等效为一个()。
- A. 电压源- B. 电阻- C. 电容3. 在并联电路中,总电阻的倒数等于各并联电阻的倒数之和。
这种说法是()。
- A. 正确- B. 错误4. 一个二极管的正向导通电压通常在()伏特左右。
- A. 0.3- B. 0.7- C. 1.05. 放大电路的基本功能是()。
- A. 整流- B. 滤波- C. 信号放大#### 二、填空题(每题2分,共20分)1. 在电路中,电源的内阻越小,输出的电流能力越()。
2. 一个理想电压源的特点是无论负载如何变化,其输出电压保持()。
3. 欧姆定律的公式是 V = I * R,其中 V 代表()。
4. 一个电路的功率计算公式是 P = V * I,其中 P 代表()。
5. 在分压电路中,各电阻的分压与电阻值成()。
#### 三、简答题(每题10分,共30分)1. 简述整流电路的工作原理及其应用场景。
2. 解释滤波电路的作用,并简述其基本类型。
3. 描述反馈放大电路的基本概念及其优点。
#### 四、计算题(每题15分,共30分)1. 已知一个串联电路中有三个电阻,分别为R1 = 100Ω,R2 = 200Ω,R3 = 300Ω。
求该串联电路的总电阻。
2. 假设有一个并联电路,其中包含两个电阻,R1 = 500Ω 和 R2 = 1000Ω。
求该并联电路的总电阻,并计算当总电压为 10V 时,通过R1 的电流。
3. 给定一个电路,其中包含一个 5V 的理想电压源和一个1000Ω 的电阻。
计算通过电阻的电流,并简述电路的功率。
#### 答案#### 一、选择题1. A2. A3. A4. B5. C#### 二、填空题1. 强2. 恒定3. 电压4. 功率5. 正比#### 三、简答题1. 整流电路将交流电转换为直流电,常用于电源适配器和电池充电器。
电路分析习题.doc

一、填空题:1.电流所经过的路径叫做 ,通常由 、 和 三部分组成。
2.对于理想电压源而言,不允许路,但允许路。
3.实际电压源模型“ 24V 、 8Ω”等效为电流源模型时,其电流源I SA ,内阻 R iΩ。
4、一阶电路全响应的三要素是指待求响应的值、值和。
5、三相电源作 Y 接时,由各相首端向外引出的输电线俗称 线,由各相尾端公共点向外引出的输电线俗称线,这种供电方式称为制。
6.两个具有互感的线圈顺向串联时,其等效电感为;它们反向串联时, 其等效电感为。
7.空芯变压器与信号源相连的电路称为 回路,与负载相连接的称为回路。
8. 一阶 RC 电路的时间常数 τ = ;一阶 RL 电路的时间常数 τ =。
在一阶 RC 电路中,若 C不变, R 越大,则换路后过渡过程越 。
RL 一阶电路中, L 一定时, R 值越大过渡过程进行的时间就越。
9.对称三相电路的线电压为 380V ,负载为△形连接 , 每相负载 Z=4-j3 ,则三相负载总功率为。
10、已知某正弦交流电压的有效值为 220V ,频率为 50Hz ,初相位为 - 60o , 则电压的瞬时表达式为。
已知正弦电压在 t=0 时为 120V ,其初相位为 45o ,则它的有效值为。
11.无源二端理想电路元件包括、 元件、元件和 元件。
12.电阻均为 90Ω的 形电阻网络,若等效为 Y 形网络,各电阻的阻值应为 Ω。
13.在多个电源共同作用的 电路中,任一支路的响应均可看成是由各个激励单独作用下在该支路上所产生的响应的,称为叠加定理。
14. 额定值为 220V 、40W 的灯泡,接在 110V 的电源上,其输出功率为 W 。
15、电感的电压相量于电流相量π /2 ,电容的电压相量于电流相量π /2 。
16.R 、L 、C 并联电路中,测得电阻上通过的电流为 3A ,电感上通过的电流为 8A ,电容元件上通过的电流是 4A ,总电流是A,电路呈性。
17.RLC 串联谐振电路的谐振条件是 =0。
电路分析考试题及答案

电路分析考试题及答案一、单项选择题(每题2分,共20分)1. 电路中,电压与电流相位完全相反的元件是()。
A. 电阻B. 电感C. 电容D. 二极管答案:C2. 在交流电路中,纯电阻电路的功率因数为()。
A. 0B. 0.5C. 1D. -1答案:C3. 电路中,电流的参考方向与实际方向相反时,该电流的值为()。
A. 正值B. 负值C. 不确定D. 零答案:B4. 电路中,若电阻R1和R2并联,则总电阻R的计算公式为()。
A. R = R1 + R2B. R = R1 * R2 / (R1 + R2)C. 1/R = 1/R1 + 1/R2D. R = R1 * R2答案:C5. 电路中,理想电压源与理想电流源不能()。
A. 串联B. 并联C. 直接替换D. 混合使用答案:C6. 电路中,RLC串联电路的谐振频率f0计算公式为()。
A. f0 = 1/(2π√(LC))B. f0 = 1/(2π√(L/C))C. f0 = 1/(2π√(R/L))D. f0 = 1/(2π√(R/C))答案:A7. 电路中,三相电路的星形接法中,线电压与相电压的关系为()。
A. U线 = U相B. U线= √3 * U相C. U线 = 2 * U相D. U线= √2 * U相答案:B8. 电路中,若要测量交流电路中的功率,应使用()。
A. 直流电压表B. 直流电流表C. 交流电压表D. 功率表答案:D9. 电路中,二极管正向导通时的电压降约为()。
A. 0.7VB. 1.5VC. 3VD. 5V答案:A10. 电路中,若要实现电压放大,应使用()。
A. 电阻B. 电容C. 电感D. 三极管答案:D二、填空题(每题2分,共20分)1. 电路中,欧姆定律的数学表达式为 V = ________。
答案:IR2. 电路中,电容器的容抗计算公式为 Xc = ________。
答案:1/(2πfC)3. 电路中,电感器的感抗计算公式为 Xl = ________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018年《电路分析与电子线路》综合训练题注意:2018年《电路分析与电子线路》综合训练组队共同讨论完成综合训练题目3-4题,以书面形式撰写报告,需要详细的讨论过程和仿真的结果。
请同学们自学“数值分析软件(如MATLAB等)及电路仿真软件(如Multisim或Pspice等)”。
提交书面报告时间:6月20日前。
Project 1Power SuppliesObjective: This project will show some of the basic principles of power supplies using fullwave rectifier, Zener diode, and fixed-voltage regulator circuits.Components: Bridge Rectifier (50 PIV, 1 A), Zener diode (10 V at 500 mW), 7805 regulatorIntroduction:Most of the direct current (DC) power used in electronic devices is derived by converting 60 Hz, 115 V alternating current (AC) power to direct current power. This AC to DC conversion usually involves a step-down transformer, rectifier, filter, and a regulator. The step-down transformer is used to decrease the AC line voltage from 115 V RMS to an RMS value near the DC voltage needed. The output of the step-down transformer is then fed into a diode rectifier circuit that only outputs positive halves of the input sinusoid. A filter is then used to smooth the rectifier output to achieve a nearly constant DC voltage level. A regulator can be added after the filter to ensure a constant output voltage in spite of changes in load current and input voltages.Two different types of voltage regulators will be used in this project. The first involves a Zener diode circuit and the second involves a voltage regulator circuit. A Zener diode can be used as a voltage regulator when the diode is reverse biased and operated in the breakdown region. To maintain voltage regulation, the Zener diode must be operated in the breakdown region at a current greater than the "knee" current (I ZK). Forcurrents greater than I ZK, the Zener diode characteristic curve is nearly vertical and the voltage across the diode changes very little. Of course there is a maximum current the diode can tolerate, so good regulation is provided when the diode is reverse biased with currents between I ZK and I ZMAX. Zener diodes are available with a wide variety of breakdown voltages. Another type of voltage regulator is available with the 7800 series regulators. This series of fixed-voltage regulators is numbered 78xx, where xx corresponds to the value of the output voltage. Output voltages from 5 to 24 volts are available. These regulators are easy to use and work very well.Design:1. Find approximations for the DC voltage level and AC peak to peak ripple voltage for the bridge rectifier and filter circuit of Figure 1-1.2. For the Zener diode regulator circuit of Figure 1-2 assume that the Zener diode will regulate at 10 V over a current range of 5 mA to 25 mA. Assuming that the current flowing through R is always between 5 mA and 25 mA and the Zener diode is regulating at 10 V, find the minimum values of R and R L required. You may assume the forward diode drop for the two diodes is 1 V.Lab Procedure:1. Construct the bridge rectifier circuit of Figure 1-1 without the capacitor. Use the Variac with the step-down transformer for the input voltage to the bridge rectifier. With the transformer plugged into the Variac, adjust the Variac until the secondary voltage from the transformer equals 12 V RMS. BE CAREFUL not to short the secondary terminals!Observe the secondary waveform on the oscilloscope. Put the oscilloscope on DC coupling and observe the load voltage waveform V L. Remember that both the input source and the load cannot share a common ground terminal.2. Remove power from the circuit. Insert the capacitor as shown in Figure 1-1 being sure to observe the correct polarity. Energize the circuit. With the oscilloscope on DC couplingobserve V L. Measure the DC voltage level using the digital voltmeter. With the oscilloscope on AC coupling observe the ripple voltage V R. Compare these measured values with the calculated values.3. Observe the effect of loading on the circuit by changing the load resistor from 1 kΩto 500 Ω. Measure the DC voltage level with the digital voltmeter. Observe the ripple voltage with the oscilloscope set on AC coupling. Compare these values with the previously recorded values.4. Record the Zener diode characteristic curve from the digital curve tracer. Note the value of the breakdown voltage in the breakdown region. Also note the value of the "knee" current I ZK.5. After verifying your designed values for R and R L with the instructor, construct the Zener diode regulator circuit of Figure 1-2. Measure the DC voltage level with the digital voltmeter for the minimum value of R L along with several values above and below the minimum value. Be careful not to overload the Zener diode. Comment on the circuit's operation for these different load resistances.6. Construct the 7805 regulator circuit of Figure 1-3 being careful to observe the correct pin configuration of the regulator. Measure the load voltage for R L equal to 300 Ω, 200 Ω, and 100 Ω. Calculate the current for each of these cases. Does the value of the load resistor affect the output voltage?7. Using R L equal to 200 Ω, record the 7805 regulator input voltage (pin 1) and output voltage (pin 3). Decrease the regulator input voltage by decreasing the setting of the Variac. For each decrease in amplitude, record the regulator input and output voltages. Continue decreasing the amplitude until the output of the regulator drops a measurable amount below 5 V. What is the minimum input voltage needed for the 7805 regulator to produce a 5 V output?Questions:1. Why can't the input source and load have a common ground in the bridge rectifier circuit?2. Can the Zener diode be used as a conventional diode? Explain your answer and verify with a curve from the curve tracer.3. Would the value of the output filter capacitor have to increase, decrease, or remain the same to maintain the same ripple voltage if the bridge rectifier were changed to a half-wave rectifier? Explain your answer.4. How would increasing the frequency of the input source affect the ripple voltage assuming all components remained the same?Project 2Analog Applications of the Operational AmplifierObjective:This project will demonstrate some of the analog applications of an operational amplifier through a summing circuit and a bandpass filter circuit.Components: 741 op-ampIntroduction:Figure 2-1 shows a weighted summer circuit in the inverting configuration. This circuit can be used to sum individual input signals with a variable gain for each signal. The virtual ground at the inverting input terminal of the op-amp keeps the input signals isolated from each other. This isolation makes it possible for each input to be summed with a different gain.The bandpass filter shown in Figure 2-2 uses an op-amp in combination with resistors and capacitors. Since the op-amp can increase the gain of the filter, the filter is classified as an active filter. This bandpass filter circuit is extremely useful because the center frequency can be changed by varying a resistor instead of changing the values of the capacitors. The center frequency is given by:The center frequency can be changed by varying the variable resistor R3. Increasing R3 decreases the center frequency while decreasing R3 increases the center frequency. The bandwidth is given by:Notice that the bandwidth is independent of the variable resistor R3 so the center frequency may be varied without changing the value of the bandwidth. The gain at the center frequency of the bandpass filter is given by:Design:1. Find the relationship between the output and inputs for the weighted summer circuit of Figure 2-1.2. Design a bandpass filter with a center frequency of 2.0 kHz and a bandwidth of 200 Hz. Let the voltage gain at the center frequency be 20. Check your design with PSPICE®. Use ± 15 V supplies for the op-amp. Use R L = 2.4 kΩ.Figure 2 - 1: Weighted SummerFigure 2 - 2: Bandpass FilterLab Procedure:1. Construct the summing amplifier of Figure 2-1. Design for the transfer function to be V O = -2 V IN1 - V IN2. Use ± 15 V supplies for the op-amp. Use R L = 2.4 kΩ.2. Let V IN1be a 1 V peak sine wave at 1 kHz and V IN2equal to 5 V DC. Verify the amplifier's operation by monitoring the output waveform on the oscilloscope.3. Construct the bandpass filter of Figure 2-2. Use the designed values for the resistors and capacitors. Use ±15 V supplies for the op-amp. Use R L = 2.4 k .4. Record and plot the frequency response (you may want to use computer control for the sweep and data collection). Find the center frequency, corner frequencies, bandwidth, and center frequency voltage gain to verify that the specifications have been met.5. Change R3to lower the center frequency from 2.0 kHz to 1.0 kHz. Repeat part 4 for the new frequency response. Verify that the new center frequency is 1.0 kHz. What is the new bandwidth? What is the new center frequency voltage gain? Compare with the measurements of Procedure 4.Questions:1. Could the summer circuit be used with the inputs connected to the noninverting terminal and produce the same affect without the inversion? Explain.2. What is/are the benefit(s) of using an op-amp circuit to produce a bandpass filter over using an RLC circuit with a noninverting op-amp at the output of the RLC circuit?Project 3Analog Computer Applications using the Operational AmplifierObjective:This project will focus on the use of the operational amplifier in performing the mathematical operations of integration and differentiation. The design of a simple circuit (analog computer) to solve a differential equation will also be included.Components: 741 op-ampIntroduction:Figures 3-1 and 3-2 illustrate two op-amp based circuits designed to perform differentiation and integration respectively. The operations are performed "real-time" and can be helpful in observing both initialtransients and steady state response. The analysis of the circuits is based on the "ideal" op-amp assumptions and performed in the time domain. The resistor R I shown in the two circuits is included to help with stability and for general circuit protection. The value for R I is nominally set equal to the feedback resistor (Figure 3-1) or the input resistor (Figure 3-2). The purpose of the optional resistor is left for student investigation in conjunction with the summary questions.The differentiator and integrator circuits may be combined with "standard" inverting and non-inverting op-amp circuits to provide the building blocks for analog computers. The resultant analog computer circuits are designed to solve differential and/or integral/differential equations in a real time environment. The ability to easily include, and change, initial conditions and forcing functions are additional benefits of the analog computers. Figure 3-3 illustrates a circuit designed to solve the second order differential equation KY - Y = 0 with the initial condition Y(0) = - V X and K = R1R2C1C2. The initial condition is "set" by using the momentary contact switch to force the output to equal the applied voltage at t = 0 (the time the switch is closed).While the major advances in digital computers and digital signal processing have reduced the use of these three circuits, they are still a fast and relatively inexpensive method for process control and stability/operation analysis for systems that can be represented in terms of differential equations.Design:1. Derive the expressions relating the input and output signals for the circuits shown in Figures 3-1 and 3-2.2. Design an analog computer to solve with y(0) = 2.Solve the differential equation when f(t) = 0 and verify your results using PSpice®.Figure 3 - 1: DifferentiatorFigure 3 - 2: IntegratorFigure 3 - 3: Analog Computer (linear, second order, homogenousdifferential equation)Lab Procedure:1. Construct the circuit shown in Figure 3-1. Use ± 15 V supplies for the op-amp and a load resistance of ≈2.4 kΩ.2. Verify the operation of the circuit using a 500 mV peak, 50 Hz sinewave as the input signal. Be sure to design the "gain" such that the output does not saturate.3. Repeat step 2 with a sinewave frequency of 500 Hz. Does the circuit still operate correctly? What changes need to be made to prevent output saturation?4. Repeat steps 2 and 3 using a triangle wave and then using a square wave with the same magnitudes and frequencies as used in steps 2 and 3.5. Construct the circuit shown in Figure 3-2. Again, use ± 15 V supplies for the op-amp and a load resistance of ≈ 2.4 kΩ.6. Repeat steps 2 through 4 for this circuit. Be sure to adjust your "gain" as necessary to maintain an output signal within the saturation limits of ≈± 12 V.7. Construct the circuit designed to solve the differential equation in part 2 of the design section. Verify the operation of the design using three different input waves (sine, triangle, and square). Determine the operation for at least three differentfrequencies -- 10 Hz, 1 kHz, and 100 kHz. Explain any differences in operation of the circuit. What affect does the initial condition have on the result?Questions:1. How could you use the differentiator to obtain an estimate of the slew rate for the op-amp?2. Why should you include a resistor in parallel with the capacitor in the integrator?3. What is the purpose of the resistor in series with the input capacitor in the differentiator?4. Is it possible to design a circuit to perform the differentiation and integration functions using the non-inverting input? Explain your answer.Project 4Common Emitter Amplifier(designed for two lab periods)Objective: This project will show how the h-parameters for a BJT can be measured and used in an equivalent circuit model for the BJT. A CE small signal amplifier will be biased and designed to specifications along with both low and high frequency response and adjustment. Series-series feedback will also be used to control the bandwidth and input impedance of the CE amplifier.Components: 2N2222 BJTIntroduction:In order for circuits involving transistors to be analyzed, the terminal behavior of the transistor must be characterized by a model. Two of the models often used for a BJT are the hybrid-π and the h-parameter models. The complete hybrid-πcircuit model for the BJT is shown in Figure 9-1. This model includes the internal capacitances and output resistance of the BJT. Inclusion of the internal transistor capacitances makes the hybrid-π model valid throughout the entire frequency range of the transistor. Typical data sheet values of Cπ and Cμ are 13 pF and 8 pF respectively. These values are so small that Cπ and Cμ may be considered open circuits for midband frequencies. The resistance r x typically has a value in the tens of ohms and can be considered a short circuit while rμand r o are usually extremely large in value and can be considered open circuits.The h-parameter small signal model for the BJT is characterized by the four h-parameters and is shown in Figure 9-2. Unlike the hybrid-πmodel, the h-parameter model does not ordinarily include frequency related effects and components and is therefore generally valid only at midband frequencies and below . However the h-parameter model is very useful since the h-parameters can be easily measured for a BJT. The value of h re is usually on the order of 10-4 and can be considered a short circuit. The value of h oe is usually on the order of 10-5 S making 1/h oe effectively an open circuit for most circuit configurations and biases. Making the same assumptions, the hybrid-π and h-parameter models are equivalent at midband frequencies.For a transistor to operate as an amplifier, it must have a stable bias in the active region. To bias a transistor, a constant DC currentmust be established in the collector and emitter. This current should be as insensitive as possible to variations in temperature and β (or h fe). The voltage across the base-emitter junction decreases about 2 mV for each 1 °C rise in temperature, therefore it is important to stabilize V BE to ensure that the transistor does not overheat. The circuit shown in Figure 9-3 is the biasing scheme most often used for discrete transistor circuits. For this circuit, the base is supplied with a fraction of the supply voltage V CC through the voltage divider R B1, R B2. For ease of circuit analysis, the Thevenin equivalent circuit shown in Figure 9-4 can replace the voltage divider network. To ensure that the emitter current is insensitive to variations in β and V BE, V BB should be much greater than V BE and R BB should be much less than βR E. R BB is usually 20-30% of the product βR E. The voltage across R E is also usually 2-3 volts for good βstabilization. This same biasing scheme can be used for all three of the BJT amplifier configurations (CB, CC, CE).The BJT CE amplifier is shown in Figure 9-5. The signal source and resistive load are capacitively coupled to the amplifier. The coupling capacitors C1and C2, emitter bypass capacitor C E, and internal transistor capacitances shape the frequency response of the amplifier. A typical amplifier frequency response curve is shown in Figure 9-6. The low half power corner frequency F L is controlled by the input and output coupling capacitors and the emitter bypass capacitor. The high half power corner frequency F H is controlled by the internal transistor capacitances and any separate load capacitor. The bandwidth is the difference between the high and low corner frequencies (F H - F L). As the signal frequency drops below midband, the impedance of the coupling capacitors C1 and C2 and emitter bypass capacitor C E increases. The coupling capacitors drop more signal voltage and the emitter bypass capacitor begins to open up and causes increased series-series feedback resulting in a reduction of the gain. One method of relating C1, C2, and C E to the low cutoff frequency is the short circuit time constant method. The time constant method is advantageous because it provides an approximate value for the cutoff frequencies without exactly finding all the poles and zeros of a circuit. The time constant method also helps show which capacitors are dominant in determining the corner frequencies. The short circuit time constant method relates F L and circuit capacitors by:where F L is the low half power frequency, n c is the number of coupling and bypass capacitors in the circuit, and C i is the value, in Farads, of the ith capacitor. R is is the resistance facing the ith capacitor withthe ith capacitor removed and all other coupling and bypass capacitors replaced by short circuits and the input signal reduced to zero. This resistance calculation is repeated for each coupling and bypass capacitor in the circuit.The internal capacitances of a transistor have values in the picofarad (pF) range that begin to decrease the gain of the amplifier for frequencies above midband. A method of relating the internal transistor capacitances Cπ and C m to the high cutoff frequency is the open circuit time constant method. This method relates F H and the internal transistor capacitances by:where F H is the high half power frequency, n c is the number of internal transistor capacitors in the circuit, and C i is the value, in Farads, of the ith capacitor. R io is the resistance facingthe ith capacitor with the ith capacitor removed and all internal transistor capacitors replaced by open circuits and the input signal reduced to zero. This resistance calculation is repeated for each internal transistor capacitor in the circuit.When the emitter resistor of the CE amplifier is left unbypassed, the input current signal flows through the unbypassed emitter resistor as does the output signal current. This unbypassed emitter resistor in the CE amplifier produces series-series feedback. The feedback resistor is R E. Feedback is used in amplifiers to control input and output impedances, extend bandwidth, enhance signal-to-noise ratio, and reduce parameter sensitivity. These feedback performance improvements are all at the expense of gain in the amplifier.Figure 4 - 1: Hybrid-π BJT ModelFigure 4 - 2: h Parameter BJT ModelFigure 4 - 3: BJT Typical Biasing CircuitFigure 4 - 4: Thevenin Equivalent Biasing CircuitFigure 4 - 5: Common Emitter AmplifierFigure 4 - 6: Typical Amplifier Frequency Bode DiagramDesign:Design a common emitter amplifier with R E [R E1 + R E2] completely bypassed with the following specifications:1. use a 2N2222 BJT and a 12 volt DC supply2. midband gain V O/V S≥ 503. low cutoff frequency F L between 100 Hz and 200 Hz4. input impedance as seen by the source ≥ 1 kΩ5. V O symmetric swing ≥ 2.0 volts peak (4 V p-p)6. load resistor R L = 1.5 kΩ7. source resistance R S = 50 Ω (this is in addition to the function generator'sinternal resistance)Lab Procedure: (steps 1 and 2 may be omitted if done prior to this lab period and the same BJT is used)1. From the digital curve tracer, find the value of βDC and βAC at the designed Q-point of the CE amplifier. Remember βDC= I C/I B and βAC= ∆I C/∆I B. How do the two β values compare?2. Determine the values of h oe and h ie from the digital curve tracer. The slope of the transistor I C-V CE curves in the active region is h oe. Find h ie by looking at the base-emitter junction as a diode on the curve tracer. The tangent slope of the I B-V BE curve at the I BQ point is 1/h ie.3. Construct the CE amplifier of Figure 9-5. Remember R S is installed in addition to the internal 50 Ωresistance of the function generator. Note that (R E1+ R E2) should equal the designed value for R E and R E1≈R E2. Verify that the specifications have been met by measuring the Q-point, midband voltage gain, and peak symmetric output voltage swing. Note any distortion in the output signal.4. Observe the loading affect by replacing R L first by 150 Ω and then by 15 kΩ. Note any changes in the output signal and comment on the loading affect.5. Use computer control to record and plot the frequency response. Find the corner frequencies and bandwidth to verify that the specifications have been met.6. Measure the input impedance seen by the source [look at the current through R S and the node voltage on the transistor side of R S] and the output impedance seen by the load resistor [look at the open circuit voltage and the current through and voltageacross R L = 1.5 kΩ]. Verify that the input impedance specification has been met.7. Now adjust the bypass capacitor C E so that R E1 is not bypassed (which is a series-series feedback configuration). Measure the Q-point and midband voltage gain. Note any distortion in the output signal.8. Repeat steps 4 - 6.9. Remove the bypass capacitor C E completely. Measure the Q-point and midband voltage gain. Note any distortion in the output signal.10. Repeat steps 4 - 6.Questions:1. Compare the measurements in Lab Procedures 3-10 to the theoretical predictions such as those obtained using PSPICE®. Note how increasing the feedback affects the gain, bandwidth, and input and output impedances.2. Can you think of a way to vary the amount of feedback (gain) using a potentiometer of a value equal to R E without affecting the Q point?3. How can F H be reduced using external components?4. Why is the value of F H measured in the lab generally different from (lower than) the value of F H determined using PSPICE® or manual calculations?Project 5Common Collector AmplifierObjective:This project will show the biasing, gain, frequency response, and impedance properties of a common collector amplifier.Components: 2N2222 BJTIntroduction:The common collector amplifier as shown in Figure 10-1 is one of the most useful small-signal amplifier configurations. The same biasing scheme and frequency response approximation technique as used for the common emitter amplifier can also be used for the common collector amplifier. The only change that needs to be made in biasing is that the voltage across the emitter resistor R E is usually larger for the common collector to allow a greater output voltage swing. The collector resistor is also usually omitted in the common collector configuration. The main characteristics of the common collector amplifier are high input impedance, low output impedance, less than unity voltage gain, and high current gain. This amplifier is most often used as a buffer or isolation amplifier to connect a high impedance source to a low impedance load without loss of signal. The load seen by the amplifier's signal sourceis the input impedance of the amplifier. With a high input impedance, the CC amplifier loads the source very lightly. Therefore the signal source is largely isolated or buffered from the rest of the circuit. The maximum current gain for the CC amplifier is β+ 1. This high current gain allows the CC amplifier to increase the power of the signal. These power and current gains make the CC amplifier a practical choice as an output stage amplifier driving several devices and/or low impedance loads.Design:Design a common collector amplifier with the following specifications:1. use a 2N2222 BJT and a 12 volt DC supply2. midband gain V O/V S≥ 0.53. low cutoff frequency F L between 100 Hz and 200 Hz4. input impedance seen by the source ≥ 10 kΩ5. V O symmetric swing ≥ 3.0 volts peak (6 V p - p)6. load resistor R L = 200 Ω7. source resistance R S = 50 Ω (this is in addition to the function generator's internal resistance)Figure 5- 1: Common Collector AmplifierLab Procedure:1. Construct the CC amplifier of Figure 10-1. Remember R S is installed in addition to the internal 50 Ω resistance of the function generator. Verify the amplifier operation by measuring the Q-point and midband voltage gain. Monitor the output on the oscilloscope to make sure the waveform is not clipped. Note any distortion in the output signal.2. Adjust the input signal level to get a3.0 volt peak symmetric output voltage swing.3. Determine the midband current gain I L/I S[measure I S by looking at the current through R S] What is the overall power gain?4. Observe the loading affect by replacing R L first by ≈ 50 Ω and then by ≈750 Ω. Note any changes in the output signal and comment on the loading affect.5. Use computer control to record and plot the frequency response. Find the corner frequencies and bandwidth to verify that the specifications have been met.6. Measure the input impedance seen by the source [look at the current through R S and the node voltage on the transistor side of R S] and the output impedance seen by the load resistor [look at the open circuit voltage and the current through and voltageacross R L]. Verify that the input impedance specification has been met.Questions:1. How can you achieve maximum power transfer from the input signal source to the amplifier circuit? Is the load resistance a factor in the answer?2. What value of load resistance results in maximum voltage gain? What load resistance results in maximum power transfer to the load?3. Compare the results of the current gain found in Lab Procedure 3 with the maximum possible gain of β +1. Comment on any differences.4. Compare the measurements in Lab Procedures 1-6 to the theoretical predictions such as those obtained using PSPICE®. Note that you must adjust the circuit file to determine the output impedance.5. What other method could be used to measure R O?。
