九年级(上)数学期中考试卷(含答案)

合集下载

江西省九江市第三中学2024-2025学年九年级上学期期中考试数学试卷(含答案)

江西省2025届九年级期中综合评估数学▶上册◀说明：共有六个大题，23个小题，满分120分，考试时间120分钟.一、单项选择题（本大题共6小题，每小题3分，共18分）在每小题列出的四个备选项中只有一项是最符合题目要求的，请将其代码填入题后括号内错选、多选或未选均不得分.1.若关于的函数是二次函数，则的值为（）A.1B.2C.0D.32.以下是几种化学物质的结构式，其中文字上方的结构式图案属于中心对称图形的是（）A.甲醛B.甲烷 C.水 D.乙酸3.已知关于的一元二次方程有一个根为，则另一根为（）A.7B.3C.D.4.如图，四边形是的内接四边形，连接，，若，则的度数是（）A. B. C. D.5.在平面直角坐标系中，将抛物线绕顶点旋转得到新抛物线，再将新抛物线沿轴翻折得到抛物线，则，，的值分别是（）A.2，，11B.2，，5C.，，11D.，8，56.某校计划举办劳动之星颁奖典礼，想在颁奖现场设计一个如图1所示的抛物线型拱门入口.要在拱门上顺次粘贴“劳”“动”“之”“保”（分别记作点，，，）四个大字，要求与地面平行，且，抛物线最高点的五角星（点）到的距离为，，，如图2所示，则点到的距离为（）图1 图221.124.1~x 31my x x =-+m x 2520x x m -+=2-7-3-ABCD O OA OC 86AOC ∠=︒ADC ∠94︒127︒136︒137︒285y ax x =-+P 180︒x22y x bx c =++a b c 8-8-2-8-2-A B C D BC BC AD ∥E BC 0.6m 2m BC =4m AD =C ADA. B. C. D.二、填空题（本大题共6小题，每小题3分，共18分）7.一元二次方程的解为______.8.在平面直角坐标系中，点关于原点对称的点的坐标是______.9.如图，是半圆的直径，，为的中点，连接，，则的度数为______.10.《九章算术》“勾股”章有一题：“今有二人同所立.甲行率七，乙行率三.乙东行，甲南行十步而斜东北与乙会，问甲、乙行各几何.”大意是说：已知甲、乙两人同时从同一地点出发，甲每单位时间走7步，乙每单位时间走3步.乙一直向东走，甲先向南走10步，后又斜向北偏东方向走了一段后与乙相遇.那么相遇时，甲、乙各走了多远？设甲走了步（步为古代长度单位，类似于现在的米），根据题意可列方程：____________.（结果化为一般式）11.在平面直角坐标系中，若抛物线向左平移2个单位长度后经过点，则的最大值为______.12.如图，在矩形中，连接，，，将线段绕点顺时针旋转，得到线段，连接，，当时，的周长为______三、解答题（本大题共5小题，每小题6分，共30分）13.（1）解方程：.（2）如图，将绕点逆时针旋转得到，若，且于点，求的度数.14.某件夏天T 恤的售价为100元，因换季促销，在经过连续两次降价后，现售价为81元，求平均每次降价的百分率.15.自古以来，景德镇就是中国陶瓷文化的象征，生产的瓷器闻名四方，远销世界各地.如图，这是景德镇2m 1.8m 2.4m 1.5m290x -=()2,4-BC OAB AC =D AC OD BD BDO ∠x ()()220y a x c a =-+≠()1,6-ac ABCD AC 1AB =60BAC ∠=︒AB B ()0180a α︒<≤︒BP CP DP 12PCB BAC ∠=∠DPC △()()()2131x x x x +=++ABC △A 28︒AB C ''△40C ∠'=︒AB BC '⊥E BAC ∠生产的某种瓷碗正面的形状示意图，是的一部分，是的中点，连接，与弦交于点，连接，.已知，碗深，求的长.16.如图，是的直径，点，点在上，，，请仅用无刻度的直尺按下列要求作图（保留作图痕迹）.（1）如图1，在上作一点，使得是以为底边的等腰三角形.（2）如图2，在上方作一点，使得为等边三角形.图1图217.在平面直角坐标系中，已知抛物线与轴没有交点.（1）求的取值范围.（2）请直接写出抛物线顶点所在的象限.四、解答题（本大题共3小题，每小题8分，共24分）18.如图，在平面直角坐标系中，抛物线经过点.（1）求的值，并求出此抛物线的顶点坐标.（2）当时，请利用图象，直接写出的取值范围.（3）当时，请利用图象，直接写出的取值范围.19.如图，在中，，将绕点顺时针旋转，得到，连接，.（1）求证：点，，在同一条直线上.（2）若，，求的面积.AB O D AB OD AB C OA OB 18cm AB =6cm CD =OA AB O C D O 60COA ∠=︒OD AB ⊥OD E OCE △OC AB F ABF △214y x x c =-++x c 222y x xc c c =-+-24y x mx =-++()3,4A -m 20x -≤≤y 0y ≤x ABC △135BCA ︒∠=ACB △A 90︒ADE △CD CE B C D 2BC=AC =CDE △20.某主播销售一种商品，已知这种商品的成本价为20元/个，规定销售价格不低于成本价，且不高于成本价的2倍，通过前几天的销售发现，该商品每天的销售量（单位：个）与销售价格（单位：元/个）之间满足一次函数关系，部分对应数据如下表：/（元/个） (23252811)/个…540500440…（1）求出关于的函数关系式，并直接写出的取值范围.（2）求销售该商品每天的最大利润.五、解答题（本大题共2小题，每小题9分，共18分）21.追本溯源题（1）来自课本中的习题，请你完成解答，提炼方法并解答题（2）.（1）如图1，，比较与的长度，并证明你的结论.方法应用（2）如图2，，是的两条弦，点，分别在，上，连接，，且，是的中点.①求证：.②若圆心到的距离为3，的半径是6，求的长.图1 图222.如图，在平面直角坐标系中，抛物线与轴相交于点和点（点在点的左侧），与轴相交于点，点与点关于轴对称，为该抛物线上一点，连接，，，.（1）求该抛物线的解析式.（2）若的面积与的面积相等，请直接写出点的横坐标.y x x y y x x AD BC = AB CDMB MD O A C MBMD AB CD AB CD =M AC BM DM =O DM O DM 25y x bx =-++x A ()5,0B A B y C D A y E AC CD DE BE BDE △ACD △E（3）当点在第一象限时，连接，设的面积为，求的最大值.六、解答题（本大题共12分）23.综合与实践如图，是等边内一点，，连接，将线段绕点顺时针旋转得到，连接.初步感知（1）如图1，的延长线与交于点，求的度数.特例应用（2）如图2，作点关于的对称点，若点在的角平分线上.①当点与点重合时，的长为______；②当点与点不重合时，判断四边形的形状，并证明.拓展延伸（3）如图2，在（2）的条件下，取的中点，记为，当点从点运动到点时，请直接写出点运动的路径长.图1图2E CE ECD △S S P ABC △2AB =CP CP C 60︒CE AE BP AE Q AQB ∠E ACF P ABC △BD P F BP P F BPEF FPG P B D G江西省2025届九年级期中综合评估数学参考答案1.B2.C3.A4.D5.A 提示：由旋转和翻折可知，，抛物线的顶点的坐标为.点关于轴的对称点的坐标为，最后得到的抛物线的解析式为，.故选A.6.B 提示：建立如图所示的平面直角坐标系.由题意易知点的坐标为，点的坐标为，则点的坐标为，故设抛物线的解析式为，将点的坐标代入上式，得，抛物线的解析式为.点的横坐标为2，点的纵坐标为，点到的距离为.故选B.7.8.9.10.11.912.3或或提示：，，，，，.如图1，当时，此时.易证得为等边三角形，的周长为；2a =8b =-∴2285y x x =-+P ()2,3- ()2,3P -x ()2,3∴()222232811y x x x =-+=-+11c ∴=C ()1,0B ()1,0-E ()0,0.6()()11y a x x =+-E 0.6a =-∴()()0.611y x x =-+- D ∴D ()()0.62121 1.8-⨯+⨯-=-∴C AD 1.8m 3x =±()2,4-22.5︒24020049x x -=2+3+1AB = 90ABC ∠=︒60BAC ∠=︒1CD ∴=22AC AB ==BC ∴==60α=︒1302PCB BAC ∠=︒=∠DPC △DPC ∴△33CD =如图2，当时，此时，，.易证得，，的周长为；如图3，当时，此时，，，.的周长为.综上所述，的周长为3或或.图1 图2 图313.（1）（解法不唯一）解：，，，.（2）解：将绕点逆时针旋转得到.，.又，，.14.解：设平均每次降价的百分率为.由题意得，解得，（舍去）.答：平均每次降价的百分率为.15.解：是的中点，，.设，则.在中，由勾股定理得，120α=︒1302PCB BAC ∠=︒=∠30PBC PCB ∴∠=∠=︒1PC BP ∴==DCP BPC ≌△△DP BC ∴==DPC ∴△2CD PC DP ++=+180a =︒1302PCB BAC ∠=︒=∠2PC AC ∴==22AP AB ==DP ∴===DPC ∴△123CD PC DP ++=+=+DPC △2+3+()()()2131x x x x +=++ ()()1230x x x ∴+--=11x ∴=-23x = ABC △A 28︒AB C ''△28BAE ∴∠=︒40C C ∠'=∠=︒AB BC '⊥ 9050EAC C ∴∠=︒-∠=︒285078BAC BAE EAC ∴∠=∠+∠=︒+︒=︒x ()2100181x -=10.110%x ==2 1.9x =10%DAB OD AB ∴⊥19cm 2AC BC AB ∴===cm OA r =()6cm OC r =-Rt OAC △222OC AC OA +=即，解得，的长为.16.解：（1）如图1，即所求.（2）如图2，即所求.图1 图217.解：（1）抛物线与轴没有交点，，即，解得.（2）第二象限.提示：，该抛物线的顶点坐标为.，，点在第二象限.18.解：（1）把代入，得，解得.，抛物线的顶点坐标为.（2）当时，的取值范围是.（3）当时，的取值范围是或.19.解：（1）证明：是由绕点顺时针旋转得到的，，，，.()22269r r -+=394r =OA ∴39cm 4OCE △ABF △ x 240b ac ∴∆=-<10c +<1c <-()2222y x xc c c x c c =-+-=-- ∴(),c c -1c <- 1c ∴->∴(),c c -()3,4A -24y x mx =-++9344m --+=3m =-223253424y x x x ⎛⎫=--+=-++ ⎪⎝⎭∴325,24⎛⎫- ⎪⎝⎭20x -≤≤y 2544y ≤≤0y ≤x 4x ≤-1x ≥ADE△ACB △A 90︒ACB ADE ∴≌△△90CAD ∠=︒AC AD ∴=()1180452ACD ADC CAD ∴∠=∠=︒-∠=︒又，，点，，在同一条直线上.（2）由（1）可知，，.，.，.20.解：（1）设关于的函数关系式为.将，代入上式.得解得.（2）设销售该商品每天的利润为元.由题意得.，，当时，取得最大值，且最大值为4500.答：销售该商品每天的最大利润为4500元.21.解：（1）.证明：，，，即.（2）①证明：是的中点，.，，，，.②如图，过点作，是垂足，连接.135BCA ∠=︒ 13545180BCA ACD ∴∠+∠=︒+︒=︒∴B C D 90CAD ∠=︒AC AD=6CD ∴===135ADE BCA ︒∠=∠= 90CDE ADE ADC ︒∴∠=∠-∠=2DE BC == 1162622CDE S CD DE ∴=⋅=⨯⨯=△y x y kx b =+()23,540()25,50023540,25500,k b k b +=⎧⎨+=⎩20,1000,k b =-⎧⎨=⎩()2010002040y x x ∴=-+≤≤W ()()()22202010002014002000020354500W x x x x x =--+=-+-=--+200-< 203540<<∴35x =W AB CD=AD BC = AD BC∴= AD AC BC AC ∴+=+ AB CD=M AC AM CM∴=AB CD = AB CD∴= AB AM CMCD ∴+=+ BMDM ∴=BM DM ∴=O ON MD ⊥N OM在中，，，22.解：（1）∵抛物线与轴相交于点和点，，解得，该抛物线的解析式为.（2.（3），令，即，解得，，点的坐标为.点与点关于轴对称，点的坐标为.设点的坐标为.设直线的解析式为.由点，的坐标可知，解得直线的解析式为.如图，过点作轴，交于点.当时，，点的坐标为，， Rt OMN △3ON =6OM =MN ∴==2DM MN ∴==25y x bx =-++x A ()5,0B 25550b ∴-++=4b =∴245y x x =-++245y x x =-++ ∴0y =2450x x -++=11x =-25x =∴A ()1,0- D A y ∴D ()1,0-E ()2,45m m m -++CE y kx t =+()0,5C ()2,45E m m m -++25,45,t mk t m m =⎧⎨+=-++⎩4,5,k m t =-+⎧⎨=⎩∴CE ()45y m x =-++D DF y ∥CE F 1x =()459y m m =-++=-+∴F ()1,9m -+9DF m ∴=-则，当时，的值最大，且最大值为，故的最大值为.23.解：（1），，即.又，，（SAS ），.，.（2②四边形为平行四边形.证明：如图1，连接.图1在等边中，平分，.又，关于对称，，，，.在等边中，，，.在等边中，，，，，，，.平分，，，，为等边三角形，()2111981922228E S DF x m m m ⎛⎫=⋅⋅=-=--+ ⎪⎝⎭∴92m =S 818S 81860ACB PCE ∠=∠=︒ ACB ACP PCE ACP ∴∠-∠=∠-∠BCP ACE ∠=∠BC AC = CP CE =BCP ACE ∴≌△△CBP CAE ∴∠=∠CBP ACB CAE AQB ∠+∠=∠+∠ 60AQB ACB ︒∴∠=∠=BPEF CF ABC △BD ABC ∠BD AC ∴⊥E F AC AF AE ∴=CF CE =AC EF ∴⊥EF BP ∴∥ PCE △60PCE ∠=︒PC CE PE ==CF PC ∴= ABC △AC BC =60ACB ∠=︒ACB PCE ∴∠=∠PCB ACE ∴∠=∠()SAS BCP ACE ∴≌△△CAE CBP ∴∠=∠BP AE =BD ABC ∠30CBP ︒∴∠=30CAE FAC CBP ∴∠=∠=∠=︒60FAE ∴∠=︒AFE ∴△，.，，四边形为平行四边形.（3.提示：将图1中与的交点记为.由（2）易知.，，，即，易求得，，.如图2，当点从点运动到点时.图2，点的运动路径为图2中的长，为的中点，连接，.，同理可得，是等边三角形.是的中点，，易求得.AE EF ∴=BP EF ∴=BP EF ∥BP EF =∴BPEF AF BP M BP AF =30FAB ABP ∠=∠=︒ AM BM∴=BP BM AF AM ∴-=-PM FM =∴30MPF ∠=︒MPF ABP ∴∠=∠PF AB ∴∥P B D PF AB ∥∴G GH H AB DH HF 112DF AB == 1DH HF ==DFH ∴△G DF 1DH DF ==∴GH =。

四川省眉山市仁寿县2024届九年级上学期11月期中考试数学试卷(含答案)

A．∠D＝∠B B．∠
10．学校图书馆去年年底有图书
平均增长率为x，则列出下列方程正确的是（
A．2:5B．2:3
12．如图，在菱形ABCD中，∠
一点（不与端点重合），连接线段
A．①②③B．①④
二、填空题（每小题4分，共
13．若3
x+是二次根式，则
17．若将一条线段AB 分割成长、短两条线段即PB AP AP AB =，则可得出这一比值等于段AB 的黄金分割点，黄金分割总能给人以美的享受，从人体审美学的角度看，若一个人上半身长与下半身长之比满足黄金比的话，则此人符合和谐完美的身体比例．一芭蕾舞演员的身高为18．如图，过线段34A A 、……1-n n A A 31n B B -=．
三、计算题（19题、20题各8分，19．（1）计算：()012132222
--++--()
(1)求证：2
=
CD AD
AC=，AB=
(2)若4
24．电商平台某服装销售商家在销售中发现某品牌童装平均每天可售出
了迎接“双11”，电商决定采取适当的降价措施，扩大销售量，增加盈利，减少库存．经市场调查发现，如果每件童装每降价4
(1)求证：PBE QAB ∽△△．
(2)你认为PBE △和BAE 相似吗？如果相似，给出证明，如果不相似，请说明理由．
(3)如图（3），沿AG 折叠，使点E 落在AD 上为点H ，连结HG 交的中线等于斜边的一半）
∵
1
2
OQ AB OB
==，OB=
∴OQ OB BQ
==，
∴BOQ
△是等边三角形，。

河南省郑州外国语中学2024-2025学年九年级上学期期中考试数学试卷(含答案)

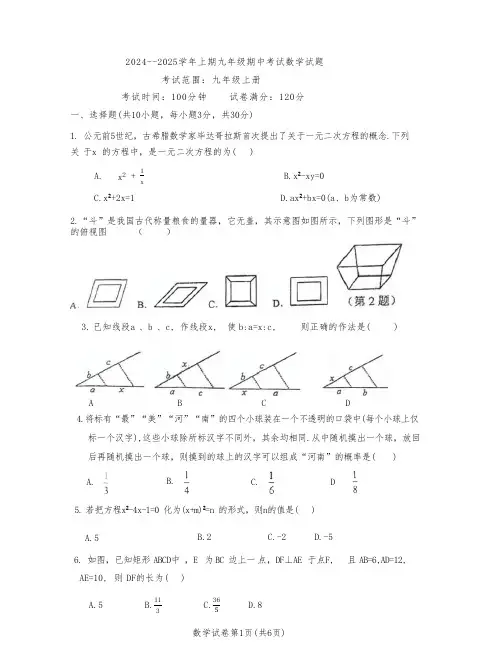
2024--2025学年上期九年级期中考试数学试题考试范围：九年级上册考试时间：100分钟试卷满分：120分一、选择题(共10小题，每小题3分，共30分)1. 公元前5世纪，古希腊数学家毕达哥拉斯首次提出了关于一元二次方程的概念.下列关于x 的方程中，是一元二次方程的为( )A. x2+1xB.x²-xy=0C.x²+2x=1D.ax²+bx=0(a、b为常数)2.“斗”是我国古代称量粮食的量器，它无盖，其示意图如图所示，下列图形是“斗”的俯视图（）3. 已知线段a 、b 、c, 作线段x, 使b:a=x:c, 则正确的作法是( )A B C D4.将标有“最”“美”“河”“南”的四个小球装在一个不透明的口袋中(每个小球上仅标一个汉字),这些小球除所标汉字不同外，其余均相同.从中随机摸出一个球，放回后再随机摸出一个球，则摸到的球上的汉字可以组成“河南”的概率是( )A. B. C. D5. 若把方程x²-4x-1=0 化为(x+m)²=n 的形式，则n的值是( )A.5B.2C.-2D.-56. 如图，已知矩形ABCD中，E 为BC 边上一点，DF⊥AE 于点F, 且AB=6,AD=12, AE=10, 则DF的长为( )A.5B.113 C.365D.8数学试卷第1页(共6页)7.如图是某地下停车场的平面示意图，停车场的长为40 m,宽为22m. 停车场内车道的宽都相等，若停车位的占地面积为520m ².求车道的宽度(单位：m). 设停车场内车道的宽度为xm, 根据题意所列方程为（ )A.(40-2x)(22-x)=520B.(40-x)(22-x)=520C.(40-x)(22-2x)=520D.(40x)(22+x)=520 8.下列给出的条件不能得出△ABD O △ACB 的是( )A.ADAB =BDBC B.∠ADB=∠ACB C.AB 2=AD.AC D.∠ADB=∠ABC9.如图，在平面直角坐标系中，正方形ABCD 与正方形BEFG 是以原点O 为位似中心的位似图形，且相似比13, 点A 、B 、E 在x 轴上，若正方形BEFG 的边长为6，则点D 的坐标为( )A. (12,2) B. (13,1) C. (14,2)D.(1,2)图一图二第9题第10题10.如图(1).正方形ABCD 的对角线相交于点O. 点 P 为OC 的中点，点M 为边BC 上的一个动点，连接OM,过点O 作OM 的亚线交CD 于点N, 点 M 从点B 出发匀速运动到点C, 设BM=x.PN=y.y 随 x 变化的图象如图(2)所示，图中m 的值为( )A.22B.1C.2D.2数学试卷第2页(共6页)二、填空题(共5小题，每小题3分，共15分)11.已知x=1 是关于x 的一元二次方程x+kx-6=0 的一个根，则k 的值为12.工人师傅做铝合金窗框分下面三个步骤进行：先截出两对符合规格的铝合金窗料(如图①),使AB=CD 、EF=GH:然后摆放成如图②四边形；将直角尺紧靠窗框的一个角(如图③)调整窗框的边框，当直角尺的两条直角边与窗框无缝隙时(如图4),说明窗框合格，这时窗框是形，根据的数学原理是：13.如图，四边形ABCD 是菱形，∠DAB=46°, 对角线AC,BD 于点O ，DH ⊥AB 于H, 连接OH, 则∠DHO= 度.14.如图，在平行四边形ABCD 中，E 是线段AB 上一点，连接AC,DE,A C 与 DE 相交于点F,若AE EB=23则S △ADFS△AEF=15.如图，在矩形纸片ABCD 中，AD=22,AB=2, 点P 是AB 的中点，点Q 是BC边上的一个动点，将△PBQ 沿PQ 所在直线翻折，得到△PE Q,连接DE,CE, 则当 △DEC 是以DE 为腰的等腰三角形时，BQ 的长是三、解答题(共8小题，共75分) 16. (8分)解方程：(1)x ²-6x+3=0; (2)3x ²-2x-1=0.数学试卷第3页(共6页)17. (8分)在一个不透明的袋子里装了只有颜色不同的黑、白两种颜色的球共50个，某学习小组做摸球试验，将球搅匀后从中随机摸出一个球记下颜色，再把它放回袋中，不断重复，下表是活动进行中的一组统计数据：摸球的次数n1002003005008001000摸到黑球的次数m65118189310482602摸到黑球的频m0.590.630.620.6030.602n a(1)当n 很大时，摸到黑球的频率将会趋近(精确到0.1);(2)某小组成员从袋中拿出1个黑球，3个白球放入一个新的不透明袋子中，随机摸出两个球，请你用列表或树状图的方法求出随机摸出的两个球颜色不同的概率.18. (9分)一张矩形纸ABCD, 将点B 翻折到对角线AC 上的点M 处，折痕CE 交AB 于点E. 将点D 翻折到对角线AC 上的点H 处，折痕AF 交DC 于点F, 折叠出四边形AECF.(1)求证；AF//CE;(2)当∠BAC= _度时，四边形AECF是菱形.数学试卷第4页(共6页)19 . (9分)已知关于x 的一元二次方程x²-ax+a-1=0.(1)求证：该方程总有两个实数根；(2)若方程的两个实数根x1、x₂满足| x1-x₂|=3, 求a 的值；20 . (8分)2024年巴黎奥运会顺利闭幕，吉祥物“弗里热”深受奥运迷的喜爱，一商场以20元的进价进一批“弗里热”纪念品，以30元每个的价格售出，每周可以卖出500 个，经过市场调查发现，价格每涨10元，就少卖100个.若商场计划一周的利润达到 8000元，并且更大优惠让利消费者，售价应定为多少钱?21. (11分)求证：相似三角形对应边上的中线之比等于相似比.要求：①根据给出的△ABC 及线段A'B',∠A'(∠A'=∠A), 以线段A'B'为一边，在给出的图形上用尺规作出△AB'C, 使得△A'B'C'心△ABC, 不写作法，保留作图痕迹；②在已有的图形上画出一组对应中线(不用尺规作图),并据此写出已知、求证和证明过程.数学试卷第5页(共6页)22. (10分)一数学兴趣小组为了测量校园内灯柱AB 的高度，设计了以下三个方案：方案一：在操场上点C 处放一面平面镜，从点C 处后退1m 到点D 处，恰好在平面镜中看到灯柱的顶部A 点的像；再将平面镜向后移动4m ( 即FC=4m)放在F 处 . 从点 F 处向后退1.8m 到点H 处，恰好再次在平面镜中看到灯柱的顶部A 点的像，测得的眼睛距地面的高度ED 、GH 为1.5m, 已知点B,C,D,F,H 在同一水平线上，且GH ⊥FH,ED ⊥CD,AB ⊥BH. (平面镜的大小忽略不计)方案二：利用标杆CD 测量灯柱的高度，已知标杆CD 高1.5m, 测得DE=2m,CE= 2.5m.方案三：利用自制三角板的边CE 保持水平，并且边CE 与点M 在同一直线上，已知两条边CE=0.4m,EF=0.2m,测得边CE 离地面距离DC=0.3m.三种方案中，方案不可行，请根据可行的方案求出灯柱的高度.23 . (12分)在△ABC 中，AB=AC,∠BAC=α,点 D 为线段CA 延长线上一动点，连接 DB, 将线段DB 绕点D 逆时针旋转，旋转角为α,得到线段DE, 连接 BE,CE.(1)如图1,当α=60°时， ADCE 的值是 ;∠DCE 的度数为 ;(2)如图2,当α=90°时，请写出 ADCE的值和∠DCE 的度数，并就图2的情形说明理由；(3)如图3,当α=120°时，若AB=8,BD=7,请直接写出点E 到 CD 的距离.数学试卷第6页(共6页)参考答案1--10DCBDCBACB11.5 12.矩形有一个角是90度的平行四边形是矩形 13.23度 14.5/2 15.1或216.x1=3+ 6 x2=3-617. （1）0.25 （2）略18.(1)【证明】∵四边形ABCD为矩形，∴AD//BC,∴∠DAC=∠BCA.由翻折知，, ∠BCE =∴∠HAF=∠MCE,∴AF//CE.(2)【解】当∠BAC=30° 时，四边形 A E CF 为菱形.理由如下：∵四边形AB CD是矩形，∴∠D=∠BAD=90°,AB// CD,由(1)得AF//CE,∴四边形A ECF 是平行四边形.∵当四边形AECF 是菱形时，CF=AF,∴∠FCA=∠FAC.∵FC//AE, ∴∠FCA=∠CAB.又∵∠DAF=∠FAC,∴∠DAF=∠FAC=∠CAB.∵∠DAB=90°,∴∠BAC=30° .(2)30度19.(1)证明：∵△=(-a)²-4(a- 1)=a²-4a+4=(a-2)²≥0,∴该方程总有两个实数根；……………(2)解：由根与系数的关系得x₁+x₂=a,x₁x₂= a-1,∵Ix₁-x₂I=√(x₁-x₂)²=√a²-4(a-1)=√(a-2)²=3, ∴a-2=3 或a-2=-3,解得a=5 或a=-1.20.(1)设售价应定为x元，由题意可得：c²-100x+2400=0,解得：x₁=40,X₂=60,更大优惠让利消费者，∴x=40,答：售价应定为40元；(2)设这两周的平均增长率为y,由题意：解得：y₁=0.1=10%,y2=-2.1 (不合题意舍去),答：这两周的平均增长率为10%.21.(1)如图所示，△A'B'C '即为所求；(2)已知，如图，△A B C∽△A'B'C',D 是AB 的中点，D'是A'B'的中点，求证：证明：∵·D是A B的中点，D'是A'B'的中点，△ABC∽△A'B'C',△A'C'D'△ACD,22. 方案二、三不可行选方案一，∵∠ECD=∠ACB,∠EDC=∠ABC, ∴△ABC∽△EDC,设BC=xm,则AB=1.5xm,同理可得△ABF∽△GHF,·AB=1.5cm,BF=BC+CF=(4+x)m,GH=1.5m ,FH=1.5m,解得：x=8,∴AB=1.5x=12(m).23.∴△ABC 是等边三角形，∴∠ACB=∠ABC=60°,AB=BC,同理可得：△BDE 是等边三角形，∴∠BDE=60°,BD=BE, ∴∠BDE=∠ABC,∴∠BDA=∠EBC,∴△ABD≌△CBE(SAS), ∴AD=CE,∠BCE=∠BAD=180°—∠BAC=120°,∠DCE=∠BCE一∠ACB=60°,故答案为：1,60;(2))∵AB=AC,∠BAC=90°, ∴∠ACB=∠ABC=45°,同理可得：∠BDE=40°,∴∠BDA=∠EBC, ∴△ABD∽△CBE,∠BCE=∠BAD=180°-∠BAC=90°, ∴∠DCE=∠BCE-∠ACB=45°;(3)如图1,图1作BF⊥CD于F,作EG⊥CD于G,作DHLCE, 交CE 的延长线于H,在Rt△AEF 中，AB=8,∠EAF=180°—∠BAC=60°, ∴AF=8·cos 60°=4,BF=8 sin 60°=4√3,在Rt△BDF 中，BD=7,BF=4√3,∵DF=√7²-(4√3)²=1,∴AD=AF 一DF=3, ∴CD=AD+AC=11,同理(2)可得：∠BCE=∠BAD=60°, ∴CE=√3AD=3√3,∠DCE=∠BCE—∠ACB=30°,在Rt△CDH 中，CD=11,∠DCE=30°,如图2,图2由上知：DF=1, AF=4,∴CD=13,AD=5,CE=√3AD=5√3,综上所述：点E 到CD 的距离为：。

江苏省徐州市邳州市2024—2025学年上学期期中考试九年级数学试卷(含答案)

2024~2025学年度第一学期期中检测九年级数学试题注意事项1．本卷共6页，满分140分，考试时间100分钟。

2．答题前，请将姓名、文化考试证号用0.5毫米黑色字迹签字笔填写本卷和答题卡的指定位置。

3．答案全部涂、写在答题卡上，写在本卷上无效。

考试结束后，将答题卡交回。

一、选择题（本大题共8小题，每小题3分，共24分．在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确选项前的字母代号填涂在答题卡相应位置）1．方程的解是（）A ．，B ．C ．，D ．，2．的半径长为4，若点P 到圆心的距离为3，则点P 与的位置关系是（）A ．点P 在内B ．点P 在上C ．点P 在外D ．无法确定3．方程的两根为、，则（）A ．6B ．－6C ．3D ．－34．下列函数的图象与的图象形状相同的是（）A ．B ．C ．D ．5．如图，A 、B 、C 、D 为一个正多边形的顶点，O 为正多边形的中心．若，则这个正多边形的边数为（）A ．7B ．8C ．9D ．10（第5题）6．如图，在半径为5的中，弦，点C 是弦AB 上的一动点，若OC 长为整数，则满足条件的点C 有（）240x x -=12x =-22x =4x =10x =24x =14x =-24x =O e O e O e O e O e 2261x x -=1x 2x 25y x =22y x=252y x =-+251y x x =++51y x =-20ADB ∠=︒O e 8AB =（第6题）A ．3个B ．4个C ．5个D ．6个7．为响应“坚持绿色低碳，建设一个清洁美丽的世界”的号召，已知某市一共有285个社区，第一季度已有60个社区实现垃圾分类，第二、三季度实现垃圾分类的小区个数较前一季度平均增长率为x ，要在第三季度将所有社医都进行垃圾分类，下列方程正确的是（）A ．B ．C ．D ．8．当时，函数的最小值为1，则a 的值为（）A ．0B ．2C ．0或2D ．0或3二、填空题（本大题共8小题，每小题4分，共32分．不需写出解题过程，请将答案直接填写在答题卡相应位置）9．一元二次方程的根是______．10．请在横线上写一个常数，使得关于x 的方程有两个相等的实数根．11．若是一元二次方程的一个根，则______．12．如图，是的内切圆，若，，则______°．（第12题）13．已知二次函数的图像经过点、，则______（填“>”“<”或“＝”）．14．如图，将一个圆锥展开后，其侧面是一个圆心角为108°，半径为12cm 的扇形，则该圆锥的底面圆的半径为______cm．()2601285x +=()2601285x -=()()2601601285x x +++=()()260601601285x x ++++=1a x a -≤≤221y x x =-+213x -=26______0x x -+=1x =20x mx n --=2024m n ++=O e ABC △60ABC ∠=︒50ACB ∠=︒BOC ∠=()()210y a x c a =-+<()11,y -()24,y 1y 2y（第14题）15．平面直角坐标系中，若平移二次函数的图象，使其与x 轴交于两点，且此两点的距离为1个单位，则平移方式为______．16．已知如图，二次函数的图像交x 轴于A 、B 两点，交y 轴于C 点，连接BC ，点M 是BC 上一点，射线MN 与以A 为圆心，1为半径的相切于点N ，则线段MN 的最小值是______．（第16题）三、解答题（本大题共9小题，共84分，请在答题卡指定区域内作答，解答时写出相应文字说明、证明过程或演算步骤）17．（本题10分）解下列方程：（1）；（2）．18．（本题8分）已知关于x 的一元二次方程．求证：不论m 为何值，该方程总有两个实数根．19．（本题8分）如图，AB 是的直径，弦AD 平分，，垂足为E ．试判断DE 与的位置关系，并说明理由．（第19题）()()202420254y x x =--+2y =+A e 2420x x --=()()323x x x +=+210x mx m ++-=O e BAC ∠DE AC ⊥O e20．（本题8分）某小区有一块矩形绿地，长为20m ，宽为8m ．为美化小区环境，现进行如下改造，将绿地的长减少a m ，宽增加a m ，改造后的面积比原来增加，求a 的值．21．（本题10分）已知y 是x 的函数，下表中给出了几组x 、y 的对应值：x …－2－1.5－101 4.55…y…3m－2－31.3753…（1）建立直角坐标系，以表中各对对应值为坐标描出各点，用平滑曲线顺次连接，由图像可知，它是我们学过的哪类函数？求出函数表达式，并直接写出m 的值；（2）结合图像回答问题：当x 的取值范围是____________时，．（第21题）22．（本题10分）如图，在中，，以AB 为直径作，分别交AC 、BC 于点D 、E ．（1）求证：；（2）当时，求的度数；（3）过点E 作的切线，交AB 的延长线于点F ，当时，求图中阴影部分面积．（第22题）23．（本题10分）商场将进货价为40元每件的某商品以50元售出，平均每月能售出700件，调查表明：售价在50元至100元范围内，这种商品的售价每上涨1元，其销售量就将减少10件，设商场决定每件商品的售价为元．（1）该商场平均每月可售出______件商品（用含x 的代数式表示）；（2）商品售价定为多少元时，每月销售利润最大？227m 0y ≥ABC △AB AC =O e BE CE =40BAC ∠=︒ADE ∠O e 2AO BE ==()50100x x <<（3）该商场决定每销售一件商品就捐赠a 元利润给希望工程，通过销售记录发现，每件商品销售价格大于85元时，扣除捐款后每天的利润随x 增大而减小，求a 的取值范围．24．（本题10分）（1）如图①，点A 、B 、C 、D 在上，，则______°：（2）如图②，A 、B 两点分别在x 轴和y 轴上，是的外接圆，利用直尺和圆规在第一象限内作出一点P ，使，且；（保留作图痕迹）（3）如图③，已知线段AB 和直线l ，利用直尺和圆规在l 上作出点P ，使；（保留作图痕迹）（4）如图④，在平面直角坐标系的第一象限内有一点B ，坐标为，过点B 作轴，轴，垂足分别为A 、C ，若点P 在线段AB 上滑动（点P 可以与点A 、B 重合），使得的位置有两个，则m 的取值范围为______．（第24题）25．（本题10分）如图，二次函数的图像与x 轴交于点、，与y 轴交于点C ．连接AC 、BC ．（1）填空：______，______；（2）如图①，若点D 是此二次函数图像的第一象限上一点，设D 点横坐标为m ，当四边形OCDB 的面积最大时，求m 的值；（3）如图②，若点P 在第四象限，点Q 在PA 的延长线上，当时，求点P 的坐标．（第25题）()1a ≥O e 35BAC ∠=︒BOC ∠=C e AOB △OPA OBA ∠=∠OP AP =30APB ∠=︒()2,m AB y ⊥BC x ⊥45OPC ∠=︒212y x bx c =-++()1,0A -()4,0B b =c =45CAQ CBA ∠=∠+︒2024~2025学年度第一学期期中检测九年级数学参考答案一、选择题（本大题共8小题，每小题3分，共24分）题号12345678答案CACBCCDD二、填空题（本大题共8小题，每小题4分，共32分）9．，10．911．202512．12513．>14．3.615．向下平移4个单位长度16三、解答题（本大题共9小题，共84分）17．（本题10分）解：（1）移项，得配方，得即直接开平方，得∴（2）移项，得因式分解，得∴或∴，18．（本题8分）解：∵，，∴∵不论m 为何值∴不论m 为何值，该方程总有两个实数根．19．（本题8分）解：DE 与相切理由是：连接OD∵∴∵AD 平分∴∴∴∵∴∴DE 与相切．12x =22x =-242x x -=24424x x -+=+()226x -=2x -=12x =+22x =()()3230x x x +-+=()()230x x -+=20x -=30x +=12x =23x =-1a =b m =1c m =-()2²4411b ac m m -=-⨯⨯-²44m m =-+()22m =-()220m -≥O e OD OA =ODA OAD∠=∠BAC ∠OAD CAD ∠=∠ODA CAD ∠=∠AC OD ∥DE AC ⊥OD DE ⊥O e（第19题）20．（本题8分）解：根据题意得：即：解得：，答：a 的值为3或9．21．（本题10分）（1）描点、连线如图是二次函数，设函数的表达式为：把点，，代入得解得：∴函数得表达式为（2）或．22．（本题10分）（1）证明：连接AE∵AB 是直径∴∴∵∴()()20820827a a -+-⨯=212270a a -+=13a =29a =()20y ax bx c a =++≠()1,0-()0,2-()1,3-023a b c c a b c -+=⎧⎪=-⎨⎪++=-⎩12322a b c ⎧=⎪⎪⎪=-⎨⎪=-⎪⎪⎩213222y x x =--1.375m =1x ≤-4x ≥O e 90AEB ∠=︒AE BC ⊥AB AC =BE CE=（第22题）（2）解：∵，∴∵四边形ABED 是的内接四边形∴∴．（3）解：连接OE 则∵∴∴是等边三角形∴∵EF 是切线∴∴∴∴∴阴影部分的面积．23．（本题10分）（1）（2）设每月销售利润为y 元则∵，∴当时，y 有最大值16000答：商品售价定为80元时，每月销售利润最大；（3）设每月销售利润为y 元则∴对称轴为直线∵∴当时，y 随x 得增大而减小∵每件商品销售价格大于85元时，扣除捐款后每天的利润随x 增大而减小∴解得：∵∴a 的取值范围是．24．（本题10分）（1）35，702分AB AC =40BAC ∠=︒180180407022BAC ABC ︒-∠︒-︒∠===︒O e 180ADE ABC ∠+∠=︒180********ADE ABC ∠=︒-∠=︒-︒=︒OE OA OB==2OA BE ==OA OB BE ==OBE △60BOE ∠=︒O e OE EF ⊥30F ∠=︒24OF OE ==EF ===2160π222π23603OEF BOE S S ⨯=-=⨯⨯=-扇形△101200x -+()()()224010120010160048000108016000y x x x x x =--+=-+-=--+100-<50100x <<80x =()()()24010120010160010480001200y x a x x a x a=---+=-++--()160010802102a a x +=-=+⨯-100-<802ax >+80852a+≤10a ≤1a ≥110a ≤≤（2）如图（3）如图（4）25．（本题10分）（1），2（2）∵点D 横坐标为m ，且点D 在二次函数的图像上∴点D 坐标为对于二次函数，当时，∴设BC ：则解得：∴BC ：21m ≤<32213222y x x =-++213,222m m m ⎛⎫-++ ⎪⎝⎭213222y x x =-++0x =2y =()0,2C y kx b =+402k b b +=⎧⎨=⎩122k b ⎧=-⎪⎨⎪=⎩122y x =-+过点D 作轴，交BC 于点E 则∴∴到DE 的距离到DE 的距离（C 到DE 的距离到DE 的距离）∵，∴当时，有最大值8∴．（3）∵，，∴，，∴∴设，则∵∴∴DE y ∥1,22E m m ⎛⎫-+ ⎪⎝⎭2213112222222DE m m m m m ⎛⎫=-++--+=-+ ⎪⎝⎭OBC BCD OCDB S S S =+四边形△△OBC CDE BDES S S =++△△△1122OC OB DE C =⨯⨯+⨯⨯12DE B +⨯⨯112422DE =⨯⨯+⨯⨯B +1442DE =+⨯⨯214222m m ⎛⎫=+-+ ⎪⎝⎭244m m =-++()()22804m m =--+<<10a =-<04m <<2m =OCDB S 四边形2m =()1,0A -()4,0B ()0,2C 25AC =220BC =225AB =222AC BC AB +=90ACB ∠=︒ABC x ∠=90CAB x∠=︒-45CAQ CBA ∠=∠+︒45CAQ x ∠=+︒()()180459045PAB x x ∠=︒-+︒-︒-=︒设直线AP 交y 轴于F则∴设AP ：则解得：∴AP ：设∵点P 在二次函数的图象上∴解得：，（舍去）当时，∴点P 的坐标为．1OF OA ==()0,1F -y kx b =+01k b b -+=⎧⎨=-⎩11k b =-⎧⎨=-⎩1y x =--()(),10P n n n -->213222y x x =-++2132122n n n -++=--16n =21n =-6n =17n --=-()6,7-。

重庆市南开中学校2024-2025学年九年级上学期期中数学试题(解析版)

重庆南开中学2024-2025学年度上学期期中考试初2025届数学试题（全卷共三个大题，满分150分，考试时间120分钟）一、选择题：（本大题10个小题，每小题4分，共40分）在每个小题的下面，都给出了代号为A、B、C、D的四个答案，其中只有一个是正确的，请将答题卡．．．上题号右侧正确答案所对应的方框涂黑．1.17−的相反数是( )．A.17− B.17C. −7D. 7【答案】B【解析】【分析】本题考查了相反数的定义，解答本题的关键是熟练掌握相反数的定义，只有符号不同的两个数是互为相反数， 0的相反数是0．【详解】解：17−的相反数是17，故选：B．2. 下列化学仪器示意图中，是轴对称图形的是（）A. 蒸馏烧瓶B. 烧杯C. 圆底烧瓶D. 分液漏斗【答案】C【解析】【分析】本题考查了轴对称图形的定义，熟练掌握轴对称图形的定义是解答本题的关键．根据轴对称图形的定义逐项分析即可．【详解】解：选项A、B、D均不能找到这样的一条直线，使图形沿该直线对折后直线两旁的部分能够完全重合，所以不是轴对称图形，选项C能找到这样的一条直线，使图形沿该直线对折后直线两旁的部分能够完全重合，所以是轴对称图形．故选C ．3. 二次函数()20y ax bx c a ++≠的图象如图所示，则下列选项正确的是（）A. 0a >B. 0b >C. 240b ac −<D. 0c >【答案】A【解析】【分析】本题考查根据二次函数图象判断各项系数和式子的符号，熟练掌握二次函数图象与系数的关系是解题的关键．根据抛物线的开口方向和对称轴的位置确定a 、b 的符号，由抛物线与x 轴的交点个数确定∆的符号，由抛物线与y 轴的交点位置确定c 的符号，即可得出答案．【详解】解：A 、∵抛物线的开口向上，∴0a >，故此选项符合题意；B 、∵抛物线的对称轴在y 轴右侧，∴02b a−>， ∵0a >，∴0b <，故此选项不符合题意；C 、∵抛物线与x 轴的两个交点，∴240b ac ∆=−>，故此选项不符合题意；D 、∵抛物线与y 轴的交点在负半轴上，∴0c <，故此选项不符合题意；故选：A ．4. 将ABC 沿BC 方向平移至DEF ，点A ，B ，C 的对应点分别是D ，E ，F ，使得:5:3BC EC =，则ABC 与GEC 的周长之比为（）A. 2:3B. 2:5C. 5:3D. 3:5【答案】C【解析】【分析】本题考查平移的性质，相似三角形的判定与性质，熟练掌握平移的性质、相似三角形的判定与性质是解题的关键．根据平移的性质得到AB GE ∥，从而可得到ABC GEC △∽△，利用相似三角形周长于相似比可得答案．【详解】解：∵ABC 沿BC 方向平移至DEF ，∴AB DE ∥，即AB GE ∥，∴A EGC ∠=∠,B GEC ∠=∠,∴ABC GEC △∽△，∴ABC 与GEC 的周长之比:5:3BCEC =，故选：C ．5. 中国选手郑钦文顺利入围2024年WTA 年终总决赛女子单打项目，该项目第一阶段采用组内循环赛制，即每两名选手之间比赛一场．现计划安排28场组内循环赛，共有几名选手参加组内循环赛？设一共有x 名选手参加组内循环赛，根据题意可列方程为（）A. ()128x x −=B. ()128x x +=C. ()11282x x +=D. ()11282x x −= 【答案】D【解析】【分析】此题主要考查了有实际问题抽象出一元二次方程，解决本题的关键是得到比赛总场数的等量关系，注意2队之间的比赛只有1场，最后的总场数应除以2．设一共有x 名选手参加组内循环赛，则每个队参加()1x −场比赛，则共有()112x x −场比赛，可以列出一个一元二次方程．【详解】解：由题意可列方程为：()11282x x −=，故选：D ．6. 估计+）A. 6和7之间B. 7和8之间C. 8和9之间D. 9和10之间【答案】D【解析】【分析】本题考查二次根式的混合运算，无理数的估算，解题的关键是熟练掌握二次根式的运算法则．先利用二次根式的运算法则将原式化简，再对无理数进行估算．【详解】解：++，3<<∵67∴9310+<故选：D．7. 南南用相同的小圆圈按照一定的规律摆成了“中”字，第①个图形中有10个小圆圈，第②个图形中有16个小圆圈，第③个图形中有22个小圆圈，…，按照此规律排列下去，则第⑧个图形中小圆圈的个数是（）A. 42B. 52C. 46D. 58【答案】B【解析】【分析】考查了图形的变化类问题，解题的关键是仔细观察图形并找到进一步解题的规律，难度不大．仔细观察图形变化，找到图形变化规律，利用规律求解．×+=个小圆圈，【详解】第①个图形中一共有16410×+=个小圆圈，第②个图形中一共有26416×+=个小圆圈，第③个图形中一共有36422…，∴第n 个图形中一共有()64n +个小圆圈，∴第⑧个图形中小圆圈的个数是86452×+=，故选：B ．8. 如图，AB 是O 的直径，AE 、CE 、CB 为O 的弦，132AO =，12AE =，则sin BCE ∠=（）A. 512B. 1312C. 513D. 125【答案】C【解析】【分析】本题考查了圆周角定理，求一个角的正弦值，勾股定理；根据AB 是O 的直径，得出90AEB ∠=°，再运用勾股定理算出5BE ，再结合 EBEB =，则BCE BAE ∠=∠，所以5sin sin 13BE BCE BAE AB ∠=∠==，即可作答．【详解】解：连接BE ，如图：∵AB 是O 的直径，∴90AEB ∠=°， ∵132AO =， ∴13AB =，在Rt ABE △中，5BE ，∵ EBEB =，∴BCE BAE ∠=∠， ∴5sin sin 13BE BCE BAE AB ∠=∠==，故选：C ． 9. 如图，在正方形ABCD 中，O 是对角线BD 的中点，E 为正方形内的一点，连接BE ，CE ，使得CB CE =，延长BE 与ECD ∠的角平分线交于点F ．若BEC α∠=，连接OF ，则FOD ∠的度数为（）A. 290α−°B. 1452α°+C. 1902α°−D. 245α−°【答案】A【解析】【分析】连接DF ，先证明∴()SAS CEF CDF ≌，得到CEF CDF ∠=∠，从而得180CDF CEF α∠=∠=°−，继而90BFD ∠=°，然后利用直角三角形的性质，得出OF OB =，从而有45OFB OBF α∠=∠=−°，然后由三角形外角的性质可求解．【详解】解：连接DF ，如图，∵正方形ABCD∴BC CD =，45CBD CDB ∠=∠=°，∵CB CE =∴CE CD =，CBE BEC α∠=∠=， ∴45DBE α∠=−°，∵CF 是ECD ∠角平分线∴ECF DCF ∠=∠ ∵CF CF =，ECF DCF ∠=∠，CE CD =， ∴()SAS CEF CDF ≌∴CEF CDF ∠=∠，∴180CDF CEF α∠=∠=°−∴18045135BDFCDF CDB αα∠=∠−∠=°−−°=°− ∴1354590BDF DBE αα∠+∠=°−+−°=° ∴90BFD ∠=°∵O 是对角线BD 的中点，∴OF OB =∴45OFB OBF α∠=∠=−° ∴4545290FOD OFB OBF ααα∠=∠+∠=−°+−°=−° 故选：A ．【点睛】本题考查正方形的性质，直角三角形的性质，等腰三角形的性质，三角形外角的性质，全等三角形的判定与性质，证明90BFD ∠=°是解题的关键．10. 给定三个互不相等的代数式，先将任意两个代数式作差（相同的两个代数式只作一次差），再将这些差“绝佳操作”．例如：对于m ，n ，p 作“绝佳操作”，得到m n m p n p −+−+−．下列说法：①对2，4−，5作“绝佳操作”结果是18；②对m ，n ，p 作“绝佳操作”的结果一共有8种；③对22a ，66a −，42a 作“绝佳操作”的结果为28，则a的值为1−或1−；其中正确的个数为（）A. 0B. 1C. 2D. 3【答案】B【解析】【分析】本题考查新定义和绝对值化简，解一元二次方程，理解万岁新定义是解题的关键，注意分类讨论．利用绝对值的性质进行逐个计算判断即可．【详解】解：①()242545−−+−+−−的的18=，故①正确；②当m n p >>时，则22m n m p n p m n m p n p m p −+−+−=−+−+−=−，当m p n >>时，则22m n m p n p m n m p n p m n −+−+−=−+−−+=−，当n m p >>时，则22m n m p n p m n m p n p n p −+−+−=−++−+−=−，当n p m >>时，则22m n m p n p m n m p n p n m −+−+−=−+−++−=− 当p m n >>时，则22m n m p n p m n m p n p p n −+−+−=−−+−+=−当p n m >>时，则22m n m p n p m n m p n p p m −+−+−=−+−+−+=− ∴对m ，n ，p 作“绝佳操作”的结果一共有6种，故②错误；③当226642a a a >−>−时，则()()()22266242664228a a a a a a −−+−−+−−−=，化简得：2260a a −−=，解得：1a =+1a =−；当224266a a a >−>−时，则()()()22266242664228a a a a a a −−+−−+−−−=，化简得：2340a a −−=，解得：4a =（舍去）或1a =−；当266242a a a −>>−时，则()()()22266242664228a a a a a a −−+−−+−−−=，化简得：6828a −=，解得：6a =（舍去）；当266422a a a −>−>时，则()()()22266242664228a a a a a a −−+−−+−−−=，化简得：23100a a −+=，∵()234110310∆=−−××=−<∴无解；当242266a a a −>>−时，则()()()22266242664228a a a a a a −−+−−+−−−=，化简得：8a −=，解得：8a =−（舍去），当242662a a a −>−>时，则()()()22266242664228a a a a a a −−+−−+−−−=，化简得：4828a −+=，解得：5a =−（舍去），综上，a 的值为11−，故③错误；∴只有①正确，共1个，二、填空题：（本题共8个小题，每小题4分，共32分）请将每个小题的答案直接填在答题．．卡．中对应的横线上． 11. 计算：()01tan3012−°−−=________．【答案】12##0.5 【解析】【分析】本题主要考查实数混合运算，零指数幂，负整理指数幂，特殊角的三角函数，解题的关键是掌握分负整数指数幂、零指数幂的规定，熟记特殊锐角的三角函数值．【详解】解：()01tan3012−°−−112 =−−112=− 12=．故答案为：12． 12. 正八边形每个外角的度数为_____．【答案】45°##45度【解析】【分析】本题主要考查了正多边形外角和定理，根据任何一个多边形的外角和都是360°求解即可．【详解】解：因为任何一个多边形的外角和都是360°，所以正八边形的每个外角的度数是：360845°÷=°．故答案为：45°．13. 为了全面推进素质教育，助力学生健康成长，公能学校开设了多门选修课程．其中南南和开开想从刺绣、糖画、国家疆土、巧匠工坊中选修一门课程，两名同学恰好选修同一门课程的概率为________．【答案】14【解析】【分析】本题考查了列表法与树状图法：利用列表法或树状图法展示所有等可能的结果n ，再从中选出符合事件A 或B 的结果数目m ，然后利用概率公式计算事件A 或事件B 的概率．画树状图展示所有16种等可能的结果数，再找出他们两人恰好选修同一门课程的结果数，然后根据概率公式求解．【详解】解：用A 、 B 、C 、D 分别表示刺绣、糖画、国家疆土、巧匠工坊，画树状图如图，共有16种等可能的结果，其中他们两人恰好选修同一门课程的结果数为4，所以他们两人恰好选修同一门课程的概率为：41164=． 14. 如图，点A 在反比例函数()0k yk x=≠图象上，过点A 作AB x ⊥轴于点B ，连接OA ，若ABO 的面积为2，则k =________．【答案】4【解析】【分析】本题考查反比例函数系数k 的几何意义，过双曲线上的任意一点分别向两条坐标轴作垂线，与坐标轴围成的矩形面积就等于k ．本知识点是中考的重要考点，同学们应高度关注．根据在反比例函数的图象上任意一点向坐标轴作垂线，这一点和垂足以及坐标原点所构成的三角形的面积是122k =，再根据反比例函数的图象位于第二象限即可求出k 的值．【详解】解：根据题意可知：221AOB S k == ，又反比例函数的图象位于第一象限，0k >，则4k =．故答案为：4．15. 若二次函数232y x x =−+过点(),3m ，则代数式2262023m m −+=________．【答案】2025【解析】【分析】本题考查的是抛物线的性质．掌握“点在抛物线上，则点的坐标满足函数解析式”是解本题的关键．由于抛物线经过点(),3m ，则231m m −=，把2262023m m −+整理后整体代入即可．【详解】∵二次函数232y x x =−+过点(),3m ， ∴2323m m −+=， ∴231m m −=，∴()222620232320232120232025m m m m −+=−+=×+=．故答案为：2025．16. 关于x 的一元一次不等式组()341221x x x x m − ≤−+≥−+至少有2个整数解，且关于y 的分式方程13222m y y−=−−−的解为非负整数，则符合条件的整数m 的值之和为________．【答案】2 【解析】【分析】本题考查了分式方程的解，以及解一元一次不等式组，掌握相应的计算方法是关键．先解不等式组，确定m 的取值范围25<≤m ，再把分式方程去分母转化为整式方程，解得22m y −=，由分式方程有非负整数解，确定出的值，即可解答．【详解】解：()341221x x x x m − ≤−+≥−+①② 解①得：2x ≤，解②得：23m x −≥， ∴223m x −≤≤， ∵不等式组至少有2个整数解， ∴213m −≤，解得：5m ≤；13222m y y−=−−−，去分母得：1243m y −=−+，解得：2my =， ∵分式方程的解为非负整数，且2y ≠ ∴0m ≥且4m ≠的偶数，又∵5m ≤ ∴2m =，0∴符合条件的整数m 的值之和为202+=．故答案：2．17. 如图，在矩形ABCD 中，4=AD ，点E 为AB 中点，将矩形沿着EF 所在的直线翻折至矩形ABCD 所在的平面，点B ，C 的对应点分别是B ′，C ′，B E ′与CD 交于点G ，使得CF GF =，连接AB ′，B F ′，AF ，若25B G GF ′=，则GF =________；AB F S ′= ________．【答案】 ①. 5 ②. 985【解析】【分析】过点G 作GH C F ′⊥，则四边形B C HG ′′是矩形，根据矩形的性质，结合折叠的性质可得4GH B C ′′==，GF GE =，令5GF CF a ==，则2B G C H a ′′==，5CF C F a ′==，可知3HF C F C H a ′′=−=，根据勾股定理即可求解，则2B G ′=，7BE B E ′==，令AB ′与CD 交于点O ，过点B ′作B M CD ′⊥，则90D B MO ′∠=∠=°，再证明B OG B AE ′′△∽△，DOA MOB ′△∽△，结合相似三角形的性质求得2855B M AD ′==，由1122AB F AOF B OF S S S OF AD OF B M ′′′=+=⋅+⋅△△△，即可求解．【详解】解：在矩形ABCD 中，4AD BC ==，AB CD =，90B C D ∠==∠=°，AB CD ∥，则BEF DFE ∠=∠，由折叠可知，BE B E ′=，CF C F ′=，4BC B C ′′==，90C C ′∠=∠=°，90EB C B ′∠=∠=°，BEF B EF ′∠=∠，则B EF DFE ′∠=∠， ∴GF GE =，为过点G 作GH C F ′⊥，则四边形B C HG ′′是矩形， ∴4GHB C ′′==，B G C H ′′=， ∵25B G GF ′=，CF GF =，令5GFCF a ==，则2B G C H a ′′==，5CF C F a ′==， ∴3HF C F C H a ′′=−=，由勾股定理可得：222GH GF HF =−，即：()()222453a a =−，解得：1a =，∴5GF =，则2B G ′=，7BEB E ′==，令AB ′与CD 交于点O ，过点B ′作B M CD ′⊥，则90D B MO ′∠=∠=°，∵点E 是AB 的中点，∴7AE BE ==，即14ABCD ==， ∵AB CD ∥，∴B OG B AE ′′△∽△，B G B O GF OA ′′==∴OG B GAE B E ′=′，即277OG =， ∴2OG =，∴7OF OG GF =+=，则2OD CD OF CF =−−=， ∵DOA MOB ′∠=∠ ∴DOA MOB ′△∽△，∴25B M B O AD OA ′′==，则2855B M AD ′==， ∴1118987422255AB F AOF B OF S S S OF AD OF B M ′′′=+=⋅+⋅=××+=，故答案为：5，985．【点睛】本题考查矩形与折叠问题，勾股定理，相似三角形的判定及性质，平行线分线段成比例等知识点，熟练掌握相关图形的性质是解决问题的关键．18. 一个四位数M 各数位上的数字均不为0，若将M 的千位数字和个位数字对调，百位数字和十位数字对调，得到新的四位数N ，则称N 为M 的“翻折数”，规定()11M NF M +=．例如：1235的“翻折数”为5321，()12355321123559611F +==，则()2678F =________；若()5001200101M x y =+++（M ，y 为整数，59x ≤≤，18y ≤≤），M 的“翻折数”N 能被17整除，则()F M 的最大值为________．【答案】 ①. 1040 ②. 757 【解析】【分析】根本题主要考查了有理数的混合运算，二元一次方程的解，列代数式，本题是阅读型题目，准确理解题干中的定义和公式并熟练应用是解题的关键．据()11M NF M +=代入求解()2678F 即可；首先表示出s 和t 的“翻折数”，然后求出3153x y ++的取值范围，进而分类讨论求得x ，y 的值，然后代入()11M NF M +=求解即可．【详解】根据题意可得，()267887622678104011F +==；∵()5001200101M x y =+++（M ，y 为整数59x ≤≤，18y ≤≤）， ∴M 的千位数字为6，百位数字为210x −，十位数字为1y +，个位数字为1， ∴M 的“翻折数”N 为()()10001001102106y x +++−+201001006x y =++()175593153x y x y =+++++，∵59x ≤≤，18y ≤≤， ∴333153150x y ≤++≤， ∵M 的“翻折数”N 能被17整除， ∴3153x y ++能被17整除， ∵x ，y 都是整数， ∴3153x y ++是整数，∴431533x y +=+，51，68，85，102，119，136，∴当431533x y +=+时，x ，y 无整数解，当131535x y +=+时，13x y = = （舍去）或62x y = =，当831536x y +=+时，x ，y 无整数解，当531538x y +=+时，x ，y 无整数解，当2315310x y +=+时，36x y == （舍去）或85x y = = ，当9315311x y +=+时，x ，y 无整数解，当6315313x y +=+时，x ，y 无整数解，∴当62x y = =时，()5001200610216231M =+×+×+=，1326N =，()6231132668711F M +==，当85x y = =时，()5001200810516661M =+×+×+=，1666N =，()6661166675711F M +==， ∴()F M 的最大值为757，故答案为：1040，757．三、解答题：（本大题共8个小题，第19题8分，其余每题10分，共78分）解答时每小题必须给出必要的演算过程或推理步骤，画出必要的图形（包括辅助线），请将解答过程书写在答题卡．．．中对应的位置上． 19. 计算：（1）()22()m m n m n +−+（2）2214123a a a a −+÷ +【答案】（1）2n −；（2）321a a +−．【解析】【分析】本题考查了整式的运算和分式的混合运算．解题的关键是掌握整式和分式混合运算顺序和运算法则．（1）利用完全平方公式和单项式乘多项式展开，再合并即可；（2）原式括号中两项通分并利用同分母分式的加法法则计算，同时利用除法法则变形，约分得到最简结果即可．【小问1详解】解：()22()m m n m n +−+2222(2)m mn m mn n =+−++22222m mn m mn n =+−−− 2n =−；【小问2详解】解：2214123a a a a −+÷ + 2221413a a a a a+−÷+ ()()()321·2121a a a a a a ++=+− 321a a +=−． 20. 为了全面了解学生对校史的掌握情况，公能学校开展了校史知识竞赛．现从七、八年级的学生中各随机抽取20名学生的比赛成绩（百分制）进行收集、整理、描述、分析．所有学生的成绩均高于60分（成绩得分用x 表示，共分为四组：A ．90100x <≤；B ．8090x <≤；C ．7080x <≤；D ．6070x <≤；），下面给出了部分信息：七年级20名学生的竞赛成绩为：68，76，78，79，84，85，86，86，86，86， 88，89，89，91，91，94，94，95，95，100．八年级20名学生的竞赛成绩在B 组的数据为：80，83，86，87，87，89，89．七、八年级所抽学生的校史知识竞赛成绩统计表年级七年级八年级平均数8787中位数 87 b众数 a92根据以上信息，解答下列问题：（1）填空：a =________；b =________；m =________；（2）根据以上数据分析，你认为在此次知识竞赛中，该校七、八年级中哪个年级学生对校史的掌握情况更好？请说明理由（写出一条理由即可）；（3）公能学校七年级有500名学生、八年级有600名学生参加此次校史知识竞赛，请估计七、八年级参加此次知识竞赛的成绩优秀(90)x >的学生共有多少人？【答案】（1）86；87；40（2）八年级学生安全知识竞赛成绩较好，理由见解析（3）415 【解析】【分析】（1）根据众数和中位数定义求a 、b 值，先求出B 组人数占的百分比为35%，即可由%110%15%35%m =−−−求出m 值；（2）根据两个年级成绩的平均数相同，但八年级的中位数高于七年级，可得出结论；（3）用各年级的总人数乘以年级的优秀率，再相加，列式计算即可求解. 【小问1详解】解：在七年级20名学生的竞赛成绩中86出现的次数最多，故众数86a =； ∵八年级20名学生的竞赛成绩在B 组的数据为：80，83，86，87，87，89，89． ∴B 组人数占的百分比为：7100%35%20×=， ∵C 组人数占的百分比为15%，D 组人数占的百分比为10%， ∴A 组人数占的百分比为%110%15%35%40%m =−−−=，即40m =． ∴八年级20名学生竞赛成绩的中位数在B 组，的∴把八年级20名学生的竞赛成绩从小到大排列，排在中间的两个数分别是87，89，故中位数8789872b +=，故答案：86；87；40．【小问2详解】解：八年级学生安全知识竞赛成绩较好，理由如下：因为两个年级成绩的平均数相同，但八年级的中位数高于七年级，所以得到八年级学生安全知识竞赛成绩较好（答案不唯一）；【小问3详解】解：750060040%20×+× 175240+415=（人），答：估计该校七、八年级参加此次安全知识竞赛成绩优秀()90x >的学生人数大约是415人．【点睛】本题考查众数，中位数，统计表，扇形统计图，用样本估计总体，掌握相关统计量的意义以及计算方法是解答本题的关键．21. 在学习了平行四边形与正方形的相关知识后，智慧小组进行了更深入的探究．他们发现，如图所示的正方形ABCD ，分别取BC ，CD 的中点M ，N ，连接AM ，DN 交于点E ，过B 作AM 的垂线，交AM 于点Q ，交AD 于点P ．则四边形BPDN 是平行四边形．（1）用尺规完成以下基本作图：过B 作AM 的垂线，交AM 于点Q ，交AD 于点P （只保留作图痕迹）．（2）根据（1）中所作图形，智慧小组发现四边形BPDN 是平行四边形成立，并给出了证明，请补全证明过程．证明：∵四边形ABCD 是正方形，∴AD CD BC ==，90ADC C ∠=∠=°，AD BC ∥．又∵M ，N 分别为BC ，CD 的中点，∴12DM CD =，12CN BC =，∴ ① ，在ADM 与DCN 中，为AD CD ADM C DM CN =∠=∠ =∴()ADM DCN SAS ≌．∴ ② ．又∵90CDN ADN ∠+∠=°，∴90DAM ADN ∠+∠=°，∴90AED ∠=°，又∵BP AE ⊥，∴90AQP AED ∠=∠=°，∴ ③ ．又∵DP BN ∥ ∴四边形BPDN 是平行四边形．进一步思考，智慧小组发现任取BC ，CD 的上点N ，M （M 不与C ，D 重合），DM CN =，连接AM ，DN ，过B 作AM 的垂线，交AD 于点P ，则四边形BPDN 是 ④ ．【答案】（1）见解析（2）DM CN =；DAM CDN ∠=∠；∥BP DN ；进一步思考：四边形BPDN 是平行四边形【解析】【分析】（1）利用尺规基本作图——经过直线外一点作已知直线的第一线作法作出图形即可；（2）先证明()SAS ADM DCN ≌，得到DAM CDN ∠=∠．从而证得90AQP AED ∠=∠=°，即可得到∥BP DN ．又由正方形的性质得DP BN ∥，即可得出结论；进一步思考：证明()SAS ADM DCN ≌，得到DAM CDN ∠=∠，再证明∥BP DN ，又由正方形的性质得DP BN ∥，即可得出结论．【小问1详解】解：如图所示，BP 就是所求作的经过点B 垂直于AM 于Q ，交AD 于P 的直线，【小问2详解】证明：∵四边形ABCD 是正方形，∴AD CD BC ==，90ADC C ∠=∠=°，AD BC ∥．又∵M ，N 分别为BC ，CD 的中点， ∴12DM CD =，12CN BC =， ∴DM CN =，在ADM 与DCN 中，AD CD ADM C DM CN =∠=∠ =∴()SAS ADM DCN ≌． ∴DAM CDN ∠=∠．又∵90CDN ADN ∠+∠=°， ∴90DAM ADN ∠+∠=°， ∴90AED ∠=°，又∵BP AE ⊥，∴90AQP AED ∠=∠=°， ∴∥BP DN ．又∵DP BN ∥∴四边形BPDN 是平行四边形．进一步思考：如图，∵四边形ABCD 是正方形，∴AD CD BC ==，90ADC C ∠=∠=°，AD BC ∥．在ADM 与DCN 中，AD CD ADM C DM CN =∠=∠ =∴()SAS ADM DCN ≌． ∴DAM CDN ∠=∠．又∵90CDN ADN ∠+∠=°， ∴90DAM ADN ∠+∠=°， ∴90AED ∠=°，又∵BP AE ⊥，∴90AQP AED ∠=∠=°， ∴∥BP DN ．又∵DP BN ∥∴四边形BPDN 是平行四边形．故答案为：平行四边形．【点睛】本题考查正方形的性质，全等三角形的判定与性质，尺规基本作图—作垂线，平行四边形的判定．熟练掌握正方形的性质，和平行四边形的判定是解题的关键．22. 重庆金沙天街某家蛋糕店推出了“流沙羊角”和“开心果羊角”两款特色蛋糕．（1）购买1个“流沙羊角”和1个“开心果羊角”需要37元，购买1个“流沙羊角”和2个“开心果羊角”需要54元，求“流沙羊角”和“开心果羊角”的单价分別为多少元？（2）国庆节当天，蛋糕店进行促销活动，将“流沙羊角”的单价降低了2m 元，“开心果半角”单价降低了m 元，节日当天“流沙羊角”的销量是“开心果羊角”销量的1.2倍，且“流沙羊角”的销售额为960元，“开心果羊角”的销售额为750元，求m 的值．【答案】（1）“流沙羊角”的单价为20元，“开心果羊角”的单价为17元（2）2 【解析】【分析】本题考查二元一次方程组的应用，分式方程的应用，正确列出方程组或方程是解题的关键．（1）设“流沙羊角”的单价为x “开心果羊角”的单价为y 元，根据购买1个“流沙羊角”和1个“开心果羊角”需要37元，购买1个“流沙羊角”和2个“开心果羊角”需要54元，列出方程组，求解即可．（2）根据销量等于销售额除以销售单价，以“流沙羊角”的销量是“开心果羊角”销量的1.2倍，列出分式方程求解即可．【小问1详解】解：设“流沙羊角”的单价为x 元，“开心果羊角”的单价为y 元，根据题意，得37254x y x y +=+= ，解得：2017x y = =，答：“流沙羊角”的单价为20元，“开心果羊角”的单价为17元．【小问2详解】解：根据题意，得960750 1.220217m m=×−−，解得：2m =，经检验，2m =是方程的解且符合题意， ∴m 的值为2．23. 如图1，在菱形ABCD 中，5AB =，8BD =，动点P 从点A 出发，沿着A B C −−的路线运动，到达C 点停止，过点P 作PQ BD ∥交菱形的另一边于点Q ．设动点P 行驶的路程为x ，点P 、Q 的距离为y ．（1）请直接写出y 关于x 的函数表达式，并注明自变量x 的取值范围；（2）在给定的平面直角坐标系中画出函数y 的图象，并写出函数y 的一条性质；（3）函数11y x b 2=+与函数y 只有一个交点，求b 的取值范围．【答案】（1）()()80558165105x x y x x ≤≤ =−+<≤ ；（2）作图见解析，当05x ≤≤时，y 随x 的增大而增大；当510x <≤时，y 随x 的增大而减小；（3）50b −≤<或112b =．【解析】【分析】（1）分点P 在AAAA 上和点P 在BC 上两种情况讨论，利用相似三角形的判定及性质构造等量关系，即可得到答案；（2）根据（1）所得函数关系式，利用描点法画图，再写出该函数的性质即可；（3）结合函数图象，将()5,8、()0,0和()10,0代入11y x b 2=+，分别求出b 的值，即可得出b 的取值范围．【小问1详解】解：如图，点P 在AAAA 上时，05x ≤≤，∵PQ BD ∥， ∴APQ ABD ∽，∴AP PQ AB BD =即58x y=， ∴85y x =， ∵5AB =，如图，点P 在BC 上时，∵四边形ABCD 是菱形， ∴5BC AB ==， ∴10PC x =−，当点P 在BC 上时，510x <≤， ∵PQ BD ∥， ∴CPQ CBD ∽，∴CP PQ CB BD =即1058x y −=， ∴8165y x =−+，综上可知，y 关于x 的函数表达式为()()80558165105x x y x x ≤≤ =−+<≤ 【小问2详解】解：由（1）所得关系式可知，x0 5 8 10 y83.2函数图象如下：性质：当05x ≤≤时，y 随x 的增大而增大；当510x <≤时，y 随x 的增大而减小；（答案不唯一）【小问3详解】解：如图，由图象可知，函数11y x b 2=+的图象在3l 和2l 之间时，与函数y 只有一个交点，将()5,8代入11y x b 2=+，得：1852b =×+，解得：112b =，将()0,0代入11y x b 2=+，得：0b =，将()10,0代入11y x b 2=+，得：5b =−， ∴b 的取值范围为50b −≤<或112b =．【点睛】本题考查了菱形的性质，相似三角形的判定及性质，求一次函数解析式，描点法画函数图象，一次函数图象和性质，两直线交点问题等知识，利用数形结合和分类讨论的思想解决问题是关键．24. 如图，M 为沙坪坝区物流中心，N ，P ，Q 为三个菜鸟驿站，N 在M 的正南方向4.3km 处，Q 在M 的正东方向，P 在Q 的南偏西37°方向2.5km 处，N 在P 南偏西64°方向．（sin370.60°≈，cos370.80°≈，tan370.75°≈，sin640.90°≈，cos640.44°≈，tan64 2.05°≈）（1）求驿站P ，驿站N 之间的距离（结果精确到0.1km ）；（2）“双11”期间，派送员从沙坪坝区物流中心M 出发，以30km/h 的速度沿着M N P Q ———的路线派送快递到各个驿站，派送员途径N ，P 两个驿站各停留6min 存放快递，请计算说明派送员能否在40min 内到达驿站Q ？【答案】（1）5.2km （2）能，理由见解析【解析】【分析】本题考查解直角三角形的应用，将实际问题转化成解直角三角形的问题，利用解直角三角形的知识求解是解题的关键．（1）过点P 作PA MN ⊥于A ，PB MQ ⊥于B ，先解Rt PBQ △，求得2km PB =，再证明2km AM PB ==，从而得出 2.3km AN =，然后解Rt PAN △，即可求解．（2）求出派送员所需总时间，再与40min 比较即可得出答案．【小问1详解】解：过点P 作PA MN ⊥于A ，PBMQ ⊥于B ，如图，根据题意，得37BPQ PQD ∠=∠=°，64PNA NPC ∠=∠=°， 4.3km MN =， 2.5km PQ =，在Rt PBQ △中，∵cos PB BPQ PQ∠=， ∴()cos 2.5cos37 2.50.802km PBPQ BPQ =⋅∠=×°≈×=， ∵PA MN ⊥，PBMQ ⊥，90NMQ ∠=°，∴四边形AMBP 是矩形， ∴2km AM PB ==，∴()4.32 2.3km AN MN AM =−=−=，在Rt PAN △中，∵cos PNA ∠∴()2.3 2.3 5.2km cos cos 640.44ANPNPNA ==≈≈∠°，答：驿站P ，驿站N 之间的距离约为5.2km ．【小问2详解】解：∵30km/h 0.5km/min =，∴()()4.3 5.2 2.50.56236min ++÷+×=， ∵36min<40min ，∴派送员能在40min 内到达驿站Q ．25. 如图1，在平面直角坐标系中，直线112y x =−+与抛物线()230y ax x a =−+≠交于A ，B 两点，且点A 在x 轴上，直线与y 轴交于点C ．（1）求抛物线的表达式；（2）P 是直线AB 上方抛物线上一点，过P 作PQ y ∥轴交直线AB 于点Q ，求PQ AQ 的最大值，并求此时点P 的坐标；（3）在（2）PQ AQ 的最大值的条件下，连接BP ，将抛物线沿射线BA 方向平移，使得点A 在新抛物线的对称轴上，M 是新抛物线上一动点，当MAB BPQ ∠=∠时，直接写出所有符合条件的点M 的坐标．【答案】（1）2134y x x =−−+（2）PQ AQ +的最大值为4，()2,4P −（3）点M 的坐标为()2,2或【解析】【分析】（1）先由一次函数解析式求出点()2,0A ，再把()2,0A 代入23y ax x =−+，求出a 值即可；（2）延长PQ 交y 轴于D ，证明OAC DAQ ∽，得AC OC AQ DQ =1DQ =，求得DQ AQ =，再设21,34P x x x −−+ ，则1,12Q x x−+ ，则211242PQ x x =−−+，112QD x =−+，所以()21244PQ AQ PQ QD PD x +=+==−++，利用二次函数最值即可求解．（3）根据平移的性质求得抛物线平移后的解析式为2114y x x =−++，再分两种情况：当点M 在直线AB 上方时，当点M 在直线AB 下方时，分别求解即可．【小问1详解】解：对于直线112y x =−+，令0y =，则1102x −+=，解得：2x =， ∴()2,0A ，把()2,0A 代入23y ax x =−+，得0423a −+，解得：14a =−， ∴抛物线的表达式2134y x x =−−+．【小问2详解】解：延长PQ 交y 轴于D ，对于直线112y x =−+，令0x =，则1y =， ∴CC (0,1)， ∵()2,0A∴AC ==∵PQ y ∥轴，即QD OC ∥， ∴OAC DAQ ∽∴AC OC AQ DQ =1DQ=，∴DQ AQ =，设21,34P x x x −−+ ，则1,12Q x x −+，∴2211113124242PQ x x x x x=−−+−−+=−−+，112QD x =−+∴()221132444PQ AQ PQ QD PD x x x =+==−−+=−++ ∵104−< ∴当2x =−时，PQ AQ +的最大值为4； ∴()2,4P −．【小问3详解】解：联立，2134112y x x y x =−−+=−+，解得：1143x y =− = ，2220x y = = ，∴()4,3B −，由（2）知，在PQ AQ +的最大值的条件下，抛物线的顶点为点()2,4P −，对称为直线PQ ，当2x =−时，则()12122y =−×−+=， ∴()2,2Q −，则2PQ =，PB QB∴BPQ BQP ∠=∠， ∵将抛物线沿射线BA 方向平移，使得点A 在新抛物线的对称轴上， ∴点Q 平移后与点A 重合， ∵()2,2Q −，()2,0A ，∴抛物线沿射线BA 方向平移，是向下平移了2个单位，向右平移了4个单位，∴抛物线顶点()2,4P −平移后到点()2,2P ′，点()4,3B −平移后到点()0,1B ′，即B ′与C 重合，∴BPQ B P A ′′ ≌，抛物线平移后的解析式为()221122144y x x x =−−+=−++，∴BPQ B P A ′′∠=∠， ∵()0,1B ′，()2,2P ′，∴P B =′=′∵()0,1B ′，()2,0A ，∴AB ′=，∴P B AB ′′′=， ∴B AP B P A ′′′′∠=∠，当点M 在直线AB 上方时，∵MAB BPQ ∠=∠， ∴MAB B P A ′′∠=∠， ∴点M 与点P ′重合， ∴()2,2M ，当点M 在直线AB 下方时，设21,14M x x x−++，过点M 作ME PQ ∥，交AB 于E ，交x 轴于N ，则MEA BQP ∠=∠，1,12E x x−+，则AOC ANE △∽△，∴AC OCAE EN=，则E AE EN AC =⋅=， ∵MAB BPQ ∠=∠， ∴BPQ MAE △∽△，∴BQ PQ ME AE=，则BQ ME PQ AE =，=，整理得：32E M y y =−，即：231111224x x x −+=−−++，解得：x =（x =，此时，M y =∴M ，综上，符合条件的点M 的坐标为()2,2或．【点睛】本题属二次函数综合题目，主要去向不明了待定系数法求抛物线解析式，抛物线的性质，抛物线的平移，相似三角形的判定与性质，综合性较强，熟练掌握相关性质是解题的关键．26. 在ABC 中，AC BC =，D 为线段AB 上一点，连接CD ．（1）如图1，若30B ∠=°，AC AD =，过A 作AE CD ⊥于O ，交BC 于E ，2CE =，求线段BE 的长；（2）如图2，过点B 作BF CD ⊥交CD 延长线于点F ，以BC 为斜边在ABC 的右侧作等腰直角三角形BCG ，过点G 作GH AB ∥，交DC 的延长线于点H ，HC FB =．猜想线段AD ，BD ，CD 的数量关系，并证明你的猜想；（3）如图3，60ACB ∠=°，过A 作AQ BC ⊥于Q ，作ACB ∠的角平分线交AQ 于M ，取CM 的中点N ，连接QN ．点K 为直线BC 上的动点，连接NK ，将QKN 沿着NK 所在直线翻折至ABC 所在平面得到Q KN ′ ，连接MQ ′，取MQ ′中点P ，连接CP ．将12CD 绕着点D 顺时针旋转至直线AB 上方DR 处，使得BDR ACD ∠=∠．当CP 取得最小值时，连接AP ，PR ，AR ，当ARP △以AP 为腰的等腰三角形时，请直接写出DR AP的值．【答案】（1）（2）AD BD =+（3 【解析】【分析】（1）利用等腰三角形的性质得120ACB ∠=°，75ACD ∠=°，得45DCE ∠=°，根据线段垂直平分线性质，得2CE DE ==，得90CED ∠=°，即得BE = （2）过点C 作CI AB ⊥于I ，得AI BI =，根据等腰直角BCG 中，90BG CG BGC =∠=°，，BF CD ⊥，得点G 、C 、F 、B 在以BC 为直径的圆上，得GCH GBF ∠=∠，结合HC FB =，得()SAS GCH GBF ≌，得GF GH BGF CGH =∠=∠，，得90FGH ∠=°，证明45IDC H ∠=∠=°，得DI =，根据BI BD DI =+，AD AI DI =+，即得AD BD =+；（3）证明当'Q 与C 重合时，点P 与点N 重合，PC 取得最小值，当AP AR =时，设CD 中点为T ，连接RT BR CR ，，，由对称性知，点R 在ABC ∠的平分线上，得CR AR =，由BDR ACD ∠=∠，得60CDR CAD ∠=∠=°，根据RT DT CT ==，得DTR 是等边三角形，得30RCT ∠=°，90CRD ∠=°，得tan DR DCR CR ∠=；②延长CM 交AB 于L ，过B 作BS AC ∥，交DR 延长线于S ，连接CS ，则AL BL =，60CBS ACB ∠=∠=°，得60CBS CDS ∠=∠=°，得B 在过C 、D 、S 三点的圆上，得60CSD CBD ∠=∠=°，得 CDS 是等边三角形，当D 与点B 重合时，T 与Q 重合，点R 在BS 上，根据150NQB NQR ∠=∠=°，BQ RQ NQ NQ ==，，得()SAS BQN RQN ≌,得BN RN =，得AN RN =，设ABC 的边长为2，则1AL =，CL =，根据23CM CL =，N 是CM 中点，得NL =，得AN =DR AP =【小问1详解】解：AC BC = ，30B ∠=°。

山西省大同市平城区三校联考2024届九年级上学期期中考试数学试卷(含答案)

山西省大同市平城区2023－2024（1）初三阶段性测试（数学）试题一、选择题（每小题3分，共30分，在每小题给出的四个选项中，只有一个选项正确）1.如图图案中既是轴对称图形又是中心对称图形的是（）A .B .C .D .2.将方程x 2－8x ＝10化为一元次方程的一般形式，其中二次项系数为1，一次项系数、常数项分别是（）A .－8、－10B .－8、10C .8、－10D .8、103.等腰三角形、等边三角形、矩形、正方形和圆这五种图形中，既是轴对称图形又是中心对称图形的图形种数是（）A .2B .3C .4D .54.已知关于x 的一元二次方程（a －5）x 2－4x －1＝0有实数根，则a 的取值范围是（）A .a ≥1B .a ＞1且a ≠5C .a ≥1且a ≠5D .a ≠55.将抛物线y ＝－2x 2＋1向右平移1个单位，再向上平移2个单位后所得到的抛物线为（）A .y ＝－2（x ＋1）2－1B .y ＝－2（x ＋1）2＋3C .y ＝－2（x －1）2＋1D .y ＝－2（x －1）2＋36、4张扑克牌如图（1）所示放在桌子上，小敏把其中一张旋转180°后得到如图（2）所示，那么她所旋转的牌从左起是（）图（1）图（2）A .第一张、第二张B .第二张、第三张C .第三张、第四张D .第四张、第一张7、如图，⊙O 的直径AB 垂直于弦CD ，垂足为E ，∠A ＝22.5°，OC ＝4，CD 的长为（）A.B.4C.D.88.如图，AB，CD是⊙O的两条直径，E是劣弧 BC的中点，连接BC，DE．若∠ABC＝22°，则∠CDE 的度数为（）A.22°B.32°C.34°D.44°9、如图，某小区计划在一块长为32m，宽为20m的矩形空地上修建三条同样宽的道路，剩余的空地上种植草坪，使草坪的面积为570m2，若设道路的宽为xm，则下面所列方程正确的是（）A.（32－2x）（20－x）＝570B.32x＋2×20x＝32×20－570C.（32－x）（20－x）＝32×20－570D.32x＋2×20x－2x2＝57010.如图，已知抛物线y＝ax2＋bx＋c的对称轴为直线x＝1，给出下列结论：①ac＜0；②b2－4ac＞0；③2a－b＝0；④a－b＋c＝0，其中，正确的结论有（）A.1个B.2个C.3个D.4个第Ⅱ卷（非选择题，共90分）二、填空题（本大题共5小题，每小题3分，共15分）11、若x＝2是方程x2－mx＋2＝0的根，则m＝．12、某村种的水稻前年平均每公顷产7200kg，今年平均每公顷产8450kg．设这两年该村水稻每公顷产量的年平均增长率为x，根据题意，所列方程为．'''的位置，旋转角为α（0°＜α＜90°）．若13、如图，将矩形ABCD绕点A顺时针旋转到矩形AB C D∠1＝110°，则α＝．14、如图，直线y＝x＋m和抛物线y＝x2＋bx＋c都经过点A（1，0）和B（3，2），不等式x2＋bx＋c＞x ＋m解集为．15、如图，点P是等边三角形ABC内一点，且PA6，PB2，PC＝2，则这个等边三角形ABC 的边长为．三、解答题（本题共8个小题，共75分，解答应写出文字说明、证明过程或演算步骤）16、（每小题4分，共8分）解下列方程：（1）x2－2x－1＝0（2）（x－2）2＝2x－417、（8分）如图，在平面直角坐标系中，△ABC的顶点坐标分别为A（－1，0），B（－4，1），C（－2，2）．（1）直接写出点B关于点C对称的点B'的坐标：；A B C；（2）请画出△ABC关于点O成中心对称的△111A B C．（3）画出△ABC绕原点O逆时针旋转90°后得到的△22218、（6分）如图，杂技团进行杂技表演，演员从跷跷板右端A处弹跳到人梯顶端椅子B处，其身体（看成一点）的路线是抛物线y＝－0.5x2＋3x＋1的一部分．（1）求演员弹跳离地面的最大高度；（2）已知人梯高BC＝5米，在一次表演中，人梯到起跳点A的水平距离是4米，问这次表演是否成功？请说明理由．=，∠OPB＝45°．19、（8分）如图，已知⊙O中，弦AB＝8，点P是弦AB上一点，OP32（1）求OB的长；（2）过点P作弦CD与弦AB垂直，求证：AB＝CD．20、（10分）如图，AB 为⊙O 的切线，B 为切点，过点B 作BC ⊥OA ，垂足为点E ．交于点C ，延长CO 与AB 的延长线交于点D ．（1）求证：AC 为⊙O 的切线；（2）若OC ＝2，OD ＝5，求线段AD 和AC 的长．21、（10）某水果商店销售一种进价为40元/千克的优质水果，若售价为50元/千克，则一个月可售出500千克；若售价在50元/千克的基础上每涨价1元，则月销售量就减少10千克．（1）当月利润为8750元时，每千克水果售价为多少元？（2）当每千克水果售价为多少元时，获得的月利润最大？22.（12分）在数学兴趣小组活动中，小明进行数学探究活动，如图①所示，已知直角三角形ABC 中，BC ＝AC ，点E ，D 为AC 、BC 边的中点．操作探究将△ECD 以点C 为旋转中心逆时针旋转，得到△E CD ''，连接,AE BD ''．图①图②图③图④（1）如图②，判断线段AE '与BD '的数量关系与位置关系，并说明理由；（2）如图③，当B ，D '，E '三点在同一直线上时，∠E 'AC ＝20°，求旋转角的度数；（3）如图④，当旋转到某一时刻，CD BD ''⊥，延长BD '与AE '交于点F ，请判断四边形D CE F ''的形状，并说明理由；23、（13分）如图，在平面直角坐标系xOy 中，抛物线y ＝－x 2＋bx ＋c 与x 轴相交于原点O 和点B （4，0），点A （3，m ）在抛物线上．（1）求抛物线的表达式，并写出它的对称轴；（2）若点P为线段OA上方抛物线上的点，过点P作x轴的垂线，交OA于点Q，求线段PQ长度的最大值．（3）在抛物线的对称轴上是否存在一点N，使得△BAN为以AB为腰的等腰三角形，若不存在，请说明理由，若存在，请直接写出点N的坐标．2023－2024学年第一学期九年级数学期中考试答案一、选择题12345678910D A B C D AC C A C 二、填空题11.312.7200（1＋x ）2＝845013.20°14.x ＜11或x ＞3三、解答题16.（8分）（1）x 2－2x －1＝0x 2－2x －1＋2＝2x 2－2x ＋1＝2（x －1）2＝2x －1∴x －1或x －11211x x ==+（2）（x －2）2＝2x －4（x －2）2－2x ＋4＝0X 2－4x ＋4－2x ＋4＝0X 2－6x ＋8＝0（x －2）（x －4）＝01224x x ==17.（8分）（1）（4，－1）（2）如图所示，△111A B C 为所求作的图形；（3）如图所示，△222A B C 为所求作的图形．18.（6分）（1）y ＝－0.5x 2＋3x ＋1a ＝－12b ＝3c ＝1h ＝331222b a -=-=⎛⎫⨯- ⎪⎝⎭221413429112 5.5142242ac b k a ⎛⎫⨯-⨯- ⎪----⎝⎭=====--⎛⎫⨯- ⎪⎝⎭∴顶点（3，5.5）答：演员弹跳离地面的最大高度为5.5米．（2）当x ＝4，代入21312y x x =-++2143412y =-⨯+⨯+1161212=-⨯++＝－8＋12＋1＝5∵5＝5∴这次表演成功了．19.（8分）（1）过O 作OH ⊥AB 90OHB OHA ∠∠∴==142AH BH AB ===45OPB ∠=∴△OHP 为等腰直角三角形设OH ＝PH ＝x在Rt △PHO 中OH 2＋PH 2＝OP 2222x x +=2x 2＝18x 2＝93x =±1233x x ==-（舍）∴OH ＝PH ＝3在Rt △DHB 中OB =5∴OB ＝5（2）过O 作OE ⊥CD ∴90OEP ∠= 190,2OEP BPC OHP CE DE CD ∠∠∠===== ∴四边形OEPH 为矩形又∵OH ＝PH∴四边形OEPH 为正方形∴OE ＝OH ＝3连接OC∴OC ＝OB ＝５在Rt △CEO 中CE =＝4∴CD ＝2CE ＝8∴AB ＝CD ＝820.（10分）（1）连接OB∵OB ，OC 为⊙O 半径∴OB ＝OC∵CB ⊥OA∴∠OED ＝∠BEO ＝90°在Rt △CED 和Rt △BED 中CO BOOE OE=⎧⎨=⎩∴Rt △CED ≌Rt △BED （HL ）COE BOE ∠∠∴=在△AOC 和△AOB 中OC OBCOE BOE AO AO∠∠=⎧⎪=⎨⎪=⎩∴△AOC ≌△AOB （SAS ）90ACO ABO ∠∠∴== AC OC∴⊥∵OC 为⊙O 半径∴AC 为⊙O 的切线．（2）∵△AOC ≌△AOB∴AB ＝AC OB ＝OC ＝2∵AB 为⊙O 的切线90OBD ∠∴=在Rt △BOD 中BD ===设AB ＝AC ＝x ，则AD x+∵AC 为⊙O 的切线90ACD ∠∴=CD ＝OC ＋OD ＝2＋5＝7在Rt △ACD 中AC 2＋CD 2＝AD 22227)x x +=+224921x x +=++28=14=x =142121=2213=∴AC ＝AB 2213=∴AD ＝AB ＋BD 22152133==21.（10分）（1）解：设水果涨价了x 元，则少售出10x 千克（500－10x ）（50＋x －40）＝8750（500－10x ）（10＋x ）＝87505000＋500x －100x －10x 2＝8750－10x 2＋400x ＝3750－x 2＋40x －375＝0x 2－40x ＋275＝0（x －25）（x －15）＝0122515x x ==当x ＝25时，50＋x ＝75当x ＝15时，50＋x ＝65答：当月利润为8750元时，水果售价为75元或65元．（2）设月利润为WW ＝（500－10x ）（50＋x －40）＝（500－10x ）（10＋x ）＝5000＋500x －100x －10x 2＝－10x 2＋400x ＋5000a ＝－10b ＝400c ＝50004002022(10)b h a =-=-=⨯-∵a ＝－10开口向下∴当x ＝20时，月利润最大售价＝50＋20＝70（元）答：当售价为70元时，获得的月利润最大．22.（12分）（1）AE BD AE BD ''=⊥''∵AB ＝AC ，E 、D 为AC 、BC 中点E C CD '∴='又∵△ABC 为Rt △∠C ＝90°90E CD ACB ∠∠'∴=='即1290ACD ACD ∠∠∠∠''+=+=12∠∠∴=在△ACE '与△BCD '中12AC BC E C D C ∠∠⎪'=⎧⎪=⎨'=⎩∴△ACE '≌△BCD '（SAS ）AE BD EAC DBC∠∠'∴''∴==∵AC ＝BC ，∠ACB ＝90°∴∠CAB ＝∠CBA ＝45°反向延长BD '，交AE '于F45CBD ABF ∠∠'+= 45EAC ABF ∠∴∠+= ∴180()AFB EAC ABF CAB ∠∠∠∠'=-+- =180455049=--∴BF ⊥AF（2）由（1）知BD AE '⊥'，设BD '交AC 于F 90AE B ∠∴='20E AC ∠'=180902070AFE ∠'∴=--=70CFD ACE ∠∠∴'=='CD CE ''= 90E CD ∠=''45CD E ∠'∴'=180704655ACD ∠'∴=--=90=906525D CB ACD ∠∠''∴=--= ∴旋转角为25°．（3）BD CD ''⊥ 90BD C ∠'∴'= 又90D CE ∠'='90BD C D CE ∠∠∴''=='' //CE BD ''∴由（1）知BD AE '⊥'90BFE ∠'∴=∵//CE BD ''180AE C BFE ∠∠''∴+= 90AE C BFE ∠∠'∴=='又90D CE ∠''=90AE C BFE D CE ∠∠∠''''∴=== 即四边形D CE F ''为矩形又CE CD ''= ∴四边形D CE F ''为正方形．23.（13分）（1）y ＝－x 2＋bx ＋ca ＝－1设()()12y a x x x x =--设120,4x x ==代入y ＝－x （x －4）＝－x 2＋4x4222(1)24b h a =-=-=-=⨯--∴抛物线表达式：y ＝－x 2＋4x 抛物线对称轴为直线x ＝2（2）将x ＝3代入y ＝－x 2＋4x 2343y =-+⨯＝－9＋12＝3∴A 的坐标为（3，3）设OA 的解析式为y ＝kx将点A （3，3）代入3＝3kk ＝1∴OA 的解析式为y ＝x设P 的坐标为（x ，－x 2＋4x ）则Q 的坐标（x ，x ）p y QP> P PQ y QP ∴=-＝－x 2＋4x －x 23PQ y x x=-+a ＝－1b ＝33322(1)2h b a =-=-=⨯-2243944(1)4ac b k a --===⨯-∴PQ 长度的最大值为94．（3）存在，N 的坐标为(2,，（2，0），．。

广东省韶关市翁源县2024-2025学年九年级上学期11月期中考试数学试题(含答案)

2024-2025学年度第一学期期中考试九年级数学注意事项：1．全卷共6页，满分为120分，考试用时为120分钟．2．答卷前，考生务必用黑色字迹的签字笔或钢笔在答题卡填写自己的准考证号、姓名、考场号、座位号，用2B 铅笔把对应的号码的标号涂黑．3．在答题卡上完成作答，答案写在试卷上无效．一、选择题：本大题共10小题，每小题3分，共30分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．下列图形中，既是中心对称图形又是轴对称图形的是（）A ．B ．C ．D ．2．关于的一元二次方程的二次项系数、一次项系数、常数项分别是（）A ．1，2，5B ．C ．D ．3．已知和关于原点对称，则的值为（）A ．B ．1C ．D ．54．二次函数的图象顶点坐标是（）A ．B ．C ．D ．5．将抛物线先向下平移1个单位长度，再向右平移3个单位长度，所得到的抛物线为（）A ．B ．C ．D ．6．如图，已知点，将线段绕点按顺时针方向旋转，旋转后点的对应点坐标为（）A ．B ．C ．D ．7．如图，已知一菜园为长10米，宽7米的矩形，为了方便浇水和施肥，修建了同样宽的四条互相垂直的“井”x 2250x x -+-=1,2,5--1,2,5-1,2,5-(),2A a ()3,B b a b +5-1-23(1)2y x =-+-()1,2-()1,2-()1,2()1,2--22y x =+2(3)1y x =++2(3)3y x =-+2(3)3y x =++2(3)1y x =-+()1,2P PO O 90︒P ()1,2-()2,1-()2,1-()2,1字形道路，余下的部分种青菜，已知种植青菜的面积为54平方米，设小路的宽为米，则根据题意列出的方程是（）A ．B ．C ．D ．8．关于的一元二次方程的一个根是1，则的值为（）A ．1或B ．C ．1D ．9．设是抛物线上的三点，则的大小关系为（）A ．B ．C ．D ．10．如图，在正方形中，点的坐标分别是，点在抛物线的图象上，则的值是（）A ．B．C ．D ．二、填空题：本大题共5小题，每小题3分，共15分．11．若方程是关于的一元二次方程，则的取值范围是_______．12．若二次函数与轴只有1个交点，则_______．13．数学课堂上，为探究旋转的性质，同学们进行了如下操作：如图所示，将一个三角形硬纸板，放置在一张白纸上，描出硬纸板的形状，并用图钉固定点，将三角形硬纸板绕点顺时针旋转一定角度后，再描出形状得到，经测量，则_______．x ()()1027254x x --=()()10754x x --=()()107254x x --=()()1027254x x +-=x ()22120a x x a -++-=a 2-2-1-()()()1233,,2,,2,A y B y C y --22y x x c =--+123,,y y y 321y y y >>123y y y >>132y y y >>213y y y >>ABCD A C 、()()1,17,3-、D 21y x bx =+-b 32-3212-12()2230a x x -+-=x a 22y x x m =-+x m =ABC △A A ADE △50,15BAC CAD ∠=︒∠=︒CAE ∠=14．设是方程的两个实数根，则的值为_______．15．如图，在中，，将绕点逆时针旋转得到，当点的对应点恰好落在边上时，则的长为_______三、解答题（一）：本大题共3小题，每小题7分，共21分．16．（7分）解方程：17．（7分）如图，在平面直角坐标系中，点的坐标分别为．（1）画出关于点的中心对称图形；（2）将绕点顺时针方向旋转后得，画出．18．（7分）如图，是二次函数的图象．12,x x 23210x x --=1212x x x x --ABC △3,1AB AC ==ABC △C 90︒CDE △A D AB AE ()330x x x --+=A B C 、、()()()1,1,2,3,4,2ABC △O 111A B C △111A B C △O 90︒222A B C △222A B C △2y ax bx c =++（1）求二次函数解析式；（2）根据图象直接写出关于的不等式的解集．四、解答题（二）：本大题共3小题，每小题9分，共27分．19．（9分）如图，四边形为矩形，，将对角线绕点逆时针旋转得，作交于点．（1）证明：；（2）连接，求的长．20．（9分）乐昌马蹄是广东韶关的特产，韶关乐昌有着“马蹄之乡”的美称．乐昌马蹄以个头大、清甜多汁、爽脆无渣为特点而闻名全国，畅销国内外．某农产品商以每斤5元的价格收购乐昌马蹄，若按每斤10元出售，平均每天可售出100斤．市场调查反映：如果每斤降价1元，每天销售量相应增加50斤．（1）若该农产品商想要日销售利润达到600元，测每斤马蹄应降低多少元？（2）日销售利润能否达到700元？如果能，请计算出每斤马蹄降价多少元；如果不能，请说明理由．21．（9分）为解方程，我们可以将视为一个整体，然后设，则原方程化为，解此方程得．当时，．当时，原方程的解为．以上方法叫做换元法解方程，达到了降次的目的，体现了转化思想．根据以上阅读材料内容，解决下列问题，并写出解答过程．（1）请用上述方法解方程：．x 20ax bx c ++>ABCD 3,4AB BC ==AC A 90︒AF FE AD ⊥AD E ABC AEF △≌△DF DF ()()22237360x x ---+=23x -23x t -=2760t t -+=121,6t t ==1t =231,2x x -=∴=±6t =236, 3.x x -=∴=±∴12342,2,3,3x x x x ==-==-42540x x -+=（2）已知实数满足，求的值．五、解答题（三）：本大题共2小题，第22题13分，第23题14分，共27分．22．（13分）如图，直线与抛物线相交于和．（1）求抛物线的解析式；（2）点是线段上的动点，过点作轴，交抛物线于点．是否存在这样的点，使线段的长有最大值？若存在，求出这个最大值；若不存在，请说明理由；（3）轴上是否存在点，使得为等腰三角形？若存在，求出点的坐标；若不存在，请说明理由．23．（14分）【阅读理解】半角模型是指有公共顶点，锐角等于较大角的一半，且组成这个较大角的两边相等．通过旋转或截长补短，将角的倍分关系转化为角的相等关系，并进一步构成全等三角形，用以解决线段关系、角度、面积等问题，【初步探究】如图1，在正方形中，点分别在边上，连接．若，将绕点顺时针旋转，点与点重合，得到．易证：．（1）根据以上信息，填空：（1）_______°；（2）线段之间满足的数量关系为_______；【迁移探究】（2）如图2，在正方形中，若点在射线上，点在射线上，，猜想线段之间的数量关系，请证明你的结论；【拓展探索】（3）如图3，已知正方形的边长为，连接分别交于点，若点恰好为线段的三等分点，且，求线段的长．,x y ()()2222222222150x y x y +-+-=22x y +2y x =-()220y ax bx a =++≠()1,1A -(),2B m C AB C CD x ⊥D C CD x M ABM △M ABCD ,E F ,BC CD ,,AE AF EF 45EAF ∠=︒ADF △A 90︒D B ABG △AEF AEG △≌△EAG ∠=BE EF DF 、、ABCD E CB F DC 45EAF ∠=︒BE EF DF 、、ABCD 45EAF ∠=︒BD AE AF 、M N 、M BD BM DM <MN2024-2025学年度第一学期期中考试九年级数学参考答案及评分标准一、选择题：本大题共10小题，每小题3分，共30分．1-5CBADD 6-10CABDB二、填空题：本大题共5小题，每小题3分，共15分．11． 12．1 13． 14． 15三、解答题（一）：本大题共3小题，每小题7分，共21分．解答要求写出文字说明、证明过程或演算步骤．16．解：．解得：．（方法不唯一，酌情给分）17．解：（1）如图所示：即为所求．（2）如图所示：即为所求．18．解：（1）设二次函数解析式为：2a ≠35︒1-()()330x x x -+-=()()130x x +-=121,3x x =-=111A B C △111A B C △()()()240y a x x a =+-≠把点代入得：解得：（2）．四、解答题（二）：本大题共3小题，每小题9分，共27分．解答要求写出文字说明、证明过程或演算步骤．19．（1）证明：四边形为矩形绕点逆时针旋转得，，，在和中．（2）解：四边形为矩形，，，在中，根据勾股定理得：20．解：（1）设每斤马蹄降价元根据题意得解得答：若该农商想要日销售利润达到600元，则每斤马蹄应降低1元或2元．（2）日销售利润不能达到700元．理由如下：设每斤马蹄降价元则化简得方程无实数根日销售利润不能达到700元．()0,484a -=12a =-24x -<< ABCD 90B BAD ∴∠=∠=︒90BAD CAD ∴∠+∠=︒AC A 90︒AF,90BC EF CAF ∴=∠=︒90EAF CAD ∴∠+∠=︒BAD EAF∴∠=∠FE AD ⊥ 90AEF ∴∠=︒B AEF∴∠=∠ABC △AEF △BAD EAF B AEFAC AF ∠=∠⎧⎪∠=∠⎨⎪=⎩()AAS ABC AEF ∴△≌△ ABCD 4AD BC ∴==ABC AEF △≌△3,4AB AE BC EF ∴====431DE AD AE ∴=-=-=FE AD ⊥ 90DEF ∴∠=︒Rt DEF △DF ===x ()()10510050600x x --+=111,2x x ==a ()()10510050700a a --+=2340a a -+=2(3)4470=--⨯=-<△∴∴21．解：（1）设则原方程化为：解得：当时当时原方程的解为：（2）设则原方程化为：解得：，，．五、解答题（三）：本大题共2小题，第22题13分，第23题14分，共27分．解答要求写出文字说明、证明过程或演算步骤．22．解：（1）把代入直线得，，在抛物线上，，解得，抛物线的解析式为．（2）存在．理由如下：设动点的坐标为，则点的坐标为，点是线段上的动点，当时，线段有最大值且为．（3）存在．设点①当时，2y x=2540y y -+=121,4y y ==1y =2,1,1x x =∴=±4y =2,4,2x x =∴=±∴12341,1,2,2x x x x ==-==-2222w x y=+22150w w --=125,3w w ==-22220x y +≥ 22225x y ∴+=2252x y ∴+= (),2B m 2y x =-4m =()4,2B ∴()()1,14,6A B - 、22y ax bx =++2116422a b a b ++=-⎧∴⎨++=⎩14a b =⎧⎨=-⎩∴242y x x =-+C (),2n n -D ()2,42n n n -+()()2242PC n n n ∴=---+254n n =-+-25924n ⎛⎫=--+ ⎪⎝⎭ C AB 14n ∴≤≤∴52n =PC 94(),0M c AB AM =解得：或．②当时，解得：或．③当时，解得：，综上所述，为等腰三角形时，点的坐标为或或或或23．（1）①45 ②．（2）解：．证明如下：如图在上截取，连接，和中，，，，即，，，在和中，，2222(14)(12)(1)(10)c -+--=-+--121,1c c =+=+)1,0M ∴+()1,0M +AB BM =2222(14)(12)(4)(20)c -+--=-+-124,4c c =+=)4,0 M ∴+()4,0M +AM BM =2222(1)(10)(4)(20)c c -+--=-+-3c =()3,0M ∴∴ABM △M )1,0+()1,0+)4,0+()4,0+()3,0BE DF EF +=BE EF DF +=DC DH BE =AH ABE △ADH △,AB AD ABE D BE DH =⎧⎪∠=∠⎨⎪=⎩()SAS ABE ADH ∴△≌△,AE AH BAE DAH ∴=∠=∠90BAE BAH BAH DAH ∴∠+∠=∠+∠=︒90EAH BAD ∠=∠=︒45EAF ∠=︒ 45EAF FAH ∴∠=∠=︒EAF △HAF △AE AH EAF HAF AF AF =⎧⎪∠=∠⎨⎪=⎩，，，，（3）将绕点顺时针旋转得到，连接，由旋转可得，，又，，，设，则，在中，，，解得，；()SAS EAF HAF ∴△≌△EF HF ∴=DF DH HF =+ DF BE EF ∴=+ADN △A 90︒ABK △KM 90AB AD ADC ==∠=︒6BD ∴==12,43BM BD DM BD BM ∴===-=,90ADN ABK KAN ∠=︒△≌△,,45AK AN BK DN ABK ADB ∴==∠=∠=︒90KBM ABK ABD ∴∠=∠+∠=︒90,45KAN MAN ∠=︒∠=︒45KAM MAN ∴∠=∠=︒AM AM = AMK AMN ∴△≌△KM MN ∴=∴MK MN x ==4BK DN x ==-Rt BMK △222BK BM MK +=222(4)2x x ∴-+=2.5x = 2.5MN ∴=。

上海市普陀区2024-2025学年九年级上学期数学期中考试试卷(含答案)

2024学年第一学期九年级数学学科期中考试试卷2024.10（时间：100分钟，满分：150分）一、选择题（本大题共6题，每题4分，满分24分）【下列各题的四个选项中，有且只有一个是正确的，选择正确项的代号并填涂在答题纸的相应位置上】1.下列函数中，一定为二次函数的是（）A. B. C. D.2.已知点P是线段AB的黄金分割点，且，那么下列结论正确的是（）A. B.C.D.3.如图，在中，点D、E和F分别在边AB、AC和BC上，，，如果，那么下列结论中正确的是（）A. B. C. D.4.下列关于向量的说法中，正确的是（）A.如果，那么B.如果，，那么C.已知是单位向量，如果，那么D.如果，，其中是非零向量，那么5.在同一平面直角坐标系中，画出直线与抛物线，这个图形可能是（）A. B.21yx=()()11y x x=+-2y ax=()21y x x x=-+BP AP>2BP AP AB=⋅2AP BP AB=⋅APAB=BPAP=ABC△DE BC∥DF AC∥34ADBD=34DEBC=34BFCF=37CFBC=37DFAC=k=0ka=2a=1b=2a b=e4a=4ea=23a b c+=2b c=ca b∥y ax b=+2y ax b=+C. D.6.已知在中，点D 、E 分别在边AB 和AC 上，联结CD 、BE 交于点F ，下列条件中，不一定能得到和相似的是（）A. B. C. D.二、填空题（本大题共12题，每题4分，满分48分）【请将结果直接填入答题纸的相应位置】7.已知，且，那么_______.8.抛物线与y 轴的交点坐标为_______.9.已知二次函数的图像经过点、，那么该二次函数图像的对称轴为直线_______.10.已知二次函数的图像在对称轴的左侧部分是上升的，那么m 的取值范围是_______.11.如图，已知在中，，CD 是边AB 上的高，如果，，那么_______.12.如图，在中，，点D 和点E 在边BC 上，，，那么_______.13.如图，已知，且，那么_______.ABC △ADE △ABC △DF EF BF CF =DF EF CF BF=BDE BFC ∠=∠BDF CEFS S =△△234a b c k ===0k ≠c a c b-=+223y x x =+-()20y x bx c a =++≠()1,1A --()5,1B -()21y m x =+ABC △90ACB ∠=︒3AD =2BD =CD =ABC △3AB AC ==4BE =BAE ADC ∠=∠CD =AD EF BC ∥∥::2:5:7AD EF BC =:AE AB =14.如图，在中，点D 在边BC 上，线段AD 经过重心G ，向量，向量，那么向量______.（用向量、表示）15.如图，一条河的两岸有一段是平行的，在河的南岸边每隔10米种一棵树，在北岸边每隔50米有一根电线杆.小丽站在离南岸边15米的点P 处看北岸，发现北岸有两根相邻的电线杆恰好被南岸的两棵树遮住，并且在这两棵树之间还有一棵树，那么这段河的宽度为_______米.16.如图，在中，点D 在边AB 上，，点E 和F 分别在边BA 和CA 的延长线上，且，如果，那么_______.17.定义：如果将抛物线上的点的横坐标不变，纵坐标变为点A 的横、纵坐ABC △BA a = BC b = AG =a b ABC △ACD B ∠=∠CD EF ∥::3:4:2EA AD DB =AEF ABCS S =△△()20y ax bx c a =++≠(),A x y标之和，就会得到一个新的点，我们把这个点叫做点A 的“简朴点”，已知抛物线上一点B 的简朴点是，那么该抛物线上点的简朴点的坐标为_______.18.如图，在矩形ABCD 中，，在边CD 上取一点E ，将沿直线BE 翻折，使点C 恰好落在边AD 上的F 处，的平分线与边AD 交于点M ，如果，那么_______.三、解答题（本大题共7题，满分78分）19.（本题满分10分）如图，已知两个不平行的向量、，求作，满足.（不要求写作法，但要保留作图痕迹，并指出所作图中表示结论的向量.）20.（本题满分10分，第（1）小题5分，第（2）小题5分）已知点在二次函数的图像上.（1）求二次函数图像的对称轴和顶点坐标；（2）将二次函数的图像先向左平移4个单位，再向上平移t 个单位后图像经过点，求的值.21.（本题满分10分，第（1）小题5分，第（2）小题5分）已知二次函数的图像经过原点，顶点坐标为.（1）求二次函数的解析式；（2）如果二次函数的图像与x 轴交于点A （不与原点重合），联结OP 、AP ，试判断的形状并说明理由.22.（本题满分10分，第1小题5分，第2小题5分）如图，已知在中，点D 在边AC 上，过点A 作，交BD 的延长线于点E ，点F 是BE 延长线上一点，联结CF ，如果.（1）求证：；（2）如果，，求的值.()1,A x x y +1A 241y ax x =-+()12,3B ()1,C m 1C 1AB =BCE △ABF ∠2AD MF =BC =a bx x ()2a x b x -=- ()3,1-2y x bx b =-++()1,5-t ()2,2P -AOP △ABC △AE BC ∥2BD DE DF =⋅AB CF ∥2DE =6EF =AB CF23.（本题满分12分，第（1）小题5分，第（2）小题7分）如图，在中，CD 是AB 边上的高，点E 是边AC 的中点，联结ED 并延长交CB 的延长线于点F ，且.（1）求证：；（2）如果，求证：.24.（本题满分12分，第（1）小题4分，第（2）小题4分，第（3）小题4分）如图，在平面直角坐标系xOy 中，二次函数的图像与x 轴交于点，与y 轴交于点.（1）求该二次函数的解析式；（2）如果点是二次函数图像对称轴上的一点，联结AD 、BD ，求的面积；（3）如果点P 是该二次函数图像上位于第二象限内的一点，且，求点P 的横坐标.ABC △BD BF =ADE FDB ∽△△2DF AC CF AD=2BC BD AB =⋅22y x bx c =-++()2,0A -()0,4B (),1D m -ABD △PB AB ⊥25.（本题满分14分，第（1）小题4分，第（2）小题6分，第（3）小题4分）如图，在矩形ABCD 中，，，点E 是射线D A 上的一点，点F 是边AB 延长线上的一点，且.联结CE 、EF ，分别交射线DB 于点O 、点P ，联结CF 、CP .（1）当点E 在边AD 上时，①求证：；②设，，求y 关于x 的函数解析式；（2）过点E 作射线DB 的垂线，垂足为点Q ，当时，请直接写出DE 的长.2AB =1BC =2DE BF =DCE BCF ∽△△DE x =CP y =14OQ PQ =2024学年第一学期九年级数学学科期中考试卷2024.10参考答案及评分说明一、选择题：（本大题共6题，每题4分，满分24分）1.B ；2.A ；3.C ；4.D ；5.D ；6.C.二、填空题：（本大题共12题，每题4分，满分48分）7.；8.；9.；10.；；12.；13.；14.；15.；16.；17.；18.三、解答题：（本大题共7题，其中第19—22题每题10分，第23、24题每题12分，第25题14分，满分78分）19.解：，20.解：（1）∵点在二次函数的图像上，∴把，代入，得.解得.∴二次函数的解析式为.∴对称轴为直线.顶点的坐标为.（2）二次函数的解析式化为.∵将二次函数的图像先向左平移4个单位，再向上平移t 个单位，∴平移后新二次函数的解析式为.∵平移后图像经过点，∴把，代入，得.解得.21.解：（1）∵二次函数图像的顶点坐标为，∴设二次函数的解析式为.∵二次函数的图像经过原点，∴把，代入得..27()0,3-2x =1m <-94352133a b -+ 45238()1,05322a x b x -=- 2x a b =- ()3,1-2y x bx b =-++3x =1y =-2y x bx b =-++193b b -=-++2b =222y x x =-++1x =()1,3()213y x =--+()233y x t =-+++()1,5-1x =5y =-()233y x t =-+++5163t -=-++8t =()2,2P -()222y a x =--0x =0y =()222y a x =--()20022a =--解得.∴这个二次函数的解析式为.（2）∵二次函数的图像与x 轴交于点A ，∴把，代入得，（舍去）.得点A 的坐标为.∴.∵，∴.∵，∴是等腰直角三角形.22.解：（1）∵，∴.∵，∴.∴∴.（2）∵，，∴.∵，∴.∵，∴，∴.23.证明：（1）∵，∴.∵CD 是AB 边上的高，点E 是边AC 的中点，∴在中.又∵，∴.∴.∵，∴.∴.（2）∵，∴.∴.∵，∴∴∴.∵，∴.∴.∴.24.解：（1）∵二次函数的图像与x 轴交于点，与y 轴交于点，12a =()21222y x =--0y =()21222y x =--14x =20x =()4,04OA =OP ==AP ==OP AP =222OP AP OA +=AOP △AE BC ∥AD DE CD BD=2BD DE DF =⋅DE BD BD DF=AD BD CD DF=AB CF ∥2DE =6EF =8DF DE EF =+=216BD DE DF =⋅=4BD =AB CF ∥AB BD CF DF =12AB CF =BD BF =F BD ∠=∠Rt ACD △12DE AC =12AE AC =AE DE =A ADE ∠=∠ADE BDF ∠=∠A F ∠=∠ADE FDB ∽△△2DF AC CF AD =DF AE CF AD =DF CF AE AD=A F ∠=∠ADE FCD ∽△△ADE FCD ∠=∠A FCD ∠=∠ABC CBD ∠=∠ABC CBD ∽△△BD BC BC AB=2BC BD AB =⋅22y x bx c =-++()2,0A -()0,4B得解得.∴二次函数的解析式为.（2）∵点是二次函数图像对称轴上的一点，又∵二次函数图像的对称轴为直线.∴，点D 坐标为.设直线AB 的表达式为.∵直线AB 经过，，得，解得，∴直线AB 的表达式为.设抛物线的对称轴与直线AB 交于点E ，得点E 坐标为.∴.∴.（3）过点P 作轴，垂足为H .设点.∴，.∵，又∵，∴.∵，∴.∴.∴.∴（舍去），.即点P 的横坐标是.25.解：（1）∵四边形ABCD 是矩形，∴，，∵，∴.()202224b c c⎧=-⨯--+⎪⎨=⎪⎩2b =-2224y x x =--+(),1D m -12x =-12m =-1,12⎛⎫-- ⎪⎝⎭()0y px q p =+≠()2,0A -()0,4B 024p q q =-+⎧⎨=⎩24p q =⎧⎨=⎩24y x =+1,32⎛⎫- ⎪⎝⎭4DE =1142422ABD ADE BDE S S S DE AO =+=⋅=⨯⨯=△△△PH y ⊥()2,224P t t t --+PH t =-222BH t t =--ABO ABP P PHB ∠+∠=∠+∠90ABP PHB ∠=∠=︒ABO BPH ∠=∠90AOP PHB ∠=∠=︒ABO BPH ∽△△PH BH BO AO =22242t t t ---=10t =234t =-34-2AB CD ==90CDE ABC ∠=∠=︒90CBF ∠=︒CDE CBF ∠=∠∵，∴.∵，∴.∴.∴.（2）∵，∴.即.∵，∴.∴.∴.∵，∴.∴.又∵且，∴.∴.∵，∴.∴.∴.∵在中，，，∴.同理可得∴∴（3）1BC =12BC CD =2DE BF =12BF DE =BF BC DE CD=DCE BCF ∽△△DCE BCF ∠=∠DCE BCE BCF BCE ∠+∠=∠+∠BCD ECF ∠=∠,CD CE CB CF =CD CB CE CF=DCB ECF ∽△△PEC BDC ∠=∠EOP DOC ∠=∠EOP DOC ∽△△OE OP OD OC=OE OD OP OC=DOE COP ∠=∠DOE COP ∽△△EDO PCO ∠=∠EDO DBC ∠=∠PCE DBC ∠=∠ECP DBC ∽△△PC EC BC BD=Rt CDE △DE x =2CD =CE =BD =1y =y =1DE =2DE =3DE =。

湖北省荆州市2024-2025学年九年级上学期11月期中考试数学试题(含答案)

2024～2025学年度上学期学情监测九年级数学试题（本试卷共4页，满分120分，考试时间120分钟）注意事项：1.答卷前，考生务必将自己的姓名、准考证号填写在试卷和答题卡上，并将准考证号条形码粘贴在答题卡上指定位置。

2.选择题的作答：每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑。

写在试卷、草稿纸和答题卡上的非答题区域均无效。

3.非选择题的作答：用黑色签字笔直接答在答题卡上对应的答题区域内，写在试卷、草稿纸和答题卡上的非答题区域均无效，作图一律用2B 铅笔或黑色签字笔。

一、选择题（共10题，每题3分，共30分，在每题给出的四个选项中，只有一项符合题目要求）1.中国航天取得了举世瞩目的成就，为人类和平贡献了中国智慧和中国力量，下列是有关中国航天的图标，其文字上方的图案是中心对称图形的是（）A.B. C. D.2.一元二次方程根的情况是（）A.有两个相等的实数根B.有两个不相等的实数根C.没有实数根D.两根互为相反数3.如图，紫荆花绕它的旋转中心，按下列角度旋转，能与其自身重合的是（）A. 60°B. 120°C. 144°D. 180°4.如图，是的直径，，则的度数是（）A. 30°B. 40°C. 50°D. 60°5.若是方程的一个根，则的值为（）A. 2024B. C. D. 10156.用配方法解方程时，配方正确的是（）2210x x --=AB O e 30CDB ∠=︒ABC ∠x m =2210090x x --=2246m m -+2012-1003-2840x x --=A. B. C. D.7.函数和函数（a 是常数，且）在同一平面直角坐标系中的图象可能是（）A.B. C. D.8.小聪以二次函数的图象为模型设计了一款杯子，如图为杯子的设计稿，若，，则杯子的高为（）A. B. C. D.9.如图，小程爸爸用一段长的铁丝网围成一个一边靠墙（墙长）的矩形鸭舍，其面积为，在鸭舍侧面中间位置留一个宽的门（由其它材料制成），则的长为（）A. 8m 或5mB. 4m 或2.5mC. 8mD. 5m 10.如图，开口向上的抛物线（）与x 轴交于点，其对称轴为直线，结合图象给出下列结论：①；②；③当时，y 随x 的增大而减小；④当时，关于x 的一元二次方程有两个不相等的实数根.其中正确的结论是（）A.①③④ B.②③④ C.②③ D.①②④二、填空题（共5题，每题3分，共15分）11.在平面直角坐标系中，点关于原点对称的点的坐标是______.12.抛物线向左平移2个单位长度，向下平移1个单位长度后的图象解析式为______.13.如图，是的直径，弦于点E ，，，则的长为______cm.()2412x -=()2420x -=()2868x -=()2860x -=y ax a =+221y ax x =--+0a ≠()292616y x =-+8cm AB =4cm DE =CE 13cm 12cm 15cm 9cm12m 6m 220m 1m BC 2y ax bx c =++0a ≠()4,01x =a c b +>20a b +=0x <m a b c >++2ax bx c m ++=()2,3-()2234y x =-+AB O e CD AB ⊥16cm CD =4cm BE =OC14.已知关于x 的方程，若等腰三角形的一边长，另外两边长b ，c 恰好是这个方程的两个根，则这个三角形的周长为______.15.如图，的半径为2，圆心M 的坐标为，点P 是上的任意一点，，且，与x 轴分别交于A ，B 两点，若点A ，点B 关于原点O 对称，则的最小值为______.三、解答题（共9题，共75分，解答应写出文字说明、证明过程或演算步骤）16.（6分）解方程：（1），（2）.17.（6分）已知二次函数.（1）写出该函数图象的开口方向；（2）求出该函数图象的对称轴和顶点坐标；（3）当x 满足什么条件时，y 随x 增大而减小？18.（6分）如图，在平面直角坐标系中，已知点，，.（1）画出关于原点O 成中心对称的；（2）画出绕点逆时针旋转90°后得到的.19.（8分）已知关于x 的一元二次方程有两个不相等的实数根.（1）求m 的取值范围；（2）若该方程的两个实数根分别为，，且，求m 的值.20.（8分）如图，已知抛物线和直线相交于点和.()23230x k x k -+++=4a =M e ()3,4M e PA PB ⊥PA PB AB 2240x x --=23100x x --=247y x x =-+-()2,0A ()1,1B ()4,2C ABC △111A B C △ABC △()0,1Q -222A B C △()222110x m x m -++-=1x 2x 22124x x +=21y x bx c =-++21522y x =+()1,A m -(),4B n（1）求m 和n 的值；（2）求抛物线的解析式；（3）结合图象直接写出满足的x 的取值范围.21.（8分）如图，为的直径，点C ，D 为直径同侧圆上的点，且点D 为的中点，过点D 作于点E ，交于点G ，延长，交于点F .图① 图②（1）如图①，若，求证：；（2）如图②，若，，求的半径.22.（10分）我市某镇是全国著名的蓝莓产地，某蓝莓基地近几年不断改良种植技术，产量明显增加，2022年的产量是5000千克，2024年的产量达到7200千克。

九年级上学期数学期中考试试卷及答案解析

九年级上学期数学期中考试试卷及答案解析一、选择题（每题4分，共40分）1. 有下列四个数：-1, 0, 1, √2，其中无理数是（）A. -1B. 0C. 1D. √2答案：D解析：无理数是指不能表示为两个整数比的数，√2无法表示为两个整数的比，故选D。

2. 下列各数中，与-3的平方相等的是（）A. 3B. -3C. 9D. -9答案：C解析：-3的平方为9，故选C。

3. 已知a = 2，b = -3，则a² - 2ab + b²的值为（）A. 25B. -25C. 1D. -1答案：A解析：将a和b的值代入a² - 2ab + b²，得(2)² -22(-3) + (-3)² = 4 + 12 + 9 = 25，故选A。

4. 下列等式中，正确的是（）A. (a²)³ = a⁶B. (a³)² = a⁶C. (a²)³ = a⁹D. (a³)² = a⁹答案：B解析：幂的乘方规则，(a³)² = a³² = a⁶，故选B。

5. 已知|a| = 5，且a < 0，则a的值为（）A. 5B. -5C. 10D. -10答案：B解析：绝对值表示一个数的非负值，|a| = 5表示a的绝对值为5，由于a < 0，所以a = -5，故选B。

6. 下列函数中，奇函数是（）A. y = x²B. y = x³C. y = |x|D. y = x² + 1答案：B解析：奇函数的定义是f(-x) = -f(x)，y = x³满足这个条件，故选B。

7. 下列关于x的不等式中，有解的是（）A. x² < 0B. x² ≤ 0C. x² > 0D. x² ≥ 0答案：D解析：任何数的平方都是非负数，所以x² ≥ 0对所有的x都有解，故选D。

九年级数学上册期中考试试卷及答案

九年级数学上册期中考试试卷及答案（试卷满分：150分；考试时间：120分钟）一.选择题（共10小题,每小题4分，共40分）1.﹣2023的绝对值是（）A.﹣2023B.12023C.﹣12023D．20232.如图所示图形绕直线旋转一周，可以得到圆柱的是（）A．B．C．D．3.2023年10月1日，国庆假期第一天，天下第一泉（济南趵突泉）风景区接待游客超过291200人次．将数字291200用科学记数法表示应为（）A.2912×102B.29.12×104C.2.912×105D.2.912×1064.在数8，﹣0.5，﹣|﹣2|，0，（﹣3）2，﹣12中，负数的个数是（）A.2B.3C.4D.55.计算机层析成像（CT）技术的工作原理与几何体的切截相似，只不过这里的“截”不是真正的截，“几何体”是病人的患病器官，“刀”是射线．如图，用一个平行于圆锥底面的平面截圆锥，截面的形状是（）A．B．C．D．6．下列各式正确的是（）A.﹣（x+6）＝﹣x﹣6B.﹣y2﹣y2＝0C.9a2b﹣9ab2＝0D.a+a2＝a37.下列说法中正确的是（）A.﹣的系数是﹣5B.单项式x的系数为1，次数为0C.﹣22xyz2的次数是6D.xy+x﹣1是二次三项式8.若代数式2x2﹣x+3的值是4，则代数式﹣4x2+2x+5的值是（）A．2 B．3 C．7 D．109.有理数a，b，c在数轴上的对应点的位置如图所示，则正确的结论是（）A.a＞﹣3B.a＞bC.ab＞0D.﹣a＞c①当n为奇数时，F（n）＝3n+1；②当n为偶数时，F（n）＝（其中k是使F（n）为奇数的正整数）……，两种运算交替重复进行，例如，取n＝24，则：若n＝13，则第2022次“F”运算的结果是（）A.1B.4C.2020D.42020二．填空题（共6小题，每小题4分，24分共）11.比较大小：﹣7﹣5．12.《九章算术》中注有“今两算得失相反，要令正负以名之”，意思是：今有两数若其意义相反，则分别叫做正数与负数，若气温为零上10℃记作+10℃，则﹣3℃表示气温为．13．如图，是正方体的一种表面展开图，各面都标有数字，则数字为﹣4的面与它对面的数字之和是．14.若代数式﹣2x3y b与2x a y2的和为0，则b﹣a＝．15.用符号（a，b）表示a、b两数中较小的一个数，用符号[a，b]表示a、b两数中较大的一个数，计算[﹣2，1]﹣（﹣1，﹣2.5）＝．16.现有一列数a1，a2，a3，…，a98，a99，a100，其中a3＝22，a7＝2002，a95＝﹣2023，且满足任意相邻三个数的和为同一个常数，则a1+a2+a3+…+a98+a99+a100的值为．三．解答题（共7小题）17.（12分）（1）（﹣12）﹣5+（﹣14）﹣（﹣39）（2）（﹣+﹣）×（﹣24）（3）（﹣）÷+（﹣）÷（﹣15）（4）﹣14﹣×[2﹣（﹣3）2]18．（6分）（1）把下列各数：，|﹣4|在数轴上表示出来；（2）将上列各数用“＜”号从小到大连接．19．（6分）化简．（1）（6m﹣5n）﹣（7m﹣8n）（2）5（3x2y﹣xy2）﹣4（﹣xy2+2x2y）20.（8分）先化简，再求值：﹣a2b+（﹣8ab2﹣a2b）﹣2（5ab2﹣a2b），其中a＝﹣1，b＝．21.（6分）如图，是一些棱长为2cm的小立方块组成的几何体．（1）请在上面方格纸中分别画出从左面、上面看到的这个几何体的形状图．（2）该几何体的体积是．22.（8分）老师在黑板上书写了一个正确的演算过程，随后用手掌捂住了一个多项式，形式如﹣（2x2﹣2x+1）＝﹣x2﹣4x﹣3，则所捂住的多项式是____．（1）求所捂的二次三项式；（2）当x＝﹣2时，求所捂二次三项式的值．23.（12分）校运动会，小明负责在一条东西赛道上为同学们拍照，这天他从主席台出发，最后停留在A处．规定以主席台为原点，以向东的方向为正方向，步行记录如下（单位：米）：+10，﹣8，+6，﹣13，+7，﹣12，+2，﹣2（1）小明离主席台最远是米；（2）以主席台为原点，用1个单位长度表示1m，请在数轴上表示点A；（3）在主席台东边5米处是仲裁处，小明经过仲裁处次；（4）若小明每步行1米消耗0.04卡路里，那么他在拍照过程中步行消耗的卡路里是多少？24.（10分）书籍是人类进步的阶梯!为爱护书本我们一般都会将书本用包书纸包好．现有一本如图所示的数学课本，长为26cm、宽为18.5cm、厚为1cm，小海打算用一张长方形包书纸包好这本数学书．第一步，他将包书纸沿虚线折出折痕，封面和封底各折进去x cm；第二步，将阴影部分沿虚线剪掉，请帮助小海解决以下问题：（1）小海第一步中所用的长方形包书纸周长是多少厘米？（用含x的代数式表示）（2）若封面和封底沿虚线各折进去2cm，剪掉阴影部分后，包书纸的面积是多少？25.（12分）探索规律．（1）观察上面的图，发现：图①空白部分小正方形的个数是22﹣12＝2+1；图②空白部分小正方形的个数是42﹣32＝4+3；图③空白部分小正方形的个数是52﹣42＝+．（2）像这样继续排列下去，你会发现一些有趣的规律，﹣n2＝+．（3）运用规律计算：（20242﹣20232+20222﹣20212+20202﹣20192+…+22﹣12）÷1012．26.（12分）已知|a+30|+（c﹣20）2＝0，在数轴上点A表示的数是a，点C表示的数是c，A，C两点之间的距离AC＝|a﹣c|．（1）直接写出a、c的值，a＝，c＝；（2）若数轴上有一点D满足CD＝3AD，且点D在A，C之间，则D点表示的数为；（3）点M从原点O出发在O，A之间以v1的速度沿数轴负方向运动，点N从点C出发在O，C之间以v2的速度沿数轴负方向运动，运动时间为t，点Q为O，N之间一点，且QN＝AN，若M，N运动过程中MQ的值固定不变，求的值．参考答案一．选择题（共10小题）1．﹣2023的绝对值是（）A．﹣2023B．C．D．2023【分析】一个数在数轴上对应的点到原点的距离即为这个数的绝对值，正数的绝对值是它本身，负数的绝对值是它的相反数，0的绝对值是0，据此即可求得答案．【解答】解：|﹣2023|＝2023故选：D．【点评】本题考查绝对值的定义及绝对值的性质，此为基础且重要知识点，必须熟练掌握．2．如图所示图形绕直线旋转一周，可以得到圆柱的是（）A．B．C．D．【分析】根据每一个几何体的特征判断即可．【解答】解：A、将所示图形绕直线旋转一周，可以得到圆柱，故A符合题意；B、将所示图形绕直线旋转一周，可以得到球体，故B不符合题意；C、将所示图形绕直线旋转一周，可以得到圆锥，故C不符合题意；D．将所示图形绕直线旋转一周，可以得到圆台，故D不符合题意；故选：A．【点评】本题考查了点、线、面、体，熟练掌握每一个几何体的特征是解题的关键．3．2023年10月1日，国庆假期第一天，天下第一泉（济南趵突泉）风景区接待游客超过291200人次．将数字291200A．2912×102B．29.12×104C．2.912×105D．2.912×106【分析】科学记数法的表现形式为a×10n的形式，其中1≤|a|＜10，n为整数，确定n的值时，要看把原数变成a 时，小数点移动了多少位，n的绝对值与小数点移动的位数相同，当原数绝对值大于等于10时，n是正整数，当原数绝对值小于1时，n是负整数；由此进行求解即可得到答案．【解答】解：291200＝2.912×105．故选：C．【点评】本题主要考查了科学记数法，解题的关键在于能够熟练掌握科学记数法的定义．4．在数8，﹣0.5，﹣|﹣2|，0，（﹣3）2，﹣12中，负数的个数是（）A．2B．3C．4D．5【分析】根据绝对值、有理数的乘方、负数解决此题．【解答】解：∵8＞0，﹣0.5＜0，﹣|﹣2|＝﹣2＜0，0，（﹣3）2＝9＞0，﹣12＝﹣1＜0∴负数有﹣0.5，﹣|﹣2|，﹣12，共3个．故选：B．【点评】本题主要考查绝对值、有理数的乘方、负数，熟练掌握绝对值、有理数的乘方、负数是解决本题的关键．5．计算机层析成像（CT）技术的工作原理与几何体的切截相似，只不过这里的“截”不是真正的截，“几何体”是病人的患病器官，“刀”是射线．如图，用一个平行于圆锥底面的平面截圆锥，截面的形状是（）A．B．C．D．【分析】根据用一个平行于圆锥底面的平面截圆锥，截面的形状是圆即可得出答案．【解答】解：用一个平行于圆锥底面的平面截圆锥，截面的形状是圆故选：B．【点评】本题考查了截一个几何体，掌握用一个平行于圆锥底面的平面截圆锥，截面的形状是圆是解题的关键．6．下列各式正确的是（）A．﹣（x+6）＝﹣x﹣6B．﹣y2﹣y2＝0C．9a2b﹣9ab2＝0D．a+a2＝a3【分析】A．根据去括号法则，去掉括号，进行判断即可；B．根据合并同类项法则，进行合并，然后判断；C，D选项均观察各个加数是不是同类项，能否合并，进行判断即可．【解答】解：A．∵﹣（x+6）＝﹣x﹣6，∴此选项计算正确，故符合题意；B．∵﹣y2﹣y2＝﹣2y2，∴此选项计算错误，故不符合题意；D．∵a和a2不是同类项，不能合并，∴此选项计算错误，故不符合题意；故选：A．【点评】本题主要考查了整式的加减运算，解题关键是熟练掌握去括号法则和合并同类项法则．7．下列说法中正确的是（）A．﹣的系数是﹣5B．单项式x的系数为1，次数为0C．﹣22xyz2的次数是6D．xy+x﹣1是二次三项式【分析】根据单项式的系数、次数：单项式中的数字因数叫做单项式的系数，一个单项式中所有字母的指数的和叫做单项式的次数；几个单项式的和叫做多项式，每个单项式叫做多项式的项．多项式中次数最高的项的次数叫做多项式的次数进行分析即可．【解答】解：A、﹣的系数是﹣，此选项错误；B、单项式x的系数为1，次数为1，此选项错误；C、﹣22xyz2的次数是4，此选项错误；D、xy+x﹣1是二次三项式，此选项正确；故选：D．【点评】此题主要考查了单项式，关键是掌握单项式的系数、次数的定义，以及多项式的次数的计算方法．8．若代数式2x2﹣x+3的值是4，则代数式﹣4x2+2x+5的值是（）A．2B．3C．7D．10【分析】由代数式2x2﹣x+3的值是4，可得2x2﹣x＝1，再将﹣4x2+2x+5转化为﹣2（2x2﹣x）+5，再整体代入计算即可．【解答】解：∵2x2﹣x+3的值是4，即2x2﹣x+3＝4∴2x2﹣x＝1∴﹣4x2+2x+5＝﹣2（2x2﹣x）+5＝﹣2×1+5＝﹣2+5＝3故选：B．【点评】本题考查代数式求值，将﹣4x2+2x+5转化为﹣2（2x2﹣x）+5是正确解答的关键．9．有理数a，b，c在数轴上的对应点的位置如图所示，则正确的结论是（）A．a＞﹣3B．a＞b C．ab＞0D．﹣a＞c【分析】根据数轴上点的位置，先确定a、b、c对应点的数，再逐个判断得结论．【解答】解：A、由数轴知：﹣4＜a＜﹣3，故选项A错误；B、由数轴知，a＜b，故选项B错误；C、因为a＜0，b＞0，所以ab＜0，故选项C错误；D、因为﹣4＜a＜﹣3，所以3＜﹣a＜4，因为2＜c＜3，所以﹣a＞c，故选项D正确．故选：D．【点评】本题考查了数轴及有理数乘法的符号法则．认真分析数轴得到有用信息是解决本题的关键．10．定义一种对正整数n的“F”运算：①当n为奇数时，F（n）＝3n+1；②当n为偶数时，F（n）＝（其中k是使F（n）为奇数的正整数）……，两种运算交替重复进行，例如，取n＝24，则：若n＝13，则第2022次“F”运算的结果是（）A．1B．4C．2020D．42020【分析】通过计算可知从第4次开始，运算结果1，4循环出现，则第2022次“F”运算的结果与第1次运算结果相同，再求解即可．【解答】解：当n＝13时第1次运算结果为13×3+1＝40第2次运算结果为＝5第3次运算结果为5×3+1＝16第4次运算结果为＝1第5次运算结果为1×3+1＝4第6次运算结果为＝1第7次运算结果为1×3+1＝4……∴从第4次开始，运算结果1，4循环出现∵（2022﹣3）÷2＝1009 (1)∴第2022次“F”运算的结果是1故选：A．二．填空题（共6小题）11．比较大小：﹣7 ＜﹣5．【分析】根据两个负数，绝对值大的其值反而小判断即可．【解答】解：∵|﹣7|＝7，|﹣5|＝5而7＞5∴﹣7＜﹣5．故答案为＜．【点评】本题考查了有理数大小比较，关键是掌握有理数大小比较法则：正数都大于0；负数都小于0；正数大于一切负数；两个负数，绝对值大的其值反而小．12．《九章算术》中注有“今两算得失相反，要令正负以名之”，意思是：今有两数若其意义相反，则分别叫做正数与负数，若气温为零上10℃记作+10℃，则﹣3℃表示气温为零下3℃．【分析】根据正数与负数的意义可直接求解．【解答】解：若气温为零上10℃记作+10℃，则﹣3℃表示气温为零下3℃．故答案为零下3℃．【点评】本题主要考查正数与负数，理解正数与负数的意义是解题的关键．13．如图，是正方体的一种表面展开图，各面都标有数字，则数字为﹣4的面与它对面的数字之和是﹣7．【分析】根据正方体的表面展开图找相对面的方法，“Z”字两端是对面，判断即可．【解答】解：由图可知：﹣4与﹣3相对∴﹣4+（﹣3）＝﹣7故答案为：﹣7．【点评】本题考查了正方体相对两个面上的文字，熟练掌握根据正方体的表面展开图找相对面的方法是解题的关键．14．若代数式﹣2x3y b与2x a y2的和为0，则b﹣a＝﹣1．【分析】根据同类项的定义判断出a，b的值，可得结论．【解答】解：由题意a＝3，b＝2∴b﹣a＝2﹣3＝﹣1．故答案为：﹣1．【点评】本题考查整式的加减，解题的关键是理解题意，灵活运用所学知识解决问题．1，﹣2.5）＝ 3.5．【分析】根据定义，所求式子可化为1﹣（﹣2.5），再求值即可．【解答】解：[﹣2，1]﹣（﹣1，﹣2.5）＝1﹣（﹣2.5）＝1+2.5＝3.5故答案为：3.5．【点评】本题考查有理数的加减法，熟练掌握有理数的加减法运算，会比较有理数的大小，弄清定义是解题的关键．16．现有一列数a1，a2，a3，…，a98，a99，a100，其中a3＝22，a7＝2002，a95＝﹣2023，且满足任意相邻三个数的和为同一个常数，则a1+a2+a3+…+a98+a99+a100的值为2035．【分析】根据题中所给“任意相邻三个数的和为同一个常数”可求出这一列数，进而可解决问题．【解答】解：由题知因为这列数中任意相邻三个数的和为同一个常数所以a1+a2+a3＝a2+a3+a4则a1＝a4．同理可得a1＝a4＝a7＝…＝a100a2＝a5＝a8＝…＝a98a3＝a6＝a9＝…＝a99所以这列数按2002，﹣2023，22循环出现．又因为100÷3＝33余1且2002+（﹣2023）+22＝1所以a1+a2+a3+…+a98+a99+a100＝1×33+2002＝2035．故答案为：2035．【点评】本题考查数字变化的规律，能根据题意得出这列数按2002，﹣2023，22循环出现是解题的关键．三．解答题（共7小题）17．（1）（﹣12）﹣5+（﹣14）﹣（﹣39）；（2）（﹣+﹣）×（﹣24）；（3）（﹣）÷+（﹣）÷（﹣15）；（4）﹣14﹣×[2﹣（﹣3）2]．【分析】（1）先把减法转化为加法，再根据加法法则计算即可；（2）根据乘法分配律计算即可；（3）先算除法，再算加法即可；（4）先算乘方和括号内的式子，再算括号外的乘法，最后算减法即可．【解答】解：（1）（﹣12）﹣5+（﹣14）﹣（﹣39）＝（﹣12）+（﹣5）+（﹣14）+39＝8；（2）（﹣+﹣）×（﹣24）＝﹣×（﹣24）+×（﹣24）﹣×（﹣24）＝20+（﹣9）+6＝17；（3）（﹣）÷+（﹣）÷（﹣15）＝（﹣）×9+（﹣）×（﹣）＝﹣24+＝﹣23；（4）﹣14﹣×[2﹣（﹣3）2]＝﹣1﹣×（2﹣9）＝﹣1﹣×（﹣7）＝﹣1+＝．【点评】本题考查有理数的混合运算，熟练掌握运算法则是解答本题的关键，注意乘法分配律的应用．18．（1）把下列各数：，|﹣4|在数轴上表示出来；（2）将上列各数用“＜”号从小到大连接．【分析】（1）在数轴上准确找到各数对应的点，即可解答；（2）利用（1）的结论，即可解答．【解答】解：（1）如图：（2）由（1）可得：．【点评】本题考查了有理数的大小比较，数轴，绝对值，准确熟练地在数轴上找到各数对应的点是解题的关键．19．化简．（1）（6m﹣5n）﹣（7m﹣8n）；（2）5（3x2y﹣xy2）﹣4（﹣xy2+2x2y）；【分析】（1）先去括号，再合并同类项即可；（2）先去括号，再合并同类项即可；【解答】解：（1）（6m﹣5n）﹣（7m﹣8n）＝6m﹣5n﹣7m+8n＝﹣m+3n；（2）5（3x2y﹣xy2）﹣4（﹣xy2+2x2y）＝15x2y﹣5xy2+4xy2﹣8x2y＝7x2y﹣xy2；20．先化简，再求值：﹣a2b+（﹣8ab2﹣a2b）﹣2（5ab2﹣a2b），其中a＝﹣1，b＝．﹣a2b+（﹣8ab2﹣a2b）﹣2（5ab2﹣a2b）＝﹣a2b﹣8ab2﹣a2b﹣10ab2+2a2b＝﹣18ab2当a＝﹣1，b＝时原式＝﹣18×（﹣1）×（）2＝2．【分析】原式去括号合并得到最简结果，把a与b的值代入计算即可求出值．【点评】此题考查了整式的加减﹣化简求值，熟练掌握运算法则是解本题的关键．21．如图，是一些棱长为2cm的小立方块组成的几何体．（1）请在上面方格纸中分别画出从左面、上面看到的这个几何体的形状图．（2）该几何体的体积是48cm3．【分析】（1）根据三视图的定义画图即可．（2）用1个小立方块的体积乘以小方块的个数即可．【解答】解：（1）如图所示．（2）该几何体的体积是23×6＝48（cm3）．故答案为：48cm3．【点评】本题考查作图﹣三视图，解题的关键是理解三视图的定义，难度不大．22．老师在黑板上书写了一个正确的演算过程，随后用手掌捂住了一个多项式，形式如﹣（2x2﹣2x+1）＝﹣x2﹣4x﹣3，则所捂住的多项式是____．（1）求所捂的二次三项式；（2）当x＝﹣2时，求所捂二次三项式的值．【分析】（1）根据题意可知：所捂的二次三项式是：（﹣x2﹣4x﹣3）+（2x2﹣2x+1），然后计算即可；（2）将x＝﹣2代入（1）中的结果计算即可．【解答】解：（1）由题意可得所捂的二次三项式是：（﹣x2﹣4x﹣3）+（2x2﹣2x+1）＝﹣x2﹣4x﹣3+2x2﹣2x+1＝x2﹣6x﹣2；（2）当x＝﹣2时，x2﹣6x﹣2＝（﹣2）2﹣6×（﹣2）﹣2＝4+12﹣2＝14．【点评】本题考查整式的加减、代数式求值，解答本题的关键是明确去括号法则和合并同类项的方法．23．校运动会，小明负责在一条东西赛道上为同学们拍照，这天他从主席台出发，最后停留在A处．规定以主席台为原点，以向东的方向为正方向，步行记录如下（单位：米）：+10，﹣8，+6，﹣13，+7，﹣12，+2，﹣2（1）小明离主席台最远是10米；（2）以主席台为原点，用1个单位长度表示1m，请在数轴上表示点A；（3）在主席台东边5米处是仲裁处，小明经过仲裁处4次；（4）若小明每步行1米消耗0.04卡路里，那么他在拍照过程中步行消耗的卡路里是多少？【分析】（1）分别求出小明每次运动后的位置，即可得到答案；（2）结合（1），在数轴上标出最后位置即可；（3）由运动过程可求出经过仲裁处的次数；（4）根据每步行1米消耗0.04卡路里列式计算即可．【解答】解：（1）∵+10﹣8＝2；2+6＝8；8﹣13＝﹣5；﹣5+7＝2，2﹣12＝﹣10；﹣10+2＝﹣8；﹣8﹣2＝﹣10；∴小明离主席台最远是10米；故答案为：10；（2）如图所示，点A即为所求；（3）从主席台出发，+10经过仲裁处，由+10到﹣8经过仲裁处，﹣8到+6经过仲裁处，+6到﹣13经过仲裁处∴经过仲裁处4次；故答案为：4；（4）（10+8+6+13+7+12+2+2）×0.04＝60×0.04＝2.4（卡路里）答：小明在拍照过程中步行消耗2.4卡路里．【点评】本题考查有理数混合运算，解题的关键是读懂题意，理解小明的运动过程．24．书籍是人类进步的阶梯!为爱护书本我们一般都会将书本用包书纸包好．现有一本如图所示的数学课本，长为26cm、宽为18.5cm、厚为1cm，小海打算用一张长方形包书纸包好这本数学书．第一步，他将包书纸沿虚线折出折痕，封面和封底各折进去x cm；第二步，将阴影部分沿虚线剪掉，请帮助小海解决以下问题：（1）小海第一步中所用的长方形包书纸周长是多少厘米？（用含x的代数式表示）（2）若封面和封底沿虚线各折进去2cm，剪掉阴影部分后，包书纸的面积是多少？【分析】（1）由题意列式计算即可；（2）当x＝2cm时，求出包书纸长和宽，即可解决问题．【解答】解：（1）小海所用包书纸的周长为：2（18.5×2+1+2x）+2（26+2x）＝2（38+2x）+2（26+2x）＝（8x+128）cm答：小海所用包书纸的周长为（8x+128）cm；（2）当x＝2cm时，包书纸长为：18.5×2+1+2×2＝42（cm）包书纸宽为：26+2×2＝30（cm）∴包书纸的面积＝42×30﹣2×2×4﹣2×1×2＝1240（cm2）答：包书纸的面积为1240cm2．【点评】本题考查了矩形的性质以及列代数式，熟练掌握矩形的性质是解题的关键．25．探索规律．（1）观察上面的图，发现：图①空白部分小正方形的个数是22﹣12＝2+1；图②空白部分小正方形的个数是42﹣32＝4+3；图③空白部分小正方形的个数是52﹣42＝5+4．（2）像这样继续排列下去，你会发现一些有趣的规律，（n+1）2﹣n2＝n+1+n．（3）运用规律计算：（20242﹣20232+20222﹣20212+20202﹣20192+…+22﹣12）÷1012．【分析】（1）根据所给的等式的形式进行求解即可；（2）根据（1）进行总结，从而可求解；（3）利用（2）中的规律进行求解即可．【解答】解：（1）由题意得：图③空白部分小正方形的个数是52﹣42＝5+4故答案为：5，4；（2）（n+1）2﹣n2＝n+1+n故答案为：（n+1）2，n+1，n；（3）（20242﹣20232+20222﹣20212+20202﹣20192+…+22﹣12）÷1012＝（2024+2023+2022+2021+2020+2019+2018+…+2+1）÷1012＝[（2024+1）+（2023+2）+（2022+3）+…+（1013+1012）]÷1012＝2025×1012÷1012＝2025．【点评】本题主要考查数字的变化规律，解答的关键是由所给的等式总结出存在的规律．26．已知|a +30|+（c ﹣20）2＝0，在数轴上点A 表示的数是a ，点C 表示的数是c ，A ，C 两点之间的距离AC ＝|a ﹣c |．（1）直接写出a 、c 的值，a ＝ ﹣30 ，c ＝ 20 ；（2）若数轴上有一点D 满足CD ＝3AD ，且点D 在A ，C 之间，则D点表示的数为 ﹣ ；（3）点M 从原点O 出发在O ，A 之间以v 1的速度沿数轴负方向运动，点N 从点C 出发在O ，C 之间以v 2的速度沿数轴负方向运动，运动时间为t ，点Q 为O ，N 之间一点，且QN ＝AN ，若M ，N 运动过程中MQ 的值固定不变，求的值．【分析】（1）根据绝对值和平方的非负性求解即可；（2）根据两点间距离公式求解即可；（3）写出MQ 距离的代数式，根据MQ 距离不变，得出v 1，v 2的比值即可．【解答】解：（1）∵|a +30|≥0，（c ﹣20）2≥0，|a +30|+（c ﹣20）2＝0∴|a +30|＝0，（c ﹣20）2＝0∴a ＝﹣30，c ＝20故答案为：﹣30，20．（2）设D 点表示的数为x则有：20﹣x ＝3{x ﹣（﹣30）}解得：x ＝﹣故答案为：﹣．（3）OM 的长度为：v 1t ，CN 的长度为v 2t∴AM ＝﹣v 1t ﹣（﹣30）＝﹣v 1t +30，AN ＝20+20﹣v 2t ＝50﹣v 2t∵QN ＝AN∴AQ ＝AN ＝（50﹣v 2t ）∴MQ ＝AQ ﹣AM ＝（50﹣v 2t ）﹣（﹣v 1t +30）＝+（v 1﹣v 2）t∵MQ 的长度不随t 的变化而变化∴v 1﹣v 2＝0 ∴＝．【点评】本题主要考查了数轴，确定MQ 长度不变的条件是本题解题的关键．。

河南省新乡市河南师范大学附属中学联考2024-2025学年九年级上学期11月期中数学试题(含答案)

2024-2025学年第一学期九年级期中考试数学试卷一、选择题（每小题3分，共30分）1．下列图形中，既是轴对称图形，又是中心对称图形的是（）A ．B ．C ．D ．2．已知的半径为，圆心O 到直线l 的距离为，则直线l 与的位置关系是（）A ．相离 B ．相交C ．相切D ．无法判断3．一元二次方程经过配方变形为，则k 的值是（）A ．B ．C ．1D ．74．如图，A 、B 、C 为圆O 上的三点，，则的度数是（）A ．B ．C ．D ．5．关于二次函数，下列说法正确的是（）A ．图象的对称轴在y 轴的右侧B ．图象的顶点坐标为C ．与x 轴交于点和D ．当时，y 随着x 的增大而减小6．如图，是由绕点O 顺时针旋转后得到的图形，若点D 恰好落在AB 上，且，则的度数是（）A ．B ．C ．D ．7．如果关于x 的一元二次方程有实数根，则a 的取值范围是（）O e 5cm 4cm O e 2430x x -+=2(2)x k -=3-7-78AOB ∠=︒ACB ∠35︒36︒37︒39︒2(1)9y x =+-(1,9)-(2,0)-(4,0)1x <-ODC △OAB △40︒105AOC ∠=︒C ∠55︒45︒42︒40︒20x x a +-=A ．B ．C ．D ．8．如图，已知的半径为5，弦AB 的长为8，P 是AB 的延长线上一点，，则OP 等于（）A ． B ．C．D ．9．已知二次函数（m 为常数），当时，函数值y 的最小值为，则m 的值是（）A ．或B ．或C ．2或D ．2或10．如图1，动点P 从菱形ABCD 的点A 出发，沿边匀速运动，运动到点C时停止．设点P 的运动路程为x ，PO 的长为y ，y 与x 的函数图象如图2所示，当点P 运动到BC 中点时，PO 的长为（）图1图2A ．2 B ．3 C D ．二、填空题（每小题3分，共15分）11．把抛物线先向右平移1个单位再向上平移1个单位，所得到抛物线的解析式为________________．12．某种植物的主干长出若干个分支，每个支干又长出同样个数的小分支，主干、支干、小分支的总数是241，设每个支干长出小分支的个数是x ，则可列方程为________________。

四川省达州市高级中学校2024届九年级上学期期中考试数学试卷(含解析)

数学试卷本试卷分为第Ⅰ卷（选择题、填空题）和第Ⅱ卷（解答题）两部分，第Ⅰ卷1至2页，第Ⅱ卷3至6页．考试时间120分钟，满分150分．第Ⅰ卷一、选择题：（每小题4分，共40分；每小题选出正确答案后，请用2B 铅笔把机读卡上对应题号的答案标号涂黑．否则不得分．）1.下列方程中是关于x 的一元二次方程的是（）A.2210x x+= B.20ax bx c ++= C.()()121x x -+= D.223250x xy y --=答案：C 解析：详解：解：A 、2210x x+=是分式方程，选项说法错误，不符合题意；B 、当0a =时，20ax bx c ++=不是一元二次方程，选项说法错误，不符合题意；C 、(1)(2)1x x -+=，即230x x +-=是一元二次方程，选项说法正确，符合题意；D 、223250x xy y --=是二元二次方程，选项说法错误，不符合题意；故选C ．2.已知四边形ABCD 是平行四边形，对角线AC 与BD 相交于点O ，下列结论中不正确的是（）A.当AB BC =时，四边形ABCD 是菱形B.当AC BD ⊥时，四边形ABCD 是菱形C.当OA OB =时，四边形ABCD 是矩形D.当ABD CBD ∠=∠时，四边形ABCD 是矩形答案：D 解析：详解：解：如图：A 、∵四边形ABCD 是平行四边形，AB BC =，∴四边形ABCD 是菱形；A 选项正确；B 、∵四边形ABCD 是平行四边形，AC BD ⊥，∴四边形ABCD 是菱形；B 选项正确；C 、∵四边形ABCD 是平行四边形，∴OA OC =，OB OD =，又∵OA OB =，∴OA OB OC OD ===，∴四边形ABCD 是矩形；C 选项正确；D 、∵四边形ABCD 是平行四边形，∴AB CD ，∴ABD BDC ∠=∠，又∵ABD CBD ∠=∠，∴BDC CBD ∠=∠，∴BC CD =，∴四边形ABCD 是菱形；不能证明四边形ABCD 是矩形，D 选项错误，故选：D ．3.端午节吃粽子是中华民族的传统习俗，妈妈买了2只红豆粽、3只碱水粽、5只干肉粽，粽子除内部馅料不同外其它均相同，小颖随意吃一个，吃到红豆粽的概率是（）A.110B.15C.13D.12答案：B 解析：详解：解：根据概率的定义，一共有10只粽子，其中红豆粽有2个，所以吃到红豆粽的概率是21105=．故选B ．4.如图，正方形ABCD 的边长是4，∠DAC 的平分线交DC 于点E ，若点P 、Q 分别是AD 和AE 上的动点，则DQ+PQ 的最小值（）A.2B.4C.D.答案：C 解析：详解：作D 关于AE 的对称点D′，再过D′作D′P′⊥AD 于P′，∵DD′⊥AE ，∴∠AFD=∠AFD′，∵AF=AF ，∠DAE=∠CAE ，∴△DAF ≌△D′AF ，∴D′是D 关于AE 的对称点，AD′=AD=4，∴D′P′即为DQ+PQ 的最小值，∵四边形ABCD 是正方形，∴∠DAD′=45°，∴AP′=P′D′，∴在Rt △AP′D′中，P′D′2+AP′2=AD′2，AD′2=16，∵AP′=P′D’，2P′D′2=AD′2，即2P′D′2=16，∴，即DQ+PQ 的最小值为2，故答案为C ．5.已知ABC 如图，则下列4个三角形中，与ABC 相似的是（）A. B. C. D.答案：D 解析：详解：∵由图可知，675AB AC B ==∠=︒，，∴75C ∠=︒，18030A B C ∠=︒-∠-∠=︒，A ．选项中三角形是等边三角形，各角的度数都为60︒，不与ABC 相似；B ．选项中三角形各角的度数分别是52.5︒，52.5︒，75︒，不与ABC 相似；C ．选项中三角形各角的度数分别为40︒，70︒，70︒，不与ABC 相似；D ．选项中三角形各角的度数分别为30，︒75︒，75︒，与ABC 相似；故选：D ．6.若578a b ck ===且323a b c -+=，则243a b c +-的值是（）A.14 B.42C.7D.143答案：D 解析：详解：解：578a b ck ===，5,7,8a k b k c k ∴===，323a b c -+= ，352783k k k ∴⨯-⨯+=，解，得13k =，578,333a b c ∴===578142432433333a b c ∴+-=⨯+⨯-⨯=，故选：D ．7.某市2020年底已有绿化面积300公顷，经过两年绿化、绿化面积逐年增加，到2022年底增加到363公顷．设绿化面积平均每年的增长率为x ，由题意，所列方程正确的是（）A.()3001363x +=B.()23001363x +=C.()30012363x += D.()23631300x -=答案：B 解析：详解：解：设绿化面积平均每年的增长率为x ，根据题意得，()23001363x +=故选：B ．8.张华在一次数学活动中，利用“在面积一定的矩形中，正方形的周长最短”的结论，推导出“式子1x x +（0x >）的最小值是2”．其推导方法如下：在面积是1的矩形中设矩形的一边长为x ，则另一边长是1x，矩形的周长是12x x ⎛⎫+⎪⎝⎭；当矩形成为正方形时，就有1x x=（0x >），解得1x =，这时矩形的周长124x x ⎛⎫+= ⎪⎝⎭最小，因此1x x +（0x >）的最小值是2．模仿张华的推导，你求得式子225x x+（0x >）的最小值是（）A.10B.5C.15D.20答案：A 解析：详解：解：∵0x >，∴在原式中分母分子同除以x ，即22525x x x x+=+；在面积是25的矩形中设矩形的一边长为x ，则另一边长是25x，矩形的周长是252x x ⎛⎫+⎪⎝⎭；当矩形成为正方形时，就有25x x=（0x >），解得：5x =，这时矩形的周长25220x x ⎛⎫+= ⎪⎝⎭最小，因此225x x+（0x >）的最小值是10．故选：A ．9.如图，点C 是线段AB 的黄金分割点（AC BC >），下列结论错误的是（）A.AC BCAB AC= B.2•BC AC AB =C.12AC AB -= D.0.618≈BCAC答案：B 解析：详解：解：∵AC ＞BC ，∴AC 是较长的线段，根据黄金分割的定义可知：AB ：AC=AC ：BC ，故A 正确，不符合题意；AC 2=AB•BC ，故B 错误，12AC AB -=，故C 正确，不符合题意；0.618≈BCAC，故D 正确，不符合题意．故选B ．10.如图，在ABC 中60A ∠=︒，BM AC ⊥于点M ，CN AB ⊥于点N ，P 为BC 边的中点，连接PM PN ，，则下列结论：①PM PN =；②AM ANAB AC=；③PMN 为等边三角形；④当=45ABC ∠︒时，BN =．其中正确个数是（）A.1个B.2个C.3个D.4个答案：D 解析：详解：解：①∵BM AC ⊥于点M ，CN AC ⊥于点N ，P 为BC 边的中点，∴点P 是Rt MBC 和Rt NBC 的斜边的中点，∴12MP NP BC ==，故①正确；②∵BM AC ⊥于点M ，CN AC ⊥于点N ，∴90AMB ANC ∠=∠=︒，又∵A A ∠=∠，∴AMB ANC ∽ ，∴AM ANAB AC=，故②正确；③∵BM AC ⊥于点M ，CN AC ⊥于点N ，P 为BC 边的中点，∴点P 是Rt MBC 和Rt NBC 的斜边的中点，∴12MP NP BP CP BC ====，∴点M ，N ，B ，C 共圆，∴2NPM ABM ∠=∠，在Rt ABM 中，60A ∠=︒，∴30ABM ∠=︒，∴60NPM ∠=︒，∵PN PM =，∴PMN 是等边三角形，故③正确；④当=45ABC ∠︒时，BNC 为以BC 为斜边的等腰直角三角形，∴22BN BC =，故④正确；故选：D ．二、填空题：（本大题共6小题，每小题4分，满分24分，请把答案填写在答题卷上，否则不得分．）11.菱形的两条对角线长分别是方程214480x x -+=的两实根，则菱形的面积为______．答案：24解析：详解：解：x 2﹣14x +48=0，则有（x -6）(x -8)=0解得：x =6或x =8．所以菱形的面积为：（6×8）÷2=24．菱形的面积为：24．故答案为：24．12.已知关于x 的方程x 2+mx ﹣6=0的一个根为2，则m =___，另一个根是___．答案：①.1②.-3解析：详解：根据题意，得4+2m −6=0，即2m −2=0，解得，m =1，由韦达定理，知：12x x m +=-，∴221x +=-，解得：2 3.x =-故答案为：1，−3.13.关于x 的方程kx 2﹣2x +1＝0有两个不相等的实数根，则k 的取值范围是_____．答案：k ＜1且k ≠0．解析：详解：解：∵关于x 的一元二次方程kx 2﹣2x +1＝0有两个不相等的实数根，∴k ≠0且△＞0，即(﹣2）2﹣4×k ×1＞0，解得k ＜1且k ≠0．∴k 的取值范围为k ＜1且k ≠0．故答案为：k ＜1且k ≠0．14.如图，△ABC 中，DE ∥BC ,23DE BC =,△ADE 的面积为8，则△ABC 的面积为______答案：18.解析：详解：∵在△ABC中，DE∥BC，∴△ADE∽△ABC．∵23 DEBC=，∴2224()(39 ADEABCS DES BC===，∴9184ABC ADES S==．故选：18．15.将一副三角尺如图所示叠放在一起，则AEED的值是_______．答案：33133解析：详解：解：90BAC ACD∠=∠=︒，∴AB CD，∴30BAE EDC∠=∠=︒，45ABE ECD∠=∠=︒，∴ABE DCE∽，∴AE ABED CD=，∵AC AB=，∴AE ACED CD=，∵3tan 3AC D CD ∠==，∴3AE ED =，故答案为：33．16.在平面直角坐标系中，正方形ABCD 的位置如图所示，点A 的坐标为()1,0，点D 的坐标为()0,2．延长CB 交x 轴于点1A ，作正方形111A B C C ；延长11C B 交x 轴于点2A ，作正方形2221A B C C 1…按这样的规律进行下去，第2014个正方形的面积为______答案：4026352⎛⎫⋅ ⎪⎝⎭解析：详解：解：∵正方形ABCD 的点A 的坐标为()1,0，点D 的坐标为()0,2．∴1OA =，2OD =，由勾股定理得，AD =12OA OD =，∵90ADO DAO ∠+=︒，190DAO BAA ∠+=︒，∴1ADO BAA ∠=，由题意得190DOA ABA ∠==︒，则1DOA ABA ∽，∴112A B OA AB OD ==，∵AD AB ==∴152A B =，则第二个正方形的面积为2221153522S A C ⎛⎫===⋅ ⎪⎝⎭⎭，同理可得第三个正方形的面积为2422215135352222S A C ⎛⎫⎛⎫==+⨯=⋅ ⎪ ⎪ ⎪⎝⎭⎝⎭，依此类推，第n 个正方形的面积为()21352n n S -⎛⎫=⋅ ⎪⎝⎭，则第2014个正方形的面积为：40262014352S ⎛⎫=⋅ ⎪⎝⎭．故答案为：4026352⎛⎫⋅ ⎪⎝⎭．第Ⅱ卷三、解答题：（本大题4个小题，共86分）解答时每小题需给出必要的演算过程或推理步骤．17.解方程：（1）22210x x --=（2）()()22320x x ---=答案：（1）112x +=，212x =（2）12x =，25x =解析：小问1详解：原方程变形为212x x -=配方得21344x x -+=，即21324x ⎛⎫-= ⎪⎝⎭，∴12x -=，∴1132x +=，2132x =．小问2详解：原方程可以变形为()()2230x x ---=，∴20x -=或230x --=，∴12x =，25x =．18.如图，在平面直角坐标系中，已知△ABC 三个顶点的坐标分别为A （﹣1，2），B （﹣3，4）C （﹣2，6）.（1）画出△ABC 绕点A 顺时针旋转90°后得到的△A 1B 1C 1；（2）以原点O 为位似中心，画出将△A 1B 1C 1三条边放大为原来的2倍后的△A 2B 2C 2．答案：（1）见解析；（2）见解析.解析：详解：（1）如图：△A 1B 1C 1即为所求；（2）如图：△A 2B 2C 2即为所求.19.已知关于x 的一元二次方程()22110x k x k +---=．（1）试判断此一元二次方程根的存在情况；（2）若方程有两个实数根x 1和x 2，且满足12111x x +=，求k 的值．答案：（1）有两个不相等的实数根（2）2k =解析：小问1详解：解：()()222Δ214144144450k k k k k k =----=-+++=+> ，()22110x k x k ∴+---=有两个不相等的实数根；小问2详解：由一元二次方程根与系数的关系可知：1212x x k +=-，121x x k ⋅=--，121212111x x x x x x ++==⋅ ，1211k k -∴=--，解得：2k =．20.第三届亚洲沙滩运动会服务中心要在某校选拔一名志愿者．经笔试、面试，结果小明和小颖并列第一．评委会决定通过抓球来确定人选．抓球规则如下：在不透明的布袋里装有除颜色之外均相同的2个红球和1个绿球，小明先取出一个球，记住颜色后放回，然后小颖再取出一个球．若取出的球都是红球，则小明胜出；若取出的球是一红一绿，则小颖胜出．你认为这个规则对双方公平吗？请用列表法或画树状图的方法进行分析．答案：见解析解析：详解：解：根据题意，用A 表示红球，B 表示绿球，列表如下：A A BAA A A AB A AA A A AB A B A B A B B B由此可知，共有9种等可能的结果，其中，两红球及一红一绿各有4种结果，(P ∴都是红球)=49，(1P 红1绿球)=49．(P 都是红球)(1P =红1绿球)，∴这个规则对双方是公平的．21.某水果批发商场经销一种水果，如果每千克盈利10元，每天可售出400千克．经市场调查发现，在进货价不变的情况下，若每千克涨价1元，日销售量将减少20千克．（1）若商场只要求保证每天的盈利为4320元，同时又可使顾客得到实惠，每千克应涨价多少元？（2）若该商场经理想让这种水果每天的盈利为4600元，商场经理的想法能实现吗？如果能请求出每千克应涨价多少元，如果不能请说明理由．答案：（1）2元（2）不能，见解析解析：小问1详解：设每千克应涨价x 元，则()()10400204320x x =＋－，解得2x =或8x =，为了使顾客得到实惠，所以2x =，所以每千克应涨价2元．小问2详解：该商场经理想法不能实现．设每千克应涨价x 元，则()()10400204600x x =＋－，整理，得210300x x -+=，∵()2104130200∆=--⨯⨯=-<，∴该方程无解，∴不可能．22.如图，△ABC 中，AB =AC ，AD 是△ABC 的角平分线，点O 为AB 的中点，连接DO 并延长到点E ，使OE =OD ，连接AE ，BE ，（1）求证：四边形AEBD 是矩形；（2）当△ABC 满足什么条件时，矩形AEBD 是正方形，并说明理由．答案：（1）证明见解析；（2）当∠BAC =90°时，矩形AEBD 是正方形．理由见解析．解析：详解：（1）证明：∵点O 为AB 的中点，连接DO 并延长到点E ，使OE =OD ，∴四边形AEBD 是平行四边形，∵AB =AC ，AD 是∠BAC 的角平分线，∴AD ⊥BC ，∴∠ADB =90°，∴平行四边形AEBD 是矩形；（2）当∠BAC =90°时，理由如下：∵∠BAC =90°，AB =AC ，AD 是∠BAC 的角平分线，∴AD =BD =CD ，∵由（1）得四边形AEBD 是矩形，∴矩形AEBD 是正方形．23.如图，在ABC 中，90C ∠=︒，AD 是CAB ∠的平分线，BE AE ⊥，垂足为点E ．求证：2BE DE AE =⋅．答案：见详解解析：详解：证明：∵AD 是CAB ∠的平分线，∴CAD BAD ∠=∠，∵90C ∠=︒，∴90CAD ADC ∠+∠=︒，又∵BE AE ⊥，∴90E ∠=︒，∴90EBD BDE ∠+∠=︒，而ADC BDE ∠=∠，∴CAD DBE BAE ∠=∠=∠，∴BDE ABE ∽△△，∴::BE AE DE BE =，∴2BE DE AE =⋅．24.阅读理解：如图1，在四边形ABCD 的边AB 上任取一点E （点E 不与点A 、点B 重合），分别连接ED ，EC ，可以把四边形ABCD 分成三个三角形，如果其中有两个三角形相似，我们就把E 叫做四边形ABCD 的边AB 上的相似点；如果这三个三角形都相似，我们就把E 叫做四边形ABCD 的边AB 上的强相似点．解决问题：（1）如图1，55A B DEC ∠=∠=∠=︒，试判断点E 是否是四边形ABCD 的边AB 上的相似点，并说明理由；（2）如图2在矩形ABCD 中，52AB BC ==，，且A ，B ，C ，D 四点均在正方形网格（网格中每个小正方形的边长为1）的格点（即每个小正方形的顶点）上，试在图2中画出矩形ABCD 的边AB 上的一个强相似点E ；拓展探究：（3）如图3，将矩形ABCD 沿CM 折叠，使点D 落在AB 边上的点E 处．若点E 恰好是四边形ABCM的边AB 上的一个强相似点，当BC =时，试求出AB 的值．答案：（1）是，理由见解析；（2）见解析；（3）2解析：详解：（1）点E 是四边形ABCD 的边AB 上的相似点．理由：55A ∠=︒ ，125ADE DEA ∴∠∠=︒＋，55DEC ∠=︒ ，125BEC DEA ∴∠∠=︒＋．ADE BEC ∴∠=∠，A B ∠=∠ ，ADE BEC ∴∽V V ，∴点E 是四边形ABCD 的AB 边上的相似点．（2）作图如下：点E 即为所求（下图中二选其一即可）（3）∵点E 是四边形ABCM 的边AB 上的一个强相似点，AEM BCE ECM ∴∽∽ ，BCE ECM AEM ∴∠=∠=∠,由折叠可知ECM DCM ：≌， ECM DCM CE CD ∴∠=∠=，，1303BCE BCD ∴∠=∠=︒，111222BE CE DC AB ∴===．在Rt BCE 中，设BE 为x ，CE 为2x ，根据勾股定理，222BC BE EC +=，可得2234x x +=，解得1x =±，0x >，1x ∴=，2CE =∴，即2AB =．25.如图，在平面直角坐标系内，已知点()0,6A 、点()8,0B ，动点P 从点A 开始在线段AO 上以每秒1个单位长度的速度向点O 移动，同时动点Q 从点B 开始在线段BA 上以每秒2个单位长度的速度向点A 移动，设点P 、Q 移动的时间为t秒．（1）求直线AB 的解析式；（2）当t 为何值时，APQ △与AOB 相似．（3）当t 为何值时，APQ △的面积为165个平方单位．答案：（1）y ＝－34x ＋6（2）3011秒或5013秒（3）1秒或4秒解析：小问1详解：解：设直线AB 的解析式为y kx b=+由题意，得680b k b =⎧⎨+=⎩，解得346k b ⎧=-⎪⎨⎪=⎩所以，直线AB 的解析式为364y x =-+．小问2详解：解：由68AO BO ==，得10AB =，∴102AP t AQ t ==-，，①当APQ AOB ∠=∠时，APQ AOB ∽．∴102610t t -=，解得3011t =②当AQP AOB ∠=∠时，AQP AOB ∽．∴102106t t -=，解得5013t =∴当t 为3011秒或5013秒时，APQ △与AOB 相似；小问3详解：解：过点Q 作QE 垂直AO 于点E ．在Rt AOB △中，4sin 5BO BAO AB ∠==在Rt AEQ △中，()48·sin 102855QE AQ BAO t t =∠=-=-，21184168422555APQ S AP QE t t t t ⎛⎫=⋅=⨯-=-+= ⎪⎝⎭ 解得，1t =（秒）或4t =（秒）∴当1t =秒或4t =秒时，APQ △的面积为165个平方单位．。

重庆市江津区12校2024届九年级上学期期中考试数学试卷(含答案)

2023-2024学年度上期期中测试数学题卷(满分150分，考试时间120分钟)注意事项：1.试题的答案书写在答题卡上，不得在试卷上直接作答。

2.作答前认真阅读答题卡上的注意事项。

3.考试结束，监考人员将试题卷和答题卡一并收回。

4.参考公式：抛物线的顶点坐标为，对称轴为.一、选择题（每小题4分，共40分）1.下列方程一定是一元二次方程的是（）A ．212023x x -=B ．30y x -=C ．2350x x -=D ．3210x x ++=2.将抛物线y ＝x 2﹣1向上平移3个单位，再向右平移1个单位后，得到的抛物线所对应的函数表达式为（）A ．y ＝（x ﹣1）2﹣1B ．y ＝（x ﹣1）2+2C ．y ＝（x +1）2+2D ．y ＝（x +1）2﹣13.下列方程中，没有实数根的是（）A. B.C.D.4.下列关于抛物线()2314y x =+-的结论，正确的是（）A ．开口方向向下B ．对称轴为直线x =-1C ．顶点坐标是（1，-4）D ．当x =-1时，函数有最大值为-45.一元二次方程x 2-6x +5=0配方可变形为()A.(x -3)2=14B.(x -3)2=4C.(x +3)2=14D.(x +3)2=46.点()()()11223331P y P y P y -，、，、2，均在二次函数244y x x =--的图象上，则y 1，y 2，y 3的大小关系是（）A ．123y y y >>B ．312y y y >>C ．231y y y >>D ．213y y y >>7.已知二次函数y =ax 2+bx +c 的图象如图所示，根据图中提供的信息，可求得使y ≥1成立的x 的取值范围是（）A ．-1≤x ≤3B ．x ≥3C ．x ≤-1D ．x ≤-1或x ≥38.关于x 的一元二次方程()22210x a a x a +-+-=两个实数根互为相反数，则a 的值为（）A.2B.0C.1D.2或09.已知二次函数2y ax bx c =++的图象如图所示，顶点为（﹣1，0），则下列结论：①0abc <；②240b ac -=；③20a b -=；④2a >；⑤420a b c -+<．其中正确结论的个数是（）A ．2个B ．3个C ．4个D ．5个10.对于实数a 、b ，定义新运算()()22*a ab a b a b b ab a b ⎧-≥⎪=⎨-<⎪⎩ ，若二次函数()2*1y x x =-，则下列结论正确的有（）①方程()2*10x x -=的解为x =0或x =−1；②关于x 的方程()2*1x x m-=有三个解，则102m ≤<；③当x <−1时，y 随x 增大而增大；④当x >−1时，函数()2*1y x x =-有最大值0．A ．1个B ．2个C ．3个D ．4个二、填空题（每小题4分，共32分）11.一元二次方程的解是.12.抛物线21252y x x =-+-的顶点坐标是.13.有一个人患了新冠病毒，经过两轮传染后共有169人患了流感，每轮传染中平均一个人传染了个人.14.若直角三角形的两边长分别是方程的两根，则该直角三角形的面积是.15.已知m 、n 是一元二次方程2250x x +-=的两个实数根，则m 2+mn +2m 的值为.第7题图第9题图16.如图，已知二次函数223y x x =-的图象与正比例函数1y x =的图象在第一象限交于点，与轴正半轴交于点，若，则的取值范围是.17.使得关于x 的不等式组6101131282x a x x -≥-⎧⎪⎨-+<-+⎪⎩有且只有4个整数解，且关于x 的方程()25410a x x -++=有实数根的所有整数a 的值之和为.18.对于一个四位自然数M ，若它的千位数字比个位数字多6，百位数字比十位数字多2，则称M 为“天真数”．如：四位数7311，∵716-=，312-=，∴7311是“天真数”；四位数8421，∵816-≠，∴8421不是“天真数”。

浙江温州实验中学2024年九年级11月期中考试数学试卷+答案

2024-2025学年浙江省温州实验中学九年级（上）期中数学试卷一、选择题（本题有10小题，每小题3分，共30分．每小题只有一个选项是正确的，不选、多选、错选，均不给分）1．（3分）已知⊙O半径为5，若点A在⊙O内，则线段OA的长可能是（）A．4.5B．5C．5.5D．62．（3分）若，则＝（）A．B．C．D．3．（3分）将抛物线y＝2（x﹣1）2先向左平移3个单位、再向下平移2个单位后，所得新抛物线的表达式是（）A．y＝2（x﹣4）2+2B．y＝2（x﹣4）2﹣2C．y＝2（x+2）2﹣2D．y＝2（x+2）2+24．（3分）已知△ABC∽△DEF，若给定其相似比和DF的长，则下列线段长度能确定的是（）A．AB B．DE C．AC D．EF5．（3分）如图，已知四边形ABCD是⊙O的内接四边形，E为AD延长线上一点，则∠CDE等于（）A．64°B．60°C．54°D．52°6．（3分）如图，已知等边△ABC，以BC为直径的圆分别交边AB，E，若BC＝2，则的长为（）A．B．C．D．7．（3分）一个不透明的袋子里装有4个白球和若干个黑球，这些球除颜色外都相同．从袋子中随机摸一个球，记下颜色后放回搅匀，并绘制了如图所示的统计图．估计袋子里黑球的个数为（）A．16B．18C．20D．228．（3分）如图，在△ABC中，∠BAC＝90°，且BD＝1，CD＝3．连接AD，连结BE，DE（）A．B．C．3D．9．（3分）二次函数y＝ax2+bx+1（a≠0）的图象的顶点在第二象限，且过点（1，0）（）A．1B．0.5C．﹣0.5D．﹣110．（3分）如图，已知A，B，C，D是⊙O上依逆时针顺序排列的四个点，设弦BC＝x，AD＝y，则在x，y值的变化过程中（）A．x+y B．xy C．x2+y2D．二、填空题（本题有6小题，每小题4分，共24分）11．（4分）已知线段a＝2cm，b＝8cm，那么线段a和b的比例中项为cm．12．（4分）如图，AD∥BE∥CF，直线l1，l2与这三条平行线分别交于点A，B，C和点D，E，F．若，则DE的长为．13．（4分）某游乐场的圆形喷水池中心O有一雕塑OA，从A点向四周喷水，喷出的水柱为抛物线，以水平方向为x轴，点O为原点建立直角坐标系，x轴上的点C，D为水柱的落水点，则两个水柱的最高点M，N之间的距离为m．14．（4分）如图，如果圆内接四边形ABCD两组对边的延长线分别相交于点E，F，且∠E＝40°，那么∠A＝．15．（4分）已知二次函数y＝x2﹣（﹣1≤x≤t），当x＝﹣1时，函数取得最大值，函数取得最小值，则t的取值范围是．16．（4分）如图1是我校小杰同学设计的“温”字图案，图2是他在设计图案前所绘制的基本框架图，其中△DEF是等腰三角形，四边形EBGF是正方形且点E在BC上，DB，I．已知△DEH∽△DBE，C，D，F在同一直线上，则．三、解答题（本题有7小题，共66分．解答需写出必要的文字说明、演算步骤或证明过程）17．（7分）如图，D，E分别是AB，AC上的点，相似比是．（1）若DE＝4cm，求BC的长．（2）若∠C＝35°，∠A＝20°，求∠EDA的度数．18．（7分）如图，已知⊙O的一条弦AB和该圆上的一点C．（1）请按尺规作图的要求作出⊙O上的点D，使得∠DAC＝∠AOB；（2）在（1）的条件下，连结OA，若∠DAC＝40°，⊙O的半径为119．（8分）某校开展数学文化节活动，其中八年级的活动项目是现场说题比赛，每位参赛的学生都需要从A，B（1）甲同学抽到题卡A的概率为．（2）用画树状图或列表的方法，求甲、乙两位同学抽到不同题卡的概率．20．（10分）如图，已知抛物线经过点（0，1），，B两点（B在A的右边）．（1）求抛物线的函数表达式．（2）过点A作x轴的平行线分别交y轴与抛物线于C，D．若A是线段CD的中点，求t的值．21．（10分）如图，△ABC和△ABD内接于⊙O，直径AC与BD相交于点E，OB，∠BAC+2∠CBD＝90°．（1）求证：BC∥OD．（2）若BE＝OE，CE＝2，求OE的长度．22．（12分）已知二次函数y＝ax2+bx+c（a，b，c是常数，a≠0）．（1）当a＝1时，①若该函数图象的对称轴为直线x＝2，且过点（1，4），求该函数的表达式．②若该函数的图象与x轴有且只有一个交点，求证：．（2）当时，若该函数的图象经过点（1，m），（3，n），（5，p）且满足m﹣n＝4 23．（12分）如图1，在圆内接四边形ABCD中，点A是，使∠AEB＝∠ABD．（1）若∠AEB＝70°，求∠CBD的度数．（2）求证：CE＝BD．（3）如图2，若BD为直径，BE＝2，2024-2025学年浙江省温州实验中学九年级（上）期中数学试卷参考答案与试题解析一、选择题（本题有10小题，每小题3分，共30分．每小题只有一个选项是正确的，不选、多选、错选，均不给分）1．（3分）已知⊙O半径为5，若点A在⊙O内，则线段OA的长可能是（）A．4.5B．5C．5.5D．6【分析】根据点与圆的位置关系解答即可．【解答】解：∵⊙O半径为5，点A在⊙O内，∴OA＜5，∴线段OA的长可能是5.5．故选：A．【点评】本题考查的是点与圆的位置关系，熟知点与圆的位置关系有3种．设⊙O的半径为r，点P到圆心的距离OP＝d，则有：点P在圆外⇔d＞r；点P在圆上⇔d＝r；点P在圆内⇔d＜r是解题的关键．2．（3分）若，则＝（）A．B．C．D．【分析】利用比例的性质，进行计算即可解答．【解答】解：∵，∴＝3+＝1+＝，故选：A．【点评】本题考查了比例的性质，熟练掌握比例的性质是解题的关键．3．（3分）将抛物线y＝2（x﹣1）2先向左平移3个单位、再向下平移2个单位后，所得新抛物线的表达式是（）A．y＝2（x﹣4）2+2B．y＝2（x﹣4）2﹣2C．y＝2（x+2）2﹣2D．y＝2（x+2）2+2【分析】根据“左加右减”的平移法则即可得到答案．【解答】解：将抛物线y＝2（x﹣1）2先向左平移3个单位、再向下平移2个单位后7﹣2＝2（x+4）2﹣2，故选：C．【点评】本题考查二次函数图象与几何变换，解题的关键是掌握“左加右减”的平移法则．4．（3分）已知△ABC∽△DEF，若给定其相似比和DF的长，则下列线段长度能确定的是（）A．AB B．DE C．AC D．EF【分析】根据相似三角形的性质解答即可．【解答】解：∵△ABC∽△DEF，∴＝＝，∵给定其相似比和DF的长，∴线段AC长度能确定．故选：C．【点评】熟知相似三角形的对应角相等，对应边的比相等是解题的关键．5．（3分）如图，已知四边形ABCD是⊙O的内接四边形，E为AD延长线上一点，则∠CDE等于（）A．64°B．60°C．54°D．52°【分析】根据圆周角定理先求出∠ABC＝64°，再根据圆内接四边形的性质求出∠ADC的度数，最后根据邻补角的定义即可求出答案．【解答】解：∵∠AOC＝128°，∴∠ABC＝64°，∵四边形ABCD是⊙O的内接四边形，∴∠ADC＝180°﹣64°＝116°，∴∠CDE＝180°﹣∠ADC＝64°．故答案为：A．【点评】本题主要考查圆周角定理、圆内接四边形的性质等，灵活运用以上知识点是解题的关键．6．（3分）如图，已知等边△ABC，以BC为直径的圆分别交边AB，E，若BC＝2，则的长为（）A．B．C．D．【分析】根据等边三角形的性质，得到△OBD，△OCE均为等边三角形，进而求出∠DOE的度数，利用弧长公式进行求解即可．【解答】解：连接OD，OE，∵△ABC为等边三角形，∴∠B＝∠C＝60°，∵BC为直径，BC＝2，∵OD＝OB＝OC＝OE＝1，∴△OBD，△OCE均为等边三角形，∴∠BOD＝∠COE＝60°，∴∠DOE＝180°﹣60°﹣60°＝60°，∴弧DE的长为；故选：B．【点评】本题考查弧长的计算，等边三角形的性质，关键是等边三角形性质的应用．7．（3分）一个不透明的袋子里装有4个白球和若干个黑球，这些球除颜色外都相同．从袋子中随机摸一个球，记下颜色后放回搅匀，并绘制了如图所示的统计图．估计袋子里黑球的个数为（）A．16B．18C．20D．22【分析】根据统计图找到摸到白球的频率稳定到的常数，再根据大量重复试验中事件发生的频率等于事件发生的概率求解即可．【解答】解：观察发现：随着实验次数的增加频率逐渐稳定到常数0.2附近，∴估计摸到白球的概率为7.2，∴共有小球4÷4.2＝20（个），∴估计袋子里黑球的个数为20﹣4＝16（个）．故选：A．【点评】本题主要考查利用频率估计概率，大量重复实验时，事件发生的频率在某个固定位置左右摆动，并且摆动的幅度越来越小，根据这个频率稳定性定理，可以用频率的集中趋势来估计概率，这个固定的近似值就是这个事件的概率．8．（3分）如图，在△ABC中，∠BAC＝90°，且BD＝1，CD＝3．连接AD，连结BE，DE（）A．B．C．3D．【分析】根据旋转的性质得出AD＝AE，∠DAE＝90°，再根据SAS证明△EAB≌△DAC得出∠C＝∠ABE＝45°，CD＝BE，得出∠EBC＝90°，再根据勾股定理即可求解．【解答】解：∵线段AD绕点A顺时针旋转90°得到线段AE，∴AD＝AE，∠DAE＝90°∴∠EAB+∠BAD＝90°，在△ABC中∠BAC＝90°，AB＝AC，∴∠BAD+∠CAD＝90°，∠C＝∠ABC＝45°，∴∠EAB＝∠CAD，∴△EAB≌△DAC（SAS），∴∠C＝∠ABE＝45°，CD＝BE，∴∠EBC＝∠EBA+∠ABC＝90°，∵BD＝1，CD＝3，∴CD＝BE＝4，∴．故选：D．【点评】本题考查了全等三角形的判定与性质，勾股定理，旋转的性质，根据SAS证明△EAB≌△DAC 是解题的关键．9．（3分）二次函数y＝ax2+bx+1（a≠0）的图象的顶点在第二象限，且过点（1，0）（）A．1B．0.5C．﹣0.5D．﹣1【分析】依据题意，首先根据题意确定a、b的符号，然后进一步确定a的取值范围．【解答】解：∵抛物线的顶点在第二象限，且过点（1，∴开口向下．∴a＜0，﹣＜0，∴b＜0，且b＝﹣a﹣8，∴﹣a﹣1＜0，得﹣8＜a＜0，∴a的值可能是﹣0.8，故选：C．【点评】本题主要考查了二次函数的图象与系数的关系，二次函数图象上点的坐标特征，解答此题的关键是分别求出a、b的取值范围．10．（3分）如图，已知A，B，C，D是⊙O上依逆时针顺序排列的四个点，设弦BC＝x，AD＝y，则在x，y值的变化过程中（）A．x+y B．xy C．x2+y2D．【分析】过点A作⊙O直径AE，过点B作⊙O的直径BF，连接DE，CF，依题意得∠E+∠F＝90°，∠E+∠A＝90°，则∠A＝∠F，由此可依据“AAS”判定△ADE和△FCB全等，则DE＝BC，然后在Rt△ADE中，由勾股定理即可得出答案．【解答】解：过点A作⊙O直径AE，过点B作⊙O的直径BF，CF ∵，∴+＝180°，∴∠E+∠F＝90°，∵AE，BF是⊙O的直径，∴AE＝BF＝20，∠ADE＝∠FCB＝90°，∴∠E+∠A＝90°，∴∠A＝∠F，在△ADE和△FCB中，，∴△ADE≌△FCB（AAS），∴DE＝BC＝x，在Rt△ADE中，AD＝y，AE＝20，由勾股定理得：DE2+AD2＝AE5，即x2+y2＝400，∴在x，y值的变化过程中7+y2的值不变．故选：C．【点评】此题主要考查了圆心角、弧、弦的关系，圆周角定理，全等三角形的判定和性质，理解圆心角、弧、弦的关系，圆周角定理，熟练掌握全等三角形的判定和性质是解决问题的关键．二、填空题（本题有6小题，每小题4分，共24分）11．（4分）已知线段a＝2cm，b＝8cm，那么线段a和b的比例中项为4cm．【分析】比例的基本性质：两外项之积等于两内项之积．【解答】解：根据比例中项的概念结合比例的基本性质，得：比例中项的平方等于两条线段的乘积．设它们的比例中项是x，则x2＝2×2，x＝±4（线段是正数．故答案为4．【点评】考查了比例中项的概念，注意：求两条线段的比例中项的时候，应舍去负数．12．（4分）如图，AD∥BE∥CF，直线l1，l2与这三条平行线分别交于点A，B，C和点D，E，F．若，则DE的长为6．【分析】根据平行线分线段成比例定理列出比例式，把已知数据代入计算即可．【解答】解：∵AD∥BE∥CF，∴＝＝，∵EF＝3，∴＝，∴DE＝6．故答案为：6．【点评】本题考查了平行线分线段成比例定理，根据定理得出比例式是解答此题的关键，注意：一组平行线截两条直线，所截得的对应线段成比例．13．（4分）某游乐场的圆形喷水池中心O有一雕塑OA，从A点向四周喷水，喷出的水柱为抛物线，以水平方向为x轴，点O为原点建立直角坐标系，x轴上的点C，D为水柱的落水点，则两个水柱的最高点M，N之间的距离为10m．【分析】利用二次函数图象上点的坐标特征可求出点M、N的坐标，进而可得出MN之间的距离．【解答】解：由二次函数y＝﹣（x﹣7）2+6的图象可知，当x＝2时，y＝6，故N点的坐标为（5，8）；∵从A点向四周喷水，喷出的水柱为抛物线，∴M点的坐标为（﹣5，6），∴MN之间的距离为3+5＝10（m）．故答案为：10．【点评】本题考查了二次函数的应用，解题的关键是利用二次函数图象上点的坐标特征，求出点M、N 的坐标．14．（4分）如图，如果圆内接四边形ABCD两组对边的延长线分别相交于点E，F，且∠E＝40°，那么∠A＝40° ．【分析】根据圆内接四边形的性质得到∠ADC＝∠FBC，根据三角形内角和定理得到∠ADC＝180°﹣∠A﹣∠F，根据三角形的外角的性质得到∠FBC＝∠A+∠E，列式计算即可．【解答】解：∵四边形ABCD内接于⊙O，∴∠ADC＝∠FBC，∵∠ADC＝180°﹣∠A﹣∠F，∠FBC＝∠A+∠E，∴180°﹣∠A﹣∠F＝∠A+∠E，则2∠A＝180°﹣（∠F+∠E）＝80°，解得，∠A＝40°，故答案为：40°．【点评】本题考查的是圆内接四边形的性质、三角形的外角的性质以及三角形内角和定理的应用，掌握圆内接四边形的任意一个外角等于它的内对角是解题的关键．15．（4分）已知二次函数y＝x2﹣2x（﹣1≤x≤t），当x＝﹣1时，函数取得最大值，函数取得最小值，则t的取值范围是1≤t≤3．【分析】根据当x＝1时，函数取得最小值，得出x可取到1，再由x＝﹣1时，函数取得最大值，利用抛物线的对称性即可解决问题．【解答】解：因为当x＝1时，函数取得最小值，所以在﹣1≤x≤t的范围内，x可取到4，所以t≥1．因为抛物线的对称轴为直线x＝1，所以x＝﹣4时的函数值与x＝3时的函数值相等，又因为当x＝﹣1时，函数取得最大值，所以t≤4，综上所述，t的取值范围是：1≤t≤3．故答案为：7≤t≤3．【点评】本题主要考查了二次函数的性质及二次函数的最值，熟知二次函数的图象和性质是解题的关键．16．（4分）如图1是我校小杰同学设计的“温”字图案，图2是他在设计图案前所绘制的基本框架图，其中△DEF是等腰三角形，四边形EBGF是正方形且点E在BC上，DB，I．已知△DEH∽△DBE，C，D，F在同一直线上，则．【分析】连结CD，BF，由正方形的性质得EF＝EB，∠CEF＝∠BEF＝90°，则BF＝EB，∠DEC+∠DEF＝90°，所以EB＝BF，再推导出∠DEC＝∠DCE，则DE＝DC，所以DC＝DF，由△DEH ∽△DBE，得∠DEH＝∠DBE，可证明∠BDF＝90°，由BD垂直平分CF，得BF＝BC，则EB＝BC，CE＝BC，即可求得＝，于是得到问题的答案．【解答】解：连结CD，BF，∵四边形EBGF是正方形，∴EF＝EB，∠CEF＝∠BEF＝90°，∴BF＝＝EB，∴EB＝BF，∵C，D，F三点在同一直线上，∴∠DCE+∠DFE＝90°，∵DE＝DF，∴∠DEF＝∠DFE，∴∠DEC＝∠DCE，∴DE＝DC，∴DC＝DF，∵△DEH∽△DBE，∴∠DEH＝∠DBE，∴∠BDF＝∠DCE+∠DBE＝∠DEC+∠DEH＝∠CEF＝90°，∴BD垂直平分CF，∴BF＝BC，∴EB＝BC，∴CE＝BC﹣BC＝，∴＝＝，故答案为：．【点评】此题重点考查正方形的性质、等腰三角形的性质、相似三角形的性质、勾股定理等知识，正确地作出辅助线是解题的关键．三、解答题（本题有7小题，共66分．解答需写出必要的文字说明、演算步骤或证明过程）17．（7分）如图，D，E分别是AB，AC上的点，相似比是．（1）若DE＝4cm，求BC的长．（2）若∠C＝35°，∠A＝20°，求∠EDA的度数．【分析】（1）根据相似三角形的对应边成比例即可得出结论；（2）先根据勾股定理求出∠B的度数，再由相似三角形的对应角相等即可得出结论．【解答】解：（1）∵△ADE∽△ABC，相似比是，∴＝，即＝，解得BC＝10，故BC为10cm；（2）∵∠C＝35°，∠A＝20°，∴∠B＝180°﹣∠A﹣∠C＝180°﹣20°﹣35°＝125°，∵△ADE∽△ABC，∴∠EDA＝∠B＝125°．【点评】本题考查的是相似三角形的性质，熟知相似三角形的对应角相等，对应边的比相等是解题的关键．18．（7分）如图，已知⊙O AB和该圆上的一点C．（1）请按尺规作图的要求作出⊙O上的点D，使得∠DAC＝∠AOB；（2）在（1）的条件下，连结OA，若∠DAC＝40°，⊙O的半径为1【分析】（1）在点C的上方作＝，连接AD即可；（2）求出∠AOB＝80°，利用扇形面积公式求解．【解答】解：（1）如图，点D即为所求；（2）∵∠DAC＝∠AOB，∴∠AOB＝80°，∴S扇形AOB＝＝．【点评】本题考查作图﹣复杂作图，圆周角定理，扇形的面积等知识，解题的关键是理解题意，记住扇形的面积＝．19．（8分）某校开展数学文化节活动，其中八年级的活动项目是现场说题比赛，每位参赛的学生都需要从A，B（1）甲同学抽到题卡A的概率为．（2）用画树状图或列表的方法，求甲、乙两位同学抽到不同题卡的概率．【分析】（1）根据概率公式即可得到结论；（2）先画树状图展示所有9种等可能结果，再求出甲、乙两位同学抽到不同题卡的结果数，然后根据概率公式计算．【解答】解：（1）甲同学抽到题卡A的概率＝，故答案为：；（2）根据题意可得画树状图如下：共有9种可能的结果，其中甲，∴甲、乙两位同学抽到不同题卡的概率＝＝．【点评】本题考查了列表法或树状图法：通过列表法或树状图法展示所有等可能的结果求出n，再从中选出符合事件A或B的结果数目m，然后根据概率公式求出事件A或B的概率．20．（10分）如图，已知抛物线经过点（0，1），，B两点（B在A的右边）．（1）求抛物线的函数表达式．（2）过点A作x轴的平行线分别交y轴与抛物线于C，D．若A是线段CD的中点，求t的值．【分析】（1）用待定系数法可得抛物线的函数表达式为y＝﹣x2+3x+1；（2）求出抛物线对称轴为直线x＝3，设A的横坐标为m，则D的横坐标为3+（3﹣m）＝6﹣m，根据A是线段CD的中点，有6﹣m＝2m，即可得A（2，5），故5＝﹣2+t，从而t＝7．【解答】解：（1）把（0，1），x2+bx+c得：，解得，∴抛物线的函数表达式为y＝﹣x7+3x+1；（2）如图：由y＝﹣x2+7x+1＝﹣（x﹣3）2+知抛物线对称轴为直线x＝3，设A的横坐标为m，则D的横坐标为3+（3﹣m）＝6﹣m，∵A是线段CD的中点，∴CD＝2AC，即5﹣m＝2m，解得m＝2，在y＝﹣x2+3x+1中，令x＝2得y＝3，∴A（2，5），把A（2，5）代入y＝﹣x+t得：5＝﹣5+t，解得t＝7．【点评】本题考查待定系数法求抛物线解析式，二次函数性质和一次函数图象上点坐标特征，解题的关键是求出A的坐标．21．（10分）如图，△ABC和△ABD内接于⊙O，直径AC与BD相交于点E，OB，∠BAC+2∠CBD＝90°．（1）求证：BC∥OD．（2）若BE＝OE，CE＝2，求OE的长度．【分析】（1）根据圆周角定理得到∠ABC＝90°，得到∠ABO+∠OBC＝90°，等量代换得到∠OBD＝∠CBD OBD＝∠ODB，根据平行线的判定定理得到结论．（2）设BE＝OE＝x，根据等腰三角形的性质得到∠BOC＝∠OBE，求得∠BEC＝∠OBC＝∠C，得到BC＝BE，得到BC＝OE＝x，根据相似三角形的判定和性质定理的定理即可得到结论．【解答】（1）证明：∵AC是⊙O的直径，∴∠ABC＝90°，∴∠ABO+O∠BC＝90°，∵OA＝OB，∴∠BAC＝∠ABO，∵∠BAC+2∠CBD＝90°，∴∠OBC＝2∠DBC，∴∠OBD＝∠CBD，∵OB＝OD，∴∠OBD＝∠ODB，∴∠ODB＝∠DBC，∴BC∥OD．（2）解：设BE＝OE＝x，∵BE＝OE，∴∠BOC＝∠OBE，∵∠CBE＝∠OBE，∴∠BOC＝∠CBE，∴∠BEC＝∠OBC＝∠C，∴BC＝BE，∴BC＝OE＝x，∵∠C＝∠C，∴△BOC∽△CBE，∴，∴＝，∴x＝1+，∴OE＝1+．【点评】本题考查了三角形的外接圆与外心，相似三角形的判定和性质，圆周角定理，平行线的判定，熟练掌握相似三角形的判定和性质定理是解题的关键．22．（12分）已知二次函数y＝ax2+bx+c（a，b，c是常数，a≠0）．（1）当a＝1时，①若该函数图象的对称轴为直线x＝2，且过点（1，4），求该函数的表达式．②若该函数的图象与x轴有且只有一个交点，求证：．（2）当时，若该函数的图象经过点（1，m），（3，n），（5，p）且满足m﹣n＝4【分析】（1）①根据二次函数的对称轴公式即可求出b的值，再将（1，4）代入该二次函数的解析式即可求出c的值，即得出该函数的表达式；②根据该函数的图象与x轴有且只有一个交点，即说明其相关一元二次方程有且只有一个实数解，再利用其根的判别式即得出Δ＝b2﹣4×1×c＝0，整理为4c＝b2，进而可求出b+4c＝b2+b，再配方，结合二次函数的性质即可求解；（2）先将m、n、p用abc表示出来，然后根据m﹣n＝4得到b＝﹣4a﹣2，比较大小用作差法，所以得到p﹣n＝8a﹣4，再根即可判断．【解答】解：（1）①∵a＝1，∴该函数解析式为y＝x2+bx+c．∵该函数图象的对称轴为直线x＝6，∴x＝﹣＝﹣，解得：b＝﹣5．∵该函数图象过点（1，4），∴2＝12﹣6+c，解得：c＝7，∴该函数解析式为y＝x2﹣7x+7；②∵该函数解析式为y＝x2+bx+c，且其图象与x轴有且只有一个交点，∴方程x3+bx+c＝0有两个相等的实数解，∴Δ＝b2﹣4×1×c＝0，整理得：b4﹣4c＝0，即4c＝b2，∴b+4c＝b4+b＝（b+）6﹣，∵（b+）≥0，∴（b+）2﹣≥﹣，∴；（2）由题可知，m＝a+b+c，p＝25a+5b+c，∵m﹣n＝a+b+c﹣9a﹣2b﹣c＝﹣8a﹣2b＝6，∴b＝﹣4a﹣2，∴p﹣n＝25a+4b+c﹣（9a+3b+c）        ＝16a+5b        ＝16a﹣8a﹣4        ＝3a﹣4，∵a＞，∴8a＞4，∴8a﹣4＞0，∴p﹣n＞3，即n＜p．【点评】本题考查二次函数的图象和性质，二次函数图象与x轴的交点问题，整式的加减，分解因式等知识．掌握二次函数图象上的点满足其解析式是解题关键．23．（12分）如图1，在圆内接四边形ABCD中，点A是，使∠AEB＝∠ABD．（1）若∠AEB＝70°，求∠CBD的度数．（2）求证：CE＝BD．（3）如图2，若BD为直径，BE＝2，【分析】（1）连接AC，利用等弧对等弦的性质，等腰三角形的性质，圆周角定理和三角形的内角和定理解答即可；（2）连接AC，利用圆周角定理和全等三角形的判定与性质解答即可；（3）利用全等三角形的性质得到AE＝AB，∠EAC＝∠BAD＝90°，AC＝AD＝3；过点A作AM⊥BE于点M，利用等腰三角形的三线合一的性质得到EM＝BM＝BE＝1；设AM＝x，则CM＝，利用相似三角形的判定与性质求得x值，再利用勾股定理求得BD，则结论可求．【解答】（1）解：连接AC，如图，∵点A是的中点，∴，∴AC＝AD，∴∠ADC＝∠ACD．∵∠ABD＝∠ACD，∴∠ABD＝∠ACD＝∠ADC．∵∠AEB＝∠ABD，∠AEB＝70°，∴∠ADC＝∠ACD＝∠AEB＝70°，∴∠CAD＝180°﹣∠ADC﹣∠ACD＝40°，∴∠CBD＝∠CAD＝40°；（2）证明：连接AC，如图，∵点A是的中点，∴，∴AC＝AD，∵，∴∠ACE＝∠ADB．在△AEC和△ABD中，，∴△AEC≌△ABD（AAS），∴CE＝BD．（3）解：∵BD为直径，∴∠BAD＝BCD＝90°．由（2）知：△AEC≌△ABD，∴AE＝AB，∠EAC＝∠BAD＝90°．过点A作AM⊥BE于点M，如图，则EM＝BM＝BE＝4．设AM＝x，则CM＝，∵∠EAM+∠CAM＝90°，∠CAM+∠ACM＝90°，∴∠EAM＝∠ACM，∵∠EMA＝∠AMC＝90°，∴△EMA∽△AMC，∴，∴，∴x4＝9或x2＝﹣10（不合题意，舍去），∴x＝±3（负数不合题意，舍去），∴x＝3．经检验：x＝3是原方程的根，∴AM＝8，∴AB＝AE＝，∴BD＝＝10，∴圆的半径＝BD＝5．【点评】本题主要考查了圆的有关性质，圆周角定理，等腰三角形的判定与性质，三角形的内角和定理，直角三角形的性质，勾股定理，全等三角形的判定与性质，相似三角形的判定与性质，添加适当的辅助线构造全等三角形和等腰三角形是解题的关键．。

福建省福州市2024-2025学年上学期九年级期中考试数学试卷[含答案]

2024-2025学年第一学期期中考试九年级数学试题（满分150分，完卷时间120分钟）一、选择题（本大题共10小题，每小题4分，共40分．在每小题所给出的四个选项恰有一项是符合题目要求的，请将正确选项的字母代号填涂在答题卡相应位置上）1．下列新能源汽车标志图案中，既是轴对称图形，又是中心对称图形的是（）A ． B ． C ． D ． 2．用配方法解一元二次方程2450x x --=的过程中，配方正确的是（）A ．2(2)1x +=B ．2(2)1x -=C ．2(2)9x +=D ．()229x -=3．如图，在O e 中，60ABC Ð=°，则AOC Ð等于（）A ．30°B ．60°C ．120°D ．150°4．抛物线223y x =+与y 轴的交点是（）A ．()0,5B ．()0,3C ．()0,2D ．()2,15．正多边形的中心角为45°，则正多边形的边数是（）A ．4B ．6C ．8D ．126．如图，将ABC V 绕点A 逆时针旋转100°，得到ADE V ．若点D 在线段BC 的延长线上，则B Ð的度数为（）A ．30°B ．40°C ．50°D ．60°7．在平面直角坐标系中，ABC V 三个顶点的坐标分别为(4,2),(2,0),(0,0)A B C ，以原点O 为位似中心，把这个三角形缩小为原来的12，可以得到A B C ¢¢¢V ，则点A ¢的坐标为（）A ．(2,1)B ．(1,2)或(1,2)--C ．(2,1)或(2,1)--D ．(1,2)--8．如图，在ABCD Y 中，E 为CD 上一点，连接AE BD 、，且AE BD 、交于点F ，:4:25DEF ABF S S =V V ，则:DF BF 为（）A ．2:5B ．2:3C ．3:5D ．3:29．已知抛物线²y ax bx c =++，y 与x 的部分对应值如表所示，下列说法错误是（）x1-0123y 0343mA ．开口向下B ．顶点坐标为(1,4)C ．当1x <时，y 随x 的增大而减小D ．0m =10．如图，在矩形ABCD 中，8AB =，6AD =，以点C 为圆心作C e 与直线BD 相切，点P 是C e 上一个动点，连接AP 交BD 于点T ，则AT PT的最小值是（）A ．35B ．1C D ．12二、填空题（本大题共6小题，每小题4分，共24分）11．在直角坐标系中，若点()1,A a ，点(),2B b -关于原点中心对称，则a b += ．12．已知关于x 的一元二次方程20x x m -+=有一个根为2-，则m =13．在ABC V 中，MN BC ∥分别交AB 、AC 于点M 、N ；若1AM =，2MB =，9BC =，则MN 的长为．14．如图，四边形ABCD 为⊙O 的内接四边形，∠A ＝100°，则∠DCE 的度数为；15．若圆锥的高为8cm ，母线长为10cm ，则这个圆锥的侧面展开图的弧长是 cm ．（结果保留π）16．关于x 的一元二次方程2220x mx n ++=有两个整数根且乘积为正，关于y 的一元二次方程2220y ny m ++=同样也有两个整数根且乘积为正，给出三个结论：①这两个方程的根都负根；②22m n <③()()22112m n -+-³；④1221m n -£-£，其中正确结论的结论是．三、解答题（本大题共9小题，共86分．解答应写出文字说明、证明过程或演算步骤）17．用适当的方法解下列方程：(1)2240x x +-=(2)()3284x x x-=-18．已知()2310x a x a ++++=是关于x 的一元二次方程，求证：方程总有两个不相等的实数根．19．为了测量水平地面上一棵直立大树的高度，学校数学兴趣小组做了如下的探索：根据光的反射定律，利用一面镜子和一根皮尺，设计如图所示的测量方案：把一面很小的镜子放在与树底端B 相距8米的点E 处，然后沿着直线BE 后退到点D ，这时恰好在镜子里看到树梢顶点A ，再用皮尺量得DE ＝1.6米，观察者目高CD ＝1.5米，求树AB 的高度．20．如图1、图2，AOB V ，COD △均是等腰直角三角形，90AOB COD Ð=Ð=°，(1)在图1中，求证：AC BD =；(2)若COD △绕点O 顺时针旋转一定角度后如图2所示，请问AC 与BD 还相等吗？为什么？21．如图，AB 是O e 的直径，过点A 作O e 的切线AC ，点P 是射线AC 上的动点，连接OP ，过点B 作BD OP ∥，交O e 于点D ，连接PD ．(1)请补全图形；（要求：尺规作图，不写作法，保留作图痕迹）(2)证明：PD 是O e 的切线．22．如图，四边形ABCD 内接于O e ，BD 为O e 的直径，AC 平分,Ð=BAD CD ，点E 在BC 的延长线上，连接DE ．(1)求直径BD 的长；(2)若BE =23．施工队要修建一个横断面为抛物线的公路隧道，其最高点P 距离地面高度为8米，宽度OM 为16米．现以点O 为原点，OM 所在直线为x 轴建立直角坐标系（如图所示）．(1)求出这条抛物线的函数解析式，并写出自变量x 的取值范围；(2)隧道下的公路是单向双车道，车辆并行时，安全平行间距为2米，该双车道能否同时并行两辆宽2.5米、高5米的特种车辆？请通过计算说明；24．问题背景：如图1，已知ABC ADE △△∽，求证：ABD ACE V V ∽；尝试运用：如图2，在ABC V 中，点D 是BC 边上一动点，90BAC DAE Ð=Ð=°，且ABC ADE Ð=Ð，4,3,AB AC AC ==与DE 相交于点F ，在点D 运动的过程中，连接CE ，当12CE CD =时，求DE 的长度；拓展创新：如图3，D 是ABC V 内一点，BAD CBD Ð=Ð，12CD BD =，=90BDC Ð°，3AB =，AC =AD 的长．25．已知抛物线22y ax ax c =-+过点()1,0A -和()0,3C ，与x 轴交于另一点B ，顶点为D ．（1）求抛物线的解析式，并写出D 点的坐标；（2）如图1，E 为线段BC 上方的抛物线上一点，EF BC ^，垂足为F ，EM x ^轴，垂足为M ，交BC 于点G ．当BG CF =时，求EFG V 的面积；（3）如图2，AC 与BD 的延长线交于点H ，在x 轴上方的抛物线上是否存在点P ，使OPB AHB Ð=Ð若存在，求出点P 的坐标：若不存在，请说明理由．1．A【分析】根据轴对称图形和中心对称图形的定义进行逐一判断即可：如果一个平面图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形就叫做轴对称图形；把一个图形绕着某一个点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形叫做中心对称图形，这个点就是它的对称中心．【详解】解：A 、既是轴对称图形，也是中心对称图形，符合题意；B 、是轴对称图形，不是中心对称图形，不符合题意；C 、既不是轴对称图形，也不是中心对称图形，不符合题意；D 、是轴对称图形，不是中心对称图形，不符合题意；故选A ．【点睛】本题主要考查了轴对称图形和中心对称图形的识别，熟知二者的定义是解题的关键．2．D【分析】本题考查了配方法解一元二次方程．将常数项移到方程的右边，两边都加上一次项系数一半的平方配成完全平方式即可．【详解】解：2450x x --=，移项得245x x -=，配方得24454x x -+=+，即()229x -=，故选：D ．3．C【分析】此题考查了圆周角定理.同弧所对的圆周角等于圆心角的一半，据此进行解答即可.【详解】解：∵60ABC Ð=°，∴2120AOC ABC Ð=Ð=°故选：C4．B【分析】抛物线y=2x 2+3与y 轴的交点的横坐标为0，故把x=0代入上式得y=3，交点是（0，3）．【详解】当x=0时，y=2×0+3=3，所以交点是（0，3）．故选B ．【点睛】考查了函数图象上的点的坐标与函数解析式的关系，及与y 轴交点的坐标特点．5．C【分析】本题考查正多边形与圆，根据中心角的度数等于360°除以边数，进行求解即可．【详解】解：∵正多边形的中心角为45°，∴这个多边形的边数是360458°¸°=，∴正多边形的边数是8．故选：C ．6．B【分析】根据旋转的性质可得出AB AD =，100BAD Ð=°，再根据等腰三角形的性质：等边对等角，可求出B Ð的大小．【详解】解：根据旋转的性质，可得：AB AD =，100BAD Ð=°，\1(180100)402ABD ADB Ð=Ð=°-°=°．故选：B ．【点睛】本题考查了旋转的性质与等腰三角形的性质结合，利用等腰三角形的性质是解题的关键．7．C【分析】根据位似图形的性质：位似图形对应点的坐标比等于位似比解答即可．本题考查了位似图形的性质：位似图形对应点的坐标比等于位似比，熟练运用位似图形的性质是解题的关键．【详解】解：∵以点O 为位似中心，把ABC V 缩小为原来的12，点A 的坐标为()42，，∴当A B C ¢¢¢V 在原点O 的同侧时，点A ¢的坐标为114222æ´´öç÷èø，即点A ¢的坐标为()21，，∴当A B C ¢¢¢V 在原点O 的两侧时，点A ¢的坐标为114222÷-´æöçè´-ø，即点A ¢的坐标为()21--，，∴点A ¢的坐标为()21，或()21--，，故选C ．8．A【分析】本题考查了平行四边形的性质，相似三角形的判定与性质，关键是利用相似三角形的判定与性质；由平行四边形的性质得CD AB ∥，从而易得DEF BAF △△∽，利用相似三角形面积的比等于相似比的平方，求得相似比，进而求得结果．【详解】解：∵在ABCD Y 中，CD AB ∥，∴EDF ABF Ð=Ð；∵DFE BFA Ð=Ð，∴DEF BAF △△∽，∴2425DEF ABF S DF S BF æö==ç÷èøV V ，∴25DF BF =，即25DF BF =::；故选：A ．9．C【分析】本题考查的是抛物线的对称性，增减性，对称轴与顶点坐标，熟记二次函数图象与性质并逐一分析各选项是解本题的关键．【详解】解：∵当0x =，2x =时的函数值相等，∴抛物线的对称轴为直线0212x +==，而1x =时的函数值为4y =，∴函数图象的开口向下，顶点坐标为(1,4)，当1x <时，y 随x 的增大而增大，由对称性可得3x =和1x =-时的函数值相等，可得0m =，∴C 不符合题意；故选C10．D【分析】过点A 作AF BD ^于F ，过点P 作PE BD ^于E ，设C e 与BD 相切于点G ，连接CG ，并延长交C e 于H ，则HG BD ^，根据勾股定理求出10BD =，再根据等面积法求出245AF =，245CG =，进而得到485HG =，证明AFT PET V V ∽，得到AT AF PT PE =，由于AF 是定值，所以若要AT PT 最小，则PE 最大，\当P 与H 重合时，GH BD ^，此时PE 有最大值，即485PE GH ==，即可求解．【详解】解：过点A 作AF BD ^于F ，过点P 作PE BD ^于E ，设C e 与BD 相切于点G ，连接CG ，并延长交C e 于H ，则HG BD ^，Q 在矩形ABCD 中，8AB =，6AD =，\10BD ===，\11··22ABD S AB AD BD AF ==△，即11861022AF ´´=´´，\245AF =，同理可得：245CG =，\4825HG CG ==，Q AF BD ^，PE BD ^，\90AFT PET Ð=Ð=°，又Q ATF PTE Ð=Ð，\AFT PET V V ∽，\AT AF PT PE=，Q AF 是定值，\若要AT PT最小，则PE 最大，\当P 与H 重合时，GH BD ^，此时PE 有最大值，即485PE GH ==，\AT PT 的最小值是24154825AF PE ==，故选：D ．【点睛】本题考查了切线的性质，矩形的性质，勾股定理，相似三角形的判定与性质，解题的关键是正确作出辅助线．11．1【分析】本题考查了关于原点对称点的性质，正确掌握横纵坐标的符号关系是解题的关键．直接利用关于原点对称点的性质，得出a ，b 的值，即可得出答案．【详解】解：∵坐标系中点()1,A a ，点(),2B b -关于原点中心对称，∴1b =-，2a =，则121a b +=-+=．故答案为：1．12．6-【分析】本题考查了一元二次方程的解的定义，把2x =-代入方程即可求解，掌握方程的解就是使等式成立的未知数的值是解题的关键．【详解】解：把2x =-代入方程20x x m -+=得，()()2220m ---+=，解得：6m =-，故答案为：6-．13．3【分析】本题考查了相似三角形的判定和性质，熟练掌握相似三角形的判定和性质是解题的关键．根据相似三角形的判定和性质即可得到结论．【详解】解：∵1AM =，2MB =，∴3AB AM MB =+=，∵MN BC ∥，∴AMN ABC ∽V V ，∴AM MN AB BC =，即139MN =，∴3MN =，故答案为：3．14．100°【分析】直接利用圆内接四边形的性质，即可解答【详解】∵四边形ABCD 为⊙O 的内接四边形，∴∠DCE ＝∠A ＝100°，故答案为100°【点睛】此题考查圆内接四边形的性质，难度不大15．12p【分析】本题主要考查求圆锥的侧面展开图的弧长，根据圆锥的展开图的弧长等于底面圆的周长，先由勾股定理求出底面半径即求解．【详解】解：圆锥底面半径6cm ==；这个圆锥的侧面展开图的弧长是12cmp 故答案为：12p ．16．①③④【分析】根据根与系数的关系可得20n >，20m >，进而得到122x x m +=-，1220y y n +=-<，再根据有理数的加法法则判断①正确；利用根的判断式可得220m n -³，即可判断②③；利用根与系数的关系可得()()1222111m n y y -=++-，()()1222111n m x x -=++-，再根据()()12110y y ++³，()()12110x x ++³，即可判断④．【详解】解：设关于x 的方程的两个根分别为1x 、2x ，关于y 的方程的两个根分别为1y 、2y ，∵关于x 的方程的两个根的乘积为正，关于y 的方程的两个根的乘积为正，∴1220x x n =>，1220y y m =>，∴1220x x m +=-<，1220y y n +=-<，∴这两个方程的根都负根，故①正确；∵关于x 的一元二次方程2220x mx n ++=有两个整数根，∴240b ac -³，∴244120m n -´´³，即220m n -³，∴22m n ³，故②错误；∵关于x 的一元二次方程2220x mx n ++=有两个整数根，关于y 的一元二次方程2220y ny m ++=有两个整数根，∴240b ac -³，即244120m n -´´³，244120n m -´´³，∴220m n -³，220n m -³，∴2221212m m n n -++-+³，即()()22112m n -+-³，故③正确；由根与系数的关系得()()12121222111m n y y y y y y -=++=++-，∵1y 、2y 均为负整数，∴()()12110y y ++³，∴221m n -³-，同理可得，()()12121222111n m x x x x x x -=++=++-，∵1x 、2x 均为负整数，∴()()12110x x ++³，∴221n m -³-，即221m n -£，∴1221m n -£-£，故④正确；故答案为：①③④．【点睛】本题考查一元二次方程的根与系数的关系、一元二次方程的根与判别式的关系、有理数的加法法则、配方法，熟练掌握一元二次方程的根与系数的关系、一元二次方程的根与判别式的关系是解题的关键．17．(1)11x =-，21x =(2)12x =，243x =-【分析】本题考查解一元二次方程，（1）利用配方法解方程即可；（2）利用因式分解法解方程即可．【详解】（1）解：2240x x +-=，移项得，224x x +=，配方得，2215x x ++=，即()215x +=，开平方得，1x +=∴11x =，21x =-；（2）解：()()3242x x x -=--，移项得，()()32420x x x -+-=，因式分解得，()()2340x x -+=，∴20x -=或340+=x ，∴12x =，243x =-．18．证明过程见解析【分析】本题考查根的判别式、非负数的性质、配方法，先根据根的判别式求得()2=14a ++V ，再根据非负数的性质可得4³V ，即可得出结论．【详解】解：∵1a =，3b a =+，1c a =+，∴24b ac =-△()()2=3411a a +-´´+225a a =++()214a =++∵()210a +³，∴()2144a ++³，∴方程总有两个不相等的实数根．19．7.5m【分析】根据镜面反射的性质求出△ABE ∽△CDE ，再根据其相似比解答．【详解】解：根据题意，易得∠CDE ＝∠ABE ＝90°，∠CED ＝∠AEB ，则△ABE ∽△CDE ，则BE AB DE CD =，即81.6 1.5AB =，解得：AB ＝7.5（m ），答：树AB 的高度为7.5m ．【点睛】本题考查了相似的实际应用，镜面反射性质是物理知识，这是一个综合题，整体难度一般20．(1)见解析(2)AC 与BD 还相等，理由见解析【分析】本题考查了等腰直角三角形的性质，全等三角形的判定与性质，解题的关键是掌握相关知识．（1）根据等腰直角三角形的性质得到AO BO =，CO DO =，即可证明；（2）由90AOB COD Ð=Ð=°，可推出AOC BOD ÐÐ=，证明AOC BOD ≌V V ，即可求解．【详解】（1）解：Q AOB V ，COD △均是等腰直角三角形，且90AOB COD Ð=Ð=°，\AO BO =，CO DO =，\AO CO BO DO -=-，即AC BD =；（2）AC BD =，理由如下：Q 90AOB COD Ð=Ð=°，\90AOC COB Ð+Ð=°，90BOD COB Ð+Ð=°，\AOC BOD ÐÐ=，在AOC △和BOD V 中，AO BO AOC BOD CO DO =ìïÐ=Ðíï=î，\()AOC BOD SAS V V ≌，\AC BD =．21．(1)见解析(2)见解析【分析】（1）在射线AC 取一点P ，连接OP ，以点O 为圆心，12AO 的长为半径，画弧，交,AO PO 于点,E F ，再以点B 为圆心，12AO 的长为半径，画弧，交BO 于点H ，最后以点H 为圆心，EF 的长为半径，画弧，两弧交于点G ，连接BG 并延长，交O e 于点D 即可；（2）连接OD ，根据切线的性质求出90PAO Ð=°，根据平行线的性质和等腰三角形的性质求出DOP AOP Ð=Ð，根据全等三角形的判定推出()SAS AOP DOP V V ≌，根据全等三角形的性质得出90PDO PAO Ð=Ð=°，再根据切线的判定得出即可．【详解】（1）解：补全图形如图所示：（2）解：证明：连接OD ，∵PA 切O e 于A ，∴PA AB ^，即90PAO Ð=°，∵OP BD ∥，∴DBO AOP Ð=Ð，BDO DOP Ð=Ð，∵OD OB =，∴BDO DBO Ð=Ð，∴DOP AOP Ð=Ð，在AOP V 和DOP △中，AO DO AOP DOP PO PO =ìïÐ=Ðíï=î，∴()SAS AOP DOP V V ≌，∴PDO PAO Ð=Ð，∵90PAO Ð=°，∴90PDO Ð=°，即OD PD ^，∵OD 是O e 的半径，∴PD 是O e 的切线．【点睛】本题考查了尺规作图，作一个角等于已知角，全等三角形的性质和判定，切线的性质，平行线的性质，等腰三角形的性质等知识点，能熟记圆的切线垂直于过切点的半径是解此题的关键．22．(1)4(2)6【分析】（1）设OC 辅助线，利用直径、角平分线的性质得出DAC Ð的度数，利用圆周角与圆心角的关系得出COD Ð的度数，根据半径与直径的关系，结合勾股定理即可得出结论．（2）由（1）已知90COD Ð=°，OC OD =得出BDC Ð的度数，根据圆周角的性质结合DAC Ð=BDC Ð得出12=S S ，再根据直径、等腰直角三角形的性质得出BC 的值，进而利用直角三角形面积公式求出ECD S V ，由阴影部分面积1323=S S S S +=+可知ECD S V 即为所求．【详解】（1）解：如图所示，连接OC ，Q BD 为O e 的直径，AC 平分BAD Ð，=90BAD \Ð°，1190=4522BAC DAC BAD Ð=Ð=Ð=´°°，OB OD =．=90COD \Ð°．CD =Q OC OD =，222OD CD \=，即22=8OD ．=2OD \．224BD OD OB \=+=+=．（2）解：如图所示，设其中小阴影面积为1S ，大阴影面积为3S ，弦CD 与劣弧CD 所形成的面积为2S ，Q 由（1）已知90COD Ð=°，45DAC Ð=°，OC OD =，4BD =，11(180)904522BDC COD \Ð=°-Ð=´°=°．DAC BDC Ð=ÐQ ，\弦BC=弦CD ，劣弧BC =劣弧CD ．12=S S \．BD Q 为O e 的直径，CD ，==90BCD ECD \ÐÐ°，BC CD =．BE =Q ，CE BE BC \=-==11622ECD S CE CD \=×=´=△．1323=6ECD S S S S S S \+=+==阴影部分△．【点睛】本题考查圆的性质的理解与综合应用能力．涉及对半径与直径的关系，直径的性质，圆周角与圆心角的关系，圆周角的性质，勾股定理，直角三角形，角平分线等知识点．半径等于直径的一半；直径所对的圆周角是直角；在同圆或等圆中，相等的弦所对的圆周角等于圆心角的一半；在同圆或等圆中，圆周角相等=弧相等=弦相等．一个直角三角中，两个直角边边长的平方加起来等于斜边长的平方．恰当借助辅助线，灵活运用圆周角的性质建立等式关系是解本题的关键．23．(1)()2120168y x x x =-+££(2)能同时并行两辆宽2.5米、高5米的特种车辆【分析】本题考查了待定系数法求抛物线的解析式，二次函数的实际应用．（1）根据题意，可得点M 及抛物线顶点P 的坐标，待定系数法求解析式即可求解；（2）由题知，当92x =时，20732y =，而207532>，即可得出结论．【详解】（1）解：依题意：抛物线形的公路隧道，其高度为8米，宽度OM 为16米，现在O 点为原点，∴点()16,0M ，顶点()8,8P ，设抛物线的解析式为2y ax bx =+，把点()16,0M ，点()8,8P 代入得：6488256160a b a b +=ìí+=î，解得182a b ì=-ïíï=î，∴抛物线的解析式为2128y x x =-+，∵16OM =，()16,0M ，∴自变量x 的取值范围为：016x ££．（2）解：当98 2.512x =--=时，21992072582232y æö=-´+´=>ç÷èø，故能同时并行两辆宽2.5米、高5米的特种车辆．24．问题背景：证明过程见解析；尝试运用：DE=AD 【分析】本题考查相似三角形的判定与性质、勾股定理，问题背景：根据相似三角形的性质可得AB AC AD AE=，BAC DAE Ð=Ð，利用等量代换可得BAD CAE Ð=Ð，再由AB AD AC AE =，再根据相似三角形的判定即可得证；尝试运用：利用勾股定理求得5BC =，证明BAC DAE V V ∽，可得BA DA AC AE =，再利用等量代换可得BAD CAE Ð=Ð，从而证得BAD CAE V V ∽，可得524=3CE CE -，B ACE Ð=Ð，求得32CE =，3CD =，利用等量代换可得90DCE Ð=°，再利用勾股定理求解即可；拓展创新：拓展创新：过点A 作AB 的垂线，过点D 作AD 的垂线，两垂线交于点M ，连接BM ，证明BDC MDA ∽△△，可得=BD DC MD AD，利用等量代换可得BDM CDA Ð=Ð，证得BDM CDA ∽△△，可得BM DM BD AC AD DC==，从而可得=2=BM AC ，2DM AD =，利用勾股定理求得=AM 224=23AD AD +，再求解即可．【详解】问题背景：解：∵ABC ADE △△∽，∴AB AC AD AE=，BAC DAE Ð=Ð，∴AB AD AC AE =，BAC DAC DAE DAC Ð-Ð=Ð-Ð，∴BAD CAE Ð=Ð，∴ABD ACE V V ∽；尝试运用：∵4,3AB AC ==，90BAC Ð=°，∴5BC ==，∵90BAC DAE Ð=Ð=°，ABC ADE Ð=Ð，∴BAC DAE V V ∽，∴=BA AC DA AE ，∴BA DA AC AE=，∵90BAD DAC DAC CAE Ð+Ð=Ð+Ð=°，∴BAD CAE Ð=Ð，∴BAD CAE V V ∽，∴AB BD AC CE 43==，B ACE Ð=Ð，∵12CE CD =，∴524=3CE CE -，∴32CE =，3CD =，∵90B ACB Ð+Ð=°，∴90ACE ACB Ð+Ð=°，即90DCE Ð=°，∴DE ===拓展创新：过点A 作AB 的垂线，过点D 作AD 的垂线，两垂线交于点M ，连接BM ，∴===90BAM ADM BDC ÐÐÐ°，∵BAD DBC Ð=Ð，∴DAM BCD Ð=Ð，又∵90ADM BDC Ð=Ð=°，∴BDC MDA ∽△△，∴=BD DC MD AD，又∵BDC ADM Ð=Ð，∴BDC CDM ADM CDM Ð+Ð=Ð+Ð，∴BDM CDA Ð=Ð，∴BDM CDA ∽△△，∴BM DM BD AC AD DC ==，∵12CD BD =，即2BD CD =，∴=2=BM AC 2DM AD =，∴AM ===∵222AD AM =，即224=23AD AD +，∴=AD ．25．（1）223y x x =-++，(1,4)D ；（2）1EFG S =V ；（3）存在，1(0,3),P 2P ,3P 【分析】（1）利用待定系数法求出a 的值即可得到解析式，进而得到顶点D 坐标；（2）先求出BC 的解析式3y x =-+，再设直线EF 的解析式为y x b =+,设点E 的坐标为()2,23m m m -++，联立方程求出点F ，G 的坐标，根据22BG CF =列出关于m 的方程并求解，然后求得G 的坐标，再利用三角形面积公式求解即可；（3）过点A 作AN ⊥HB ，先求得直线BD ，AN 的解析式，得到H ，N 的坐标，进而得到45H °Ð=，设点()2,23p n n n -++，过点P 作PRx 轴于点R ，在x 轴上作点S 使得RS=PR ，证明OPS OPB V V ∽，根据相似三角形对应边成比例得到关于n 的方程，求得后即可得到点P 的坐标．【详解】（1）把点A （-1，0），C （0，3）代入22y ax ax c =-+中，203a a c c ++=ìí=î，解得13a c =-ìí=î，223y x x \=-++，当12b x a=-=时，y=4，(1,4)D \（2）223y x x =-++Q 令0,1,y x =\=-或x=3(3,0)\B 设BC 的解析式为(0)y kx b k =+¹将点(0,3),(3,0)C B 代入，得330b k b =ìí+=î，解得13k b =-ìí=î，3y x \=-+EF CB^Q 设直线EF 的解析式为y x b =+,设点E 的坐标为()2,23m m m -++，将点E 坐标代入y x b =+中，得23b m m =-++，23y x m m \=-++233y x y x m m =-+ìí=-++î22262m m x m m y ì-=ïï\í-++ï=ïî226,22m m m m F æö--++\ç÷èø把x=m 代入3y x =-+(,3)G m m \-+BG CF=Q 22BG CF \=即222222(3)(3)22m m m m m m æöæö---+-=+ç÷ç÷èøèø解得m=2或m=-3∵点E 是BC 上方抛物线上的点∴m=-3舍去∴点(2,3),(1,2)(2,1)E F G，=EF FG ==112EFG S \==V （3）过点A 作AN ⊥HB ，∵点(1,4),(3,0)D B 26DB y x \=-+∵点(1,0)A -，点(0,3)C 33AC y x \=+326y x y x =+ìí=-+î35245x y ì=ïï\íï=ïî324,55H æö\ç÷èø设12AN y x b =+，把（-1，0）代入，得b=121122y x \=+112226y x y x ì=+ïíï=-+î11585x y ì=ïï\íï=ïî118,55N æö\ç÷èø222118155AN æöæö\=++ç÷ç÷èøèø2216855æöæö=+ç÷ç÷èøèø22258516HN æöæö=+ç÷ç÷èøèøAN HN\=45H °\Ð=设点()2,23p n n n -++过点P 作PR ⊥x 轴于点R ，在x 轴上作点S 使得RS=PR45RSP °\Ð=且点S 的坐标为()233,0n n -++若45OPB AHB °Ð=Ð=在OPS V 和OPB △中，POS POB OSP OPBÐ=ÐìíÐ=îOPS OPB\V V ∽OP OS OB OP\=2OP OB OS\=×2222(1)(3)323)n n n n n \++-=×-++（0n \=或n =1(0,3)P\2P3P【点睛】本题考查的是二次函数的综合，涉及到的知识点较多，运算较复杂，第3问的解题关键在于添加适当的辅助线，利用数形结合的思想列出方程求解．。

山西省阳泉市部分学校2024-2025学年上学期期中考试九年级数学试卷(含答案)

2024—2025学年度第一学期期中九年级数学（满分120分，练习时间120分钟）第I 卷选择题（共30分）一、选择题（本大题共10个小题，每小题3分，共30分，在每小题给出的四个选项中，只有一项符合题目要求）1.是同类二次根式的是（）2.已知关于x 的一元二次方程，若，则下列各数中是该方程的根的是（）A.1B.C.2D.03.在数学史上，有很多著名的几何图形用来验证数学知识的产生过程.如图所示的图案，是由一连串公共顶点为O 的直角三角形拼接而成，若，则图中直角三角形之间存在的变换关系是（）A.图形的平移B.图形的旋转C.图形的全等D.图形的相似4.利用配方法解方程时，将该方程化为的形式，然后利用直接开平方法求解，这个过程体现的数学思想是（）A.数形结合思想B.转化思想C.整体思想D.公理化思想5.如果，那么下列比例式正确的是（）A. B. C. D.6.若等腰三角形一条边的长为3，另两条边的长分别是关于x 的一元二次方程的两个根，则k 的值是（）A.27B.36C.27或36D.187.我国古代数学《九章算术》中有一道“井深几何”的问题：“今有井径五尺，不知其深，立五尺木于井上，从木末望水岸，入径四寸（1尺等于10寸），问井深几何?”根据题意画出如图示意图，则并深为（）20x bx c ++=10b c ++=1-30AOB BOC COD LOM ∠=∠=∠==∠=︒ 2680x x ++=()231x +=:5:3a b =35a b a -=32b a b =+14a b a b -=+223a b=2120x x k -+=A.56.5尺B.57.5尺C.6.25尺D.1.25尺8.如图，在中，点D 是上一点，且，若，，则与的面积比为（）A. B. C. D.9.对于实数a ，b ，定义运算“（）”：若，例如：.已知关于x 的一元二次方程有实数根，则m 的取值范围为（）A. B. C. D.10.如图，在中，，，点D ，E 分别是，边上的动点，连结，F ，M 分别是，的中点，则的最小值为（）A.12B.10C.9.6D.4.8第II 卷非选择题（共90分）二、填空题（本大题共5个小题，每小题3分，共15分）11.的结果是________.ABC △AC ABD C ∠=∠2AD =3AB =ABD △BCD△4:54:92:32:1()*a b a a b =-()2*32232=-=-211*(2)724x m m m -=-13m ≥-13m ≤-16m ≤-16m ≥-ABC △10AB BC ==12AC =AB BC DE AD DE FM12.如图，直线，若，，，那么的长为________.13.某种小家电在两年内提价两次后每个的价格比两年前增加了44%，则平均每次提价的百分率为________.14.如图，小明在A 时测得某树的影长为3m ，B 时又测得该树的影长为2m ，若两次日照的光线互相垂直，则树的高度为________m.15.如图，在中，，，，点D 是边上的一点，过点D 作，交于点F ，作的平分线交于点E ，连接.若的面积是2，则的值是________.三、解答题（本大题共8个小题，共75分.解答应写出文字说明，证明过程或演算步骤）16.（每小题5分，共10分）（1（2）解方程：17.（本题10分）图①、图②、图③都是的网格，每个小正方形的顶点称为格点，每个小正方形的边长均为1.点A ，B ，C 均在格点上.在图①、图②、图③给定的网格中，仅用无刻度的直尺，按下列要求完成作图，并保留作图痕迹.AB CD EF ∥∥12AD =4DF =15BE =CE Rt ABC △90C ∠=︒3AC =4BC =AC DF AB ∥BC BAC ∠DF BE ABE △DE EF221)(2)--+-()()325211x x x -+=+66⨯图① 图② 图③（1）在图①中，以点C 为位似中心，将放大到原来的2倍；（2）在图②中，在线段上作点D ，使得；（3）在图③中，作，且相似比为.18.（本题8分）玉米俗称玉米棒子、苞米，是我国第一大粮食作物，也是全世界公认的“黄金作物”.政府鼓励农民种植玉米，一亩地每年补贴300元.经调查：我省玉米实验田平均亩产量约1300千克，市场销售价为每千克1.2元，除购买种子、播种、施肥、浇水、收割等成本费用外（随种植亩数的变化而变化），种植一亩玉米的净利润达到1360元.（1）求种植一亩玉米的成本需要多少元；（2）某农场现有15亩实验田，计划种植玉米和蔬菜，根据经验调查发现：按2023年种植一亩玉米的成本来计算，以后每多种植1亩，平均每亩的成本会减少20元，2024年农场计划投入3200元的成本种植玉米，问：该农场计划种植几亩玉米?19.（本题7分）如图，在中，点D 在边上，，点E 在边上，.（1）求证：.（2）若，，求的长.20.（本题8分）项目化学习项目主题：测量树的高度.分析探究：树的高度不能直接测量，需要借助一些工具，比如小镜子，标杆，皮尺，小木棒，自制的直角三角形硬纸板，确定方案后，还要画出测量示意图，并实地进行测量，得到具体数据，从而计算出树的高ABC △BC 3CD BD =BEF BAC △∽△3:4ABC △BC DAC B ∠=∠AD CD CE =ABD CAE △△∽9AB =6AC BD ==AE度.成果展示：下面是某小组进行交流展示时的部分测量方案及测量数据：测量工具标杆，皮尺测量方案选一名同学作为观测者，在观测者与树之间的地面直立一根标杆，使树的顶端、标杆的顶端与观测者的眼睛恰好在一条直线上.这时再测出观测者的脚到树底端的距离，以及观测者的脚到标杆底端的距离，然后测出标杆的高.测量示意图测量数据线段表示树，标杆，观测者的眼睛到地面的距离，观测者的脚到树底端的距离，观测者的脚到标杆底端的距离.……请同学们继续完善上述成果展示：任务一：根据测量数据，求出树的高度；任务二：写出求树的高度时所利用的数学知识________________________________________.（写出一个即可）21.（本题8分）阅读下列材料，并按要求完成相应的任务.两千多年前，古希腊数学家欧多克索斯（Eudoxus ，约前400-前347）发现：如图1，将一条线段分割成长、短两条线段，，若较短线段与较长线段的比等于较长线段与原线段的比，即（此时线段叫做线段，的比例中项）比值为黄金比，P 为线段的黄金分割点. 图1采用如下方法可以得到黄金分割点：如图2，设是已知线段，经过点B 作，且，连接，在上截取，在上截取，则C 就是线段的黄金分割点.任务：AB 3.2m EF = 1.7m CD =14m DB =2m DF =AB AB AP BP BP AP AP AB =AP BP AB AB AB BD AB ⊥12BD AB =AD AD DE DB =AB AC AE =AB图2（1）求证：C 是线段的黄金分割点.（2）若，则的长为________.22.（本题12分）综合与实践（1）如图①，在中，，，点D 在边上，点E 在边上.若，求证：.图①（2）如图②，在矩形中，，，点E 在边上，连接，过点E 作，交于点F .图②i ）若，求的长；ii ）若点F 恰好与点D 重合，求的长.23.（本题12分）综合与探究如图1，在矩形中，，，点E 是对角线上任意一点，交于点G ，交于点F .（1）当点E 为的中点时，________. 图1（2）如图2，将四边形绕点B 逆时针旋转，连结，.在旋转过程中，是否发生变化，若不变化，求出的值，若发生变化，请说明理由.AB 1BD =BC Rt ABC △90ACB ∠=︒AC BC =AB BC 45CDE ∠=︒ACD BDE △∽△ABCD 4cm AB =10cm BC =BC AE EF AE ⊥CD :1:9BE EC =CF BE ABCD 6cm AB =4cm AD =BD EG CD ∥BC EF AD ∥AB BD DE CG=BFEG CG DE DE CG DE CG图2（3）如图3，将四边形绕点B 逆时针旋转，连结，.请直接写出旋转过程中的值. 图3BFEG AF DE DE AF九年级数学答案一、1、C2、A3、D4、B5、C6、B7、B8、A9、D10、D二、11、412、13、20%1415、三、16、解：（1（2），，，，，.17、（1）如图，即为所求（2）如图，点D 即为所求（3）如图，即为所求18、（1）设种植一亩玉米的成本需要x 元，154372211111)(2)(21)21444---+-=--+=-+-+=-2315210211x x x x +--=+238110x x --=14∆==81423x ±=⨯1113x =21x =-11A B C △BEF △依题意得：，解得.答：种植一亩玉米的成本最高需要500元.（2）设该农场计划种植y 亩玉米，则每亩的成本为依题意得：，整理得：，解得：，（不合题意，舍去）。

江苏省盐城市盐城经济技术开发区2024-2025学年九年级上学期11月期中考试数学试题(含答案)

2024年秋学期九年级数学期中考试试卷一、选择题（每题3分，计24分）1. 下列方程是一元二次方程的是（）A. 3x 2－6x ＋2B. ax 2－bx ＋c ＝0C.D. x 2＝02. 用配方法解方程，配方正确是（）A. B. C. D. 3. 如图，已知四边形是的内接四边形，且，那么等于（）A B. C. D. 4. 一个等腰三角形的两条边长分别是方程x 2﹣9x +18＝0的两根，则该等腰三角形的周长是（）A. 12B. 9C. 15D. 12或155．如图，小球从口往下落，在每个交叉口都有向左或向右两种可能，且可能性相同，则小球最终从口落出的概率为（）A. B. C. D.6．电影（长津湖》讲述了一段波澜壮阔的历史，一上映就获得全国人民的追捧，某地第一天票房约亿元，三天后票房收入累计达亿元，若把增长率记作（）A ．；B ．；C ．；D ．7．如图，是的直径，圆上的点D 与点C ，E 分布在直线的两侧，，则（）的.212x x +=2240x x --=()213x -=()214x -=()215x -=()213x +=ABCD O e 120ABC ∠=︒AOC ∠125︒120︒110︒100︒A G 18161412310x ()3110x +=()23110x +=()233110x ++=()()23313110x x ++++=AB O e 50BCD ∠=︒AED =∠A ．B ．C ．D ．8．图1是一个地铁站入口的双翼闸机．如图2，它的双翼展开时，双翼边缘的端点与之间的距离为，双翼的弧与弧的长都为，且与闸机侧立面夹角．当双翼收起时，可以通过闸机的物体的最大宽度为（）A ．B ．C ．D ．二、填空题（每题3分，计30分）9．一组数据19，15，10，x ，4，它的中位数是13，则这组数据的平均数是．10．已知一元二次方程的其中一个根为，则的值为．11．关于的一元二次方程有两个实数根，那么的取值范围是．12．已知，如图，是的弦，，点在弦上，连结并延长交于点，，则的度数是．14．设m 、n 为关于x 的方程x 2+4x ﹣2023＝0的两个实数根，则m 2+5m +n ＝．60︒50︒45︒40︒A B 10cm AP BQ 12π30PCA BDQ ︒∠=∠=72cm 10cm 10cm 82cm 250ax bx +-=2x =1632a b +-x ()22114x m x m +-=-m AB AD O e 30B ∠=︒C AB CO O e D 35D ∠=︒BAD ∠15．某天的体育课上，老师测量了班级同学的身高，恰巧小明今日请假没来，经过计算得知，除了小明外，该班其他同学身高的平均数为170cm ，方差为acm 2．第二天，小明来到学校，老师帮他补测了身高，发现他的身高也是170cm ，此时全班同学身高的方差为bcm 2，那么a 与b 的大小关系是a b ．（填“＜”，“＞”或“＝”）D=_______°．18．如图，在矩形ABCD 中，AB=3，⊙O 与边BC ，CD 相切，现有一条过点B 的直线与⊙O 相切于点E ，连接BE ，△ABE 恰为等边三角形，则⊙O 的半径为.第17题第18题三、解答题（共9题，计96分）19．解方程：（1）；（2）；20．“秋风响，蟹脚痒”，正是食蟹好时节．某蟹农在今年五月中旬向自家蟹塘投放蟹苗1200只，为赶在食蟹旺季前上市销售，该蟹农于九月中旬在蟹塘中随机试捕了4次，获得如下数据：（1）、四次试捕中平均每只蟹的质量为____________；（2）、若蟹苗的成活率为，试估计蟹塘中蟹的总质量为_______；（3）、若第3次试捕的蟹的质量（单位：g ）分别为：166，170，172，a ，169，167．①____________；②求第3次试捕所得蟹的质量数据的方差．21．唐代李皋发明了“桨轮船”，这种船是原始形态的轮船，是近代明轮航行模式之先导．如图，某桨轮船数量/只平均每只蟹的质量/g 第1次试捕4166第2次试捕4167第3次试捕6168第4次试捕6170()24190x --=2250x x --=g 75%kg =a的轮子被水面截得的弦AB 长8m ，设圆心为O ，OC ⊥AB 交水面AB 于点D ，轮子的吃水深度CD 为2m ，求该桨轮船的轮子直径．22．已知，内接于，为的直径，点为优弧的中点．(1)如图1，连接，求证：；(2)如图2，过点作，垂足为．若，求的半径．23．已知关于的一元二次方程．求证：无论取何值，方程总有两个不相等的实数根．ABC V O e AC O e D BC OD DO BC ⊥D DE AC ⊥E 38AE BC ==,O e x 22(3)10x m x m ++-+=m（2）已知关于 x 的方程﹣（m ﹣1）x ﹣m ＝0（m 是常数）是“邻根方程”，求 m 的值；（3）若关于 x 的方程 a +bx+1＝0（a 、b 是常数，a ＞0）是“邻根方程”，令 t ＝8a-，试求 t 的最大值．25．小明大学毕业后和同学创业，合伙开了一家网店，暑期销售原创设计的手绘图案T 恤衫．已知每件T 恤衫的成本价为60元，当销售价为100元时，每天能售出20件；经过一段时间销售发现，当销售价每降低1元时，每天就能多售出2件．(1)若降价8元，则每天销售T 恤衫的利润为多少元？(2)小明希望每天获得的利润达到1050元并且优惠最大，则每件T 恤衫的销售价应该定为多少？26.如图，是直角三角形的外接圆，直径，过C 点作的切线，与延长线交于点D ，M 为的中点，连接，，且与相交于点N ．(1)求证：与相切；(2)当时，在的圆上取点F ，使，补全图形，并求点F 到直线的距离．27．（1）如图1，四边形ABCD 为⊙O 的内接四边形，AC 为⊙O 的直径，则∠B =∠D = 度，∠BAD +∠BCD = 度．（2）如果⊙O 的内接四边形ABCD 的对角线AC 不是⊙O 的直径，如图2，求证：圆内接四边形的对角互补．知识运用（3）如图3，等腰三角形ABC 的腰AB 是⊙O 的直径，底边和另一条腰分别与⊙O 交于点 D ，E ，F 是线段CE 的中点，连接DF ，求证：DF 是⊙O 的切线．2x 2x 2b O e ABC 4AC =O e AB CD BM OM BC OM BM O e 60A ∠=︒O e 15ABF ∠=︒AB参考答案1-4DCBC 5-8CDDD9.12.2 10.7 11.12. 13.86 14.2019 15.>16.b>-3 17．3018．19.（1），（2），20.（1）168（2）（3）①164 ②721.解：设半径为rm，则OA ＝OC ＝rm ，∴OD ＝（r ﹣2）m ．∵AB ＝8m ，OC ⊥AB ，∴AD ＝4m ．在Rt △ODA 中有OA 2＝OD 2+AD 2，即r 2＝（r ﹣2）2+4，解得r ＝5m则该桨轮船的轮子直径为10m ．22.（1）（1）证明：如下图，延长交于，∵点为优弧的中点，∴，12m ≤65︒112x =-252x =11x =21x =151200DO BC F D BC »»BD CD =∴，即；（2）23.证明：一元二次方程中，a =2，，，，一元二次方程总有两个不相等的实数根．24.（1）不是邻根方程；是邻根方程（2）或（3）25.（1）解：由题意得，每天销售T 恤衫的利润为：（元）．答：降价8元，则每天销售T 恤衫的利润为1152元．（2）解：设此时每件T 恤衫降价x 元，由题意得，，整理得，解得或．又∵优惠最大，∴．∴此时售价为（元）．答：小明希望每天获得的利润达到1050元并且优惠最大，则每件T 恤衫的销售价应该定为75元．26.（1）根据题意可得，根据直径所对的圆周角是直角，得出，进而得出，证明，得出，即可得证；(2)DF BC ⊥DO BC ⊥256()22310x m x m ++-+=3b m =+1c m =-+24b ac∴∆=-()()23421m m =+-⨯⨯-+26988m m m=+++-2217m m =-+()22116m m =-++()21160m =-+>∴()22310x m x m ++-+=260x x --=2210x -=0m =2m =-4t =最大值()()10086020281152--⨯+⨯=()()100602021050x x --+=2301250x x -+=5x =25x =25x =1002575-=OM AD ∥90ABC ∠=︒OM BC ⊥OBM OCM V V ≌90OBM ∠=︒21-27.（1）∵四边形ABCD为⊙O的内接四边形，AC为⊙O的直径，∴∠B=∠D=90度，∵∠BAD+∠BCD+∠B+∠D=360°∴∠BAD+∠BCD=360°−∠B−∠D=180°故答案为：90，180(2)证明：如图，连接AO并延长，交⊙O于点E，连接BE，DE.由(1)可知，∠ABE=90°，∠ADE=90°，∴∠ABE+∠ADE=180°∴∠BAD+∠BED=180°∵∠BED=∠C，∠CDE=∠CBE∴∠BAD+∠C=180°，∠ABC+∠ADC=180°即圆内接四边形的对角互补（3）证明:连接OD，DE，如图所示.∵OB=OD，∴∠B=∠ODB∵AB=AC，∴∠B=∠C∴∠ODB=∠C∴OD∥AC∵四边形ABDE是圆内接四边形，∴∠B+∠AED=180°∵∠DEC+∠AED=180°，∴∠B=∠DEC∴∠C=∠DEC∴DC=DE∵F是线段CE的中点，∴DF⊥AC∴DF⊥OD∵OD是⊙O的半径，∴DF是⊙O的切线。

北京市海淀区北京大学附属中学2024-2025学年九年级上学期期中考试数学试卷(含答案)

2024～2025学年度第一学期期中练习九年级数学学科试卷2024年11月考生须知：1．本试卷共8页，共三道大题，28道小题．满分100分．考试时间120分钟．2．在试卷和答题卡上准确填写班级、姓名．3．答案一律填涂或书写在答题卡相应位置上，用黑色字迹签字笔作答．4．考试结束，只交答题卡，并妥善保管试卷．一、选择题（共16分，每题2分）第1～8题均有四个选项，符合题意的选项只有一个．1．下列图形中，既是中心对称图形也是轴对称图形的是（）．A ．B ．C ．D ．2．在平面直角坐标系内，点关于原点的对称点Q 的坐标为（）．A ．B ．C ．D ．3．一元二次方程的解是（）．A ．，B ．C ．，D ．，4．抛物线的顶点坐标是（）．A ．B ．C ．D ．5．如图是一个标准的五角星，若将它绕旋转中心旋转一定角度后能与自身重合，则至少应将它旋转的度数是（）．A ．B ．C ．D ．6．北京市2021年人均可支配收入为7.5万元，2023年达到8.18万元，若2021年至2023年间每年人均可支配收入的增长率都为x ，则下面所列方程正确的是（）．A ．B．()3,2P -()3,2-()3,2()2,3-()3,2--20x x +=10x =21x =121x x ==11x =-21x =10x =21x =-()212y x =-+()1,2()1,2-()1,2-()1,2--144︒90︒72︒60︒()28.1817.5x +=()27.518.18x +=C ．D ．7．如图所示，在4×4的正方形网格中，绕某点旋转一定的角度，得到，则其旋转中心是（）．A ．点AB ．点BC ．点CD ．点D8．如图，是边长为4的等边三角形，D 是BC 的中点，E 是直线上的一个动点，连接，将线段绕点C 逆时针旋转得到，连接．下列说法中正确的个数是（）．①；②；③；④点E 的运动过程中，的最小值是1．A ．1个B ．2个C ．3个D ．4个二、填空题（共16分，每题2分）9．请写出一个图象开口向上，且与y 轴交于点）的二次函数的解析式__________．10．关于x 的一元二次方程有一个根是，则__________．11．若关于x 的方程有两个相等的实数根，则实数a 的值是__________．12．如图，为的直径，点C 是上的一点，，则__________°．13．点，在抛物线上，则__________（填“＞”“＜”或“＝”）．14．如图，在平面直角坐标系中，点，，以点B 为旋转中心，把线段顺时针旋转得到线段，则点C 的坐标为__________．()27.518.18x -=+()28.1817.5x -=MNP △111M N P △ABC △AD EC EC 60︒FC DF 2DC =FCD ECA ∠=∠CE CF =DF ()0,1230x x m -+=1x =m =20x x a -+=AB O e O e 70ABC ∠=︒BAC ∠=()13,A y -()22,B y 22y x =1y 2y xOy ()0,2A ()1,0B BA 90︒BC15．如图，将绕顶点C 逆时针旋转得到，且点B 刚好落在上，若，，则等于__________°．16．已知函数，下列结论：①若该函数图象与x 轴只有一个交点，则；②方程至少有一个整数根；③若，则的函数值都是负数；④不存在实数a ，使得对任意实数x 都成立．所有正确结论的序号是__________．三、解答题（共68分，第17题8分，18～25题每题5分，第26题6分，第27、28题每题7分）解答应写出文字说明、演算步骤或证明过程．17．解方程：（1）；（2）．18．如图，在平面直角坐标系中，抛物线的部分图象经过点，．（1）求该抛物线的解析式；（2）结合函数图象，直接写出时，x 的取值范围．19．已知m 是方程的一个根，求代数式的值．20．已知：如图，为锐角三角形，．求作：一点P ，使得．ABC △A B C ''△A B ''25A ∠=︒45BCA =∠'︒A BA '∠()211y ax a x =-++1a =()2110ax a x -++=11x a<<()211y ax a x =-++()2110ax a x -++≤24250x -=2280x x +-=xOy 22y ax x c =++()0,3A -()1,0B 0y <2220x x --=()()()22111m m m -+-+ABC △AB AC =APC BAC ∠=∠作法：①以点A 为圆心，长为半径画圆；②以点B 为圆心，长为半径画弧，交于点C ，D 两点；③连接并延长交于点P ．点P 即为所求．（1）使用直尺和圆规，依作法补全图形（保留作图痕迹）；（2）完成下面的证明：证明：连接，．∵，∴点C 在上．∵，∴∠______＝∠______．∴．∵点D ，P 在上，∴．（__________）（填推理的依据）∴．21．如图，是等边三角形，点D 在边上，以为边作等边，连接，．求证：．22．已知关于x 的一元二次方程．（1）求证：方程总有两个实数根；（2）若方程两个根差为1，求此时m 的值．23．学校计划利用一片空地建一个长方形自行车车棚，其中一面靠墙，墙的长度为8米．在与墙平行的一面开一个2米宽的门，已知现有的木板材料可修建的总长为26米，且全部用于除墙外其余三面外墙的修建．（1）长方形车棚与墙垂直的一面至少为__________米；（2）如图，为了方便学生取车，施工单位决定在车棚内修建几条等宽的小路（如图中阴影），若车棚与墙AB BC A e DA A e PC BD AB AC =A e BC BD =12BAC CAD ∠=∠A e 12CPD CAD ∠=∠APC BAC ∠=∠ABC △AC CD CDE △BD AE BD AE =()2320m x x m -+++=垂直的一面长按（1）中的最小长度，则停放电动车的区域面积能否达到54平方米，若能，此时小路的宽度是多少米？若不能，请说明理由．24．如图，是直径，是的一条弦，且于点E ，连接、和．（1）求证：；（2）若，，求的半径．25．有机肥作为一种富含有机质及多样营养元素的优质肥料，对于土壤改良及肥力提升具有显著效果．将其应用于小树施肥，不仅能有效供给必要的养分，还能优化土壤结构，进而促进小树的茁壮成长．在针对金叶女贞和连翘这两种植物的培育过程中，我们统一施用了A 种有机肥，并确保了它们在浇水、松土、除草等抚育管理措施上的一致性．以下表格详细记录了A 种有机肥对这两种植物增长高度的影响：天数t /天1530456090金叶女贞增长的高度 3.3 6.39.612.615.919.3连翘增长的高度 1.14.09.115.636.2（1）通过分析数据，发现与t 之间近似满足正比例函数关系．请在给出的平面直角坐标系中，画出关于t 的函数的图象；（2）观察图象，补全表格（结果保留小数点后一位）；（3）实验前，测量金叶女贞的高度为，连翘的高度为，大概在第__________天时，连翘和金叶女贞一样高（结果保留到整数）．26．已知关于x 的二次函数上两个不同的点，．（1）求顶点坐标；（2）若且时，总有，求m 的取值范围．27．已知，点D 是直线上一动点（不含B 点），连接，将线段绕点A 逆时针旋转得到线段，连接线段，过点E 作交直线于点F ．AB O e CD O e CD AB ⊥AC BD OC ACO D ∠=∠2BE =CD =O e 1cm h 2cmh 1h 2h 43.6cm 31.2cm 221y mx mx m =-+-()11,A x y ()22,B x y 145x <<221x m =-12y y <60ABC ∠=︒BC AD AD 60︒AE ED EF AB ⊥AB图1备用图（1）如图1，点D 在点B 右侧时，①依题意补全图形；②用等式表示与的数量关系，并证明；③用等式表示线段，，之间的数量关系，并证明；（2）当点D 在直线上运动时，请直接写出线段，，之间的数量关系．28．在平面直角坐标系中，点，点为定点，对于点P 作如下变换，将点P 绕点M 逆时针旋转得到点，再将点绕点N 逆时针旋转后得到点Q ，则称点Q 为点P 的“双逆转点”．备用图1 备用图2（1）若点P 为线段上的一点，则在点，，中，点P 的“双逆转点”可能为__________；（2）若点P 的“双逆转点”在x 轴上，请写出一个满足条件的点P 的坐标__________；（3）若点P 坐标为，点Q 为点P 的“双逆转点”，①当长度最短时，求m 的值；②已知半径为2，若存在过点Q 的直线被所截得的弦长为2，则m 的取值范围为__________．EAB ∠EDB ∠BF BD AB BC BF BD AB xOy ()0,2M ()1,0N 90︒1P 1P 90︒MN ()1,1A --()1,0B -()2,1C -(),4m m +PQ N e N e初三第一学期期中练习答案和评分标准数学2024.11一、选择题（本题共6分，每小题2分）题号12345678答案CADACBBD二、填空题（本题共16分，每小题2分）9．（答案不唯一） 10．2 11．12．2013．＞14．15．40 16．②④（答对一个给1分，多选或错选不得分）三、解答题（共68分，第17题8分，18～25题每题5分，第26题6分，第27、28题每题7分）17．（1）（一个答案2分，如果只会移项给1分）（2），，．（不限方法，不全对的酌情给分）18．（1）由题意知，（2分）解得，解析式为．（3分）（2）．（5分）19．解．原式．（3分）∵，∴，（4分）∴原式．（5分）20．（1）如图所示．（2分）（2），，一条弧所对的圆周角等于它所对圆心角的一半．（5分）21．证明：∵，均为等边三角形，∴，，．21y x =+14()3,152x =±2280x x +-=14x =-22x =3230c a =-⎧⎨+-=⎩31c a =-⎧⎨=⎩223y x x =+-31x -<<()()222212123m m m m m =--++=--2220m m --=222m m -=231=-=-BAC BAD ABC △CDE △AC BC =CD CE =60ACB ACE ∠=∠=︒在与中，，∴≌（SAS ），（4分）∴．（5分）22．（1）∵，∴方程总有两个实数根．（2分）（2）解：∵，∴，∴，．∵方程两个根的差为1，∴或0．∴或．（5分）23．解：（1）．（2分）（2）设小路的宽为a 米，根据题意得，．（4分）整理得；，解得：（舍去），．（5分）答：小路的宽为1米．24．（1）证明；∵，∴，∵，∴．（2分）（2）解，设的半轻为r ，则．∵，∴（3分）在中，，解得．（ 5分）25．（1）（2分）（2）23～30之间均可．（4分）（3）78～86之间均可．（5分）26．（1）由题意可知：，∵，∴顶点坐标为．（2分）BCD △ACE △60AC BC ACB ACE CD CE =⎧⎪∠=∠=︒⎨⎪=⎩BCD △ACE △BD AE =()()()234210m m m ∆=+-+=+≥()2320x m x m -+++=()()210x m x ---=12x m =+21x =22m +=0m =2-10x ≥()()821054a a --=214130a a -+=13a =1a =OA OC =ACO A ∠=∠A D ∠=∠ACO D ∠=∠O e 2OE r =-CD AB ⊥1122CE DE CD ===⨯=Rt OCE △(()2222r r +-=3r =0m ≠()()2222121111y mx mx m m x x m x =-+-=-+-=--()1,1-法2：对称轴，当时，，∴顶点坐标为．（2分）（2）当时，对称轴是直线，当时，y 随x 的增大而增大；当时，y 随x 的增大而减小．∵，∴点始终在对称轴右侧，若A 、B 在对称轴右侧，，即时，∵，∴，∴，若A 、B 在对称轴异侧，，即时，关于对称轴的对称点是．∵，∴，即，∴（舍）．综上所述：．（4分）当时，对称轴是直线，当时，y 随x 的增大而减小；当时，y 随x 的增大而增大．∵，，∴，，关于对称轴的对称点是．∵，∴，即，2122b m x a m-=-=-=1x =211y m m m =-+-=-()1,1-0m >1x =1x ≥1x <145x <<()11,A x y 2211x m =->1m >12y y <215m -≥3m ≥2211x m =-<1m <()22,B x y ()222,B x y '-12y y <225x -≥()2215m --≥1m ≤-3m ≥0m <1x =1x ≥1x <221x m =-145x <<2211x m =-<1145x <<<()22,B x y ()222,B x y '-12y y <224x -≤()2214m --≤∴，∴．（6分）综上所述：或．27．（1）①补全图形，如图所示（1分）②，（2分）理由如下：∵线段绕点A 逆时针旋转得到线段，∴，，∴是等边三角形，∴．∵，∴．∵在四边形中，，∴，∴．（3分）③，理由如下：（4分）延长线段至点G 使得，连结，．∵，，∴．∵是等边三角形，∴．在和中，，∴≌（SAS ），（5分），∴．∵，∴．∵，，，∴．（6分）（2）当点D 在点B 右侧时，，当点D 在点B 左侧时，．（7分）12m ≥-102m -≤<102m -≤<3m ≥180EAB BDE ∠+∠=︒AD 60︒AE AE AD =60EAD ∠=︒AED △60AED ∠=︒60ABC ∠=︒180120ABD ABC ∠=︒-∠=︒ABDE 360EAB ABD BDE DEA ∠+∠+∠+∠=︒12060360EAB BDE ∠+︒+∠+︒=︒180EAB BDE ∠+∠=︒2BF AB BD =+BA AG BD =EG EB 180EAG EAB ∠+∠=︒180EAB EDB ∠+∠=︒EAG EDB ∠=∠AED △EA ED =EGA △EBD △EA EDEAG EDB GA BD =⎧⎪∠=∠⎨⎪=⎩EGA △EBD △EG EB =EF BF ⊥GF FB =BG BA GA =+GA BD =2BG BF =2BF BA BD =+2BF AB BD =+2BF AB BD =-28．（1）A ，C ．（2分）（2）答案不唯一，纵坐标为1即可．（3分）（3）①（5分）②或（7分）2m =-m≥m ≤。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

中考期中考试试卷数学科(内容：21章-23章)题号一二三四五总分 19 20 21 22 23 24 得分说明：１、考试时间：100分钟；２、全卷满分：150分。

一、选择题（本大题共8小题，每小题４分，共32分） 1. 下列各式中，是最简二次根式的是( ) A ．18 B ．b a 2 C ．22b a + D ．32 2. 下列方程有两个不相等实数根的是（）A ．012=--x xB ． 022=+xC ．012=+-x xD ．0122=+-x x3. 下列图形中，是中心对称图形，但不是轴对称图形的是 ( )A. 正方形B. 矩形C. 菱形D. 平行四边形 4. 若代数式6432+-x x 的值为9，则6342+-x x 的值为( ) A ．7 B ．18C ．12D ．95. 如果点P (3-m ,1-2m )关于原点O 的对称点P 1在第二象限，那么当m 取偶数时，点P 关于x 轴对称的点P 2的坐标为（）A ．(1,-3)B ．(1,3)C ．(2,-1)D ．(2,1) 6．已知（x －1）2＋2y +=0，则（x ＋y ）2的算术平方根是（）A ．1B ．±1 C．－1 D ．07．如图，将△ABC 绕着点C 按顺时针方向旋转20°，B 点落在B '位置，A 落在A '位置，若B A AC ''⊥，则BAC ∠的度数是（） A ．50° B ．60° C ．70° D ．80° 8. 把mm 1-根号外的因式移到根号内，得（） A ．m B ．m - C ．m -- D ．m -学校：班级：姓名：座号D EC AB二、填空题（每题4分，共２０分）（请将正确答案填在每题后面的横线上） 9、函数32-+=x x y 中自变量x 的取值范围是。

10、在实数范围内因式分解：44_____________________x -=。

11、在直角坐标平面内，点M （-4，0）绕原点O 逆时针旋转1200后得到的点的坐标是。

12、若3的整数部分是a ，小数部分是b ，则=-b a 3 。

13、如图，在△ABC 中，AC=BC=2，∠ACB=90°，D 是BC 边的中点，E 是AB 边上一动点，则EC+ED 的最小值是。

三、解答下列各题（每小题7分，共35分） 14. 计算：0)15(282218-+--15. 解方程: 3（x-2）+x 2-2x=016. 某商场今年2月份的营业额为300万元，3月份的营业额比二月份增加了10％，5月份的营业额达到475.2万元，求３月份到５月份营业额的平均月增长率。

17.已知：x ＋y=5,xy=1,求x y18. 如图，方格纸中的每个小方格都是边长为1个单位的正方形，在建立平面直角坐标系后，△ABC 的顶点均在格点上，点B 的坐标为．（1）画出△ABC 关于x 轴对称的△A 1B 1C 1；（2）画出将△ABC 绕原点O 按逆时针方向旋转所得的△A 2B 2C 2。

(1,0)90四、解答下列各题(每小题9分，共27分)19.某商厦服装柜在销售中发现:“乐乐”牌童装平均每天可售出20件，每件盈利40元，为了迎接“六·一”国际儿童节，商场决定采取适当的降价措施，扩大销售量，增加盈利，减少库存。

经市场调查发现：如果每件童装每降价4元，那么平均每天就可多售出8件，要想平均每天在销售这种童装上盈利1200元，那么每件童装应降价多少元？20. 已知关于x的k x2+2x－1=0有实数根。

（1）求k的取值范围;（2）当k＝1时，请用配方法解此方程。

21．观察下图所包含规律（图中三角形均是直角三角形，且一条直角边始终为1，四边形均为正方形。

S 1，S 2，S 3，……S n 依次表示正方形的面积，每个正方形边长与它左边相邻的直角三角形斜边相等），再回答下列问题。

（1）填表：直角边 A 1B 1 A 2B 2 A 3B 3 A 4B 4 … A n B n 长度1…（2）当s 1＋s 2＋s 3＋s 4＋……＋s n ＝495时，求n 。

……A 1 A 2A 3A 4S 1 S 2 S 3 S 4 B 1 C 1B 2 B 3 B 4C 2 C 3 C 4 1 11 1 1 学校：班级：姓名：座号：五、解答下列各题(每小题12分，共36分)22．已知，如图在△ABC中，AB=AC，若将△ABC绕点C顺时针旋转180°得到△FEC。

（1）试猜想AE与BF有何关系？说明理由；（2）若△ABC的面积为3cm2，求四边形ABFE的面积；（3）当∠ACB为多少度时，四边形ABFE为矩形？说明理由。

F EC BA23. 将一条长为20cm 的铁丝剪成两段，并以每一段铁丝的长度为周长做成一个正方形。

(1)要使这两个正方形的面积之和等于172cm ，那么这段铁丝剪成两段后的长度分别是多少？（6分）(2)两个正方形的面积之和可能等于102cm 吗？若可能，求出两段铁丝的长度，若不可能，请说明理由。

（6分）24.如图，在等腰直角三角形ABC 中，O 是斜边AC 的中点，P 是斜边AC 上的一个动点，D 为BC 上的一点，且PE=BO ，DE AC ,垂足为点E . (1)求证： PB=PD;(2)设AC=8，AP=x ，四边形PBDE 的面积为y ，求y 与x 之间的函数关系式，并写出自变量的取值范围。

OPAEDB参考答案一、选择题：1、C ；2、A ； 3、D ； 4、A ；5、B;6、A;7、C ；8. C. 二、填空题：9、x ≥-2且x ≠3; 10. )2)(2)(2(2-++x x x ; 11、)32,2(-; 12、1; 13、5. 三、解答下列各题：14．解：原式=23-2-2+1 =2+115．解：)2(3-x +)2(-x x =0 0)3)(2(=+-x x0)3(0)2(=+=-x x 或 ∴3221-==x x ， 16．解：设３月份到５月份营业额的平均月增长率x,依题意得300（1+10％2.475)1)(2=+x解得不合题意舍去）(2.2,2.021-==x x 答：３月份到５月份营业额的平均月增长率为20％.17．解：∵x ＋y=5＞0, xy=1＞0 ∴x 与y 必同号，即x ＞0, y ＞0∴原式=xy y x xy y xy x )(+=+=5×51=18．解：（1）如图所示；（2）如图所示。

19．解：设每件童装应降价x 元,依题意得 (40-x)(20+2x)=1200 整理,得x 2-30x+200=0,解得x 1=10 x 2=20因要尽量减少库存,故x 应取20。

答:每件童装应降价20元。

20．解：（1）① 当k ≠0时，∵一元二次方程有实数根， ∴b 2-4ac ≥0 即：4+4k ≥0 解得，k ≥-1又∵k ≠0，∴k ≥-1且k ≠0②当k=0时，方程可化为：2x －1=0，有一个实根。

综合上述可得，k 的取值范围为k ≥-1。

（2）当k ＝1时，方程可化为x 2+2x=1 移项，得 x 2+x=1配方x 2+2x+1=-1+1 (x+1)2=2由此可得 x+1＝±2 ∴ x 1=12-, x 2=－12- 21. 解：（1）填表：（2）∵s 1=,2)2(2= s 2=4)4(,3)3(232===s …1)1(,)(221+=+===-n n s n n s n n∴当s 1＋s 2＋s 3＋s 4＋……＋s n ＝495时，2+3+4+…+n+n+1=495整理得4962)1(=++n n n解得不合题意舍去）(33,3021-==n n∴n=30.22.解：（1）AE=BF理由如下：∵△ABC 绕点C 顺时针旋转180°得到△FEC 。

∴△AB C ≌△FEC ∴ AC=FC,BC=EC∴四边形ABFE 是平行四边形 ∴AE=BF（2）由（1）知: BC=EC,△ABC 与△ACE 等底同高 ∴△ACE 的面积为3 cm 2 ∴四边形ABFE 的面积为4×3=12 cm 2（3）当∠ACB=60°时，四边形ABFE 为矩形. 理由如下：∵∠ACB=60°，AB=AC∴△ABC 为等边三角形，∠ABC=60° ∴AC= BC又AC=FC ∴BC= FC ∴∠CB F=∠C F B=21∠ACB=30° ∴∠AB F=∠CB F+∠ABC=30°+60°=90°由（1）知：四边形ABFE 是平行四边形 ∴四边形ABFE 为矩形.当∠ACB=60°时，四边形ABFE 为矩形23. 解：（1）设这段铁丝剪成一段铁丝的长度是xcm ，则另每一段铁丝的长度为（20-x ）cm,依题意得17)420()4(22=-+x x 整理得064202=+-x x解得x 1=4，x 2=16当x 1=4时，20-x=16；当x 2=16时，20-x=4。

答：这段铁丝剪成两段后的长度分别是4cm ，16cm 。

（2）设这段铁丝剪成一段铁丝的长度是ycm ，则另每一段铁丝的长度为（20-y ）cm,依题意得 10)420()4(22=-+y y 整理得0120202=+-y y∵120142)20(42⨯⨯--=-ac b=400-480＜0∴该方程没有实数解。

∴不可能剪成两个正方形的面积之和等于102cm 。

24.解：证明：（1）∵点O 是等腰直角△ABC 斜边AC 的中点∴BO=OC=21AC, B O ⊥AC ∴∠C=∠OBC=45°∵DE AC ⊥ ∴∠BOP=∠PED=90°∵PE=BO,PE=PO+OE,OC=OE+EC∴PO=EC在Rt △DEC 中，DE=EC∴PO=DE∴△PBO ≌△DPE∴PB=PD解：(2) ∵AC=8,AP= x ∴AO=BO=PE=4 DE=PO=EC=4- x, EO= x∴四边形PBDE 的面积y=BDEO PBO s s 梯形三角形+ =x x x )8(21)4(421-+-⨯=82212++-x x 自变量x 的取值范围是0＜x ＜4.。