23.2相似三角形判定__直角三角形相似判定定理
三角形相似的5个判定方法
三角形相似的5个判定方法
相似三角形是指具有相同形状但大小不同的三角形。
下面是五个判定方法来判断三角形是否相似：
1. AAA判定法，如果两个三角形的对应角度相等，那么它们是相似的。
这意味着如果两个三角形的三个角分别相等，那么它们是相似的。
2. AA判定法，如果两个三角形的一个角相等，并且它们的对应边成比例，那么它们是相似的。
这意味着如果两个三角形的两个角分别相等，并且它们的对应边成比例，那么它们是相似的。
3. SSS判定法，如果两个三角形的对应边成比例，那么它们是相似的。
这意味着如果两个三角形的三条边分别成比例，那么它们是相似的。
4. SAS判定法，如果两个三角形的一个角相等，并且它们的两个对应边分别成比例，那么它们是相似的。
这意味着如果两个三角形的一个角相等，并且它们的两个对应边分别成比例，那么它们是相似的。
5. 直角三角形的判定法，如果一个三角形是直角三角形，且两个直角三角形的一个角相等，那么它们是相似的。
这意味着如果一个三角形是直角三角形，且两个直角三角形的一个角相等，那么它们是相似的。
这些判定方法可以帮助我们确定三角形是否相似，从而在几何学中应用相似三角形的性质。
通过这些方法，我们可以更好地理解和解决与相似三角形相关的问题。
直角三角形相似判定定理
直角三角形相似判定定理
一、定义法
如果两个直角三角形的三条边对应成比例，那么这两个直角三角形相似。
二、定理法
1.勾股定理：在直角三角形中，勾股定理表述了直角三角形的两条直角边的
平方和等于斜边的平方。
如果两个直角三角形的斜边相等，那么这两个直角三角形相似。
2.毕达哥拉斯定理：在直角三角形中，毕达哥拉斯定理表述了直角三角形的
两条直角边的平方和等于斜边的平方。
如果两个直角三角形的两条直角边对应相等，那么这两个直角三角形相似。
三、斜边中线法
在直角三角形中，斜边上的中线等于斜边的一半。
如果两个直角三角形的斜边中线对应相等，那么这两个直角三角形相似。
四、两锐角对应相等
如果两个直角三角形的两个锐角对应相等，那么这两个直角三角形相似。
五、夹边中线法
在直角三角形中，夹边上的中线等于夹边的一半。
如果两个直角三角形的夹边中线对应相等，那么这两个直角三角形相似。
六、两边对应成比例且夹角相等
如果两个直角三角形的两边对应成比例且夹角相等，那么这两个直角三角形相似。
七、两边对应成比例且夹边平行
如果两个直角三角形的两边对应成比例且夹边平行，那么这两个直角三角形相似。
八、两锐角对应相等且夹边平行
如果两个直角三角形的两锐角对应相等且夹边平行，那么这两个直角三角形相似。
九、两角对应相等且夹边平行
如果两个直角三角形的两角对应相等且夹边平行，那么这两个直角三角形相似。
三角形相似的定义与判定方法
三角形相似的定义与判定方法三角形是几何学中研究的基本形状之一，它们的相似性是几何分析中一个重要的概念。
在本文中，我们将探讨三角形相似的定义与判定方法。
一、三角形相似的定义两个三角形被认为是相似的，如果它们的对应角度相等，并且对应边的比例相等。
换句话说，如果两个三角形的内角相等，并且三边的比值相等，那么它们就是相似的。
二、判定方法一：AA相似定理AA相似定理是判定两个三角形相似性的常用方法。
根据该定理，如果两个三角形的两个角分别相等，那么它们就是相似的。
三、判定方法二：SAS相似定理SAS相似定理是另一种常用的判定方法。
根据该定理，如果两个三角形之间存在一个对应的边长比例，并且这两个边的夹角相等，那么它们就是相似的。
四、判定方法三：SSS相似定理SSS相似定理是另一种用于判定三角形相似性的方法。
根据该定理，如果两个三角形的三条边长比例相等，那么它们就是相似的。
五、判定方法四：底角相等定理对于两个三角形的底边的边长比例相等，并且两个三角形的顶角都相等，那么它们就是相似的。
这条定理也可以用来判定三角形的相似性。
六、判定方法五：割线定理割线定理是基于圆的相关性质中的一个重要定理。
如果两个三角形的两边分别平行于另一个三角形的两边，并且这些边是由同一个圆的弦所连接的，那么这两个三角形是相似的。
七、应用举例通过上述相似定理和判定方法，我们可以解决许多与三角形相似性相关的问题。
例如，当两个三角形的两个内角相等时，我们可以利用AA相似定理判定它们的相似性。
同样地，当两个三角形的边长比例相等时，我们可以使用SAS相似定理来判定它们是否相似。
结论：在几何学中，相似性是一个非常基础且重要的概念。
通过扩展对三角形的定义与判定方法的了解，我们可以更好地理解和应用相似性的概念。
相似性在许多实际应用中发挥着关键的作用，包括图像处理、地理测量等领域。
因此，深入了解三角形相似的定义与判定方法对我们的学习和应用有着重要的意义。
通过以上讨论，我们希望读者能够对三角形相似的定义与判定方法有更清晰的认识，并且能够在实际问题中正确应用这些知识。
相似三角形的判定条件
相似三角形的判定条件相似三角形是指具有相同形状但可能不同大小的三角形。
判定两个三角形是否相似的条件包括三个方面：对应角相等、对应边成比例和三边对应比例相等。
1. 对应角相等两个三角形的对应角相等是判断其相似性最基本的条件之一。
如果两个三角形的三个内角分别相等，则它们是相似的。
具体地，设三角形ABC和三角形DEF，如果∠A=∠D、∠B=∠E、∠C=∠F，则可以判定三角形ABC相似于三角形DEF。
2. 对应边成比例相似三角形的另一个判定条件是对应边成比例。
在两个相似三角形中，对应边的比值要保持一致。
设三角形ABC和三角形DEF，如果AB/DE=BC/EF=AC/DF，则可以判定三角形ABC相似于三角形DEF。
3. 三边对应比例相等除了对应角相等和对应边成比例外，相似三角形还需要满足三边对应比例相等的条件。
具体地，设三角形ABC和三角形DEF，如果AB/DE=BC/EF=AC/DF，则可以判定三角形ABC相似于三角形DEF。
基于以上判定条件，我们可以利用相似三角形的特点进行问题求解和证明。
例如，当我们已知一些三角形的角度或边的比例时，可以利用相似三角形的判定条件来推导出其他相关的角度或边的比例关系，从而解决一些三角形的性质和应用问题。
需要注意的是，相似三角形的判定条件是充要条件，即满足此条件的三角形一定是相似的，但只满足部分条件并不能保证三角形之间的相似性。
因此，在应用相似三角形的定理时，我们需要确保已满足了所有的判定条件。
综上所述，相似三角形的判定条件是对应角相等、对应边成比例和三边对应比例相等。
通过判定这三个条件是否满足，我们可以准确地判断两个三角形是否相似，并可以利用相似三角形的性质进行问题求解和证明。
相似三角形及判定
相似三角形及判定在我们的数学世界中，相似三角形是一个非常重要的概念。
它不仅在数学理论中有着关键的地位，还在实际生活中的许多领域有着广泛的应用。
首先，咱们来弄清楚啥是相似三角形。
简单来说，相似三角形就是形状相同但大小不一定相同的三角形。
这就好比是同一个模子印出来的不同大小的图形。
两个三角形相似，它们对应的角相等，对应的边成比例。
那怎么判定两个三角形相似呢？这就有几个关键的方法。
第一种方法是“两角对应相等，两三角形相似”。
比如说，有两个三角形，其中一个三角形的两个角分别和另一个三角形的两个角相等，那这两个三角形就是相似的。
这就好比咱们拿着两把同样角度的扇子，不管大小，形状就是相似的。
第二种判定方法是“两边对应成比例且夹角相等，两三角形相似”。
想象一下，有两个三角形，其中两条边的比例一样，而且它们之间的夹角也相等，那这两个三角形就相似啦。
接下来是“三边对应成比例，两三角形相似”。
这个比较好理解，如果一个三角形的三条边和另一个三角形的三条边的比例都一样，那它们就是相似的。
就好像是用不同长度的三根棍子按照相同的比例搭成的两个架子。
为了更好地理解相似三角形的判定，咱们来看几个实际的例子。
比如说在建筑设计中，设计师要根据小模型来设计出实际的大楼。
小模型中的三角形结构和实际大楼中的某些三角形结构就是相似的。
通过对小模型中三角形的测量和计算，再运用相似三角形的判定和性质，就能准确地设计出大楼的尺寸和形状。
在地图绘制中也能看到相似三角形的身影。
地图上的一个区域和实际的那个区域可以看作是相似的。
通过测量地图上的距离，再利用相似三角形的知识，就能算出实际的距离。
相似三角形的判定在数学考试中也是经常出现的考点。
很多同学在做这类题的时候，可能会因为概念不清楚或者判定方法没掌握好而出错。
所以，一定要把这些判定方法理解透彻，多做一些练习题来巩固。
咱们再深入思考一下，相似三角形的知识其实和我们的生活是紧密相连的。
比如在摄影中，通过调整镜头的角度和焦距，可以拍出不同大小但形状相似的画面。
23.2.2 相似三角形的判定定理(2)
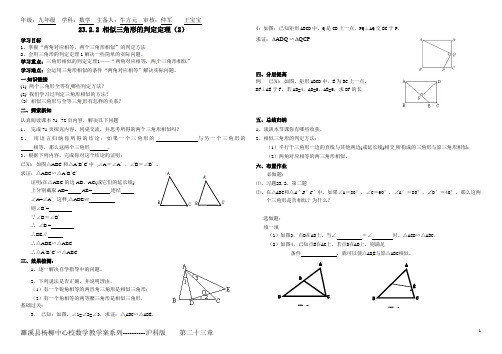
年级：九年级 学科：数学 主备人：牛方元 审核：仲军 王宝宝濉溪县杨柳中心校数学教学案系列----------沪科版 第二十三章123.2.2 相似三角形的判定定理（2）学习目标1、掌握“两角对应相等，两个三角形相似”的判定方法2、会用三角形的判定定理1解决一些简单的实际问题。
学习重点：三角形相似的判定定理1——“两角对应相等，两个三角形相似” 学习难点：会运用三角形相似的条件“两角对应相等”解决实际问题。
一.知识链接(1) 两个三角形全等有哪些判定方法？ (2) 我们学习过判定三角形相似的方法？(3) 相似三角形与全等三角形有怎样的关系？ 二、探索新知认真阅读课本71--72页内容，解决以下问题1、 完成71页探究内容，同桌交流，并思考所得的两个三角形相似吗？2、 用语言归纳你所得的结论：如果一个三角形的 与另一个三角形的相等，那么这两个三角形 。
3、根据下列内容，完成你对这个结论的证明：已知：如图△ABC 和△A`B`C`中 ,∠A ＝∠A` ，∠B ＝∠B` 。
求证：△ABC ∽△A`B`C`证明:在△ABC 的边AB 、AC(或它们的延长线) 上分别截取AD= ,AE= ,连结 . ∠A=∠A`, 这样,△ADE ≌ . 则∠B`= ∵∠B ＝∠B` ∴ ∠B = ∴DE ∥ ∴△ADE ∽△ABC ∴△A`B`C`∽△ABC 三、效果检测：1、逐一解决自学指导中的问题。
2、下列说法是否正确，并说明理由．（1）有一个锐角相等的两直角三角形是相似三角形； （2）有一个角相等的两等腰三角形是相似三角形． 基础过关：3、 已知：如图，∠1=∠2=∠3，求证：△ABC ∽△ADE ．4：如图：已知矩形ABCD 中，Q 是CD 上一点，PQ ⊥AQ 交BC 于P ， 求证：ADQ ∆∽QCP ∆四、分层提高例 已知：如图，矩形ABCD 中，E 为BC 上一点， DF ⊥AE 于F ，若AB=4，AD=5，AE=6，求DF 的长五、总结归纳1、谈谈本节课你有哪些收获．2、相似三角形的判定方法： （1）平行于三角形一边的直线与其他两边(或延长线)相交,所构成的三角形与原三角形相似; （2）两角对应相等的两三角形相似。
相似三角形与三角函数
初三数学---相似三角形和解直角三角形一、相似三角形1．相似三角形判定定理：（1）平行于三角形一边的直线和其他两边（或两边的延长线）相交，所构成的三角形与原三角形相似. （2）判定定理1如果一个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似．即“两角对应相等，两三角形相似”．（3）判定定理2如果一个三角形的两条边与另一个三角形的两条边对应成比例，并且夹角相等，那么这两个三角形相似．即“两边对应成比例且夹角相等，两三角形相似”．（4）判定定理3如果一个三角形的三条边与另一个三角形的三条边对应成比例，那么这两个三角形相似．即“三边对应成比例，两三角形相似”．（5）若△1∽△2、△2∽△3、则△1∽△3．对于直角三角形相似，还有如下判定定理：（6）如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例，那么这两个直角三角形相似．（7）直角三角形被斜边上的高分成的两个直角三角形和原三角形相似．2．相似三角形的性质（1）相似三角形的对应角相等；（2）相似三角形的对应边成比例；（3）相似三角形的对应高的比、对应中线的比与对应角平分线的比都等于相似比；（4）相似三角形周长比等于相似比；（5）相似三角形面积的比等于相似比的平方．二、锐角三角函数1．掌握锐角三角函数的定义，准确地进行计算．2．互余角的三角函数间的关系（1）sin（90°－）＝cos；（2）cos（90°－）＝sin；（3）．3．同角三角函数间的关系（1）；（2）．三、解直角三角形1．如图，在Rt△ABC中，∠C＝90°，（1）三边之间的关系：a2＋b2＝c2；（2）两锐角之间的关系：∠A＋∠B＝90°；（3）边与角之间的关系：，，．2．如图，若直角三角形ABC中，CD⊥AB于点D，设CD＝h，AD＝q，DB＝p，则由△CBD∽△ABC，得a2＝pc；由△CAD∽△BAC，得b2＝qc；由△ACD∽△CBD，得h2＝pq；由△ACD∽△ABC或由△ABC的面积，得ab＝ch．从三角函数的角度考虑，有由，得a2＝pc；同理，得b2＝qc；由，得h2＝pq；由，得ab＝ch．在有关直角三角形的相似问题中，可以尝试运用三角函数的知识来解题，即“三角法”．3．如图1，若CD是直角三角形ABC中斜边上的中线，则（1）CD＝AD＝BD＝；（2）点D是Rt△ABC的外心，外接圆半径．4．如图2，若r是直角三角形ABC的内切圆半径，则．图1 图2 图3 5．直角三角形的面积：（1）如图2，S△ABC．（2）如图3，S△ABC．6B＝90°－A，，，由求角A，B＝90°－A，由求角A，B＝90°－A例题分析例1．如图，等腰梯形ABCD中，AD∥BC，AD＝3，BC＝7，∠B＝60°，P为下底BC上一点（不与B，C重合），连接AP，过P点作PE交DC于E，使得∠APE＝∠B．（1）你认为图中哪两个三角形相似，为什么?（2）当点P在底边BC上自点B向C移动的过程中，是否存在一点P，使得DE∶EC＝5∶3?如果存在，求BP的长；如果不存在，请说明理由．例2．如图，正方形ABCD的边长为4，M，N分别是BC，CD上的两个动点，当M点在BC上运动时，保持AM和MN垂直．（1）求证：Rt△ABM∽Rt△MCN；（2）设BM＝x，梯形ABCN的面积为y，求y与x之间的函数关系式；当M点运动到什么位置时，四边形ABCN的面积最大，并求出最大面积；（3）当M点运动到什么位置时，Rt△ABM∽Rt△AMN，并求x的值．例3．如图，在△ABC中，∠BAC＝120°，AB＝10，AC＝5，求sin B·sin C的值．例4．如图，D是AB上一点，且CD⊥AC于C，S△ACD∶S△CDB＝2∶3，，AC＋CD＝18，求tan A的值和AB的长．5．如图，△OAB是边长为2的等边三角形，过点A的直线y＝与x轴交于点E．求点E的坐标．6．已知：如图（a），梯形ABCD中，AB∥CD，∠C＝90°，AB＝BC＝4，CD＝6．（1）E为BC边上一点，EF∥AD，交CD边于点F，FG∥EA，交AD边于点G，若四边形AEFG为矩形，求BE的长；（2）如图（b），将（1）中的∠AEF绕E点逆时针旋转为∠A′EF′，EF′交CD边于F′点，且F′点与D点不重合，射线EA′交AB边于点M，作F′N∥EA′交AD边于点N，设BM为x，△NF′D中，F′D边上的高为y，求y关于x的函数解析式及自变量x的取值范围．图（a）图（b）答案例1、解：（1）△ABP∽△PCE．其理由是除∠B＝∠C外，由于∠APE＝∠B＝60°，∠APC＝∠B＋∠BAP＝∠APE＋∠CPE，∴∠BAP＝∠CPE．由“两角对应相等，两三角形相似”可得△ABP∽△PCE．说明：此图形结构可以称为“一线三等角问题”．（2）作DF⊥BC于F，由已知可得CF＝，腰长AB＝CD＝2CF＝4，这样原问题转化为在底边BC上是否存在一点P，使得CE＝1.5．假设存在P点，使CE＝1.5，由△ABP∽△PCE，得，可得BP·PC＝AB·CE＝6．设BP＝x，∵BC＝BP＋PC＝7，∴PC＝7－x．∴x（7－x）＝6，即x2－7x＋6＝0．解得x1＝1，x2＝6．答：当BP＝1或BP＝6时，使得DE∶EC＝5∶3．例2、解：（1）在正方形ABCD中，AB＝BC＝CD＝4，∠B＝∠C＝90°．∵AM⊥MN，∴∠AMN＝90°．∴∠CMN＋∠AMB＝90°．在Rt△ABM中，∠MAB＋∠AMB＝90°，∴∠MAB＝∠CMN．∴Rt△ABM∽Rt△MCN．（2）∵Rt△ABM∽Rt△MCN，，即．．．当x＝2时，y取最大值，最大值为10．（3）∵∠B＝∠AMN＝90°，∴要使△ABM ∽△AMN，只需．由（1）知．∴BM＝MC．∴当点M运动到BC的中点时，△ABM∽△AMN，此时x＝2．例3、分析:为求sin B，sin C，需将∠B，∠C分别置于直角三角形之中，另外已知∠A的邻补角是60°，若要使其充分发挥作用，也需要将其置于直角三角形中，所以应分别过点B，C，向CA，BA的延长线作垂线段，即可顺利求解．解：过点B作BD⊥CA的延长线于点D，过点C作CE⊥BA的延长线于点E．∵∠BAC＝120°，∴∠BAD＝60°．；．又∵CD＝CA＋AD＝10，，．同理，可求得．．说明：由于锐角的三角函数是在直角三角形中定义的，因此若要求某个角的三角函数值，一般可以通过作垂线段等方法将其置于直角三角形中．例4、解：作DE∥AC交CB于E，则∠EDC＝∠ACD＝90°．∵，设CD＝4k（k＞0），则CE＝5k，由勾股定理得DE＝3k．∵△ACD和△CDB在AB边上的高相同，∴AD∶DB＝S△ACD∶S△CDB＝2∶3．．即．．∵AC＋CD＝18，∴5k＋4k＝18．解得k＝2．．．说明：本章解题的基本思路是将问题转化为解直角三角形的问题，转化的目标主要有两个，一是构造可解的直角三角形；二是利用已知条件通过设参数列方程．在解直角三角形时，常用的等量关系是：勾股定理、三角函数关系式、相等的线段、面积关系等．例5、解：作AF⊥x轴于F．∴OF＝OA·cos60°＝1，AF＝OF·．∴点A坐标为（1，）．代入直线解析式，得．．．当y＝0即时，x＝4．∴点E坐标为（4，0）．例6、解：（1）作AH⊥CD于点H（如图（c））可得∠1＝∠2＝∠D．由AB＝BC＝CH＝4可得HD＝CD－CH＝2．．．∴BE＝2，即E为BC的中点．（2）图（d），作NP⊥CD于点P，则PN＝y．可得∠4＝∠5＝∠6，它们的正切值相等．，即．，．，，∵CD＝CF′＋PF′＋PD，，即．整理，得．若点F′与点D重合（见图（e）），则∠BEM＝∠EDC，．．．∴x的取值范围为。
相似三角形判定定理
探讨相似三角形判定定理的逆命题
9字
两三角形如果对应边成比例， 那么这两个三角形是否一定 相似？
9字
两三角形如果面积比等于相 似比的平方，那么这两个三 角形是否一定相似？
9字
回答是肯定的。如果两个三 角形的对应边成比例，那么 它们的对应角必然相等，因 此这两个三角形一定相似。
9字
回答也是肯定的。如果两个 三角形的面积比等于相似比 的平方，那么它们的对应边 必然成比例，因此这两个三 角形一定相似。
该定理是相似三角形判定的基础，也是 应用最广泛的判定方法之一。
判定定理二：两边对应成比例且夹角相等
如果一个三角形的两条边与另一个三角形的两条边对应成比例， 并且夹角相等，则这两个三角形相似。
该定理是相似三角形判定的另一种方法，适用于已知两边和夹 角的情况。
判定定理三：三边对应成比例
如果一个三角形的三条边与另一个三角形的三条边对应成比例，则这两个三角形相 似。
该定理是相似三角形判定的另一种方法，适用于已知三边长度的情况。
以上三个判定定理是相似三角形判定的主要方法，它们在实际应用中具有广泛的适 用性和实用性。同时，这些定理也是学习相似三角形知识的基础和关键。
03
相似三角形证明方法
综合法证明
综合运用相似三角形的性质
01
通过已知条件，结合相似三角形的对应角相等、对应边成比例
飞机的位置。
建筑设计中的应用
比例缩放
在建筑设计中，相似三角形可以帮助 设计师按比例缩放模型，使得不同大 小的建筑保持相同的比例和美感。
透视绘图
在绘制建筑透视图时，相似三角形原 理可以帮助准确表现物体的远近关系 和立体感。
结构分析
在建筑结构分析中，相似三角形可以 帮助工程师理解和计算结构的稳定性 和承重能力。
直角三角形相似的判定
A D C E F B
证明：
(1)
CD是斜边AB上的高 ADF ACE 90 又 AE AD AF AC AE AC AF AD
b a
b
C
b a BD
2
2
A
ΔABC∽ΔBDC，
a
D 图（2）
B a b2 a 2 BD b 2 a a b 2 a 2 有两个三角形相似 答： BD 或 BD 当 b b
2.如图，在RtΔABC中，CD是斜边AB上的高，E是 BC上的一点，AE交CD于点F，AE•AD＝AF•AC， 求证：(1) AE是∠CAB的平分线； (2) AB•AF＝AC•AE。
又
∠CAE=∠EAB
ΔACF∽ΔABE
AC AF AB AE
(2)
ΔAEC∽ΔAFD ∠CAE=∠BAE AE是∠CAB的角平分线 ∠ACD+∠CAB=90°
∠B+∠CAB=90°
AB•AF=AC•AEC E F BA∠ACD=∠BD
思考：
如图，在RtΔABC中， ∠C=90°，CD是AB边上的高。 求证： (1)
(1) ∠A＝25°，∠B'＝65°； (2) AC=3，BC＝4，A'C'＝6，B'C'＝8； (3) AB＝10，AC＝8，A'B'＝15，B'C'＝9．
(1) ∠A＝25°，∠B'＝65°；
A 25° B' 65° C 65° B A'
三角形相似的判定方法
三角形相似的判定方法三角形是初中数学中的重要内容，而三角形的相似性是其中的重要概念之一。
在数学学习中，我们经常会遇到需要判定三角形是否相似的问题，因此，了解三角形相似的判定方法是十分重要的。
接下来，我们将介绍三角形相似的判定方法，希望能够帮助大家更好地理解和掌握这一知识点。
首先，我们来看一下什么是相似三角形。
两个三角形的对应角相等，并且对应边的比值相等时，我们称这两个三角形是相似的。
在实际问题中，我们通常需要通过给定的条件来判定三角形是否相似。
下面，我们将介绍几种常见的判定方法。
1. AAA判定法。
AAA判定法是指如果两个三角形的对应角分别相等，那么这两个三角形是相似的。
这是最为简单的相似三角形的判定方法之一。
例如，如果两个三角形的对应角分别为∠A、∠B、∠C和∠A'、∠B'、∠C'，且满足∠A=∠A'、∠B=∠B'、∠C=∠C'，那么这两个三角形就是相似的。
2. AA判定法。
AA判定法是指如果两个三角形的两个对应角分别相等，那么这两个三角形是相似的。
例如，如果两个三角形的对应角分别为∠A、∠B和∠A'、∠B'，且满足∠A=∠A'、∠B=∠B'，那么这两个三角形就是相似的。
3. SSS判定法。
SSS判定法是指如果两个三角形的对应边的比值相等，那么这两个三角形是相似的。
例如，如果两个三角形的对应边分别为AB/AB'、BC/BC'、AC/AC'，且满足AB/AB'=BC/BC'=AC/AC'，那么这两个三角形就是相似的。
4. 直角三角形的判定法。
对于直角三角形，我们还可以利用斜边和直角边的长度比来判定是否相似。
如果两个直角三角形的斜边和直角边的比值相等，那么这两个三角形是相似的。
需要注意的是，判定三角形相似时，至少需要满足三个条件中的一个。
在实际问题中，我们可以根据已知条件来选择合适的判定方法，从而判定三角形是否相似。
相似三角形判定定理的证明核心知识
相似三角形判定定理的证明核心知识首先，我们来看一下相似三角形的定义。
两个三角形ABC和DEF是相似的，当且仅当它们的对应角度相等，并且对应边的比值相等。
数学符号表示为：∠A=∠D，∠B=∠E，∠C=∠F，且AB/DE=BC/EF=AC/DF。
现在，我们来证明相似三角形的判定定理。
相似三角形判定定理分为三种情况，即AAA（角-角-角）判定定理、AA（角-角）判定定理和SSS（边-边-边）判定定理。
接下来，我们将分别对这三种情况进行证明。
首先，我们证明AAA判定定理。
假设有两个三角形ABC和DEF，它们的对应角度分别为∠A、∠B、∠C和∠D、∠E、∠F。
我们假设∠A=∠D，∠B=∠E，∠C=∠F，要证明这两个三角形是相似的，我们需要证明它们的对应边的比值相等。
根据正弦定理和余弦定理，我们可以得到三角形的边长与角度的关系。
通过计算可以得到AB/DE=BC/EF=AC/DF，因此，根据对应角度相等和对应边的比值相等的条件，我们可以得出相似三角形判定定理中的AAA判定定理。
接下来，我们证明AA判定定理。
假设有两个三角形ABC和DEF，它们的对应角度分别为∠A、∠B、∠C和∠D、∠E、∠F。
我们假设∠A=∠D，∠B=∠E，要证明这两个三角形是相似的，我们需要证明它们的对应边的比值相等。
首先，我们可以得到∠C=180°-∠A-∠B，∠F=180°-∠D-∠E。
然后，根据正弦定理和余弦定理，我们可以得到三角形的边长与角度的关系。
通过计算可以得到AB/DE=BC/EF，因此，根据对应角度相等和对应边的比值相等的条件，我们可以得出相似三角形判定定理中的AA判定定理。
最后，我们证明SSS判定定理。
假设有两个三角形ABC和DEF，它们的对应边分别为AB、BC、AC和DE、EF、DF。
我们假设AB/DE=BC/EF=AC/DF，要证明这两个三角形是相似的，我们需要证明它们的对应角度相等。
根据余弦定理和正弦定理，我们可以得到三角形的角度与边长的关系。
相似三角形的定义及判定方法
相似三角形的定义及判定方法相似三角形是初中数学中的一个重要概念，在几何学中有着广泛的应用。
了解相似三角形的定义及判定方法对于解决相关问题非常有帮助。
本文将介绍相似三角形的定义，以及根据三个条件来判定两个三角形是否相似。
首先，让我们来了解相似三角形的定义。
相似三角形是指具有相同形状但可能不相等的三角形。
两个三角形相似的条件是：对应角相等且对应边成比例。
换句话说，如果两个三角形的对应角相等，并且对应边之间的比例相等，那么这两个三角形就是相似的。
接下来，我们来讨论判定两个三角形相似的方法。
根据相似三角形的定义，我们可以得出以下三种判定方法。
方法一：AAA相似判定法如果两个三角形的三个对应角分别相等，那么它们就是相似的。
例如，如果两个三角形的三个角分别为∠A、∠B、∠C和∠A'、∠B'、∠C'，如果有∠A=∠A'、∠B=∠B'、∠C=∠C'，那么这两个三角形就是相似的。
方法二：AA相似判定法如果两个三角形的两个对应角相等，那么它们就是相似的。
例如，如果两个三角形的两个角分别为∠A、∠B和∠A'、∠B'，如果有∠A=∠A'、∠B=∠B'，那么这两个三角形就是相似的。
方法三：边比例相等判定法如果两个三角形的对应边的比例相等，那么它们就是相似的。
例如，如果两个三角形的三条边分别为AB、BC、CA和A'B'、B'C'、C'A'，如果有AB/A'B' = BC/B'C' = CA/C'A'，那么这两个三角形就是相似的。
需要注意的是，上述的方法一般只适用于已知两个三角形相似的情况。
在实际问题中，我们往往需要根据已知条件来判定两个三角形是否相似。
综上所述，了解相似三角形的定义及判定方法对于解决相关问题非常重要。
相似三角形的定义是指具有相同形状但可能不相等的三角形，判定方法包括AAA相似判定法、AA相似判定法和边比例相等判定法。
相似三角形判定定理
相似三角形判定定理三角形是几何学中最基本的几何图形之一，而相似三角形是几何学中常见且重要的概念之一。
在数学中，两个三角形被称为相似三角形，如果它们的对应角相等，并且对应边的比例相等。
相似三角形有着许多有趣的性质和定理，其中最基本也是最重要的之一就是相似三角形判定定理。
相似三角形判定定理对于两个三角形ABC和DEF，如果它们满足以下条件之一，则这两个三角形是相似的：1.三个对应角相等：∠A = ∠D，∠B = ∠E，∠C = ∠F2.两个角相等且夹在两个相等的边之间：∠A = ∠D，∠B = ∠E，且AB/DE = BC/EF相似三角形判定定理的证明方法主要基于几何学中的基本原理和引理。
其中重要的一点是对应角相等的性质，即如果两个角相等，则它们的对应边的比例也相等，这是相似三角形判定定理的关键。
相似三角形的应用相似三角形在解决实际问题中有着广泛的应用。
例如在测量高楼的高度时，可以利用相似三角形来计算。
另外，在地图绘制和图像处理中，也常常需要利用相似三角形的性质来实现缩放和变换。
常见的相似三角形相关题目1.已知两个三角形的三个顶点坐标，判定它们是否相似。
2.已知三角形的三个顶点，求出相似三角形的比例。
3.已知两个三角形的某一条边，以及与该边夹的两个角度，判定它们是否相似。
在解决这些问题时，相似三角形判定定理往往是一个非常有用的工具，并且可以帮助我们简化计算过程，快速得出结论。
总之，相似三角形判定定理是几何学中一个基础而重要的定理，它在几何学的研究和实际应用中都有着广泛的应用价值。
通过理解和掌握这一定理，我们可以更好地理解和运用相似三角形的性质，从而解决各种与相似三角形相关的问题。
相似三角形的判定与性质
相似三角形的判定与性质一、学习要求1．了解相似多边形的概念，知道相似多边形的性质；2．了解两个三角形相似的概念，会利用相似三角形的性质与判定进行简单的推理和计算；3．会利用相似三角形的知识解决一些实际问题；认识现实生活中物体的相似；会运用相似多边形的性质解决简单的问题；利用图形的相似解决一些简单实际问题.二、知识梳理及例题分析1．相似三角形的概念：在和中，如果，，，，我们就说和相似，记作∽，就是它们的相似比(注意：要把表示对应顶点的字母写在对应的位置上).思考：在中,点是边的中点,，交于点，与有什么关系？猜想：与相似. 证明：在与中，∴，.过点作，交于点在中，，，∴. 又，∴∴，∴∽(对应角相等，对应边的比相等的两三角形相似)，相似比为.改变点在上的位置，可以进一步猜想以上两个三角形依然相似.2．相似三角形的判定定理：平行于三角形一边的直线和其他两边相交，所构成的三角形与原三角形相似.小结：判定三角形相似的方法：(1)相似三角形的定义；(2)由平行线得相似.思考：对比三角形全等判定的简单方法()，看是否也有简便的方法？已知：在和中，.求证：∽.分析：要证明∽，可以先作一个与全等的三角形，证明它与相似，这里所作的三角形是证明的中介，它把与联系起来证明：在线段(或它的延长线)上截取，过点作，交于点，根据前面的结论可得∽. ∴又，∴∴同理：∴≌∴∽相似三角形的判定定理：如果两个三角形的三组对应边的比相等，那么这两个三角形相似.可简单说成：三边对应成比例，两三角形相似.思考：若，，与是否相似呢？相似三角形的判定定理：如果两个三角形的两组对应边的比相等，并且相应的夹角相等，那么这两个三角形相似可简单说成：两边对应成比例且夹角相等，两三角形相似.进一步引申：若，，与是否相似呢？不一定问：全等中的边边角不能用，那么边边角也不能证相似，反例同全等.例1.根据下列条件，判断与是否相似，并说明理由：(1)，，；，，.(2)，，；，，.解：(1)，∴又∴∽问：这两个相似三角形的相似比是多少？(答：是)(2)，，∴与的三组对应边的比不等，它们不相似.问：要使两三角形相似，不改变的长，的长应当改为多少？(答：)例2.要做两个形状相同的三角形框架，其中一个三角形框架的三边的长分别为4、5、6，另一个三角形的一边长为2，怎样选料可使这两个三角形相似？注：此题没说2与哪条边是对应边，所以要进行分类讨论.可以是：，3；或，；或，.注：当两三角形相似而边不确定时，要注意分类讨论.相似三角形的判定定理：如果一个三角形的两个角与另一个三角形的两个角对应相等的，那么这两个三角形相似.简单说成：两角对应相等，两三角形相似.3．三角形相似的判定的应用例3.如图，弦和弦相交于内一点，求证：.分析:题目中求证的是等积式，我们可以转化为比例式，从而找到应证哪两个三角形相似.同时圆当中同弧或等弧所对的圆周角相等要会灵活应用.证明：连接，.在∴∽∴.例4.已知：如图，在中，于点.(1)求证：∽∽；(2)求证：；；(此结论称之为射影定理)(3)若，求.(4)若，求.分析：(1)利用两角相等证相似；(2)把相似三角形的相似比的比例式改为乘积式即可；(3)利用射影定理和勾股定理直接求；(4)利用上面的定理和方程求.进一步引申：在中，于点，这个条件可以放在圆当中，是直径，是圆上任意一点，于点，则可得到双垂直图形.例.已知：∽，分别是两个三角形的角平分线.求证：.分析：先利用相似三角形的性质得到，，再利用角平分线的定义，得到，从而可证得∽，则比例式可证得得到：相似三角形对应角的平分线的比等于相似比.那么对应中线的比，对应高线的比呢？4．相似三角形的性质(1)相似三角形的对应角相等，对应边的比相等，都等于相似比.(2)相似三角形对应高的比，对应角的平分线的比，对应中线的比都等于相似比.(3)相似三角形周长的比等于相似比；相似多边形周长的比等于相似比.证明：如果∽，相似比为，那么.因此，，.从而，.同理可得相似多边形对应周长的比也等于相似比.如图，已知：∽，相似比为.分别作出与的高和和都是直角三角形，并且，∽相似多边形面积的比等于相似比的平方.对于两个相似多边形，可以把他们分成若干个相似三角形证明.例5.如图，在和中，，，，的周长是24，面积是48，求的周长和面积.解：在和中，，又∽，相似比为.的周长为，的面积是.例6.已知点P在线段AB上，点O在线段AB的延长线上.以点O为圆心，OP为半径作圆，点C是圆O上的一点.(1)如图，如果AP=2PB，PB=BO.求证：△CAO∽△B CO；(2)如果AP=m(m 是常数，且)，BP=1，OP是OA、OB的比例中项.当点C在圆O 上运动时，求的值(结果用含m的式子表示)；(3)在(2)的条件下，讨论以BC为半径的圆B和以CA为半径的圆C的位置关系，并写出相应m的取值范围.分析：此题第1问：利用两边的比相等，夹角相等证相似. 即，第2问：设∵是的比例中项，∴是的比例中项即∴解得又∵第3问：∵ ，，即当时，两圆内切；当时，两圆内含；当时，两圆相交.例7.如图，已知中，，，，，点在上，(与点不重合)，点在上.(1)当的面积与四边形的面积相等时，求的长.(2)当的周长与四边形的周长相等时，求的长.(3)在上是否存在点，使得为等腰直角三角形？要不存在，请说明理由；若存在，请求出的长.解：(1)，∽(2)∵的周长与四边形的周长相等∽(3)在线段上存在点，使得为等腰直角三角形.过作于，则，设交于若，则.∵∽若，同理可求. 若，∽∴ 在线段上存在点，使得为等腰直角三角形，此时，或.三、总结归纳：1、相似三角形的判定：(1)相似三角形的定义；(2)平行得相似；(3)三边的比相等；(4)两边的比相等，夹角相等；(5)两角对应相等.三角形相似判定的方法较多，要根据已知条件适当选择.3、相似三角形的常见图形及其变换：4、证明四条线段成比例的常用方法：(1)线段成比例的定义(2)三角形相似的预备定理(3)利用相似三角形的性质(4)利用中间比等量代换(5)利用面积关系证明题常用方法归纳：(1)通过“横找”“竖看”寻找三角形，即横向看或纵向寻找的时候一共各有三个不同的字母，并且这几个字母不在同一条直线上，能够组成三角形，并且有可能是相似的，则可证明这两个三角形相似，然后由相似三角形对应边成比例即可证的所需的结论.(2)若没有三角形(即横向看或纵向寻找的时候一共有四个字母或者三个字母，但这几个字母在同一条直线上)，则需要进行“转移”(或“替换”)，常用的“替换”方法有这样的三种：等线段代换、等比代换、等积代换.(3)若上述方法还不能奏效的话，可以考虑添加辅助线(通常是添加平行线)构成比例.以上步骤可以不断的重复使用，直到被证结论证出为止.。
相似三角形及判定
相似三角形及判定在数学的奇妙世界中，相似三角形就像是一组神秘而有趣的密码，等待着我们去解读和探索。
相似三角形不仅在数学理论中占据重要地位，在实际生活中的应用也十分广泛。
那到底什么是相似三角形呢？简单来说，如果两个三角形的形状相同，但大小不一定相同，那么这两个三角形就是相似的。
这就好比是两个不同大小的同款风筝，它们的形状是一样的，只是一个大一个小。
相似三角形有很多有趣的性质。
比如说，它们的对应角相等。
想象一下，有两个相似三角形，其中一个三角形的三个角分别是 30 度、60 度和 90 度，那么另一个相似三角形对应的三个角也必然是 30 度、60度和 90 度。
再比如，它们的对应边成比例。
如果一个三角形的三条边分别是 3、4、5，而另一个与其相似的三角形的对应边分别是 6、8、10，那么 3 与 6 的比值、4 与 8 的比值、5 与 10 的比值都是相等的。
接下来，咱们重点聊聊相似三角形的判定方法。
这可是解决相似三角形问题的关键钥匙。
第一种判定方法是“两角分别相等的两个三角形相似”。
这很好理解，因为三角形的内角和是固定的 180 度，如果两个三角形有两个角分别相等，那么第三个角自然也相等。
就像两个人，眼睛和鼻子长得一样，那嘴巴大概率也长得差不多，整体长相也就相似了。
第二种判定方法是“两边成比例且夹角相等的两个三角形相似”。
比如说，一个三角形的两条边分别是 4 和 6，夹角是 60 度；另一个三角形对应的两条边是 8 和 12，夹角也是 60 度，那么这两个三角形就是相似的。
第三种判定方法是“三边成比例的两个三角形相似”。
假如一个三角形的三边分别是 3、4、5，另一个三角形的三边分别是 6、8、10，因为 3 比 6 等于 4 比 8 等于 5 比 10，所以这两个三角形相似。
咱们通过几个实际的例子来看看这些判定方法是怎么运用的。
假设在一个三角形 ABC 中，角 A 等于 30 度，角 B 等于 60 度，在另一个三角形 DEF 中，角 D 等于 30 度，角 E 等于 60 度。
三角形相似的判定方法6种
三角形相似的判定方法6种三角形相似是几何学中的一个重要概念，它描述了两个三角形形状相同，大小可能不同的关系。
判断两个三角形是否相似，主要依靠六种判定方法，它们分别是：AA相似、SSS相似、SAS相似、ASA相似、AAS相似以及HL相似（仅限于直角三角形）。
本文将详细阐述这六种判定方法，并辅以例题和图形说明，力求全面、深入地讲解三角形相似的判定。
一、 AA相似（角角相似）如果两个三角形的两个角对应相等，那么这两个三角形相似。
这是最常用的相似判定方法，其简洁性使其在解题中应用广泛。
原理：两个角对应相等，则第三个角也必然相等（因为三角形内角和为180°）。
三个角对应相等，保证了两个三角形的形状完全一致，从而判定它们相似。
图形说明：A A'/ \ / \/ \ / \/ \ / \B-------C B'-------C'如果∠A = ∠A’ 且∠B = ∠B’，则△ABC ∽△A’B’C’。
例题1：已知△ABC中，∠A = 60°，∠B = 80°；△DEF中，∠D = 60°，∠E = 80°。
判断△ABC与△DEF是否相似，并说明理由。
解答：因为∠A = ∠D = 60°，∠B = ∠E = 80°，根据AA相似判定定理，△ABC ∽△DEF。
二、 SSS相似（边边边相似）如果两个三角形的对应边成比例，那么这两个三角形相似。
这是基于比例关系的相似判定方法。
原理：对应边成比例意味着两个三角形形状相同，只是大小不同。
比例关系保证了三角形的形状不变，从而判定它们相似。
图形说明：A A'/ \ / \/ \ / \/ \ / \B-------C B'-------C'如果AB/A’B’ = BC/B’C’ = AC/A’C’，则△ABC ∽△A’B’C’。
例题2：已知△ABC的三边长分别为6cm、8cm、10cm；△DEF的三边长分别为3cm、4cm、5cm。
相似三角形的判定
相似三角形的判定在数学的奇妙世界里，相似三角形是一个非常重要的概念。
它不仅在几何问题中频繁出现，对于解决实际生活中的许多测量和计算问题也具有关键作用。
而要准确地判断两个三角形是否相似，就需要掌握一些特定的判定方法。
首先，我们来谈谈“两角分别相等的两个三角形相似”这一判定方法。
想象一下，有两个三角形，它们对应的两个角分别相等。
就好像一个三角形是另一个三角形的“放大版”或者“缩小版”，角度却保持不变。
这是因为三角形的内角和是固定的 180 度，当两个角分别相等时，第三个角也必然相等。
比如说，一个三角形的三个角分别是 30 度、60 度和90 度，另一个三角形也有同样的 30 度、60 度和 90 度的角，那么这两个三角形就是相似的。
接下来是“两边成比例且夹角相等的两个三角形相似”。
假设我们有两个三角形，其中一组对应边的比例相同，并且它们所夹的角也相等。
这就好比我们按照一定的比例缩放了一个三角形，并且角度没有发生变化。
例如，一个三角形的两条边分别是 4 和 6，夹角是 60 度；另一个三角形对应的两条边是 8 和 12，夹角也是 60 度，那么这两个三角形就是相似的。
再说说“三边成比例的两个三角形相似”。
如果两个三角形的三条边对应成比例，那就像是把一个三角形均匀地放大或缩小了一样。
比如说，一个三角形的三条边分别是3、4、5，另一个三角形的三条边是6、8、10，它们的边长比例都是 1:2，所以这两个三角形是相似的。
为了更好地理解这些判定方法，我们通过一些具体的例子来看看。
假设在一个三角形 ABC 中，角 A 是 50 度，角 B 是 70 度，在另一个三角形 DEF 中，角 D 是 50 度，角 E 是 70 度。
因为三角形的内角和是 180 度，所以在三角形 ABC 中，角 C 是 60 度；在三角形 DEF 中，角 F 也是 60 度。
由于两个三角形的三个角分别相等，所以三角形ABC 和三角形 DEF 相似。
沪科版23.2相似三角形的判定第2课时说课稿
相似三角形的判定课堂说课稿1 .教材分析：对于相似三角形的研究,实际上是对平面几何中两个封闭图形关系研究的进一步,是在原来研究三角形全等基础上的深入.它是初中阶段研究比例式的主要途径.既是全等三角形研究的继续,也为后面测量和研究三角函数做了铺垫.因此必须熟练掌握三角形相似的判定,学会灵活运用相似三角形的判定.。
在学习平面几何中起着承上启下的作用。
2 .学生的认知起点分析：学生通过前面的学习已了解了三角形相似的概念，掌握了相似三角形判定的预备定理，这为探究三角形相似的条件做好了知识上的准备.另外，学生也具备了识别三角形全等的知识，通过类比,使学生能主动参与本节课的探究。
3、教法分析与学法指导教法分析：为了充分调动学生学习的积极性，变被动学习为主动学习，使课堂教学生动、有趣、高效，本节课我将采用自主探索、启发引导、.合作交流、反馈测试展开教学，并采用多媒体辅助课堂教学，激励学生积极参与、观察、发现其知识的内在联系，使每个学生都能积极思维，这样一方面可以激发学生学习的兴趣，提高学生学习的效率，另一方面拓展学生的思维空间，培养学生用创造性思维去学习体会。
学法指导：在学法指导上，充分引导学生积极思维，鼓励学生进行合作学习，让每个学生都动口、动手、动脑，体会数学内容之间的联系，在解决问题的过程中，深化对其本质属性的理解，培养学生学习的主动性和积极性，让学生在愉悦的气氛中感受到数学学习的无穷乐趣。
4 .教学目标：（1）．掌握判定两个三角形相似的方法：如果一个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似。
（2）．培养学生的观察﹑发现﹑比较﹑归纳能力，感受两个三角形相似的判定方法1与全等三角形判定方法（AAS﹑ASA）的区别与联系，体验事物间特殊与一般的关系。
（3）．让学生经历从实验探究到归纳证明的过程，发展学生的合情推理能力。
5.教学的重点与难点：重点：三角形相似的判定定理1及应用。
难点：三角形相似的判定定理1的发现和证明。
三角形相似的判定方法
三角形相似的判定方法相似三角形是指三角形的对应角相等，对应边成比例。
在几何学中，判定三角形是否相似是一个常见的问题。
下面我们将介绍三角形相似的判定方法。
1. AAA相似判定法。
如果两个三角形的对应角相等，则这两个三角形是相似的。
这是最简单的相似判定方法之一。
例如，如果三角形ABC和三角形DEF的对应角分别相等，即∠A=∠D，∠B=∠E，∠C=∠F，则可以判定三角形ABC与三角形DEF是相似的。
2. AA相似判定法。
如果两个三角形的一个角相等，且它们的对应边成比例，则这两个三角形是相似的。
例如，如果∠A=∠D，∠B=∠E，并且AB/DE=BC/EF，则可以判定三角形ABC与三角形DEF是相似的。
3. SSS相似判定法。
如果两个三角形的对应边成比例，则这两个三角形是相似的。
例如，如果AB/DE=BC/EF=AC/DF，则可以判定三角形ABC与三角形DEF是相似的。
4. 直角三角形的相似判定方法。
对于直角三角形，如果一个角相等，且斜边成比例，则这两个直角三角形是相似的。
例如，如果∠A=∠D，且AB/DE=AC/DF，则可以判定直角三角形ABC与直角三角形DEF是相似的。
5. 重要提示。
在判定三角形相似时，需要注意以下几点：判定相似时，必须保证对应角相等，并且对应边成比例。
对应边成比例时，可以利用辅助线或者相似三角形的性质来进行判定。
在判定时，要注意排除特殊情况，例如对应角相等但对应边不成比例的情况。
总结。
三角形相似的判定方法主要包括AAA相似判定法、AA相似判定法、SSS相似判定法以及直角三角形的相似判定方法。
在实际问题中，通过这些方法可以准确地判定三角形是否相似，从而解决各种相关的几何问题。
希望通过本文的介绍，读者能够掌握三角形相似的判定方法，提高对几何学知识的理解和运用能力。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
A
BC 和 AC
BC AC
都是正数
AB AB
AC AC
AB2 AB2 AC 2 AC2
BC BC AC AC
即:
BC AC BC AC
C
B
A'
又 C C 90
C'
B'
AB2 AC 2 AC 2
AB2 AC2 AC2
A
E
O
C
B
D
学习小结
1、如何判定两个直角三角形相似呢？ 答：一个锐角对应相等或两边对应成比例的 两个直角三角形相似。 2、直角三角形相似的判定定理的简单应用。 3、初步了解转移比例的证法。
作业 布置
课堂作业： 必做题：课本76页11 基础训练42页 4 选做题： 课外作业： 基础训练
∠A DE= ∠C= ∠C ' = 900
A D =A'C' A E =A'B'
ADE ≌ A'C'B'
E B
A'
C' B'
△ABC ∽ △A' B' C'
已知：∠C=∠C‘=90°，A'B':AB＝A'C'：AC， 求证： Rt△A'B'C' ∽Rt △ABC
证法(2):
AB AC AB AC
已知：∠C=∠C‘=90°，A'B':AB＝A'C'：AC， 求证： Rt△A'B'C' ∽Rt △ABC
证法（1）: 分别在A C ，A B上截取AD =A'C'，A
A E =A'B'，连结DE。
D
AB
AC
=
A'B'
A'C'
AE
AD
C
A'C'=A D，A'B'=A E
=
AB
AC
∠A = ∠A
A DE ∽ A C B
C
分析：
E
(1)要证明AE是∠CAB的平分线， 只要证明RtΔACE∽RtΔＡＤＦ A
F
B
即可
D
(2)要证明AB•AF＝AC•AE，只要 证明ΔACF∽ΔＡＢＥ
(1) CD是斜边AB上的高
又 ∠CAE=∠EAB
ADF ACE 90 又 AE AD AF AC
AE AC AF AD
4、AB=10，BC=6， A′B′=5， A′C′=_4_____. 5、AC：AB=1：3， A′C′=a, A′B′=__3_a__
例题解析
例：如图所示，已知∠ABC=∠CDB=90°，AC=a，
BC=b，当BD与a,b之间满足怎样的关系式时，
⊿分A析BC：∽要⊿C使DRBt？⊿ABC∽Rt⊿CDB
直角三角形相似的判定
A
cb
B
a ∟C
A′
B′
C′
回顾与反思☞
1、到目前为止我们总共学过几种判定两个三 角形相似的方法？ 答2(、1）两相个似等三腰角三形角判定形的一预定备相定似理吗？两个等边 （三2角）两形角一对定应相相似等吗的两?两个个三直角角形三相角似形。一定相似
吗？
（33、）判两定边两对应个成直比角例三且角夹形角相相等似的有两几个种三方角法形？相似。
ΔABC∽ΔA'B'C‘
由勾股定理得
BC 2 AC 2
BC2 AC2
是真是假 练习一
在Rt△ABC和Rt△A′B′C′中，已知 ∠C=∠C′=90°。依据下列各组条件判定这 两个三角形是不是相似，并说明为什么。
1、∠A=25°，∠A′=65°。
2、AC=3，BC=4，A′C′=6，B′C′=8。
ΔAEC∽ΔAFD
ΔACF∽ΔABE
AC AF
AB AE 即，AB•AF=AC•AE
∠CAE=∠BAE
C
即：AE是∠CAB的角平分线
E
(2) ∠ACD+∠CAB=90° F
∠B+∠CAB=90°
A
B
∠ACD=∠B
D
2.如图 ：高线CE交△ABC的高线AD于点 O，交AB 于E，写出图中的相似三角形。
b2 (BD )
a
a
C
b
b a2 b2 BD
a
B
D
答：当 BD b2
a
或 BD b a2 b2 a
这两个三角形相似
3、如图，在RtΔABC中，CD是斜边AB上的高，E
是BC上的一点，AE交CD于点F，AE•AD＝AF•AC，
求证：(1) AE是∠CAB的平分线；
(2) AB•AF＝AC•AE。
行讨论，切不可凭主观想象，只解一种情况，而忽略其他的解。
1，当AC与BC，BC与BD对应时：RtΔABC∽RtΔCDB （过程略）
2，如图： ABC CDB 90
当 AC BC
AB 时， BD
ΔABC∽ΔBDC，
即当 a a2 b2 时， ΔABC∽ΔBDC，
A
b BD
aC
而题中已经知道Rt⊿ABC的斜边和一直A
角边及Rt⊿CDB的斜边，利用今天讲的 这个定理可知只须加上条件
b
BD
= 即可。
如图所示，已知∠ABC=∠CDB=90°，AC=a，
BC=b，当BD与a,b之间满足怎样的关系式时，
⊿ABC∽⊿CDB？
a
ABC CDB 90, A
C
当 AC BC
（4）三边对应成比例的两个三角形相似。 答：一个锐角对应相等或两直角边对应成比例。
探索思考
判定两个三角形相似，除了用 一般的判定定理外，是否象判定 两个三角形全等一样，还有特殊 的判定方法？
探求 新知
直角三角形相似判定定理：
如果一个直角三角形的斜边和 一条直角边与另一个直角三角 形的斜边和一条直角边对应成 比例，那么这两个直角三角形 相似。
BBDC 时，ΔABC∽ΔCDB
即
a b
b 时， BD
ΔABC∽ΔCDB
BD b2
a
b
B
D
答: 当 BD b0°，
AC=a，BC=b， 当BD与a，b之间
满足怎样的关系时，图中⊿ABC与
⊿CDB？相似？ A a
C
b
B
D
分析：对条件探索性问题，在解题时应分类对每一种情况进
3、AB=10，AC=8，A′B′=15， A′C′=9。
练习二
在Rt△ABC和Rt△A′B′C′中，已知 ∠C=∠C′=90°。要使Rt△ABC∽ Rt△A′B′C′，应 加什么条件？
1、∠A=35° ，∠B′=__5_5_°____。 2、AC=5，BC=4，A′C′=15，B′C′=_1_2_。 3、AB=5，AC=_3__，A′B′=10， A′C′=6。