Semiclassical Droplet States in Matrix Quantum Hall Effect
华南师范大学学报(自然科学版)2019年(1-6期)总目次

华南师范大学学报(自然科学版)2019年(1~6期)总目次2019年第I期-物理学与光学工程•基于锥形天线的超宽带微带-波导转换的研究.......许文涛,朱玮玮,林峻,王剑莹,张涵(1)具有诱导超导电性和自旋轨道耦合作用的半导体纳米线零偏压电导峰的研究王媛,陈佐满,卢金兰,赵家隆,陈钰淇,胡梁宾(5)CO2和CO分子在五边形石墨烯表面的吸附行为...............................张灿鹏,邵志刚(11)工作气压对氩射频电感耦合等离子体模式转换的影响..........熊文文,陈俊芳,王燕,王勇(16)•化学与环境•碘掺杂Bi4O5Br2可见光催化降解2,4-二羟基苯甲酸甲酯...................................................................................卢明莉,肖信,张玲,刘飞,南俊民(22)取代基和配体的负离子效应对(TPFC)Mn(V)O轴向配位作用的影响...................................................................................徐艳,章小慧,徐志广,陈华彬,刘海洋(28)MoS2@ZnO异质结纳米材料的制备及光催化性能.....张辉,宋海燕,阮舒红,黄雯倩,高志红(35)热碱解-水解预处理剩余污泥的效果研究............................李哲,林嘉薇,胡勇有(42)4种常用铁基材料非均相芬顿降解四环素的研究.....陈俊毅,易云强,方战强,晏晓敏,郑刘春(49)累托石对左氧氟沙星的吸附研究....................杨凤,曾丽璇,罗继文,张秋云,康园(56)•生物学与生物工程•水稻C2H2型锌指蛋白OsZAT12转化拟南芥功能的初步研究............陈宗新,陈俊飞,王亚琴(63)去势对成年雄性斑胸草雀HVC神经元电生理特性的影响..............周文丽,许小冰,李东风(68)•地理科学与技术•位置服务大数据下广州市土地利用类型模拟探讨...............................刘望保,谢智豪(75)腾格里沙漠南缘末次冰消期微量元素反映的古气候环境....................................................李芳,温小浩,李保生,杨庆江,黄嘉慧,陈思宏,李俊覃(84)•数学与应用数学•模糊市场中含有投资约束的最优投资消费问题......................杨舟,吕漫妮,魏智健(93)液晶流方程在弱V空间中的解的存在性............................林俊宇,龚伟华,徐晓杰(97)s-quantale同余的进一步刻画...............................................李婷玉,张霞(104)具有唯一左单位的二元关系半群P r(A x A)...............................................................................林屏峰(107)•计算机科学与软件工程•主颜色提取算法及其在服装图像检索中的应用陈倩,陶彬娇,潘中良,李萍,刘寿强(111)基于内容和最近邻算法的多臂老虎机推荐算法.................................王高智,肖菁(120)《华南师范大学学报(自然科学版)》征稿简则(128)I](川丿[第2期-物理学与光学工程•基于极化码的单步量子密钥分发后处理........................李锦,蒋琳,林旭城,方俊彬(1)六角晶格中Dirac准粒子的动力学模拟与操控.......黄肖健,许文刚,廖开宇,黄巍,李志(7)基于单/多参数的DC-DC模块电源健康评估技术研究姜伟,张春雷,时林林,贾寒光,俞鹏飞,周振威(14)基于棱镜耦合的双循环法测量液体复折射率............................张敬,邓剑勋,黄佐华(21)•化学与环境•肠溶型饲料添加剂甘氨酸亚铁的制备与表征纳米AgBr热力学性质的测定及温度效应研究舒绪刚,林羽,胡洪超,付志欢,龚圣(27)覃方红,肖碧源,张美婷,吕勇,钟婧晗,邱江源,黄在银(34)碱式铜盐包覆CU2O催化剂的形成机理及催化性能直接回收锰酸锂制备超级电容器MnS材料的研究黄小燕,古颖,钟嘉豪,陈可清,万霞(39)缪建麟,常毅,蔡俊超,朱显峰,赵瑞瑞(45)复合光催化剂AgCl/AgBr降解水中四溴双酚A的研究高大方,张冈弭50)Fe-Mn-MCM-41分子筛催化臭氧氧化控制含溴水中溴酸盐的生成..................................................................................................薛颖,李旭凯,吴颖,李来胜(56)•生物学与生物工程•金钗石斛转基因体系的建立.................................八角中茴香油与莽草酸的提取和分离纯化....................王昊,邓柠檬,张雅文,梁山(62)吕琪,张耀元,倪贺,李海航(69)-地理科学与技术•粤北锦江扶溪段河流阶地的光释光测年.....邹小娟,周尚哲,谢金明,孙永,黄耀婷,杨虹(76)土壤理化性质对珠江口红树林湿地土壤氮磷质量分数的影响...................................................................................牛安逸,马姣娇,杨文槐,黄金辉,徐颂军(86)•数学与应用数学•截面曲率有上界的4维收缩的梯度Ricci孤立子.......................................张珠洪(95)非线性抛物积分微分方程非常规Hermite型矩形元的高精度分析................李先枝,范中广(98)—类Riemann-Liouville型分数阶微分方程正解的存在性................薛益民,戴振祥,刘洁(105)有限级代数体函数的Borel方向.....................................张晓梅,孙道椿,柴富杰(110)•计算机科学与软件工程•基于矩阵分解与随机森林的多准则推荐算法...................................林栢全,肖菁(117)时态拟序数据索引TQD-tree更新技术......................陈瑛,吴明珠,卢莉,叶小平(123)《华南师范大学学报(自然科学版)》征稿简则.. (128)n-物理学与光学工程•一种具有安全特性的压缩全息成像方法.....李军,王尚媛,李娇声,雷苗,尹振兴,唐志列(1)硫化铅量子点的能带调控.................................................曾鹏菀,李炜(8)透射式透明薄膜厚度的在线测量.....................................陈方涵,赵光宇,蒋仕龙(12)•化学与环境•系列氮唑类含能配合物的合成及其性质.........................................李莲玉,谭淑莲,谢晓丹,汤颖欣,何春凤,陈俊彬,区泳聪,吴建中(18)一种2-肼基苯并噻唑衍生物作为Ag+荧光探针的研究...................................................................................古雯蕾,劳珊珊,许佳如,钟慧贤,马立军(24)混凝助凝强化ZTI重金属捕集法对烧结脱硫废水中铊的去除研究...................................................................................郑进熙,王奕非,杨余维,黄志华,黄振雄(29)热碱解-好氧消化联合工艺处理剩余污泥的效能及抗性基因变化研究..................................................................................................吴学深,胡勇有,陈元彩,程建华(36)铁碳微电解耦合反硝化菌削减河道黑臭底泥污染物及净化水质的研究……王颖,林嘉薇,胡勇有(47)•生物学与生物工程•去势对成年雄性斑胸草雀LMAN神经元电生理特性的影响.....................吴丽,李东风(57)2种光强下生长的4种木本植物叶片的光保护物质积累能力与光合能力的关系...................................................................................俞正超,刘晓涛,郑晓婷,黄姮栋,彭长连(62)•地理科学与技术•南岭亚高山泥炭地现代有壳变形虫环境指示意义的初步研究——以湖南省大坪泥炭地为例..........魏志强,钟巍,欧阳军,叶素素,商圣潭,杨坤有,唐小雯,薛积彬,Robert K BOOTH(70)长江中游城市群经济联系能力比较...................................郭卫东,钟业喜,傅钰(79)基于多细节路网Voronoi层次模型的最优路径算法............................胡正华,王尚媛(88)•数学与应用数学•具有机会约束的多阶段可信性M-AD投资组合优化..................张鹏,黄梅雨,彭壁玉(94)关于不定方程/+4”=y9的整数解...........................................尤利华,蔡小群(103)一类二重积分不等式中未知函数的估计............................黄星寿,王五生,罗日才(108)Bloch-Orlicz型空间上的一类紧积分型算子...................................何忠华,江剑韬(112)•计算机科学与软件工程•基于Ring-LPN的高效公钥加密方案.................................艾志娟,马昌社,徐碧霞(116)基于深度学习的图像去雾算法...............................................张泽浩,周卫星(123)皿ZnO陷光结构材料的制备及其太阳能电池性能的研究..........................贺冠南,黄波(1)单层含硫空位MoS2光伏效应的第一性原理研究......................罗文铭,邵志刚,杨谋(7)利用单波长椭偏仪对各向异性薄膜光学常数和欧拉角的研究……冀丽娜,邓剑勋,汪娟,黄佐华(14)•化学与环境•Na2Ca2.92Si6O,6:0.08Eu3+荧光粉的制备及其发光特性研究...................................................................................高世杰,王华,张珊珊,乔利,毛近隆(21)双丹酰基组氨酸作为Fe3+荧光探针的研究............邓乐芳,苏晓萍,李敏,古雯蕾,马立军(26)表面分子印迹固相萃取微球的制备及其在谷氨酸分离检测中的应用.....何佩玲,陈时远,胡小刚(32)铁碳微电解耦合苦草原位处理河道黑臭污水的研究......................陈超,胡勇有,谢玲彩(39)•生物学与生物工程•斜纹夜蛾精巢的发育和精子的发生…文靓,陈丰,陈亚青,周来娣,刘玉成,冯启理,刘琳(47)黄皮种质资源果汁中有机酸成分的分析.....彭程,陈喆,常晓晓,林志雄,邱继水,陆育生(57)雷州半岛东海岸玉蕊群落的干扰机制及潜在生态损失分析...................................................................郭程轩,陈祁琪,徐颂军,陈虹羽,李婉盈,潘亭君(67)•地理科学与技术•基于WT-MB方法的OLI图像融合—以宁夏回族自治区吴忠市的OLI图像和P5图像为例..........................郭小丹(76)—太阳辐射变化对光伏电站最佳倾角的影响分析..........................张俊,俞文政,申彦波(86)•数学与应用数学•线性互补问题的广义松弛两步模基矩阵分裂迭代法...................................彭小飞(93)类不变子空间与不变子空间的关系...........................................古雯,倪军娜(100)右e-wlpp半群的平移壳结构定理...................................................王春茹(104)整函数差分算子的唯一性...................................................李倩,吴小英(108)•计算机科学与软件工程•基于卷积神经网络的食品图像识别廖恩红,李会芳,王华,庞雄文(113)一种基于聚类算法的机会网络路由算法何志立,潘达儒,宋晖(120)冷原子系统中不同色散准粒子波包动力学的模拟..............李志,黄育蕾,陈李梅,廖开宇(1)基于脑电图的新型情绪识别特征提取方法....................张克军,韩娜,陈欣然,缪睿(6)智能车追寻信标灯过程的图像处理..........................唐小煜,苏思伟,翁哲,陈群元(12)•化学与环境•镍铁钻磷化物纳米片阵列的制备及其电催化析氧性能............................张璋,胡先标(18)g-C3N4@Ag的光催化性能及原位热动力学研究....................................................覃方红,万婷,王素素,邱江源,肖碧源,贺子君,黄在银(25)生物炭负载金属硒化物复合材料的储锂性能..................苏炽权,汝强,石正禄,赵灵智(32)铁碳内电解耦合蘿菜(Ipomoea aquatica)对黑臭污水脱氮效果的研究.....陈胜男,廖子聪,胡勇有(38)基于水环境数学模型的竹桥河流域综合整治成效模拟分析...................................................................许文卿,梁康,黄志华,黄振雄,杨余维,高源濛(49)化工园区水环境中优控化学品的污染特征及风险评估.........................................刘强,陈晓雯,刘嘉烈,卓丽,蔡凤珊,严骁,胡立新,石运刚(58)•生物学与生物工程•1株副干酪乳酸菌S-4对致病弧菌的抑制特性研究...................................................................梁晓明,曾嘉颖,王安利,叶剑敏,冯娟,廖绍安(66)变形球囊霉(Glomus versiforme)和钢渣复合处理对玉米生长和积累镉/铅的影响...................................................................卓逢,张小凤,颜廷秀,胡尊河,黄丹,靖元孝(75)•地理科学与技术•铀系不平衡在粤北花岗岩风化速率研究中的应用................................杨虹,周尚哲(84)多源数据结合的高分一号土地利用/覆盖分类方法研究................欧健滨,罗文斐,刘畅(92)•数学与应用数学•基于信息干预的SIRS传染病模型稳定性分析.................................李小妮,张启敏(98)一类二阶整数矩阵方程的解.........................................尹倩倩,梁欣然,袁平之(104)按饱和顶点分类的完美匹配数的递推求法.....................................唐保祥,任韩(110)•计算机科学与软件工程•SDN中一种基于网络的分布式移动管理方案.................................张奇支,赵淦森(115)TLRank:一种新的社会化协同排序推荐算法..................李改,徐清振,李磊,黄锦涛(121)V新型二维碳材料net-Y光学性质的第一性原理研究............................邵志刚,李白(1)节点面晶体的拓扑特性.....................................李润泽,陈李梅,黄育蕾,李志(7)全反射比较法测量液体折射率色散的研究............................白芸,汪娟,黄佐华(12)•化学与环境•钛酸锶钡拉曼光谱的理论计算与实验研究............................陈文烁,孟耀勇,顾凤龙(18)手性联二萘侧基聚(3,3'-联咔唑对苯二腈)的合成及其聚集诱导发光和圆偏振发光性能研究..................................................................................................张敏敏,唐小勇,许炳佳,石光(24)新型电润湿显示油墨材料分散剂的制备及应用…王宵,邓勇,叶德超,李诗,唐彪,李笑然,Reinder COEHOORN,李明,周国富(31)a-Fe2O3/CuO/rGO非均相芬顿催化剂的制备及其降解苯酚的性能.....杨镇杉,李耀威,吴宏海(36)硫化纳米零价铁对五氯苯酚的脱氯及其增强反应.....张苑芳,吴宏海,寇卓瑶,张鹏,管玉峰(42)24种个人护理品在鱼血浆中的富集特征及风险...................................................................姚理,窦文渊,马艳芳,周漪波,刘有胜,赵建亮(51)•生物学与生物工程•…刘海粟,付胜利,邱铭,林妙华,王安利,叶剑敏(61)水体铅对草鱼幼鱼肠道结构与功能的影响…淀粉加工型甘薯茎尖的成分分析与利用研究..................洪炜嘉,石帅帅,倪贺,李海航(69)•地理科学与技术•基于地理加权回归的江南市镇发展动力机制分析(1736—1949年)..............陈浩东,张伟然(76)明清时期东南沿海地区的台风重建及影响因素分析……孙力,毕硕本,潘威,陈昌春,许志慧(88)•数学与应用数学•一类平面三次多项式系统的平衡点分析........................................龙能,梁海华(98)群作用下逆极限空间和乘积空间中的强G-跟踪性....................冀占江,张更容,涂井先(103)广义泊松计数模型及其统计推断......................................吴琴,刘寅,阮建(107)•计算机科学与软件工程•一种D2D缓存网络的延时与能耗优化方案....................刘志错,宋晖,潘达儒,吴群英(111)基于PNCC与基频的鲁棒电话语音性别检测方案...................................................................钟顺明,况鹏,庄豪爽,冯韩德,王剑莹,张涵(118)•其他•铱配合物专利的发展现状及转化策略研究.....................................杨宝杰,张寅(123)。
【计算机科学】_学习算法_期刊发文热词逐年推荐_20140722
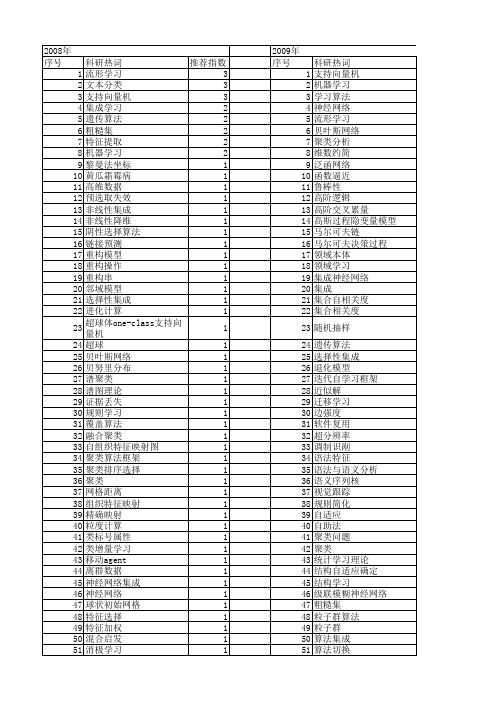
科研热词 支持向量机 机器学习 学习算法 神经网络 流形学习 贝叶斯网络 聚类分析 维数约简 泛函网络 函数逼近 鲁棒性 高阶逻辑 高阶交叉累量 高斯过程隐变量模型 马尔可夫链 马尔可夫决策过程 领域本体 领域学习 集成神经网络 集成 集合自相关度 集合相关度 随机抽样 遗传算法 选择性集成 退化模型 迭代自学习框架 近似解 迁移学习 边强度 软件复用 超分辨率 调制识剐 语法特征 语法与语义分析 语义序列核 视觉跟踪 规则简化 自适应 自助法 聚类问题 聚类 统计学习理论 结构自适应确定 结构学习 级联模糊神经网络 粗糙集 粒子群算法 粒子群 算法集成 算法切换 算法
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106
2008年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
【国家自然科学基金】_wigner分布函数_基金支持热词逐年推荐_【万方软件创新助手】_20140801

2014年 序号 1 2 3 4 5
2014年 科研热词 高阶厄密高斯模 量子光学 压缩态光场 光学参量放大器 wigner准概率分布函数 推荐指数 1 1 1 1 1
2008年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27
科研热词 推荐指数 频率 1 集合多晶体 1 量子玻尔兹曼方程 1 量子层析 1 量子修正项 1 重排 1 超声波速 1 织构系数 1 线性调频 1 算法 1 立方晶粒各向异性 1 真空压缩态光场 1 时频分析 1 弹性张量 1 平滑伪分布 1 平滑伪wigner-ville分布 1 局部放电 1 局域波分解 1 参数估计 1 分频谱 1 内蕴模式函数 1 光学参量振荡器 1 伪码 1 wigner分布函数 1 wigner分布 1 wigner准概率分布函数 1 clebsch-gordan表达式 1
2012年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32
科研热词 推荐指数 量子光学 3 边缘分布 3 wigner函数 3 维格纳分布函数 2 激光光学 2 大气湍流 2 大气光学 2 部分相干平顶光束 1 部分相干双曲正弦高斯光束 1 超声波测量 1 统计性质 1 织构系数 1 立方晶粒正交材料 1 玻色子 1 湍流距离 1 束宽扩展 1 斜程传输 1 截断光束 1 归一化因子 1 弹性张量 1 复高斯展开法 1 压缩相干态 1 创造者 1 光子数分布 1 介观rlc电路 1 二阶矩矩阵 1 weyl-wigner理论 1 tomogram函数 1 non-gaussian state, hermite polynomial, 1 squeezed m2因子 1 hermite多项式 1 clebsch-gordan表达式 1
基于非凸熵最小化与高斯混合模型聚类的电容层析成像图像重建

基于非凸熵最小化与高斯混合模型聚类的电容层析成像图像重
建
张立峰;卢栋臣;刘卫亮
【期刊名称】《计量学报》
【年(卷),期】2024(45)2
【摘要】基于压缩感知原理提出了一种构建非凸熵(NE)函数作为正则化项的方法,在有效缓解电容层析成像(ECT)病态性逆问题的同时可保证解的稀疏性,并采用快速迭代阈值收缩算法(FISTA)求解以加快收敛速度。
对所得解通过高斯混合模型(GMM)进行阈值寻优,采用期望最大化算法(E-M)更新模型参数,从而构建NE-GMM算法。
仿真及实验结果均表明:与LBP、Landweber、迭代硬阈值(IHT)、ADMM-L1及NE算法进行了对比,该算法所得重建图像质量最优,对中心分布及多物体分布的保真度进一步提高,仿真实验重建图像的平均相对误差和相关系数分别为0.4611及0.8827,优于其他5种算法。
【总页数】7页(P207-213)
【作者】张立峰;卢栋臣;刘卫亮
【作者单位】华北电力大学自动化系
【正文语种】中文
【中图分类】TB937
【相关文献】
1.基于双循环改进landweber电容层析成像图像重建
2.基于卷积神经网络及有限元仿真的电容层析成像图像重建
3.基于卷积稀疏编码的电容层析成像图像重建
4.基于改进ResNet-18网络的电容层析成像图像重建
5.基于彩色-深度传感器的电容层析成像图像重建方法
因版权原因,仅展示原文概要,查看原文内容请购买。
一维空间注意力机制

一维空间注意力机制一维空间注意力机制是一种用于在序列数据中学习和提取关键信息的强大工具。
在自然语言处理、语音识别、机器翻译等任务中,一维空间注意力机制被广泛应用,以帮助模型更好地理解和处理输入序列。
一维空间注意力机制的基本原理是根据输入序列中每个位置的重要性,为每个位置分配一个权重。
这些权重可以用于加权求和,从而聚焦于输入序列中最重要的部分。
一维空间注意力机制的关键在于计算每个位置的权重,通常使用softmax函数对输入进行加权。
在一维空间注意力机制中,首先通过一个线性变换将输入序列映射到一个低维空间。
这个映射可以是一个全连接层,用于将输入序列的每个位置表示映射到一个低维向量。
然后,对映射后的向量应用softmax函数,得到每个位置的权重。
一维空间注意力机制的优势在于能够在序列中动态地选择和聚焦于重要的部分。
这使得模型能够更好地处理长序列,提取关键信息。
与传统的固定窗口方法相比,一维空间注意力机制能够更灵活地适应不同长度的输入序列。
在自然语言处理任务中,一维空间注意力机制常被用于处理文本分类、命名实体识别、情感分析等任务。
例如,在文本分类任务中,模型可以通过一维空间注意力机制自动关注关键词,从而更好地理解和分类文本。
在命名实体识别任务中,模型可以通过一维空间注意力机制聚焦于识别实体的关键上下文。
除了在自然语言处理任务中的应用,一维空间注意力机制还被广泛应用于语音识别和机器翻译等任务中。
在语音识别任务中,一维空间注意力机制可以帮助模型更好地理解语音信号的不同部分。
在机器翻译任务中,一维空间注意力机制可以帮助模型更好地对输入序列和输出序列之间的对应关系进行建模。
一维空间注意力机制是一种强大的工具,可以帮助模型更好地理解和处理序列数据。
它的优势在于能够动态地选择和聚焦于重要的部分,提取关键信息。
一维空间注意力机制在自然语言处理、语音识别、机器翻译等任务中有着广泛的应用前景。
未来随着深度学习的不断发展,一维空间注意力机制将继续发挥重要作用,推动这些任务的进一步发展和改进。
代数英语

(0,2) 插值||(0,2) interpolation0#||zero-sharp; 读作零井或零开。
0+||zero-dagger; 读作零正。
1-因子||1-factor3-流形||3-manifold; 又称“三维流形”。
AIC准则||AIC criterion, Akaike information criterionAp 权||Ap-weightA稳定性||A-stability, absolute stabilityA最优设计||A-optimal designBCH 码||BCH code, Bose-Chaudhuri-Hocquenghem codeBIC准则||BIC criterion, Bayesian modification of the AICBMOA函数||analytic function of bounded mean oscillation; 全称“有界平均振动解析函数”。
BMO鞅||BMO martingaleBSD猜想||Birch and Swinnerton-Dyer conjecture; 全称“伯奇与斯温纳顿-戴尔猜想”。
B样条||B-splineC*代数||C*-algebra; 读作“C星代数”。
C0 类函数||function of class C0; 又称“连续函数类”。
CA T准则||CAT criterion, criterion for autoregressiveCM域||CM fieldCN 群||CN-groupCW 复形的同调||homology of CW complexCW复形||CW complexCW复形的同伦群||homotopy group of CW complexesCW剖分||CW decompositionCn 类函数||function of class Cn; 又称“n次连续可微函数类”。
Cp统计量||Cp-statisticC。
ssnmf 稀疏半非负矩阵
ssnmf 稀疏半非负矩阵SSNMF(Sparse Semi-Negative Matrix Factorization)是一种用于高维数据分析的矩阵分解方法。
它可以有效地提取出数据中的稀疏和半非负特征,广泛应用于图像处理、文本挖掘、社交网络分析等领域。
SSNMF通过将原始数据矩阵分解为两个低秩矩阵的乘积,来实现特征提取和数据降维的目的。
其中,一个矩阵包含了数据中的稀疏特征,另一个矩阵包含了数据中的半非负特征。
在SSNMF中,稀疏特征矩阵表示了原始数据中的稀疏性信息。
稀疏性是指数据中只有少数几个元素具有较大的值,而大部分元素都接近于零。
通过提取出稀疏特征,我们可以发现数据中的重要模式和结构。
与稀疏特征相对应的是半非负特征矩阵。
半非负特征是指数据中的元素都是非负的,但不一定是稀疏的。
通过提取出半非负特征,我们可以捕捉到数据中的整体趋势和分布情况。
SSNMF的关键在于如何选择合适的约束条件和优化算法来进行矩阵分解。
一种常用的约束条件是稀疏性约束,通过最小化稀疏特征矩阵中的非零元素个数,来实现稀疏特征的提取。
另一种常用的约束条件是非负性约束,通过要求矩阵中的元素都为非负数,来实现半非负特征的提取。
SSNMF的优化算法通常采用迭代的方式进行求解。
常用的方法包括交替最小二乘法(Alternating Least Squares, ALS)、梯度下降法(Gradient Descent, GD)等。
这些算法通过不断更新稀疏特征和半非负特征矩阵,使其逐渐逼近原始数据矩阵,从而得到更好的分解结果。
SSNMF的应用非常广泛。
在图像处理领域,可以利用SSNMF提取图像的纹理特征、边缘特征等,从而实现图像分类、图像检索等任务。
在文本挖掘领域,可以利用SSNMF提取文档的主题特征、关键词特征等,从而实现文本聚类、文本分类等任务。
在社交网络分析领域,可以利用SSNMF提取用户的兴趣特征、社区特征等,从而实现用户推荐、社区发现等任务。
类内离散度矩阵和类间离散度
类内离散度矩阵和类间离散度The concept of intra-class scatter matrix and inter-class scatter matrix is fundamental in statistics and pattern recognition, especially in the field of machine learning and image processing. These matrices provide a quantitative measure of the variability and separability of different classes in a dataset.类内离散度矩阵和类间离散度矩阵在统计学和模式识别中具有基础性的概念,特别是在机器学习和图像处理领域。
这些矩阵为数据集中不同类别的可变性和可分性提供了定量度量。
The intra-class scatter matrix represents the dispersion or variance within each individual class. It is calculated by summing the covariance matrices of all the samples belonging to a particular class. A low intra-class scatter indicates that the samples within a class are tightly clustered together, whereas a high scatter suggests greater diversity or noise within the class.类内离散度矩阵表示每个类别内部的离散度或方差。
它是通过计算属于特定类别的所有样本的协方差矩阵之和来得到的。
非齐型空间上奇异积分算子的加权不等式
非齐型空间上奇异积分算子的加权不等式
在非齐型空间上,奇异积分算子的加权不等式是推动研究人员发现数学世界的
神奇之旅的一个重要工具。
它可以帮助我们研究它的应用场景,可以深入剖析功能的优缺点,从而更有效地改善模型的准确性。
首先,空间上的加权不等式能够让我们预估空间上变量的各种值,从而实现动
态追踪非齐性空间上特定地方的状态变量,在多目标最优化中也得到广泛应用。
此外,奇异积分算子也能用来搜索给定实例的最佳解,计算复杂模型下的空间参数,或者基于奇异积分算子构建多元非线性方程组。
该算子还可用于表达的函数的解析求极,研究复杂系统的稳定性,以及考虑一些复杂函数特性的情况下评估优化算法的收敛性,使其具有显著的优势。
此外,研究表明,对于某些复杂模型来说,使用加权不等式可以有效应用,有
利于巩固其准确性。
此外,它也可以极大地提高运行效率,增强搜索结果的有效性,并降低计算成本。
总的来说,空间上的加权不等式给研究者带来了无限的可能性,可以帮助我们在实际应用中更加精准地模拟模型,更准确地估算变量的各种值,更有效地改善模型的准确性。
因此,在非齐型空间上的研究者们都会把加权不等式看作一张重要而又神奇的后路,来发现更多有趣的数学世界。
Graph Regularized Nonnegative Matrix
Ç
1 INTRODUCTION
HE
techniques for matrix factorization have become popular in recent years for data representation. In many problems in information retrieval, computer vision, and pattern recognition, the input data matrix is of very high dimension. This makes learning from example infeasible [15]. One then hopes to find two or more lower dimensional matrices whose product provides a good approximation to the original one. The canonical matrix factorization techniques include LU decomposition, QR decomposition, vector quantization, and Singular Value Decomposition (SVD). SVD is one of the most frequently used matrix factorization techniques. A singular value decomposition of an M Â N matrix X has the following form: X ¼ UÆVT ; where U is an M Â M orthogonal matrix, V is an N Â N orthogonal matrix, and Æ is an M Â N diagonal matrix with Æij ¼ 0 if i 6¼ j and Æii ! 0. The quantities Æii are called the singular values of X, and the columns of U and V are called
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
refer to [15] for an introduction to noncommutative theories of the quantum Hall effect.
1
matrix extension of the Landau levels, where the gauge-invariant many-body states are given by matrix generalizations of Slater determinants. Although the degeneracy of matrix states grows exponentially with energy, it was possible to control it by introducing suitable projections in the theory. We showed that the constraint (Aab )m ≈ 0, ∀a, b, projects the theory to the “lowest m matrix Landau levels”, with m = 1, 2, . . .; the m-th reduced theory naturally possesses non-degenerate homogeneous ground states with filling fractions of the Jain series, ν = m/(mk + 1) [19] (see section 2). Indeed, the solutions of the gauge invariance conditions and of the constraint Am ≈ 0 give raise to a rather surprising structure of ground states that corresponds to the Jain composite-fermion construction of ansatz wave functions [18]. These g = 0 states exactly match the phenomenological Jain wave functions under matrix diagonalization, that is formally achieved at g = ∞. Therefore, we conjectured that these matrix ground states have smooth deformations for g > 0 into the physical g = ∞ states, namely that no phase transitions are found for 0 < g < ∞ when the system is at the specific densities [19]. A number of problems remained to be further investigated: • Understand the matrix Jain states, e.g. compute their densities and observables quantities. • Understand the projections (Aab )m ≈ 0 in more physical terms. • Study the phase diagram of the theory for 0 < g < ∞ at the relevant densities. In the present paper, after reminding earlier results [19] (section 2), we find the gauge invariant form of the projection Am ≈ 0 and its semiclassical physical meaning in terms of single-particle occupancy (section 3). Next, we study the matrix Jain states in the semiclassical approximation, by analytically solving the classical equations of motion, further constrained by the Gauss law and the semiclassical version of the Am ≈ 0 condition (section 4). The ground states are found to be two-step droplets of incompressible fluid with piecewise constant density; this is the same density shape of the phenomenological Jain states before projection to the lowest Landau level [18] (where the density of incompressible fluids becomes strictly constant). The fact that the matrix Jain states at g = 0 already have the expected droplet density of physical g = ∞ states, supports our earlier claim that these ground states could remain stable while varying 0 < g < ∞ [19]. Other ground states corresponding to generalized Jain constructions with different filling fraction, although possible in the g = 0 theory, are found not 2
1 Introduction
In this paper we continue the study of noncommutative and matrix gauge theories [1][2][3] that can be used as effective non-relativistic theories∗ [4][5] of the fractional Hall effect [6]. The original Susskind proposal was based on the noncommutative Chern-Simons theory [7]: it developed in the Polychronakos Chern-Simons matrix model [8], that was analysed by several authors [9] [10] [11] [12] [13] [14] [15][16]. This model is a U (N ) gauge theory in one dimension (i.e. time) with Chern-Simons kinetic term; it involves two Hermitean matrix coordinates, X1 (t ), X2(t ), that are noncommuting, [X1 , X2] = i θ I , where θ is a constant “background charge” and I is the identity matrix. In the semiclassical limit [7], the matrix model describes two-dimensional incompressible fluids in strong magnetic field B with Laughlin’s values of the filling fraction, ν = 1/(k + 1), where k = Bθ is integer quantized [17]. At the full quantum level, some problems were found in matching the matrix model to the physics of the fractional Hall effect: one point was that the theory reduced to the eigenvalues, λa , a = 1, . . . , N , of X = X1 + i X2 , does not really describe electrons in the lowest Landau level with coordinates λa ; owing to matrix noncommutativity, the Laughlin wave function is deformed at short distances [11][15]. Another issue was that this model cannot easily describe the general Hall states with Jain’s filling fractions: ν = m/(mk ± 1), m = 2, 3, . . . [18]. In our earlier paper [19], we showed that these problems can be overcome by upgrading the Chern-Simons model to the Maxwell-Chern-Simons matrix theory. This includes an additional kinetic term quadratic in time derivatives and the potential, V = −gTr [X1, X2 ]2 , with the coupling g ≥ 0 that controls matrix noncommutativity. All terms in the action are determined by the gauge principle because they can be obtained by dimensional reduction of Maxwell-Chern-Simons gauge theory, as discussed in the literature of D0-branes in string theory [3]. The Maxwell-Chern-Simons matrix theory reduces to the earlier Chern-Simons model for large values of B (with finite g). However, in the different g = ∞ limit (with finite B), corresponding to [X1 , X2 ] = 0, it does provide a sensible physical description of the fractional Hall effect: after reduction to eigenvalues, one finds electrons in Landau levels interacting with a two-dimensional potential of Calogero type, 1/|λa − λb |2 (see section 2.2). For general B < ∞, the additional coupling g in the theory allows one to interpolate between matrix (g = 0) and electron (g = ∞) dynamics. Furthermore, the theory is exactly solvable at g = 0 [19]: it was found to describe a
