六年级分数解方程
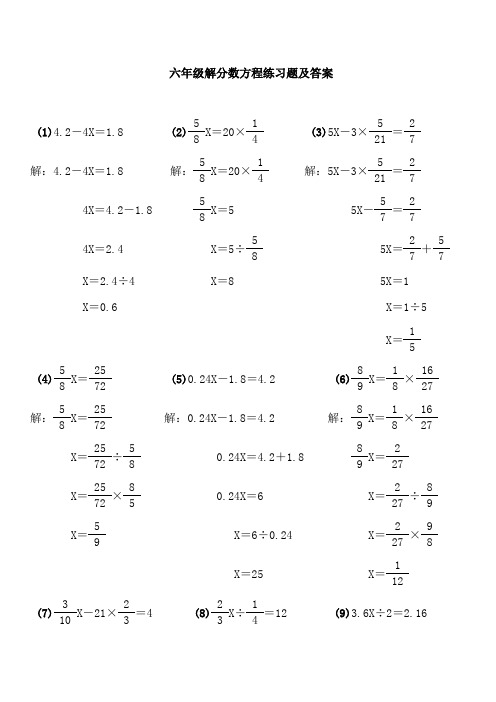
六年级解分式方程练习题及答案
(40)4X-3×9=29(41) X+ = (42)X- X=12
解:4X-3×9=29 X+ = X- X=12
4X-27=29 X= - X=12
4X=29+27 X= X=12÷
4X=56X= ÷ X=21
X=56÷4X=
X=14
(43)3X+5×0.3=4.5(44) X= (45)X-15%X=68
(22)X-0.25= (23)4+0.7X=102(24) X+ X=42
解:(22)X-0.25= 解:4+0.7X=102解: X+ X=42
X- = 0.7X=102-4 X=42
X= + 0.7X=98X=42÷
X= X=98÷0.7X=42×
X=140X=36
(25)4X-6× =2(26) ÷X= (27)9X÷0.7=9
X= 2X= - 6X=13.4-5
X= ÷ 2X= 6X=8.4
X= × X= ÷2X=8.4÷6
X= X= X=1.4
(49) X=20× (50)5X-2.4×5=8(51) (X-4.5)=6
解: X=20× 解:5X-2.4×5=8解: (X-4.5)=6
X=55X-12=8X-4.5=6÷
六年级解分数方程练习题及答案
(1)4.2-4X=1.8(2) X=20× (3)5X-3× =
解:4.2-4X=1.8解: X=20× 解:5X-3× =
4X=4.2-1.8 X=55X- =
4X=2.4 X=5÷ 5X= +
X=2.4÷4 X=85X=1
X=0.6 X=1÷5
X=
(4) X= (5)0.24X-1.8=4.2(6) X= ×
解:3X+5×0.3=4.5解: X= 解:X-15%X=68
六年级上册解决问题的解方程

六年级上册解决问题的解方程一、分数运算相关的方程。
1. (3)/(4)x + (1)/(2) = (5)/(6)- 解析:- 为了消去方程左边的(1)/(2),我们在等式两边同时减去(1)/(2),得到(3)/(4)x=(5)/(6)-(1)/(2)。
- 计算右边式子,(5)/(6)-(1)/(2)=(5)/(6)-(3)/(6)=(1)/(3)。
- 然后,为了求出x,因为x前面的系数是(3)/(4),所以在等式两边同时除以(3)/(4),即x = (1)/(3)÷(3)/(4)=(1)/(3)×(4)/(3)=(4)/(9)。
2. (2)/(3)x-(1)/(4)=(1)/(6)- 解析:- 等式两边同时加上(1)/(4),得到(2)/(3)x=(1)/(6)+(1)/(4)。
- 计算右边式子,(1)/(6)+(1)/(4)=(2 + 3)/(12)=(5)/(12)。
- 再等式两边同时除以(2)/(3),x=(5)/(12)÷(2)/(3)=(5)/(12)×(3)/(2)=(5)/(8)。
3. x-(3)/(5)x=(4)/(9)- 解析:- 先计算左边式子,x-(3)/(5)x=(5)/(5)x-(3)/(5)x=(2)/(5)x。
- 所以方程变为(2)/(5)x=(4)/(9),等式两边同时除以(2)/(5),x=(4)/(9)÷(2)/(5)=(4)/(9)×(5)/(2)=(10)/(9)。
4. (4)/(7)x+(3)/(14)x = (5)/(14)- 解析:- 先将左边式子相加,(4)/(7)x+(3)/(14)x=(8)/(14)x+(3)/(14)x=(11)/(14)x。
- 方程变为(11)/(14)x=(5)/(14),等式两边同时除以(11)/(14),x=(5)/(14)÷(11)/(14)=(5)/(14)×(14)/(11)=(5)/(11)。
六年级分数解方程计算题100道

六年级分数解方程计算题100道一、题目。
1. (1)/(2)x + (1)/(3) = (5)/(6)2. (2)/(3)x - (1)/(4) = (5)/(12)3. (3)/(4)x+(1)/(5)=(19)/(20)4. (4)/(5)x - (1)/(6)=(19)/(30)5. (1)/(3)x+(1)/(7)=(10)/(21)6. (5)/(6)x-(1)/(8)=(19)/(24)7. (2)/(5)x+(1)/(9)=(23)/(45)8. (3)/(7)x - (1)/(10)=(23)/(70)9. (4)/(9)x+(1)/(11)=(53)/(99)10. (5)/(8)x - (1)/(12)=(13)/(24)11. (1)/(4)x+(2)/(5)=(13)/(20)12. (3)/(5)x-(2)/(7)=(11)/(35)13. (5)/(7)x+(3)/(8)=(61)/(56)14. (2)/(9)x - (3)/(10)=( - 7)/(90)15. (4)/(7)x+(5)/(12)=(83)/(84)16. (1)/(6)x-(3)/(13)=( - 5)/(78)17. (3)/(8)x+(4)/(15)=(67)/(120)18. (5)/(9)x - (4)/(17)=(47)/(153)19. (2)/(7)x+(5)/(18)=(71)/(126)20. (4)/(11)x - (5)/(21)=(31)/(231)二、解析。
1. 对于方程(1)/(2)x+(1)/(3)=(5)/(6)- 将方程两边同时减去(1)/(3),得到(1)/(2)x=(5)/(6)-(1)/(3)。
- 计算右边式子:(5)/(6)-(1)/(3)=(5 - 2)/(6)=(3)/(6)=(1)/(2)。
- 然后方程两边同时除以(1)/(2),x = (1)/(2)÷(1)/(2)=1。
六年级分数解方程题

六年级分数解方程题题目 1:(2)/(3)x = 12解析:方程两边同时乘以(3)/(2),得到x = 12×(3)/(2) = 18题目 2:(3)/(4)x - 5 = 10解析:先在方程两边同时加 5,得到(3)/(4)x = 15,然后方程两边同时乘以(4)/(3),得到x = 15×(4)/(3) = 20题目 3:x - (1)/(5)x = 8解析:合并同类项,得到(4)/(5)x = 8,方程两边同时乘以(5)/(4),得到x = 8×(5)/(4) = 10题目 4:(2)/(5)x + (1)/(3)x = 14解析:通分计算左边,得到(6)/(15)x + (5)/(15)x = (11)/(15)x,方程两边同时乘以(15)/(11),得到x = 14×(15)/(11) = (210)/(11)题目 5:(3)/(7)x + 7 = 28解析:方程两边先同时减 7,得到(3)/(7)x = 21,然后方程两边同时乘以(7)/(3),得到x = 21×(7)/(3) = 49题目 6:x - (3)/(8)x = 15解析:合并同类项,得到(5)/(8)x = 15,方程两边同时乘以(8)/(5),得到x = 15×(8)/(5) = 24题目 7:(1)/(4)x - (1)/(6)x = 3解析:通分计算左边,得到(3)/(12)x - (2)/(12)x = (1)/(12)x,方程两边同时乘以12,得到x = 3×12 = 36题目 8:(5)/(6)x - 8 = 2解析:方程两边同时加 8,得到(5)/(6)x = 10,然后方程两边同时乘以(6)/(5),得到x = 10×(6)/(5) = 12题目 9:(3)/(5)x + (1)/(2)x = 21解析:通分计算左边,得到(6)/(10)x + (5)/(10)x = (11)/(10)x,方程两边同时乘以(10)/(11),得到x = 21×(10)/(11) = (210)/(11)题目 10:x + (2)/(7)x = 36解析:合并同类项,得到(9)/(7)x = 36,方程两边同时乘以(7)/(9),得到x = 36×(7)/(9) = 28题目 11:(4)/(9)x + 5 = 13解析:方程两边先同时减 5,得到(4)/(9)x = 8,然后方程两边同时乘以(9)/(4),得到x = 8×(9)/(4) = 18题目 12:(1)/(3)x - 4 = 8= 12×3 = 36题目 13:(5)/(8)x + (1)/(4)x = 24解析:通分计算左边,得到(5)/(8)x + (2)/(8)x = (7)/(8)x,方程两边同时乘以(8)/(7),得到x = 24×(8)/(7) = (192)/(7)题目 14:x - (5)/(12)x = 18解析:合并同类项,得到(7)/(12)x = 18,方程两边同时乘以(12)/(7),得到x = 18×(12)/(7) = (216)/(7)题目 15:(2)/(7)x + 10 = 20解析:方程两边先同时减 10,得到(2)/(7)x = 10,然后方程两边同时乘以(7)/(2),得到x = 10×(7)/(2) = 35题目 16:(3)/(8)x - 6 = 3解析:方程两边同时加 6,得到(3)/(8)x = 9,然后方程两边同时乘以(8)/(3),得到x = 9×(8)/(3) = 24题目 17:(1)/(6)x + (1)/(8)x = 14解析:通分计算左边,得到(4)/(24)x + (3)/(24)x = (7)/(24)x,方程两边同时乘以(24)/(7),得到x = 14×(24)/(7) = 48题目 18:(4)/(5)x + 8 = 16得到x = 8×(5)/(4) = 10题目 19:x - (7)/(9)x = 6解析:合并同类项,得到(2)/(9)x = 6,方程两边同时乘以(9)/(2),得到x = 6×(9)/(2) = 27题目 20:(5)/(7)x - 10 = 5解析:方程两边同时加 10,得到(5)/(7)x = 15,然后方程两边同时乘以(7)/(5),得到x = 15×(7)/(5) = 21。
六年级上册分数解方程计算题

六年级上册分数解方程计算题一、题目。
1. (1)/(2)x + (1)/(3)x = 5- 解析:先通分,将方程左边的分数相加,(1)/(2)x+(1)/(3)x=(3)/(6)x+(2)/(6)x=(5)/(6)x,则方程变为(5)/(6)x = 5,两边同时除以(5)/(6),x = 5÷(5)/(6)=5×(6)/(5)=6。
2. (2)/(3)x-(1)/(4)x=(5)/(6)- 解析:通分,(2)/(3)x-(1)/(4)x=(8)/(12)x-(3)/(12)x=(5)/(12)x,方程变为(5)/(12)x=(5)/(6),两边同时除以(5)/(12),x=(5)/(6)÷(5)/(12)=(5)/(6)×(12)/(5) = 2。
3. x+(1)/(5)x=(12)/(5)- 解析:x+(1)/(5)x=(5)/(5)x+(1)/(5)x=(6)/(5)x,方程变为(6)/(5)x=(12)/(5),两边同时除以(6)/(5),x=(12)/(5)÷(6)/(5)=(12)/(5)×(5)/(6)=2。
4. (3)/(4)x - (1)/(2)x=(1)/(4)- 解析:通分,(3)/(4)x-(1)/(2)x=(3)/(4)x-(2)/(4)x=(1)/(4)x,方程变为(1)/(4)x=(1)/(4),两边同时除以(1)/(4),x = 1。
5. (5)/(8)x+(1)/(4)x=(7)/(8)- 解析:通分,(5)/(8)x+(1)/(4)x=(5)/(8)x+(2)/(8)x=(7)/(8)x,方程变为(7)/(8)x=(7)/(8),两边同时除以(7)/(8),x = 1。
6. x-(1)/(6)x=(5)/(6)- 解析:x-(1)/(6)x=(6)/(6)x-(1)/(6)x=(5)/(6)x,方程变为(5)/(6)x=(5)/(6),两边同时除以(5)/(6),x = 1。
六年级上册分数解方程应用题

六年级上册分数解方程应用题一、分数解方程应用题的基础知识1. 分数方程的概念方程中含有分数的方程叫做分数方程。
例如:公式。
2. 解方程的步骤去分母(根据等式的性质,在方程两边同时乘以各分母的最小公倍数)。
去括号(运用乘法分配律将括号去掉)。
移项(把含未知数的项移到方程一边,常数项移到另一边,注意移项要变号)。
合并同类项(将同类项进行合并)。
系数化为1(在方程两边同时除以未知数的系数)。
例如:解方程公式。
去分母,方程两边同时乘以6(2和3的最小公倍数),得到公式。
合并同类项得公式。
系数化为1,公式。
二、分数解方程应用题的典型题目及解析1. 题目某工厂有职工200人,其中男职工占总人数的公式,后来又调进一批男职工,这时男职工占总人数的公式,问调进了多少男职工?2. 解析原来男职工的人数为公式人,设调进了公式名男职工。
调进男职工后总人数为公式人,男职工人数为公式人。
根据这时男职工占总人数的公式,可列出方程公式。
去分母,方程两边同时乘以公式得到:公式。
去括号得公式。
移项得公式。
合并同类项得公式。
系数化为1得公式(人)。
3. 题目一桶油,第一次用去这桶油的公式,第二次用去第一次的公式,这时桶里还剩22千克油。
这桶油原来有多少千克?4. 解析设这桶油原来有公式千克。
第一次用去公式千克,第二次用去公式千克。
可列出方程公式。
合并同类项得公式,即公式。
系数化为1得公式千克。
5. 题目学校图书馆有科技书和文艺书共630本,其中科技书占总数的公式,后来又买来一些科技书,这时科技书占总数的公式。
又买来多少本科技书?6. 解析原来科技书的数量为公式本,设又买来公式本科技书。
买来科技书后总数为公式本,科技书数量为公式本。
根据这时科技书占总数的公式,可列出方程公式。
去分母,方程两边同时乘以公式得到公式。
去括号得公式。
移项得公式。
合并同类项得公式。
系数化为1得公式本。
六年级分数解方程练习题
六年级分数解方程练习题六年级分数解方程练习题在六年级的数学学习中,解方程是一个重要的内容。
通过解方程,我们可以找到未知数的值,从而解决各种实际问题。
今天,我们来练习一些关于分数的解方程题目。
1. 问题一:小明和小红一起做数学作业,他们两个人一共用了2个小时。
如果小明独自完成这个作业,他需要3个小时,那么请问小红一个人独立完成这个作业需要多长时间?解题思路:设小红一个人独立完成作业需要的时间为x小时。
根据题意,小明一个人独立完成作业需要3小时,小红和小明一起完成作业需要2小时。
根据工作量的原理,我们可以得到以下等式:1/3 + 1/x = 1/2。
解方程:将等式两边的分数通分,得到2/6 + 6/x = 3/6。
将等式两边的分数相加,得到8/x = 1/6。
两边同时乘以x,得到8 = x/6。
将等式两边同时乘以6,得到48 = x。
所以小红一个人独立完成作业需要48分钟。
2. 问题二:一辆汽车以60公里/小时的速度行驶,行驶了4个小时后,发现还剩下120公里的路程没有到达目的地。
请问这段路程的长度是多少?解题思路:设这段路程的长度为x公里。
根据题意,汽车以60公里/小时的速度行驶4个小时后,还剩下120公里的路程。
根据速度、时间和路程的关系,我们可以得到以下等式:60 * 4 + 120 = x。
解方程:计算等式左边的数值,得到240 + 120 = x。
所以这段路程的长度是360公里。
3. 问题三:小明和小红一起做数学练习,他们两个人一共做了5/6的练习题。
如果小明独自完成这些练习题需要1个小时,那么请问小红一个人独立完成这些练习题需要多长时间?解题思路:设小红一个人独立完成练习题需要的时间为x小时。
根据题意,小明一个人独立完成练习题需要1个小时,小红和小明一起完成练习题需要5/6个小时。
根据工作量的原理,我们可以得到以下等式:1 + 1/x = 5/6。
解方程:将等式两边的分数通分,得到6/6 + 6/x = 5/6。
六年级分数解方程的公式法
六年级分数解方程的公式法一、分数解方程的基本原理。
1. 等式的基本性质。
- 等式两边同时加上(或减去)同一个整式,等式仍然成立。
例如:如果a = b,那么a + c=b + c,a - c=b - c。
- 等式两边同时乘或除以同一个不为0的整式,等式仍然成立。
即若a = b,那么ac = bc(c≠0),a÷ c=b÷ c(c≠0)。
2. 分数方程的定义。
- 方程中含有分数(分式)的方程叫做分数方程。
例如(1)/(2)x+(1)/(3)=(1)/(4)x + 1。
二、分数解方程的步骤(以人教版六年级知识为例)1. 去分母。
- 找到方程中所有分母的最小公倍数。
例如方程(x)/(2)+(x - 1)/(3)=1,分母2和3的最小公倍数是6。
- 方程两边同时乘以这个最小公倍数,将分数方程化为整式方程。
对于上述方程,两边同时乘以6得到:6×(x)/(2)+6×(x - 1)/(3)=6×1,化简后为3x + 2(x - 1)=6。
2. 去括号(如果有括号的话)- 根据乘法分配律去括号。
在3x + 2(x - 1)=6中,2(x - 1)=2x-2,方程变为3x+2x - 2 = 6。
3. 移项。
- 把含有未知数的项移到方程的一边,常数项移到方程的另一边。
注意移项要变号。
在3x+2x - 2 = 6中,将-2移到右边变为+2,得到3x+2x=6 + 2。
4. 合并同类项。
- 对同类项进行合并。
在3x+2x=6 + 2中,3x+2x = 5x,方程变为5x=8。
5. 求解未知数。
- 方程两边同时除以未知数的系数。
在5x = 8中,两边同时除以5,得到x=(8)/(5)。
6. 检验(非常重要)- 把求得的未知数的值代入原方程进行检验。
将x = (8)/(5)代入(x)/(2)+(x - 1)/(3)=1中,- 左边=(frac{8)/(5)}{2}+(frac{8)/(5)-1}{3}=(4)/(5)+(frac{3)/(5)}{3}=(4)/(5)+(1)/(5)=1,右边=1,左边等于右边,所以x=(8)/(5)是原方程的解。
六年级分数乘除方程练习题
六年级分数乘除方程练习题题一:1. 解方程:3/5 * x = 9/10解析:为了解这个方程,我们需要消去分数的除法。
为此,我们可以通过两边乘以10来消去x分母上的5,所以方程变为:3/5 * x = 9/10(3/5) * (10/1) * x = 9/10 * 10/13 * 2 * x = 96x = 9x = 9/6x = 3/2所以方程的解为 x = 3/2。
答案:x = 3/2题二:2. 解方程:2/3 ÷ y = 8/15解析:为了解这个方程,我们需要消去分数的除法。
为此,我们可以通过两边乘以y来消去y分母上的2/3,所以方程变为:2/3 ÷ y = 8/152/3 ÷ y * y = 8/15 * y2/3 = 8/15 * y(2/3) * (15/8) = y1/1 * 5/2 = y5/2 = y所以方程的解为 y = 5/2。
答案:y = 5/2题三:3. 解方程:4/9 * x = 2/3解析:为了解这个方程,我们需要消去分数的除法。
为此,我们可以通过两边乘以9来消去x分母上的4/9,所以方程变为:4/9 * x = 2/3(4/9) * (9/1) * x = 2/3 * 9/14 * x = 64x = 6x = 6/4x = 3/2所以方程的解为 x = 3/2。
答案:x = 3/24. 解方程:3/10 ÷ y = 5/9解析:为了解这个方程,我们需要消去分数的除法。
为此,我们可以通过两边乘以y来消去y分母上的3/10,所以方程变为:3/10 ÷ y = 5/93/10 ÷ y * y = 5/9 * y3/10 = 5/9 * y(3/10) * (9/5) = y1/1 * 3/2 = y3/2 = y所以方程的解为 y = 3/2。
答案:y = 3/2题五:5. 解方程:2/3 * x = 4/9解析:为了解这个方程,我们需要消去分数的除法。
六年级数学上册第三单元 分数解方程
到引用源。
源。
X = 错误!未找到引用源。
源。
+ X = 错误!未找到引用源。
X÷错误!未找到引用源。
= 10错误!未找到引用源。
X = 错误!未找到引用源。
X ×错误!未找到引用源。
×错误!未找到引用源。
= 3X÷错误!未找到引用源。
= 8X + 错误!未找到引用源。
= 错误!未找到引用源。
980X÷错误!未找到引用源。
= 错误!未找到引用源。
错误!未找到引用源。
X = 错误!未找到引用源。
X÷错误!未找到引用源。
= 19错误!未找到引用源。
X + X = 错误!未找到引用源。
错误!未找到引用源。
X÷错误!未找到引用源。
= 错误!未找到引用源。
X÷3.5 = 错误!未找到引用源。
错误!未找到引用源。
X = 错误!未找到引用源。
错误!未找到引用源。
X = 24源。
X + 错误!未找到引用源。
= 错误!未找到引用源。
源。
X = 2.4 源。
+ 错误!未找到引用源。
X =错误!未找到引用源。
源。
X = 错误!未找到引用源。
错误!未找到引用源。
X÷错误!未找到引用源。
= 错误!未找到引用源。
错误!未找到引用源。
X = 错误!未找到引用源。
错误!未找到引用源。
X + 错误!未找到引用源。
×错误!未找到引用源。
= 错误!未找到引用源。
错误!未找到引用源。
X - 错误!未找到引用源。
= 错误!未找到引用源。
错误!未找到引用源。
X = 错误!未找到引用源。
X - 错误!未找到引用源。
= 18X + 错误!未找到引用源。
X = 错误!未找到引用源。
7X÷错误!未找到引用源。
= 错误!未找到引用源。
7X- 错误!未找到引用源。
X = 错误!未找到引用源。
错误!未找到引用源。
X + 错误!未找到引用源。
= 错误!未找到引用源。
错误!未找到引用源。
X÷错误!未找到引用源。
= 错误!未找到引用源。
错误!未找到引用源。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
六年级分数解方程
引言
在六年级研究中,我们经常会遇到一些关于分数的方程问题。
解决这些问题需要掌握一些基本的解方程方法。
本文将介绍几种常见的六年级分数解方程方法供大家参考。
一、通分法
当我们遇到含有不同分母的分数方程时,可以通过通分的方法将分数的分母变得相同,从而简化方程。
假设我们有以下方程:
$\frac{2}{3}x + \frac{1}{4} = 2$
我们可以将分数的分母都乘以一个相同的数,从而得到相同分母的方程:
$4\times\frac{2}{3}x + 4\times\frac{1}{4} = 4\times2$
化简得到:
$\frac{8}{12}x + \frac{4}{12} = 8$
继续化简得到:
$\frac{8x + 4}{12} = 8$
接下来,我们可以通过消去分母的方法求解方程,得到:$8x + 4 = 8\times12$
化简得到:
$8x + 4 = 96$
继续化简得到:
$8x = 96 - 4$
化简得到:
$8x = 92$
最后,我们可以通过除以常数的方法解出未知数x的值,得到:$x = \frac{92}{8}$
化简得到:
$x = \frac{23}{2}$
因此,方程的解为$x = \frac{23}{2}$。
二、化简法
有些分数方程可能存在化简的机会,利用化简可以更快地解决
方程。
例如,我们有以下方程:
$\frac{3}{5} + \frac{1}{5}x = 2$
我们可以首先通过化简将方程简化为:
$\frac{3 + x}{5} = 2$
接下来,我们可以将等式两边都乘以5,得到:
$3 + x = 2\times5$
化简得到:
$3 + x = 10$
最后,我们可以通过减去常数的方法解出未知数x的值,得到:$x = 10 - 3$
化简得到:
$x = 7$
因此,方程的解为$x = 7$。
三、分数相消法
在一些分数方程中,可能会存在可以相消的分数。
例如,我们有以下方程:
$x - \frac{2}{3} = \frac{4}{5}$
我们可以通过将两个分数的分母相乘,得到分数相消的机会。
首先,我们将方程转化为相同分母的方程:
$5x - \frac{10}{3} = \frac{4}{5}\times5$
化简得到:
$5x - \frac{10}{3} = 4$
接下来,我们可以相消分数,得到:
$5x = 4 + \frac{10}{3}$
化简得到:
$5x = \frac{12}{3} + \frac{10}{3}$
继续化简得到:
$5x = \frac{22}{3}$
最后,我们可以通过除以常数的方法解出未知数x的值,得到:$x = \frac{22}{3}\div5$
化简得到:
$x = \frac{22}{15}$
因此,方程的解为$x = \frac{22}{15}$。
结论
通过通分法、化简法和分数相消法,我们可以解决六年级分数解方程问题。
这些方法可以帮助我们更好地理解和解决方程问题,提升数学能力。
以上为六年级分数解方程的学习文档,希望对大家有所帮助。
