CEI对静止轨道共位卫星的轨道确定
轨道卫星运动位置计算

轨道卫星运动位置计算轨道卫星的位置计算是航天领域中的重要任务之一,它对于实现通信、导航、气象监测等功能起着至关重要的作用。
本文将介绍轨道卫星运动位置计算的基本原理和方法。
一、轨道卫星的运动模型轨道卫星的运动可以用开普勒运动模型来描述。
开普勒运动模型假设行星围绕太阳运动,且太阳是一个质点,不考虑行星之间的相互作用。
同样,我们也可以假设卫星围绕地球运动,且地球是一个质点,不考虑卫星之间的相互作用。
根据开普勒第一定律,轨道卫星围绕地球运动的轨道是一个椭圆。
椭圆的两个焦点分别为地球的中心和轨道中心。
卫星在轨道上运动时,地球的位置可以通过确定轨道的半长轴、半短轴、离心率和轨道的倾角等参数来计算。
二、轨道卫星位置计算方法轨道卫星的位置计算方法主要包括传统方法和现代方法。
传统方法主要是利用开普勒的数值解来计算卫星的位置。
现代方法主要是利用数值计算方法和遥测数据来进行计算。
1.传统方法传统的轨道卫星位置计算方法主要有两种:开普勒法和摄动法。
开普勒法是根据开普勒第三定律和数值解方法来计算卫星的位置。
它首先确定半长轴、离心率和轨道的倾角等参数,然后通过数值积分的方法来模拟卫星的运动,得到卫星的位置和速度。
摄动法是在开普勒法的基础上考虑了一些外力的作用,如地球引力、月球引力和太阳引力等。
这些外力会对卫星的轨道产生一定的影响,通过考虑这些影响可以提高计算的精度。
2.现代方法现代方法主要是利用数值计算方法和遥测数据来计算轨道卫星的位置。
数值计算方法主要是利用数值积分的方法来模拟卫星的运动。
通过数值计算模型,可以根据卫星的初始位置和速度来计算卫星在未来一些时刻的位置和速度。
遥测数据是通过各种测量手段来获取的卫星的相关数据,如卫星的位置、速度和加速度等。
通过分析这些数据,可以获得卫星的运动状态,并进一步计算出卫星的位置。
在实际的轨道卫星位置计算中,通常会结合使用传统方法和现代方法,以提高计算的准确性和稳定性。
三、轨道卫星位置计算的应用轨道卫星的位置计算应用广泛,主要包括通信、导航、气象监测和科学研究等领域。
基于Ku波段CEI的GEO卫星定轨特性

导航定位学报Journal of Navigation and Positioning 第9卷第1期2021年2月Vol.9, No. 1Feb., 2021引文格式:刘泽军,杜兰,张栩晨,等.基于Ku 波段CEI 的GEO 卫星定轨特性[J].导航定位学报,2021, 9(1): 38-43. (LIU Zejun,DULan,ZHANG Xuchen,et al.Analysis on orbit determination of GEO satellite based on Ku-band CEI[J].Journal of Navigation and Positioning, 2021, 9(1): 38-43.) DOI: 10.16547/ki. 10-1096.20210107.基于Ku 波段CEI 的GEO 卫星定轨特性刘泽军1,杜 兰1,张栩晨1,黄晓霞2(1.信息工程大学,郑州 450001; 2. 61085部队,杭州 311200)摘要:为了进一步提高共位地球静止轨道(GEO )卫星实时监测的精度,提出1种GEO 卫星轨道确定方法:利用L型正交双基线Ku 频段连续干涉测量(CEI )测量系统进行干涉测量;利用双行轨道根数(TLE )作为先验轨道信息,确 定整周模糊度,采用批处理算法获得GEO 卫星的精密轨道。
实验结果表明:Ku 频段受对流层影响显著,冬季大气较夏季更稳定,信号空间传输路径中的对流层误差基本可以抵消,使得观测数据质量明显好于夏季;夏季的晚间数据质量好 于白天;冬季和夏季的内符合精度差别较小,而冬季的外符合精度明显高于夏季;外符合精度变化规律一致,且存在明显的趋势项,表明夏季和冬季观测数据都存在一定的系统误差。
关键词:连线干涉测量;Ku 波段;地球静止轨道卫星;轨道确定中图分类号:P 228 文献标志码:A 文章编号:2095-4999(2021)01-0038-06Analysis on orbit determination of GEO satellite based on Ku-band CEILIU Zejun 1, DU Lan', ZHANG Xuchen', HUANG Xiaoxia(1. Information Engineering University, Zhengzhou 450001, China; 2. Troops 61085, Hangzhou 311200, China )Abstract : In order to further improve the real-time monitoring accuracy of co-located Geostationary Earth Orbit (GEO) satellites, the paper proposed a GEO orbit determination method: the L-type orthogonal double baseline Ku band of Connected Element Interferometry (CEI) measurement system was used to do interferometry; meanwhile, Two Line Element(TLE) was used as prior orbit information to determine the ambiguity of the whole cycle, and the precise orbit of GEO satellite was obtained by batch processing algorithm. Experimental result showed that: due to the significant effect of thetroposphere on Ku band, the atmosphere would be more stable in winter than in summer, and the troposphere error in thesignal spatial transmission path could be basically offset, leading to the better observation data of winter compared to summer; while the data quality of evening would be better than that of daytime in summer; there would be little difference of internalcoincidence accuracy between winter and summer, while the external coincidence accuracy in winter would be significantlyhigher than that in summer; moreover, in addtion to an obvious trend term, the variation law of external coincidence accuracyin both seasons could be consistent, indicating that there would be certain systematic error in the observation data of bothsummer and winter.Keywords: connected-element interferometry; Ku band; geostationary Earth orbit satellite; orbit determination0引言为了充分利用有限的地球静止轨道(geostationary Earth orbit, GEO )资源,分属不同收稿日期:2020-07-01基金项目:国家自然科学基金项目(41804034, 41774038)。
gps星座轨道参数

gps星座轨道参数1.引言1.1 概述概述部分的内容是对GPS星座轨道参数这个主题进行简要介绍。
在这一部分,我们可以提到GPS星座是由一组卫星组成的系统,其目的是为全球定位系统(GPS)提供准确的定位信息。
每颗卫星都绕地球以特定的轨道运行,这些轨道参数对于GPS系统的正常运行至关重要。
GPS星座轨道参数包括卫星的轨道高度、轨道倾角、升交点经度以及轨道偏心率等。
轨道高度决定了卫星与地球之间的距离,而轨道倾角则影响了卫星在天空中的位置。
升交点经度表示了卫星轨道与地球赤道的交点位置,而轨道偏心率则反映了卫星轨道的离心程度。
通过精确控制GPS星座轨道参数,可以保证卫星系统的稳定性和可靠性。
这些轨道参数的调整需要考虑许多因素,如地球引力、大气阻力和其他卫星的相互干扰等。
同时,精确的轨道参数还能够为GPS用户提供更准确的定位和导航服务。
在本文中,我们将详细介绍GPS星座轨道参数的相关知识,并分析其对于GPS系统性能的影响。
通过深入探讨这些参数的特点和调整方法,我们旨在为读者提供更全面、准确的了解,并为相关领域的研究和应用提供参考依据。
1.2 文章结构文章结构部分内容如下:文章结构部分将介绍本文的组织结构和章节安排,以帮助读者更好地了解全文的内容。
本文共分为三个部分:引言、正文和结论。
在引言部分,我们将概述本文的主题和背景,并说明本文的目的。
首先,我们将简要介绍GPS星座和其在定位导航系统中的重要性。
接下来,我们将阐述全文的目标和意义,以引发读者的兴趣并概括本文的核心内容。
正文部分是本文的主体部分,分为两个小节:GPS星座和轨道参数。
在GPS星座小节中,我们将详细介绍GPS星座的概念、构成和功能。
我们将讨论GPS星座的组成要素,包括卫星和地面控制部分,并解释它们在GPS系统中的作用。
然后,我们将深入探讨轨道参数的重要性和定义,并解释它们对GPS星座的影响。
结论部分将对本文进行总结并展望未来的发展方向。
我们将概括本文的主要观点和结论,并提供一些关于GPS星座轨道参数研究的展望。
一种基于CEI的GEO目标滑窗式机动探测方法

一种基于CEI的GEO目标滑窗式机动探测方法
黄俊迦;杜兰;刘泽军;张中凯;周佩元;刘隆迪
【期刊名称】《导航定位学报》
【年(卷),期】2024(12)1
【摘要】为了进一步提升地面跟踪站的监视预警能力,提出一种基于连线相位干涉测量(CEI)的地球静止轨道(GEO)目标滑窗式机动探测方法:立足于CEI的GEO短弧段定轨和预报,基于GEO卫星位保机动的持续小推力和轨道缓慢渐变特性,提出一种针对GEO目标尤其是非合作GEO目标的滑窗式准实时机动探测方法;并利用亚太七号和中星十号卫星的CEI仿真和实测数据进行机动探测。
结果表明,东西机动和南北机动捕获与卫星发动机的点火时刻基本保持一致,机动探测延迟量均小于10 min;能够实现GEO目标的准实时机动告警。
【总页数】6页(P79-84)
【作者】黄俊迦;杜兰;刘泽军;张中凯;周佩元;刘隆迪
【作者单位】信息工程大学地理空间信息学院
【正文语种】中文
【中图分类】P228
【相关文献】
1.一种高超声速机动目标双(多)基地雷达探测方法
2.基于滑窗式单帧红外弱小目标检测方法研究
3.基于图像叠加的GEO目标探测方法
4.基于超同步轨道的GEO目标天基近实时探测方法
5.一种多雷达机动目标探测高阶运动特征估计方法
因版权原因,仅展示原文概要,查看原文内容请购买。
判断卫星同轨的方法

判断卫星同轨的方法卫星同轨现象在航天领域具有重要的研究价值,对于了解宇宙空间环境、保障卫星安全运行等具有重要意义。
本文将详细介绍如何判断卫星同轨的方法。
一、卫星同轨概念卫星同轨是指两颗或多颗卫星在空间轨道上的位置和速度相同或相近,使得它们在一段时间内相对静止或保持相对稳定的距离。
这种现象通常出现在地球同步轨道、太阳同步轨道等特定轨道上。
二、判断卫星同轨的方法1.观测数据分析通过对卫星的观测数据进行处理和分析,可以判断卫星是否处于同轨状态。
观测数据包括卫星的轨道根数、位置、速度等。
具体方法如下:(1)计算卫星之间的相对距离和相对速度。
若相对距离较小,且相对速度接近零,则可能表明卫星处于同轨状态。
(2)分析卫星轨道根数的差值。
若两颗卫星的轨道根数(如半长轴、偏心率、倾角等)相差很小,说明它们可能处于同轨状态。
2.卫星轨道预报通过对卫星轨道进行预报,可以预测卫星在未来一段时间内的相对位置关系。
若预测结果显示卫星在一段时间内保持相对静止或相对稳定距离,则可以判断它们处于同轨状态。
具体方法如下:(1)利用卫星轨道动力学模型,如开普勒定律、牛顿运动定律等,对卫星轨道进行预报。
(2)根据预报结果,分析卫星之间的相对位置和速度关系,判断是否满足同轨条件。
3.卫星跟踪与测距通过卫星跟踪和测距技术,可以实时监测卫星之间的相对位置和距离。
以下方法可用于判断卫星同轨:(1)使用地面跟踪站对卫星进行跟踪观测,获取卫星的位置和速度数据。
(2)利用卫星激光测距、雷达测距等技术,精确测量卫星之间的距离。
(3)分析测量数据,判断卫星是否处于同轨状态。
三、结论通过以上方法,我们可以较为准确地判断卫星是否处于同轨状态。
这些方法为航天领域的研究提供了有力支持,有助于了解宇宙空间环境,保障卫星安全运行。
航天器制导与控制课后题答案(西电)

航天器制导与控制课后题答案(西电)1.3 航天器的基本系统组成及各部分作用?航天器基本系统一般分为有效载荷和保障系统两大类。
有效载荷:用于直接完成特定的航天飞行任务的部件、仪器或分系统。
保障系统:用于保障航天器从火箭起飞到工作寿命终止, 星上所有分系统的正常工作。
1.4 航天器轨道和姿态控制的概念、内容和相互关系各是什么?概念:轨道控制:对航天器的质心施以外力, 以有目的地改变其运动轨迹的技术; 姿态控制:对航天器绕质心施加力矩, 以保持或按需要改变其在空间的定向的技术。
内容:轨道控制包括轨道确定和轨道控制两方面的内容。
轨道确定的任务是研究如何确定航天器的位置和速度, 有时也称为空间导航, 简称导航; 轨道控制是根据航天器现有位置、速度、飞行的最终目标, 对质心施以控制力, 以改变其运动轨迹的技术, 有时也称为制导。
姿态控制包括姿态确定和姿态控制两方面内容。
姿态确定是研究航天器相对于某个基准的确定姿态方法。
姿态控制是航天器在规定或预先确定的方向( 可称为参考方向)上定向的过程, 它包括姿态稳定和姿态机动。
姿态稳定是指使姿态保持在指定方向, 而姿态机动是指航天器从一个姿态过渡到另一个姿态的再定向过程。
关系:轨道控制与姿态控制密切相关。
为实现轨道控制, 航天器姿态必须符合要求。
也就是说, 当需要对航天器进行轨道控制时, 同时也要求进行姿态控制。
在某些具体情况或某些飞行过程中,可以把姿态控制和轨道控制分开来考虑。
某些应用任务对航天器的轨道没有严格要求, 而对航天器的姿态却有要求。
1.5 阐述姿态稳定的各种方式, 比较其异同。
姿态稳定是保持已有姿态的控制, 航天器姿态稳定方式按航天器姿态运动的形式可大致分为两类。
自旋稳定:卫星等航天器绕其一轴(自旋轴) 旋转, 依靠旋转动量矩保持自旋轴在惯性空间的指向。
自旋稳定常辅以主动姿态控制, 来修正自旋轴指向误差。
三轴稳定: 依靠主动姿态控制或利用环境力矩, 保持航天器本体三条正交轴线在某一参考空间的方向。
【国家自然科学基金】_精密轨道确定_基金支持热词逐年推荐_【万方软件创新助手】_20140801
2014年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
2014年 科研热词 测定轨 星间链路 全球卫星导航系统 中高轨航天器 飞行器 雷达测量 识别算法 精密轨道确定 空间相机 空间目标 稀疏数据 法方程叠加 姿态参数 坐标变换 初始轨道 分网定轨 igs站 gps导航星座 推荐指数 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1
推荐指数 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2013年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42
2008年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22
科研热词 高分辨力可见光相机 非差 谱分析 精密定轨 空间相机 测距偏差 模型补偿 抗差估计 小波分析 导航卫星 定轨 天基空间目标监视系统 天体测量学 地心运动 可观测性 初轨确定 光学系统设计 光学传递函数 panda软件 giove-a galileo卫星导航系统 champ
推荐指数 3 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2011年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27
基于CEI的航天器交会对接段的轨道监控
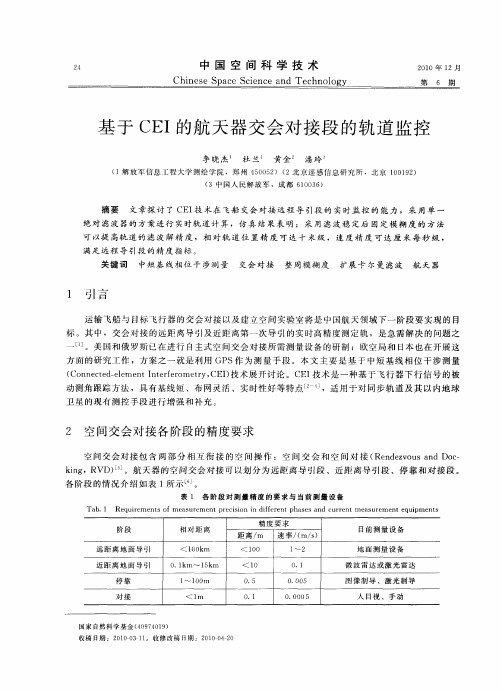
+ N 一 一 一 JA £ 一,£ J j ) ( J A。k P +△ …+£ () R ( ) ( ) — R ( ~, 。 )+C t +△ … 1 0 1
式中 和 N 分别 为相 位观 测量 和整 周模 糊 度 ; 为卫 星 下 行波 段
的信号 波长 ;r币 、R 眦 分别 为卫 星 和基 线 两端 台 站 A、B的位 置 向量 ;A 为 两 站 钟差 互 差 ;△ 为 站 问 大 气传 播 延 迟 的残 已在进行 自主式 空间交会 对接所需 测量设 备 的研 制 ;欧空局 和 日本也 在开展 这
方面 的研 究工作 ,方案 之一就 是利用 GP S作 为测 量手 段 。本 文 主要是 基 于 中短基 线 相位 干涉 测 量
( o n ce —lme tItreo ty C I技 术展开讨 论 。C I C n etde e n n efr mer , E ) E 技术 是一种 基 于飞行器 下行 信号 的被
关键词 中短 基线相位 干 涉测量 交会 对接
整周模 糊度
扩展卡 尔曼滤波
航 天器
1 引 言
运输 飞船 与 目标 飞行器 的交会对 接 以及建 立空 问实验室将 是 中国航天 领域下 一阶段 要实现 的 目 标 。其 中 ,交会 对接 的远距离 导引及 近距离第 一次导 引 的实 时高精度 测定轨 ,是 急需 解决 的问题 之
差 ,包括对 流层 和 电离 层 的传 播误 差 的影 响 ;A 为仪 器 延迟 引起 p 的距离误差 ;e 观测 噪 声 。这 样 ,每 个 时刻 均 得 到 两条 基 线 上 的 为 两 个高精度 观测量 。由于卫 星轨 道误 差 绝 大部 分体 现 在它 在 有效 基 线 方 向上 的投影 ,因此 两条 正交 基线 是 决定 静地 卫 星 二维 角 坐标 及 其变 化信息 所必需 的 ,结 合 卫 星 的动力 学模 型 ,就 能 够确 定完 整 的
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第36卷第5期2011年5月武汉大学学报 信息科学版Geo matics and Informat ion Science of W uhan U niver sity V ol.36N o.5M ay 2011收稿日期:2011 03 15。
项目来源:国家自然科学基金资助项目(40974019)。
文章编号:1671 8860(2011)05 0605 04文献标志码:ACEI 对静止轨道共位卫星的轨道确定李晓杰1 杜 兰1 黄 金2(1 信息工程大学测绘学院,郑州市陇海中路66号,450052)(2 61768部队,三亚市田独镇2019信箱,572011)摘 要:主要考察了CEI 对静止轨道共位卫星的轨道确定能力。
仿真结果表明,利用CEI 对共位卫星进行定轨时,需采用基线阵列。
对于110 E 共位卫星采用三亚 昆明基线阵列、10km 基线和2d 的数据,可使绝对轨道精度达百米级;外推至14d 时,相对轨道精度保持在m 级。
同样,要使绝对和相对轨道精度达到相同的量级,对于80 E 共位卫星,需选用昆明 三亚基线阵列、100km 基线和1d 的观测弧段;对于140 E 共位卫星,需选用上海 三亚基线阵列、50km 基线和2d 的观测弧段。
关键词:CEI;地球静止轨道;多星共位;基线阵列;精密定轨中图法分类号:P228.1自20世纪70年代末国外提出地球静止轨道多星共位技术以来,一点多星技术既充分利用了轨道资源,又增加了某一轨道位置的通信容量。
目前,采用多星共位技术共位卫星的数量多为2颗,双星共位技术的研究是今后多星共位发展的基础[1]。
在共位卫星所研究的问题中,防止卫星相互碰撞是最基本的问题。
为了防止在同一经度窗口中的共位卫星发生潜在的相互碰撞,应对其进行高精度的轨道确定和轨道预报,间隔一定的时间进行一次定点保持机动[2 4]。
相位干涉测量是一种基于飞行器下行信号的被动测角跟踪方法,其中中短基线相位干涉测量(co nnected element interferometry,CEI)通过一条光纤通信链路向相距10~100km 的两个地面站发送同一个频率标准,两站之间形成一条短基线,用它可以精确测量航天器发射来的载波信号在两个站之间的相位延迟,从而精确测角,是国外广泛使用的一种中精度角度测量系统。
CEI 技术具有基线短、布网灵活、实时性好等特点,非常适用于对同步轨道及其以内地球卫星的现有测控手段进行增强和补充[5,6]。
日本早在80年代末已将短基线相位干涉技术用于并轨的同步卫星间的实时精密轨道监控,而俄罗斯一直把短基线相位干涉作为低轨卫星的日常监测技术[7]。
我国短基线相位干涉技术多年来集中应用在技术侦察部门,具有较好的设备和技术力量。
本文以CEI 差分相位延迟为观测量,讨论了采用单组CEI 基线和基线阵列时定点在110 E 共位双星的绝对、相对轨道精度,并给出了分别定点在80 E 和140 E 共位双星的轨道精度。
1 CEI 差分相位干涉延迟测量的定轨原理对测量精度要求较高的近距离导引段两航天器的距离较近,影响测量精度的各种误差具有较强的相关性,因此,观测量选取差分CEI,组差以后可以消去大部分误差项。
相位干涉测量得到的是同一个信号波前到达基线两端天线的相对相位。
选择合适的两条长度为数十至数百公里的正交基线建立三个测站,每条基线上,如果在某时段内能同时观测到目标附近的一个轨道精确已知的参考源(如射电源或其他GEO 卫星等),则有差分相位干涉观测方程[5]:+ N =R A (t 1)-r(t 0)-RB (t 2)-r(t 0)-R A (t 1)-r0(t 0)+RB (t 2)-r0(t 0)+ atm + ins + d + (1)其中, 和 N 分别为相位观测量之差和整周模武汉大学学报 信息科学版2011年5月糊度之差;R A、R B、r 和r 0分别为测站1、测站2、目标星和参考星在天球坐标系中的位置向量;a tm是大气传播延迟的残余误差; ins是仪器延迟引起的距离误差; d为测角系统延迟偏差; 为观测噪声。
这样,每个时刻均得到两条基线上的两个高精度差分相位观测量。
由于卫星轨道误差绝大部分体现在它在有效基线方向上的投影,因此两条正交基线是决定静地卫星二维角坐标及其变化信息所必需的,结合卫星的动力学模型,就能够确定完整的轨道状态。
2 轨道仿真方案确定2.1 仿真条件1)卫星的初始时刻轨道选取。
初始历元时刻为U TC2008 7 112:00:00,该时刻定点在80 E、110 E、140 E上的GEO共位卫星分别是sat1和sat2、sat3和sat4、sat5和sat6,其轨道数据由STK生成(见表1,其中 =42162.5km),精确的轨道用于观测量的模拟。
2)自然摄动以及定点误差的共同作用使卫表1 各卫星的初始轨道根数T ab.1 Initia l O rbit Ro ots of Satellit es卫星e i/( ) /( ) /( )M/( )星下点经度s at1/3/50.0002310.063328133.729/163.729/193.729259.823146.24680.005/110.005/140.005 s at2/4/60.00021470.088195.624/225.625/255.624253.96390.220179.986/109.986/139.986星相对于标称经度存在长期漂移。
在ST K中,可以仿真得到共位双星4d内的星下点轨迹图。
3)两颗共位卫星的面质比相同,1d内相对距离在16.83~60.05km之间变化,相对于测控站的夹角在0.01 以内,在测控站天线的同一波束角内。
3)由于GEO卫星的静地特性,在短弧段内,可将各基线测角系统延迟偏差等效为常值系统误差,其对共位双星之差取为1cm,观测噪声误差取为8mm。
4)动力学模型中,采用JGM 3的20 20阶重力场、日月引力摄动和光压摄动力模型。
两颗卫星的状态量同时进行求解,待估参数还包括光压参数和常值系统参数。
初始轨道位置误差为1 km,速度误差为0.1m/s。
2.2 仿真流程及精度评定方法[8,9]为更真实地反映各误差源对定轨结果的影响,可采用统计的方法[10]对外符合精度进行评定。
仿真流程如下: 首先模拟一条真实轨道,并根据观测方程模拟含有随机噪声和系统噪声的观测数据文件(假定相位模糊度之差已知); 根据先验轨道的误差,采用批处理的方法解算初始时刻的轨道[11]; 重新产生随机噪声进行轨道解算。
利用40组观测数据文件的解算结果进行统计分析。
在每个观测及外推时刻,分别比较 真实轨道 和解算出的轨道在径向(R)、沿迹向(T)、法向(N)上的位置误差,得到 i,再利用式(2)得到位置三分量的误差 ,=i2N=(x i-a)2N(2)其中,x i(i=1, ,N)为由历元的定轨结果进行轨道外推的一列轨道量;a为由历元的标准轨道进行轨道外推值。
将计算出的标准误差 作为此次定轨的绝对轨道精度,每个观测时刻及外推时刻的绝对位置误差作差即为此时刻的相对位置误差,仍以式(2)得到此次定轨的相对轨道精度。
2.3 轨道仿真方案考察CEI正交双基线组对卫星的绝对及相对定轨能力,从以下几方面进行分析: 对于110 E的共位卫星,分别考察单组基线、基线阵列的绝对、相对定轨能力; 采用不同的观测弧长、不同的基线长度进行轨道计算,当观测弧长为1d 时,外推弧段取至7d;当观测弧长为2d时,外推弧段取至14d; 采用基线阵列对定点于80 E、140 E的共位卫星进行轨道计算。
3 110 E共位卫星的定轨结果分析3.1 采用单组基线的定轨精度对于单颗卫星,单组基线应布设在离星下点最近的位置;相同的基线长度,正交基线组以V型布设时,定轨精度最高[13]。
因此,单组基线以V型布设在三亚,基线长度分别取10km、50km、100km,观测弧段分别取1d、2d。
绝对、相对定轨结果见表2。
10km基线采用2d观测弧段的相对轨道外推图见图1(a),其外推弧段中R、T、N方向的最大误差值分别为-22.2m、-14.5m、-0.9m。
606第36卷第5期李晓杰等:CEI对静止轨道共位卫星的轨道确定图1 外推相对轨道在R 、T 、N 方向的误差图Fig.1 Relat ive O rbit Er ro r in R,T ,N in theEx tr apo lation A rc由表2中不同基线长度和观测弧段下的定轨结果可知: 利用单组基线对共位卫星进行定轨,绝对轨道精度较差。
10km 基线采用2d 的数据或采用50km 和100km 基线时,绝对轨道精度达百m 级; 相对定轨精度可达几十m 级甚至m 级,10km 采用2d 的数据或采用50km 和100km 基线时,相对轨道精度达m 级; 观测弧长越长,基线长度越长,定轨精度越高。
由图1(a)可以看出,相对轨道误差随着时间的推移而逐步放大,当外推到第14d 时,误差在R 、T 方向分别达到了22.2m 、14.5m,值较大。
要把相对轨道误差值控制在10m 以内,就只能外表2 各卫星的绝对和相对定轨精度T ab.2 Absolute and Relative Or bit Determ inat ion A ccuracy基线长度/k m 1d/m 2d/m R /mT /mN /msat3sat4s at3sat41d 2d 1d 2d 1d 2d 不同基线长度、不同观测弧度下的定轨精度105316.95306.7576.3572.210.89 2.6423.859.280.710.1650517.4516.8397.9399.3 3.670.568.68 1.070.340.39100490.4490.1398.3400.5 1.840.33 4.210.570.390.42昆明 三亚基线阵列的定轨精度106896.16903.4417.3417.3 6.140.8015.40 1.870.350.4350698.7699.6159.4159.52.480.145.571.160.310.03推至4d,外推弧段较短。
3.2 采用基线阵列的定轨精度单组基线分别布设在昆明和三亚,两组基线的配置相同,定轨结果见表2。
10km 基线长度采用2d 观测弧段的相对轨道外推图见图1(b)。
由表2中昆明 三亚基线阵列的定轨结果可知,采用1d 弧段时,绝对轨道精度有所降低,主要是因为昆明站的加入所致;单站定轨时,三亚站的定轨精度高于昆明站,并且弧段较短。
基线阵列的绝对定轨精度(2d 弧段)和相对定轨精度均高于单站,但无量级上的提高。
但由图1(a)可以看出,当轨道外推至第14d 时,相对轨道各方向的误差仍在m 级以内。
