电场强度及其叠加原理
场强叠加原理公式

场强叠加原理公式
电场场强叠加原理公式:
电场场强叠加原理公式表达的是两个电场的场强叠加,其数学表达式可以用下列公式表示:
E=E1+E2
其中E是两个电场在某一空间点的叠加电场强度,E1表示第一个电场在该点的电场强度,E2表示第二个电场在该点的电场强度。
磁场场强叠加原理公式:
磁场场强叠加原理公式也可以表示为两个磁场的场强叠加,其数学表达式可以用下列公式表示:
B=B1+B2
其中B是两个磁场在某一空间点的叠加磁场强度,B1表示第一个磁场在该点的磁场强度,B2表示第二个磁场在该点的磁场强度。
电磁波场强叠加原理公式:
电磁波场强叠加原理公式可以表示为两个电磁波的场强叠加,其数学表达式可以用下列公式表示:
E=E1+E2
B=B1+B2
其中E和B分别是两个电磁波在某一空间点的叠加电场和叠加磁场强度;E1和B1表示第一个电磁波在该点的电场和磁场强度;E2和B2表示第二个电磁波在该点的电场和磁场强度。
总之,场强叠加原理公式是电磁学中十分重要的公式,它可以帮助我们计算和预测电磁场的变化和传播规律。
在实际应用中,我们可以利用该原理来分析、设计和优化电磁设备和系统,从而提高其性能和可靠性。
电场叠加原理

电场叠加原理
电场叠加原理是电学中的一个重要概念,它描述了当存在多个电荷或电场时,它们对某一点的作用效果等于各个电荷或电场分别作用时的效果之和。
这一原理在电学领域有着广泛的应用,对于理解和分析电场的行为具有重要意义。
首先,我们来看一下电场叠加原理的基本表达式。
设有n个点电荷q1、q2、
q3...qn,分别位于r1、r2、r3...rn处,那么在某一点P处的电场强度E等于各个点电荷对该点产生的电场强度之和,即E=E1+E2+E3...+En。
其中Ei表示第i个点电荷对点P产生的电场强度。
这就是电场叠加原理的数学表达形式。
接下来,我们来看一些电场叠加原理的应用。
在实际问题中,往往会存在多个电荷或电场对某一点产生作用的情况,这时就可以利用电场叠加原理来求解问题。
比如,当有多个点电荷分布在空间中时,我们可以通过叠加原理来计算某一点的电场强度,从而分析该点的受力情况。
又如,在电容器中,如果存在多个电荷,我们也可以利用叠加原理来计算电容器的总电荷或总电场强度。
此外,电场叠加原理还可以帮助我们理解电场的叠加规律。
在空间中,如果存在多个电场,它们会相互叠加,形成一个合成的电场分布。
这时,我们可以利用叠加原理来分析合成电场的性质,从而更好地理解电场的行为。
总的来说,电场叠加原理是电学中一个非常重要的概念,它对于理解和分析电场问题具有重要意义。
通过对叠加原理的理解和运用,我们可以更好地解决电场问题,提高对电场行为的认识,为实际问题的分析和应用提供有力的支持。
因此,在学习电学知识的过程中,我们应该深入理解电场叠加原理,并灵活运用它来解决问题。
电场强度的叠加原理

电场强度的叠加原理
电场强度是描述电场强度大小的物理量,它的单位是高斯。
对于任意的一个点电荷,电场线的位置由该点电荷所受电场力的
方向和该点位置与该点电荷的电势差的方向共同决定。
我们知道,电场强度只与电荷有关,与电荷位置无关。
那么,电场强度的大小又由什么决定呢?这是因为:
(1)点电荷所在的位置与该点处电场强度的方向是互相垂
直的;
(2)一个点电荷所受电场力与它所在位置之间没有空间距离;
(3)一个点电荷所受电场力,是由它周围电场强度的叠加
而成的。
因此,在某一点附近,在一定范围内,其电场力之和等
于该点所受电场力。
我们可以这样来理解:如果我们在一个平面内画出一条平行线,那么在这条平行线上所有点的电场力之和等于它在这条平行
线上各点所受电场力之和。
很明显,电场强度可以看作是一种均
匀分布的力。
— 1 —
这样我们就把电场强度描述为场强叠加原理在整个空间中任意一点附近所产生的场强。
这样我们就得到了一个矢量,即:场强=电场强度矢量+电势差。
— 2 —。
用叠加原理求电场强度和电场力

用叠加原理求电场强度和电场力叠加原理是一种基本的电磁学原理,用于求解由多个电荷产生的电场的问题。
该原理基于电场是一个线性物理量的事实,即当有多个电荷同时存在时,它们各自产生的电场矢量可以简单地叠加在一起。
根据叠加原理,如果在空间中有多个电荷,那么在其中一点的电场强度是所有电荷在该点产生的电场强度的矢量和。
假设有n个电荷qi(i=1,2,...,n),其位置矢量为ri(i=1,2,...,n),则该点的电场强度E为:E=E1+E2+...+En其中,Ei是电荷qi在该点产生的电场强度。
根据库仑定律,电荷qi产生的电场强度Ei可以表示为:Ei = k * qi / ri^2 * ri/,ri其中,k为库仑常数,ri^2为电荷qi与该点的距离的平方, ri/,ri,为单位化的位置矢量。
由于电场是一个矢量量,所以叠加原理不仅适用于电场强度的叠加,也适用于电场力的叠加。
根据叠加原理,多个电荷对其中一点的电场力可以简单地叠加在一起。
假设有两个电荷q1和q2,在其中一点产生的电场力F可以表示为:F=F1+F2其中,F1为电荷q1对该点的电场力,F2为电荷q2对该点的电场力。
根据库仑定律,电荷q1对该点的电场力F1可以表示为:F1=k*q1*q/r^2*r/,r类似地,电荷q2对该点的电场力F2可以表示为:F2=k*q2*q/r^2*r/,r其中,r是该点与电荷q的距离,r/,r,是单位化的位置矢量。
通过以上的推导,我们可以使用叠加原理来求解由多个电荷产生的电场强度和电场力。
只需要计算每个电荷对其中一点的电场强度和电场力,然后将它们简单地叠加在一起即可。
需要注意的是,在实际应用中,叠加原理适用于处于远距离的电荷,也就是说两个电荷之间的距离要相对较大,以保证不会发生明显的相互作用影响。
如果两个电荷之间的距离较小,则必须考虑它们之间的相互作用效应,此时只使用叠加原理将得到不准确的结果。
除了叠加原理,还有一种更简单的方法来求解由多个电荷产生的电场强度和电场力,那就是使用超级叠加原理。
电场强度的叠加原理

电场强度的叠加原理嘿,咱们今天来聊聊电场强度的叠加原理。
你知道吗,这电场强度的叠加原理就像是一群小伙伴一起用力推一个大箱子。
每个人使的力大小和方向都不太一样,但是最后箱子受到的总的推力,就是把每个人的力加起来。
就说我之前有一次去看孩子们拔河比赛吧。
两队小朋友,每队都有十来个人,大家都紧紧拽着绳子,拼命往后拉。
这时候,每个人的力量就好像是电场中的一个电场强度。
有的小朋友力气大,有的小朋友力气小,有的往左边使劲儿,有的往右边使劲儿。
但是最后决定绳子往哪边移动的,可不是看某一个人的力量,而是把所有人的力量加在一块儿。
咱们回到电场强度的叠加原理上来。
假如在一个空间里,有两个点电荷,一个带正电,一个带负电。
那么正电荷会产生一个向外的电场,负电荷会产生一个向里的电场。
这两个电场在空间中的每一点相互叠加。
就好像拔河比赛中两队小朋友的力量在绳子上的每一点相互作用一样。
再比如说,在一个房间里,同时开着几台风扇。
每台风扇吹出的风都有自己的方向和速度,这就相当于每个点电荷产生的电场。
而房间里最终感受到的风的情况,就是把每台风扇吹出的风加在一起。
这就是电场强度的叠加原理在生活中的一个类比。
如果空间中有多个点电荷,那情况就更复杂啦。
但原理还是一样,就是把每个点电荷在某一点产生的电场强度按照矢量的加法法则加起来。
这就像是一群小朋友在操场上乱跑,每个人的速度和方向都不一样,要想知道在某个点上,这群小朋友总的运动趋势,就得把每个人的速度矢量加起来。
咱们来做个简单的计算。
假设有一个正电荷 Q1 在坐标原点,产生的电场强度为 E1;还有一个负电荷 Q2 在(a, 0) 点,产生的电场强度为 E2。
那么在点(x, y) 处的总电场强度 E 就等于 E1 + E2。
通过库仑定律和电场强度的公式,咱们就能算出具体的数值和方向。
在实际应用中,电场强度的叠加原理用处可大了。
比如说在电路设计中,电子在导线中流动会产生电场,多个电子的电场叠加起来,就会影响电流的分布和传输。
电场叠加原理

电场叠加原理
电场叠加原理是指在某个空间中,如果有多个电荷或电荷分布存在,那么在该空间中任一点的电场强度等于每个电荷或电荷分布所产生的电场强度的矢量和。
简言之,电场的叠加是线性的。
具体来说,如果在某一点P处有n个电荷qi(i=1,2,...,n),它们与该点的距离分别为ri,则该点处的电场强度可以表示为:
E=k*(q1/r1^2)*r1̂+k*(q2/r2^2)*r2̂+...+k*(qn/rn^2)*rn̂
其中,k为电场常数,r1̂、r2̂、...、rn̂分别为从电荷qi到点P的矢量方向,r1、r2、...、rn为它们的长度。
这一原理可以用于计算任意分布的电荷所产生的电场分布。
在实际应用中,我们可以将电荷分布离散化为若干小电荷,然后对每个小电荷的电场进行计算,并将结果进行叠加得到总电场分布。
需要注意的是,在考虑电场叠加时,应该同时考虑静电场和电磁场的叠加。
对于静电场,叠加原理适用于任意空间,而对于电磁场,则需要考虑相对论效应和场的传播特性等因素,可能会导致电磁场的非线性叠加。
总之,电场叠加原理是电学中的基本概念之一,它为我们计算和描述电场提供了重要的方法和工具。
在实际应用中,我们可以利用这一原理进行诸如电场分析、电场测量、电场模拟等方面的研究和设计。
第三讲 电场 电场强度 场强叠加原理 点电荷系的场强
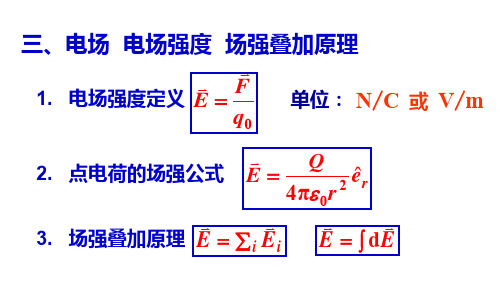
0q F E=1. 电场强度定义 单位: 2. 点电荷的场强公式 re r QE ˆπ420ε= 3. 场强叠加原理 N /C或 V /m三、电场 电场强度 场强叠加原理∑=i i E E ⎰=E Ed在电场中某一点的电场强度定义为 ,若该点没有试验电荷,那么该点的电场强度又如何,为什么?Q1.3.1答:不变。
0q F EQ1.3.2在地球表面上通常有一竖直方向的电场,电子在此电场中受到一个向上的力,电场强度的方向朝上还是朝下?答:朝下。
两个点电荷相距一定距离,已知在这两点电荷连线中点处电场强度为零。
你对这两个点电荷的电荷量和符号可作什么结论? 答:q 1 q 2 O q 1 q 2Q1.3.3在点电荷的电场强度公式中,若 r → 0,则电场强度的大小 E 将趋于无限大,对此,你有什么看法呢? 答:当 r → 0 时,公式没有意义。
r e rQ E ˆπ420ε= Q1.3.4Q1.3.5电力叠加原理和场强叠加原理是彼此独立没有联系的吗?答:不是。
∑==n i iF F 1 01q F n i i∑== 若带电体由 n 个点电荷组成, 由电力叠加原理 由场强定义 P ∑==n i i q F 10 ∑==n i i E 1q i q 1 0q F E=q 0r >> l 电偶极子 的方向由 -q 指向 +q +qO -qPr l 定义 电偶极矩 (electric moment ) lq p =p如图所示,一电偶极子的电偶极矩 ,P 点到电偶极子中心 O 的距离为 r ,r 与 l 的夹角为 q 。
在 r >> l 时,求 P 点的电场强度 在 方向的分量 E r 和垂直于 r方向上的分量 E q 。
-q +q l P r OQ1.3.6 l q p = OP r = q E22cos 21-+⎪⎭⎫ ⎝⎛-=q l r r 解: -q +q l -r +r +E -E P r O a - a + q 20π41++=r q E ε--++-=a a cos cos E E E r 20π41--=r q E ε; 1cos 1cos ≈≈-+a a ; ⎪⎭⎫ ⎝⎛+≈q cos 112r l r ⎪⎭⎫ ⎝⎛-≈⎪⎭⎫ ⎝⎛+=--q q cos 11cos 21222r l r l r r式中 又 q εεcos 2π411π430220r l q r r q E r ≈⎪⎪⎭⎫ ⎝⎛-=-+--+++=a a q sin sin E E E -q +q -r +r +E -E P r O l a - a + q q a a sin 2sin sin r l ≈≈-+⎪⎪⎭⎫ ⎝⎛+=-+22011sin 2π4r r r l q E q εq q εsin π430r l q ≈30cos 2π41r p q ε=30sin π41rp q ε=如图所示是一种电四极子,它由两个相同的电偶极子组成,这两个电偶极子在一直线上,但方向相反,它们的负电荷重合在一起。
场强叠加原理

场强叠加原理
场强叠加原理是物理学中一个重要的概念,用于描述由多个电荷或其他场源产生的电场、磁场或重力场等的总效应。
根据场强叠加原理,对于多个电荷或场源而言,产生的场强可以通过将每个电荷或场源单独产生的场强矢量进行矢量求和得到。
这意味着对于一个给定点的场强,可以通过将所有与该点相关的电荷或场源产生的场强矢量相加获得。
具体来说,如果有n个电荷或场源,它们分别产生的场强矢量分别为E1、E2、E3...En,则在给定点的总场强矢量E是它们的矢量和,即E = E1 + E2 + E3 + ... + En。
这个原理在电学、磁学和重力学等领域都有应用。
在电学中,例如当有多个点电荷在给定点产生的电场时,可以通过场强叠加原理求解电场强度。
在磁学中,当有多个电流元或磁石在给定点产生的磁场时,也可以使用这个原理。
在重力学中,当有多个质点在给定点产生的重力场时,同样可以使用场强叠加原理求解重力场强度。
需要注意的是,场强叠加原理只适用于线性场。
如果存在非线性场源,例如强度与距离平方成反比的引力场,叠加原理则不再适用。
此外,在实际应用中还需要考虑其他因素,如超完整性原理和边缘效应等。
总之,场强叠加原理是一种基本的物理原理,能够帮助我们理
解和计算由多个场源产生的场强。
在实际问题中,它为我们提供了一个简单而有效的方法,用于处理复杂的场分布情况。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
University Physics
§8.3 电通量 高斯定理
一.电场线(电力线)
• 起始于正电荷(或无穷 远处),终止于负电荷 (或无穷远处)
• 场强方向沿电力线切线
方向,场强大小决定电
力线的疏密
E dN dS
解 dq dl
E dE
dE
1
1
4π 0
dr4q2πr00
dqn dE cos
由于圆环上电荷分布关于x 轴对称 E 0
x
dE
dEx
P
dE
r
RO dq
Ex
1
4π 0 cos r (R2
x
P
O
R1
R2
补 偿法
E
2 0
[1
(R2
x x2
)1/ 2
]i
E ER2 ER1
x 2 0
[(R12
1 x 2 )1/ 2
(R
2 2
1 x
2
)1
/
2
]i
Xu Zhongfeng, Xi’an Jiaotong University, 2010
University Physics
(2) 由电场强度求电场力 F qE
适用各种电场
F
1
4 0
qq0 r2
r0
用于点电荷的电场
例1 已知圆环带电量为q ,杆
qR
的线密度为 ,长为L
dq L
求 杆对圆环的作用力
解 dq dx
O
Ex x
圆环在 dq 处产生的电场
dF Exdq Exdx
Xu Zhongfeng, Xi’an Jiaotong University, 2010
University Physics
(3)
E
x
2 0
R2 R1
(r 2
rdr x2
)3/
2
i
x 2 0
[ (R12
1 x2 )1/ 2
(R22
1 x2 )1/ 2
]i
e
de
E dS
S
闭合曲面向外为正,向内为负。
(2) 电通量是代数量
dΦe1
E
dS1
0
dΦe2 E dS2 0
穿入为负 穿出为正
投影,写出
dEx
,
dEy ,
dEz
(3) 统一变量,计算积分
Ex dEx Ey dEy Ez dEz
Xu Zhongfeng, Xi’an Jiaotong University, 2010
University Physics
例3 半径为R 的均匀带电细圆环,带电量为q
求 圆环轴线上任一点P 的电场强度
解 F qE
F qE
相对于O点的力矩
M
F
1 l sinθ 2
F
1 l sinθ 2
qlE sinθ
M
ql E
p
E
F
q
l
O
θ
q
F
p
E
讨论
(1) θ 2
(2) 0
(3)
力偶矩最大 力偶矩为零 (电偶极子处于稳定平衡) 力偶矩为零 (电偶极子处于非稳定平衡)
Ex
1
4 0
(R 2
qx x 2 )3/ 2
F
L 0
qxdx 4 0 (R2 x2 )3
2
qλ
4 0
(1 R
1) R2 L2
Xu Zhongfeng, Xi’an Jiaotong University, 2010
University Physics
例2 求电偶极子在均匀电场中受到的力偶矩。
dq cosθ r2 x r x2 )1/ 2
1
4π 0
E
cos
r2
1q
dq 4π0 r 2
1
4π 0
(R2
qx x2 )3/2
cos
讨论
(1) 当 x = 0(即P点在圆环中心处)时 E 0
(2) 当 x >> R 时
E
1
4π 0
q x2
Xu Zhongfeng, Xi’an Jiaotong University, 2010
• 电场线是非闭合曲线 • 电场线不相交
dN
E
dS
Xu Zhongfeng, Xi’an Jiaotong University, 2010
University Physics
二.电通量
穿过任意曲面的电场线
条数称为电通量
e
1.dS 面元的电通量
n
de dN EdS
dEScnos E dS
x
2 0
R rdr
0 (r2 x2 )3/2 i
x
20 [1 (R2 x2 )1/2 ]i
E1
讨论
P
r RO
E1
E1
(1) 当R >> x,圆板可 视为无限大薄板
E 2 0
E2
E2
E2
(2) EI E1 E2 0
EII
E1
E2
0
EIII E1 E2 0
University Physics
Xi’an Jiaotong University Zhongfeng Xu 04 / 29 / 2010
Xu Zhongfeng, Xi’an Jiaotong University, 2010
University Physics
电场强度及其叠加原理
E
F
q0
E
1
q r0
40 r 2
E
dq
4 0r
2
r0
dl (线分布) : 电荷线密度 dq dS (面分布) : 电荷面密度
dV (体分布) : 电荷体密度
解题思路:
(1) 选取 dq (dl, ds, dV )
确定 dE
(2)
建立恰当的坐标系,将
dE
矢量面元
dS
dS
n
de E dS
dS
dS
dS E
2.曲面的电通量
e
de
E
S
dS
Xu Zhongfeng, Xi’an Jiaotong University, 2010
University Physics
对于闭合曲面
说明
(1) n 方向的规定:
University Physics
例4 面密度为 的圆板在轴
线上任一点的电场强度
1
qx
E 4π0 (R2 x2 )3/ 2
x dE
解 dq 2π rdr
dE
1
4π 0
(r 2
xdq x2 )3/2
x 2 0
(r 2
rdr x2 )3/2
E
dEi
