电势以及叠加原理
电势

得圆盘在P点的电势为
24
5-7 电势
1 V 4πε0
讨论
R
2πrdr
x r
2 2
0
2ε0
( x 2 R 2 x)
P点在很远:x R
2 R 2 2 x R x 2x
dr
r
R
x2 r 2
圆盘在P点的电势为:
Q V 4πε0 x
o
x
P
x
25
5-7 电势
R
o
rA
A
rB
B
r
17
5-7 电势
0 r R 解: 球面内外电场为 E Q r R 2 4ε r 0
(1)球面外两点间的电势差为 rB VA VB E dr rA Q rB dr A dr o 2 R r 4πε0 A r rA r Q 1 1 rB ( ) 4πε0 rA rB
Q 4 πε0 R
dr R r 2
rR
球面内和球面上任一点电势相等。
V
Q 4 π 0 R
Q 4π 0 r
R
o
A rA
rB
B
r
o
R
r
21
5-7 电势
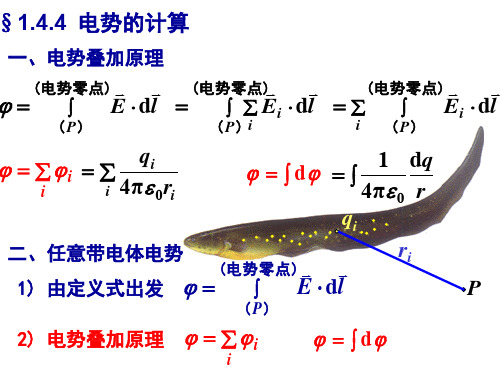
例4 正电荷q均匀分布在半径为R的细圆环上。 求环轴线上距环心为x处的点P的电势。 解:在圆环上任取一电荷元,电势为 1 dq dVP 4πε0 r dq 得圆环在点P的电势为:
5-7 电势
5-7 电势
宝宝玩滑梯:
秋天宝宝玩滑梯时,如果下面有人接住的话, 宝宝为什么会感觉手很强烈的麻木感?
2
5-7 电势
电势2

解:取半径为r,宽度为 dr的圆
环,圆环上电量为dq= 2rdr,
它在P点的电势为
dU
dq
4 0 r 2 x 2
整个圆盘在P点的电势:
dr r
R
x P· x
U dU
R
dq
0 4 0 r 2 x2
R rdr
(
0 2 0 r 2 x 2 2 0
R2 x2 x)
A、大小不变,方向改变
B、大小改变,方向不变
√C、大小和方向都不变
D、大小和方向都改变
H.M.Qiu
测验题
2、下列说法正确的是: A、如高斯面上E处处为零, 则该面内必无电荷; B、如高斯面内无电荷, 则高斯面上E处处为零; C、如高斯面上E处处不为零,则该面内必有电荷; D、如高斯面内有电荷,则高斯面上E处处不为零;
当常量C取等间隔数值时, 可以得到一系列的等势面
U12 U23
若U0,则
U1
U2
U3 n
U En
等势面的疏密反映了场的强弱
H.M.Qiu
(二) 电力线与等势面的关系
1. 电力线处处垂直等势面
在等势面上任取两点 a、b,则
b
等势
a E dl Ua Ub
= 0 E dl
方向如图
其中: 1 dx dx
r ab x
a b
x x+dx
o
b a+b x
H.M.Qiu
测验题
dx
dE
20r 20 (a b x)
EP dE
r P dE
b
电势知识点总结

电势知识点总结电势是电荷在电场中所具有的能力。
它是刻画电场强度的物理量,通常用V表示。
电势是标量,它的方向与电场强度的方向相反。
电势的定义很简单,就是单位正电荷在电场中所具有的势能。
如果把距离无限远处的电势设定为零,那么其他地方的电势就是相对于这个参考点的。
1. 电势的定义电势是电场场强E在电场中沿电场方向线积分的数值:V = -∫E•ds其中ds为位移,E为电场强度。
2. 电势的单位电势的单位是伏特(V),它是国际单位制中电位单位的一种。
1V等于1焦耳/库仑。
3. 电势的性质(1)电势是标量,没有方向。
(2)电势与电场之间的关系是:电势是电场的功,单位正电荷在电场中沿某一路径的单位正功率。
(3)电势差等于两点之间的电势差。
电势差可以理解为电场中两点间移动单位正电荷所做的功。
4. 电势与电场强度的关系电场强度与电势之间有如下关系:E = -▽V其中▽V表示电势V的梯度。
这个关系式的含义是:电场强度E是电势V的梯度的相反数。
5. 电势的叠加原理电势是一种标量,因此它服从叠加原理。
如果在某一点上存在多个电荷产生的电势,则这些电势可以相互叠加。
即如果在某一点上同时存在多个电荷,则该点上的总电势等于所有电荷产生的电势之和。
6. 静电势能在电场中存在着复杂的电势能变化。
当电荷在电势差V下做功时,它的势能会发生改变。
这种势能改变称为静电势能。
7. 电势的分布规律在特定情况下,电势具有特定的分布规律,这有助于我们在实际应用中研究电场的特性。
例如:(1)均匀带电直棒:在空间各点上的电势相等,并且大小与距离直棒的距离成反比。
(2)均匀带电球壳:在球表面上的电势相等,并且光滑地变化。
8. 电势的应用电势是电场中非常重要的一个物理量,它在实际应用中有着广泛的用途:(1)电势与电势差可用来描述电场中电荷的势能和静电势能。
(2)电势与电势差可用来计算电场中单位正电荷所受的力和电势能。
(3)电势可用来描述导体中的电场分布。
高二必修三物理电势知识点

高二必修三物理电势知识点物理学中的电势是一个重要的概念,它在理解电场、电力和电荷分布等方面起着至关重要的作用。
对于高二学生来说,掌握物理电势的知识是必不可少的。
本文将为大家详细介绍高二必修三物理电势的知识点。
一、电势的定义及基本概念电势是指单位正电荷在电场中具有的势能。
常用符号为V,单位是伏特(V)。
电势既可以是标量,也可以是矢量,具体是根据具体情况而定。
在电场中,电势是一个点的属性,表示该点单位正电荷所具有的电势能。
二、电势的计算方法根据电势的定义,我们可以通过电场力和电荷之间的关系来计算电势。
电势的计算公式是V = kQ/r,其中V为电势,k为电场力常量,Q为电荷量,r为距离。
通过这个公式,可以计算任意一个点的电势。
三、电势与电势差的关系电势差是指两个点之间的电势差别。
单位电荷从高电势点移动到低电势点时,会受到电势差的作用。
电势差的计算公式是ΔV = V2 - V1,其中ΔV为电势差,V2为低电势点的电势,V1为高电势点的电势。
四、电势与电场的关系电势是电场的一种表现形式,电场是由电荷产生的力场。
在电场中,电荷会受到电场力的作用,而电势则体现了电场力对电荷的影响。
电势的方向与电场力的方向相反,即从高电势点指向低电势点。
五、电势能与电势的关系电势能是指电荷在电场中具有的势能。
电势能与电势之间的关系可以通过公式Ep = qV得到,其中Ep为电势能,q为电荷量,V为电势。
当电荷在电场中移动时,它的电势能会发生变化,从而产生电场力。
六、电势线与等势面电势线是用来表示电场分布情况的一种图形表达方式。
在电场中,电势线与电场线的方向相同,即从高电势点指向低电势点。
等势面则是指电势相等的点构成的面。
等势面与电势线垂直相交,而且等势面上的点沿着同一条线没有电势差。
七、电势的叠加原理对于复杂的电场,可以将其分解为若干简单的电场,然后再根据电势叠加原理将其电势进行叠加。
根据叠加原理,电势是一个标量,可以直接进行叠加运算。
电势11.3--电势叠加原理

一、 点电荷系的电势
q1
r1
E2
v v
p
E dl
p
q2
r2 P E1
q1 dr
r1 40r12
q2
r2 40r22
dr
q1
4 0 r1
q2
4 0 r2
n
对n 个点电荷
qi
i1 4 0ri
注意:电势零点P0 必须是共同的。
电势的零点的;而当激发电场的电荷分布延伸到无穷远时,不 宜把电势的零点选在无穷远点,否则将导致场中任一点的电势 值为无限大。这时只能根据具体问题,在场中选择某点为电势 的零点。
(1)电势叠加法 例题1(课本P37):电荷q均
匀分布在半径为 R 的细圆环上, 求圆环轴线上距环心x处的点P的 电势。
解:在圆环上取任意电荷
即点电荷系电场中某点的电势,等于各点电荷单独存在时在该 点的电势的叠加(代数和)。这个结论叫做静电场的电势叠加原 理。
2.连续型——连续分布电荷电场中的电势
若场源为电荷连续分布的带电体,可
以把它分成无穷多个电荷元 dq ,每个电荷
元都可以看成点电荷,在场点产生的电势
为
dV dq
4 0 r
该点电势为这些元电荷的叠加:
uur r R Ew dl 0
R
q 40r
2
dr
q 40
R
球面内各点电势相等,均等于球面上各点电势。
V-r曲线如图,可见在r=R的球壳处,电势是连续的,而 前面我们知道,带电球壳在r=R处的场强是跃变的。其次, 我们发现可见场强为零处,电势不一定为零。
例题3(课本P41)求无限长均匀带 电直导线外任一点 P 处的电势,已 知线电荷密度为λ。
物理 电磁学 第11讲 电势叠加原理及电势的计算
R2
Q1 Q2 4 π R 4 π R ( r R1 ) 0 1 0 2 Q2 Q1 ( R1 r R2 ) 4 π r 4 π R 0 0 2 Q1 Q2 4 π r ( r R2 ) 0
[例] 均匀带电球层 ,内外半径为 R1,R2,求:A、B 两点的电势。 解:取带电球面 1. 求 A
Q1 ( r R ) 1 4 π R 0 1 1 Q1 ( r R ) 1 4 π 0 r
Q2 ( r R ) 2 4 π R 0 2 2 Q2 ( r R ) 2 4 π 0 r
Q2
区域 r < R1 R1 < r < R2 r > R2
Q1 O R1
R2
外壳贡献 总电势
内壳贡献
Q1 1内 4π 0 R1
Q1 1外 4π 0 r Q2 2外 4π 0 r
Q2 2内 4π 0 R2
1内 2内
1外 2内
1外 2外
解: 总电势分布为
1 2
Q2
Q1 O R1
P
[例] 己知:均匀带电圆盘,总电量 Q,半径 R。 求:圆盘轴线上任意点 P 处的电势。 解:利用电势积分法。
1.分割合适电荷元
dq dS Q π R2 dS 2π d
O d
r x P dq
2.电荷元 dq 在 P 处电势 3.总电量 Q 在 P 处电势
dq d 4π 0 r
1 q 4π 0 r
OP r
P r+
r- r
[例] 求距电偶极子相当远处的电势。
大物电磁学 第三章 电势

方向沿径向向外 方向沿径向向外
18
AQ
(r R1) E3 40r2
方向沿径向向外
(3)球内、外各点的电势
注意: 求各点电势(电势分布)时,要分 区域讨论,分区方式与场强相同。
电势零点位置选择:如无特殊说明,对球状
带电体产生的电场,选
取无穷远处为电势零点。
即:令 0
19
R oP1
二、公式 静电场力的功 = 电势能差 电势差 公式 电势公式
三、解题方法 求场强时的填补法,叠加法; 求电势的方法,电势差的方法
28
作业:P87 3.2 3.3 3.7 3.9
29
课后思考题: 如图,两个同心的半球面相对放置,半径分别 为 R 1 和 R 2 ( R1 R2 ),都均匀带电,电荷面 密度分别为 1 和 2 .试求大的半球底面圆直 径AOB上得电势. B
总
ቤተ መጻሕፍቲ ባይዱ
n i 1
1
4 0
qi ri
r i : 第 i个点电荷到场点的距离
0
qi
.P
3、连续带电体的电场中的电势 令
d 1 dq 40 r
r : 所取的任意位置的电荷元
到场点的距离
0
dq
+q
r
.P
32
总电势
dq
4 电荷分布范围 0r
( 0)
注意:电势是标量,上式可直接积分,电势 迭加比电场迭加要简便。
P20( x2R2x)
( 0)
39
3-5 电荷在外电场中的静电势能
八、电势能差、电场力的功及电势、电 场四者之间的关系
Wa Wb Aab
b
b
q 0a E d l q 0a E c o sd l
第11章电势

[ 例 11.3] 计算电偶极子电场中任 11. 一点的电势分布
y
P(x, y)
解:P的电势为
l θ+ −O ϕp = ϕ+ +ϕ− x q − q q(r1 − r2 ) = + = 4πε0r2 4πε0r 4πε0r2r1 1 2 Qr >> l ∴r r2 ≈ r r1 − r2 ≈ l cosθ 1
R
12
q
R
讨论: 讨论: 球壳内任一点的电势与 球壳的电势相等(等势) 球壳的电势相等(等势) 球壳外的电势与球壳上 的电荷集中于球心的点 电荷的电势相同
U
0
R
r
13
[例11.2]求无限长均匀带电直线外任一点 11. a处的电势。已知电荷线密度为λ 处的电势。 解:无限长均匀带电直线 的场强大小为
31
[ 例 1] 应用电势梯度的概念 , 计算半径为 R 、 应用电势梯度的概念, 计算半径为R 电荷面密度为 σ 的均匀带电圆盘轴线上任一 点P的电场强度
c
E θ
3
• 在q1、q2、…qn点电荷系电场中移动
b
1 q0q ∴Aab = ∫ qoEdr = ∫ dr 2 a ra 4 πε0 r q0q 1 1 = ( − ) ----与路径无关 ----与路径无关 4πε0 ra rb
b
rb
v v v v v b v Aab = q0 ∫ E ⋅ dl = q0 ∫ (E1 + E2 +L+ En ) ⋅ dl a a q0qi 1 1 ----与路径无 =∑ ( − ) ----与路径无 πε ia rib 关 i 4 0 r
v r a
dq
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第六讲电势
内容:§9-6
1.电势和电势差
2.电势叠加原理
3.电势的计算
要求:
1.掌握电势叠加原理;
2.掌握电势的两种计算方法。
重点与难点:
3.电势的计算方法。
作业:
习题:P39:21,22
意大利物理学家。
伏打在物理学方面做出了许多重要贡献,他发明过起电盘,发明过验电器、储电器等多种静电实验仪器。
伏打最显赫的功绩是发明了伏打电池。
伏打电池的出现对电学的发展却产生的深远的影响,开创了一个新的广阔天地,成为人类征服自然的最有力的武
伽伐尼在1786年和1792年在实验中观察到用铜钩挂起来的蛙腿在碰到铁架时会发生痉挛。
他认为这是生物电产生的效果。
伏打认为上述现象的产生是由于两种不同金属接触时所产生的电效应。
两种观点曾引起了十年之久的争论。
3.电势差
在静电场中,任意两点-=V U。
