303-电势、电势叠加原理 (1)
电工技术:叠加定理解题步骤ppt课件

I 故,各支路电流也增加到原来的3.63倍,即:
1
I2
k
I
' 1
k
I
' 2
4 .7 6 A 7 .6 2 A
I3
k
I
' 3
3 .9 9 A
I4
k
I
' 4
3 .6 3
A
编辑版pppt
9
二、齐次定理
若给定电压变为80V,这相当于电压增
加到原来的2.42倍 (k 80 2.42) 33.02
故,各支路电流也增加到原来的2.42倍,即 :
递推法
编辑版pppt
8
二、齐次定理
• 递推法 设I4' 1A
若给定电压为120V,这相 当于电压增加到原来的
UB' D22V I3' 1.1A
3.63倍 (k 120 3.63) 33.02
I2' 2.1A
I k I ' 1 2 .3 8 A
UA' D26.2V
I1' 1.31A I ' 3.41A U ' 33.02V
二齐次定理若给定电压为120v这相当于电压增加到原来的363倍1203633302bd22若给定电压变为80v这相当于电压增加到原来的242倍故各支路电流也增加到原来的242倍即二齐次定理802423302感谢亲观看此幻灯片此课件部分内容来源于网络如有侵权请及时联系我们删除谢谢配合
叠加定理(2)
叠加定理解题步骤;齐次定理
编辑版pppt
1
一、叠加定理的应用
叠加定理
(三步走: 1分,2解,3求和 )
应用 例1:如图电路,求U 。 解: (1)画出分电路图
归纳电工基础ppt课件叠加定理

回顾
怎样用支路电流法的分析复杂直流 电路?
有没有更容易理解,计算更简单 思考 的分析直流电路的方法呢?
..........
2
本标准适用于已投入商业运行的火力 发电厂 纯凝式 汽轮发 电机组 和供热 汽轮发 电机组 的技术 经济指 标的统 计和评 价。燃 机机组 、余热 锅炉以 及联合 循环机 组可参 照本标 准执行 ,并增 补指标 。
..........
I″ I″1 R1
I 2″ R2
Is
I 3″ R3
-+ U″
R4 I ″4
(c)
7
本标准适用于已投入商业运行的火力 发电厂 纯凝式 汽轮发 电机组 和供热 汽轮发 电机组 的技术 经济指 标的统 计和评 价。燃 机机组 、余热 锅炉以 及联合 循环机 组可参 照本标 准执行 ,并增 补指标 。
假设E2单独作用时:
..........
5
本标准适用于已投入商业运行的火力 发电厂 纯凝式 汽轮发 电机组 和供热 汽轮发 电机组 的技术 经济指 标的统 计和评 价。燃 机机组 、余热 锅炉以 及联合 循环机 组可参 照本标 准执行 ,并增 补指标 。
讲授新课
叠加定理的内容图示
E1和E2同时作用时
例题分析
(2) 当电流源单独作用时, 电压源短路, 如图(c)
所示, 则各支路电流为
I
" 1
R3 R1 R3
Is
3 1 0.6 A 23
I
" 2
R4 R2 R4
Is
0.5 1 1 0.5
0.333 A
I"
I
" 1
I
" 2
(0.6
电势电势差
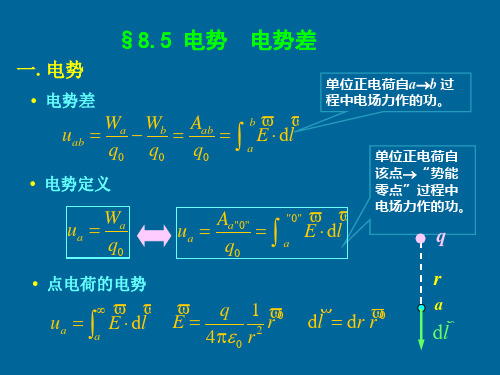
w
W V
1 2
0
E
2
(适用于所有电场)
不均匀电场中 dW wdV
W
dW
V
V
1
2
0
E
2dV
例 已知均匀带电的球体,半径为R,带电量为Q
求 从球心到无穷远处的电场能量
解
E1
Qr
4 0 R3
E2
Q
4 0r 2
Q
R r
取体积元 dV 4r2dr
W1
R
0
1
2
0
E12dV
Q2
40 0R
W2
R12 0 E2 2dV
a
-Q
R2 R1
R2
h R1
l
u R2 Q dr Q ln R2
R1 20lr
20l R1
C Q 20l
u ln(R2 R1)
讨论
R2
h R1
l
若R1>>R2-R1 ,则 C = ?
ln( R2 R1 1) R2 R1
R1
R1
C 0S
d
u
C Q 20l
u ln(R2 R1)
• 电容器的应用:
解
D dS
S
q0i,内
0
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
i
DS 0S D 0
' - - - - - - - - -
电势一解答
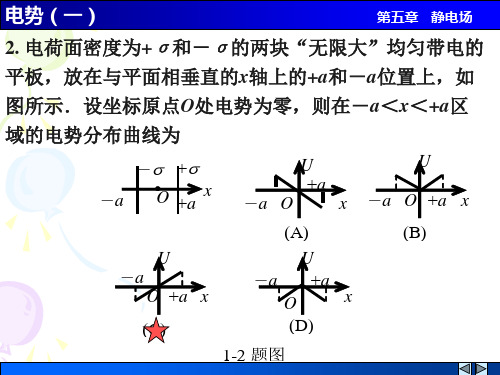
(B) E=0,U=
Q
4 0
1 R1
R12.
(C) E=
Q
4 0r2 ,U=
Q
4 0 r
Q
R1 r
P
O R2
(D) E=
Q
4 0r 2 , U=
Q
4 0 R1
1-3 题图
电势(一)
解: 由高斯定理可得场强分布为:
E 0(0 r R1)
Q
E 4 0r 2 (R1 r R2 )
U p (r)
P
又因电场线从高电势→低电势,
O
所以UP<UO
2-1题图
电势(一)
第五章 静电场
2. 电荷分别为q1,q2,q3的三个点电荷分别位于同一圆周 的三个点上,如图所示.设无穷远处为电势零点,圆半径
为R,则b点处的电势U= 1 8 0 R
2q1 q2 2q3
由电势的叠加原理可得:
U Uq1 Uq2 Uq3
电势(一)
第五章 静电场
5.有N个电量均为q的点电荷,以两种方式分布在相同半
径的圆周上:一种是无规则地分布,另一种是均匀分布.
比较这两种情况下在过圆心O并垂直于圆平面的Z轴上任
z
一点p的场强与电势,则有p(A)场强Fra bibliotek等,电势相等.
(B)场强不等,电势不等.
(C)场强分量Ez相等,电势相等. (D)场强分量Ez相等,电势不等.
定远处Q外1、力Q所3的作情的况功下_,__将8__QQ_22_0从d__Q__1、__Q3连F1线3 中点d 移至Q无2 穷
由题意Q.1所受的合力为零
Q1 F12 o
Q3
Q1
Q2
4 0d 2
第六章(第三讲)电势

静电场的环路定理和电势
一、静电场的环路定理 二、电势与电势差 三、电势叠加原理 四、电势的计算
1
§6.4 静电场的环路定理和电势 一 电场力作功的特点 B 1. 点电荷的电场
dA q0 E dl
qq0 r dl 3 rB 4 π 0 r r dl rdl cos rdr qq0 dA dr 2 rA 4 π 0 r q qq0 rB dr A A rA r 2 4 π 0 qq0 1 1 ( ) q 0 E dl 0 L 4 π 0 rA rB
大小
dU E dl n
方向
相反,由高电势处指向低电势处. 与 e n
23
§6.5、等势面 电势的梯度 物理意义 (1)空间某点电场强度的大小取决于该点领 域内电势 U 的空间变化率.
(2)电场强度的方向恒指向电势降落的方向. 直角坐标系中
讨 论
U U U E ( i j k ) gradU x y z
§6.5、等势面 二
电势的梯度
电场线和等势面的关系
1)电场线与等势面处处正交. (等势面上移动电荷,电场力不做功.)
2)等势面密处电场强度大;等势面疏处电梯度 三 电场强度与电势梯度
将单位正电荷由A经 l 移动到B
U U
B
U AB U B U A) E l ( El cos E cos El
q
dl dr E
q
q U 4 π 0 r
q 0,U 0
7
q 0, U 0
r
§6.4
静电场的环路定理和电势
点电荷系 E E i
U A E dl E i dl
电势、电压

四)点电荷系、带电体电场的电势、电势叠加 原理。 + 设一点电荷系:q1、q2----qn qn a 产生电场 E E1 E2 En q1 + q2 + U a E dl ( E1 E2 En ) dl a a q3 +
dr
r
x
2rdr rdr 2 2 2 2 40 r x 2 0 r x
Y
+ + + + +o + + R ++ + ++ Z
dr
p
r
Up
X
R
rdr
2 0 r x
2 2
0
2 2 Up ( R x x) 2 0
2 2 x ( R x x) 2 0
ds
Y
dq
2 2 2 U2 ( R x x) r r xp 2 0
p R 讨论: X 1)x 0 U p x 2 0 2)x R
1 2
dr
2 2 Up ( R x x) 2 0 2
2
1 1 2 (1 Z ) 1 Z Z 2 24
+ d + + + + o+ + R + + + Z ++
ds
Y
dq
p
另解: 分割成点电荷 X
r
x dr
dq
ds rddr dq rddr
R
dU
rddr
电场叠加原理.ppt

p r3
方向如图。
40
(r
ql 2
l2 4
)3
2
思考: 任意点的场 强如何求?
p 40r
3
方向如图。
例7、无限大均匀带电平面中间有一圆孔,求轴上 E =?
R
E
x
两种方法
圆环 R
相减法
例8、均匀带电球面,求轴上 E =?
dl
d R
r
E
dq
dE
dq 40 R 2
Rd 40 R 2
d
R
dE y
y
dEx
dE
Ex
dE x
dE cos
0
2
40
R
cos
d
x
40
E
R
E y
dEy
2
dE sin
sind
0 4 0 R
4 0 R
2、电场有能的性质: 电场力可以移动电场中的带电体。 (电场力对带电体做功)
3、电场
对导体产生静电感应现象。 对绝缘体(介质) 产生极化现象。
二定1、、义电电:场E场强强度度FE
q0
:
电场
(N c
“力的性质”
, V m)
用E
Q
大小:等于单位正电荷受到的力。
描述。
q0
E
F
方向:沿正电荷受力方向。
方向相反。
四 电场强度叠加原理 试验电荷 q0 在点电荷系q1、
大学物理第三章电势

8
P
电荷分布在有限空间, 取无穷远为 U= 0 点。
电位零点的选取: 电荷分布在无限空间, 取有限远点为U= 0 点。 一般工程上, 选大地或设备外壳为U=0点。
9
解题技巧:当场源带电体是球状带电体和柱状带 电体时,无论电势零点取在什么位置, 积分路径都应沿径向向外。此时,
dl dr
19
本题令 U r l 0 电场中任一点的电势 U P P 柱体内 ( r R)
U P1
电势零点 P 1
电势零点
E cosdr
U P E cosdr
电势零点
P
E cosdr E1dr E2 dr R
R r
l
柱外筒内 ( R r R1 )
7
五、电势 (Electric Potential) *场中任一点P的电势
U P E cos dl
P c
当取电场中某一点c为电势零点(即:令Uc = 0)时,
电势零点
P
E cos dl
即:电场中任意一点P的电势等于电场强度从P点 经任一路径到电势零点的积分。
U P E cos dl
qo
5
二、 静电场的保守性(静电场环路定理)
L
E dl 0
a
L2
.
qo
L1
b
.
在静电场中,场强沿任意闭合路径的线积 分等于零。即:对任何静电场,电场强度的 线积分都只取决于起点和终点的位置,而与连 接起点和终点间的路径无关。
6
三、电势能差
Aab Wa Wb qo a 实验电荷qo 在静电场中从a运动到b时,静电场力
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
电势、电势叠加原理1.选择题1.静电场中某点电势在数值上等于()A 试验电荷0q 置于该点时具有的电势能; ()B 单位试验电荷置于该点时具有的电势能;()C 单位正电荷置于该点时具有的电势能;()D 把单位正电荷从该点移到电势零点外力所作的功。
〔 〕2.边长为0.3m 的正三角形 abc ,顶点a 处有一电量为810C -的正点电荷,顶点b 处有一电量为810C-的负电荷,则顶点c 处的场强E 和电势U 的大小分别为92-201910N m C 4πε⎡⎤=⨯⋅⋅⎢⎥⎣⎦:()A 0E =,0U =; ()B 1000(V/m)E =,600V U =; ()C 1000(V/m)E =,0V U =; ()D 2000(V/m)E =,600V U =。
〔 〕3.如图所示,下面表述中正确的是:()A A B C E E E >> A B CU U E >>; ()B A B C E E E << A B C U U E >>; ()C A B C E E E >> A B CU U E <<; ()D A B C E E E << A B CU U E <<。
〔 〕4.边长为a 的正方形,在其四个顶角上各放一个等量的点电荷,若正方形中心处的场强和电势都为零(设无穷远处电势为零),则:()A 在四个顶角上都应放上正电荷。
()B 在四个顶角上都应放上负电荷。
()C 在两个对顶角上应放上正电荷,而另外两个对顶角上应放上负电荷。
()D 在两个相邻的顶角上应放上正电荷,而另外两个相邻的顶角上应放上负电荷。
〔 〕5.真空中有一点电荷Q ,在与它相距为r 的a 点处有一试验电荷q 。
现使试验电荷q 从a 点沿半圆弧轨道运动到b 点,如图所示。
则电场力对q 作功为()A 22042Qq r r επ⋅π; ()B 2024Qq r r πε; ()C 204Qq r r ππε; ()D 0. 〔 〕6.如图所示,a 、b 、c 是电场中某条电场线上的三个点,由此可知:()A a b c E E E >> ; ()B a b c E E E << ;()C a b c U U E >> ; ()D a b c U U E << 。
〔 〕7.如图所示,直线MN 长为2l ,弧OCD 是以N 点为中心,l 为半径的半圆弧,N 点有正电荷q +,M 点有负电荷q -。
今将一试验电荷0q +从O 点出发沿路径OCDP 移到无穷远处,设无穷远处电势为零,则电场力作功()A A <0, 且为有限常量;()B A>0 ,且为有限常量; ()C A=∞; ()D A =0。
〔 〕8.已知某电场的电场线分布情况如图所示.现观察到一负电荷从M 点移到N 点.有人根据这个图作出下列几点结论,其中哪点是正确的? ()A 电场强度M N E E <; ()B 电势M N U U <;()C 电势能M N W W < ; ()D 电场力的功0A >。
〔 〕9.点电荷Q -位于圆心O 处,a 是一固定点,b 、c 、d 为同一圆周上的三点,如图所示。
现将一试验电荷从a 点分别移动到b 、c 、d 各点,则()A 从a 到b ,电场力作功最大;()B 从a 到到c ,电场力作功最大;()C 从a 到d ,电场力作功最大;()D 从a 到各点,电场力作功相等。
〔 〕10.已知均匀带正电圆盘的静电场的电力线分布如图所示。
由这电力线分布图可断定圆盘边缘处一点P 的电势与中心O 处的电势的大小关系是: ()A P O U U =; ()B P O U U <;()C P O U U >; ()D 无法确定的(因不知场强公式)。
〔 〕11.在静电场中,电场线为均匀分布的平行直线的区域内,在电场线方向上任意两点的电场强度E 和电势U 相比较:()A E 相同,U 不同; ()B E 不同,U 相同; ()C E 不同,U 不同; ()D E 相同,U 相同。
〔 〕12.有四个等量点电荷在OXY 平面上的四种不同组态,所有点电荷均与原点等距。
设无穷远处电势为零,则原点O 处电场强度和电势均为零的组态是 :〔 〕13.在点电荷q +的电场中,若取图中P 点处为电势零点,则M 点的电势为:()Aaq 04πε; ()Baq 08πε; ()C aq 04πε-; ()D aq 08πε-。
〔 〕2.判断题1.静电场中某点电势值的正负取决于电势零点的选取。
2.静电场中某点电势值的正负取决于产生电场的电荷的正负。
3.在已知静电场分布的条件下,任意两点1P 和2P 之间的电势差决定于1P 和2P 两点的位置。
4.电荷在电势高的地方静电势能一定大。
5.正电荷在电势高的地方,电势能也一定高。
6.电场强度的方向总是指向电势降落的方向。
7.场强和电势都是矢量。
3.填空题1.可以引入电位(势)来描述静电场的原因是 。
2.如图所示,在静电场中,一电荷0q 沿正三角形的一边从a 点移动到b 点,电场力作功为0A ,则当该电荷0q 沿正三角形的另二条边从b 点经c 点到a 点的过程中,电场力做功A = 。
3.两个点电荷的带电量分别为Q 和q ,它们相距为a 。
当q 由2Q 变到4Q时,在它们的连线中点处的电势变为原来的 倍。
(以无限远处的电势为零)4.一半径为R 的均匀带电球面,带有电荷Q 。
若规定该球面上的电势值为零,则无限远处的电势将等于 。
5.图中所示以O 为圆心的各圆弧为静电场的等势线图, 已知123U U U << ,则a 、b 两点电场强度的大小:a E ________b E (填 >、=、<)。
6.如图所示,在电荷为q 的点电荷的静电场中,将一电荷为0q 的试验电荷从a 点经任意路径移动到b 点,外力所作的功A =___ _______。
a bc7.如图所示,两个点电荷q +和3q -,相距为d ,若选无穷远处电势为零。
则两点电荷之间电势0U =的点与电荷为q +的点电荷相距多远? 。
8.一个半径为R 的均匀带电球面,带电量为Q 。
若规定该球面上电势为零,则球面外距球心r 处的P 点的电势P U =______________________。
9.一电量为Q 的点电荷固定在空间某点上,将另一电量为q 的点电荷放在与Q 相距r 处。
若设两点电荷相距无限远时电势能为零,则此时的电势能e W =_________________。
10.如图所示,半径为R 的均匀带电球面,总电荷为Q ,设无穷远处的电势为零,则球内距离球心为r 的P 点处的电势为_________________。
11.电量为q 的三个点电荷分别位于同一个圆周的三个点上,如图所示。
设无穷远处为电势零点,圆半径为R ,则b 点处的电势U 是______________。
4.计算题1.(1)(本小题5分)一根长为L 的细棒,弯成半圆形,其上均匀带电,电荷线密度为λ+,试求在圆心O 点的电势。
(2)(本小题5分)如图所示,在A ,B 两点处放有电量分别为q +,q -的点电荷,AB 间距离为2R ,现将另一正试验点电荷0q 从O 点经过半圆弧移到C 点,求:移动过程中电场力作的功(无穷远为电势零点)。
2.(1)(本小题5分)两个带等量异号电荷的均匀带电同心球面,半径分别为10.03m R =和20.10m R =。
已知两者的电势差为450V ,求:内球面上所带的电荷。
[92201910N m /C 4πε=⨯⋅](2)(本小题5分)电荷q 均匀分布在长为2l 的细杆上。
求:在杆外延长线上与杆端距离为a 的P 点的电势(设无穷远处为电势零点)。
3.电荷以相同的面密度σ分布在半径为110cm r =和220cm r =的两个同心球面上。
设无限远处电势为零,球心处的电势为0300V U =。
[92201910N m /C 4πε=⨯⋅](1) 求电荷面密度σ;(2) 若要使球心处的电势也为零,外球面上应放掉多少电荷?4.如图所示,在电偶极矩为e p的电偶极子的电场中,将一电荷为q 的点电荷从A 点沿半径为R 的圆弧(圆心与电偶极子中心重合,R >>电偶极子正负电荷之间距离)移到B 点,(1)以圆弧的圆心为座标原点,求电偶极子的电势分布;(2)在此过程中电场力所作的功(设无穷远处为电势零点)。
5.如图所示,有三个点电荷1Q ,2Q ,3Q 沿一条直线等间距分布,已知其中任一点电荷所受合力均为零,且13Q Q Q ==。
求在固定1Q ,3Q 的情况下,将2Q 从O 点推到无穷远处外力所作的功。
6.如图所示,AO=OB=R ,OCD 为以B 为中心的半圆弧,A 、B 两点分别放置电荷+q 和-q ,求:(1) O 点与D 点的电势 O U 与 D U (设无穷远处电势为零);(2) 把正电荷0q 从O 点沿弧OCD 移到D 点,电场力做的功;(3) 把单位正电荷从D 点沿AB 延长线移到无穷远处电场力做的功。
