网格编码调制(TCM)
第7章 TCM编码调制
映射的本质：
–8PSK信号星座图各点之间的欧式距离不 同。有些点之间的距离大，有些点之间 的距离小。
7 0 1 2
6
5 4 3
问题：能否将重要的比特映射成之间距离 远的点，将不重要的比特映射成距离近的 点。 2015-1-16 14 天津大学电子信息工程学院通信系
引出两个问题
– 哪点之间的距离近，哪些点之间的距离 远？（分割问题） – 采用什么样的映射方法？（映射问题）
282015天津大学电子信息工程学院通信系29有平行状态的4状态网格图0426153726043715282015天津大学电子信息工程学院通信系3074tcm74tcm译码译码估计信息遍历网格的路径在所有的可能路径中选择与接收序列z最相近中寻找与接收序列z最相似的u相当于在网格图中寻找一条与接收序列差异最小的路径
23
7.3 TCM编码 7.3.1 Ungerboeck提出的TCM方案 为了最大化自由欧式距离，Ugerboeck最 先提出采用分割和映射TCM方案。 分割：将调制信号星座图集进行分割:
–首先，将调制信号的星座图相继分割成具有 递增最小距离d0< d1< d2……的子集 ； –随后进行信道比特到波形的映射；
天津大学电子信息工程学院通信系 12
2015-1-16
5、4状态8PSK-TCM波形映射
– 4状态8PSK-TCM编码器的结构如图所示：
y0
x1
M1
M2
y1 y2
映 8PSK 调制 射
去发射机
x2
问题：
– 能否像卷积码那样，波形的映射满足一定的关 系？映射成网格图上的一条路径？
2015-1-16 天津大学电子信息工程学院通信系 13
一种基于TCM网格编码调制技术的高速数据传输方法与实现的开题报告
一种基于TCM网格编码调制技术的高速数据传输方法与实现的开题报告一、选题背景与意义随着互联网的快速普及，人们对于数据传输速度的需求也越来越高，而传统的数据传输技术已经不能满足这一需求。
因此，需要通过新的技术手段来实现高速数据传输。
传输渠道的带宽并非无限，而大规模的并行化传输会产生不同的输入输出数据之间的冲突，因此，如何充分利用传输资源，有效地提高传输速率是现代通信领域的研究热点。
近年来，基于高效编码调制技术的数据传输方法受到了越来越多的关注。
而传统调制方式往往基于FFT等信号处理算法实现，需要使用大量的计算资源，从而导致高成本、复杂度较高等问题。
而TCM是通过建立特殊网格，使得调制方式直接通过异或运算实现，具有简单、高效、抗干扰等优点，因此成为了一种十分有潜力的调制技术。
基于上述，本课题计划研究和探讨一种基于TCM网格编码调制技术的高速数据传输方法，旨在提高数据传输速率以及减少计算资源的消耗。
二、研究内容和方案1. TCM网格编码调制原理研究TCM网格编码调制技术是利用“距离谱”的思想，构造出多个网格并将数据映射到不同的网格中，最终通过简单的异或运算实现调制。
因此，本课题需要深入研究TCM网格编码调制技术的原理和特点，探讨其优势和局限性。
2. 高速数据传输方法和算法的设计与实现本课题基于TCM网格编码调制的技术特点，将其应用于高速数据传输中，通过合理的算法设计，提高数据传输的速率，实现数据的高效传输。
3. 系统性能测试与分析设计完毕后，需要对本课题中提出的高速数据传输方案进行测试并进行系统性能分析，测试内容包括系统的可行性、正确性、响应速度等多个维度指标。
三、预期成果和意义通过本课题研究，可以实现基于TCM网格编码调制技术的高速数据传输方法，并且在实际应用中对比传统技术进行性能分析。
预期成果包括：1. 基于TCM网格编码调制技术的高速数据传输方法的实现；2. 系统性能测试数据以及系统性能分析；3. 相关研究论文和期刊发表。
TCM编码
y引言y调制信号空间的分解y TCM编码y TCM译码y性能分析y应用2y TCM(Trellis-Coded Modulation)是一种将信道编码和调制相结合的技术。
调制相结合的技术3y在采用相同调制信号的前提下，(n, k)分组码和(K,R=k/n)卷积码都是通过扩展信道带宽(1/R倍）来获得编码增益。
适合于功率受限而频带不受限的系统。
y在频带受限系统中，为了获得编码增益，即节省功率，必须采用不同的调制信号集。
4未进行8kb QPSK调制信道纠错编码8kbps4kHzQPSKR=2/3功率受限8kbps 12kbps 6kHz调制卷积码频带不受限pp8PSK R=2/3功率受限8kbps12kbps4kHz调制卷积码K>7频带受限5y如系统中信号未编码时采用QPSK调制信号传输；卷积码编码后为不增加信道带宽y经过R=2/3卷积码编码后，为不增加信道带宽，则需采用8PSK调制信号来传输；y而8PSK信号为了获得与QPSK信号相同的误码率，功率需增加4dB;y因此要求卷积码的编码增益超过4dB, 才能节省功率；y这就要求采用长约束长度（如K>7)卷积码，因而增加了设备的复杂度增加了设备的复杂度。
6技术相结合在不增y TCM技术通过将编码和调制技术相结合，在不增加信道带宽的前提下，获得显著的编码增益。
的编码增益y简单的4状态TCM可获得3dB的编码增益；y复杂的TCM可获得6dB,甚至更高的编码增益。
y这些增益是在不增加信道带宽或降低信息传输速率的前提下得到的。
7y TCM技术特别适合频带和功率同时受限的通信系统，如卫星通信系统。
y TCM技术最早在1976年由Ungerboeck提出。
目前对技术的论研究和实际应用得到速y TCM技术的理论研究和实际应用得到迅速发展。
G. David Forney, Jr., Gottfried Ungerboeck, “Modulation and Coding for LinearGaussian Channels”, IEEE Transactions on Information T heory, Vol.44, No. 6,October 1998.8y引言y调制信号空间的分解y TCM编码y TCM译码y性能分析y应用9调制信号空间的分解y所谓调制信号空间的分解，是将信号空间的调制信号与二进制序列一一对应起来。
tcm_网格编码(MATLAB程序)
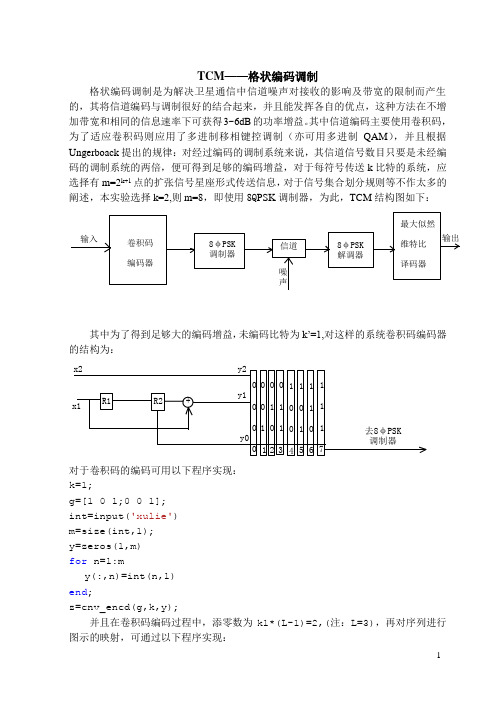
TCM——格状编码调制格状编码调制是为解决卫星通信中信道噪声对接收的影响及带宽的限制而产生的，其将信道编码与调制很好的结合起来，并且能发挥各自的优点，这种方法在不增加带宽和相同的信息速率下可获得3~6dB的功率增益。
其中信道编码主要使用卷积码，为了适应卷积码则应用了多进制移相键控调制（亦可用多进制QAM），并且根据Ungerboack提出的规律：对经过编码的调制系统来说，其信道信号数目只要是未经编码的调制系统的两倍，便可得到足够的编码增益，对于每符号传送k比特的系统，应选择有m=2k+1点的扩张信号星座形式传送信息，对于信号集合划分规则等不作太多的阐述，本实验选择k=2,则m=8，即使用8Q PSK调制器，为此，TCM结构图如下：卷积码编码器8φPSK调制器信道8φPSK解调器最大似然维特比译码器输入噪声输出其中为了得到足够大的编码增益，未编码比特为k’=1,对这样的系统卷积码编码器的结构为：x2x1R1R211111111111101234567去8φPSK调制器+y2y1y0对于卷积码的编码可用以下程序实现：k=1;g=[1 0 1;0 0 1];int=input('xulie')m=size(int,1);y=zeros(1,m)for n=1:my(:,n)=int(n,1)end;z=cnv_encd(g,k,y);并且在卷积码编码过程中，添零数为k1*(L-1)=2,(注：L=3)，再对序列进行图示的映射，可通过以下程序实现：tyu=length(z)/2;s=zeros(1,3*tyu);for i=1:ms(:,3*i-2)=int(i,2)ends(:,3*m+1)=0;s(:,3*(m+1)+1)=0;for j=1:tyus(:,3*j-1)=z(2*j-1)end;for k2=1:tyus(:,3*k2)=z(2*k2)end;uu=reshape(s,3,tyu);kk=uu'；（注意：对添零后卷积编码的处理），将编码处理后的信号进行调制，相位调制实现比较容易，对于通过信道后的解调，有两种实现途径：①接收信号通过相关器后，将接收到的信号矢量映射到M个可能发送的信号矢量上去，并且选出对应于最大映射的矢量；②亦可计算接收信号矢量的相位，并从M个可能发送的信号矢量中选出相位最接近的信号。
基于网格编码调制TCM技术的水声通信系统及DSP实现
"7 -
@AB 主程序流程
系 统 的 主 要 功 能 由 8K 公 司 的 @AB 芯 片
8LA-"#M$&" 软件完成，发送端和接收端主程序流程 如图 ** 及图 *" 所示。
-
结论
些值的附近。所以， 接收端的映射规则如表 " 所示。 "7 "7 " /012340 译码 /231040 算法是一种关于解卷积的最大似然译码 法。它不是在网格上依次比较所有的可能路径， 而是 接收一段， 计算一段， 保留最有可能的路径， 从而达到 整个码序列是一个最大似然序列。 译码过程就是根据接收到的数据符号， 按最大似 然译码准则找出编码器在网络图上所走过的路径。
/
水下无线通信系统的 ?’@ 实现
基于 <=! 技术的通信系统如图 / 所示， 图中所示
6
<=! 技术原理
最佳编码调制系统按编码序列的欧氏距离作为
信道， 在本文中为水声信道。 采用 <> 公司的 ?’@ 芯片 <!’9/4=53/ J: K作为通信 系统的主控芯片，实现发送端的卷积编码、相位调
调制设计的量度， 将编码器和调制器当做统一体综合 设计时， 可使二者级联后产生的编码信号具有最大的 欧氏自由距离。从信号空间的角度看， 这种最佳编码 调制的设计实际上是一种对信号空间的最佳分割， 这 就是 <=! 的技术基础。 在 <=! 系统中，信道编码使符号序列映射到信 号空间所形成的路径之间的最小欧氏距离为最大 1 这 样的符号结构具有最大的抗干扰能力。 信道译码通常 采用 +$F&#L$ 算法译码。这种方法是一种最大似然译 码方法， 能够减轻译码工作量； 同时由于采用边译码
TCM编码
y引言y调制信号空间的分解y TCM编码y TCM译码y性能分析y应用2y TCM(Trellis-Coded Modulation)是一种将信道编码和调制相结合的技术。
调制相结合的技术3y在采用相同调制信号的前提下，(n, k)分组码和(K,R=k/n)卷积码都是通过扩展信道带宽(1/R倍）来获得编码增益。
适合于功率受限而频带不受限的系统。
y在频带受限系统中，为了获得编码增益，即节省功率，必须采用不同的调制信号集。
4未进行8kb QPSK调制信道纠错编码8kbps4kHzQPSKR=2/3功率受限8kbps 12kbps 6kHz调制卷积码频带不受限pp8PSK R=2/3功率受限8kbps12kbps4kHz调制卷积码K>7频带受限5y如系统中信号未编码时采用QPSK调制信号传输；卷积码编码后为不增加信道带宽y经过R=2/3卷积码编码后，为不增加信道带宽，则需采用8PSK调制信号来传输；y而8PSK信号为了获得与QPSK信号相同的误码率，功率需增加4dB;y因此要求卷积码的编码增益超过4dB, 才能节省功率；y这就要求采用长约束长度（如K>7)卷积码，因而增加了设备的复杂度增加了设备的复杂度。
6技术相结合在不增y TCM技术通过将编码和调制技术相结合，在不增加信道带宽的前提下，获得显著的编码增益。
的编码增益y简单的4状态TCM可获得3dB的编码增益；y复杂的TCM可获得6dB,甚至更高的编码增益。
y这些增益是在不增加信道带宽或降低信息传输速率的前提下得到的。
7y TCM技术特别适合频带和功率同时受限的通信系统，如卫星通信系统。
y TCM技术最早在1976年由Ungerboeck提出。
目前对技术的论研究和实际应用得到速y TCM技术的理论研究和实际应用得到迅速发展。
G. David Forney, Jr., Gottfried Ungerboeck, “Modulation and Coding for LinearGaussian Channels”, IEEE Transactions on Information T heory, Vol.44, No. 6,October 1998.8y引言y调制信号空间的分解y TCM编码y TCM译码y性能分析y应用9调制信号空间的分解y所谓调制信号空间的分解，是将信号空间的调制信号与二进制序列一一对应起来。
TCM调制讲稿
3 格形（格栅）编码调制（Trellis Coded Modulation ）技术，即TCM 技术。
现代通信新技术，陈显治 第 4 章在差错控制编码中，发送端的编码和调制是分开进行的，接收端的解码和解调也是分开的。
在码流中增加监督比特可达到检错或纠错的目的。
但此时码流的比特速率将增加，从而使码流速率增加，即增加了传输带宽，这实际上是用频带利用率下降的代价换取功率利用率的改善。
在带限的信道中，我们总是希望提高频带的利用率。
那么能否在不增加信道传输带宽的前提下降低差错率呢？办法是有的，就是将编码和调制统一设计。
在M 元数字载波调制中，引入信号空间的分析方法。
如果不增加信号空间的维数，只增加信号点的数目，引入多余度，它既可以不增加传输带宽，又可以利用这种多余度编码，按某种规则安排信号点的位置，使它与输入数码之间建立某种映射关系。
高效利用频带的数字载波调制技术主要有两类：一是多电平／多相位调制，如多元的QAM 和 PSK 调制；二是连续相位调制，典型的如 MSK 。
相应的编码与调制相结合的技术也有两类，即编码的多电平／多相位调制和编码的连续相位调制。
编码的多电平／多相位调制也称为格形（格栅）编码调制（Trellis Coded Modulation ），即TCM 。
TCM 调制有两个基本特点：（1）在信号空间中，信号点的数目比调制时对应的信号点的数目多一倍。
（2）采用卷积码编码规则，在一系列信号点之间引入依赖关系，使得只有某些信号点图样或序列是许可使用的信号序列，并可模型化为格状网络，因此又称为格形（格栅）编码。
在格状结构中，通常把信号点之间的距离称码距。
其中最短距离称为最小码距，记为min d 。
利用空间划分计算差错率时，最小距离是影响差错率的一个重要参数。
当编码调制后的信号序列经过一个加性高斯白噪声的信道后，在接收端采用最大似然解调和解码，用维特比算法寻找最佳格状路径，以最小码距为准则解出接收的信号序列。
tcm码123
0 10 2
1 10 6
0 01 1
1 01 5
0 11 3
1 11 7
图 8-20 8PSK集分割示意图
第8章 数字电视
图8-21是16QAM信号星座的集分割示意图， 分割 级数为8， 假设d0=1， d1 2 ， d2=2， d3 2 2 。
第8章 数字电视
d0 ＝ 1 d1 ＝ 2
第8章 数字电视
3. 格形编码调制(TCM， Trellis Code Modulation)
在传统的数字传输系统中， 纠错编码与调制是分 别设计并实现的。 昂格尔博克 (Ungerboeck) 提出的网 格编码调制(TCM)将两者作为一个整体来考虑。 编码 器和调制器级连后产生的编码信号序列具有最大的欧 氏自由距离。 在不增加系统带宽的前提下， 这种方案 可获得3～6 dB的性能增益。
第8章 数字电视
b －k 比特 b 比特 k 比特 卷积编码器 k ＋r比特
信号点 选择器 子集选择器
多电平、多相 位输出信号
图 8-19 通用TCM编码调制器结构示意图
第8章 数字电视
TCM码要构成信号星座到2k+r个子集的一种分割，
分割采用最小距离最大化的原则， 即分割后子集内信 号点之间的最小欧氏距离最大。 每经过一次分割， 子 集数加倍， 每个子集内的信号点数减半， 最小平方欧 氏距离随之增大。 设经过i级分割之后子集内的最小欧 氏距离为di， 则有d0＜d1＜d2＜…。 用二叉树可以表示 集分割， 定义最后一次分割得到的子集数为分割的级 数， 显然图8-19的TCM编码调制器使用的分割级数应 该是2k+r 。
0 11 3
1 11 7
图 8-21 16QAM集分割示意图
网格编码调制TCM
Yn 2 = Xn2 Yn 1= Xn1 Yn 0= Sn0
Xn2Xn1
•
Sn1Sn0
Xn2 1
Xn2 0
00
Xn2 10 Xn2 00
01
Xn2 11 Xn2 01
10
Xn2 10 Xn2 00
•
11
Xn2 11 Xn2 01
–9
000 100 010 110
•
010 110
•
000 100
001
–2
网格编码调制是一种信号集空间编码(signalspace code)，它利用信号集旳冗余度，保持符号 率和功率不变，用大星座传送小比特数而获取纠 错能力。为此，先将小比特数编码成大比特数， 再设法按一定规律映射到大星座上去。
上述过程中，冗余比特旳产生属于编码范围 ，信号集星座旳扩大与映射属于调制范围，两者 结合就是编码调制。例如，用具有携带3比特信 息能力旳8ASK或8PSK调制方式来传播2比特信 息，叫做信号集冗余度，我们正是利用这种信号 集空间(星座)旳冗余度来获取纠错能力旳。
(6-2)
本例 d2seq = dis2[(C0,C0,C0), (C1,C2,C1)]
= dis2(C0,C1) + dis2(C0,C2) + dis2(C0,C1)
= 12+02+12 =( )2+2(2sin(/8))2+( )2 =2 4.586
d2par = 22 = 22 = 4
d
2 f
000 110 100 010
C=
101 111 001 011
=
110 000 010 100
111 101 011 001
浅谈TCM调制技术
护信号点的每 一个二进制 向量元 素。每一级编码器的码型选择也是 以欧 氏 距离最大化为依据 的。在接收端 ， 每个码字都经过多级译码 ， 从最低级开始 的， 高级考虑前一级的译码结果。Ｍ Ｌ Ｃ 方案码率设计灵活、 可实现不等错误 保护度、 易于使用信道容量规则， 是Ｒ ａ ｙ ｌ ｅ ｉ ｇ ｈ 衰落信道下有 效的编码调制方
案之一。
的发展历程 ， 我们可 以得到这样的启示： 通过系统 内部的组合优化 ， 可 以使 系统的整体性 能得到极大的提高。 Ｔ Ｃ Ｍ对数字通信领域变革 的影响广阔深 远。Ｔ ＣＭ技术方兴未艾 ， 正在迈向新 的高峰 。■ 参考文献 ［ １ ］ 樊昌信 ， 曹丽娜． 通信原理 （ 第六版） 【 Ｍ】 Ｂ 京： 国防工业出版社 ， ２ ０ ０ ９ ．
格状编码调制
格状编码调制
格状编码调制（Trellis Coded Modulation，TCM）是一种数字通信技术，它结合了编码和调制的概念，以提高通信系统的性能。
TCM 的基本思想是在调制过程中引入额外的编码信息，以增加信号的冗余度。
通过在信号星座图中引入多个状态，TCM 可以在接收端利用这些状态之间的关系进行纠错。
这种编码信息通常以格状结构的形式表示，因此称为格状编码。
TCM 的主要优点包括：
1. 提高频谱效率：通过引入编码信息，TCM 可以在相同的带宽内传输更多的数据。
2. 提高抗噪声性能：TCM 引入的编码信息可以帮助接收端更好地纠正由于噪声引起的错误。
3. 降低误码率：TCM 可以通过在信号星座图中引入多个状态来降低误码率。
4. 简化接收机设计：由于TCM 引入了编码信息，接收机可以使用简单的解调算法来实现。
TCM 已经广泛应用于各种数字通信系统，如卫星通信、移动通信、数字电视等。
网格编码调制_毕设论文
摘要摘要传统的数字通信系统中，信道编码和调制是独立设计的，系统性能的改善以带宽的扩展为代价。
网格编码调制技术是用卷积码产生取得编码增益所需的冗余，然后通过采用高阶调制而不是增加发送符号的数目来保持带宽不变。
本文首先用一个例子阐明了编码与调制联合设计的原因，然后分析了Ungerboeck TCM和实用化TCM（Pragmatic TCM）的设计过程，并对两个简单的方案进行了性能仿真。
接着，本文对TCM的旋转不变性行了分析，介绍了旋转不变TCM的基本设计思想。
最后介绍了多维TCM，详细的分析了WEI提出的4维TCM方案，并对其在AWGN信道上的性能进行了仿真。
理论与仿真结果均表明采用TCM相对于未编码系统可以取得较高的编码增益，将TCM 引入通信系统可以显著的提高系统性能。
【关键词】信道编码网格编码调制实用化TCM旋转不变TCM多维TCMABSTRACTABSTRACTIn conventional digital communication systems,channel coding and modulation are separately designed,and system performance is improved with the cost of bandwidth expansion.Trellis-Coded Modulation(TCM)is to use a convolutional code to generate the redundancy necessary to achieve a coding gain,while preventing bandwidth expansion by increasing the size of the constellation rather than the number of transmitted symbols.In this thesis,the reason to combine modulation and coding is illustrated by an example firstly,then we show the design procedures of Ungerboeck TCM and pragmatic TCM,followed by computer simulations of two simple TCM schemes.After that,the concept of rotational invariant TCM is introduced,general meth-ods to analyze these schemes are also discussed.Finally,multidimensional TCM is studied,and we describe the construction procedures of WEI's four-dimensional TCM scheme in detail.Per-formance evaluation of this code in AWGN channels is conducted by simulation.Theoretical analysis and simulation results both show that system performance can be efficiently improved by applying TCM.Keywords:channel coding Trellis-coded modulation pragmatic TCM rotational in-variant TCM multidimensional TCM目录i目录第一章绪论11.1网格编码调制的背景 (1)1.2本文的安排 (2)第二章网格编码调制简介32.1通信系统效率的描述 (3)2.2TCM系统的渐进编码增益 (5)2.3编码与调制联合设计的原因 (5)第三章TCM方案设计93.1Ungerboeck的TCM方案 (9)3.1.1集合分割映射 (9)3.1.2TCM的Viterbi译码 (10)3.2实用化TCM (12)3.3性能仿真 (14)第四章旋转不变TCM174.1相位模糊导致星座旋转的原因 (17)4.2差分编译码 (18)4.3旋转不变TCM (20)第五章多维TCM265.1多维TCM的优势 (26)5.24D TCM方案 (27)5.34D Viterbi译码 (32)5.4仿真结果 (32)第六章结束语34ii网格编码调制致谢35参考文献38第一章绪论1第一章绪论1.1网格编码调制的背景数字通信系统的基本组成如图1.1所示。
tcm网格编码MATLAB程序
TCM——格状编码调制格状编码调制是为解决卫星通信中信道噪声对接收的影响及带宽的限制而产生的，其将信道编码与调制很好的结合起来，并且能发挥各自的优点，这种方法在不增加带宽和相同的信息速率下可获得3~6dB的功率增益。
其中信道编码主要使用卷积码，为了适应卷积码则应用了多进制移相键控调制（亦可用多进制QAM），并且根据Ungerboack提出的规律：对经过编码的调制系统来说，其信道信号数目只要是未经编码的调制系统的两倍，便可得到足够的编码增益，对于每符号传送k比特的系统，应选择有m=2k+1点的扩张信号星座形式传送信息，对于信号集合划分规则等不作太多的阐述，本实验选择k=2,则m=8，即使用8Q PSK调制器，为此，TCM结构图如下：卷积码编码器8φPSK调制器信道8φPSK解调器最大似然维特比译码器输入噪声输出其中为了得到足够大的编码增益，未编码比特为k’=1,对这样的系统卷积码编码器的结构为：x2x1R1R211111111111101234567去8φPSK调制器+y2y1y0对于卷积码的编码可用以下程序实现：k=1;g=[1 0 1;0 0 1];int=input('xulie')m=size(int,1);y=zeros(1,m)for n=1:my(:,n)=int(n,1)end;z=cnv_encd(g,k,y);并且在卷积码编码过程中，添零数为k1*(L-1)=2,(注：L=3)，再对序列进行图示的映射，可通过以下程序实现：tyu=length(z)/2;s=zeros(1,3*tyu);for i=1:ms(:,3*i-2)=int(i,2)ends(:,3*m+1)=0;s(:,3*(m+1)+1)=0;for j=1:tyus(:,3*j-1)=z(2*j-1)end;for k2=1:tyus(:,3*k2)=z(2*k2)end;uu=reshape(s,3,tyu);kk=uu'；（注意：对添零后卷积编码的处理），将编码处理后的信号进行调制，相位调制实现比较容易，对于通过信道后的解调，有两种实现途径：①接收信号通过相关器后，将接收到的信号矢量映射到M个可能发送的信号矢量上去，并且选出对应于最大映射的矢量；②亦可计算接收信号矢量的相位，并从M个可能发送的信号矢量中选出相位最接近的信号。
TCM调制技术
浅谈TCM调制技术摘要：网格编码调制技术（tcm）是一种将编码与调制有机结合起来的编码调制技术，它既不增加频带宽度，又不降低信息传输速率，可使系统的频带利用率和功率资源同时得到有效利用。
本文首先介绍tcm的发展背景与研究现状，进而引出tcm的基本原理与特点，最后描述tcm的未来及发展趋势。
关键词：tcm的现状 tcm的原理 tcm的发展1.tcm调制技术的发展背景与现状随着数字移动通信的发展，频带资源日益宝贵，对数据传输质量的要求也越来越高。
因此，如何提高信息传输系统的有效性和可靠性，便成为了该领域研究的重要课题。
把编码调制技术应用于高速信息传输的通信中，较好地解决了这一问题。
一般的纠错编码技术对信息传输性能的改善是建立在带宽扩展的基础上的。
因此，在带宽受限的信道中，依靠传统的纠错编码技术是难于提高信道利用率的。
1974年messy根据shannon信息理论最早证明了将编码与调制作为一个整体考虑的最佳设计，就可大大改善系统的性能。
1982年，ungerboeck在ieee trans information theory上发表题为“channel coding with multilevel/phase signals”的论文，正式宣布了人们研究多年的调制编码相结合的网格编码调制（trellis coded modulation，简记为tcm）技术的诞生。
该技术把信道编码和调制结合在一起进行设计，可以在既不增加信道频带宽度、也不降低信息传输速率的情况下，获得3～6db的编码增益，宣告了一个划时代的、新的纠错编码技术的开始，成为继shannon奠基以来信道编码技术发展的一个新的里程碑。
随后，对tcm技术进行研究的热潮迅速的在全球范围内兴起，tcm研究领域取得了众多令人瞩目的成就，使得tcm技术从理论研究阶段逐步进入实用阶段。
目前，tcm技术在无线通信、微波通信、卫星通信以及移动通信等各个领域中的应用前景非常广阔。
网格编码调制(TCM)
d0＝2sin( π8 )＝ 2· 2
0
d1＝ 2 0
d1 1
d2＝ 2
0
1
d2
0
1
d0
1 0
0
1
1
0
1
000
100
010
110
001
101
图10.13描述了最简单的传输2比特码字的8PSK四 状态TCM编码方案。它采用了效率为1/2的卷积码编码器.
图8-11 8PSK四状态TCM编码方案
对应的格图如图所示。
10.6 Turbo码
1. Turbo
典型的Turbo码编码器结构如图10.14所示。它由两 个成员码编码器、一个交织器和一个截取复接器组成。 第一个编码器直接对信源信息序列的分组进行编码，第 二个编码器对经过交织器交织后的信息序列的分组进行 编码，最后的编码输出由信息序列和两个编码器产生的 校验序列经截取和复接后得到。
图10.16 Turbo码译码器
•
在Turbo码出现以前，编码界对于级联码的次优译
码算法进行了大量的研究，包括多个（通常是两个）
译码器协同循环译码。其译码算法可采用逐符号MAP
算法，又常被称为BCJR算法、BAHL
现代通信原理
现代通信原理
网格编码调制(TCM)
网络编码调制技术, 是利用编码效率为n/(n+1)的卷积码，并 将每一码段映射为2n+1个调制信号集中的一个信号。在收端信 号解调后经反映射变换为卷积码， 再送入维特比译码器译码。 它有两个基本特点：
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
–7
6.1.2 4状态8PSK TCM码结构
以4状态8PSK网格编码调制为例，如图6-2，它 是Ungerboeck 1975研究出的第一种TCM码。
第一部分 第二部分 差分编码 卷积编码 D Xn2 ’ Xn2 Y n2 第三部分 分集映射 010 011 001 000
Xn1’
–11
为此，我们将8PSK星座对半又对半地划分成子 集(set partitioning),使每级子集具有逐级增大的 距离，然后把并行转移的一组码字映射到点数 相符的同一子集上，以保证并行转移具有最大 的距离，这个过程叫作分集映射(mapping by set partitioning)，它使并行转移总是对应到星座的 最远点距子集上。8PSK分集过程及各级距离 0 、 0、 1、 2见图6-4。
000 110 100 010
C0 C1
C =
110 000 010 100
101 111 001 011 =
C2 C3
(6-1)
C1 C0
111 101 011 001
C3 C2
从编码矩阵看，每一行、每一列的子集具有相同 的上级子集， C0～C3出现次数相同，分布规则。 凡相差180°的两星座点，比如C0的000、100，其 后两位Yn1Yn0总是相同的，不受180°相移影响； 其第一位Yn2采用差分编码，可抗180°相位混淆。
–20
引入差分编码后就不怕180度相位混淆了，比如
原信息位： … 0 0 0 1 0 1 1 0 0 1 0 …
差分编码:
…0 0 0 1 1 0 1 1 1 0 0 …
180相位差: … 1 1 1 0 0 1 0 0 0 1 1 … 差分译码: … 0 0 0 1 0 1 1 0 0 1 0 … 可见，相位混淆不再影响收码的正确性。
–9
00 01 10 11
000 100 010 110
ห้องสมุดไป่ตู้
010 110
000 100 001 101 011 111 011 111
Sn+11 = Sn0 Sn+10= Sn1⊕Xn1
Xn2Xn1 Sn 1 S n 0
00 01 10 11
Xn Xn2 10 Xn2 11 Xn2 10 Xn2 11
图6-4 8-PSK星座的子集分割
–13
分集的结果产生了4个子集C0～C3，每子集与一组 并行转移对应，对应的原则是： (1).从某一状态发出的子集源于同一个上级子集， 比如C0、C1就是源于同一上级子集B0。 (2).到达某一状态的子集源于同一个上级子集。 (3).各子集在编码矩阵中出现的次数相等，并呈现 出一定的对称性。 另外，由于接收端载波恢复时会造成不同程 度的相位不定度，比如对于8PSK，一般的载波提 取可产生45、90、135、180…等相位不定度， 如采用判决反馈情况好些，但还存在180°的相位 混淆。
–19
图6-2前部的差分编码是为了克服相位混淆而设计 的。这是因为Viterbi译码时的相似度是以路径间 的距离来衡量的，而本题的路径距离体现为各分 支对应子集间的欧氏距离。如果子集不同，在相 似度上会有所体现；但如果子集相同而同一子集 内的点搞错，比如点000混淆为100、010混淆为 110，则Viterbi译码时察觉不到。其结果是，如果 接收端的载波恢复相差180度，那么收到的所有 信号将相差180度，即收端星座是发端星座的180 度旋转体，发端的000点变为收端100点、发端 001点变为收端101点…，依此类推，见图6-2。简 2 2 1 0 言之，码字 Y n Y n Y中的 Y n 将由0变为1或由1变 n 为0而Viterbi译码察觉不到，造成译码差错。
–12
B0
2
1
0
100
C0 000
距离
010 C1
C2 101 011 C3
110 001
A B0 B1
0 1
B1
C0 C1 C2 C3 2
111
0=2sin(/8) 1=
第0级
第1级
2
第2级
2=2
–3
C (比特/符号) 6 5
½ log2(1+SNR) 4
3 10-5
〇
16PSK
8PSK
10-5
〇
2
1 0┸ 0 10-5 〇 4.7 5.9
10-5
〇
4PSK
2PSK
12.9
SNR
4 8 12 16 20 24 dB 图6-1 带限AWGN信道PSK调制时 信道容量与SNR的关系曲线
–4
┸ ┸ ┸ ┸ ┸ ┸ ┸ ┸ ┸ ┸ ┸ ┸ ┸
式中， d 2un是不编码时信号点集的最小距离，Ec 、Eun分别是编码、不编码条件下信号集的平均能 量。本例不编码时无需信号点集冗余度，只要 4PSK即可传送2比特/符号信息，4PSK的最小距离 是d 2un= 12 = ( 2 )2 = 2，而4PSK、8PSK平均能量 相同，于是得编码增益 = 10 log(d 2f / d 2un) = 10 log(4/2) = 3.01dB
2
状态 C0 00 C1 01 C1 C0 10 C3 C2 C3 11 C2
000 100 C1
C0
C0
C2
C1
–17
为了定量说明编码前后的变化，定义编码增益为 = 10 log (
d
2 f
/ Ec / E un
d
2 un
)
(6-3)
–1
八十年代以来，一种将编码和调制结合在一 起，利用状态的记忆和适当的映射来增大码字序 列之间距离的方法诞生了，这就是网格编码调制 （TCM- Trellis Coded Modulation）。TCM码是 1982年由Ungerboeck.G [29] 提出的。这种方法既 不降低频带利用率，也不降低功率利用率，而是 以设备的复杂化为代价换取编码增益。在当前集 成电路高速发展、传输媒体成本高于终端设备成 本而成为通信成本的第一考虑因素时，这种方法 无疑是非常吸引人的。现在，这种网格编码调制 已在频带、功率同时受限的信道如太空、卫星、 微波、同轴、对绞线等通信中大量应用，占据了 统治地位。
–10
并行转移影响了卷积码的自由距离。如前述， 自由距离是指从零状态分叉又回到零状态、与 全0路径距离最小的那条路径的距离。对于如图 6-3码字(100)是与全零码(000)的并行转移，严 格意义上它并没有“从零状态分叉又回到零状 态”，但它的确是“与全0路径分叉又回到全0 路径”的一条路径，因此在计算自由距离时也 必须包括并行距离，即自由距离不可能大于并 行转移的距离。正因为如此，并行转移所对应 的码距越大越好。对于二进码就是汉明距离越 大越好，对于两维调制如PSK或QAM，就是星 座上码字对应信号点的欧氏距离越大越好。
–18
可以想象，如果进一步增加编码器的复 杂度，使TCM具有8状态、16状态、32 状态…，一定可以得到更大的编码增益 。实际情况确是如此，通过计算机模拟 发现，码率m/m+1的TCM码，8状态时 最大可得3.97dB编码增益(理论值)，而 16、32、64、128状态时的最大编码增 益分别是4.39、5.11、5.44、6.02 dB。
网格编码调制（TCM） 6.1 网格编码调制的基本概念 任何纠错码纠错能力的获取都是以冗余度为基 础的，即通过编码使误码率降低是要付出代价的。 这种代价或者是频带利用率的降低，或者是功率利 用率的降低，或者是设备变得比较复杂，昂贵。 比如采用(n,k)分组或卷积码后， ▬或者信源速率不变而提高信道传输速率，意味着 占用更大带宽，频带利用率下降了。 ▬或者带宽不变而采用多电平（或多相）调制。在 误码率即信号星座各点间距离不变条件下，意味着 要增大平均功率，则功率利用率下降了。
这个7db增益是指理论极限值，目前工程可实 现的TCM码的最大编码增益不超过6dB。
–5
各类信道的信噪比(SNR)有一个典型值。 比如微波信道的SNR典型值取50dB, 移动信 道取10～15 dB, 模拟电话信道取28dB等。 以电话信道，由对数值10lg(S/N)=28得信 噪比S/R=631。电话信道标称带宽300～ 3400Hz，但适合数据传输的频段仅是600～ 3000Hz，带宽2400Hz。代入香农公式， C=2400log2(1+631)=22320比特/秒，考虑到 其它一些因素，当时认为极限数据速率是 23500比特/秒（见IEEE J-SA, Sept. 1984, pp632-634）。
21
20
001 101
从网格图看，从一个状态转移到另一状态 的路径不唯一，存在两条，称为“并行转移”。 产生并行转移的原因是输入信息Xn2没有参与卷 积编码，编码器状态转移仅与Xn1有关，而与Xn2 (即Yn2)究竟是1还是0无关，所以它的两种取值就 构成了1Yn1Yn0和0Yn1Yn0两条并行转移路径。 从另一角度看，每次输入的两位信息共有 22=4种组合，而其中只有一位对状态转移产生影 响即只有21=2种转移，所以每转移应对应42=2 种Xn2Xn1组合即2种码字即一对并行转移（一条 转移路线对应一种码字）。
–2
网格编码调制是一种信号集空间编码(signalspace code)，它利用信号集的冗余度，保持符号 率和功率不变，用大星座传送小比特数而获取纠 错能力。为此，先将小比特数编码成大比特数， 再设法按一定规律映射到大星座上去。 上述过程中，冗余比特的产生属于编码范畴 ，信号集星座的扩大与映射属于调制范畴，两者 结合就是编码调制。比如，用具有携带3比特信 息能力的8ASK或8PSK调制方式来传输2比特信 息，叫做信号集冗余度，我们正是利用这种信号 集空间(星座)的冗余度来获取纠错能力的。