(完整版)高一数学直线方程知识点归纳及典型例题
高一数学直线的一般式方程

它表示为斜率为 – A/B,纵截距为- C/B的直线。
⑵B=0时,由于A,B不同时为零所以A≠0,此时,Ax+By+ C=0可化为x= -C / A,它表示为与Y轴平行(当C=0时)或重合 (当C=0时)的直线。
思考:直线与二元一次方程具有什么样的关系?
结论:(1)直线方程都是关于x,y的二元一次方程 (2)关于x,y的二元一次图象又都是一条直线。 我们把方程Ax+By+c=0(A,B不同时为零)叫做 直线方程的一般式。所以直线和二元一次方程是 一一对应。
1、直线方程的一般式Ax+By+c=0(A,B不同时为零)的两 方面含义:
(1)直线方程都是关于x,y的二元一次方程 (2)关于x,y的二元一次图象又都是一条直线
2、掌握直线方程的一般式与特殊式的互化。
布置作业:
7· 2
8,9,10
;/ 商场展柜;
仙吧,要不然你把这个家伙给灭了?咱们抢了他们の宝物の话,应该就差不多了""小子,你以为魔仙是阿猫阿狗吗?说灭就灭,脑子有病"对于根汉の想法,红柳只能甩他壹个白眼了,想将魔仙说灭就灭,那可不是随便壹个人就能做到の丶;猫补中文肆0肆0未知领域(猫补中文)哪个魔仙不是通天の 人物,要是这么容易被人灭了,这魔仙の名头也白让人给叫了丶"呵呵,也没说要杀了他嘛,不如你将他给引开,咱将这剩下の十来人给收了,如何?"根汉笑了笑丶"别想了,这里の强者可不少,魔仙绝对不止壹两位。"红柳白了他壹眼,传音道:"要抓他们也不急于现在,不如跟着他们,等他们离开 了这里,到了没什么人の地方倒是可以。""只不过这三个年轻人,竟然还有魔仙做守卫,背后の实力壹定很强大。&#
高中数学直线方程知识点

高中数学直线方程知识点
高中数学直线与方程知识点总结
1.直线的倾斜角
(1)定义:当直线l与x轴相交时,取x轴作为基准,x轴正向与直线l向上方向之间所成的角叫做直线l的倾斜角.当直线l与x轴平行或重合时,规定它的倾斜角为0°.
(2)范围:直线l倾斜角的范围是[0°,180°).
2.斜率公式
(1)若直线l的倾斜角α≠90°,则斜率k=tan_α.
(2)P1(x1,y1),P2(x2,y2)在直线l上且x1≠x2,则l的斜率k=(y2-y1)/(x2-x1).
3.直线方程的五种形式
题组一思考辨析
1.判断下列结论是否正确(请在括号中打“√”或“×”)
(1)根据直线的倾斜角的大小不能确定直线的位置.(√)
(2)坐标平面内的任何一条直线均有倾斜角与斜率.(×)
(3)直线的倾斜角越大,其斜率就越大.(×)
(4)若直线的斜率为tanα,则其倾斜角为α.(×)
(5)斜率相等的两直线的倾斜角不一定相等.(×)
(6)经过任意两个不同的点P1(x1,y1),P2(x2,y2)的直线都可以用方程(y-y1)(x2-x1)=(x-x1)(y2-y1)表示.(√)
2.若过点M(-2,m),N(m,4)的直线的斜率等于1,则m的值为( )
A.1 B.4
C.1或3 D.1或4
综上可知,直线m的方程为x-2y+2=0或x=2.
(2)直线l过点P(1,0),且与以A(2,1),B(0,√3)为端点的线段有公共点,则直线l斜率的取值范围为___________________.答案(-∞,-]∪[1,+∞)
解析如图
直线方程的综合应用
课时作业:。
(完整版)高一数学直线方程知识点归纳及典型例题

直线的一般式方程及综合【学习目标】1.掌握直线的一般式方程;2.能将直线的点斜式、两点式等方程化为直线的一般式方程,并理解这些直线的不同样形式的方程在表示直线时的异同之处;3.能利用直线的一般式方程解决有关问题. 【要点梳理】要点一:直线方程的一般式关于 x 和 y 的一次方程都表示一条直线.我们把方程写为 Ax+By+C=0 ,这个方程 (其中 A 、B 不全为零 )叫做直线方程的一般式.要点讲解:1.A 、 B 不全为零才能表示一条直线,若 A 、 B 全为零则不能够表示一条直线 .当 B ≠0时,方程可变形为 yA x C ,它表示过点 0,C,斜率为A的直线.B BBB当 B=0 , A ≠0时,方程可变形为Ax+C=0 ,即 xCx 轴垂直的直线.,它表示一条与A由上可知,关于 x 、 y 的二元一次方程,它都表示一条直线.2.在平面直角坐标系中,一个关于x 、y 的二元一次方程对应着唯一的一条直线,反过来,一条直线可以对应着无数个关于 x 、y 的一次方程 (如斜率为 2,在 y 轴上的截距为 1 的直线,其方程能够是 2x ―y+1=0 ,也能够是 x 1 y 1 0 ,还可以够是 4x ― 2y+2=0等.)2 2要点二:直线方程的不同样形式间的关系 直线方程的五种形式的比较以下表:名称方程的形式 常数的几何意义适用范围 点斜式y ―y( x 1, y 1)是直线上必然点, k 是斜率 不垂直于 x 轴1=k(x ―x 1)斜截式y=kx+bk 是斜率, b 是直线在 y 轴上的截距不垂直于 x 轴 两点式y y 1 x x 1 ( x 1, y 1 ),(x 2 ,y 2)是直线上两定点不垂直于 x 轴和 y 轴y 2 y 1x 2x 1截距式x y a 是直线在 x 轴上的非零截距,b 是直不垂直于 x 轴和 y 轴,a1线在 y 轴上的非零截距b且但是原点 一般式Ax+By+C=0 ( A 2+B 2≠0) A 、B 、 C 为系数任何地址的直线要点讲解:在直线方程的各种形式中,点斜式与斜截式是两种常用的直线方程形式,要注意在这两种形式中都要求 直 线 存 在 斜 率 , 两 点 式 是 点 斜 式 的 特 例 , 其 限 制 条 件 更 多 ( x 1≠x 2, y 1 ≠y 2), 应 用 时 若 采 用 (y 2―y 1)(x ―x 1) ― (x 2―x 1)(y ―y 1)=0 的形式,即可除掉限制性.截距式是两点式的特例,在使用截距式时,第一要判断可否满足 “直线在两坐标轴上的截距存在且不为零 ”这一条件.直线方程的一般式包含了平面上的所有直线形式.一般式常化为斜截式与截距式.若一般式化为点斜式,两点式,由于取点不同样,获取的 方程也不同样.要点三:直线方程的综合应用1.已知所求曲线是直线时,用待定系数法求.2.依照题目所给条件,选择合适的直线方程的形式,求出直线方程.关于两直线的平行与垂直,直线方程的形式不同样,考虑的方向也不同样.( 1)从斜截式考虑已知直线 l 1 : y k 1 x b 1 , l 2: y k 2 x b 2 ,l 1 // l 2 1 2k 1 k 2 (b 1 b 2 ) ;l 1 l 2tancot1 k 1k 211212k 12k 2于是与直线 y kx b 平行的直线能够设为 ykx b 1 ;垂直的直线能够设为y1 x b2 . ( 2)从一般式考虑:kl 1 : A 1x B 1 y C 1 0, l 2 : A 2 x B 2 y C 2l 1 l 2 A 1 A 2 B 1B 2l 1 // l 2A 1B 2 A 2B 1 0且 A 1C 2 A 2C 1 0 或 B 1C 2 B 2C 1 0 ,记忆式( A 1 B 1C1 )A 2B 2C 2l 1 与 l 2 重合, A 1B 2 A 2 B 1 0 , A 1C 2 A 2C 1 0 , B 1C 2 B 2C 1 0于 是 与 直 线 Ax By C 0 平 行 的 直 线 可 以 设 为 AxBy D 0 ; 垂 直 的 直 线 可 以 设 为Bx Ay D0 .【典型例题】种类一:直线的一般式方程例 1.依照以下条件分别写出直线的方程,并化为一般式方程.1 (1)斜率是,经过点 A ( 8, ―2);2(2)经过点 B ( 4, 2),平行于 x 轴;(3)在 x 轴和 y 轴上的截距分别是3,―3;2(4)经过两点 P 1( 3,―2), P 2( 5, ―4).【答案】( 1) x+2y ―4=0 ( 2) y ―2=0 ( 3) 2x ―y ―3=0 ( 4) x y 1 0【剖析】( 1)由点斜式方程得 y( 2)1( x 8) ,化成一般式得 x+2y ― 4=0.2(2)由斜截式得 y=2,化为一般式得 y ―2=0 .(3)由截距式得xy1 ,化成一般式得 2x ―y ―3=0 .3 32(4)由两点式得y 2x3,化成一般式方程为x y 1 0 .4 ( 2)5 3【总结升华】本题主若是让学生领悟直线方程的各种形式,以及各种形式向一般式的转变,关于直线方程的一般式,一般作以下约定: x 的系数为正, x ,y 的系数及常数项一般不出现分数,一般按含 x 项、 y 项、常数项序次排列.求直线方程的题目,无特别要求时,结果写成直线方程的一般式.贯穿交融:【变式 1】已知直线 l 经过点 B(3, 1) ,且倾斜角是 30 ,求直线的点斜式方程和一般式方程.【答案】 y 13(x3) 3x 3y3 3 3 03【剖析】由于直线倾斜角是30 ,所以直线的斜率 ktantan 303 ,所以直线的点斜式方程3为: y 13(x 3) ,化成一般式方程为:3x 3 y 3 3 30 .3例 2. ABC 的一个极点为 A( 1, 4) , B 、 C 的均分线在直线y 1 0和 x y 10 上,求直线 BC 的方程 .【答案】 x 2 y3 0【剖析】由角均分线的性质知,角均分线上的任意一点到角两边的距离相等,所以可得 A 点关于B 的均分线的对称点 A ' 在 BC 上, B 点关于C 的均分线的对称点 B ' 也在 BC 上.写出直线 A ' B ' 的方程,即为直线 BC 的方程 .例 3.求与直线 3x+4y+1=0 平行且过点( 1, 2)的直线 l 的方程.【答案】 3x+4y ―11=0 【剖析】解法一:设直线l 的斜率为 k ,∵ l 与直线 3x+4y+1=0 平行,∴ k3 .4又∵ l 经过点( 1, 2),可得所求直线方程为 y 23(x 1) ,即 3x+4y ― 11=0.4解法二:设与直线 3x+4y+1=0 平行的直线 l 的方程为 3x+4y+m=0 ,∵ l 经过点( 1, 2),∴ 3×1+4×2+m=0 ,解得 m=―11 .∴所求直线方程为 3x+4y ―11=0 .【总结升华】( 1)一般地, 直线 Ax+By+C=0 中系数 A 、B 确定直线的斜率, 所以,与直线 Ax+By+C=0平行的直线可设为 Ax+By+m=0 ,这是常采用的解题技巧.我们称 Ax+By+m=0 是与直线 Ax+By+C=0 平行的直线系方程.参数m 能够取 m ≠C 的任意实数,这样就获取无数条与直线Ax+By+C=0平行的直线.当m=C 时, Ax+By+m=0 与 Ax+By+C=0 重合.(2)一般地,经过点 A (x 0 ,y 0),且与直线 Ax+By+C=0 平行的直线方程为 A(x ―x )+B(y ―y )=0 .(3)近似地有:与直线 Ax+By+C=0 垂直的直线系方程为Bx ―Ay+m=0 ( A , B 不同样时为零) .贯穿交融:【变式 1】已知直线 l 1 : 3mx+8y+3m-10=0 和 l 2 :x+6my-4=0 . 问 m 为何值时 :(1) l 1 与 l 2 平行( 2) l 1 与 l 2 垂直 . 【答案】( 1) m2 ( 2) m3【剖析】当 m0 时, l 1 : 8y-10=0 ; l 2 : x-4=0 , l 1 l 2当 m 0 时, l 1 : y3m 10 3m: y 1x4x 8 ; l 2 6m86m由 3m1 ,得 m2 ,由 10 3m 4 得 m 2 或 886m38 6m 3 3 而 (3m ) ( 1 ) 1无解8 6m2综上所述( 1) m, l 1 与 l 2 平行.( 2) m 0 , l 1 与 l 2 垂直.3【变式 2】 求经过点 A ( 2, 1),且与直线 2x+y ―10=0 垂直的直线 l 的方程. 【答案】 x - 2y=0【剖析】由于直线 l 与直线 2x+y ―10=0 垂直,可设直线 l 的方程为 x 2y m 0 ,把点 A (2,1)代入直线 l 的方程得: m0 ,所以直线 l 的方程为: x -2y=0 .种类二:直线与坐标轴形成三角形问题例 4.已知直线 l 的倾斜角的正弦值为3,且它与坐标轴围成的三角形的面积为6,求直线 l 的方程.5【思路点拨】知道直线的倾斜角就能求出斜率,进而引进参数—— 直线在 y 轴上的截距 b ,再依照直线与坐标轴围成的三角形的面积为 6,即可求出 b .也能够依照直线与坐标轴围成的三角形的面积为6,设截距式直线方程,进而得出1| ab | 6 ,再依照它的斜率已知,进而获取关于a ,b 的方程组,解之即可.3 x23 x【答案】 y3 或 y 344【剖析】解法一:设 l 的倾斜角为,由 sin33,得 tan.3544设 l 的方程为yx b ,令 y=0,得 x4 b .3∴直线 l 与 x 轴、 y 轴的交点分别为 4 ,( 0,b ).b,03∴ S1 4b | b | 2b 2 6 ,即 b 2=9,∴ b=±3.23 3故所求的直线方程分别为y 3 x 3 或 y3 x 3 .44解法二:设直线l 的方程为xy 1,倾斜角为,由 sin3 ,得 tan3 .a b541| a | | b |6a 4∴2b3 ,解得.b 3a4故所求的直线方程为x y 1或 xy 1.4 3 4 3【总结升华】( 1)本例中,由于已知直线的倾斜角(与斜率有关)及直线与坐标轴围成的三角形的面积(与截距有关) ,所以可选择斜截式直线方程,也可采用截距式直线方程,故有“题目决定解法 ”之说.(2)在求直线方程时,要合适地选择方程的形式,每种形式都拥有特定的结论,所以依照已知条件恰 当地选择方程的种类经常有助于问题的解决.比方:已知一点的坐标,求过这点的直线方程,平时采用点 斜式,再由其他条件确定该直线在y 轴上的截距;已知截距或两点,选择截距式或两点式.在求直线方程的过程中,确定的种类后,一般采用待定系数法求解,但要注意对特别情况的谈论,省得遗漏.贯穿交融:【变式 1】( 2015 春 启东市期中)已知直线m : 2x ― y ―3=0 , n :x+y ―3=0 .( 1)求过两直线 m ,n 交点且与直线 l : x+2y ―1=0 平行的直线方程; (2)求过两直线 m , n 交点且与两坐标轴围成面积为4 的直线方程.【思路点拨】( 1)求过两直线 m , n 交点坐标,结合直线平行的斜率关系即可求与直线l : x+2y ―1=0平行的直线方程;( 2)设出直线方程,求出直线和坐标轴的交点坐标,结合三角形的面积公式进行求解即可.【答案】( 1) x+2y ―4=0 ;( 2)2x y 3 0 x 2 【剖析】( 1)由y3 ,解得y,x 01即两直线 m , n 交点坐标为( 2, 1),设与直线 l : x+2y ―1=0 平行的直线方程为 x+2y+c=0 ,则 2+2×1+c=0,解得 c=―4, 则对应的直线方程为 x+2y ―4=0 ;(2)设过( 2, 1)的直线斜率为 k ,( k ≠0),则对应的直线方程为 y ―1= k(x ―2) ,令 x=0, y=1―2k ,即与 y 轴的交点坐标为 A ( 0, 1―2k ) 令 y=0,则 x2 1 2k 1 ,即与 x 轴的交点坐标为 B(2k 1,0) ,k kk 则△AOB 的面积 S1 | 2k 1||1 2k | 4 ,2 k即 (2k 1)2 8 k ,即 4k 24k 8 k1 0 ,若 k > 0,则方程等价为 4k 212k1 0 ,解得 k3 2 2或 k 3 2 2 ,22若 k < 0,则方程等价为 4k 24k1 0 ,解得 k1 .2综上直线的方程为y 11( x 2) ,或 y 13 2 2 ( x 2) ,或 y 13 2 2( x 2)222即 y1 x2 ,或 y3 2 23 2 2x 2 2 22 x 2 2 2 ,或 y22种类三:直线方程的本质应用例 6.( 2015 春 湖北期末)光辉从点 A ( 2,3)射出,若镜面的地址在直线 l : x+y+1=0 上,反射光辉经过 B ( 1, 1),求入射光辉和反射光辉所在直线的方程,并求光辉从 A 到 B 所走过的路线长.【思路点拨】求出点 A 关于 l 的对称点,就可以求出反射光辉的方程,进一步求得入射点的坐标,从而可求入射光辉方程,可求光辉从A 到B 所走过的路线长.【答案】 41【剖析】设点 A 关于 l 的对称点 A '( x 0, y 0),x 0 2 y 0 3 1 0 x 04∵AA '被 l 垂直均分,∴2 2 ,解得y 0 3y 03x 0 12∵点 A '(―4, ―3), B (1, 1)在反射光辉所在直线上, ∴反射光辉的方程为y 3 x4,即 4x ―5y+1=0,1 3 1 44x 5y 1 0( 2 ,1) . 解方程组x y 10 得入射点的坐标为3 3y 1x 2由入射点及点 A 的坐标得入射光辉方程为3 3,即 5x ―4y+2=0 ,31 2 233光辉从 A 到 B 所走过的路线长为 | A' B |( 4 1)2 ( 3 1)241 .【总结升华】本题要点观察点关于直线的对称问题,观察入射光辉和反射光辉,解题的要点是利用对称点的连结被对称轴垂直均分.线 贯穿交融:【变式 1】( 2016 春 福建厦门期中)一条光辉从点 A (- 4,- 2)射出,到直线y=x 反射到 y 轴上的 C 点,又被 y 轴反射,这时反射光辉恰好过点 D (- 1,6).求 【答案】 10x - 3y+8=0【剖析】如图, A (- 4,- 2), D (- 1,6),y=x 上的 B 点后被直BC 所在直线的方程.由对称性求得 A (- 4,- 2)关于直线 y=x 的对称点 A '(- 2,- 4), D 关于 y 轴的对称点 D '( 1, 6),则由入射光辉和反射光辉的性质可得:过 A ' D '的直线方程即为 BC 所在直线的方程.由直线方程的两点式得: y 4 x 2 . 整理得: 10x - 3y+8=0 .64 1 2例 7.如图,某房地产公司要在荒地ABCDE 上划出一块长方形土地(不改变方向)建筑一幢8 层的公寓,如何设计才能使公寓占地面积最大?并求出最大面积.(精确到 1 m 2)【答案】 6017【剖析】建立坐标系,则 B ( 30, 0), A ( 0, 20).∴由直线的截距方程获取线段AB 的方程为x y 1 (0≤ x ≤ )30.30 202x . 设点 P 的坐标为( x , y ),则有 y203∴公寓的占地面积为S (100 x) (80y) (100 x) (80 20 2x)2 x 2 20 x 6000 (0≤ x ≤ )30.3 3 3 ∴当 x=5 , y50 时, S 取最大值,最大值为 S2 52 20 5 6000 6017(m 2 ) .333即当点 P 的坐标为 (5,50) 时,公寓占地面积最大,最大面积为6017 m 2.3P 的地址由两个条件确定,一是 A 、 P 、 B 三点共线,【总结升华】本题是用坐标法解决生活问题,点 二是矩形的面积最大.借三点共线追求x 与 y 的关系,利用二次函数知识研究最大值是办理这类问题常用的方法.。
直线方程经典例题及解析

直线方程经典例题及解析直线是我们在几何学中经常遇到的基本概念之一,研究直线方程是数学中的一个重要分支。
本文将介绍几个经典的直线方程例题,并逐步解析它们的求解过程。
例题1:求过两点的直线方程已知直线上有两个点A(x1, y1)和B(x2, y2),请求出通过这两个点的直线方程。
解析:我们知道,直线的方程可以表示为y = kx + b的形式,其中k是斜率,b是与y 轴交点的纵截距。
首先我们需要计算斜率k,根据斜率公式:k = (y2 - y1) / (x2 - x1)然后,我们可以使用其中一个点(例如A点),将点坐标带入方程:y1 = kx1 + b可以得到b的值:b = y1 - kx1因此,通过这两个点的直线方程为:y = (y2 - y1) / (x2 - x1) * x + (y1 - (y2 - y1) / (x2 - x1) * x1)这就是通过两个已知点求直线方程的方法。
例题2:求与两直线的交点已知直线L1的方程为y = k1x + b1,直线L2的方程为y = k2x + b2,求两直线的交点坐标。
解析:假设L1和L2的交点坐标为(x, y)。
那么根据直线方程,我们可以得到:k1x + b1 = k2x + b2整理后可得:(k1 - k2)x = b2 - b1从而得到交点横坐标x的值:x = (b2 - b1) / (k1 - k2)将x的值带入任意一条直线方程中,可以求出交点纵坐标y的值。
综上所述,我们可以通过以上步骤求得直线L1和L2的交点坐标。
例题3:已知截距和斜率求直线方程已知直线L的斜率为k,与y轴的截距为b,请求直线L的方程。
解析:根据直线方程y = kx + b,我们已知直线L的截距和斜率。
根据已知信息,我们可以直接写出直线L的方程:y = kx + b就是这么简单!我们只需将已知的斜率k和截距b带入直线方程即可求得直线L的方程。
例题4:已知直线与坐标轴的交点已知直线L与x轴和y轴的交点分别为A(2,0)和B(0,3),求直线L的方程。
直线与方程知识点总结

直线与方程知识点总结一、直线的表示1、比例表达式:对于任意的两个不同的点A(x1,y1)与B(x2,y2),它们所连成的直线上任意的一点P(x,y)都满足比例关系:$$\frac{y-y_1}{y_2-y_1}=\frac{x-x_1}{x_2-x_1}$$2、斜截式:也叫斜率表达式:对于任意的两个不同的点A(x1,y1)与B(x2,y2),它们所连成的直线可用如下斜率表达式:$$y-y_1=k(x-x_1)$$其中,k为斜率,可以根据两点A(x1,y1)与B(x2,y2),计算得出:$$k=\frac{y_2-y_1}{x_2-x_1}$$3、标准方程:直线可以用标准方程表达:$$Ax+By+C=0$$其中,A、B、C可以根据两点A(x1,y1)与B(x2,y2),计算得出:$$A=y_2-y_1,B=x_1-x_2,C=x_2y_1-x_1y_2$$二、方程的表示1、一元一次方程:一元一次方程可以按如下形式表示:$$Ax+B=0$$其中,A、B为常数,A≠0,解析解可以表示为:$$x=-\frac{B}{A}$$2、一元二次方程:一元二次方程可以按如下形式表示:$$Ax^2+Bx+C=0$$其中,A、B、C为常数,A≠0,解析解可以表示为:$$x=\frac{-B\pm\sqrt{B^2-4AC}}{2A}$$3、二元一次方程:二元一次方程可以按如下形式表示:$$Ax+By+C=0$$其中,A、B、C为常数,解析解可以表示为:$$x=\frac{-B\pm\sqrt{B^2-4AC}}{2A}$$$$y=\frac{-A\pm\sqrt{B^2-4AC}}{2B}$$4、同次及非同次线性方程组:。
(完整版)高一数学直线方程知识点归纳与典型例题

直线的一般式方程及综合【学习目标】1. 掌握直线的一般式方程;2 .能将直线的点斜式、两点式等方程化为直线的一般式方程,并理解这些直线的不同形式的方程在表示直线时的异同之处;3 .能利用直线的一般式方程解决有关问题.【要点梳理】要点一:直线方程的一般式关于x和y的一次方程都表示一条直线.我们把方程写为Ax+By+C=0 ,这个方程(其中A、B不全为零)叫做直线方程的一般式.要点诠释:1 . A、B不全为零才能表示一条直线,若A、B全为零则不能表示一条直线..、一、. A C ............................................ 一C . A ...................................当B照时,万程可变形为y —x g ,它表示过点°,甘,斜率为E的直线.C …一—………当B=0 , AP时,万程可变形为Ax+C=0,即x 只,它表示一条与x轴垂直的直线.由上可知,关于x、y的二元一次方程,它都表示一条直线.2 .在平面直角坐标系中,一个关于x、y的二元一次方程对应着唯一的一条直线,反过来,一条直线可以对应着无数个关于x、y的一次方程(如斜率为2,在y轴上的截距为1的直线,其方程可以是2x — y+1=0 ,— 1 1也可以是x —— 0 ,还可以是4x — 2y+2=0 等.)要点二:直线方程的不同形式间的关系直线方程的五种形式的比较如下表:方程的形式常数的几何意义适用范围名称求直线存在斜率,两点式是点斜式的特例,其限制条件更多(X1方2 , yi句2 ),应用时若采用(y2 —y i)(x — x i) 一(X2— x i)(y — y i)=0的形式,即可消除局限性.截距式是两点式的特例,在使用截距式时,首先要判断是否满足直线在两坐标轴上的截距存在且不为零”这一条件.直线方程的一般式包含了平面上的所有直线形式.一般式常化为斜截式与截距式.若一般式化为点斜式,两点式,由于取点不同,得到的方程也不同.要点三:直线方程的综合应用i •已知所求曲线是直线时,用待定系数法求.2. 根据题目所给条件,选择适当的直线方程的形式,求出直线方程.对于两直线的平行与垂直,直线方程的形式不同,考虑的方向也不同.(i) 从斜截式考虑已知直线l i: y k〔x n,l2:y k2x b2,l i //12 i 2k i k2(b i b2);.. ,,,i …/l i 12 i 2 tan i cot 2 k i k i k2 ik 2于是与直线y kx (2)从般式考虑: b平行的直线可以设为y kx b| ;垂直的直线可以设为y1 -xk b2.11: A1x B1y C1I1 I2 AA20,l2: A2x B2y C2B1B20I1 //12 A1B2A2B1 0 且A1C2 A2C10或B1C2 B2C1 0,记忆式( A1A2邑B2C1C2l i与12 重合,AB2 A2B1 0, A1C2 A2C1 0, B1C2 B2C1 0于是与直线Ax By C 0平行的直线可以设为Ax By D 0 ;垂直的直线可以设为Bx Ay D 0.【典型例题】类型一:直线的一般式方程例1 .根据下列条件分别写出直线的方程,并化为一般式方程.(1) 斜率是1 ,经过点A (8 , — 2);(2) 经过点B (4 , 2 ),平行于x轴;(3) 在x轴和y轴上的截距分别是 -,—3 ;2(4)经过两点P1 (3,一2), P2 (5, — 4).【答案】(1) x+2y — 4=0(2) y-2=0 (3) 2x — y — 3=0 (4) x y 1 01 .. ...... ...................... ....【解析】(1)由点斜式方程碍y ( 2) — (x 8),化成一般式得x+2y — 4=0 .(2) 由斜截式得y=2,化为一般式得y — 2=0 .(3) 由截距式得—1,化成一般式得2x — y — 3=0 .3 32(4) 由两点式得y 2 M化成一般式方程为x y 1 0.4(2) 5 3【总结升华】本题主要是让学生体会直线方程的各种形式,以及各种形式向一般式的转化,对于直线方程的一般式,一般作如下约定:x的系数为正,x, y的系数及常数项一般不出现分数,一般按含x项、y项、常数项顺序排列.求直线方程的题目,无特别要求时,结果写成直线方程的一般式.举一反三:【变式1】已知直线l 经过点B (3, 1),且倾斜角是 【答案】y 1——(x 3) 3x 3y 3 3 3 0 3【解析】因为直线倾斜角是 30,所以直线的斜率 k tan tan30为:y 1 ■■— (x 3),化成一般式方程为:J 3x 3 y3/33 0.3例2. ABC 的一个顶点为 A ( 1, 4) , B 、 C 的平分线在直线 y 和x y 1 0上,求直线BC 的方程.【答案】x 2y 3 0【解析】由角平分线的性质知,角平分线上的任意一点到角两边的距离相等 ,所以可得A 点关于 B 的平分线的对称点 A 在BC 上,B 点关于 C 的平分线的对称点B 也在BC 上.写出直线 AB 的方程,即为直线 BC 的方程.例3 .求与直线3x+4y+1=0 平行且过点(1 , 2)的直线l 的方程.【答案】3x+4y —11=0 【解析】3 解法一:设直线l 的斜率为k, -. l 与直线3x+4y+1=0 平仃,.•• k -.43又..•l 经过点(1 , 2),可得所求直线万程为 y 2 一(x 1),即3x+4y —11=0 .4解法二:设与直线 3x+4y+1=0 平行的直线l 的方程为3x+4y+m=0 ,•• l 经过点(1 , 2), .-.3 刈+4 X2+m=0 ,解得 m= —11 . 所求直线方程为3x+4y —11=0 .【总结升华】(1 )一般地,直线Ax+By+C=0 中系数A 、B 确定直线的斜率,因此,与直线Ax+By+C=0 平行的直线可设为 Ax+By+m=0,这是常采用的解题技巧.我们称 Ax+By+m=0是与直线 Ax+By+C=0平行的直线系方程.参数m 可以取m 北的任意实数,这样就得到无数条与直线 Ax+By+C=0 平行的直线.当 m=C 时,Ax+By+m=0 与 Ax+By+C=0 重合.(2) 一般地,经过点 A (x o, y o),且与直线 Ax+By+C=0 平行的直线方程为 A(x — x o )+B(y — y o )=0 . (3)类似地有:与直线30 ,求直线的点斜式方程和一般式方程_3 3所以直线的点斜式方程Ax+By+C=0 垂直的直线系方程为 Bx — Ay+m=0(A , B 不同时为零).举一反三:【变式1】已知直线11 : 3mx+8y+3m-10=0 和12 : x+6my-4=0 . 问m 为何值时: (1) l i 与12平行(2) l i 与I 2垂直.2-【答案】(1) m -(2) m 03【解析】当 m 0时,11 : 8y-10=0 ; 12 : x-4=0 ,1112当m 。
《直线的方程》全章知识点总结及典型例题
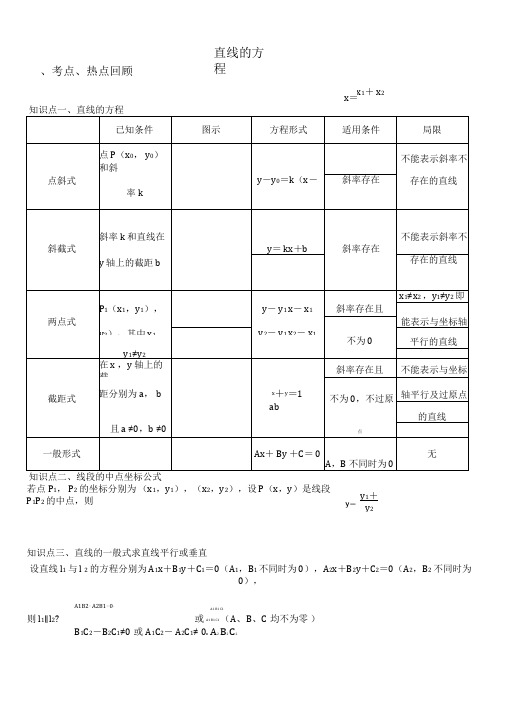
、考点、热点回顾已知条件图示方程形式适用条件 局限 点斜式点 P (x 0, y 0)和斜不能表示斜率不y -y 0=k (x -x )斜率存在存在的直线率k斜率 k 和直线在不能表示斜率不斜截式y = kx +b斜率存在y 轴上的截距 b存在的直线x 1≠x 2 ,y 1≠y 2 即P 1(x 1,y 1),P (x ,y - y 1 x - x 1斜率存在且两点式能表示与坐标轴y 2),其中 x 1y 2- y 1 x 2- x 1不为 0平行的直线y 1≠y 2在 x ,y 轴上的截斜率存在且不能表示与坐标截距式距分别为 a , bx+y =1不为 0,不过原轴平行及过原点ab的直线且 a ≠0,b ≠0点一般形式Ax + By +C = 0A ,B 不同时为 0无知识点二、线段的中点坐标公式若点 P 1, P 2的坐标分别为 (x 1,y 1),(x 2,y 2),设 P (x ,y )是线段 P 1P 2 的中点,则知识点三、直线的一般式求直线平行或垂直设直线 l 1与 l 2的方程分别为 A 1x +B 1y +C 1=0(A 1,B 1 不同时为 0),A 2x +B 2y +C 2=0(A 2,B 2不同时为0),A1B2- A2B1= 0,A1 B1 C1 则 l 1∥l 2?或 A1 B1 C1(A 、B 、C 均不为零 )B 1C 2-B 2C 1≠0或A 1C 2- A 2C 1≠ 0. A 2B 2C 2直线的方程x =x 1+ x 2 y 1+y 2l1⊥ l2? A1A2+B1B2= 0.二、典型例题考点一、直线的点斜式方程例 1、写出下列直线的点斜式方程.(1)经过点 A(2,5),且与直线 y=2x+ 7 平行;(2)经过点 C(-1,- 1),且与 x轴平行;(3)经过点 D(1,2),且与 x 轴垂直.变式训练 1、(1)经过点 (-3,1)且平行于 y 轴的直线方程是__ .(2) ________________________________________________________________________ 直线 y=2x +1绕着其上一点 P(1,3)逆时针旋转 90°后得到直线 l,则直线 l 的点斜式方程是_________________ .(3) ______________________________________________________________________________ 一直线 l1过点 A(-1,-2),其倾斜角等于直线 l2:y=33x的倾斜角的 2 倍,则 l1的点斜式方程为_________ .考点二、直线的斜截式方程例 2、 (1) 倾斜角为 60°,与 y 轴的交点到坐标原点的距离为 3 的直线的斜截式方程是 ___ __.(2)已知直线 l1的方程为 y=- 2x+ 3, l 2的方程为 y=4x-2,直线 l与 l 1平行且与 l2在y轴上的截距相同,求直线 l 的方程.变式训练 2、已知直线 l 的斜率为1,且和两坐标轴围成面积为 3 的三角形,求 l 的斜截式方程.6考点三、直线过定点问题例 3、求证:不论 m 为何值时,直线 l:y=(m-1)x+2m+1 总过第二象限 .变式训练 3、已知直线 l:5ax-5y- a+ 3= 0.求证:不论 a 为何值,直线 l 总经过第一象限考点四、直线的两点式方程例4、已知 A(-3,2),B(5,-4),C(0,-2),在△ABC 中,(1)求 BC 边的方程;(2)求 BC 边上的中线所在直线的方程.变式训练 4、若点 P(3,m)在过点 A(2,- 1),B(- 3,4)的直线上,则 m=_考点五、直线的截距式方程6 的直线方程是 ( )例 5、过点 P(1,3) ,且与 x 轴、 y 轴的正半轴围成的三角形的面积等于A.3x+y-6=0 B.x+ 3y- 10= 0C.3x- y=0 D.x-3y+8= 0变式训练 5、直线 l 过点 P(34, 2),且与两坐标正半轴围成的三角形周长为 12,求直线 l 的方程.3A.2 条 B.3 条 C.4 条 D .无数多条变式训练 6、过点 P(2,3)且在两坐标轴上的截距相等的直线有 ( )A.1 条 B.2 条 C.3条 D.无数多条考点六、直线的一般式方程(1)斜率是 3,且经过点 A(5,3) ;(2)斜率为 4,在 y 轴上的截距为- 2;(3)经过点 A(- 1,5),B(2,- 1)两点;(4)在 x轴,y 轴上的截距分别为- 3,-1.变式训练 7、根据条件写出下列直线的一般式方程:1(1)斜率是-21,且经过点 A(8,- 6)的直线方程为 ____________ ;(2)经过点 B(4,2),且平行于 x 轴的直线方程为 ______________ ;3(3) __________________________________________________ 在 x轴和 y轴上的截距分别是2和-3 的直线方程为 ________________________________________________________________(4) ____________________________________________ 经过点 P1(3,- 2),P2(5,- 4)的直线方程为 _____________________________________________________________________ .例 8、设直线 l 的方程为(m2- 2m- 3)x-(2m2+m- 1)y+ 6-2m= 0.(1)若直线 l 在 x 轴上的截距为- 3,则 m=;(2)若直线 l 的斜率为 1,则 m= __ .变式训练 8、若方程(a2+5a+6)x+(a2+2a)y+ 1=0 表示一条直线,则实数 a 满足.考点七、由直线的一般式研究直线的平行与垂直命题角度 1 利用两直线的位置关系求参数例 9、(1)已知直线 l 1: 2x+(m+ 1)y+4= 0与直线 l2:mx+3y-2=0 平行,求 m的值;(2)当 a 为何值时,直线 l1:(a+2)x+(1-a)y-1=0 与直线 l2:(a-1)x+(2a+3)y+2=0互相垂直?变式训练 9、已知直线 l1:ax+2y-3=0,l2:3x+(a+1)y-a=0,求满足下列条件的 a 的值.(1)l1∥ l2;(2)l1⊥l2.例 10、已知直线 l 的方程为 3x+ 4y-12= 0,求满足下列条件的直线 l′的方程:(1)过点(-1,3),且与 l 平行;(2)过点(-1,3),且与 l 垂直.变式训练 10、已知点 A(2,2)和直线 l:3x+ 4y-20=0. 求:(1)过点 A 和直线 l 平行的直线方程;(2)过点 A 和直线 l 垂直的直线方程.三、课后练习一、选择题(每小题只有一个正确答案)1.不论 m为何值,直线(m- 1)x+(2m- 1)y= m- 5 恒过定点()1A. 1,B. (- 2,0)C. (2,3)D. (9 ,- 4)范围为()A. B. C. D.3.若直线 l1:x+ay+6=0与 l2:(a-2)x+3y+2a=0平行,则 l1与 l2之间的距离为()A. B. C. D.4.若点A 1,1 关于直线y kx b 的对称点是B 3,3 ,则直线y kx b 在y 轴上的截距是()A. 1B. 2C. 3D. 4 5.已知直线l1 :x y 1 0,动直线l2 : k 1 x ky k 0 k R ,则下列结论错误..的是()A. 存在k,l1使得l2的倾斜角为 90° B. 对任意的k,l1与l2都有公共点C. 对任意的k,l1与l2都不.重合D. 对任意的k,l1与l2都不.垂.直.6.设点A 2, 3 ,B 3, 2 ,直线 l 过点P 1,1 ,且与线段AB 相交,则 l 的斜率k 的取值范围()33A. k 或k 4B. 4 k 44C. 3k 4D. 以上都不对47.图中的直线l1,l2,l3的斜率分别是k1,k2,k3 ,则有()A. k1 k2 k3 B. k3k1k2 C. k3k2k1 D. k2k3k18.直线x 3y1 0 的倾斜角为().A. B. C. D.9.直线的斜率和在轴上的截距分别是()A. B. C. D.10 .过点,且平行于向量的直线方程为()2.已知不等式组表示的平面区域为18.已知 的三个顶点坐标分别为 , , .11.过点 A (3,3) 且垂直于直线 的直线方程为二、填空题13.已知 a,b, c 为直角三角形的三边长, c 为斜边长,若点 M m,n 在直线 l :ax by 2c 0上,则 m 2 n 2的 最小值为 __________ .14.m R ,动直线 l 1:x my 1 0过定点 A ,动直线 l 2:mx y 2m 3 0过定点 B ,若直线 l 与l 2相交于 点 P (异于点 A,B ),则 PAB 周长的最大值为 ________15.过点 (2,- 3)且在两坐标轴上的截距互为相反数的直线方程为 _________ .16.定义点 到直线 的有向距离为 .已知点 到直线 的有向距离分别是 ,给出以下命题: ① 若 ,则直线 与直线 平行; ② 若 ,则直线 与直线 平行; ③若,则直线与直线 垂直;④若 ,则直线 与直线 相交;其中正确命题的序号是 _______________ . 三、解答题17.求符合下列条件的直线方程: ( 1)过点 ,且与直线 平行; ( 2)过点 ,且与直线垂直;( 3)过点, 且在两坐标轴上的截距相等.1)求边 上的高所在直线的一般式方程;A. B. C. D.12.在平面直角坐标系中,已知 A 1,2, 3,0 ,那么线段 AB 中点的坐标为().A. 2, 1B. 2,1C. 4,D.1,22)求边上的中线所在直线的一般式方程19.已知直线l :3x y 2 2 x 4y 2 0( 1)求证:直线 l 过定点。
直线方程知识点归纳总结

直线方程知识点归纳总结一、直线的倾斜角与斜率。
1. 倾斜角。
- 定义:直线l向上的方向与x轴正方向所成的最小正角α,叫做直线l的倾斜角。
- 范围:0^∘≤slantα < 180^∘。
2. 斜率。
- 定义:直线的倾斜角α≠90^∘时,k = tanα叫做直线的斜率。
- 经过两点P_1(x_1,y_1),P_2(x_2,y_2)(x_1≠ x_2)的直线的斜率k=(y_2 -y_1)/(x_2 - x_1)。
二、直线方程的几种形式。
1. 点斜式。
- 方程:y - y_0=k(x - x_0),其中(x_0,y_0)是直线上一点,k是直线的斜率。
- 适用范围:斜率存在的直线。
2. 斜截式。
- 方程:y = kx + b,其中k是斜率,b是直线在y轴上的截距。
- 适用范围:斜率存在的直线。
3. 两点式。
- 方程:(y - y_1)/(y_2 - y_1)=(x - x_1)/(x_2 - x_1)(x_1≠ x_2,y_1≠ y_2),其中(x_1,y_1),(x_2,y_2)是直线上两点。
- 适用范围:不垂直于坐标轴的直线。
4. 截距式。
- 方程:(x)/(a)+(y)/(b)=1(a≠0,b≠0),其中a是直线在x轴上的截距,b是直线在y轴上的截距。
- 适用范围:不垂直于坐标轴且不过原点的直线。
5. 一般式。
- 方程:Ax + By+C = 0(A,B不同时为0)。
- 可以表示平面内任意一条直线。
三、直线的平行与垂直。
1. 平行。
- 设直线l_1:y = k_1x + b_1,l_2:y = k_2x + b_2。
- 当k_1 = k_2且b_1≠ b_2时,l_1∥ l_2;对于直线l_1:A_1x + B_1y + C_1 = 0,l_2:A_2x + B_2y + C_2 = 0,当(A_1)/(A_2)=(B_1)/(B_2)≠(C_1)/(C_2)时,l_1∥l_2。
2. 垂直。
- 设直线l_1:y = k_1x + b_1,l_2:y = k_2x + b_2。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
直线的一般式方程及综合【学习目标】1.掌握直线的一般式方程;2.能将直线的点斜式、两点式等方程化为直线的一般式方程,并理解这些直线的不同形式的方程在表示直线时的异同之处;3.能利用直线的一般式方程解决有关问题.【要点梳理】要点一:直线方程的一般式关于x和y的一次方程都表示一条直线.我们把方程写为Ax+By+C=0,这个方程(其中A、B不全为零)叫做直线方程的一般式.要点诠释:1.A、B不全为零才能表示一条直线,若A、B全为零则不能表示一条直线.当B≠0时,方程可变形为A Cy xB B=--,它表示过点0,CB⎛⎫-⎪⎝⎭,斜率为AB-的直线.当B=0,A≠0时,方程可变形为Ax+C=0,即CxA=-,它表示一条与x轴垂直的直线.由上可知,关于x、y的二元一次方程,它都表示一条直线.2.在平面直角坐标系中,一个关于x、y的二元一次方程对应着唯一的一条直线,反过来,一条直线可以对应着无数个关于x、y的一次方程(如斜率为2,在y轴上的截距为1的直线,其方程可以是2x―y+1=0,也可以是1122x y-+=,还可以是4x―2y+2=0等.)要点二:直线方程的不同形式间的关系直线方程的五种形式的比较如下表:要点诠释:在直线方程的各种形式中,点斜式与斜截式是两种常用的直线方程形式,要注意在这两种形式中都要求直线存在斜率,两点式是点斜式的特例,其限制条件更多(x1≠x2,y1≠y2),应用时若采用(y2―y1)(x―x1)―(x2―x1)(y―y1)=0的形式,即可消除局限性.截距式是两点式的特例,在使用截距式时,首先要判断是否满足“直线在两坐标轴上的截距存在且不为零”这一条件.直线方程的一般式包含了平面上的所有直线形式.一般式常化为斜截式与截距式.若一般式化为点斜式,两点式,由于取点不同,得到的方程也不同.要点三:直线方程的综合应用1.已知所求曲线是直线时,用待定系数法求.2.根据题目所给条件,选择适当的直线方程的形式,求出直线方程.对于两直线的平行与垂直,直线方程的形式不同,考虑的方向也不同.(1)从斜截式考虑已知直线111:b x k y l +=,222:b x k y l +=,12121212//()l l k k b b αα⇒=⇒=≠;12121211221tan cot 12l l k k k k παααα⊥⇒-=⇒=-⇒=-⇒=- 于是与直线y kx b =+平行的直线可以设为1y kx b =+;垂直的直线可以设为21y x b k=-+. (2)从一般式考虑:11112222:0,:0l A x B y C l A x B y C ++=++=1212120l l A A B B ⊥⇔+=121221//0l l A B A B ⇔-=且12210A C A C -≠或12210B C B C -≠,记忆式(111222A B C A B C =≠) 1l 与2l 重合,12210A B A B -=,12210A C A C -=,12210B C B C -=于是与直线0Ax By C ++=平行的直线可以设为0Ax By D ++=;垂直的直线可以设为0Bx Ay D -+=.【典型例题】类型一:直线的一般式方程例1.根据下列条件分别写出直线的方程,并化为一般式方程. (1)斜率是12-,经过点A (8,―2); (2)经过点B (4,2),平行于x 轴; (3)在x 轴和y 轴上的截距分别是32,―3; (4)经过两点P 1(3,―2),P 2(5,―4).【答案】(1)x+2y―4=0(2)y―2=0(3)2x―y―3=0(4)10x y +-= 【解析】 (1)由点斜式方程得1(2)(8)2y x --=--,化成一般式得x+2y―4=0. (2)由斜截式得y=2,化为一般式得y―2=0. (3)由截距式得1332x y +=-,化成一般式得2x―y―3=0. (4)由两点式得234(2)53y x +-=----,化成一般式方程为10x y +-=.【总结升华】本题主要是让学生体会直线方程的各种形式,以及各种形式向一般式的转化,对于直线方程的一般式,一般作如下约定:x 的系数为正,x ,y 的系数及常数项一般不出现分数,一般按含x 项、y 项、常数项顺序排列.求直线方程的题目,无特别要求时,结果写成直线方程的一般式.举一反三:【变式1】已知直线l 经过点(3,1)B -,且倾斜角是30︒,求直线的点斜式方程和一般式方程. 【答案】31(3)3y x +=- 333330x y ---=【解析】因为直线倾斜角是30︒,所以直线的斜率3tan tan 303k α==︒=,所以直线的点斜式方程为:31(3)3y x +=-,化成一般式方程为:333330x y ---=. 例2.ABC ∆的一个顶点为(1,4)A --,B ∠、C ∠ 的平分线在直线10y +=和10x y ++=上,求直线BC 的方程. 【答案】230x y +-=【解析】由角平分线的性质知,角平分线上的任意一点到角两边的距离相等 ,所以可得A 点关于B ∠的平分线的对称点'A 在BC 上,B 点关于C ∠的平分线 的对称点'B 也在BC 上.写出直线''A B 的方程,即为直线BC 的方程.例3.求与直线3x+4y+1=0平行且过点(1,2)的直线l 的方程. 【答案】3x+4y―11=0 【解析】解法一:设直线l 的斜率为k ,∵l 与直线3x+4y+1=0平行,∴34k =-. 又∵l 经过点(1,2),可得所求直线方程为32(1)4y x -=--,即3x+4y―11=0. 解法二:设与直线3x+4y+1=0平行的直线l 的方程为3x+4y+m=0, ∵l 经过点(1,2),∴3×1+4×2+m=0,解得m=―11. ∴所求直线方程为3x+4y―11=0. 【总结升华】(1)一般地,直线Ax+By+C=0中系数A 、B 确定直线的斜率,因此,与直线Ax+By+C=0平行的直线可设为Ax+By+m=0,这是常采用的解题技巧.我们称Ax+By+m=0是与直线Ax+By+C=0平行的直线系方程.参数m 可以取m≠C 的任意实数,这样就得到无数条与直线Ax+By+C=0平行的直线.当m=C 时,Ax+By+m=0与Ax+By+C=0重合.(2)一般地,经过点A (x 0,y 0),且与直线Ax+By+C=0平行的直线方程为A(x―x 0)+B(y―y 0)=0. (3)类似地有:与直线Ax+By+C=0垂直的直线系方程为Bx―Ay+m=0(A ,B 不同时为零). 举一反三:【变式1】已知直线1l :3mx+8y+3m-10=0 和 2l :x+6my-4=0 .问 m 为何值时: (1)1l 与2l 平行(2)1l 与2l 垂直. 【答案】(1)23m =-(2)0m = 【解析】当0m =时,1l :8y-10=0;2l :x-4=0,12l l ⊥当0m ≠时,1l :310388m m y x -=-+;2l :1466y x m m =-+由3186m m-=-,得23m =±,由103486m m -=得2833m =或 而31()()186m m-⋅-=-无解综上所述(1)23m =-,1l 与2l 平行.(2)0m =,1l 与2l 垂直.【变式2】 求经过点A (2,1),且与直线2x+y―10=0垂直的直线l 的方程. 【答案】x -2y=0【解析】因为直线l 与直线2x+y―10=0垂直,可设直线l 的方程为20x y m -+=,把点A (2,1)代入直线l 的方程得:0m =,所以直线l 的方程为:x -2y=0.类型二:直线与坐标轴形成三角形问题例4.已知直线l 的倾斜角的正弦值为35,且它与坐标轴围成的三角形的面积为6,求直线l 的方程. 【思路点拨】知道直线的倾斜角就能求出斜率,进而引进参数——直线在y 轴上的截距b ,再根据直线与坐标轴围成的三角形的面积为6,便可求出b .也可以根据直线与坐标轴围成的三角形的面积为6,设截距式直线方程,从而得出1||62ab =,再根据它的斜率已知,从而得到关于a ,b 的方程组,解之即可. 【答案】334y x =±或334y x =-±【解析】解法一:设l 的倾斜角为α,由3sin 5α=,得3tan 4α=±. 设l 的方程为34y x b =±+,令y=0,得43x b =±.∴直线l 与x 轴、y 轴的交点分别为4,03b ⎛⎫±⎪⎝⎭,(0,b ). ∴2142||6233S b b b ∆=±⋅==,即b 2=9,∴b=±3. 故所求的直线方程分别为334y x =±或334y x =-±. 解法二:设直线l 的方程为1x y a b +=,倾斜角为α,由3sin 5α=,得3tan 4α=±.∴1||||6234a b b a⎧⋅=⎪⎪⎨⎪-=±⎪⎩,解得43a b =±⎧⎨=±⎩.故所求的直线方程为143x y +=±或143x y-=±.【总结升华】(1)本例中,由于已知直线的倾斜角(与斜率有关)及直线与坐标轴围成的三角形的面积(与截距有关),因而可选择斜截式直线方程,也可选用截距式直线方程,故有“题目决定解法”之说.(2)在求直线方程时,要恰当地选择方程的形式,每种形式都具有特定的结论,所以根据已知条件恰当地选择方程的类型往往有助于问题的解决.例如:已知一点的坐标,求过这点的直线方程,通常选用点斜式,再由其他条件确定该直线在y 轴上的截距;已知截距或两点,选择截距式或两点式.在求直线方程的过程中,确定的类型后,一般采用待定系数法求解,但要注意对特殊情况的讨论,以免遗漏.举一反三: 【变式1】(2015春 启东市期中)已知直线m :2x ―y ―3=0,n :x +y ―3=0. (1)求过两直线m ,n 交点且与直线l :x +2y ―1=0平行的直线方程; (2)求过两直线m ,n 交点且与两坐标轴围成面积为4的直线方程. 【思路点拨】(1)求过两直线m ,n 交点坐标,结合直线平行的斜率关系即可求与直线l :x +2y ―1=0平行的直线方程;(2)设出直线方程,求出直线和坐标轴的交点坐标,结合三角形的面积公式进行求解即可. 【答案】(1)x +2y ―4=0;(2)【解析】(1)由23030x y x y --=⎧⎨+-=⎩,解得21x y =⎧⎨=⎩,即两直线m ,n 交点坐标为(2,1),设与直线l :x +2y ―1=0平行的直线方程为x +2y +c =0, 则2+2×1+c =0,解得c =―4,则对应的直线方程为x +2y ―4=0; (2)设过(2,1)的直线斜率为k ,(k ≠0), 则对应的直线方程为y ―1=k (x ―2),令x =0,y =1―2k ,即与y 轴的交点坐标为A (0,1―2k )令y =0,则1212k x k k -=-=,即与x 轴的交点坐标为21(,0)k B k -,则△AOB 的面积121|||12|42k S k k-=⨯-=,即2(21)8k k -=, 即244810k k k --+=,若k >0,则方程等价为241210k k -+=,解得32k +=32k -=, 若k <0,则方程等价为24410k k ++=, 解得12k =-.综上直线的方程为11(2)2y x -=-- ,或31(2)2y x +-=-,或31(2)2y x --=-即122y x =-+,或322y x +=--322y x -=-+ 类型三:直线方程的实际应用例6.(2015春 湖北期末)光线从点A (2,3)射出,若镜面的位置在直线l :x +y +1=0上,反射光线经过B (1,1),求入射光线和反射光线所在直线的方程,并求光线从A 到B 所走过的路线长.【思路点拨】求出点A 关于l 的对称点,就可以求出反射光线的方程,进一步求得入射点的坐标,从而可求入射光线方程,可求光线从A 到B 所走过的路线长.【解析】设点A 关于l 的对称点A '(x 0,y 0),∵AA '被l 垂直平分,∴0000231022312x y y x ++⎧++=⎪⎪⎨-⎪=-⎪⎩,解得0043x y =-⎧⎨=-⎩∵点A '(―4,―3),B (1,1)在反射光线所在直线上, ∴反射光线的方程为341314y x ++=++,即4x ―5y +1=0, 解方程组451010x y x y -+=⎧⎨++=⎩得入射点的坐标为21(,)33--.由入射点及点A 的坐标得入射光线方程为1233123233y x ++=++,即5x ―4y +2=0, 光线从A 到B所走过的路线长为|'|A B ==.【总结升华】本题重点考查点关于直线的对称问题,考查入射光线和反射光线,解题的关键是利用对称点的连结被对称轴垂直平分.举一反三: 【变式1】(2016春 福建厦门期中)一条光线从点A (-4,-2)射出,到直线y =x 上的B 点后被直线y =x 反射到y 轴上的C 点,又被y 轴反射,这时反射光线恰好过点D (-1,6).求BC 所在直线的方程.【答案】10x -3y +8=0【解析】如图,A (-4,-2),D (-1,6),由对称性求得A (-4,-2)关于直线y =x 的对称点A '(-2,-4), D 关于y 轴的对称点D '(1,6),则由入射光线和反射光线的性质可得:过A 'D '的直线方程即为BC 所在直线的方程. 由直线方程的两点式得:426412y x ++=++. 整理得:10x -3y +8=0.例7.如图,某房地产公司要在荒地ABCDE 上划出一块长方形土地(不改变方向)建造一幢8层的公寓,如何设计才能使公寓占地面积最大?并求出最大面积.(精确到1 m 2)【答案】6017【解析】 建立坐标系,则B (30,0),A (0,20). ∴由直线的截距方程得到线段AB 的方程为13020x y+=(0≤x≤30). 设点P 的坐标为(x ,y ),则有2203y x =-. ∴公寓的占地面积为2(100)(80)(100)(8020)3S x y x x =-⋅-=-⋅-+2220600033x x =-++(0≤x≤30). ∴当x=5,503y =时,S 取最大值,最大值为222205560006017(m )33S =-⨯+⨯+≈.即当点P 的坐标为50(5,)3时,公寓占地面积最大,最大面积为6017 m 2.【总结升华】本题是用坐标法解决生活问题,点P 的位置由两个条件确定,一是A 、P 、B 三点共线,二是矩形的面积最大.借三点共线寻求x 与y 的关系,利用二次函数知识探求最大值是处理这类问题常用的方法.。
