第一章 例题讲解
第一章-集合与命题

第一章 集合与命题 (一)集合的概念与运算 【集合的基本概念】❖ 知识点归纳 1. 集合的定义: 2. 集合的特征: 3. 集合的表示法: 4. 集合的分类: 5. 数集: 6. 集合的关系: 7. 集合的运算: 8. 集合的运算性质:❖ 例题讲解 例1(1) 已知集合{}3M x x n n ==∈Z ,,{}31N x x n n ==+∈Z ,,{}31P x x n n ==-∈Z ,,且a M ∈,b N ∈,c P ∈,设d a b c =-+,则( ).A. d M ∈B. d N ∈C. d P ∈D. 以上都不正确 (2) 若集合2442k k A x x k B x x k ⎧⎫⎧⎫ππππ==+∈==+∈⎨⎬⎨⎬⎩⎭⎩⎭Z Z ,,,,则( ).A. A B =B. B ⊂≠AC. A ⊂≠BD.AB =∅例2 写出满足{},M a b ⊆的所有集合M .例3 已知集合{}2340A x x x x =--<∈R ,,求A N 的真子集的个数.例4 已知全集{}1,2,3,4,5,6,7,8,9U =,{}2A B =,∁{}()1,9U A B =,∁{}4,6,8U A B =,求集合A 、B .(1) {}{}2223213A y y x x x B y y x x x ==--∈==-++∈R R ,,,;(2) {}{}22(,)23(,)213A x y y x x x B x y y x x x ==--∈==-++∈R R ,,,;(3) {}{}2223213A y y x x x B y y x x x ==--∈==-++∈Z Z ,,,.例6同时满足下列两个条件: ①{}1,2,3,4,5M ⊆,②若a M ∈,则6a M -∈,这样的集合M 有多少个? 写出这些 集合. 例7 已知集合{}{}222280320A x x x x B x x ax a x =--<∈=-+=∈R R ,,, (1) 实数a 在什么范围内取值时,B ⊂≠A ?(2) 实数a 在什么范围内取值时,AB =∅.❖ 回顾反思 1. 主要方法:① 解决集合问题,首先要分析集合中的元素是什么; ② 抓住集合中元素的3个性质,对互异性要注意检验;③ 弄清集合元素的本质属性,正确进行“集合语言”和“文字语言”的相互转化; ④ 了解空集的意义,在解题中强化空集的意识; ⑤ 借助数轴和文氏图进行求解. 2. 易错、易漏点:① 辨清: 子集、真子集、非空真子集的区别。
沪教版六年级上册 第一章 1.1 整数和整除 讲义(无答案)

整数与整除(后附难点题型)一、知识要点:要点1:在数物体的时候,用来表示物体个数的数1、2、3、4……叫做正整数.在正整数1、2、3、4…,的前面添上“—”号,得到的数-1、-2、-3、-4……叫做负整数.要点2:零和正整数统称为自然数.正整数、零和负整数,统称为整数.要点3:整数a除以整数b,如果除得的商正好是整数而余数为零,我们就说a能被b整除,或者说b能整除a.(1)注意整除的两种表述方法(2)归纳整除的条件;除数、被除数都是整数.被除数除以除数,商是整数而且没有余数.要点4:整数a能被整数b整除,a就叫做b的倍数,b就叫做a的因数(也称为约数).例如:35能被7整除,所以35是7的倍数,7是35的约数一个数的因数是有限,其中最小的因数是1,最大的因数是它本身.(倍数和因数是相互依存的)例如:10的因数有:1、2、5、10,其中最小的因数是1,最大的因数是10。
一个数的倍数的个数是无限的,其中最小的倍数是它本身。
例如:3的倍数有:3、6、9、12……其中最小的倍数是3 ,没有最大的倍数。
要点5:能被2整除的整数叫做偶数,不能被2整除的数叫做奇数.个位上是0、2、4、6、8的整数都能被2整除.例如:202、480、304,都能被2整除.个位上是0或者是5的整数都能被5整除.例如:5、30、405都能被5整除.整数:自然数(正整数、0)、负整数自然数:0和正整数正整数:奇数和偶数(按能否被2整除分)二、例题讲解:例1:把下列各数填在适当的圈内: 12、 -6、 0、 1.23、76、 2005、 -19.6、 9 正整数 自然数 整数思考:1、最小的自然数、最小的正整数是同一个数吗?不是同一个数,那么分别是什么?2、是否有最大的正整数、负整数、自然数?3、是否有最小的正整数、负整数、自然数?例2:观察下面两组算式卡片中的运算有什么异同? (1)24÷2 = 12 (2) 6÷5 = 1.2 48÷8 = 6 17÷5 = 3.416÷4 = 4 35÷6 = 5 (5)例3:下列哪一个算式的被除数能被除数整除?10÷3 48÷8 6÷4 解:因为10÷3=3……1 48÷8=6 6÷4=1.5所以,被除数能被除数整除的算式是48÷8思考:2.6÷1.3=2,能不能说2.6能被1.3整除?说明理由 2.5÷5=0.5,能说2.5被5整除? 6÷4=1.5,能说6被4整除?例4:找因数和倍数(1)找出36的所有因数?方法1:想乘法算式:36×1=36,36和1是36的因数;18×2=36,18和2是36的因数;12×3=36,12和3是36的因数;9×4=36,9和4是36的因数;6×6=36,6是36的因数。
第一章 集合 课程讲义

1.1 集合的含义及其表示一、知识梳理1.集合的定义2.元素与集合的关系3.集合中元素的特性:确定性、互异性、无序性4.常用数集及其记法:5.集合的表示方法:二、例题讲解例1:集合M中的元素为1,x,x2-x,求x的范围?例2:三个元素的集合1,a,ba,也可表示为0,a2,a+b,求a2005+ b2006的值.例3:集合A中的元素由(a∈Z,b∈Z)组成,判断下列元素与集合A的关系?(1)0 (2(3例4.用描述法表示下列集合:(1)所有被3整除的整数的集合;(2)使yx=有意义的x的集合;(3)方程x2+x+1=0所有实数解的集合;(4)抛物线y=-x2+3x-6上所有点的集合;例5.已知A={a|6,3N a Za∈∈-},试用列举法表示集合A.例6.已知集合P={-1,a,b},Q={-1,a2,b2},且Q=P,求1+a2+b2的值.三、巩固练习1、用∈或∉填空________N________R0_______N* π________R 227_______Q cos300_______Z2、由实数-x,|x|x,组成的集合最多含有元素的个数是_________________个.3、用列举法表示下列集合:(1) {x|x为不大于10的正偶数}(2){(x,y)|0≤x ≤2,0≤y<2,x ,y ∈Z}4、用描述法表示下列集合:(1)不等式2x-3>5的解集;(2)直角坐标平面内属于第四象限的点的集合;5、集合A={x|y=x 2+1},B={t|p=t 2+1},,这三个集合的关系? 6、已知A={x|12,6N x N x∈∈-},试用列举法表示集合A .1.2 子集、全集、补集一、知识梳理1.子集的概念及记法:2.子集的性质:① A ⊆ A② A ∅⊆3.真子集的概念及记法:4.真子集的性质:①∅是任何非空集合的真子集5.全集的概念:6. 补集的概念:二、例题讲解例1:以下各组是什么关系,用适当的符号表示出来.(1)a 与{a} 0 与 ∅(2)∅与{20,35,∅} (3)S={-2,-1,1,2},A={-1,1},B={-2,2};(4)S=R ,A={x|x ≤0,x ∈R},B={x|x>0 ,x ∈R };例2:设集合A={x|x 2+4x=0,x ∈R},B={x|x 2+2(a+1)x+a 2-1=0,x ∈R},若B ⊆A ,求实数a 的取值范围.例3:①方程组210360x x +>⎧⎨-≤⎩的解集为A ,U=R ,试求A 及u C A . ②设全集U=R ,A={x|x>1},B={x|x+a<0},B 是R C A 的真子集,求实数a 的取值范围.三、巩固练习1.指出下列各组中集合A 与B 之间的关系.(1) A={-1,1},B=Z ;(2)A={1,3,5,15},B={x|x 是15的正约数};(3) A = N*,B=N(4) A ={x|x=1+a 2,a ∈N*},B={x|x=a 2-4a+5,a ∈N*}2.(1)已知{1,2 }⊆M ⊆{1,2,3,4,5},则这样的集合M 有多少个?(2)已知M={1,2,3,4,5,6, 7,8,9},集合P 满足:P ⊆M ,且若P α∈,则10-α∈P ,则这样的集合P 有多少个?3.若U=Z ,A={x|x=2k ,k ∈Z},B={x|x=2k+1, k ∈Z},则U C A ___________ U C B ___________:4.设全集是数集U={2,3,a 2+2a-3},已知A={b ,2},U C A ={5},求实数a ,b 的值.5.已知集合A={x|x 2-1=0 },B={x|x 2-2ax+b=0},B ⊆ A ,求a ,b 的取值范围.1.3 交集、并集一、知识梳理1.交集的定义:注意: 当集合A 与B 没有公共元素时,不能说A 与B 没有交集,而是A ∩B=∅.2.交集的常用性质:(1)(A ∩B)∩C =A ∩(B ∩C);(2) A ∩B ⊆A , A ∩B ⊆B3.区间的表示法:4.并集的定义:注意:并集(A ∪B )实质上是A 与B 的所有元素所组成的集合,但是公共元素在同一个集合中要注意元素的互异性.5.并集的常用性质:(1)(A ∪B)∪C =A ∪(B ∪C);(2) A ⊆A ∪B , B ⊆A ∪B二、例题讲解例1. (1)设A={-1,0,1},B={0,1,2,3},求A ∩B ;(2)设A={x|x>0},B={x|x≤1},求A∩B;(3)设A={x|x=3k,k∈Z},B={y|y=3k+1 k∈Z },C={z|z=3k+2,k∈Z},D={x|x=6k+1,k∈Z},求A∩B;A∩C;C∩B;D∩B;例2:已知数集 A={a2,a+1,-3},数集B={a-3,a-2,a2+1},若A∩B={-3},求a的值.例3:(1)设集合A={y|y=x2-2x+3,x∈R},B={y|y=-x2+2x+10,x∈R},求A∩B;(2)设集合A={(x,y)|y=x+1,x∈R},B={(x,y)|y=-x2+2x+34,x∈R},求A∪B;例4:已知集合A={x|x2-1=0 },B={x|x2-2ax+b=0},A∪B=A,求a,b的值或a,b所满足的例5:若A={x|x2-ax+a2-19=0},B={x|x2-5x+6=0},C={x|x2+2x-8=0},(1)若A∪B=A∩B,求a的值;(2)∅ A∩B,A∩C=∅,求a的值.例6:已知集合A={2,5},B={x|x2+px+q=0,x∈R}(1)若B={5},求p,q的值.(2)若A∩B= B ,求实数p,q满足的条件.例10、已知集合A={x|-2<x<-1,或x>0},B={x|a≤x≤b},满足A∩B={x|0<x≤2},A∪B={x|x>-2},求a、b的值。
必修二第一章(柱锥台及三视图)
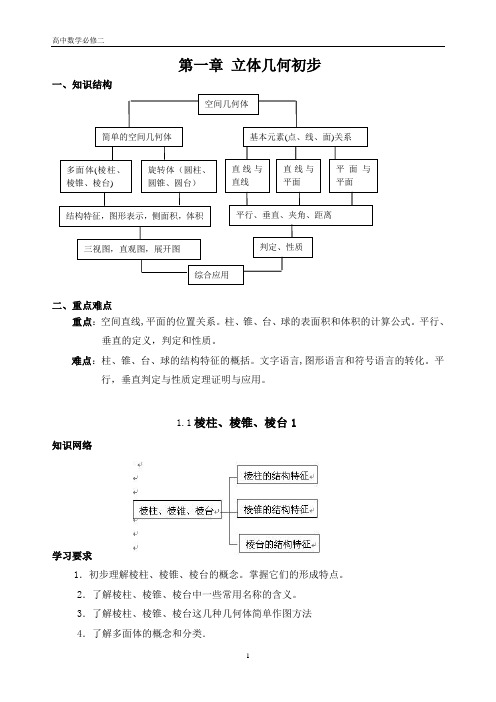
第一章 立体几何初步一、知识结构二、重点难点重点:空间直线,平面的位置关系。
柱、锥、台、球的表面积和体积的计算公式。
平行、垂直的定义,判定和性质。
难点:柱、锥、台、球的结构特征的概括。
文字语言,图形语言和符号语言的转化。
平行,垂直判定与性质定理证明与应用。
1.1棱柱、棱锥、棱台1知识网络学习要求1.初步理解棱柱、棱锥、棱台的概念。
掌握它们的形成特点。
2.了解棱柱、棱锥、棱台中一些常用名称的含义。
3.了解棱柱、棱锥、棱台这几种几何体简单作图方法4.了解多面体的概念和分类.空间几何体简单的空间几何体 基本元素(点、线、面)关系多面体(棱柱、棱锥、棱台) 旋转体(圆柱、圆锥、圆台) 直线与直线 直线与平面 平面与平面结构特征,图形表示,侧面积,体积 平行、垂直、夹角、距离三视图,直观图,展开图判定、性质综合应用1.多面体:多面体是由若干个所围成的几何体。
围成多面体的各个多边形叫做多面体的;相邻的两个面的公共边叫做多面体的;棱和棱的公共点叫做多面体的;连接不在同一个面上的两个顶点的线段叫做多面体的;2.凸多面体:把一个多面体的任意一个面延展为平面,如果其余的各面 ,则这样的多面体就叫做凸多面体。
3。
截面:一个几何体和相交所得到的平面图形(包含它的内部),叫做这个几何体的截面。
4。
棱柱:从运动的观点看:棱柱可以看成一个多边形(包括图形围成的平面部分)上各点都沿着移动的距离所形成的几何体.5。
棱柱的主要特征性质:(1)有两个互相的面。
(2)夹在这两个平行平面间的每相邻两个面的交线都互相。
棱柱的两个互相平行的面叫棱柱的______,其余各面叫____________,两侧面的公共边叫___________;棱柱两底面之间的距离叫做棱柱的______。
棱柱用表示_______________________字母来表示。
6。
棱柱的分类:(1)按底面多边形的边数可以分为:棱柱、棱柱、棱柱……(2)按侧棱和底面是否垂直分为: 棱柱和棱柱。
南京大学《物理化学》每章典型例题讲解

第一章 热力学第一定律与热化学例题1 1mol 理想气体于27℃ 、101325Pa 状态下受某恒定外压恒温压缩到平衡,再由该状态恒容升温到97 ℃ ,则压力升到1013.25kPa 。
求整个过程的W 、Q 、△U 及△H 。
已知该气体的C V ,m 恒定为20.92J ∙mol -1 ∙K -1。
解题思路:需先利用理想气体状态方程计算有关状态: (T 1=27℃, p 1=101325Pa ,V 1)→(T 2=27℃, p 2=p 外=?,V 2=?)→(T 3=97℃, p 3=1013.25kPa ,V 3= V 2)例题2水在 -5℃ 的结冰过程为不可逆过程,计算时要利用0℃ 结冰的可逆相变过程,即H 2O (l ,1 mol ,-5℃ ,θp )(s ,1 mol ,-5℃,θp )↓△H 2 ↑△H 4H 2O (l ,1 mol , 0℃,θp ) O (s ,1 mol ,0℃,θp )∴ △H 1=△H 2+△H 3+△H 4例题3 在 298.15K 时,使 5.27 克的甲醇(摩尔质量为32克) 在弹式量热计中恒容燃烧,放出 119.50kJ 的热量。
忽略压力对焓的影响。
(1) 计算甲醇的标准燃烧焓 θm c H ∆。
(2) 已知298.15K 时 H 2O(l) 和CO 2(g)的标准摩尔生成焓分别为-285.83 kJ·mol -1、-393.51 kJ·mol -1,计算CH 3OH(l)的θm f H ∆。
(3) 如果甲醇的标准蒸发焓为 35.27kJ·mol -1,计算CH 3OH(g) 的θm f H ∆。
解:(1) 甲醇燃烧反应:CH 3OH(l) +23O 2(g) → CO 2(g) + 2H 2O(l) Q V =θm c U ∆=-119.50 kJ/(5.27/32)mol =-725.62 kJ·mol -1Q p =θm c H ∆=θm c U ∆+∑RT v)g (B= (-725.62-0.5×8.3145×298.15×10-3)kJ·.mol -1 =-726.86 kJ·mol-1(2) θm c H ∆=θm f H ∆(CO 2) + 2θm f H ∆(H 2O )-θm f H ∆ [CH 3OH(l)] θm f H ∆[CH 3OH (l)] =θm f H ∆ (CO 2) + 2θm f H ∆ (H 2O )-θm c H ∆= [-393.51+2×(-285.83)-(-726.86) ] kJ·mol -1=-238.31 kJ·mol -1(3) CH 3OH (l) →CH 3OH (g) ,θm vap ΔH= 35.27 kJ·.mol -1θm f H ∆[CH 3OH (g)] =θm f H ∆[CH 3OH (l)] +θmv ap H ∆= (-38.31+35.27)kJ·.mol-1=-203.04 kJ·mol -1第二章 热力学第二定律例1. 1mol 理想气体从300K ,100kPa 下等压加热到600K ,求此过程的Q 、W 、U 、H 、S 、G 。
人教版七年级上册数学第一章《1.3.2有理数的减法》(2课时,教案+课件)

人教版七年级上册数学第一章《1.3.2 有理数 的减法 》(2 课时, 教案+课 件)
达标检测
2. 一电脑公司仓库在8月1日库存某种型号 的电脑20台,8月2日到6日该种型号的电脑 进出记录如下表,问到8月6日止,库存该 种电脑多少台
人教版七年级上册数学第一章《1.3.2 有理数 的减法 》(2 课时, 教案+课 件)
尝试应用
把下式写成省略加号的和的形式,并把它读出来 (-3)+(-8)-(-6)+(-7)
解:原式=(-3)+(-8)+(+6)+(-7) =-3-8+6-7
读作“-3,-8,+6,-7的和 或负3减8加6减7
人教版七年级上册数学第一章《1.3.2 有理数 的减法 》(2 课时, 教案+课 件)
课文讲解
算式 (20) (3) (5) (7)
是-20,3,5,-7 这四个数的和,为书写简单, 可以省略算式中的括号和加号,把它写为
20 3 5 7
这个算式可以读作“负20、正3、正5、负7的 和”,或读作“负20加3加5减7”.
人教版七年级上册数学第一章《1.3.2 有理数 的减法 》(2 课时, 教案+课 件)
知识探究
在数轴上,点 A,B 分别表示 a,b.利用有理数减法, 分别计算下列情况下点 A,B 之间的距离;
a=2,b=6;a=0,b=6;a=2,b=-6; a=-2,b=-6. 你能发现点 A, B 之间的距离与数 a,b 之间的关系吗? A,B之间的距离就是a,b中较大的数减去较小的数的差
人教版七年级上册数学第一章《1.3.2 有理数 的减法 》(2 课时, 教案+课 件)
(完整版)高中数学必修五第一章(1)
第一章解三角形章节总体设计(一)要求本章的中心内容是如何解三角形,正弦定理和余弦定理是解三角形的工具,最后落实在解三角形的应用上。
通过本章学习,学生应当达到以下学习目标:(1)通过对任意三角形边长和角度关系的探索,掌握正弦定理、余弦定理,并能解决一些简单的三角形度量问题。
(2)能够熟练运用正弦定理、余弦定理等知识和方法解决一些与测量和几何计算有关的生活实际问题。
(二)教学内容及课时安排建议1.1正弦定理和余弦定理(约课时)1.2应用举例(约课时)1.3实习作业(约课时)(三)评价建议1.要在本章的教学中,应该根据教学实际,启发学生不断提出问题,研究问题。
在对于正弦定理和余弦定理的证明的探究过程中,应该因势利导,根据具体教学过程中学生思考问题的方向来启发学生得到自己对于定理的证明。
如对于正弦定理,可以启发得到有应用向量方法的证明,对于余弦定理则可以启发得到三角方法和解析的方法。
在应用两个定理解决有关的解三角形和测量问题的过程中,一个问题也常常有多种不同的解决方案,应该鼓励学生提出自己的解决办法,并对于不同的方法进行必要的分析和比较。
对于一些常见的测量问题甚至可以鼓励学生设计应用的程序,得到在实际中可以直接应用的算法。
2.适当安排一些实习作业,目的是让学生进一步巩固所学的知识,提高学生分析问题的解决实际问题的能力、动手操作的能力以及用数学语言表达实习过程和实习结果能力,增强学生应用数学的意识和数学实践能力。
教师要注意对于学生实习作业的指导,包括对于实际测量问题的选择,及时纠正实际操作中的错误,解决测量中出现的一些问题。
第1课时课题: §1.1.1正弦定理●教学目标 知识与技能:通过对任意三角形边长和角度关系的探索,掌握正弦定理的内容及其证明方法;会运用正弦定理与三角形内角和定理解斜三角形的两类基本问题。
过程与方法:让学生从已有的几何知识出发,共同探究在任意三角形中,边与其对角的关系,引导学生通过观察,推导,比较,由特殊到一般归纳出正弦定理,并进行定理基本应用的实践操作。
第一章 集合
第一章 集合第一单元 集合的概念及运算知识点一 集合及其表示方法1、 集合:能够确切指定的对象集在一起组成的整体叫做集合。
元素:集合中的每个对象叫做这个集合的元素。
2、集合的表示方法⎪⎩⎪⎨⎧象的集合表示和运算。
韦恩图法:主要用于抽不可数或很多时使用。
描述法:集合中元素为使用。
中元素为可数且较少时列举法:主要用于集合 (1){ … } 如{我校的篮球队员},{太平洋,大西洋,印度洋,北冰洋} (2)用拉丁字母表示集合:A={我校的篮球队员},B={1,2,3,4,5}3、集合的分类⎪⎩⎪⎨⎧的集合空集:不含有任何元素多个的集合无限集:元素个数无限的集合有限集:元素个数有限例题讲解1、观察下列实例:①小于11的全体非负偶数; ②整数12的正因数; ③抛物线12+=x y 图象上所有的点; ④所有的直角三角形; ⑤高一(1)班的全体同学; ⑥班上的高个子同学。
回答下列问题:(1)哪些对象能组成一个集合。
(2)用适当的方法表示它。
(3)指出以上集合哪些集合是有限集。
2、用适当的方法表示以下集合: (1)平方后与原数相等的数的集合。
(2)设b a ,为非零实数,bb aa +可能表示的数的取值集合。
(3)不等式62<x 的解集。
(4)坐标轴上的点组成的集合。
(5)第二象限内的点组成的集合。
(6)方程组⎩⎨⎧=-=+15y x y x 的解集。
课堂练习1、下列给出的对象中,能表示集合的是( )A 、一切很大的数B 、无限接近零的数C 、聪明的人D 、方程x 2=2的实数根 2、用适当的方法表示下列集合: (1)平方后仍等于原数的数集。
(2)方程29x =的解集。
(3)使得函数612-+=x x y 有意义的实数x 的集合。
(4)方程组1232x y x y +=⎧⎨=-⎩的解集。
(5)方程224941250x y x y +-++=的解集。
3、方程0652=+-x x 的解集可表示为_____________________。
2014-2015学年第2学期 温州大学控制工程基础-复习例题(2015.06)
1 2+
1
+
5
s
2
s +
4
温州大学 机电工程学院
第二章 习题解答
3) x′′(t) + 2x′(t) + 5x(t) = 3, x(0) = 0, x′(0) = 0
s2 X (s) + 2sX (s) + 5X (s) = 3 s
X
(s)
=
s2
+
1 2s
+
5
⋅
3 s
ห้องสมุดไป่ตู้
=
0.6
1 s
−
0.6
(s
s+2 +1)2 +
4)
=
1 s
−
2
s
1 +
2
+
s2
s +
+1 2s +
4
=
1 s
−
2
s
1 +
2
+
(s
s +1 +1)2 +
3
g(t) = L−1[G(s)] = 1− 2e−2t + e−t cos 3t, t ≥ 0
13)G(s)
=
1
s(s2 + ω2)
=
1
ω2
1 s
−
1
ω2
s2
s
+ω2
g (t )
=
L−1[G(s)]
数值,求此温度计的时间常数T。若给容器加热,使水温以
10°C/min 的速度变化,问此温度计的稳态指示误差是多少?
( ) 解:温度计的单位阶跃响应为: xo (t )
第一章轴对称图形讲义
第一章轴对称图形一、基础知识点知识点一:轴对称图形如果一个图形沿一条折叠,直线两旁的部分能够这个图形就叫做轴对称图形。
这条直线就是它的对称轴知识点二:轴对称把一个图形沿着某一条直线折叠,如果它能够与重合,那么就说这两个图形关于这条直线成轴对称。
这条直线就是对称轴,两个图形中的对应点(即两个图形重合时互相重叠的点)叫做对称点。
知识点三:关于某条直线成轴对称的图形的性质特征1、成轴对称的两个图形全等.如果把一个轴对称图形沿对称轴分成两个图形,这两个图形全等,并且也是成轴对称的.2、轴对称图形和关于直线成轴对称有什么区别和联系?区别:①轴对称是指两个图形沿某直线对折能够完全重合,而轴对称图形是指一个图形的两个部分沿某直线对折能完全重合。
②轴对称是反映两个图形的特殊位置、大小关系;轴对称图形是反映一个图形的特性。
联系:①两部分都完全重合,都有对称轴,都有对称点。
②如果把成轴对称的两个图形看成是一个整体,这个整体就是一个轴对称图形;如果把一个轴对称图形的两旁的部分看成两个图形,这两个部分图形就成轴对称。
常见的轴对称图形有:圆、正方形、长方形、菱形、等腰梯形、等腰三角形、等边三角形、角、线段、相交的两条直线等知识点四:垂直平分线的定义经过线段并且这条线段的直线,叫做这条线段的垂直平分线知识点五:线段垂直平分线的性质(1)线段垂直平分线的性质:线段垂直平分线上的与这条线段的距离思考:反过来,如果PA=PB,那么点P是否在线段AB的垂直平分线上?(2)与一条线段两个端点距离相等的点,在这条线段的上.知识点六:轴对称的性质以及轴对称图形:性质:⑴成轴对称的两个图形全等。
⑵如果两个图形成轴对称,那么对称轴是对称点连线的垂直平分线。
画轴对称图形时,应先确定对称轴,再找出对称点。
知识点七:用坐标表示轴对称1.关于x轴与y轴对称的点的坐标的规律;(1)点(x,y)关于x轴对称的点的坐标为________;(2)点(x,y)关于y轴对称的点的坐标为________.(3)点(x,y)关于原点对称的点的坐标为________.2.图形关于坐标轴对称一个图形内任一点的横坐标保持不变,纵坐标乘以-1所得的图形与原图形关于________轴对称.专题:等腰三角形知识点一:等腰三角形有相等的三角形是等腰三角形;相等的两边叫作,另一边叫作,两腰的夹角叫作,底边和腰的夹角叫作.练习1:1.如图(1):△ABC中,若则△ABC是等腰三角形,是腰、是底边、是顶角,是底角.2.等腰三角形的两边长分别为3cm和6cm,这个三角形的周长为________.知识点二:等腰三角形的性质问题:如图,已知△ABC中,AB=AC,AD是底边上的中线.求证:∠B=∠C;AD平分∠A,AD⊥BC.归纳性质:(1)等腰三角形的两个相等(简写成“等边对”);C BA图(1)DC BA(2)等腰三角形的顶角 、底边上的 线、底边上的 互相重合(通常称作“三线合一”);友情提醒:(1)等边对等角的边角必须是同一个三角形的边与角;(2)等腰三角形的“三线合一”不要与三角形全等混淆.练习2:1.等腰三角形的顶角的度数是底角的4倍,则它的顶角是_______.2.已知等腰三角形一个内角的度数为30°,那么它的底角的度数是__ _ ___ _. 3.如果等腰三角形的一个外角是125°,则底角为 .注:已知等腰三角形一个角的度数,求另外两角的度数,常有两种情况,需要分类讨论. 4.等腰三角形一腰上的高与底边的夹角为45°,则这个三角形是( ) A .锐角三角形 B .钝角三角形 C .等腰直角三角形 D .等边三角形 5.如图,在△ABC 中,AB=AC ,点D 在AC 上,且BD=BC=AD ,求△ABC 各个内角的度数.知识点三: 等腰三角形的判定活动:如图(4),位于海上A 、B 两处的两艘救生船接到O 处遇险船只的报警,当时测得∠A =∠B .如果这两艘救生船以同样的速度同时出发,能不能大约同时赶到出事地点(不考虑风浪因素)?COBA图(4)DC BA归纳:证明边相等或角相等,一般需要构造全等的三角形.判定定理:如果一个三角形有两个 相等,那么这两个角所对的 也相等(简写成“等角对 ”).练习3:1.如图(5),CD 、BD 平分∠BCA 及∠ABC ,EF 过D 点且EF ∥BC , 则图中的等腰三角形有 个,它们是2.在△ABC 中,∠B =36°,D 、E 在BC 边上,且AD 和AE 把∠BAC 三等分,则图中等腰三角形的个数( )A . 3B . 4C . 5D . 63.如图(6),∠CAE 是△ABC 的一个外角,∠1=∠2,AD//BC , 求证:AB=AC .4.如图(7),在△ABC 中,AE 平分∠BAC ,∠DCB =∠B -∠ACB , 求证:△DCE 是等腰三角形.知识点四:等边三角形相等的三角形是等边三角形,它是特殊的等腰三角形,也叫 ;图(6)21EDCBA 图(5)图(7)练习4:如果一个等边三角形的一条边长为6cm,那么这个等边三角形的周长是.知识点五:等边三角形的性质(1)等边三角形的三个都相等,且都等于;(2)等边三角形是轴对称图形,且有对称轴;(3)等边三角形每条边上的、和三线合一,它们所在的直线都是等边三角形的.友情提醒:等边三角形是一种特殊的等腰三角形,容易知道等边三角形的三条高(或三条中线、三条角平分线)都相等.练习5:1.△ABC中,AB=BC,∠B=∠C,则∠A=_____度.2.如图,C是线段AB上的一点,△ACD和△BCE是等边三角形,连结AE,BD.求证:AE=BD.知识点六:等边三角形的判定(1)三条都相等的三角形是等边三角形;(2)三个都相等的三角形是等边三角形;(3)有一个角是的三角形是等边三角形.练习6:1.已知△ABC中,AB=AC, ∠A+∠B=120°,那么∠A= ;△ABC是三角形;2.下面给出的几种三角形:①有两个角为60°的三角形;②三个外角都相等的三角形;③一边上的高也是这边上中线的三角形;④有一个角为60°的等腰三角形.•其中是等边三角形的个数是()A .4个B .3个C .2个D .1个3. 如图,在△ABC 中,点D 是AB 上的一点,且AD=DC=DB ,∠B=30°,求证:△ADC 是等边三角形.分析:由已知条件知△ADC 是等腰三角形,要想证明它还是等边三角形,只需要说明这个三角形中有一个内角等于60°即可.4.如图,△ABC 是等边三角形,点D 、E 、F 分别是线段AB 、BC 、AC 上的点, (1)若AD=BE=CF ,问△DEF 是等边三角形吗?试证明你的结论; (2)若△DEF 是等边三角形,问AD=BE=CF 成立吗?试证明你的结论.规律技巧总结:要说明一个三角形是等边三角形,可以考虑: ①利用定义证明; ②证明三个角相等;③证明它是等腰三角形并且有一个角是60°知识点七:有一个角是30°的直角三角形在直角三角形中30°的角所对的 为斜边的 . 练习7:三角形三内角度数之比为1:2:3,最大边长是8cm ,则最小边的长是______.AC BDAFaDBEC二、典型例题讲解(2010无锡)如图,△ABC中,DE垂直平分AC交AB于E,∠A=30°,∠ACB=80°,则∠BCE=____°。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、点的落影概念及求作
点在平面上的落影:用光线三角形法求影。 空间光线 A
S
s a 空间光线在P 面上的投影 P
S s
AP
△AaAP称为光线三角形
利用光线三角形求点的落影
S
s
A
AP
a
P
光线三角形法
2
点在投影面上的落影:用光线迹点法求影。
S s
B
S
Bv F
V
fv
b
(BH)
fH
光线迹点法
3
点在立体表面上的落影:用光截面法求影。
A
V
S
Av
虚影
S
(AH)
s
C s
CH
折影点
av
Ⅰo
a
c
3、直线段的落影规律
1)平行规律:
① 若直线平行于承影面,则其影 与直线平行且等长﹙直线段﹚
B
S s
C
S S
BP
s
s
c P
CP
b
② 一直线在诸平行承影面上的落影彼此平行。
A
S
AP B BP bP AQ
s
aP
bQ
P
BQ
aQ
Q
③ 诸平行直线在同一承影面上的落影彼此平行。
A C
S s
B D BP bP dP DP AP CP
P
aP
cP
④ 诸平行直线在诸平行承影面上的落影彼此平行。
A C
S s
B D BP DP dP AP
CP
bP
P
G
aP cP
⑤ 平行于光线的直线其落影积聚为一点。
A
S
s
B AP BP bP
aP P
2)相交规律: ⑥ 若直线与承影面相交,则影必过交点。
c
3)垂直规律: ⑨ 若直线垂直于承影面,则落影与光线在该承影面 上的投影方向平行。
A
S s AH
B
BH
H
三、平面图形的阴影
V 1、平面图形落 影的概念
A
三角形平 面的落影
Av
B
(AH)
S s
X
BH
Ⅱo
av Ⅰo O
C
CH
2、平面图形落影的求作:通常 是用平面图形轮廓线上各点同 面落影连线来求作影线。当各 点的影不在同一平面上时,应 利用假影求得折影点,再与其 真影相连。
Do d Co Bo
阴线
C
D
阳面
B
A
s
s
S
阳 阳 面 面
c
S s
s
a
s
b
s
其余表面为阴面
2、棱锥的阴影
作阴影步骤:
1)、首先定出锥顶之影,再 作锥之影; 2)、再确定棱锥的阴线; 3)、着色。
T
S
To (F) s E
t
C
D
A
直线和四棱锥 的阴影
注意:直 线在锥面 上的落影, 是利用直 线及锥面 B 的各棱线 在地面上 的落影的 重影点用 返回光线 b 法作出。
Ⅰ
T
S
S
Ⅱ Ⅲ Ⅰo
To
(F)
(Bo)
(Ⅳ)
(Ⅲo) (Ⅱo) Ⅰo
Ao
E
t
C
D
a
3、圆柱的阴影
作阴影步骤:
1)、根据光线方向确定阴、 阳面,从而定出阴线; 2)、逐段求出各段阴线的 落影;(即为圆柱落影的 轮廓线) 3)、着色。 Ⅳo Ⅲo Ⅲ Ⅱ
S
Ⅳ Ⅴ
s
Ⅴo
Ⅰ
4
Ⅱo Ⅰo 2 3
5
s
1
4、圆筒内壁的阴影
S
A
E
s
P B
F
Ap
e 光截面 D
(AH)
b
c
a G
f
2)、斜线在斜面上的落影
E
S s e
A Ap
B
F
(Ao)
b
f
D
P
R J a c
G
本章小结
1、通过本讲应掌握作轴测图阴影的基本步骤和基本方法
基本步骤:
1) 2) 3) 4)
确定光线方向; 由光线方向确定阴、阳面及阴线; 求各段阴线的落影; 着色。
§1-1 阴影的基础知识
一、阴影的形成
阳面
阳面与阴面的分界线
阴面 影
阴线 影线 承影面
阴点
承 影 面
影点 阴影三要素: 光源、形体、承影面
二、图样中加绘阴影的作用与光线方 向及作阴影的方法
作用:
更生动、真实、富有表现力
方法:
1、光线三角形法
3、回投光线法
2、光截面法 4、延棱扩面法
§1-2
1
轴测图中的阴影
本章结束
D
s
S
30
d0
a0
Ⅲo
Ⅱo Ⅰo
e
B
Eo
圆柱的阴线
承影面 M
2、台阶的阴影
作影思路:
(用延棱扩面法求影)
1)、由已知点A的影A0,定 出空间光线S,用延棱扩面 法求出光线的H投影s; 2)、根据光线方向定出 台阶及挡板的阴线;
C s′ V
Ⅲ
Dd Ⅱ Ⅰ
B
ⅡH ⅢH ⅠH CH
t
A 3
S
s
c
五、建筑细部的阴影
1、方帽圆柱的阴影(用光线三角法求影)
作影思路:
1)、据已知点A的影A0,定 出空间光线S及其H投影s, △Aa0A0为光线三角形.
2)、以光线的H投影s与圆 C 柱顶圆相切得d0,过切点d0 的素线为圆柱面的阴线. 3)、柱面阴线及柱面右轮 廓线上的影点D0、E0,是过 d0 、e0作s返回定出D 、E 再由D 、E作光线S而求得. 4)、各光线三角形中最 小的光线三角形Ⅰ10Ⅰ0 中的Ⅰ0点为落影的最高 点(因Ⅰ10最短) 5)、作色
b
a
c
H
例题:
已知圆O所在的平面为正平面,其水平投影积聚为直 线段1-5;光线的方向为S,其水平投影为s,求圆O在 水平面上的落影。
Ⅶ
Ⅷ
Ⅵ
S s
Ⅰ
O
圆平 面的 落影
Ⅶh
Ⅴ Ⅳ
Ⅷh
Ⅱ
Ⅲ
Ⅵh Ⅴh
Ⅰh
Ⅱh Ⅲh
Ⅳh
1
8(2)
7(3)
6(4)
5
四、基本几何体的阴影
1、棱柱的阴影
作阴影步骤:
1)、根据光线方向确定阴、 阳面,从而定出阴线; 2)、由直线段落影规律逐 段求出上述阴线的落影; (即为棱柱落影的轮廓线) 3)、将阴、影涂暗色。
S s
21 31 41 51 Ⅵ
Ⅴ0 Ⅴ
Ⅳ
Ⅰ
Ⅱ
Ⅲ
Ⅳ0
Ⅱ0 Ⅲ0
5、圆锥的阴影
作阴影步骤:
1)、首先定出锥顶之影,再 作锥之影; 2)、定圆锥面上的阴线; 3)、着色。
T S
TH
B S s s t
A
C T
直线和圆锥的阴影
注意:直线在圆锥面 上的落影,是利用直 线及圆锥面上的各素 线在地面上落影的重 影点用返回光线法作 出。 TH
A
S s
B
AP
BP aP P
bP C cP、CP
点属于平面 其影为自身
⑦ 相交两直线的同面落影必相交,且交点的落影 即两直线落影的交点。
A
S
s
C BP CP B AP
a
P
b
c
⑧ 一直线落于两相交承影面上的影为一折线, 折影点在两承影面的交线上。
A V
S
Av
S
AH
折影点
s C s
a av
CH Ⅰo
V
B VI
阴线
B0
E
IV S s A
3)、用延棱扩 面法求影线;
4)、着色。
s′
H2 V2 C D
A0
s
a1 III
Cv DH
H1
V1 H
a
s
阴线
6、直线在斜面上的落影
1) 、铅垂线在斜面上的落影 A S
s
e
(介绍光截面法)
E
P F
D
f
a
G
例题:
已知直线Aa为铅垂线;平面P为倾斜面,平面P在水平面上的投影为四 边形DefG;光线方向为S,S在水平面上的投影为s,求直线Aa的落影。
C S s S
F
C0
c
s
用光截面法
二、 直线的落影及其落影规律
1、直线段的落影概念: A S s
光平面
直线段的落影是含该直线段的 一组光线所构成的光平面与承影 面的交线。 S
AP
C s a c
CP
2、直线段落影的求法: A S s AP s
CP 1)、直线段在一个平面上落影的求法
S
C
a
c
2)、直线段在两相交平面上落影的求法
基本方法:
1) 光线三角形法 2) 光线迹点法 3) 光截面法 5) 回头光线法 4) 延棱扩面法
2、应熟悉各种位置直线的落影规律 3、轴测图中求影应具备以下基本功: 1) 凭点的落影要能熟练地定出光线及其在各坐 标面上的投影方向。(S、s、); 2) 在任何情况下,能求出空间任意一点落在任 何表面上的影。
