教师导学案NO.35直角三角形的判定
直角三角形的性质与判定教案

直角三角形的性质与判定教案直角三角形是指其中一个内角为90°的三角形。
在本教案中,我们将学习直角三角形的性质与判定方法。
通过本教案,我们将了解到直角三角形的特点以及如何利用这些特点进行判定。
一、直角三角形的性质1. 边长关系:在直角三角形中,直角边是相对于直角的两条边。
我们可以使用勾股定理来描述直角三角形的边长关系。
根据勾股定理,直角三角形的两个直角边的平方和等于斜边的平方。
即,设直角三角形的直角边分别为a和b,斜边为c,那么有a² + b²= c²。
2. 角度关系:在直角三角形中,直角为90°,而其余两个角的和为90°。
即,设直角三角形的一个角为α,另一个角为β,那么有α + β = 90°。
二、直角三角形的判定方法根据直角三角形的性质,我们可以通过以下方法来判定一个三角形是否为直角三角形:1. 根据边长关系判定:若一个三角形的三条边满足勾股定理中的等式关系,即a² + b² = c²或c² = a² + b²,则该三角形是直角三角形。
例如,若一个三角形的边长为3、4、5,则满足3² + 4² = 5²,因此该三角形是直角三角形。
2. 根据角度关系判定:若一个三角形的一个角为90°,则该三角形是直角三角形。
例如,若一个三角形的一个角为90°,另一个角度为45°,则这个三角形是直角三角形,因为90° + 45° = 135°。
3. 综合判定:在某些情况下,我们可以综合使用边长关系和角度关系来判定直角三角形。
例如,若一个三角形的两条边长为5和12,并且夹角为90°,则这个三角形是直角三角形。
因为5² + 12² = 13²,同时夹角为90°。
直角三角形的性质和判定(2)导学案
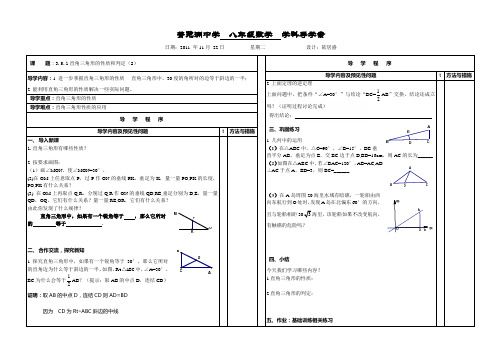
2 上面定理的逆定理 上面问题中,把条件“∠A=30°”与结论“BC= 吗?(证明过程讨论完成) 得出结论: 三、巩固练习 1 几何中的运用 (1)在△ABC 中,△C=90°,∠B=15°,DE 垂 直平分 AB, 垂足为点 E, BC 边于点 D,BD=16cm, 交 则 AC 的长为______ (2) 如图在△ABC 中, 若∠BAC=120°, AB=AC,AD ⊥AC 于点 A,BD=3,则 BC=______. (3)在 A 岛周围 20 海里水域有暗礁,一轮船由西 向东航行到 O 处时, 发现 A 岛在北偏东 60°的方向, 且与轮船相距 30 3 海里,该轮船如果不改变航向, 有触礁的危险吗?
菁芜洲中学
日期:2011 年 11 月 22 日 课 题:3.5.1 直角三角形的性质和:陆居盛 导 学 程 导学内容及预见性问题 序 t 方法与措施
导学内容:1 进一步掌握直角三角形的性质----直角三角形中,30 度的角所对的边等于斜边的一半; 2 能利用直角三角形的性质解决一些实际问题。 导学重点:直角三角形的性质 导学难点:直角三角形性质的应用 导 学 程 序 导学内容及预见性问题 t 方法与措施 一、 导入新课 1.直角三角形有哪些性质? 2 按要求画图: (1)画∠MON,使∠MON=30°, (2)在 OM 上任意取点 P,过 P 作 ON 的垂线 PK,垂足为 K,量一量 PO,PK 的长度, PO,PK 有什么关系? (3) 在 OM 上再取点 Q,R,分别过 Q,R 作 ON 的垂线 QD,RE,垂足分别为 D,E,量一量 QD,OQ,它们有什么关系?量一量 RE,OR,它们有什么关系? 由此你发现了什么规律? M 直角三角形中,如果有一个锐角等于 ,那么它所对 P 的 等于 .
八年级数学-直角三角形的判定导学案

直角三角形的判定导学案 学习目标:(1)探索并掌握勾股定理逆定理;(2)会应用勾股逆定理判别一个三角形是否是直角三角形;(3)通过三角形三边的数量关系来判断它是否为直角三角形,体会数形结合的思想。
一、课前预习:1、(回忆)直角三角形的性质: (1)有一个角是 , (2)两个锐角的和为 (互余);(3) 的平方和等于 的平方,即: 。
2、在△ABC 中,∠C=︒90(1)若5=a ,12=b ,则c=____;(2)若7=a ,4=c ,则b=____;3、以小组为单位,准备长度分别5 cm 、6 cm 、9 cm 、12cm 、13cm 、15cm 的小棒。
二、合作探究:(以小组为单位进行)1、拼三角形:从长度分别为3cm 、 4cm 、5 cm 、6 cm 、9 cm 、12cm 、13cm 、15cm 的小棒中选出三根:(1)6、9、13;(2)9、12、 15;(3)5、12、13拼出三个三角形。
(1)三角形的两条较短的边的平方和与最长边的平方满足 时,这个三角形是直角三角形; 边所对的角是直角。
(2)你们的结论:三角形的三边长a 、b 、c 有 关系时,这个三角形是直角三角形。
4、思考:如果三角形的两条较短的边的平方和不等于最长边的平方,那么这个三角形还是直角三角形吗?5、归纳总结:在一个三角形中:只要 的平方和等于 的平方,这个三角形就是直角三形,其中 所对的角是直角。
三、当堂练习:用上面的结论看能否解决下列问题。
1 、下面以a 、b 、c 为边长的△ABC 是不是直角三角形?如果是,那么哪一个角是直角?(1) a=12, b=16, c=20 ; 。
(2) a=10, b=9, c=5 ; 。
(3) a=8 ,b=12 ,c=15 ; 。
2、若△ABC 的两边长为3和5,则能使 △ABC 是直角三角形的第三边的平方是( )A 、16B 、34C 、4D 、16或343、满足下列条件△ABC ,不是直角三角形的是( )A 、b 2 = a 2 -c 2B 、a ∶b ∶c=3∶4∶5C 、∠C=∠A -∠BD 、∠A ∶∠B ∶∠C=3∶4∶5四、反思提升我的收获:我的疑惑:我还想知道…….五、反馈练习:1、下列各组线段中,能组成直角三角形的是( )A. 5,6,7B. 32,42,52C. 5,11,12D. 5,12,132、小蒋要求△ABC 的的最长边上的高,测得AB=8cm ,AC=6cm ,BC=10cm 。
八年级 勾股定理--直角三角形的判定导学案

八年级数学导学案学科:数学 主备人: 审核人_____ 班级____ 姓名____ 课题:勾股定理-----------直角三角形的判定一、自主学习(一)学习目标(重、难点)会用勾股定理判定一个三角形是否是直角三角形(二)自学指导我们都知道:一个直角三角形的两条直角边的平方的和等于斜边的平方。
反之,如果一个三角形的两条边的平方的和等于第三边的平方,那么,这样的三角形是直角三角形吗?如果是,又该怎样判定一个三角形是否是直角三角形?带着问题去预习吧!(三)合作探究1.判断由下列各组线段a 、b 、c 的长,能组成的三角形是不是直角三角形,并说明理由.(1)a =6.5,b =7.5,c =4; (2)a =11,b =60,c =61;(3)a =38,b =2,c =310; (4)a =433,b =2,c =414;2. 如图,已知在△ABC 中,CD ⊥AB 于D ,AC =20,BC =15,DB =9.(1)求DC 的长.(2)求AB 的长.(3)求证: △ABC 是直角三角形.二、学生展示C A BD三、学习检测(一)基础题1.如图,下列三角形中是直角三角形的是( )2.在下列长度的各组线段中,能组成直角三角形的是( ).A .12,15,17B .9,16,25C .5a ,12a ,13a (a>0)D .2,3,43.在△ABC 中,∠A 、∠B 、∠C 的对边分别是a 、b 、c ,AB =8,BC =15,CA =17,则下列结论不正确的是( ).A .△ABC 是直角三角形,且AC 为斜边B .△ABC 是直角三角形,且∠ABC =90°C .△ABC 的面积是60D .△ABC 是直角三角形,且∠A =60°4.在△ABC 中,∠A 、∠B 、∠C 的对边分别是a 、b 、c ,且a :b :c =1:3:2,则下列说法错误的是( ).A .∠C =90°B .c 2-a 2=b 2C .c 2=2a 2D .若a =k ,则c =2k (k>0)5.在△ABC 中,∠A 、∠B 、∠C 的对边分别是a 、b 、c.则满足下列条件但不是直角三角形的是( ).A .∠A =∠B -∠C B .∠A :∠B :∠C =1:1:2C .a :b :c =4:5:6D .a 2-c 2=b 26.若一三角形铁皮余料的三边长为12cm ,16cm ,20cm ,则这块三角形铁皮余料的面积为cm 2.(二)综合题在△ABC 中,∠A 、∠B 、∠C 的对边分别是a 、b 、c. a =n 2-16,b =8n ,c =n 2+16(n>4).求证: ∠C=90°.(三)拓展题如图,AD=7,AB =25,BC =10,DC =26,DB =24,求四边形ABCD 的面积.四、小结反思D 5 12 13 C 5 6 7 B 7 5 8 A 6 3 5A B C D。
直角三角形的判定教案

直角三角形的判定教案
哎呀,同学们,今天咱们要来好好聊聊直角三角形的判定!
先来说说啥是直角三角形,就是有一个角是直角的三角形呗!那怎么才能知道一个三角形是不是直角三角形呢?
咱们来看第一种方法,要是一个三角形的两条边的平方和等于第三边的平方,那它就是直角三角形啦!这就好比咱们搭积木,两边的积木长度平方加起来正好和第三边的积木长度平方一样,那这个三角形就能稳稳地立成直角啦!
比如说,有一个三角形,三条边分别是3、4、5。
那3 的平方是9,4 的平方是16,加起来是25,正好是5 的平方。
这不就说明它是直角三角形嘛!
老师再给你们举个例子,假如有个三角形三条边是5、12、13,那5 的平方是25,12 的平方是144,加起来是169,正好是13 的平方,这不就又证明它是直角三角形啦?
那同学们,你们想想,如果给你们一个三角形,三条边分别是6、8、10,它是不是直角三角形呢?
还有一种方法哦,要是一个三角形有一个内角是直角,那它不就是直角三角形嘛!这多简单呀,就好像你一眼就能看出桌子上的苹果和梨,直角也能一眼就看出来呀!
那怎么才能知道一个角是不是直角呢?咱们可以用三角板去量一量呀!
好啦,同学们,咱们学了这两种判定直角三角形的方法,以后遇到三角形,是不是就能很快判断它是不是直角三角形啦?
我的观点是:学会了直角三角形的判定方法,咱们就能在数学的世界里更厉害啦,遇到相关的问题都能轻松解决,多棒呀!。
直角三角形全等的判定导学案
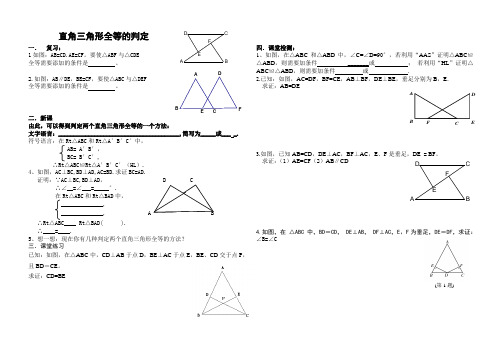
FE DCB A A B D FC E FE D C B A 直角三角形全等的判定一. 复习:1如图:AB=CD.AE=CF 。
要使△ABF 与△CDE全等需要添加的条件是 。
2.如图:AB ∥DE ,BE=CF ,要使△ABC 与△DEF 全等需要添加的条件是 。
二.新课由此,可以得到判定两个直角三角形全等的一个方法:文字语言:________________________________________,简写为_____或___ _. 符号语言:在Rt △ABC 和Rt △A ′B ′C ′中,AB= A ′B ′,BC= B ′C ′,∴Rt △ABC ≌Rt △A ′B ′C ′(HL ).4、如图,AC ⊥BC,BD ⊥AD,AC=BD.求证BC=AD. 证明:∵AC ⊥BC,BD ⊥AD , D C ∴∠__=∠___=_____°.在Rt △ABC 和Rt △BAD 中, ______________, ______________, A B∴Rt △ABC____ Rt △BAD( ). ∴____=____.5、想一想:现在你有几种判定两个直角三角形全等的方法? 三.课堂练习已知:如图,在△ABC 中,CD ⊥AB 于点D ,BE ⊥AC 于点E ,BE 、CD 交于点P ,且BD =CE 。
求证:CD=BE四.课堂检测:1、如图,在△ABC 和△ABD 中,∠C=∠D=90°,若利用“AAS ”证明△ABC ≌△ABD ,则需要加条件 _______或 ; 若利用“HL ”证明△ABC ≌△ABD ,则需要加条件 或 . 2.已知:如图,AC=DF ,BF=CE ,AB ⊥BF ,DE ⊥BE ,垂足分别为B ,E . 求证:AB=DE3.如图,已知AB=CD ,DE ⊥AC ,BF ⊥AC ,E 、F 是垂足,DE = BF 。
求证:(1)AE=CF (2)AB ∥CD4.如图,在 △ABC 中,BD =CD , DE ⊥AB , DF ⊥AC ,E 、F 为垂足,DE =DF ,求证: ∠B=∠CF E D CB A(第1题)G F E D CB AGF E DC B A1.能判定两个直角三角形全等的是( ) A .有一锐角对应相等 B .有两锐角对应相等 C .两条边分别相等D .斜边与一直角边对应相等2.如图,AB=CD ,DF ⊥AC 于F ,BE ⊥AC 于E ,DF=BE ,求证:AF=CE.3.如图,AB=CD ,AE ⊥BC ,DF ⊥BC ,CE=BF. 求证:AE=DF4.如图,在△ABC 中,AB ⊥AC ,且AB =AC ,点E 在AC 上,点D 在BA 的延长线上,AD =AE .求证:(1)△ADC ≌△AEB ;(2)BE=CD .5.已知:如图,AB=CD ,DE ⊥AC ,BF ⊥AC ,E ,F 是垂足,DE=BF . 求证:(1)AF=CE ;(2)AB ∥CD .6.如图所示,A 、E 、F 、C 在同一条直线上,AE=CF ,DE ⊥AC ,BF ⊥AC ,垂足分别为E 、F 。
直角三角形的判定(导学案)定稿
14.1.2 直角三角形的判定导学案学习目标1.探索发现直角三角形的判定定理,感受它与勾股定理的关系;2.经历“观察——猜想——论证”的探索过程,培养探究能力和合作精神,体会数形结合思想;3.能运用勾股定理的逆定理解决简单的证明问题.学习探究问题1.分组活动:第1,2,3大组用直尺和圆规分别画第113页的“试一试”的(1)(2)(3)小题的三角形.画完后观察所画三角形的形状,并计算a 2+b 2= ,c 2= ,发现三角形的形状 (填是或不是)直角三角形,且a 2+b 2 c 2(填=或≠).第4大组用三角板画直角△ABC ,满足条件:∠C =90°,两直角边分别为AC=3,BC=4 发现你们画的所进行的形状和大小与一组的怎样?为什么呢?归纳:三角形的三边满足什么数量关系时,该三角形是直角三角形?如图,△ABC 中,若 ,则∠C =90°.直角三角的判定定理:A CB a cb已知:如图△ABC 中,AB=a,BC=b,AC=c,且a 2+b 2=c 2,求证:∠C =90°证明:【学习反馈】:设三角形的三边长分别等于下列各组数,试判断各三角形是否是直角三角形。
若是,指出哪一条边所得的角是直角.(不写过程)(1)12,16,20;(2)1.5,2,2.5;(3)3,4,7;(4)13,5,12问题2.已知△ABC ,AB=n 2-1,BC=2n ,AC= n 2+1(n 为大于1的正整数)。
试问△ABC 是直角三角形吗?若是,哪一条边所对的角是直角?请说明理由。
小结:1.我们今天都学习了些什么?应注意什么?2.在学习的过程中,体验到哪些数学思想方法?A CB ac b。
初中数学 导学案:直角三角形的性质和判定
课题:直角三角形的性质和判定(Ⅱ)(1)【学习目标】1.了解勾股定理的发现过程,掌握勾股定理的内容,会用面积法证明勾股定理。
2.会简单的应用勾股定理。
【学习重点】勾股定理的内容及证明。
【学习难点】勾股定理的证明【学习过程】一、知识链接(用学过的知识完成下列填空)①含有一个的三角形叫做直角三角形.②已知Rt△ABC中的两条直角边长分别为a、b ,则S△ABC= .③已知梯形上下两底分别为a和b,高为(a+b),则该梯形的面积为 .④完全平方公式:(a±b)2= .⑤在Rt△ABC中,已知∠A=30°,∠C=90°,直角边BC=1,则斜边AB = .二、自主学习1、如图1-9,在方格纸上(设小方格边长为单位1) 画一个顶点都在格点上的直角三角形,使其两直角边分别为3、4,量出这个直角三角形斜边的长度.合作探究2、在方格纸上,以图1-9 中的Rt△ABC的三边为边长分别向外作正方形,得到三个大小不同的正方形,如图1-10,那么这三个正方形的面积S1,S2 ,S3 之间有什么关系呢?3、如图1-11,任作一个Rt△ABC,∠C= 90°,若BC= a,AC= b,AB= c,那么a2 + b2 = c2是否成立呢?三、当堂检测CABD1、在Rt △ABC 中,∠C=90°,①若a=5,b=12,则c=___________;②若a=15,c=25,则b=___________;③若c=61,b=60,则a=__________;④若a ∶b=3∶4,c=10则S Rt△ABC =________。
2、一个直角三角形中,两直角边长分别为3和4,下列说法正确的是( )A .斜边长为25B .三角形周长为25C .斜边长为5D .三角形面积为203、如图,已知在△ABC 中,CD ⊥AB 于D ,AC =20,BC =15,DB =9。
(1)求DC 的长。
(2)求AB 的长。
直角三角形全等的判定导学案
直角三角形全等的判定【教学目标】:1、掌握直角三角形全等的判定定理,并能应用定理解决与直角三角形有关的问题。
2、进一步掌握推理证明的方法,拓发展演绎推理能力,培养思维能力。
【教学重难点】:理解,掌握直角三角形全等的条件:HL .【自学指导】:一 、学生看P13---P14并思考一下问题:1、 “HL ”中“H ”代表什么?“L ”代表什么?“HL ”表示的是什么意思?2、 如何验证“HL ”可以判定两个三角形全等?3、 到目前为止,我们学习了几种三角形全等的判别方法?各是什么?那么对于直角三角形全等的判别方法有几种?4、 运用“HL ”证明直角三角形全等通常写成什么格式?通常写成下面的格式:在Rt △ABC 与Rt △DEF 中,∵⎩⎨⎧AC =DF BC =EF∴Rt △ABC ≌Rt △DEF (HL )二、自学检测:1.请判断满足下列条件的两个直角三角形是否全等,若不全等,在括号内打“×”,若全等,在括号内注明理由。
1.一个锐角和这个锐角的对边对应相等; ( )2.一个锐角及和锐角相邻的一直角边对应相等;( )3.一锐角与斜边对应相等; ( )4.两直角边对应相等; ( )5.两边分别相等; ( )6.斜边和一条直角边对应相等的两个三角形. ( )2.如图,CE ⊥AB ,DF ⊥AB ,垂足分别为E 、F ,(1)若AC//DB ,且AC=DB ,则△ACE ≌△BDF ,根据(2)若AC//DB ,且AE=BF ,则△ACE ≌△BDF ,根据(3)若AE=BF ,且CE=DF ,则△ACE ≌△BDF ,根据(4)若AC=BD ,AE=BF ,CE=DF 。
则△ACE ≌△BDF ,根据F E D C B A (5) 若AC=BD ,CE=DF (或AE=BF ),则△ACE ≌△BDF ,根据3.如图,AB ⊥BD ,CD ∥AB ,AB =CD ,点E 、F 在BD 上,且AE =CF .试说明AE ∥CF .三、师生共同探讨,总结:@@@思考:证明线段相等,证明两个角相等我们现在用什么方法?由三角形全等到线段相等,角相等,还可由角相等到线平行。
初中数学 导学案2:直角三角形的性质和判定
直角三角形的性质和判定(1)导学案学习目标:1.探索并掌握直角三角形两锐角互余。
2.掌握有两锐角互余的三角形是直角三角形。
3.探索并掌握直角三角形斜边上的中线等于斜边的一半.学习过程:一、知识链接:三角形内角和定理:三角形的内角和等于。
二、自主学习、探究新知探究1:直角三角形ABC可表示为:(1)已知,在 ABC中,∠B=90°,那么∠A+∠C= 。
由此得出:直角三角形的性质定理1:。
(2)已知,在 ABC中,∠A+∠C=90°,那么∠B=由此得出:直角三角形的判定定理:。
探究2:自学课本第一节。
由此得出:直角三角形的性质定理2探究3:直角三角形中,如果有一个锐角等于30°,那么它所对的直角边为什么等于斜边的一半。
Rt △ABC 中,∠A=30°,BC 为什么会等于12AB ?(提示:取AB 的中点D ,连结CD ) 证明:取AB 的中点D ,连结CD 则AD=BD ( )因为 CD 为Rt △ABC 斜边的中线所以 ( )又因为 ∠A=30°所以∠B=所以 △CDB 为 三角形得出结论:三、展示提升:完成课本练习四、达标检测(1)在直角三角形中,有一个锐角为52°,那么另一个锐角度数(2)在Rt △ABC 中,∠C=90°,∠A -∠B =30°,那么∠A= ,∠B= 。
(3)在△ABC 中,∠ACB=90°,CE 是AB 边上的中线,那么与CE 相等的线段有_________,与∠A 相等的角有_________,若∠A=35°,那么∠ECB= _________。
(4)在△ABC 中,△C=90°,∠B=15°,DE 垂直平分AB ,垂足为点E ,交BC 边于点D,BD=16cm ,则AC 的长为______(5)如图在△ABC 中,若∠BAC=120°,AB=AC,AD ⊥AC 于点A ,BD=3,则BC=______.(6) 如图,在△ABC 中,∠ACB=90°,CD 是斜边AB 上的高,那么,与 ∠B 互余的角有 ,与∠A 相等的角有 ,与∠B 相等的角有 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
义务教育 八年级 数学(华师版) 课型 新授 主备人 赵艳华 审核: 年级主任: 使用时间 2013 年 12 月 6 日
NO.35直角三角形的判定
【学习目标】
1.掌握直角三角形的判定条件,并能进行简单运用.
2.经历探索直角三角形的判定条件的过程,理解勾股定理.
3.激发学生解决问题的愿望,体会勾股定理逆向思维所获得的结论,明确其应用范围和实际价值.
【学习重点】:理解和应用直角三角形的判定方法 【学习难点】:.运用直角三角形判定方法解决问题.
【预习案】
学法指导
1.勾股定理的逆定理具体内容是什么?
2.什么是勾股数?
预习点拨:认真阅读P112-P114的内容,完成P114的练习。
二、预习自测 (课件展示)
1、以下面每组中的三条线段为边的三角形中,是直角三角形的是( )
A 5cm ,12cm ,13cm
B 5cm ,8cm ,11cm
C 5cm ,13cm ,11cm
D 8cm ,13cm ,11cm ⊿ABC 中,如果三边满足关系2
BC =2
AB +2
AC ,则⊿ABC 的直角是( )
A ∠ C
B ∠A
C ∠B
D 不能确定 3、由下列线段组成的三角形中,不是直角三角形的是
( )
A a=7,b=25,c=24
B a=2.5,b=2,c=1.5
C a= ,b=1,c=
D a=15,b=20,c=25 4、三角形的三边长a 、b 、c 满足 ,则此三角形是( )
A. 直角三角形
B.锐角三角形
C.钝角三角形
D.等腰三角形
探究部分:
自主探究
1.勾股定理的逆定理
如果三角形的三边长a,b,c ,当 时,那么这个三角形是直角三角形,且边c 所对的角为直角。
2.能够成为直角三角形三条边长的 ,称为勾股数。
3试画出三角形的三边长度分别为如下数据的三角形,看看它们是一些什么样的三角形: (1)3cm, 4cm, 5cm (2)5cm , 13cm , 12cm (3)45mm ,60mm ,75 mm
例1,设三角形三边长分别为下列各组数.试判断各三角形是否是直角三角形.
(1)7,24,25; (2)12,35,37; (3)13,11,9
教师教学设计
教师姓名 任教班级
、
453
2
ab c b a 2)(22=-+
阳光高效课堂导学稿
例2:如图,已知AB=4,BD=12,CD=13,CA=3,AB ⊥AC ,求证:
△ABC 是直角三角形。
例 3.已知a,b,c 是△ABC 三边的长,且满足关系式
2
22=-+--b a b a c ,求△ABC 的形状。
当堂检测
1.下列各组数是三角形的三边长,不能构成直角三角形的是( )
A.3,4,5
B.5,12,13
C.7,24,25
D.12,15,20
2.三角形的三边长分别为6,8,10,则最短边上的高为( )
A. 6
B. 4.5
C. 2.4
D. 8
3..三角形的三边长为a, b, c ,且满足(a+b)2
-c 2
=2ab ,
则此三角形是( )
A. 锐角三角形
B.直角三角形
C. 钝角三角形
D.等边三角形
训练案
1、若一个三角形的三边长分别是m+1,m+2,m+3,则当m= ,它是直角三角形。
2、在⊿ABC 中,若5,7,252
222==-=+c b a b a ,则最大
边上的高为 。
3、一个三角形的三边之比为13:12:5,且周长为60cm ,
则它的面积是 2
cm 。
4、三角形的两边长为5和4,要使它成为直角三角形,则第三边的平方为 。
5、小明画了一个如图所示的四边形,其中AB=4,BC=12,CD=13,DA=3,∠A=
90,你能求出四边形ABCD 的面积吗?
6.已知在⊿ABC 中,AB=AC=5,BC=6,求⊿ABC 的面积。
教师教学设计
教师姓名 任教班级
A
C
D
B
A
C
B
D。
