拉曼光谱1
激光拉曼光谱-1详解

2021/4/1
28
Raman and Infrared Spectra of H-C≡C-H
Asymmetric C-H Stretch
Symmetric C-H Stretch C≡C Stretch
2021/4/1
29
2941,2927cm-1 ASCH2 2854cm-1 SCH2 1444,1267 cm-1 CH2
Stocks lines
anti-Stockes lines
2021/4/1
12
3.拉曼光谱的经典解释 拉曼光谱与分子极化率的关系
分子在静电场E中,极化感应偶极距p
p= αE α为极化率
诱导偶极矩与外电场的强度之比为分子极化率 分子中两原子距离最大时,α也最大 拉曼散射强度与极化率成正比例关系
32
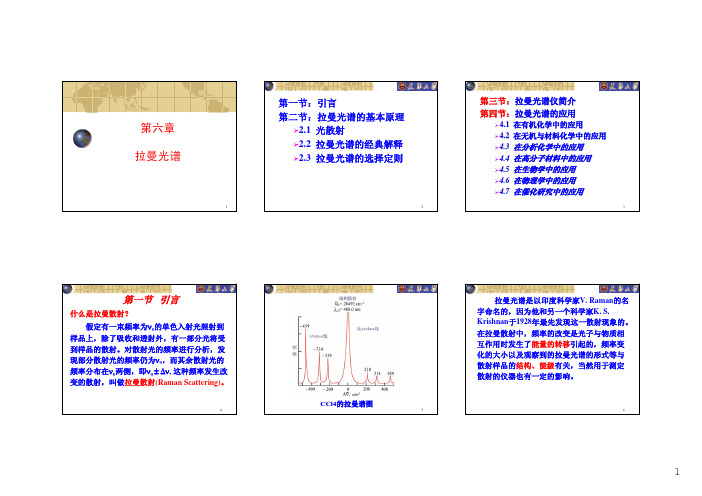
Infrared and Raman Spectrum of CCl4
Infrared spectrum
776 cm-1
314 cm-1
Raman spectrum
463 cm-1 219 cm-1
2021/4/1
33
红外光谱:基团; 拉曼光谱:分子骨架测定;
2021/4/1
34
2.无机化学中的应用
延德尔散射 弹性散射
瑞利散射
I与λ无关 I正比于1/λ4
2021/4/1
8
2.基本理论
2021/4/1
λ
λ
拉 曼
增减散 大小射
变
λ
样
透过光λ不变
品
池
瑞 利
散
射
λ
不 变
9
最低激发 E1 电子能级 E0
激发虚态
第五章拉曼光谱
1第六章拉曼光谱2第一节:引言第二节:拉曼光谱的基本原理 2.1 光散射2.2 拉曼光谱的经典解释 2.3 拉曼光谱的选择定则3第三节:拉曼光谱仪简介第四节:拉曼光谱的应用4.1 在有机化学中的应用 4.2 在无机与材料化学中的应用 4.3 在分析化学中的应用 4.4 在高分子材料中的应用 4.5 在生物学中的应用 4.6 在物理学中的应用 4.7 在催化研究中的应用4第一节引言什么是拉曼散射?假定有一束频率为ν0的单色入射光照射到样品上,除了吸收和透射外,有一部分光将受到样品的散射。
对散射光的频率进行分析,发现部分散射光的频率仍为ν0,而其余散射光的频率分布在ν0两侧,即ν0 ±∆ν, 这种频率发生改变的散射,叫做拉曼散射(Raman Scattering)。
5CCl4的拉曼谱图6拉曼光谱是以印度科学家V. Raman 的名字命名的,因为他和另一个科学家K. S.Krishnan 于1928年最先发现这一散射现象的。
在拉曼散射中,频率的改变是光子与物质相互作用时发生了能量的转移引起的,频率变化的大小以及观察到的拉曼光谱的形式等与散射样品的结构、能级有关,当然用于测定散射的仪器也有一定的影响。
7拉曼光谱的用途:主要用于分子内部转动和振动跃迁的研究。
拉曼散射频率的变化值±∆ν与分子内部的转动和振动能级密切相关。
分子转动能级和几乎所有振动能级的拉曼波数都在0~3500 cm -1之间,当采用400~600 nm 范围任一波长的光作为辐射源,拉曼光谱都处于可见光区域。
用拉曼光谱研究分子的转动和振动,只需一种色散系统和一种探测器。
8在红外光谱中,有些振动模是红外非活性的,如CO 2的对称振动模,这些振动频率可以用拉曼光谱测得,拉曼光谱和红外光谱具有互补性,它们是研究振动和转动的最有效方法,两者缺一不可。
9拉曼光谱的特点:波长位移在中红外区。
有红外及拉曼活性的分子,其红外光谱和拉曼光谱近似。
拉曼光谱拉曼谱是以印度物理学家拉曼(C.V.Raman)命名的一种散射光谱

拉曼光谱拉曼谱是以印度物理学家拉曼(C.V.Raman)命名的一种散射光谱.1928年拉曼和克利希南(K.S.Krishnan)在研究单色光在液体中散射时,不仅观察到与入射光频率相同的瑞利散射,而且还发现有强度很弱,与入射光频率不同的散射光谱.同年,前苏联的曼迭利斯塔姆和兰兹贝尔格在石英的散射中也观察到了这一现象.这种新谱线对应于散射分子中能级的跃迁,为研究分子结构提供了一种重要手段,引起学术界极大兴趣,拉曼也因此荣获1930年的诺贝尔物理学奖.但由于拉曼光谱很弱,受当时光源和检测手段的限制,它的发展曾停滞了一段时期.19世纪60年代激光技术的出现使拉曼光谱得以迅速发展,再加上近年来发展的高分辨率的单色仪和高灵敏度的光电检测系统,使拉曼光谱学进入崭新的阶段,应用领域遍及物理、化学、生物、医学等.利用各种类型的材料作为散射物质,几乎都可能得到相应的拉曼谱.这种新型的实验技术正日益显示其重要意义。
通过实验了解激光拉曼光谱仪的基本结构与工作原理;了解拉曼散射的原理及其在现代科学研究中的作用;测量典型的CCl4拉曼散射谱。
一、实验原理当一束单色光入射在固、液或气态介质上时,从介质中有散射光向四面八方射出.散射光中较强的是瑞利散射,其频率与入射光频率ν0相同,其强度和数量级约为入射光强的10-4~10-3.除瑞利散射外还有拉曼散射,拉曼散射的散射光频率ν与入射光频率相比有明显的变化,即ν=ν0±|Δν|,其强度数量级约为瑞利散射的10-8-10-6,最强的也只是瑞利散射的10-3.瑞利线ν0长波一侧出现的散射线ν=ν0-|Δν|称为斯托克斯(Stokes)线,又称为红伴线;把短波一侧出现的ν=ν0+|Δν|称为反斯托克斯(anti-Stokes)线,又称紫伴线.斯托克斯线比反斯托克斯线通常要强一些.散射光频率ν相对于入射光频率ν0的偏移,即拉曼光谱的频移Δν,是拉曼谱的一个重要特征量.散射线的±|Δν|相对于瑞利线是对称的,而且这些谱线的频移Δν不随入射光频率而变化,只决定于散射物质的性质.换句话说,在不同频率单色光的入射下都能得到类似的拉曼谱.拉曼散射是由分子振动,固体中的光学声子等元激发与激发光相互作用产生的非弹性散射。
拉曼光谱的原理及应用

拉曼光谱的原理及应用拉曼光谱是将激发的样品通过分析散射光的频率而得到的一种光谱技术。
它是基于拉曼散射效应,即光与物质相互作用后,光的频率发生变化而产生散射光谱。
拉曼光谱的原理及应用如下。
原理:拉曼散射是指当物质被激发后,光通过与物质分子或晶体相互作用而发生频率改变的现象。
当光与物质相互作用后,其中一部分光的频率会发生变化,其频率的差值与物质分子或晶体的振动和转动能级有关。
这种频率发生变化的光被称为拉曼光,而拉曼光谱则是分析和记录这种光的技术和结果。
应用:1.化学分析:拉曼光谱可以用于分析化学物质的成分、结构和浓度。
不同化学物质的分子结构和振动能级不同,因此它们与光相互作用后会产生不同的拉曼光谱。
通过对比样品的拉曼光谱与数据库中已知物质的拉曼光谱,可以确定样品的成分和结构。
2.材料科学:拉曼光谱在材料科学中有广泛的应用。
例如,可以通过拉曼光谱来分析材料中的应变、晶格缺陷、晶体结构及化学组成等。
由于拉曼光谱对物质的表面敏感性较强,因此它在研究纳米材料和杂质掺杂材料的结构和性质方面特别有用。
3.生物医学:拉曼光谱在生物医学领域有多种应用。
例如,可以使用拉曼光谱来识别肿瘤组织与正常组织的差异,从而在肿瘤诊断和治疗中发挥重要作用。
此外,拉曼光谱还可以用于分析生物分子的结构变化和相互作用,以及研究细胞功能和代谢过程。
4.环境分析:拉曼光谱可以用于环境样品的分析和监测,例如水质、大气污染物、土壤和废物中的化学物质。
通过拉曼光谱技术,可以对这些环境样品中的有机和无机成分进行定性和定量分析,从而提供可靠的环境数据。
5.药品质量检测:拉曼光谱可用于对药物的质量进行快速和准确的检测。
通过对药物样品的拉曼光谱进行分析,可以确定药物的成分、结构和纯度,以保证药物的质量和疗效。
总结:拉曼光谱技术以其非破坏性、快速、准确的特点在各个领域得到广泛应用。
基于拉曼散射现象,拉曼光谱能够提供关于样品成分、结构和相互作用的信息。
它已成为化学、材料科学、生物医学、环境分析和药品质量检测等领域中不可或缺的分析工具,为科研和工业应用提供了重要支持。
拉曼光谱

• 拉曼光谱在化学研究中的应用
拉曼光谱在有机化学方面主要是用作结构鉴定和分 子相互作用的手段,它与红外光谱互为补充,可以鉴别特 殊的结构特征或特征基团。拉曼位移的大小、强度及拉曼 峰形状是鉴定化学键、官能团的重要依据。利用偏振特性, 拉曼光谱还可以作为分子异构体判断的依据。在无机化合 物中金属离子和配位体间的共价键常具有拉曼活性,由此 拉曼光谱可提供有关配位化合物的组成、结构和稳定性等 信息。另外,许多无机化合物具有多种晶型结构,它们具 有不同的拉曼活性,因此用拉曼光谱能测定和鉴别红外光 谱无法完成的无机化合物的晶型结构。
发展前景
• 激光技术 现在国际上推出的从事非线性光谱研究的超快(飞秒或皮 秒)激光器,技术上已经达到比较成熟地步,可以成套购 买,也较稳定。非线性拉曼光谱技术已经在生命科学领域 研究中发挥它的独特和重要作用。例如,美国哈佛大学的 谢晓亮教授在开拓并运用相干反斯托克斯拉曼光谱显微学 (CARS Microscopy)研究活细胞内部三维结构方面取得 一系列重要成果。高质量的超快激光器还推动了另一个极 具前途的表面光谱技术,就是合频(SFG)技术的发展, 它作为具有独特的界面选择性的非线性光谱方法,已经在 界面和表面科学、材料乃至生命领域研究中发挥着越来越 重要的作用。
拉曼光谱
• 拉曼光谱(Raman spectra),是一种散射 光谱。拉曼光谱分析法是基于印度科学家 C.V.拉曼(Raman)所发现的拉曼散射效 应,对与入射光频率不同的散射光谱进行 分析以得到分子振动、转动方面信息,并 应用于分子结构研究的一种分析方法。最 常用的红外及拉曼光谱区域波长是 2.5~25μm。(中红外区)
拉曼光谱的应用 • 拉曼光谱技术以其信息丰富,制样简单,水的干 扰小等独特的优点,在化学、材料、物理、高分 子、生物、医药、地质等领域有广泛的应用。 • 通过对拉曼光谱的分析可以知道物质的振动转动 能级情况,从而可以鉴别物质,分析物质的性质. 例如:天然鸡血石和仿造鸡血石的拉曼光谱有本 质的区别,前者主要是地开石和辰砂的拉曼光谱,后 者主要是有机物的拉曼光谱,利用拉曼光谱可以区 别二者;鉴别毒品;利用拉曼光谱可以监测物质 的制备;监测水果表面残留的农药。 • 激光拉曼光谱法的应用有以下几种:在有机化学 上的应用,在高聚物上的应用,在生物方面上的 应用,在表面和薄膜方子对光子的一种非弹性散射效应。当用一定 频率的激发光照射分子时,一部分散射光的频率和入射光 的频率相等。这种散射是分子对光子的一种弹性散射。只 有分子和光子间的碰撞为弹性碰撞,没有能量交换时,才 会出现这种散射。该散射称为瑞利散射。还有一部分散射 光的频率和激发光的频率不等,这种散射成为拉曼散射。 Raman散射的几率极小,最强的Raman散射也仅占整个 散射光的千分之几,而最弱的甚至小于万分之一。 • 处于振动基态的分子在光子的作用下,激发到较高的、不 稳定的能态(称为虚态),当分子离开不稳定的能态,回 到较低能量的振动激发态时,散射光的能量等于激发光的 能量减去两振动能级的能量差。
拉曼光谱

拉曼光谱(Raman spectra),是一种散射光谱。光照射到物质上发生弹性散射和非弹性散射.弹性散射的散射光是与激发光波长相同的成分,非弹性散射的散射光有比激发光波长长的和短的成分,统称为拉曼效应。拉曼效应是光子与光学支声子相互作用的结果。
拉曼光谱-原理 拉曼效应起源于分子振动(和点阵振动)与转动,因此从拉曼光谱中可以得到分子振动能级(点阵振动能级)与转动能级结构的知识。用虚的上能级概念可以说明了拉曼效应:
c.一般情况下,斯托克斯线比反斯托克斯线的强度大。这是由于Boltzmann分布,处于振动基态上的粒子数远大于处于振动激发态上的粒子数。
.24H-SiC
图4为橙色区域(纵切片上边缘的三角形区域)SiC晶体的显微拉曼光谱图。分析得到各拉曼峰对应的声子模及其简约波矢、对称性分别为:205.8cm-1(FTA,x=0.5,E2),267.1cm-1(FTA,x=1,E1);612.0cm-1(FLA,x=1,A1);778.8cm-1(FTO,x=0.5,E2),796.3cm-1(FTO,x=0,E1);970.0cm-1(LOPC模)。4H-SiC的六方百分比为0.5。简约波矢x=0.5的FTA模(205.8cm-1)和FTO模(778.8cm-1)的强度分别大于其它简约波矢的FTA和FTO模的强度,且其它拉曼峰也与4H-SiC的文献报道值[5]相符,可以判断橙色区域为4H-SiC。值得注意的是,拉曼光谱中出现了187.5cm-1的拉曼峰,这是由于4H-SiC简约波矢x=0.5的FTA模峰形展宽造成的,说明4H-SiC的结晶质量一般[5]。实验测得橙色区域4H-SiC的导电类型也为n-型,说明载流子主要为自由电子。970.0cm-1的拉曼峰为4H-SiC的LOPC模,与本征4H-SiC的FLO模(964.0cm-1,x=0,A1)[Байду номын сангаас]相比较,其拉曼位移值仅仅增大了6.0cm-1;且LOPC模的强度仍可与778.8cm-1(FTO,x=0.5)的强度相比拟,这说明橙色区域4H-SiC晶体中的载流子(主要为自由电子)浓度不高[8]。这说明在掺氮6H-SiC单晶的生长条件下,4H-SiC与6H-SiC的掺氮效应存在明显差异。
拉曼光谱 归一化
拉曼光谱归一化
拉曼光谱的归一化处理是对原始光谱数据进行预处理的一种方法,目的是消除光谱仪器的误差、光强波动等因素对测量结果的影响,提高光谱数据的可比性和可靠性。
以下是一些关于拉曼光谱归一化的方法:
1.谱线归一化:将拉曼光谱的每一个波长对应的峰强度进行归一化处理,即将每个峰的最大强度归一化为1,从而使不同实验条件下获得的拉曼光谱具有可比性。
2.谱带归一化:将拉曼光谱的每一个谱带对应的峰强度进行归一化处理,即将每个谱带的总强度归一化为1,以便更好地比较不同实验条件下同一物质的不同拉曼光谱。
3.全光谱归一化:将整个拉曼光谱的强度进行归一化处理,即将整个光谱的总强度归一化为1,以便比较不同实验条件下不同物质的拉曼光谱。
总之,对拉曼光谱进行归一化处理是一种非常重要的预处理步骤,可以提高测量结果的准确性和可靠性,有助于更好地理解和分析物质的结构和性质。
拉曼光谱和荧光光谱的区别
拉曼光谱和荧光光谱的区别拉曼光谱和荧光光谱是分析物质结构和特性的重要手段,在光谱学领域具有广泛的应用。
尽管两者都属于光谱技术,但它们在原理和应用方面存在一些显著的区别。
以下是拉曼光谱和荧光光谱的区别:一、原理1. 拉曼光谱:拉曼光谱是指当物质受到激发光源照射时,分子通过与光子相互作用而发生的散射现象。
在拉曼散射中,被测物质中的分子在与入射光相互作用后,其散射光的频率会发生微弱的变化。
这种频率变化被称为拉曼位移,可以提供关于物质的结构和化学成分的信息。
2. 荧光光谱:荧光光谱是指物质受到激发光照射后,在激发能级上的电子跃迁到低能级并发射光子的过程。
荧光光谱的特点是物质吸收能量后会发射出具有较长波长的光。
物质的荧光光谱可以提供关于物质的结构、浓度和环境等信息。
二、激发方式1. 拉曼光谱:拉曼光谱的激发方式通常采用单色激光束进行。
入射的单色光可以通过光栅或干涉仪进行分光,以获得更高的分辨率和更准确的谱线信息。
2. 荧光光谱:荧光光谱的激发方式通常是使用紫外线或可见光照射样品。
被激发的样品会吸收能量并发射出具有较长波长的荧光光。
三、检测方法1. 拉曼光谱:拉曼光谱通常采用光散射的方式进行检测。
被测样品散射的光经过分光装置后,由光谱仪进行检测和记录。
2. 荧光光谱:荧光光谱的检测通常采用荧光光谱仪进行。
荧光光谱仪具有一个激发源、一个样品舱和一个探测器,用于检测样品发射的荧光光。
四、应用领域1. 拉曼光谱:拉曼光谱广泛应用于材料科学、生物化学、环境监测等领域。
它可以用于分析化学物质、溶液中的有机化合物、无机物等,以及表面增强拉曼光谱和显微拉曼光谱等高级技术。
2. 荧光光谱:荧光光谱在生物医学、光电子学、环境监测等领域得到广泛应用。
例如,荧光光谱可以用于分析药物、检测环境中的有毒物质、研究生物分子的相互作用等。
综上所述,拉曼光谱和荧光光谱在原理、激发方式、检测方法和应用领域上都存在一定的差异。
这些光谱技术在不同领域的研究和应用中发挥着重要的作用,为我们深入了解物质的结构和性质提供了有力的工具。
拉曼光谱
拉曼光谱(RAMAN SPECTRA)的原理(续)
Mid IR Stokes Raman Rayleigh Anti-Stokes Raman Fluorescence
红外 斯托克斯拉曼
瑞利散射 反斯托克斯拉曼
荧光
Real States 真实能级
Virtual State 虚能级
Vibrational States 振动能级 i
的研究员充满吸引力。
拉曼光谱仪的主要厂商及相关仪器
美国PerkinElmer公司的RamanStation 400系列拉曼光 谱仪
全球唯一的运用中阶梯光栅及二维面阵CCD 检测器组合成的二维色散型拉曼光谱仪,集 中了宽波段,高分辨率及检测速度快等特点, 摒弃了传统的获取高分辨率图谱所惯用的多 次测量不同谱带再进行拼接的方法,可在一 秒钟内获取覆盖整个波段的高分辨率拉曼图 谱。 分光系统采用中阶梯光栅技术,不含任何可 移动元件,保证系统的高度稳定性 高灵敏度二维CCD检测器,使得整个波段的 数据同时获取,避免了光谱失真 采用超稳定785nm的激光光源,减弱了荧光 背景的产生。
拉曼光谱(RAMAN SPECTRA)的原理(续)
设散射物分子原来处于基电子态,振动能级如图所示。 当受到入射光照射时,激发光与此分子的作用引起的 极化可以看作为虚的吸收,表述为电子跃迁到虚态 (Virtual state),虚能级上的电子立即跃迁到下能级而 发光,即为散射光。设仍回到初始的电子态,则有如 图所示的三种情况。因而散射光中既有与入射光频率 相同的谱线,也有与入射光频率不同的谱线,前者称 为瑞利线,后者称为拉曼线。在拉曼线中,又把频率 小于入射光频率的谱线称为斯托克斯线,而把频率大 于入射光频率的谱线称为反斯托克斯线。
--拉曼光谱简介
反斯托克斯线 h(v0+v1)
(v0+v1)
v=1 hv1
v=0
3
拉曼光谱的基本原理
Raman spectrum of CCl4
处于基态的分子总是占绝大多数,所以斯托克斯线强度远远高于反斯托克斯线 强度。斯托克斯线与反斯托克斯线的强度比可用这样一个式子表示:
I反斯托克斯
/ I斯托克斯
(0 (0
Raman Intensity
Over-The-Counter Tablet, 785 laser
0
3000
2500
2000
1500
1000
500
Raman shift (cm-1)
31
Highly fluorescent sample:Poly(9-vinylcarbazole)
32
镜头的选择
FT-IR Transmission Spectrum
80 60 40 20
4 Raman Spectrum
3 2 1
4000
3000
2000
1000
9
项目
红外光谱
拉曼光谱
分子结构与光 谱活性
分子结构测定 范围
测试对象与品 种
极性分子及基团通常是红 非极性分子及基团通常是
外活性的
拉曼活性的
适于分子端基的测定
50 0 -0
Hale Waihona Puke 1 4001 200
1 000 cm-1
8 00
6 00
30 25 20 15 10 5 0
24
10 micron depth
Raman Intensity
17 micron depth
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例:线形分子CO2 ,有四个( 3N-5 ) 简正振动模。每个振动过程中极化率和偶 极矩的变化示于下图。
例:非线形分子SO2 ,有三个( 3N-6 ) 简正振动模。每个振动过程中极化率和 偶极矩的变化示于下图。
3.互不相容原理 具有对称中心的分子:
红外活性的振动模,拉曼非活性 拉曼活性的振动模,红外非振动 红外+拉曼→全部振动谱 一般有: 同核双原子分子: 非极性晶体: 异核双原子分子: 极性晶体:
I as Is
= (ν
(ν 0 +ν k ) 4
0
−ν k )
4
exp(−hν k / kT )
斯托克斯线和反斯托克斯线对称分布在瑞利线两侧,且反斯克 斯线一般较弱,通常我们只测斯托克斯线。
五 振动自由度和光谱选律
1.振动自由度 每个原子的运动可以用固定坐标系的直角 坐标(x,y,z )表示,如果分子中有N个原子,就 需要3N 个(x,y,z )表示,即具有3N个自由度。 分子的三个平动和三个转动自由度对分子 的振动无贡献,因而非线性分子有3N-6振动自 由度
当一束光照射到介质上时,大部分光被介质反射或 透过介质,另一小部分的光则被介质向四面八方散射 早晚东西方的天空中出现红色霞光,晴朗的天 空呈蓝色,广阔的大海呈深兰色等,都属于光散射 现象 早在1871年,这种现象就可以用大气和海水对太阳 光的瑞利散射予以解释,瑞利散射的强度与入射光波 长的四次方成反比(I∝1∕λ4)。
类似的过程也可能发生在处于激发态E 类似的过程也可能发生在处于激发态Eν = 1 的激发而跃迁到受激虚态, 的分子受入射光子hυ0的激发而跃迁到受激虚态, 同样因为虚态是不稳定的而立即跃迁到激发态 此过程对应于弹性碰撞, Eν = 1,此过程对应于弹性碰撞,跃迁频率等于 为瑞利散射。 υ0,为瑞利散射。 处于虚态的分子也可能跃迁到基态E 处于虚态的分子也可能跃迁到基态Eν = 0, 此过程对应于非弹性碰撞, 此过程对应于非弹性碰撞,光子从分子的振动 或转动中得到部分能量, 或转动中得到部分能量,跃迁频率等于 ),为拉曼散射的反斯托克斯线 (υ0+υ1),为拉曼散射的反斯托克斯线
I ∝
..
2
P
,
Ias Is
∝ (ν −ν )4 ≈1
0 k
(ν0 +νk )
4
式中Ias 为反斯托克斯线强度,Is斯托克斯线 强度。通常ν0>>νk则反斯托克斯线强度和斯托 克斯线强度相当,与实验结果不符。
CCl4的拉曼光谱
四 拉曼散射的量子理论
按照量子理论,频率为υ0的单色光可以视 为具有能量为hυ0的光子,h是普朗克常数。当 光子作用于分子时,可能发生弹性和非弹性两 种碰撞. 在弹性碰撞过程中,光子与分子之间不发生 能量交换,光子仅仅改变其运动方向,而不改 变其频率,这种弹性散射过程对应于瑞利散射;
1923年,斯迈克尔(Smekal)从理论上 预测,当频率为υ0的入射光经试样散射 后,散射光中应含有υ0±Δυ的辐射。
拉曼散射υ0-Δυ
υ0
斯托克斯线
样 品
瑞利散射
υ0
拉曼散射 υ0+Δυ 反斯托克斯线
1928年,印度物理学家拉曼第一次经 实验在液态苯中发现了这种效应,因 而称作拉曼效应(拉曼散射、 拉曼光 谱) 同时前苏联及法国的学者也相继独 立地在实验中观察到这种效应。
斯托克斯和反斯托克斯线与瑞利线之间的频率差分别为:
υ0-(υ0-υk)=υk和υ0-(υ0+υk)=-υk
其数值相等,符号相反,说明拉曼谱线对称地分布在瑞利线的 两侧。 根据玻尔兹曼定律,常温下处于基态Eν = 0的分子数比处于激 发态Eν = 1的分子数多,遵守玻尔兹曼分布,因此斯托克斯线的强 度(Is)大于反斯托克斯线的强度(Ias),和实验结果相符。
这里Qk0是简正坐标的振幅,νk是分子的简 正振动频率,单色光的电场可以写成: E=E0cos(2πν0t) 式中,E0是单色光的振幅,ν0是单色光频率;
只考虑一个分量,有 P= αk E =α0E0cos(2πν0t)+αk’E0Qk0cos(2πν0t )cos(2πνkt) =α0E0cos(2πν0t) + αk’E0 Qk0{cos[2π(ν0-νk)t]+cos[2π(ν0+νk)t]}/2
α ij = (α ) + ∑ (
ij 0
k
∂α ij ∂Q k
) 0 Qk
式中(αij)0 是分子在平衡位置的αij 值,通常 是不变的,Qk,…是分子振动的简正坐标,这 里已略去二次项及高次项。为简单起见,只 考虑一个(第k个)简正振动
假定分子的振动是简谐振动, 相位因子等于 0,于是有:
Qk = Qk 0 cos(2πν κ t )
光谱选律的直观说法是,如果某一简正振动对应的分 子偶极矩变化不为零,即 (∂∂QP )0 ≠ 0则是红外活性的;反 之,是红外非活性的。
k
( ∂Q k
∂ α ij
如果某一简正振动对应于分子的感生极化率变化不为零,即 ) ≠ 0 则是拉曼活性的,反之,是拉曼非活性的
0
如果某一简正振动对应的分子偶极矩和感生极化率同时发 生变化(或不变化),则是红外和拉曼活性的(或非活性的)
拉曼散射 斯托克斯 线
hυ0 hυ0
hυ0 hυ0
h(υ 0 –υk)
振动能极
瑞利散射
拉曼散射 反斯托克斯线
图3 拉曼和瑞利散射能级图
处于基态 Eν = 0的分子受入射光hυ0的激发而 跃迁到一个受激虚态。因为这个受激虚态是不稳 定的能级(一般不存在),所以分子立即跃迁到 基态Eν = 0。此过程对应于弹性碰撞,跃迁辐射的 频率等于υ0,为瑞利散射线。 处于虚态的分子也可能跃迁到激发态Eν = 1, 此过程对应于非弹性碰撞, 跃迁频率等于 (υ0-υk),光子的部分能量传递给分子,为拉曼 散射的斯托克斯线。
在非弹性碰撞过程中,光子与分子之 间发生能量交换,光子不仅改变其运动方 向,同时光子的一部分能量传递给分子, 转变为分子的振动或转动能,或者光子从 分子的振动或转动得到能量。 光子得到能量的过程对应于频率增 加的反斯托克斯拉曼散射;光子失去能 量的过程对应于频率减小的斯托克斯拉 曼散射。
虚态能极 h(υ 0 -υk) Eυ=1 Eυ=0 hυk
黄昆先生 黄昆
1954年在英国出版与波恩合著的名著 《晶格动力学理论》,成为声子物理和拉 曼散射的经典理论著作。 1988建立起超晶格拉曼散射理论 2002年获国家科技奖。
在拉曼效应被发现后的十余年间,共发表了 约2000篇研究论文,报道了约4000个化合物的拉 曼光谱图。 尽管当时拉曼光谱在实验技术上有很多困 难,例如拉曼散射光的强度只有瑞利散射强度 的10-3 ~10-6,但与刚发展起来的红外光谱在实验 技术上的困难相比,拉曼光谱仍不失为一种方 便易行的测试方法。 1946年前后,商品化的红外分光光度计问世, 使红外光谱测试技术的方便程度大大超过了拉 曼光谱,这种状态一直持续到50年代末期。
(1)纯化样品 (2)强激光长时间照射样品
虽然无法解释为什么用激光长时间照射样品 能够有效的消除荧光干扰,但在很多情况下用 这种方法确实能达到消除荧光干扰的效果。
(3)加荧光灭剂
有时在样品中加入少量荧滤灭剂,如硝基 苯,KBr, AgI等 ,可以有效地淬灭荧光干扰。
(4)利用脉冲激光光源
当激光照射到样品时,产生荧光和拉曼散 射光的时间过程不同,若用一个激光脉冲照射 样品,将在10-11~10-13S内产生拉曼散射光,而荧 光则是在10-7∽10-9S后才出现
I as Is
= (ν
(ν 0 +ν )4
0
−ν )
4
exp(−hν / kT)
七 拉曼光谱的退偏比
一个确定取向的分子,在偏振的入射光 的作用下,所产生的拉曼散射也是完全偏 振的,由于液体和气体样品的分子取向是 无规的,因此完全偏振的入射光所产生的 散射光则不一定是完全偏振的,称做散射 光的退偏,为了描述拉曼谱带的偏振性能 变化的程度,引进了退偏比的概念。
Z
Ez E’z
样 品
Y
E’y
入射光
Iz
检偏器
探测器
X
退偏比的测量-Iz
Z
Ez E’z
样 品
Y
E’y
入射光
Iy
检偏器
探测器
X
退偏比的测量-Iy
设X,Y,Z为空间坐标系,分子固定在坐标系 的原点,偏振方向在Z轴 (E Z ) 的入射光沿-Y轴方 向入射,在X轴方向观测散射光(见图 ),散射 光中不仅含有沿Z轴也含有沿Y轴(E Z' , E Y' )方向的 偏振分量,一般来说散射光中的这两个偏振分 量的强度不相等。这些分量的强度可以分别从 实验上测得。在散射光处插进一个光学装置— 检偏器,按其取向透过一个偏振分量,然后转 90º透过另一个偏振分量。
红外非活性 红外非活性 红外活性 红外活性
拉曼活性 拉曼活性 拉曼非活性 拉曼具体分析
ห้องสมุดไป่ตู้
六.发光(荧光)的抑制和消除
在拉曼光谱测试中,往往会遇到荧光 的干扰,由于拉曼散射光极弱,所以一旦 样品或杂质产生荧光,拉曼光谱就会被荧 光所淹没。通常荧光来自样品中的杂质, 但有的样品本身也可发生萤光,常用抑制 或消除萤光的方法有以下几种
拉 曼 光 谱
左 健
理化中心-213,3602814(O) zuoj@
拉曼光谱的发现与发展 光散射现象与拉曼光谱 拉曼光谱的经典理论及量子理论 光谱选律 发光(荧光)的抑制和消除 拉曼光谱的退偏比 晶体偏振谱的测量
晶格动力学基础 群论在振动光谱中的应用 拉曼光谱的实验装置 拉曼光谱的一些应用
60年代初期问世的激光技术给拉曼光谱带 来了新的生机 由于高分辨率,低杂色光的双联或三联光栅 单色仪,以及高灵敏度的光电接收系统(光电 倍增管和光子计数器)的应用,使拉曼光谱测 量达到与红外光谱一样方便的水平 和红外光谱相比,拉曼光谱有制样简单,水 的干扰小,可做活体实验等优点
