倍数含量筛法与恒等式(a b b a 1×=)的妙用
《化学计量在实验中的应用》-课时作业(含解析) (246)
第2节化学计量在实验中的应用第4课时暑假作业1、属于定量仪器的是()A. 蒸馏烧瓶B. 容量瓶C. 干燥器D. 分液漏斗2、实验室配制250mL 0.5mo1·L﹣1NaCl溶液,不需要用到的仪器是()A. 玻璃棒B. 酒精灯C. 胶头滴管D. 容量瓶3、配制一定体积、一定物质的量浓度的溶液,实验结果偏高影响的是( )A. 容量瓶中原有少量蒸馏水B. 溶解所用的烧杯未洗涤C. 定容时仰视观察刻度线D. 定容时俯视观察刻度线4、某学生配制了100 mL 1 mol/L的硫酸溶液.然后,对溶液浓度做精确测定,且测定过程中一切操作都正确.结果测得溶液的物质的量浓度低于1 mol/L.那么,在配制过程中,下列操作可能导致溶液浓度偏低的是()①量筒用蒸馏水洗净后立即用来量取浓硫酸②将浓硫酸在烧杯中稀释,转移到容积为100 mL的容量瓶中后,没有洗涤烧杯③在转移过程中用玻璃棒引流,因操作不慎有少量溶液流到了容量瓶外面④最后定容时,加水超过了刻度,马上用胶头滴管吸去多余的水,使溶液凹液面刚好与刻度线相切A.②③④B.③④C.①②③D.①②③④5、以下仪器,用蒸馏水洗净后便可立即使用而不.会对实验结果造成误差的是()①中和滴定用的锥形瓶②中和滴定用的滴定管③容量瓶④配制一定体积、一定物质的量浓度的NaOH溶液,用于称量的小烧杯⑤量筒(量取浓H 2SO 4用)A.①②⑤B.①③C.②④⑤D.①⑤6、将a %的某物质的水溶液加热蒸发掉m g 水(溶质不挥发,且蒸发过程中无溶质析出),所得溶液体积为V L ,溶质的质量分数为蒸发前的2倍.设溶质的相对分子质量为M ,则蒸发后所得溶液的物质的量浓度为( )A .mol/L 2VM maB .mol/L 100MV maC .mol/L 220MV maD .mol/L 50MVma 7、铜与1mol/L 的硝酸反应,如果NO 浓度下降0.2mol/L ,则溶液中c(H +)同时下降(溶液体积变化忽略不计)A .0.2mol·L1- B .0.4mol·L 1- C .0.6mol·L 1- D .0.8mol·L 1- 8、下列所得溶液的物质的量浓度等于0.1mol·L -1的是A .将0.1mol 氨充分溶解在1L 水中B .将10g 质量分数为98%的硫酸与990g 水混合C .将8g 三氧化硫溶于水并配成1L 溶液D .将0.1mol 氧化钠溶于水并配成1L 溶液 9、某学生的实验报告中有下列数据,其中合理的是 ( )①用托盘天平称取11.7g 氯化钠 ②用100mL 的量筒量取21.48mL 盐酸 ③用容量瓶配制216mL 1mol·L -1的氯化钠溶液 ④用酸式滴定管量取25.00mL H 2SO 4溶液⑤用广泛pH 试纸测定H 2SO 4溶液的pH 的3.2A .①④B .②④C .③⑤D .②⑤10、将标准状况下的NH 3(g)溶于水中,得到密度为b g·cm -3的氨水a g ,物质的量浓度为c mol·L -1,则溶于水中的NH 3(g)的体积是A.174.22c LB.b ac 10004.22 LC. LD. L11、用固体样品配制一定物质的最浓度的溶液,需经过称量、溶解、转移溶液、定容等操作。
2022届高三化学一轮复习实验专题强基练18定量型综合实验探究评价提高题含解析

定量型综合实验探究评价(提高题)填空题(精选15题)1.草酸铵[()4242NH C O ]为无色柱状晶体,不稳定,受热易分解,是一种有机合成中间体,可用于测定2Ca +、2Mg +的含量。
Ⅰ.某同学利用如图所示实验装置检验草酸铵的分解产物。
(1)反应开始前通入氮气的目的是___________。
(2)装置C 的作用是___________。
(3)实验过程中,观察到浸有酚酞溶液的滤纸变红,装置B 中澄清石灰水变浑浊,说明分解产物中含有___________(填化学式);若观察到___________,说明分解产物中含有CO 。
(4)除CO 外,还有一种分解产物在一定条件下也能还原CuO ,并生成一种无污染的气体,该反应的化学方程式为___________。
Ⅱ.该同学利用草酸铵测定血液中钙元素的含量。
(5)取20.00mL 血液样品,定容至100mL ,分别取三份体积均为25.00mL 稀释后的血液样品,加入草酸铵,生成草酸钙沉淀,过滤,将该沉淀溶于过量稀硫酸中,然后用0.0101mol L -⋅ 4KMnO 溶液进行滴定。
滴定至终点时的实验现象为___________。
三次滴定实验消耗4KMnO 溶液的体积分别为0.43mL ,0.41mL ,0.52mL ,则该血液样品中含钙元素的量为___________1mol L -⋅。
2.I.二氯化二硫(S 2Cl 2)在工业上用于橡胶的硫化,还可以作为贵金属的萃取剂。
可由硫和氯气在100~110℃直接化合而成。
实验室用以下装置制备S 2Cl 2并对尾气进行回收利用。
已知S 2Cl 2的熔点:-77℃,沸点:137℃。
S 2Cl 2遇水剧烈反应。
(1)B 中所装试剂名称为______(2)S 2Cl 2遇水会生成一种黄色单质、一种能使品红褪色的气体(化合物)及酸雾,写出该反应的化学方程式______。
(3)A 、B 装置中的空气可以通过控制K 2、K 3来去除,具体方法为______,写出E 中发生的氧化还原的化学方程式______(4)由于存在系统缺陷,实验制得的二氯化二硫可能不纯,故需增加一个盛有固体试剂的装置克服缺陷,则装置中的试剂可以选用______。
倍数含量筛法与恒等式(a b b a 1×=)的妙用

3.2. 加强方法
4 13 1 1 在筛除 2,3 的倍数时,我们不妨用 和 代替原来的 2,3 的倍数(含量)占有比例 , ,在筛除 2 3 7 36 1 筛除,这种筛除方法我们称之为倍数含量加强比 pi ( i ≥ 3) 的倍数时,依据引理 2(覆盖定理)按照比例 pi −1
例单筛法。
1 4 13 1 1 n 1 − 1 − 1 − 1 − 1 − , pk −1 , pk ≤ 2n为最大素数 p 7 36 3 5 k −1
1 1 1 1 210 1 − 1 − 1 − 1 − = 48 2 3 5 7
291
鲁思顺
3. 加强比例单筛法
3.1. 覆盖定理[2]
引理 2(覆盖定理):设 pi ( i ≥ 3) 为小于 n 的素数,即使间隔最小,即 pi , pi −1 为孪生素数时,仍有
(
)
4. 等差项同数列及其性质[2]
大偶数 2n 表为两数和的式子共有 n 种形式:
n n 2n = 1 + ( 2n − 1) =+ 2 ( 2n − 2 ) =+ 3 ( 2n − 3) =+ ai } {1,2,3,4,5,, n} , {= 后项集合: B ={bi } ={2n − 1,2n − 2,2n − 3,, n} ,
记作:
2 = C−D
其中 C(D)为有序对偶集合
= C = D ci } {3,4,5,6,, n} {= d i } {1,2,3,4,, n − 2} {=
如果把 C(D)中的数是合数的都筛除干净,若能证明剩余的式子有无穷多,则说明存在无穷多相差为 2 的素数对。
高中化学第2讲 物质的量浓度(练)解析版

第2讲物质的量浓度【练基础】1.配制一定物质的量浓度的溶液是一个重要的定量实验,下列有关说法正确的是()A.容量瓶用蒸馏水洗净后,必须干燥才能用于配制溶液B.配制1 L 0.1 mol·L-1的NaCl溶液时,用托盘天平称量NaCl固体时药品砝码左右位置颠倒,对实验结果无影响C.配制一定物质的量浓度的溶液时,定容时仰视刻度线会导致所配溶液浓度偏高D.用浓盐酸配制稀盐酸,量取浓盐酸时仰视量筒的刻度线会导致所配溶液浓度偏高【答案】D【解析】配制溶液时需加水定容,所以容量瓶用蒸馏水洗净后,不需要干燥就能用于配制溶液,A错误;配制1 L 0.1 mol·L-1的NaCl溶液时,用托盘天平称量NaCl固体时药品砝码左右位置颠倒,称取食盐的质量偏小,配制溶液的浓度偏低,B错误;配制一定物质的量浓度的溶液时,定容时仰视刻度线,溶液体积偏大,导致所配溶液浓度偏低,C错误;用浓盐酸配制稀盐酸,量取浓盐酸时仰视量筒的刻度线,量取浓盐酸体积偏大,会导致所配溶液浓度偏高,D正确。
2.配制100 mL 1.0 mol·L-1Na2CO3溶液,下列操作正确的是()A.称取10.6 g无水碳酸钠,置于100 mL容量瓶中,加水溶解、定容B.称取10.6 g无水碳酸钠置于烧杯中,加入100 mL蒸馏水,搅拌、溶解C.转移Na2CO3溶液时,未用玻璃棒引流,直接倒入容量瓶中D.定容后,塞好瓶塞,反复倒转、摇匀【答案】D【解析】固体不能直接在容量瓶中溶解,A项错误;配制100 mL 1.0 mol·L-1Na2CO3溶液,所用水的体积并不是100 mL,而是加水至100 mL,B项错误;转移液体时,要用玻璃棒引流,C项错误;定容后,塞好瓶塞,要进行摇匀操作,D项正确。
3.用已准确称量的氢氧化钠固体配制0.20 mol·L-1的氢氧化钠溶液250 mL,需要用到的仪器是()①250 mL容量瓶①托盘天平①烧瓶①胶头滴管①烧杯①玻璃棒①试管①药匙A.①①①①B.①①①①C.①①①①①①D.全部【答案】A【解析】用已准确称量的NaOH固体配制0.20 mol·L-1的NaOH溶液250 mL,需要用到的仪器是①①①①,故选A。
湖北省荆门市2024高三冲刺(高考数学)统编版摸底(拓展卷)完整试卷

湖北省荆门市2024高三冲刺(高考数学)统编版摸底(拓展卷)完整试卷一、单选题:本题共8小题,每小题5分,共40分 (共8题)第(1)题函数的图像大致为A.B.C.D.第(2)题“”是“”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件第(3)题同位素测年法最早由美国学者Willard Frank Libby在1940年提出并试验成功,它是利用宇宙射线在大气中产生的C的放射性和衰变原理来检测埋在地下的动植物的死亡年代,当动植物被埋地下后,体内的碳循环就会停止,只进行放射性衰变.经研究发现,动植物死亡后的时间n(单位:年)与死亡n年后的含量满足关系式(其中动植物体内初始的含量为).现在某古代祭祀坑中检测出一样本中的含量为原来的70%,可以推测该样本距今约(参考数据:,)()A.2750年B.2865年C.3050年D.3125年第(4)题在中,,D为AB的中点,,P为CD上一点,且,则()A.B.C.D.第(5)题把4个相同的红球,4个相同的白球,全部放入4个不同的盒子中,每个盒子放2个球,则不同的放法种数有()A.12B.18C.19D.24第(6)题已知,若存在实数(),当()时,满足,则的取值范围为()A.B.C.D.第(7)题某企业对目前销售的四种产品进行改造升级,经过改造升级后,企业营收实现翻番,现统计了该企业升级前后四种产品的营收占比,得到如下饼图:下列说法不正确的是()A.产品升级后,产品的营收是升级前的4倍B.产品升级后,产品的营收是升级前的2倍C.产品升级后,产品的营收减少D.产品升级后,产品营收的总和占总营收的比例不变第(8)题设是两个单位向量,若在上的投影向量为,则()A.B.C.D.二、多选题:本题共3小题,每小题6分,共18分 (共3题)第(1)题已知向量,则下列命题正确的是()A.存在,使得B.当时,与垂直C.对任意,都有D.当时,第(2)题已知双曲线,()A.B.若的顶点坐标为,则C.的焦点坐标为D.若,则的渐近线方程为第(3)题下列物体中,能够被整体放入棱长为1(单位:m)的正方体容器(容器壁厚度忽略不计)内的有()A.直径为的球体B.所有棱长均为的四面体C.底面直径为,高为的圆柱体D.底面直径为,高为的圆柱体三、填空题:本题共3小题,每小题5分,共15分 (共3题)第(1)题在平面直角坐标系xOy中,双曲线上一点M,点M的横坐标是3,则M到双曲线右焦点的距离是__________第(2)题设,则的最小值为______________.第(3)题已知,,则___________四、解答题:本题共5小题,每小题15分,最后一题17分,共77分 (共5题)第(1)题已知等差数列满足,数列是以1为首项,公比为3的等比数列.(1)求和;(2)令,求数列的最大项.第(2)题网购是当前民众购物的新方式,某公司为改进营销方式,随机调查了100名市民,统计其周平均网购的次数,并整理得到如下的频数分布直方图,这100名市民中,年龄不超过40岁的有65人,将所抽样本中周平均网购次数不小于4次的市民称为网购迷,且已知其中有5名市民的年龄超过40岁.(1)根据已知条件完成下面的列联表,能否在犯错误的概率不超过0.10的前提下认为网购迷与年龄不超过40岁有关?网购迷非网购迷合计年龄不超过40岁年龄超过40岁合计(2)若将所抽取样本中周平均网购次数为6次的市民称为超级网购迷,且已知超级网购迷中有2名年龄超过40岁,若从超级网购迷中任意挑选2名,求至少有一名市民年龄超过40岁的概率.(附:)0.150.100.050.012.0722.7063.8416.635第(3)题在中,角A,,所对的边分别为,,,,,且.(1)若,,求的周长;(2)若,,求的最大值.第(4)题已知函数(1)当时,求的单调区间;(2)已知,求证:当时,恒成立;(3)设,求证:当函数恰有一个零点时,该零点一定不是函数的极值点.第(5)题选修4-1:几何证明选讲如图,从圆外一点引圆的切线及割线,为切点,,垂足为.(1)求证:;(2)若依次成公差为1的等差数列,且,求的长.。
2022届高三化学一轮复习实验专题强基练17定量型综合实验探究评价基础题含解析
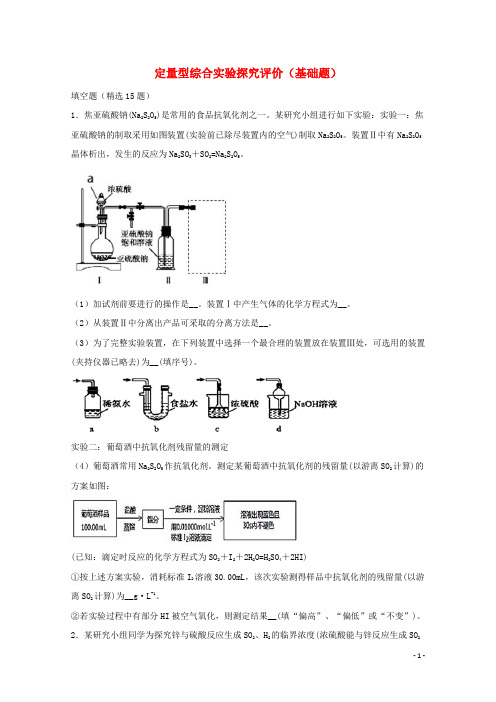
定量型综合实验探究评价(基础题)填空题(精选15题)1.焦亚硫酸钠(Na2S2O5)是常用的食品抗氧化剂之一。
某研究小组进行如下实验:实验一:焦亚硫酸钠的制取采用如图装置(实验前已除尽装置内的空气)制取Na2S2O5。
装置Ⅱ中有Na2S2O5晶体析出,发生的反应为Na2SO3+SO2=Na2S2O5。
(1)加试剂前要进行的操作是__。
装置Ⅰ中产生气体的化学方程式为__。
(2)从装置Ⅱ中分离出产品可采取的分离方法是__。
(3)为了完整实验装置,在下列装置中选择一个最合理的装置放在装置Ⅲ处,可选用的装置(夹持仪器已略去)为__(填序号)。
实验二:葡萄酒中抗氧化剂残留量的测定(4)葡萄酒常用Na2S2O5作抗氧化剂。
测定某葡萄酒中抗氧化剂的残留量(以游离SO2计算)的方案如图:(已知:滴定时反应的化学方程式为SO2+I2+2H2O=H2SO4+2HI)①按上述方案实验,消耗标准I2溶液30.00mL,该次实验测得样品中抗氧化剂的残留量(以游离SO2计算)为__g·L-1。
②若实验过程中有部分HI被空气氧化,则测定结果__(填“偏高”、“偏低”或“不变”)。
2.某研究小组同学为探究锌与硫酸反应生成SO2、H2的临界浓度(浓硫酸能与锌反应生成SO2的最低浓度)设计了如下实验。
在大试管A中加入100mLl 8mol/L硫酸,向连接在塑料棒上的多孔塑料球内加入足量的锌粒(塑料棒可以上下移动),在试剂瓶D中加入足量的浓NaOH溶液(加热和夹持装置已省略)。
已知:锌与浓硫酸接触,开始时反应缓慢,可以适当加热以加速其反应,当有大量气泡生成时,该反应速率会明显加快并伴有大量的热放出。
(1)请写出锌与硫酸反应产生SO2的化学方程式______________。
(2)在组装仪器之后,加入试剂之前必须进行的操作是__________。
(3)长导管B的作用是______,如果没有这个设计,最终测定的临界浓度会_________。
小升初数学七大专题知识点

小升初数学七大专题知识点数学是小升初考试中的一个重要科目,所以我们在小升初总复习的时候,都会把数学作为一个重点。
本文为大家汇总了一部分2017年小升初数学知识点,内容很详细,具体到各个题型的不同解法,赶紧来看看吧!计算扎实的算功是学好数学的必要条件。
聪明在于勤奋,知识在于积累。
积累一些常见数是必要的。
如1/8,1/4,3/8,1/2,5/8,3/4,7/8的分数,小数,百分数,比的互化要脱口而出。
100以内的质数要信手拈来。
1-30的平方,1-10的立方的结果要能提笔就写。
对于整除的判定仅仅积累2,3,5的是不够的。
9的整除判定和3的方法是一样的。
还有就是2和5的n次方整除的判定只要看末n位。
如4和25的整除都是看末2位,末2位能被4或25整除则这个数可以被4或25整除。
8和125就看末3位。
7,11,13的整除判定就是割开三位。
前面部分减去末三位就可以了如果能整除7或11或13,这个数就是7或11或13的倍数。
这其实是判定1001的方法。
此外还有一种方法是割个位法,望同学们至少掌握20以内整除的判定方法。
接下来讲下数论的积累。
搞清楚什么是完全平方数,完全平方数个位只能是0,1,4,5,6,9.奇数的平方除以8余1,偶数的平方是4的倍数。
要掌握如何求一个数的约数个数,所有约数的和,小于这个数且和这个数互质数的个数如何求。
如何估计一个数是否为质数。
计算分为一般计算和技巧计算。
到底用哪个呢?首先基本的运算法则必须很熟悉。
不要被简便运算假象迷惑。
这里重点说下技巧计算。
首先要熟练乘法和除法的分配律,其次要熟练a-b-c=a-(b+c)a-(b-c)=a-b+c还有连除就是除以所有除数的积等。
再者对于结合交换律都应该很熟悉。
分配律有直接提公因数,和移动小数点或扩大缩小倍数来凑出公因数。
甚至有时候要强行创造公因数。
再单独算尾巴。
分数的裂项:裂和与裂差等差数列求和,平方差,配对,换元,拆项约分,等比定理的转化等都要很熟悉。
(完整版)化学计算题解题方法(含答案)

高中化学计算题常用的一些巧解和方法一、差量法差量法是根据物质变化前后某种量发生变化的化学方程式或关系式,所谓“差量”就是指一个过程中某物质始态量与终态量的差值。
它可以是气体的体积差、物质的量差、质量差、浓度差、溶解度差等。
该法适用于解答混合物间的反应,且反应前后存在上述差量的反应体系。
【例1】把22.4g铁片投入到500gCuSO4溶液中,充分反应后取出铁片,洗涤、干燥后称其质量为22.8g,计算(1)析出多少克铜? (2)反应后溶液的质量分数多大?Cu 完全反应,反应后的溶液为FeSO4溶液,不能轻解析“充分反应”是指CuSO4中2率地认为22.8g就是Cu!(若Fe完全反应,析出铜为25.6g),也不能认为22.8-22.4=0.4g 就是铜。
分析下面的化学方程式可知:每溶解56gFe,就析出64g铜,使铁片质量增加8g(64-56=8),反过来看:若铁片质量增加8g,就意味着溶解56gFe、生成64gCu,即“差量” 8与方程式中各物质的质量(也可是物质的量)成正比。
所以就可以根据题中所给的已知“差量”22.8-22.4=0.4g 求出其他有关物质的量。
设:生成Cu x g,FeSO4 y gFe+CuSO4 =FeSO4+Cu 质量增加56 152 64 64-56=8y x 22.8-22.4=0.4故析出铜3.2克铁片质量增加0.4g,根据质量守恒定律,可知溶液的质量必减轻0.4g,为500-0.4=499.6g。
【巩固练习】将N2和H2的混合气体充入一固定容积的密闭反应器内,达到平衡时,NH3的体积分数为26%,若温度保持不变,则反应器内平衡时的总压强与起始时总压强之比为1∶______。
解析:由阿伏加德罗定律可知,在温度、体积一定时,压强之比等于气体的物质的量之比。
所以只要把起始、平衡时气体的总物质的量为多少mol表示出来即可求解。
方法一设起始时N2气为a mol, H2为b mol,平衡时共消耗N2气为xmolN2+3H22NH3起始(mol) a b ?0变化(mol) x 3x 2x平衡(mol) a-x b-3x 2x起始气体:a+bmol平衡气体:(a-x)+( b-3x)+2x=(a+b-2x)mol又因为:体积比=物质的量比(注意:若N 2为1mol ,H 2为3mol ,是不够严密的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
291
鲁思顺
3. 加强比例单筛法
3.1. 覆盖定理[2]
引理 2(覆盖定理):设 pi ( i ≥ 3) 为小于 n 的素数,即使间隔最小,即 pi , pi −1 为孪生素数时,仍有
Open Access
1. 引言
1.1. 偶数 2n 表为两自然数和的式子共有 n 种形式
2n = 1 + ( 2n − 1) =+ 2 ( 2n − 2 ) =+ 3 ( 2n − 3 ) = =+ n n
记作 2n = A + B 为有序对偶集合:
= A ai } {1, 2,3, , n} {=
1 1 ,非 pk +1 的倍数含量占有( 1 − ) pk + 1 pk +1
证明:用数学归纳法证明 (I) 当 j = 1 时 在 A = {ai } 中,根据倍数含量的定义, p1 , 及推论 1,易得
n n 1 1 1 。 − ⋅ = n 1 − ⋅ p2 p1 p2 p 1 p2 1 1 1 1 1 n 1 − − n 1 − ⋅ = n 1 − 1 − 。 p p p p p 1 1 2 1 2
摘
要
本文挖掘出倍数含量及等差项同数列的概念,根据倍数含量重叠规律及等差项同数列的性质,对自然数 列中倍数出现规律作了深入的探讨。作为应用,我们证明了偶数哥德巴赫猜想与孪生素数猜想。
文章引用: 鲁思顺. 倍数含量筛法与恒等式()的妙用[J]. 理论数学, 2017, 7(4): 288-296. https:///10.12677/pm.2017.74038
(1)
非 pk 的倍数含量为:
k −1 k 1 1 1 1− = n ⋅ ∏ 1 − 1 − ⋅ n ⋅ ∏ pk pj pj = j 1= j 1
(2)
290
鲁思顺
下边证明当 j =
( k − 1) + 1 =
k 时,命题成立。
Pure Mathematics 理论数学, 2017, 7(4), 288-296 Published Online July 2017 in Hans. /journal/pm https:///10.12677/pm.2017.74038
倍数含量为 n −
1 n = n 1 − 。 p p
易知, p 的倍数含量与 n 成正比例关系, p 的倍数个数与 p 的倍数含量的正负误差的绝对值小于 1。
289
鲁思顺
2.2. 倍数含量重叠规律
引理 1 [1]:在 A = {ai } 里 p 的倍数含量中, q 的部分倍数含量,也就是 p 的倍数的含量中的 pq 的倍 数含量,占有
n⋅
= =
k −1 1 1 1 ⋅ n ⋅ ∏ 1 − ⋅ 1 − pk +1 pj pk j =1 k 1 1 ⋅ n ⋅ ∏ 1 − pk +1 pj j =1
(5)
(2)~(5)
k k 1 1 1 n ⋅ ∏ 1 − − ⋅ n ⋅ ∏ 1 − pj pj j 1= j 1 = pk + 1 k 1 1 =n ⋅ ∏ 1 − ⋅ 1 − pj pk +1 j =1 k +1 1 = n ⋅ ∏ 1 − pj j =1
n n 在连续的 n 个自然数的集合 A = {ai } 中,自然数 p 的倍数个数有 或 + 1 ( [ ] 为去尾取整)。 p p n 定义 1:A = {ai } 中数的个数 n 与自然数 p ( p ≥ 2 ) 的比值 , 叫做自然数 p 的倍数含量.在 A 中非 P 的 p
Sieve of Multiple Content and a b Subtle Effects of × = 1 b a
Sishun Lu
Linyi University, Linyi Shandong Received: Jun. 23 , 2017; accepted: Jul. 7 , 2017; published: Jul. 13 , 2017
3.2. 加强方法
4 13 1 1 在筛除 2,3 的倍数时,我们不妨用 和 代替原来的 2,3 的倍数(含量)占有比例 , ,在筛除 2 3 7 36 1 筛除,这种筛除方法我们称之为倍数含量加强比 pi ( i ≥ 3) 的倍数时,依据引理 2(覆盖定理)按照比例 pi −1
例单筛法。
1 4 13 1 1 n 1 − 1 − 1 − 1 − 1 − , pk −1 , pk ≤ 2n为最大素数 p 7 36 3 5 k −1
由 p 的任意性及假设可知: k −1 1 pk , pk +1 , pk pk +1 在 n ⋅ ∏ 1 − 中的倍数含量分别是: pj j =1
k −1 1 1 ⋅ n ⋅ ∏ 1 − pk pj j =1 k −1 1 1 ⋅ n ⋅ ∏ 1 − pk + 1 pj j =1
rd th th
Abstract
We introduce the notions of multiple content and parallel arithmetic series. Based on the overlap law of multiple contents and properties of parallel arithmetic progressions, we discuss the appearance rule of multiples in the series of natural numbers. As applications, we prove the even number Goldbach’s conjecture and the twin prime conjecture.
前项集合: = A
要是把前项集合 A,后项集合 B 中 pi ( 1 ≤ i ≤ k , pk ≤ 2n 的最大素数)倍数的式子都筛除干净,若还 有剩余的式子,就说明大偶数能表为两素数和的式子。 问题是,筛去 A 中的一个素数的倍数(如 3 的倍数,是一个数列),要带走 B 中的一个数列,这两个 数列,都是等差数列,项数相同。下面我们看它们之间有什么性质。
鲁思顺
关键词
倍数含量,重叠规律,覆盖定理,等差项同数列,两筛法
Copyright © 2017 by author and Hans Publishers Inc. This work is licensed under the Creative Commons Attribution International License (CC BY). /licenses/by/4.0/
n n > + 1 pi −1 pi
证明:因为 pi −1 ≤ Pi − 2 ( pi , pi −1 为孪生素数时,等号取得)
n n n n − ≥ = − pi −1 pi pi − 2 pi 2n >1 pi ( pi − 2 )
(p −2< p < n)
i i
所以
n n n > + 1 ≥ + 1 。证毕 pi −1 pi pi
n n n , , 。 p1 p1 p2 p2
则命题成立。 (II) 假设当 j= k − 1 时命题成立 k −1 1 即在 n ⋅ ∏ 1 − 中 pk 的倍数含量为 pj j =1
k −1 1 1 ⋅ n∏ 1 − pk pj j =1
(
)
4. 等差项同数列及其性质[2]
大偶数 2n 表为两数和的式子共有 n 种形式:
n n 2n = 1 + ( 2n − 1) =+ 2 ( 2n − 2 ) =+ 3 ( 2n − 3) =+ ai } {1,2,3,4,5,, n} , {= 后项集合: B ={bi } ={2n − 1,2n − 2,2n − 3,, n} ,
Keywords
Multiple Content, Overlap Law, Covering Theorem, Parallel Arithmetic Series, Sieve of Both Sides
a b 倍数含量筛法与恒等式( × = 1)的妙用 b a
鲁思顺
临沂大学,山东 临沂
收稿日期:2017年6月23日;录用日期:2017年7月7日;发布日期:2017年7月13日
n n n 1 − = n − 。证毕 q pq pq
n 由推论 1 知,筛除 p 的倍数含量之后,欲筛除剩余部分中 q 的倍数含量,只需对剩余部分 n − , p 1 再筛除 ,即可。 q
推论 2 [2]:在 A = {ai } 中的 n 个数中,依次筛除 p j ( j = 1,2,3,, k ) 的倍数含量后,在非 p j 的倍数含 量中, pk +1 的倍数含量占有
B ={bi } ={2n − 1, 2n − 2, 2n − 3, , n}
如果把 A(B)中的加数是合数及 1 的式子都筛除干净, 若还有剩余的式子, 说明偶数 2n 能表示为两素 数之和。
1.2. 小于 n 的相差为 2 的数对共有 n-2 种形式
2 = 3 − 1 = 4 − 2 = 5 − 3 = = n − (n − 2)
1 q
