信号与系统 第三章 陈后金 习题解答
信号与系统习题答案第三章

第三章习题基础题3.1 证明cos t , cos(2)t , …, cos()nt (n 为正整数),在区间(0,2)π的正交集。
它是否是完备集?解:(积分???)此含数集在(0,2)π为正交集。
又有sin()nt 不属于此含数集02sin()cos()0nt mt dt π=⎰,对于所有的m 和n 。
由完备正交函数定义所以此函数集不完备。
3.2 上题的含数集在(0,)π是否为正交集?解:由此可知此含数集在区间(0,)π内是正交的。
3.3实周期信号()f t 在区间(,)22T T-内的能量定义为222()TT E f t dt -=⎰。
如有和信号12()()f t f t +(1)若1()f t 与2()f t 在区间(,)22T T-内相互正交,证明和信号的总能量等于各信号的能量之和;(2)若1()f t 与2()f t 不是相互正交的,求和信号的总能量。
解:(1)和信号f(t)的能量为[]222222222221212222()12()()()()()()T T T T T T T T T T E f t dt dtf t dt f t dt f t f t dtf t f t -----===+++⎰⎰⎰⎰⎰(少乘以2)由1()f t 与2()f t 在区间内正交可得2122()()0T T f t f t dt -=⎰则有 22221222()()T T T T E f t dt f t dt --=+⎰⎰即此时和信号的总能量等于各信号的能量之和。
和信号的能量为(2)[]222222222221212222()12()()()()()()T T T T T T T T T T E f t dt dtf t dt f t dt f t f t dtf t f t -----===+++⎰⎰⎰⎰⎰(少乘以2吧?)由1()f t 与2()f t 在区间(,)22T T-内不正交可得2122()()0T T f t f t dt K -=≠⎰则有2222222212122222()()()()T T T T T T T T E f t dt f t dt K f t dt f t dt ----=++≠+⎰⎰⎰⎰即此时和信号的总能量不等于各信号的能量之和。
信号与系统 陈后金 第二版 课后习题答案(完整版)

(1) f (t) = 3sin 2t + 6 sinπ t
(2) f (t) = (a sin t) 2
(8)
f
(k)
=
cos⎜⎛ ⎝
πk 4
⎟⎞ ⎠
+
sin⎜⎛ ⎝
πk 8
⎟⎞ ⎠
−
2
cos⎜⎛ ⎝
πk 2
⎟⎞ ⎠
解:(1)因为 sin 2t 的周期为π ,而 sin πt 的周期为 2 。
显然,使方程
−∞
0
2-10 已知信号 f (t) 的波形如题 2-10 图所示,绘出下列信号的波形。
f (t)
2
1
−1 0
t 2
题 2-10 图
(3) f (5 − 3t) (7) f ′(t) 解:(3)将 f (t) 表示成如下的数学表达式
(5) f (t)u(1 − t)
由此得
⎧2
f
(t)
=
⎪ ⎨ ⎪ ⎩
f (t)u(1− t) 2
1
0.5
t
−1 0
1
(7)方法 1:几何法。由于 f (t) 的波形在 t = −1处有一个幅度为 2 的正跳变,所以 f ′(t) 在 此处会形成一个强度为 2 的冲激信号。同理,在 t = 0 处 f ′(t) 会形成一个强度为 1 的冲激信 号(方向向下,因为是负跳变),而在 0 < t < 2 的区间内有 f ′(t) = −0.5 (由 f (t) 的表达式可
第 1 页 共 27 页
《信号与系统》(陈后金等编)作业参考解答
(2)显然,该系统为非线性系统。 由于
T{f (t − t0 )}= Kf (t − t0 ) + f 2 (t − t0 ) = y(t − t0 )
信号与系统习题答案第三章

第三章习题基础题3.1 证明cos t , cos(2)t , …, cos()nt (n 为正整数),在区间(0,2)π的正交集。
它是否是完备集?解:(积分???)此含数集在(0,2)π为正交集。
又有sin()nt 不属于此含数集02sin()cos()0nt mt dt π=⎰,对于所有的m 和n 。
由完备正交函数定义所以此函数集不完备。
3.2 上题的含数集在(0,)π是否为正交集?解:由此可知此含数集在区间(0,)π内是正交的。
3.3实周期信号()f t 在区间(,)22T T-内的能量定义为222()TT E f t dt -=⎰。
如有和信号12()()f t f t +(1)若1()f t 与2()f t 在区间(,)22T T-内相互正交,证明和信号的总能量等于各信号的能量之和;(2)若1()f t 与2()f t 不是相互正交的,求和信号的总能量。
解:(1)和信号f(t)的能量为[]222222222221212222()12()()()()()()T T T T T T T T T T E f t dt dtf t dt f t dt f t f t dtf t f t -----===+++⎰⎰⎰⎰⎰(少乘以2)由1()f t 与2()f t 在区间内正交可得2122()()0T T f t f t dt -=⎰则有 22221222()()T T T T E f t dt f t dt --=+⎰⎰即此时和信号的总能量等于各信号的能量之和。
和信号的能量为(2)[]222222222221212222()12()()()()()()T T T T T T T T T T E f t dt dtf t dt f t dt f t f t dtf t f t -----===+++⎰⎰⎰⎰⎰(少乘以2吧?)由1()f t 与2()f t 在区间(,)22T T-内不正交可得2122()()0T T f t f t dt K -=≠⎰则有2222222212122222()()()()T T T T T T T T E f t dt f t dt K f t dt f t dt ----=++≠+⎰⎰⎰⎰即此时和信号的总能量不等于各信号的能量之和。
信号与系统第3章 习题答案

第3章 傅里叶变换与连续系统的频域分析3.1 证明函数集{}0cos ,0,1,2,n t n ω=在区间()00,2πω内是正交函数集。
证明: 对任意的自然数n,m (n ≠m),有220000011cos cos [cos()+cos()]22n t m tdt n m t n m t dt ππωωωωωω=+-⎰⎰=0证毕 3.2 一个由正弦信号合成的信号由下面的等式给出:()10cos(800)7cos(1200)5cos(1600)43x t t t t πππππ=++-- (1)画出这个信号的频谱图,表明每个频率成分的复数值。
对于每个频率的复振幅,将其实部和虚部分开或者将其幅度和相位分开来画。
(2)()x t 是周期信号吗?如果是,周期是什么?(提示:按照最小公倍数计算) (3)现在考虑一个新的信号:()()5cos(1000)2y t x t t ππ=++,请问,频谱如何变化?()y t 是周期信号吗?如果是,周期是什么?解:(1)频谱图如下ωX(j ω) 05107 800π 1600π1200π107 -5振幅图(2)()x t 三项都是周期信号,周期分别为1/400、1/600、1/800,所以()x t 是周期信号,周期为为1/400、1/600、1/800的最小公倍数为1/200。
(3)根据频谱的分析()y t 比()x t 多了一个频谱分量,频率为1/500,所以()y t 还是周期信号,周期为1/200和1/500的最小公倍数1/100。
3.3 求下列每个信号的傅里叶级数表示式。
(1)200j te; (2)(1)cos 4t π-⎡⎤⎢⎥⎣⎦; (3)cos 4sin 8t t +;(4)()x t 是周期为2的周期信号,且(),11t x t e t -=-<<(5)()x t ,如题图3.3所示。
题图3.3(6)()x t 是周期为4的周期信号,且sin 02()024t t x t t π≤≤⎧=⎨≤≤⎩(7)2sin tω)(ωϕ800π1200π4π-3π相位图解(1)该信号为虚指数信号,自身就是指数级数,频0200ω=,周期100T π=三角级数为200cos(200)sin(200)j t e t j t =+ (2)基频04πω=,周期8T = 三角级数(1)2cos cos sin 4244t t t πππ-⎡⎤⎡⎤⎛⎫⎛⎫=+ ⎪ ⎪⎢⎥⎢⎥⎣⎦⎝⎭⎝⎭⎣⎦指数级数44444422()cos sin 24422222(1)(1)44t t t tj j j j t tj j t t e e j e e j e j e ππππππππ---⎡⎤⎡⎤+-⎛⎫⎛⎫⎢⎥+=+⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎣⎦⎢⎥⎣⎦=-++ (3)自身为三角级数cos 4sin 8t t +,基频04ω=,周期2T π=指数级数44888448()cos 4sin8222222j t j t j t j t j t j t j t j t e e j e e je e e je t t -----+-+=+=++-(4)周期T=2;基频0ωπ=11011 1.17522t e e a e dt ----===⎰11212(1)()cos()21()n t n e e a e n t dt n ππ----+==+⎰ 11212()(1)sin()21()n t n e e n b e n t dt n πππ-----==+⎰ 三角级数:1() 1.175[cos()sin()]nn n x t an t b n t ππ∞-=++∑1(1)11111(1)()22(1)2(1)jn jn k t jn t n e e e e F e e dt jn jn πππππ+-+-------===++⎰ 指数级数:11(1)()()2(1)k jntjn tnn n e e x t F ee jn ππ-∞∞=-∞=-∞--==+∑∑(5)由图可知,周期T=2;基频0ωπ=,且该信号为奇信号00n a a ==11022sin()(1)n n b t n t dt n ππ-==-⎰三角级数:111122(1)()(1)sin()sin()n n n n x t n t n t n n ππππ-∞∞-==-=-=∑∑111(1)2n n n F jb n π-=-=- 指数级数:11()(1)jntn jn t n n n x t F ee n ππ∞∞-=-∞=-∞==-∑∑ (6)周期T=4;基频02πω=2001sin()04a t dt π==⎰ 21sin()cos(/2)2n a t n t dt ππ==⎰⎪⎩⎪⎨⎧-为偶数为奇数n 0n ,)n 4(42π201sin()sin(/2)2n b t n t dt ππ==⎰0 三角级数:11()[cos(/2)n n x t a n t ππ∞==+∑/22/2202sin(/2)21sin()(4)402jn jn t n j n e n F t e dt n n πππππ--⎧≠±⎪==-⎨⎪=±⎩⎰指数级数: ()jntnn x t F e∞=-∞=∑(7)21cos(2)sin 2t t -=2211()24j tj t e e -=-+三角级数为0211,22a a ==-,其他系数为0 指数级数: x(t)=2211()24j tj t e e --+ 3.4 给定周期方波()x t 如图题图3.4所示,求该信号的傅里叶级数(包括三角形式和指数形式)。
信号与系统课后习题与解答第三章
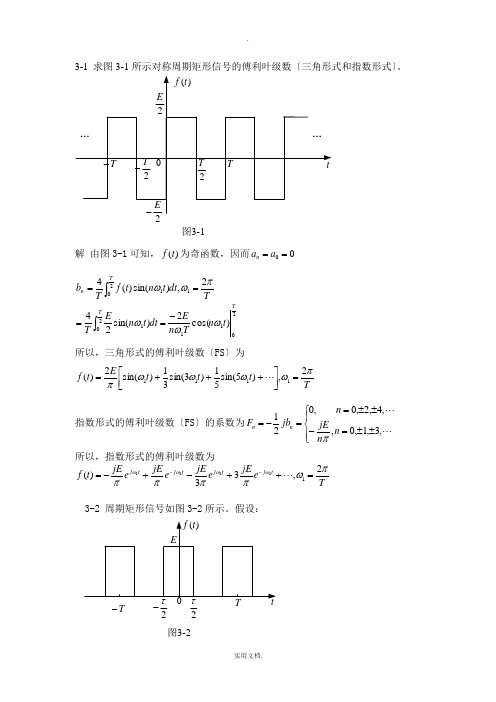
3-1 求图3-1所示对称周期矩形信号的傅利叶级数〔三角形式和指数形式〕。
图3-1解 由图3-1可知,)(t f 为奇函数,因而00==a a n2112011201)cos(2)sin(242,)sin()(4T T T n t n T n Edt t n E T T dt t n t f T b ωωωπωω-====⎰⎰所以,三角形式的傅利叶级数〔FS 〕为T t t t E t f πωωωωπ2,)5sin(51)3sin(31)sin(2)(1111=⎥⎦⎤⎢⎣⎡+++=指数形式的傅利叶级数〔FS 〕的系数为⎪⎩⎪⎨⎧±±=-±±==-= ,3,1,0,,4,2,0,021n n jE n jb F n n π所以,指数形式的傅利叶级数为T e jE e jE e jE e jE t f t j t j t j t j πωππππωωωω2,33)(11111=++-+-=--3-2 周期矩形信号如图3-2所示。
假设:图3-22τT-2τ-重复频率kHz f 5= 脉宽 s μτ20=幅度 V E 10=求直流分量大小以及基波、二次和三次谐波的有效值。
解 对于图3-2所示的周期矩形信号,其指数形式的傅利叶级数〔FS 〕的系数⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛====⎰⎰--22sin 12,)(1112212211τωττωππωττωωn Sa T E n n E dt Ee T T dt e t f T F tjn TT t jn n那么的指数形式的傅利叶级数〔FS 〕为∑∑∞-∞=∞-∞=⎪⎭⎫⎝⎛==n tjn n tjn ne n Sa TE eF t f 112)(1ωωτωτ 其直流分量为T E n Sa T E F n ττωτ=⎪⎭⎫ ⎝⎛=→2lim100 基波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-2sin 2111τωπEF F 二次谐波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-22sin 122τωπEF F 三次谐波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-23sin 32133τωπE F F 由所给参数kHz f 5=可得s T s rad 441102,/10-⨯==πω 将各参数的值代入,可得直流分量大小为V 110210201046=⨯⨯⨯--基波的有效值为())(39.118sin 210101010sin 210264V ≈=⨯⨯⨯- πππ二次谐波分量的有效值为())(32.136sin 251010102sin 21064V ≈=⨯⨯⨯- πππ三次谐波分量的有效值为())(21.1524sin 32101010103sin 2310264V ≈=⨯⨯⨯⨯- πππ3-3 假设周期矩形信号)(1t f 和)(2t f 的波形如图3-2所示,)(1t f 的参数为s μτ5.0=,s T μ1= ,V E 1=; )(2t f 的参数为s μτ5.1=,s T μ3= ,V E 3=,分别求:〔1〕)(1t f 的谱线间隔和带宽〔第一零点位置〕,频率单位以kHz 表示; 〔2〕)(2t f 的谱线间隔和带宽; 〔3〕)(1t f 与)(2t f 的基波幅度之比; 〔4〕)(1t f 基波与)(2t f 三次谐波幅度之比。
信号与系统陈后金版答案

第二步:求差分方程的齐次 解: 2 求差分方程的齐次 第二步 h [ 0 ] = C 1 + C 2 r −5r /6 +1/ 6 = 0 1 k1 1 k 1 特征方程为: [ ( + 特征方程为=hCk1 ] = )[3 (C 2) ( −) 2 ( 求 ] u [ C ] = 3, C 2 = − 2 h [1] ⇒ ) 出 k1 ∴r =1/ 2, r2 =1/3 2 3 3 1 2
(3) 计算固有响应与强迫响应 计算固有响应与强迫响应:
1 7 1 k 4 1 k y[k ] = [ − ( ) + ( ) ]u[k ] 完全响应: 完全响应 2 2 2 3 3 7 1 k 4 1 k 固有响应: yh [k ] = [− ( ) + ( ) ]u[ k ] 固有响应 2 2 3 3 1 强迫响应: 强迫响应 y p [k ] = u[k ] 2 (4) 计算瞬态响应与稳态响应 计算瞬态响应与稳态响应:
特征根为 s1 = -2, s2 = -5, 又因为 n > m , 所以: 则 h ( t ) = K 1e − 2 t u ( t ) + K 2 e − 5 t u ( t )
h '(t ) = − 2 K 1e −2 t u (t ) + K 1δ (t ) − 5 K 2 e −5 t u (t ) + K 2δ (t ) = − 2 K 1e −2 t u (t ) − 5 K 2 e −5 t u (t ) + ( K 1 + K 2 )δ (t ) h ''(t ) = 4 K 1e −2 t u (t ) − 2 K 1δ (t ) + 25 K 2 e −5 t u (t ) − 5 K 2δ (t ) + ( K 1 + K 2 )δ '(t ) 代入方程有: = K 1 + K 2 = '( t ) = 2 K 2δ ( t ) + 5 K∴K2 + (7/3; K1 )δ −1/3; 2δ '( t ) + 3δ ( t ) 1δ ( t )
陈后金《信号与系统》(第2版)配套题库【名校考研真题+课后习题+章节题库+模拟试题】(上册)

图2-2
3.有一离散时间信号
(1)画出
(2)求序列 学]
使之满足
解:(1)
又 比较上述两式可得: 故如图2-3所示。
[电子科技大
图2-3
4.已知 如图2-4(a),画出
和
的波形。[北
京理工大学]
解:将 反转得 如图2-4(b)所示,将它们相加、减得 ,波形如图2-4(c)、(d)所示。
图2-4 5.已知f(t)的波形如图2-5所示,令r(t)=tu(t)。
大学]
图1-2 解:因为:
故:
y2(t)的波形如图1-3所示。
图1-3 3.将如图1-4(a)、(b)所示的连续信号展成如下形式:
给出信号
最简单的解析表达形式。[北京航空航天大学]
图1-4
解:(a)该信号可分为两段:
和
可化简为
故
,即:
(b)该信号可分为三段: 可化简为 故
,即
4.求
的值。[北京航空航天大学2006研]
,应该与齐次解有关,即系统的特征根为-1和-3,故特征方程应为 ,即a0=4,a1=3。
(2)设系统对激励 rzs(t),则
的零输入响应和零状态响应分别为rzi(t)和
由于
,则由线性时不变系统的微分特性可知
同时,设系统的单位冲激响应为h(t),则由线性时不变系统的叠加性 可知
由式(1)、式(2),并设
陈后金《信号与系统》(第2版)配 套模拟试题及详解
第一部分 名校考研真题 第1章 信号与系统分析导论 一、选择题
1.方程 天大学2007研] A.线性时不变 B.非线性时不变 C.线性时变 D.非线性时变 E.都不对 【答案】B
描述的系统是( )。[北京航空航
信号与系统第三章习题部分参考答案

(7) (1 − t) f (1 − t) ;
(2) [1 + m f (t)]cosω0 t
(4) (t + 2) f (t); ( ) (6) e− jω0 t df t
dt
(8) f (t)∗ f (t − 3);
t
(9) ∫τ f (τ )dτ −∞
1−t / 2
(11) ∫ f (τ )dτ −∞
2π (sin π t )2 ↔ 2π (1− ⎜w⎜)[ε(w + 2π ) − ε(w − 2π )]
πt
2π
即 (sin π t )2 ↔ (1− ⎜w⎜)[ε(ω + 2π ) − ε(w − 2π )]
πt
2π
(3)双边指数信号
∵ e−a⎜t⎜
↔
2a a2 + w2
(−∞
<
t
<
+∞)
∴ 2a a2 + w2
(13) f (t)∗ Sa(2t) (15) t df (1 − t)
dt
t+5
(10) ∫ f (τ )dτ −∞
(12) df (t) + f (3t ) − 2 e− jt ;
dt
(14) f (t) u(t)
(16) (t − 2) f (t)e j2(t−3)
解:(1) f 2 (t) + f (t) = f (t). f (t) + f (t) ↔ 1 [F (w}* F (w)] + F (w)
又 f (t) = 2 + cos⎜⎛ 2πt ⎟⎞ + 4sin⎜⎛ 5πt ⎟⎞
⎝3⎠
