信号与系统(陈生潭)习题答案1-4章部分1
信号与系统PPT电子书陈生谭版课后习题答案

1.22 在题 1.21 的基础上,若还已知 f(t)=ε(t),x1(0-)=0,x2(0-)=0 时,有 y(t)=2+e-t+2e-3t,t≥0 试求当 f(t)=3ε(t),x1(0-)=2,x2(0-)=5 时的系统响应 y(t)。 解: 记,f(t)=ε(t),x1(0-)=0,x2(0-)=0 时,系统响应 yf(t)=y(t)=2+e-t+2e-3t,t≥0 则当 f(t)=3ε(t),x1(0-)=2,x2(0-)=5 时的系统全响应 y(t)为: y(t)=3yf(t)+2y1(t)+5y2(t)
解:
(1)
is
(t)
=
i(t
)
+
ic
(t )
+
iR
(t )
=
i (t )
+
Cuc′
(t )
+
1 2
u (t )
----⑴
而 uC (t) = u(t)
对回路①,有:
⎧− ⎩⎨iL
3i(t) (t) =
+ is
LiL′ (t) + u(t) (t) − i(t)
=
0
⇒
u(t)
=
3i(t
)
−
Lis′
(t)
− p 1+ p
−1
3p 0
−p
− p 0 1+ p +1/ p
− p f (t) i2 (t) = 3 p − p
信号与系统第四版习题解答精选全文完整版

可编辑修改精选全文完整版《信号与系统》(第四版)习题解析高等教育2007年8月目录第1章习题解析1第2章习题解析5第3章习题解析14第4章习题解析21第5章习题解析29第6章习题解析39第7章习题解析47第8章习题解析52第1章习题解析1-1题1-1图示信号中,哪些是连续信号?哪些是离散信号?哪些是周期信号?哪些是非周期信号?哪些是有始信号?(c) (d)题1-1图解(a)、(c)、(d)为连续信号;(b)为离散信号;(d)为周期信号;其余为非周期信号;(a)、(b)、(c)为有始(因果)信号。
1-2给定题1-2图示信号f( t ),试画出下列信号的波形。
[提示:f( 2t )表示将f( t )波形压缩,f (2t)表示将f ( t )波形展宽。
](a) 2 f (t - 2 ) (b) f ( 2t )(c)f (2t )(d)f (-t +1 )题1-2图解以上各函数的波形如图p1-2所示。
图p1-21-3 如图1-3图示,R 、L 、C 元件可以看成以电流为输入,电压为响应的简单线性系统S R 、S L 、S C ,试写出各系统响应电压与激励电流函数关系的表达式。
S RS LS C题1-3图解各系统响应与输入的关系可分别表示为)()(t i R t u R R ⋅= tt i Lt u L L d )(d )(= ⎰∞-=tC C i C t u ττd )(1)(1-4 如题1-4图示系统由加法器、积分器和放大量为-a 的放大器三个子系统组成,系统属于何种联接形式?试写出该系统的微分方程。
题1-4图解系统为反馈联接形式。
设加法器的输出为x ( t ),由于)()()()(t y a t f t x -+=且)()(,d )()(t y t x t t x t y '==⎰故有)()()(t ay t f t y -='即)()()(t f t ay t y =+'1-5已知某系统的输入f ( t )与输出y ( t )的关系为y ( t ) = | f ( t )|,试判定该系统是否为线性时不变系统?解设T 为系统的运算子,则可以表示为)()]([)(t f t f T t y ==不失一般性,设f ( t ) = f 1( t ) +f 2( t ),则)()()]([111t y t f t f T ==)()()]([222t y t f t f T ==故有)()()()]([21t y t f t f t f T =+=显然)()()()(2121t f t f t f t f +≠+即不满足可加性,故为非线性时不变系统。
信号与系统--完整版答案--纠错修改后版本
1)
3)
5)
3.8、求下列差分方程所描述的离散系统的单位序列响应。
2)5)
3.9、求图所示各系统的单位序列响应。
(a)
(c)
3.10、求图所示系统的单位序列响应。
3.11、各序列的图形如图所示,求下列卷积和。
(1)(2)(3)(4)
4.34 某LTI系统的频率响应,若系统输入,求该系统的输出。
4.35 一理想低通滤波器的频率响应
4.36 一个LTI系统的频率响应
若输入,求该系统的输出。
4.39 如图4-35的系统,其输出是输入的平方,即(设为实函数)。该系统是线性的吗?
(1)如,求的频谱函数(或画出频谱图)。
(2)如,求的频谱函数(或画出频谱图)。
(1) (2) (3) (4) (5)
4.19 试用时域微积分性质,求图4-23示信号的频谱。
图4-23
4.20 若已知,试求下列函数的频谱:
(1)(3) (5)
(8)(9)
4下列方式求图4-25示信号的频谱函数 (1)利用xx和线性性质(门函数的频谱可利用已知结果)。
(1)
5-18 已知系统函数和初始状态如下,求系统的零输入响应。
(1),
(3),
5-22 如图5-5所示的复合系统,由4个子系统连接组成,若各子系统的系统函数或冲激响应分别为,,,,求复合系统的冲激响应。
5-26 如图5-7所示系统,已知当时,系统的零状态响应,求系数a、b、c。
5-28 某LTI系统,在以下各种情况下起初始状态相同。已知当激励时,其全响应;当激励时,其全响应。
(7)(8)
1-7 已知序列的图形如图1-7所示,画出下列各序列的图形。
信号与系统(第三版)陈生潭第一章课后答案

信号与系统 电子教案
1.3 阶跃信号与冲激信号
n
f ( n)
©西安电子科技大学电路与系统教研中心
k
第1-16页
■
信号与系统 电子教案
1.3 阶跃信号与冲激信号
1.3 阶跃信号与冲激信号
一 序列函数定义
1.阶跃信号
(t )
A (t t 0 )
1
ε (t)
∆→0
0 t
2
1 o t
A
0
t0
t
0 (t ) t 1
广义函数:为避开变量点上没有确定函数值的情况, 广义函数采用它与另一个函数相互作用(如相乘后积 分)后的效果来定义:
第1-20页
■
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案
1.3 阶跃信号与冲激信号
g (t )(t )dt Ng[(t )]
可理解为:在试验函数集{(t)}中,对每一函数 (t),按一定规则Ng,分配一个函数值Ng[(t)]. 注意: (t)是普通函数,满足连续、有任意阶导数。 且(t)及各阶导数在|t|时要比|t|的任意次幂更 快的趋于零;
f (t) 1 o 1 t
反转 t → - t
1 -1
f (- t )
o
t
第1-9页
■
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案
1.2 信号的运算
2.平移
将 f (t) → f (t – t0) , f (k) → f (t – k0)称为对信号f (· )的 平移或移位。若t0 (或k0) >0,则将f (· )右移;否则左移。 如: f (t- 1)
信号与系统课后习题答案

习 题 一 第一章习题解答基本练习题1-1 解 (a) 基频 =0f GCD (15,6)=3 Hz 。
因此,公共周期3110==f T s 。
(b) )30cos 10(cos 5.0)20cos()10cos()(t t t t t f ππππ+==基频 =0f GCD (5, 15)=5 Hz 。
因此,公共周期5110==f T s 。
(c) 由于两个分量的频率1ω=10π rad/s 、1ω=20 rad/s 的比值是无理数,因此无法找出公共周期。
所以是非周期的。
(d) 两个分量是同频率的,基频 =0f 1/π Hz 。
因此,公共周期π==01f T s 。
1-2 解 (a) 波形如图1-2(a)所示。
显然是功率信号。
t d t f TP T TT ⎰-∞→=2)(21lim16163611lim 22110=⎥⎦⎤⎢⎣⎡++=⎰⎰⎰∞→t d t d t d T T T W(b) 波形如图1.2(b)所示。
显然是能量信号。
3716112=⨯+⨯=E J (c) 能量信号 1.0101)(lim101025=-===⎰⎰∞∞---∞→T t ttT e dt edt eE J(d) 功率信号,显然有 1=P W1-3 解 周期T=7 ,一个周期的能量为 5624316=⨯+⨯=E J 信号的功率为 8756===T E P W 1-5 解 (a) )(4)2()23(2t tt δδ=+; (b) )5.2(5.0)5.2(5.0)25(5.733-=-=----t e t e t et tδδδ(c) )2(23)2()3sin()2()32sin(πδπδπππδπ+-=++-=++t t t t 题解图1-2(a) 21题解图1-2(b) 21(d) )3()3()(1)2(-=----t e t t et δδε。
1-6 解 (a) 5)3()94()3()4(2-=+-=+-⎰⎰∞∞-∞∞-dt t dt t t δδ(b) 0)4()4(632=+-⎰-dt t t δ(c) 2)]2(2)4(10[)]42(2)4()[6(63632=+++-=+++-⎰⎰--dt t t dt t t t δδδδ(d)3)3(3)(3sin )(1010=⋅=⎰⎰∞-∞-dt t Sa t dt ttt δδ。
信号与系统课后习题答案汇总

第一章习题参考解答1.1 绘出下列函数波形草图。
(1) ||3)(t et x -=(2) ()⎪⎪⎨⎧<≥=02021)(n n n x n n (3) )(2sin )(t t tx επ= (5) )]4()([4cos )(--=-t t t et x tεεπ(7) t t t t x 2cos)]2()([)(πδδ--=(9) )2()1(2)()(-+--=t t t t x εεε)5- (11) )]1()1([)(--+=t t dtdt x εε (12) )()5()(n n n x --+-=εε (13) ⎰∞--=td t x ττδ)1()((14) )()(n n n x --=ε1.2 确定下列信号的能量和功率,并指出是能量信号还是功率信号,或两者均不是。
(1) ||3)(t et x -=解 能量有限信号。
信号能量为:(2) ()⎪⎩⎪⎨⎧<≥=02021)(n n n x n n解 能量有限信号。
信号能量为:(3) t t x π2sin )(=解 功率有限信号。
周期信号在(∞-∞,)区间上的平均功率等于在一个周期内的平均功率,t π2sin 的周期为1。
(4) n n x 4sin)(π=解 功率有限信号。
n 4sin π是周期序列,周期为8。
(5) )(2sin )(t t t x επ=解 功率有限信号。
由题(3)知,在),(∞-∞区间上t π2sin 的功率为1/2,因此)(2sin t t επ在),(∞-∞区间上的功率为1/4。
如果考察)(2sin t t επ在),0(∞区间上的功率,其功率为1/2。
(6) )(4sin)(n n n x επ=解 功率有限信号。
由题(4)知,在),(∞-∞区间上n 4sin π的功率为1/2,因此)(4sinn n επ在),(∞-∞区间上的功率为1/4。
如果考察)(4sinn n επ在),0(∞区间上的功率,其功率为1/2。
信号与系统课后习题答案

1.1绘出下列函数波形草图。
(1) (2)
(3) (4)
(5) (6)
(7) (8)
(9) (10)
(11) (12)
(13) (14)
1.2确定下列信号的能量和功率,并指出是能量信号还Biblioteka 功率信号,或两者均不是。(1)
解 能量有限信号。信号能量为:
(2)
解 能量有限信号。信号能量为:
(3)
解 功率有限信号。周期信号在( )区间上的平均功率等于在一个周期内的平均功率, 的周期为1。
(4)
解 功率有限信号。 是周期序列,周期为8。
(5)
解功率有限信号。由题(3)知,在 区间上 的功率为1/2,因此 在 区间上的功率为1/4。如果考察 在 区间上的功率,其功率为1/2。
(6)
解功率有限信号。由题(4)知,在 区间上 的功率为1/2,因此 在 区间上的功率为1/4。如果考察 在 区间上的功率,其功率为1/2。
(1) (2)
(7)
解 非功率、非能量信号。考虑其功率:
上式分子分母对 求导后取极限得 。
(8)
解 能量信号。信号能量为:
1.3已知 的波形如题图1.3所示,试画出下列函数的波形。
(1) (2)
(3) (4)
(5) (6)
(7) (8)
(9)
(10)
(11)
(12) (13)
(14) =
1.4已知 及 的波形如题图1.4所示,试分别画出下列函数的波形,并注意它们的区别。
信号与系统课后习题附参考答案
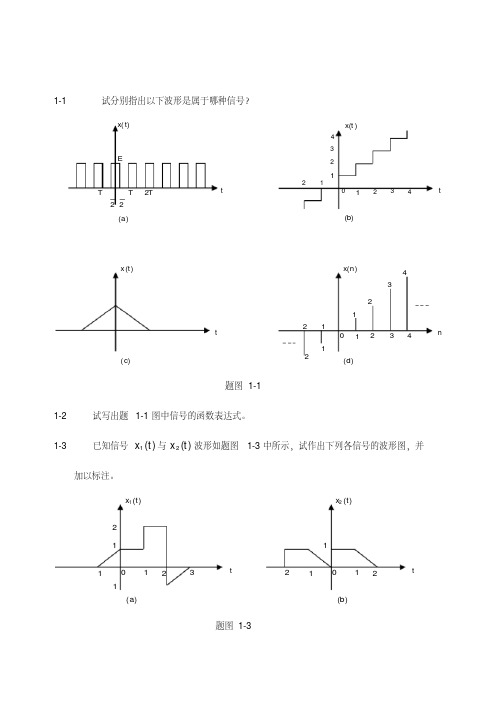
1-1试分别指出以下波形是属于哪种信号?题图1-11-2 试写出题1-1图中信号的函数表达式。
1-3已知信号)(1t x 与)(2t x 波形如题图1-3中所示,试作出下列各信号的波形图,并加以标注。
题图1-3t)(2t x )(b 12112t)(1t x )(a 121123122T T2TEt)(t x )(a t)(t x )(b 13124023412t)(t x )(c n)(n x )(d 2213012112344⑴)2(1t x ⑵)1(1t x ⑶)22(1t x ⑷)3(2tx ⑸)22(2t x ⑹)21(2t x ⑺)(1t x )(2t x ⑻)1(1t x )1(2tx ⑼)22(1t x )4(2tx 1-4 已知信号)(1n x 与)(2n x 波形如题图1-4中所示,试作出下列各信号的波形图,并加以标注。
题图1-4⑴)12(1n x ⑵)4(1n x ⑶)2(1n x ⑷)2(2n x ⑸)2(2n x ⑹)1()2(22n x n x ⑺)2(1nx )21(2n x ⑻)1(1n x )4(2nx ⑼)1(1nx )3(2nx 1-5 已知信号)25(t x 的波形如题图1-5所示,试作出信号)(t x 的波形图,并加以标注。
题图1-5t)25(t x 110232523n)(2n x )(b 2213121124n)(1n x )(a 22131142134212321231-6 试画出下列信号的波形图:⑴)8sin()sin()(t t t x ⑵)8sin()]sin(211[)(t t t x ⑶)8sin()]sin(1[)(t t t x ⑷)2sin(1)(t tt x 1-7 试画出下列信号的波形图:⑴)(1)(t u e t x t⑵)]2()1([10cos )(t u t u t e t x t⑶)()2()(t u e t x t⑷)()()1(t u et x t ⑸)9()(2tu t x ⑹)4()(2tt x 1-8试求出以下复变函数的模与幅角,并画出模与幅角的波形图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
信号与系统(陈生潭)习题答案1-4章部分1第一章,第二章,第三章,第四章,第一章:1.找两个表示信号的例子,并指出信号表示的信息(消息)。
1.1(1),1.1(5),1.1(9);1.2(4),1.2(6) ;1.3(a);1()(1)0.5*() 2.5*(1)(3)f t t t t t εεεε=++--+-1.4(6), (1)6()j t f t eπ-=, 周期信号,周期为22T ππ==1.5(10);1.6(4);1.11(3),[]00000()()()()1j t j t j t j t j t e t t t dte t dt e t t dt e e e ωωωωωδδδδ∞--∞∞∞---∞-∞----=--=-=-⎰⎰⎰1.11(7) 2221(1)()(1)()21/22(1)()2()2t t t dt t t t dt t t t dt t dtδδδδ∞∞-∞-∞∞∞-∞-∞++=++=++==⎰⎰⎰⎰1.11(8)()()221()212()2()2()tttxx x dx x x x dxx dx t δδδε-∞-∞-∞++=++==⎰⎰⎰ 1.17(a) 解:设左边加法器的输出为'()x t ,则积分器的输出为()x t 。
根据两个加法器的输入输出关系,可以得到''()()3()()()2()x t f t x t y t x t x t =-=+因此"'''"''''''''()()3()()()2()()3()2(()3())()2()3(()2())()2()3()()3()()2()x t f x x t y t x t x t f x x t f t x t f x f t x t x t f x f t y t y t y t f t f t =-=+=-+-=+-+=+-∴+=+1.17(b)"'"'()()3()2()()3()2()()y t f t y t y t y t y t y t f t =--⇒++=1.17(c) 解:设左边加法器的输出为()x k ,则()()(1)x k f k ax k =--(1)()()(1)y k x k bx k =+-(2)由 式(1)和(2)(1)(1)(2)(1)(1)(2)x k f k ax k y k x k bx k -=----=-+- 因此[][]()()(1)(1)(2)()(1)(1)(2)()(1)(1)y k f k ax k b f k ax k f k bf k a x k bx k f k bf k ay k =--+---=+---+-=+---即()(1)()(1)y k ay k f k bf k +-=+-1.17(d)()4[()2(1)3(2)]5[(1)2(2)3(3)]6[(1)2(3)3(4)]4()5(1)6(1)2[4(1)5(2)6(3)]3[4(2)5(3)6(4)]4()5(1)6(2)2(1)3(2)y k f k x k x k f k x k x k f k x k x k f k f k f k x k x k x k x k x k x k f k f k f k y k y k =+-----+---+-+---=--+-+---+-----+-=--+-+---所以,输入输出方程是()2(1)3(2)4()5(1)6(2)y k y k y k f k f k f k --+-=--+-1.18 是否为线性系统(1)否; 零输入响应2()x t 为非线性响应,零输入响应和零状态响应也不是和的关系。
(2)否;零状态响应2()f t 为非线性响应。
(3)否;(4)是;1.19 解:(1) 线性、时不变、因果、稳定;(2) 非线性(零输入响应12(0)(0)x x 为非线性响应)、时不变、因果、不稳定(响应中0()t f d ττ⎰,例如信号()()f t t ε=时,随时间增长变为无穷大。
); (3) 非线性(输出响应sin[()]f t 为非线性响应)、时不变、因果、稳定;(4) 线性、时变(响应(2)f t 和初始时间有关系)、非因果(响应(1)f t +,0t =时刻的响应和之后的时刻1t =有关系)、稳定;(5) 非线性(响应()(2)f k f k -为非线性响应)、时不变、因果、稳定; (6) 线性、时变(响应11(0)2kx ⎛⎫⎪⎝⎭为和初始时刻有关系的响应)、非因果(响应(1)(2)k f k -+,0k =时刻的响应和之后的时刻2k =有关系)、不稳定(响应中(1)(2)k f k -+,例如信号()()f k k ε=时,随k 增长变为无穷大。
);1.21 解:零输入线性,包括零输入齐次性和零输入可加性。
因为激励()0f t =,故系统零状态响应()0fyt =。
对于零输入响应,已知3121(0)1,(0)0()23,0ttx x x y t e e t ----==→=+≥3122(0)0,(0)1()42,0t t x x x y t e e t ----==→=-≥ 根据零输入线性,可得12123(0)5,(0)3()5()3()229,0x x x t tx x y t y t y t e e t ----==→=+=+≥响应;3()()229,0tt xy t y t ee t --==+≥1.23 解: 设初始状态12(0)1,(0)2x x --==时,系统的零输入响应为1()x y t ;输入()()f t t ε=时,系统的零状态响应为 1()f y t ,则有11231231()()65()3()87t tx f t t x f y t y t e e y t y t e e----⎧+=-⎪⎨+=-⎪⎩联立,解方程组得12312354t t x t t f y e e y e e----⎧=-⎪⎨=-⎪⎩根据系统的线性特性,求得 (1)23154,0t t x x y y e e t --==-≥(2)输入为()2()f t t ε=时的零状态响应12322(),0ttff y y e e t --==-≥# 离散信号()f n : # (3)()()(3)t t t t εεεε-=-- # )()()()(02t d d e d e tttεττδττδττδτ===⎰⎰⎰∞-∞-∞--1.4(6), (1)6()j t f t eπ-=, 周期信号,周期为22T ππ==# 系统结构框图如图所示,该系统的单位冲激响应h(t) 满足的方程式为dh t dt h t t ()()()+=δ)()()()()()()()();()()()()()()()()()()()()()()()('''''t t h dtt dh t t h t h t t x t h t y t x t y t y t y t x t s t x t s t y t s t y t s t x t s δδδ=+=+===+-=-===-=代入第二章:2.3(3)()434()()()(1)()(1)f t f t f t t t t δδδ*=*+++-444(1)()(1)(2)(1)(1)(2)f t f t f t t t t t εεεε=+++-=+++----2.3(4) 45()()((1)(1))((1)(4))f t f t t t t t εεεε*=+--*---235()|()|()|()|t t t t t t t t t t t t t t t t εεεε→→-→-→-=--+()(2)(2)(3)(3)(5)(5)t t t t t t t t εεεε=------+--2.4(4)122200()()()()()()11()22ttf t f t t t t t d d t t εετετετττττε∞-∞*=*=-===⎰⎰2.4(8)122()()(1)(2)(2)(1)(1)t f t f t t e t e t d e t d ττεεετεττεττ∞-∞-∞*=-*-=---=--⎰⎰当 12t -< 即 3t <时 1112()()t t f t f t e d e ττ---∞*==⎰当 12t -≥ 即 3t ≥时 2212()()f t f t e d e ττ-∞*==⎰故 21(3)(1)(2)(3)tt e t t e t e t εε-⎧≥-*-=⎨<⎩2.4(9) 2312()()(1)(3)tt f t f t et e t εε--*=-*+22(1)93(3)(1)(3)t t e e t e e t εε----+=-*+72(1)3(3)723137232724362331((1)(3))(()())|()()|()(2)()(2)t t t t t t t t t t t t t t e e t e t e e t e t e e e t e e e t e e t εεεεεεε---+--→-+--→+-----+-+=-*+=*=-=-+=-+2.612013111()()53()123323t or t t t f t f t t t t t <->⎧⎪+-≤<⎪⎪*=⎨--≤<⎪⎪-≤≤⎪⎩2.7(1)112222[(2)(1)]2[(2)(1)]23t t t d d εετετετττττ∞-∞--*+--=+--===-⎰⎰2.7(2)11()()()()1t tn n n n t t t d d t t n εετεττττε+-∞*===+⎰⎰ [()0]ε-∞= 2.7(3)''()()()()[()()]tt et t t e t t t εδεεδε--**=** [()0]ε-∞='()[()()]()[()()]()()()t t tte t t t e t t t e t t e t εδεεδδεδε----=**=**=*=2.7(4)由于 ()0t t t ε=-∞=2"2'2'22()()()()()[()()]()()()()()()()t t ttte t t t t e t t t t t e t t t e t t t e t εδεεδεδεδεεδδε-----**=**+=**=**=2.8123()()[(2)2(1)](1)(2)(1)2(1)(1)()2()(3)(3)2()t t t t f t f t t t t t t t t t t t t t t t t εεεεεεεεεεε→+→*=-++-*+=-+*++-*+=-+=-+++(1)(13)2f -=--+=-;(0)(03)03f =-++=-(1)(13)2112f =-++⋅⋅=-2.9 由图可知 1()(2)(3)f t t t εε=---,(1)2()(1)t f t et ε-+=+因此(1)(1)12213112(1)(2)(1)(1)()()()(2)(1)(3)(1)[()()][()()](1)()(1)()(1)(1)(1)(2)01112(t t t t t t t t t t t t t t t t t t f t f t f t t e t t e t t e t t e t e t e t e t e t t e t e e εεεεεεεεεεεε-+-+----→-+→-+→-→---------=*=-*+--*+=*-*=---=-----<=-≤<1)2t ⎧⎪⎨⎪-≥⎩# ()()()()t f t t f t δδ**= # ())()(2121t t t f tt t t f --=-*-δ# 已知函数()f t ,则函数0()f tat -可以把函数()f at -右移0t a 得到。
