实验四Matlab神经网络及应用于近红外光谱的汽油辛烷值预测
汽油组分及汽油辛烷值预测方法研究进展_仇爱波

关键词:辛烷值;汽油;汽油组分;拓扑指数法;基团贡献法
中 图 分 类 号 :TE62
文 献 标 识 码 :A
文 章 编 号 :1001-9219(2014)02-62-05
辛烷值是在内燃机的燃烧室中未燃混合气受已 燃气压缩和热传递时汽油抑制过早燃烧的表现数 值,是汽油性能最重要的指标之一,过早燃烧不仅过 度消耗了汽油资源, 还可能会在发动机工作时产生 爆炸性威胁,并且对发动机有所损害。汽油辛烷值是 用 ASTM-CFR 内 燃 机 在 相 同 测 试 条 件 下 与 测 试 汽 油达到相同爆震强度时异辛烷和正庚烷混合物的异 辛烷的体积分数表示的, 根据发动机的转速及进气 温 度 分 为 研 究 法 辛 烷 值 (RON) 和 马 达 法 辛 烷 值 (MON)。 随着汽车发动机压缩比的增加,对汽油辛 烷值的要求也越来越高, 如对每一个可能提高辛烷 值的物质进行合成, 再利用仪器对其辛烷值进行测 定, 这不仅花费大量的时间, 更花费大量的研究经 费, 因此通过各种算法来建立辛烷值的预测模型受 到广泛的关注,在早期一些文献[1]只报道了辛烷值与 化合物结构之间的一些定性关系, 随着各种计算软 件的研究开发,各种定量计算的方法才逐步被提出。
的含氧类化合物对辛烷值有所提高,并认为在整个 燃烧过程中自由基的形成来源于羰基结构,在燃烧 过程中影响着整个自由基的传递和终止, 确定了 α 位的 C-H 键对产生自由基起着决定性的作用。 通过 对影响分子键强度的现象分析,确定烯醇-酮的互变 异构的气象常数和形成最稳定的烯醇二聚物时烯 丙基氢的数量对自由基的传递起着决定性的作用。 基团贡献法的适用范围较广,主要注重分子结构的 拆解,要想拥有较高的相关性,则更要保证拆解的 正确性, 不过利用该方法获得的标准偏差相对较 大。 1.3 仪器分析法
基于DMD哈达玛变换近红外光谱仪的汽油辛烷值检测

基于DMD哈达玛变换近红外光谱仪的汽油辛烷值检测斯中发;王月;韦紫玉【摘要】应用近红外光谱分析检测技术建立一种汽油研究法辛烷值的快速定量分析方法.收集来自不同地区共100个汽油样品,应用化学计量学方法建立近红外光谱原始数据信息与研究法辛烷值之间的定量分析模型,结果表明:对原始光谱进行归一化处理后,采用偏最小二乘回归建立数学模型,其校正集与预测集相关系数分别为0.9300和0.9322,校正集均方根误差与预测集均方根误差分别为0.6700和0.6577,表明模型准确可靠,可应用于汽油辛烷值的快速检测.【期刊名称】《浙江化工》【年(卷),期】2018(049)007【总页数】5页(P50-54)【关键词】汽油辛烷值;哈达玛变换;近红外光谱仪【作者】斯中发;王月;韦紫玉【作者单位】浙江华才检测技术有限公司, 浙江诸暨 311800;浙江华才检测技术有限公司, 浙江诸暨 311800;河池市粮油质量监督检测中心, 广西河池 547000【正文语种】中文近红外光谱(Near Infrared Spectrum,NIR)作为一种快速、无损检测分析技术,广泛应用于食品、石油化工、纺织等多个领域,其利用有机物中含有的各种含氢基团(如C-H、O-H、N-H等)的倍频与合频谱带在近红外区域具有特征性振动信息,结合化学计量方法建立光谱信息与样品成分含量之间的定量关系,从而实现样品中指标含量的快速测定[1-2]。
近红外光谱分析技术最早应用于汽油辛烷值的分析测量,而后关于石油产品其他性质的检测日渐增多,并得到石化行业的认可与推广。
近年来,随着NIR研究和应用领域的不断扩展,各种新型近红外光谱仪也层出不穷,如何应用便携式或微型近红外光谱仪设备实现石油相关品质属性的移动、快速、准确、简便检测成为研究热点。
数字变换式微型近红外光谱仪主要包括傅里叶变换式和哈达玛变换式两种模式[3]。
傅里叶变换光谱仪因存在可动部件,且对外界环境要求较高,主要用于实验室离线分析。
汽油辛烷值神经网络预测模型的设计

汽油辛烷值神经网络预测模型的设计
秦秀娟;陈宗海
【期刊名称】《控制与决策》
【年(卷),期】1999(14)2
【摘要】针对催化重整工艺仿真数学模型中遇到的汽油辛烷值预测方面的困难,
提出一种将定量计算与神经网络计算相结合的催化重整工艺汽油辛烷值的预测模型。
此预测模型综合考虑了反应器温度。
【总页数】5页(P151-155)
【关键词】汽油;辛烷值;神经网络;预测模型;设计
【作者】秦秀娟;陈宗海
【作者单位】中国科学技术大学自动化系
【正文语种】中文
【中图分类】TE626.21
【相关文献】
1.汽油精制过程中的辛烷值损失预测模型 [J], 杜明洋;张甜甜;薄其高;许文文
2.基于BP神经网络对汽油辛烷值损失预测模型的构建 [J], 王宁宁
3.基于BP神经网络对汽油辛烷值损失预测模型的构建 [J], 王宁宁
4.基于改进PCA-RFR算法的汽油辛烷值损失预测模型的构建与分析 [J], 蒋伟;佟
国香
5.基于汽油催化裂化过程实时数据的辛烷值损失预测模型 [J], 韩庆珏;邹敏;霍皓灵
因版权原因,仅展示原文概要,查看原文内容请购买。
基于数据挖掘的汽油精制过程辛烷值损失预测模型
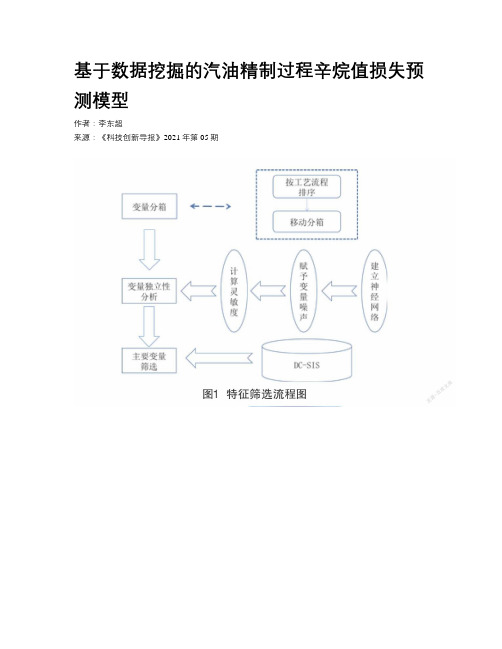
基于数据挖掘的汽油精制过程辛烷值损失预测模型作者:***来源:《科技创新导报》2021年第05期摘要:汽油精制过程中造成的辛烷值损失会降低汽油的燃烧效率,如何降低汽油精制过程中辛烷值的损失量是目前相关企业面临的一个重要课题。
本文利用我国某石化企业在催化裂化汽油精制过程中积累的数据,建立基于神经网络、测量误差模型以及DC-SIS数据降维方法的两阶段特征筛选模型,选择出对辛烷值影响比较大的因素。
设计了一种基于XGBoost和神经网络的辛烷值预测模型,可以实现对不同原材料和不同操作下精制后辛烷值的预测,经验证,模型的均方误差为0.06876,所设计模型在处理辛烷值预测问题时可以达到比较好的预测效果。
关键词:辛烷值高维降维测量误差模型神经网络 XGBoost中图分类号:TP274 文獻标识码:A 文章编号:1674-098X(2021)02(b)-0092-05Prediction Model of Octane Number Loss in Gasoline Refining Process Based on Data Mining LI Dongchao(School of Mathematics and Statistics, Nanjing University of Information Science & Technology, Nanjing, Jiangsu Province, 210044 China)Abstract: The loss of octane number in the process of gasoline refining will reduce the combustion efficiency of gasoline. How to reduce the loss of octane number in the process of gasoline refining is an important issue facing related enterprises. This paper uses the data accumulated by a petrochemical enterprise during the refining process of catalytic cracking gasoline to establish a two-stage feature screening model based on neural network, measurement error model and DC-SIS data dimensionality reduction method, and select the one that has a greater impact on the octane number factor. An octane number prediction model based on XGBoost and neural network is designed,which can predict the octane number after refining under different raw materials and different operations. After verification, the mean square error of the model is 0.06876. A better prediction effect can be achieved in the alkane number prediction problem.Key Words: Octane number; High dimensionality reduction; Neural networks; XGBoost汽油是小型车辆的主要燃料,汽油燃烧产生的尾气排放对大气环境有重要影响。
基于近红外光谱的汽油分子组成预测

基于近红外光谱的汽油分子组成预测
蔡广庆;张莉;李春澎;胡益炯;王弘历;杨诗棋;纪晔
【期刊名称】《油气与新能源》
【年(卷),期】2023(35)1
【摘要】汽油分子信息解析耗时较长的问题制约着其在炼厂实时优化中的应用前景。
依据汽油的近红外光谱及其对应的色谱分子组成数据,采用欧氏距离与多元线性回归方法拟合待测光谱,并把拟合参数代入对应的汽油分子数据库,建立了由近红外光谱快速预测汽油分子组成的模型。
模型的预测值与实验值吻合较好,验证集的汽油分子组成预测平均绝对误差为0.0356,证明了此模型不但具有广泛适用性,而且满足炼厂汽油分子解析的精度要求。
基于近红外光谱预测汽油分子组成的方法可以应用于炼厂的实时在线分析优化中,并且对炼厂反应过程模型和油品调和模型的建立具有重要意义。
【总页数】6页(P111-116)
【作者】蔡广庆;张莉;李春澎;胡益炯;王弘历;杨诗棋;纪晔
【作者单位】中国石油天然气股份有限公司规划总院;北京无线电计量测试研究所【正文语种】中文
【中图分类】TE622
【相关文献】
1.甲基叔丁基醚含量对近红外光谱法测定汽油族组成的影响
2.基于支持向量机的汽油族组成近红外光谱分析方法研究
3.汽油族组成的近红外光谱快速测定
4.化学计
量学方法在近红外光谱分析中的应用--近红外光谱法测定汽油辛烷值5.基于近红外光谱快速预测石脑油单体烃分子组成
因版权原因,仅展示原文概要,查看原文内容请购买。
数学建模实验四:Matlab神经网络以及应用于汽油辛烷值预测

实验四:Matlab 神经网络以及应用于汽油辛烷值预测专业年级: 2014级信息与计算科学1班姓名: 黄志锐 学号:201430120110一、实验目的1. 掌握MATLAB 创建BP 神经网络并应用于拟合非线性函数2. 掌握MATLAB 创建REF 神经网络并应用于拟合非线性函数3. 掌握MATLAB 创建BP 神经网络和REF 神经网络解决实际问题4. 了解MATLAB 神经网络并行运算二、实验内容1. 建立BP 神经网络拟合非线性函数2212y x x =+第一步 数据选择和归一化根据非线性函数方程随机得到该函数的2000组数据,将数据存贮在data.mat 文件中(下载后拷贝到Matlab 当前目录),其中input 是函数输入数据,output 是函数输出数据。
从输入输出数据中随机选取1900中数据作为网络训练数据,100组作为网络测试数据,并对数据进行归一化处理。
第二步 建立和训练BP 神经网络构建BP 神经网络,用训练数据训练,使网络对非线性函数输出具有预测能力。
第三步 BP 神经网络预测用训练好的BP 神经网络预测非线性函数输出。
第四步 结果分析通过BP 神经网络预测输出和期望输出分析BP 神经网络的拟合能力。
详细MATLAB代码如下:27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54disp(['神经网络的训练时间为', num2str(t1), '秒']);%% BP网络预测% 预测数据归一化inputn_test = mapminmax('apply', input_test, inputps); % 网络预测输出an = sim(net, inputn_test);% 网络输出反归一化BPoutput = mapminmax('reverse', an, outputps);%% 结果分析figure(1);plot(BPoutput, ':og');hold on;plot(output_test, '-*');legend('预测输出', '期望输出');title('BP网络预测输出', 'fontsize', 12);ylabel('函数输出', 'fontsize', 12);xlabel('样本', 'fontsize', 12);% 预测误差error = BPoutput-output_test;figure(2);plot(error, '-*');title('BP神经网络预测误差', 'fontsize', 12);ylabel('误差', 'fontsize', 12);xlabel('样本', 'fontsize', 12);figure(3);plot((output_test-BPoutput)./BPoutput, '-*');title('BP神经网络预测误差百分比');errorsum = sum(abs(error));MATLAB代码运行结果截图如下所示:MATLAB代码运行结果如下所示:图1 BP神经网络预测输出图示图2 BP神经网络预测误差图示图3 BP 神经网络预测误差百分比图示2. 建立RBF 神经网络拟合非线性函数22112220+10cos(2)10cos(2)y x x x x ππ=-+-第一步 建立exact RBF 神经网络拟合, 观察拟合效果详细MATLAB 代码如下:MATLAB代码运行结果如下所示:图4 RBF神经网络拟合效果图第二步建立approximate RBF神经网络拟合详细MATLAB代码如下:13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41F = 20+x1.^2-10*cos(2*pi*x1)+x2.^2-10*cos(2*pi*x2); %% 建立RBF神经网络% 采用approximate RBF神经网络。
近红外光谱预测汽油辛烷值

前言烃加工工业中,连续在线监测关键石油物流的性质,是强化过程控制和炼厂信息系统集成的重要环节,为表征石油物流这一高度复杂的烃类混合物,引入了一系列测试手段和标准指标,总的来说,这些指标测试费用高、重复性差、试样用量大,在线实现时维护代价高,响应速度慢。
七十年代以来,近红外光谱(NIR)技术在分析机理、仪器制造、数据处理方面有了很大发展,与传统分析仪器相比,近红外分析仪有显著优势:光纤远程信号传输,可实现非接触式测量;一谱多用,只要建立模型,可同时测量多个指标;预处理简单,分析中不需化学试剂;响应速度快;易于制成小型紧凑的过程分析仪,在农作物分析等方面已建立实用标准[47]。
八十年代末,西雅图华盛顿大学过程分析化学中心(CPAC)进行了将近红外技术用于石油化学领域的研究,最重要的工作是测量汽油辛烷值,族组成和其它几个关键指标,随后在世界范围内的众多试验室和炼厂开展了这方面的研究工作,例如位于法国的BP拉菲尔炼厂将近红外技术大量用于过程控制,效益显著:在调合工艺中,一套近红外分析仪可替代两台辛烷机和一套雷德蒸汽压测试仪和其它蒸馏测试装置,月维护时间减小到数小时,光学仪器发生故障的平均时间间隔能够提高到几百小时,辛烷值测量范围增宽,重复性偏差小于0.1,该厂借助于近红外分析系统对乙烯蒸汽裂解炉的进料进行高频监测和优化,年收益百万美元,分析设备的投资可很快回收,还有利于下游分馏塔的稳定操作尽管NIR预测的重复性很好,在数学模型的设计上仍要谨慎从事。
因为近红外技术用于石油物流性质的预测是基于ASTM系列测定的二次方法,NIR模型只有在其适用范围内,才能获得与ASTM测试一样的准确性,当对象物流由于进料、工艺等原因偏离原模型的适用范围时,NIR模型必须重新标定。
如何提取NIR光谱和目标性质的统计关系是这门技术软件方面的关键。
一些典型的数学方法有主因子分析(PCA)、偏最小二乘法(PLS)、多元线性回归(MLR)、判别分析(DA)、聚类分析和人工神经网络(ANN)等,这些基本属于计量化学问题。
近红外光谱预测汽油辛烷值和辛烷值仪的研制

第19卷,第5期 光 谱 学 与 光 谱 分 析Vol 119,No 15,pp 68426861999年10月 Sp ectro scop y and Sp ectral A nalysisO ctober ,1999 近红外光谱预测汽油辛烷值和辛烷值仪的研制 王宗明 华伟英 韦占凯 张弧弘 武惠忠石油化工科学研究院,100083 北京 北京精密光学仪器公司,100015 北京摘 要 本文报道用近红外光谱预测汽油马达法辛烷值、研究法辛烷值和抗爆指数的方法。
用多重线性回归和偏最小二乘法回归建立辛烷值的预测模型。
基于此模型,首次研制成功光学多道近红外辛烷值仪。
主题词 光学多道近红外辛烷值仪, 多重线性回归, 偏最小二乘法, 汽油辛烷值 1998203226收,1998210213接受;王宗明,1935年生,石油化工科学研究院教授级高级工程师1 近红外光谱法测定汽油的辛烷值用化学计量学方法通过光谱研究性质和组成的关系与日俱增。
通过近红外光谱预测汽油辛烷值有重要的工业应用价值。
前文我们报道了用汽油烃分子CH 伸缩振动二倍频预测汽油辛烷值,并研制成功了傅里叶变换近红外辛烷值仪[1,2]。
考虑到炼油厂过程控制的需要[3],本工作建立了用三倍频预测汽油辛烷值的方法,并研制成功近红外光学多道辛烷值仪。
111 实验仪器使用北京精密光学仪器公司研制的近红外光学多道分析仪。
以溴钨灯作为近红外光源,硅光二极管阵列作为多道探测器。
光谱分辨率实测为18c m -1,光谱范围为9000~14000c m -1。
112 实验方法在室温下,将汽油试样(15mL )放于干净的光程为5c m 的液槽中,以不放液槽时的空白透过率作为参比本底,测量9000~14000c m -1的近红外吸收光谱。
测量一个光谱所需的全部时间为7秒(对光谱背景和样品光谱各扫描100次的时间)。
113 模型的建立和汽油辛烷值预测结果分别用多重线性回归(M L R )和偏最小二乘方回归(PL S )法[1~6,7,8]建立辛烷值预测模型。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
在理论上,RBF 网络和 BP 网络一样能以任意精度逼近任何非线性函数。但由于它们使 用的激活函数不同,其逼近性能也不相同。Poggio 和 Girosi 已经证明,RBF 网络是连续函数 的最佳逼近,而 BP 网络不是。BP 网络使用的 Sigmoid 函数具有全局特性,它在输入值的很 大范围内每个节点都对输出值产生影响,并且激活函数在输入值的很大范围内相互重叠,因 而相互影响,因此 BP 网络训练过程很长。此外,由于 BP 算法的固有特性,BP 网络容易陷 入局部极小的问题不可能从根本上避免,并且 BP 网络隐层节点数目的确定依赖于经验和试 凑,很难得到最优网络。采用局部激活函数的 RBF 网络在很大程度上克服了上述缺点,RBF 不仅有良好的泛化能力,而且对于每个输入值,只有很少几个节点具有非零激活值,因此只 需很少部分节点及权值改变。学习速度可以比通常的 BP 算法提高上千倍, 容易适应新数据, 其隐含层节点的数目也在训练过程中确定,并且其收敛性也较 BP 网络易于保证,因此可以 得到最优解。
BP 网络是一种多层前馈神经网络,其神经元的传递函数为 S 型函数,因此输出量为 0 到 1 之间的连续量,它可以实现从输入到输出的任意的非线性映射。由于其权值的调整是利 用实际输出与期望输出之差,对网络的各层连接权由后向前逐层进行校正的计算方法,故而 称为反向传播(Back-Propogation)学习算法,简称为 BP 算法。BP 算法主要是利用输入、 输出样本集进行相应训练,使网络达到给定的输入输出映射函数关系。算法常分为两个阶段: 第一阶段(正向计算过程)由样本选取信息从输入层经隐含层逐层计算各单元的输出值;第 二阶段(误差反向传播过程)由输出层计算误差并逐层向前算出隐含层各单元的误差,并以 此修正前一层权值。
径向基神经网络的神经元结构如图 3 所示。径向基神经网络的激活函数采用径向基函数, 通常定义为空间任一点到某一中心之间欧氏距离的单调函数。由图 3 所示的径向基神经元结
构可以看出,径向基神经网络的激活函数是以输入向量和权值向量之间的距离 dist 作为自
变量的。径向基神经网络的激活函数(高斯函数)的一般表达式为
径向基函数的阈值 b1可以调节函数的灵敏度,但实际工作中更常用另一参数 C(称为
扩展常数)。 b1和 C 的关系有多种确定方法,在 MATLAB 神经网络工具箱中, b1和 C 的关
系为 b1i 0.8326 / Ci ,此时隐含层神经元的输出变为:
giq
exp(( W1i X q
0.8326)2 ) Ci
RBF 网络的结构与多层前向网络类似,它是一种三层前向网络。输入层由信号源节点组 成;第二层为隐含层,隐单元数视所描述问题的需要而定,隐单元的变换函数 RBF()是对 中心点径向对称且衰减的非负非线性函数;第三层为输出层,它对输入模式的作用作出响应。 从输入空间到隐含层空间的变换是非线性的,而从隐含层空间的输出层空间变换是线性的。
输出为:
n
yq riq w2i i 1
RBF 网络的训练过程分为两步:第一步为无教师式学习,确定训练输入层与隐含层间的
权值W1;第二步为有教师式学习,确定训练隐含层与输出层间的权值W 2 .在训练以前需要
提供输入向量 X 、对应的目标向量 T 和径向基函数的扩展常数 C。训练的目的是求取两层 的最终权值W1,W 2 和阈值 b1, b2 。
传递函数 purelin,正切 S 型传递函数 tansig,对数 S 型传递函数 logsig. BTF:训练函数,包括梯度下降 BP 算法训练函数 traingd,动量反传的梯度下降 BP 算法训
练函数 traingdm.动态自适应学习率的梯度下降 BP 算法训练函数 traingda,动量反传 和动态自适应学习率的梯度下降 BP 算法训练函数 traingdx、Levenberg_Marquardt 的 BP 算法训练函数 trainlm。 BLF: 网络学习函数,包括 Bp 学习规则 learngd、带动量项的 BP 学习规则 learngdm。 PF: 性能分析函数,包括均值绝对误差性能分析函数 mae、均方差性能分析函数 mse. IPF: 输入处理函数。 OPF: 输出处理函数。 DDF: 验证数据划分函数。
wij
E w1ij
ij p j
0 1 (η为学习系数)
其中:
ij ei f1'
s2
ei
ki w2ki
k 1
由此可以看出:①调整是与误差成正比,即误差越大调整的幅度就越大。②调整量与输
入值大小成比例,在这次学习过程中就显得越活跃,所以与其相连的权值的调整幅度就应该
越大,③调整是与学习系数成正比。通常学习系数在 0.1~0.8 之间,为使整个学习过程加快,
二、实验原理
2.1 BP神经网络
2.1.1 BP 神经网络概述 BP神经网络 Rumelhard 和 McClelland 于1986年提出。从结构上将,它是一种典
型的多层前向型神经网络,具有一个输入层、一个或多个隐含层和一个输出层。层与层之间 采用权连接的方式,同一层的神经元之间不存在相互连接。理论上已经证明,具有一个隐含 层的三层网络可以逼近任意非线性函数。
2.4 BP 神经网络与 RBF 神经网络的 MATLAB 实现
2.4.1 BP 神经网络的相关函数 (1) newff: BP 神经网络参数设置函数
函数功能:构建一个 BP 神经网络 函数形式:net=newff(P, T, S, TF, BTF, BLF, PF, IPF, OPF, DDF)
P: 输入数据矩阵(训练集的输入向量作为列构成的矩阵) T: 输出数据矩阵(训练集的期望向量作为列构成的矩阵) S: 隐合层节点数 TF: 节点传递函数,包括硬限幅传递函数 hardlim,对称硬限幅传递函数 hardlims,线性
在 RBF 网络训练中,隐含层神经元数量的确定是一个关键问题,简便的做法是使其与输 入向量的个数相等(称为精确(exact) RBF)。显然,在输入向量个数很多时,过多的隐含层单 元数是难以让人接受的。其改进方法是从 1 个神经元开始训练,通过检查输出误差使网络自 动增加神经元。每次循环使用,使网络产生的最大误差所对应的输入向量作为权值向量,产 生一个新的隐含层神经元,然后检查新网络的误差,重复此过程直到达到误差要求或最大隐 含层神经元数为止(称为近似(approximate) RBF)。
在 MATLAB 神经网络工具箱中,C 值用参数 spread 表示,由此可见,spread 值的大小
实际上反映了输出对输入的响应宽度。spread 值 越大,隐含层神经元对输入向量的响应范
围将越大,且神经元间的平滑度也较好。
输出层的输入为各隐含层神经元输出的加权求和。由于激活函数为纯线性函数,因此
a2k
f2
S1 i 1
w2ki a1i
ห้องสมุดไป่ตู้
b2k ,
i 1,2,s2
其中 f1(·), f2 (·)分别为隐含层和输出层的传递函数。 2)输出误差逆传播
在第一步的样本顺传播计算中我们得到了网络的实际输出值,当这些实际的输出值与期
望输出值不一样时,或者说其误差大于所限定的数值时,就要对网络进行校正。
RBF 网络的基本思想是:用 RBF 作为隐单元的“基”构成隐含层空间,这样就可以将输 入向量直接(即不需要通过权接)映射到隐空间。当 RBF 的中心点确定以后,这种映射关系 也就确定了。而隐含层空间到输出空间的映射是线性的,即网络的输出是隐单元输出的线性 加权和。此处的权即为网络可调参数。由此可见,从总体上看,网络由输入到输出的映射是 非线性的,而网络输出对可调参数而言却又是线性的。这样网络的权就可由线性方程直接解 出,从而大大加快学习速度并避免局部极小问题。
一般在使用过程中设置前面 6 个参数,后面 4 个参数采用系统默认参数。
注意:Matlab R2011a 之后的版本开始用新函数 feedforwardnet 替代函数 newff, 其用 法为
值,使网络的实际输出与期望输出接近一致(图 2)。
实际上针对不同具体情况,BP 网络的训练有相应的学习规则,即不同的最优化算法,
沿减少期望输出与实际输出之间误差的原则,实现 BP 网络的函数逼近、向量分类和模式识
别。
2.2 RBF神经网络
图 2 神经网络的训练
2.2.1 RBF 神经网络概述
1985 年,Powell 提出了多变量插值的径向基函数(Radical Basis Function, RBF)方 法。1988 年,Moody 和 Darken 提出了一种神经网络结构,即 RBF 神经网络,属于前向神经 网络类型,它能够以任意精度逼近任意连续函数,特别适合于解决分类问题。
BP 网络的学习过程主要由以下四部分组成: 1)输入样本顺传播 输入样本传播也就是样本由输入层经中间层向输出层传播计算。这一过程主要是 输入样本求出它所对应的实际输出。 ① 隐含层中第 i 个神经元的输出为
a1i
f1
R
w1ij p j
j 1
b1i
i 1,2,, s1
② 输出层中第 k 个神经元的输出为:
首先,定义误差函数
1 s2
E(w,b)=
2 k 1
(tk a2k ) 2
其次,给出权值的变化
① 输出层的权值变化
从第 i 个输入到第 k 个输出的权值为:
w2ki
E w2ki
ki a1i
其中:
ki ek f 2' , ek lk a2k
② 隐含层的权值变化
从第 j 个输入到第 i 个输出的权值为:
隐含层中的神经元多采用 S 型传递函数,输出层的神经元多采用线性传递函数。图1所 示为一个典型的BP神经网络。该网络具有一个隐含层,输入层神经元数据为 R,隐含层神 经元数目为 S1,输出层神经元数据为 S2,隐含层采用 S 型传递函数 tansig,输出层传递函 数为 purelin。
