Abaqus6.14有限元仿真分析视频教程-实例篇(上)
合集下载
基于Abaqus的自行车车架的有限元分析
基于Abaqus的自行车车架的有限元分析
卢磊;张明容;晋战喜
【期刊名称】《中国自行车》
【年(卷),期】2024()1
【摘要】此文利用有限元技术对自行车车架结构的静态特性做了详细的分析,采用Solidwork软件设计了自行车车架的3D数模,并通过有限元软件Abaqus搭建装配体的有限元分析模型,对自行车车架进行了静强度分析和模态分析,获得了自行车车架的静强度结果和模态振型及频率特性,为自行车车架的设计和改进提供依据。
【总页数】4页(P124-127)
【作者】卢磊;张明容;晋战喜
【作者单位】广州城市理工学院工程研究院;佛山镁利好自行车配件有限公司【正文语种】中文
【中图分类】TP3
【相关文献】
1.基于ABAQUS的FSAE赛车车架有限元分析
2.基于ABAQUS的某车架静态结构强度的有限元分析
3.基于ABAQUS的双箱自卸半挂车车架有限元分析
4.基于ABAQUS的某车载迫击炮车架结构有限元分析
5.基于ABAQUS的钻机车架板结构有限元分析
因版权原因，仅展示原文概要，查看原文内容请购买。
有限元仿真利器ABAQUS-PPT课件
怎么用abaqus建空间网架结构？ 在平面坐标中建立某个平面内的主框架的sketch，然后生成一个part，然后就 可在3D空间中构建你想要得框架的。 用写input的方式可以很快的建立这 个模型。 input文件的格式和大多数有限元程序差不多比如： *HEADING AN ANALYSIS FOR 8STORY FRAME STRUCTURE . **CREATE THE NODES *NODE 1, 0.0000, TE NODES *NGEN, NSET=S0 1, 17, 1 *NSET, NSET=Base 1, 17 *NSET, NSET=Middle 9 *ELEMENT, TYPE=B23 1, 1, 2 *ELGEN, ELSET=level0 1, 16, 1, 1, *BEAM SECTION, ELSET=B8, MATERIAL=steel, SECTION=I 0.375, 0.75, 0.40, 0.40, 0.036, 0.036, 0.019 0.,0.,-1. **DEFINE MATERIAL
ABAQUS中约定的边界条件类型有哪些？ ABAQUS模型中的6个自由度，其中的坐标中编号是1.2.3而不是常用的X.Y.Z。因 为模型的坐标系也可以是主坐标系或球坐标系等。边界条件的定义方法主要 有两种，这两种方法可以混合使用： 自由度1（U1）：沿坐标轴1方向上的平移自由度。 自由度2（U2）：沿坐标轴2方向上的平移自由度。 自由度3（U3）：沿坐标轴3方向上的平移自由度。 自由度4（UR1）：沿坐标轴1上的旋转自由度。 自由度5（UR1）：沿坐标轴2上的旋转自由度。 自由度6（UR1）：沿坐标轴3上的旋转自由度。 2、约定的边界条件类型： XSYMM：对称边界条件，对称面为与坐标轴1垂直的平面，即U1＝UR2＝UR3=0; YSYMM：对称边界条件，对称面为与坐标轴2垂直的平面，即U2＝UR1＝UR3=0; ZSYMM：对称边界条件，对称面为与坐标轴3垂直的平面，即U3＝UR1＝UR2=0; XASYMM：反对称边界条件，对称面为与坐标轴1垂直的平面，即U2＝U3＝ UR1=0; YASYMM：反对称边界条件，对称面为与坐标轴2垂直的平面，即U1＝U3＝ UR2=0; ZASYMM：反对称边界条件，对称面为与坐标轴3垂直的平面，即U1＝U2＝ UR3=0; PINNED：约束所有平移自由度，即U1=U2=U3=0; ENCASTRE：约束所有自由度（固支边界条件），即 U1=U2=U3=UR1=UR2=UR3=0.
Abaqus有限元仿真培训教程
Create Cut（创建切除）
Create Cut的方法依次为： Extrude、Revolve、Sweep、Loft和Circular hole。
Create Cut与Create Solid类似。现以Circular hole 为例说明如何Create Cut：
1、选择孔的类型：通孔或盲孔
2、选择草绘平面
Introduction to ABAQUS/CAE
分析时最常接触的一些参数：应力σ、应变ε、屈服强度σs、抗 拉强度σb、位移U
应力σ：单位面积上的内力称为应力。
应变ε：应变表示长度的相对变化量,是形变量与原来长度尺寸的比值, 即ε=ΔL/L,无量纲,常用百分数表示。
屈服强度σs ：是金属材料发生屈服现象时的屈服极限，即抵抗微量塑 性变形的应力。对于无明显屈服的金属材料，规定以产生0.2%残余变 形的应力值为其屈服极限。大于此极限的外力作用，将会使零件永久 失效，无法恢复，零件将会产生永久变形。
3、确定孔的方向（Flip反向）
4、选择基准边，并指定距离
Introduction to ABAQUS/CAE
5、设置孔的直径
倒角
Create Round or Fillet倒圆角与Creaste Chamfer倒直角。
现以Create Round or Fillet为例说明如何倒圆角： 1、选择要进行倒圆角的边（按住Shift，左键拾取可 进行多选） 2、指定圆角半径
Introduction to ABAQUS/CAE
在了解分析之前，我们先来熟悉一些 刚强度分析中的一些常识
静力学刚强度分析到底我们计算什么？ 可以简单理解为： 1.计算工件的刚度，即变形 2.计算工件的强度，即应力
《ABAQUS有限元分析常见问答解答》常见问答汇总
《ABAQUS有限元分析常见问答解答》常见问答汇总1.什么是ABAQUS有限元分析?ABAQUS是一种有限元分析软件，用于模拟和分析结构、材料、流体等物体的力学行为。
它通过将实际物体离散化成有限数量的元素，并利用数值方法，计算出这些元素的力学行为。
ABAQUS可以模拟各种静态和动态问题，并且在工程和科学研究中被广泛应用。
2.如何创建一个模型?在ABAQUS中创建模型的第一步是定义几何形状。
可以通过绘制几何形状、导入CAD文件或使用预定义的几何模板来创建几何模型。
接下来，需要定义材料属性、边界条件和加载条件。
最后，生成网格并进行求解，得到模型的力学行为。
3.如何选择适当的网格密度?网格密度是指模型中网格单元的数量。
选择适当的网格密度是非常重要的，因为粗网格会导致模型不准确，而细网格则会增加计算时间。
通常，需要根据具体问题的复杂程度和计算资源的限制来选择适当的网格密度。
4.是否需要考虑材料非线性?当材料的应力-应变关系不是线性的时候，需要考虑材料的非线性行为。
ABAQUS提供了各种材料模型来模拟不同类型的非线性行为，如弹塑性、强化、断裂等。
5.如何处理接触问题?在模拟接触问题时，需要定义接触对面并选择适当的接触算法。
ABAQUS提供了多种接触算法，如基于面间距离的接触和基于面接触力的接触。
还可以定义接触的摩擦性质。
6.如何评估模拟结果的准确性?评估模拟结果的准确性可以通过与实验结果进行比较来实现。
可以比较模拟结果和实验数据之间的有关物理量，如应力、位移、应变等。
此外，还可以进行敏感性分析和验证分析来评估模拟结果的稳健性和可靠性。
7.如何处理大变形问题?当分析问题涉及到大变形时，需要使用ABAQUS中的非线性分析功能。
非线性分析可以考虑材料的非线性行为和结构的大变形。
此外，还需要定义适当的材料模型和边界条件。
8.如何处理复杂的加载条件?ABAQUS提供了各种加载条件的定义方法，如施加预定义的位移、施加预定义的力和施加定义的速度。
[断裂与失效] ABAQUS6.9版本XFEM(扩展有限元)例子的详细图解
![[断裂与失效] ABAQUS6.9版本XFEM(扩展有限元)例子的详细图解](https://img.taocdn.com/s3/m/ceb37c09941ea76e59fa043e.png)
[断裂与失效] ABAQUS6.9版本XFEM(扩展有限元)例子的详细图解step by step 〔By SIMWE wylxl2001 〕一、part模块中的操作： 1.生成一个新的part，取名为plate，本part选取3D deformable solid extrusion类型〔如图1〕 2.通过Rectangle工具画出一长3，高6的矩形。
考虑使用工具栏add-dimension和edit dimension来画出准确长度的模型。
强烈建议此矩形的左上角坐标为〔0，3〕，右下角坐标为〔3，-3〕〔如图2〕 3.完成后拉伸此矩形，深度为1.〔如图3〕图1，图2，图34.生成一个新的part，取名为crack，本part选取3D deformable shell extrusion 类型〔如图4〕5.生成一条线，此线的左端点坐标为〔0，0.08〕，右端点坐标为〔1.5，0.08〕6 .完成后拉伸此线，深度为1.〔如图6〕7.保存此模型为XFEMtutor〔如图7〕，以后经常保存模型，不再累述。
8.在part Plate中分别创立4个集合，分别为：all，bottom，top和fixZ，各局部的内容如图8～11所示。
二、Material模块中的操作： 1.创立材料elsa，其弹性参数为E=210GPa，泊松比为0.3〔如图12〕最大主应力失效准那么作为损伤起始的判据，最大主应力为84.4MPa〔如图13〕损伤演化选取基于能量的、线性软化的、混合模式的指数损伤演化规律，有关参数为G1C=G2C=G3C=42200N/m， =1.〔如图14〕2.创立一个Solid Homogeneous的section，名为solid，此section与材料elsa 相联，并将此section赋给plate part〔也就是集合all〕3.赋予材料取向，分别如图18～21所示。
三、划分网格：网格控制为：Hex型structured〔如图22〕，单元类型为C3D8R 〔如图23〕设置plate各边的网格种子为8，26，36〔如图24〕，各边种子的个数不能改变〔如图25〕四、装配模块：选中plate和crack两个part，分别生成2个实体〔如图26〕，生成一个参考点，参考点的坐标为〔1.5，-3，0〕〔如图27，28〕。
abaqus带孔平板的有限元分析
5.
组装零件 (Context Bar: Module Assemble) Toolbox Area: click Instance Part Create Instance Window: select Parts: plate; click OK
6.
定义加载步 (Context Bar: Module Step)
-2-
9.
Байду номын сангаас
ABAQUS step-by-step 建模分析实例 1
S11; click OK 11. 计算结果的验证： 对于以上计算方案，由图 4 得到最大 Von Mises 等效应力为：288.342 MPa；由图 5 得 到最大的 x 方向主应力为：300.013 MPa。
-3-
ABAQUS step-by-step 建模分析实例 1
实例 1：带孔平板的有限元分析
y 100 p R5 50 100 50 x 单位: mm p=100N/mm2 t=1 mm E=210000N/mm2 =0.3
图 1 平面问题的计算分析模型
1.
进入 ABAQUS/CAE 开始 程序 ABAQUS 6.xx ABAQUS CAE
-1-
ABAQUS step-by-step 建模分析实例 1
Toolbox Area: click Create Step Create Step window: input Name: Tension; select Procedure type: General > Static, General; click Continue… Edit Step Window: click OK 7. 定义载荷与边界条件 (Context Bar: Module Load) Toolbox Area: click Create Load Create Load Window: input Name: pressure; select Step: Tension, Category: Mechanical, Types for Selected Step: Pressure; click Continue… Viewport: click the right edge of the plate Prompt Area: click Done Edit Load Window: input Magnitude: -100; click OK Toolbox Area: click Create Boundary Condition Create Boundary Condition Window: input Name: Fix Left Bottom Corner; select Step: Initial, Category: Mechanical, Types for Selected Step: Symmetry/Antisymmetry/Encastre; click Continue... Viewport: click the left bottom corner of the plate Prompt Area: click Done Edit Boundary Condition Window: select ENCASTRE(U1=U2=U3=UR1=UR2=UR3=0); click OK Toolbox Area: click Create Boundary Condition Create Boundary Condition Window: input Name: Fix Left Edge Horizontally; select Step: Initial, Category: Mechanical, Types for Selected Step: Displacement/Rotation; click Continue… Viewport: click the left edge of the plate Prompt Area: click Done Edit Boundary Condition Window: set U1: ON, U2: OFF, UR3: OFF; click OK 8. 划分网格 (Context Bar: Module Mesh) Menu Bar: select Seed > Edge by Number Viewport: select the inner circle Prompt Area: click Done Prompt Area: input 16 enter Viewport: shift select the outer four edges Prompt Area: click Done Prompt Area: input 8 enter Prompt Area: click Done Toolbox Bar: click Assign Element Type Element Type Window: (Quad Tab) set Reduced integration: OFF; click OK Toolbox Bar: click Mesh Part Instance Prompt Area: click Yes 计算分析 (Context Bar: Module Job) Toolbox Bar: click Create Job Create Job Window: input Name: Plate; click Continue… Edit Job Window: click OK Toolbox Bar: click Job Manager Job Manager Window: click Submit; click Monitor plate Monitor Window: click Dismiss when job is completed Job Manger Window: click Results 10. 后处理 (Context Bar: Module Visualization) 显示 Von Mises 应力云图：Toolbox Bar: click Plot Contour 显示应力的最大最小值：Menu Bar: select Viewport > Viewport Annotation Options… Viewport Annotation Options Window: (Legend Tab) select show min/max values: ON; click OK 显示 x 方向主应力云图：Menu Bar: select Result > Field Output… Field Output Window: select Primary Variable: S Stress components at integration points, Component:
ABAQUS有限元分析实例详解 3PPT课件
L
F2EA(U2U1) L
11
既
F F1 2 E LA1 , 1,1 1 U U1 2
FKU
[K]单元刚度阵，{F}载荷，{U}位移向量
每一种类型单元都有自己的单元刚度 矩阵，对于复杂的单元是基于能量原理 来确定的。
12
3）总刚度矩阵 结构有限元是用有限个基本单元来
逼近结构模型，把有限个基本单元的单 元刚度矩阵组装到一起，形成总刚度矩 阵。
四或八节点四边形板元 CQUAD4、CQUAD8 四节点剪力板元 CSHEAR
21
体单元 六面体单元 CHEXA 五面体单元 CPENTA 四面体单元 CTETRA
约束元（刚体元 RBE2） 其它单元 质量元 CONM2
22
2、输入文件结构 执行控制（求解类型、允许时间、系统 诊断） 情况控制（输出请求、选择模型数据集） 数据：节点、单元（结构模型定义）、 几何和材料性质、载荷、约束（求解条 件参数)
一、简介
一般来说工程分析可分为两大类： 数值法
（有限元法是数值法的一种）
1
经典法：
经典法直接采用控制微分方程来求 解场问题，其方法是基于物理原理而建 立的。闭合性的精确解仅对于几何、载 荷与边界条件最简单的情况才有可能得 到。精确解离大多数实际工程问题较远。 经典法可以验证数值解的解题精度。
2
AP1_2000计算结果与理论解对比
\\ 执行控制\\
TITLE=FIXED PLATE DISP=ALL STRESS=ALL SPC=1 LOAD=1
\\4种控制\\
25
BEGIN BULK
\\数据集\\
GRID 1 0 0. 0. 0.
GRID 2 0 2. 0. 0.
ABAQUS有限元软件基本操作说明.
2．选中“将部件实体化” 。
(3) “分析步”完成类型、频率、频率阶数的设定。具体操作见下图： 1．切换到分析步。
2．名称自定义。
3．类型由 ”通用 ”改为“线性摄动” ，同 时选择“频率” ，然后继续进行参数设置。
4 ．描述自定义。
5．特征值求解器选择 “子空 默认，无需自己设置。
6．阶数与频率大小有关，频率 波动范围越大， 所需阶数越多。
8．以上参数完成后单击“确定” 。分析步完成。
(4) “载荷”步完成边界条件的设定。具体操作见下图：
1．切换到“载荷”步。
2．双击“边界条件设定”
3． “名称”必须定义。
4．两者选其一均可 5．单击“继续”
6．选择要施加边界条件的端 面。 (注：存在多个边界条件 请一个一个单独设定，方便 后面边界条件的修改 )
1.计算分析完成后 ,切换到 ”可视化 ”。
(7) “可视化”步，查看计算结果和模拟动画，输出计算结果、动画视频。具体操作见下图：
2.双击 ”输出数据库 ”,输出计算结果。
字体放大 :视口→视口注释选项→图例→设
置字体。该块还可以看出各部位位移大小。
网格隐藏 :选项→通用→基本信息→可见边
(设为无 )。
(6) “作业提交”步，具体操作见下图：
1.单击“创建作业”和“继续” ，进入编辑作业窗口，里面内容全部默认。
2.单击“确定”，完成作业创建。
3.单击“作业管理器” ，弹出下侧窗口。 4.单击“提交”，提交作业。弹出下面 窗口，点击“确定”进入计算中。
5.当跳出“ completed successfully”,计算完成 ,关闭作业管理器。
如下图所示：
1
2
3 4
5.时间值不易过大。 6
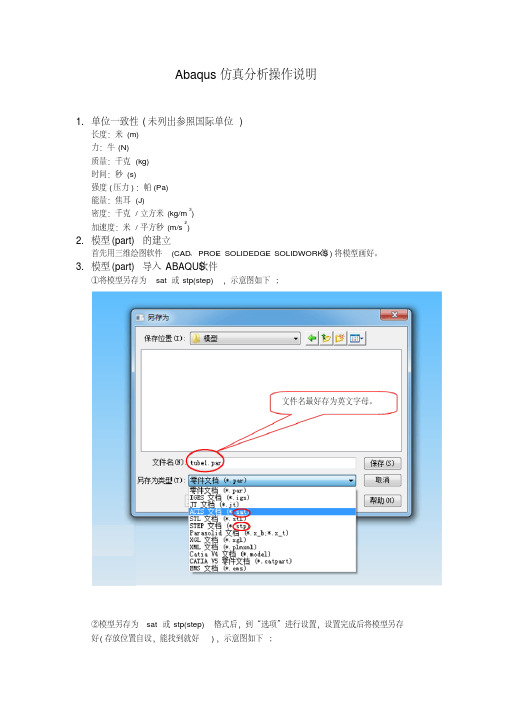
(3) “分析步”完成类型、频率、频率阶数的设定。具体操作见下图： 1．切换到分析步。
2．名称自定义。
3．类型由 ”通用 ”改为“线性摄动” ，同 时选择“频率” ，然后继续进行参数设置。
4 ．描述自定义。
5．特征值求解器选择 “子空 默认，无需自己设置。
6．阶数与频率大小有关，频率 波动范围越大， 所需阶数越多。
8．以上参数完成后单击“确定” 。分析步完成。
(4) “载荷”步完成边界条件的设定。具体操作见下图：
1．切换到“载荷”步。
2．双击“边界条件设定”
3． “名称”必须定义。
4．两者选其一均可 5．单击“继续”
6．选择要施加边界条件的端 面。 (注：存在多个边界条件 请一个一个单独设定，方便 后面边界条件的修改 )
1.计算分析完成后 ,切换到 ”可视化 ”。
(7) “可视化”步，查看计算结果和模拟动画，输出计算结果、动画视频。具体操作见下图：
2.双击 ”输出数据库 ”,输出计算结果。
字体放大 :视口→视口注释选项→图例→设
置字体。该块还可以看出各部位位移大小。
网格隐藏 :选项→通用→基本信息→可见边
(设为无 )。
(6) “作业提交”步，具体操作见下图：
1.单击“创建作业”和“继续” ，进入编辑作业窗口，里面内容全部默认。
2.单击“确定”，完成作业创建。
3.单击“作业管理器” ，弹出下侧窗口。 4.单击“提交”，提交作业。弹出下面 窗口，点击“确定”进入计算中。
5.当跳出“ completed successfully”,计算完成 ,关闭作业管理器。
如下图所示：
1
2
3 4
5.时间值不易过大。 6
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1．回归教材，注重基础
试卷遵循了考查基础知识为主体的原则，尤其是考试说明中的大部分知识点均有涉及，其中应用题与抗战胜利70周年为背景，把爱国主义教育渗透到试题当中，使学生感受到了数学的育才价值，所有这些题目的设计都回归教材和中学教学实际，操作性强。
2．适当设置题目难度与区分度
选择题第12题和填空题第16题以及解答题的第21题，都是综合性问题，难度较大，学生不仅要有较强的分析问题和解决问题的能力，以及扎实深厚的数学基本功，而且还要掌握必须的数学思想与方法，否则在有限的时间内，很难完成。
3．布局合理，考查全面，着重数学方法和数学思想的考察
在选择题，填空题，解答题和三选一问题中，试卷均对高中数学中的重点内容进行了反复考查。包括函数，三角函数，数列、立体几何、概率统计、解析几何、导数等几大版块问题。这些问题都是题的解答过程之中。
【举一反三】
【相似较难试题】【2014高考全国，22】已知抛物线C：y2＝2px(p>0)的焦点为F，直线y＝4与y轴的交点为P，与C的交点为Q，且|QF|＝ |PQ|.
（1）求C的方程；
（2）过F的直线l与C相交于A，B两点，若AB的垂直平分线l′与C相交于M，N两点，且A，M，B，N四点在同一圆上，求l的方程．
1.对学生的考查要求上完全一致。
即在考查基础知识的同时，注重考查能力的原则，确立以能力立意命题的指导思想，将知识、能力和素质融为一体，全面检测考生的数学素养，既考查了考生对中学数学的基础知识、基本技能的掌握程度，又考查了对数学思想方法和数学本质的理解水平，符合考试大纲所提倡的“高考应有较高的信度、效度、必要的区分度和适当的难度”的原则．
二、亮点试题分析
1．【试卷原题】11.已知 是单位圆上互不相同的三点，且满足 ，则 的最小值为（ ）
A．
B．
C．
D．
【考查方向】本题主要考查了平面向量的线性运算及向量的数量积等知识，是向量与三角的典型综合题。解法较多，属于较难题，得分率较低。
【易错点】1．不能正确用 ， ， 表示其它向量。
2．找不出 与 的夹角和 与 的夹角的倍数关系。
【解题思路】1．把向量用 ， ， 表示出来。
2．把求最值问题转化为三角函数的最值求解。
【解析】设单位圆的圆心为O，由 得， ，因为 ，所以有， 则
设 与 的夹角为 ，则 与 的夹角为2
所以，
即， 的最小值为 ，故选B。
【举一反三】
【相似较难试题】【2015高考天津，理14】在等腰梯形 中,已知 ,动点 和 分别在线段 和 上,且, 则 的最小值为.
由题设得 ＋ ＝ × ，解得p＝－2(舍去)或p＝2，
所以C的方程为y2＝4x.
（2）依题意知l与坐标轴不垂直，故可设l的方程为x＝my＋1(m≠0)．
代入y2＝4x，得y2－4my－4＝0.
设A(x1，y1)，B(x2，y2)，
则y1＋y2＝4m，y1y2＝－4.
故线段的AB的中点为D(2m2＋1，2m)，
由于线段MN垂直平分线段AB，
故A，M，B，N四点在同一圆上等价于|AE|＝|BE|＝ |MN|，
从而 |AB|2＋|DE|2＝ |MN|2，即
4(m2＋1)2＋ ＋ ＝
，
化简得m2－1＝0，解得m＝1或m＝－1，
故所求直线l的方程为x－y－1＝0或x＋y－1＝0.
三、考卷比较
本试卷新课标全国卷Ⅰ相比较，基本相似，具体表现在以下方面：
2．【试卷原题】20.（本小题满分12分）已知抛物线 的焦点 ，其准线与 轴的交点为 ，过点 的直线 与 交于 两点，点 关于 轴的对称点为 ．
（Ⅰ）证明：点 在直线 上；
（Ⅱ）设 ，求 内切圆 的方程.
【考查方向】本题主要考查抛物线的标准方程和性质，直线与抛物线的位置关系，圆的标准方程，韦达定理，点到直线距离公式等知识，考查了解析几何设而不求和化归与转化的数学思想方法，是直线与圆锥曲线的综合问题，属于较难题。
【试题分析】本题主要考查向量的几何运算、向量的数量积与基本不等式.运用向量的几何运算求 ，体现了数形结合的基本思想，再运用向量数量积的定义计算 ，体现了数学定义的运用，再利用基本不等式求最小值，体现了数学知识的综合应用能力.是思维能力与计算能力的综合体现.
【答案】
【解析】因为 ， ，
， ，
当且仅当 即 时 的最小值为 .
【试题分析】本题主要考查求抛物线的标准方程,直线和圆锥曲线的位置关系的应用,韦达定理,弦长公式的应用,解法及所涉及的知识和上题基本相同.
【答案】（1）y2＝4x.
（2）x－y－1＝0或x＋y－1＝0.
【解析】（1）设Q(x0，4)，代入y2＝2px，得x0＝ ，
所以|PQ|＝ ，|QF|＝ ＋x0＝ ＋ .
|AB|＝ |y1－y2|＝4(m2＋1)．
又直线l ′的斜率为－m，
所以l ′的方程为x＝－ y＋2m2＋3.
将上式代入y2＝4x，
并整理得y2＋ y－4(2m2＋3)＝0.
设M(x3，y3)，N(x4，y4)，
则y3＋y4＝－ ，y3y4＝－4(2m2＋3)．
故线段MN的中点为E ，
|MN|＝ |y3－y4|＝ .
【易错点】1．设直线 的方程为 ，致使解法不严密。
2．不能正确运用韦达定理，设而不求，使得运算繁琐，最后得不到正确答案。
【解题思路】1．设出点的坐标，列出方程。
2．利用韦达定理，设而不求，简化运算过程。
3．根据圆的性质，巧用点到直线的距离公式求解。
【解析】（Ⅰ）由题可知 ，抛物线的方程为
则可设直线 的方程为 ， ，
故 整理得 ，故
则直线 的方程为 即
令 ，得 ，所以 在直线 上.
（Ⅱ）由（Ⅰ）可知 ，所以 ，
又 ，
故 ，
则 ，故直线 的方程为 或
，
故直线 的方程 或 ，又 为 的平分线，
故可设圆心 ， 到直线 及 的距离分别为 -------------10分
由 得 或 （舍去）.故圆 的半径为
所以圆 的方程为
Abaqus6.14有限元仿真分析视频教程-实例篇(上)
江西省南昌市2015-2016学年度第一学期期末试卷
（江西师大附中使用）高三理科数学分析
一、整体解读
试卷紧扣教材和考试说明，从考生熟悉的基础知识入手，多角度、多层次地考查了学生的数学理性思维能力及对数学本质的理解能力，立足基础，先易后难，难易适中，强调应用，不偏不怪，达到了“考基础、考能力、考素质”的目标。试卷所涉及的知识内容都在考试大纲的范围内，几乎覆盖了高中所学知识的全部重要内容，体现了“重点知识重点考查”的原则。
试卷遵循了考查基础知识为主体的原则，尤其是考试说明中的大部分知识点均有涉及，其中应用题与抗战胜利70周年为背景，把爱国主义教育渗透到试题当中，使学生感受到了数学的育才价值，所有这些题目的设计都回归教材和中学教学实际，操作性强。
2．适当设置题目难度与区分度
选择题第12题和填空题第16题以及解答题的第21题，都是综合性问题，难度较大，学生不仅要有较强的分析问题和解决问题的能力，以及扎实深厚的数学基本功，而且还要掌握必须的数学思想与方法，否则在有限的时间内，很难完成。
3．布局合理，考查全面，着重数学方法和数学思想的考察
在选择题，填空题，解答题和三选一问题中，试卷均对高中数学中的重点内容进行了反复考查。包括函数，三角函数，数列、立体几何、概率统计、解析几何、导数等几大版块问题。这些问题都是题的解答过程之中。
【举一反三】
【相似较难试题】【2014高考全国，22】已知抛物线C：y2＝2px(p>0)的焦点为F，直线y＝4与y轴的交点为P，与C的交点为Q，且|QF|＝ |PQ|.
（1）求C的方程；
（2）过F的直线l与C相交于A，B两点，若AB的垂直平分线l′与C相交于M，N两点，且A，M，B，N四点在同一圆上，求l的方程．
1.对学生的考查要求上完全一致。
即在考查基础知识的同时，注重考查能力的原则，确立以能力立意命题的指导思想，将知识、能力和素质融为一体，全面检测考生的数学素养，既考查了考生对中学数学的基础知识、基本技能的掌握程度，又考查了对数学思想方法和数学本质的理解水平，符合考试大纲所提倡的“高考应有较高的信度、效度、必要的区分度和适当的难度”的原则．
二、亮点试题分析
1．【试卷原题】11.已知 是单位圆上互不相同的三点，且满足 ，则 的最小值为（ ）
A．
B．
C．
D．
【考查方向】本题主要考查了平面向量的线性运算及向量的数量积等知识，是向量与三角的典型综合题。解法较多，属于较难题，得分率较低。
【易错点】1．不能正确用 ， ， 表示其它向量。
2．找不出 与 的夹角和 与 的夹角的倍数关系。
【解题思路】1．把向量用 ， ， 表示出来。
2．把求最值问题转化为三角函数的最值求解。
【解析】设单位圆的圆心为O，由 得， ，因为 ，所以有， 则
设 与 的夹角为 ，则 与 的夹角为2
所以，
即， 的最小值为 ，故选B。
【举一反三】
【相似较难试题】【2015高考天津，理14】在等腰梯形 中,已知 ,动点 和 分别在线段 和 上,且, 则 的最小值为.
由题设得 ＋ ＝ × ，解得p＝－2(舍去)或p＝2，
所以C的方程为y2＝4x.
（2）依题意知l与坐标轴不垂直，故可设l的方程为x＝my＋1(m≠0)．
代入y2＝4x，得y2－4my－4＝0.
设A(x1，y1)，B(x2，y2)，
则y1＋y2＝4m，y1y2＝－4.
故线段的AB的中点为D(2m2＋1，2m)，
由于线段MN垂直平分线段AB，
故A，M，B，N四点在同一圆上等价于|AE|＝|BE|＝ |MN|，
从而 |AB|2＋|DE|2＝ |MN|2，即
4(m2＋1)2＋ ＋ ＝
，
化简得m2－1＝0，解得m＝1或m＝－1，
故所求直线l的方程为x－y－1＝0或x＋y－1＝0.
三、考卷比较
本试卷新课标全国卷Ⅰ相比较，基本相似，具体表现在以下方面：
2．【试卷原题】20.（本小题满分12分）已知抛物线 的焦点 ，其准线与 轴的交点为 ，过点 的直线 与 交于 两点，点 关于 轴的对称点为 ．
（Ⅰ）证明：点 在直线 上；
（Ⅱ）设 ，求 内切圆 的方程.
【考查方向】本题主要考查抛物线的标准方程和性质，直线与抛物线的位置关系，圆的标准方程，韦达定理，点到直线距离公式等知识，考查了解析几何设而不求和化归与转化的数学思想方法，是直线与圆锥曲线的综合问题，属于较难题。
【试题分析】本题主要考查向量的几何运算、向量的数量积与基本不等式.运用向量的几何运算求 ，体现了数形结合的基本思想，再运用向量数量积的定义计算 ，体现了数学定义的运用，再利用基本不等式求最小值，体现了数学知识的综合应用能力.是思维能力与计算能力的综合体现.
【答案】
【解析】因为 ， ，
， ，
当且仅当 即 时 的最小值为 .
【试题分析】本题主要考查求抛物线的标准方程,直线和圆锥曲线的位置关系的应用,韦达定理,弦长公式的应用,解法及所涉及的知识和上题基本相同.
【答案】（1）y2＝4x.
（2）x－y－1＝0或x＋y－1＝0.
【解析】（1）设Q(x0，4)，代入y2＝2px，得x0＝ ，
所以|PQ|＝ ，|QF|＝ ＋x0＝ ＋ .
|AB|＝ |y1－y2|＝4(m2＋1)．
又直线l ′的斜率为－m，
所以l ′的方程为x＝－ y＋2m2＋3.
将上式代入y2＝4x，
并整理得y2＋ y－4(2m2＋3)＝0.
设M(x3，y3)，N(x4，y4)，
则y3＋y4＝－ ，y3y4＝－4(2m2＋3)．
故线段MN的中点为E ，
|MN|＝ |y3－y4|＝ .
【易错点】1．设直线 的方程为 ，致使解法不严密。
2．不能正确运用韦达定理，设而不求，使得运算繁琐，最后得不到正确答案。
【解题思路】1．设出点的坐标，列出方程。
2．利用韦达定理，设而不求，简化运算过程。
3．根据圆的性质，巧用点到直线的距离公式求解。
【解析】（Ⅰ）由题可知 ，抛物线的方程为
则可设直线 的方程为 ， ，
故 整理得 ，故
则直线 的方程为 即
令 ，得 ，所以 在直线 上.
（Ⅱ）由（Ⅰ）可知 ，所以 ，
又 ，
故 ，
则 ，故直线 的方程为 或
，
故直线 的方程 或 ，又 为 的平分线，
故可设圆心 ， 到直线 及 的距离分别为 -------------10分
由 得 或 （舍去）.故圆 的半径为
所以圆 的方程为
Abaqus6.14有限元仿真分析视频教程-实例篇(上)
江西省南昌市2015-2016学年度第一学期期末试卷
（江西师大附中使用）高三理科数学分析
一、整体解读
试卷紧扣教材和考试说明，从考生熟悉的基础知识入手，多角度、多层次地考查了学生的数学理性思维能力及对数学本质的理解能力，立足基础，先易后难，难易适中，强调应用，不偏不怪，达到了“考基础、考能力、考素质”的目标。试卷所涉及的知识内容都在考试大纲的范围内，几乎覆盖了高中所学知识的全部重要内容，体现了“重点知识重点考查”的原则。