Eviews应用案例——通货膨胀预测分析
应用eviews分析数据和预测

统计预测与决策论文摘要:随着市场经济的多元化发展。
统计软件被广泛的应用,企业应用统计软件进行对下一期的生产值进行预测。
从而能更准确的做出决策。
本文利用eviews对某企业的下几期的生产值进行预测,便于企业做出最准确的决策。
关键字:平稳序列,模型识别,模型定阶,模型参数估计,模型检验,模型预测。
下表是某企业近期一百个生产数据值。
1、模型识别绘制序列时序图7680848892255075100125150175200PRODUCTI ON2模型定阶绘制序列相关图从相关图看出,自相关系数迅速衰减为0,说明序列平稳,但最后一列白噪声检验的Q 统计量和相应的伴随概率表明序列存在相关性,因此序列为平稳非白噪声序列。
模型定阶:由图2-5看出,偏自相关系数在k=3后很快趋于0即3阶截尾,尝试拟合AR (3);自相关系数在k=1处显著不为0,当k=2时在2倍标准差的置信带边缘,可以考虑拟合MA (1)或MA (2);同时可以考虑ARMA (3,1)模型等。
原序列做描述统计分析见图481216207880828486889092Series: PRODUCTION Sample 1 201Observations 201Mean 84.11940Median 84.10000Maximum 91.70000Minimum 76.50000Std. Dev. 2.906625Skewness 0.107191Kurtosis 2.752406Jarque-Bera 0.898321Probability0.638164可见序列均值非0,我们通常对0均值平稳序列做建模分析,所以需要在原序列基础上生成一个新的0均值序列。
这个序列是0均值的平稳非白噪声序列,新序列的描述统计量见图 048121620-8-6-4-22468Series: XSample 1 201Observations 201Mean 2.99e-06Median -0.019400Maximum 7.580600Minimum -7.619400Std. Dev. 2.906625Skewness 0.107191Kurtosis 2.752406Jarque-Bera 0.898321Probability0.6381643模型参数估计由伴随概率可知,AR (i )(i=1,2,3)均高度显著,表中最下方给出的是滞后多项式φ-1(x )=0的倒数根,只有这些值都在单位圆内时,过程才平稳。
计量经济学模型-eviews应用
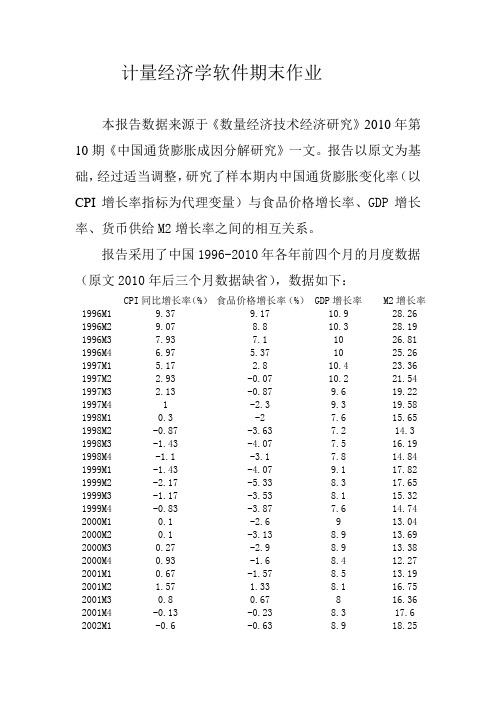
计量经济学软件期末作业本报告数据来源于《数量经济技术经济研究》2010年第10期《中国通货膨胀成因分解研究》一文。
报告以原文为基础,经过适当调整,研究了样本期内中国通货膨胀变化率(以CPI增长率指标为代理变量)与食品价格增长率、GDP增长率、货币供给M2增长率之间的相互关系。
报告采用了中国1996-2010年各年前四个月的月度数据(原文2010年后三个月数据缺省),数据如下:CPI同比增长率(%)食品价格增长率(%)GDP增长率M2增长率1996M1 9.37 9.17 10.9 28.26 1996M2 9.07 8.8 10.3 28.19 1996M3 7.93 7.1 10 26.81 1996M4 6.97 5.37 10 25.26 1997M1 5.17 2.8 10.4 23.36 1997M2 2.93 -0.07 10.2 21.54 1997M3 2.13 -0.87 9.6 19.22 1997M4 1 -2.3 9.3 19.58 1998M1 0.3 -2 7.6 15.65 1998M2 -0.87 -3.63 7.2 14.3 1998M3 -1.43 -4.07 7.5 16.19 1998M4 -1.1 -3.1 7.8 14.84 1999M1 -1.43 -4.07 9.1 17.82 1999M2 -2.17 -5.33 8.3 17.65 1999M3 -1.17 -3.53 8.1 15.32 1999M4 -0.83 -3.87 7.6 14.74 2000M1 0.1 -2.6 9 13.04 2000M2 0.1 -3.13 8.9 13.69 2000M3 0.27 -2.9 8.9 13.38 2000M4 0.93 -1.6 8.4 12.27 2001M1 0.67 -1.57 8.5 13.19 2001M2 1.57 1.33 8.1 16.75 2001M3 0.8 0.67 8 16.36 2001M4 -0.13 -0.23 8.3 17.6 2002M1 -0.6 -0.63 8.9 18.252002M2 -1.07 -1.23 8.9 14.74 2002M3 -0.77 -0.5 9.2 16.57 2002M4 -0.63 -0.03 9.1 16.87 2003M1 0.5 2.47 10.8 18.54 2003M2 0.67 1.83 9.7 20.83 2003M3 0.83 2.13 10.1 20.67 2003M4 2.67 7.27 10 19.58 2004M1 2.77 7.17 10.4 19.16 2004M2 4.4 12 10.9 16.35 2004M3 5.27 13.83 10.5 14.14 2004M4 3.17 6.93 9.5 14.46 2005M1 2.83 6.13 10.5 14.17 2005M2 1.73 2.67 10.5 15.67 2005M3 1.33 1.17 10.4 17.92 2005M4 1.37 1.7 10.4 17.99 2006M1 1.2 1.87 11.4 17.35 2006M2 1.37 1.93 12 17.03 2006M3 1.27 1.47 11.8 15.46 2006M4 2.03 4.07 11.6 15.67 2007M1 2.73 6.23 11.7 17.27 2007M2 3.6 8.9 12.2 17.06 2007M3 6.1 16.83 12.2 18.45 2007M4 6.63 17.5 11.9 16.73 2008M1 8.03 20.97 10.6 16.19 2008M2 7.77 19.77 10.4 17.29 2008M3 5.27 11.47 9.9 15.21 2008M4 2.53 6.2 9 17.79 2009M1 -0.6 0.5 6.1 25.5 2009M2 -1.53 -1 7.1 28.38 2009M3 -1.27 0.27 7.7 29.26 2009M4 0.67 3.37 8.7 27.58 2010M1 2.2 5.1 11.9 22.5其中,被解释变量为CPI增长率(以cpi表示),解释变量为食品价格增长率(以foodprice表示)、GDP增长率(以gdp 表示)、货币供给M2增长率(以M2表示)。
基于Eviews计量经济学软件X11方法的季度GDP预测

基于Eviews软件X11方法的季度GDP预测1.数据导入及时间序列分解将1992年第1季度至2013年第1季度的季度GDP时间序列录入或者导入到Eviews 软件,命名为Y序列。
双击打开序列Y,点击菜单栏中的PROC,在下拉菜单选择Seasonal Adjustment,在弹出的菜单中选择X11方法。
这时会弹出的X11季节调整对话框,在Adjustment Method 下,选择乘法模型(multiplicative),系统默认季节调整后的序列名为YSA,我们定义季节因子序列为YYZ,忽略贸易日和节假日因素。
然后选择确定,这时,工作文件中多了两个序列:YSA,YYZ。
我们建立包含序列Y和这两个序列的组,命名为g1,在其窗口栏单击View| Graphs Options选项,在Multiple中选择Multiple Graphs将得到单独显示着3个序列的线性图。
从图中我们可以看出,原始的时间序列Y在图的最上方,数据有向上增加的趋势,序列呈现锯齿状的波动。
根据原始序列分解出的1-4季度的季节因子分别为0.8765、0.9403、0.9589和1.2239。
2.基于时间序列分解方法的季度GDP预测用季节调整后的序列进行预测。
根据最小二乘法,采用1992年第1季度至2013年第1季度数据建立对数回归方程,在Eviews软件中建立一个取值从1至85序列t,然后在软件的命令行键入:L S LOG(YSA) C T然后按Enter键,得到如下结果LOG(YSA) = 8.9655 + 0.03382*T,其中,t取值为1、2、3、…该方程的拟合优度R2=0.98,拟合效果非常好,常数项和自变量参数的t统计量分别为389.87,72.81,检验的P值均近似为零,故认为这两个参数的估计都是显著的;模型的F值为5301.81,检验的P值近似为零,故认为该模型是显著的。
预测2013年第2季度经季节调整的GDP值,此时t=86:LOG(YSA) = 8.9655 + 0.03382*86 YSA=143489.91假定没有特殊情况发生,不规则因素I=1,2季度季节因子YYZ=0.9403,预测2013年第2季度的GDP为:Y=YSA×YYZ=143489.91×0.9403=134922.70同样方法可以得出2013年第3季度的经季节调整的GDP值,此时t=87:YSA=148425.73 Y=142325.43。
用Eviews建立ARMA模型预测CPI
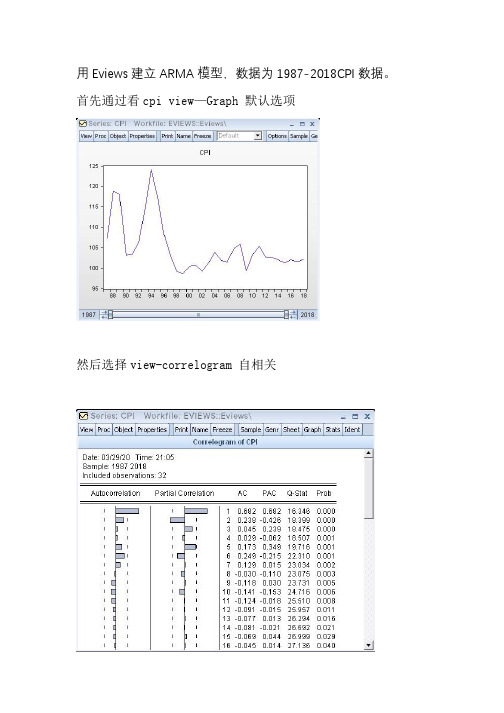
用Eviews建立ARMA模型,数据为1987-2018CPI数据。
首先通过看cpi view—Graph 默认选项
然后选择view-correlogram 自相关
可以看出自相关系数自二阶开始没有超过虚线,而偏相关自二阶开始阻尼震荡,所以自相关系数出现截尾现象,偏相关系数出现拖尾现象,因此考虑建立ARMA(01)模型
下面开始模型估计
看模型是否很好拟合数据,建立残差序列
紧接着看残差数列的自相关偏相关图
因为自相关和偏相关的函数估计值均在两倍标准差内,可以认为残差数列不存在自相关现象,回归拟合较好.
然后回到回归页面点击Resids残差页面
绿色是cpi拟合值,红色是真实值……
然后在添加2019,在框里填写expand 1987 2019,然后再一次回归,后点dorecast(动态方法)
紧接着用静态方法forcast
预测完毕打开看到
预测2019CPI为105.9521。
(注:可编辑下载,若有不当之处,请指正,谢谢!)。
eviews实验心得与体会

eviews实验心得与体会作为一位经济学专业的学生,在学习和研究经济数据的过程中,Eviews无疑是一个非常有用和必要的工具。
作为一款专门用于经济和金融数据分析的统计软件,Eviews提供了丰富的功能和工具,让我们能够更好地理解和解释经济现象。
在这篇文章中,我将分享我在使用Eviews进行实验和研究的心得与体会。
首先,作为一个统计软件,Eviews拥有强大的数据处理和分析能力。
在实验进行之前,我需要先收集到相关的经济数据,这些数据包含了许多指标和变量,例如国内生产总值(GDP)、通货膨胀率、失业率等。
使用Eviews,我可以方便地导入数据并进行预处理,包括数据清洗、缺失值处理和数据变换等。
这使得我能够更好地准备数据,以便后续的分析和研究。
其次,Eviews提供了多种统计方法和模型,可以帮助我进行深入的经济数据分析。
例如,我可以使用Eviews进行描述统计分析,了解数据的分布和趋势;我也可以使用Eviews进行回归分析,探究变量之间的关系和影响。
此外,Eviews还支持时间序列分析和面板数据分析等高级技术,使得我能够从多个角度和维度揭示经济现象的本质。
在实验过程中,我最喜欢的一个功能是Eviews的可视化工具。
通过绘制图表和图形,我可以更直观地观察数据的变化和趋势。
Eviews提供了多种图表类型,例如折线图、柱状图和散点图等,可以根据实际情况选择合适的图表。
这对于展示研究结果和解释模型的效果非常有帮助,同时也为我自己更深入地理解数据提供了手段。
除了数据分析和模型建立外,Eviews还可以帮助我进行经济预测和决策分析。
Eviews可以根据历史数据和模型进行未来走势的预测,这对于政府决策和企业战略制定具有重要意义。
同时,Eviews还可以进行灵敏度分析和假设检验,帮助我评估不同情境下的经济风险和可行性。
这让我能够在实际问题中更加准确和全面地评估不同策略的影响和效果。
然而,尽管Eviews具有众多强大的功能和工具,但在使用过程中也存在一些挑战和限制。
利用EVIEWS研究中国通货膨胀诱因
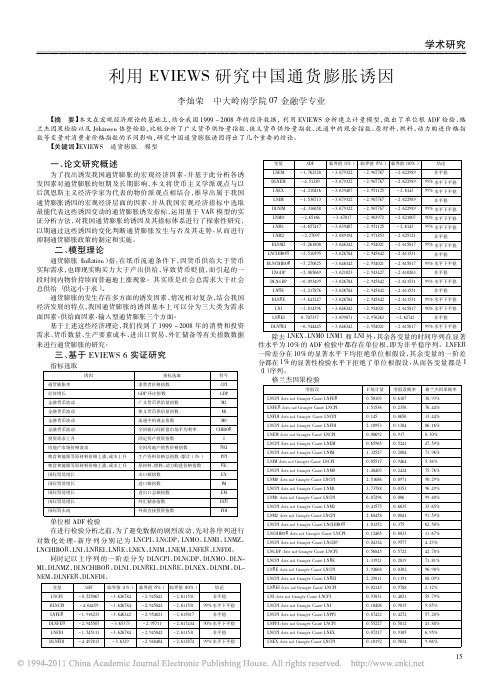
一、 论文研究概述
为了找出诱发我国通货膨胀的宏观经济因素, 并基于此分析各诱 本文将货币主义学派观点与以 发因素对通货膨胀的短期及长期影响, 后凯恩斯主义经济学家为代表的物价派观点相结合, 推导出属于我国 并从我国宏观经济指标中选取 通货膨胀诱因的宏观经济层面的因素, 运用基于 VAR 模型的实 最能代表这些诱因变动的通货膨胀诱发指标, 证分析方法, 对我国通货膨胀的诱因及其指标体系进行了探索性研究, 以期通过这些诱因的变化判断通货膨胀发生与否及其走势, 从而进行 抑制通货膨胀政策的制定和实施 。
Ml LNFDI does not Granger Cause LNCPI M0 LNCPI does not Granger Cause LNFDI CHIBOR LNEM does not Granger Cause LNCPI I LNCPI does not Granger Cause LNEM REI LNCPI does not Granger Cause LNIM PPI LNIM does not Granger Cause LNCPI RE LNCPI does not Granger Cause LNM0 EX LNM0 does not Granger Cause LNCPI IM LNCPI does not Granger Cause LNM1 EM LNM1 does not Granger Cause LNCPI FER LNCPI does not Granger Cause LNM2 FDI LNM2 does not Granger Cause LNCPI LNCPI does not Granger Cause LNCHIBOR LNCHIBOR does not Granger Cause LNCPI LNCPI does not Granger Cause LNGDP LNGDP does not Granger Cause LNCPI LNCPI does not Granger Cause LNRE LNRE does not Granger Cause LNCPI LNCPI does not Granger Cause LNREI LNREI does not Granger Cause LNCPI LNI does not Granger Cause LNCPI LNCPI does not Granger Cause LNI LNCPI does not Granger Cause LNPPI LNPPI does not Granger Cause LNCPI LNCPI does not Granger Cause LNEX LNEX does not Granger Cause LNCPI
eviews面板数据实例分析(包会)-

eviews面板数据实例分析(包会)-Eviews是一种流行的面板数据分析软件,广泛用于经济学及财务学领域。
本文将以一个面板数据实例为例,介绍Eviews的一些基本功能及应用。
数据说明本数据集为横截面面板数据,共包含11个国家(美国、加拿大、英国、法国、德国、意大利、荷兰、比利时、奥地利、瑞典、日本)在1970年至1986年间的年度数据。
变量说明如下:- gdpercap:人均GDP- invest:投资/GDP比率- consump:消费/GDP比率- inflation:通货膨胀率- popgrowth:人口增长率- literacy:成年人识字率- female:女性劳动力占比数据导入及面板设置首先,在Eviews中新建一个工作文件,并将数据导入。
打开数据文件后,我们可以看到数据已经被正确读入。
然后,我们需要将数据设为面板数据。
在Eviews中,选择“View”菜单下的“Structure of Workfile”选项,可以进入工作文件结构设置。
在弹出的窗口中,选择“Panel Data”选项,并按照数据的属性设置面板变量。
在本例中,我们选择“Country”作为单位维度,“Year”作为时间维度。
设置完成后,Eviews会自动进行面板数据检测。
检测结果显示,数据格式符合面板数据要求。
面板数据描述及汇总统计接下来,我们可以对数据进行初步的描述性统计和汇总统计。
选择“Quick”菜单下的“Descriptive Stats”选项,Eviews会自动生成数据的描述性统计报告,展示各变量在不同国家和不同年份的均值、标准差、最小值、最大值等基本信息。
我们也可以手动计算其他统计量。
例如,选择“Proc”菜单下的“Panel Data”选项,可以对选定的变量进行面板数据汇总统计。
下面是在Eviews中计算人均GDP和消费/GDP比率两个变量的面板均值统计结果:面板数据变量之间的相关性分析在分析面板数据时,我们通常需要考虑不同变量之间的相关性。
应用案例-通货膨胀预测分析

应用案例-通货膨胀预测分析引言通货膨胀是一个经济学术语,它指的是商品和服务的价格普遍上涨,导致货币价值下降。
通货膨胀对经济和人们的生活产生了深远的影响,因此准确预测通货膨胀的发展趋势对个人和企业非常重要。
本文将介绍一种基于数据分析和机器学习的方法来预测通货膨胀,并提供一个应用案例。
数据收集与准备通货膨胀预测的核心是基于历史数据来识别和利用潜在趋势。
因此,我们需要收集和准备一组包含经济指标和相关数据的时间序列数据。
这些经济指标可以包括国内生产总值(GDP)、消费者物价指数(CPI)、就业数据、产业产值等。
通过收集这些数据,我们可以建立一个包含时间和相应指标值的数据集。
数据准备的过程通常包括数据清洗、数据平滑以及特征工程等步骤。
在数据清洗阶段,我们需要处理数据中的缺失值、异常值和重复值,以确保数据集的质量。
对于数据平滑,我们可以使用Moving Average、Exponential Smoothing等技术来降低数据的噪音。
特征工程是一项重要的任务,它可以帮助我们从原始数据中提取有用的特征并构建合适的输入变量。
数据分析与建模在数据准备完成后,我们可以进行数据分析和建模。
通货膨胀预测通常使用时间序列分析和机器学习的方法。
下面介绍两种主要的建模方法:时间序列分析时间序列分析是一种用于研究随时间变化的数据的方法。
通货膨胀数据通常具有时间相关性和季节性。
因此,在时间序列分析中,我们可以使用ARIMA模型(自回归-滑动平均模型)来预测通货膨胀。
ARIMA模型是一种广泛应用于时间序列分析的模型,它考虑了自回归、差分和滑动平均的特性。
该模型可以分为三个部分:自回归(AR)、差分(I)和滑动平均(MA)。
在应用ARIMA模型进行通胀预测时,我们可以根据历史数据的相关性来选择适当的AR、I和MA的参数。
机器学习方法机器学习是一种从数据中学习模式并做出预测的方法。
与时间序列分析不同,机器学习方法可以考虑更多的影响因素,如经济数据、社会因素、政治因素等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、Eviews预测基础
预测的误差和方差 假定真实模型为:
yt xt' t
其中, 是t 服从独立同分布且均值为零的随机扰动项,β是未知参 数向量。
放宽“ t是独立的”这个约束条件 使用真实模型得到的y是不可知的,但是我们估计得到未知参数β
的估计值b,设定误差项为零。对y的点估计可以从下式中取得: yˆt xt'b
一、Eviews预测基础
系数的不确定性
在随机模式下,回归等式中的估计得到系数b不同于真实的系数β。 在回归等式输出界面给出的估计系数的标准差可以衡量估计参数 反映参数的真实值的准确程度。
系数不确定性的影响程度取决于外生变量。在计算预测值的过程 中,由于估计系数与外生变量x相乘,所以外生变量与其平均值相 差越多,预测的不确定性越大。
一、Eviews预测基础
调整缺失项 预测值的缺失项生成有两种情况:一种是某个自变量有缺失值,
另一种是某个所需的回归变量的值在工作簿的时间范围之外。
如果预测方程中没有动态变量(例如:没有滞后内生变量或 ARMA误差项),那么预测序列中的缺失值将不会影响以后各期 的预测值。
如果有动态项,预测序列中单个缺失值就会影响到未来所有的预 测值。此时,EViews会向前期移动预测样本的开始点,直至包含 一个有效预测值。如果不进行这些调整,使用者就必须自行指定 某个合适的值,否则,预测结果将会全部由缺失值组成。
预测是有误差的,这个误差其实就是实际值与预测值的差,即 et yt xt'b
一、Eviews预测基础
假设模型是正确设定的,那么预测误差 来源有两种:
残差不确定性 系数不确定性
一、Eviews预测基础
残差的不确定性
公式中的残差ε在预测期是未知的并被它们的期望值代替。残差的 期望为零,但是个别值不为零,个别误差的变化越大,预测的总 体误差就越大。
如果在预测设定窗口中关掉Insert actuals for out-of-sample选 项,那么预测序列中预测样本外的值将设为缺失值(NA)。
如果使用已经存在的预测序列的名称,每次预测后预测值序列的 所有数据将会被重写,预测序列中已经存在的数值将会丢失
一、Eviews预测基础
点预测值
对于预测样本的每个观测值,EViews都会利用估计得到参数、外 生自变量、滞后内生变量的实际值或拟合值以及残差值,来计算 出因变量的拟合值。
生成预测值的方法主要取决于预测使用的模型及用户设置。
一、Eviews预测基础
点预测——以不包含滞后内生自变量和ARMA项的线性回归模型为 例
假定已经估计了下面的模型: ycxz
一般使用回归标准差来衡量误差的变化程度(在回归等式输出界 面中用“S.E. of regression”表示),残差的不确定性是预测误 差的主要来源。
在动态预测中,残差不确定性是复合形成的,这是由于滞后因变 量和ARMA项取决于滞后残差。EViews同样将这些值设置为等于 它们的期望值,然而这些期望值与真实值是不同的。这种额外的 预测不确定性的来源有超过预测区间的趋势,导致这种动态预测 有越来越多的预测误差。
一、Eviews预测基础
预测的不确定性
预测的不确定性由预测标准差来衡量。对于一个不包含滞后因变 量或者ARMA项的回归方程,预测标准误差计算公式如下: forecast se s 1 xt' ( X ' X )1 xt 其中s是回归标准差
预测标准差同时解释了残差不确定性和系数不确定性。利用通过 最小二乘法估计得到的线性回归模型进行的点估计预测,这从某 种意义上讲是最优的,因为它们在线性无偏估计的预测中拥有最 小的预测方差。此外,如果残差呈正态分布,那么预测误差将呈 现t分布,预测值分布的区间也就很容易确定了。
单击估计等式结果上方工具栏中的Forecast按钮,指定预测期 对预测期的每个观测值,EViews都会利用估计参数和自变量的对应
值(即X和Z),yˆt来生cˆ成(1)Y的cˆ拟(2合)x值t , c即ˆ(3:)zt
需要确保预测期内的所有观测值对应的外生变量均为有效值。如果 预测样本中有数据缺失,那么对应的预测值将为缺失值(NA)。
◦ 所有样本数据可分为两段,试数据集,用以测试训练出的模型的估计效果
一、Eviews预测基础
对于预测序列中不包含在预测样本中的值,有两个处理方式可供 选择。
默认情况下,EViews将把预测值序列中预测样本外的部分赋予因 变量的实际值,
一、Eviews预测基础
假定使用者想用下列方程项进行动态预测: y c y(-1) ar(1)
此时如果设定预测样本和工作簿时间范围的起始点相同,那么 EViews将会把预测样本向后推迟两期,然后使用预测样本前面的 观测值作为滞后变量来进行预测。
向后推迟两期,是因为滞后内生变量使得残差损失一期观测值, 所以对误差项的预测只能从第三期开始。
一、Eviews预测基础
如果在进行预测时,在预测标准差(S.E.)对话框中输入一个 名称,那么EViews会计算出预测标准差序列并将其保存在工 作簿中。预测标准差可以用来确定预测区间。
如果选择Do graph选项进行输出,EViews会通过加减两个标 准差得到预测区间,并绘制预测图。这两个标准差的范围提供 了大约95%的预测区间。也就是说如果假设你进行了很多次预 测,那么因变量的实际值会有95%的机率落在区间内。
第四章 Eviews应用案例——通货膨胀预测分析
本章内容概要
Eviews预测基础
在Eviews中进行预测分析 利用Eviews进行中国CPI预测
一、Eviews预测基础
(一)预测的基础知识
预测序列是指在Eviews调用“预测(Forecast)”选项的预测设定 窗口后储存预测结果的序列。
预测样本指的是EViews计算预测值(拟合值)的样本区间。如果 预测值是不可计算的,那么就将返回一个缺失值(NA)。有些 情况下,EViews会对样本进行自动调整,以防止出现预测序列全 部为缺失值的情况。需要注意的是,预测样本有可能会与估计方 程所用的样本区间重叠。
