高中数学选修2-3知识点、考点、附典型例题
数学人教B版选修2-3知识点总结(含例题)
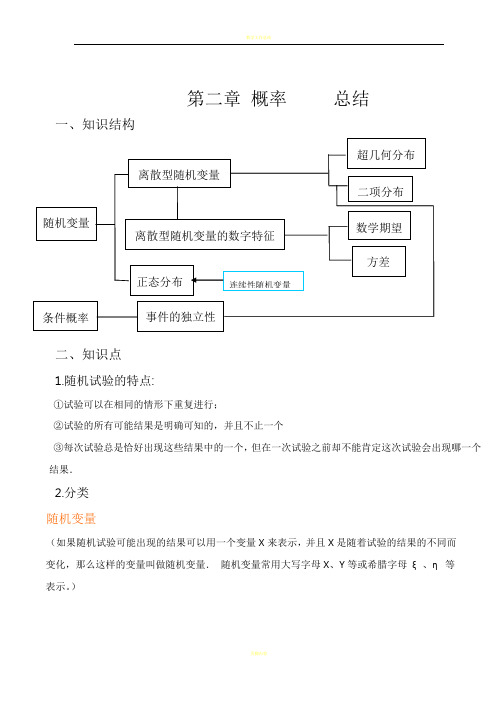
第二章概率总结一、知识结构二、知识点1.随机试验的特点:①试验可以在相同的情形下重复进行;②试验的所有可能结果是明确可知的,并且不止一个③每次试验总是恰好出现这些结果中的一个,但在一次试验之前却不能肯定这次试验会出现哪一个结果.2.分类随机变量(如果随机试验可能出现的结果可以用一个变量X来表示,并且X是随着试验的结果的不同而变化,那么这样的变量叫做随机变量.随机变量常用大写字母X、Y等或希腊字母ξ、η等表示。
)离散型随机变量在上面的射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.连续型随机变量对于随机变量可能取的值,可以取某一区间内的一切值,这样的变量就叫做连续型随机变量.连续型随机变量的结果不可以一一列出.3.离散型随机变量的分布列一般的,设离散型随机变量X可能取的值为x1,x2, ,x i , ,x nX取每一个值xi(i=1,2,)的概率P(ξ=x i)=P i,则称表为离散型随机变量X 的概率分布,简称分布列性质:①pi≥0, i =1,2,…;②p1 + p2 +…+p n= 1.③一般地,离散型随机变量在某一范围内取值的概率等于它取这个范围内各个值的概率之和。
4.求离散型随机变量分布列的解题步骤例题:篮球运动员在比赛中每次罚球命中得1分,不中得0分,已知某运动员罚球命中的概率为0.7,求他罚球一次的得分的分布列.解:用随机变量X表示“每次罚球得的分值”,依题可知,X可能的取值为:1,0且P(X=1)=0.7,P(X=0)=0.3因此所求分布列为:引出超几何分布一般地, 设总数为N件的两类物品,其中一类有M件,从所有物品中任取n(n≤N)件,这n件中所含这类物品件数X是一个离散型随机变量,则它取值为k时的概率为()(0,1,2,,)k n kM N MnNC CP X k k mC--===,其中{}min,m M n=,且*,,,,n N M N n M N N∈≤≤则称随机变量X的分布列为超几何分布列,且称随机变量X服从参数N、M、n的超几何分布注意:二点分布如果随机变量X的分布列为:其中0<p<1,q=1-p,则称离散型随机变量X服从参数p的二点分布二点分布的应用:如抽取彩票是否中奖问题、新生婴儿的性别问题等.nNnMNMCCC-nNnMNMCCC11--nNmnMNmMCCC--(1)超几何分布的模型是不放回抽样;(2)超几何分布中的参数是N 、M 、n ,其意义分别是总体中的个体总数、N 中一类的总数、样本容量解题步骤:例题、在某年级的联欢会上设计了一个摸奖游戏,在一个口袋中装有10个红球和20个白球,这些球除颜色外完全相同.游戏者一次从中摸出5个球.至少摸到3个红球就中奖,求中奖的概率 解:设摸出红球的个数为X,则X 服从超几何分布,其中30,10,5N M n === X 可能的取值为0,1,2,3,4, 5. 由题目可知,至少摸到3个红球的概率为(3)(3)(4)(5)P X P X P X P X ==+=+=≥324150102010201020555303030C C C C C C C C C =++ ≈0.191答:中奖概率为0.191.条件概率1.定义:对任意事件A 和事件B ,在已知事件A 发生的条件下事件B 发生的概率,叫做条件概率.记作P 读作A 发生的条件下B 的概率2.事件的交(积):由事件A 和事件B 同时发生所构成的事件D ,称为事件A 与事件B 的交(或积作D=A ∩B 或D=AB3.条件概率计算公式:P(B|A)相当于把A 看作新的基本事件空间,求A∩B发生的概率:.0)(,)()()|(>=A P A P AB P A B P 发生的条件下样本点数在包含的样本点数发生的条件下在A B A )A |B (=P解题步骤:例题、10个产品中有7个正品、3个次品,从中不放回地抽取两个,已知第一个取到次品,求第二取到次品的概率.解:设 A = {第一个取到次品}, B = {第二个取到次品},所以,P(B|A) = P(AB) / P(A)= 2/9 答:第二个又取到次品的概率为2/9.相互独立事件1.定义:事件A(或B)是否发生对事件B(或A)发生的概率没有影响,这样的两个事件叫做相互独立事包含的样本点数包含的样本点数A AB =总数包含的样本点数总数包含的样本点数//AB A =)(P(AB)A P =.1)|(0)()|()(0)A (P ≤≤⋅=>A B P A P A B P AB P (乘法公式);,则若.151)(21023==⇒C C AB P .103)(=A P2.相互独立事件同时发生的概率公式两个相互独立事件同时发生的概率,等于每个事件发生的概率的积。
(word完整版)高中数学选修2-3知识点及章节练习,文档.docx

数学选修 2-3 第一章计数原理知识点什么是分加法数原理?答:做一件事情,完成它有 n 法,在第一法中有m1种不同的方法,在第二法中有 m2种不同的方法⋯在第 n 法中有 m n种不同的方法。
那么完成件事情共有N m1m2m n种不同的方法。
1.什么是分步乘法数原理?答:做一件事情,完成它需要 n 个步,做第一个步有m1种不同的方法,做第二个步有 m2种不同的方法⋯⋯做第 n 个步有 m n种不同的方法。
那么完成件事情共有N m1m2m n种不同的方法。
2.排列的定是什么?答:一般地,从n 个不同的元素中任取m m n 个元素,按照一定的序排成一列,叫做从 n 个不同的元素中任取 m 个元素的一个排列。
3.合的定是什么?答:一般地,从n 个不同的元素中任取m m n 个元素并成一,叫做从 n 个不同的元素中任取 m 个元素的一个合。
4.什么是排列数?答:从 n 个不同的元素中任取m m n 个元素的所有排列的个数,叫做从 n 个不同的元素中任取 m 个元素的排列数,作 A n m。
5.什么是合数?答:从 n 个不同的元素中任取m m n 个元素的所有合的个数,叫做从n 个不同的元素中任取m 个元素的合数,作C n m。
7.排列数公式有哪些?答:( 1)A m n n 1 n 2n m 1或nA n mn!;n m !(2)A n n n!,定0! 1。
8.合数公式有哪些?答:( 1)C n m n n 1 n 2n m 1 或m!C n m n!;m! n m !( 2)C n m C n n m,定 C n01。
9.排列与合的区是什么?答:排列有序,合无序。
10.排列与合的系是什么?答:A n m C n m A m m,即排列就是先合再全排列。
11.排列与合的性有哪些?答:两个性公式:(1)排列的性公式:A n m1 A n m mA n m 1( 2)合的性公式: C n m C n n m;C n m1C n m C n m 112.二式定理是什么?答:a b n C n0a n C n1a n 1b C n2a n 2b2C n r a n r b rC n n b n n N13二展开式的通是什么?答: T r 1C n r a n r b r 0 r n, r N , n N。
人教A版高中数学选修2-3讲义及题型归纳:分类加法计数原理和分步乘法原理

目录考点一:基本计数原理 (2)题型一、分布加法原理 (2)题型二、分布乘法原理 (4)题型三、基本计数原理的综合运用 (5)课后综合巩固练习 (6)考点一:基本计数原理加法原理分类计数原理:做一件事,完成它有n 类办法,在第一类办法中有1m 种不同的方法,在第二类办法中有2m 种方法,……,在第n 类办法中有n m 种不同的方法.那么完成这件事共有12nN m m m =+++种不同的方法.又称加法原理. 乘法原理分步计数原理:做一件事,完成它需要分成n 个子步骤,做第一个步骤有1m 种不同的方法,做第二个步骤有2m 种不同方法,……,做第n 个步骤有n m 种不同的方法.那么完成这件事共有12n N m m m =⨯⨯⨯种不同的方法.又称乘法原理.加法原理与乘法原理的综合运用如果完成一件事的各种方法是相互独立的,那么计算完成这件事的方法数时,使用分类计数原理.如果完成一件事的各个步骤是相互联系的,即各个步骤都必须完成,这件事才完成,那么计算完成这件事的方法数时,使用分步计数原理.分类计数原理、分步计数原理是推导排列数、组合数公式的理论基础,也是求解排列、组合问题的基本思想方法,这两个原理十分重要必须认真学好,并正确地灵活加以应用.题型一、分布加法原理1.用10元、5元和1元来支付20元钱的书款,不同的支付方法有( ) A .3B .5C .9D .12【分析】用列举法求解.【解答】解:用10元、5元和1元来支付20元钱的书款,有以下几类办法: ①用2张10元钱支付;②用1张10元钱和2张5元钱支付;③用1张10元钱、1张5元钱5张1元钱支付; ④用1张10元钱和10张1元钱支付; ⑤用1张5元钱和15张1元钱支付; ⑥用2张5元钱和10张1元钱支付;⑦用3张5元钱和5张1元钱支付; ⑧用4张5元钱支付; ⑨用20张1元钱支付. 故共有9种方法. 故选:C .【点评】本题考查不同的付款方式共有多少种的求法,是基础题,解题时要认真审题,注意列举法的合理运用.2.一个三层书架,分别放置语文书12本,数学书14本,英语书11本,从中取出一本,则不同的取法共有( ) A .3种B .1848种C .37种D .6种【分析】分情况讨论:选择拿语文书:有12种不同的拿法,数学书有14种不同的拿法,英语书有11种不同的拿法,然后把这三种情况的数量加在一起即可.【解答】解:由题意可知选择拿语文书:有12种不同的拿法,数学书有14种不同的拿法,英语书有11种不同的拿法, 共有:12141137++=. 故选:C .【点评】本题先确定拿哪种类型的书,考查分类计数原理的应用,考查两种原理的区别. 3.已知集合{1M=,2-,3},{4N =-,5,6,7}-,从两个集合中各选一个数作为点的坐标,则这样的坐标在直角坐标系中可表示第三、四象限内多少个不同点( ) A .18个B .10个C .16个D .14个【分析】根据第三、四象限内点的坐标的性质,分2种情况讨论,①取M 中的数作横坐标,取N 中的数作纵坐标坐标,②取N 中的数作横坐标,取M 中的数作纵坐标坐标,易得每种情况下的数目,进而由加法原理可得答案.【解答】解:第三、四象限内点的纵坐标为负值,横坐标无限制;分2种情况讨论,①取M 中的数作横坐标,取N 中的数作纵坐标坐标,有326⨯=种情况, ②取N 中的数作横坐标,取M 中的数作纵坐标坐标,有414⨯=种情况; 共有6410+=种情况, 故选:B .【点评】本题考查分类计数原理的运用,解题的切入点为四个象限的点的坐标的性质.题型二、分布乘法原理1.设函数:f N N ++→满足:对于任意大于3的正整数n ,()3f n n =-,且当3n 时,2()3f n ,则不同的函数()f x 的个数为()A .1B .3C .6D .8【分析】通过()3f n n =-,结合映射的定义,根据2()3f n ,确定函数的个数.【解答】解:3n ,2()3f n ,f∴(1)2=或3,且f(2)2=或3 且f(3)2=或3.根据分步计数原理,可得共2228⨯⨯=个不同的函数. 故选:D .【点评】本题主要考查映射的定义,以及分步计数原理的应用,比较基础. 2.将一枚骰子向桌面先后抛掷2次,一共有( )种不同结果. A .6B .12C .36D .216【分析】由分步计数原理知有66⨯种结果,问题得以解决 【解答】解:由分步计数原理知有6636⨯=种结果 故选:C .【点评】本题考查了分步计数原理,属于基础题3.古代“五行”学认为:“物质分金、木、土、水、火五种属性,金克木,木克土,土克水,水克火,火克金.”将五种不同属性的物质任意排成一列,但排列中属性相克的两种物质不相邻,则这样的排列方法有多少种(结果用数字表示).( ) A .5B .10C .20D .120【分析】由题意,可看作五个位置排列五种事物,由分步原理求解即可,本题需要考虑的因素:相克的两种物质不相邻,注意满足此规则,计算符合条件的排列方法种数【解答】解:由题意,可看作五个位置排列五种事物,第一位置有五种排列方法,不妨假设排上的是金,则第二步只能从土与水两者中选一种排放,故有两种选择不妨假设排上的是水, 第三步只能排上木,第四步只能排上火,第五步只能排上土, 故总的排列方法种数有5211110⨯⨯⨯⨯= 故选:B .【点评】本题考查排列排列组合及简单计数问题,解答本题关键是理解题设中的限制条件及“五行”学说的背景,利用分步原理正确计数,本题较抽象,计数时要考虑周详,本题以实际问题为背景,有着实际背景的题在现在的高考试卷上有逐步增多的趋势题型三、基本计数原理的综合运用1.将5种不同的花卉种植在如图所示的四个区域中,每个区域种植一种花卉,且相邻区域花卉不同,则不同的种植方法种数是( )A .420B .180C .64D .25【分析】由于规定一个区域只涂一种颜色,相邻的区域颜色不同,可分步进行,区域A 有5种涂法,B 有4种涂法,讨论A ,D 同色和异色,根据乘法原理可得结论.【解答】解:由题意,由于规定一个区域只涂一种颜色,相邻的区域颜色不同,可分步进行, 区域A 有5种涂法,B 有4种涂法,A ,D 不同色,D 有3种,C 有2种涂法,有5432120⨯⨯⨯=种, A ,D 同色,D 有4种涂法,C 有3种涂法,有54360⨯⨯=种,∴共有180种不同的涂色方案.故选:B .【点评】本题考查排列组合的应用,涉及分步计数原理的应用,注意分析图形中区域相邻的情况. 2.5名同学排成一列,某个同学不排排头的排法种数为 (用数字作答).【分析】先排不在排头的这个学生,方法有4种,其他学生任意排,有44A 种,根据分步计数原理,求得结果.【解答】解:先排不在排头的这个学生,方法有4种,其他学生任意排,有44A 种,根据分步计数原理,所有的排列方法共有44496A =种,故答案为:96.【点评】本题主要考查分步计数原理的应用,注意特殊元素优先排列,属于基础题.3.已知集合{1M ∈,2-,3},{4N ∈-,5,6,7}-,从两个集合中各取一个元素作为点的坐标,求这样的坐标在直角坐标系中可表示第一、二象限内不同的点的个数.【分析】本题首先分类在每一类中又分步,M中的元素作点的横坐标,N中的元素作点的纵坐标,N中的元素作点的横坐标,M中的元素作点的纵坐标,分别可以得到在第一和第二象限中点的个数,根据分类加法原理得到结果.【解答】解:由题意知本题是一个分类和分步的综合问题,⨯个,M中的元素作点的横坐标,N中的元素作点的纵坐标,在第一象限的点共有22在第二象限的点共有12⨯个.⨯个,N中的元素作点的横坐标,M中的元素作点的纵坐标,在第一象限的点共有22在第二象限的点共有22⨯个.∴所求不同的点的个数是2212222214⨯+⨯+⨯+⨯=(个).【点评】本题考查分步计数原理和分类计数原理,是一个综合题目,首先分类,每类方法并不都是一步完成的,必须在分类后又分步,综合利用两个原理解决.课后综合巩固练习1.某一数学问题可用综合法和分析法两种方法证明,有5位同学只会用综合法证明,有3位同学只会用分析法证明,现任选1名同学证明这个问题,不同的选法种数有()种.A.8B.15C.18D.30【分析】本题是一个分类计数问题,解决问题分成两个种类,一是可以用综合法证明,有5种方法,一是可以用分析法来证明,有3种方法,根据分类计数原理知共有358+=种结果.【解答】解:由题意知本题是一个分类计数问题,解决问题分成两个种类,一是可以用综合法证明,有5种方法,一是可以用分析法来证明,有3种方法,根据分类计数原理知共有358+=种结果,故选:A.【点评】本题看出分类计数问题,本题解题的关键是看清楚完成这个过程包含两种方法,看出每一种方法所包含的基本事件数,相加得到结果.2.将一张面值1元的人民币全部换成面值1角,2角和5角的硬币,则换法总数为.【分析】设1角硬币有x枚,2角硬币有y枚,5角硬币有z枚,构造三元一次方程,然后利用列举法得到所有可能的情况,可得答案.【解答】解:设1角硬币有x 枚,2角硬币有y 枚,5角硬币有z 枚 则2510x y z ++= 满足方程的解有:10x =,0y =,0z = 8x =,1y =,0z = 6x =,2y =,0z = 4x =,3y =,0z = 2x =,4y =,0z = 0x =,5y =,0z =5x =,0y =,1z = 0x =,0y =,2z = 3x =,1y =,1z = 1x =,2y =,1z =共十种不同情况 故答案为:10【点评】解决此类问题要用列举法,把所有的情况都一一排查,找出问题的答案. 3.乘积123123412345()()()a a a b b b b c c c c c +++++++++展开后共有 项.【分析】根据多项式的乘法法则,分析易得在123()a a a ++中取一项有3种取法,在1234()b b b b +++中取一项有4种取法,在12345()c c c c c ++++中取一项有5种取法,进而由分步计数原理计算可得答案.【解答】解:根据多项式的乘法法则,123123412345()()()a a a b b b b c c c c c +++++++++的结果中每一项都必须是在123()a a a ++、1234()b b b b +++、12345()c c c c c ++++三个式子中任取一项后相乘,得到的式子,而在123()a a a ++中有3种取法,在1234()b b b b +++中有4种取法,在12345()c c c c c ++++中有5种取法,由乘法原理,可得共有34560⨯⨯=种情况,则123123412345()()()a a a b b b b c c c c c +++++++++的展开式中有60项; 故答案为60.【点评】本题考查分步计数原理的运用,是常见的题目;平时要多加训练.4.在66⨯的表中停放3辆完全相同的红色车和3辆完全相同的黑色车,每一行、每一列都只有一辆车,每辆车占一格,共有 种停放方法.(用数字作答)【分析】利用分步计数原理,第一步先选车,第二种再排列,问题得以解决【解答】解:第一步先选车有36C 种,第二步因为每一行、每一列都只有一辆车,每辆车占一格,从中选取一辆车后,把这辆车所在的行列全划掉,依次进行,则有11111166543216C C C C C C A =种,根据分步计数原理得;366614400C A =种.故答案为:14400.【点评】本题考查了分步计数原理的应用,关键是如何求出每辆车所在行列的可能性5.对于各数互不相等的正数数组1(i ,2i ,⋯,)(n i n 是不小于2的正整数),如果在p q <时有p q i i <,则称“p i 与q i ”是该数组的一个“顺序”,一个数组中所有“顺序”的个数称为此数组的“顺序数”.例如,数组(2,4,3,1)中有顺序“2,4”、“2,3”,其“顺序数”等于2.若各数互不相等的正数数组1(a ,2a ,3a ,4a ,5)a 的“顺序数”是4,则5(a ,4a ,3a ,2a ,1)a 的“顺序数”是 . 【分析】根据题意,假设出一种情况,倒序后输出顺序数即可.【解答】解:根据题意,各数互不相等的正数数组1(a ,2a ,3a ,4a ,5)a 的“顺序数”是4,假设12a a <,13a a <,14a a <,15a a <,且后一项都比前一项小,因此可以判断出23a a >,34a a >,45a a >, 则5(a ,4a ,3a ,2a ,1)a 的“顺序数”是6, 故填:6.【点评】本题考查了新定义,理解好定义是解题的先决条件,另外,要大胆假设.本题属基础题.。
高中数学选修2-3 二项式

1、二项式定理: nn n r r n r n n n n n n b C b a C b a C a C b a +++++=+--ΛΛ110)( 2、通项公式: 3、特例: (1)对称性: 二项式系数的性质与首末两端“等距离”的两个二项式系数相等. (2)增减性与最大值:从第一项起至中间项,二项式系数逐渐增大,随后又逐渐减小.因此,当n 为偶数时,中间一项的二项式系数取得最大值;当n 为奇数时,中间两项的二项式系数 、 相等且同时取得最大值(3)各二项式系数的和例1:在二项式(2x-3y )9的展开式中,求: (1)二项式系数之和; (2)各项系数之和; (3)所有奇数项系数之和; (4)系数绝对值的和。
解:设(2x-3y )9=a 0x 9+a 1x 8y+a 2x 7y 2+…+a 9y 9,1(0,1,2,)r n r rr n T C a br n -+==L n n n r r n n n n xC x C x C x C x ++++++=+ΛΛ22111)(m n mn nC C -=0122r nnn n n n n C C C C C ++++++=L L 131202-=⋅⋅⋅++=⋅⋅⋅++n n n n n C C C C(1)二项式系数之和为;(2)各项系数之和为a0+a1+a2+…+a9,令x=1,y=1,∴a0+a1+a2+…+a9=(2-3)9=-1;(3)由(2)知a0+a1+a2+…+a9=-1,令x=1,y=-1,可得:a0-a1+a2-…-a9=59,将两式相加除以2可得:a0+a2+a4+a6+a8=,即为所有奇数项系数之和;(4)|a0|+|a1|+|a2|+…+|a9|=a0-a1+a2-a3+…-a9,令x=1,y=-1,则|a0|+|a1|+|a2|+…+|a9|=a0-a1+a2-a3+…-a9=59。
1、已知(2x+1)10=a0x10+ a1x9+ a2x8+……+a9x+ a10, (1)求a0+ a1+ a2+…… +a9+ a10的值(2)求a0+ a2+ a4+…… + a10的值答案 :1结论:3.( 1﹣x ) 13 的展开式中系数最小的项是 ( ) C (A)第六项 (B)第七项 (C )第八项 (D)第九项求n的值。
高二数学选修2-3 (2)

高二数学选修2-3一、知识点概述高二数学选修2-3是高中数学的选修课程,主要内容包括以下几个方面:1.组合与二项式定理:介绍组合的基本概念,以及组合的性质和计算方法;讲解二项式定理及其应用。
2.排列与多项式:引入排列的概念,介绍全排列和循环排列的性质;讲解多项式的定义、运算和因式分解的方法。
3.概率与统计:介绍概率的基本概念、性质和计算方法;讲解统计的基本概念和统计图表的绘制方法。
4.空间解析几何:引入空间直角坐标系,讲解空间中直线和平面的方程及其性质;讲解空间几何体的性质和计算方法。
本文将逐个知识点进行详细介绍,并给出相关的应用示例和习题。
二、组合与二项式定理1. 组合的基本概念组合是从给定的若干个不同元素中任意地选择出一些元素排成一组的方法数。
用符号C(n, m)表示从n个不同元素中选取m个元素的组合数。
2. 组合的性质和计算方法(1)组合的性质:组合有以下几个基本性质:交换律、加法原理、乘法原理和二项式定理。
(2)组合的计算方法:组合的计算可以使用公式C(n, m) = n! / (m!(n-m)!)进行求解,也可以通过递推公式C(n, m) = C(n-1, m) + C(n-1, m-1)进行计算。
3. 二项式定理及其应用二项式定理是代数中的一个重要定理,它给出了两个数之和的n次方展开后的表达式。
二项式定理的公式为:(a+b)^n = C(n, 0) * a^n * b^0 + C(n, 1) * a^(n-1) * b^1 + … + C(n, n) * a^0 * b^n。
二项式定理在代数运算和概率计算中有很多应用。
三、排列与多项式1. 排列的基本概念排列是从给定的若干个不同元素中任意地选择出一些元素并按照一定顺序排列的方法数。
用符号P(n, m)表示从n个不同元素中选取m个元素进行排列的方法数。
2. 排列的性质和计算方法(1)排列的性质:排列有以下几个基本性质:乘法原理、加法原理和递推关系式。
高中数学知识点总结选修2-3

高中数学知识点总结选修 2-3第一章计数原理1.1 分类加法计数与分步乘法计数分类加法计数原理:完成一件事有两类不同方案,在第第 2 类方案中有n 种不同的方法,那么完成这件事共有“不重不漏”。
1 类方案中有m 种不同的方法,在N=m+n 种不同的方法。
分类要做到分步乘法计数原理:完成一件事需要两个步骤。
做第1步有m种不同的方法,做第2步有n 种不同的方法,那么完成这件事共有N=m× n 种不同的方法。
分步要做到“步骤完整”。
n 元集合A={a1 , a2?, an} 的不同子集有2n 个。
1.2 排列与组合1.2.1 排列一般地,从n 个不同元素中取出m(m≤n)个元素,按照一定的顺序排成一列,叫做从n 个不同元素中取出m 个元素的一个排列(arrangement)。
从 n 个不同元素中取出m(m≤n) 个元素的所有不同排列的个数叫做从n 个不同元素中取出m 个元素的排列数,用符号Amn 表示。
排列数公式:n个元素的全排列数规定: 0!=11.2.2 组合一般地,从 n 个不同元素中取出m(m≤n) 个元素合成一组,叫做从n个不同元素中取出元素的一个组合(combination) 。
从 n 个不同元素中取出m(m≤n) 个元素的所有不同组合的个数,叫做从n 个nm 不同元素中取出m 个元素的组合数,用符号Cn 或 m 表示。
m 个组合数公式:mm∵ Amn=Cn?Am∴规定: ?? =组合数的性质:1.3 二项式定理1.3.1 二项式定理 (binomial theorem)*注意二项展开式某一项的系数与这一项的二项式系数是两个不同的概念。
1.3.2杨“辉三角”与二项式系数的性质*表现形式的变化有时能帮助我们发现某些规律!(1)对称性(2)当 n 是偶数时,共有奇数项,中间的一项Cnn+12 取得最大值;n+1当 n 是奇数时,共有偶数项,中间的两项Cn ,Cn 同时取得最大值。
(3)各二项式系数的和为012kn2n=Cn+Cn+Cn+ ?+Cn+ ?+Cn(4)二项式展开式中,奇数项二项式系数之和等于偶数项二项式系数之和:024135Cn+Cn+Cn+ ?=Cn+Cn+Cn+ ? n-1(5)一般地,rrrrr+1Cr+Cr+1+Cr+2+ ?+Cn-1=Cn(n> )第二章随机变量及其分布2.1 离散型随机变量及其分布2.1.1 离散型随机变量随着试验结果变化而变化的变量称为随机变量(random variable) 。
人教版高中数学【选修2-3】[知识点整理及重点题型梳理] 二项式定理(理)(提高)
人教版高中数学选修2-3知识点梳理重点题型(常考知识点)巩固练习二项式定理【学习目标】1.理解并掌握二项式定理,了解用计数原理证明二项式定理的方法. 2.会用二项式定理解决与二项展开式有关的简单问题.【要点梳理】 要点一:二项式定理1.定义一般地,对于任意正整数n ,都有:nn n r r n r n n n n n n b C b a C b a C a C b a +++++=+-- 110)((*N n ∈),这个公式所表示的定理叫做二项式定理, 等号右边的多项式叫做n b a )(+的二项展开式。
式中的rn rr n C ab -做二项展开式的通项,用T r+1表示,即通项为展开式的第r+1项:1r n r rr nT C a b -+=, 其中的系数rn C (r=0,1,2,…,n )叫做二项式系数, 2.二项式(a+b)n 的展开式的特点:(1)项数:共有n+1项,比二项式的次数大1;(2)二项式系数:第r+1项的二项式系数为rn C ,最大二项式系数项居中;(3)次数:各项的次数都等于二项式的幂指数n .字母a 降幂排列,次数由n 到0;字母b 升幂排列,次数从0到n ,每一项中,a ,b 次数和均为n ;3.两个常用的二项展开式:①011()(1)(1)n n n r r n r r n n nn n n n a b C a C a b C a b C b ---=-++-⋅++-⋅(*N n ∈)②122(1)1n r r n n n n x C x C x C x x +=++++++要点二、二项展开式的通项公式公式特点:①它表示二项展开式的第r+1项,该项的二项式系数是rn C ; ②字母b 的次数和组合数的上标相同; ③a 与b 的次数之和为n 。
要点诠释:(1)二项式(a+b)n 的二项展开式的第r+1项r n r r nC a b -和(b+a)n 的二项展开式的第r+1项r n r r n C b a -是有区别的,应用二项式定理时,其中的a 和b 是不能随便交换位置的.(2)通项是针对在(a+b)n 这个标准形式下而言的,如(a -b)n 的二项展开式的通项是1(1)r r n r rr n T C a b -+=-(只需把-b 看成b 代入二项式定理)。
高中数学选修2-3(人教B版)第二章随机变量及其分布2.2知识点总结含..
描述:例题:高中数学选修2-3(人教B版)知识点总结含同步练习题及答案第二章 随机变量及其分布 2.2 条件概率与事件的独立性一、学习任务1. 了解条件概率的定义及计算公式,并会利用条件概率解决一些简单的实际问题.2. 能通过实例理解相互独立事件的定义及概率乘法公式,并能综合利用互斥事件的概率加法公式及独立事件的概率乘法公式.3. 理解独立重复试验的概率及意义,理解事件在 次独立重复试验中恰好发生 次的概率公式,并能利用 次独立重复试验的模型模拟 次独立重复试验.二、知识清单事件的独立性与条件概率独立重复试验与二项分布三、知识讲解1.事件的独立性与条件概率条件概率的概念一般地,设 ,为两个事件,且 ,称为在事件 发生的条件下,事件 发生的条件概率(conditional probability).读作 发生的条件下 发生的概率.条件概率的性质①条件概率具有概率的性质,任何事件的条件概率都在 和 之间,即.②如果 和 是两个互斥事件,则相互独立事件的概念设 ,为两个事件,若 ,则称事件 与事件 相互独立(mutually independent).相互独立事件同时发生的概率:如果事件 ,,, 相互独立,那么这 个事件同时发生的概率等于每个事件发生概率的积,即n k n n A B P (A )>0P (B |A )=P (AB )P (A )A B P (B |A )A B 0 1 0≤P (B|A)≤1 B CP (B ∪C |A )=P (B |A )+P (C |A ).A B P (AB )=P (A )P (B )A B A 1A 2⋯A n n P (⋯)=P ()P ()⋯P ().A 1A 2A n A 1A 2A n 甲、乙两地都位于长江下游,根据一百多年气象记录,知道甲、乙两地一年中雨天占的比例分别20%18%12%为 和 ,两地同时下雨的比例为 ,问:(1)乙地为雨天时甲地也为雨天的概率是多少?(2)甲地为雨天时乙地也为雨天的概率是多少?解:设“甲地为雨天”, “ 乙地为雨天”,则根据题意有(1)乙地为雨天时甲地也为雨天的概率(2)甲地为雨天时乙地也为雨天的概率是20%18%12%A =B =P (A )=0.20,P (B )=0.18,P (AB )=0.12.P (A |B )==≈0.67.P (AB )P (B )0.120.18P (B |A )===0.60.P (AB )P (A )0.120.20如图,四边形 是以 为圆心,半径 的圆内接正方形,将一颗豆子随机地扔到该圆内,用 表示事件“豆子落在正方形 内”, 表示事件“豆子落在扇形 (阴影部分)内”,则(1)______;(2)______.解:;圆 的面积是,正方形 的面积是 ,扇形 的面积是 ,由几何概型概率公式得 ,由条件概率公式得EFGH O 1A EFGH B OHE P (A )=P (B |A )=2π14O πEF GH 2OHE π4P (A )=2πP (B |A)===.P (AB )P (A)12π2π14掷一枚正方体骰子一次,设事件 :“出现偶数点”,事件 :“出现 点或 点”,则事件 , 的关系是( )A.互斥但不相互独立 B.相互独立但不互斥 C.互斥且相互独立 D.既不相互独立也不互斥解:B事件 ,事件 ,事件 ,基本事件空间 .所以,,,即 ,因此,事件 与 相互独立.当“出现 点”,事件 , 同时发生,所以 , 不是互斥事件.A B 36A B A ={2,4,6}B ={3,6}AB ={6}Ω={1,2,3,4,5,6}P (A )==3612P (B )==2613P (AB )==×161213P (AB )=P (A )P (B )A B 6A B A B 甲、乙两人在罚球线投球命中的概率分别为与 .(1)甲、乙两人在罚球线各投球一次,求恰好命中一次的概率;(2)甲、乙两人在罚球线各投球二次,求这四次投球均不命中的概率.解:记“甲投一次命中”为事件 ,“乙投一次命中”为事件 ,则 ,1225A B P (A )=12213,,.(1)恰好命中一次的概率为(2)设事件“甲、乙两人在罚球线各投球二次均不命中”的概率为 ,则2P (B )=25P ()=A ¯¯¯12P ()=B ¯¯¯35P =P (A ⋅)+P (⋅B )B ¯¯¯A ¯¯¯=P (A )⋅P ()+P ()⋅P (B )B ¯¯¯A ¯¯¯=×+×12351225=.12P 1P 1=P (∩∩∩)A ¯¯¯A ¯¯¯B ¯¯¯B ¯¯¯=P ()⋅P ()⋅P ()⋅P ()A ¯¯¯A ¯¯¯B ¯¯¯B ¯¯¯=(1−(1−12)225)2=9100在一个选拔项目中,每个选手都需要进行 轮考核,每轮设有一个问题,能正确回答者进入下一轮考核,否则被淘汰.已知某选手能正确回答第一、二、三、四轮问题的概率分别为,,,,且各轮问题能否正确回答互不影响.(1)求该选手进入第三轮才被淘汰的概率;(2)求该选手至多进入第三轮考核的概率;解:设事件 ( ,,, )表示“该选手能正确回答第 轮问题”,由已知得,,,.(1)设事件 表示“该选手进入第三轮才被淘汰”,则(2)设事件 表示“该选手至多进入第三轮考核”,则456453413A i i =1234i P ()=A 156P ()=A 245P ()=A 334P ()=A 413B P (B )=P ()A 1A 2A ¯¯¯3=P ()P ()P ()A 1A 2A ¯¯¯3=××(1−)564534=.16C P (C )=P (++)A ¯¯¯1A 1A ¯¯¯2A 1A 2A ¯¯¯3=P ()+P ()+P ()A ¯¯¯1A 1A ¯¯¯2A 1A 2A ¯¯¯3=+×+××(1−)165615564534=.12描述:例题:2.独立重复试验与二项分布独立重复试验一般地,在相同条件下重复做的 次试验,称为次独立重复试验(independent andrepeated trials).二项分布一般地,在 次独立重复试验中,用表示事件发生的次数,设每次试验中事件发生的概率为,则此时称随机变量服从二项分布(binnomial distribution),记作 ),并称为成功概率.n n n X A A p P (X =k )=(1−p ,k=0,1,2,⋯,n .C kn pk )n −k X X ∼B (n ,p ) p 下列随机变量 的分布列不属于二项分布的是( )A.投掷一枚均匀的骰子 次, 表示点数 出现的次数B.某射手射中目标的概率为 ,设每次射击是相互独立的, 为从开始射击到击中目标所需要的射击次数C.实力相等的甲、乙两选手举行了 局乒乓球比赛, 表示甲获胜的次数D.某星期内,每次下载某网站数据后被病毒感染的概率为 , 表示下载 次数据后电脑被病毒感染的次数解:B选项 A,试验出现的结果只有两个:点数为 和点数不为 ,且点数为 的概率在每一次试验都为 ,每一次试验都是独立的,故随机变量 服从二项分布;选项 B,,故随机变量 不服从二项分布;选项 C,甲、乙的获胜率都相等,举行 次比赛,相当于进行了 次独立重复试验,故 服从二项分布;选项 D,由二项分布的定义可知,被感染次数 .X 5X 6p X 5X 0.3X n 66616X P (X =1)=p ,P (X =2)=(1−p )p ,P (X =k )=(1−p p )(k −1)X 55X X ∼B (n ,0.3)口袋中有 个白色乒乓球, 个黄色乒乓球,从中选取 次,每次取 个后又放回,则 次中恰有 次取到白球的概率是( )A. B. C. D . 解:D任意取球 次,取得白球 次的概率是5551531235C 35C 510⋅C 350.5553P (X =3)=(1−0.5=⋅C 350.53)5−3C 350.55甲、乙两名同学进行三分球投篮比赛,甲每次投中的概率为 ,乙每次投中的概率为 ,每人分别进行三次投篮.(1)设甲投中的次数为 ,求 的分布列;(2)求乙至多投中 次的概率;(3)求乙恰好比甲多投中 次的概率.1312ξξ221四、课后作业 (查看更多本章节同步练习题,请到快乐学)解:(1), 的可能取值为 ,,,. 的分布列为:(2)设“乙至多投中 次”为事件 ,则(3)设“乙比甲多投中 次”为事件 ,“乙恰投中 次且甲恰投中 次”为事件,“乙恰投中 次且甲恰投中 次”为事件 ,则 ,, 为互斥事件,则所以乙恰好比甲多投中 次的概率为.ξ∼B (3,)13ξ0123P(ξ=0)=(=,C 0323)3827P (ξ=1)=()(=,C 131323)249P (ξ=2)=(()=,C 2313)22329P (ξ=3)=(=.C 3313)3127ξξP082714922931272A P (A )=1−(=.C 3312)3782A 120B 131B 2=∪A 1B 1B 2B 1B 2P (A )=P ()+P ()=×+×=.B 1B 282738491816216答案:解析:1. 某一批花生种子,如果每 粒发芽的概率为 ,那么播下 粒种子恰有 粒发芽的概率是 A .B .C .D .B 概率为 .14542()1662596625192625256625=C 24()452(1−)45296625答案:2. 某地区空气质量监测资料表明,一天的空气质量为优良的概率是 ,连续两天为优良的概率是,已知某天的空气质量为优良,则随后一天的空气质量为优良的概率是 A .B .C .D .A0.750.6()0.80.750.60.453. 某厂生产电子元件,其产品的次品率为 ,现从一批产品中任意地连续取出 件,其中次品数 的5%2ξ高考不提分,赔付1万元,关注快乐学了解详情。
高中数学选修2-3(人教A版)第一章计数原理1.2知识点总结含同步练习及答案
1 6 7 12 C0 12 < C12 < ⋯ < C12 > C12 > ⋯ > C12 ,所以 2x − 3 ⩾ 5 且 2x ⩽ 12 解得 4 ⩽ x ⩽ 6.
高考不提分,赔付1万元,关注快乐学了解详情。
− A5 9
= =
8 × 7 × 6 × 5 × (8 + 7) 8 × 7 × 6 × 5 × (24 − 9) = 1.
2×8×7×6×5×4+7×8×7×6×5 8×7×6×5×4×3×2×1−9×8×7×6×5
(3)根据原方程,可得
3x(x − 1)(x − 2) = 2(x + 1)x + 6x(x − 1).
0 10 (1)计算:C5 10 ⋅ C10 − C10 ; m−1 (2)证明:mCm n = nCn−1 .
解:(1)原式= (2)证明:因为
10 × 9 × 8 × 7 × 6 × 1 − 1 = 252 − 1 = 251 ; 5×4×3×2×1
Cm n =
n! , m!(n − m)! (n − 1)! n(n − 1)! n m−1 n n! ⋅ = = . Cn−1 = m m (m − 1)!(n − m)! m ⋅ (m − 1)!(n − m)! m!(n − m)!
正整数 1 到 n 的连乘积,叫做 n 的阶乘,用 n! 表示.另外,我们规定 0! = 1 .所以排列数公 式还可以写成
Am n =
(n − m)!
n!
.
组合的定义 一般地,从 n 个不同元素中取出 m (m ⩽ n )个元素合成一组,叫做从 n 个不同元素中取出 m 个元素的一个组合(combination). 组合数及组合数的公式 从 n 个不同元素中取出 m (m ⩽ n )个元素的所有不同组合的个数,叫做从 n 个不同元素中取 出 m 个元素的组合数,用符号 Cm n 表示.
人教版高中数学【选修2-3】[知识点整理及重点题型梳理]组合(理)(基础)
精品文档用心整理人教版高中数学选修2-3知识点梳理重点题型(常考知识点)巩固练习组合1.理解组合的概念.2.能利用计数原理推导组合数公式.3.能解决简单的实际问题.4.理解组合与排列之间的联系与区别.要点一:组合1.定义:一般地,从n 个不同元素中取出m (m n )个元素并成一组,叫做从n 个不同元素中取出m 个元素的一个组合.要点诠释:①从排列与组合的定义可知,一是“取出元素”;二是“并成一组”,“并成一组”即表示与顺序无关.排列与元素的顺序有关,而组合与元素的顺序无关,这是它们的根本区别.②如果两个组合中的元素相同,那么不管元素的顺序怎样都是相同的组合;只有当两个组合中的元素不完全相同时,才是不同的组合. 因此组合问题的本质是分组问题,它主要涉及元素被取到或未被取到.要点二:组合数及其公式1)组合数的定义:从n 个不同元素中取出m (m n )个元素的所有组合的个数,叫做从n 个不同元素中取出m 个元素的组合数.记作C n m.要点诠释:“组合”与“组合数”是两个不同的概念:精品文档用心整理一个组合是指“从n 个不同的元素中取出m(m≤ n)个元素并成一组”,它不是一个数,而是具体的一件事;组合数是指“从n 个不同元素中取出m(m≤n)个元素的所有组合的个数”,它是一个数.例如,从 3 个不同元素a,b,c 中取出2 个元素的组合为ab,ac,bc,其中每一种都叫做一个组合,而数字3 就是组合数.2.组合数的公式及推导求从n 个不同元素中取出m个元素的排列数An m,可以按以下两步来考虑:精品文档 用心整理 第一步,先求出从这 n 个不同元素中取出 m 个元素的组合数 C nm ;第二步,求每一个组合中 m 个元素的全排列数 A m m.根据分步计数原理,得到An mCn m Am m.A n mn(n 1)(n 2) (n m 1)A m m m!这里 n , m ∈ N+,且m ≤ n ,这个公式叫做组合数公式.因为A n mn! ,所以组合数公式还可表示(n m )!!2) ) Cn m( m 、 n N ,且 m n )m!(n -m)!要点诠释:上面第一个公式一般用于计算,但当数值 m 、 n 较大时,利用第二个式子计算组合数较为方便,在对含有字母的组合数的式子进行变形和论证时,常用第二个公式. 要点三 : 组合数的性质 性质 1: Cn mCn n m( m 、 n N ,且 m n )性质2:Cn m1 Cn mCn m 1( m 、n N ,且 m n )要点诠释: 规定:Cn 01 .要点四、纯组合问题常见题型1) “含有”或“不含有”某些元素的组合题型:“含” ,则先将这些元素取出,再由另外元素补足; “不含” ,则先将这些元素剔除,再从剩下的元素为: C n mn! m!(n m)!要点诠释:组合数公在以后学习排列组合的混合问题时, 一般都是按先取(1) n(n-1)(n-2) (n-m1) m! m 、 n N ,且 m n )m n精品文档用心整理如:现从 5 位男同学、 4 位女同学中选出 5 名代表,若男甲、女A都必须当选,有多少种不同的选法女A 必须当选,只需从剩下7 人中任选3 人即可满足题目的要求,故有C7335 种不同的选法.精品文档 用心整理 ( 2) “至少”或“最多”含有几个元素的题型:解这类题必须十分重视“至少”与“最多”这两个关键词的含义,谨防重复与漏解.用直接法和间接法都可以求解,但通常用直接法分类复杂时,考虑逆向思维,用间接法处理.如( 1 )中,将问题改为至少有一名女同学当选,有多少种不同的选法 ?则在全部的选法中,排除全部男生当选的情况即可,故有 C 95 C 55125种不同的选法.3)分堆问题平分到指定位置 堆数的阶乘例如 将 6 本不同的书平均分成三份,每份两本,求不同的分法数.222C62C42C2215(种) .3!②分堆但不平均,其分法数为 相同数量的堆数阶乘之积 分到指定位置例如,将 12 本不同的书分成五份,分别为 2 本、 2 本、 2 本、 3 本、 3 本,求不同的分法数.依据上述公式,分到指定位置数为 C 122C 120C 82C 62C 33.( 4)定序问题.对于某些元素的顺序固定的排列问题,可先全排,再除以定序元素的全排,或先在总位置中选出定序元素的位置而不参加排列,然后对其他元素进行排列.例: 5 人站成一排,如果甲必须站在乙的左边,则不同的排法有多少种? 法一 :5 人不加限制的排列方法有 A55种, “甲在乙的左边”和“甲在乙的右边”的排法是相对的,所1A55 60 (种) . 25法二 : 第一步,在 5 个位置中选2 个位置给甲、乙二人有 C 52种选法;323第二步,剩下三个位置由剩下三人全排,有A3 种排法,共有 C 5 A3 60 (种); 法三 : 从 5 个位置选3 个位置由除甲、乙两人之外的①平均分堆,其分法数为:依据上述公式,其分法为其中两本的有三堆,故除以 3! ; 3 本的有两堆,要除以 2! ,故分法数为C122C120C82C62C3! 2!精品文档用心整理三人排列有A53 60 种(剩下两个位置,甲、乙随之确定).(5)指标问题用“隔板法”:如,将10 个保送生预选指标分配给某重点中学高三年级六个班,每班至少一名,共有多少种分配方案?将10 个名额并成一排,名额之间有9个空,用 5 块隔板插入9 个空,就可将10 个名额分为 6 部分,每一种插法就对应一种分配法,故有C95种方案.注意:隔板法与插空法是不同的,要予以“区分”.隔板法只适用于相同元素的分配问题.要点五、组合组合的综合应用处理排列、组合综合题时,应遵循四大原则:(1 )先特殊后一般的原则( 2)先取后排的原则( 3)先分类后分步的原则( 4)正难则反、等价转化原则.【典型例题】类型一、组合概念及组合数公式例1.判断下列问题是组合问题还是排列问题.( 5))设集合A={a,b,c,d,e},则集合A的子集中含有3 个元素的有多少个?( 6)铁路线上有5 个车站,则这条线上共需准备多少种车票?多少种票价?( 3)3 人去干5 种不同的工作,每人干一种,有多少种分工方法?(4)把3 本相同的书分给 5 个学生,每人最多得 1 本,有几种分配方法?【思路点拨】排列与顺序有关,组合与顺序无关.【解析】(1 )因为本问题与元素顺序无关,故是组合问题.(2)因为甲站到乙站车票与乙站到甲站车票是不同的,故是排列问题,但票价与顺序无关,甲站到乙站与乙站到甲站是同一种票价,故是组合问题.(3)因为分工方法是从 5 种不同的工作中取出3 种,按一定次序分给 3 个人去干,故是排列问题.(4)因为3 本书是相同的,无论把 3 本书分给哪三人,都不需考虑他们的顺序,故是组合问题.【总结升华】区分排列与组合问题,关键是利用排列与组合的定义,组合是“只选不排、并成一组,与顺序无关”举一反三:精品文档用心整理【变式1 】平面内有10 个点,(1)以其中每 2 个点为端点的线段共有多少条?(2)以其中每 2 个点为端点的有向线段共有多少条?【解析】线段不考虑线段两个端点的顺序,是组合问题;有向线段考虑线段两个端点的顺序,是排列问题.(1)以每 2 个点为端点的线段的条数,就是从10 个不同元素中取出 2 个元素的组合数,2 10 9即以其中每 2 个点为端点的线段共有C12010 9 45(条)2(2)由于有向线段的两个端点中一个是起点,一个是终点,以每2 个点为端点的有向线段的条数,就是从10 个不同元素中取出 2 个元素的排列数,即以其中每2个点为端点的有向线段共A120 10 9 90(条)【变式2】计算:(1)C74;(2)C170;精品文档 用心整理组合应用题例 2. 某医院有内科医生 12 名 , 外科医生 8 名 , 现要选派 5 名参加赈灾医疗队 , 则(1)某内科医生必须参加 , 某外科医生不能参加 , 有几种选法 ?(2)至少有一名内科医生和至少有一名外科医生参加 , 有几种选法?【思路点拨】要正确理解题意中的关键性词语 , 从“在”与“不在” “至少”中寻求解题思路(1) 某内科医生参加 , 某外科医生不参加, 只需从剩下的 18 名医生中选 4 名即可 , 故有 C148 =3 060 种 .(2) 方法一 ( 直接法 ):至少有一名内科医生和至少有一名外科医生当选可分为四类 : 一内四外 ; 二内三外 ; 三内二外 ; 四内一 外 , 共有 C 112C 48+C 212C 38+C 312C 28+C 412C 18=14 656( 种 ).方法二 ( 排除法 ):事件“至少有一名内科医生和至少有一名外科医生”的反面是“全部为内科医生或外科医生” , 共有C 512+C 58种选法 , 则 C 520-(C 512+C 58)=14 656 种 . 【总结升华】本题属有限制条件的组合问题 , “含”与“不含” , “最多”与“至少”是常见题型 .“含有”一般先将这些元素取出 , 不足部分由另外的元素补充 , “不含”可将这些元素剔除 , 再从剩下的元素中去取 . 解“最多”与“至少”问题 , 是用直接法还是排除法 , 要具体问题具体分析 , 一般是正难则反. 举一反三:【变式 1 】 ( 2015 西宁校级模拟) 某学校开设“蓝天工程博览课程”,组织 6个年级的学生外出参观包括甲博物馆在内的 6 个博物馆,每个年级任选一个博物馆参观,则有且只有两个年级选择甲博物馆的方案有 ()24 24 2 4 24 A . A6A5 种 B . A6 5 种 C . C6 A5 种 D . C6 5 种【答案】因为有且只有两个年级选择甲博物馆,2)解法 1: 解法 2: 76544! 35;C170 10 9 8 7 6 5 4 7!120.C17010! 10 9 8 7!3! 3!120. 类型二、用心整理所以参观甲博物馆的年级有C62种情况,其余年级均有5 种选择,所以共有54种情况,根据乘法原理可得C6254种情况,故选D。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
111--++=⋅+=m nm n m n m m m n m n mA A C A A A 高中数学 选修2-3知识点总结第一章 计数原理 知识点:1、分类加法计数原理:做一件事情,完成它有N 类办法,在第一类办法中有M 1种不同的方法,在第二类办法中有M 2种不同的方法,……,在第N 类办法中有M N 种不同的方法,那么完成这件事情共有M 1+M 2+……+M N 种不同的方法。
2、分步乘法计数原理:做一件事,完成它需要分成N 个步骤,做第一 步有m1种不同的方法,做第二步有M 2不同的方法,……,做第N 步有M N 不同的方法.那么完成这件事共有 N=M 1M 2...M N 种不同的方法。
3、排列:从n 个不同的元素中任取m(m ≤n )个元素,按照一定顺序......排成一列,叫做从n 个不同元素中取出m 个元素的一个排列4、排列数:从n 个不同元素中取出m (m≤n )个元素排成一列,称为从n 个不同元素中取出m 个元素的一个排列. 从n 个不同元素中取出m 个元素的一个排列数,用符号m n A 表示。
),,()!(!)1()1(N m n n m m n n m n n n A m ∈≤-=+--=5、公式:,11--=m n m n nA A6、组合:从n 个不同的元素中任取m (m ≤n )个元素并成一组,叫做从n 个不同元素中取出m 个元素的一个组合。
7、公式:)!(!!!)1()1(m n m n C m m n n n A A C m nm mm n mn-=+--== )!(!!!)1()1(m n m n C m m n n n A A C m n m m m n m n -=+--==;m n n m n C C -=m n m n m n C C C 11+-=+8、二项式定理:()a b C a C a b C a b C a b C b n n n n n n n n r n r r n n n+=++++++---011222…… 9、二项式通项公式展开式的通项公式:,……T C a b r n r nr n r r+-==101() 考点:1、排列组合的运用2、二项式定理的应用★★1.我省高中学校自实施素质教育以来,学生社团得到迅猛发展。
某校高一新生中的五名同 学打算参加“春晖文学社”、“舞者轮滑俱乐部”、“篮球之家”、“围棋苑”四个社团。
若 每个社团至少有一名同学参加,每名同学至少参加一个社团且只能参加一个社团,且同 学甲不参加“围棋苑”,则不同的参加方法的种数为 ( ) A .72 B .108 C .180 D .216★★2.在243)1(xx +的展开式中,x 的幂的指数是整数的项共有( )A .3项B .4项C .5项D .6项★★3.现有12件商品摆放在货架上,摆成上层4件下层8件,现要从下层8件中取2件调整到上层,若其他商品的相对顺序不变,则不同调整方法的种数是A .420B .560C .840D .20160★★4.把编号为1,2,3,4的四封电子邮件分别发送到编号为1,2,3,4的四个网址,则至多有一封邮件的编号与网址的编号相同的概率为★★5.81()x x-的展开式中2x 的系数为 ( )A .-56B .56C .-336D .336第二章 随机变量及其分布 知识点:1、随机变量:如果随机试验可能出现的结果可以用一个变量X 来表示,并且X 是随着试验的结果的不同而变化,那么这样的变量叫做随机变量. 随机变量常用大写字母X 、Y 等或希腊字母 ξ、η等表示。
2、离散型随机变量:在上面的射击、产品检验等例子中,对于随机变量X 可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.3、离散型随机变量的分布列:一般的,设离散型随机变量X 可能取的值为x 1,x 2,..... ,x i ,......,x nX 取每一个值 x i (i=1,2,......)的概率P(ξ=x i )=P i ,则称表为离散型随机变量X 的概率分布,简称分布列4、分布列性质① p i ≥0, i =1,2, … ;② p 1 + p 2 +…+p n = 1.5、二项分布:如果随机变量X 的分布列为:其中0<p<1,q=1-p ,则称离散型随机变量X 服从参数p 的二点分布6、超几何分布:一般地, 设总数为N 件的两类物品,其中一类有M 件,从所有物品中任取n(n ≤N)件,这n 件中所含这类物品件数X 是一个离散型随机变量,则它取值为k 时的概率为()(0,1,2,,)k n k M N MnNC C P X k k m C --===,其中{}min,m M n =,且*,,,,n N M N n M N N ∈≤≤7、条件概率:对任意事件A 和事件B ,在已知事件A 发生的条件下事件B 发生的概率,叫做条件概率.记作P(B|A),读作A 发生的条件下B 的概率 8、公式:.0)(,)()()|(>=A P A P AB P A B P9、相互独立事件:事件A(或B)是否发生对事件B(或A)发生的概率没有影响,这样的两个事件叫做相互独立事件。
)()()(B P A P B A P ⋅=⋅10、n 次独立重复事件:在同等条件下进行的,各次之间相互独立的一种试验11、二项分布: 设在n 次独立重复试验中某个事件A 发生的次数,A 发生次数ξ是一个随机变量.如果在一次试验中某事件发生的概率是p ,事件A 不发生的概率为q=1-p ,那么在n 次独立重复试验中)(k P =ξkn k k n q p C -=(其中 k=0,1, ……,n ,q=1-p )于是可得随机变量ξ的概率分布如下:这样的随机变量ξ服从二项分布,记作ξ~B(n ,p) ,其中n ,p 为参数12、数学期望:一般地,若离散型随机变量ξ的概率分布为则称 E ξ=x1p1+x2p2+…+xnpn +… 为ξ的数学期望或平均数、均值,数学期望又简称为期望.是离散型随机变量。
13、两点分布数学期望:E(X)=np 14、超几何分布数学期望:E (X )=M n N⋅. 15、方差:D(ξ)=(x 1-E ξ)2·P 1+(x 2-E ξ)2·P 2 +......+(x n -E ξ)2·P n 叫随机变量ξ的均方差,简称方差。
16、集中分布的期望与方差一览:17.正态分布:若概率密度曲线就是或近似地是函数期望 方差两点分布 E ξ=pD ξ=pq ,q=1-p超几何分布的超几何分布服从参数为n ,M ,N ξNM n ⋅=ξED (X )=np (1-p )* (N-n )/(N-1)(不要求) 二项分布,ξ ~ B (n,p )E ξ=npD ξ=qE ξ=npq ,(q=1-p )几何分布,p(ξ=k)=g(k ,p)1p2p q D =ξ),(,21)(222)(+∞-∞∈=--x e x f x σμσπ的图像,其中解析式中的实数0)μσσ>、(是参数,分别表示总体的平均数与标准差. 则其分布叫正态分布(,)N μσ记作:,f( x )的图象称为正态曲线。
18.基本性质:①曲线在x 轴的上方,与x 轴不相交. ②曲线关于直线x=μ对称,且在x=μ时位于最高点.③当时μ<x ,曲线上升;当时μ>x ,曲线下降.并且当曲线向左、右两边无限延伸时,以x 轴为渐近线,向它无限靠近.④当μ一定时,曲线的形状由σ确定.σ越大,曲线越“矮胖”,表示总体的分布越分散;σ越小,曲线越“瘦高”,表示总体的分布越集中.⑤当σ相同时,正态分布曲线的位置由期望值μ来决定.⑥正态曲线下的总面积等于1. 19. 3σ原则:从上表看到,正态总体在 )2,2(σμσμ+- 以外取值的概率 只有4.6%,在 )3,3(σμσμ+-以外取值的概率只有0.3% 由于这些概率很小,通常称这些情况发生为小概率事件.也就是说,通常认为这些情况在一次试验中几乎是不可能发生的.考点:1、概率的求解2、期望的求解3、正态分布概念★★★1.(本小题满分12分)某项考试按科目A 、科目B 依次进行,只有当科目A 成绩合格时,才可以继续参加科目B 的考试。
每个科目只允许有一次补考机会,两个科目成绩均合格方可获得该项合格证书,现在某同学将要参加这项考试,已知他每次考科目A 成绩合格的概率均为23,每次考科目B 成绩合格的概率均为12。
假设他在这项考试中不放弃所有的考试机会,且每次的考试成绩互不影响,记他参加考试的次数为X 。
(1)求X 的分布列和均值;(2)求该同学在这项考试中获得合格证书的概率。
★★★2(本小题满分12分)济南市有大明湖、趵突泉、千佛山、园博园4个旅游景点,一位客人浏览这四个景点的概率分别是0.3,0.4,0.5,0.6,且客人是否游览哪个景点互不影响,设ξ表示客人离开该城市时游览的景点数与没有游览的景点数之差的绝对值。
(1)求ξ=0对应的事件的概率; (2)求ξ的分布列及数学期望。
★★★3. 袋子中装有8个黑球,2个红球,这些球只有颜色上的区别。
(1)随机从中取出2个球,ξ表示其中红球的个数,求ξ的分布列及均值。
(2)现在规定一种有奖摸球游戏如下:每次取球一个,取后不放回,取到黑球有奖,第一个奖100元,第二个奖200元,…,第k 个奖100⨯k 元,取到红球则要罚去前期所有奖金并结束取球,按照这种规则,取球多少次比较适宜?说明理由。
第三章 统计案例 知识点:1、独立性检验假设有两个分类变量X 和Y ,它们的值域分另为{x 1, x 2}和{y 1, y 2},其样本频数列联表为: y 1 y 2 总计 x 1 a b a+b x 2 c d c+d 总计a+cb+da+b+c+d若要推断的论述为H 1:“X 与Y 有关系”,可以利用独立性检验来考察两个变量是否有关系,并且能较精确地给出这种判断的可靠程度。
具体的做法是,由表中的数据算出随机变量K^2的值(即K 的平方) K 2 = n (ad - bc) 2 / [(a+b)(c+d)(a+c)(b+d)],其中n=a+b+c+d 为样本容量,K 2的值越大,说明“X 与Y 有关系”成立的可能性越大。
K 2≤3.841时,X 与Y 无关; K 2>3.841时,X 与Y 有95%可能性有关;K 2>6.635时X 与Y 有99%可能性有关2、回归分析回归直线方程bx a y+=ˆ其中xSS SP x x y y x x x n x y x n xy b =---=--=∑∑∑∑∑∑∑222)())(()(11, x b y a -= 考点:无。
