浅析机械臂轨迹伺服控制的Matlab仿真
基于MATLAB与ADAMS的机械臂联合仿真研究

基于MATLAB与ADAMS的机械臂联合仿真研究一、本文概述随着机器人技术的快速发展,机械臂作为机器人执行机构的重要组成部分,其运动性能和控制精度对于机器人整体性能具有决定性影响。
为了提升机械臂的设计水平和控制性能,研究者们不断探索新的仿真技术。
在此背景下,基于MATLAB与ADAMS的机械臂联合仿真研究应运而生,为机械臂的设计优化和控制策略的开发提供了有力支持。
本文旨在探讨基于MATLAB与ADAMS的机械臂联合仿真的方法与技术,并对其进行深入的研究。
介绍了MATLAB和ADAMS软件的特点及其在机械臂仿真中的应用优势。
阐述了机械臂联合仿真的基本原理和步骤,包括模型的建立、动力学方程的求解、控制算法的设计等。
接着,通过实例分析,展示了联合仿真在机械臂运动学性能分析和控制策略验证方面的实际应用。
总结了联合仿真的研究成果,并展望了未来的发展方向。
本文的研究不仅有助于提升机械臂的设计水平和控制性能,也为相关领域的研究者提供了有益的参考和借鉴。
通过不断深入研究和完善联合仿真技术,将为机器人技术的发展注入新的活力。
二、MATLAB与ADAMS联合仿真的理论基础在进行MATLAB与ADAMS的机械臂联合仿真研究时,理解两种软件的理论基础和它们之间的交互方式是至关重要的。
MATLAB作为一种强大的数值计算环境和编程语言,广泛应用于算法开发、数据可视化、数据分析以及数值计算等多个领域。
而ADAMS(Automated Dynamic Analysis of Mechanical Systems)则是一款专门用于多体动力学仿真的软件,特别适用于复杂机械系统的运动学和动力学分析。
MATLAB与ADAMS的联合仿真理论基础主要包括以下几个方面:接口技术:MATLAB与ADAMS之间的数据交换和通信是联合仿真的核心。
通常,这需要通过特定的接口技术来实现,如ADAMS提供的Control接口或MATLAB的Simulink接口。
matlab机械臂端点轨迹

matlab机械臂端点轨迹
机械臂的端点轨迹在MATLAB中可以通过多种方法实现。
一种常
见的方法是使用正运动学和逆运动学来计算机械臂的轨迹。
正运动
学可以根据关节角度计算出末端执行器的位置,而逆运动学则可以
根据末端执行器的期望位置来计算所需的关节角度。
下面我将从这
两个方面来介绍如何在MATLAB中实现机械臂的端点轨迹。
首先,我们可以使用正运动学来计算机械臂末端执行器的位置。
假设我们有一个3自由度的平面机械臂,我们可以通过正运动学方
程将关节角度转换为末端执行器的位置。
在MATLAB中,我们可以编
写一个函数来实现这个计算过程,然后通过给定的关节角度来得到
末端执行器的位置。
其次,我们可以使用逆运动学来计算机械臂的轨迹。
假设我们
希望机械臂沿着一条特定的轨迹移动,我们可以通过逆运动学计算
出每个时间点上机械臂的关节角度,然后将这些关节角度输入到正
运动学方程中得到对应的末端执行器位置。
在MATLAB中,我们可以
编写一个循环来计算每个时间点上的末端执行器位置,从而得到整
个轨迹。
除了正逆运动学外,MATLAB还提供了机器人工具箱(Robotics Toolbox),其中包含了许多用于机器人运动学和轨迹规划的函数和工具。
使用这个工具箱,我们可以更方便地实现机械臂的端点轨迹规划。
总的来说,在MATLAB中实现机械臂的端点轨迹可以通过正逆运动学计算以及机器人工具箱来实现。
这些方法可以帮助我们计算机械臂末端执行器在特定轨迹上的位置,从而实现端点轨迹控制。
基于MATLAB的机器人柔性手臂控制系统设计与仿真【毕业作品】

任务书设计题目:基于MATLAB的机器人柔性手臂控制系统设计与仿真1.设计的主要任务及目标学生应通过本次毕业设计,综合运用所学过的基础理论知识,在深入了解反馈控制系统工作原理的基础上,掌握机械系统建模、分析及校正环节设计的基本过程;初步掌握运用MATLAB/Simulink相关模块进行控制系统设计与仿真的方法,为学生在毕业后从事机械控制系统设计工作打好基础。
2.设计的基本要求和内容(1)根据已有的机器人柔性手臂系统相关资料,对其结构特点及工作原理进行分析;(2)建立柔性手臂系统的数学模型;(3)应用极点配置对系统进行状态反馈设计;(4)运用MATLAB/SIMULINK对系统进行仿真计算;(5)通过动态仿真设计优化系统参数,对反馈系数K进行确定;3.主要参考文献[1] 刘白燕等编,机电系统动态仿真-基于MATLAB/SIMULINK[M].北京:机械工业出版社,2005.7[2] 王积伟,吴振顺等著,控制工程基础[M].北京:高等教育出版社2001.8[3] (日)末松良一. 机械控制入门[M].北京:科学出版社,2000[4] 徐昕等著. MATLAB工具箱应用指南.北京:电子工业出版社,2000 4.进度安排基于MATLAB的机器人柔性手臂控制系统设计与仿真摘要:机械臂未来的发展趋势是高速、高精度和轻型化、操作灵活的柔性机械臂。
柔性机械臂系统的动力学特点是大范围刚体运动的同时,伴随着柔性臂杆的小幅弹性运动。
柔性臂杆的弹性振动将极大地影响机械臂末端的定位精度。
本设计结合机器人柔性手臂的结构特点,对机器人柔性手臂进行了受力分析,建立了柔性手臂系统的集中参数模型。
对柔性手臂系统的特性、系统的可控制性和可观测性进行了分析,用极点配置求取状态反馈系数K对系统进行反馈。
使柔性手臂系统的振动快速达到稳态,用MATLAB仿真确认控制效果。
关键词:柔性机械臂,控制系统,MATLAB仿真Design and simulation system for flexible manipulator control basedon MATLABAbstract:The trend of the development of mechanical arm is high speed, high precision and light-duty, flexible operation of the flexible manipulator. The dynamics of flexible manipulator system is characterized by a wide range of rigid motion at the same time, with flexible arm slightly elastic movement. The elastic vibration of flexible arm will greatly influence the mechanical arm at the ends of the positioning accuracy. This design with the structure characteristics of a flexible robot arm, has carried on the stress analysis of flexible robot arms, established the lumped parameter model of the flexible arm system. Characteristics of the flexible arm system, system controllability and observability are analyzed, using pole assignment for state feedback coefficient K to feedback system. To make the vibration of the flexible arm system to reach steady state quickly, MATLAB simulation confirm the control effect.Key words:Flexible manipulator, Control system, MATLAB simulation目录1概述 (1)1.1引言 (1)1.2研究目的及意义 (2)1.3国内外柔性机械臂的研究现状 (3)1.3.1柔性臂动力学建模的研究现状 (3)1.3.2柔性机械臂的主动控制 (4)2柔性手臂的建模过程 (5)2.1柔性手臂对机器人的重要性 (5)2.2柔性手臂的试验模型 (6)2.3状态方程的建立 (8)2.3.1集中参数模型 (8)2.3.2系统参数和变量的定义 (8)2.3.3数学模型 (10)3系统的特性分析 (13)3.1实验参数 (13)3.2比例变换 (14)3.3系统矩阵的特征值和手臂的振型 (15)3.4可控制性和可观测性 (20)4用极点配置法进行设计和仿真 (22)4.1状态反馈设计 (22)4.2控制系统设计方法选择 (22)4.3利用仿真确认控制效果 (24)5控制系统的实现 (26)总结 (27)参考文献 (29)致谢 (30)附录 (31)1 概述1.1 引言随着人类科技水平的不断进步,机器人的应用越来越广泛。
matlab机械臂运动轨迹代码

MATLAB机械臂运动轨迹代码一、概述机械臂是一种通过电力、液压或气动装置驱动,按一定程序控制,并具有自主操作功能的机电一体化机器人。
它可以灵活地完成包括搬运、焊接、喷涂等各种动作,被广泛应用于工业生产和科研领域。
在机械臂的研发和应用过程中,运动轨迹的设计和控制是至关重要的一环。
MATLAB作为一种强大的科学计算软件,提供了丰富的工具和函数,可以帮助工程师和研究人员快速有效地进行机械臂运动轨迹的设计和仿真。
二、MATLAB中的机械臂运动轨迹设计1.创建机械臂模型在MATLAB中,可以利用Robotics System Toolbox工具箱创建机械臂模型。
首先需要定义机械臂的结构,包括关节数、关节类型、关节参数等。
然后可以使用自带的机械臂模型库,或者自行建立机械臂的正运动学和逆运动学模型。
通过这些步骤,可以在MATLAB中构建出准确的机械臂模型,为后续的运动轨迹设计和控制打下基础。
2.运动轨迹规划机械臂的运动轨迹设计是指按照一定的规划算法和路径规划原则,生成机械臂末端执行器的轨迹,使其能够完成特定的任务。
在MATLAB中,可以利用Robotics System Toolbox提供的函数和算法来进行机械臂运动轨迹的规划。
常用的方法包括插补算法、最优控制算法、遗传算法等。
用户可以根据具体的应用需求,选择相应的规划方法,并使用MATLAB进行仿真验证。
3.编写控制代码一旦确定了机械臂的运动轨迹,就需要编写控制代码来实现对机械臂的精确控制。
在MATLAB中,可以利用Robotics System Toolbox 提供的控制函数和API接口,编写控制程序。
用户可以通过MATLAB 与实际的机械臂硬件进行连接,实时地发送控制指令,控制机械臂按照设计好的运动轨迹进行运动。
三、MATLAB机械臂运动轨迹代码示例以下是一个简单的MATLAB机械臂运动轨迹代码示例,该示例基于Robotics System Toolbox,实现了一个三自由度的SCARA型机械臂的圆形运动轨迹规划和控制。
基于matlab的机械结构仿真程序

基于matlab的机械结构仿真程序基于Matlab的机械结构仿真程序是一种用于模拟和分析机械系统动态行为的工具。
通过使用Matlab编程语言和Simulink仿真环境,我们可以构建出具有各种结构和运动特性的机械系统,并对其进行仿真和优化。
以下是一个基于Matlab的机械结构仿真程序的探讨:1. 简介在介绍这个仿真程序之前,我们首先明确一下机械结构仿真的定义和意义。
机械结构仿真是指通过建立数学模型和运用仿真技术,对机械系统进行虚拟化,以便通过模拟和分析机械系统的行为,获得系统的性能指标和设计优化。
2. Matlab的仿真环境Matlab是一种强大的科学计算软件,具有丰富的工具箱和编程语言。
Simulink是Matlab的一个附属工具,用于建立、模拟和分析动态系统。
Simulink提供了一个直观的图形化界面,使得机械结构仿真程序的搭建更加便捷。
3. 机械结构建模在进行机械结构仿真前,我们需要首先建立机械系统的数学模型。
这包括建立机械结构的几何模型、物理模型和动力学模型。
通过使用Matlab的数学工具箱,可以方便地表示机械结构的运动学和动力学方程,从而实现仿真程序的搭建。
4. 动力学仿真一旦机械结构的数学模型建立完毕,我们可以使用Matlab的仿真工具对机械系统的动态行为进行仿真。
仿真可以模拟机械结构在不同工况下的运动和响应,例如负载变化、初始条件变化等。
通过对仿真数据的分析,我们可以获得机械系统的性能指标,如速度、加速度、力矩等。
5. 仿真结果分析仿真结果的分析是机械结构仿真程序中非常重要的一环。
通过使用Matlab的数据处理和可视化工具,我们可以对仿真结果进行综合分析。
通过绘制机械系统的运动轨迹图、动力学响应曲线和频谱图,我们可以更直观地理解系统的行为特性,并进一步对机械结构进行优化。
6. 优化设计基于仿真结果的分析,我们可以对机械结构的设计进行优化。
通过改变机械结构的几何参数、材料选择和工艺参数等,可以改善系统的性能和可靠性。
伺服驱动与控制建模与Matlab仿真分析共53页

31、只有永远躺在泥坑里的人,才不会再掉进坑里。——黑格尔 32、希望的灯一旦熄灭,生活刹那间变成了一片黑暗。——普列姆昌德 33、希望是人生的乳母。——科策布 34、形成天才的决定因素应该是勤奋。——郭沫若 35、学到很多东西的诀窍,就是一下子不要学很多。——洛克
伺服驱动与控制建模与 Matlab仿真分析
41、实际上,我们想要的不是针对犯 罪的法 律,而 是针对 疯狂的 法律。 ——马 克·吐温 42、法律的力量应当跟随着公民,就 像影子 跟随着 身体一 样。— —贝卡 利亚 43、法于情 理。— —托·富 勒
matlab伺服系统仿真
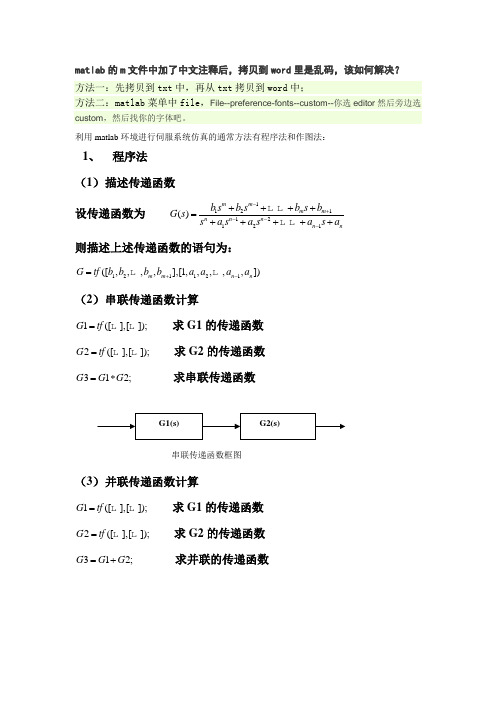
matlab 的m 文件中加了中文注释后,拷贝到word 里是乱码,该如何解决? 方法一:先拷贝到txt 中,再从txt 拷贝到word 中;方法二:matlab 菜单中file ,File--preference-fonts--custom--你选editor 然后旁边选custom ,然后找你的字体吧。
利用matlab 环境进行伺服系统仿真的通常方法有程序法和作图法:1、 程序法 (1) 描述传递函数设传递函数为 112112121()m m m m n n n n nb s b s b s b G s s a s a s a s a -+---++++=+++++ 则描述上述传递函数的语句为:121121([,,,,],[1,,,,,])m m n n G tf b b b b a a a a +-=(2) 串联传递函数计算1([],[]);G tf = 求G1的传递函数 2([],[]);G tf = 求G2的传递函数 312;G G G =* 求串联传递函数(3) 并联传递函数计算1([],[]);G tf = 求G1的传递函数 2([],[]);G tf = 求G2的传递函数 312;G G G =+ 求并联的传递函数串联传递函数框图(4) 求闭环传递函数1([],[]);G tf = 求G1的传递函数 2([],[]);G tf = 求G2的传递函数(1,2);GB feedback G G =闭环系数只与G1,G2相关(5) 求阶跃响应1([],[]);G tf = 求G1的传递函数step(G1) 求G1的单位阶跃响应 (6) 求频率特性1([],[]);G tf = 求G1的传递函数bode(G1); 求G1的幅频特性和相频特性 (7) 求稳定裕度闭环传递函数框图并联传递函数框图1([],[]);G tf = 求G1的传递函数margin(G1); 求G1的幅值裕度和相位裕度 例题一:闭环传递函数与G1无关G1=tf([0.06],[0.0000024,1]); G2=tf([0.0044,1],[0.0002,0]); G3=tf([28],[0.0001,1]); G4=tf([0.6],[0.005,1]); G5=tf([0.06],[0.0000024,1]); GK=G1*G2*G3*G4; figure; bode(GK); grid ontitle('开环特性曲线');GB=feedback(G2*G3*G4,G5); figure bode(GB); grid ontitle('闭环特性曲线'); figure step(GB); grid ontitle('阶跃响应');G1G2G3G4例题2:G1=tf([0.15,1],[0.051,0]);G2=tf([70],[0.0067,1]);G3=tf([0.21],[0.15,1]);G4=tf([0.1],[0.01,1]);GB1=feedback(G1*G2*G3,G4);G5=tf([0.17,1],[0.085,0]);G6=tf([1],[0.01,1]);G7=tf([0.0044],[0.01,1]);G8=tf([130],[1,0]);GK=G5*G6*GB1*G7*G8; %求开环传递函数figurebode(GK); %求开环频率特性grid on %打坐标title('开环频率特性曲线');figure;margin(GK); %求幅值裕度与相位裕度GB=feedback(G5*G6*GB1*G8,G7); %求闭环传递函数bode(GB); %求闭环频率特性grid ontitle('闭环频率特性曲线');figure;margin(GB);step(GB);grid ontitle('阶跃响应特性曲线');2、作图法利用Matlab提供的SIMULINK动态系统仿真环境进行仿真。
伺服系统Matlab仿真教学幻灯片

应用领域与前景
应用领域
伺服系统广泛应用于工业自动化、机器人、数控机床、航空航天、军事装备等领域,是实现高精度、高效率、高 自动化生产的关键技术之一。
介绍Matlab中信号处理相关的工具,如滤 波器设计、信号处理算法实现等。
02
01
仿真结果分析与可视化
讲解如何对仿真结果进行分析和可视化处理 ,如数据绘图、性能指标计算等。
04
03
03 伺服系统建模与仿真
伺服系统数学模型
状态空间模型
描述系统的内部状态和输入/输出关系,适 用于多输入多输出系统和非线性系统。
Matlab界面与基本操作
讲解Matlab的界面组成、常用命令、变量 与数据类型等。
Matlab编程基础
介绍Matlab的编程语法、控制结构、函数 编写与调试等。
仿真模型建立方法
系统建模方法
01
讲解物理系统建模的一般方法,如机理建模、系统辨
识等。
Matlab/Simulink建模
02 介绍如何使用Matlab/Simulink建立系统仿真模型,
案例介绍:典型伺服系统仿真实验
实验目的
验证伺服系统对复杂轨迹的 跟踪能力。
实验步骤
设置目标轨迹,观察实际轨 迹跟随情况,记录误差数据 。
结果分析
通过误差数据评估伺服系统 对复杂轨迹的跟踪精度和稳 定性。
实验结果分析与讨论
位置控制实验结果
展示位置误差曲线、跟随性能等指标。
速度控制实验结果
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
需要按曲线的输出次序进行相应的说明。示例如下:
459(2035):1783-1800.
%用 xlabel()显示横轴名称:时间 t/s
[2] 邹创铭.小波变换在奇异信号探测中应用及 MATLAB 仿
xlabel('\rm 时间\it t\rm/s');
真[J].通信与信息技术,2008(04):74-75.
一般考虑计算机计算量,选择合适的步长即可。
关内容包括框体(坐标轴)和曲线的线型及线粗,文字的字形及
3.2 采用 ode45 函数方法
字号。示例如下:
%状态向量初值
%设置框体线宽为 1
x(1,:)=[x1 x2 …x2n]; %仿真时间 0~10s tspan=[0 10];
set(gca,'linewidth',1); %用 plot 输出坐标 q1 的变化曲线为虚线,线宽为 1 plot(t,x(:,1),'--k','linewidth',1);
常用的方法是 ode45 函数方法。ode45 是 Matlab 系统内置的
%初始条件,前 n 项为广义坐标,后 n 项为广义速度 x(1,:)=[x1 x2 …x2n]; %采用 for 循环编写四阶龙哥库塔函数
一个微分方程数值求解函数,采用四阶、五阶 Runge-Kutta 算 法,属于变步长算法。而采用自编四阶龙哥库塔方法,步长可
4.2 图形文字添加
的应用,对机械臂控制及其他方面的仿真研究都非常有用。
一般,为了使图形的显示更明了,有必要添加文字说明。
文字内容包括坐标名称、曲线名称、图形名称等,添加方式常 参考文献:
用的有 xlabel()、ylabel()、zlabel()、gtext()、legend()等。前三个 [1] Udwadia F E.A new perspective on the tracking control of
38
—— 科协论坛 · 2013 年第 11 期(下) ——
与 工程技术 产业经济
x(i+1,:)=x(i,:)+h/6*(k1+2*k2+2*k3+k4);
legend('e_x','e_y')
end
4.3 线型及文字格式设置
四阶龙哥库塔方法选取的步长越小,数值计算精度越高,
图形的显示应该美观,因此线型及文字格式要协调。相
2.邹创铭 小波变换在奇异信号探测中应用及MATLAB仿真[期刊论文]-通信与信息技术 2008(04)
3.薛定宇 基于MATLAB/Simulink的系统仿真技术与应用 2011
本文链接:/Periodical_kxlt-x201311018.aspx
[t,x]= ode45(@RK,tspan,x(1,:),options);
为^,下角标为_等。
在调用 ode45 函数的语句中,t 为时间变量,x 为返回的与 4.4 特殊处理
时间对应的状态值。与自编龙哥库塔方法不同,该算法无需
在机械臂轨迹伺服控制中,可能出现需要曲线局部放大,
对步长进行设定,系统将采用变步长。
是对坐标轴名称的添加,第四个可在图形任意位置添加说明
nonlinear structural and mechanical systems[J].Proceedings:
文字,通过鼠标来指定位置,最后一个用于对多条曲线的说明,
Mathematical,Physical and Engineering Sciences,2003,
dx(2)=x(n+2);
械臂的控制技术。然而,伺服电机及需要配置的传感器价格
...
昂贵,使得采用实体机械臂的轨迹控制研究难以普遍实现。
dx(n)=x(2n);
Matlab 作为计算机辅助分析设计仿真工具,相比之下,成本低,
%广义速度微分方程,结果先赋给向量 temp
周期短,使用方便,在各学科领域得到了应用广泛。将机械臂
%相对误差精度为 10-6
%用 gtext()显示图形名称伺服控制为楷体,14 号字
options=odeset('RelTol',1e-6);
gtext('\fontname{楷体}\fontsize{14}伺服控制');
%调用 ode45()函数
此外字体格式还有正体\rm 与斜体\it,加粗为\bf,上角标
可以采用 axes()函数表示,该函数视原框体位置为[0,0,1,1],
4 仿真图形处理
前两个数值代表框体左下角的坐标,后两个数值为其长高值,
4.1 图形输出方式
示例如下:
Matlab 仿真的结果要以形象、直观的方式展示出来。机 械臂轨迹及误差图形的常用输出方式主要有两种:二维曲线
%将误差 ex 在 3~5 秒的变化曲线放大显示 %区域:左下角位置为[0.3,0.3],长为 0.4,高为 0.3
%用 gtext()显示图形名称:伺服控制
[3] 薛定宇.基于 MATLAB/Simulink 的系统仿真技术与应用
gtext('伺服控制');
[M].北京:清华大学出版社,2011.
%用 legend()对误差曲线说明,分别为:ex 和 ey
—— 科协论坛 · 2013 年第 11 期(下) ——
for i=1:k t(i+1)=t(i)+h;
根据情况自己设定。
k1=RK(t(i),x(i,:));
仿真编程的步骤如下:
k2=RK(t(i)+h/2,x(i,:)+k1*h/2);
第一步,根据动力学方程建立 RK.m 文件。 function dx=RK(t,x)
k3=RK(t(i)+h/2,x(i,:)+k2*h/2); k4=RK(t(i+1),x(i,:)+k3*h);
39
浅析机械臂轨迹伺服控制的Matlab仿真
作者: 作者单位: 刊名:
英文刊名: 年,卷(期):
孟为来, 平昭琪 长安大学工程机械学院 陕西·西安 710064
科协论坛(下半月) Science & Technology Association Forum 2013(11)
参考文献(3条) 1.Udwadia F E A new perspective on the tracking control of nonlinear structural and mechanical systems[外文期刊] 2003(2035)
该特别注意的是尽量避免出现奇异点,利用 Matlab 自带的小 波分析工具箱(wavelet toolbox)可以检测信号奇异点。
%输出机械臂末端自然坐标(x0,y0)随时间的变化曲线 plot3(x0,y0,t); 若要求输出图形框体仅显示横纵坐标轴两条框线,则需
5 结论 针对机械臂轨迹伺服控制的简化模型及所用到的 Matlab
temp=M^-1*( +H+G);
的控制技术与 Matlab 编程仿真方法结合起来,对于机械臂轨
dx(n+1)=temp(1);
迹控制的研究非常重要。
dx(n+2)=temp(2);
机械臂轨迹控制的方法很多,如 PID 控制、自适应控制、
...
鲁棒控制以及智能控制方法,伺服控制是一种基于机械臂动
dx(2n)=temp(n);
迹控制及仿真的研究。
关键词:机械臂 伺服控制 仿真 Matlab
中图分类号:TP241.2
文献标识码:A
文章编号:1007-3973(2013)011-038-02
1 引言
%广义坐标微分方程
进入 21 世纪,机器人工业已经进入高速崛起的时代,机
dx(1)=x(n+1);
械臂是机器人的操作终端,有一大批机器人爱好者在研究机
与 工程技术 产业经济
浅析机械臂轨迹伺服控制的 Matlab 仿真
□ 孟为来 平昭琪
(长安大学工程机械学院 陕西·西安 710064)
摘 要:针对基于 Matlab 的机械臂轨迹伺服控制仿真,通过一个简化的伺服控制模型,进行仿真编程分析,对比
ode45 算法与自编四阶龙哥库塔方法,并阐述仿真中经常用到的一些函数及图形格式处理方法,有利于机械臂轨
仿真内容进行了阐述,并对 ode45 的调用程序与自编龙哥库塔
在图形输出之前,加上一个语句:
方法程序进行了介绍,图形的处理仅对机械臂控制仿真中常
hold on;
用的一些函数及格式设置作了分析。Matlab 作为计算机辅助
这样就可以隐藏上边框线和右边框线。
分析设计仿真工具,掌握 Matlab 编程语言及自带专业工具箱
%初始时刻为 0
此得到
t(1)=0;
%设定仿真时间为 0~T(s),此处 T 为常数,如 T=10
根据参考文献[1] 就可以确定 的值,因此,下文视其为已
%循环次数 k
知量,且初始条件为:
。
k=10/h;
3 基于 Matlab 的数值积分编程 在机械臂轨迹控制仿真中,利用 Matlab 编程解微分方程,
力学模型的控制方法,本文将浅析基于 Matlab 的机械臂轨迹
第二步,建立主文件 control.m
伺服控制仿真技术。
3.1 采用自编四阶龙哥库塔方法
2 机械臂轨迹伺服控制的简化模型
clear all;
一般机械臂的运动模型可以根据拉格朗日方程得到
%步长为固定值如 0.01s,可以更改
h=0.01;
其中:、H、G 为 n 维列向量,M 为 nЧn 正定对称矩阵,由
和三维曲线。
