圆内极点与极线性质简证
20.极点与极线的性质
第15讲:极点与极线的性质 125第15讲:极点与极线的性质极点与极线是高等几何中的基本且重要的概念,虽然中学数学没有介绍,但以此为背景命制的高考试题经常出现.掌握极点与极线的初步知识,可使我们“登高望远”,抓住问题的本质,确定解题方向,寻找简捷的解题途.定义:已知曲线G:ax 2+bxy+cy 2+dx+ey+f=0,则称点P(x 0,y 0)和直线l:ax 0x+b200y x x y ++cy 0y+d 20x x ++e 2y y ++f=0是曲线G 的一对极点与极线,点P 称为直线l 关于曲线G 的极点;直线l 称为点P 关于曲线G 的极线.称点P 与直线l 有“配极关系”,或“对偶关系”,相互为对方的“配极元素”,或“对偶元素”.特别地,当点P 在曲线G 上时,点P 关于曲线G 的极线是曲线G 在点P 处的切线;圆锥曲线的焦点对应的极线是该焦点对应的准线;圆锥曲线的准线对应的极点是该准线对应的焦点.[位置关系]:已知点P 关于圆锥曲线G 的极线是直线l,则三者的位置关系是:①若点P 在曲线G 上,则直线l 是曲线G 在点P 处的切线;②若点P 在曲线G 外,则直线l 是由点P 向曲线G 引两条切线的切点弦;③若点P 在曲线G 内,则直线l 是经过点P 的曲线G 的弦的两端点处的切线交点轨迹.如图:l l l P M P A D M PN C N B[配极原则]:如果点P 的极线通过点Q,则点Q 的极线也通过点P.证明:设圆锥曲线G:ax 2+bxy+cy 2+2dx+2ey+f=0,点P(x p ,y p ),Q(x Q ,y Q ),则点P 、Q 关于曲线G 的极线方程分别为p:ax p x+b2yx x y p p ++cy p y+d2p x x ++e2p y y ++f=0,q:ax Q x+b2yx x y Q Q ++cy Q y+d2Q x x ++e2Q y y ++f=0,则点P 的极线通过点Q ⇔ax p x Q +b2Qp Q p y x x y ++cy p y Q +d2pQ x x ++e 2pQ y y ++f=0⇔点P(x p ,y p )在直线q:ax Q x+b2y x x y Q Q ++cy Q y+d2Q x x ++e2Q y y ++f=0上⇔点Q 的极线也通过点P.推论1:两点连线的极点是此二点极线的交点,两直线交点的极线是此二直线极点的连线;证明:设两点A 、B 连线的极点是P,即点P 的极线经过点A 、B,由配极原则知点A 、B 的极线均过点P,即点P 是此二点极线的交点;同理可证:两直线交点的极线是此二直线极点的连线.推论2(共点共线):共线点的极线必共点;共点线的极点必共线.证明:设点A 、B 均在直线l 上,直线l 对应的极点为P,由配极原则知点A 、B 的极线均过点P,即点A 、B 的极线必共点;同理可证:共点线的极点必共线.推论3(中点性质):若圆锥曲线G 过点P 的弦AB 平行于点P 的极线,则点P 是弦AB 的中点.证明:设P(x 0,y 0),曲线G:ax 2+bxy+cy 2+2dx+2ey+f=0,则点P 的极线方程:ax 0x+b200y x x y ++cy 0y+d 20x x ++e 2y y + +f=0,故可设AB:ax 0x+b200y x x y ++cy 0y+d 20x x ++e 20y y ++λ=0,由点P(x 0,y 0)在直线AB 上⇒ax 02+bx 0y 0+cy 02+2dx 0+2ey 0+λ=0⇒λ=-(ax 02+bx 0y 0+cy 02+2dx 0+2ey 0)⇒直线AB:ax 0x+b 200y x x y ++cy 0y+d 20x x ++e 20y y +=ax 02+bx 0y 0+cy 02+2dx 0+2ey 0⇒ ax 0x+b200y x x y ++cy 0y+d 20x x ++e 20y y ++f=ax 02+bx 0y 0+cy 02+2dx 0+2ey 0+f,而该直线为以为P 中点的中点弦方程,即点P 是弦AB 的中点.[比例定理]:若过点P(x 0,y 0)的直线l 与曲线G:ax 2+bxy+cy 2+dx+ey+f=0相交于A 、B 两点,与直线:ax 0x+b200yx x y ++ 126 第15讲:极点与极线的性质cy 0y+d20x x ++e 2y y ++f=0交于点Q,则|PA||QB|=|QA||PB|. 证明:设直线l:⎩⎨⎧+=+=θθsin cos 00t y y t x x (t 为参数),代入ax 0x+b 200y x x y ++cy 0y+d 20x x ++e 20y y ++f=0得:(2ax 0cos θ+bx 0sin θ+by 0cos θ+2cy 0sin θ)t+2(ax 02+bx 0y 0+cy 02+dx 0+ey 0+f)=0⇒t 0=-2θθθθsin 2cos sin cos 2000000200020cy by bx ax f ey dx cy y bx ax ++++++++;代入ax 2+bxy+cy 2+2dx+2ey+f=0得:(acos 2θ+bcos θsin θ+csin 2θ)t 2+(2ax 0cos θ+bx 0sin θ+by 0cos θ+2cy 0sin θ)t+(ax 02+bx 0y 0+cy 02+dx 0 +ey 0+f)=0⇒t 1+t 2=-θθθθθθθθ220000sin cos sin cos sin 2cos sin cos 2c b a cy by bx ax +++++,t 1t 2=θθθθ2200200020sin cos sin cos c b a fey dx cy y bx ax +++++++⇒t 0=21212t t t t +;而|PA||QB|= |QA||PB|⇔|t 1||t 2-t 0|=|t 1-t 0||t 2|⇔t 0=21212t t t t +成立. [面积定理]:已知点P 关于圆锥曲线G 的极线为l,过点P 的直线与圆锥曲线G 相交于A 、B 两点,分别过点A 、B 的两条平行线与直线l 交于点D 、C,记△APD 、△CPD 、△BPC 的面积分别为S 1,S 2,S 3,则:S 22=4S 1S 2.证明:以椭圆G:22a x +22b y =1(a>b>0)为例,设P(x 0,y 0),则极线l:12020=+b y y a x x .设A(x 1,y 1),B(x 2,y 2),并分别过点A 、B作l 的垂线,垂足分别为D 1、C 1,则||||11BC AD =|1||1|220220210210-+-+by y a x x b y y a x x =||||2220220222102102b a y y a x x b b a y y a x x b -+-+(注意到:a 2b 2=b 2x 12+a 2y 12,a 2b 2=b 2x 22+a 2y 2) =||||222222202202212212102102y a x b y y a x x b y a x b y y a x x b --+--+=|)()(||)()(|0222022201120112y y y a x x x b y y y a x x x b -+--+-(注意到:0101x x y y --=0202x x y y --=k)=||||0201x x x x --⋅||||22221212x b ky a x b ky a ++.又因||||BP AP =||||0201x x x x --,以下只需证||||22221212x b ky a x b ky a ++=1,即|a 2ky 1+b 2x 1|=|a 2ky 2+b 2x 2|,由⎪⎩⎪⎨⎧=+=+2222222222212212ba y a xb b a y a x b ⇒b 2(x 1-x 2)(x 1+x 2)+a 2(y 1- y 2)(y 1+y 2)=0⇒b 2(x 1+x 2)+a 2k(y 1+y 2)=0⇒a 2ky 1+b 2x 1=-(a 2ky 2+b 2x 2)⇒|a 2ky 1+b 2x 1|=|a 2ky 2+b 2x 2|⇒||||BP AP =||||11BC AD ,由△ADD 1∽△BCC 1⇒||||BC AD =||||BP AP ,设AC 与BD 交于点Q,由AD ∥BC ⇒||||BC AD =||||QC AQ ⇒||||BP AP =||||QC AQ ⇒PQ ∥BC ∥AD ⇒S △BAC =S △BDC ,两边同减S △BQC 得S △QAB =S △QDC ,又因S △PQA =S △PQD ,S △PQB =S △PQC ⇒S △PCD =S △QCD +S △PQD +S △PQC =S △QCD +S △PQA +S △PQB =S △QCD +S △QAB =2S △QAB ⇒S △QAD =S △PAD =S 1,S△QBC=S △PBC =S 3,S △QAB =21S △PCD =21S 2,注意到:QAB QBC QAB QAD S S S S ∆∆∆∆⋅=||||||||QA QC QB QD ⋅=1⇒2QAB S ∆=S △QAD S △QBC ⇒S 22=4S 1S 2. 例1:极点与极线的位置关系.[始源问题]:(2010年湖北高考试题)已知椭圆C:22x +y 2=1的两焦点为F 1 ,F 2,点P(x 0,y 0)满足0<220x +y 02<1,则|PF 1|+|PF 2|的取值范围为 ,直线20xx +y 0y=1与椭圆C 的公共点个数为 . [解析]:由0<220x +y 02<1知,点P 在椭圆C 内,所以直线20x x +y 0y=1与椭圆C 相离⇒公共点个数为0;2c ≤PF 1|+|PF 2|<2a ⇒ 2≤PF 1|+|PF 2|<22⇒|PF 1|+|PF 2|的取值范围为[2,22).[原创问题]:已知椭圆C:42x +32y =1,点P(x 0,y 0)满足42x +320y >1(x 0≠0),直线l:40x x +30y y =1.(Ⅰ)求直线l 与椭圆C 的公共点个数;(Ⅱ)若射线OP 与直线l 、椭圆C 分别交于点Q 、M,求证:|OP||OQ|=|OM|2.[解析]:(Ⅰ)因椭圆C:42x +32y =1⇔⎩⎨⎧==θθsin 3cos 2y x ,θ∈[0,2π),所以,直线l 与椭圆C 的公共点个数⇔关于θ的方程第15讲:极点与极线的性质 12720x cos θ+330y sin θ=1解的个数⇔直线:20x x+330y y=1与圆:x 2+y 2=1的公共点个数;由圆心O(0,0)到直线:20x x+330y y=1的距离d=341220y x +<1⇒直线:20x x+330y y=1与圆:x 2+y 2=1的公共点个数=2⇒直线l 与椭圆C 的公共点个数=2;(Ⅱ)因射线OP:y=00x y x(x 与x 0同号),与40x x +30y y =1联立得:40x x +0203x x y =1⇒x=202004312y x x +⇒y=202004312y x y +⇒Q(202004312y x x +,22004312y x y +)⇒|OP||OQ|=2020202043)(12y x y x ++;由y=00x y x 与42x +32y =1联立得:42x +20203x y x 2=1⇒x 2=2020204312y x x +⇒y 2=2020204312y x y +⇒|OM|2=x 2+y 2=2020204312y x x ++2020204312y x y +=2020202043)(12y x y x ++⇒|OP||OQ|=|OM|2.例2:抛物线中的共线性质.[始源问题]:(2010年大纲卷Ⅰ高考试题)已知抛物线C:y 2=4x 的焦点为F,过点K(-1,0)的直线l 与C 相交于A 、B 两点,点A 关于x 轴的对称点为D. (Ⅰ)证明:点F 在直线BD 上; (Ⅱ)设FB FA ⋅=98,求△BDK 的内切圆M 的方程. [解析]:(Ⅰ)设A(x 1,y 1),B(x 2,y 2),直线l:y=k(x+1)(k ≠0),则D(x 1,-y 1),由⎩⎨⎧=+=xy x k y 4)1(2⇒ky 2-4y+4k=0⇒y 1+y 2=k 4,y 1y 2= 4;所以,点F 在直线BD 上⇔FB ∥FD ⇔(x 2-1):(x 1-1)=y 2:(-y 1)⇔y 1(k y 2-2)+y 2(ky1-2)=0⇔y 1y 2-k(y 1+y 2)=0; (Ⅱ)由FB FA ⋅=(x 1-1)(x 2-1)+y 1y 2=(k y 2-2)(k y 1-2)+y 1y 2=(1+21k )y 1y 2-k 2(y 1+y 2)+4=4(1+21k )-28k +4=8-24k=98⇒k=±43; 根据对称性,不妨设k=43,则直线AB:3x-4y+3=0,且k KD =43⇒KF 平分∠AKD ⇒圆M 的圆心M 在x 轴上;(x 2-x 1)2=(x 1+x 2)2- 4x 1x 2=7162⇒k BD =1212y y x x +-=73⇒直线BD:3x-7y-3=0;设M(t,0)(-1<t<1),则由点M 到直线AB 与BD 的距离相等⇒5|1|3+t=4|1|3-t ⇒t=91⇒圆M:(x-91)2+y 2=94. [原创问题]:已知抛物线y 2=2px 及定点A(a,b),B(-a,0)(ab ≠0,b 2≠2pa),M 是抛物线上的点,设直线AM,BM 与抛物线的另一交点分别为M 1,M 2.求证:当M 点在抛物线上变动时(只要M 1,M 2存在且M 1≠M 2),直线M 1M 2恒过一个定点,并求出这个定点的坐标.[解析]:设M(2pt 2,2pt),M 1(2pt 12,2pt 1),M 2(2pt 22,2pt 2),则点B,M,M 2对应的极线分别为:x=a,2ty=x+2pt 2,2t 2y=x+2pt 22,由B,M,M 2三点共线⇒三线x=a,2ty=x+2pt 2,2t 2y=x+2pt 22共点⇒a=2ptt 2⇒t 2=pta2,点A,M 1对应的极线分别为:by=px+ap, 2t 1y=x+2pt 12,由A,M,M 1三点共线⇒三线by=px+ap,2ty=x+2pt 2,2t 1y=x+2pt 12共点⇒bp(t+t 1)=2p 2tt 1+ap ⇒t 1=ptb bta 2--,由⎪⎩⎪⎨⎧+=+=2222112222pt x y t pt x y t ⇒⎩⎨⎧+==)(22121t t p y t pt x ⇒⎪⎪⎩⎪⎪⎨⎧--=--=)2(2)2()2()(2pt b pt t p a b y pt b t bt a a x ⇒x-a=)2(22pt b t t p a --=b a 2y ⇒M 1,M 2对应极线的交点在定直线b p 2y=x+a, 即b p 22y=2p 2a x +上⇒直线M 1M 2恒过一个定点(a,bpa2). 128 第15讲:极点与极线的性质例3:抛物线中的比例性质.[始源问题]:(2009年全国高中数学联赛湖北初赛试题)已知抛物线C:y=21x 2与直线l:y=kx-1没有公共点,设点P 为直线l 上的动点,过P 作抛物线C 的两条切线,A 、B 为切点. (Ⅰ)证明:直线AB 恒过定点Q;(Ⅱ)若点P 与(Ⅰ)中的定点Q 的连线交抛物线C 于M 、N 两点.证明:||||PN PM =||||QN QM . [解析]:(Ⅰ)设A(x 1,y 1),B(x 2,y 2),P(x 0,y 0),则抛物线y=21x 2在点A 、B 处的切线方程分别为x 1x=y+y 1、x 2x=y+y 2,由点P(x 0,y 0)在这两切线上得:⎩⎨⎧+=+=02200110y y x x y y x x ⇒直线AB:x 0x=y+y 0(注意到:y 0=kx 0-1)⇒x 0x=y+kx 0-1⇒直线AB 过定点Q(k,1);(Ⅱ)设直线MN:⎩⎨⎧+=+=θθsin cos 00t y y t x x ,代入直线AB:x 0x=y+y 0,得:t Q =θθcos sin 20020x y x --;代入y=21x 2得:t 2cos 2θ+2(x 0cos θ-sinθ)t+x 02-2y 0=0⇒t 1+t 2=2⋅θθθ20cos cos sin x -,t 1t 2=θ2020cos 2y x -⇒21212t t t t +=θθcos sin 20020x y x --⇒t Q =21212t t t t +;所以,||||PN PM =||||QN QM ⇔21t t= QQ t t t t --21⇔t Q =21212t t t t +成立. [原创问题]:已知抛物线C:x 2=4y 与直线l:y=x-2,设点P 为直线l 上的动点,过P 作抛物线C 的两条切线,A 、B 为切点.(Ⅰ)证明:直线AB 恒过定点T;(Ⅱ)若过点P 的直线l 交抛物线C 于M 、N 两点,与直线AB 交于点Q.证明||PM ||PN ||PQ [解析]:(Ⅰ)设A(x 1,y 1),B(x 2,y 2),P(x 0,y 0),则抛物线C:x 2=4y 在点A 、B 处的切线方程分别为x 1x=2(y+y 1)、x 2x=(y+y 2),由点P(x 0,y 0)在这两切线上得:⎩⎨⎧+=+=)(2)(202200110y y x x y y x x ⇒直线AB:x 0x=2(y+y 0)(注意到:y 0=x 0-2)⇒x 0x=2y+2x 0-4⇒直线AB 过定点T(2,2);(Ⅱ)设直线MN:⎩⎨⎧+=+=θθsin cos 00t y y t x x ,代入直线AB:x 0x=2(y+y 0),得:t Q =θθcos sin 240020x y x --;代入x 2=4y 得:t 2cos 2θ+2(x 0cos θ-2sin θ)t+x 02-4y 0=0⇒t 1+t 2=2⋅θθθ20cos cos sin 2x -,t 1t 2=θ2020cos 4y x -⇒21212t t t t +=θθcos sin 240020x y x --⇒t Q =21212t t t t +;所以||PM ||PN ||PQ ⇔11t21t =Q t 2⇔t Q =21212t t tt +成立. 例4:抛物线中的面积关系.[始源问题]:(2009年湖北高考试题)过抛物线y 2=2px(p>0)的对称轴上一点A(a,0)(a>0),的直线与抛物线相交于M 、N两点,自M 、N 向直线l:x=-a 作垂线,垂足分别为M 1、N 1. (Ⅰ)当a=2p时,求证:AM 1⊥AN 1; (Ⅱ)记△AMM 1、△AM 1N 1、△ANN 1的面积分别为S 1、S 2、S 3,是否存在λ,使得对任意的a>0,都有S 22=λS 1S 3成立.若存在,求出λ的值;若不存在,说明理由.[解析]:(Ⅰ)当a=2p 时,A(2p ,0),设M(2pm 2,2pm),N(2pn 2,2pn),则M 1(-2p ,2pm),N 1(-2p ,2pn),由AM ∥AN ⇒(2pm 2- 2p ):(2pn 2-2p )=2pm:2pn ⇒mn=-41⇒1AM ⋅1AN =p 2+4p 2mn=0⇒AM 1⊥AN 1;第15讲:极点与极线的性质 129(Ⅱ)由AM ∥AN ⇒(2pm 2-a):(2pn 2-a)=2pm:2pn ⇒2pmn+a=0;因||||11NN MM =2222pn a pm a ++;当MN ⊥/x 轴时,||||AN AM =|2||2|22pn a a pm --=2222pn a a pm --;所以,||||11NN MM =||||AN AM ⇔2222pn a pm a ++=2222pn a a pm --⇔4p 2m 2n 2=a 2成立;当MN ⊥x 轴时,显然有||||11NN MM =||||AN AM ;设MN 1与NM 1交于点Q(点Q 即原点O),由MM 1∥NN 1⇒||||1QN MQ =||||11NN MM =||||AN AM ⇒AQ ∥MM 1∥NN 1;设∠MQM 1=α,则S 1=21|QM||QM 1|sin α,S 3 =21|QN||QN 1|sin α;又S △QMN =11N QM S ∆⇒S 2=11N QM S ∆+(1AQM S ∆+1AQN S ∆)=11N QM S ∆+(S △AQM +S △AQN )=11N QM S ∆+S △QMN =2S △QMN ;S 1S 3=21|QM||QM 1|sin α⋅21|QN||QN 1|sin α=21|QM||QN|sin α⋅21|QM 1||QN 1|sin α=S △QMN 11N QM S ∆=41S 22⇒S 22=4S 1S 3⇒存在λ=4,使得对任意的a>0,都有S 22=λS 1S 3成立.[原创问题]:已知抛物线C:y 2=4x,直线l:y=2x+2,过点P(1,1)的直线与抛物线C 交于A 、B 两点,A 、B 两点在直线l 上的射影点分别为N 、M,记△PAN 、△PMN 、△PBM 的面积分别为S 1、S 2、S 3. (Ⅰ)当AB ∥直线l 时,求证:P 是AB 的中点; (Ⅱ)求证:S 22=4S 1S 3.[解析]:(Ⅰ)设A(x 1,y 1),则y 12=4x 1;由P 是AB 的中点⇒B(2-x 1,2-y 1)⇒(2-y 1)2=4(2-x 1)⇒y 1=2x 1+1⇒点A 在直线y=2x+1上,同理可得点B 也在直线y=2x+1上⇒直线AB:y=2x+1⇒AB ∥直线l;由统一法知,当AB ∥直线l 时, P 是AB 的中点;(Ⅱ)设直线AB:⎩⎨⎧+=+=θθsin 1cos 1t y t x (t 为参数),代入y 2=4x 得:t 2sin 2θ+2(sin θ-2cos θ)t-3=0⇒t 1+t 2=2⋅θθθ2sin sin cos 2-,t 1t 2=-θ2sin 3;点A(1+t 1cos θ,1+t 1sin θ)到直线l 的距离|AN|=5|3sin cos 2|11+-θθt t ,点B(1+t 2cos θ,1+t 2sin θ)到直线l 的距离|BM|=5|3sin cos 2|22+-θθt t ⇒||||BM AN =|3sin cos 2||3sin cos 2|2211+-+-θθθθt t t t (由点A 、B 在直线l 的同侧⇒2t 1cos θ-t 1sin θ+3与t 2cos θ-t 2sin θ+3同号)=3sin cos 23sin cos 22211+-+-θθθθt t t t ;而||||PB PA =||||21t t (点A 、B 在点P 的异侧)=-21t t;所以,||||BM AN =||||PB PA ⇔3sin cos 23sin cos 22211+-+-θθθθt t t t=-21t t ⇔2(2cos θ-sin θ)t 1t 2+3(t 1+t 2)=0⇔2(2cos θ-sin θ)(-θ2sin 3)+3⋅2⋅θθθ2sin sin cos 2-=0成立; 以下同例题可证:S 22=4S 1S 3.例5:椭圆中的共线性质.[始源问题]:(2012年北京高考试题)已知曲线C:(5-m)x 2+(m-2)y 2=8(m ∈R).(Ⅰ)若曲线C 是焦点在x 轴点上的椭圆,求m 的取值范围;(Ⅱ)设m=4,曲线C 与y 轴的交点为A,B(点A 位于点B 的上方),直线y=kx+4与曲线C 交于不同的两点M 、N,直线y=1与直线BM 交于点G.求证:A,G,N 三点共线.[解析]:(Ⅰ)由曲线C 是焦点在x 轴点上的椭圆⇔m-2>5-m>0⇔27<m<5.故m 的取值范围是(27,5); (Ⅱ)当m=4时,曲线C:x 2+2y 2=8⇒A(0,2),B(0,-2);设M(x 1,y 1),N(x 2,y 2),由⎩⎨⎧=++=82422y x kx y ⇒(2k 2+1)x 2+16kx+24=0⇒△= 32(2k 2-3)>0⇒k 2>23;且x 1+x 2=-12162+k k ,x 1x 2=12242+k ;又由直线BM:y=112x y +x-2⇒G(2311+y x ,1),即G(6311+kx x ,1)⇒k AG =-1136x kx +=-3k -12x ,k AN =222x y -=222x kx +=k+22x ⇒k AN -k AG =34k +12x +22x =34k +2⋅2121x x xx +=34k +2⋅2416k -=0⇒A,G,N 三点共线.第(Ⅱ)问是本题的特色与亮点,其实质是共轭点的性质:设点P 与Q 是二次曲线G 的一对共轭点,过点Q 的直线AC 与曲线G 相交于A 、C 两点,AP 与曲线G 相交于另一点B,BQ 与曲线G 相交于另一点D,则P 、C 、D 三点共线.其中共轭点的定义:130 第15讲:极点与极线的性质若直线PQ 与圆锥曲线G 相交于A 、B 两点,且PA ⋅QB +PB ⋅QA =0,则称点P 与Q 是圆锥曲线G 的一对共轭点.[原创问题]:已知椭圆C:2222b y a x +=1(a>b>0)过点D(-1,e),其中,e 是椭圆C 的离心率,椭圆C 的左、右顶点分别为A(-2,0)、B(2,0). (Ⅰ)求椭圆C 的方程;(Ⅱ)过点E(4,0)的直线l 与椭圆C 交于M 、N 两点,求证:直线AM 与BN 的交点P 在一条定直线上.[解析]:(Ⅰ)由a=2,21a +22b e =1⇒1+22b c =a 2⇒b 2=1⇒椭圆C:42x +y 2=1; (Ⅱ)设M(x 1,y 1),N(x 2,y 2),直线l:y=k(x-4),由⎩⎨⎧=+-=44)4(22y x x k y ⇒(1+4k 2)x 2-32k 2x+64k 2-4=0⇒x 1+x 2=224132k k +,x 1x 2=2241464k k +- ⇒k 2=)(4322121x x x x +-+,x 1x 2(1+4k 2)=64k 2-4⇒x 1x 2⋅)(8821x x +-=)(8]8)(5[42121x x x x +--+⇒2x 1x 2=5(x 1+x 2)-8;又由直线AM:y=211+x y (x+2),直线BN:y=222-x y (x-2)⇒直线AM 与BN 的交点P 的横坐标x 满足:211+x y (x+2)=222-x y (x-2)⇒2)4(11+-x x k (x+2)= 2)4(22--x x k (x-2)⇒x=83262122121----x x x x x x =83268)(5122121-----+x x x x x x =1⇒点P 在一条定直线x=1上.例6:椭圆中的中点性质.[始源问题]:(2008年全国高中数学联赛湖南初赛试题)如图,过直线l:5x-7y-70=0上的点P 作椭圆252x +92y =1的两条切线PM 、PN,切点分别为M 、N.(Ⅰ)当点P 在直线l 上运动时,证明:直线MN 恒过定点Q; (Ⅱ)当MN ∥l 时,定点Q 平分线段MN.[解析]:(Ⅰ)设P(7t+7,5t-5),则直线MN 的方程为:2577+t x+955-t y=1⇒(257x+95y)t+(257x-95y-1)=0,由257x+95y=0,且257x-95y-1=0⇒x=1425,y=-109⇒直线MN 恒过定点Q(1425,-109);(Ⅱ)MN ∥l ⇔2577+t :955-t =5:(-7)⇔t=53392⇒直线MN 的方程为:5x-7y-35533=0,代入椭圆方程252x +92y =1得:275332⨯x2 -23753325⨯x+25[(275533⨯)2-9]=0,设M(x 1,y 1),N(x 2,y 2),则x 1+x 2=725⇒定点Q 平分线段MN. [原创问题]:过点Q(1,1)作己知直线l:3x+4y=12的平行线交椭圆C:42x +32y =1于点M 、N. (Ⅰ)分别过点M 、N 作椭圆C 的切线l 1、l 2.证明:三条直线l 1、l 2、l 交于一点; (Ⅱ)证明:点Q 是线段MN 的中点;(Ⅲ)设P 为直线l 上一动点,过点P 作椭圆C 的切线PA 、PB,切点分别为A 、B,证明:点Q 在直线AB 上.[解析]:(Ⅰ)设M(x 1,y 1),N(x 2,y 2),切线l 1、l 2交于点P(x 0,y 0),由切线l 1:41x x+31y y=1,切线l 2:42x x+32yy=1均过点P(x 0, y 0)⇒41x x 0+31y y 0=1,42x x 0+32yy 0=1⇒直线MN:40x x+30y y=1;又由直线MN 过点Q(1,1)⇒40x +30y =1⇒3x 0+4y 0=12⇒点P 在直线l 上⇒三条直线l 1、l 2、l 交于一点; (Ⅱ)由直线MN ∥直线l ⇒40x :30y =41:31,又40x +30y =1⇒x 0=y 0=712⇒直线MN:3x+4y=7⇒点Q 是线段MN 的中点; (Ⅲ)设P(x 0,y 0),则直线AB:3x 0x+4y 0y=12⇒3x 0x+(12-3x 0)y=12⇒点Q 在直线AB 上.第15讲:极点与极线的性质 131例7:椭圆中的比例性质.[始源问题]:(2011年山东高考试题)在平面直角坐标系xOy 中,已知椭圆C:32x +y 2=1.如图所示,斜率为k(k>0)且不过原点的直线l 交椭圆C 于A,B 两点,线段AB 的中点为E ,射线OE 交椭圆C 于点G 交直线x=-3于点D(-3,m).(Ⅰ)求m 2+k 2的最小值(Ⅱ)若|OG|2(i)求证:直线l 过定点(ii)试问点B,G 能否关于x 轴对称？若能,求出此时△ABG 的外接圆方程;若不能,请说明理由.[解析]:(Ⅰ)设E(-3λ,m λ),A(-3λ+t,m λ+kt),则B(-3λ-t,m λ-kt).由点A 、B 都在椭圆C 上⇒⎪⎩⎪⎨⎧=-+--=+++-3)(3)3(3)(3)3(2222kt m t kt m t λλλλ,两式相减得mk=1⇒m 2+k 2≥2mk=2,当且仅当m=k=1时等号成立,所以m 2+k 2的最小值=2.(Ⅱ)(i)设直线OG 与椭圆C 相交于另一点T,则由椭圆C 关于原点对称得:|OT|=|OG|.所以,|OG|2=|OD||OE|⇔DT EG ⋅+DG ET ⋅=0,由轨迹1知,点E 在直线-x+my=1上,即直线l 的方程为:-x+my=1⇒直线l 过定点(-1,0);(ii)若点B,G 关于x 轴对称⇒点G(-3λ-t,-m λ+kt),由点G 在直线OE 上⇒(-3λ-t):(-3λ)=(-m λ+kt):m λ⇒6m λ+mt =3kt(注意到mk=1)⇒m 2(6λ+t)=3t ⇒t=2236mm -λ,又由点E 在直线l 上⇒3λ+m 2λ=1⇒λ=231m +⇒B(-233m -,-23m m -)⇒31(233m -)2+(23mm -)2=1⇒m=1,k=1,λ=41,t=43⇒A(0,1),B(-23,-21),G(-23,21)⇒△ABG 的外接圆方程:(x+21)2+y 2=45. [原创问题]:已知椭圆C:2222b y a x +=1(a>b>0)内一点P(2,1),射线OP 与椭圆C 交于点N,与直线l 0:x+y-12=0交于点M,满足|OP||OM|=|ON|2,且椭圆C 在N 处的切线平行于直线l 0. (Ⅰ)求椭圆C 的方程;(Ⅱ)过点P 的任意一条直线l 与直线l 0交于点Q,与椭圆C 交于A 、B 两点(A 在P 与Q 之间),求证:|QA||PB|=|QB||PA|.[解析]:(Ⅰ)由射线OP:y=21x(x ≥0),直线l 0:x+y-12=0⇒M(8,4);设N(2t,t)(t>0),由|OP||OM|=|ON|2⇒5⋅80=4t2+t 2⇒t=2⇒N(4,2)⇒216a+24b=1,椭圆C 在N 处的切线:24ax +22by =1;由切线平行于直线l 0⇒24a=22b⇒a 2=2b 2⇒b 2=12,a2=24⇒椭圆C:242x +122y =1; (Ⅱ)设直线l:⎩⎨⎧+=+=θθsin 1cos 2t y t x (t 为参数),代入242x +122y =1得:(2sin 2θ+cos 2θ)t 2+4(sin θ+cos θ)t-18=0⇒t 1+t 2=-θθθθ22cos sin 2)cos (sin 4++,t 1t 2=-θθ22cos sin 218+;代入x+y-12=0得:(sin θ+cos θ)t-9=0⇒t Q =θθcos sin 9+;而|QA||PB|=|QB||PA|⇔(t Q -t 1)(-t 2)=(t Q -t 2)t 1⇔(t 1+t 2)t Q -2t 1t 2=0⇔-θθθθ22cos sin 2)cos (sin 4++⋅θθcos sin 9+-2(-θθ22cos sin 218+)=0成立. [原创问题]:已知椭圆C:2222b y a x +=1(a>b>0)内一点P(2,1),过点P 且平行于x 轴直线被椭圆C 截得的弦长为46,过点P 且平行于y 轴直线被椭圆C 截得的弦长为210. (Ⅰ)求椭圆C 的方程;(Ⅱ)过点P 的任意一条直线l 与直线l 0:x+y-12=0交于点Q,与椭圆C 交于A 、B 两点,若QA =λAP ,QB =μBP .求证:λ+132 第15讲:极点与极线的性质μ为定值.[解析]:(Ⅰ)由2222by ax +=1,令y=1得:|x|=ba12-b ;令x=2得:|y|=ab 42-a ;由题知,ba 12-b =26,ab 42-a =10⇒a 2=12422-b b ,22a b (a 2-4)=10⇒2412-b (12422-b b -4)=10⇒b 2=12⇒a 2=24⇒椭圆C:242x +122y =1;(Ⅱ)设直线l:⎩⎨⎧+=+=θθsin 1cos 2t y t x (t 为参数),代入242x +122y =1得:(2sin 2θ+cos 2θ)t 2+4(sin θ+cos θ)t-18=0⇒t 1+t 2=-θθθθ22cos sin 2)cos (sin 4++,t 1t 2=-θθ22cos sin 218+;代入x+y-12=0得:(sin θ+cos θ)t-9=0⇒t Q =θθcos sin 9+;由QA =λAP ,QB =μBP⇒λ=11t t t Q -,μ=22t t t Q -⇒λ+μ=2-t Q ⋅2121t t t t +=2-θθcos sin 9+⋅9)cos (sin 2θθ+=0. 例8:椭圆中的共线性质.[始源问题]:(2002年澳大利亚数学奥林匹克试题)己知△ABC 为锐角三角形以AB 为直径的⊙K 分别交AC 、BC 于P 、Q,分别过A 和Q 作⊙K 的两条切线交于点R,分别过B 和P 作⊙K 的两条切线交于点S.证明:点C 在线段RS 上[解析]:设⊙K:x 2+y 2=r 2,R(-r,a),S(r,b)⇒点R,S 对应的极线分别为:AQ:-rx+ay=r 2,BP:rx+by=r 2⇒Q(2222)(r a r r a +-,2222r a ar +),P(-2222)(r b r r b +-,2222r b br +⇒AP:y=r b (x+r),BQ:y=-r a (x-r),由⎪⎪⎩⎪⎪⎨⎧+=--=)()(r x r b y r x r a y ⇒⎪⎪⎩⎪⎪⎨⎧+=+-=b a ab y r b a b a x 2⇒C(b a b a +-r,b a ab +2)⇒点C 对应的极线为:(a-b)rx+2aby=(a+b)r 2,由三线:-rx+ay=r 2,BP:rx+by=r 2,(a-b)rx+2aby=(a+b)r 2共点于(ba ba +-r, ba r +22)⇒R,C,S 三点共线⇒点C 在线段RS 上. 该题是平面几何定理:“过非等腰三角形的三个顶点作其外接圆的切线,顶点处的切线与其对边所在直线的交点共线.”的变形,以该定理为始源,取其特殊情况,并把圆压缩为椭圆得:[原创问题]:若对任意θ∈[0,2π),直线l:xcos θ+2ysin θ-2=0与椭圆C:2222b y a x +=1(a>b>0)均只有一个交点M.(Ⅰ)求椭圆C 的方程; (Ⅱ)当θ∈(0,2π)时,若直线l 与x 轴交于点N,椭圆C 的左、右顶点分别为A 、B,直线BM 上的点Q 满足QA ⊥x 轴,直线AM 与NQ 交于点P,求点P 的轨迹方程.[解析]:(Ⅰ)由⎩⎨⎧=-+=-+002sin 2cos 222222b a y a x b y x θθ⇒(a 2cos 2θ+4b 2sin 2θ)y 2-8b 2ysin θ+4b 2-a 2b 2cos 2θ=0⇒△=64b 4sin 2θ-4(a 2cos 2θ +4b 2sin 2θ)(4b 2-a 2b 2cos 2θ)=0⇒a 2-4+(4b 2-a 2)sin 2θ=0恒成立⇒a 2-4=0,4b 2-a 2=0⇒a 2=4,b 2=1⇒椭圆C:42x +y 2=1; (Ⅱ)由xcos θ+2ysin θ-2=0⇒N(θcos 2,0);(Ⅰ)知,M(2cos θ,sin θ)⇒直线AM:y=2cos 2sin +θθ(x+2),BM:y=2cos 2sin -θθ(x-2)⇒Q(-2,θθcos 1sin 2-)⇒直线NQ:y=-cot θ(x-θcos 2);令2cos 2sin +θθ(x+2)=-cot θ(x-θcos 2)⇒(2cos 2sin +θθ+θθcos sin )x=θsin 2-1cos sin +θθ⇒x=2⇒点P 的轨迹方程x=2(0<y<2).。
极点与极线
极点与极线对于高考而言，在全国卷大一统的形势下，纵观历年全国卷的解析几何试题，以极点极线为背景的题目，不断出现，不过基本上也是基础类型．所以，极点极线，我们还是按照一些题型来进入分类总结．极点极线的定义1．二次曲线的替换法则对于一般式的二次曲线22Ax Bxy Cy Dx ϕ+++：0Ey F ++=，用0xx 代2x ，用0yy 代2y ，用002x y xy +代xy ，用02x x +代x ，用02y y +代y ，常数项不变，可得方程：0000022x y xy x x Axx B Cyy D ++++++ 002y y E F ++= ．2．极点极线的代数定义高中阶段，常见的二次曲线的极点极线的方程如下：（1）圆：①极点00()P x y ，关于圆222x y r +=的极线方程是200xx yy r +=；②极点00()P x y ，关于圆222()()x a y b r -+-=的极线方程是200()()()()x a x a y b y b r --+--=；③极点00()P x y ，关于圆220x y Dx Ey F ++++=的极线方程是：0000022x x y y xx yy D E F ++++++= ．（2）椭圆：极点00(,)P x y 关于椭圆22221x y a b +=的极线方程是：00221xx yy a b +=．（3）双曲线：极点00(,)P x y 关于双曲线22221x y a b -=的极线方程是：00221xx yy a b-=．（4）抛物线极点00(,)P x y 关于抛物线22y px =的极线方程是：00()y y p x x =+．注：①极点极线是成对出现的；②焦点和焦点对应的准线就是最常见的极点极线；③已知定比分点，则其调和分点一定位于其对应极线上！3．极点极线的几何意义（1）若极点P 在二次曲线上，则极线是过点P 的切线方程．（2）若极点P 在二次曲线内部，则极线是过点P 的弦两端端点的切线交点的轨迹．如图所示，过点P 的弦AB 、CD 的两端端点作切线，得到的直线MN 即为点P 对应的极线轨迹．【极线和二次曲线必定相离】（3）若极点P 在二次曲线外部，分成两种情况：①极线在二次曲线内的部分是点P 对二次曲线的切点弦；【极线和二次曲线必定相交】②极线在二次曲线外的部分是过点P 的弦两端端点的切线交点的轨迹．4．极点极线的配极性质①点P 关于二次曲线C 的极线p 经过点Q ⇔点Q 关于二次曲线C 的极线q 经过点P ．②直线p 关于二次曲线C 的极点P 在直线q 上⇔直线q 关于二次曲线C 的极点Q 在直线p 上．①②表达点P 和点Q 是二次曲线的一组调和共轭点，也是定比点差常说到的定比分点和调和分点．极点极线的综合模型——自极三角形极点极线的几何意义:（1）若点P 是圆锥曲线上的点，则过点P 的切线即为极点p 对应的极线．（2）如图所示（以椭圆图形为例），若点P 是不在圆锥曲线上的点，且不为原点O ，过点P 作割线P AB 、PCD 依次交圆锥曲线于A 、B 、C 、D 四点，连结直线AD 、BC 交于点M ，连结直线AC 、BD 交于点N ，则直线MN l 为极点P 对应的极线．类似的，也可得到极点N 对应的极线为直线PM l ，极点M 对应的极线为直线PN l ，因此，我们把PMN △称为自极三角形．【即PMN △的任一顶点作为极点，则顶点对应的边即为对应的极线，“补全自极三角形”这个技巧很常用，后面结合例题了解！】如图所示，如果我们连结直线NM 交圆锥曲线于点E 、F ，则直线PE 、PF 恰好为圆锥曲线的两条切线，此时，直线EF l 不仅是极点P 的极线，我们也称直线EF l 为渐切线．下面的共轭点模型，实际都是极点在坐标轴上的特例模型的应用，也是高考题常见．自极三角形的定点定值我们先来尝试一下抛物线的极点极线证明：如图，A 、B 、C 、D 分别为抛物线px y 22=上四点，且AB 与CD 交于)0(，m M ，则AC 与BD 的交点N 一定在定直线m x -=上．令MB AM λ=，MD CM μ=，所以m x A λ=，λpm y A 2=，λmx B =，λpmy B 2-=，m x c μ=，μpm y C 2=，μmx D =，μpmy D 2-=．三点共线:)()(D N D B D B D C N C A C A C N x x x x y y y x x x x y y y y ---+=---+=，)(2)(2D N DB DC N C A C N x x y y p y x x y y p y y -++=-++=所以)(2)(21(2μλμμμ+--=+=-pm m x p pm y y N D C )(2)(2μλλμμ+--+pm m x p N ，所以=+++)1(μλμλμm μλλμμm x x m N N +--，所以=+)1(λμm )1(λμ+-N x ，所以m x N -=．接下来我们来参考2020年的全国1卷，也是一种常见的自极三角形．【例17】（2020•新课标Ⅰ）已知A ，B 分别为椭圆222:1(1)x E y a a +=>的左、右顶点，G 为E 的上顶点，8AG GB = ．P 为直线6x =上的动点，PA 与E 的另一交点为C ，PB 与E 的另一交点为D ．（1）求E 的方程；（2）证明：直线CD 过定点．模型总结已知极点在长（短）轴上，证明极线相对简单，只需要利用定比设点法表达出来再联立，消掉变量即可，但是在已知极线反推极点的时候，就要将引入的比例系数λ消除，构造0+0=0λ⨯模型，此类型题目均可以快速拿满分（曲线系处理最快）；抛物线通常利用对称的定比设点法，证明极点极线非常轻松，大家可以试试手．【训练18】（2021•金华模拟）如图，已知抛物线24y x =，过点(11)P -，的直线l 斜率为k ，与抛物线交于A ，B 两点．（1）求斜率k 的取值范围；（2）直线l 与x 轴交于点M ，过点M 且斜率为2k -的直线与抛物线交于C ，D 两点，设直线AC 与直线BD 的交点N 的横坐标为0x ，是否存在这样的k ，使05x =-，若存在，求出k 的值，若不存在，请说明理由．【训练19】（2021•湖南模拟）已知椭圆C ：22221(0)x y a b a b +=>>的左右焦点分别为1F ，2F ，点3(1)2P ，在C 上，且221PF F F ⊥．（1）求C 的标准方程；（2）设C 的左右顶点分别为A ，B ，O 为坐标原点，直线l 过右焦点2F 且不与坐标轴垂直，l 与C 交于M ，N 两点，直线AM 与直线BN 相交于点Q ，证明点Q 在定直线上．【例18】已知椭圆134:22=+y x C ，斜率为1的直线l 与椭圆交于A 、B 两点，点)04(，M ，直线AM 与椭圆交于点1A ，直线BM 与椭圆交于1B ，求证：直线11B A 过定点．模型总结若过)0(，m P 交椭圆于1AA ，1BB 两条线，若①t k AB=，②11B A 过定点)22(22t m m a m a m -+，，两者互为充要条件．大家可以自行证明．本章节到此告一段落，关于极点极线的其它性质，比如等角定理、比如斜率等差模型、斜率比值模型、焦准距的平方和共圆模型、椭圆的平行弦模型、蝴蝶定理初步，会在《高考数学满分突破》之秒杀压轴题系列2（2022年新版本）中详细阐述，二轮复习在于以题型入手的思维巩固，在于以不变应万变，秒系列在于思维深挖拓展，对一个问题的看法更加立体，也是数学爱好者的江湖情怀！【训练20】（2018•北京文）已知椭圆2222:1x y M a b+=(0)a b >>的离心率为36，焦距为22．斜率为k 的直线l 与椭圆M 有两个不同的交点A 、B ．（1）求椭圆M 的方程；（2）若1=k ，求AB 的最大值；（3）设)0,2(-P ，直线PA 与椭圆M 的另一个交点为C ，直线PB 与椭圆M 的另一个交点为D ．若C ，D 和点41,47(-Q 共线，求k ．【训练21】（2021•广东七校联考）已知椭圆2222:1x yCa b+=(0)a b>>的左顶点为(20)A-，，两个焦点与短轴的一个顶点构成等腰直角三角形，过点(10)P，且与x轴不重合的直线l与椭圆交于M、N不同两点．（1）求椭圆方程；（2）若过点P且平行于AM的直线交直线52x=于点Q，求证：直线NQ过定点．【训练22】（2020•北京）已知椭圆2222:1x yCa b+=过点(21)A--，，且2a b=．（1）求椭圆C的方程；（2）过点(40)B-，的直线l交椭圆C于点M，N，直线MA，NA分别交直线4x=-于点P，Q．求|| || PB BQ的值．。
圆曲极点极线和等角定理
圆曲极点极线和等角定理1.引言1.1 概述概述在几何学中，圆曲极点极线和等角定理是非常重要的概念和定理。
圆曲极点极线是指通过一个给定点外切于一个给定圆的直线，而等角定理是指两个相交弧所对的圆心角相等。
本文将逐步介绍这两个概念的定义、性质以及它们在几何学中的应用。
首先，我们将详细讨论圆曲极点极线。
我们将介绍其定义和基本性质，包括通过给定点作圆曲极点极线的方法和圆曲极点极线与圆的切线之间的关系。
此外，我们还将探讨圆曲极点极线在几何学中的应用，例如在三角形内切圆的构造中的应用以及它在求解几何问题中的重要作用。
接下来，我们将转向等角定理的讨论。
我们将介绍等角定理的定义和原理，以及如何使用等角定理来证明两个相交弧所对的圆心角相等。
此外，我们还将探讨等角定理在几何学中的应用，例如在相似三角形的证明中的应用以及它在解决几何问题时的重要性。
最后，我们将对圆曲极点极线和等角定理进行总结，并对它们在几何学中的重要性进行讨论。
我们将探讨这些概念和定理在几何学中的广泛应用，以及它们对于解决几何问题的帮助和影响。
通过本文的学习，读者将能够充分了解圆曲极点极线和等角定理的概念、定义和原理，并能够应用它们解决几何学中的问题。
这些概念和定理在几何学中具有广泛的应用和重要性，对于进一步研究和理解几何学都具有重要意义。
1.2文章结构文章结构:本文主要分为三个部分：引言、正文和结论。
引言部分首先概述了本文的研究对象——圆曲极点极线和等角定理，并介绍了文章的结构和目的。
正文部分分为两大章节：圆曲极点极线和等角定理。
在圆曲极点极线章节中，将对其定义和性质进行详细的阐述，解释其背后的原理和基本概念。
同时，还将探讨圆曲极点极线在实际问题中的作用和应用，提供具体的例子和案例分析。
在等角定理章节中，将对其定义和原理进行深入探讨，并给出其证明过程。
此外，还会探讨等角定理在几何学中的应用场景，以及在实际问题中的应用实例。
结论部分将总结整篇文章的主要内容和观点，并展开对圆曲极点极线和等角定理重要性的讨论。
极点极线详解-概述说明以及解释
极点极线详解-概述说明以及解释1.引言1.1 概述极点极线是复数函数理论中重要的概念，它们在解析几何和数学物理等领域均有广泛的应用。
极点是函数在复平面上的奇点，它表现为函数在该点处无穷大或无穷小的特性，而极线则是连接这些极点的曲线。
极点和极线的研究不仅有助于深入理解复函数的性质，还在实际问题的求解中发挥着重要作用。
本文将详细介绍极点和极线的定义、特性、关系以及应用，旨在帮助读者更好地理解和应用这一重要的数学概念。
1.2 文章结构文章结构部分的内容可以按照以下方式进行编写:文章结构部分本文将按照以下结构来论述极点极线的相关内容:2. 正文2.1 极点的定义和特性2.2 极线的定义和特性2.3 极点极线的关系2.4 极点极线的应用在正文部分，我们将依次介绍和探讨极点和极线在计算机视觉领域中的重要性以及相关概念、定义和特性。
首先，我们将详细讲解极点的定义和其特性，包括极点在图像处理和计算机视觉中的作用以及其在数学中的定义。
然后，我们将介绍极线的定义和特性，重点关注极线在立体视觉和图像对几何关系解决中的重要性。
接下来，我们将讨论极点和极线的关系，包括如何通过极点和极线之间的投影关系来求解立体视觉和图像重建中的几何关系。
最后，我们将探讨极点极线在实际应用中的具体应用场景，包括目标识别、图像配准和三维重建等领域，并介绍一些相关的案例和算法。
通过以上结构，我们希望能够全面而系统地介绍极点极线的相关内容，使读者对其有一个清晰的认识和理解。
在这个过程中，我们将尽可能地提供详细的解释和示例，以帮助读者更好地理解和应用极点极线的概念和方法。
在接下来的章节中，我们将从极点的定义和特性开始，逐步展开对极点极线的讨论。
让我们一起深入了解极点极线的奥秘吧。
1.3 目的本文的目的在于探讨和详解极点极线的概念、定义、特性以及其在实际应用中的重要性。
通过对极点和极线的定义和特性的介绍，我们将深入了解这一数学概念的内涵和本质。
同时，我们还将研究极点和极线之间的关系以及它们在几何学、计算机视觉和图像处理领域的应用。
极点极线的又一性质_张留杰
＞ ｒ ａ
ｍ
ｉ Ｔ ＇
４４， ＞
ｋ
－
－
Ｊ
？
１
ｒ．
，
＋
ｌｉ
＝
， １
ｍ ｎ
是曰 焦此 点 ｉ
定 圆
的
方程为
Ｖ ＋
２
ｙ
＝
在 上 椭 ｙ 轴 的
圆 ．
⑴ 存 在 零 妨 斜 零 证 明 ：
当 都 Ｏ ５
？ ？ ／
，＊
＊
非 斜率时 ， 不
Ｈ ｘ ＼
￣
＾ ２
￣尤
丨
尤 一
〇
ｍｘ Ｑ＋ ｎｙ＼ －１
ｋ ｘ ２ ＋ ｂ－ ｔ
＋ ｋ ｘ
（
＿
ｌ
ｘ － ０）
ｋｘ ０
ｂ ￣ｔ ＋
ｍｘ 〇
ｊＱ＋ ｎ ｙ 〇
ｎ ７ ＾ ￣ ￣ 〇
＾ ｋ
、
ｘ
ｘ ￣
两点 ，
＜＾ 椭 圆 上 任 意 两 点
使得 乙
则直线
仙 的 斜率 为 定值？ 又 Ｐ 点 满足 ＋
所 有 ＝ １
以
？
，
ａ
ｂ
斜 率 定 值 上 Ｂ 的 ４ ＜
？
为
＝
？
．
２
Ｖ 因 此 ￣ ２
ｙ
＿ ｍ ，
／ｃ ４ Ｂ
＝
．
ａ ｍ
＝
Ｖ ‘
＝
Ｈ
＝２
友
＿ （
ｙ〇
＿ ｔ ）
ｘ
线 线 抛 物 线 时 结 论 也 容 证 ｍ
2023全国乙卷理科第20题 极点极线
2023全国乙卷理科第20题极点极线【导读】极点与极线是解析几何中的重要概念，它们在数学领域中有着广泛的应用。
本文将深入探讨极点与极线的定义、性质和应用，并共享对这一主题的个人理解。
【正文】一、极点与极线的定义1. 极点的定义极点是与给定圆的两条切线相交的一个点，这两条切线是从极点到圆上的两个不同点的切线。
在平面直角坐标系中，给定一点 P(x1, y1)，以及一个圆 C：(x - a)² + (y - b)² = r²。
点 P 是圆 C 的极点，当且仅当从 P 到圆 C 上的任意一点 Q 的斜率相等。
即∠OPQ为直角，其中O(a, b) 是圆 C 的圆心。
2. 极线的定义过给定点和给定圆的两条切线所确定的交点的轨迹叫做极线。
根据定义，极线是由圆 C 的所有极点所决定。
在平面直角坐标系中，假设圆的方程是(x - a)² + (y - b)² = r²，圆的极线可以表示为下面形式的方程：xx1 + yy1 = a(x + x1) + b(y + y1) + r²。
这里，(x1, y1) 是圆的极点。
二、极点与极线的性质1. 极点的性质（1）极点坐标的性质通过上述定义，可得到极点P(x1, y1) 的坐标对称形式是P′(-x1, -y1)。
意味着，极点 P 关于圆心 O 对称。
（2）极点的存在性对于给定圆 C，如果有直角坐标系中的点 P（x，y）满足OP⊥OQ，那么点 P 就是圆 C 的极点。
2. 极线的性质（1）极线的对称性已知圆 C 关于 X 轴和 Y 轴的极线方程为 a1x + b1y + c1 = 0 和 a2x + b2y + c2 = 0。
易得，关于 X 轴和 Y 轴的两条极线方程互为对称。
（2）极线的交点性质两条极线的交点坐标为(-ab/a1 - a2, -ab/b1 - b2, 非常重要)。
三、极点与极线的应用1. 应用一：极点极线在密码学中的应用极点极线广泛应用于密码学领域，尤其是在椭圆曲线密码学中。
20.极点与极线的性质
20.极点与极线的性质第15讲:极点与极线的性质125第15讲:极点与极线的性质极点与极线是高等几何中的基本且重要的概念,虽然中学数学没有介绍,但以此为背景命制的高考试题经常出现.掌握极点与极线的初步知识,可使我们“登高望远”,抓住问题的本质,确定解题方向,寻找简捷的解题途.定义:已知曲线G:ax 2+bxy+cy 2+dx+ey+f=0,则称点P(x 0,y 0)和直线l:ax 0x+b200y x x y ++cy 0y+d 20x x ++e 2y y ++f=0是曲线G 的一对极点与极线,点P 称为直线l 关于曲线G 的极点;直线l 称为点P 关于曲线G 的极线.称点P 与直线l 有“配极关系”,或“对偶关系”,相互为对方的“配极元素”,或“对偶元素”.特别地,当点P 在曲线G 上时,点P 关于曲线G 的极线是曲线G 在点P 处的切线;圆锥曲线的焦点对应的极线是该焦点对应的准线;圆锥曲线的准线对应的极点是该准线对应的焦点.[位置关系]:已知点P 关于圆锥曲线G 的极线是直线l,则三者的位置关系是:①若点P 在曲线G 上,则直线l 是曲线G 在点P 处的切线;②若点P 在曲线G 外,则直线l 是由点P 向曲线G 引两条切线的切点弦;③若点P 在曲线G 内,则直线l 是经过点P 的曲线G 的弦的两端点处的切线交点轨迹.如图:l l l P M P A D M PN C N B[配极原则]:如果点P 的极线通过点Q,则点Q 的极线也通过点P.证明:设圆锥曲线G:ax 2+bxy+cy 2+2dx+2ey+f=0,点P(x p,y p),Q(x Q,y Q),则点P 、Q 关于曲线G 的极线方程分别为p:ax p x+b 2yx x y p p ++cy p y+d2p x x ++e2p y y ++f=0,q:ax Q x+b2yx x y Q Q ++cy Q y+d2Q x x ++e2Q y y ++f=0,则点P 的极线通过点Q⇔ax p x Q +b 2Qp Q p y x x y ++cy p y Q +d 2pQ x x ++e2pQ y y ++f=0⇔点P(x p ,y p )在直线q:ax Q x+b2y x x y Q Q ++cy Q y+d2Q x x ++e2Q y y ++f=0上⇔点Q 的极线也通过点P.推论1:两点连线的极点是此二点极线的交点,两直线交点的极线是此二直线极点的连线;证明:设两点A 、B 连线的极点是P,即点P 的极线经过点A 、B,由配极原则知点A 、B 的极线均过点P,即点P 是此二点极线的交点;同理可证:两直线交点的极线是此二直线极点的连线.推论2(共点共线):共线点的极线必共点;共点线的极点必共线.证明:设点A 、B 均在直线l 上,直线l 对应的极点为P,由配极原则知点A 、B 的极线均过点P,即点A 、B 的极线必共点;同理可证:共点线的极点必共线.推论3(中点性质):若圆锥曲线G 过点P 的弦AB 平行于点P 的极线,则点P 是弦AB 的中点. 证明:设P(x 0,y 0),曲线G:ax 2+bxy+cy 2+2dx+2ey+f=0,则点P 的极线方程:ax 0x+b200y x x y ++cy 0y+d 20x x ++e 2y y + +f=0,故可设AB:ax 0x+b200y x x y ++cy 0y+d 20x x ++e 20y y ++λ=0,由点P(x 0,y 0)在直线AB 上⇒ax 02+bx 0y 0+cy 02+2dx 0+2ey 0+λ=0⇒λ=-(ax 02+bx 0y 0+cy 02+2dx 0+2ey 0)⇒直线AB:ax 0x+b 200y x x y ++cy 0y+d 20x x ++e 20y y +=ax 02+bx 0y 0+cy 02+2dx 0+2ey 0⇒ ax 0x+b200y x x y ++cy 0y+d 20x x ++e 20y y ++f=ax 02+bx 0y 0+cy 02+2dx 0+2ey 0+f,而该直线为以为P 中点的中点弦方程,即点P 是弦AB 的中点.[比例定理]:若过点P(x 0,y 0)的直线l 与曲线G:ax 2+bxy+cy 2+dx+ey+f=0相交于A 、B 两点,与直线:ax 0x+b200yx x y ++ 126 第15讲:极点与极线的性质cy 0y+d20x x ++e 2y y ++f=0交于点Q,则|PA||QB|=|QA||PB|. 证明:设直线l:⎩⎨⎧+=+=θθsin cos 0t y y t x x (t 为参数),代入ax 0x+b 200y x x y ++cy 0y+d 20xx ++e2y y ++f=0得:(2ax 0cos θ+bx 0sin θ+by 0cos θ+2cy 0sin θ)t+2(ax 02+bx 0y 0+cy 02+dx 0+ey 0+f)=0⇒t 0=-2θθθθsin 2cos sin cos 2000000200020cy by bx ax fey dx cy y bx ax ++++++++;代入ax 2+bxy+ cy 2+2dx+2ey+f=0得:(acos 2θ+bcos θsin θ+csin 2θ)t 2+(2ax 0cos θ+bx 0sin θ+by 0cos θ+2cy 0sinθ)t+(ax 02+bx 0y 0+cy 02+dx 0 +ey 0+f)=0⇒t 1+t 2=-θθθθθθθθ220000sin cos sin cos sin 2cos sin cos 2c b a cy by bx ax +++++,t 1t 2=θθθθ2200200020sin cos sin cos c b a fey dx cy y bx ax +++++++⇒t 0=21212t t t t +;而|PA||QB|=|QA||PB|⇔|t 1||t 2-t 0|=|t 1-t 0||t 2|⇔t 0=21212t t t t +成立. [面积定理]:已知点P 关于圆锥曲线G 的极线为l,过点P 的直线与圆锥曲线G 相交于A 、B 两点,分别过点A 、B 的两条平行线与直线l 交于点D 、C,记△APD 、△CPD 、△BPC 的面积分别为S 1,S 2,S 3,则:S 22=4S 1S 2.证明:以椭圆G:22ax +22by =1(a>b>0)为例,设P(x 0,y 0),则极线l:12020=+b y y ax x .设A(x 1,y 1),B(x 2,y 2),并分别过点A 、B 作l 的垂线,垂足分别为D 1、C 1,则||||11BC AD =|1||1|220220210210-+-+b y y a x x b y y a x x =||||2220220222102102b a y y a x x b b a y y a x x b -+-+(注意到:a 2b 2=b 2x 12+a 2y 12,a 2b 2=b 2x 22+a 2y 2) =||||222222202202212212102102y a x b y y a x x b y a x b y y a x x b --+--+=|)()(||)()(|0222022201120112y y y a x x x b y y y a x x x b -+--+-(注意到:0101x x y y --=0202x x y y --=k)=||||0201x x x x --⋅||||22221212x b ky a x b ky a ++.又因||||BP AP =||||0201x x x x --,以下只需证||||22221212x b ky a x b ky a ++=1,即|a 2ky 1+b 2x 1|=|a 2ky 2+b 2x 2|,由⎪⎩⎪⎨⎧=+=+2222222222212212ba y a xb b a y a x b ⇒b 2(x 1-x 2)(x 1+x 2)+a 2(y 1- y 2)(y 1+y 2)=0⇒b 2(x 1+x 2)+a 2k(y 1+y 2)=0⇒a 2ky 1+b 2x 1=-(a 2ky 2+b 2x 2)⇒|a 2ky 1+b 2x 1|=|a 2ky 2+b 2x 2|⇒||||BP AP =||||11BC AD ,由△ADD 1∽△BCC 1⇒||||BC AD =||||BP AP ,设AC 与BD 交于点Q,由AD ∥BC ⇒||||BC AD =||||QC AQ ⇒||||BP AP =||||QC AQ ⇒PQ ∥BC ∥AD ⇒S △BAC =S △BDC ,两边同减S △BQC 得S △QAB =S △QDC ,又因S △PQA =S △PQD ,S △PQB =S △PQC ⇒S △PCD =S △QCD +S △PQD +S △PQC =S △QCD +S △PQA +S △PQB =S △QCD +S △QAB =2S △QAB ⇒S △QAD =S △PAD =S 1,S△QBC=S △PBC =S 3,S △QAB =21S △PCD =21S 2,注意到:QAB QBC QAB QAD S S S S ∆∆∆∆⋅=||||||||QA QC QB QD ⋅=1⇒2QAB S ∆=S △QAD S △QBC ⇒S 22=4S 1S 2. 例1:极点与极线的位置关系.[始源问题]:(2010年湖北高考试题)已知椭圆C:22x +y 2=1的两焦点为F 1 ,F 2,点P(x 0,y 0)满足0<220x +y 02<1,则|PF 1|+|PF 2|的取值范围为 ,直线20xx +y 0y=1与椭圆C 的公共点个数为 . [解析]:由0<220x +y 02<1知,点P 在椭圆C 内,所以直线20x x +y 0y=1与椭圆C 相离⇒公共点个数为0;2c ≤PF 1|+|PF 2|<2a ⇒2≤PF 1|+|PF 2|<22⇒|PF 1|+|PF 2|的取值范围为[2,22).[原创问题]:已知椭圆C:42x +32y =1,点P(x 0,y 0)满足420x +320y >1(x 0≠0),直线l:40x x +30y y =1. (Ⅰ)求直线l 与椭圆C 的公共点个数;(Ⅱ)若射线OP 与直线l 、椭圆C 分别交于点Q 、M,求证:|OP||OQ|=|OM|2.[解析]:(Ⅰ)因椭圆C:42x +32y =1⇔⎩⎨⎧==θθsin 3cos 2y x ,θ∈[0,2π),所以,直线l 与椭圆C 的公共点个数⇔关于θ的方程第15讲:极点与极线的性质12720x cos θ+330y sin θ=1解的个数⇔直线:20x x+330y y=1与圆:x 2+y 2=1的公共点个数;由圆心O(0,0)到直线:20x x+330y y=1的距离d=3412020y x +<1⇒直线:20x x+330y y=1与圆:x 2+y 2=1的公共点个数=2⇒直线l 与椭圆C 的公共点个数=2;(Ⅱ)因射线OP:y=00x y x(x 与x 0同号),与40x x +30y y =1联立得:40x x +0203x x y =1⇒x=202004312y x x +⇒y=202004312y x y +⇒Q(202004312y x x +,22004312y x y +)⇒|OP||OQ|=2020202043)(12y x y x ++;由y=00x y x 与42x +32y =1联立得:42x +20203x y x 2=1⇒x 2=2020204312y x x +⇒y 2=2020204312y x y +⇒ |OM|2=x 2+y 2=2020204312y x x ++2020204312y x y +=2020202043)(12y x y x ++⇒|OP||OQ|=|OM|2.例2:抛物线中的共线性质.[始源问题]:(2010年大纲卷Ⅰ高考试题)已知抛物线C:y 2=4x 的焦点为F,过点K(-1,0)的直线l 与C 相交于A 、B 两点,点A 关于x 轴的对称点为D. (Ⅰ)证明:点F 在直线BD 上; (Ⅱ)设FB FA ⋅=98,求△BDK 的内切圆M 的方程. [解析]:(Ⅰ)设A(x 1,y 1),B(x 2,y 2),直线l:y=k(x+1)(k ≠0),则D(x 1,-y 1),由⎩⎨⎧=+=xy x k y 4)1(2⇒ky 2-4y+4k=0⇒y 1+y 2=k 4,y 1y 2= 4;所以,点F 在直线BD 上⇔FB ∥FD ⇔(x 2-1):(x 1-1)=y 2:(-y 1)⇔y 1(ky 2-2)+y 2(k y1-2)=0⇔y 1y 2-k(y 1+y 2)=0;(Ⅱ)由FB FA ⋅=(x 1-1)(x 2-1)+y 1y 2=(k y 2-2)(k y 1-2)+y 1y 2=(1+21k )y 1y 2-k 2(y 1+y 2)+4=4(1+21k )-28k +4=8-24k=98⇒k=±43;根据对称性,不妨设k=43,则直线AB:3x-4y+3=0,且k KD =43⇒KF 平分∠AKD ⇒圆M 的圆心M 在x 轴上;(x 2-x 1)2=(x 1+x 2)2- 4x 1x 2=7162⇒k BD =1212y y x x +-=73⇒直线BD:3x-7y-3=0;设M(t,0)(-1<t<1),则由点M 到直线AB 与BD 的距离相等⇒5|1|3+t =4|1|3-t ⇒t=91⇒圆M:(x-91)2+y 2=94. [原创问题]:已知抛物线y 2=2px 及定点A(a,b),B(-a,0)(ab ≠0,b 2≠2pa),M 是抛物线上的点,设直线AM,BM与抛物线的另一交点分别为M 1,M 2.求证:当M 点在抛物线上变动时(只要M 1,M 2存在且M 1≠M 2),直线M 1M 2恒过一个定点,并求出这个定点的坐标.[解析]:设M(2pt 2,2pt),M 1(2pt 12,2pt 1),M 2(2pt 22,2pt 2),则点B,M,M 2对应的极线分别为:x=a,2ty=x+2pt 2,2t 2y=x+2pt 22,由B,M,M 2三点共线⇒三线x=a,2ty=x+2pt 2,2t 2y=x+2pt 22共点⇒a=2ptt 2⇒t 2=pta2,点A,M 1对应的极线分别为:by=px+ap, 2t 1y=x+2pt 12,由A,M,M 1三点共线⇒三线by=px+ap,2ty=x+2pt 2,2t 1y=x+2pt 12共点⇒bp(t+t 1)=2p 2tt 1+ap ⇒t 1=ptb bta 2--,由⎪⎩⎪⎨⎧+=+=2222112222pt x y t pt x y t ⇒⎩⎨⎧+==)(22121t t p y t pt x ⇒⎪⎪⎩⎪⎪⎨⎧--=--=)2(2)2()2()(2pt b pt t p a b y pt b t bt a a x ⇒x-a=)2(22pt b t t p a --=b a 2y ⇒M 1,M 2对应极线的交点在定直线b p 2y=x+a, 即b p 22y=2p 2a x +上⇒直线M 1M 2恒过一个定点(a,bpa2).128 第15讲:极点与极线的性质例3:抛物线中的比例性质.[始源问题]:(2009年全国高中数学联赛湖北初赛试题)已知抛物线C:y=21x 2与直线l:y=kx-1没有公共点,设点P 为直线l 上的动点,过P 作抛物线C 的两条切线,A 、B 为切点. (Ⅰ)证明:直线AB 恒过定点Q;(Ⅱ)若点P 与(Ⅰ)中的定点Q 的连线交抛物线C 于M 、N 两点.证明:||||PN PM =||||QN QM .[解析]:(Ⅰ)设A(x 1,y 1),B(x 2,y 2),P(x 0,y 0),则抛物线y=21x 2在点A 、B 处的切线方程分别为x 1x=y+y 1、x 2x=y+y 2,由点P(x 0,y 0)在这两切线上得:⎩⎨⎧+=+=02200110y y x x y y x x ⇒直线AB:x 0x=y+y 0(注意到:y 0=kx 0-1)⇒x 0x=y+kx 0-1⇒直线AB 过定点Q(k,1);(Ⅱ)设直线MN:⎩⎨⎧+=+=θθsin cos 00t y y t x x ,代入直线AB:x 0x=y+y 0,得:t Q =θθcos sin 20020x y x --;代入y=21x 2得:t 2cos 2θ+2(x 0cos θ-sinθ)t+x 02-2y 0=0⇒t 1+t 2=2⋅θθθ20cos cos sin x -,t 1t 2=θ2020cos 2y x -⇒21212t t t t +=θθcos sin 20020x y x --⇒t Q =21212t t t t +;所以,||||PN PM =||||QN QM ⇔21t t= QQ t t t t --21⇔t Q =21212t t t t +成立. [原创问题]:已知抛物线C:x 2=4y 与直线l:y=x-2,设点P 为直线l 上的动点,过P 作抛物线C 的两条切线,A 、B 为切点.(Ⅰ)证明:直线AB 恒过定点T;(Ⅱ)若过点P 的直线l 交抛物线C 于M 、N 两点,与直线AB 交于点Q.证明||PM ||PN =||PQ [解析]:(Ⅰ)设A(x 1,y 1),B(x 2,y 2),P(x 0,y 0),则抛物线C:x 2=4y 在点A 、B 处的切线方程分别为x 1x=2(y+y 1)、x 2x=(y+y 2),由点P(x 0,y 0)在这两切线上得:⎩⎨⎧+=+=)(2)(202200110y y x x y y x x ⇒直线AB:x 0x=2(y+y 0)(注意到:y 0=x 0-2)⇒x 0x=2y+2x 0-4⇒直线AB 过定点T(2,2); (Ⅱ)设直线MN:⎩⎨⎧+=+=θθsin cos 00t y y t x x ,代入直线AB:x 0x=2(y+y 0),得:t Q =θθcos sin 240020x y x --;代入x 2=4y 得:t 2cos 2θ+2(x 0cos θ-2sin θ)t+x 02-4y 0=0⇒t 1+t 2=2⋅θθθ20cos cos sin 2x -,t 1t 2=θ2020cos 4y x -⇒21212t t t t +=θθcos sin 240020x y x --⇒t Q =21212t t t t +;所以||PM ||PN ||PQ ⇔11t21t =Q t 2⇔t Q =21212t t tt +成立. 例4:抛物线中的面积关系.[始源问题]:(2009年湖北高考试题)过抛物线y 2=2px(p>0)的对称轴上一点A(a,0)(a>0),的直线与抛物线相交于M 、N 两点,自M 、N 向直线l:x=-a 作垂线,垂足分别为M 1、N 1. (Ⅰ)当a=2p时,求证:AM 1⊥AN 1; (Ⅱ)记△AMM 1、△AM 1N 1、△ANN 1的面积分别为S 1、S 2、S 3,是否存在λ,使得对任意的a>0,都有S 22=λS 1S 3成立.若存在,求出λ的值;若不存在,说明理由.[解析]:(Ⅰ)当a=2p 时,A(2p ,0),设M(2pm 2,2pm),N(2pn 2,2pn),则M 1(-2p ,2pm),N 1(-2p ,2pn),由AM ∥AN ⇒(2pm 2-2p ):(2pn 2-2p )=2pm:2pn ⇒mn=-41⇒1AM ⋅1AN =p 2+4p 2mn=0⇒AM 1⊥AN 1;第15讲:极点与极线的性质129(Ⅱ)由AM ∥AN ⇒(2pm 2-a):(2pn 2-a)=2pm:2pn ⇒2pmn+a=0;因||||11NN MM =2222pn a pm a ++;当MN ⊥/x 轴时,||||AN AM =|2||2|22pn a a pm --=2222pn a a pm --;所以,||||11NN MM =||||AN AM ⇔2222pn a pm a ++=2222pn a a pm --⇔4p 2m 2n 2=a 2成立;当MN ⊥x 轴时,显然有||||11NN MM =||||AN AM ;设MN 1与NM 1交于点Q(点Q 即原点O),由MM 1∥NN 1⇒||||1QN MQ =||||11NN MM =||||AN AM ⇒AQ ∥MM 1∥NN 1;设∠MQM 1=α,则S 1=21|QM||QM 1|sin α,S 3 =21|QN||QN 1|sin α;又S △QMN =11N QM S ∆⇒S 2=11N QM S ∆+(1AQM S ∆+1AQN S ∆)=11N QM S ∆+(S △AQM +S △AQN )=11N QM S ∆+S △QMN =2S △QMN;S 1S 3=21 |QM||QM 1|sin α⋅21|QN||QN 1|sin α=21|QM||QN|sin α⋅21|QM 1||QN 1|sin α=S △QMN 11N QM S ∆=41S 22⇒S 22=4S 1S 3⇒存在λ=4,使得对任意的a>0,都有S 22=λS 1S 3成立.[原创问题]:已知抛物线C:y 2=4x,直线l:y=2x+2,过点P(1,1)的直线与抛物线C 交于A 、B 两点,A 、B 两点在直线l 上的射影点分别为N 、M,记△PAN 、△PMN 、△PBM 的面积分别为S 1、S 2、S 3. (Ⅰ)当AB ∥直线l 时,求证:P 是AB 的中点; (Ⅱ)求证:S 22=4S 1S 3.[解析]:(Ⅰ)设A(x 1,y 1),则y 12=4x 1;由P 是AB 的中点⇒B(2-x 1,2-y 1)⇒(2-y 1)2=4(2-x 1)⇒y 1=2x 1+1⇒点A 在直线y=2x+1上,同理可得点B 也在直线y=2x+1上⇒直线AB:y=2x+1⇒AB ∥直线l;由统一法知,当AB ∥直线l 时, P 是AB 的中点;(Ⅱ)设直线AB:⎩⎨⎧+=+=θθsin 1cos 1t y t x (t 为参数),代入y 2=4x 得:t 2sin 2θ+2(sin θ-2cos θ)t-3=0⇒t 1+t 2=2⋅θθθ2sin sin cos 2-,t 1t 2=-θ2sin 3;点A(1+t 1cos θ,1+t 1sin θ)到直线l 的距离|AN|=5|3sin cos 2|11+-θθt t ,点B(1+t 2cos θ,1+t 2sin θ)到直线l 的距离|BM|=5|3sin cos 2|22+-θθt t ⇒||||BM AN =|3sin cos 2||3sin cos 2|2211+-+-θθθθt t t t (由点A 、B 在直线l 的同侧⇒2t 1cos θ-t 1sin θ+3与t 2cos θ-t 2sin θ+3同号)=3sin cos 23sin cos 22211+-+-θθθθt t t t ;而||||PB PA =||||21t t (点A 、B 在点P 的异侧)=-21t t;所以,||||BM AN =||||PB PA ⇔3sin cos 23sin cos 22211+-+-θθθθt t t t=-21t t ⇔2(2cos θ-sin θ)t 1t 2+3(t 1+t 2)=0⇔2(2cos θ-sin θ)(-θ2sin 3)+3⋅2⋅θθθ2sin sin cos 2-=0成立; 以下同例题可证:S 22=4S 1S 3.例5:椭圆中的共线性质.[始源问题]:(2012年北京高考试题)已知曲线C:(5-m)x 2+(m-2)y 2=8(m ∈R).(Ⅰ)若曲线C 是焦点在x 轴点上的椭圆,求m 的取值范围;(Ⅱ)设m=4,曲线C 与y 轴的交点为A,B(点A 位于点B 的上方),直线y=kx+4与曲线C 交于不同的两点M 、N,直线y=1与直线BM 交于点G.求证:A,G,N 三点共线.[解析]:(Ⅰ)由曲线C 是焦点在x 轴点上的椭圆⇔m-2>5-m>0⇔27<m<5.故m 的取值范围是(27,5); (Ⅱ)当m=4时,曲线C:x 2+2y 2=8⇒A(0,2),B(0,-2);设M(x 1,y 1),N(x 2,y 2),由⎩⎨⎧=++=82422y x kx y ⇒(2k 2+1)x 2+16kx+24=0⇒△= 32(2k 2-3)>0⇒k 2>23;且x 1+x 2=-12162+k k ,x 1x 2=12242+k ;又由直线BM:y=112x y +x-2⇒G(2311+y x ,1),即G(6311+kx x ,1)⇒k AG =-1136x kx +=-3k -12x ,k AN =222x y -=222x kx +=k+22x ⇒k AN -k AG =34k +12x +22x =34k +2⋅2121x x xx +=34k +2⋅2416k -=0⇒A,G,N 三点共线.第(Ⅱ)问是本题的特色与亮点,其实质是共轭点的性质:设点P 与Q 是二次曲线G 的一对共轭点,过点Q 的直线AC 与曲线G 相交于A 、C 两点,AP 与曲线G 相交于另一点B,BQ 与曲线G 相交于另一点D,则P 、C 、D 三点共线.其中共轭点的定义:130 第15讲:极点与极线的性质若直线PQ 与圆锥曲线G 相交于A 、B 两点,且PA ⋅QB +PB ⋅QA =0,则称点P 与Q 是圆锥曲线G 的一对共轭点.[原创问题]:已知椭圆C:2222b y a x +=1(a>b>0)过点D(-1,e),其中,e 是椭圆C 的离心率,椭圆C 的左、右顶点分别为A(-2, 0)、B(2,0).(Ⅰ)求椭圆C 的方程;(Ⅱ)过点E(4,0)的直线l 与椭圆C 交于M 、N 两点,求证:直线AM 与BN 的交点P 在一条定直线上.[解析]:(Ⅰ)由a=2,21a +22b e =1⇒1+22b c =a 2⇒b 2=1⇒椭圆C:42x +y 2=1; (Ⅱ)设M(x 1,y 1),N(x 2,y 2),直线l:y=k(x-4),由⎩⎨⎧=+-=44)4(22y x x k y ⇒(1+4k 2)x 2-32k 2x+64k 2-4=0⇒x 1+x 2=224132k k +,x 1x 2=2241464k k +-⇒k 2=)(4322121x x x x +-+,x 1x 2(1+4k 2)=64k 2-4⇒x 1x 2⋅)(8821x x +-=)(8]8)(5[42121x x x x +--+⇒2x 1x 2=5(x 1+x 2)-8;又由直线AM:y=211+x y (x+2),直线BN:y=222-x y (x-2)⇒直线AM 与BN 的交点P 的横坐标x 满足:211+x y (x+2)=222-x y (x-2)⇒2)4(11+-x x k (x+2)= 2)4(22--x x k (x-2)⇒x=83262122121----x x x x x x =83268)(5122121-----+x x x x x x =1⇒点P 在一条定直线x=1上.例6:椭圆中的中点性质.[始源问题]:(2008年全国高中数学联赛湖南初赛试题)如图,过直线l:5x-7y-70=0上的点P 作椭圆252x +92y =1的两条切线PM 、PN,切点分别为M 、N. (Ⅰ)当点P 在直线l 上运动时,证明:直线MN 恒过定点Q;(Ⅱ)当MN ∥l 时,定点Q 平分线段MN.[解析]:(Ⅰ)设P(7t+7,5t-5),则直线MN 的方程为:2577+t x+955-t y=1⇒(257x+95y)t+(257x-95y-1)=0,由257x+95y=0,且257x-95y-1=0⇒x=1425,y=-109⇒直线MN 恒过定点Q(1425,-109); (Ⅱ)MN ∥l ⇔2577+t :955-t =5:(-7)⇔t=53392⇒直线MN 的方程为:5x-7y-35533=0,代入椭圆方程252x +92y =1得:275332⨯x2 -23753325⨯x+25[(275533⨯)2-9]=0,设M(x 1,y 1),N(x 2,y 2),则x 1+x 2=725⇒定点Q 平分线段MN.[原创问题]:过点Q(1,1)作己知直线l:3x+4y=12的平行线交椭圆C:42x +32y =1于点M 、N.(Ⅰ)分别过点M 、N 作椭圆C 的切线l 1、l 2.证明:三条直线l 1、l 2、l 交于一点; (Ⅱ)证明:点Q 是线段MN 的中点;(Ⅲ)设P 为直线l 上一动点,过点P 作椭圆C 的切线PA 、PB,切点分别为A 、B,证明:点Q 在直线AB 上.[解析]:(Ⅰ)设M(x 1,y 1),N(x 2,y 2),切线l 1、l 2交于点P(x 0,y 0),由切线l 1:41x x+31y y=1,切线l 2:42x x+32y y=1均过点P(x 0, y 0)⇒41x x 0+31y y 0=1,42x x 0+32yy 0=1⇒直线MN:40x x+30y y=1;又由直线MN 过点Q(1,1)⇒40x +30y =1⇒3x 0+4y 0=12⇒点P 在直线l 上⇒三条直线l 1、l 2、l 交于一点; (Ⅱ)由直线MN ∥直线l ⇒40x :30y =41:31,又40x +30y =1⇒x 0=y 0=712⇒直线MN:3x+4y=7⇒点Q 是线段MN 的中点; (Ⅲ)设P(x 0,y 0),则直线AB:3x 0x+4y 0y=12⇒3x 0x+(12-3x 0)y=12⇒点Q 在直线AB 上.第15讲:极点与极线的性质131例7:椭圆中的比例性质.[始源问题]:(2011年山东高考试题)在平面直角坐标系xOy 中,已知椭圆C:32x +y 2=1.如图所示,斜率为k(k>0)且不过原点的直线l 交椭圆C 于A,B 两点,线段AB 的中点为E ,射线OE 交椭圆C 于点G 交直线x=-3于点D(-3,m).(Ⅰ)求m 2+k 2的最小值; D y (Ⅱ)若|OG|2=|OD||OE|. G A (i)求证:直线l 过定点; E(ii)试问点B,G 能否关于x 轴对称？若能,求出 -3 O x 此时△ABG 的外接圆方程;若不能,请说明理由.[解析]:(Ⅰ)设E(-3λ,m λ),A(-3λ+t,m λ+kt),则B(-3λ-t,m λ-kt).由点A 、B 都在椭圆C 上⇒⎪⎩⎪⎨⎧=-+--=+++-3)(3)3(3)(3)3(2222kt m t kt m t λλλλ,两式相减得mk=1⇒m 2+k 2≥2mk=2,当且仅当m=k=1时等号成立,所以m 2+k 2的最小值=2.(Ⅱ)(i)设直线OG 与椭圆C 相交于另一点T,则由椭圆C 关于原点对称得:|OT|=|OG|.所以,|OG|2=|OD||OE|⇔DT EG ⋅+DG ET ⋅=0,由轨迹1知,点E 在直线-x+my=1上,即直线l 的方程为:-x+my=1⇒直线l 过定点(-1,0);(ii)若点B,G 关于x 轴对称⇒点G(-3λ-t,-m λ+kt),由点G 在直线OE 上⇒(-3λ-t):(-3λ)=(-m λ+kt):m λ⇒6m λ+mt=3kt(注意到mk=1)⇒m 2(6λ+t)=3t ⇒t=2236mm -λ,又由点E 在直线l 上⇒3λ+m 2λ=1⇒λ=231m+⇒B(-233m-,-23m m -)⇒31(233m -)2+(23mm -)2=1⇒m=1,k=1,λ=41,t=43⇒A(0,1),B(-23,-21),G(-23,21)⇒△ABG 的外接圆方程:(x+21)2+y 2=45.[原创问题]:已知椭圆C:2222b y a x +=1(a>b>0)内一点P(2,1),射线OP 与椭圆C 交于点N,与直线l 0:x+y-12=0交于点M,满足|OP||OM|=|ON|2,且椭圆C 在N 处的切线平行于直线l 0. (Ⅰ)求椭圆C 的方程;(Ⅱ)过点P 的任意一条直线l 与直线l 0交于点Q,与椭圆C 交于A 、B 两点(A 在P 与Q 之间),求证:|QA||PB|=|QB||PA|.[解析]:(Ⅰ)由射线OP:y=21x(x ≥0),直线l 0:x+y-12=0⇒M(8,4);设N(2t,t)(t>0),由|OP||OM|=|ON|2⇒5⋅80=4t2+t 2⇒t=2⇒N(4,2)⇒216a +24b =1,椭圆C 在N 处的切线:24a x +22by =1;由切线平行于直线l 0⇒24a =22b ⇒a 2=2b 2⇒b 2=12,a2=24⇒椭圆C:242x +122y =1; (Ⅱ)设直线l:⎩⎨⎧+=+=θθsin 1cos 2t y t x (t 为参数),代入242x +122y =1得:(2sin 2θ+cos 2θ)t 2+4(sin θ+cos θ)t-18=0⇒t 1+t 2=-θθθθ22cos sin 2)cos (sin 4++,t 1t 2=-θθ22cos sin 218+;代入x+y-12=0得:(sin θ+cos θ)t-9=0⇒t Q =θθcos sin 9+;而|QA||PB|=|QB||PA|⇔(t Q -t 1)(-t 2)=(t Q -t 2)t 1⇔(t 1+t 2)t Q -2t 1t 2=0⇔-θθθθ22cos sin 2)cos (sin 4++⋅θθcos sin 9+-2(-θθ22cos sin 218+)=0成立. [原创问题]:已知椭圆C:2222b y a x +=1(a>b>0)内一点P(2,1),过点P 且平行于x 轴直线被椭圆C 截得的弦长为46,过点P 且平行于y 轴直线被椭圆C 截得的弦长为210.(Ⅰ)求椭圆C 的方程;(Ⅱ)过点P 的任意一条直线l 与直线l 0:x+y-12=0交于点Q,与椭圆C 交于A 、B 两点,若QA =λAP ,QB =μBP .求证:λ+132 第15讲:极点与极线的性质μ为定值.[解析]:(Ⅰ)由2222by ax +=1,令y=1得:|x|=ba 12-b ;令x=2得:|y|=ab 42-a ;由题知,ba12-b =26,ab 42-a =10⇒a 2=12422-b b ,22a b (a 2-4)=10⇒2412-b (12422-b b -4)=10⇒b 2=12⇒a 2=24⇒椭圆C:242x +122y =1; (Ⅱ)设直线l:⎩⎨⎧+=+=θθsin 1cos 2t y t x (t 为参数),代入242x +122y =1得:(2sin 2θ+cos 2θ)t 2+4(sin θ+cos θ)t-18=0⇒t 1+t 2=-θθθθ22cos sin 2)cos (sin 4++,t 1t 2=-θθ22cos sin 218+;代入x+y-12=0得:(sin θ+cos θ)t-9=0⇒t Q =θθcos sin 9+;由QA =λAP ,QB =μBP⇒λ=11t t t Q -,μ=22t t t Q -⇒λ+μ=2-t Q ⋅2121t t t t +=2-θθcos sin 9+⋅9)cos (sin 2θθ+=0. 例8:椭圆中的共线性质.[始源问题]:(2002年澳大利亚数学奥林匹克试题)己知△ABC 为锐角三角形, R以AB 为直径的⊙K 分别交AC 、BC 于P 、Q,分别过A 和Q 作⊙K 的两条切线交 C 于点R,分别过B 和P 作⊙K 的两条切线交于点S.证明:点C 在线段RS 上. P Q S[解析]:设⊙K:x 2+y 2=r 2,R(-r,a),S(r,b)⇒点R,S 对应的极线分别为:AQ:-rx+ay=r 2,BP:rx+by=r 2⇒Q(2222)(r a r r a +-,2222r a ar +),P(-2222)(r b r r b +-,2222r b br +) A K B⇒AP:y=r b (x+r),BQ:y=-r a (x-r),由⎪⎪⎩⎪⎪⎨⎧+=--=)()(r x r b y r x r a y ⇒⎪⎪⎩⎪⎪⎨⎧+=+-=b a ab y r b a b a x 2⇒C(b a b a +-r,b a ab +2)⇒点C 对应的极线为:(a-b)rx+2aby=(a+b)r 2,由三线:-rx+ay=r 2,BP:rx+by=r 2,(a-b)rx+2aby=(a+b)r 2共点于(ba ba +-r, ba r +22)⇒R,C,S 三点共线⇒点C 在线段RS 上. 该题是平面几何定理:“过非等腰三角形的三个顶点作其外接圆的切线,顶点处的切线与其对边所在直线的交点共线.”的变形,以该定理为始源,取其特殊情况,并把圆压缩为椭圆得:[原创问题]:若对任意θ∈[0,2π),直线l:xcos θ+2ysin θ-2=0与椭圆C:2222b y a x +=1(a>b>0)均只有一个交点M.(Ⅰ)求椭圆C 的方程; (Ⅱ)当θ∈(0,2π)时,若直线l 与x 轴交于点N,椭圆C 的左、右顶点分别为A 、B,直线BM 上的点Q 满足QA ⊥x 轴,直线AM 与NQ 交于点P,求点P 的轨迹方程.[解析]:(Ⅰ)由⎩⎨⎧=-+=-+002sin 2cos 222222b a y a x b y x θθ⇒(a 2cos 2θ+4b 2sin 2θ)y 2-8b 2ysin θ+4b 2-a 2b 2cos 2θ=0⇒△=64b 4sin 2θ-4(a 2cos 2θ+4b 2sin 2θ)(4b 2-a 2b 2cos 2θ)=0⇒a 2-4+(4b 2-a 2)sin 2θ=0恒成立⇒a 2-4=0,4b 2-a 2=0⇒a 2=4,b 2=1⇒椭圆C:42x +y 2=1; (Ⅱ)由xcos θ+2ysin θ-2=0⇒N(θcos 2,0);(Ⅰ)知,M(2cos θ,sin θ)⇒直线AM:y=2cos 2sin +θθ(x+2),BM:y=2cos 2sin -θθ(x-2)⇒Q(-2,θθcos 1sin 2-)⇒直线NQ:y=-cot θ(x-θcos 2);令2cos 2sin +θθ(x+2)=-cot θ(x-θcos 2)⇒(2cos 2sin +θθ+θθcos sin )x=θsin 2-1cos sin +θθ⇒x=2⇒点P 的轨迹方程x=2(0<y<2).。
极点极线10个二级结论
极点极线10个二级结论摘要：一、引言二、极点极线的概念1.极点2.极线三、10 个二级结论1.极点与极线的关系2.极点与极线的性质3.极点与极线的应用四、结论正文：【引言】极点极线是数学中的一个基本概念，它在几何学、微积分学等学科中都有着广泛的应用。
本文将详细介绍极点极线的概念以及10 个二级结论，帮助读者更好地理解和掌握这一重要概念。
【极点极线的概念】极点是数学中的一个点，它满足某个函数在此点处的导数等于零。
换句话说，极点是函数的局部最小值或最大值点。
极线是与极点相关的直线，它表示函数在极点处的切线。
【10 个二级结论】1.极点与极线的关系：极点处的切线就是极线。
极线是函数在极点处的局部性质，反映了函数在极点处的变化趋势。
2.极点与极线的性质：极点与极线是相互关联的，它们共同决定了函数在极点处的局部性质。
极点的性质包括局部最小值、局部最大值等，极线的性质包括切线的斜率、切线方程等。
3.极点与极线的应用：极点与极线在数学的许多分支中都有着广泛的应用。
例如，在微积分学中，极点与极线可以用来求解函数的极值；在几何学中，极点与极线可以用来分析图形的性质。
4.函数的极值与极点极线的关系：函数的极值点就是极点，函数在极值点处的导数值就是极线的斜率。
5.函数的单调性与极点极线的关系：函数的单调区间与极点极线密切相关。
在单调递增的区间，函数的导数大于零，极线是上升的；在单调递减的区间，函数的导数小于零，极线是下降的。
6.函数的凹凸性与极点极线的关系：函数的凹凸性决定了极点极线的性质。
在凹函数的区间，极点是局部最小值点，极线是下凸的；在凸函数的区间，极点是局部最大值点，极线是上凸的。
7.极点极线在微分方程中的应用：微分方程中的极点极线可以用来分析系统的稳定性和动态行为。
例如，在常微分方程中，极点可以表示系统的平衡状态，极线可以表示系统在平衡状态下的动态行为。
8.极点极线在数值分析中的应用：极点极线在数值分析中有着广泛的应用，例如在插值和拟合问题中，极点极线可以用来提高算法的收敛性和准确性。
圆的极点极线定理
圆的极点极线定理
圆的极点极线定理，又称为极轴定理，是描述在平面直角坐标系
中的圆上的一个点（极点）和与该点相切圆的切线（极线）之间的关系。
具体来说，对于一个圆C和其中一点P，过P点作圆C的切线，切点为T，那么PT的斜率等于圆C关于点P的极线的斜率。
具体而言，假设圆C的方程为(x-a)²+(y-b)²=r²，其中a,b是圆C 的圆心坐标，r是半径。
假设点P的坐标为(x0,y0)，则过P点的切线
方程为(x-a)x0+(y-b)y0=r²。
根据斜率的定义，切线的斜率为(y0-
b)/(x0-a)。
根据极点极线定理，圆C关于点P的极线的斜率等于切线
的斜率，也就是(y0-b)/(x0-a)。
因此，圆的极点极线定理可以表述为：在平面直角坐标系中，对于任意一条与圆相交的直线L，它在圆上的任意一点P处的切线PT，PT的斜率等于L关于圆的极线的斜率。
反
过来也成立，即如果过圆上的一点P和极线相交的直线L，在PT处切圆，则L关于圆的极线的斜率等于PT的斜率。
极点极线定理可以用于很多几何证明中，例如在求解某些几何问
题的过程中，可以利用圆的对称性质，把问题转化为一个求解极点极
线的问题，进而求出所求的几何量。
圆内极点极线的结论
为调和点列， QCJ ′D为调和点列，于是 H 与 H ′重合，J 与 J ′ 重合，故 HJP 三点共线，所
以得到 S、T、H、J、I、P 六点共线。 为了研究极点与极线的其他性质，我们找到了一些特殊情况，试图在特殊情况中得出极
极点极线的简单应用
内容摘要：我们平时在做几何题时，经常可以看到一些十分类似的图形。在一个圆中，由圆外一点做他的 两条切线，然后连接切点弦，再引出了一系列的问题。其实这些问题都与极点极线有关，极点与极线在几 何中有着广泛的性质，如果我们把他的性质研究透彻，便可以很快的解出一些较难的几何题。 关键词：极点 极线 调和点列 完全四边形
AH AH AH
AB
AB
JQ = CJ + CQ = CQ +1 = 1+ CQ + DQ = 2 DQ
CJ CJ CJ
CD CD
考察 ∆ACQ 被直线 PBD 所截 应用梅涅劳斯定理可知 1 = CP ⋅ AB ⋅ QD = CP ⋅ AH PA BQ DC PA HQ
⋅ QN 所以 PHJ 共线，从而 STHJP 五点共线。 CN
直线，即 P 点关于圆的极线。 从而看出极点与极线在几何中有着广泛的性质，如果我们把他的性质研究透彻，便可以
很快的解出一些较难的几何题。 二、性质
由上面的证明过程中，我们总结出性质 1。 性质 1 P 点与过 P 点作任意割线与圆和其关于圆的极线所交形成的三点为调和点列。 在研究性质 1 的过程中，我们发现了关于极点与极线一个十分特殊的例子，六点共线。 如图（4），连线 ST 为 Q 关于圆 O 的极线，任意作两条割线 QAB、QCD 分别交 ST 于 H、 J，联结 AD、CB 交于 I，延长 CA 与 DB 交于 P，则 P、T、H、I、J、S 六点共线。
数学复习：极点与极线
数学复习：极点与极线知识与方法极点极线是射影几何中的重要内容，在中学教材中并未提及，但纵观历年高考的解析几何大题，可以发现诸多试题都有极点极线的背景，所以了解极点极线，可以让我们站在更高处来看待问题．这一小节我们先介绍极点极线的几何定义、代数定义和一些常用的性质，再辅以若干典型的高考真题的极点极线观点，来加深大家的理解.1．极点极线的几何定义：以椭圆为例，如图1所示，设P 为椭圆外一点，过P 作椭圆的两条割线分别与椭圆相交于A 、B 和C 、D 四点，AC 与BD 交于点M ，AD 与BC 交于点N ，则称点P 为直线MN 关于椭圆的极点，直线MN 为点P 关于椭圆的极线.另一方面，图1也可以这么来看，从椭圆外的点N 作椭圆的两条割线分别交椭圆于A 、D 和B 、C 四点，AC 与BD 交于点M ，AB 与CD 交于点P ，所以点N 和直线PM 也是一对极点极线，事实上，点M 和直线PN 也是一对极点极线，因此在PMN 中，以其中一个顶点作为极点，那么该顶点的对边所在的直线就是对应的极线，从而我们将PMN 称为“自极三角形”，为了加以区分，图中画成了虚线．这个图形有两种特殊情况：（1）如图2所示，当四边形ABCD 有一组对边平行时，如∥AD BC ，此时我们看成AD 和BC 的交点N 在无穷远处，那么以M 为极点，对应的极线是图2中的PN 2，其中∥PN BC 2；以P 为极点，那么极线是MN 1，其中∥MN BC 1；（2）如图3所示，当其中一条割线变成切线时，此时D 、M 、N 几个点就都与切点C 重合，从而点C 和切线PC 是一对极点极线.2．极点极线的代数定义：在平面直角坐标系xOy 中，设有圆锥曲线C （圆、椭圆、双曲线、抛物线均可）和不与C 的对称中心重合的点P x y ,00)(，在圆锥曲线C 的方程中，用x x 0替换x 2，y y 0替换y 2，+x x 20替换x ，+y y20替换y ，得到的方程即为以P 作为极点的极线l 的方程.例如，设椭圆C 的方程为+=y x 2122，极点为P 2,4)(，则与P 对应的极线为+=y x 2412，即+−=x y 410；又如，设抛物线C 的方程为=y x 22，极点为P 2,4)(，则与P 对应的极线为=⋅+y x2422，即−+=x y 420.可以看到，极点与极线是一个成对的概念，且若给定极点，求极线的规则是统一的，与圆锥曲线的类型无关，与极点P 的位置无关，下面以椭圆为例，说明极点P 在不同位置时，极线l 的情形：（1）当点P 在椭圆C 上时，极线l 为椭圆C 在P 处的切线，如图4所示；（2）当点P 在椭圆C 外部时，极线l 为点P 对椭圆C 的切点弦所在直线，如图5所示；（3）当点P 在椭圆C 内部时，过点P 任作椭圆C 的一条割线交C 于A 、B 两点，椭圆C 在A 、B 两点处的切线交于点Q ，则当割线AB 绕着点P 旋转时，点Q 的轨迹就是极线l ，如图6所示.3．极点极线的常用性质：（下面以椭圆为例）（1）如图7所示，O 为椭圆中心，点P 在椭圆内，延长OP 交椭圆于点Q ，交椭圆与点P 对应的极线l 于点M ，则OP 、OQ 、OM 成等比数列；当P 恰好为弦AB 的中点时，直线AB 的方程为+=+a b a bx x y y x y 2222000022，且极线l 和椭圆在点Q 处的切线均与AB 平行.（2）调和分割性：如图8所示，设极点P 的极线是直线l ，过P 作椭圆的一条割线交椭圆于A 、B 两点，交极线l 于点Q ，则P 、A 、Q 、B 成调和点列，即=PBQBPA QA （或写成=+PQ PA PB211） （3）配极原理：若点P 关于椭圆的极线过点Q ，则点Q 关于椭圆的极线也过点P .由此出发，我们可以得出共线点的极线必然共点，共点极线的极点必然共线，如图9所示，极点P 1、P 2、P 3的极线分别为l 1、l 2、l 3，则P 1、P 2、P 3共线⇔l 1、l 2、l 3共点.提醒：极点极线的分析方法只能让我们在看到问题时能够迅速“窥得天机”，不能作为正式的作答，我们在学习时，仍然应该以基本方法为主，技巧偏方为辅，不能本末倒置.典型例题【例1】（2021·新高考Ⅱ卷·多选）已知直线+−=l ax by r :02与圆+=C x y r :222，点A a b ,)(则下列说法正确的是（ ）A.若点A 在圆C 上，则直线l 与圆C 相切B.若点A 在圆C 内，则直线l 与圆C 相离C.若点A 在圆C 外，则直线l 与圆C 相离D.若点A 在直线l 上，则直线l 与圆C 相切【解析】解法1：A 项，若点A 在圆C 上，则+=a b r 222，圆心C 到直线l 的距离=d r ，所以直线l 与圆C 相切，故A 项正确；B 项，若点A 在圆C 内，则+<a b r 222，圆心C 到直线l 的距离==>d r 2，所以直线l 与圆C 相离，故B 项正确；C 项，若点A 在圆C 外，则+>a b r 222，圆心C 到直线l 的距离==d r 2，所以直线l 与圆C 相交，故C 项错误；D 项，若点A 在直线l 上，则+−=a b r 0222，即+=a b r 222，圆心C 到直线l 的距离==d r ，所以直线l 与圆C 相切，故D 项正确.解法2：显然对于圆C ，以A a b ,)(作为极点，那么极线就是+−=l ax by r :02A 项，若极点A 在圆C 上，则极线l 是圆C 的切线，故A 项正确；B 项，若极点A 在圆C 内，则极线l 与圆C 相离，故B 项正确；C 项，若极点A 在圆C 外，则极线l 是圆C 的切点弦，应与圆C 相交，故C 项错误；D 项，若极点A 在直线l 上，这是极线恰好为切线，极点为切点的情形，故D 项正确. 【答案】ABD【例2】（2011·四川）椭圆有两个顶点−A 1,0)(，B 1,0)(，过其焦点F 0,1)(的直线l 与椭圆交于C 、D 两点，并与x 轴交于点P ，直线AC 与BD 交于点Q .（1）当=CD 时，求直线l 的方程； （2）当P 点异于A 、B 两点时，证明：⋅OP OQ 为定值.【解析】（1）由题意，椭圆的短半轴长=b 1，半焦距=c 1，所以长半轴长=a ，故椭圆的方程为+=x y 2122，当=CD 2时，易得直线l 与x 轴垂直，故可设l 的方程为=+y kx 1≠≠±k k 0,1)(， 设C x y ,11)(，D x y ,22)(，联立⎩⎪+=⎨⎪⎧=+x y y kx 21122消去y 整理得：++−=k x kx 221022)(， 判别式∆=+>k 8102)(，由韦达定理，②①⎩+⎪=−⎪⎨+⎪⎪+=−⎧k x x k x x k 2122212212，所以=−==CD x x 12=k 所以直线l的方程为=+y 1.（2）极点极线看问题：设P m ,0)(，以P 为极点，则对应的极线为=mx 1，即=mx 1， 显然点Q 在极线上，所以=m x Q 1，不难发现⋅=⋅+⋅=mOP OQ m y Q 011. 注意：上面的过程不能作为正式的作答，卷面上可以按下面两个解法来写.解法1：直线AC 的斜率为+=x k y AC 111，其方程为+=+x y x y1111)(③，直线BD 的斜率为−=x k y BD 122，其方程为−=−x y x y1122)(④，用式③除以式④整理得：−−=++x y x x y x 11111221)()(，即−−=++x y x y x x Q Q 11111221)()(， 而−+−−+−==++++++y x kx x kx x kx x kx x kx x y x kx x 111111111212121212212121)()()()()()(，所以−−+−=++++x kx x kx x kx x kx x x Q Q 111112121221，由①知+=−−k x x k22212， 故⎝⎭+++ ⎪++−−−−+−⎛⎫−+−+===+++−+−+−−++−−−k k k k x k x x x k k k k k k k k k x kx x k x k kk k Q Q 222111121212221111212222222222222)()()()()()(，解得：=−x k Q ，易得⎝⎭⎪−⎛⎫k P ,01，故⋅==−⋅−=k OP OQ x x k P Q 11)(，即⋅OP OQ 为定值1.解法2：直线AC 的斜率为+=x k y AC 111，其方程为+=+x y x y1111)(③，直线BD 的斜率为−=x k y BD 122，其方程为−=−x y x y1122)(④，用式③除以式④整理得：−−=++x y x x y x 11111221)()(，即−−=++x y x y x x Q Q 11111221)()(⑤ 所以⎝⎭−−−−−−−++ ⎪ ⎪====+++++++⎛⎫−+y x x x x x x x x x x y x x x x x x x x x x Q Q 121111111111121112121212122222212112122122222)()()()()()()()()()()()( ++−++⎝⎭+ ⎪=++⎛⎫−−−+k k k k k k k k22111222111222222， 因为x 1，∈−x 1,12)(，所以−<+x x 10121，结合⑤可得−+x x Q Q 11与y y 12异号， 又++++=++=+++=−−+==−+−k k k k y y kx kx k x x k x x k k k k k 222211112222112222121212122222)()()()()(++=−⋅−+k k k k 2112122)(， 所以y y 12与+−k k 11异号，即y y 12与+−k k 11异号，从而−+x x Q Q 11与+−k k 11同号，所以−+=−+x k k x Q Q 1111，解得：=−x k Q ，易得⎝⎭⎪−⎛⎫k P ,01，故⋅==−⋅−=k OP OQ x x k P Q 11)(，即⋅OP OQ 为定值1.【例3】（2020·新课标Ⅰ卷）已知A 、B 分别为椭圆+=>aE y a x :11222)(的左、右顶点，G为E 的上顶点，⋅=AG GB 8，P 为直线=x 6上的动点，PA 与E 的另一交点为C ，PB 与E 的另一交点为D . （1）求E 的方程；（2）证明：直线CD 过定点.【解析】（1）由题意，−A a ,0)(，B a ,0)(，G 0,1)(，故=AG a ,1)(，=−GB a ,1)(， 所以⋅=−=AG GB a 182，解得：=a 3或−3（舍去），故E 的方程为+=y x 9122.（2）极点极线看问题：如图1，设AB 和CD 交于点Q ，AD 和CB 交于点M ，则PQM 为自极三角形，所以点Q 和直线PM 是一对极点极线，设Q m ,0)(，则极线PM 的方程为=mx91，即=m x 9，又点P 在直线=x 6上，所以=m 69，从而=m 23，故⎝⎭⎪⎛⎫Q 2,03，这样就得到了直线CD 过定点⎝⎭⎪⎛⎫2,03.注意：上面的过程不能作为正式的作答，卷面上可以按下面两个解法来写. 解法1：由（1）知−A 3,0)(，B 3,0)(，设P t 6,)(，C x y ,11)(，D x y ,22)(，当≠t 0时，直线PA 的方程为=−t x y 39，代入+=y x 9122消去x 化简得：⎝⎭⎪+−=⎛⎫t t y y 90815422， 解得：=y 0或+t t 962，所以+=t y tC 962，故+=−=−t t x y t C C 93927322，从而⎝⎭++ ⎪−⎛⎫t t C t t 99,2736222，直线PB 的方程为=+t x y 33，代入+=y x 9122消去x 化简得：⎝⎭⎪++=⎛⎫t t y y 9091822，解得：=y 0或+−t t 122，所以+=−t y t D 122，从而+=+=−t t x y t D D 1333322，故⎝⎭++ ⎪−−⎛⎫t t D t t 11,332222，设⎝⎭ ⎪⎛⎫T 2,03，则⎝⎭++ ⎪= ⎪−⎛⎫t t TC t t 299,2796222)(，⎝⎭++ ⎪=− ⎪−⎛⎫t t TD t t 211,392222)(，即+=−+t TC TD t 93122)(，故∥TC TD ，所以T 、C 、D 三点共线，从而直线CD 过定点⎝⎭⎪⎛⎫T 2,03，当=t 0时，易得C 、D 分别与B 、A 重合，所以直线CD 即为x 轴，显然直线CD 也过点T ，综上所述，直线CD 过定点⎝⎭⎪⎛⎫T 2,03解法2：由（1）知−A 3,0)(，B 3,0)(，设C x y ,11)(，D x y ,22)(，P y 6,0)(当≠y 00时，由图2可知点C 不与点B 重合，因为+=y x 911122，所以=−y x 9911122)(，故CA 、CB 的斜率之积为+−−⋅=⋅==−x x x k k y y y CA CB 3399111121112① 又PA 的斜率==k k y PA CA 90，PB 的斜率==k k y PB BD 30，所以=k k CA BD 31， 代入式①化简得：BC 、BD 的斜率之积⋅=−k k BC BD 31，显然CD 不与y 轴垂直，否则AC 与BD 的交点在y 轴上，故可直线CD 的方程为=+x my t ，联立⎩⎪=++=⎨⎪⎧x my y tx 9122消去x 整理得：+++−=m y mty t 9290222)(， 判别式∆=−+−>m t m t 449902222)()(，所以+−>m t 9022， 由韦达定理，++=−m y y mt 92212，+=−m y y t 992122，所以++=++=m x x m y y t t 921821212)(，+=+++=−m x x m y y mt y y t t m 99921212122222)(，−−−++⋅=⋅==−x x x x x x k k y y y y BC BD 3339311212121212)(，故−=−++y y x x x x 339121212)(，即+++−⋅=−⋅+−−m m m t t m t 99933999918222222，整理得：−+=t t 29902，解得：=t 23或3，若=t 3，则C 、D 中有一个点与B 重合，不合题意，所以=t 23，满足∆>0，即直线CD 过定点⎝⎭ ⎪⎛⎫2,03，当=y 00时，易得C 、D 分别与B 、A 重合，所以直线CD 即为x 轴，也过点⎝⎭ ⎪⎛⎫2,03，综上所述，直线CD 过定点⎝⎭⎪⎛⎫2,03【例4】（2018·新课标Ⅰ卷）设椭圆+=C y x 2:122的右焦点为F ，过F 的直线l 与C 交于A 、B 两点，点M 的坐标为2,0)(.（1）当l 与x 轴垂直时，求直线AM 的方程； （2）设O 为坐标原点，证明：∠=∠OMA OMB .【解析】（1）由题意，F 1,0)(，当l 与x 轴垂直时，其方程为=x 1， 由⎩⎪+=⎨⎪⎧=y x x 21122解得：=y ，即点A的坐标为⎝⎭ ⎪ ⎪⎛⎫21,， 当点A的坐标为⎝⎭ ⎛2时，直线AM的方程为=y x 2， 当点A的坐标为⎝⎭⎛1,时，直线AM的方程为=−y . （2）极点极线看问题：如图，设'A 、'B 分别为A 、B 关于x 轴的对称点， 则显然四边形''AA BB 构成等腰梯形，其对角线的交点为F ，以F 1,0)(为极点， 则对应的极线为+⋅=⋅y x2011，即=x 2，而'BA 和'B A 的交点应该在极线上， 从而M 2,0)(就是'BA 和'B A 的交点， 由图形的对称性不难发现∠=∠OMA OMB . 且这一结论还可以推广，若F 不是焦点， 而是椭圆内x 轴正半轴上的一个一般的点， 比如可设为t ,0)(，那么它的极线为+⋅=y tx201，即=t x 2，所以点⎝⎭⎪⎛⎫t M ,02必定也能使∠=∠OMA OMB注意：上面的过程不能作为正式的作答，卷面上可以按下面的解法来写. 解：当⊥l y 轴时，易得∠=∠=︒OMA OMB 0当l 不与y 轴垂直时，可设其方程为=+x my 1，设A x y ,11)(，B x y ,22)(， 联立⎩⎪+=⎨⎪⎧=+y x x my 21122消去x 整理得：++−=m y my 221022)(，易得判别式∆>0， 由韦达定理，++=−m y y m 22212，+=−m y y 21212， −−−−−−+=+==−+−+−+x x x x x x k k y y y x y x x y x y y y AM BM 222222222121212121221122112)()()()()()()( 而+−+x y x y y y 2122112)(=+++−+=−+my y my y y y my y y y 11221221121212)()()()( ⎝⎭⎝⎭++ ⎪ ⎪=⋅−−−=⎛⎫⎛⎫m m m m 22201222，所以+=k k AM BM 0，从而∠=∠OMA OMB ， 综上所述，∠=∠OMA OMB .【例5】（2008·安徽）设椭圆+=>>a bC a b x y :102222)(过点M)，且左焦点为F 1)(.（1）求椭圆C 的方程；（2）当过点P 4,1)(的动直线l 与椭圆C 相交于两个不同的点A 、B 时，在线段AB上取点Q ，满足⋅=⋅AP QB AQ PB ，求证：点Q 在某定直线上.【解析】（1）由题意，⎩⎪+=⎨⎪−=⎧ab a b 12122222，解得：=a 42，=b 22，所以椭圆C 的方程为+=x y 42122. （2）极点极线看问题：因为⋅=⋅AP QB AQ PB ，所以=PBQBAP AQ ，故P 、A 、Q 、B 是一组调和点列，从而点Q 必定在点P 的极线上，因为点P 的坐标为4,1)(，所以它的极线为+=⋅x y42141，化简得：+−=x y 220，从而点O 在定直线+−=x y 220上. 注意：上面的过程不能作为正式的作答，卷面上可以按下面的定比点差法来写. 解：设Q x y ,)(，A x y ,11)(，B x y ,22)( 因为⋅=⋅AP QB AQ PB ，所以=PBQBAP AQ ，设==λPBQBAP AQ >≠λλ0,1)(，则=λPA PB ，=λAQ QB ，而=−−PA x y 4,111)(，=−−PB x y 4,122)(，=−−AQ x x y y ,11)(，=−−QB x x y y ,22)(所以⎩⎪−=−⎨⎪⎧−=−λλy y x x 11441212)()(，且⎩⎪−=−⎨⎪⎧−=−λλy y y y x x x x 1212)()(，从而②①⎩−⎪=⎪−⎨−⎪⎪=⎧−λλλλy y x x 11141212，且④③⎩+⎪=⎪+⎨+⎪⎪=⎧+λλλλy y y x x x 111212，①×③得：−=−λλx x x 14212222，②×④得：−=−λλy y y 1212222，所以−−+⋅=+−−λλλλx yx x y y 11242221212222222，即−=++−+λλx y x y x y 142222112222222)(⑤ 又A 、B 在椭圆C 上，所以⎩⎪+=⎪⎨⎪⎪+=⎧x y x y 42142122221122， 从而⎩⎪+=⎨⎪+=⎧x y x y 242422221122，代入⑤的：−=+−λλx y 1424422， 化简得：+−=x y 220，即点Q 始终在直线+−=x y 220上.强化训练1.（★★★）对于抛物线=C y x :22，设点P x y ,00)(满足<y x 2002，则直线=+l y y x x :00与抛物线C （ ） A.恰有1个交点B.恰有2个交点C.没有交点D.有1个或2个交点【解析】显然直线l 是点P 对应的极线，因为<y x 2002，所以点P 在抛物线内部，从而直线l 与抛物线C 没有交点. 【答案】C2.（★★★）已知椭圆+=C y x 2:122的右焦点为F ，过点A 2,2)(的直线与椭圆C 在x 轴上方相切于点B ，则直线BF 的方程为______.【解析】由题意，F 1,0)(，以F 为极点，则极线为=x21，即=x 2，所以点A 在极线上，根据配极原理，以A 为极点的极线过点F ，所以该极线就是BF ，其方程为+=y x2212，即+=x y 21【答案】+=x y 213.（★★★）过点P 2,1)(的直线l 与椭圆+=y x 4122相交于点A 和B ，且=λAP PB ，点Q 满足=−λAQ QB ，若O 为原点，则OQ 的最小值为________.【解析】由题意，==λPBQAPA QA所以点Q 是对应极点P 的极线与直线l 的交点，如图，易求得极线l 的方程为+=y x412，即+−=x y 220，所以点Q在该极线上，从而==OQ 5min .【答案】54.（★★★★）设椭圆+=>>a bC a b x y :102222)(的左、右顶点分别为A 、B ，上顶点为D ，点P 是椭圆C 上异于顶点的动点，已知椭圆C的离心率=e ，短轴长为2. （1）求椭圆C 的方程； （2）如下图所示，直线AD 与直线BP 交于点M ，直线DP 与x 轴交于点N ，证明：直线MN 过定点，并求出该定点.【解析】（1）由题意，=b 22，所以=b 1，椭圆C的离心率=e ，所以=a 2，故椭圆C 的方程为+=y x 4122.（2）极点极线看问题：如图，连接AP 、BD 交于点Q ，显然点Q 的极线是直线MN ， 当P 在椭圆上运动的过程中，点Q 会在直线BD 上运动，根据共线极点的极线必然共点不难发现直线MN 是过定点的直线，易求得直线BD 的方程为+=x y 22，所以可设−Q t t 22,)(，那么极线MN 的方程为+=−ty t x4122)(，整理得：−−−=x t x y 220)(，所以直线MN 过的定点是2,1)(．下面给出规范的作答过程.解：由（1）可得D 0,1)(，B 2,0)(，−A 2,0)(，可设直线BP 的方程为=+x my 2≠≠±m m 0,2)(， 联立⎩⎪+=⎨⎪⎧=+y x x my 41222消去x 整理得：++=m y my 44022)(，解得：=y 0或+−m m 442，所以+=−m y m p 442，从而+=+=−m x my m p p 428222，故⎝⎭++ ⎪−−⎛⎫m m P m m 44,824222，从而直线DP 的斜率为+−−−===+−−−+−−m m m m k m m m m mDP 482228244421422222)(故直线DP 的方程为−=++m y x m 2212)(，联立⎩−⎪=+⎨+⎪⎧=m y x m y 2212)(解得：+=−m x m 222)(，所以⎝⎭+ ⎪⎛⎫−m N m 2,022)(， 直线AD 的方程为−+=x y 211，即−+=x y 220，联立⎩=+⎨⎧−+=x my x y 2220，解得：⎩−⎪=−⎪⎨−⎪⎪=−⎧+m y m x m 24224，所以点M 的坐标为⎝⎭−− ⎪−−⎛⎫+m m m 22,244，设G 2,1)(， 则⎝⎭−− ⎪=−−⎛⎫+m m GM mm 22,42，⎝⎭+ ⎪=−−⎛⎫m GN m 2,14， 从而−=+m GM GN m 22，故G 、M 、N 三点共线， 即直线MN 过定点G 2,1)(.【反思】求解这道题时，可以先在草稿纸上用极点极线的知识去找到定点G 2,1)(，那么在严格求解时，心中就有答案了，可以通过证明GM 与GN 共线，从而得出直线MN 过定点G . 5.（★★★★）如下图所示，椭圆+=E x y 43:122的左、右顶点分别为A 、B ，左焦点为F ，过F 的直线与椭圆E 交于不与A 、B 重合的C 、D 两点，记直线AC 和BD 的斜率分别k 1，k 2，证明：k k 21为定值.【解析】极点极线看问题：由题意，−F 1,0)(，椭圆E 的极点F 对应的极线为+=−⋅⋅x y43110，即=−x 4，如图，AC 与BD 的交点P 应在极线上，所以可设−P y 4,0)(，显然−A 2,0)(，B 2,0)(，所以直线AC 的斜率==−k k y PA 210，直线BD 的斜率==−k k yPB 620， 从而=k k 321.下面给出严格求解过程. 解：由题意，−F 1,0)(，直线CD 不与y 轴垂直，可设其方程为=−x my 1，设C x y ,11)(，D x y ,22)(，联立⎩⎪⎨⎪⎧−+==x my x y 143122消去x 整理得：+−−=m y my 3469022)(， 易得判别式∆>0， 由韦达定理，++=m y y m 346212，+=−m y y 349212， 所以=−+my y y y 231212)( 显然−A 2,0)(，B 2,0)(，所以直线AC 的斜率+=x k y 2111， 直线BD 的斜率−=x k y 2222， 从而−++−−+++======−−−−+−−−y y y y y k x y my y my y y k my y y y x y my y y y y y 222213313222323339312212212121221121121212112)()()()()()(.6.（★★★★）已知椭圆+=>>a b C a b x y :102222)(的上、下顶点分别为A 和B ，左焦点为F ， 原点O 到直线FA的距离为2. （1）求椭圆C 的离心率； （2）设=b 2，直线=+y kx l :4与椭圆C 交于不同的两点M 、N ，证明：直线BM 与直线AN 的交点G 在定直线上.【解析】（1）由题意，原点O 到直线FA的距离===⋅AFa d bc OA OF ， 所以椭圆C的离心率==a e c 2. （2）极点极线看问题：由题意，直线l 与y 轴交于定点P 0,4)(，显然点G 在点P 对应的极线上，当=b 2时，易求得椭圆C 的方程为+=x y 84122，从而该极线的方程为+=⋅x y 84104，即=y 1，所以点G 在定直线=y 1上．下面给出严格求解过程.解：由题意，A 0,2)(，−B 0,2)(，设M x y ,11)(，N x y ,22)(， 联立⎩⎪+=⎨⎪⎧=+x y y kx 841422消去y 整理得：+++=k x kx 121624022)(，判别式∆=−+⨯>k k 1641224022)()(所以<k 2或>k 2，由韦达定理，②①⎩+⎪=⎪⎨+⎪⎪+=−⎧k x x k x x k 12241216212212直线BM 的方程为+=+x y x y 2211，直线AN 的方程为−=−x y x y 2222，联立⎩⎪−=⎪−⎨⎪⎪+=⎧+x y xy x y x y 22222211消去x 可得：−−=++y y x y y x 22222112)()(，从而−−++===++++y y x kx x kx x x kx x x y y x kx x G G 2222622621211211221212)()()()(③， 接下来给出以下两种计算非对称结构++kx x x kx x x 26121122的方法：法1：由①②知=−+kx x x x 231212)(， 代入式③得：−++−+===−+−++−+x x x x x kx x x kx x x x x x x x 222223133222663391211212112212212)()(， 从而−=+y y G G 232，解得：=y G 1，所以点G 在定直线=y 1上. 法2：由①知+=−−k x x k1216212代入式③得：⎝⎭+++ ⎪+−−−−⎛⎫+===−+++++k k k x x kx x x k k k k k kx x x x x k k12121222224168312126662424222221211222222从而−=−+y y G G 232，解得：=y G 1，所以点G 在定直线=y 1上.。
专题十：与椭圆有关的极点、极线问题
专题之十与椭圆有关的极点、极线问题我们知道，对于椭圆C:x2a2+y2b2=1(a>b>0)有如下的两个结论：(1)过椭圆C：x2a2+y2b2=1(a>b>0)上一点P(x0，y0)，椭圆C的切线方程为：x0xa2+y0yb2=1.(2)过椭圆C：x2a2+y2b2=1(a>b>0)外一点P(x0，y0)，椭圆C的切点弦方程为：x0xa2+y0yb2=1.简证(1)设过点P(x0，y0)椭圆C的切线方程为y-y0=k (x-x0).可用两种方法求得k=−b2x0a2y0.(法1.利用∆=0;法2.利用求隐函数的导数).于是可得切线方程为y-y0=−b2x0a2y0 (x-x)，a2y0y-a2y02=−b2x0x+b2x02,∴ b2x0x+a2y0y=b2x02+a2y02=a2b2,即x0xa2+y0yb2=1.(2)设过椭圆C：x2a2+y2b2=1(a>b>0)外一点P(x0，y0)向椭圆所作两条切线的切点分别为A(x1，y1)，B(x2，y2),于是切线AP x1xa2+y1yb2=1，∵ P∈AP，∴x1x0a2+y1y0b2=1①同理x2x0a2+y2y0b2=1②由①②知点A、B∈直线x0xa2+y0yb2=1. 即切点弦方程为x0xa2+y0yb2=1.如果把点P(x0，y)放到椭圆x2a2+y2b2=1(a>b>0)的内部，我们仍然可以写出一条直线方程x0xa2+y0yb2=1.那么这条直线与点P(x0，y0)间有怎样的关系呢？首先我们给出如下的概念：将点P(x0，y)与直线x0xa2+y0yb2=1分别称为椭圆x2 a2+y2b2=1(a>b>0)的一对极点和极线，其中，点P不为原点.于是我们易得椭圆x2a2+y2b2=1(a>b>0)极点和极线的如下性质：1.每给出一个极点，就可以唯一确定一条对应的极线.2.每给出一条极线，就可以唯一确定一个对应的极点.3.若极点在椭圆x 2a2+y2b2=1上，则极线为椭圆x2a2+y2b2=1在点P处的切线x0xa2+y0yb2=1.4.若极点在椭圆x 2a2+y2b2=1外，则极线为椭圆x2a2+y2b2=1过点P的切点弦x0xa2+y0yb2=1.5.若极点在椭圆x 2a2+y2b2=1内，则极线与椭圆x2a2+y2b2=1相离；若极点在椭圆x 2a2+y2b2=1外，则极线与椭圆x2a2+y2b2=1相交.(切点弦).6.当极点P 是椭圆x 2a 2+y 2b 2=1的右焦点(c ，0)时，极线为右准线 x=a 2c . 当极点P 是椭圆x 2a 2+y 2b 2=1的左焦点(-c ，0)时，极线为左准线 x=−a 2c.7.当极点P 在椭圆x 2a 2+y 2b 2=1的对称轴上时，极线垂直于极点所在的对称轴.即极点为P(m ，0)时，极线为x=a 2m ；极点为P(0，n)时，极线为y=b 2n . 8.设极点P(x 0，y 0)，对应极线的斜率为k ，则kk 0P =−b 2a 2.9.极点P(x 0，y 0)在椭圆x 2a 2+y 2b 2=1内部时，以P 为中点的弦与极线平行. 10.设极点P 对应的极线为l P ，极点Q 对应的极线为l Q .则l P 过点Q ⇔l Q 过点P.下面给出其中部分结论的简略证明： 证5：将椭圆x 2a 2+y 2b 2=1和极线x 0xa 2+y 0y b 2=1联立，可得其∆=a 2b 2(x 02a 2+y 02b 2−1),点P 在椭圆x 2a 2+y 2b 2=1外⇔∆>0⇔极线与椭圆x 2a 2+y 2b 2=1相交. 点P 在椭圆x 2a 2+y 2b 2=1内⇔∆<0⇔极线与椭圆x 2a 2+y 2b 2=1相离. 证6、7:将极点的坐标带入对应的极线方程x 0xa 2+y 0yb 2=1中，即可得.证8:由1知极线x 0xa 2+y 0y b 2=1的斜率k=−b 2x 0a 2y 0，又k 0P =y 0x 0，∴ kk 0P =−b 2a 2.证9:设以点P 为中点的弦交椭圆x 2a 2+y 2b 2=1于A(x 1，y 1)、B(x 2，y 2)，∴ x 12a 2+y 12b 2=1 (1) x 22a 2+y 22b 2=1 (2) (1)-(2)得k AB =y 1−y 2x 1−x 2=-−b 2x0a 2y 0,其中x 0=x 1+x 22, y 0=y 1+y 22. 与极线x 0x a 2+y 0yb2 =1的斜率k=−b 2x0a 2y 0相等， ∴ 结论正确.证10:∵极点P 对应的极线为l P :x Pxa 2+y P yb 2=1，极点Q 对应的极线为l Q ：x Qxa2+y Q y b 2=1.∴ l P 过点Q ⇔x P x Q a 2+y P y Q b 2 =1⇔l Q 过点P.命题1.设射线OP 与椭圆x 2a 2+y 2b 2=1(a>b>0)交于点R ，与点P 对应的极线交于点Q.如图1.则|OP||OQ|=|OR|2.特别地，当点P 在x 轴上时，|OP||OQ|=a 2. 证明：设点P(x 0，y 0)，则点P 对应的极线为x 0xa 2+y 0yb 2=1. 当点P 不在x 轴上时，直线OP ：y =y 0x 0x ，yxORQ P. . .图1联立{x 0xa 2+y 0y b 2=1y =y 0x 0x，解得Q(a 2b 2x 0b 2x 02+a 2y 02，a 2b 2y 0b 2x 02+a 2y 02),联立{x 2a 2+y 2b 2=1y =y 0x 0x，可得|OR|2=a 2b 2x 02b 2x 02+a 2y 02+a 2b 2y 02b 2x 02+a 2y 02.∵|OP|=√x 02+y 02,|OQ|=a 2b 2√x 02+y 02b 2x 02+a 2y 02，∴ |OP||OQ|=|OR|2.特别地，当点P 在x 轴上时，设P(m ，0)，则对应的极线为x=a 2m , ∴ |OP||OQ|=a 2，此时点R(a ，0)也成立.下面我们来研究当极点P 不在椭圆上时，怎样画出对应的极线. 如图2，过点P(x 0，y 0)作椭圆C: x 2a 2+y 2b 2=1 的两条割线，分别交椭圆C 于A 、B 、C 、D 四点. 设PA ⃗⃗⃗⃗⃗ =λPB ⃗⃗⃗⃗⃗ ，PD ⃗⃗⃗⃗⃗ =μPC ⃗⃗⃗⃗⃗ .A(x 1，y 1)，B(x 2，y 2)， C(x 3，y 3)，D(x 4，y 4).由PA⃗⃗⃗⃗⃗ =λPB ⃗⃗⃗⃗⃗ ， 得{x 1−λx 2=(1−λ)x 0 ①y 1−λy 2=(1−λ)y 0 ②， ∵ 点A 、B ∈椭圆C ，{b 2x 12+a 2y 12=a 2b 2 ③b 2x 22+a 2y 22=a 2b 2 ④. ③-λ2④得 b 2(x 12−λ2x 22)+ a 2(y 12−λ2y 22)= a 2b 2(1−λ2)，∴ b 2(x 1−λx 2)(x 1+λx 2)+ b 2(y 1−λy 2)(y 1+λy 2)= a 2b 2(1−λ2)，将①、②代入上式得b 2x 0(x 1+λx 2)+b 2y 0(y 1+λy 2)= a 2b 2(1+λ)， ∴x 0(x 1+λx 2)a 2(1+λ)+y 0(y 1+λy 2)b 2(1+λ)=1，令M(x 1+λx 21+λ，y 1+λy 21+λ),由定比分点公式知：直线AB 上存在一点M ，使得PA ⃗⃗⃗⃗⃗ =λPB ⃗⃗⃗⃗⃗ 与AM ⃗⃗⃗⃗⃗⃗ =λMB ⃗⃗⃗⃗⃗⃗ 同时成立，且点M 恰好在椭圆C 的极线上.同理，我们在直线CD 上可以找到一点N ，使得点N 既在椭圆C 的极线上，同时又满足PD ⃗⃗⃗⃗⃗ =μPC ⃗⃗⃗⃗⃗ 与DN⃗⃗⃗⃗⃗⃗ =μNC ⃗⃗⃗⃗⃗ .如图2. 定义：我们称满足|MA||MB|=|PA||PB|(内分比=外分比)的点P 、A 、M 、B 为一组调和点列.于是满足|ND||NC|=|PD||PC|(内分比=外分比)的点P 、D 、N 、C 为另一组调和点列.注意：调和点列与椭圆C 无关，只要满足内分比=外分比即可.我们把这种性质称为调和性.进一步我们可以证明，AC 与BD 的交点及AD 与BC 的交点都在直线MN 上.这 个问题的证明要用到平面几何中的梅涅劳斯定理和塞瓦定理.此处略.由此我们得到椭圆C 的极点P 所对应极线的确定方法为：过点P 作椭圆C:yxO P图2ABDCMNx 2a 2+y 2b 2=1的两条割线，分别交椭圆C 于A 、B 、C 、D 四点，如图2.则极线必是直线AC 、BD 的交点与直线AD 、BC 交点的连线.命题2.设四边形ABCD 为椭圆C 的内接四边形，且AC ∩BD=P ，AB ∩CD=Q ，AD ∩BC=R.则点P 的极线为QR ；点Q 的极线为PR ；点R 的极线为PQ.如图3.命题3.若四边形ABCD 为椭圆C 的内接梯形，AD ∥BC ，如图4.则点P 对应的极线经过AC 、BD 的交点Q 且与AD 平行.命题4.若四边形ABCD 为椭圆C 的内接梯形，AD ∥BC ∥y 轴，如图5.则点P 对应的极线经过AC 、BD 的交点Q 且与y 轴平行.并满足OP ⃗⃗⃗⃗⃗ ∙OQ⃗⃗⃗⃗⃗⃗ =|OR|2=a 2. 这是因为当AD ∥BC ∥y 轴时，由椭圆的对称性知AC 、BD 的交点Q 必在x 轴 上.再由命题1知OP⃗⃗⃗⃗⃗ ∙OQ ⃗⃗⃗⃗⃗⃗ =|OR|2=a 2.我们称此为a 2模型. 特别地，若点P 是椭圆的右准线，则点Q 为右焦点，且x 轴平分∠APC.【应用举例】例1.如图6.椭圆有两个顶点A(-1，0)，B(1，0).过其焦点F(0，1)的直线l 与椭圆交于C 、D 两点，并与x 轴交于点P ，直线AC 、BD 交于点Q.当点P 异于A 、B 两点时，求证：OP ⃗⃗⃗⃗⃗ ∙OQ ⃗⃗⃗⃗⃗⃗ 为定值. 分析：由前面的性质7知，点P 的极线与x 轴垂直； 又由前面的讨论知，点P 的极线过点Q ，即点P的极线为过点Q 且垂直于x 轴的直线l 1.设直线l 1与x 轴交于点R.则由数量积的几何意义及a 2模型知： OP ⃗⃗⃗⃗⃗ ∙OQ⃗⃗⃗⃗⃗⃗ =|OP||OR|= a 2=1.例2.如图7.已知椭圆C:x 29+y 25=1的左、右顶点为A 、B ，右焦点为F.设过点T(9，m)的直线TA 、TB 与椭圆C 交于M 、N 两点，其中m >0.求证：MN 必过x 轴上一定点(其坐标与m 无关).分析：设MN 与x 轴交于点K.则极点T 对应的极线经过点K ；极点K 对应的极线l 经过点T 且与x 轴垂直.设直线l 与x 轴交于点P,则|OP|=9.由a 2模型知： |OK||OP|=|OB|2.可得|OK|=1，即点K(1，0)与F(1，0) 重合，所以 MN 必过x 轴上一定点F.yQx O 图3 A B D C R P yxO P图4AB DC Q yx O P 图5 B A D CQ R y P xO 图6A BDCl 1QR yTx BO MKA 图7N P例3.设椭圆C ：x 2a 2+y 2b 2=1(a>b>0)过点M(√2，1)，且左焦点F 1(−√2，0). (1)求椭圆C 的方程；(2)当过点P(4，1)的动直线l 与椭圆C 交于不同的两点A 、B 时，在线段AB 上取点Q ，满足|AP||QB|=|AQ||PB|.求证：点Q 总在某定直线上. 分析：(1)由已知易得椭圆C 的方程为：x 24+y 22=1.(2)∵ |AP||QB|=|AQ||PB|，∴ |AP||PB|=|AQ||QB|，即内分比=外分比，∴ 点Q 必在点P 所对应的极线上，又∵ 点P 所对应的极线方程为： 4×x 4+1×y 2=1， ∴ 点Q 总在定直线2x+y -2=0上.例4.椭圆C ：x 2a 2+y 2b 2=1(a>b>0)的离心率为√32，且a+b=3.(1)求椭圆C 的方程；(2)如图8.A 、B 、D 为椭圆C 的顶点，点P 是椭圆C 上异于顶点的任意一点. DP ∩x 轴=N ，AD ∩BP=M.设k PB =k ，k MN =m.求证：2m-k 为定值. 分析:(1)易求得椭圆C 的方程为：x 24+y 2=1.(2)设AP ∩BD=E.极点N 对应的极线过ME 且与 x 轴垂直，由a 2模型知x M x N =a 2=4.设N(t ，0)，则x M =4t .又∵ M ∈AD,l AD :y=x2+1，∴ M(4t ，2t +1). ∵ B(2，0)，∴ 2m-k=4t +24t−t -2t +14t−2=4+2t 4−t 2−2+t 4−2t =22−t −2+t 4−2t =12.例5.如图9.设椭圆C ：x 2a 2+y 2b 2=1(a>b>0)的一个焦点为，对应的准线为l .(1)若过点F 的直线与C 交于M 、N 两点，则M 、N两点处的切线的交点Q 必在准线l 上，且FQ ⊥MN.(2)若过准线l 上的一点Q 作C 的两条切线，切点分别 为M 、N 两点，则直线MN 必过交点F ，且FQ ⊥MN.(3)若过点F 的直线与C 交于M 、N 两点，过F 作FQ MN 交准线于Q ，则QM ，QN 是C 的两条切线. 分析:(1)由已知点F 的极线为准线l ，点Q 的极线为MN. ∵ 点F 在点Q 对应的极线MN 上， ∴ 点Q 必在点F 所对应的极线l 上. 设点Q(a 2c ，m ),则k MN =−b 2×a 2ca 2×m =−b 2cm ；k FQ =m−0a 2c−c=cm b 2.∴ FQ ⊥MN.(2)由已知MN 是点Q 所对应的极线，准线l 是点F 所对应的极线，且点Q在准线l 上，∴ 点F 必在MN 上.yExB MDOAPN 图8 yQ xMO FN 图9设点Q(a 2c ，m ),则k MN =−b 2×a 2ca 2×m =−b 2cm ；k FQ =m−0a 2c−c=cm b 2.∴ FQ ⊥MN.(3)设点Q(a 2c ，m ),F(c ，0). ∵ k FQ =m−0a 2c−c=cm b 2，且FQ ⊥MN∴ k MN =−b 2×a 2ca 2×m =−b 2cm ，因此直线MN 的方程为：y =−b 2cm (x −c)， 即 xc +my b 2=1与过点Q 的极线方程一致，∴ QM ，QN 是C 的两条切线.想一想①：1.已知曲线C ：x 2+2y 2=8与y 轴交于A 、B 两点(点A 在点B 的上方如图10).直线y=kx+4与曲线C 交于不 同的两点M 、N ，直线y=1与直线BM 交于点G. 求证：A 、G 、N 三点共线.2.已知椭圆C ：x 24+y 22=1.过点P(0，1)的动直线l 交椭圆C 于不同的两点A 、B.问是否存在异于点P 的定点Q 使得|AP||PB|=|AQ||QB|恒成立？若存在，求出点Q 的坐标. 3.设椭圆C ：x 2a 2+y 2b 2=1(a>b>0)的左、右焦点分别为F 1、F 2，离心率e=12，过F 1的直线交椭圆C 于A 、B 两点，且∆ABF 1的周长为8.(1)求椭圆C 的方程；(2)设动直线y=kx+m 与椭圆C 只有一个公共点P ，且与直线x=4交于点Q.试探究：是否存在定点M ，使得以PQ 为直径的圆恒过定点M?与椭圆类似，对于抛物线y 2=2px(p>0)，设极点P(x 0，y 0)，对应的极线为：y 0y=p(x+x 0). x 2=2py(p>0)的极点、极线分别为极点P(x 0，y 0)，对应的极线x 0x=p(y+y 0). 其极点和极线有如下性质：1.若极点在抛物线y 2=2px(p>0)上，则极线为在点P 处的切线y 0y=p(x+x 0). 若极点在抛物线x 2=2py(p>0) 上，则极线为在点P 处的切线x 0x=p(y+y 0).2.若极点在抛物线y 2=2px(p>0)外，则极线为过点P 处的切点弦y 0y=p(x+x 0). 若极点在抛物线x 2=2py(p>0)外，则极线为在点P 处的切点弦x 0x=p(y+y 0).3.当极点P 是抛物线y 2=2px(p>0)的焦点 (p2，0)时，极线为其准线x=−p2. 4.对于抛物线y 2=2px(p>0)，当极点为P(m ，0)时，极线为x=-m. 对于抛物线x 2=2py(p>0)，当极点为P(0，m)时，极线为y=-m.5.极点P(x 0，y 0)在抛物线y 2=2px(p>0)内部时，以P 为中点的弦与极线平行.6.设极点P 对应的极线为l P ，极点Q 对应的极线为l Q .则l P 过点Q ⇔l Q 过点P.7.设四边形ABCD 为抛物线C 的内接四边形，且AC ∩BD=P ，AB ∩CD=Q ，AD ∩BC=R.则点P 的极线为QR ；点Q 的极线为PR ；点R 的极线为PQ.8.若四边形ABCD 为抛物线C 的内接梯形，AD ∥BC ，则点P 对应的极线经过AC 、 BD 的交点Q 且与AD 平行.yG xBMO K APN图109.若四边形ABCD 为抛物线C 的内接梯形，AD ∥BC ∥y 轴，则点P 对应的极线经过AC 、BD 的交点Q 且与y 轴平行.10.设抛物线C ：y 2=2px(p>0)的焦点为F ，对应的准线为l .(1)若过点F 的直线与交C 于M 、N 两点，则M 、N 两点处的切线的交点Q 必在准线l 上，且FQ ⊥MN.(2)若过准线l 上的一点Q 作C 的两条切线，切点分别为M 、N 两点，则直线MN 必过交点F ，且FQ ⊥MN.(3)若过点F 的直线与C 交于M 、N 两点，过F 作FQ ⊥MN 交准线于Q ，则QM ，QN 是C 的两条切线.对于双曲线x 2a 2−y 2b 2=1(a>0，b>0)，当极点为P(x 0，y 0)时，对应的极线方程为：x 0x a 2−y 0y b 2=1.其极点、极线也有与椭圆类似的性质和结论.下面略举两例说明之.例6.已知抛物线C ：x 2=4y 的焦点为F.A 、B 是C 上的两动点， 且AF⃗⃗⃗⃗⃗ =μFB ⃗⃗⃗⃗⃗ (μ>0).过A 、B 分别作C 的切线，设其交 于点P.(1)求证：FP ⃗⃗⃗⃗⃗ ∙AB ⃗⃗⃗⃗⃗ 为定值；(2)设S 为∆ABP 的面积，求S min .解析：(1)设点P(x 0，-1)，A(x 1，y 1)，B(x 2，y 2). ∴ F 、A 、B 三点对应的极线方程分别为：y=-1，x 1x=2(y 1+y)，x 2x=2(y 2+y).由于F 、A 、B 三点共线，∴ 这三条极线都共线于点P(x 0，-1)，代入极线方程有{x 1x 0=2(y 1−1)x 2x 0=2(y 2−1)，两式相减得 x 0(x 1−x 2)=2(y 1−y 2). 又∵ FP ⃗⃗⃗⃗⃗ =(x 0，-2)， AB ⃗⃗⃗⃗⃗ =(x 2−x 1，y 2−y 1)，∴ FP ⃗⃗⃗⃗⃗ ∙AB ⃗⃗⃗⃗⃗ =x 0(x 2−x 1)−2(y 2−y 1)=0. (2)设直线AB 的方程为y=kx+1，与其极线方程x 0x=2(y 0+y)进行比较知，极线AB 所对应的极点为P(2k ，-1).右弦长公式可得|AB|=4(1+k 2)， ∴ S=12|AB||FP|=2(1+k 2)√4(1+k 2)，显然，当k=0时S min =4.例7.已知以原点为中心，F(√5，0)为右焦点的双曲线C的离心率e=√52. (1)求双曲线的方程和渐近线的方程； (2)如图12.已知过点M(x 1，y 1)的直线l 1:x 1x+4y 1y=4 与过点N(x 2，y 2)( x 1≠x 2)的直线l 2:x 2x+4y 2y=4的交点 E 在双曲线C 上.直线MN 与C 的两条渐近线分别交于 点G 、H.求0G ⃗⃗⃗⃗⃗ ∙OH⃗⃗⃗⃗⃗⃗ 的值. 解析:(1)双曲线C 的方程为：x 24−y 2=1; 渐近线方程为：y =±x2.yF xO AB图11FyxOMH 图12GNl 2l 1(2)直线l 1:x 1x+4y 1y=4与直线l 2:x 2x+4y 2y=4显然是椭圆x 2+4y 2=4的两条切线.由已知点E(x E ，y E )同在l 1和l 2上，∴ MN 是椭圆的极点E 对应的极线，于是 MN 的方程为：x E x+ 4y E y=4. 联立{x E x +4y E y =2x −2y =0 及{x E x +4y E y =2x +2y =0 ，解得G(4xE +2y E，2xE +2y E)，H(4xE −2y E，−2xE −2y E).∴ 0G ⃗⃗⃗⃗⃗ ∙OH ⃗⃗⃗⃗⃗⃗ =12x E2−4y E2，又∵ 点E 在双曲线x 24−y 2=1，∴ x E 2−4y E 2=4， 故 0G ⃗⃗⃗⃗⃗ ∙OH⃗⃗⃗⃗⃗⃗ =3. 想一想②：已知抛物线E ：y 2=4x 的焦点为F.过点K(-1，0)的直线与R 交于A 、B 两点，点A 关于x 轴的对称点为D.求证：直线BD 过定点.说明：我们在考试时，作为解答题，是不能用上述极点、极线的方式解题的，还是 要用常规方法解答.我们在此之所以要介绍关于极点、极线的相关知识，主要作用有二：一是在解选填题时，用它可以快速得到结论；二是作为解答题(特别是探索题型)，我们可以先由极点、极线的方式得到结论，在明确目标的前提下，再作一般性的论证.即使一般性的论证完成不了，起码可得到猜想结论分.习题：1.已知椭圆C ：x 2+4y 2=4的左、右顶点为A 、B.设直线x=my+1与椭圆C 交于P 、Q 两点，直线AP 交直线BQ 于S,试问当m 变化时，点S 是否恒在一条定直线上？若是，写出这条直线的方程.2.如图13，已知椭圆C ：x 2+3y 2=3.斜率为k(k>0)且不 过原点的直线l 交椭圆C 于不同的两点A 、B.线段 AB 的中点为E ，射线OE 交椭圆C 于点G ，交直线 x=-3于点D(-3，m). (1)求m 2+k 2的最小值；(2)若|OG|2=|OD||OE|，求证：直线l 过定点.3.如图14.设椭圆E:x 2+2y 2=2的右焦点为F ，过点F 的直线l 交椭圆E 于A 、B 两点,点M(2，0). (1)当直线l 垂直于x 轴时，求直线AM 的方程；(2)设O 为坐标原点，求证：∠OMA=∠OMB. 4.已知椭圆C ：x 24+y 23=1.过点P(4，0)的直线与椭圆C 交于点A 、B 两点.作点A关于x 轴的对称点Q ，连接QB.求证：直线QB 过定点.5.已知椭圆C ：x 28+y 24=1.过点F(2，0)作倾角互补的两条直线交椭圆C 于A 、B 两点(A 、B 两点均在x 轴的同侧). 求证：直线AB 过定点.6.已知椭圆C ：x 2a 2+y 2b 2=1(a>b>0)过的P(1，e)(e 为椭圆的离心率).其左、右顶点为A(-2，0)，B(2，0). (1)求椭圆C 的方程; (2)过点E(4，0)的直线交椭圆C 于yxD E AO lGB图13yM Ax O FB 图14 2M、N两点.设AM与BN交于点P.求证：点P在定直线上.参考答案：想一想①：1.∵直线y=kx+4过定点P(0，4)在y轴上，点P对应的极线方程为y=b2n=1. 即直线是点P对应的极线. 又∵直线MB与直线y=1(极线)交于点Q，∴直线AN必过点Q.2.∵点P(0，1)在y轴上，∴点P对应的极线方程为y=b2n=2，设y轴与极线 y=2交于点Q(0，2)，则点Q满足条件.3.(1)x 24+y23=1. (2)由例5知F2P的斜率与点Q对应的极线的斜率相同，又∵点F2对应的极线为直线x=4，设Q(4，m), ∵k F2P=−3m，k F2Q =m4−1=m3，∴ PF2⊥QF2,故以PQ为直径的圆恒过定点F2.想一想②：直线BD过定点F. 提示：作点B关于x轴的对称点E.利用抛物线的性质9，注意到点K极线过焦点F.习题1.设PQ与x轴交于点M，极点S对应的极线过点M(1，0)；极点M对应的极线过点S且垂直于x轴，∴点S必在直线x=a 2m=4上.2.(1)设A(x1，y1)，B(x2，y2).用点差法易得k OE=-13k , ∴直线OE的方程为y=-13kx,解得m=1k . ∴m2+k2=1k2+ k2≥2.(2)设AD∩x轴=M，M(m，0).由|OG|2=|OD||OE|，知点D的极线是l，又点D的极线过M，则点M的极线过点D且于x轴垂直.∴-3m=-3，得m=1.3(1)x+√2y−2=0.(2)利用命题4及后面“特别地…”.4.利用命题4.5.延长AF交椭圆C于P，延长BF交椭圆C于Q.则易知点B与点P，点A与点Q 均关于x轴对称.所以BA必过准线x=4与x轴的交点M(4，0).6.(1) x2+4y2=4. (2)利用例1的结论知，定直线为过点R且与x轴垂直的直线x=1.。
圆锥曲线中的极点极线问题(学生版)
圆锥曲线中的极点极线问题考情探究命题规律及备考策略【命题规律】本节内容是新高考卷的选考内容，设题不定，难度中等或偏难，分值为5-17分【备考策略】1.理解、掌握圆锥曲线极点极线的定义2.理解、掌握圆锥曲线的极点极线问题及其相关计算【命题预测】本节内容是新高考卷的常考内容，小题和大题都会作为载体命题，同学们要会结合公式运算，需强化训练复习知识讲解1.极点极线的定义如图,设P 是不在圆雉曲线上的一点,过P 点引两条割线依次交圆锥曲线于四点E ,F ,G ,H ,连接EH ,FG 交于N ,连接EG ,FH 交于M ,则直线MN 为点P 对应的极线.若P 为圆雉曲线上的点,则过P 点的切线即为极线.同理,PM 为点N 对应的极线,PN 为点M 所对应的极线.因而将△MNP 称为自极三点形.设直线MN 交圆锥曲线于点A ,B 两点,则P A ,PB 恰为圆锥曲线的两条切线.2.其他定义对于圆锥曲线C :Ax 2+Bxy +Cy 2+Dx +Ey +F =0,已知点P x 0,y 0 (非中心)及直线l :Ax 0x +B ⋅x 0y +y 0x 2+Cy 0y +D ⋅x +x 02+E ⋅y 0+y 2+F =0,则称点P x 0,y 0 是直线l 关于圆锥曲线C 的极点,直线l 称为点P 关于圆锥曲线C 的极线。
配极原则:共线点的极线必共点,共点线的极点必共点。
3.替换原则x0x →x 2,x 0y +y 0x 2→xy ,y 0y →y 2,x +x 02→x ,y +y 02→y .4.极点极线的几何意义(以椭圆为例)已知椭圆方程:x2a2+y2b2=1,设点P x0,y0的极线l:x0xa2+y0yb2=1.(1)当点P x0,y0在椭圆上时,极线l是以点P为切点的切线。
(极点在极线上)(2)当点P在椭圆外时,极线l与椭圆相交,且为由P点向椭圆所引切线的切点弦所在直线。
(3)当点P在椭圆内时,极线l与椭圆相离,极线l为经过点P的弦在两端点处的切线交点的轨迹,且极线l与以点P为中点的弦所在的直线平行。
极点与极线的性质
.极点与极线的性质————————————————————————————————作者：————————————————————————————————日期：第15讲:极点与极线的性质 125第15讲:极点与极线的性质极点与极线是高等几何中的基本且重要的概念,虽然中学数学没有介绍,但以此为背景命制的高考试题经常出现.掌握极点与极线的初步知识,可使我们“登高望远”,抓住问题的本质,确定解题方向,寻找简捷的解题途.定义:已知曲线G:ax 2+bxy+cy 2+dx+ey+f=0,则称点P(x 0,y 0)和直线l:ax 0x+b200y x x y ++cy 0y+d 20x x ++e 2y y ++f=0是曲线G 的一对极点与极线,点P 称为直线l 关于曲线G 的极点;直线l 称为点P 关于曲线G 的极线.称点P 与直线l 有“配极关系”,或“对偶关系”,相互为对方的“配极元素”,或“对偶元素”.特别地,当点P 在曲线G 上时,点P 关于曲线G 的极线是曲线G 在点P 处的切线;圆锥曲线的焦点对应的极线是该焦点对应的准线;圆锥曲线的准线对应的极点是该准线对应的焦点.[位置关系]:已知点P 关于圆锥曲线G 的极线是直线l,则三者的位置关系是:①若点P 在曲线G 上,则直线l 是曲线G 在点P 处的切线;②若点P 在曲线G 外,则直线l 是由点P 向曲线G 引两条切线的切点弦;③若点P 在曲线G 内,则直线l 是经过点P 的曲线G 的弦的两端点处的切线交点轨迹.如图:l l l P M P A D M PN C N B[配极原则]:如果点P 的极线通过点Q,则点Q 的极线也通过点P.证明:设圆锥曲线G:ax 2+bxy+cy 2+2dx+2ey+f=0,点P(x p ,y p ),Q(x Q ,y Q ),则点P 、Q 关于曲线G 的极线方程分别为p:ax p x+b2yx x y p p ++cy p y+d2p x x ++e2p y y ++f=0,q:ax Q x+b2yx x y Q Q ++cy Q y+d2Q x x ++e2Q y y ++f=0,则点P 的极线通过点Q ⇔ax p x Q +b2Qp Q p y x x y ++cy p y Q +d2pQ x x ++e 2pQ y y ++f=0⇔点P(x p ,y p )在直线q:ax Q x+b2y x x y Q Q ++cy Q y+d2Q x x ++e2Q y y ++f=0上⇔点Q 的极线也通过点P.推论1:两点连线的极点是此二点极线的交点,两直线交点的极线是此二直线极点的连线;证明:设两点A 、B 连线的极点是P,即点P 的极线经过点A 、B,由配极原则知点A 、B 的极线均过点P,即点P 是此二点极线的交点;同理可证:两直线交点的极线是此二直线极点的连线.推论2(共点共线):共线点的极线必共点;共点线的极点必共线.证明:设点A 、B 均在直线l 上,直线l 对应的极点为P,由配极原则知点A 、B 的极线均过点P,即点A 、B 的极线必共点;同理可证:共点线的极点必共线.推论3(中点性质):若圆锥曲线G 过点P 的弦AB 平行于点P 的极线,则点P 是弦AB 的中点.证明:设P(x 0,y 0),曲线G:ax 2+bxy+cy 2+2dx+2ey+f=0,则点P 的极线方程:ax 0x+b200y x x y ++cy 0y+d 20x x ++e 2y y + +f=0,故可设AB:ax 0x+b200y x x y ++cy 0y+d 20x x ++e 20y y ++λ=0,由点P(x 0,y 0)在直线AB 上⇒ax 02+bx 0y 0+cy 02+2dx 0+2ey 0+λ=0⇒λ=-(ax 02+bx 0y 0+cy 02+2dx 0+2ey 0)⇒直线AB:ax 0x+b 200y x x y ++cy 0y+d 20x x ++e 20y y +=ax 02+bx 0y 0+cy 02+2dx 0+2ey 0⇒ ax 0x+b200y x x y ++cy 0y+d 20x x ++e 20y y ++f=ax 02+bx 0y 0+cy 02+2dx 0+2ey 0+f,而该直线为以为P 中点的中点弦方程,即点P 是弦AB 的中点.[比例定理]:若过点P(x 0,y 0)的直线l 与曲线G:ax 2+bxy+cy 2+dx+ey+f=0相交于A 、B 两点,与直线:ax 0x+b200yx x y ++ 126 第15讲:极点与极线的性质cy 0y+d20x x ++e 2y y ++f=0交于点Q,则|PA||QB|=|QA||PB|. 证明:设直线l:⎩⎨⎧+=+=θθsin cos 00t y y t x x (t 为参数),代入ax 0x+b 200y x x y ++cy 0y+d 20x x ++e 20y y ++f=0得:(2ax 0cos θ+bx 0sin θ+by 0cos θ+2cy 0sin θ)t+2(ax 02+bx 0y 0+cy 02+dx 0+ey 0+f)=0⇒t 0=-2θθθθsin 2cos sin cos 2000000200020cy by bx ax f ey dx cy y bx ax ++++++++;代入ax 2+bxy+cy 2+2dx+2ey+f=0得:(acos 2θ+bcos θsin θ+csin 2θ)t 2+(2ax 0cos θ+bx 0sin θ+by 0cos θ+2cy 0sin θ)t+(ax 02+bx 0y 0+cy 02+dx 0 +ey 0+f)=0⇒t 1+t 2=-θθθθθθθθ220000sin cos sin cos sin 2cos sin cos 2c b a cy by bx ax +++++,t 1t 2=θθθθ2200200020sin cos sin cos c b a fey dx cy y bx ax +++++++⇒t 0=21212t t t t +;而|PA||QB|= |QA||PB|⇔|t 1||t 2-t 0|=|t 1-t 0||t 2|⇔t 0=21212t t t t +成立. [面积定理]:已知点P 关于圆锥曲线G 的极线为l,过点P 的直线与圆锥曲线G 相交于A 、B 两点,分别过点A 、B 的两条平行线与直线l 交于点D 、C,记△APD 、△CPD 、△BPC 的面积分别为S 1,S 2,S 3,则:S 22=4S 1S 2.证明:以椭圆G:22a x +22b y =1(a>b>0)为例,设P(x 0,y 0),则极线l:12020=+b y y a x x .设A(x 1,y 1),B(x 2,y 2),并分别过点A 、B作l 的垂线,垂足分别为D 1、C 1,则||||11BC AD =|1||1|220220210210-+-+by y a x x b y y a x x =||||2220220222102102b a y y a x x b b a y y a x x b -+-+(注意到:a 2b 2=b 2x 12+a 2y 12,a 2b 2=b 2x 22+a 2y 2) =||||222222202202212212102102y a x b y y a x x b y a x b y y a x x b --+--+=|)()(||)()(|0222022201120112y y y a x x x b y y y a x x x b -+--+-(注意到:0101x x y y --=0202x x y y --=k)=||||0201x x x x --⋅||||22221212x b ky a x b ky a ++.又因||||BP AP =||||0201x x x x --,以下只需证||||22221212x b ky a x b ky a ++=1,即|a 2ky 1+b 2x 1|=|a 2ky 2+b 2x 2|,由⎪⎩⎪⎨⎧=+=+2222222222212212ba y a xb b a y a x b ⇒b 2(x 1-x 2)(x 1+x 2)+a 2(y 1- y 2)(y 1+y 2)=0⇒b 2(x 1+x 2)+a 2k(y 1+y 2)=0⇒a 2ky 1+b 2x 1=-(a 2ky 2+b 2x 2)⇒|a 2ky 1+b 2x 1|=|a 2ky 2+b 2x 2|⇒||||BP AP =||||11BC AD ,由△ADD 1∽△BCC 1⇒||||BC AD =||||BP AP ,设AC 与BD 交于点Q,由AD ∥BC ⇒||||BC AD =||||QC AQ ⇒||||BP AP =||||QC AQ ⇒PQ ∥BC ∥AD ⇒S △BAC =S △BDC ,两边同减S △BQC 得S △QAB =S △QDC ,又因S △PQA =S △PQD ,S △PQB =S △PQC ⇒S △PCD =S △QCD +S △PQD +S △PQC =S △QCD +S △PQA +S △PQB =S △QCD +S △QAB =2S △QAB ⇒S △QAD =S △PAD =S 1,S△QBC=S △PBC =S 3,S △QAB =21S △PCD =21S 2,注意到:QAB QBC QAB QAD S S S S ∆∆∆∆⋅=||||||||QA QC QB QD ⋅=1⇒2QAB S ∆=S △QAD S △QBC ⇒S 22=4S 1S 2. 例1:极点与极线的位置关系.[始源问题]:(2010年湖北高考试题)已知椭圆C:22x +y 2=1的两焦点为F 1 ,F 2,点P(x 0,y 0)满足0<220x +y 02<1,则|PF 1|+|PF 2|的取值范围为 ,直线20xx +y 0y=1与椭圆C 的公共点个数为 . [解析]:由0<220x +y 02<1知,点P 在椭圆C 内,所以直线20x x +y 0y=1与椭圆C 相离⇒公共点个数为0;2c ≤PF 1|+|PF 2|<2a ⇒ 2≤PF 1|+|PF 2|<22⇒|PF 1|+|PF 2|的取值范围为[2,22).[原创问题]:已知椭圆C:42x +32y =1,点P(x 0,y 0)满足42x +320y >1(x 0≠0),直线l:40x x +30y y =1.(Ⅰ)求直线l 与椭圆C 的公共点个数;(Ⅱ)若射线OP 与直线l 、椭圆C 分别交于点Q 、M,求证:|OP||OQ|=|OM|2.[解析]:(Ⅰ)因椭圆C:42x +32y =1⇔⎩⎨⎧==θθsin 3cos 2y x ,θ∈[0,2π),所以,直线l 与椭圆C 的公共点个数⇔关于θ的方程第15讲:极点与极线的性质 12720x cos θ+330y sin θ=1解的个数⇔直线:20x x+330y y=1与圆:x 2+y 2=1的公共点个数;由圆心O(0,0)到直线:20x x+330y y=1的距离d=341220y x +<1⇒直线:20x x+330y y=1与圆:x 2+y 2=1的公共点个数=2⇒直线l 与椭圆C 的公共点个数=2;(Ⅱ)因射线OP:y=00x y x(x 与x 0同号),与40x x +30y y =1联立得:40x x +0203x x y =1⇒x=202004312y x x +⇒y=202004312y x y +⇒Q(202004312y x x +,22004312y x y +)⇒|OP||OQ|=2020202043)(12y x y x ++;由y=00x y x 与42x +32y =1联立得:42x +20203x y x 2=1⇒x 2=2020204312y x x +⇒y 2=2020204312y x y +⇒|OM|2=x 2+y 2=2020204312y x x ++2020204312y x y +=2020202043)(12y x y x ++⇒|OP||OQ|=|OM|2.例2:抛物线中的共线性质.[始源问题]:(2010年大纲卷Ⅰ高考试题)已知抛物线C:y 2=4x 的焦点为F,过点K(-1,0)的直线l 与C 相交于A 、B 两点,点A 关于x 轴的对称点为D. (Ⅰ)证明:点F 在直线BD 上; (Ⅱ)设FB FA ⋅=98,求△BDK 的内切圆M 的方程. [解析]:(Ⅰ)设A(x 1,y 1),B(x 2,y 2),直线l:y=k(x+1)(k ≠0),则D(x 1,-y 1),由⎩⎨⎧=+=xy x k y 4)1(2⇒ky 2-4y+4k=0⇒y 1+y 2=k 4,y 1y 2= 4;所以,点F 在直线BD 上⇔FB ∥FD ⇔(x 2-1):(x 1-1)=y 2:(-y 1)⇔y 1(ky 2-2)+y 2(k y1-2)=0⇔y 1y 2-k(y 1+y 2)=0;(Ⅱ)由FB FA ⋅=(x 1-1)(x 2-1)+y 1y 2=(k y 2-2)(k y 1-2)+y 1y 2=(1+21k )y 1y 2-k 2(y 1+y 2)+4=4(1+21k )-28k +4=8-24k=98⇒k=±43;根据对称性,不妨设k=43,则直线AB:3x-4y+3=0,且k KD =43⇒KF 平分∠AKD ⇒圆M 的圆心M 在x 轴上;(x 2-x 1)2=(x 1+x 2)2- 4x 1x 2=7162⇒k BD =1212y y x x +-=73⇒直线BD:3x-7y-3=0;设M(t,0)(-1<t<1),则由点M 到直线AB 与BD 的距离相等⇒5|1|3+t=4|1|3-t ⇒t=91⇒圆M:(x-91)2+y 2=94. [原创问题]:已知抛物线y 2=2px 及定点A(a,b),B(-a,0)(ab ≠0,b 2≠2pa),M 是抛物线上的点,设直线AM,BM 与抛物线的另一交点分别为M 1,M 2.求证:当M 点在抛物线上变动时(只要M 1,M 2存在且M 1≠M 2),直线M 1M 2恒过一个定点,并求出这个定点的坐标.[解析]:设M(2pt 2,2pt),M 1(2pt 12,2pt 1),M 2(2pt 22,2pt 2),则点B,M,M 2对应的极线分别为:x=a,2ty=x+2pt 2,2t 2y=x+2pt 22,由B,M,M 2三点共线⇒三线x=a,2ty=x+2pt 2,2t 2y=x+2pt 22共点⇒a=2ptt 2⇒t 2=pta2,点A,M 1对应的极线分别为:by=px+ap, 2t 1y=x+2pt 12,由A,M,M 1三点共线⇒三线by=px+ap,2ty=x+2pt 2,2t 1y=x+2pt 12共点⇒bp(t+t 1)=2p 2tt 1+ap ⇒t 1=ptb bta 2--,由⎪⎩⎪⎨⎧+=+=2222112222pt x y t pt x y t ⇒⎩⎨⎧+==)(22121t t p y t pt x ⇒⎪⎪⎩⎪⎪⎨⎧--=--=)2(2)2()2()(2pt b pt t p a b y pt b t bt a a x ⇒x-a=)2(22pt b t t p a --=b a 2y ⇒M 1,M 2对应极线的交点在定直线b p 2y=x+a, 即b p 22y=2p 2a x +上⇒直线M 1M 2恒过一个定点(a,bpa2). 128 第15讲:极点与极线的性质例3:抛物线中的比例性质.[始源问题]:(2009年全国高中数学联赛湖北初赛试题)已知抛物线C:y=21x 2与直线l:y=kx-1没有公共点,设点P 为直线l 上的动点,过P 作抛物线C 的两条切线,A 、B 为切点. (Ⅰ)证明:直线AB 恒过定点Q;(Ⅱ)若点P 与(Ⅰ)中的定点Q 的连线交抛物线C 于M 、N 两点.证明:||||PN PM =||||QN QM . [解析]:(Ⅰ)设A(x 1,y 1),B(x 2,y 2),P(x 0,y 0),则抛物线y=21x 2在点A 、B 处的切线方程分别为x 1x=y+y 1、x 2x=y+y 2,由点P(x 0,y 0)在这两切线上得:⎩⎨⎧+=+=02200110y y x x y y x x ⇒直线AB:x 0x=y+y 0(注意到:y 0=kx 0-1)⇒x 0x=y+kx 0-1⇒直线AB 过定点Q(k,1);(Ⅱ)设直线MN:⎩⎨⎧+=+=θθsin cos 00t y y t x x ,代入直线AB:x 0x=y+y 0,得:t Q =θθcos sin 20020x y x --;代入y=21x 2得:t 2cos 2θ+2(x 0cos θ-sinθ)t+x 02-2y 0=0⇒t 1+t 2=2⋅θθθ20cos cos sin x -,t 1t 2=θ2020cos 2y x -⇒21212t t t t +=θθcos sin 20020x y x --⇒t Q =21212t t t t +;所以,||||PN PM =||||QN QM ⇔21t t= QQ t t t t --21⇔t Q =21212t t t t +成立. [原创问题]:已知抛物线C:x 2=4y 与直线l:y=x-2,设点P 为直线l 上的动点,过P 作抛物线C 的两条切线,A 、B 为切点.(Ⅰ)证明:直线AB 恒过定点T;(Ⅱ)若过点P 的直线l 交抛物线C 于M 、N 两点,与直线AB 交于点Q.证明:||1PM +||1PN =||2PQ .[解析]:(Ⅰ)设A(x 1,y 1),B(x 2,y 2),P(x 0,y 0),则抛物线C:x 2=4y 在点A 、B 处的切线方程分别为x 1x=2(y+y 1)、x 2x=(y+y 2),由点P(x 0,y 0)在这两切线上得:⎩⎨⎧+=+=)(2)(202200110y y x x y y x x ⇒直线AB:x 0x=2(y+y 0)(注意到:y 0=x 0-2)⇒x 0x=2y+2x 0-4⇒直线AB 过定点T(2,2);(Ⅱ)设直线MN:⎩⎨⎧+=+=θθsin cos 00t y y t x x ,代入直线AB:x 0x=2(y+y 0),得:t Q =θθcos sin 240020x y x --;代入x 2=4y 得:t 2cos 2θ+2(x 0cos θ-2sin θ)t+x 02-4y 0=0⇒t 1+t 2=2⋅θθθ20cos cos sin 2x -,t 1t 2=θ2020cos 4y x -⇒21212t t t t +=θθcos sin 240020x y x --⇒t Q =21212t t t t +;所以,||1PM +||1PN =||2PQ ⇔11t21t =Q t 2⇔t Q =21212t t tt +成立. 例4:抛物线中的面积关系.[始源问题]:(2009年湖北高考试题)过抛物线y 2=2px(p>0)的对称轴上一点A(a,0)(a>0),的直线与抛物线相交于M 、N两点,自M 、N 向直线l:x=-a 作垂线,垂足分别为M 1、N 1. (Ⅰ)当a=2p时,求证:AM 1⊥AN 1; (Ⅱ)记△AMM 1、△AM 1N 1、△ANN 1的面积分别为S 1、S 2、S 3,是否存在λ,使得对任意的a>0,都有S 22=λS 1S 3成立.若存在,求出λ的值;若不存在,说明理由.[解析]:(Ⅰ)当a=2p 时,A(2p ,0),设M(2pm 2,2pm),N(2pn 2,2pn),则M 1(-2p ,2pm),N 1(-2p ,2pn),由AM ∥AN ⇒(2pm 2- 2p ):(2pn 2-2p )=2pm:2pn ⇒mn=-41⇒1AM ⋅1AN =p 2+4p 2mn=0⇒AM 1⊥AN 1;第15讲:极点与极线的性质 129(Ⅱ)由AM ∥AN ⇒(2pm 2-a):(2pn 2-a)=2pm:2pn ⇒2pmn+a=0;因||||11NN MM =2222pn a pm a ++;当MN ⊥/x 轴时,||||AN AM =|2||2|22pn a a pm --=2222pn a a pm --;所以,||||11NN MM =||||AN AM ⇔2222pn a pm a ++=2222pn a a pm --⇔4p 2m 2n 2=a 2成立;当MN ⊥x 轴时,显然有||||11NN MM =||||AN AM ;设MN 1与NM 1交于点Q(点Q 即原点O),由MM 1∥NN 1⇒||||1QN MQ =||||11NN MM =||||AN AM ⇒AQ ∥MM 1∥NN 1;设∠MQM 1=α,则S 1=21|QM||QM 1|sin α,S 3 =21|QN||QN 1|sin α;又S △QMN =11N QM S ∆⇒S 2=11N QM S ∆+(1AQM S ∆+1AQN S ∆)=11N QM S ∆+(S △AQM +S △AQN )=11N QM S ∆+S △QMN =2S △QMN ;S 1S 3=21|QM||QM 1|sin α⋅21|QN||QN 1|sin α=21|QM||QN|sin α⋅21|QM 1||QN 1|sin α=S △QMN 11N QM S ∆=41S 22⇒S 22=4S 1S 3⇒存在λ=4,使得对任意的a>0,都有S 22=λS 1S 3成立.[原创问题]:已知抛物线C:y 2=4x,直线l:y=2x+2,过点P(1,1)的直线与抛物线C 交于A 、B 两点,A 、B 两点在直线l 上的射影点分别为N 、M,记△PAN 、△PMN 、△PBM 的面积分别为S 1、S 2、S 3. (Ⅰ)当AB ∥直线l 时,求证:P 是AB 的中点; (Ⅱ)求证:S 22=4S 1S 3.[解析]:(Ⅰ)设A(x 1,y 1),则y 12=4x 1;由P 是AB 的中点⇒B(2-x 1,2-y 1)⇒(2-y 1)2=4(2-x 1)⇒y 1=2x 1+1⇒点A 在直线y=2x+1上,同理可得点B 也在直线y=2x+1上⇒直线AB:y=2x+1⇒AB ∥直线l;由统一法知,当AB ∥直线l 时, P 是AB 的中点;(Ⅱ)设直线AB:⎩⎨⎧+=+=θθsin 1cos 1t y t x (t 为参数),代入y 2=4x 得:t 2sin 2θ+2(sin θ-2cos θ)t-3=0⇒t 1+t 2=2⋅θθθ2sin sin cos 2-,t 1t 2=-θ2sin 3;点A(1+t 1cos θ,1+t 1sin θ)到直线l 的距离|AN|=5|3sin cos 2|11+-θθt t ,点B(1+t 2cos θ,1+t 2sin θ)到直线l 的距离|BM|=5|3sin cos 2|22+-θθt t ⇒||||BM AN =|3sin cos 2||3sin cos 2|2211+-+-θθθθt t t t (由点A 、B 在直线l 的同侧⇒2t 1cos θ-t 1sin θ+3与t 2cos θ-t 2sin θ+3同号)=3sin cos 23sin cos 22211+-+-θθθθt t t t ;而||||PB PA =||||21t t (点A 、B 在点P 的异侧)=-21t t;所以,||||BM AN =||||PB PA ⇔3sin cos 23sin cos 22211+-+-θθθθt t t t=-21t t ⇔2(2cos θ-sin θ)t 1t 2+3(t 1+t 2)=0⇔2(2cos θ-sin θ)(-θ2sin 3)+3⋅2⋅θθθ2sin sin cos 2-=0成立; 以下同例题可证:S 22=4S 1S 3.例5:椭圆中的共线性质.[始源问题]:(2012年北京高考试题)已知曲线C:(5-m)x 2+(m-2)y 2=8(m ∈R).(Ⅰ)若曲线C 是焦点在x 轴点上的椭圆,求m 的取值范围;(Ⅱ)设m=4,曲线C 与y 轴的交点为A,B(点A 位于点B 的上方),直线y=kx+4与曲线C 交于不同的两点M 、N,直线y=1与直线BM 交于点G.求证:A,G,N 三点共线.[解析]:(Ⅰ)由曲线C 是焦点在x 轴点上的椭圆⇔m-2>5-m>0⇔27<m<5.故m 的取值范围是(27,5); (Ⅱ)当m=4时,曲线C:x 2+2y 2=8⇒A(0,2),B(0,-2);设M(x 1,y 1),N(x 2,y 2),由⎩⎨⎧=++=82422y x kx y ⇒(2k 2+1)x 2+16kx+24=0⇒△= 32(2k 2-3)>0⇒k 2>23;且x 1+x 2=-12162+k k ,x 1x 2=12242+k ;又由直线BM:y=112x y +x-2⇒G(2311+y x ,1),即G(6311+kx x ,1)⇒k AG =-1136x kx +=-3k -12x ,k AN =222x y -=222x kx +=k+22x ⇒k AN -k AG =34k +12x +22x =34k +2⋅2121x x xx +=34k +2⋅2416k -=0⇒A,G,N 三点共线.第(Ⅱ)问是本题的特色与亮点,其实质是共轭点的性质:设点P 与Q 是二次曲线G 的一对共轭点,过点Q 的直线AC 与曲线G 相交于A 、C 两点,AP 与曲线G 相交于另一点B,BQ 与曲线G 相交于另一点D,则P 、C 、D 三点共线.其中共轭点的定义:130 第15讲:极点与极线的性质若直线PQ 与圆锥曲线G 相交于A 、B 两点,且PA ⋅QB +PB ⋅QA =0,则称点P 与Q 是圆锥曲线G 的一对共轭点.[原创问题]:已知椭圆C:2222b y a x +=1(a>b>0)过点D(-1,e),其中,e 是椭圆C 的离心率,椭圆C 的左、右顶点分别为A(-2,0)、B(2,0). (Ⅰ)求椭圆C 的方程;(Ⅱ)过点E(4,0)的直线l 与椭圆C 交于M 、N 两点,求证:直线AM 与BN 的交点P 在一条定直线上.[解析]:(Ⅰ)由a=2,21a +22b e =1⇒1+22b c =a 2⇒b 2=1⇒椭圆C:42x +y 2=1; (Ⅱ)设M(x 1,y 1),N(x 2,y 2),直线l:y=k(x-4),由⎩⎨⎧=+-=44)4(22y x x k y ⇒(1+4k 2)x 2-32k 2x+64k 2-4=0⇒x 1+x 2=224132k k +,x 1x 2=2241464k k +- ⇒k 2=)(4322121x x x x +-+,x 1x 2(1+4k 2)=64k 2-4⇒x 1x 2⋅)(8821x x +-=)(8]8)(5[42121x x x x +--+⇒2x 1x 2=5(x 1+x 2)-8;又由直线AM:y=211+x y (x+2),直线BN:y=222-x y (x-2)⇒直线AM 与BN 的交点P 的横坐标x 满足:211+x y (x+2)=222-x y (x-2)⇒2)4(11+-x x k (x+2)= 2)4(22--x x k (x-2)⇒x=83262122121----x x x x x x =83268)(5122121-----+x x x x x x =1⇒点P 在一条定直线x=1上.例6:椭圆中的中点性质.[始源问题]:(2008年全国高中数学联赛湖南初赛试题)如图,过直线l:5x-7y-70=0上的点P 作椭圆252x +92y =1的两条切线PM 、PN,切点分别为M 、N.(Ⅰ)当点P 在直线l 上运动时,证明:直线MN 恒过定点Q; (Ⅱ)当MN ∥l 时,定点Q 平分线段MN.[解析]:(Ⅰ)设P(7t+7,5t-5),则直线MN 的方程为:2577+t x+955-t y=1⇒(257x+95y)t+(257x-95y-1)=0,由257x+95y=0,且257x-95y-1=0⇒x=1425,y=-109⇒直线MN 恒过定点Q(1425,-109); (Ⅱ)MN ∥l ⇔2577+t :955-t =5:(-7)⇔t=53392⇒直线MN 的方程为:5x-7y-35533=0,代入椭圆方程252x +92y =1得:275332⨯x2 -23753325⨯x+25[(275533⨯)2-9]=0,设M(x 1,y 1),N(x 2,y 2),则x 1+x 2=725⇒定点Q 平分线段MN. [原创问题]:过点Q(1,1)作己知直线l:3x+4y=12的平行线交椭圆C:42x +32y =1于点M 、N. (Ⅰ)分别过点M 、N 作椭圆C 的切线l 1、l 2.证明:三条直线l 1、l 2、l 交于一点; (Ⅱ)证明:点Q 是线段MN 的中点;(Ⅲ)设P 为直线l 上一动点,过点P 作椭圆C 的切线PA 、PB,切点分别为A 、B,证明:点Q 在直线AB 上.[解析]:(Ⅰ)设M(x 1,y 1),N(x 2,y 2),切线l 1、l 2交于点P(x 0,y 0),由切线l 1:41x x+31y y=1,切线l 2:42x x+32yy=1均过点P(x 0, y 0)⇒41x x 0+31y y 0=1,42x x 0+32yy 0=1⇒直线MN:40x x+30y y=1;又由直线MN 过点Q(1,1)⇒40x +30y =1⇒3x 0+4y 0=12⇒点P 在直线l 上⇒三条直线l 1、l 2、l 交于一点; (Ⅱ)由直线MN ∥直线l ⇒40x :30y =41:31,又40x +30y =1⇒x 0=y 0=712⇒直线MN:3x+4y=7⇒点Q 是线段MN 的中点; (Ⅲ)设P(x 0,y 0),则直线AB:3x 0x+4y 0y=12⇒3x 0x+(12-3x 0)y=12⇒点Q 在直线AB 上.第15讲:极点与极线的性质 131例7:椭圆中的比例性质.[始源问题]:(2011年山东高考试题)在平面直角坐标系xOy 中,已知椭圆C:32x +y 2=1.如图所示,斜率为k(k>0)且不过原点的直线l 交椭圆C 于A,B 两点,线段AB 的中点为E ,射线OE 交椭圆C 于点G ,交直线x=-3于点D(-3,m). (Ⅰ)求m 2+k 2的最小值; D y (Ⅱ)若|OG|2=|OD||OE|. G A (i)求证:直线l 过定点; E(ii)试问点B,G 能否关于x 轴对称？若能,求出 -3 O x 此时△ABG 的外接圆方程;若不能,请说明理由.[解析]:(Ⅰ)设E(-3λ,m λ),A(-3λ+t,m λ+kt),则B(-3λ-t,m λ-kt).由点A 、B 都在椭圆C 上⇒⎪⎩⎪⎨⎧=-+--=+++-3)(3)3(3)(3)3(2222kt m t kt m t λλλλ,两式相减得mk=1⇒m 2+k 2≥2mk=2,当且仅当m=k=1时等号成立,所以m 2+k 2的最小值=2.(Ⅱ)(i)设直线OG 与椭圆C 相交于另一点T,则由椭圆C 关于原点对称得:|OT|=|OG|.所以,|OG|2=|OD||OE|⇔DT EG ⋅+DG ET ⋅=0,由轨迹1知,点E 在直线-x+my=1上,即直线l 的方程为:-x+my=1⇒直线l 过定点(-1,0);(ii)若点B,G 关于x 轴对称⇒点G(-3λ-t,-m λ+kt),由点G 在直线OE 上⇒(-3λ-t):(-3λ)=(-m λ+kt):m λ⇒6m λ+mt =3kt(注意到mk=1)⇒m 2(6λ+t)=3t ⇒t=2236mm -λ,又由点E 在直线l 上⇒3λ+m 2λ=1⇒λ=231m +⇒B(-233m -,-23m m -)⇒31(233m -)2+(23mm -)2=1⇒m=1,k=1,λ=41,t=43⇒A(0,1),B(-23,-21),G(-23,21)⇒△ABG 的外接圆方程:(x+21)2+y 2=45. [原创问题]:已知椭圆C:2222b y a x +=1(a>b>0)内一点P(2,1),射线OP 与椭圆C 交于点N,与直线l 0:x+y-12=0交于点M,满足|OP||OM|=|ON|2,且椭圆C 在N 处的切线平行于直线l 0. (Ⅰ)求椭圆C 的方程;(Ⅱ)过点P 的任意一条直线l 与直线l 0交于点Q,与椭圆C 交于A 、B 两点(A 在P 与Q 之间),求证:|QA||PB|=|QB||PA|.[解析]:(Ⅰ)由射线OP:y=21x(x ≥0),直线l 0:x+y-12=0⇒M(8,4);设N(2t,t)(t>0),由|OP||OM|=|ON|2⇒5⋅80=4t2+t 2⇒t=2⇒N(4,2)⇒216a+24b=1,椭圆C 在N 处的切线:24ax +22by =1;由切线平行于直线l 0⇒24a=22b⇒a 2=2b 2⇒b 2=12,a2=24⇒椭圆C:242x +122y =1; (Ⅱ)设直线l:⎩⎨⎧+=+=θθsin 1cos 2t y t x (t 为参数),代入242x +122y =1得:(2sin 2θ+cos 2θ)t 2+4(sin θ+cos θ)t-18=0⇒t 1+t 2=-θθθθ22cos sin 2)cos (sin 4++,t 1t 2=-θθ22cos sin 218+;代入x+y-12=0得:(sin θ+cos θ)t-9=0⇒t Q =θθcos sin 9+;而|QA||PB|=|QB||PA|⇔(t Q -t 1)(-t 2)=(t Q -t 2)t 1⇔(t 1+t 2)t Q -2t 1t 2=0⇔-θθθθ22cos sin 2)cos (sin 4++⋅θθcos sin 9+-2(-θθ22cos sin 218+)=0成立. [原创问题]:已知椭圆C:2222b y a x +=1(a>b>0)内一点P(2,1),过点P 且平行于x 轴直线被椭圆C 截得的弦长为46,过点P 且平行于y 轴直线被椭圆C 截得的弦长为210. (Ⅰ)求椭圆C 的方程;(Ⅱ)过点P 的任意一条直线l 与直线l 0:x+y-12=0交于点Q,与椭圆C 交于A 、B 两点,若QA =λAP ,QB =μBP .求证:λ+132 第15讲:极点与极线的性质μ为定值.[解析]:(Ⅰ)由2222by ax +=1,令y=1得:|x|=ba12-b ;令x=2得:|y|=ab 42-a ;由题知,ba 12-b =26,ab 42-a =10⇒a 2=12422-b b ,22a b (a 2-4)=10⇒2412-b (12422-b b -4)=10⇒b 2=12⇒a 2=24⇒椭圆C:242x +122y =1;(Ⅱ)设直线l:⎩⎨⎧+=+=θθsin 1cos 2t y t x (t 为参数),代入242x +122y =1得:(2sin 2θ+cos 2θ)t 2+4(sin θ+cos θ)t-18=0⇒t 1+t 2=-11 θθθθ22cos sin 2)cos (sin 4++,t 1t 2=-θθ22cos sin 218+;代入x+y-12=0得:(sin θ+cos θ)t-9=0⇒t Q =θθcos sin 9+;由QA =λAP ,QB =μBP ⇒λ=11t t t Q -,μ=22t t t Q -⇒λ+μ=2-t Q ⋅2121t t t t +=2-θθcos sin 9+⋅9)cos (sin 2θθ+=0. 例8:椭圆中的共线性质.[始源问题]:(2002年澳大利亚数学奥林匹克试题)己知△ABC 为锐角三角形, R以AB 为直径的⊙K 分别交AC 、BC 于P 、Q,分别过A 和Q 作⊙K 的两条切线交 C于点R,分别过B 和P 作⊙K 的两条切线交于点S.证明:点C 在线段RS 上. P Q S[解析]:设⊙K:x 2+y 2=r 2,R(-r,a),S(r,b)⇒点R,S 对应的极线分别为:AQ:-rx+ay=r 2,BP:rx+by=r 2⇒Q(2222)(r a rr a +-,2222r a ar +),P(-2222)(r b rr b +-,2222r b br +) A K B⇒AP:y=r b (x+r),BQ:y=-r a (x-r),由⎪⎪⎩⎪⎪⎨⎧+=--=)()(r x r b y r x r a y ⇒⎪⎪⎩⎪⎪⎨⎧+=+-=b a ab y r b a b a x 2⇒C(b a b a +-r,b a ab +2) ⇒点C 对应的极线为:(a-b)rx+2aby=(a+b)r 2,由三线:-rx+ay=r 2,BP:rx+by=r 2,(a-b)rx+2aby=(a+b)r 2共点于(b a b a +-r, ba r +22)⇒R,C,S 三点共线⇒点C 在线段RS 上. 该题是平面几何定理:“过非等腰三角形的三个顶点作其外接圆的切线,顶点处的切线与其对边所在直线的交点共线.”的变形,以该定理为始源,取其特殊情况,并把圆压缩为椭圆得:[原创问题]:若对任意θ∈[0,2π),直线l:xcos θ+2ysin θ-2=0与椭圆C:2222b y a x +=1(a>b>0)均只有一个交点M. (Ⅰ)求椭圆C 的方程;(Ⅱ)当θ∈(0,2π)时,若直线l 与x 轴交于点N,椭圆C 的左、右顶点分别为A 、B,直线BM 上的点Q 满足QA ⊥x 轴,直线AM 与NQ 交于点P,求点P 的轨迹方程.[解析]:(Ⅰ)由⎩⎨⎧=-+=-+002sin 2cos 222222b a y a x b y x θθ⇒(a 2cos 2θ+4b 2sin 2θ)y 2-8b 2ysin θ+4b 2-a 2b 2cos 2θ=0⇒△=64b 4sin 2θ-4(a 2cos 2θ +4b 2sin 2θ)(4b 2-a 2b 2cos 2θ)=0⇒a 2-4+(4b 2-a 2)sin 2θ=0恒成立⇒a 2-4=0,4b 2-a 2=0⇒a 2=4,b 2=1⇒椭圆C:42x +y 2=1; (Ⅱ)由xcos θ+2ysin θ-2=0⇒N(θcos 2,0);(Ⅰ)知,M(2cos θ,sin θ)⇒直线AM:y=2cos 2sin +θθ(x+2),BM:y=2cos 2sin -θθ(x-2) ⇒Q(-2,θθcos 1sin 2-)⇒直线NQ:y=-cot θ(x-θcos 2);令2cos 2sin +θθ(x+2)=-cot θ(x-θcos 2)⇒(2cos 2sin +θθ+θθcos sin )x=θsin 2-1cos sin +θθ ⇒x=2⇒点P 的轨迹方程x=2(0<y<2).。
微专题二圆与圆锥曲线中的二级结论
圆与圆锥曲线中的二级结论一、极点极线：设点00(,)P x y 是平面上任意一点，点00(,)P x y 对应的极线为l ①圆222()(),x a y b r -+-= 极线200:()()()()l x a x a y b y b r --+--= ②椭圆22221x y a b +=，极线0022:1x x y y l a b +=③双曲线22221x y a b-=，极线0022:1x x y y l a b -=④抛物线22y px =，极线00:()l y y p x x =+（其余三种类推）性质：（Ⅰ）点P 在曲线上，则在点P 处的切线即为极线l（Ⅱ）点P 在曲线外，则极线l 为过点P 处作曲线的两条切线的切点弦所在的直线方程 （Ⅲ）点P 在曲线内，则极线l 为过点P 的割线两端点处的切线交点的轨迹例1、（2020年全国Ⅰ）已知22:2220,M x y x y +---=直线:220,l x y ++=P 为l 上的动点。
过点P 作M 的切线,,PA PB 切点为,A B ，当PM AB ⋅最小时，直线AB 的方程为A 、210x y --=B 、210x y +-=C 、210x y -+=D 、210x y ++=【分析】22:(1)(1)4M x y -+-=，由等面积关系可得PM AB ⋅=显然当PM 最小时即PM l ⊥时，PM AB ⋅最小，此时PM 方程为210x y -+=，由210(1,0)220x y P x y -+=⎧⇒-⎨++=⎩则AB 的方程为21x y ++跟踪训练：在平面直角坐标系xOy 中，过点(1,4)P 向圆222:()5(16)C x m y m m -+=+<<引两条切线，切点分别为,A B ，则直线AB 过定点A 、1(,1)2-B 、3(1,)2-C 、13(,)22-D 、1(1,)2-例2、（2020海南名校联考）过点(1,1)H -作抛物线24x y =的两条切线,,HA HB 切点分别为,A B ，则直线AB 的方程为A 、220x y -+=B 、220x y --=C 、220x y +-=D 、220x y -+= 【分析】 由极点极线可得AB 的方程为12(1)x y ⋅=-即220x y -+=跟踪训练：已知F 为抛物线22y x =的焦点，A 为抛物线上的动点，点1(,0)2B -，当AB AF 取得最大值时，AB 的值为A 、2BCD 、1PM ABBA PQ 二、抛物线中的二级结论 1、2、抛物线中的阿基米德三角形则0PA PB ⋅=⇔直线AB图1图2例3、设F 为抛物线24y x =的焦点，,A B 为抛物线上两点，若20,FA FB += 则2FA FB += 【分析】由 20,FA FB +=得,,F A B 三点共线，且2FA FB = 则24FA FB FB +=，由11232BF BF AF p +=⇒=，所以26FA FB += 跟踪训练：（2020衡阳一模）已知抛物线2:4C y x =的焦点为F ，过F 的直线与C 交于,A B 两点，且线段AB 中点的纵坐标为2，O 为坐标原点，则AOB ∆的面积为 例4、（2018全国Ⅲ）已知点(1,1)M -和抛物线2:4,C y x =过C 的焦点且斜率为k 的直线与C 交于,A B 两点。
可以讲讲圆曲里的极点和极线相关问题和定理推导吗？
圆曲线是一种特殊的二次曲线，它具有很多独特的性质和定理。
其中，极点和极线是圆曲线中最重要的概念之一。
极点和极线是描述圆曲线上的点和直线之间的关系的数学工具。
我们将深入探讨圆曲线中的极点和极线相关问题和定理推导。
一、极点和极线的定义极点是圆曲线上的一个点，它具有一个特殊的性质：如果通过这个点画一条直线，那么这条直线和圆曲线的交点将是一对共轭点。
换句话说，极点是圆曲线上的一个点，它与圆曲线上的每个点都有一对共轭点。
极线是圆曲线上的一条直线，它具有一个特殊的性质：如果通过这条直线画一条过圆曲线上的任意一点的直线，那么这条直线和极线的交点将是一对共轭点。
换句话说，极线是圆曲线上的一条直线，它与圆曲线上的每个点都有一对共轭点。
二、极点和极线的性质1、极点和极线是一一对应的。
也就是说，圆曲线上的每个点都对应着一条唯一的极线，而圆曲线上的每条直线都对应着一个唯一的极点。
2、圆曲线上的任意两个点的共轭点都在同一条直线上。
这条直线就是它们的极线。
3、圆曲线上的任意两条直线的交点都在同一个点上。
这个点就是它们的极点。
4、圆曲线上的任意一点和它的极线上的任意一点都是共轭点。
5、圆曲线上的任意一条直线和它的极点上的任意一点都是共轭点。
三、极点和极线的定理1、极点定理对于圆曲线上的任意一条直线L和任意一点P，如果P不在L上，那么P在L上的投影点P'是P关于L的极点。
证明：设P关于L的投影点为P'，那么P和P'是共轭点。
P'在圆曲线上的任意一条直线L'上的投影点P''是P'关于L'的极点。
又因为P'在L上，所以P''在L'上。
P''是P关于L'的投影点。
由于P和P'是共轭点，所以P'是P关于L的极点。
2、极线定理对于圆曲线上的任意一点P和任意一条直线L，如果P不在L上，那么L是P关于圆曲线的极线。
高考数学总复习考点知识专题讲解18 极点与极线探秘
高考数学总复习考点知识专题讲解专题18极点与极线探秘极点与极线是高等几何中的重要概念，虽然不是《高中数学课程标准》规定的学习内容，也不属于高考考查的范围，但由于极点与极线是圆锥曲线的一种基本特征，因此在高考试题中必然会有所反映，自然也会成为高考试题的命题背景．由于极点极线内容较多，本文也难以全部介绍，故根据近年高考和一些常见模考题作为背景来阐述重点，更多的极点极线内容，欢迎大家去参考本人编写的2024版《高中数学新思路——圆锥曲线高考数学总复习考点知识专题讲解 专题》书.知识点一极点和极线的定义和性质 在圆锥曲线方程中，以x x 0替换2x ，以20xx +替换x ，以0y y 替换2y ，以02y y +替换y ，即可得到点),(00y x P 的极线方程．已知圆锥曲线22:220Ax Cy Dx Ey F Γ++++=，则称点00(,)P x y 和直线0000:()()0l Ax x Cy y D x x E y y F ++++++=是圆锥曲线Γ的一对极点和极线．从定义我们共同思考和讨论几个问题:1．若点),(00y x P 在椭圆上，则其对应的极线是什么?椭圆的两个焦点对应的极线分别是什么?（1）对于椭圆()b a b y a x ≠=+12222，与点),(00y x P 对应的极线方程为12020=+byy a x x ；当),(00y x P 为其焦点)0,(c F 时，极线12020=+b y y ax x 变成ca x 2=，恰是椭圆的右准线． （2）对于双曲线12222=-b y a x ，与点),(00y x P 对应的极线方程为12020=-byy a x x ；当),(00y x P 为其焦点)0,(c F 时，极线12020=-b y y ax x 变成ca x 2=，恰是双曲线的右准线． （3）对于抛物线22px y =，与点),(00y x P 对应的极线方程为)(00x x p y y +=．当),(00y x P 为其焦点)0,2(p F 时，极线)(00x x p y y +=变为2px -=，恰为抛物线的准线． 2．过椭圆上（外、内）任意一点),(00y x P ，如何作出相应的极线？ （1）当点P 在圆锥曲线Γ上时，其极线是曲线Γ在点P 点处的切线；（2）当点P 在Γ外时，其极线l 是曲线Γ从点P 所引两条切线的切点所确定的直线（即切点弦所在的直线）；（3）当点P 在Γ内时，其极线l 是曲线Γ过点P 的任一割线两端点处的切线交点的轨迹． 为了表达方便，我们给出圆锥曲线内部和外部的定义．圆、椭圆是封闭图形其内部和外部很好界定，抛物线、双曲线不是封闭的是开的，对双曲线和抛物线的内部和外部给出如下定义：焦点所在的平面区域称为该曲线的内部，不含焦点的平面区域称为曲线的外部，曲线上的点既不在内部也不在外部．注意：证明书写过程请参考上一讲《抛物线切线与阿基米德三角形》中的“导、同、差、代”即可，这里不作详述．知识点二极点与极线的作图（几何意义）如图1，设P 是不在圆锥曲线上的一点，过P 点引两条割线依次交圆锥曲线于四点,,,E F G H ，连接,EH FG 交于N ，连接,EG FH 交于M ，则直线MN 为点P 对应的极线．若P 为圆锥曲线上的点，则过P 点的切线即为极线．由图1同理可知，PM 为点N 对应的极线，PN 为点M 所对应的极线．因而将MNP 称为自极三角形．设直线MN 交圆锥曲线于点,A B 两点，则,PA PB 恰为圆锥曲线的两条切线．图1 图2如图2，设点P关于圆锥曲线Γ的极线为l，过点P任作一割线交Γ于,A B，交l于Q，则PA PB=①；反之，若有①成立，则称点,P Q调和分割线段AB，或称点P与Q关于ΓAQ BQ调和共轭，或称点P(或点Q)关于圆锥曲线Γ的调和共轭点为点Q(或点P)．点P关于圆锥曲线Γ的调和共轭点是一条直线，这条直线就是点P的极线．注意：关于分割和调和分割问题，在《秒1》的定比点差法破解极点与极线中有阐述，可以参考．图3配极原则：点P关于圆锥曲线Γ的极线p过点⇔Q点Q关于Γ的极线q经过点P；直线p 关于Γ的极点P在直线q上⇔直线q关于Γ的极点Q在直线p．由此可知，共线点的极线必共点；共点线的极点必共线．极点极线垂直定理:如图3，设圆锥曲线Γ的一个焦点为F，与F相应的准线为l．（1）若过点F的直线与圆锥曲线Γ相交于NM,两点处的切线的M,两点，则Γ在N交点Q在准线l上，且MNFQ⊥；（2）若过准线l 上一点Q 作圆锥曲线Γ的两条切线，切点分别为N M ,，则直线MN 过焦点F ，且MN FQ ⊥；（3）若过焦点F 的直线与圆锥曲线Γ相交于N M ,两点，过F 作MN FQ ⊥交准线l 于Q ，则连线QN QM ,是圆锥曲线Γ的两条切线．知识点三切线方程和切点弦方程求法的书写过程我们尝试来求椭圆12222=+by a x 上一点)(00y x P ，处的切线方程，法一(参数换元+判别式)：令⎩⎨⎧==θθsin cos 00b y a x ，过点)(00y x P ，的切线方程为)cos (sin θθa x k b y -=-，代入椭圆方程联立得：-+-++θθθsin [()cos sin (2)(222222b a x ak b k a x b a k 0])cos 22=-b ak θ0])cos sin ([4222222=--+=∆θθak b b a k b a ，所以0)cos sin (2=+θθb ka ，所以θθsin cos a b k -=， 所以)cos (sin cos sin θθθθa x a b b y --=-，所以ab b x a y =⋅+⋅θθcos sin ，即12020=+byya xx ． 注意：如果是证明切线方程为12020=+b yy a xx ，那么可以将⎪⎪⎩⎪⎪⎨⎧=+=+1120202222b yy a xx b y a x ，联立方程消除y ，计算判别式为0．法二（分类求导）当点)(00y x P ，位于第一或第二象限时，221ax b y -=，求导得22222211122ax a bx a x a xb y k -⋅-=--⋅='=，当0x x =时，b y a x 02201=-，故0202y a x b k -=，代入切线方程)(00x x k y y -=-得：12020=+b yy a xx ；当点),(00y x P 位于第三或第四象限时，221a x b y --=，求导得=--⋅-='=222122a x a x b y k22211a x a bx-⋅，当0x x =时，b y a x 0221-=-，故0202y a x b k -=，代入切线方程)(00x x k y y -=-得：12020=+b yy a xx ．注意：如果按照隐函数求导，那么可以一次性解决切线方程问题，但是现行高考政策下，以上两种方法最为保险．我们再来看看切点弦方程，过点)(00y x P ，作椭圆的两条切线PA 和PB ，则切点弦AB 的方程为：12020=+b yy a xx ．【证明】法一（点差法）令),(11y x A ，),(22y x B ，根据其切线方程可知⎪⎪⎩⎪⎪⎨⎧=+=+1:1:22222121b yy a xx l byy a xx l PB PA 由于点)(00y x P ，均在两直线上，故满足⎪⎪⎩⎪⎪⎨⎧=+=+②①11220220210210b y y a x x by y a x x ，①－②得：0)()(22102210=-+-b y y y a x x x ，即0202y a x b k AB -=，再代入AB 的方程)(11x x k y y AB -=-得：0120120202x x b y y a xx b yy a +=+，同除以22b a 得：12012012020=+=+by y ax x byy axx ，故切点弦AB 的方程为：12020=+b yy a xx ．法二（同构方程）点)(11y x A ，满足方程1210210=+by y ax x ，点)(22y x B ，也满足方程1220220=+b y y a x x ，故A 、B 均在同构方程12020=+b y y a x x 上，根据两点确定一直线方程原理，则AB 方程为：12020=+b yy a xx ．显然，选择同构方程的证法更能体现圆锥曲线的本质，两点确定一直线，两根确定一二次方程，就是二次方程的核心思想。
蝴蝶定理证极点极线
蝴蝶定理证极点极线1. 蝴蝶定理内容。
- 设M为圆内弦PQ的中点，过M作弦AB和CD。
设AD和BC分别交PQ 于点X和Y，则M是XY的中点。
- 设圆O的方程为x^2+y^2=r^2，点P(x_0,y_0)关于圆O的极线方程为xx_0+yy_0=r^2。
- 过点P作两条相交弦AB、CD，设AB与极线xx_0+yy_0=r^2的交点为M，CD与极线的交点为N。
- 设A(x_1,y_1)，B(x_2,y_2)，C(x_3,y_3)，D(x_4,y_4)。
- 由圆的方程与直线AB（设直线AB的方程为y = k_1(x - x_0)+y_0）联立可得x^2+[k_1(x - x_0)+y_0]^2=r^2。
- 展开并整理得(1 + k_1^2)x^2+2k_1(y_0-k_1x_0)x+(y_0-k_1x_0)^2-r^2=0。
- 根据韦达定理，x_1+x_2=-frac{2k_1(y_0-k_1x_0)}{1 + k_1^2}。
- 同理对于直线CD（设直线CD的方程为y = k_2(x - x_0)+y_0）与圆联立也可得到类似韦达定理的结果。
- 设AD与BC相交于点Q。
- 根据蝴蝶定理的结构，把圆中的相关线段和交点对应起来。
- 设AD的方程为y - y_1=frac{y_4-y_1}{x_4-x_1}(x - x_1)，BC的方程为y - y_2=frac{y_3-y_2}{x_3-x_2}(x - x_2)。
- 联立AD与BC的方程求出交点Q的坐标（过程较为复杂，涉及大量的代数运算）。
- 然后分别求出A、B、C、D到极线xx_0+yy_0=r^2的距离d_1、d_2、d_3、d_4（根据点到直线距离公式d=(| Ax + By+C|)/(√(A^2)+B^{2)}）。
- 通过一系列的比例关系和蝴蝶定理中的等量关系（如(XM)/(MY)=(XA·XB)/(YC· YD)等，这里X、Y是相关线段与极线的交点）。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
圆内极点与极线性质简证
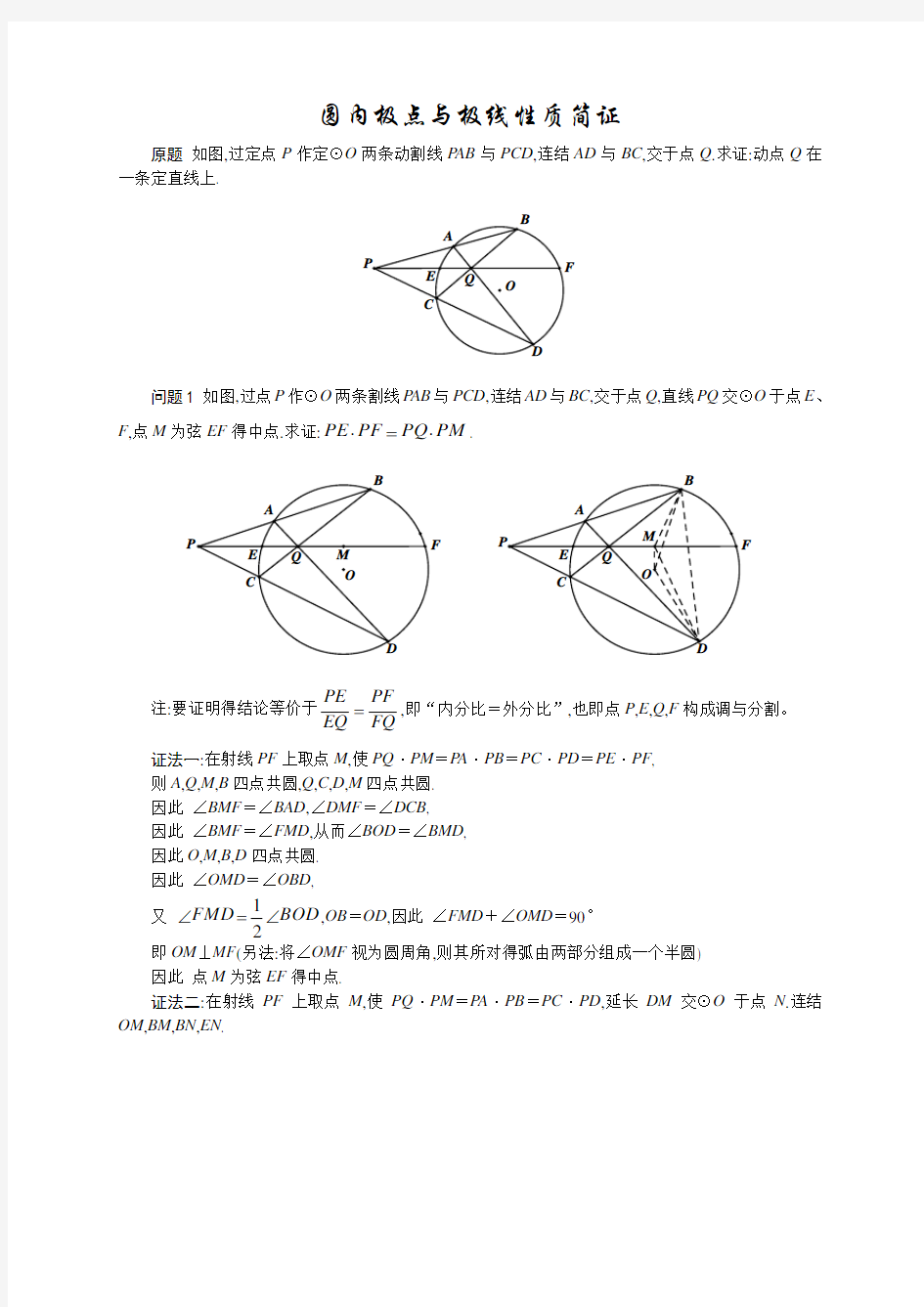
原题 如图,过定点P 作定⊙O 两条动割线P AB 与PCD ,连结AD 与BC ,交于点Q .求证:动点Q 在一条定直线上.
问题1 如图,过点P 作⊙O 两条割线P AB 与PCD ,连结AD 与BC ,交于点Q ,直线PQ 交⊙O 于点E 、F ,点M 为弦EF 得中点.求证:PM PQ PF PE ⋅=⋅.
注:要证明得结论等价于
FQ
PF
EQ PE =,即“内分比＝外分比”,也即点P ,E ,Q ,F 构成调与分割。
证法一:在射线PF 上取点M ,使PQ ·PM ＝P A ·PB ＝PC ·PD ＝PE ·PF , 则A ,Q ,M ,B 四点共圆,Q ,C ,D ,M 四点共圆. 因此 ∠BMF ＝∠BAD ,∠DMF ＝∠DCB ,
因此 ∠BMF ＝∠FMD ,从而∠BOD ＝∠BMD , 因此O ,M ,B ,D 四点共圆. 因此 ∠OMD ＝∠OBD , 又 BOD FMD ∠=
∠2
1
,OB ＝OD ,因此 ∠FMD ＋∠OMD ＝90° 即OM ⊥MF (另法:将∠OMF 视为圆周角,则其所对得弧由两部分组成一个半圆) 因此 点M 为弦EF 得中点.
证法二:在射线PF 上取点M ,使PQ ·PM ＝P A ·PB ＝PC ·PD ,延长DM 交⊙O 于点N .连结OM ,BM ,BN ,EN .
由于 C ,Q ,M ,D 四点共圆,Q ,A ,B ,M 四点共圆.
因此 ∠BQF ＝∠NDC ＝∠NBC 因此 NB ∥EF 因此 NE ＝BF ,∠NEF ＝∠BFE
又 ∠NME ＝∠BCD ＝∠BAD ＝∠BMF 因此 △NME ≌△BMF (AAS ) 因此 EM ＝FM ,下略.
证法三:这题可以用“面积正弦法”解决,您可以随便找三角形来构成正弦比
.
QA PA
DE BE QA PA QAE PAE S S EQ PE QAE PAE ⋅=⋅∠∠==∆∆sin sin QA
PA
DF BF QA PA QAF PAF S S FQ PF QAF PAF ⋅=⋅∠∠==∆∆sin sin 因此只要证明
DF
BF
DE BE =
,这可以由下面得推导得到: DF
BF
AE CE CD AB AE CE QC QA AE CE DPE BPE DE PE PE BE DE BE =⋅=⋅=⋅∠∠=⋅=sin sin (由∠BAD ＝∠BCD 得∠P AQ ＝∠PCQ ) 从而得证.
证法四:设直线PQ 为
x 轴,直线AB ,CD ,AD ,BC 方程为
0),(1=y x f ,0),(2=y x f ,0),(3=y x f ,0),(4=y x f ;P (p ,0),Q (q ,0),E (e ,0),F (f ,0)、
(f ,0)
P (
则圆O 可表为0),(),(),(),(4321=⋅⋅+⋅⋅y x f y x f y x f y x f μλ、其中λ,μ就是待定参数、 令y = 0,得到0)0,()0,()0,()0,(4321=⋅⋅+⋅⋅x f x f x f x f μλ(*) 两根为e ,f , 注意到一次方程0)0,(1=x f ,0)0,(2=x f 得解均为x = p , 故2
121)()0,()0,(p x k x f x f -=⋅ (1k 为待定系数)、
同理2
243)()0,()0,(q x k x f x f -=⋅ (2k 为待定系数)、
(*)可变为0)()(2
221=-⋅⋅+-⋅⋅q x k p x k μλ、
将x ＝ e ,f 带入上式,消去待定系数,得到2
2
22)
()()()(q f p f q e p e --=-- 故
FQ
FP
EQ EP =、 上述证明本质上证明了射影几何中得Desargues 对合定理,但就是并没有动用射影几何得概念,仅仅用了高中平面解析几何得二次曲线系与初中二次函数两点式理论,可以说就是初等得、
推广:
如图,点P 在⊙O 外,P AB 、PCD 、PEF 为⊙O 得三条割线,A 、B 、C 、D 、E 、F 为割线与⊙O 得交点,割线PEF 交AD 、BC 于点S 、T .求证:
PT
PS PF PE 1
111+
=+.
N
证法一:分别过点A 、C 作割线PEF 得平行线,交⊙O 于点L 、N ,连结AN 、CL ,分别交PF 于X 、
Y .取EF 得中点M ,连结OM ,则OM ⊥PF .
∵ ∠B ＝∠L ＝∠PXA ∴ A 、B 、X 、T 四点共圆
∴ PX ·PT ＝P A ·PB ＝PE ·PF ∴ PX
PF
PE PT ⋅= 同理,∠PYC ＝∠LCN ＝∠D ∴ C 、D 、Y 、S 四点共圆
∴ PY ·PS ＝PC ·PD ＝PE ·PF ∴ PY
PF
PE PS ⋅=
∴ PF
PE PF PE PF PE PF PE PM PF PE PY PX PT PS 11211+
=⋅+=⋅=⋅+=+ 注:当点S 与点T 重合为点Q 时,点X 与点Y 则重合为中点M . 证法二:设割线PEF 为x 轴,直线
AB ,CD ,AD ,BC
方程为
0),(1=y x f ,0),(2=y x f ,0),(3=y x f ,0),(4=y x f ;P (p ,0),E (e ,0),F (f ,0) ,S (s ,0) ,T (t ,0)、
P (p (f ,0)
则圆O 可表为0),(),(),(),(4321=⋅⋅+⋅⋅y x f y x f y x f y x f μλ、其中λ,μ就是待定参数、 令y = 0,得到0)0,()0,()0,()0,(4321=⋅⋅+⋅⋅x f x f x f x f μλ(*) 两根为e ,f , 注意到一次方程0)0,(1=x f ,0)0,(2=x f 得解均为x = p , 故2
121)()0,()0,(p x k x f x f -=⋅ (1k 为待定系数)、
而一次方程0)0,(3=x f ,0)0,(4=x f 得解分别为x = s 与x = t . 故))(()0,()0,(243t x s x k x f x f --=⋅ (2k 为待定系数)、 (*)可变为0))(()(22
1=--⋅⋅+-⋅⋅t x s x k p x k μλ、
将x ＝ e ,f 带入上式,消去待定系数,得到)
)(()
)(()()(22t f s f t e s e p f p e ----=
-- 即 FT FS ET
ES PF
PE ⋅⋅=2
2,由此得 ))(())((22PT PF PS PF PE PT PE PS PF PE ----=,
整理得
PT
PS PF PE 1
111+
=+、 问题2 如图,过定点P 得动直线交定⊙O 于点E 、F ,点M 为弦EF 得中点,求证:满足PE ·PF ＝PQ ·PM 得动点Q 在一条定直线上.
证明:如图,作直线OP ,交⊙O 于点E '、F ',取点H 使PO PH F P E P ⋅='⋅'.连结OM .
因为 F P E P PF PE '⋅'=⋅, 所以 PO PH PM PQ ⋅=⋅.
因此 Q ,H ,O ,M 四点共圆,从而 QH ⊥OP .
下面证明点H 为定点.设⊙O 得半径为R ,由PO PH F P E P ⋅='⋅'得,
OP OH OP R OP R OP ⋅-=+⋅-)()()(,整理得 2R OH OP =⋅,因此点P 为定点.
故动点Q 得轨迹为过定点H 且与OP 垂直得直线.
当直线PEF 成为⊙O 得切线时,点E 与F 重合为切点,因此定直线QH 为切点弦所在得直线.。