高等光学教程-第4章参考答案
物理光学教程第四章题目详解
4.4 波长为 546nm 的绿光垂直照射缝宽为 1mm 的狭缝，在狭缝后面放置一个焦距为 1m 的 透镜，将衍射光聚集在透镜后焦面的观察屏。试求：
(1) 衍射图形中央亮斑的宽度和角宽度； (2) 衍射图形中央两侧 2mm 处的辐照度与中央辐照度的比值。
答案： (1)
L x L0sin c2
2
9 56.25% 16
（3）图(b)圆环 L环 0, 0 R12 R22 2 9 56.25%
L孔 0, 0
R14
16
问题：有人应用 Babinet 原理，有必要吗？
补充题一：利用单缝夫琅和费衍射原理，可以在线检测拉丝机生产的金属细 丝的直径误差。（1） 自行设计检测装置，画出原理示意图；说明其工作原 理及装置构造。
4.14 光谱范围为 400~700nm 的可见光经光栅衍射后被展成光谱。 (1) 若光栅常数 d=2μm，试求一级光谱的衍射角范围； (2) 欲使一级光谱的线范围为 50mm，试问应选用多大焦距的透镜？ (3) 问可见光的一级与二级光谱、二级与三级光谱会不会重叠？
答案：（1）应用 1 级光栅方程： sin1 d 一级衍射角11.50 1 20.50 ， 90
（2） f 293.37mm
（3）同样应用
2
级和
3
级光栅方程： sin
m
d
m
2,3 ，求出短波
（400nm）的 2、3 级衍射角和长波（700nm）的 1、2 级衍射角，可知：
1－2 级光谱不重叠，2－3 级光谱重叠。
4.15 用宽度为 50mm，每毫米有 500 条刻线的光栅分析汞光谱。已知汞的谱线有：λ1=404.7nm， λ2=435.8nm，λ3=491.6，λ4=546.1nm，λ5=577nm，λ6=579nm 等，假设照明光正入射。 (1) 试求一级光谱中上述各谱线的角距离；（2）试求一级光谱中汞绿线(λ4)附近的角色散； (2) 用此光栅能否分辨一级光谱的两条汞黄线(λ5，λ6)？ (3) 用此光栅最多能观察到 λ6 的几级光谱？
《光学教程》课后习题解答
对 的第三个次最大位
即：
9、波长为的平行光垂直地射在宽的缝上，若将焦距为的透镜紧贴于缝的后面，并使光聚焦到屏上，问衍射图样的中央到⑴第一最小值；⑵第一最大值；⑶第三最小值的距离分别为多少？
解：⑴第一最小值的方位角为：
⑵第一最大值的方位角为：
⑶第3最小值的方位角为：
10、钠光通过宽的狭缝后，投射到与缝相距的照相底片上。所得的第一最小值与第二最小值间的距离为，问钠光的波长为多少？若改用X射线（）做此实验，问底片上这两个最小值之间的距离是多少？
解：
⑴
⑵级光谱对应的衍射角为：
即在单缝图样中央宽度内能看到条（级）光谱
⑶由多缝干涉最小值位置决定公式：
第3xx 几何光学的基本原理
1、证明反射定律符合费马原理
证明：
设A点坐标为，B点坐标为
入射点C的坐标为
光程ACB为：
令
即：
*2、根据费马原理可以导出近轴光线条件下，从物点发出并会聚到像点的所有光线的光程都相等。由此导出薄透镜的物像公式。
另一个气泡
， 即气泡离球心
13、直径为的球形鱼缸的中心处有一条小鱼，若玻璃缸壁的影响可忽略不计，求缸外观察者所看到的小鱼的表观位置和横向放大率。
解：由球面折射成像公式：
解得 ，在原处
14、玻璃棒一端成半球形，其曲率半径为。将它水平地浸入折射率为的水中，沿着棒的轴线离球面顶点处的水中有一物体，利用计算和作图法求像的位置及横向放大率，并作光路图。
解：
由球面折射成像公式：
15、有两块玻璃薄透镜的两表面均各为凸球面及凹球面，其曲率半径为。一物点在主轴上距镜处，若物和镜均浸入水中，分别用作图法和计算法求像点的位置。设玻璃的折射率为，水的折射率为。
光学教程课后习题答案
光学教程课后习题答案光学教程课后习题答案光学作为物理学的一个重要分支，研究光的传播、反射、折射、干涉、衍射等现象，是一门既有理论基础又有实践应用的学科。
在学习光学的过程中，课后习题是巩固知识、提高理解能力的重要环节。
下面我将为大家提供一些光学教程课后习题的答案，希望对大家的学习有所帮助。
1. 什么是光的折射？折射定律是什么？光的折射是指光线从一种介质传播到另一种介质时，由于介质的光密度不同，光线的传播方向发生改变的现象。
折射定律是描述光的折射现象的基本规律，它可以用一个简单的数学公式表示：n₁sinθ₁ = n₂sinθ₂，其中n₁和n₂分别表示两种介质的折射率，θ₁和θ₂分别表示光线在两种介质中的入射角和折射角。
2. 什么是光的干涉？干涉定律是什么？光的干涉是指两束或多束光线相遇时产生的明暗交替的干涉条纹的现象。
干涉定律是描述光的干涉现象的基本规律，它可以用一个简单的数学公式表示：d·sinθ = mλ，其中d表示两个光源之间的距离，θ表示干涉条纹的倾斜角，m 表示干涉条纹的序数，λ表示光的波长。
3. 什么是光的衍射？衍射定律是什么？光的衍射是指光通过一个孔或绕过一个障碍物后，发生偏折和扩散的现象。
衍射定律是描述光的衍射现象的基本规律，它可以用一个简单的数学公式表示：a·sinθ = mλ，其中a表示衍射孔的尺寸，θ表示衍射角，m表示衍射条纹的序数，λ表示光的波长。
4. 什么是光的反射？反射定律是什么？光的反射是指光线从一种介质射向另一种介质的界面时，由于介质的光密度不同，光线发生改变方向的现象。
反射定律是描述光的反射现象的基本规律，它可以用一个简单的数学公式表示：θ₁ = θ₂，其中θ₁和θ₂分别表示光线在入射介质和反射介质中的入射角和反射角。
5. 什么是光的色散？色散定律是什么？光的色散是指光通过一个介质时，由于介质的折射率与波长有关，不同波长的光线被折射的角度不同，从而产生彩虹色的现象。
《光学教程》（姚启钧）课后习题解答
《光学教程》（姚启钧）课后习题解答《光学教程》（姚启钧）课后习题解答 - 百度文库《光学教程》（姚启钧）习题解答第一章光的干涉1 、波长为的绿光投射在间距为的双缝上，在距离处的光屏上形成干涉条纹，求两个亮条纹之间的距离。
若改用波长为的红光投射到此双缝上，两个亮纹之间的距离为多少？算出这两种光第2 级亮纹位置的距离。
解：改用两种光第二级亮纹位置的距离为：2 、在杨氏实验装置中，光源波长为，两狭缝间距为，光屏离狭缝的距离为，试求：⑴光屏上第1 亮条纹和中央亮纹之间的距离；⑵若 P 点离中央亮纹为问两束光在 P 点的相位差是多少？⑶求 P 点的光强度和中央点的强度之比。
解：⑴⑵由光程差公式⑶中央点强度：P 点光强为：3 、把折射率为的玻璃片插入杨氏实验的一束光路中，光屏上原来第5 级亮条纹所在的位置变为中央亮条纹，试求插入的玻璃片的厚度。
已知光波长为解：，设玻璃片的厚度为由玻璃片引起的附加光程差为：4 、波长为的单色平行光射在间距为的双缝上。
通过其中一个缝的能量为另一个的倍，在离狭缝的光屏上形成干涉图样，求干涉条纹间距和条纹的可见度。
解：由干涉条纹可见度定义：由题意，设，即代入上式得5 、波长为的光源与菲涅耳双镜的相交棱之间距离为，棱到光屏间的距离为，若所得干涉条纹中相邻亮条纹的间隔为，求双镜平面之间的夹角。
解：由菲涅耳双镜干涉条纹间距公式6 、在题1.6 图所示的劳埃德镜实验中，光源S 到观察屏的距离为，到劳埃德镜面的垂直距离为。
劳埃德镜长，置于光源和屏之间的中央。
⑴若光波波长，问条纹间距是多少？⑵确定屏上可以看见条纹的区域大小，此区域内共有几条条纹？（提示：产生干涉的区域 P 1 P 2 可由图中的几何关系求得）解：由图示可知：①②在观察屏上可以看见条纹的区域为 P 1 P 2 间即，离屏中央上方的范围内可看见条纹。
7 、试求能产生红光（）的二级反射干涉条纹的肥皂膜厚度。
已知肥皂膜折射率为，且平行光与法向成 30 0 角入射。
光学教程第二版习题答案(一至七章)
∴ d1
=
h1 − h2 tan u1′
= 1.5 −1 0.015
= 33.33mm
tan u2 ′ = tan u2
+
h2 f 2′
= 0.015 +
1 = 0.011
− 250
∴d2
=
h2 − h3 tan u2 ′
1 − 0.9 =
0.011
= 9.091mm
2－13 一球形透镜，直径为 40mm，折射率为 1.5，求其焦距和主点位置。
= −200mm
lH
= dϕ2 ϕ
= 50 × 5 = −100mm − 2.5
2－11
有三个透镜，
f1′
= 100mm，
f2′
= 50mm，
f
′
3
=
−50mm，其间隔 d1
= 10mm，
d 2 = 10mm ，设该系统处于空气中，求组合系统的像方焦距。
解：设 h1 = 100mm， u1 = 0 ，则：
tan u3′
= tan u3 +
h3 f3′
= 2.8 +
62 − 50
= 1.56
∴组合系统的像方焦距为：
f
′=
h1 tan u3′
100 =
1.56
= 64.1mm
2－12
一个三 片型望远镜 系统，已知
f
′
1
= 100mm，
f
′
2
=
−250mm ，
f
′
3
= 800mm，入
射平行光在三个透镜上的高度分别为： h1 = 1.5mm， h2 = 1mm ， h3 = 0.9mm ，试求合成
高等光学4章
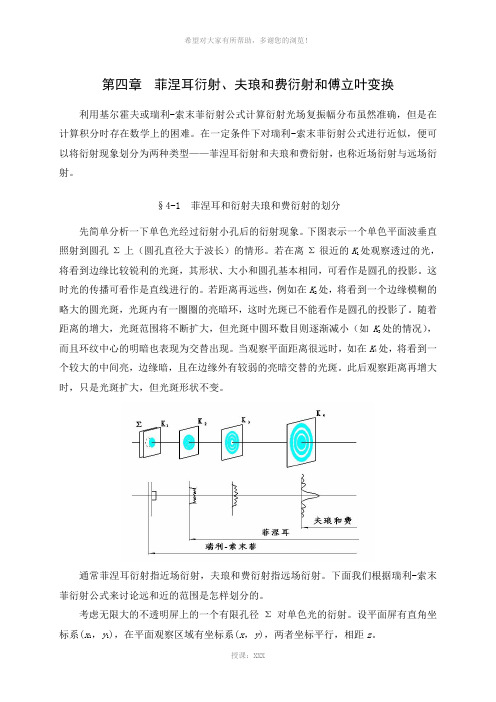
第四章菲涅耳衍射、夫琅和费衍射和傅立叶变换利用基尔霍夫或瑞利-索末菲衍射公式计算衍射光场复振幅分布虽然准确，但是在计算积分时存在数学上的困难。
在一定条件下对瑞利-索末菲衍射公式进行近似，便可以将衍射现象划分为两种类型——菲涅耳衍射和夫琅和费衍射，也称近场衍射与远场衍射。
§4-1 菲涅耳和衍射夫琅和费衍射的划分先简单分析一下单色光经过衍射小孔后的衍射现象。
下图表示一个单色平面波垂直照射到圆孔Σ上（圆孔直径大于波长）的情形。
若在离Σ很近的K1处观察透过的光，将看到边缘比较锐利的光斑，其形状、大小和圆孔基本相同，可看作是圆孔的投影。
这时光的传播可看作是直线进行的。
若距离再远些，例如在K2处，将看到一个边缘模糊的略大的圆光斑，光斑内有一圈圈的亮暗环，这时光斑已不能看作是圆孔的投影了。
随着距离的增大，光斑范围将不断扩大，但光斑中圆环数目则逐渐减小（如K3处的情况），而且环纹中心的明暗也表现为交替出现。
当观察平面距离很远时，如在K4处，将看到一个较大的中间亮，边缘暗，且在边缘外有较弱的亮暗交替的光斑。
此后观察距离再增大时，只是光斑扩大，但光斑形状不变。
通常菲涅耳衍射指近场衍射，夫琅和费衍射指远场衍射。
下面我们根据瑞利-索末菲衍射公式来讨论远和近的范围是怎样划分的。
考虑无限大的不透明屏上的一个有限孔径Σ对单色光的衍射。
设平面屏有直角坐标系(x1，y1)，在平面观察区域有坐标系(x，y)，两者坐标平行，相距z。
一、 菲涅耳衍射（近场衍射）在第三章里我们已经得到开孔的瑞利-索末菲衍射公式是⎰⎰∑=dS K re P U j P U jkr)()(1)(10θλ 在图所示的坐标系下，上式可以写为⎰⎰∑-+-+-+-+=1121212)()(110)()()(),(1),(21212dy dx K y y x x z ey x U j y x U y y x x z jk θλ 假设观察屏和衍射屏的距离z 远远大于Σ的线度和观察范围的线度，那么在z 轴附近1)(≈θK 。
光学教程第四版姚启钧课后题答案
目录第一章光的干涉 (3)第二章光的衍射 (15)第三章几何光学的基本原理 (27)第四章光学仪器的基本原理 (49)第五章光的偏振 (59)第六章光的吸收、散射和色散 (70)第七章光的量子性 (73)第一章光的干涉.波长为的绿光投射在间距d 为的双缝上，在距离处的光屏1nm 500cm 022.0cm 180上形成干涉条纹，求两个亮条纹之间的距离.若改用波长为的红光投射到此双缝上,nm 700两个亮条纹之间的距离又为多少?算出这两种光第级亮纹位置的距离.2解：由条纹间距公式得λd r y y y j j 01=-=∆+cm 328.0818.0146.1cm146.1573.02cm818.0409.02cm573.010700022.0180cm 409.010500022.018021222202221022172027101=-=-=∆=⨯===⨯===⨯⨯==∆=⨯⨯==∆--y y y drj y d rj y d r y d r y j λλλλ2．在杨氏实验装置中,光源波长为,两狭缝间距为,光屏离狭缝的距离为nm 640mm 4.0.试求：(1)光屏上第亮条纹和中央亮条纹之间的距离；（2）若p 点离中央亮条纹为cm 501，问两束光在p 点的相位差是多少？（3）求p 点的光强度和中央点的强度之比.mm 1.0解：（1）由公式λdr y 0=∆得=λd r y 0=∆cm 100.8104.64.05025--⨯=⨯⨯（2）由课本第20页图1-2的几何关系可知52100.01sin tan 0.040.810cm 50y r r d d dr θθ--≈≈===⨯521522()0.8106.4104r r πππϕλ--∆=-=⨯⨯=⨯由公式得(3)2222121212cos 4cos 2I A A A A A ϕϕ∆=++∆=8536.042224cos18cos 0cos 421cos 2cos42cos 422202212212020=+=+==︒⋅=∆∆==πππϕϕA A A A I I pp .把折射率为1.5的玻璃片插入杨氏实验的一束光路中,光屏上原来第5级亮条纹所3在的位置为中央亮条纹,试求插入的玻璃片的厚度.已知光波长为6×10-7m .解：未加玻璃片时，、到点的光程差，由公式可知为1S 2S P 2rϕπλ∆∆=Δr =215252r r λπλπ-=⨯⨯=现在发出的光束途中插入玻璃片时，点的光程差为1S P ()210022r r h nh λλϕππ'--+=∆=⨯=⎡⎤⎣⎦所以玻璃片的厚度为421510610cm 10.5r r h n λλ--====⨯-4.波长为500nm 的单色平行光射在间距为0.2mm 的双狭缝上.通过其中一个缝的能量为另一个的2倍,在离狭缝50cm 的光屏上形成干涉图样.求干涉条纹间距和条纹的可见度.解：6050050010 1.250.2r y d λ-∆==⨯⨯=mm122I I =22122A A=12A A =()()122122/0.94270.941/A A V A A ∴===≈+5.波长为700nm 的光源与菲涅耳双镜的相交棱之间距离为20cm ，棱到光屏间的距离L 为180cm ,若所得干涉条纹中相邻亮条纹的间隔为1mm ，求双镜平面之间的夹角θ。
光学教程四章节New-
S
r
倾斜因子为：
F 比(例0常,数) 为c：o0s2cos
C 1 i
2020/7/2
12
光 学 第四章 光的衍射
Kirchoff衍射积分公式
由基尔霍夫衍射积分公式可得：
E ~(P )i1 S0E ~(Q )1 reikc r o 02 sco d sS
1. 次波在各个方向上的振幅是不相等的；正
2020/7/2
7
光 学 第四章 光的衍射
惠更斯－－菲涅耳原理（1818）
波传到的任何一点都是子波的波源；设S是某光波的波阵面
，在其上任一面元dsi都可看作是次波的光源，各子波在空间
某点的相干叠加，就决定了该点处光波的强度。若dsi在波阵
面前面一点P产生的电场矢量为dEi，则S在P点产生的合电场
为n
奇 偶
由于： 0 0
F()1cos
2
a2a21a23,a4a23a25,
A( p) a1 an 22
奇 偶
2020/7/2
26
光 学 第四章 光的衍射
菲涅耳半波带法
对自由空间传播的球面波：
An
(
p)
a1 2
半波带法要求波面恰好能够分成若干个完整的 半波带，若半波带不完整，则不易得到定量的 结果。
1. 子波球面次波的频率与初波相同； 2. 子波源的初相与初波到达Q点时同相； 3. 次波在P点的振幅与初波在Q点的振幅成 正比；
2020/7/2
9
光 学 第四章 光的衍射
Fresnel衍射积分公式 由上所述，dS在P点的振幅为：
dE ~(P)cE ~(Q)1eikF r()dS
r
代入积分得：
E ~(P)c E ~(Q)1eikF r()dS
光学第04章答案_理想光学系统
2.单薄透镜成像时，若共轭距(物与像之间的距离)为250mm ， 求下列情况下透镜应有的焦距：1)实物，β=－4；2)实物，β=－1/4；3)虚物，β=－4；4)实物，β=4；5)虚物， β=4。
解：由薄透镜的物象位置关系''111fl l =-和l l '=β，共轭距mm l l 250'=-（1） 实物，β=－4。
由mm l l 250'=-和4'-==ll β,解得mm l 200'=，mm l 50-=,代入''111fl l =-得到焦距40'=f mm （2） 实物，β=－1/4。
由mm l l 250'=-和41'-==l l β,解得mm l 50'=，mm l 200-=,代入''111fl l =-得到焦距40'=f mm （3） 虚物，β=－4。
由mm l l 250'=-和4'-==ll β,解得mm l 200'-=，mm l 50=,代入''111fl l =-得到焦距40'-=f mm （4） 实物，β=4。
由mm l l 250'=-和4'==l l β,解得mm l 31000'-=，mm l 3250-=,代入''111fl l =-得到焦距11.111'=f mm （5） 虚物， β=4。
由mm l l 250'=-和4'==l l β，解得mm l 31000'=，mm l 3200=,代入''111fl l =-得到焦距11.111'-=f mm 。
3.一个f '＝80mm 的薄透镜当物体位于其前何处时，正好能在1)透镜之前250mm 处；2) 透镜之后250mm 处成像？ 解: 由薄透镜的物象位置关系''111fl l =- （1）l’=-250代入'111'l l f -=得l=-60.6061mm（2）l’=250代入'111'l l f -=得l=-117.647mm 4.有一实物被成一实像于薄透镜后300mm 处时，其放大率正好为1倍。
高等光学答案最终PDF版
1-2 从麦克斯韦方程组出发，导出电磁场在两种电介质分界面处的边值关系。
解：(ⅰ)ln t E E l d E ∆×⋅−=⋅∫)()(21当回路短边趋于零时，回线面积为零，而t B ∂∂有限，所以0)()(21=⋅∂∂−=∆×⋅−=⋅∫∫∫Σσd t B l n t E E l d E高等光学作业习题参考答案2012.12.10即l E E n t ∆−⋅×)()(21l E E n t ∆−×⋅=))((210=得0)(21=−×E E n，即t t E E 21=(ⅱ)l t d t DJ l n t H H l d H ∆⋅=⋅∂∂+=∆×⋅−=⋅∫∫∫Σασ)()()(21t H H n t n t H H⋅=−×⋅=×⋅−α))(()()(2121当没有电流分布时0=α，得,0)(21=−×H H n即t t H H 21=(ⅲ)s n D D ds n D d D ∆⋅−=⋅=⋅∫∫)(21σ当不存在自由电荷时，0=sρ，积分0=∫∫∫Ωdv s ρ，所以0)(21=∆⋅−s n D D，即n n D D 21=(ⅳ)0)(21=∆⋅−=⋅=⋅∫∫s n B B ds n B d Bσ即n n B B 21=1-5 已知电场E 和磁场H 在直角坐标中的分量分别为：)cos(t kz A E x ω−=；);sin(wt kz B E y −=0=z E )sin(t kz B H x ωε−−=；)cos(t kz A H y ωε−=；0=z H试求电磁场的能量密度w 和玻印亭矢量S 。
解：HB E D µε==,电磁场能量密度)(21B H D E w ⋅+⋅=)(2122H E µε+= )]()([21222222z y x z y x H H H E E E +++++=µε )](sin )(cos [2)1(2222t kz B t kz A ωωµε−+−+=玻印亭矢量H E S ×=zyxz y xH H H E E E z y x =z H E H E y H E H E x H E H E x y y x z x x z y z z y)()()(−+−+−=z H E H E x y y x)(−=z t kz B t kz A))]((sin ))((cos [2222ωεωε−+−=1-6 设某一无限大介质中，,0,0==σρε、µ只是空间坐标的函数，试从麦克斯韦方程和物质方程出发证明：{}0)](ln [)()(ln 22=∇⋅∇+×∇×∇++∇εµεµωE E E E证明：)(),(r rµµεε==H B E Dµε==,E E E D⋅∇+⋅∇=⋅∇=⋅∇εεε由麦克斯韦方程 0=⋅∇D得 (ln )EE E εεε∇⋅∇⋅=−=−∇⋅取麦克斯韦方程组微分式第一式的旋度，)()(B tE ×∇∂∂−=×∇×∇其中，E E E 2)()(∇−⋅∇∇=×∇×∇2[(ln )]E E ε=−∇∇⋅−∇)()(H tB t µ×∇∂∂−=×∇∂∂− )(H H t×∇+×∇∂∂−=µµ)(µµµB t Dt×∇+∂∂∂∂= t B tE ∂∂×∇+∂∂= )(ln 22µεµ)()(ln 22E t E×∇×∇−∂∂=µεµ)()(B tE ×∇∂∂−=×∇×∇即222(ln )()[(ln )]0E E E E t εµµε∂∇−+∇×∇×+∇∇⋅=∂若ti e E E ω0 =，则22(ln )()[(ln )]0E E E E εµωµε∇++∇×∇×+∇∇⋅=1-7 从麦克斯韦方程组出发导出电磁场在有色散的非均匀介质中所满足的亥姆霍兹方程。
光学第4章答案
第四章习题答案4-1 一束电子进入1.2T 的均匀磁场时,试问电子的自旋平行于和反平行于磁场的电子的能量差为多大?解：∵磁矩为μ的磁矩，在磁场B 中的能量为：U = -μ ·B= -sz μ B电子自旋磁矩 sz μ=±B μ∴电子自旋平行于和反平行于磁场的能量差u =B μ B – (-B μB) =2B μ B ∴u = 2B μ B =2 ×0.5788×410-eV ·1T -× 1.2 T = 1.39 ×410- eV 4-2 试计算原子处于23/2D 状态的磁矩μ及投影μz 的可能值.解：由23/2D 可知 S=12 J=32L=2 ∴j g =32+12(1)(1)(1)S S L L J J +-++=32+121323223522⨯-⨯⨯=45又j μ=jg Bμ45B μ =1.55 B μ∴μ=1.55 B μ又,j z j j B m g μμ= 又3113,,,2222j m =-- ∴,142×255j z B B μμμ=±=± 或,346×255j z B B μμμ=±=±即,6226(,,,)5555j zB μμ=-- 4-3 试证实:原子在63/2G 状态的磁矩等于零,并根据原子矢量模型对这一事实作出解释.解：由63/2G 可知：S =52 J = 32L = 4 ∴ 574531(1)(1)3122··03522(1)22×22J S S L L g J J ⨯-⨯+-+=+=+=+∴0J j B μμ==即原子在63/2G 状态的磁矩等于零。
解释：∵原子的总角动量为 J L S =+，而处于63/2G 态原子各角动量为：4.47L ====2.962S ====1.94J ==== 则它们的矢量关系如图示：L 和S同时绕J 旋进，相对取向保持不变由三角形余弦定理可知：22222211()[(1)(1)(1)]22L J L J S L L J J S S ⋅=+-+++-+ =22355715[45]222222=⨯+⨯-⨯= 而222221573515()(45)2222224S J S J L ⋅=+-=⨯+⨯-⨯=- ∴相应的磁矩 2B B S Sg S S μμμ=-=-B B L g L L μμμ∆=-=-S L μμμ=+由于磁矩μ 随着角动量绕J 旋进，因而对外发生效果的是μ 在J方向上的分量。
《光学教程》姚启钧原著_第四章
当一个中央亮斑的最大值恰和另一个中央亮斑的最小值 位置重合时，两个像点刚好能分辨开。
2、分辨极限角：
刚好能分辨时，两物点对光具组入瞳中心的夹角(或两像点 对出瞳的夹角)为夫琅和费圆孔衍射中中央亮斑的角半径：
U 1 0 610
R
( R 入瞳半径, 入射光波长) 1 分辨极限角
41
牛顿反射式
几种望远镜光路图
椭球面
F ''
F1
F’
抛物面
F ''
牛顿反射物镜
格雷戈里反射物镜
抛物面
F’
双曲面
F ''
抛物面
42
卡斯格伦反射物镜
五、激光扩束器
1、定义： 激光扩束器——将激光束横截面扩大的光学仪器。 2、装置 —倒用的折射式望远镜是很好的激光扩束器 。
开氏 伽氏
F1` F2
F1` F2
要求：A、放大本领高；
B、能校正像差、色差。 2、结构：场镜+视镜+分划板（刻度尺） • 场镜： 面向物体的透镜（或透镜组） • 视镜： 接近人眼的透镜（或透镜组） • 分划板：包含透明刻度尺，用于提高测量精度。
27
二、两种目镜 1)惠更斯（Huygens）目镜
’
二镜凸面向物镜
F’2 F’1
f1 ': f 2 ': d 3 : 1 : 2
22
二、放大本领
Q’
U’ Q
l U' M l U
说明：
'
P‘
Q P U
P H H’
O
l'
高等光学2016-第4章作业参考答案
2016高等光学第4次作业答案4-8一对称型带状波导，宽度和厚度分别为a 和b ，导光层的折射率为n ，覆盖层和衬底的折射率为n 0.证明：波导的基模传输条件为a=b 。
解：薄膜波导在x 向有限，y 方向无限大；带状波导，在x 和y 向都有限，宽度为a 和b （类似于矩形波导，参考图（4.1.1））。
x 方向受限的波导稳定传输的条件为（4.2.8）0122a cos ++2i n k m θδδπ=Y 方向受限的波导稳定传输条件为'''0122b cos ++2i n k n θδδπ=基模传输，''112'112===,0mn δδδθθδ==，，， 故a=b 。
4-9 一阶跃型光纤的纤芯和包层的折射率分别为1 1.55n =,2 1.50n =,求光纤在空气中的数值孔径和最大入射孔径角0θ.若将该光纤放入水中(设水的折射率为1.33),问光纤的数值孔径是否会改变?如果改变,则改变量是多少?解:光纤的数值孔径大小与纤芯折射率,及纤芯－包层折射率差有关,表达式为:.所以将该光纤放入水中,其数值孔径不会改变. 最大入射孔径角0θ==023≈4-10 一阶跃型光纤的纤芯和包层的折射率分别为n1=1.52，n2=1.51，现欲使该光纤单模传输，问工作波长分别为λλ00=11.222222和λλ00=00.882222时，光纤的最大芯径应该是多少？解：单模光纤的归一化截止频率（查阅光纤相关资料）0V=k 2.4048≤a λ≤max max =1.2m a =2.64m =0.8m a =1.76mλµµλµµ，，。
第4章光学仪器基本原理习题及解答
第四章 光学仪器的基本原理4.1．眼睛的构造简单地可用一折射球面来表示，其曲率半径为5.55mm ，内部为折射率等于43的液体，外部是空气，其折射率近似地等于1，试计算眼球的两个焦距。
用肉眼观察月球时月球对眼的张角为01，问视网膜上月球的像多大？解：眼睛的构造简单地可用一折射球面时，其物方焦点为'1 5.551.67413nr f cm n n⨯=-=-=---其像方焦点为'''43 5.55 2.22413n r f cm n n ==⨯=-- 根据折射定律有关系式''''''sin sin sin sin n n n nθθθθθθθθθ=≈≈≈因为很小，所以，''''''11tan 2.220.02941803n y d f f cm n θθθ=≈≈=⨯⨯=4.2．把人眼的晶状体看成距视网膜2cm 的一个简单透镜。
有人能看清楚距离在100cm 到300cm 间的物体，试问：（1）此人看清远点和近点时，眼睛透镜的焦距是多少？（2）为看清25cm 远的物体，需配戴怎样的眼镜？解：根据透镜的物像公式''111s s f -= （1）远点对应的焦距 将'2s cm = 300s cm =-代入上式''1112300300 1.987151f f cm-=-==近点对应的焦距将'2s cm = 100s cm =-代入上式''1112100100 1.96151f f cm-=-==（2）此人的近点为100cm ，要看清楚25cm 的物体，需要配戴眼镜使的25cm 的物体成虚象在100cm 处，所以应该配戴凸透镜（远视镜），根据透镜的物像公式''111s s f-= 其中'100s cm =- 25s cm =-'1110.10.25f =--- '1143300D f Φ==-+==（度）4.3．一照相机对准远物时，底片距物镜18cm ，当透镜拉至最大长度时，底片与物镜相距20cm ，求目的物在镜前的最近距离？解：根据透镜的物像公式''111s s f-= 当照相机对准远物时， 1s =-∞''11111s s f -= 所以 ''118s f cm ==当照相机对准最近物时，要成像必须把底片与物镜的距离拉到最大''22111s s f-= '220s cm =''21111112018s f s -=== 2180s cm =-目的物在镜前的最近距离为180厘米4.4．两星所成的视角为'4，用望远镜物镜照相，所得两像点相距1mm ，问望远镜物镜的焦距是多少？解：根据视角与透镜焦距的关系''1y U f -=， ''1185.987460180y f cm U π-===⨯ 4.5．一显微镜具有三个物镜和两个目镜。
高等光学教程-第3章-参考答案
高等光学教程--第三章参考答案第三章光学薄膜的基本知识3.1 证明在TM 波入射的情况下单层膜的特征矩阵为=22sin cos sin cos j q jq ββββ⎛⎫- ⎪⎪⎪-⎝⎭M式中=2q 220cos /θμεn，其它参数及图示参考§3.1节中图3-2。
图p3-1解答: 模仿教材§3-1中推导TE 波入射情况下求特征矩阵所用的方法。
在界面I 处： 2II 2I 1I 1I I cos cos cos cos θθθθrt r i E E E E E '-=-= (p3.1-1) II I I I I rt r i H H H H H '+=+= (p3.1-2) 由非磁性介质中E 和的关系式H E s H ⨯=n 0με (p3.1-2)式化为 )()(II I 20I I 100I rt r i E E n E E n H '+=-=μεμε (p3.1-3) 在界面II 处： 3II 2II 2II II cos cos cos θθθt r i E E E E =-= (p3.1-4)II II II II t r i H H H H =+= (p3.1-5)由(p3.1-3)式，(p3.1-5)式化为II 30II II 200II )(t r i E n E E n H μεμε=+=(p3.1-6) 两个界面上的电矢量有关系式II tI II II j i j r r E E eE E eββ-⎧=⎪⎨'=⎪⎩ (p3.1-7)(p3.1-8)由(p3.1-7)和(p3.1-8)两式，(p3.1-4)、(p3.1-6)两式化为II tI 2I 2II2tI I cos cos (p3.1-9)(p3.1-10)()j j r j j r E E e E e H E e E e ββββθθ--'⎧=-⎪⎨'=+⎪⎩由(p3.1-9)和(p3.1-10)两式解出tI 2II 2II cos E E θ⎫=⎪⎪⎭H + (p3.1-11) 和 βθμεμεθj re n E n H E --='220II 20II 2II cos 2cos (p3.1-12)将(p3.1-11)、(p3.1-12)式代入(p3.1-1)式，并令有 II 2II 1sin cos H q j E E ββ-=(p3.1-13) 22q =用同样的方法得到II II 2I cos sin H E jq H ββ+-= (p3.1-14)由(p3.1-13)和(p3.1-14)式⎥⎦⎤⎢⎣⎡⎥⎥⎦⎤⎢⎢⎣⎡--=⎥⎦⎤⎢⎣⎡II II 22I I cos sin sin cos H E jq q jH E ββββ ⎥⎥⎦⎤⎢⎢⎣⎡--=ββββcos sin sin cos 22I jq q j M∴式中 2202cos θμεn q =3.2 如图p3-2所示，有一单层介质膜，入射光由折射率为的介质经过界面I 、单层膜及界面II 后进入折射率为 的衬底，入射光在界面I 和界面II 一次反射的振幅反射率分别为和，一次透射的振幅透射率分别为和。
光学第四章习题解答ppt课件
∴ 透镜为有效光阑，也是整个光具组的入射光瞳和 出射光瞳， 对主轴上P点的位置均为12cm，其大小 为6cm。
1 1 1 (2) . s s f 1 1 1 1 1 1 1 7 s f s 5 12 5 12 60 60 故：s 8.57（cm) 8.6 (cm) . 7
4.10 有一光阑直径为5cm，放置在薄透镜后3厘 米处，透镜焦距为5cm，孔径为6cm，现有一高为 3cm的物PQ置于透镜前12cm处，试求：（1）计算对 主轴上P点的入射光瞳和出射光瞳的大小和位置； （2）象的位置；（3）作光路图。 解：（1）首先计算光阑对其前面的透镜所成 的象的位置和大小 1 1 1 f 5 cm s 3 c m s s f
（3）注意光阑经透镜L成象时，其实图中F是象 方焦点，但PQ经透镜L成象时，F为物方焦点。
A´ Q O P F
s
A
光阑
2.5 7.5
6.25
P´ Q´ B´
B
若为凹透镜，则 s = - 3.53cm
4.11 图中 H H 为光具组的主点， F F 为焦点， E为对于物点P的入射光瞳，EO为其半径。 已知 EO ， 2 , HP 20 , HF 15 , HO 5 , H F 15 物长 PQ 0.5 （单位都是cm）。作光路图计算：（1） 像的位置；（2）像长；（3）入射孔径角；（4）对 P点的出射光瞳半径和出射孔径角。
1 1 1 s s f
1 1 1 5 1 1 2 1 0 0 f近 0 0
1 0 0 f近 1 .9 6 1 c m 5 1
3 0 0 f 1 . 9 8 7 c m 远 1 5 1
高等光学教程-第4章参考答案
cos cos （3） At ,
a cos cos a sinc
cos cos cos cos a cos cos （4） At , , a sinc
当 R 时，有 r ，所以这时有
cos(n, r ) 1 U exp( jkr ) 1 exp( jkr ) jkU jk jkU r r n r2
当 R 时，上式分母中的 r 可用 R 来代替，于是
U exp( jkr ) 1 lim R jkU lim R lim (cos kr j sin kr ) 2 R R n R R R
Xx 2 XY sinc di
夫琅和费衍射图样
Yy sinc diΒιβλιοθήκη y cos di
U ( x, y )
jk 2 Xx Yy y 1 exp( jkz )exp ( x y 2 ) 2 XY sinc sinc cos j d i 2d i di di di
（P4.2-2）
~ 对于互为镜像点的 P0 和 P0 来说，有
cos(n, r01 ) cos(n, ~ r01 )
将以上关系式代入（P4.2-2）式，得到
r01 ~ r01
（P4.2-3）
G 0 n
（P4.2-4）
（2）根据（4-22）式，观察点 P0 的光扰动可以用整个平面 S1 上的光扰动 U 和它的法向导数 来表示
高等光学教程-第4章参考答案
第四章 标量衍射理论基础4.1证明（4-21）式所示的索末菲辐射条件成立。
证明：球面2S 是中心位于1S 面上的发散球面波的波面，假定2S 面 上的光场分布表示为 rjkr )exp(=U 式中r 表示产生发散球面波的点光源到球面2S 上任意一点的距离。
1exp()cos()cos(,)r jkr jk n r n r r r ∂∂∂∂⎛⎫===- ⎪∂∂∂∂⎝⎭U U U n,r n r 当∞→R 时，有∞→r ，所以这时有1),cos(≈r n2)exp()exp(1rjkr jk r jkr r jk jk n -≅-⎪⎭⎫ ⎝⎛-=-∂∂U U U 当∞→R 时，上式分母中的r 可用R 来代替，于是 2exp()1lim lim lim (cos sin )R R R jkr R jk R kr j kr n R R →∞→∞→∞∂⎛⎫⎡⎤⎛⎫-=-=-+⎪ ⎪⎢⎥∂⎝⎭⎣⎦⎝⎭U U lim 0jkrR e R →∞⎛⎫=-= ⎪⎝⎭4.2 参考图4-8，考虑在瑞利—索末菲理论中采用下式所表示的格林函数，即010110101exp()exp()()jkr jkr P r r +=+G %%(1) 证明+G 的法线方向的导数在孔径平面上为零。
(2) 利用这个格林函数，求出用孔径上的任意扰动来表示0()p U 的表达式，要得到这个结果必须用什么样的边界条件。
(3) 利用(2)的结果，求出当孔径被从2P 点发散的球面波照明时0()p U 的表达式 证明: 下面是教材中图4-8（1）)(1P +G 由两项迭加而成，它们分别表示从互为镜像的点0P 和0~P 发出的两个初相位相同的单位振幅的球面波。
孔径平面1S 上任一点1P 的+G 值为010101011~)~exp()exp()(r r jk r jkr P +=+G （P4.2-1） 1()P +G 的法向导数为0101010101010101~)~exp(~1)~,cos()exp(1),cos(r r r r n r n G jk jk r jkr r jk n ⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛-=∂∂+ （P4.2-2） 对于互为镜像点的0P 和0~P 来说，有)~,cos(),cos(0101r n r n -= 0101~r r = （P4.2-3）将以上关系式代入（P4.2-2）式，得到0n+∂=∂G （P4.2-4） （2）根据（4-22）式，观察点0P 的光扰动可以用整个平面1S 上的光扰动U 和它的法向导数来表示⎰⎰⎪⎪⎭⎫ ⎝⎛∂∂-∂∂=1d 41)(0S s n n P G U G U U π（P4.2-5） 由0101~r r =，得01011)exp(2)(r jkr P =+G （P4.2-6）将上式和（P4.2-4）式一同代入（P4.2-5）式，得到⎰⎰⎰⎰∂∂=∂∂=+11d )exp(21d 41)(01010S S s r jkr n s G n P U U U ππ（P4.2-7）为了将上式所表示的结果进一步简化，根据孔径∑上的场去计算0P 点的复振幅分布)(0P U ，只需要规定如下两个边界条件：（a ）在孔径∑上，场分布的法向导数n U ∂与不存在衍射屏时的值完全相同。
光学教程第三四章答案
1. 证：设两个均匀介质的分界面是平面，它们的折射率为n 1和n2。
光线通过第一介质中指定的A 点后到达同一介质中指定的B 点。
为了确定实际光线的路径，通过A,B 两点作平面垂直于界面，O O '是他们的交线，则实际 光线在界面上的反射点C 就可由费马原理来确定（如右图）。
（1）反正法：如果有一点C '位于线外，则对应于C '，必可在O O '线上找到它的垂足C ''.由于C A >C A ,B C >B C ,故光谱B C A '总是大于光程B C A ''而非极小值，这就违背了费马原理，故入射面和反射面在同一平面内得证。
（2）在图中建立坐oxy 标系，则指定点A,B 的坐标分别为（y x 11,）和（y x22,），未知点C 的坐标为（0,x ）。
C 点在B A '',之间是，光程必小于C 点在B A ''以外的相应光程，即xx x 21<<，于是光程ACB为：y x x n y x x n n n n 2211221221111)()(+-++-=+=根据费马原理，它应取极小值，即：i i 11='，∴0)(1=ACB n dxd取的是极值，符合费马原理。
故问题得证。
0)sin (sin )()()()()()(21112222211212111=-='-'=+---+--=i i n CB B C AC C A n y x x x x n y x x x x n ACB n dx d2.(1)证：如图所示，有位于主光轴上的一个物点S 发出的光束 经薄透镜折射后成一个明亮的实象点S '。
由于球面AC 是由S 点 发出的光波的一个波面，而球面DB 是会聚于S '的球面波的一个 波面，固而SB SC =,BS D S '='.又光程FD EF n CE CEFD ++=，而光程AB n AB =。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
u ( P0 , t )
1 j
cos( n, r01 ) j 2 t d ds jkr exp( ) U (P 01 1 , ) e r01
当 P1 点在 之外时， u ( P1 , t ) 0 ，上式改写为
u ( P0 , t )
cos cos （3） At ,
a cos cos a sinc
cos cos cos cos a cos cos （4） At , , a sinc
2 2 cos cos dJ 1 d cos cos 解答 .（1） At , 2 2 cos cos 2
Xx 2 XY sinc di
夫琅和费衍射图样
Yy sinc di
y cos di
U ( x, y )
jk 2 Xx Yy y 1 exp( jkz )exp ( x y 2 ) 2 XY sinc sinc cos j d i 2d i di di di
（P4.2-2）
~ 对于互为镜像点的 P0 和 P0 来说，有
cos(n, r01 ) cos(n, ~ r01 )
将以上关系式代入（P4.2-2）式，得到
r01 ~ r01
（P4.2-3）
G 0 n
（P4.2-4）
（2）根据（4-22）式，观察点 P0 的光扰动可以用整个平面 S1 上的光扰动 U 和它的法向导数 来表示
4
2 2 cos cos dJ 1 d cos cos cos cos （2） At , , 2 2 cos cos 2
U n 0 。
2
根据上述边界条件
U ( P0 )
1 4
n G ds 2 n
U
1
U exp( jkr01 ) ds r01
（P4.2-8）
（3）参考教材中图 4-5，孔径 由位于 P2 点的发散球面波照明，即
U ( P1 )
A exp( jkr21 ) r21
2 2 x y 2
4
（2）运用(4-118)式 代入数据，得
max
0.25m 3 2
取 z 2.5m
3
3
得 z 1.36m
z
2
2
max
2 z 1636m
，
4.5 用单位振幅的单色平面波垂直照明下列衍射屏，分别求出衍射屏后表面复振幅的角谱。 （1）直径为 d 的圆孔。 （2）直径为 d 的不透明圆屏。 （3）宽度为 a 的单缝 （4）直径为 a 的金属细丝
光强分布
I U ( x, y )
2
2 XY 2 Xx sinc di di
2
2 Yy sinc di
2 y cos di
4.7 若用一个单位振幅的单色平面波垂直照明
5
（1）图 p4-7(a)所示的方形环带，图中所示的两正方形中心重合，对应边平行，大小两 正方形的边长分别为 2 L0 和 2 Li 。 （2）图 p4-7(b)所示的环状孔径，图中所示的两正方形中心重合，大小两圆的直径分别 为 2 L0 和 2 Li 。 设光波波长为 ，孔径到观察平面的距离为 z，试导出该方形环带和环状孔径的夫琅 和费衍射图样的表达式。
式中
1 j
u ( P, t )
exp( jk r01 ) cos(n, r01 ) d s r01
v
，
k
2
4.4 （1）一个半径为 1cm 的圆孔用 =500nm 的单色平面波垂直照明，希望在垂直于光轴平 面上 1cm 的观察区内观察菲涅耳衍射，求观察距离至少为多少？ （2） 有一个边长为 2.5cm 的正方形孔径， 若要观察夫琅和费衍射， 求观察距离至少为多少？ 解答： （1）运用(4-109)式，代入数据，得
第四章
标量衍射理论基础
证明： 球面 S 2 是中心位于 S1 面上的发散球面波的波面， 假定 S 2 面 上的光场分布表示为
4.1 证明（4-21）式所示的索末菲辐射条件成立。
U
exp( jkr ) r
式中 r 表示产生发
散球面波的点光源到球面 S 2 上任意一点的距离。
U U r U 1 exp( jkr ) cos( n,r ) cos( n, r ) jk n r n r r r
U ( P0 )
由 r01 ~ r01 ，得
1 4
S1
U G ds n G U n
（P4.2-5）
G ( P1 )
2 exp( jkr01 ) r01
（P4.2-6）
将上式和（P4.2-4）式一同代入（P4.2-5）式，得到
U ( P0 )
U ( P0 ) A j
1 2
Ajk cos(n, r21 )
exp( jkr21 ) exp( jkr01 ) ds r21 r01
4.3
exp[ jk (r21 r01 )] cos(n, r21 )d s r21 r01
考虑非单色扰动 u( P, t ) ，其中心频率为 而带宽为 ，定义 一个相关的复数值扰动 u ( P, t ) ，它只是由 u( P, t ) 的负频分量 构成。因此
U 1 exp( jkr21 ) A cos( n, r21 ) jk n r21 r21
因为 r21 ，即 k
1 ，因此有 r21
exp( jkr21 ) U Ajk cos( n, r21 ) n r21
将上式代入（P4.2-8）式，得到 P0 点光场的复振幅
当 R 时，有 r ，所以这时有
cos(n, r ) 1 U exp( jkr ) 1 exp( jkr ) jkU jk jkU r r n r2
当 R 时，上式分母中的 r 可用 R 来代替，于是
U exp( jkr ) 1 lim R jkU lim R lim (cos kr j sin kr ) 2 R R n R R R
2 rect rect X Y
2 rect Y
F {U ( , )} XY sinc( Xf x ) sinc(Yf y ) exp( j f y ) exp( j f y )
图 p4-7(a) 解答： (1)
图 p4-7(b)
t ( , ) rect rect rect 2 L0 2 L0 2 Li
2
rect 2 Li
2
2 L0 x 2L y 2 Li x 2L y 4 I ( x, y ) L2 sinc 0 L2 sinc i o sinc i sinc z z z z z
j 2 U ( P1
r j 2 t 01 v , )e d d s
u ( P, t ) 的中心频率为 ，带宽为 。当 ( 2 , 2) 时，上式中第一个积
分才不为 0，在 的条件下， 变化很小，因此可以用 代替 并将它拿出积分号 之外。在 r01 v 的条件下用 exp( j 2 r01 v) 代替 exp( j 2 r01 v) ，因此有方程
e jkr lim R R 0
4.2 参考图 4-8，考虑在瑞利—索末菲理论中采用下式所表示的格林函数，即
G ( P 1)
01 ) exp( jkr01 ) exp( jkr 01 r01 r
(1) 证明 G 的法线方向的导数在孔径平面上为零。 要得到这个结 (2) 利用这个格林函数， 求出用孔径上的任意扰动来表示 U ( p0 ) 的表达式， 果必须用什么样的边界条件。 (3) 利用(2)的结果，求出当孔径被从 P2 点发散的球面波照明时 U ( p0 ) 的表达式 证明: 下面是教材中图 4-8
1 4
S1
U 1 G d s n 2
S1
U exp( jkr01 ) ds n r01
（P4.2-7）
为了将上式所表示的结果进一步简化，根据孔径 上的场去计算 P0 点的复振幅分布
U ( P0 ) ，只需要规定如下两个边界条件：
（a）在孔径 上，场分布的法向导数 U n 与不存在衍射屏时的值完全相同。 （b）在 S1 面上除去孔径 外的其余部分，即位于衍射屏的几何阴影区的那一部分上面
1
~ （1） G ( P1 ) 由两项迭加而成，它们分别表示从互为镜像的点 P0 和 P0 发出的两个初相位相
同的单位振幅的球面波。孔径平面 S1 上任一点 P1 的 G 值为
G ( P1 )
r01 ) exp( jkr01 ) exp( jk~ ~ r01 r01
（P4.2-1）
u ( P , t )