数图形方法总结
数图形方法总结
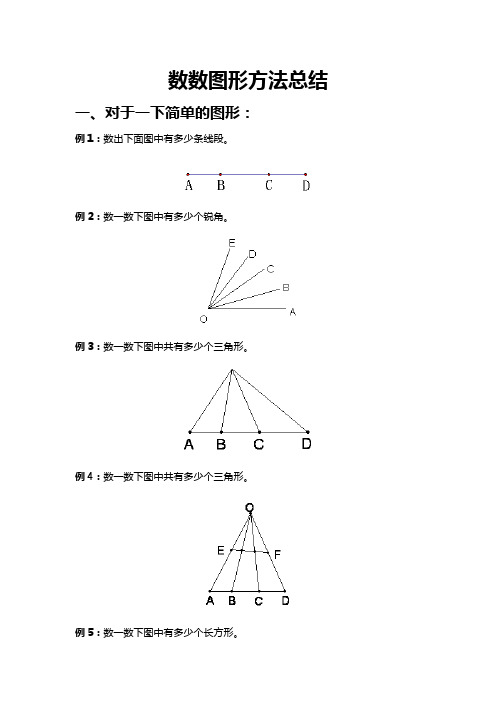
数数图形方法总结一、对于一下简单的图形:
例1:数出下面图中有多少条线段。
例2:数一数下图中有多少个锐角。
例3:数一数下图中共有多少个三角形。
例4:数一数下图中共有多少个三角形。
例5:数一数下图中有多少个长方形。
以上这些简单的图形分割后的个数,通过实际的计数不难发现它们都存在同意个规律,即都可以根据如下公式计算:
1+2+3……(端点数-1),这样学生即可以简化了数的烦恼,还可快速正确
的数出图形的个数。
二、下面是复杂图形的个数的计算方法:
例1:数一数下图中有多少个长方形?
数长方形可以用下面的公式:
长边上的线段×短边上的线段=长方形的个数
例2:数一数,下图中有多少个正方形?(每个小方格是边长为1的正方形)
由相同的n×n个小方格组成的几行几列的正方形其中所含的正方形总数为:1×1+2×2+…+n×n。
例3:数一数下图中有多少个正方形?(其中每个小方格都是边长为1个长度单位的正方形)
一般情况下,如果一个长方形的长被分成m等份,宽被分成n等份(长和宽的每一份都是相等的)那么正方形的总数为:mn+(m-1)(n-1)+(m-2)(n-2)+…+(m-n+1)
例5:数线段的实际应用
求下列图中线段长度的总和。
(单位:厘米)
如果设线段上的点数为n,基本线段分别为a1、a2、…a(n-1)。
以上各线段长度的总和为L,那么L= a1×(n-1)×1+ a2×(n-2)×2+ a3×(n-3)×3+…+ a(n-1)×1×(n-1)。
二年级专题第四讲:数几何图形的个数

⼆年级专题第四讲:数⼏何图形的个数第四讲:数⼏何图形的个数“数⼏何图形的个数”是趣味图形问题的⼀种。
数图形虽然很简单,但重复计数和遗漏是经常出现的错误,在细⼼的同时还要掌握⽅法和技巧。
⼀、数线段1. 数出下列每条线段上线段的总条数。
分析与解:数线段的时候⼀定按⼀定的顺序数,否则就会出现重复或遗漏。
数时可以先数最基本的⼩线段,再数两条基本线段组成的线段,再数三条基本线段组成的线段,……,最后把各种“线段”条数相加起来。
法⼀:照下⾯的⽅法数(以第2⼩题为例):3+2+1=6(条)法⼆:(规律) 线段总条数都是从1开始的⼏个连续⾃然数的和,⽽且最后⼀个加数正好和最基本线段数相同。
(1)(条)(2)(条)(3)(条)⼆、数⾓2. 数出右图中总共有多少个⾓.分析与解:在∠AOB内有三条⾓分线OC1、OC2、OC3,∠AOB被这三条⾓分线分成4个基本⾓,那么∠AOB内总共有多少个⾓呢?⾸先有这4个基本⾓,其次是包含有2个基本⾓组成的⾓有3个(即∠AOC2、∠C1OC3、∠C2OB),然后是包含有3个基本⾓组成的⾓有2个(即∠AOC3、∠C1OB),最后是包含有4个基本⾓组成的⾓有1个(即∠AOB),所以∠AOB内总共有⾓:4+3+2+1=10(个).令狐⽼师注:数⾓的⽅法可以采⽤例1数线段的⽅法来数,就是⾓的总数等于从1开始的⼏个连续⾃然数的和,这个和⾥⾯的最⼤的加数是⾓分线的条数加1,也就是基本⾓的个数. 【巩固】数⼀数右图中总共有多少个⾓?分析与解:因为∠AOB内⾓分线OC1、OC2…OC9共有9条,即9+1=10个基本⾓.所以总共有⾓:10+9+8+…+4+3+2+1=55(个).三、数三⾓形3. 如右图中,各个图形内各有多少个三⾓形?分析与解:⽅法⼀:(1)先数图中包含⼀个⼩三⾓形个数:△ABD、△ADE、△AEF、△AFC 共4个三⾓形.(2)再数由两个⼩三⾓形组合在⼀起的三⾓形个数:△ABE、△ADF、△AEC 共3个三⾓形,(3)以三个⼩三⾓形组合在⼀起的三⾓形:△ABF、△ADC 共2个三⾓形,(4)最后数以四个⼩三⾓形组合在⼀起的只有△ABC⼀个.所以图中三⾓形的个数总共有:4+3+2+1=10(个).⽅法⼆:我们就可以把数三⾓形问题转化为数线段问题了。
3年级奥数-数数图形(教师版)

数数图形教学目标认识了解线段、角、三角形、长方形等基本图形;学会数基本图形的个数;掌握数图形的规律。
知识梳理一、学会数图形同学们,你想学会数图形的方法吗?要想不重复也不遗漏地数出线段、角、三角形、长方形……那就必须要有次序、有条理地数,从中发现规律,以便得到正确的结果。
要正确数出图形的个数,关键是要从基本图形入手。
首先要弄清图形中包含的基本图形是什么,有多少个,然后再数出由基本图形组成的新的图形,并求出它们的和。
当我们识了线段、角、三角形、长方形等基本图形后,这些图形重重叠叠地交错在一起时就构成了复杂的几何图形。
要想准确地计数这类图形中所包含的某一种基本图形的个数,就需要仔细地观察,灵活地运用有关的知识和思考方法,掌握数图形的规律,才能获得正确的结果。
二、解题策略要准确、迅速地计数图形必须注意以下几点:1.弄清被数图形的特征和变化规律。
2.要按一定的顺序数,做到不重复,不遗漏。
典例分析考点一:基本图形例1、数出下图中有多少条线段?【解析】方法一:我们可以采用以线段左端点分类数的方法。
以A点为左端点的线段有:AB、AC、AD3条;以B点为左端点的线段有:BC、BD2条;以C点为左端点的线段有:CD1条。
所以,图中共有线段3+2+1=6(条)。
方法二:把图中线段AB、BC、CD看做基本线段来数,那么,由1条基本线段构成的线段有:AB、BC、CD3条;由2条基本线段构成的线段有:AC、BD2条;由3条基本线段构成的线段有:AD1条。
所以,图中一共有3+2+1=6(条)线段。
例2、数出图中有几个角?【解析】数角的个数可以采用与数线段相同的方法来数。
方法一:以OA为一边的角有:∠AOB、∠AOC、∠AOD3个;以OB为一边的角还有:∠BOC、∠BOD2个;以OC为一边的角还有:∠COD1个。
所以,图中共有角3+2+1=6(个)。
方法二:把图中∠AOB、∠BOC、∠COD看做基本角来数,那么,由1个基本角构成的角有:∠AOB、∠BOC、∠COD3个;由2个基本角构成的角有:∠AOC、∠BOD2个;由3个基本角构成的角有:∠AOD1个。
数图形的技巧

数图形的技巧
自古以来,人们就一直喜欢把数学和图形联系起来。
这些技巧可以让数学变得更有深度,也让我们能够更容易理解数学概念。
图形可以有助于我们更好地理解数学术语,数据的关系以及统计学的基础知识。
首先,图形可以帮助我们更好地理解数学概念。
在绘制图形时,我们可以使用一些简单的图标来代表数学概念,比如数字,平面几何图形,圆形,矩形等等。
这些图标不仅可以节省时间,而且可以更清晰地表达相关概念。
例如,通过使用圆形来表示圆周率可以让我们更直观地理解这一概念。
其次,图形可以帮助我们更好地理解数据之间的关系。
通过使用图表,我们可以更容易的观察数据之间的规律,从而获得更多的信息。
比如,可以使用折线图或饼图来展示不同离散类别之间的关系,从而获得更多的信息。
最后,图形可以帮助我们更好地理解统计学的基础知识。
绘制统计图形可以更清楚的说明数据的分布规律,比如质量,比例,概率等等,而且可以清楚的表示出这些数据之间的联系。
此外,绘制统计图形也可以用来表示数据之间的因果关系,从而帮助我们更好地分析问题。
总之,数图形技巧可以有效节约我们的时间,更加直观地了解数学概念,理解数据之间的关系,以及更好地理解统计学的基础知识。
在数学教学中,引入数图形技巧可以加深学生的理解力,提高学生的
学习效果。
与其他教学方法相比,使用数图形技巧可以让学生能够更深入了解数学概念,进而更好地掌握和应用知识。
举一反三第7周---数数图形

D
方法二:三角形的个数正好与三角形左面边
上的线段条数相同。
E
A
举一反三
3.下图中,图②比图①多几条线段? ①
②
王牌例题②
数一数,下图中共有多少条线段?
A
G
F
B
C
D
E
H
思路启发 能不能直接用公式进行计算?
知识点总结
>数图形要注意:
① 有顺序; ② 适当分类; ③ 不能随意使用公式;
举一反三
1.数一数,下图中共有多少条线段?
第7周 数数图形 主讲人:
课前热身 下面这只小鸟是用什么图形画出来的呢?你能找出来吗?
本课学什么
>数数图形: ①线段的数法 ②三角形的分层数法 ③组合图形数正方形 ④立体图形数正方形
王牌例题①
数一数,下图中共有多少条线段?
A
B
C
D
思路启发
方法一:从最左边的端点A开始找起。 方法二:从“基本线段”数找起。
2.观察下图,数一数图中共有多少条线段?
举一反三 3.小红在纸上画了一条线段,小亮又拿起笔,在小红画的线段上 点了2个点,然后问小红:“你知道现在这条线段上又多出了多 少条线段吗?”小红一会就说出了结果。你知道又多出了几条线 段吗?
思路启发 画图表示,找出多出的线段。
王牌例题③
数一数,下图中共有多少个三角形?
思路启发 先数上层,再数下层。
知识点总结 分层三角形的问题:我们可以先数一层,再合并起来数。
举一反三
1.数一数,下列各图中有多少三角形?
①
②
③
④
⑤
王牌例题④
数一数,下图中共有多少个正方形?
v
数正方形个数的方法

数正方形个数的方法
将正方形的一角作为初始点,分别向两边写上正方形的个数,标好个数之后再用两边相对应的数字进行相乘,然后将乘的积进行相加,最终所得的和就是正方形的个数。
正方形的两组对边分别平行,四个角都是90°,邻边互相垂直,对角线互相垂直、平分且相等,每条对角线都平分一组对角,正方形是矩形的特殊形式,也是菱形的特殊形式。
数图形时要有次序、有条理,才能不遗漏、不重复,一般步骤应是:仔细观察,发现规律,应用规律。
长方形是用“点”或者“线”来数的,而正方形是用“块”来数的。
数正方形个数的公式:
假设大正方形的每边有N个小正方形,则在大正方形这个图形中有正方形的个数为:(即数正方形个数的公式)1*1+2*2+3*3+……+N*N。
在这里用1乘以1,2乘以2,这样简单的表达学生叫形象理解,容易掌握。
数图形常用方法

分析与解答 : 怎样数 角的个数 呢?联想数线段 的方法 , 易知这 种数角的问题与数线段的方法类似 , 图中两条射线对应一个角 , 因 分析与解答 : 一般长方形( 正方形除外) 的长大于宽。 为了便 于 此要数 出图中角 的个数 , 只要利 用例 l 的公式来解答就可 以了。 弄清计数 , 把图形分解来观察 : 后 先 图中共有 6 条射线 , 则所数角 的个数是 :
分析 与解答 : 图形 比较 复杂 , 直接数 比较 困难 , 以利用例 1 可
从上 面的分类讨论 中可 以看 出 ,图形 中正方 形的总数与该 图 形 中最 大正方形 的边被等分成几段有关 系。 再观察 以上数据 , 从图 ( ) 图( )正方形 的个数 从 l l开始 , 1至 3, x 逐渐增加 2 2 3 3 最后 x ,x , 个加数正好是最大正方形的边被等分的线段条数相乘 。 这样 , 可
() 3 图中 9个小正方形又可 以组成 1 大正 个 分析与解答 : 这是一个数线段 的问题 。有两种数法 : 方形 。 方 法一 : 以线段 端点为顺序 , 按从 左到右顺序观察 , 以一个 点 因此 ,图 中共 有正方 形 的个数 是 : + + = 9 4 1 为起点 , 数出以这个点为端点 的线段有哪几条 : 1 ( ) 4个 。 () 1 以点 A为左端点的线段 有 AC A AE A 有 4 。 、 D、 、 B, 条 数正方形 的个数 , 还可 以按正方形 的边分类 () 2 以点 C为左端点 的线段有 C C 、 8, 3条。 D、 E C 有 去数 , 探索规律 。 () 3 以点 D为左端点的线段 有 D D 有 2 。 E、 B, 条 设下面各图中 , 每一个小方格是边长 为 1的正方形 , 分别数一 () 4 以点 E为左端点 的线段有 E , 1 B 有 条。 数各图中正方形 的总数 : 因此 , 图中线段 的总数是 :+ + + = 0 条 ) 4 3 2 1 1( 。 方法二 : A C D E 把 C、D、 E、B称为基本线段。 () 1 由一条基本线段组成的线段有 JC C D E 有 4条。 4 、 D、 E、 B,
数图形有绝招小学奥数

3 13
3
3+3+3+1=
20个
设想大 长方形消失则 有15+10-1=24个
还原大长方形则增4个
28 总共24+4= 总共2个8个
谢谢使用
2023
拓展21. 数一数,图中有多少个正方形?
15+6+1=
个
22
9+2=
个
11
拓展22. 数一数,图中 有多少个正方形?
5+11=
个
5
11
16
拓展23. 数一数,图中有多 少三角方形?
20+16+8+4=
个
48
20
16
8
4
4
1
拓展24. 数一数,图中有多 少个正方形?
5+4+1=
个
5
10
拓展25. 数一数,图中有多少个长方形?
总共(4+3+2+1)×3=
个
30
拓展15. 数一数,图中有多少个长方形?
(4+3+2+1)×(4+3+2+1)=
个
6+5+4+3+2+1=
个
100
21
拓展16. 数一数,图中有
多少个正方形?
4
或
32
55
A
B
25 10
16
6×3+5×2+4×1=
个
9
1
5×5+4×4+3×3+2×2+
1=
个
C
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数数图形方法总结一、对于一下简单的图形:
例1:数出下面图中有多少条线段。
例2:数一数下图中有多少个锐角。
例3:数一数下图中共有多少个三角形。
例4:数一数下图中共有多少个三角形。
例5:数一数下图中有多少个长方形。
以上这些简单的图形分割后的个数,通过实际的计数不难发现它们都存在同意个规律,即都可以根据如下公式计算:
1+2+3……(端点数-1),这样学生即可以简化了数的烦恼,还可快速正确
的数出图形的个数。
二、下面是复杂图形的个数的计算方法:
例1:数一数下图中有多少个长方形?
数长方形可以用下面的公式:
长边上的线段×短边上的线段=长方形的个数
例2:数一数,下图中有多少个正方形?(每个小方格是边长为1的正方形)
由相同的n×n个小方格组成的几行几列的正方形其中所含的正方形总数为:1×1+2×2+…+n×n。
例3:数一数下图中有多少个正方形?(其中每个小方格都是边长为1个长度单位的正方形)
一般情况下,如果一个长方形的长被分成m等份,宽被分成n等份(长和宽的每一份都是相等的)那么正方形的总数为:mn+(m-1)(n-1)+(m-2)(n-2)+…+(m-n+1)
例5:数线段的实际应用
求下列图中线段长度的总和。
(单位:厘米)
如果设线段上的点数为n,基本线段分别为a1、a2、…a(n-1)。
以上各线段长度的总和为L,那么L= a1×(n-1)×1+ a2×(n-2)×2+ a3×(n-3)×3+…+ a(n-1)×1×(n-1)。
