《信号与系统分析基础》第1章习题解答
信号与系统王明泉第一章习题解答
第1章信号与系统的概述1.1 学习要求(1)了解信号与系统的基本概念与定义,会画信号的波形;(2)了解常用基本信号的时域描述方法、特点与性质,并会灵活应用性质;(3)深刻理解信号的时域分解、运算的方法,会求解;(4)深刻理解线性是不变系统的定义与性质,会应用性质求解系统1.2 本章重点(1)基本的连续时间信号的时域描述和时域特性;(2)单位冲激信号的定义、性质与应用;(3)信号的时域运算及其综合应用;(4)线性时不变系统的性质与应用。
1.3 本章的知识结构1.4 本章的内容摘要1.4.1信息、消息和信号的概念所谓信息,是指存在于客观世界的一种事物形象,一般泛指消息、情报、指令、数据和信号等有关周围环境的知识。
消息是指用来表达信息的某种客观对象,如电报中的电文、电话中的声音、电视中的图像和雷达探测的目标距离等等都是消息。
所谓信号,是指消息的表现形式,是带有信息的某种物理量,如电信号、光信号和声信号等等。
信号代表着消息,消息中又含有信息,因此信号可以看作是信息的载体。
1.4.2信号的分类以信号所具有的时间函数特性来加以分类,可以将信号分为确定信号与随机信号、连续时间信号与离散时间信号、周期信号与非周期信号、能量信号与功率信号、实信号与复信号等等。
1.4.3 常用信号 (1)正弦型信号)cos()(ϕω+=t A t f (1-3)(2)指数信号st Ae t f =)( (1-8)(3)矩形脉冲⎪⎩⎪⎨⎧><=2/02/1)(ττt t t f(4)三角脉冲⎪⎩⎪⎨⎧>≤-=2/02/21)(τττt t tt f (1-18)(5)抽样信号ttt sin )Sa(=(1-19)性质:(1))Sa()Sa(t t =-,偶函数 (2)1)Sa(,0==t t ,即1)Sa(lim 0=→t t(3)π,0)Sa(n t t ±==, 3,2,1=n (4)⎰∞=02πd sin t t t ,⎰∞∞-=πd sin t tt(5)0)Sa(lim =±∞→t t该函数的另一表示式是辛格函数,其表示式为ttsi t c ππn )(sin =(1-20) (6) 斜变信号⎩⎨⎧≥<=000)(t t t t f (1-24)(7)单位阶跃信号⎩⎨⎧><=0100)(t t t u 或⎩⎨⎧><=-0100)(000t t t t u如果矩形脉冲对于纵坐标左右对称,则可用)(t G T)2()2()(Tt u T t u t G T --+= 下标T 表示其矩形脉冲宽度。
信号与系统(第1章)上册课后习题答案

0, 0 等幅 0, 0 增幅振荡 0, 0 衰减
第 21 页
4.抽样信号(Sampling Signal)
O
2
2
第 37 页
c.表示符号函数 符号函数:(Signum)
1 sgn( t ) 1
1 u( t ) [sgn( t ) 1] 2
sgnt
t 0 t0
O
t
sgn( t ) u( t ) u( t ) 2u( t ) 1
第 38 页
e
j t
cost j sint
第 20 页
3.复指数信号
f ( t ) Ke st
Ke t cos t jKe t sin t
为复数,称为复频率
( t )
s j
, 均为实常数
的量纲为1 /s , 的量纲为rad/s 讨论
瞬态信号:除准周期信号外的 一切可以用时间函数描述的非 周期信号。
第 10 页
3.连续信号和离散信号
连续时间信号:信号存在的 时间范围内,任意时刻都有定 义(即都可以给出确定的函数 值,可以有有限个间断点)。 用t表示连续时间变量。 离散时间信号:在时间上是 离散的,只在某些不连续的规 定瞬时给出函数值,其他时间 没有定义。 用n表示离散时间变量。
f t f at a 0 波形的压缩与扩展,尺度变换
f (t ) f t 2
f t
2
1
t f 2
2
信号与系统课后习题答案

习 题 一 第一章习题解答基本练习题1-1 解 (a) 基频 =0f GCD (15,6)=3 Hz 。
因此,公共周期3110==f T s 。
(b) )30cos 10(cos 5.0)20cos()10cos()(t t t t t f ππππ+==基频 =0f GCD (5, 15)=5 Hz 。
因此,公共周期5110==f T s 。
(c) 由于两个分量的频率1ω=10π rad/s 、1ω=20 rad/s 的比值是无理数,因此无法找出公共周期。
所以是非周期的。
(d) 两个分量是同频率的,基频 =0f 1/π Hz 。
因此,公共周期π==01f T s 。
1-2 解 (a) 波形如图1-2(a)所示。
显然是功率信号。
t d t f TP T TT ⎰-∞→=2)(21lim16163611lim 22110=⎥⎦⎤⎢⎣⎡++=⎰⎰⎰∞→t d t d t d T T T W(b) 波形如图1.2(b)所示。
显然是能量信号。
3716112=⨯+⨯=E J (c) 能量信号 1.0101)(lim101025=-===⎰⎰∞∞---∞→T t ttT e dt edt eE J(d) 功率信号,显然有 1=P W1-3 解 周期T=7 ,一个周期的能量为 5624316=⨯+⨯=E J 信号的功率为 8756===T E P W 1-5 解 (a) )(4)2()23(2t tt δδ=+; (b) )5.2(5.0)5.2(5.0)25(5.733-=-=----t e t e t et tδδδ(c) )2(23)2()3sin()2()32sin(πδπδπππδπ+-=++-=++t t t t 题解图1-2(a) 21题解图1-2(b) 21(d) )3()3()(1)2(-=----t e t t et δδε。
1-6 解 (a) 5)3()94()3()4(2-=+-=+-⎰⎰∞∞-∞∞-dt t dt t t δδ(b) 0)4()4(632=+-⎰-dt t t δ(c) 2)]2(2)4(10[)]42(2)4()[6(63632=+++-=+++-⎰⎰--dt t t dt t t t δδδδ(d)3)3(3)(3sin )(1010=⋅=⎰⎰∞-∞-dt t Sa t dt ttt δδ。
奥本海姆信号与系统第一章部分习题答案

(e)
x[n], n 1
y[n] 0,
n0
x[n 1], n 1
(e)
Байду номын сангаас[n], n 1
y[n] 0,
n0
x[n 1], n 1
(g )
y[n] x[4n 1]
+++
1.31 在本题中将要说明线性时不变性质的重要结果之一,即一旦知道了一个线性
∴ 1 = 3,1 = 0,2 = −3,2 =1(或-1)
1.19判定下列输入-输出关系的系统是否具有线性性质、时不变性质,或两者俱有。
线
性: 3 = 1 + 2
时不变性: 2 = 1 ( − 0 )
(a) = 2 ( − 1)
∴ 是线性的
∴ 不是时不变的
基波周期0 : 使[] = + 成立的最小正整数。
离散时间复指数信号的周期: 0 , 0 = 是有理数,则是周期的,
2
2 0
且和无公因子时,基波周期为,角频率为 =
常数通常不讨论它的周期性,但可以认为周期为1。
1
4
2
=
= ,1 = 7
2 7 × 2 7
1
3
1
[] = [cos + cos( )]
2
4
4
N1
2
* m 8, m 3
3 / 4
N1
∴ 是周期的,基波周期为 =8
2
* m 8, m 1
/4
+ + + 1.27 这一章介绍了系统的几个一般性质,这就是一个系统可能是或不是:
信号与系统课后习题答案—第1章

第1章 习题答案1-1 题1-1图所示信号中,哪些是连续信号?哪些是离散信号?哪些是周期信号?哪些是非周期信号?哪些是有始信号?解: ① 连续信号:图(a )、(c )、(d ); ② 离散信号:图(b ); ③ 周期信号:图(d );④ 非周期信号:图(a )、(b )、(c ); ⑤有始信号:图(a )、(b )、(c )。
1-2 已知某系统的输入f(t)与输出y(t)的关系为y(t)=|f(t)|,试判定该系统是否为线性时不变系统。
解: 设T 为此系统的运算子,由已知条件可知: y(t)=T[f(t)]=|f(t)|,以下分别判定此系统的线性和时不变性。
① 线性1)可加性不失一般性,设f(t)=f 1(t)+f 2(t),则y 1(t)=T[f 1(t)]=|f 1(t)|,y 2(t)=T[f 2(t)]=|f 2(t)|,y(t)=T[f(t)]=T[f 1(t)+f 2(t)]=|f 1(t)+f 2(t)|,而|f 1(t)|+|f 2(t)|≠|f 1(t)+f 2(t)|即在f 1(t)→y 1(t)、f 2(t)→y 2(t)前提下,不存在f 1(t)+f 2(t)→y 1(t)+y 2(t),因此系统不具备可加性。
由此,即足以判定此系统为一非线性系统,而不需在判定系统是否具备齐次性特性。
2)齐次性由已知条件,y(t)=T[f(t)]=|f(t)|,则T[af(t)]=|af(t)|≠a|f(t)|=ay(t) (其中a 为任一常数)即在f(t)→y(t)前提下,不存在af(t)→ay(t),此系统不具备齐次性,由此亦可判定此系统为一非线性系统。
② 时不变特性由已知条件y(t)=T[f(t)]=|f(t)|,则y(t-t 0)=T[f(t-t 0)]=|f(t-t 0)|,即由f(t)→y(t),可推出f(t-t 0)→y(t-t 0),因此,此系统具备时不变特性。
依据上述①、②两点,可判定此系统为一非线性时不变系统。
信号与系统教程习题解析(前七章)

2e
第2章
连续时间信号
2-1 设有如下函数f t ,试分别画出它们的波形。 (a) f t 2ε t 1 2ε t 2 (b) f t sinπt ∙ ε t ε t 6 解 (a)和(b)的波形如图 p2-1 所示。
2
图 p2-1
2-2 试用阶跃函数的组合表示题 2-2 图所示信号。 解 (a) f t ε t 2ε t 1 ε t 2
信号与系统的频域分析
4-1 求题 4-1 图所示周期信号的三角函数形式的傅里叶级数表示式。
题 4-1(a) 图
解 对于周期锯齿波信号,在周期( 0,T )内可表示为
ft
A T
t
T
At T
A
a
1 T
f t dt
1 T
At T
A dt
A T
t 2T
t
A 2
∵ ω T 2π, ∴ sinnω tdt
cosnω tdt 0
⇒t
2f
t
↔
j
dF ω dω
2F ω
df t dt
↔ jωF ω
⇒
t
df t dt
↔
j
d
jωF ω dω
4-9 对于如题 4-9 图所示的三角波,试求其频谱函数。
13
题 4-9 图
解 过原点的三角波函数是偶函数,其表达式为
ft
A1
|t| τ
,
|t|
0,
|t|
Fω
fte
dt 2
A1
t τ
cosωtdt
2A
1 ω
sinωt|
1 τ
信号与系统教程习题解析(前七章)
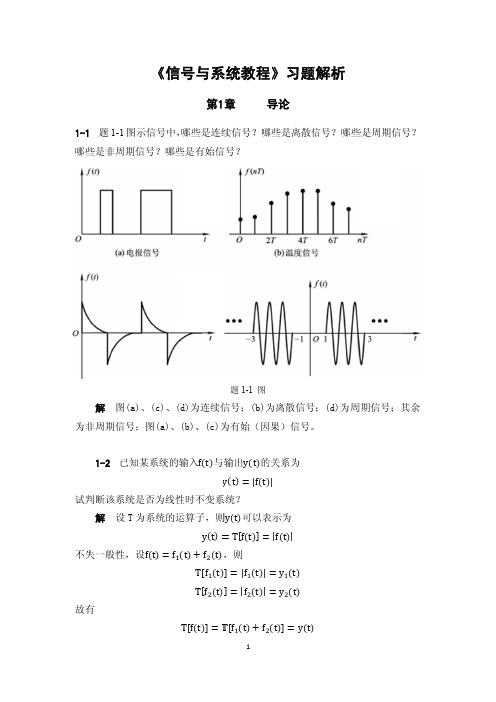
题 4-1(a) 图
解
对于 于周期锯齿波 波信号,在 在周期( 0,T )内可表示 示为 At A f t t T A T T a 1 T f t dt d 1 T At T A dt A T t 2T t A 2 0
∵ω T 2 T 2A 2 T b 2 T
2π, 2 ∴
sinnω tdt t 2 2A T
《信 信号与系 系统教程 程》习题 题解析
第1 章 导论 导
1-1 题 1-1 图示信号中, 图 哪些是连续 续信号?哪 哪些是离散信 信号?哪些 些是周期信号 号? 哪些 些是非周期 期信号?哪些 些是有始信 信号?
题 1-1 图
解
图(a a)、(c)、( (d)为连续信 信号;(b)为 为离散信号 号;(d)为周 周期信号;其 其余
(a)和(b)的波形如图 p2-1 所示。
2
图 p2-1
2-2 试用 用阶跃函数的组合表示 示题 2-2 图所 所示信号。 解 (a) f t (b) f t ε t ε t 2ε t ε t 1 T ε t ε t 2 2T T
题 2-2 图
2-3 如题 题 2-3 图所示 示f t ,试画 画出如下信 信号的波形。 。 (a) f (b) f t (c) f t (d) f 2t (e) f t/2 (f) f 2t 2
cosn nω tdt A 2A T
a
f t cosnω ω tdt tsinnω ω t nω f t sinnω ω tdt
tcosn nω tdt
cosnω ω tdt
sinnω t dt nω 2 2A T
0 2A A T
tsinn nω tdt
sinnω tdt
《信号与系统》习题解析(燕庆明,第3版)非常详细

8
本材料由 三折网 倾情奉献
2-7 如题 2-7 图一阶系统,对 (a) 求冲激响应 i 和 uL ,对(b) 求冲激响应 uC 和 i C,并画出 它们的波形。
解 由图(a) 有
即
当 uS( t ) = δ( t ),则冲激响应 1 − t h (t ) = i ( t ) = e L ⋅ ε (t ) L di R − t h (t ) = u L (t ) = L = δ ( t ) − e L ⋅ ε (t ) dt L du C u = iS − C dt R
∫ ∫ ∫
∞
(4)
0+
0−
e −3 t δ (−t )dt = ∫ e −3 t δ (t ) dt = ∫ δ (t )dt = 1
0− 0−
0+
0+
2-6
设有题 2-6 图示信号 f( t ),对 (a) 写出 f′ ( t ) 的表达式,对 (b) 写出 f ″ ( t ) 的表达式,
并分别画出它们的波形。
(d)
题 1-1 图
题 1-2 图
解 以上各函数的波形如图 p1-2 所示。
2
本材料由 三折网 倾情奉献
1-3 如图 1-3 图示,R、L、C 元件可以看成以电流为输入,电压为响应的简单线性系统 SR、SL、SC,试写出各系统响应电压与激励电流函数关系的表达式。 SR
解 各系统响应与输入的关系可分别表示为
1-6 判断下列方程所表示的系统的性质。 df (t ) t (1) y (t ) = + ∫ f (τ )dτ 0 dt (2) y′′(t ) + y′(t) + 3 y(t) = f ′(t)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《信号与系统分析基础(第2版)》部分习题解答
姜建国,曹建中,高玉明著,清华大学出版社,2006年7月
第一章
1-3 粗略画出下列各序列的图形。
(5)1
()2
(1)n x n u n -=-
1-5 说明下列函数的信号是否是周期信号,若是,求周期T 。
(本题属于连续情况) (1)sin sin3a t b t - 解:12222, T 13
T ππ
π=
==
1
2
3T T =,为有理数
∴是周期信号,2T π=
(3)sin 4cos7a t b t + 解:122, 27T T π
π=
=
1
2
7
224
7
T T π
π=
=
为有理数 ∴是周期信号,2T π=
1-6 判断下列各序列是否是周期性的,若是,试确定其周期。
(本题属于离散情况) (1)3
()cos()7
8
x n A n π
=-
解:周期条件:22 =m kN m N k
πωπω=⋅ 本题中,314 =73m N k
πω=⋅为无理数,非周期。
(2)8
()n j x n e π-=
解: =168
N π
ω=,是周期信号,周期为16.
(3)()8
()n j x n e π-=
解:12 =168N m m πωπω
=
⋅=为无理数,非周期。
1-7 绘出下列各时间函数的波形图,注意它们的区别。
设01
= 2
t ωπ=
, 12030040(1) ()sin ()(2) ()sin ()(3) ()sin ()()(4) ()sin ()()
f t t u t f t t u t t f t t t u t t f t t t u t ωωωω=⋅=⋅-=-⋅-=-⋅
t
t
t
1-10 应用冲激信号的筛选特征(又称抽样特性),求下列个表达式的函数值。
000
0000000000 ()()()
()(2)0
-2 ()()(0)
1 (sin )()sin 6666210 ()()()()0222t f t t t dt f t e t t dt t f t t t t dt f t t t dt t t t t t t u t dt u t u t δδδππππδδ--+∞
-∞+∞
-+∞-∞
+∞-∞+∞-=-++==--=+-=+=+
≥--=-==⎰
⎰⎰
⎰⎰(1)(2) 只有在处有值,但不在积分区间。
(3)(4)(5)00
000
[()()]1j t j t j t e t t t dt e e e ωωωδδ+∞
----∞
⎧⎨
<⎩--=-=-⎰(6)
1-12 绘出下列各时间函数的波形图。
10(10-1)
1
()()11
10(10-1)10(-)(-0.1)1010
0.1t at t a
t t t t δδδδδδ==⋅
=∴=(3) 由尺度特性: 知在处有一个脉冲。
t
2()3()2
u t t π
δ+-(4)
1-13 计算下列积分:
202
020
(2)cos[(3)]cos (3)0 (1)(2)22 ()(2)2
2(2)(2) 2(42)12
j t t t dt t e dt t t dt
t t dt
t t dt
ωδωω
δδδδ-----∞
∞
∞
∞∞
--=+=-+-=+=-+=+=⎰⎰⎰⎰⎰(1)(2),t=-3不在积分区间内。
(3)
2
2
2000
1 (2)()22tu t u t dt tdt t --∞
-===⎰⎰(4)
2220
()|0
t t
t e e t dt e
λ
λλδλλ--∞
--=⎧≥-==⎨
<⎩⎰(5) 00000
2
sin10 '()
10 '()()'()sin10sin10 '()
[]1010cos10sin10 10 t t t
t dt t
t t f t dt f t t d t
t dt t dt t t t
t t δδδ--∞
+∞-∞
∞
==-=-=-=-+⎰⎰⎰(6)由得:()1
1
10 '(1)()t t
t t t d t e u t dt e e e dt
δ-∞
----===∞-=-
==⎰(7)
1-14 已知系统具有初始值0()y t ,其响应()y t 与激励()x t 有如下关系:
0023000001 ()()()()
2 ()()()
3 ()()3()
4 ()3()2()
5 ()()sin 5()
6 ()()t
y t ay t bx t dx t y t y t x t dt
y t y t t x t y t y t x d y t y t t tx t y t y t ττ=+=+=+=+=+=+⎰(), 线性时不变
(), 非线性系统(), 非线性系统,时变系统(), 线性系统,时不变系统
(), 线性系统,时变系统()23()t x t , 线性系统,时变系统
试判断它是线性系统还是非线性系统,并注明其理由。
解:判断是否线性时,应从三个方面来判断:
①可分解性,即系统的输出响应可分解为零输入与零状态响应之和;
②零输入线性,系统的零输入的响应必须对所有的初始状态呈现线性特征;
③零状态线性,系统的零状态响应必须对所有的输入信号呈现线性特性。
只有这三个条件都符合,该系统才为线性系统。
(1)0() () zi zs y y t y bx t ==∴满足可分解性 判别零输入线性: 显然 判别零状态线性: 显然 ∴是线性系统
02 (),() (), y t dx t x t dt
⋅∴()响应满足分解性
零输入为具备线性特性
零状态为不具备线性特性
是非线性系统
∴(3) 满足可分解性,但零输入不符合迭加性是非线性系统
01211220
312331204 (),()() ()2(), ()2()()()() ()2()2[()()]t
t
zs zs t zs y t x t x t y t x d y t x d x t ax t bx t y t x d ax bx ττττ
ττττ===+==+⎰⎰⎰()响应满足分解性
零输入为3具备线性特性 判别零状态线性:
设输入为、时系统的零状态响应分别为 当系统起始状态为时,系统的零状态响应为:
120
12 2()2() ()() t
t
t
zs zs d x d x d ay t by t τ
ττττ
=+=+∴⎰⎰⎰满足零状态线性
三个特性都满足,是线性系统。
005 y y , , zi zs ∴()(t)=y(t )sin5t (t)=tx(t)响应满足分解性零输入为y(t )sin5t 具备线性特性零状态为tx(t)具备线性特性是线性系统,但是时变系统。
02
6 (), 3(), y t t x t ∴()响应满足分解性
零输入为具备线性特性
零状态为具备线性特性,但是时变的是线性时变系统。
