圆的认识第一课时练习题
北师大版六年级数学上册第一单元《圆》全部课时练习附答案(共11份)
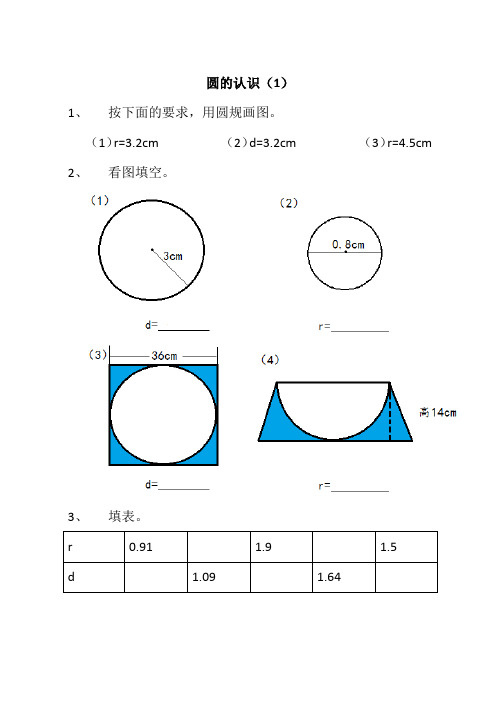
圆的认识(1)1、按下面的要求,用圆规画图。
(1)r=3.2cm (2)d=3.2cm (3)r=4.5cm 2、看图填空。
3、填表。
4、用圆规画一个半径是1.6cm的圆,并用字母o、r、d标出它的圆心、半径和直径。
参考答案1、2、(1)6cm (2)0.4cm (3)36cm (4)14cm3、填表。
4、用圆规画一个半径是1.6cm的圆,并用字母o、r、d标出它的圆心、半径和直径。
圆的认识(2)一、填空:1、画圆时,圆规两脚之间的距离为4厘米,那么这个圆的直径是()厘米。
2、在一个边长为4分米的正方形里,画一个最大的圆,这个圆的直径为( )分米,半径为( )分米。
二、判断:1、直径总比半径长。
()2、通过圆心的线段,叫做直径。
()三、操作题。
1、画一个直径为6厘米的圆。
并且用字母表示出半径、直径、圆心。
参考答案一、1、8 2、 4 2二、1、× 2、×三、圆的认识(3)1、下面的图形哪些是轴对称图形?在轴对称图形下面的()里画“√”。
()()()()2、画出下面轴对称图形的对称轴,并在()里注明它们各有几条对称轴。
()条()条()条()条()条3参考答案1.(√)(√)(√)(×)2.3.欣赏与设计1.在下面的图形中涂上颜色,设计出你喜欢的图案。
2.你能画出下面美丽的图案吗?试一试。
3.画出下面的美丽图案。
参考答案每一题,只要符合题意的答案都行。
圆的周长(1)一、用心填一填。
圆的周长和直径的()叫做圆周率。
二、火眼金睛辨对错。
1.π=3.14()2.小圆的圆周率比大圆的圆周率小。
()三、在长方形中有三个大小相等的圆,已知这个长方形的长是18cm,圆的直径是多少?长方形的周长是多少?参考答案一、比值二、 1.× 2.×三、18÷3=6(厘米)(18+6)×2=48(厘米)答:圆的直径是6厘米,长方形的周长是48厘米。
圆的周长(2)一、用心填一填。
圆的认识练习题

认识圆习题(一)基础测试1.填空。
(1)圆中心的一点叫做,用字母表达,它到圆上任意一点的距离都。
(2)叫做半径,用字母表达。
(3)叫做直径,用字母表达。
(4)在一种圆里,有条半径、有条直径。
(5)拟定圆的位置,拟定圆的大小。
(6)在一种直径是8 分米的圆里,半径是厘米。
(7)画圆时,圆规两脚间的距离是圆的。
(8)在同一圆内,全部的都相等,全部的也相等。
的长度等于长度的 2 倍。
(9)圆有条对称轴,每条对称轴都过它的。
(10)一种正方形最多能够画对称轴。
2.判断。
(1)直径都是半径的 2 倍。
()(2)同一种圆中,半径都相等。
()(3)同一圆中,在连接圆上任意两点的线段中,直径最长。
()(4)画一种直径是 4 厘米的圆,圆规两脚应叉开 4 厘米。
()(5)对称轴两侧相对的点到对称轴的距离相等。
()3.选择题。
(1)圆是平面上的()①直线图形②曲线图形③无法拟定(2)圆中两端都在圆上的线段,()①一定是圆的半径②一定是圆的直径③无法拟定(3)圆的直径有()条。
①1②2③无数4.填表。
5.下面哪些图形是轴对称图形,画出轴对称图形的对称轴。
6.按规定画圆。
(1)半径是 2 厘米。
(2)直径是 3 厘米。
综合测试1.画出下面图形的另二分之一,使它们成为轴对称图形。
2.在下面的图形中涂上你喜欢的颜色,使图案更美丽。
3.运用圆规和直尺画出下面美丽的图案。
参考答案:基础测试。
1.填空。
(1)圆心o 相等(2)连接圆心和圆上任意一点的线段r(3)通过圆心并且两端都在圆上的线段 d(4)无数无数(5)圆心半径长度(6)40(7)半径长度(8)半径直径直径半径(9)无数圆心(10)4 条2.判断。
(1)×(2)√(3)√(4)×(5)√3.选择题。
(1)②(2)③(3)③4.填表。
2 3.5 1.6 5.2 8.525.略6.略综合测试。
1.略2.略3.略。
(北师大版)六年级数学上册《圆》第1课时《圆的认识(一)》课时测评

第 1 课时
圆的认识(一)
1.填空不困难,全对不简单。
(1)在右图中,点()是圆心,线段()是半径,线段()是直径。
(2)同一圆内有()条直径,()条半径。
(3)()决定圆的大小,()决定圆的位置。
(4)用圆规画一个半径为5厘米的圆,圆规两脚间的距离是()。
如果画一个直径为6厘米的圆,则圆规两脚间的距离是()。
(5)车轮都要做成圆形的,车轴应该装在()的位置上。
2.我是小法官,对错我会判。
(1)以某一点为圆心只可以画一个圆。
()
(2)所有的半径都相等,所有的直径都相等。
()
(3)下面各图只有C图中的线段是直径。
()
3.知识全掌握,轻松做选择。
(1)在日常生活中,我们所见到的下水井盖一般都制成()形。
A.正方B.长方C.圆
(2)在同一个圆中最长的一条线段是()。
A.半径B.直径C.直线
(3)画一个直径为5厘米的圆,圆规两脚之间的距离是()。
A.5厘米B.10厘米C.2.5厘米
4.动动小脑瓜,一起画一画。
(1)用你喜欢的方法画一个圆,并标出它的圆心,半径和直径。
(2)画一个半径是1.5厘米的圆。
(3)以A点为圆心,画两个大小不等的圆。
你能想办法找出下面圆的圆心吗?。
数学六年级上册圆的认识课时习题(含答案)

《5.1圆的认识》选择题1.要画一个直径为6厘米的圆,圆规两脚尖的距离是( )厘米.A.6B.3C.12D.无法确定2.直径是通过圆心并且两端都在圆上的( )A.直线B.射线C.线段D.折线3.画圆时,( )决定圆的位置,( )决定圆的大小.A.圆规B.半径C.圆心D.无法确定4.如图中圆的直径是6厘米,则正方形的面积是()A.9.42cm2B.18cm2C.25cm2D.28.26cm25.所有的车轮都做成圆形是利用了圆的( )特性.A.曲线B.美观C.圆心到圆上任意一点的距离相等填空题6.在同一个圆里,两端在圆上的所有线段中,(________)最长。
7.用圆规画一个直径是8cm的圆,圆规两脚尖的距离应该是(___)cm.8.如图,一个圆有无数条对称轴,对折后的折痕所在的直线都是对称轴,它们都交于一点,这个点就是_____,这些折痕就是_____.9.在一个直径是10cm的圆形纸片上剪下一个最大的正方形,这个正方形的面积是cm2.10.连接圆心和圆上任意一点的线段是_____,通过圆心并且两端都在圆上的线段是_____.判断题11.两个半圆一定能拼成一个整圆.(____)12.在同一个圆内,两端在圆上的线段中,直径最长.(_____)13.彬彬说:圆的每一条对称轴都是圆的直径._____.14.半径是直径的一半。
(_______)15.每一个圆的直径都相等.(____)计算题16.口算0.6×2=9.3÷0.03= 3.14×2=×49=÷3=2.5×0.4=35.7÷0.7=3.14×0.5=×=÷=17.如图已知长方形周长30厘米,求长方形的面积.解决问题18.一个圆的半径是4cm,求阴影部分面积.19.在一个长方形内有两个相同的圆(如图),这个长方形的面积是多少平方分米?20.一个平面封闭图形,只要组成它的边中有一条边不是直线段,就将这个图形称为曲边形,例如圆、半圆、扇形等都是曲边形,在图中,共有多少个不同的曲边形?21.一块长1米20厘米,宽90厘米的铝皮,剪成直径是30厘米的铝锅底,最多可以剪几块?22.图中,圆的半径是多少厘米?圆的直径是多少厘米?参考答案1.B2.C3.CB4.B5.C6.直径7.48.圆心直径9.5010.半径直径11.×12.正确13.×14.×15.×16.1.2 310 6.28 213101 51 1.5712217.50平方厘米18.32cm2 19.72平方分米20.59个21.12块22.4厘米;8厘米。
数学六年级上册《圆的认识》一课一练(含答案)

第五单元《圆》第1课时《圆的认识》一.选择题1.两端都在圆上的线段()A.一定是直径B.不一定是直径C.一定不是直径2.在观看马戏表演的时候,人们一般都会围成圆形.这是应用了圆特征中()A.圆心决定圆的位置B.半径决定圆的大小C.同圆中的半径都相等D.同圆中直径是半径的2倍3.以一点为圆心可以画()个圆.A.1 B.2 C.无数4.世界上第一个把圆周率的值精确到六位小数的数学家是()A.刘徽B.祖冲之C.欧几里德5.以一点为圆心可以画出()个圆.A.1 B.2 C.无数D.无答案6.通过圆心并且两端都在圆上的()叫做圆的直径.A.射线B.线段C.直线7.两个大小不相等的圆,大圆的周长除以它的直径所得的商()小圆的周长除以它的直径所得的商.A.大于B.等于C.小于8.在2300多年前,()给出了圆的概念:“圆,一中同长也.”A.墨子B.希腊数学家欧几里得C.祖冲之9.圆的位置和大小分别是由()决定的.A.半径和直径B.直径和圆心C.圆心和半径二.填空题10.连接圆心和圆上任意一点的线段叫做,用字母表示.11.圆是图形,它的对称轴是,它有条这样的对称轴.12.一个圆的周长总是它的直径的.13.圆的周长与直径的比值用字母表示是,这个比值表示的是.14.圆沿一条直线滚动时,圆心也在一条上运动,并且当圆滚动一周时,圆心所走过的距离等于圆的.15.圆是图形,直径所在的直线是圆的,圆有条对称轴.三.判断题16.直径是圆内最长的线段.(判断对错)17.任意一个圆的周长与它的直径的比值是3.14..(判断对错)18.圆的周长总是它直径的3倍多一些.(判断对错)19.两个圆的大小不同,周长和直径的比值也不同..(判断对错)20.直径一定比半径长..(判断对错)四.解答题21.圆的半径的长度是直径的..22.在一个圆中画有一条线段,怎样可以判断这条线段是否是所在圆的半径?(至少写出两种方法)23.圆内所有的线段中,直径最长..24.在一个圆中画有一条线段,怎样可以判断这条线段是否是所在圆的半径?(至少写出两种方法)25.π是一个无限不循环小数..参考答案第五单元《圆》第1课时《圆的认识》一.选择题1.两端都在圆上的线段()A.一定是直径B.不一定是直径C.一定不是直径【解答】解:因为通过圆心并且两端都在圆上的线段叫做直径,所以两端都在圆上的线段不一定是直径.故选:B.2.在观看马戏表演的时候,人们一般都会围成圆形.这是应用了圆特征中()A.圆心决定圆的位置B.半径决定圆的大小C.同圆中的半径都相等D.同圆中直径是半径的2倍【解答】解:在观看马戏表演的时候,人们一般都会围成圆形.这是应用了圆特征中同圆中的半径都相等.故选:C.3.以一点为圆心可以画()个圆.A.1 B.2 C.无数【解答】解:以一点为圆心,以任意长为半径可以画无数个同心圆,故选:C.4.世界上第一个把圆周率的值精确到六位小数的数学家是()A.刘徽B.祖冲之C.欧几里德【解答】解:世界上第一个把圆周率的值精确到六位小数的数学家是祖冲之.故选:B.5.以一点为圆心可以画出()个圆.A.1 B.2 C.无数D.无答案【解答】解:以一点为圆心,以任意长为半径可以画无数个同心圆,故选:C.6.通过圆心并且两端都在圆上的()叫做圆的直径.A.射线B.线段C.直线【解答】解:通过圆心,并且两端都在圆上的线段叫做圆的直径;故选:B.7.两个大小不相等的圆,大圆的周长除以它的直径所得的商()小圆的周长除以它的直径所得的商.A.大于B.等于C.小于【解答】解:两个大小不相等的圆,大圆的周长除以它的直径所得的商等于小圆的周长除以它的直径所得的商;故选:B.8.在2300多年前,()给出了圆的概念:“圆,一中同长也.”A.墨子B.希腊数学家欧几里得C.祖冲之【解答】解:在2300多年前,墨子给出了圆的概念:“圆,一中同长也.”故选:A.9.圆的位置和大小分别是由()决定的.A.半径和直径B.直径和圆心C.圆心和半径【解答】解:圆的位置和大小分别是由圆心和半径决定的;故选:C.二.填空题10.连接圆心和圆上任意一点的线段叫做半径,用字母r表示.【解答】解:连接圆心和圆上任意一点的线段叫做半径,用字母r表示;故答案为:半径,r.11.圆是轴对称图形,它的对称轴是直径所在的直线,它有无数条这样的对称轴.【解答】解:圆是轴对称图形,它的对称轴是直径所在的直线,它有无数条对称轴.故答案为:轴对称,直径所在的直线,无数.12.一个圆的周长总是它的直径的π倍.【解答】解:根据圆周率的含义,可得:圆的周长总是它直径的π倍;故答案为:π倍.13.圆的周长与直径的比值用字母表示是π,这个比值表示的是圆周率.【解答】解:圆的周长与直径的比值用字母表示是π,这个比值表示的是圆周率;故答案为:π,圆周率.14.圆沿一条直线滚动时,圆心也在一条直线上运动,并且当圆滚动一周时,圆心所走过的距离等于圆的周长.【解答】解:圆沿一条直线滚动时,圆心也在一条直线上运动,并且当圆滚动一周时,圆心所走过的距离等于圆的周长;故答案为:直线,周长.15.圆是轴对称图形,直径所在的直线是圆的对称轴,圆有无数条对称轴.【解答】解:圆是轴对称图形,直径所在的直线都是圆的对称轴,圆有无数条对称轴;故答案为:轴对称,对称轴,无数.三.判断题16.直径是圆内最长的线段.√(判断对错)【解答】解:通过直径的定义可知:在一个圆中,圆内最长的线段是圆的直径的说法是正确的;故答案为:√.17.任意一个圆的周长与它的直径的比值是3.14.错误.(判断对错)【解答】解:由分析知:周长与直径的比值应是π,不是3.14;故答案为:错误.18.圆的周长总是它直径的3倍多一些.√(判断对错)【解答】解:根据分析可知,不管圆的大小,它的周长总是直径的3倍多一些;所以上面的说法正确.故答案为:√.19.两个圆的大小不同,周长和直径的比值也不同.×.(判断对错)【解答】解:根据圆周率的含义得出:大小不同的两个圆的周长都是它们各自直径的π倍,即周长和它的直径的比值是相同的.所以原题的说法错误.故答案为:×.20.直径一定比半径长.×.(判断对错)【解答】解:必须在同圆或等圆中,直径才比半径长.所以上面的说法是错误的.故答案为:×.四.解答题21.圆的半径的长度是直径的.×.【解答】解:在同一个圆或等圆中,圆的半径的长度是直径的.故答案为:×.22.在一个圆中画有一条线段,怎样可以判断这条线段是否是所在圆的半径?(至少写出两种方法)【解答】解:圆的半径是从圆心到圆周上任意一点的线段;方法①:把圆规的两脚放在线段的端点上,固定一端,看另一端旋转是否与圆重合;方法②:这条线段从圆心出发,另一端是否在圆周上.方法③把圆形纸片沿着线段AB对折,再对折,如果圆的边沿能够完全重合,且展开后,观察,如果B 点在两条相互垂直的折痕的交点上,这条线段就为所在圆的半径,否则不是所在圆的半径.23.圆内所有的线段中,直径最长.正确.【解答】解:根据直径的含义可知:同一圆中的所有线段,直径最长;故答案为:正确.24.在一个圆中画有一条线段,怎样可以判断这条线段是否是所在圆的半径?(至少写出两种方法)【解答】解:圆的半径是从圆心到圆周上任意一点的线段;方法①:把圆规的两脚放在线段的端点上,固定一端,看另一端旋转是否与圆重合;方法②:这条线段从圆心出发,另一端是否在圆周上.方法③把圆形纸片沿着线段AB对折,再对折,如果圆的边沿能够完全重合,且展开后,观察,如果B 点在两条相互垂直的折痕的交点上,这条线段就为所在圆的半径,否则不是所在圆的半径.25.π是一个无限不循环小数.√.【解答】解:因为π的小数数位是无限的,且没有出现循环的数字,所以π是一个无限不循环小数.故答案为:√.。
(完整版)圆认识练习

圆的认识练习部门: xxx时间: xxx整理范文,仅供参照,可下载自行编写圆的认识 <一)练习题一、填空。
1、画圆时,固定的一点叫做<),常用字母< )表示;从<)到 < )随意一点的线段叫做半径,常用字母 < )表示;通过圆心而且两头都在圆上的线段,叫做<),常用字母<)表示。
b5E2RGbCAP2、画圆时,<)确立圆的地点,<)确立圆的大小。
3、在同一个圆中,能够画<)条半径,<)条直径。
<)厘M,4、画一个直径为 4 厘M的圆,圆规两脚间的距离应取半径是 <)厘M。
二、下边的图中是半径或直径的打“√”,并标上相应的字母。
<)<)<)<)<)<)三、判断1、两头都在圆上的线段叫做直径。
<)2、半径必定比直径短。
<)3、圆的半径是一条射线,直径是一条直线。
<)4、圆有无数条直径,也有无数条半径。
<)5、圆规两脚间的距离是 5 厘 M,这个圆的直径就是 5 厘 M。
<)四、画一画。
<1 )、画一个直径是 2 厘 M的圆。
并标出圆心、直径和半径。
<2)、画一个半径是 2 厘 M的圆,并标出圆心、直径和半径。
思虑题:求出圆的半径和直径。
r = d =r = d =圆的认识 <二)练习题一、填空。
1、圆是 <)图形,直径所在的直线是圆的<),圆有<)条对称轴。
2、在同一个圆内,直径的长度是半径的<)倍,d = (>。
半径是直径的<), r = (>。
p1EanqFDPw3、一种部件的横截面是圆形,它的半径是8 厘M,它的直径是<)厘 M。
4、一个圆的直径是8 厘M,它的半径是<)厘M。
假如这个圆的直径增添 2 厘M,它的半径是<)厘M;假如这个圆的半径减少2 厘M,它的直径是<)厘M。
【强烈推荐】六年级圆的认识(一)第1课时练习题
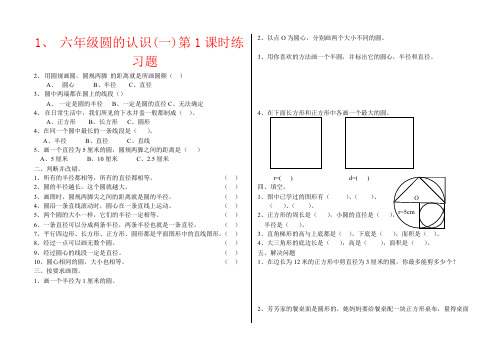
1、六年级圆的认识(一)第1课时练习题2、用圆规画圆,圆规两脚的距离就是所画圆额()A、圆心B、半径C、直径3、圆中两端都在圆上的线段()A、一定是圆的半径B、一定是圆的直径C、无法确定4、在日常生活中,我们所见的下水井盖一般都制成()。
A、正方形B、长方形C、圆形4、在同一个圆中最长的一条线段是()。
A、半径B、直径C、直线5、画一个直径为5厘米的圆,圆规两脚之间的距离是()A、5厘米B、10厘米C、2.5厘米二、判断并改错。
1、所有的半径都相等,所有的直径都相等。
()2、圆的半径越长,这个圆就越大。
()3、画图时,圆规两脚尖之间的距离就是圆的半径。
()4、圆沿一条直线滚动时,圆心在一条直线上运动。
()5、两个圆的大小一样,它们的半径一定相等。
()6、一条直径可以分成两条半径,两条半径也就是一条直径。
()7、平行四边形、长方形、正方形、圆形都是平面图形中的直线图形。
()8、经过一点可以画无数个圆。
()9、经过圆心的线段一定是直径。
()10、圆心相同的圆,大小也相等。
()三、按要求画图。
1、画一个半径为1厘米的圆。
2、以点O为圆心,分别画两个大小不同的圆。
3、用你喜欢的方法画一个半圆,并标出它的圆心,半径和直径。
4r=( ) d=( )四、填空。
1、图中已学过的图形有()、()、()、()。
2、正方形的周长是(),小圆的直径是(半径是()。
3、直角梯形的高与上底都是(),下底是(),面积是()。
4、大三角形的底边长是(),高是(),面积是()。
五、解决问题1、在边长为12米的正方形中剪直径为3厘米的圆,你最多能剪多少个?2、芳芳家的餐桌面是圆形的,她妈妈要给餐桌配一块正方形桌布,量得桌面直径是1.5米,桌子高1.2米,要使正方形桌布的四角刚好接触地面,正方形桌布的对角线应是多少米?。
圆认识第一课时复习练习题

圆的认识第一课时练习题一、目标导学1.认识圆的半径、直径的看法,认识圆的直径和半径之间的关系。
2.理解圆的特色及圆的圆心和半径的作用,会用圆规画圆。
3.能用圆来讲解简单生活现象。
二、填空。
1.圆中心的一点叫 _______, 平时用字母 _________来表示。
2. 连接_________到________任意一点的线段叫做_________。
一般用字母______表示。
用圆规画圆时,把圆规两脚分开,两脚之间的距离就是圆的_______。
3.经过 ________并且两端都在 _________的线段叫做 _______。
一般用字母______表示。
是一个圆内最长的线段。
4.一个圆有 _______个圆心,一个圆心可以画 ______个圆。
5.平时画圆所用的工具是 ___________,圆规两脚之间的距离是 _________。
6.圆规两脚之间的距离是 6 厘米能画出半径是的 ___________圆。
7. 圆规两脚之间的距离是 3 厘米能画出直径是的 ___________圆。
8. 要画出直径为10 厘米的圆,圆规两脚之间的的距离应该为___________。
9. 分针转动一周,尖端所走的行程所形成的图形是___________。
10.在同圆或等圆内 , 有_________条半径,有 ________条直径。
所有的 _______都相等,所有的直径都__________。
11.在同圆或等圆内,直径的长度是半径的______倍,用字母表示为___________;半径的长度是直径的 _________,用字母表示为 ___________。
12.__________确定圆的地址, __________确定圆的大小。
13.若是一个图形沿着一条直线对折,两侧的图形可以完好重合,这个图形是___________图, 圆是轴对称图形且有 __________条对称轴。
三、判断。
1.两端都在圆上的线段,叫做圆的直径。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
12.__________确定圆的位置,__________确定圆的大小。
13.如果一个图形沿着一条直线对折,两侧的图形能够完全重合,这个图形是___________图,圆是轴对称图形且有__________条对称轴 。
圆的认识第一课时练习题
一、目标导学
1.认识圆的半径、直径的概念,了解圆的直径和半径之间的关系。
2.理解圆的特征及圆的圆心和半径的作用,会用圆规画圆。
3.能用圆来解释简单生活现象。
二、填空。
1.圆中心的一点叫_______, 通常用字母_________来表示。
2.连接_________到________任意一点的线段叫做_________。一般用字母______表示。用圆规画圆时,把圆规两脚分开,两脚之间的距离就是圆的_______。
三、判断。
1.两端都在圆上的线段,叫做圆的直径。 ( )
2.以某一点为圆心,只可以画一个圆。 ( )
3.所有圆的直径都相等。 ( )
4.圆的半径越大,圆就越大。 ( )
5.半径是射线,直径是线段。 ( )
6.直径是8的圆比半径是5的圆大。 ( )
7.以某一点为圆心只能画一个圆。 ( )
8.在同一圆里,两条半径Байду номын сангаас是一条直径。 ( )
2.已知有图中小圆的半径为1cm,
(1)大圆的直径为( )cm。
(2)正方形的边长为( )cm。
3.通过________并且两端都在_________的线段叫做_______。一般用字母______表示。是一个圆内最长的线段。
4.一个圆有_______个圆心,一个圆心可以画______个圆。
5.通常画圆所用的工具是___________,圆规两脚之间的距离是_________。
6.圆规两脚之间的距离是6厘米能画出半径是的___________圆。
9.半径是直径的一般,直径是半径的2倍。 ( )
10.直径确定圆的位置。 ( )
四、按照要求用圆规画圆,并用字母标出圆心、半径、直径。
1.过A点画一个半径为2厘米的圆;
A.
2.以B点为圆心画两个半径分别为1厘米和2.5厘米的圆。
B.
3.以C为圆心,画一个直径为4厘米的圆。
C.
四、看图填空。
五、1.已知右图中长方形中小圆的半径为1cm,则 长方形的长为( )cm,宽为( )cm。
7.圆规两脚之间的距离是3厘米能画出直径是的___________圆。
8.要画出直径为10厘米的圆,圆规两脚之间的的距离应该为___________。
9.分针转动一周,尖端所走的路程所形成的图形是___________。
10.在同圆或等圆内,有_________条半径,有________条直径。所有的_______都相等,所有的直径都__________。
