逐次逼近法(1)
ISIGHT里面的优化方法

ISIGHT里面的优化方法大致可分为三类:1 数值优化方法数值优化方法通常假设设计空间是单峰值的,凸性的,连续的。
iSIGHT中有以下几种:(1)外点罚函数法(EP):外点罚函数法被广泛应用于约束优化问题。
此方法非常很可靠,通常能够在有最小值的情况下,相对容易地找到真正的目标值。
外点罚函数法可以通过使罚函数的值达到无穷值,把设计变量从不可行域拉回到可行域里,从而达到目标值。
(2)广义简约梯度法(LSGRG2):通常用广义简约梯度算法来解决非线性约束问题。
此算法同其他有效约束优化一样,可以在某方向微小位移下保持约束的有效性。
(3)广义虎克定律直接搜索法:此方法适用于在初始设计点周围的设计空间进行局部寻优。
它不要求目标函数的连续性。
因为算法不必求导,函数不需要是可微的。
另外,还提供收敛系数(rho),用来预计目标函数方程的数目,从而确保收敛性。
(4)可行方向法(CONMIN):可行方向法是一个直接数值优化方法,它可以直接在非线性的设计空间进行搜索。
它可以在搜索空间的某个方向上不断寻求最优解。
用数学方程描述如下:Design i = Design i-1 + A * Search Direction i方程中,i表示循环变量,A表示在某个空间搜索时决定的常数。
它的优点就是在保持解的可行性下降低了目标函数值。
这种方法可以快速地达到目标值并可以处理不等式约束。
缺点是目前还不能解决包含等式约束的优化问题。
(5)混合整型优化法(MOST):混合整型优化法首先假定优化问题的设计变量是连续的,并用序列二次规划法得到一个初始的优化解。
如果所有的设计变量是实型的,则优化过程停止。
否则,如果一些设计变量为整型或是离散型,那么这个初始优化解不能满足这些限制条件,需要对每一个非实型参数寻找一个设计点,该点满足非实型参数的限制条件。
这些限制条件被作为新的约束条件加入优化过程,重新优化产生一个新的优化解,迭代依次进行。
在优化过程中,非实型变量为重点考虑的对象,直到所有的限制条件都得到满足,优化过程结束,得到最优解。
51单片机adc0809模数转换器逐次逼近法的实现原理

51单片机adc0809模数转换器逐次逼近法的实现原
理
51单片机ADC0809模数转换器采用逐次逼近法实现模数转换。
逐次逼近法的原理是,从高位到低位逐位比较,根据比较结果不断调整待转换的数字量,直到找到一个数字量使其对应的模拟量与输入的模拟量相等或最大程度接近。
在ADC0809模数转换器中,逐次逼近法的实现过程如下:
1. 将最高位(MSB)设置为1,其余位为0,形成起始转换数字量。
2. 将该数字量输入比较器,与输入的模拟量进行比较。
3. 根据比较结果,调整数字量的最高位:如果模拟量大于数字量,则将最高位清0;否则保持为1。
4. 保持其余位不变,将调整后的数字量再次输入比较器进行比较。
5. 重复步骤3和4,直到比较器的输出为稳定状态(即最高位不再变化),此时得到的就是输入模拟量的近似值。
通过逐次逼近法,ADC0809模数转换器能够实现高精度的模数转换,并且具有较快的转换速度。
基于51单片机的简易数字电压表的设计单片机

基于51单片机的简易数字电压表的设计单片机————————————————————————————————作者:————————————————————————————————日期:2个人收集整理勿做商业用途甘肃畜牧工程职业技术学院毕业设计题目:基于51单片机的简易数字电压表的设计系部:电子信息工程系专业:信息工程技术班级:学生姓名:学号:指导老师:日期:目录毕业设计任务书 (1)开题报告 (3)摘要 (6)关键词 (7)引言 (7)第一章A/D转换器 (9)1.1A/D转换原理 (9)1.2 ADC性能参数 (11)1.2.1 转换精度 (11)1.2.2。
转换时间......................................... 错误!未定义书签。
1.3 常用ADC芯片概述 (13)第二章8OC51单片机引脚 (14)第三章ADC0809 (16)3。
1 ADC0809引脚功能 (16)3。
2 ADC0809内部结构 (18)3.3ADC0809与80C51的接口 (19)3.4 ADC0809的应用指导 (20)3.4。
1 ADC0809应用说明 (20)3.4.2 ADC0809转换结束的判断方法 (20)3。
4.3 ADC0809编程方法 (21)第四章硬件设计分析 (22)4。
1电源设计 (22)4.2 关于74LS02,74LS04 (22)4。
3 74LS373概述 (23)4。
3。
1 引脚图 (23)4。
3。
2工作原理 (23)4.4简易数字电压表的硬件设计 (24)结论 (25)参考文献 (25)附录.......................................................................................... 错误!未定义书签。
致谢 (29)毕业设计任务书学生姓名专业班级信息工程技术08。
2指导教师论文题目基于51单片机的简易数字电压表的设计研究的目标、内容及方法目标:基于MCS—51单片机,对设计硬件电路和软件程序应用的设计,使用发光二极管来显示所要测试模拟电压的数字电压值。
简述逐次逼近法的工作原理

简述逐次逼近法的工作原理
逐次逼近法是一种数值计算方法,用于求解近似解的近似值。
其主要工作原理如下:
1. 初始化:选择一个初始值作为近似解的初始近似值。
2. 迭代过程:根据某种规则进行迭代,每次迭代都会产生一个较接近真实解的近似值。
3. 收敛判断:判断近似解是否足够接近真实解。
如果接近程度满足预定的收敛准则,则输出近似解;否则返回第2步进行下一次迭代。
4. 输出结果:输出满足收敛准则的近似解作为最终结果。
逐次逼近法的核心思想是不断迭代,通过每一次迭代对近似解进行修正,逐渐接近真实解。
在迭代过程中,常用的方法有不动点迭代法、Newton-Raphson迭代法等等。
这些方法在每一步迭代中通过一定的数学计算方式来更新近似解,并不断逼近真实解。
逐次逼近法的优点是易于实现和理解,适用于一些求解复杂方程或函数的数值解问题。
然而,它的收敛速度可能很慢,对于某些问题可能无法得到满意的解。
因此,在应用中需要根据具体问题选择合适的迭代方法,以提高计算效率和准确性。
第四章逐次逼近法

(k )
( D L)1 b
令 BG ( D L)1U , fG ( D L) 1 b
则
x ( k 1) BG x ( k ) fG (k 0,1,)
3.1.2 迭代法的收敛性
考虑如下问题: ① 如何判断迭代过程是否收敛呢? ② 迭代格式收敛的充要条件、充分条件是什么? ③ 决定迭代收敛速度的因素是什么? 设某种迭代格式为
x
( k 1)
BJ x
(k )
f J (k 0,1,)
由 A D L U , 得 (D - L)x Ux b 从而
x D - L Ux D - L b
1 1
则Gauss-Seidel迭代法可以写成
x
( k 1)
( D L) Ux
则
A D L U
由 A D L U , 得 Dx ( L U ) x b 从而
x D1 L U x D1b
则Jacobi迭代法可写成为:
x
( k 1)
D
1
L U x
k
D 1b
k 0, 1, 2,
令 BJ = D 1 L U , f J D 1b, 则
定理 3.2
(k ) 迭代法 x ( k 1) Bx f 对任意 x ( 0 ) 和 f
均收敛的充要条件为: ( B) 1。
定理 3.3 (充分条件) 若 || B || 1 ,则迭代法收敛, 且有 证明
|| x
(k )
x ||
*
(1) (0) || B || (k ) ( k 1) x x || x x || 1 B 1 || B ||
非线性离散系统最优控制——逐次逼近方法

维普资讯
第 2期
刘 鹏 :非 线 性 离散 系统 最 优 控 制— — 逐 次逼 近 方 法
17 5
1 非 线 性 离 散 系统 描 述
考虑 如下 非线 性离散 系统 : 『( k+1 =S( ( ) 1 k ) k=0 1 2 … ) x k ,( ) 1 , , ,, 、 ( )= 【 O 0
() 4
除非特殊的情形 , 一般来说 I B方程 ( ) - I J 3 的解析解是不存在的。因此, 求解非线性系统的二次性能指 标 最 优控制 问题 的近 似解课题 引起 了不 少学 者 的兴趣 。 目前 , 国际上 比较 公认 的最 优控 制 的近 似 方法 可 以大体归结为 4 。第 1 类 种方法是求解非线性 I B方程的 G l k 逐次逼近法… ; 2 - I J a rn ei 第 种方法是求解非
维普资讯
第2 3卷第 2期
Vo . No. 123 2
重庆工 商 大学 学报 ( 自然科 学版 )
JC og igTc nl uiesU i, N t c E ) h nqn eh o B s s nv ( a i d n S
20 0 6年 4月
Ap .20 6 r 0
文章 编号 :6 2— 5 X( 0 6 0 0 5 0 17 0 8 2 0 ) 2— 1 6— 4
非 线 性 离 散 系统最 优 控 制
逐 次 逼 近 方 法
刘
鹏
(. 1重庆工商大学 计算 机科 学与信息工程学院 , 重庆 40 6 ) 0 0 7
摘 要 : 究 了非线性 离散 系统 最优 控制 问题 , 出一种逐 次逼 近方 法 ; 研 提 首先 将 系统 的 最优 控 制 问题 转化 为非 线性 两点边值 问题 族 , 然后 通过 构造 线 性 两 点边 值 问题 族 。 非线 性 两点 边 将
第6章 逐次逼近法

其中: BG (D L)1U, fG (D L)1b
四、迭代法的收敛性
定理:迭代法 x(k1) Bx(k) f 对任意 x(0) , f 收敛的充要条件是 (B) 1。
定理:设 x*为线性方程组的精确解,若 B 1,则迭代法 x(k1) Bx(k) f 收敛,且
有
x * x (k) B x(k) x(k1) 1 B
第 6 章 逐次逼近法
[教学目的与要求]
1.理解方程求根数值解法的基本思想; 2.掌握根的隔离的基本方法、二分法求根的基本思想与过程; 3.理解简单迭代法的基本思想、迭代函数的收敛性; 4.掌握埃特金迭代法; 5.掌握牛顿迭代法与插值法; 6.掌握迭代法的控制条件
[重点与难点]
重点:二分法、迭代法的基本思想、埃特金和牛顿迭代法。
x1 = 0.4771 x2 = 0.3939 …
x6 = 0.3758 x7 =0.3758 因为 x6 和 x7 已趋于一致,所以取 x7 = 0.3758 为原方程在[0, 1]内的一个根的近似值。 2、迭代的几何意义 3、迭代过程的收敛性 一个方程的迭代格式并不是唯一的,且迭代也不总是收敛的。如上例中取等价方程为
0
即
lim
k
xk
x*
(2)由定理中的条件得
xk1 xk x* xk (x* xk1 ) x* xk x* xk1 x* xk ( x*) (xk ) x* xk ( ) x* xk x* xk L x* xk (1 L) x* xk
x 10x 2
得迭代格式
xk1 10xk 2
仍取 x0 = 1 算得:
x1 10 2 8
x2 108 2 108
8
x3 10108 2,
突破“极限”教学难点 提升质疑创新能力——以气垫导轨实验教学为例
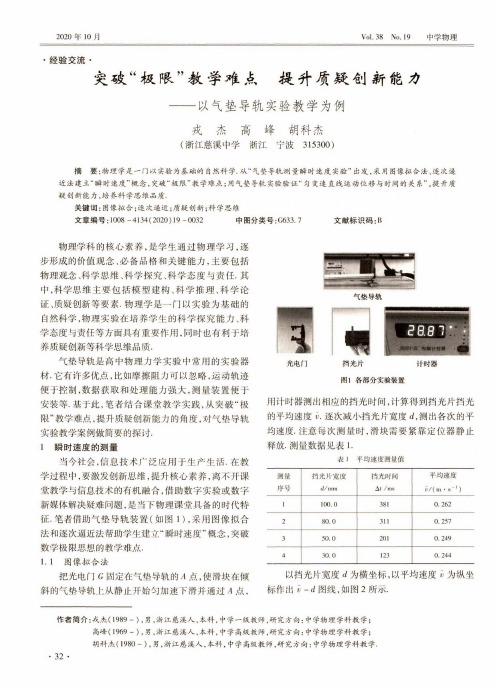
2020年10月Vol. 38 No. 19 中学物理・经验交流・突破“极限”教学堆占 提升质融创新能力——以气垫导轨实验教学为例戎杰高峰胡科杰•(浙江慈溪中学 浙江 宁波315300)摘要:物理学是一门以实验为基础的自然科学.从“气垫导轨测量瞬时速度实验”出发,采用图像拟合法、逐次逼近法建殳“瞬时速度”概念,突破“极限”教学难点;用气垫导轨实验验证“匀变速直线运动位移与时间的关系”,提升质疑创新能力,培养科学思维品质.关键词:图像拟合;逐次逼近;质疑创新;科学思维文章编号:1008 -4134(2020)19 -0032中图分类号:G633.7 文献标识码:B物理学科的核心素养,是学生通过物理学习,逐 步形成的价值观念、必备品格和关键能力,主要包括物理观念、科学思维、科学探究、科学态度与责任.其 中,科学思维主要包括模型建构、科学推理、科学论证、质疑创新等要素.物理学是一门以实验为基础的 自然科学,物理实验在培养学生的科学探究能力、科 学态度与责任等方面具有重要作用,同时也有利于培养质疑创新等科学思维品质•气垫导轨是高中物理力学实验中常用的实验器材•它有许多优点,比如摩擦阻力可以忽略,运动轨迹 便于控制,数据获取和处理能力强大,测量装置便于安装等.基于此,笔者结合课堂教学实践,从突破“极 限”教学难点,提升质疑创新能力的角度,对气垫导轨实验教学案例做简要的探讨.1瞬时速度的测量当今社会,信息技术广泛应用于生产生活•在教 学过程中,要激发创新思维,提升核心素养,离不开课堂教学与信息技术的有机融合,借助数字实验或数字 新媒体解决疑难问题,是当下物理课堂具备的时代特征•笔者借助气垫导轨装置(如图1),采用图像拟合法和逐次逼近法帮助学生建立“瞬时速度”概念,突破 数学极限思想的教学难点.1. 1图像拟合法把光电门G 固定在气垫导轨的4点,使滑块在倾斜的气垫导轨上从静止开始匀加速下滑并通过/1点,气垫导轨光电门持光片图1各部分实验装置用计时器测岀相应的挡光时间,计算得到挡光片挡光 的平均速度几逐次减小挡光片宽度d,测出各次的平均速度•注意每次测量时,滑块需要紧靠定位器静止 释放•测量数据见表1-表1平均速度测量值测量挡光片宽度挡光时间平均速度序号d/m m △/ /msv/(m • s _,)1100.03810. 262280.03110. 257350.02010.249430.01230.244以挡光片宽度d 为横坐标,以平均速度v 为纵坐标作出v -d 图线,如图2所示.作者简介:戎杰(1989 男,浙江慈溪人,本科,中学一级教师,研究方向:中学物理学科教学;高峰(1969 -),男,浙江慈溪人,本科,中学高级教师,研究方向:中学物理学科教学; 胡科杰(1980 -),男,浙江慈溪人,本科,中学高级教师,研究方向:中学物理学科教学.• 32•中学物理Vol.38No.192020年10月7 S ・®惓刘艸0.2750.2700.2650.2600.2550.2500.2450.2400.235^小0.0y=0.0003x+0.236250.0100.0y'=0.2362挡光片宽度d/mm图2平均速度与挡光片宽度的关系150.0以挡光时间M为横坐标,以平均速度”为纵坐标作出v-M图线,如图3所示.S•饅懒刘讯0.2700.2650.2600.2550.2500.2450.2400.2350.2300100200300400500挡光时间&/ms图3平均速度与挡光时间的关系测量表1中的数据时,滑块做匀加速运动的状态完全相同.当挡光片宽度变到无限小,或挡光时间d 无限短时,即或4—0时,平均速度的极限值就是挡光片通过光电门的瞬时速度.v -M图线在纵坐标轴上的截距就是d-0或时平均速度的极限值,即为滑块通过光电门G的瞬时速度”。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
设 Ax = b为一线性方程组 , A为非奇异矩阵 , x为其精确解
若常数项 b 存在误差 δ b , 则解也应存在误差 δ x
即有
A( x + δ x ) = b + δ b
--------(15)
Aδ x = δ b
所以 又因为 可得
δ x = A −1δ b
n× n
.
则称 A 为矩阵 A的范数 .
对于复空间 C n×n中的矩阵范数可以类似 定义
例2.
设 n阶方阵 A = ( aij ) n× n
类似向量的 2-范数 --------(5)
设 A
F
n n 2 = ∑ ∑ a ij i = 1 j =1
1
2
不难验证其满足定义2的4个条件
cond ( A )1 = A 1 ⋅ A cond ( A) ∞ = A
∞
−1 1 −1 ∞
T
⋅ A
1 cond ( A) 2 = A 2 ⋅ A 2 = λmax ( A A) λ min ( AT A) T λ max ( A A) = λmin ( AT A)
−1
根据定义7的定义,(18)式和(22)式可表示为
--------(8)
对于给定的向量范数 ⋅ υ 和矩阵范数 ⋅ µ , Ax ≤ A xυ
--------(9)
若 ∀x ∈ R n , A ∈ R n × n , 都有
υ µ
则称所给的向量范数 ⋅ υ 和矩阵范数 ⋅ µ 相容 .
由(8)式,可知算子范数和其对应的向量范数是相容的
根据向量的常用范数可以得到常用的矩阵算子范数
−1 −1
δx = A δb ≤ A
⋅ δb
--------(16)
b = Ax ≤ A ⋅ x
A 1 ≤ x b
--------(17)
(16)和(17)两式相乘 ,得
δx δb −1 ≤ A ⋅ A ⋅ x b
相对误差
--------(18)
(18)式表明,由常数项产生的误差,最多可将解的 −1 A ⋅ A 相对误差放大 倍
因此 A F 是不从属于任意向量范数 ⋅ υ 的矩阵范数
故而矩阵范数和算子范数并不完全是一回事
不过
A
F
n n 2 = ∑ ∑ aij i =1 j =
2 = (tr ( AT A)
1
)
1
Байду номын сангаас
2
= (tr ( AA )
T
)
1
2
A 2 = λmax ( AT A ) ≤ A Ax
(19)式化为
δ x = −( I + A δ A ) A δ A ⋅ x
--------(21)
δx ≤ ( I + A −1δA )−1 ⋅ A −1 ⋅ δA ⋅ x
A ⋅ δA δx ≤ ≤ −1 −1 1 − A ⋅ δA x 1 − A δA δA −1 A ⋅ A ⋅ A = --------(22) δA −1 1− A ⋅ A ⋅ A
2.系数矩阵A的扰动对方程组解的影响
若系数矩阵 A存在误差 δ A , 则解也应存在误差 δ x
( A + δ A)( x + δ x ) = b
δ A ⋅ x + Aδ x + δ A ⋅ δ x = 0
( A + δ A)δ x = −δ A ⋅ x
在上式能直接使用范数吗?
--------(19)
推论:设 A ∈ R n×n 可逆 , 且 A −1 ≤ α , C ∈ R n×n , A − C ≤ β , 且 αβ < 1, 则 C 可逆,且 C
−1
α ≤ 1 − αβ
( 摄动定理 )
二、误差分析简介 定义6. 对于线性方程组 Ax = b , 如果系数矩阵 A或
常数项 b的元素的微小变化 , 就会引起方程组解的 巨大变化 , 则称该方程组是 " 病态 "的 , A为" 病态 " 矩 阵.否则称为 "良态 "的.
2
F
≤ A
2
x
2
≤ A
F
x
2
因此 A F 与 x 2 相容
例4.
求矩阵A的各种常用范数
1 A = − 1 0
2
n
2 2 1
5
0 3 − 1 4 1 2
2
解:
A 1 = max ∑ aij = max { 2 ,5 , 2 } = 5
1≤ j ≤ n i =1
n
1≤ j ≤ n
( A + δ A) = A( I + A −1δ A )
如果假设
A δA < 1
I + A−1δ A非奇异 1 −1 −1 ( I + A δ A) ≤ 1 − A − 1δA
A( I + A δ A )δ x = −δ A ⋅ x
−1 −1 −1 −1
−1
--------(20)
则由定理1.,可知 且
--------(7)
Ax υ A υ = max x≠0 x υ
可以验证 A υ 满足定义 2的 4个条件
定义3. 由( 7 )式确定的 A 称为从属于给定向量 υ
范数 x υ 的矩阵范数
简称为从属范数或算子范数
显然,由定义不难推出
Ax
定义4.
υ
≤ Aυ xυ
--------(11)
(2)
A
∞
∞
A的每行绝对值之和的最大值 ,
称 A 的行范数
Ax 2 T --------(12) ( 3 ) A 2 = max = λ ( A A ) max x 2 x≠0 称 A的 λmax ( AT A)为AT A的特征值的绝对值的最 大值 2 − 范数
p p 1
并且由于
max xi ≤ ( x1
1≤ i ≤ n
+ x2
+ L + xn
1≤i≤ n
)
p
≤ ( n max xi )
1≤i≤ n
p
1
=n
x
p
1
p
max xi → max xi ( p → ∞ )
1≤i≤ n
→ x
∞
( p → ∞ 时 ), 所以 x 也是 x 的特例 ∞ p
且 x
∞
≤ x
λ max ( AT A) = 9.1428 A 2 = λmax ( AT A ) = 3.0237 A
F
= tr ( AT A) = 2 + 9 + 2 = 3.6056
A
∞
A1
容易计算
A
2
A
F
计算较复杂 对矩阵元素的 变化比较敏感 性质较好 使用最广泛
不是从属范数 较少使用
定义5. 设 A ∈ R n× n的特征值为 λ1 , λ 2 , L , λ n , 称
定义7. 设 A 为非奇异矩阵 , 称
−1
A −1 ⋅ δ A
cond ( A) = A ⋅ A
−1
--------(23)
为 A的条件数 , 其中 ⋅ 为某种算子范数 .
显然
cond ( A) = A ⋅ A
−1
≥ AA −1 = I = 1
即任意方阵的条件数必不小于1 根据算子范数的不同也有不同的条件数:
第六章
逐次逼近法
第六章 逐次逼近法
§6.1 基本概念
6.2 线性方程组的迭代法 § 6.3 非线性方程组的迭代法 § 6.4 矩阵特征值问题的数值算法 §
§6.5 迭代法的加速
本章要点 本章主要介绍线性方程组的迭代法、非线性方程组 的数值方法 主要方法 基本迭代法、G-J迭代法、G-S迭代法、 Newton迭代法、SOR方法和 Aitken加速方法
2
≤ x
1
例1.求下列向量的各种常用范数
x = ( 1 , 4 ,3 , − 1)T
解:
x x x
1
= x1 + x 2 + L + x 4 = 9
2
= ( x1 + x2 + L + x 4
= max xi = 4
1≤i≤ 4
2
2
2
) 2=
1
27 = 3 3
∞
定义2.
对于空间 R n× n中任意一个矩阵 A ,
n
若存在唯一一个实数 x ∈ R与 x对应,且满足
( 1) (正定性 ) x ≥ 0 , 且 ∀x ∈ R n , x = 0 ⇔ x = 0 ;
( 2 ) ( 齐次性 ) α x = α ⋅ x , ∀x ∈ R n , α ∈ R ;
( 3 ) ( 三角不等式 ) x + y ≤ x + y , ∀x , y ∈ R n .
例3. 判别矩阵 A的 Frobenius 范数 A F 是不是算子范数 解:
A 的 F − 范数为
A
F
n n 2 = ∑ ∑ a ij i=1 j=1
1
2
类似于向量的2-范数
但 A F 并不是从属于 x 2 的算子范数
考虑单位矩阵 I
I
F
= n
I
υ
Ix υ xυ = max = max =1 x x x≠0 x≠0 υ υ
ρ ( A ) = max{ λ 1 , λ 2 ,L , λ n }
