应用时间序列分析 第5章
统计基础知识第五章时间序列分析习题及答案

第五章时间序列分析一、单项选择题1.构成时间数列的两个基本要素是( C )(2012年1月)A.主词和宾词B.变量和次数C.现象所属的时间及其统计指标数值D.时间和次数2.某地区历年出生人口数是一个( B )(2011年10月)A.时期数列 B.时点数列C.分配数列D.平均数数列3.某商场销售洗衣机,2008年共销售6000台,年底库存50台,这两个指标是( C ) (2010年10)A.时期指标B.时点指标C.前者是时期指标,后者是时点指标D.前者是时点指标,后者是时期指标4.累计增长量( A ) (2010年10)A.等于逐期增长量之和B.等于逐期增长量之积C.等于逐期增长量之差D.与逐期增长量没有关系5.某企业银行存款余额4月初为80万元,5月初为150万元,6月初为210万元,7月初为160万元,则该企业第二季度的平均存款余额为( C )(2009年10)万元万元万元万元6.下列指标中属于时点指标的是( A ) (2009年10)A.商品库存量B.商品销售量C.平均每人销售额D.商品销售额7.时间数列中,各项指标数值可以相加的是( A ) (2009年10)A.时期数列B.相对数时间数列C.平均数时间数列D.时点数列8.时期数列中各项指标数值( A )(2009年1月)A.可以相加B.不可以相加C.绝大部分可以相加D.绝大部分不可以相加10.某校学生人数2005年比2004年增长了8%,2006年比2005年增长了15%,2007年比2006年增长了18%,则2004-2007年学生人数共增长了( D )(2008年10月)%+15%+18%%×15%×18%C.(108%+115%+118%)-1 %×115%×118%-1二、多项选择题1.将不同时期的发展水平加以平均而得到的平均数称为( ABD )(2012年1月)A.序时平均数B.动态平均数C.静态平均数D.平均发展水平E.一般平均数2.定基发展速度和环比发展速度的关系是( BD )(2011年10月)A.相邻两个环比发展速度之商等于相应的定基发展速度B.环比发展速度的连乘积等于定基发展速度C.定基发展速度的连乘积等于环比发展速度D.相邻两个定基发展速度之商等于相应的环比发展速度E.以上都对3.常用的测定与分析长期趋势的方法有( ABC ) (2011年1月)A.时距扩大法B.移动平均法C.最小平方法D.几何平均法E.首末折半法4.时点数列的特点有( BCD ) (2010年10)A.数列中各个指标数值可以相加B.数列中各个指标数值不具有可加性C.指标数值是通过一次登记取得的D.指标数值的大小与时期长短没有直接的联系E.指标数值是通过连续不断的登记取得的5.增长1%的绝对值等于( AC )(2010年1)A.增加一个百分点所增加的绝对量B.增加一个百分点所增加的相对量C.前期水平除以100D.后期水平乘以1%E.环比增长量除以100再除以环比发展速度6.计算平均发展速度常用的方法有( AC )(2009年10)A.几何平均法(水平法)B.调和平均法C.方程式法(累计法)D.简单算术平均法E.加权算术平均法7.增长速度( ADE )(2009年1月)A.等于增长量与基期水平之比B.逐期增长量与报告期水平之比C.累计增长量与前一期水平之比D.等于发展速度-1E.包括环比增长速度和定基增长速度8.序时平均数是( CE )(2008年10月)A.反映总体各单位标志值的一般水平B.根据同一时期标志总量和单位总量计算C.说明某一现象的数值在不同时间上的一般水平D.由变量数列计算E.由动态数列计算三、判断题1.职工人数、产量、产值、商品库存额、工资总额指标都属于时点指标。
第五章时间序列分析A

5月 282
6月 260
7月 270
平均库存额 (万元)
(1)将表格填写完整 (2)计算第一季度平均库存额和上半年年平均库存额
第五章A
• 2、简述时间序列的水平分析指标 • 答:发展水平、平均发展水平、增长量、 平均增长量 • 3、发展水平:又称发展量,是时间序列中 的各个指标数值,它反映现象在各个时期 (或时点)发展所达到的规模或水平,是计算 动态分析指标的基础
• 4、简述相对数时间数列计算序时平均数的 方法 • (1)分子序列和分母序列都为时期序列 • (2)分子分母都为时点序列 • (3)分子分母一个时期序列一个时点序列
1月 1日
工人数 1800
2月 1日
1850
3月 1日
1870
4月 1日
1872
职工数
2300
2350
2370
2372
一直该企业第一季度工业总产值为833.4万元
(1)该企业一季度工人占职工人数的比重
(2)一季度工人劳动生产率
月份
月初库存额 (万元)
1 280 272
时间序列分析方法第05章最大似然估计

时间序列分析方法第05章最大似然估计最大似然估计(Maximum Likelihood Estimation, MLE)是一种常用的统计学方法,用于估计时间序列模型的参数。
在时间序列分析中,最大似然估计可以用于估计自回归(AR)、移动平均(MA)、自回归滑动平均(ARMA)等模型的参数。
最大似然估计的基本思想是寻找最能解释已观测到的数据的模型参数。
具体来说,最大似然估计根据已观测到的数据样本,通过优化模型参数使得该样本的出现概率最大化。
换句话说,最大似然估计通过寻找最可能产生观测到的数据样本的模型参数值,来估计真实的未知参数值。
最大似然估计的主要步骤如下:1.选择合适的时间序列模型。
根据数据的特征和背景知识,确定适合的时间序列模型。
常见的时间序列模型包括AR、MA、ARMA、ARIMA等。
2.建立模型的似然函数。
似然函数是一个关于模型参数的函数,表示了在给定参数值的情况下,观测到数据样本的概率。
3.对似然函数取对数,得到对数似然函数。
似然函数通常非常复杂,可能难以直接处理。
取对数可以简化计算,并不改变估计值的最优性质。
4.求解对数似然函数的最大值。
通过优化算法(如牛顿法、梯度下降法)求解对数似然函数的最大值,得到最大似然估计值。
5.检验估计结果。
最大似然估计得到的估计值通常具有一些统计性质,可以进行假设检验、置信区间估计等。
最大似然估计方法在时间序列分析中具有广泛的应用,可以用于估计参数、进行模型选择和模型比较等。
然而,最大似然估计方法也有一些限制和假设,它假设数据是独立同分布的,且服从一些特定的概率分布。
对于一些时间序列数据,可能不满足这些假设,或者需要使用其他方法进行估计。
总之,最大似然估计是一种重要的时间序列分析方法,可以用于估计自回归、移动平均等模型的参数。
它通过优化模型参数,使得模型生成观测到的数据样本的概率最大化。
最大似然估计方法在实际应用中具有广泛的应用,并可以通过检验统计性质来评估估计结果的准确性和有效性。
时间序列5章例题
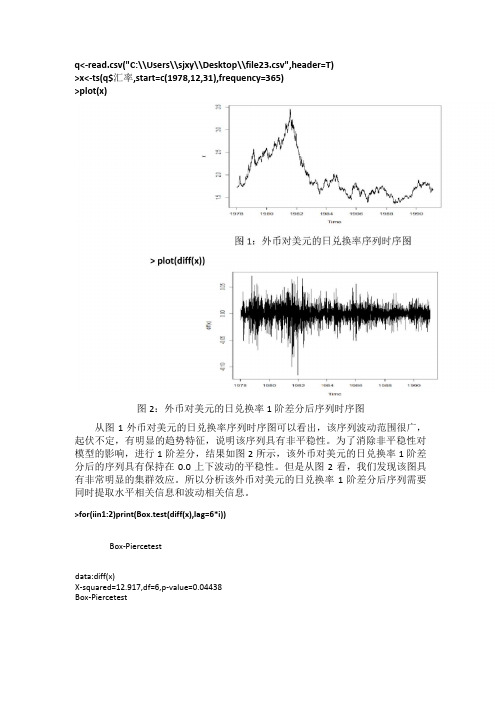
q<-read.csv("C:\\Users\\sjxy\\Desktop\\file23.csv",header=T)>x<-ts(q$汇率,start=c(1978,12,31),frequency=365)>plot(x)图2:外币对美元的日兑换率1阶差分后序列时序图从图1外币对美元的日兑换率序列时序图可以看出,该序列波动范围很广,起伏不定,有明显的趋势特征,说明该序列具有非平稳性。
为了消除非平稳性对模型的影响,进行1阶差分,结果如图2所示,该外币对美元的日兑换率1阶差分后的序列具有保持在0.0上下波动的平稳性。
但是从图2看,我们发现该图具有非常明显的集群效应。
所以分析该外币对美元的日兑换率1阶差分后序列需要同时提取水平相关信息和波动相关信息。
>for(iin1:2)print(Box.test(diff(x),lag=6*i))Box-Piercetestdata:diff(x)X-squared=12.917,df=6,p-value=0.04438Box-Piercetestdata:diff(x)X-squared=29.712,df=12,p-value=0.003085>acf(diff(x))图3:外币对美元的日兑换率1阶差分后序列自相关图>pacf(diff(x))Serie-sdifT<|x誉-Iaooaozo04o oa□oaa1oLag图4:外币对美元的日兑换率1阶差分后序列偏自相关图延迟6阶和12阶后,P值分别为p-value=0.04438、p-value=0.003085,且都小于置信水平0.05,说明该外币对美元的日兑换率1阶差分后的序列不是纯随机序列。
水平信息的提取主要是对差分后自相关与偏自相关的考察。
外币对美元的日兑换率1阶差分后序列自相关图如图3所示,该图在延迟1阶之后几乎所有值都落在2倍标准差区域内波动,具有突然衰减且衰减的速度非常快,根据衰减的速度判断,以及具有短期相关性,判断该自相关具有截尾性。
第五章、时间序列分析1

3、平均数时间数列 它是把一系列同类平均数指标按时间向后顺序 排列而成的数列 。
绝对数时间数列的分类
绝对数时间数列按数列反映时间状态的不同; 又可分为时期数列和时点数列。 时期数列
当数列中的指标为时期指标,反映现象在各段时期 内发展过程的总量时,即为时期数列。
—— 27.8 84.2 173.4
—— 27.8 56.4 89.2
—— 106.7 120.4 142.0
—— 106.7 112.8 118.0
四、增长速度
概念:由增长量与基期水平之比。 作用:说明报告期水平较基期水平增长的相对程度。 种类:增长速度也分为定基增长速度和环比增长速度。 定基增长速度的一般通式为;
a1-a0, a2-a1, a3-a2,……,an-1-an-2 ,an-an-1。
两种增长量之间关系: 各逐期增长量之和,等于相应时期的
累计增长量:
(a i a i 1) a n a 0
两相邻时期累计增长量之差,等于相 应时期的逐期增长量:
(a i a 0 ) (a i 1 a 0 ) a i a i 1
作用:说明现象报告期水平较基期水平的相对增 长结果。
种类:由基期水平选择的不同可把增长量分为累 计增长量和逐期增长量。
累计增长量是指报告期水平与固定基期水平之差。 一般通式为:
a1-a0, a2-a0, a3-a0,……,an-1-a0 ,an-a0。 逐期增长量是指报告期水平与前一期水平之差。
一般通式为:
(7) ——
(8)
举例
年份
发展水 增长量(万 平(万 元) 元) 累计 逐期
时间序列分析--第五章非平稳序列的随机分析

50
乘积季节模型
使用场合
序列的季节效应、长期趋势效应和随机波动之间有着复 杂地相互关联性,简单的季节模型不能充分地提取其中 的相关关系
构造原理
短期相关性用低阶ARMA(p,q)模型提取
季节相关性用以周期步长S为单位的ARMA(P,Q)模型提取
假设短期相关和季节效应之间具有乘积关系,模型结构
3
差分运算的实质
差分方法是一种非常简便、有效的确定 性信息提取方法
Cramer分解定理在理论上保证了适当阶 数的差分一定可以充分提取确定性信息
差分运算的实质是使用自回归的方式提 取确定性信息
d
d xt (1 B)d xt (1)i Cdi xti i0
5/10/2019
模型中有部分系数省缺了,那么该模型 称为疏系数模型。
5/10/2019
课件
34
疏系数模型类型
如果只是自相关部分有省缺系数,那么该疏系 数模型可以简记为ARIMA(( p1,, pm ), d, q)
p1,, pm 为非零自相关系数的阶数
如果只是移动平滑部分有省缺系数,那么该疏 系数模型可以简记为 ARIMA( p, d, (q1,, qn ))
26
建模
定阶
ARIMA(0,1,1)
参数估计
(1 B)xt 4.99661 (1 0.70766 B) t
Var(t ) 56.48763
模型检验
模型显著 参数显著
5/10/2019
课件
27
ARIMA模型预测
原则
最小均方误差预测原理
Green函数递推公式
一阶差分
第五章 时间序列

是一种无规律可循的偶然性的变 动,包括严格的随机变动和不规 则的突发性影响很大的变动两种 类型。比如股票的价格波动。
前三种都是可以解释的变 动,只有不规则变动是无法解 释的。
传统的时间序列分析的主 要内容就是将这些成分从时间 序列中分离出来,然后将它们 之间的关系用一定的数学关系 式予以表达,并进行分析。
1. 长期趋势(T)
现象在较长时期内受某种根 本性因素作用而形成的总的 变动趋势。比如GDP总量长 期看来具有上升趋势。
2. 季节变动(S)
现象在一年内随着季节的变化 而重复出现的有规律的周期性 变动。比如通常商业上有“销 售淡季”和“销售旺季”。
3. 周期性(C)
现象以若干年为周期所呈现出的围 绕长期趋势的一种波浪形态的有规 律的变动。比如我们常说的经济周 期,5年或者10年一个循环。
• 时期序列的主要特点有: ① 时期序列中各个观察值可以相加,相加后的观察 值表示现象在更长时期内发展过程的总量。 ② 时期序列中每个指标数值的大小与时期的长短有 直接联系,即具有时间长度。 ③ 时期序列中的指标数值一般采用连续登记办法获 得。
2.时点序列
• 当时间序列中所包含的总量指标都是反映社会经 济现象在某一瞬间上所达到的水平时,这种总量 指标时间序列即为时点序列。在时点序列中,相 邻两个时点指标之间的距离为“间隔”。
相对指标时间序列中各个指标数值都是相对数,其计算基础不同,不能直接相加。在编制相对指 标时间序列时,要注意百分号的表示及其在表中的位置和作用。
(三)平均指标时间序列
将同一平均指标的数值按其发生的时间先后顺序排列而成的数列叫做平均指数时间序列。它反映 社会经济现象一般水平的变化过程和发展趋势。
平均指标时间序列中每个指标数值都是平均数,不能相加,相加起来没有经济意义
统计学原理第5章:时间序列分析

a a
n 118729 129034 132616 132410 124000 5
127357.8
②时点序列
若是连续时点序列: 计算方法与时期序列一样; 若是间断时点序列: 则必须先假设两个条件,分别是 假设上期期末水平等于本期期初水平; 假设现象在间隔期内数量变化是均匀的。 间隔期相等的时点序列 采用一般首尾折半法计算。 例如:数列 a i , i 0,1,2, n 有 n 1 个数据,计算 期内的平均水平 a n a n 1 a 0 a1 a1 a 2
(3)联系
环比发展速度的乘积等于相应的定基发展速度,
n n i 0 i 1 i 1
相邻两期的定基发展速度之商等于后期的环比发展速度
i i 1 i 0 0 i 1
(二)增减速度
1、定义:增长量与基期水平之比 2、反映内容:现象的增长程度 3、公式:增长速度
0.55
二、时间序列的速度分析指标
(一)发展速度 (二)增长速度 (三)平均发展水平
(四)平均增长速度
(一)发展速度
1、定义:现象两个不同发展水平的比值 2、反映内容:反映社会经济现象发展变化快慢相对程度 3、公式:v 报告期水平 100%
基期水平
(1)定基发展速度
是时间数列中报告期期发展水平与固定基期发展水平对比所 得到的相对数,说明某种社会经济现象在较长时期内总的发 展方向和速度,故亦称为总速度。 (2)环比发展速度 是时间数列中报告期发展水平与前期发展水平之比,说明某 种社会经济现象的逐期发展方向和速度。
c
a
b
均为时期或时点数列,一个时期数列一个时点数列,注意平均的时间长度 ,比如计算季度的月平均数,时点数据需要四个月的数据,而时期数据则 只需要三个月的数据。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
佛山科学技术学院
应用时间序列分析实验报告
实验名称第五章非平稳序列的随机分析
一、上机练习
通过第4章我们学习了非平稳序列的确定性因素分解方法,但随着研究方法的深入和研究领域的拓宽,我们发现确定性因素分解方法不能很充分的提取确定性信息以及无法提供明确有效的方法判断各因素之间确切的作用关系。
第5章所介绍的随机性分析方法弥补了确定性因素分解方法的不足,为我们提供了更加丰富、更加精确的时序分析工具。
5.8.1 拟合ARIMA模型
【程序】
data example5_1;
input x@@;
difx=dif(x);
t=_n_;
cards;
1.05 -0.84 -1.42 0.20
2.81 6.72 5.40 4.38
5.52 4.46 2.89 -0.43 -4.86 -8.54 -11.54 -1
6.22
-19.41 -21.61 -22.51 -23.51 -24.49 -25.54 -24.06 -23.44
-23.41 -24.17 -21.58 -19.00 -14.14 -12.69 -9.48 -10.29
-9.88 -8.33 -4.67 -2.97 -2.91 -1.86 -1.91 -0.80
;
proc gplot;
plot x*t difx*t;
symbol v=star c=black i=join;
proc arima;
identify var=x(1);
estimate p=1;
estimate p=1 noint;
forecast lead=5id=t out=out;
proc gplot data=out;
plot x*t=1 forecast*t=2 l95*t=3 u95*t=3/overlay;
symbol1c=black i=none v=star;
symbol2c=red i=join v=none;
symbol3c=green I=join v=none;
2、序列difx时序图:如图1-2所示,时序图显示差分后序列difx没有明显的非平稳特征。
<拒绝原假设,1阶差分后序列difx为平稳非3、序列difx白噪声检验:图1-3所示,由结果可知Pα
5.8.2 拟合Auto-Regressive模型
【程序】
data example5_2;
input x@@;
lagx=lag(x);
t=_n_;
cards;
3.03 8.46 10.22 9.80 11.96 2.83
8.43 13.77 16.18 16.84 19.57 13.26
14.78 24.48 28.16 28.27 32.62 18.44
25.25 38.36 43.70 44.46 50.66 33.01
39.97 60.17 68.12 68.84 78.15 49.84
62.23 91.49 103.20 104.53 118.18 77.88
94.75 138.36 155.68 157.46 177.69 117.15
;
proc gplot data=example5_2;
plot x*t=1;
symbol1c=black i=join v=star;
run;
proc autoreg data=example5_2;
model x=t/ dwprob;
proc autoreg data=example5_2; model x=t/nlag=5backstep method=ml; output out=out p=xp pm=trend;
proc autoreg data=example5_2; model x=t/nlag=5backstep method=ml noint; output out=out p=xp pm=trend; proc gplot data=out; plot x*t=2 xp*t=3 trend*t=4 / overlay ; symbol2v=star i=none c=black; symbol3v=none i=join c=red w=2l=3; symbol4v=none i=join c=green w=2;
run;
proc autoreg data=example5_2; model x=lagx/lagdep=lagx;
model x=lagx/lagdep=lagx noint;
output out=out p=xp; proc gplot data=out; plot x*t=2 xp*t=3 / overlay;
symbol2v=star i=none c=black; symbol3v=none i=join c=red w=2l=3;
run;
、因变量关于时间的回归模型:
、延迟因变量回归模型
拟合GARCH模型
11。
