数学建模指导
数学老师如何帮助学生进行数学建模

数学老师如何帮助学生进行数学建模数学建模是数学教育中的重要组成部分,它旨在培养学生的创新思维、综合应用能力和问题解决能力。
作为数学教育的重要一环,数学老师在数学建模过程中发挥着重要的指导作用。
本文将探讨数学老师如何帮助学生进行数学建模,提供一些教育者在此方面可以采取的有效策略和方法。
1. 激发学生兴趣数学建模的前提是学生对数学问题感兴趣,积极主动地投入其中。
数学老师应该通过生动的教学方法和丰富的实例来激发学生的兴趣,使他们对数学建模产生浓厚的兴趣。
可以通过展示一些与实际生活相关的数学模型成功案例,让学生看到数学建模对解决实际问题的重要性和实际应用的广泛性。
2. 提供合适的教育资源数学建模需要一定的教育资源支持,数学老师应该为学生提供合适的参考书籍、文献资料和网络资源等。
这些资源可以帮助学生深入了解数学建模的基本原理、方法和技巧,并为他们提供相关案例和实例,以便学生能够更好地理解和应用数学建模。
3. 引导学生选择合适的课题数学建模的课题选择对学生的学习成果和兴趣培养至关重要。
数学老师应该对学生进行指导,帮助他们选择与日常生活紧密相关的课题,并鼓励学生思考和提出具有一定难度和挑战性的问题。
同时,老师还应该向学生介绍一些已经被研究和解决过的数学建模课题,以供学生借鉴和参考。
4. 指导学生进行建模过程在数学建模过程中,数学老师应该在学生自主探究的基础上给予适当的指导。
他们可以帮助学生梳理思路,明确问题的关键点,并提供相应的数学知识和方法。
同时,老师还应该鼓励学生进行团队合作和讨论,通过相互交流和合作解决问题。
5. 培养学生的模型评价能力数学建模的一个重要环节是对模型的评价和改进。
数学老师应该引导学生学会分析模型的优缺点,评估模型的有效性和适用性,并提出相应的改进措施。
这可以通过让学生参与模型竞赛、专题研究等活动来培养他们的模型评价能力。
6. 提供反馈和激励数学建模是一个需要持续投入和实践的过程,学生常常会面临各种困难和挑战。
杭州电子科技大学本科生数学建模指导书

杭州电子科技大学本科生数学建模指导书建模指导书方法接受参加数学建模竞赛赛前培训的同学大都需要学习诸如数理统计、最优化、图论、微分方程、计算方法、神经网络、层次分析法、模糊数学,数学软件包的使用等等“短课程”(或讲座)培训中广泛地采用的讨论班方式,同学自己报告、讨论、辩论,教师主要起质疑、答疑、辅导的作用,竞赛中一定要使用计算机及相应的软件,如Spss,Lingo,Mapple,Mathematica,Matlab甚至排版软件等。
数学建模应当掌握的十类算法1、蒙特卡罗算法(该算法又称随机性模拟算法,是通过计算机仿真来解决问题的算法,同时可以通过模拟可以来检验自己模型的正确性,是比赛时必用的方法)2、数据拟合、参数估计、插值等数据处理算法(比赛中通常会遇到大量的数据需要处理,而处理数据的关键就在于这些算法,通常使用Matlab作为工具)3、线性规划、整数规划、多元规划、二次规划等规划类问题(建模竞赛大多数问题属于最优化问题,很多时候这些问题可以用数学规划算法来描述,通常使用Lindo、Lingo软件实现)4、图论算法(这类算法可以分为很多种,包括最短路、网络流、二分图等算法,涉及到图论的问题可以用这些方法解决,需要认真准备)5、动态规划、回溯搜索、分治算法、分支定界等计算机算法(这些算法是算法设计中比较常用的方法,很多场合可以用到竞赛中)6、最优化理论的三大非经典算法:模拟退火法、神经网络、遗传算法(这些问题是用来解决一些较困难的最优化问题的算法,对于有些问题非常有帮助,但是算法的实现比较困难,需慎重使用)7、网格算法和穷举法(网格算法和穷举法都是暴力搜索最优点的算法,在很多竞赛题中有应用,当重点讨论模型本身而轻视算法的时候,可以使用这种暴力方案,最好使用一些高级语言作为编程工具)8、一些连续离散化方法(很多问题都是实际来的,数据可以是连续的,而计算机只认的是离散的数据,因此将其离散化后进行差分代替微分、求和代替积分等思想是非常重要的)9、数值分析算法(如果在比赛中采用高级语言进行编程的话,那一些数值分析中常用的算法比如方程组求解、矩阵运算、函数积分等算法就需要额外编写库函数进行调用)10、图象处理算法(赛题中有一类问题与图形有关,即使与图形无关,论文中也应该要不乏图片的,这些图形如何展示以及如何处理就是需要解决的问题,通常使用Matlab进行处理)竞赛参考书l、中国大学生数学建模竞赛,李大潜主编,高等教育出版社(1998).2、大学生数学建模竞赛辅导教材,(一)(二)(三),叶其孝主编,湖南教育出版社(1993,1997,1998).3、数学建模教育与国际数学建模竞赛《工科数学》专辑,叶其孝主编,《工科数学》杂志社,1994).国内教材、丛书。
成功组织并指导学生参加全国数学建模竞赛

成功组织并指导学生参加全国数学建模竞赛全国数学建模竞赛是中国最具影响力和参与度高的数学竞赛之一。
它旨在提高学生在数学、统计和计算科学领域的综合能力。
成功组织并指导学生参加全国数学建模竞赛对于学生的学习成果、个人发展和学校声誉都有着重要的意义。
本文将探讨如何成功组织并指导学生参加全国数学建模竞赛。
一、了解竞赛规则和要求在组织学生参加全国数学建模竞赛之前,我们首先要了解竞赛的规则和要求。
该竞赛通常由主办方发布竞赛题目,要求参赛学生在一定时间内完成,并提交解题报告和相关材料。
我们需要仔细研读竞赛题目,了解解题要求、评分标准和提交截止日期,以便顺利组织学生参赛。
二、选拔合适的参赛学生成功组织并指导学生参加全国数学建模竞赛,需要我们有明确的选拔机制,以确保选派的学生具备相应的数学基础和竞赛能力。
我们可以通过举办校内预选赛、组织数学建模培训班等方式来选拔合适的学生。
参赛学生应该具备较强的数学思维能力、解决实际问题的能力和团队合作精神。
三、制定合理的备赛计划在学生选拔完成后,我们需要制定合理的备赛计划,确保学生能够充分准备竞赛。
备赛计划可以包括以下内容:1. 深入学习数学建模相关知识:我们可以组织针对竞赛题型的培训,让学生系统学习数学建模的基础知识和方法,提高解题能力。
2. 队内合作与分工:数学建模竞赛通常是以小组形式参赛,我们需要指导学生合理分工,明确每个队员的职责和任务,培养团队合作意识。
3. 解题技巧与经验分享:我们可以邀请曾经获奖或有丰富竞赛经验的学生来分享解题技巧和经验,启发其他队员的思维,提高整个团队的竞赛水平。
四、提供良好的竞赛环境和支持为了提高学生参赛的效果和体验,我们需要为他们提供良好的竞赛环境和全面的支持:1. 提供必要的学习资源:为学生提供各类适合竞赛题目的数学教材和学习资料,帮助他们在备赛过程中有更好的准备。
2. 配备必要的设备和软件:为了便于学生进行模拟训练和实际解题过程,我们需要配备必要的计算机、软件和相关设备。
《数学建模》实验指导_03_Lingo求解线性规划问题
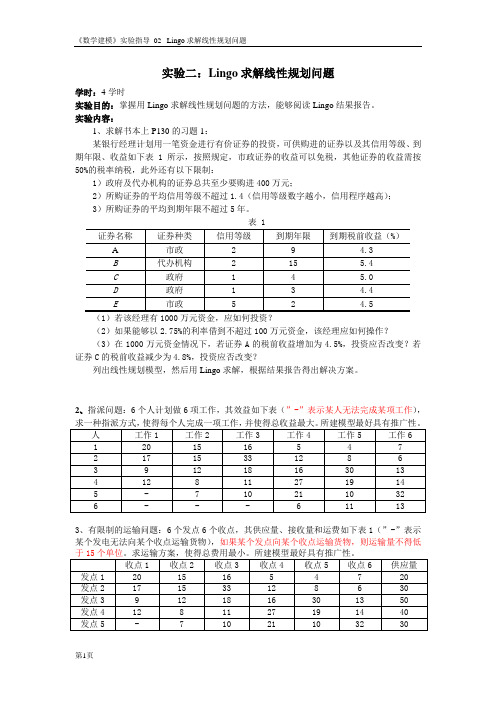
实验二:Lingo求解线性规划问题学时:4学时实验目的:掌握用Lingo求解线性规划问题的方法,能够阅读Lingo结果报告。
实验内容:1、求解书本上P130的习题1:某银行经理计划用一笔资金进行有价证券的投资,可供购进的证券以及其信用等级、到期年限、收益如下表1所示,按照规定,市政证券的收益可以免税,其他证券的收益需按50%的税率纳税,此外还有以下限制:1)政府及代办机构的证券总共至少要购进400万元;2)所购证券的平均信用等级不超过1.4(信用等级数字越小,信用程序越高);3)所购证券的平均到期年限不超过5年。
表 1(1)若该经理有1000万元资金,应如何投资?(2)如果能够以2.75%的利率借到不超过100万元资金,该经理应如何操作?(3)在1000万元资金情况下,若证券A的税前收益增加为4.5%,投资应否改变?若证券C的税前收益减少为4.8%,投资应否改变?列出线性规划模型,然后用Lingo求解,根据结果报告得出解决方案。
2、指派问题:6个人计划做6项工作,其效益如下表(”-”表示某人无法完成某项工作),3、有限制的运输问题:6个发点6个收点,其供应量、接收量和运费如下表1(”-”表示某个发电无法向某个收点运输货物),如果某个发点向某个收点运输货物,则运输量不得低使用Lingo 的一些注意事项1. “>”与“>=”功能相同。
2. 变量与系数间相乘必须用”*”号,每行用”;”结束。
3. 变量以字母开头,不能超过8个字符。
4. 变量名不区分大小写(包括关键字)。
5. 目标函数用min=3*x1+2*x2或max=3*x1+2*x2的格式表示。
6. “!”后为注释。
7. 变量界定函数实现对变量取值范围的附加限制,共4种:@bin(x) 限制x 为0或1 @bnd(L,x,U) 限制L≤x≤U@free(x) 取消对变量x 的默认下界为0的限制,即x 可以取任意实数 @gin(x) 限制x 为整数 其他可见“Lingo 教程.doc ”如书上85页的Lindo 代码可改为如下Lingo 代码: max =72*x1+64*x2; x1+x2<50;12*x1+8*x2<480; 3*x1<100;例1.1 如何在LINGO 中求解如下的LP 问题:,6002100350..32min 212112121≥≤+≥≥++x x x x x x x t s x x在模型窗口中输入如下代码:min =2*x1+3*x2; x1+x2>=350; x1>=100;2*x1+x2<=600;然后点击工具条上的按钮 即可。
小学五年级数学数学建模指导

小学五年级数学数学建模指导数学建模是一种将数学知识应用于实际问题解决的方法。
它通过建立数学模型,运用数学方法和技巧进行问题分析和求解,旨在培养学生的数学思维、创新意识以及解决实际问题的能力。
小学五年级是数学建模的理论与实践结合的重要时期。
本文将为五年级学生提供数学建模指导,包括模型建立、问题分析和解决方法等方面的内容。
一、模型建立模型是对实际问题进行抽象和描述的数学形式。
在建立数学模型时,需要考虑以下几个步骤:1.了解实际问题:首先,需要仔细阅读给定的问题描述,理解问题的背景和条件,确定问题的主要目标和约束条件。
2.确定变量和参数:根据问题的特点,确定与问题相关的各种变量和参数。
变量是随问题变化的量,参数是给定的常数。
例如,求解一个有关图书馆借书问题的模型时,可以将借书人数作为变量,图书馆的开放时间作为参数。
3.建立数学关系:根据问题描述和变量之间的关系,构建数学方程或不等式。
这些数学关系将问题的条件和目标用代数形式表达出来。
4.模型验证:建立模型后,需要进行模型的验证。
可以通过将模型应用到已知情况下进行求解,并与实际情况进行对比,检验模型的准确性和可靠性。
二、问题分析当模型建立完成后,需要进行问题分析,明确问题的求解方法和步骤。
具体分析步骤如下:1.解读问题:详细阅读问题描述,理解问题的要求和限制条件。
需要将问题分解为若干个小问题,明确每个小问题的目标和意义。
2.分析模型:根据建立的数学模型,分析模型的特点和属性。
比较模型与实际问题的差异和联系,进一步确定问题求解的方向和方法。
3.确定求解步骤:根据问题的特点和模型的要求,确定问题求解的步骤和方法。
可以通过数学计算、图表分析等方法求解问题。
三、解决方法解决数学建模问题的方法多种多样。
下面介绍一些常用的解决方法:1.数学计算:将数学模型转化为数学方程,通过计算求解问题。
常用的计算方法包括代数计算、方程求解、函数计算等。
2.图表分析:将模型转化为图形形式,通过分析图形特征和规律,解决问题。
高中数学建模竞赛指导与训练

高中数学建模竞赛指导与训练数学建模竞赛在高中阶段逐渐受到重视,它不仅能够培养学生的数学应用能力和创新思维,还对学生的综合素质提升有着重要意义。
在这篇文章中,我们将深入探讨高中数学建模竞赛的指导与训练方法,帮助同学们在竞赛中取得优异成绩。
一、认识数学建模竞赛数学建模竞赛要求参赛者运用数学知识和方法,对实际问题进行分析、假设、建立模型、求解,并对结果进行检验和改进。
其过程涉及到数学、计算机、统计学等多个学科领域的知识和技能。
在高中数学建模竞赛中,通常会给出一个具有现实背景的问题,例如城市交通规划、资源分配、环境保护等。
参赛者需要在规定的时间内,通过团队合作,将问题转化为数学语言,建立合理的数学模型,并利用数学软件或编程工具进行求解和分析。
二、竞赛前的准备1、扎实的数学基础参赛者首先需要具备扎实的高中数学知识,包括函数、数列、不等式、解析几何、概率统计等。
同时,对于高等数学中的微积分、线性代数等知识有一定的了解,也会对建模竞赛有所帮助。
2、掌握相关软件和工具熟练掌握一些数学软件和编程工具,如 Matlab、Mathematica、Python 等,可以大大提高建模的效率和准确性。
在竞赛前,同学们应该花时间学习这些工具的基本操作和常用函数。
3、培养团队合作能力数学建模竞赛通常以团队形式参赛,团队成员之间的合作至关重要。
在平时的训练中,要注重培养团队成员之间的沟通、协作和分工能力,明确各自的职责,发挥团队的优势。
4、广泛阅读和积累多读一些数学建模方面的书籍、论文和优秀案例,了解不同类型问题的建模思路和方法。
同时,关注时事热点和社会问题,拓宽自己的视野,为竞赛积累素材。
三、竞赛中的技巧1、仔细审题拿到竞赛题目后,不要急于动手建模,要仔细阅读题目,理解问题的背景、要求和限制条件。
可以对题目中的关键信息进行标注和分析,确保对问题有清晰的认识。
2、合理假设根据问题的实际情况,进行合理的假设。
假设要尽量简化问题,但又不能过于简化而失去问题的本质。
数学建模作业指导

数学建模作业指导在进行数学建模作业时,我们需要遵循一定的步骤和方法,以确保我们的成果准确、完整和可靠。
本文将介绍一些数学建模作业的指导原则和方法。
一、问题分析在进行数学建模作业前,我们首先需要仔细分析问题,确保我们对问题的理解准确。
通过仔细观察问题陈述,确定问题的关键要素和约束条件,理清问题的逻辑结构和问题类型。
二、模型建立在问题分析的基础上,我们开始着手构建数学模型。
数学模型是对实际问题进行抽象和描述的一种数学形式。
常见的数学模型包括线性规划模型、非线性规划模型、动态规划模型等。
根据问题的特点,选择合适的数学模型进行建立。
1. 建立数学表达式:将问题中的变量、约束条件和目标函数通过数学符号进行表达,并建立数学方程式或不等式。
2. 建立数学关系:将问题中的因果关系、随机关系、量变关系等通过数学方法进行建模,确保模型的准确性和可靠性。
3. 建立参数设定:确定模型中的参数值,并进行合理的设定和推导。
三、模型求解模型建立完成后,我们需要对模型进行求解,得到问题的解答。
数学建模中常用的求解方法包括优化算法、最优化工具和数值计算等。
1. 优化算法:通过优化算法寻找模型的全局最优解或局部最优解,常用的优化算法包括蚁群算法、遗传算法、模拟退火算法等。
2. 最优化工具:使用最优化软件工具,如Matlab、Gurobi等,进行模型求解和优化。
3. 数值计算:对于复杂的数学模型,可以采用数值计算方法进行求解,如差分法、积分法等。
四、模型评价当模型求解完成后,我们需要对模型的可行性和有效性进行评价。
评价模型的指标包括模型的精度、稳定性、灵敏度等。
1. 精度评价:通过与实际数据进行对比,评估模型的预测准确性和误差水平。
2. 稳定性评价:通过模型的参数稳定性和鲁棒性评估模型的可靠性和稳定性。
3. 灵敏度评价:评估模型对于输入变量和参数的敏感程度,以判断模型对于外部变化的响应能力。
五、结果分析与应用在模型评价后,我们需要对结果进行深入分析和应用。
数学建模竞赛指导方案

数学建模竞赛指导方案第一节:引言数学建模竞赛是一项旨在培养学生创新思维和实践能力的比赛,其内容涉及数学、计算机科学和实际问题。
本文将从赛事特点、参赛要求、解题技巧、团队合作和培训指导等方面介绍数学建模竞赛的一些建议,以帮助参赛者在竞赛中取得更好的成绩。
第二节:赛事特点数学建模竞赛强调对实际问题进行数学建模和解决的能力,与传统的数学竞赛有所不同。
参赛者需要运用数学模型、优化方法和计算机工具等手段,分析问题、提出解决方案并进行模拟验证。
了解赛事特点,有助于参赛者在备赛过程中有针对性地准备。
第三节:参赛要求参赛者需要具备扎实的数学基础和良好的计算机应用能力。
除此之外,团队协作能力和自主解决问题的能力也是重要的要求。
赛事组织方通常会提供参赛问题和数据,参赛者需要在规定时间内解答并撰写报告。
第四节:解题技巧解题的关键是合理运用数学方法和模型,进一步进行假设和近似。
在解题过程中,参赛者需要灵活运用数学知识,充分挖掘问题中的隐含规律和特征。
同时,借助计算机工具进行模拟实验和数据分析也是解题的有效手段。
第五节:团队合作数学建模竞赛注重展示参赛团队的团结协作和分工合作能力。
参赛者需要明确分工,分别负责问题的不同部分,并在整个解题过程中保持密切的合作与协调。
合理安排时间、高效沟通和有效解决团队内部冲突是成功的关键。
第六节:培训指导培训是参赛者备战数学建模竞赛的重要环节。
培训团队应包括数学专家、计算机专家和实际问题领域的专业人士,以确保参赛者能够获得全面的指导和专业知识。
培训内容包括数学理论、算法实现和实际问题分析等方面的内容。
第七节:备赛要点备赛阶段,参赛者需要充分了解和研究往届题目和解题方法。
通过多次练习和模拟比赛,提高解题速度和准确性。
参赛者还应该注意加强对数学模型和计算机工具的熟悉程度,并结合实际问题进行综合训练。
第八节:解题策略解题时,参赛者可以采用分析-建模-求解-验证的策略。
首先,对问题进行分析,理解问题的本质和相关约束条件。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
建模方法
接受参加数学建模竞赛赛前培训的同学大都需要学习诸如数理统计、最优化、图论、微分方程、计算方法、神经网络、层次分析法、模糊数学,数学软件包的使用等等“短课程”(或讲座)
培训中广泛地采用的讨论班方式,同学自己报告、讨论、辩论,教师主要起质疑、答疑、辅导的作用,竞赛中一定要使用计算机及相应的软件,如Spss,Lingo,Mapple,
1、蒙特卡罗算法(该算法又称随机性模拟算法,是通过计算机仿真来解决问题的算法,同时可以通过模拟可以来检验自己模型的正确性,是比赛时必用的方法)
2、数据拟合、参数估计、插值等数据处理算法(比赛中通常会遇到大量的数据需要处理,而处理数据的关键就在于这些算法,通常使用Matlab作为工具)
3、线性规划、整数规划、多元规划、二次规划等规划类问题(建模竞赛大多数问题属于最优化问题,很多时候这些问题可以用数学规划算法来描述,通常使用Lindo、
Lingo软件实现)
4、图论算法(这类算法可以分为很多种,包括最短路、网络流、二分图等算法,涉及到图论的问题可以用这些方法解决,需要认真准备)
5、动态规划、回溯搜索、分治算法、分支定界等计算机算法(这些算法是算法设计中比较常用的方法,很多场合可以用到竞赛中)
6、最优化理论的三大非经典算法:模拟退火法、神经网络、遗传算法(这些问题是用来解决一些较困难的最优化问题的算法,对于有些问题非常有帮助,但是算法的实现比较困难,需慎重使用)
7、网格算法和穷举法(网格算法和穷举法都是暴力搜索最优点的算法,在很多竞赛题中有应用,当重点讨论模型本身而轻视算法的时候,可以使用这种暴力方案,最好使用一些高级语言作为编程工具)
8、一些连续离散化方法(很多问题都是实际来的,数据可以是连续的,而计算机只认的是离散的数据,因此将其离散化后进行差分代替微分、求和代替积分等思想是非常重要的)
9、数值分析算法(如果在比赛中采用高级语言进行编程的话,那一些数值分析中常用的算法比如方程组求解、矩阵运算、函数积分等算法就需要额外编写库函数进行调用)
10、图象处理算法(赛题中有一类问题与图形有关,即使与图形无关,论文中也应该要不乏图片的,这些图形如何展示以及如何处理就是需要解决的问题,通常使用Matlab进行处理)
竞赛参考书
l、中国大学生数学建模竞赛,李大潜主编,高等教育出版社(1998).
2、大学生数学建模竞赛辅导教材,(一)(二)(三),叶其孝主编,湖南教育出版社(1993,1997,1998).
3、数学建模教育与国际数学建模竞赛《工科数学》专辑,叶其孝主编,《工科数学》杂志社,1994).
国内教材、丛书
1、数学模型,姜启源编,高等教育出版社(1987年第一版,1993年第二版,2003年第三版;第一版在 1992年国家教委举办的第二届全国优秀教材评选中获"全国优秀教材奖").
2、数学模型与计算机模拟,江裕钊、辛培情编,电子科技大学出版社,(1989).
3、数学模型选谈(走向数学从书),华罗庚,王元著,王克译,湖南教育出版社;(1991).
4、数学建模--方法与范例,寿纪麟等编,西安交通大学出版社(1993).
5、数学模型,濮定国、田蔚文主编,东南大学出版社(1994).
6..数学模型,朱思铭、李尚廉编,中山大学出版社,(1995)
7、数学模型,陈义华编著,重庆大学出版社,(1995)
8、数学模型建模分析,蔡常丰编著,科学出版社,(1995).
9、数学建模竞赛教程,李尚志主编,江苏教育出版社,(1996).
10、数学建模入门,徐全智、杨晋浩编,成都电子科大出版社,(1996).
11、数学建模,沈继红、施久玉、高振滨、张晓威编,哈尔滨工程大学出版社,(1996).
12、数学模型基础,王树禾编著,中国科学技术大学出版社,(1996).
13、数学模型方法,齐欢编著,华中理工大学出版社,(1996).
14、数学建模与实验,南京地区工科院校数学建模与工业数学讨论班编,河海大学出版社,(1996).
15、数学模型与数学建模,刘来福、曾文艺编,北京师范大学出版杜(1997).
16. 数学建模,袁震东、洪渊、林武忠、蒋鲁敏编,华东师范大学出版社.
17、数学模型,谭永基,俞文吡编,复旦大学出版社,(1997).
18、数学模型实用教程,费培之、程中瑗层主编,四川大学出版社,(1998).
19、数学建模优秀案例选编(工科数学基地建设丛书),汪国强主编,华南理工大学出版社,(1998).
20、经济数学模型(第二版)(工科数学基地建设丛书),洪毅、贺德化、昌志华编著,华南理工大学出版社,(1999).
21、数学模型讲义,雷功炎编,北京大学出版社(1999).
22、数学建模精品案例,朱道元编著,东南大学出版社,(1999),
23、问题解决的数学模型方法,刘来福,曾文艺编著、北京师范大学出版社,(1999).
24、数学建模的理论与实践,吴翔,吴孟达,成礼智编著,国防科技大学出版社,(1999).
25、数学建模案例分析,白其岭主编,海洋出版社,(2000年,北京).
26、数学实验(高等院校选用教材系列),谢云荪、张志让主编,科学出版社,(2000).
27、数学实验,傅鹏、龚肋、刘琼荪,何中市编,科学出版社,(2000).
28、数学建模与数学实验,赵静、但琦编,高等教育出版社,(2000).
国外参考书(中译本)
1、数学模型引论, E.A。
Bender著,朱尧辰、徐伟宣译,科学普及出版社(1982).
2、数学模型,[门]近藤次郎著,官荣章等译,机械工业出版社,(1985).
3、微分方程模型,(应用数学模型丛书第1卷),[美]W.F.Lucas主编,朱煜民
等译,国防科技大学出版社,(1988).
4、政治及有关模型,(应用数学模型丛书第2卷),[美W.F.Lucas主编,王国
秋等译,国防科技大学出版社,(1996).
5、离散与系统模型,(应用数学模型丛书第3卷),[美w.F.Lucas主编,成礼
智等译,国防科技大学出版社,(1996).
6、生命科学模型,(应用数学模型丛书第4卷),[美1W.F.Lucas主编,翟晓
燕等译,国防科技大学出版社,(1996).
7、模型数学--连续动力系统和离散动力系统,[英1H.B.Grif6ths和A.01dknow 著,萧礼、张志军编译,科学出版社,(1996).
8、数学建模--来自英国四个行业中的案例研究,(应用数学译丛第4号),
英]D.Burglles等著,叶其孝、吴庆宝译,世界图书出版公司,(1997)
专业性参考书
(这方面书籍很多,仅列几本供参考) :
1、水环境数学模型,[德]W.KinZE1bach著,杨汝均、刘兆昌等编纂,中国建筑
工业出版社,(1987).
2、科技工程中的数学模型,堪安琦编著,铁道出版社(1988)
3、生物医学数学模型,青义学编著,湖南科学技术出版杜(1990).
4、农作物害虫管理数学模型与应用,蒲蛰龙主编,广东科技出版社(1990).
5、系统科学中数学模型,欧阳亮编著, E山东大学出版社,(1995).
6、种群生态学的数学建模与研究,马知恩著,安徽教育出版社,(1996)
7、建模、变换、优化--结构综合方法新进展,隋允康著,大连理工大学出版社,(1986)
8、遗传模型分析方法,朱军著,中国农业出版社(1997). (中山大学数学系王
寿松编辑,2001年4月)。
