江苏省清江中学2014-2015学年高二数学午间练习(91) Word版含答案
江苏省清江中学2014-2015学年高二数学午间练习(057) Word版含答案
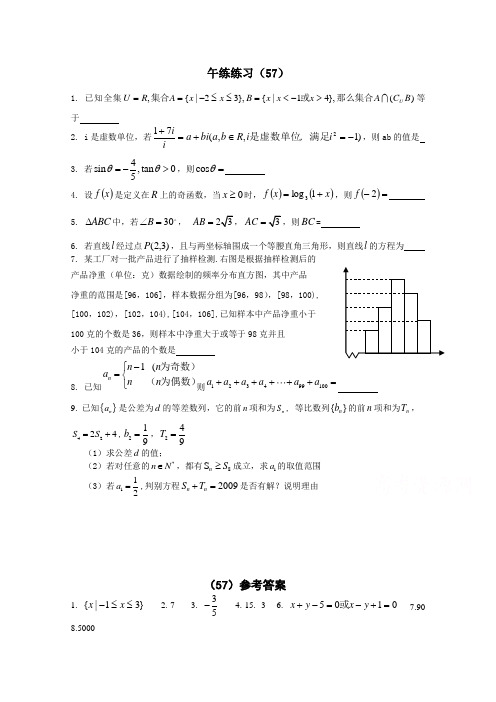
午练练习(57)1. 已知全集)(},41|{},32|{,B C A x x x B x x A R U U 那么集合或集合>-<=≤≤-==等于2. i 是虚数单位,若)1,,(712-=∈+=+i ,i R b a bi a ii 满足是虚数单位,则ab 的值是 3. 若4sin ,tan 05θθ=->,则cos θ=4. 设()x f 是定义在R 上的奇函数,当0≥x 时,()()x x f +=1log 3,则()=-2f5. ABC ∆中,若30B ∠=, 23AB =,3AC =,则BC =6. 若直线l 经过点)3,2(P ,且与两坐标轴围成一个等腰直角三角形,则直线l 的方程为7. 某工厂对一批产品进行了抽样检测.右图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106],已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是 8. 已知1(n n n a n n -⎧=⎨⎩为奇数)(为偶数)则123499100a a a a a a ++++++=9. 已知{}n a 是公差为d 的等差数列,它的前n 项和为n S , 等比数列{}n b 的前n 项和为n T ,4224S S =+,219b =,249T = (1)求公差d 的值;(2)若对任意的*n N ∈,都有8S n S ≥成立,求1a 的取值范围(3)若112a =,判别方程2009n n S T +=是否有解?说明理由(57)参考答案1. }31|{≤≤-x x2.-73. 35-4.-15. 36. 0105=+-=-+y x y x 或7.908.50009. 解:(1)∵4224S S =+,∴113442(2)42a d a d ⨯+=++-------2分 解得1d = --------------------3分(2)解法1:11(1)1n a a n d n a =+-=+- ------------4分 2111[(21)]22n n a a S n n a n +==+- ∵对任意的*n N ∈,都有8n S S ≥,∴1211517222a -≤-≤ ∴187a -≤≤-∴1a 的取值范围是[8,7]-- -----------8分 解法2:由于等差数列{}n a 的公差n 10,d S =>要取得最大值, 必须有8900a a ≤⎧⎨≥⎩ 117080a d a d +≤⎧⎨+≥⎩ 求得187a -≤≤-∴1a 的取值范围是[8,7]--解法3: ∵对任意的*n N ∈,都有8n S S ≥ 所以11(1)8(81)822n n n S na d a d -⋅-=+≥+ 由于1d = 所以1(8)(7)(8)2n n n a -⋅+-≥ 当8n = 时1a R ∈当8n > 时1max 7()82n a +≥-=- 当18n ≤< 时1min 7()72n a +≤-=- 综合:187a -≤≤-(3)由于等比数列{}n b 满足219b =,249T = 1111949b q b b q ⎧=⎪⎪⎨⎪+=⎪⎩-------------------10分 11133b q == ])31(1[21311])31(1[31n n n T -=--= 2111(1)22n S na n n d n =+-=---------12分 则方程2009n n S T +=转化为:21[1()]40183n n +-=令:21()1()3n f n n =+-, 由于21(1)()21()033n f n f n n +-=++> 所以()f n 单调递增-当163n ≤≤时,26321()63[1()]63139703f n ≤+-<+= 当64n ≥时,26421()64[1()]6440963f n ≥+->= 综合:方程2009n n S T +=无解.---------16分。
江苏省清江中学2014-2015学年高二数学 午练练习(39)苏教版

午练练习(39)1、已知集合{}(1)0P x x x =-≥,Q ={})1ln(|-=x y x ,则P Q = .2、在等比数列{n a }中,若7944,1a a a ⋅==,则12a 的值是 .3、若关于x 的不等式2260ax x a -+<的解集为(1, m),则实数m= .4、已知点()3,1--和()4,6-在直线320x y a --=的两侧,则a 的取值范围是5、若0,0>>y x ,且191=+y x ,求y x +的最小值为 .6、已知直线0=++C By Ax (其中0,222≠=+C C B A )与圆422=+y x 交于N M ,,O 是坐标原点,则OM ·ON = _________________. 7、如果实数.x y 满足不等式组22110,220x x y x yx y ≥⎧⎪-+≤+⎨⎪--≤⎩则的最小值是8、已知576*,)}({S S S n N n a d S n n >>∈且项和的前的等差数列是公差为,则下列四个命题:①0<d ;②011>S ;③012<S ;④013>S 中为真命题的序号为 . 9、已知以点)0,)(2,(≠∈t R t t t C 为圆心的圆与x 轴交于点A O ,,与y 轴交于点O 、B ,其中O 为原点。
(1)求证:OAB ∆的面积为定值;(2)设直线42+-=x y 与圆C 交于点N M ,,若ON OM =,求圆C 的方程。
(39)参考答案1.{}1/>xx.2.4. 3. 2. 4.247<<-a 5.16.6.-2.7.5 8. ①②.9、(1)略(2)()()52122=-+-yx。
清江中学2014-2015高二数学 午练练习(20)苏教版

午练练习(20)1. 设P 和Q 是两个集合,定义集合{,}P Q x x P x Q -=∈∉且,如果}1log {2<=x x P ,{21}Q x x =-<,那么P Q -= .2. 一水池有2个进水口, 1个出水口,一个口的进、出水的速度如图甲、乙所示.某天0点到6点,该水池的蓄水量如图丙所示.给出以下3个论断:进水量 出水量蓄水量甲 乙 丙(1)0点到3点只进水不出水; (2)3点到4点不进水只出水; (3)4点到6点不进水不出水.则一定不正确的论断是3. 已知函数()y f x =的图象与函数22()log (2)g x x x =++的图象关于直线2x =对称,则(3)f = .4. 若不等式142x x a +--≥0在x ∈[1,2]上恒成立,则a 的取值范围为 .5. 在公差为正数的等差数列}{n a 中,n S a a a a ,0,011101110<<+且是其前n 项和,则使n S 取最小值的n 是 。
6. 数列{an}的前n 项和Sn =n2+2n -1,则a1+a3+a5+…+a25= .7. 在ABC ∆中,若=+=C B C B A tan tan ,cos cos 2sin 则 。
40208. 设函数0)(),()(3=+-=x f b bx x x f 若方程为常数的根都在区间[-2,2]内,且函数)(x f 在区间(0,1)上单调递增,则b 的取值范围是 。
9. 某观测站C 在城A 的南20˚西的方向上,由A 城出发有一条公路,走向是南40˚东,在C 处测得距C 为31千米的公路上B 处,有一人正沿公路向A 城走去,走了20千米后,到达D 处,此时C 、D 间距离为21千米,问这人还需走多少千米到达A 城?午练练习(20) 1.}10{≤<x x 2. (2) 3. 2 4. a ≤0 5. 10 6. 350 7. 2 8. [3,4]9. 根据题意得,BC=31千米,BD=20千米,CD=21千米,∠CAB=60˚. 设∠ACD =α ,∠CDB = β .在△CDB 中,由余弦定理得2222222120311cos 2221207CD BD BC CD BD β+-+-===-⋅⋅⨯⨯,于是sin β. ()()sin sin 2040sin 60αββ=--=-︒11sin cos60cos sin 6027ββ=︒-︒=+.在△ACD中,由正弦定理得21sin 15().sin sin 60CD AD A α=⋅===︒千米。
江苏省清江中学2014-2015学年高二数学 午练练习(33)苏教版

午练练习(33)1. 已知:A=(){}0,=+y x y x ,B=(){}2,=-y x y x ,则A∩B=_________.2. 直线023=+-k y x 在两坐标轴上的截距之和为2,则实数k 的值是_____.3.ABC △的内角A B C ,,的对边分别为a b c ,,,若26120c b B ===,,,则a = .4.若3sin()25πθ+=,则cos 2θ=_________5.设向量(12)(23)==,,,a b ,若向量λ+a b 与向量(47)=--,c 共线,则=λ . 6.在等比数列{n a }中,若271086=a a a ,则=8a _____.7.函数()sin cos 1sin cos x x f x x x =++的值域是______________________8.“已知数列{}n a 为等差数列,它的前n 项和为n S ,若存在正整数(),m n m n ≠,使得m n S S =,则0m n S +=”,类比前面结论,若正项数列{}n b 为等比数列,9.在三棱锥A-BPC 中,AP ⊥PC,AC ⊥BC,M 为AB 中点,D 为PB 中点,且△PMB 为正三角形. (Ⅰ)求证:DM ∥平面APC ;(Ⅱ)求证:平面ABC ⊥平面APC ; (Ⅲ)若BC=4,AB=20,求三棱锥D-BCM 的体积._ P _ A _ B _ C_ D _ M(33)参考答案1.{(1,-1)} 2.12 3.2 4.725- 5.2 6.3 7.⎥⎦⎤ ⎝⎛--⋃⎪⎪⎭⎫⎢⎣⎡-+-212,11,212 8.它的前n 项乘积为n T ,若m n T T =,则1m n T +=4.9.(1)∵M 为AB 中点,D 为PB 中点,∴MD ∥AP ,又MD ⊄平面APC ,∴DM ∥平面APC(2)∵△PMB 为正三角形,且D 为PB 中点,∴MD ⊥PB ,又由(1)知MD ∥AP ,∴AP ⊥PB ,又已知AP ⊥PC ,PC ∩PB=P ,∴AP ⊥平面PBC ,∴AP ⊥BC ,又AC ⊥BC ,AP ∩AC=A ,∴BC ⊥平面APC , 又BC ⊂平面ABC ,∴平面ABC ⊥平面APC(3)∵AB=20,∴MB=10,∴PB=10,在直角三角形PBC 中,212846100,4==-==PC BC , ∴2122124414121=⨯⨯=⋅==∆∆BC PC S S PBC BDC , 又351020212122=-==AP MD , ∴710352123131=⨯⨯=⋅==∆--DM S V V BCD BCD M BCM D …14分。
2014-2015年江苏省淮安市清江中学高二(下)期中数学试卷(理科)和答案

2014-2015学年江苏省淮安市清江中学高二(下)期中数学试卷(理科)一、填空题:本大题共14小题,每小题5分,计70分.不需写出解答过程,请把答案写在答题纸的指定位置上.1.(5分)计算:C+C=.(用数字作答)2.(5分)二项式(3x﹣)8的展开式中第7项的二项式系数为(用数字作答)3.(5分)在矩阵变换下,点A(2,1)将会转换成.4.(5分)已知向量,若,则t=.5.(5分)在极坐标系中,圆ρ=2sinθ(0≤θ<2π)的圆心的极坐标为.6.(5分)已知矩阵M=,则M的特征值为.7.(5分)从1,2,3,4,5,6中选出3个不同的数组成3位数,并将这些三位数由小到大打排列,则第100个数是.8.(5分)参数方程的普通方程.9.(5分)已知随机变量X的概率分布如下表所示,且其数学期望E(X)=2,则随机变量X的方差是.10.(5分)某小组有4名男生,3名女生.若从男,女生中各选2人,组成一个小合唱队,要求站成一排且2名女生不相邻,共有种不同的排法?11.(5分)5555+15除以8余数是.12.(5分)一袋中装有5个白球,3个红球,现从袋中往外取球,每次取出一个,取出后记下球的颜色,然后放回,直到红球出现10次停止,停止时取球的次数X是随机变量,则P(X=12)=(用式子作答).13.(5分)(坐标系与参数方程选做题)已知直线(t为参数)与直线l2:2x﹣4y=5相交于点B,又点A(1,2),则|AB|=.14.(5分)已知数列{a n}满足a1=1,a n+a n﹣1=()n(n≥2),S n=a1•2+a2•22+…+a n•2n,类比课本中推导等比数列前n项和公式的方法,可求得3S n﹣a n•2n+1=.二、解答题:本大题共6小题,计90分.解答应写出必要的文字说明,证明过程或演算步骤,请把答案写在答题纸的指定区域内.15.(14分)已知直线l的参数方程:(t为参数)和曲线C的极坐标方程:ρ=2sin(θ+).(1)证明:判定曲线C的形状,并证明直线l和C相交;(2)设直线l与C交于A、B两点,P(0,1),求•.16.(14分)在1,2,3,…,9这9个自然数中,任取3个不同的数.(1)组成三位数“abc”,若满足a<b>c的三位数叫做凸数,这样的凸三位数有多少个?(2)设X为所取3个数中奇数的个数,求随机变量X的概率分布列及数学期望.17.(14分)在棱长为2的正方体ABCD﹣A1B1C1D1中,E,F分别为A1B1,CD 的中点.(1)求||(2)求直线EC与AF所成角的余弦值;(3)求二面角E﹣AF﹣B的余弦值.18.(16分)已知数列{a n}满足,且a2=10,(1)求a1、a3、a4;(2)猜想数列{a n}的通项公式a n,并用数学归纳法证明;(3)是否存在常数c,使数列成等差数列?若存在,请求出c的值;若不存在,请说明理由.19.(16分)已知.(1)求a2的值;(2)求展开式中系数最大的项;(3)求的值.20.(16分)已知二阶矩阵M的属于特征值﹣1的一个特征向量为,属于特征值3的一个特征向量为.(1)求矩阵M;(2)求直线l:y=2x﹣1在M作用下得到的新的直线l′方程;(3)已知向量,求.2014-2015学年江苏省淮安市清江中学高二(下)期中数学试卷(理科)参考答案与试题解析一、填空题:本大题共14小题,每小题5分,计70分.不需写出解答过程,请把答案写在答题纸的指定位置上.1.(5分)计算:C+C=84.(用数字作答)【解答】解:由组合数的性质可得C+C===84故答案为:842.(5分)二项式(3x﹣)8的展开式中第7项的二项式系数为28(用数字作答)【解答】解:二项式(3x﹣)8的展开式中第7项的二项式系数为==28,故答案为:28.3.(5分)在矩阵变换下,点A(2,1)将会转换成(2,5).【解答】解:设在矩阵变换下,点A(2,1)将会转换成A′(a,b),由=,得2+0=a,则b=2×2+1×1=5,故答案是:(2,5).4.(5分)已知向量,若,则t=0或2.【解答】解:∵,∴=2t﹣t2=0,解得t=0或2,故答案为:0或2.5.(5分)在极坐标系中,圆ρ=2sinθ(0≤θ<2π)的圆心的极坐标为(1,),或(﹣1,),.【解答】解:圆ρ=2sinθ(0≤θ<2π),即ρ2=2θsinθ,故它的直角坐标方程为x2+y2=2y,即x2+(y﹣1)2=1,故圆心的直角坐标为(0,1),故它的极坐标为(1,),也可以为(﹣1,),故答案为(1,),或(﹣1,).6.(5分)已知矩阵M=,则M的特征值为﹣1或6.【解答】解:矩阵M的特征多项式为f(λ)==(λ+1)(λ﹣6)令f(λ)=0,解得λ=﹣1或6;故答案为﹣1或6.7.(5分)从1,2,3,4,5,6中选出3个不同的数组成3位数,并将这些三位数由小到大打排列,则第100个数是564.【解答】解:由题意得,从1,2,3,4,5,6中选出3个不同的数组成3位数,∴百位上的数字是1共有:5×4=20;百位上的数字是2共有:5×4=20,…,百位上的数字是5共有:5×4=20,共有100个数,∴第100个数是百位上的数字是5的最大数:564,故答案为:564.8.(5分)参数方程的普通方程(x≥2).【解答】解:由参数方程可得,把①和②平方相减可得4x2﹣y2=16,即(x≥2),故答案为:(x≥2).9.(5分)已知随机变量X的概率分布如下表所示,且其数学期望E(X)=2,则随机变量X的方差是1.【解答】解:由随机变量X的概率分布列知:,解得a=,b=,∴D(X)=(0﹣2)2×+(1﹣2)2×+(2﹣2)2×+(3﹣2)2×=1.故答案为:1.10.(5分)某小组有4名男生,3名女生.若从男,女生中各选2人,组成一个小合唱队,要求站成一排且2名女生不相邻,共有216种不同的排法?【解答】解:完成这是事情可分为四步进行:第一步第一步,从4名男生中选2名男生,有C42=6种选法,第二步,从3名女生中选2名女生,有C32=3种选法,第三步,将选取的2名男生排成一排,有A22=2种排法,第四步,在2名男生之间及两端共3个位置选2个排2个女生,有A32=6,根据分步计数原理,不同的排法种数为6×3×2×6=216,故答案为:216.11.(5分)5555+15除以8余数是6.【解答】解:5555=(56﹣1)55=+++…++,∵展开式的前55项都能被8整除,∴展开式的前55项的和能被8整除.∵展开式的最后一项=﹣1,∴5555除以8余数的余数是7,∴5555+15除以8余数就是22除以8的余数,∵22÷8=2…6.∴5555+15除以8余数是6.故答案为:6.12.(5分)一袋中装有5个白球,3个红球,现从袋中往外取球,每次取出一个,取出后记下球的颜色,然后放回,直到红球出现10次停止,停止时取球的次数X是随机变量,则P(X=12)=••(用式子作答).【解答】解:若ξ=12,则取12次停止,第12次取出的是红球,前11次中有9次是红球,则P(ξ=12)=•••=•••故答案为:••.13.(5分)(坐标系与参数方程选做题)已知直线(t为参数)与直线l2:2x﹣4y=5相交于点B,又点A(1,2),则|AB|=.【解答】解:由,得4x+3y﹣10=0,由解得,即B(,0),所以|AB|==,故答案为:.14.(5分)已知数列{a n}满足a1=1,a n+a n﹣1=()n(n≥2),S n=a1•2+a2•22+…+a n•2n,类比课本中推导等比数列前n项和公式的方法,可求得3S n﹣a n•2n+1=n+1.【解答】解:由S n=a1•2+a2•22+…+a n•2n①得2•s n=a1•22+a2•23+…+a n•2n+1②①+②得:3s n=2a1+22(a1+a2)+23•(a2+a3)+…+2n•(a n﹣1+a n)+a n•2n+1=2a1+22×()2+23×()3+…+2n×()n+a n•2n+1=2+1+1+…+1+2n+1•a n=n+1+2n+1•a n.所以3S n﹣a n•2n+1=n+1.故答案为n+1.二、解答题:本大题共6小题,计90分.解答应写出必要的文字说明,证明过程或演算步骤,请把答案写在答题纸的指定区域内.15.(14分)已知直线l的参数方程:(t为参数)和曲线C的极坐标方程:ρ=2sin(θ+).(1)证明:判定曲线C的形状,并证明直线l和C相交;(2)设直线l与C交于A、B两点,P(0,1),求•.【解答】解:(1)曲线C的极坐标方程ρ=2sin(θ+),化为普通方程是x2+y2﹣2x﹣2y=0,即(x﹣1)2+(y﹣1)2=2;所以C是以(1,1)为圆心,半径为的圆;…(2分)直线的参数方程(t为参数),消去参数t得直线的普通方程为y=2x+1;…(4分)设圆心C(1,1)到直线l的距离为d,则d=,(或用判别式法)…(6分)所以直线l与曲线C相交.…(7分)(2)联立l与C的方程得方程组,解得或,即A(,),B(,);…(10分)所以=(,),=(,);…(12分)所以=(,)•(,)==﹣1.…(14分)又解:(用参数方程直接求)将直线参数方程直接代入圆C的普通方程得t2+(2t+1)2﹣2t﹣2(2t+1)=0,化简得:5t2﹣2t﹣1=0,所以t1t2=…(10分)所以==5t 1t2=﹣1(或者用直线参数方程的标准形式)…(14分)(几何法)过圆心C作AB的垂线交AB于H,则H平分AB,所以====PH2﹣HA2=PH2﹣(R2﹣HC2)=PC2﹣R2=﹣1.16.(14分)在1,2,3,…,9这9个自然数中,任取3个不同的数.(1)组成三位数“abc”,若满足a<b>c的三位数叫做凸数,这样的凸三位数有多少个?(2)设X为所取3个数中奇数的个数,求随机变量X的概率分布列及数学期望.【解答】解:(1)从9个自然数中,任取3个不同的数,共有=84种等可能的结果…(2分)由条件得最大的在中间,其它两个排两边,有2种排法,…(4分)所以这样的三位数共有个.…(6分)(2)由题意得X的取值范围为0,1,2,3,…(7分)P(X=0)=,P(X=1)=,P(X=2)=,P(X=3)=,∴随机变量X的分布列为:…(11分)(算对1个给(1分),不列表格或只列表格照样给分)EX=…(13分)17.(14分)在棱长为2的正方体ABCD﹣A1B1C1D1中,E,F分别为A1B1,CD 的中点.(1)求||(2)求直线EC与AF所成角的余弦值;(3)求二面角E﹣AF﹣B的余弦值.【解答】解:(1)在棱长为2的正方体ABCD﹣A1B1C1D1中,建立如图所示的空间直角坐标系.则A(2,0,0),F(0,1,0),C(0,2,0),E(2,1,2),,…(2分)∴…(4分)(2)∵,,∴…(6分)∴直线EC与AF所成角的余弦值为.…(8分)(如果把向量的夹角当成直线的夹角,扣1分)(3)平面ABCD的一个法向量为…(9分)设平面AEF的一个法向量为,∵,,∴,令x=1,则y=2,z=﹣1,…(10分)则…(12分)由图知二面角E﹣AF﹣B为锐二面角,其余弦值为.…(14分)(如果把向量的夹角当成二面角的平面角,扣2分)18.(16分)已知数列{a n}满足,且a2=10,(1)求a1、a3、a4;(2)猜想数列{a n}的通项公式a n,并用数学归纳法证明;(3)是否存在常数c,使数列成等差数列?若存在,请求出c的值;若不存在,请说明理由.【解答】解:(1)∵a2=10,将n=1代入已知等式得a1=3,同法可得a3=21,a4=36.(2)∵a1=3=1×3,a2=10=2×5,a3=3×7,a4=4×9,∴由此猜想a n=n(2n+1).下面用数学归纳法证明.①当n=1和2时猜想成立;②假设当n=k(k≥2)时猜想成立,即a k=k(2k+1),那么,当n=k+1时,因为,所以=(k+1)(2k+3)这就是说当n=k+1时猜想也成立.因此a n=n(2n+1)成立(3)假设存在常数c使数列成等差数列,则有把a1=3,a2=10,a3=21代入得.当c=0时,数列即为{2n+1}是公差为2的等差数列;当时,数列即为{2n}是公差为2的等差数列.∴存在常数使数列成等差数列.19.(16分)已知.(1)求a2的值;(2)求展开式中系数最大的项;(3)求的值.【解答】解:(1)∵(x2+1)(x﹣1)9=(x2+1)(x9﹣x8+…+x﹣)=a0+a1x+a2x2+…+a11x11,∴a2=﹣﹣=﹣37.…(4分)(2)展开式中的系数中,数值为正数的系数为a1==9,a3=+=93,a5=+=210,a7=+=162,a9=+=37,a11=,故展开式中系数最大的项为210x5.…(8分)(3)对=(x2+1)•(x﹣1)9=a0+a1x+a2x2+…+a11x11两边同时求导得:(11x2﹣2x+9)(x﹣1)8=a1+2a2x+3a3x2+…+11a11x10,令x=1,得a1+2a2+3a3+4a4+…+10a10+11a11=0,所以﹣=(a1+2a2+3a3+4a4+…+10a10+11a11)(a1﹣2a2+3a3﹣4a4+…﹣10a10+11a11)=0.…(14分)20.(16分)已知二阶矩阵M的属于特征值﹣1的一个特征向量为,属于特征值3的一个特征向量为.(1)求矩阵M;(2)求直线l:y=2x﹣1在M作用下得到的新的直线l′方程;(3)已知向量,求.【解答】解:(1)设M=,则∵二阶矩阵M的属于特征值﹣1的一个特征向量为,属于特征值3的一个特征向量为,∴,,∴a=2,b=1,c=3,d=0,∴A=…(4分)(2)设P(x0,y0)是l上任意一点,它在M作用下的对应点P′(x′,y′),则有…(6分)所以得解得…(8分)因为P(x0,y0)在l上,所以y0=2x0﹣1即化简得:3x′﹣4y′+3=0所以所求直线l′的方程为3x﹣4y+3=0…(10分)(3)设特征值λ1=﹣1时,对应特征向量=,λ2=3时,对应特征向量=.设即解得解得s=1,t=3,所以…(12分)∴=…(16分)。
2014-2015年江苏省淮安市清江中学高二(下)期中数学试卷(文科)和答案

2014-2015学年江苏省淮安市清江中学高二(下)期中数学试卷(文科)一、填空题:本大题共14小题,每小题5分,计70分.不需写出解答过程,请把答案写在答题纸的指定位置上.1.(5分)命题“∀x>4,x2>16”的否定是.2.(5分)已知cos x=(0<x<),则sin2x的值为.3.(5分)“α=”是“tanα=1”的条件.(填“充分不必要”、“必要不充分”、“充要”或“既不充分也不必要”)4.(5分)若函数,则f(x)的定义域是.5.(5分)用反证法证明时,对结论“自然数a,b,c至少有1个为偶数”的正确假设为.6.(5分)在等比数列{a n}中,若a1>0,a2a4+2a3a5+a4a6=25,则a3+a5=.7.(5分)已知向量,,若,则x=.8.(5分)已知实数x,y满足,则z=2x+y的最小值是.9.(5分)一元二次不等式ax2+bx﹣1>0的解集为{x|<x<1},则a+b=.10.(5分)函数y=2x2﹣lnx的最小值是.11.(5分)已知函数的图象的对称中心为(0,0),函数的图象的对称中心为,函数的图象的对称中心为(﹣1,0),…,由此推测,函数的图象的对称中心为.12.(5分)已知正实数x,y满足x+y=1,若的最小值为9,则正数a=.13.(5分)已知函数f(x)=对任意x1≠x2,都有>0成立,则实数a的取值范围是..14.(5分)已知等差数列{a n}的首项a1及公差d都是实数,且满足,则d的取值范围是.二、解答题:本大题共6小题,计90分.解答应写出必要的文字说明,证明过程或演算步骤,请把答案写在答题纸的指定区域内.15.(14分)已知向量=(sin A,sin B),=(cos B,cos A),=sin2C,其中A、B、C为△ABC的内角.(Ⅰ)求角C的大小;(Ⅱ)若sin A,sin C,sin B成等差数列,且,求AB的长.16.(14分)解关于x的不等式:①;②(2mx﹣1)(x﹣2)<0(m 为实常数)17.(14分)如图,在半径为3m的圆形(O为圆心)铝皮上截取一块矩形材料OABC,其中点B在圆弧上,点A、C在两半径上,现将此矩形铝皮OABC 卷成一个以AB为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设矩形的边长AB=xm,圆柱的体积为Vm3.(1)写出体积V关于x的函数关系式,并指出定义域;(2)当x为何值时,才能使做出的圆柱形罐子体积V最大?最大体积是多少?18.(16分)已知函数f(x)=x+(x>0)的最小最小值为,设点P是函数图象上的任意一点,过点P分别作直线y=x和y轴的垂线,垂足分别为M、N.(1)求a的值;(2)问:PM•PN是否为定值?若是,则求出该定值,若不是,请说明理由;(3)设O为坐标原点,求四边形OMPN面积的最小值.19.(16分)已知函数.(1)若函数f(x)的图象在点(2,f(2))处的切线方程为9x﹣y+b=0,求实数a,b的值;(2)若a≤0,求f(x)的单调减区间;(3)对一切实数a∈(0,1),求f(x)的极小值的最大值.20.(16分)已知等差数列{a n} 中,a3=7,a1+a2+a3=12,令b n=a n•a n+1,数列{}的前n项和为T n.(1)求数列{a n}的通项公式;(2)求证:T n<;(3)是否存在正整数m,n,且1<m<n,使得T1,T m,T n成等比数列?若存在,求出m,n的值,若不存在,请说明理由.2014-2015学年江苏省淮安市清江中学高二(下)期中数学试卷(文科)参考答案与试题解析一、填空题:本大题共14小题,每小题5分,计70分.不需写出解答过程,请把答案写在答题纸的指定位置上.1.(5分)命题“∀x >4,x 2>16”的否定是 ∃x >4,x 2≤16 .【解答】解:因为全称命题的否定是特称命题,所以,命题“∀x >4,x 2>16”的否定是:∃x >4,x 2≤16. 故答案为:∃x >4,x 2≤16;2.(5分)已知cos x =(0<x <),则sin2x 的值为 .【解答】解:∵cos x =,x ∈(0,),∴sin x =,∴sin2x =2sin x cos x =,故答案为:.3.(5分)“α=”是“tan α=1”的 充分不必要 条件.(填“充分不必要”、“必要不充分”、“充要”或“既 不充分也不必要”) 【解答】解:时,tan α=1;tan α=1时,,所以不一定得到;∴是tan α=1的充分不必要条件.故答案为:充分不必要. 4.(5分)若函数,则f (x )的定义域是 [﹣1,0)∪(0,1] .【解答】解:∵函数,则有 .解得﹣1≤x ≤1且x ≠0,故函数的定义域为[﹣1,0)∪(0,1],故答案为[﹣1,0)∪(0,1].5.(5分)用反证法证明时,对结论“自然数a,b,c至少有1个为偶数”的正确假设为a,b,c都是奇数.【解答】解:用反证法法证明数学命题时,应先假设要证的命题的反面成立,即要证的命题的否定成立,而命题:“自然数a,b,c中至少有一个是偶数”的否定为:“a,b,c都是奇数”,故答案为:a,b,c都是奇数.6.(5分)在等比数列{a n}中,若a1>0,a2a4+2a3a5+a4a6=25,则a3+a5=5.【解答】解:∵{a n}是等比数列,且a1>0,a2a4+2a3a5+a4a6=25,∴a32+2a3a5+a52=25,即(a3+a5)2=25.再由a3=a1•q2>0,a5=a1•q4>0,q为公比,可得a3+a5=5,故答案为:5.7.(5分)已知向量,,若,则x=3或﹣1.【解答】解:向量,,若,可得﹣(3﹣x)=x(3﹣x),解得x=3或﹣1.故答案为:3或﹣1.8.(5分)已知实数x,y满足,则z=2x+y的最小值是﹣1.【解答】解:画出可行域,得在直线x﹣y+2=0与直线x+y=0的交点A(﹣1,1)处,目标函数z=2x+y的最小值为﹣1.故答案为﹣1.9.(5分)一元二次不等式ax2+bx﹣1>0的解集为{x|<x<1},则a+b=1.【解答】解:由题意知,、1是方程ax2+bx﹣1=0的两根,且a<0,所以,解得,所以a+b=(﹣3)+4=1,故答案为:1.10.(5分)函数y=2x2﹣lnx的最小值是+ln2.【解答】解:函数y=2x2﹣lnx的定义域为(0,+∞),y′=4x﹣=,∴函数y=2x2﹣lnx在(0,)上单调递减,在(,+∞)上单调递增,∴当x=时,函数y=2x2﹣lnx有最小值,最小值为=+ln2.故答案为:+ln2.11.(5分)已知函数的图象的对称中心为(0,0),函数的图象的对称中心为,函数的图象的对称中心为(﹣1,0),…,由此推测,函数的图象的对称中心为.【解答】解:题中所涉及的函数的对称中心的横坐标依次为0,,﹣1,…,即0,,,…,由此推测,函数的图象的对称中心为故答案为:12.(5分)已知正实数x,y满足x+y=1,若的最小值为9,则正数a=4.【解答】解:∵a>0,∴=()(x+y)=1+a+≥a+1+2=(+1)2,当且仅当取等号,则有,解得a=4.故答案为:4.13.(5分)已知函数f(x)=对任意x1≠x2,都有>0成立,则实数a的取值范围是.[).【解答】解:由题意知函数f(x)在R上单调递增;∴f(x)的两段函数在各自区间上单调递增;∴1﹣2a>0,即;又e0﹣2≤(1﹣2a)•0+2a;∴﹣1≤2a;∴;∴实数a的取值范围是[).故答案为:[).14.(5分)已知等差数列{a n}的首项a1及公差d都是实数,且满足,则d的取值范围是.【解答】解:∵,由等差数列的前n项公式得(2a1+d)(2a1+3d)+(a1+d)2=﹣2,展开并化简整理得5a12+10a1d+4d2+2=0,将此式看作关于a1的一元二次方程,d 为系数.∵a1、d为实数,∴△=100d2﹣4×5×(4d2+2 )≥0.化简整理得d2﹣2≥0,∴d∈(﹣∞,﹣]∪[,+∞)故答案为:(﹣∞,﹣]∪[,+∞)二、解答题:本大题共6小题,计90分.解答应写出必要的文字说明,证明过程或演算步骤,请把答案写在答题纸的指定区域内.15.(14分)已知向量=(sin A,sin B),=(cos B,cos A),=sin2C,其中A、B、C为△ABC的内角.(Ⅰ)求角C的大小;(Ⅱ)若sin A,sin C,sin B成等差数列,且,求AB的长.【解答】解:(Ⅰ)(2分)对于△ABC中A+B=π﹣C,0<C<π∴sin(A+B)=sin C,∴(4分)又∵,∴(7分)(Ⅱ)由sin A,sin C,sin B成等差数列,得2sin C=sin A+sin B,由正弦定理得2c=a+b(9分)∵,∴,即ab cos C=18,ab=16(12分)由余弦弦定理c2=a2+b2﹣2ab cos C=(a+b)2﹣3ab,∴c2=4c2﹣3×36,,c=6(14分)16.(14分)解关于x的不等式:①;②(2mx﹣1)(x﹣2)<0(m 为实常数)【解答】解:①原不等式可化为,即,所以有,解得:,可得不等式的解集为{x|≤x<}.②对于不等式(2mx﹣1)(x﹣2)<0,当m=0时,原不等式即为﹣(x﹣2)<0解得:x>2.当m≠0时,原不等式可化为,当m<0时,得,解得它的解集为{x|}.当m>0时,原不等式可化为,当0<m<时,>2,所以不等式的解集为{x|};当m=时,=2,所以原不等式无解;当m>时,可得<2,所以不等式的解集为{x|}.综上所得:原不等式的解集为:当m<0时,解集为;当m=0时,解集为(2,+∞);当0<m<时,解集为;当m=时,解集为φ;当m>时,解集为.17.(14分)如图,在半径为3m的圆形(O为圆心)铝皮上截取一块矩形材料OABC,其中点B在圆弧上,点A、C在两半径上,现将此矩形铝皮OABC 卷成一个以AB为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设矩形的边长AB=xm,圆柱的体积为Vm3.(1)写出体积V关于x的函数关系式,并指出定义域;(2)当x为何值时,才能使做出的圆柱形罐子体积V最大?最大体积是多少?【解答】解:(1)连接OB,在Rt△OAB中,∵AB=x,∴OA=,设圆柱底面半径为r,则=2πr,即4π2r2=9﹣x2,∴V=πr2•x=,其中0<x<3.…(6分)(2)由V′==0及0<x<3,得x=,…(8分)列表如下:…(10分)所以当x=时,V有极大值,也是最大值为.…(14分)答:当x为m时,做出的圆柱形罐子体积最大,最大体积是m3.…(16分)18.(16分)已知函数f(x)=x+(x>0)的最小最小值为,设点P是函数图象上的任意一点,过点P分别作直线y=x和y轴的垂线,垂足分别为M、N.(1)求a的值;(2)问:PM•PN是否为定值?若是,则求出该定值,若不是,请说明理由;(3)设O为坐标原点,求四边形OMPN面积的最小值.【解答】解:(1)∵x>0,若a≤0,则f(x)递增,没有最小值,∴a>0,∴,∴x=时,;∴.(2)设,则,PN=x0,则PM•PN=1;(3)设,则直线PM:,由得,M;S OMPN=S△OPN+S△OPM==≥.(当且仅当,即x0=1时取等号);故四边形OMPN面积的最小值.19.(16分)已知函数.(1)若函数f(x)的图象在点(2,f(2))处的切线方程为9x﹣y+b=0,求实数a,b的值;(2)若a≤0,求f(x)的单调减区间;(3)对一切实数a∈(0,1),求f(x)的极小值的最大值.【解答】解:(1)f′(x)=ax2﹣(a+1)x+1(a∈R),…(1分)由f′(2)=9,得a=5.,…(2分)∴∴f(2)=3,∴(2,3)在直线9x﹣y+b=0上,∴b=﹣15.…(4分)(2)①若a=0,,∴f(x)的单调减区间为(1,+∞).…(6分)②若a<0,则,令f′(x)<0,得.∴,或x>1.…(9分)∴f(x)的单调减区间为,(1,+∞).…(10分)(3),0<a<1,列表:,,…(12分)∴f(x)的极小值为=.…(14分)当时,函数f(x)的极小值f()取得最大值为.…(16分)20.(16分)已知等差数列{a n} 中,a3=7,a1+a2+a3=12,令b n=a n•a n+1,数列{}的前n项和为T n.(1)求数列{a n}的通项公式;(2)求证:T n<;(3)是否存在正整数m,n,且1<m<n,使得T1,T m,T n成等比数列?若存在,求出m,n的值,若不存在,请说明理由.(1)设数列{a n}的公差为d,由解得.∴【解答】解:a n=1+(n﹣1)×3=3n﹣2.(2)∵a n=3n﹣2,a n+1=3n+1,∴b n=a n•a n+1=(3n﹣2)(3n+1),∴.∴.(3)由(2)知,,∴,,∵T1,T m,T n成等比数列,∴,即.当m=2时,,n=16,符合题意;当m=3时,,n无正整数解;当m=4时,,n无正整数解;当m=5时,,n无正整数解;当m=6时,,n无正整数解;当m≥7时,m2﹣6m﹣1=(m﹣3)2﹣10>0,则,而,所以,此时不存在正整数m,n,且1<m<n,使得T1,T m,T n成等比数列.综上,存在正整数m=2,n=16,且1<m<n,使得T1,T m,T n成等比数列.。
江苏省清江中学2014-2015学年高二数学 午练练习(91)苏教版
午练练习(91)1.若双曲线221y x m -=的一条渐近线方程是y =,则m 等于 . 2.已知p :⎩⎪⎨⎪⎧x|⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x +2≥0x -10≤0,q :{x|1-m≤x≤1+m ,m>0},若q 是p 的必要非充分条件,则实数m 的取值范围是______.3.设实数,x y 满足2025020x y x y y --≤⎧⎪+-≥⎨⎪-≤⎩ 则y x u x y =-的取值范围是 .4.已知函数()ln 2x f x x =+,若2(2)(3)f x f x +<,则实数x 的取值范围是 . 5.直线AB 、AD ⊂α,直线CB 、CD ⊂β,点E ∈AB ,点F ∈BC ,点G ∈CD ,点H ∈DA ,若直线EH∩直线FG=M ,则点M 一定在直线 上6.一直PA ,PB ,PC 两两互相垂直,且△PAB 、△PAC 、△PBC 的面积分别为1.5cm2,2cm2,6cm2,则过P ,A ,B ,C 四点的外接球的表面积为 cm2.7.已知A ,B ,P 是双曲线22221x y a b -=上不同的三点,且A ,B 连线经过坐标原点,若直线PA ,PB 的斜率乘积23PA PB k k ⋅=,则该双曲线的离心率为 . 8.给出定义:若函数()f x 在D 上可导,即()f x '存在,且导函数()f x '在D 上也可导,则称()f x在D 上存在二阶导函数,记()()()f x f x ''''=,若()0f x ''<在D 上恒成立,则称()f x 在D 上为凸函数.以下四个函数在0,2π⎛⎫ ⎪⎝⎭上不是凸函数的是 .(1)()sin cos f x x x =+ (2)()ln 2f x x x =- (3)3()21f x x x =-+-(4)()x f x xe -=-.9.已知函数()11sin 24f x x x x =-的图象在点()()00,A x f x 处的切线斜率为12,则)4tan(0π+x 的值为 .10.已知t 为常数,函数2|2|y x x t =-+在区间[0,3]上的最大值为3,则实数t =_____. 11.设数列}{n b 满足:211=b ,n n n b b b +=+21, (1)求证:11111+-=+n n n b b b ; (2)若11111121++++++=n n b b b T ,对任意的正整数n ,05log 32>--m T n 恒成立.求m 的取值范围.(91)参考答案1.3 2。
江苏清江中学14-15学年高二下学期期中考试数学(理)试题 (Word版含答案)
江苏省清江中学2014—2015学年度第二学期期中考试高二数学试卷(理科)时间:120分钟 满分:160分纸的指定位置上.1.计算:3828C C += ▲ .(用数字作答) 2.二项式(3x x2-)8的展开式中第7项的二项式系数为 ▲ (用数字作答) 3.在矩阵1021⎡⎤⎢⎥⎣⎦变换下,点A (2,1)将会转换成 ▲4.已知向量),5,2(),1,0,(2t t =-=,若⊥,则t= ▲ . 5.在极坐标系中,圆2sin ρθ=(02θπ<≤)的圆心的极坐标为 ▲ .6.已知矩阵M=⎥⎦⎤⎢⎣⎡2263,则M 的特征值为 ▲ .7.从1,2,3,4,5,6中选出3个不同的数组成3位数,并将这些三位数由小到大打排列,则第100个数是 ▲8.将参数方程()2()t tt tx e et y e e --⎧=+⎪⎨=-⎪⎩为参数化为普通方程,结果为 ▲ 9.已知随机变量X 0 3则随机变量X 的方差是 _ __▲____ .10.某小组有4名男生,3名女生.若从男,女生中各选2人,组成一个小合唱队,要求站成一排且2名女生不相邻,共有 ▲ 种不同的排法? 11.555555+除以8余数是 ▲12.一袋中装有5个白球,3个红球,现从袋中往外取球,每次取出一个,取出后记下球的颜色,然后放回,直到红球出现10次停止,设停止时,取球次数为随机变量X,则==)12(X P ▲ (只需列式,不需计算结果).13.已知直线113:()24x tl t y t=+⎧⎨=-⎩为参数与直线2:245l x y -=相交于点B ,又点(1,2)A ,则AB = ▲14.已知数列{}n a 满足11a =,11()2n n n a a -+=(2)n ≥,212222n n n S a a a =⋅+⋅++⋅,类比课本中推导等比数列前n 项和公式的方法,可求得132n n n S a +-⋅= ▲二、解答题:本大题共6小题,计90分.解答应写出必要的文字说明,证明过程或演算步骤,请把答案写在答题纸的指定区域内. 15.已知直线l 的参数方程:⎩⎨⎧+==,21,t y t x (t 为参数)和曲线C 的极坐标方程:⎪⎭⎫⎝⎛+=4sin 22πθρ。
【解析】江苏省淮安市清江中学2014-2015学年高二上学期期末考试数学(文)试卷 Word版含解析[ 高考]
2014-2015学年江苏省淮安市清江中学高二(上)期末数学试卷(文科)一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题纸相应位置上.1.命题“∃x<2,x2>4”的否定是.2.抛物线y=x2的准线方程是.3.在校英语节演讲比赛中,七位评委老师为某班选手打出的分数的茎叶图(如图所示),去掉一个最高分和一个最低分后,所剩数据的方差为.4.若复数z=a2﹣4+(a﹣2)i(a∈R)是纯虚数,则|z|= .5.某工厂甲、乙、丙三个车间生产同一种产品,数量分别为450、750、600,用分层抽样从三个车间中抽取一个容量为n的样本,且每个产品被抽到的概率为0.02,则应从乙车间抽产品数量为.6.如图是一个算法流程图,则输出S的值是.7.已知曲线 y=lnx在点P处的切线经过原点,则此切线的方程为.8.一只蚂蚁在高为3,两底分别为3和6的直角梯形区域内随机爬行,则其恰在离四个顶点距离都大于1的地方的概率为.9.已知等比数列{a n}中,有成立.类似地,在等差数列{b n}中,有成立.10.已知g(x)=x3﹣x2﹣x﹣1,如果存在x1,x2∈[0,2],使得g(x1)﹣g(x2)≥M,则满足该不等式的最大整数M= .11.“﹣4<a<2”是“方程+=1表示椭圆”的条件.(填“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”)12.函数f(x)=sinx﹣cosx﹣tx在[0,π]上单调递减,则实数t的取值范围是.13.椭圆+=1(a>b>0)的右焦点F,其右准线与x轴的交点为A,在椭圆上存在点P满足PF=AF,则﹣2(lnb﹣lna)的范围是.14.函数f(x)=+x3(x∈R),其导函数为f′(x),则f(2015)+f′(2015)+f(﹣2015)﹣f′(﹣2015)= .二、解答题:本大题共6小题,共计90分.请在答题纸指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.15.设p:复数z=(1﹣2m)+(m+2)i在复平面上对应的点在第二或第四象限;q:函数g (x)=x3+mx2+(m+)x+6在R上有极大值点和极小值点各一个.求使“p且q”为真命题的实数m的取值范围.16.高二年级从参加期末考试的学生中抽出60名学生,并统计了他们的物理成绩(成绩均为整数且满分为100分),把其中不低于50分的分成五段[50,60),[60,70)…[90,100]后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:(1)根据江苏省高中学业水平测试要求,成绩低于60分属于C级,需要补考,求抽取的60名学生中需要补考的学生人数;(2)年级规定,本次考试80分及以上为优秀,估计这次考试物理学科优秀率;(3)根据(1),从参加补考的学生中选两人,求他们成绩至少有一个不低于50分的概率.17.已知关于x的一次函数y=mx+n.(1)设集合P={﹣4,﹣1,1,2,3}和Q={﹣4,3},分别从集合P和Q中随机取一个数作为m和n,求函数y=mx+n是减函数的概率;(2)实数m,n满足条件求函数y=mx+n的图象经过一、二、四象限的概率.18.如图,在半径为30cm的半圆形(O为圆心)铝皮上截取一块矩形材料ABCD,其中点C、D在圆弧上,点A、B在两半径上,现将此矩形铝皮ABCD卷成一个以BC为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设矩形的边长BC=xcm圆柱的体积为Vcm3.(1)写出体积V关于x的函数关系式;(2)当x为何值时,才能使做出的圆柱形罐子体积V最大?19.已知椭圆E:+=1(a>b>0),以抛物线y2=8x的焦点为顶点,且离心率为(1)求椭圆E的方程;(2)已知A、B为椭圆上的点,且直线AB垂直于x轴,直线l:x=4与x轴交于点N,直线AF与BN交于点M.(ⅰ)求证:点M恒在椭圆C上;(ⅱ)求△AMN面积的最大值.20.已知函数f(x)=lnx,g(x)=﹣(a>0),设F(x)=f(x)+g(x)(Ⅰ)求函数F(x)的单调区间(Ⅱ)若以函数y=F(x)(x∈(0,3])图象上任意一点P(x0,y0)为切点的切线的斜率k ≤恒成立,求实数a的最小值(Ⅲ)是否存在实数m,使得函数y=g()+m﹣1的图象与函数y=f(1+x2)的图象恰有四个不同交点?若存在,求出实数m的取值范围;若不存在,说明理由.2014-2015学年江苏省淮安市清江中学高二(上)期末数学试卷(文科)参考答案与试题解析一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题纸相应位置上.1.命题“∃x<2,x2>4”的否定是∀x<2,x2≤4 .考点:命题的否定.专题:简易逻辑.分析:直接利用特称命题的否定是全称命题写出结果即可.解答:解:因为特称命题的否定是全称命题.所以,命题“∃x<2,x2>4”的否定是:∀x<2,x2≤4.故答案为:∀x<2,x2≤4.点评:本题考查命题的否定,特称命题与全称命题的否定关系,基本知识的考查.2.抛物线y=x2的准线方程是4y+1=0 .考点:抛物线的简单性质.专题:圆锥曲线的定义、性质与方程.分析:先根据抛物线的标准方程得到焦点在y轴上以及2p=1,再直接代入即可求出其准线方程.解答:解:因为抛物线的标准方程为:x2=y,焦点在y轴上;所以:2p=1,即p=,所以:=,∴准线方程 y=﹣=﹣,即4y+1=0.故答案为:4y+1=0.点评:本题主要考查抛物线的基本性质.解决抛物线的题目时,一定要先判断焦点所在位置.3.在校英语节演讲比赛中,七位评委老师为某班选手打出的分数的茎叶图(如图所示),去掉一个最高分和一个最低分后,所剩数据的方差为.考点:茎叶图.专题:概率与统计.分析:根据方差的定义,首先求出数据的平均数,由公式求方差.解答:解:=(84+84+86+84+87)=85S2=[3×(84﹣85)2+(86﹣85)2+(87﹣85)2]=所以所剩数据的方差为.点评:本题考查了方差的定义和公式,属于基础题.4.若复数z=a2﹣4+(a﹣2)i(a∈R)是纯虚数,则|z|= 4 .考点:复数求模.专题:数系的扩充和复数.分析:利用纯虚数的定义、模的计算公式即可得出.解答:解:∵复数z=a2﹣4+(a﹣2)i(a∈R)是纯虚数,∴,解得a=﹣2.∴z=﹣4i.则|z|=4.故答案为:4.点评:本题考查了纯虚数的定义、模的计算公式,属于基础题.5.某工厂甲、乙、丙三个车间生产同一种产品,数量分别为450、750、600,用分层抽样从三个车间中抽取一个容量为n的样本,且每个产品被抽到的概率为0.02,则应从乙车间抽产品数量为15 .考点:分层抽样方法.专题:概率与统计.分析:根据分层抽样的定义以及概率的关系即可得到结论.解答:解:∵个产品被抽到的概率为0.02,∴应从乙车间抽产品数量为750×0.02=15,故答案为:15点评:本题主要考查分层抽样的应用,比较基础.6.如图是一个算法流程图,则输出S的值是66 .考点:程序框图.专题:图表型;算法和程序框图.分析:模拟执行算法流程,依次写出每次循环得到的S,k的值,当k=11时,满足条件k >7,退出循环,输出S的值为66.解答:解:模拟执行算法流程,可得S=0,k=1不满足条件k>7,S=1,k=4不满足条件k>7,S=17,k=7不满足条件k>7,S=66,k=11满足条件k>7,退出循环,输出S的值为66.故答案为:66.点评:本题主要考查了程序框图和算法,依次写出每次循环得到的S,k的值是解题的关键,属于基本知识的考查.7.已知曲线 y=lnx在点P处的切线经过原点,则此切线的方程为y=.考点:利用导数研究曲线上某点切线方程.专题:计算题;导数的概念及应用;直线与圆.分析:设P(m,n),求出函数的导数,求得切线的斜率,运用点斜式方程求得切线方程,由切线经过原点,可得n=1,由切点在曲线上,求得m,即可得到切线方程.解答:解:设P(m,n),y=lnx的导数为y′=,即有在点P处的切线斜率为k=,则切线方程为y﹣n=(x﹣m),又切线经过原点,即有n=1,由于lnm=n,解得m=e,则有切线方程为y=.故答案为:y=.点评:本题考查导数的运用:求切线方程,主要考查导数的几何意义,运用点斜式方程和正确求导是解题的关键.8.一只蚂蚁在高为3,两底分别为3和6的直角梯形区域内随机爬行,则其恰在离四个顶点距离都大于1的地方的概率为1﹣.考点:几何概型.专题:概率与统计.分析:以四个顶点为圆心,1为半径作圆,当蚂蚁在此区域外的区域随机爬行,离顶点的距离大于1,其面积为﹣π,再用几何概型公式即得本题的概率.解答:解:如图由已知,高为3,两底分别为3和6的直角梯形面积为,离四个顶点距离都大于1的区域是如图阴影部分,即以四个顶点为圆心,1为半径作圆,当蚂蚁在除此区域外的区域随机爬行,离顶点的距离大于1的部分,其面积为=﹣π,∴蚂蚁恰在离四个顶点距离都大于1的地方的概率为P=.故答案为:1﹣.点评:本题以蚂蚁在正方形内爬行为例,求几何概型的概率.着重考查了图形面积的求法和几何概型的概率求法等知识点,属于基础题.9.已知等比数列{a n}中,有成立.类似地,在等差数列{b n}中,有成立.考点:类比推理.专题:综合题;推理和证明.分析:在等差数列中,考查的主要是若m+n=p+q,则a m+a n=a p+a q,那么对应的在等比数列中考查的应该是若m+n=p+q,则b m b n=b p b q.解答:解:等差数列与等比数列的对应关系有:等差数列中的加法对应等比数列中的乘法,等差数列中除法对应等比数列中的开方,故此我们可以类比得到结论:.故答案为:.点评:本题考查类比推理,掌握类比推理的规则及类比对象的特征是解本题的关键,本题中由等差结论类比等比结论,其运算关系由加类比乘,解题的难点是找出两个对象特征的对应,作出合乎情理的类比.10.已知g(x)=x3﹣x2﹣x﹣1,如果存在x1,x2∈[0,2],使得g(x1)﹣g(x2)≥M,则满足该不等式的最大整数M= ﹣3 .考点:利用导数求闭区间上函数的最值.专题:导数的综合应用.分析:求函数的导数,求出函数在[0,2]上的最大值和最小值即可.解答:解:函数的f(x)的导数g′(x)=3x2﹣2x﹣1,由g′(x)>0得x>1,此时函数单调递增,由g′(x)<0得0<x<1,此时函数单调递减,即函数在[0,2]上的极小值为g(1)=1﹣1﹣1﹣1=﹣2,∵g(0)=﹣1,g(2)=1,∴函数的最大值为1,最小值为﹣2,则[g(x1)﹣g(x2)]min=﹣2﹣1=﹣3,故M≤﹣3,则满足该不等式的最大整数M=﹣3,故答案为:﹣3点评:本题主要考查函数的最值的求解,利用导数求函数的最大值和最小值是解决本题的关键.11.“﹣4<a<2”是“方程+=1表示椭圆”的必要不充分条件.(填“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”)考点:椭圆的标准方程;必要条件、充分条件与充要条件的判断.专题:圆锥曲线的定义、性质与方程.分析:当a=﹣1时,a+4=2﹣a=3,方程+=1是圆;由方程+=1表示椭圆,得,由此能求出“﹣4<a<2”是“方程+=1表示椭圆”的必要不充分条件.解答:解:∵﹣4<a<2,∴,当a=﹣1时,a+4=2﹣a=3,方程+=1是圆,∴“﹣4<a<2”推不出“方程+=1表示椭圆”,∵方程+=1表示椭圆,∴,∴解得﹣4<a<﹣1或﹣1<a<2,∴“方程+=1表示椭圆”⇒“﹣4<a<2”,∴“﹣4<a<2”是“方程+=1表示椭圆”的必要不充分条件.故答案为:必要不充分.点评:本题考查椭圆的性质的应用,是基础题,解题时要认真审题,注意“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”的合理运用.12.函数f(x)=sinx﹣cosx﹣tx在[0,π]上单调递减,则实数t的取值范围是[2,+∞).考点:三角函数中的恒等变换应用.专题:导数的概念及应用.分析:求出函数f(x)的导数f′(x)=cosx+sinx﹣t,函数f(x)在[0,π]上单调递增可转化为f′(x)≤0,即cosx+sinx﹣t≥0在区间[0,π]上恒成立,变成求函数的最值问题即可求解.解答:解:∵函数f(x)=sinx﹣cosx﹣tx在[0,π]上单调递减,∴函数f(x)的导数f′(x)≤0,在区间[0,π]上恒成立,求得f′(x)=cosx+sinx﹣t,所以cosx+sinx﹣t≤0在区间[0,π]上恒成立即t≥cosx+sinx对x∈[0,π]总成立,记函数g(x)=cosx+sinx=2sin(x+),易求得g(x)在[0,π]的最大值为2,从而t≥2,故答案为:[2,+∞).点评:利用导数工具讨论函数的单调性,是求函数的值域和最值,从而得出参数t的取值范围,是解决此种问题的常用方法,解决本题同时应注意研究导函数的单调性得出导数的正负,从而得出原函数的单调性的技巧,本题属于基本知识的考查.13.椭圆+=1(a>b>0)的右焦点F,其右准线与x轴的交点为A,在椭圆上存在点P满足PF=AF,则﹣2(lnb﹣lna)的范围是[﹣ln,+∞).考点:椭圆的简单性质.专题:函数的性质及应用;导数的综合应用;圆锥曲线的定义、性质与方程.分析:求出椭圆的右焦点和右准线,求得AF的长,再由椭圆的性质,可得a﹣c≤|PF|≤a+c,进而得到a≤2c,由a,b,c的关系,可得a,b的关系,令t=,(0<t),则f(t)=t2﹣2lnt,运用导数判断单调性,即可得到所求范围.解答:解:椭圆+=1(a>b>0)的右焦点F(c,0),右准线为x=,由题意|PF|=|AF|=﹣c,由椭圆的性质可得a﹣c≤|PF|≤a+c,即有a﹣c≤﹣c≤a+c,即有c<a+c且a﹣c≤c,则有a2≤4c2=4(a2﹣b2),即为0<≤,则﹣2(lnb﹣lna)=()2﹣2ln,令t=,(0<t),则f(t)=t2﹣2lnt,由f′(t)=2t﹣在(0,]小于0,则有f(t)在(0,]递减,故f(t)的范围为[﹣ln,+∞).故答案为:[﹣ln,+∞).点评:本题考查椭圆的方程和性质,主要考查椭圆的准线方程的运用,椭圆上一点到焦点的距离的最值,同时考查导数的运用:判断单调性,属于中档题.14.函数f(x)=+x3(x∈R),其导函数为f′(x),则f(2015)+f′(2015)+f(﹣2015)﹣f′(﹣2015)= 4026 .考点:导数的运算.专题:导数的概念及应用.分析:先化简f(x),再求出f(﹣x),得到f(x)+f(﹣x)=2014+2012=4026,然后求导,得到导函数为偶函数,问题得以解决.解答:解:f(x)=+x3=+x3=2014﹣﹣x3,∴f(﹣x)=2014﹣﹣(﹣x)3=2012++x3,∴f(x)+f(﹣x)=2014+2012=4026∴f′(x)=﹣3x2,∴f′(﹣x)=﹣3x2,∴f′(x)=f′(﹣x)∴f(2015)+f′(2015)+f(﹣2015)﹣f′(﹣2015)=4026故答案为:4026点评:本题考查了导数的运算以及函数奇偶性的运用,属于中档题二、解答题:本大题共6小题,共计90分.请在答题纸指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.15.设p:复数z=(1﹣2m)+(m+2)i在复平面上对应的点在第二或第四象限; q:函数g (x)=x3+mx2+(m+)x+6在R上有极大值点和极小值点各一个.求使“p且q”为真命题的实数m的取值范围.考点:复合命题的真假.专题:简易逻辑.分析:先根据复数的定义,函数导数在极值点处的取值情况求出命题p,q下的m的取值范围,再根据p且q为真,对所得m的取值范围求交集即可.解答:解:∵复数z=(1﹣2m)+(m+2)i在复平面上对应的点在第二或第四象限,∴(1﹣2m)(m+2)<0,即m<﹣2或.…(5分)∵函数在R上有极大值点和极小值点各一个,∴有两个不同的解,即△>0.由△>0,得m<﹣1或m>4 …(10分)要使“p且q”为真命题,则p,q都是真命题,…(12分)∴.∴m的取值范围为(﹣∞,﹣2)∪(4,+∞).…(14分)点评:考查复数的定义,极值的概念,及导函数在极值点处的取值情况,p且q的真假和p,q真假的关系.16.高二年级从参加期末考试的学生中抽出60名学生,并统计了他们的物理成绩(成绩均为整数且满分为100分),把其中不低于50分的分成五段[50,60),[60,70)…[90,100]后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:(1)根据江苏省高中学业水平测试要求,成绩低于60分属于C级,需要补考,求抽取的60名学生中需要补考的学生人数;(2)年级规定,本次考试80分及以上为优秀,估计这次考试物理学科优秀率;(3)根据(1),从参加补考的学生中选两人,求他们成绩至少有一个不低于50分的概率.考点:频率分布直方图.专题:概率与统计.分析:(1)根据频率和为1,求出低于50分的频率,计算对应的频数即可;(2)根据题意,计算成绩在80及以上的分数的频率即可;(3)求出“成绩低于50分”及“[50,60)”的人数是多少,再利用古典概型计算对应的概率.解答:解:(1)因为各组的频率和等于1,故低于50分的频率为:f1=1﹣(0.015×2+0.03+0.025+0.005)×10=0.1,…(3分)所以低于60分的人数为60×(0.1+0.15)=15(人);…(5分)(2)依题意,成绩80及以上的分数所在的第五、六组(低于50分的为第一组),频率和为(0.025+0.005)×10=0.3,所以,抽样学生成绩的优秀率是30%,…(8分)于是,可以估计这次考试物理学科及格率约为30%;…(9分)(3)“成绩低于50分”及“[50,60)”的人数分别是6,9,所以从参加补考的学生中选两人,他们成绩至少有一个不低于50分的概率为:P=1﹣=.…(14分)点评:本题考查了频率分布直方图的应用问题,也考查了古典概型的应用问题,是综合性题目.17.已知关于x的一次函数y=mx+n.(1)设集合P={﹣4,﹣1,1,2,3}和Q={﹣4,3},分别从集合P和Q中随机取一个数作为m和n,求函数y=mx+n是减函数的概率;(2)实数m,n满足条件求函数y=mx+n的图象经过一、二、四象限的概率.考点:几何概型;列举法计算基本事件数及事件发生的概率.专题:概率与统计.分析:(1)由题意,写出所有满足条件的事件,由古典概型公式解答;(2)画出平面区域,计算区域面积,由几何概型的公式解答.解答:解:(1)由已知,抽取的全部结果表示为(m,n),则基本事件有:(﹣4,﹣4),(﹣4,3),(﹣1,﹣4),(﹣1,3),(1,﹣4),(1,3),(2,﹣4),(2,3),(3,﹣4),(3,3),共10个基本事件,设使函数为减函数的事件为A,m<0,则A包含的基本事件有:(﹣4,﹣4),(﹣4,3),(﹣1,﹣4),(﹣1,3),共4个基本事件,由古典概型公式,P(A)=.…(7分)(2)m、n满足条件的区域如图所示:要使函数的图象过一、二、四象限,则m<0,n>0,故使函数图象过一、二、四象限的(m,n)的区域为第二象限的阴影部分,由几何概型的概率公式得所求事件的概率为.…(14分)点评:本题考查了古典概型、几何概型的公式的运用;古典概型关键是明确事件的个数;几何概型关键是明确事件的测度,然后由公式解答.18.如图,在半径为30cm的半圆形(O为圆心)铝皮上截取一块矩形材料ABCD,其中点C、D在圆弧上,点A、B在两半径上,现将此矩形铝皮ABCD卷成一个以BC为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设矩形的边长BC=xcm圆柱的体积为Vcm3.(1)写出体积V关于x的函数关系式;(2)当x为何值时,才能使做出的圆柱形罐子体积V最大?考点:导数在最大值、最小值问题中的应用.专题:应用题;导数的综合应用.分析:(1)连接OC,在Rt△OCB中,由BC=x,利用勾股定理可得OB,设圆柱底面半径为r,则π2r2=900﹣x2,利用V=πr2•x(其中0<x<30)即可得出.(2)利用导数V′,得出其单调性即可.解答:解:(1)连结OC,因为BC=x,所以,设圆柱底面半径为r,则,即π2r2=900﹣x2,所以,其中0<x<30.…(7分)(2)由,得,又在上V′>0,在上V′<0,所以,在上是增函数,在上是减函数,所以,当时,V有最大值..…(16分)点评:熟练掌握勾股定理、圆柱的体积计算公式、利用导数研究函数的单调性极值与最值等是解题的关键.19.已知椭圆E:+=1(a>b>0),以抛物线y2=8x的焦点为顶点,且离心率为(1)求椭圆E的方程;(2)已知A、B为椭圆上的点,且直线AB垂直于x轴,直线l:x=4与x轴交于点N,直线AF与BN交于点M.(ⅰ)求证:点M恒在椭圆C上;(ⅱ)求△AMN面积的最大值.考点:椭圆的简单性质.专题:直线与圆;圆锥曲线的定义、性质与方程.分析:(1)求出抛物线的焦点,由题意可得a=2,再由离心率公式可得c,进而得到b,即有椭圆方程;(2)(i)设A(m,n),则B(m,﹣n)代入椭圆方程,通过直线方程求得交点M,代入椭圆方程的左边,检验即可得证;(ⅱ)设AM的方程为x=ty+1,代入椭圆方程,设A(x1,y1),M(x2,y2),求得|y1﹣y2|,通过对勾函数的单调性,即可得到面积的最大值.解答:解:(1)因为抛物线y2=8x的焦点为(2,0),又椭圆以抛物线焦点为顶点,所以a=2,又e==,所以c=1,b2=3,∴椭圆E的方程为=1.(2)(i)证明:由题意得F(1,0)、N(4,0).设A(m,n),则B(m,﹣n)(n≠0),=1.AF与BN的方程分别为:n(x﹣1)﹣(m﹣1)y=0,n(x﹣4)﹣(m﹣4)y=0,设M(x0,y0),则有,得x0=,由于==1,所以点M恒在椭圆C上;(ⅱ)解:设AM的方程为x=ty+1,代入=1,得(3t2+4)y2+6ty﹣9=0,设A(x1,y1),M(x2,y2),解方程得,y1=.|y1﹣y2|=,令=λ(λ≥1),令=λ(λ≥1),则|y1﹣y2|=,因为函数y=3λ+在[1,+∞)上为增函数,所以,当λ=1即t=0时,y=3λ+有最小值4,S△AMN==,所以△AMN面积最大值为.点评:本题考查椭圆的方程和性质,主要考查椭圆的离心率和方程的运用,联立直线方程,求出交点,考查函数的单调性的运用,属于中档题.20.已知函数f(x)=lnx,g(x)=﹣(a>0),设F(x)=f(x)+g(x)(Ⅰ)求函数F(x)的单调区间(Ⅱ)若以函数y=F(x)(x∈(0,3])图象上任意一点P(x0,y0)为切点的切线的斜率k ≤恒成立,求实数a的最小值(Ⅲ)是否存在实数m,使得函数y=g()+m﹣1的图象与函数y=f(1+x2)的图象恰有四个不同交点?若存在,求出实数m的取值范围;若不存在,说明理由.考点:利用导数研究函数的单调性;利用导数研究曲线上某点切线方程.专题:导数的综合应用.分析:(I)先求出其导函数,根据导函数的正负即可求出其单调区间;(II)先把问题转化为F'(x0)=≤恒成立;再结合二次函数即可求出结论;(III)先根据条件把问题转化为m=ln(1+x2)+x2+有四个不同的根;求出其导函数,找到其极值点,根据极值即可得到结论.解答:解:(I)∵F(x)=f(x)+g(x)=lnx﹣,∴F'(x)=+=,(x>0);∵x>0,a>0,∴F'(x)>0,∴F(x)在(0,+∞)上递增;(II)∵F'(x)=,(0<x≤3),则k=F'(x0)=≤恒成立;即a≤(﹣2x0)在(0,3]上恒成立,当x0=1时,(﹣2x0)取到最小值﹣,∴a≤﹣.即a的最大值为﹣.(III)y=g()+m﹣1=﹣x2+m﹣的图象与函数y=f(1+x2)=ln(1+x2)的图象恰有四个不同的交点,即,﹣x2+m﹣=ln(1+x2)有四个不同的根,亦即m=ln(1+x2)+x2+有四个不同的根;令G(x)=ln(1+x2)+x2+;则G'(x)=+x=;∴x>0时,G′(x)>0,G(x)递增,x<0时,G′(x)<0,G(x)递减,∴G(x)min=G(0)=>0,∴不存在实数m,使得函数y=g()+m﹣1的图象与函数y=f(1+x2)的图象恰有四个不同交点.点评:本题主要考察了应用导数求函数的单调区间,极值,最值,以及恒成立问题的判断.。
江苏省清江中学2014-2015学年高二下学期期中考试数学(文)试卷Word版含答案
江苏省清江中学2014—2015学年度第二学期期中考试高二数学试卷(文科)时间:120分钟 满分:160分 一、填空题:本大题共14小题,每小题5分,计70分.不需写出解答过程,请把答案写在答题纸的指定位置上.1.命题“4>∀x ,162>x ”的否定是 . 2.已知⎪⎭⎫⎝⎛<<=2053cos πx x ,则x 2sin 的值为_________. 3.“4πα=” 是“tan 1α=”的 条件.(填“充分不必要”、“必要不充分”、“充要”或“既不充分也不必要”)4.若函数()f x =,则()f x 的定义域是 .5.用反证法证明某命题时,对结论“自然数,,a b c 至少有1个偶数”的正确假设为 “ ”.6.在实数等比数列{}n a 中,10a >,若243546225a a a a a a ++=,则35a a += .7.已知向量)3,(x x -=,)3,1(x --=,若//,则x =8.已知实数,x y 满足20,0,1,x y x y x -+≥⎧⎪+≥⎨⎪≤⎩则2z x y =+的最小值为 .9.一元二次不等式210ax bx +->的解集为1{|1}3x x <<,则a b += 10.函数22ln y x x =-的最小值是 11.已知函数1y x=的图象的对称中心为(0,0),函数111y x x =++的图象的对称中心为1(,0)2-,函数11112y x x x =++++的图象的对称中心为(1,0)-,……,由此推测,函数111112y x x x x n=+++++++的图象的对称中心为 . 12.已知正数x 、y 满足1x y +=,则1ax y+的最小值是9,则正数a 的值为 13.已知函数f (x )=⎩⎨⎧+--a x a a e x 2)21(2 0>≤x x 对任意x 1≠x 2,都有0)()(2121>--x x x f x f 成立,则实数a 的取值范围是14.已知等差数列{}n a 的首项a 1及公差d 都是实数,且满足23242029S S S ++=,则d 的取值范围是 . 二、解答题:本大题共6小题,计90分.解答应写出必要的文字说明,证明过程或演算步骤,请把答案写在答题纸的指定区域内.15.已知A 、B 、C 为ABC ∆的内角,向量)sin ,(sin B A m =,)cos ,(cos A B n =,且C 2sin =⋅,(Ⅰ)求角C 的大小;(Ⅱ)若A sin ,C sin ,B sin 成等差数列,且18)(=-⋅,求AB 的长.16.解关于x 的不等式:① 2121≥--x x ; ② (2mx-1)(x-2)<0(m 为实常数)17. 如图,在半径为cm 30的41圆形(O 为圆心)铝皮上截取一块矩形材料OABC ,其中点B 在圆弧上,点A 、C 在两半径上,现将此矩形铝皮OABC 卷成一个以AB 为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设矩形的边长xcm AB =,圆柱的体积为3Vcm . (1)写出体积V 关于x 的函数关系式;(2)当x 为何值时,才能使做出的圆柱形罐子体积V 最大?并求出最大值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
午练练习(91)
1.若双曲线2
21y x m
-=
的一条渐近线方程是y =,则m 等于 . 2.已知p :⎩
⎪⎨⎪⎧
x |⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x +2≥0x -10≤0,q :{x |1-m ≤x ≤1+m ,m >0},若q 是p 的必要非充分条件,则实数m 的取值范围是______. 3.设实数,x y 满足2025020x y x y y --≤⎧⎪+-≥⎨⎪-≤⎩
则y x u x y =-的取值范围是 . 4.已知函数()ln 2x f x x =+,若2(2)(3)f x f x +<,则实数x 的取值范围是 .
5.直线AB 、AD ⊂α,直线CB 、CD ⊂β,点E ∈AB ,点F ∈BC ,点G ∈CD ,点H ∈DA ,若直线EH∩直线FG=M ,则点M 一定在直线 上
6.一直P A ,PB ,PC 两两互相垂直,且△P AB 、△P AC 、△PBC 的面积分别为1.5cm 2,2cm 2,6cm 2,则过P ,A ,B ,C 四点的外接球的表面积为 cm 2.
7.已知A ,B ,P 是双曲线22
221x y a b
-=上不同的三点,且A ,B 连线经过坐标原点,若直线P A ,PB 的斜率乘积23
PA PB k k ⋅=,则该双曲线的离心率为 . 8.给出定义:若函数()f x 在D 上可导,即()f x '存在,且导函数()f x '在D 上也可导,则称()f x 在D 上存在二阶导函数,记()()()f x f x ''''=,若()0f x ''<在D 上恒成立,则称()
f x 在D 上为凸函数.以下四个函数在0,
2π⎛⎫ ⎪⎝⎭
上不是凸函数的是 . (1)()sin cos f x x x =+ (2)()ln 2f x x x =- (3)3()21f x x x =-+-(4)()x f x xe -=-. 9.已知函数(
)11sin 24f x x x x =--的图象在点()()00,A x f x 处的切线斜率为12,则)4tan(0π
+x 的值为 .
10.已知t 为常数,函数2|2|y x x t =-+在区间[0,3]上的最大值为3,则实数t =_____.
11.设数列}{n b 满足:211=
b ,n n n b b b +=+21, (1)求证:1
1111+-=+n n n b b b ; (2)若11111121++++++=n n b b b T ,对任意的正整数n ,05log 32>--m T n 恒成立.求m 的取值范围.
(91)参考答案
1.3 2。
[9,+∞) 3。
83,32⎡⎤-⎢⎥⎣⎦ 4。
(1,2) 5。
答案:BD 6。
答案:26π.7。
e =
8.(4) 9。
答案:32+ 10。
0或-2
11、【解析】(1)∵,2
11=b )1b (b b b b n n n 2n 1n +=+=+,∴对任意的0 *,>∈n b N n . ∴,1
b 1b 1)1b (b 1b 1n n n n 1n +-=+=+即1n n n b 1b 11b 1+-=+. (2)111132211211)11()11()11(+++-=-=-++-+-=n n n n n b b b b b b b b b T ∵,b b ,0b b b n 1n 2n n 1n >∴>=-++
∴数列}b {n 是单调递增数列. ∴数列{n T }关于n 递增. ∴1
T T n ≥,∵211=b ,∴43)1(112=+=b b b ∴321221=-=b T ,∴32≥n T ,∵05log 32>--m T n 恒成立, ∴53log 2-<n T m 恒成立,∴3log 2-<m ,∴8
10<<m .。
