等效电阻的计算题(培优)
等效电阻的计算题(培优)

有关等效电阻的欧姆定律计算题一、知识梳理:1、串联、并联电路的电流、电压、电阻特点 注意:n 个相同的电阻R 1串联,总电阻R=n 个相同的电阻R 1并联,总电阻R=2、欧姆定律(注意同体性、同时性、统一单位)U =I = R =二、中考真题:如图所示.电源电压U保持不变,滑动变阻器R 2的最大阻值为20Ω,灯泡L 的电阻是10Ω。
当S 闭合,S 1断开,且滑片P 在b 端时,电流表示数为0.2A :当S 、S 1都闭合,且滑片P 在b 端时,电流表的示数为0.8A ,则电源电压为_____V ,电阻R 1的阻值为_____Ω. 三、过关检测1、 现在电阻R 1=30Ω,R 2=20Ω,(1)若将R 1,R 2串联,则总电阻是多少?(2)若将R 1、R 2并联,则总电阻是又是多少? 2、如图2所示电路,电源电压为50V ,电阻R 1=10Ω,R 2=15Ω,闭合开关后,求:(1)电路的总电阻R (2)电路中的电流I (3)R 1两端的电压U 13.如图3所示电路中,电源电压为6V ,R 1=8Ω,R 2=4Ω,闭合开关。
求:(1)电路的总电阻(2)通过R 1的电流 (3)电流表的示数(4)电压表的示数图34、如图4所示电路,R 1=3Ω,R 2=6Ω,电源电压为18V ,求:(1)R 1 、R 2并联后的总电阻是多少?(2)电流表的示数是多少?5、如图5所示,R 1=30Ω,闭合开关后,电流表的示数为0.3A ,电压表的示数为6V 。
求:(1)求R 1和R 2并联后的总电阻。
(2)R 2的电阻6、如图6所示,已知电流表的示数为0.3A ,电压表的示数是9V ,L 1的电阻R 1=20Ω,求:(1)L 1与L 2的总电阻R (2)L 2的电阻R 2 (3)L 2两端电压U 27. 在图7电路中,电阻R 1的阻值为10Ω.闭合开关S ,电流表A 的示数为0.6A ,电流表A1示数为0.3A,求:(1)通过电阻R 1的电流.(2)电源电压.(3)电阻R 2的阻值. (4)R 1与R 2的总电阻。
欧姆定律等效电路培优习题
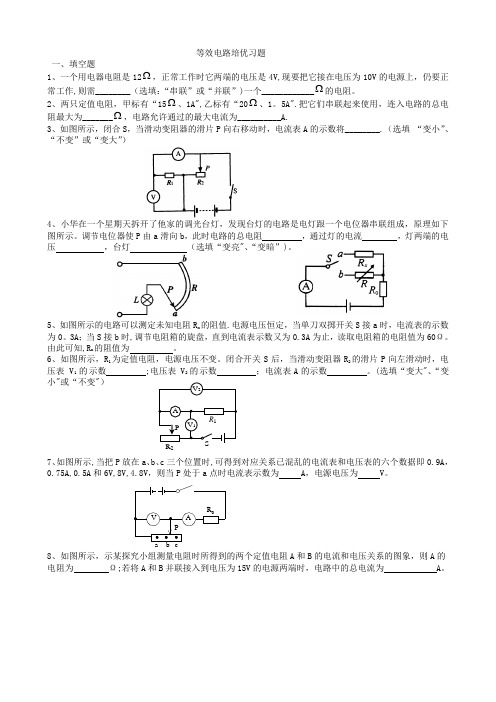
等效电路培优习题 一、填空题1、一个用电器电阻是12Ω,正常工作时它两端的电压是4V,现要把它接在电压为10V 的电源上,仍要正常工作,则需________(选填:“串联”或“并联”)一个____________Ω的电阻。
2、两只定值电阻,甲标有“15Ω、1A",乙标有“20Ω、1。
5A".把它们串联起来使用,连入电路的总电阻最大为_______Ω,电路允许通过的最大电流为__________A.3、如图所示,闭合S ,当滑动变阻器的滑片P 向右移动时,电流表A 的示数将________.(选填 “变小”、“不变”或“变大”)4、小华在一个星期天拆开了他家的调光台灯,发现台灯的电路是电灯跟一个电位器串联组成,原理如下图所示。
调节电位器使P 由a 滑向b ,此时电路的总电阻 ,通过灯的电流 ,灯两端的电压 ,台灯 (选填“变亮"、“变暗”)。
5、如图所示的电路可以测定未知电阻R x 的阻值.电源电压恒定,当单刀双掷开关S 接a 时,电流表的示数为0。
3A ;当S 接b 时,调节电阻箱的旋盘,直到电流表示数又为0.3A 为止,读取电阻箱的电阻值为60Ω。
由此可知,R x 的阻值为 。
6、如图所示,R 1为定值电阻,电源电压不变。
闭合开关S 后,当滑动变阻器R 2的滑片P 向左滑动时,电压表V 1的示数 ;电压表V 2的示数 ;电流表A 的示数 。
(选填“变大"、“变小"或“不变")7、如图所示,当把P 放在a 、b 、c 三个位置时,可得到对应关系已混乱的电流表和电压表的六个数据即0.9A ,0.75A,0.5A 和6V,8V,4.8V ,则当P 处于a 点时电流表示数为 A ,电源电压为 V 。
VPa b cAR 08、如图所示,示某探究小组测量电阻时所得到的两个定值电阻A 和B 的电流和电压关系的图象,则A 的电阻为 Ω;若将A 和B 并联接入到电压为15V 的电源两端时,电路中的总电流为 A 。
等效电阻练习题
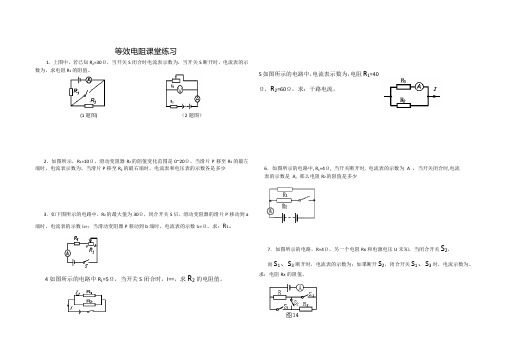
等效电阻课堂练习
1. 上图中,若已知R2=30Ω,当开关S闭合时电流表示数为,当开关S断开时,电流表的示
数为,求电阻R1的阻值。
(1题图) (2题图)
2.如图所示,R1=10Ω,滑动变阻器R2的阻值变化范围是0~20Ω。
当滑片P移至R2的最左端时,电流表示数为。
当滑片P移至R2的最右端时,电流表和电压表的示数各是多少
3.如下图所示的电路中,R2的最大值为30Ω,闭合开关S后,滑动变阻器的滑片P移动到a 端时,电流表的示数I1=;当滑动变阻器P移动到b端时,电流表的示数I2=Ω。
求:R1。
4如图所示的电路中R1=5Ω,当开关S闭合时,I==,求R2的电阻值。
5如图所示的电路中,电流表示数为,电阻R1=40
Ω,R2=60Ω,求:干路电流。
6.如图所示的电路中, R1=4Ω, 当开关断开时, 电流表的示数为A ,当开关闭合时,电流
表的示数是A, 那么电阻R2的阻值是多少
7.如图所示的电路,R=4Ω,另一个电阻Rx和电源电压U未知,当闭合开关S2,
而S1、S3断开时,电流表的示数为;如果断开S2,闭合开关S1、S3时,电流示数为。
求:电阻Rx的阻值。
电阻电路的等效变换例题
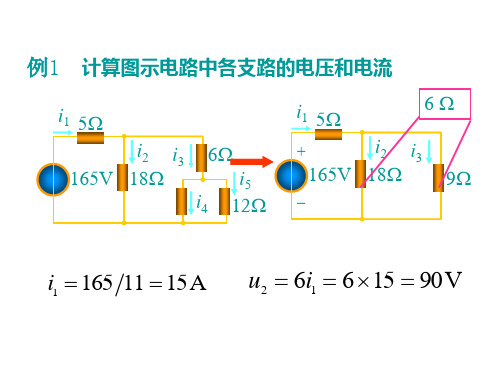
15
-
等效
5
+ 10 u_1 15
u1 15i1
i2
u1 10
1.5i1
i i1 i2 2.5i1
u 5i u1 5 2.5i1 15i1 27.5i1
Rin
u i
27.5i1 2.5i1
11Ω
Rin
5 1015 10 15
11Ω
E
R
- 3k 3k
例9 求负载电阻RL消耗的功率
30
30
20 10 10 20
20 30 20
2A
2A 30
30 40 RL
30
10 40 RL
30
I L 1A
PL
RL
I
2 L
40W
10 2A
10 10
40
IL RL
40
例10 利用电源转换简化电路计算
ab 20 100
60 40
例5 求: Rab
5
15 6
a b
20 缩短无 电阻支路
7
6
Rab=10
4 a b
15
10
20
5
a
15 b
7 6 6 4 a
b
15 7
3
• 例6 计算90电阻吸收的功率
1 +
20V
-
1 +
20V
-
1
10
4 9 90
6A
10 + 6_6V
• 1.
+ 10V
_ 10
+ 6A _10V
7A 10
电阻电路的等效变换习题及答案
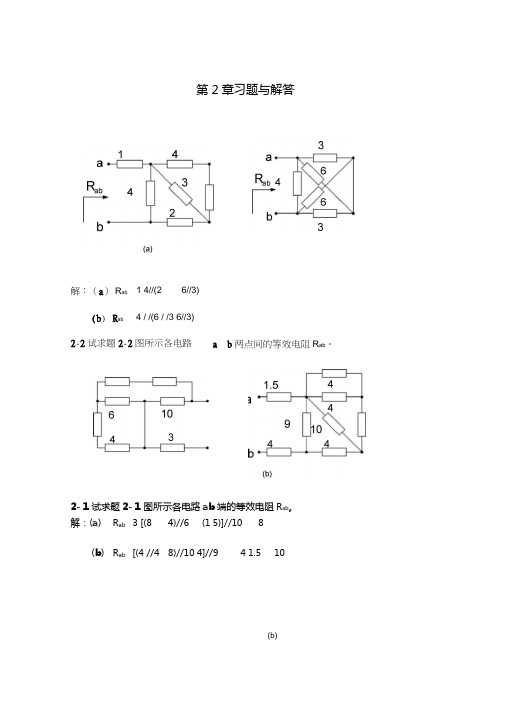
解:(a ) R ab 1 4//(26//3)(b ) R ab4 / /(6 / /3 6//3)2-2试求题2-2图所示各电路a 、b 两点间的等效电阻R ab 。
第2章习题与解答2- 1试求题2- 1图所示各电路ab 端的等效电阻R ab 。
解:(a ) R ab 3 [(84)//6(1 5)]//108(b ) R ab [(4 //4 8)//10 4]//94 1.510(b)2- 3试计算题2-3图所示电路在开关K打开和闭合两种状态时的等效电阻R ab⑻(b)解:(a)开关打开时(8 4)//4 3开关闭合时Rab4//4 2(b)开关打开时Rab(6 12)//(6 12) 9开关闭合时6//12 6//12 8题2-4图解:(a)从左往右流过1电阻的电流为l121/ (1 6//12 3//6) =21/ (1 4 2) 3A从上往下流过3电阻的电流为I3 63 2A3 6从上往下流过12电阻的电流为I 12所以I l3-l12=1A(b)从下往上流过6V电压源的电流为I(1+2) // ( 1+2) 1.5从上往下流过两条并联支路的电流分别为 2A 所以 U 2 2-1 2=2V2- 5试求题2-5图所示各电路ab 端的等效电阻 為,其中R R 211 11 )//(1 D 3 32(b )将图中的两个丫形变成△形,如图所示(b)题2-5图解:(a )如图,2.5I85即得40 21所以志 1.269 2-6计算题2-6图所示电路中a ]1I8888(a)解: 所以20 9题2- 6图(a )将图中的丫形变成△形,如图所示R ab 12//6 4(b )将图中的丫形变成△形,如图所示140 381、对-T~~110108A] I0Uab 532.5 { I—2612所以&b3//4 —2- 7对题2- 7图所示电路,应用Y—△等效变换求电路ab端的等效电阻角线电压U及总电压U ab。
诺顿定理试题及答案初中

诺顿定理试题及答案初中一、选择题1. 诺顿定理中,等效电阻的计算公式是:A. \( R_{th} = \frac{R_1 \times R_2}{R_1 + R_2} \)B. \( R_{th} = R_1 + R_2 \)C. \( R_{th} = \frac{R_1}{R_2} \)D. \( R_{th} = R_1 \times R_2 \)答案:A2. 在并联电路中,若电阻R1和R2并联,根据诺顿定理,等效电阻Rth与R1和R2的关系是:A. \( R_{th} = R_1 + R_2 \)B. \( R_{th} = \frac{1}{\frac{1}{R_1} + \frac{1}{R_2}} \)C. \( R_{th} = R_1 \times R_2 \)D. \( R_{th} = \frac{R_1}{R_2} \)答案:B二、填空题3. 根据诺顿定理,一个复杂的电路可以等效为一个______串联一个电阻。
答案:电压源4. 若电路中有两个电阻R1和R2并联,根据诺顿定理,等效电阻Rth 的计算公式为______。
答案:\( R_{th} = \frac{1}{\frac{1}{R_1} + \frac{1}{R_2}} \)三、计算题5. 给定电路中有两个电阻R1=10Ω和R2=20Ω并联,求等效电阻Rth。
解:根据诺顿定理,等效电阻Rth计算公式为 \( R_{th} =\frac{1}{\frac{1}{R_1} + \frac{1}{R_2}} \)。
代入R1和R2的值,得到 \( R_{th} = \frac{1}{\frac{1}{10} +\frac{1}{20}} = \frac{1}{\frac{3}{20}} = \frac{20}{3} \Omega \)。
答案:\( \frac{20}{3} \Omega \)6. 电路中有两个电阻R1=5Ω和R2=10Ω串联,求等效电阻Rth。
电阻计算(答案)-竞赛-培优

电阻的计算I 卷一、选择题(本题共16小题,每小题 分,共 分)1.两只阻值相同的电阻,每个电阻的阻值均为R ,现将其中一个电阻增大,另一个电阻减小,则并联后的总电阻将( ) A . 大于R B . 小于RC . 仍等于RD . 无法判断考点: 电阻的并联.分析: 电阻并联,总电阻的倒数等于支路电阻倒数之和,电阻越并越小,小于其中的任一个,据此分析判断. 解答: 解:阻越并越小,小于其中的任一个,若将其中的一个电阻减小,总电阻将小于减小后的那个电阻.故选B .点评: 明确电阻越并越小,小于其中的任一个是解本题的关键.2.用均匀电阻丝制成直径为D 的半圆图,如图所示,已知oa 两点间的电阻为R ,则bc 两点间的电阻为( )A . 8πR/(π+2)2B . 2πR/(π+2)2C .R D . 无法计算考点: 电阻的并联. 专题: 计算题.分析: 根据并联电路总电阻与支路电阻的关系进行分析.解答: 解:因为oa 两点间的电阻为R ,根据并联电路电阻的关系可得,该电阻丝的总电阻为4R ;将bc 两点接入电路,则cab 的电阻为=,cob 的电阻为根据并联电路电阻的关系可得:故选A .点评: 会根据并联电路总电阻与各支路电阻的关系计算电阻的大小.3.有一只圆片型电阻,在上面钻了一个圆孔,如图所示,在圆周的1/4处各引出四个电极A 、B 、C 、D ,比较电阻R AB 和R CD 的大小,则有( )A . R AB =R CD B . R AB >R CDC . R AB <R CDD . 无法确定考点: 电阻的并联.1423790 专题: 计算题.分析: 从图中可以看出,AB 将圆分为上下两半,并且上下两部分电阻相等;CD 将圆分为左右两半,并且右半部分的电阻大于左半部分的电阻,则四部分电阻大小关系为R 右>R 上=R 下>R 左;然后根据并联电路的总电阻小于较小电阻的阻值.解答: 解:将A 、B 接入电路时,电阻R AB 相当于上半部分电阻和下半部分电阻并联;将C 、D 接入电路时,电阻R CD 相当于左半部分电阻和右半部分电阻并联; ∵R 右>R 上=R 下>R 左 ∴R AB >R CD .故选B .点评: 本题的电路是一个并联电路,与实际相结合,较为复杂,本题的难点在于准确理解各个电阻之间的关系,根据并联电路电阻的特点进行比较.4.滑动变阻器瓷筒上缠绕的合金线应该( ) A . 所有表面都绝缘 B .所有表面都可以导通 C .与接线柱相连的线端是导通的,其余部分绝缘 D . 线端、滑片接触处是导通的,其余部分绝缘考点: 滑动变阻器的工作原理;滑动变阻器的使用. 专题: 应用题.分析: (1)滑动变阻器是将表面有绝缘层的电阻丝,绕在瓷筒上,金属杆通过滑片,与电阻丝相连;滑动变阻器通过接线柱接入电路,所以线端没有绝缘层.(2)滑动变阻器的原理是靠改变连入电路中电阻线的长度.解答:解:由滑动变阻器的构造可知,滑动变阻器的线端、滑片接触处是导通的,其余部分绝缘,故ABC错误,D正确.故选D.点评:本题主要考查学生对滑动变阻器的原理的了解和掌握,是一道基础题.5.有两个圆环A和B,均由相同粗细的铜导线围成.其中圆环A所围的面积是圆环B的两倍,则原先的两根铜导线的电阻之比为()A.2︰1 B.:1 C.4︰1 D.1︰2考点:电阻的并联;影响电阻大小的因素.专题:计算题.分析:由题知,圆环A所围的面积是圆环B的两倍,即π(r A)2=2π(r B)2,可得半径的大小关系,再根据周长公式得出两导线的长度,再根据决定电阻大小的因素判断电阻关系.解答:解:由题知,S A=S B,即:π(r A)2=2π(r B)2,∴r A:r B=:1,圆环的周长之比:L A:L B=2πr A:2πr B=r A:r B=:1,∵两导线的粗细相同、由同种材料做成,∴R A:R B=L A:L B=:1.故选B.点评:本题考查了学生对影响电阻大小因素的掌握和运用,根据圆环围成面积的大小关系得出周长(导线长度)关系是本题的关键.6.现有四个电阻R1、R2、R3和R4,其中R1=R2,R3<R4.现将R1和R3组成串联电路,R2和R4组成并联电路,则()A.串联电路的总电阻一定大于并联电路的总电阻B.串联电路的总电阻一定小于并联电路的总电阻C.串联电路的总电阻可能大于并联电路的总电阻D.串联电路的总电阻可能等于并联电路的总电阻考点:电阻的串联;电阻的并联.专题:应用题.分析:根据并联电路的电阻特点和并联电路的电阻特点、结合电阻之间的关系即可得出串联电路的总电阻与并联电路的总电阻之间的关系.解答:解:∵串联电路电阻越串越大、大于任何一个分电阻,∴R 1和R3组成串联电路的总电阻大于R1阻值;∵并联电路电阻越并越小、小于任何一个分电阻,∴R2和R4组成并联电路的总电阻小于R2的阻值;∵R1=R2,∴串联电路的总电阻一定大于并联电路的总电阻.故选A.点评:本题考查了串联电路和并联电路的电阻特点,关键是根据已知条件进行比较串联电路的总电阻与并联电路的总电阻之间的关系.7.一电阻连接在电路中,如果把该电阻两端的电压减为原来的一半.则这一电阻的阻值和通过电阻的电流() A.都变为原来的一半B.都变为原来的两倍C.阻值不变.电流变为原来的一半D.阻值变为原来的一半,电流变为原来的两倍考点:欧姆定律的应用;影响电阻大小的因素.专题:应用题.分析:电阻是导体本身的一种性质,与导体两端的电压和通过的电流无关;但可以通过电压与电流的比值求出.解答:解:电阻是导体本身具有的一种性质,与通过导体的电流和导体两端的电压无关,所以电阻不变;根据欧姆定律I=可知:在电阻一定时,电压减少一半,电流也变为原来的一半.故选C.点评:本题考查了欧姆定律的应用,关键是知道电阻是导体本身的一种性质,与导体两端的电压和通过的电流无关.8.一根均匀的电阻丝(它的电阻跟它的长度成正比,跟它的横截面积成反比),测得其电阻值为R.现将其剪掉1/3,然后将剩余的2/3部分再拉长到原长,则此时这部分电阻丝的阻值变为()A.B.R C.D.考点:影响电阻大小的因素.专题:推理法.分析:电阻的影响因素是材料、长度、横截面积,当导线被拉长后,长度变长的同时,横截面积变小,但导体的整个体积不变.解答:解:将其剪掉,剩余的被拉伸到原来的长度时,横截面接变为了原来的,因电阻跟它的横截面积成反比,故总电阻变为原来的.故选C.点评:知道导体的电阻大小与导体的长度(当材料和横截面积一定时,导线越长、电阻越大)、横截面积(当材料和长度一定时,导线越细、电阻越大)的具体关系是本题的关键.9.两块金属板M 和N之间夹有一滴水银,当金属板M和N靠近时,通过精密测量可以发现M和N之间的电阻将()A.变大B.变小C.不变D.以上三种情况都有可能考点:影响电阻大小的因素.专题:应用题.分析:导体电阻的大小与材料、长度、横截面积、温度有关,在材料和温度相同时,横截面积越小、长度越短,导体的电阻越小.解答:解:当两金属板互相靠近一些时,水银的材料和温度不变,横截面积变大、长度变短,其电阻变小;故选B.点评:本题的关键是根据影响电阻大小的因素判断当两金属板互相靠近一些时电阻的变化.10.三个相同的滑动变阻器,电阻的变化范围都是0~30欧姆,把它们并联起来后,得到最大的电阻变化范围是()A.0~10欧姆B.0~15欧姆C.0~20欧姆D.0~30欧姆考点:电阻的并联.专题:应用题.分析:根据并联电路的电阻特点:并联电路电阻越并越小、小于任何一个分电阻可知,当三个相同的滑动变阻器中的任意一个接入电路的电阻为0时会造成其它两个滑动变阻器短路,当三个滑动变阻器都达到最大阻值时并联的总电阻最大.解答:解:当三个相同的滑动变阻器中的任意一个接入电路的电阻为0时,会造成其它两个滑动变阻器短路,所以并联电路的最小总电阻为0;当三个滑动变阻器都达到最大阻值时并联的总电阻最大,所以并联电路的最大总电阻为R=×30Ω=10Ω;故得到最大的电阻变化范围为0~10Ω.故选A.点评:本题考查了电阻的并联特点,关键是知道n个相同的电阻R并联后的总电阻为R.11.如图所示,R1=3欧姆,R2=6欧姆,则电键K断开和闭合时,a 、b间的电阻分别为()A.2欧姆和2欧姆B.2欧姆和0欧姆C.9欧姆和0欧姆D.0欧姆和9欧姆考点:电阻的串联;电阻的并联.专题:计算题;应用题.分析:先判断开关闭合和断开时电路的连接情况,再根据电阻的串、并联特点求出电阻.解答:解:当开关断开时,R1和R2并联,所以,R ab===2Ω.当开关闭合时,a、b间短路,所以a、b间电阻为零.故选B.点评:本题考查了电阻的串、并联特点,属于基本内容,比较简单.正确分析电路的串、并联是解题的关键.12.某精密电子仪器中为了便于调节电路中的电流,其调节部分使用了两个滑动变阻器,如图所示.已知这两个滑动变阻器是分别用不同的电阻丝绕在相同的绝缘瓷管上制成的,其中R1的总电阻是200Ω,R2的总电阻5000Ω,开始时两变阻器都处于最大阻值.下面的几种方法中,能够既快又准确地使电流表指针指到要求位置的是()A . 先调节R 1,使电流表指针指到要求位置附近,再调节R 2B .先调节R 2,使电流表指针指到要求位置附近,再调节R 1 C .同时调节R 1和R 2,使电流表指针指到要求位置 D . 交替、反复调节R 1和R 2,使电流表指针指到要求位置考点: 滑动变阻器的使用;变阻器.分析: 由欧姆定律可知,I=,通过调节滑动变阻器阻值的大小可以改变电路中的电流.但由于电路图中有两个滑动变阻器串联,使得调节起来增加难度.但我们首先要把选项C 和D 排除,因为同时或交替调节两个变阻器有些盲目.在先调节哪个变阻器的问题上,需要考虑电阻越大,对电流的影响也越大,在电流值没有达到要求附近时,应该先调节大电阻,这样比较快速,但电流接近要求值时,改为调节小电阻则更容易精确操作.解答: 解:由题意可知,R 2比R 1大很多(R 2>>R 1),线路中电流I=.调节R 2阻值变化大,对电流影响大,所以要快速将电路中的电流调到要求位置,应先调节大电阻R 2,当电流表的指针到达要求位置附近时,若再调节R 2使指针达到准确位置就很困难,因为只要有R 2很小的调节,就会引起阻值很大的变化,电流I 就有大的改变.所以此时要调节小电阻R 1,因为它对电流的影响较小,能使指针准确地达到要求位置. 故选B .点评: 两个变阻器串联起来使用,学生接触的比较少,有新意的同时又增加了难度.不过在生活中我们会经常用到这样使用的变阻器,例如:收音机调台功能上的粗调和微调等.13.把一根电阻为R 的均匀电阻丝弯折成一个等边三角形abc ,如图所示,图中d 为底边ab 的中心.如果cd 两端的电阻R 1为9欧姆,则ab 两端的电阻R 2的阻值是( )A . 36欧姆B . 12欧姆C . 8欧姆D . 0欧姆考点: 电阻的串联;电阻的并联. 专题: 计算题.分析: 根据cd 两端的电阻R 1为9欧姆,分析电路的连接情况,求出电阻R 的阻值;然后求出电阻丝ab 、ac 、bc 、ad 、bd 的阻值,再根据电阻的串、并联特点求出ab 两端的电阻R 2的阻值.解答: 解:把一根电阻为R 的均匀电阻丝弯折成一个等边三角形abc ,所以,R ab =R ac =R bc =,d 为底边ab 的中心,R ad =R bd =,cd 两端的电阻R 1为R ac 与R ad 串联、R bc 与R bd 串联,然后并联的总电阻, R ac 与R ad 串联的总电阻为+=、R bc 与R bd 串联的总电阻也是,所以,R 1===9Ω.所以,R=36Ω.所以,R ab =R ac =R bc ==12Ω.ab 两端的电阻R 2的阻值是R ac 与R bc 串联,再与R ab 并联后的总电阻, R ac 与R bc 串联的总电阻是:24Ω, 所以,R 2==8Ω.故选C .点评: 本题考查了串、并联电路中的电阻特点,正确分析电路的连接是解题的关键.14.如图所示,变阻器的电阻丝MN 间的总电阻为R ,滑片P 从M 点向右移动到N 的过程中,a 、b 两点间的电阻的变化情况是( )A . 电阻由0增大到RB .电阻由0增大到R/2 C .电阻由0增大到R/2,再减小到0,最大值为R/2D . 电阻由0增大到R/4,再减小到0,最大值为R/4考点: 电阻的串联;电阻的并联.专题: 应用题.分析: 当滑片在M 端或者N 端时,ab 两点间的电阻均为0;在中间时,ab 间的电阻最大,为两端电阻并联. 解答: 解:(1)当滑片在M 端或者N 端时,ab 两点间的电阻均为0,在中间时,ab 间的电阻最大;(2)当滑片在中间时,长度变为原来的二分之一,横截面积变为原来的一倍,则电阻变为原来的四分之一. 即电阻由0增大到R/4,再减小到0,最大值为R/4. 故选D .点评: 本题考查影响电阻大小的因素,关键在于分析并联部分电阻的阻值,长度减半,电阻减半,增粗一倍,电阻增大一倍,故变为原来的四分之一.15.如图所示,M 和N 间的电阻为( )A . 6欧姆;B . 1.33欧姆;C . 0.75欧姆;D . 0欧姆考点: 电阻的串联. 专题: 应用题.分析: 由电路图可知,电路相当于两电阻串联,根据串联电路电阻特点求出M 和N 间的电阻. 解答: 解:∵M 和N 间的电阻相当于2Ω和4Ω的电阻串联,∴M 和N 间的电阻为2Ω+4Ω=6Ω. 故选A .点评: 本题考查了电阻的串联特点,弄清电阻的连接方式是解决本题的关键.16.图中有一个半径为r ,总电阻为R 的均匀导体圆环,环上放置两根平行直导线a 、b ,直导线电阻不计,直导线间的距离等于圆半径r .现将直导线a 、b 在环上自由移动,移动过程中a 、b 导线始终保持相互平行,距离仍为r ,并始终与导体环有良好接触,则a 、b 间电阻最小值与最大值分别是( )A ., B .,C . ,D .,考点: 电阻的并联.分析: 根据导线的电阻为零可知两导轨外侧的两个弧可以剪掉了,然后分析内侧两弧并联,再判断出两弧的长度的取值范围为圆周到圆周即可求出a 、b 间电阻最小值与最大值.解答: 解:当两根导线分别位于中间位置及与圆相切的位置时,内侧弧的长度最大,即圆周,此时a 、b 间电阻值最大,即×R=R ;当两根导线分别距圆心为r 时,内侧弧的长度最小,即圆周,此时a 、b 间电阻值最小,即×R=R .故选D点评: 本题考查电阻的并联,但是难度较大,重点是能够分析出两导轨外侧的两个弧被短路,然后根据导线移动的位置确定出内侧两弧的长度的取值范围.II 卷二、简答题(本题共3小题,每空 分,共 分)17.(2010•宝应县模拟)如图是一个电表的表盘.也许你没有学过这种电表的用法,但根据所学的其他电表的读数方法,你也能知道,它的示数是 26 ,单位是 Ω .考点: 变阻器;电阻.菁优网版权所有 专题: 应用题;压轴题. 分析: 表盘上的符号就是单位.读数时,要看清分度值,然后由指针位置读出示数.解答: 解:由表盘上的符号可知单位是Ω;从表盘上可知,20到30之间,分度值是2Ω,所以示数是26×1=26. 故答案为:26、Ω.点评: 此表的分度值不是固定的,读数时要注意看清分度值;读出示数不要忘记乘以倍数.18.如图所示,M 为一块边长比为3︰1的均匀矩形薄电阻合金片.若先将它按图(a)方连接在A 、B 之间,测得A 、B 间的电阻为R ,然后将它按图(b)方式接在C 、D 之间,则C 、D 间的电阻值为 9R .考点: 影响电阻大小的因素. 专题: 计算题;应用题;图析法.分析: (1)影响电阻大小的因素是材料、长度、横截面积,另外还有温度,一般情况下不考虑温度的影响;(2)电阻的材料称为电阻率ρ,长度为L ,横截面积为S ,则导体的电阻R=.解答: 解:(1)按图(a)方式接在A 、B 之间时,设电阻率为ρ,长度为L ,横截面积为S ,则此时AB 间电阻R=;(2)按图(b)方式接在C 、D 之间时,电阻率不变仍为ρ,长度为3L ,横截面积为S ,则此时CD 间电阻R′==9×=9R .故答案为:9R .点评: 本题考查影响电阻大小的因素材料、长度、横截面积,当这几个因素变化时,导体的电阻就会相应的变化.19.某段导线的电阻是R ,把它均匀拉伸到原长的6倍,再剪绰1/6的长度,则剩下导线的电阻为 30R . 考点: 影响电阻大小的因素. 专题: 应用题.分析: 解决此类问题的关键是知道导体的长度、材料相同时,横截面积越小,电阻越大;导体的横截面积、材料相同时,长度越长,电阻越大.解答: 解:一根粗细均匀的长为L 的金属导线,其电阻为R ,当把它均匀拉长到6L 时,长度变为原来的6倍,同时横截面变为原来的,这样使导线的电阻变为原来的36倍,为36R ;当把它再减掉的长度,其电阻又会减小原电阻的,故此时的电阻是36R ﹣36R×=30R . 故答案为:30R .点评: 知道导体的电阻大小与导体的长度(当材料和横截面积一定时,导线越长、电阻越大)、横截面积(当材料和长度一定时,导线越细、电阻越大)的具体关系是本题的关键.@{实验探究题}(本题共@{题数}小题,每空@{分数}分,共@{总分}分)三、分析计算题(本题共2小题,共 分)20.如图所示,一块电阻均匀的矩形薄片,长是宽的两倍.以长边的中点为圆心,挖一个半圆形的孔.已知ab 间电阻为R ,求证cd 间电阻为.考点: 电阻的串联;电阻的并联. 专题: 应用题;图析法.分析: 可以将挖一个半圆形孔的金属片对折为相同的两部分,ab 间的电阻可以认为是这两部分电阻串联而成,而cd 间的电阻可以认为是这两部分并联而成;然后根据串并联电路电阻的特点进行推导.解答: 解:将挖一个半圆形孔的金属片对折为相同的两部分后,因为ab 间的电阻为R ,而串联电路中总电阻等于各部分电阻之和,则对折后的电阻分别为R ;则cd 间的总电阻相当于这两部分电阻并联,故cd间的总电阻R 总==.点评: 本题考查电阻的串联和电阻的并联;关键是能够识别电阻的连接方式,并灵活应用串并联电路总电阻与分电阻的关系.21.现有两个不同材料制成的,粗细相同的圆柱形长导体,它们的电阻均会随温度变化而发生变化.下表列出了两个导体在不同温度时的电阻值(单位:KΩ).试问:(1)怎样利用这两个导体(可以截取导体的一部分或使用导体的全部)制成一个阻值最大,但不随温度变化的电阻(简述方法)?(2)这个最大电阻的阻值是多少?温度0℃10℃20℃30℃40℃50℃导体1 4 3.68 3.36 3.04 2.72 2.40导体2 1.0×10﹣2 1.06×l0﹣2 1.12×10﹣2 1.18×10﹣2 1.24×10﹣2 1.30×10﹣2考点:电阻的串联.专题:简答题.分析:两个电阻的阻值都随温度的变化而变化.观察表格可知每增加10℃,导体1电阻减小0.32Ω,导体2增加0.06×10﹣2Ω.若是导体1减少的电阻值与导体2增加的电阻值相等,可得最大电阻,且不随温度变化而变化.解答:解:取导体1的0.06×10﹣2÷0.32与导体2串联,0.32÷0.06×10﹣2=533.3.此时电阻为4×1÷533.3kΩ+1.0×10﹣2kΩ=0.0175kΩ答:(1)将导体1截取533.3分之一再与导体2串联,得到的串联电阻就是满足条件的最大电阻.(2)这个最大电阻的阻值是0.0175千欧.点评:此题考查了电阻的串联,需要仔细观察数据,从而得出结论.。
等效电阻试题及答案

等效电阻试题及答案一、单选题1. 在串联电路中,两个电阻分别为R1和R2,那么等效电阻R的计算公式是()。
A. R = R1 + R2B. R = R1 - R2C. R = R1 × R2D. R = R1 / R2答案:A2. 并联电路中,两个电阻分别为R1和R2,那么等效电阻R的计算公式是()。
A. R = R1 + R2B. R = R1 - R2C. R = R1 × R2 / (R1 + R2)D. R = R1 / R2答案:C3. 如果一个电路中有两个并联的电阻R1和R2,且R1 = 2Ω,R2 = 4Ω,那么等效电阻R的值是()。
A. 1.33ΩB. 2.67ΩC. 3.33ΩD. 5.33Ω答案:C4. 在一个复杂的电路中,如果需要计算等效电阻,以下哪个步骤是不必要的()。
A. 识别串联和并联的电阻B. 计算串联电阻的总电阻C. 计算并联电阻的总电阻D. 直接使用欧姆定律计算总电阻答案:D二、填空题5. 在一个由三个电阻R1、R2和R3串联组成的电路中,如果R1 = 3Ω,R2 = 6Ω,R3 = 9Ω,则等效电阻R等于_______Ω。
答案:18Ω6. 两个电阻R1和R2并联,已知R1 = 4Ω,R2 = 8Ω,则等效电阻R的值为_______Ω。
答案:2.67Ω三、计算题7. 一个电路中包含四个电阻,其中两个电阻R1和R2串联,另外两个电阻R3和R4并联,R1 = 5Ω,R2 = 10Ω,R3 = 3Ω,R4 = 6Ω。
求整个电路的等效电阻。
答案:首先计算R1和R2的串联电阻,R串= R1 + R2 = 5Ω + 10Ω = 15Ω。
然后计算R3和R4的并联电阻,1/R并 = 1/R3 + 1/R4 =1/3Ω + 1/6Ω = 1/2Ω,所以R并= 2Ω。
最后计算整个电路的等效电阻,R总 = R串 + R并= 15Ω + 2Ω = 17Ω。
8. 一个电路由三个电阻R1、R2和R3组成,其中R1和R2并联,然后与R3串联。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
有关等效电阻的欧姆定律计算题
一、知识梳理:
1、串联、并联电路的电流、电压、电阻特点 &
注意:n 个相同的电阻R 1串联,总电阻R=
n 个相同的电阻R 1并联,总电阻R= 2、欧姆定律(注意同体性、同时性、统一单位)
U = I =
R =
>
二、中考真题: 如图所示.电源电压U 保持不变,滑动变阻器R 2的最大阻值为20Ω,灯泡L 的电阻是10Ω。
当S 闭合,S 1断开,且滑片P 在b 端时,电流表示数为:当S 、S 1都闭合,且滑片P 在b 端时,电流表的示数为,则电源电压为_____V ,电阻R 1的阻值为_____Ω. 三、过关检测
1、 现在电阻R 1=30Ω,R 2=20Ω,(1)若将R 1,R 2串联,则总电阻是
多少(2)若将R 1、R 2并联,则总电阻是又是多少 、
2、如图2所示电路,电源电压为50V ,电阻R 1=10Ω,R 2=15Ω,闭合开关后,求:(1)电路的总电阻R (2)电路中的电流I (3)R 1两端的电压U 1
3.如图3所示电路中,电源电压为6V ,R 1=8Ω,R 2=4Ω,闭合开关。
求:(1)电路的总电阻(2)通过R 1的电流 (3)电流表的示数(4)电压表的示数
串联电路
并联电路
电路图
电流特点 串联电路中各处的电流相等。
@
公式: 在并联电路中干路里的电流等于各支路中的电流之和。
公式:
电压特点
串联电路两端的电压等于串联电路中各部分电路两端的电压之和。
公式:
在并联电路中,各支路两端的电压相等。
《
公式: 电阻特点 串联电路的总电阻等于各串联电阻之和。
公式: 并联电路的总电阻的倒数等于各支路电阻的倒数之和。
公式: 或
图2
R 1 R 2
@
R 1
R 2 V
A R 1 R 2 R 2
*
{
4、如图4所示电路,R1=3Ω,R2=6Ω,电源电压为18V,求:(1)R1、R2并联后的总电阻是多少(2)电流表的示数是多少
【
5、如图5所示,R1=30Ω,闭合开关后,电流表的示数为,电压表的示数为6V。
求:(1)求R1和R2并联后的总电阻。
(2)R2的电阻
-
6、如图6所示,已知电流表的示数为,电压表的示数是9V,L1的电阻R1=20Ω,
求:(1)L1与L2的总电阻R (2)L2的电阻R2 (3)L2两端电压U2
}
7. 在图7电路中,电阻R1的阻值为10Ω.闭合开关S,电流表A的示数为,电流表A1示数为,求:(1)通过电阻R1的电流.(2)电源电压.
(3)电阻R2的阻值.(4)R1与R2的总电阻。
8.如图8所示,已知电源电压U为6V,电阻R1=5Ω,电流表的示数为I=1.5A
(1)R1两端的电压U1;(2)R1与R2的总电阻。
(3)通过R2的电流I2;
(4)R2的阻值。
9.根据电路如图9所示,已知电源电压为
24V,电阻R2的阻值为40 Ω,闭合
图7
图9
开关后,电流表的示数为0.8 A ,求:(1)R 1的阻值;(2)电路的总电阻。
下面是小鹏对该题的计算过程,你认为正确吗如果不正确,请说明理由,并写出你的正确解答过程。
)
10、在右图10所示的电路中,电源电压不变,当开关闭合后,电流表的示数为, R 1和R 2并联后的总电阻为20Ω,求(1)电源电压U (2)若R 1的电阻为24Ω,则电阻R 2的阻值为多少
!
11、如图11所示,电阻R 1=R 2=4Ω,电源电压保持不变。
(1)当S 1、S 2都闭合时,电流表的示数为,此时电路的总电阻为多少当S 2闭合、S 1断开时,电路的总电阻是多少电流表的示数又是多少
,
12、如图12所示,R 1与R 2串联在电路中,已知R 1两端电压为2V ,R 2两端电压为4V ,其中R 2为滑动变阻器,滑片在最左端,R 1+R 2=60Ω。
求:⑴R 1的阻值和R 2的最大阻值各为多少
⑵R 2的滑片由左向右滑动时,电流表的示数大小如何变化
13、如图13所示,已知电源电压为9V ,另外手头有四个电阻R 1=15Ω,R 2=25Ω,R 3=100Ω,R 4=5Ω请你用其中的两个电阻在图中虚线框内连成电路,使图中的电流表的示数为。
请求出电路中的总电阻,并在虚线框内画出电路图,并注明
连入电路的阻值。
图11
A
R 1
R 2
S 1
S 2
图10
R 1R 2
A
图12
图13
A
Ω=Ω+Ω=+=Ω
===704030)2(308.024)1(21111R R R A
V
I U R。
