多元统计分析随机向量
多元统计分析:第二章 多元正态分布及

1 2 exp( it ) exp( s j ) 2 j 1
) E(e
isqU q
)
第二章 多元正态分布及参数的估计
§2.2
记Σ=AA′,则有以下定义。 定义2.2.2 若p维随机向量X的特征函数 t ' t 为:
X (t ) exp[ it '
,d为s×1常向量,令Z=BX+d,则
Z~Ns(Bμ+d , BΣB ).
该性质指出正态随机向量的任 意线性组合仍为正态分布.
19
第二章 多元正态分布及参数的估计
§2.2 多元正态分布的性质2
证明 因Σ ≥0, Σ可分解为Σ=AA ,其中A 为p×q 矩阵.已知X~Np(μ,Σ),由定义 2.2.1可知 X = AU+μ
是对称非负定阵. 即 =´ , ´ ≥0 (为任给的p维常量).
7
第二章 多元正态分布及参数的估计
§2.1 随机向量—
(4) Σ=L2 ,其中L为非负定阵.
由于Σ≥0(非负定),利用线性代数中实对称阵的对角化定理,存 在正交阵Γ,使
1 0 LL
1 0 ' 0 p
并设:
i 0(i 1,, q), q1 0,, p 0.
10
第二章 多元正态分布及参数的估计
§2.2
在一元统计中,若U~N(0,1),则U的任意 线性变换X=σU+μ~N(μ,σ2)。利用这一性质, 可以从标准正态分布来定义一般正态分布:
若U~N(0,1),则称X =σU+μ的分布为 一般正态分布,记为X ~N(μ, σ2 )。
如例2.1.1,证明了X1,X2均为一元正态 分布,但由(X1,X2) 联合密度函数的形式易见 它不是二元正态.
厦门大学《应用多元统计分析》习题第02章 多元正态分布的参数估计

思考与练习2.1 试述多元联合分布和边缘分布之间的关系。
2.2 设随机向量12(,)X X ′=X 服从二元正态分布,写出其联合分布密度函数和1X 、2X 各自的边缘密度函数。
2.3 已知随机向量12(,)X X ′=X 的联合分布密度函数为:()()()()()()()()()121122222,d c x a b a x c x a x c f x x b a d c −−+−−−−−2⎡⎤⎣⎦=−−其中,。
求:12,a x b c x d ≤≤≤≤⑴ 随机变量1X 和2X 各自的边缘密度函数、均值与方差。
⑵ 随机变量1X 和2X 的协方差和相关系数。
⑶ 判断1X 和2X 是否相互独立。
2.4 设随机向量12(,,,)p X X X ′=X L 服从正态分布,已知其协差阵为对角阵,证明ΣX 的分量是相互独立的随机变量。
2.5 从某企业全部职工中随机抽取一个容量为6的样本,该样本中各职工的目前工资、受教育年限、初始工资和工作经验资料如下表所示: 职工编号目前工资 (美元)受教育年限(年)初始工资 (美元)工作经验(月)11 2 3 4 5 6 57,000 40,200 21,450 21,900 45,000 28,350 15 16 12 8 15 8 27,000 18,750 12,000 13,200 21,000 12,000 144 36 381 190 138 26设职工总体的以上变量服从多元正态分布,根据样本资料求出均值向量和协差阵的最大似然估计。
2.6 均值向量和协差阵的最大似然估计量具有哪些优良性质? 2.7 试证多元正态总体的样本均值向量(,)p N μΣ1~(,p N nX μΣ)。
2.8 试证多元正态总体的样本协差阵S 为(,)p N μΣΣ的无偏估计。
2.9 设()1x 、()2x 、…、()n x 是从多元正态总体中独立抽取的一个随机样本,试求样本协差阵的分布。
多元统计分析_第2章_多元正态分布_s

第2章多元正态分布§2.1 多元分布§2.2 多元正态分布的定义及基本性质§2.3 正态分布的条件分布和独立性§2.4 矩阵正态分布§2.5 参数的极大似然估计§2.6 极大似然估计的性质13),21′=p ξξξ (ξ随机向量:pn ij ξξ×=)(随机矩阵:注:随机矩阵拉直后就是随机向量,二者都是由多个随机变量组成,只是摆放形势不同.4一、多元分布函数1212121122122.1.1 (,,,)()(,,,) ()(,,,)(,,,)(,,,)~.p p p p p pp ξξξξξξF x F x x x P ξx ξx ξx x x x x R F ξξ′===≤≤≤′=∈ 定义设是一随机向量,它的多元分布函数的联合分布函数定义为式中,记作512122112(1)(,,,)(1,2,,)(2)0(,,,)1(3)(,,,)(,,,)(,,,)0(4)(,,,)1p i p p p F x x x x i p F x x x F x x F x x F x x F =≤≤−∞=−∞==−∞=+∞+∞+∞= 是每个变量的单调非降右连续函数.多元分布函数的性质:71)( )2( ,0)( )1()(=∈∀≥⋅∫dx x f R x x f R f pR pp 当且仅当随机向量的分布密度,中某个能作为一个多元函数9二、边缘分布.)( 3.1.2)1(的边缘分布的分布称为个分量组成的随机向量的维随机向量,由它为若定义ξξξp q q p <10),,,,,,(),,,,,),,)111111)1()2()1(∞∞∞=∞≤∞≤≤≤=≤≤=≤⎟⎟⎠⎞⎜⎜⎝⎛=+ q p q q q q q u u F u ξu ξP u ξu ξP u ξP ξξξξξξ((((1)的分布函数为,则不妨假设11(1)(1212112111)(,,)(,,)q q u u u p p u u u p q p q P ξu f t t dt dt dt f t t dt dt dt dt ∞∞∞−∞−∞−∞−∞−∞−∞∞∞∞+−∞−∞−∞−∞−∞−∞≤=⎡⎤=⎢⎥⎣⎦∫∫∫∫∫∫∫∫∫∫∫∫ 若ξ有分布密度函数f (x ),则12p q p q q q dt dt t t x x f x x f ξ1111)1(),,,,,(),,(++∞∞−∞∞−∞∞−∫∫∫=的边缘分布密度为(1)13注:(1)有分布密度函数,则它的任何边缘分布也有分布密度函数;(2)若的任何边缘分布有分布密度函数,并不能推出有分布密度.ξξξ两个随机向量独立的充分必要条件:①联合分布函数等于边缘分布函数的乘积;②若随机向量为连续型的,联合分布密度等于边缘分布密度的乘积;③若随机向量为离散型,联合分布列等于边缘分布列的乘积;④联合特征函数等于边缘特征函数的乘积.1621).()(~),(~),(~,)4(t t t t ηηηξηξηξΦΦ+ΦΦξξ则量的随机向是相互独立且维数相同与若).()(),( ,)()(,,)5()2()1()2()1(t t t t t t q p ηξξΦΦ=Φ⇔ΦΦ⎟⎟⎠⎞⎜⎜⎝⎛Φ独立和则的特征函数和分别为和特征函数的表示维随机向量和分别为和若ηξηξηξηξη22(7) .p a ξξ′若为维随机向量,则它的分布由一切形如的分布所唯一决定).()exp()( ,),(~ )6(t A a t i t a A t ′Φ′=Φ+=Φξηξηξ则若ξ23).()exp()])([exp()exp()][exp()exp())]([exp()][exp()(t A a t i t A i E a t i A t i E a t i a A t i E t i E t ′Φ′=′′′=′′=+′=′=Φξηξξξη证明:(6)24.,3,,),()][exp()1( 1)][exp()( )7(:的分布它决定了知由性质的特征函数恰好是的函数把它看成得取的特征函数为证明ξξξξa a a i E t a it E t a a a Φ=′=Φ=′=Φ′′′ξξξξ25五、矩2.1.6 ()(), 1, 2, , ,1, 2, , ,()(), .ij ij ij n p E i n j p E ξξξεξξξ=×=== 定义设为随机矩阵,假定存在且有限记称为随机矩阵的均值)()( ij E ξξε=26,(1) ,,,( )(),()()A B C A B C A B CA A εξεξξεξεξ+=+=若为常数矩阵则特别当为随机向量时有注:以下总假定公式中用到的随机矩阵的矩是存在的.均值的性质:27)]([)]([)] )4()()( , )3()()( ,, )2(ξεξεξξηεξεηξεηεξεηξεA tr A tr A E n p A p n b a b a b a B A B A B A ==××+=++=+[tr()()(则常数矩阵,为随机矩阵,为若为常数,则若则为常数矩阵若注:以上四个性质均体现均值的线性性.28().),,cov()(),cov(])()][([),cov( ),,cov(,)(),), 7.2.1 2121的协方差称为时,记作当即其元素是矩阵定义为一个简称协差阵阵的协方差维随机向量,它们之间维和分别为和设定义ξξξξηξηξηεηξεξεηξηξηηηηξ===′−−=×′=′=D p n p n ξξξj i j i p n ((29() ),cov(),cov( j i ηξηξ=()),cov(),cov(j i ξξξξ=31.])(][)([)())()()( ,)2(.})(){() (),cov(,})(){() (),cov()1(′−−+=′−−=+′−′=′−′=a a D a a D a D a ξεξεξξξεξξξεξεξξεξξηεξεηξεηξ(则为常向量若特别协差阵的性质:32A AD A DB A B A B A ′=′=)()( ),cov(),cov( ,)3(ξξηξηξ特别则为常数矩阵和设协差阵的性质(续)35则记值和协差阵存在的均若随机向量定理 ),( ),( ,),,, 1.1.221ξξεμD ξξξξn =Σ=′= ()()( μμξξA A tr A E ′+Σ=′36μμμμξξξξξξA A tr A tr A Etr A Etr A E ′+Σ=′+Σ=′=′=′)()}({)()()(μμξξεξεξεξξεξ′+Σ=′′−′=) (,})(){() ()(:所以因为证明D。
多元统计分析——多元正态分布

一、多元正态分布的定义
1、一元正态分布的定义 若变量 X 的概率密度为:
x 2
2 2
1 f x e 2
, 0 ,
则称 X 服从一元正态分布,记为 X ~ N , 2 。 我们可以将上式改写为:
f x 2
1 2
1 exp x ' 2 2
量 X 的相关阵为
R rij p p
其中
rij
Var X i Var X j
covX i , X j
ij ii Байду номын сангаасj
i, j 1,2,, p
另证明:标准化数据的协方差阵正好是原始指标的相 关阵
第2节
多元正态分布
一、多元正态分布的定义 二、均值向量和协方差阵的估计 三、维希特(Wishart)分布 四、统计距离
三、多元变量的独立性
定义 3 两个随机向量 x 和 y 相互独立的充要条件为:
PX x, Y y PX x PY y
对任意的 x, y
若 F x, y 为 x, y 的联合分布函数; G x 和 H y 分别为 x 和 y 的分布函数, 则 x 与 y 独立当且仅当 F x, y G x H y 若 X ,Y ' 有密度函数 f x, y , g x 和 h y 分别表示 X 和 Y 的分布密度, X 和 Y 用 则 独立当且仅当
X 1 X 2 X p q
q
μ 1 μ 2 μ p q
q
11 21
12 21 p q
多元统计分析知识点 多元统计分析课件

多元统计分析(1)题目:多元统计分析知识点研究生专业指导教师完成日期 2013年 12月目录第一章绪论 (1)§1.1什么是多元统计分析 ....................................................................................................... 1 §1.2多元统计分析能解决哪些实际问题 ............................................................................... 2 §1.3主要内容安排 ................................................................................................................... 2 第二章多元正态分布 .. (2)§2.1基本概念 ........................................................................................................................... 2 §2.2多元正态分布的定义及基本性质 .. (8)1.(多元正态分布)定义 ................................................................................................ 9 2.多元正态变量的基本性质 (10)§2.3多元正态分布的参数估计12(,,,)p X X X X '= (11)1.多元样本的概念及表示法 (12)2. 多元样本的数值特征 ................................................................................................ 123.μ和∑的最大似然估计及基本性质 (15)4.Wishart 分布 (17)第五章 聚类分析 (18)§5.1什么是聚类分析 ............................................................................................................. 18 §5.2距离和相似系数 . (19)1.Q —型聚类分析常用的距离和相似系数 ................................................................ 20 2.R 型聚类分析常用的距离和相似系数 ...................................................................... 25 §5.3八种系统聚类方法 (26)1.最短距离法 .................................................................................................................. 27 2.最长距离法 .................................................................................................................. 30 3.中间距离法 .................................................................................................................. 32 4.重心法 .......................................................................................................................... 35 5.类平均法 ...................................................................................................................... 37 6.可变类平均法 .............................................................................................................. 38 7.可变法 .......................................................................................................................... 38 8.离差平方和法(Word 方法) (38)第六章判别分析 (39)§6.1什么是判别分析 ............................................................................................................. 39 §6.2距离判别法 (40)1、两个总体的距离判别法 (40)2.多总体的距离判别法 (45)§6.3费歇(Fisher)判别法 (46)1.不等协方差矩阵两总体Fisher判别法 (46)2.多总体费歇(Fisher)判别法 (51)§6.4贝叶斯(Bayes)判别法 (58)1.基本思想 (58)2.多元正态总体的Bayes判别法 (59)§6.5逐步判别法 (61)1.基本思想 (61)2.引入和剔除变量所用的检验统计量 (62)3.Bartlett近似公式 (63)第一章绪论§1.1什么是多元统计分析在自然科学、社会科学以及经济领域中,常常需要同时观察多个指标。
多元统计分析第二章 多元正态分布

第2章 多元正态分布多元正态分析是一元正态分布向多元的自然推广。
多元正态分布是多元分析的基础,多元分析的许多理论都是建立在多元正态总体基础上的。
虽然实际的数据不一定恰好是多元正态的,但是正态分布常常是真实的总体分布的一种有效的近似。
所以研究多元正态分布在理论上或实际上都有重大意义。
限于篇幅,本章仅简介多元正态简单理论,细节可参看王学民(2004),张尧庭(2002),余锦华(2005),Richard (2003),朱道元(1999)等。
现实世界的许多问题都可以纳入正态理论的范围内,正态分布可以作为许多统计量的近似的抽样分布。
2.1随机向量2.1.1随机向量定义2.1.1:称每个分量都是随机变量的向量为随机向量。
类似地,所有元素都是随机变量的矩阵称为随机矩阵。
设()1,,p X X X '= 是1p ⨯随机向量,其概率分布函数定义为:(){}111,,,,p p p F x x P X x X x =≤≤ ,1,,p x x 为任意实数多元分布函数()1,,p F x x 有如下性质: (1)()10,,1p F x x ≤≤ ;(2)()1,,p F x x 是每个变量,1,2,,i x i p = 的非降右连续函数; (3)(),,1F ∞∞= ;(4)()()()211,,,,,,,0p p F x x F x x F x -∞=-∞==-∞= 。
多元分布和一元分布一样也分为离散型和连续型。
连续型随机向量()1,,pX X X '= 的分布函数可以表示为 : ()()1111,,,,px x p p p F x x f t t dt dt -∞-∞=⎰⎰,()1,,pp x x R ∈ (2.1)称()1,,p f x x 是()1,,p X X X '= 的多元联合概率密度,简称多元概率密度或多元密度。
多元概率密度()1,,p f x x 有以下性质: (1)()1,,p f x x 非负; (2)()11,,1p p f x x dx dx ∞∞-∞-∞=⎰⎰ ;(3)()()111,,,,p p p nF x x f x x x x ∂=∂∂2.1.2边缘分布、条件分布和独立性 边缘分布设()1,,p X X X '= 是p 维连续型随机向量,由其q 个分量组成的向量()1X (不妨设()()11,,q X X X '= )的分布称为的边缘分布,其边缘概率密度为:()()()1111,,,,X q p q p f x x f x x dx dx ∞∞+-∞-∞=⎰⎰ (2.2)条件分布设()1,,p X X X '= 是p 维连续型随机向量,()()11,,q X X X '= ,()()()()2112,,,,,0q p X q p X X X f x x ++'=> ,在给定()2X 的条件下,()1X 的条件概率密度函数为:()()()()21111,,,,,,,,p q q p X q p f x x f x x x x f x x ++=(2.3)独立性设()1,,n X X 是连续型随机向量,则1,,n X X 相互独立当且仅当()()()111,,n n X X n f x x f x f x = 对任意1,,n x x 成立。
第二章 多元正态分布 《应用多元统计分析》 ppt课件

1
一、随机向量
在理论上,对多维随机向量的研究和对一维随机 变量的研究思路是类似的,通过分布及其特征进 行刻画。不同的是,可能要考虑变量之间的相关 关系。
在统计应用上,对多维随机向量的研究和对一维 随机变量的研究思路也是一样的,要通过样本资 料来推断总体。
19
二、多元正态分布的数字特征
若 X ~ Np μ, Σ ,则 E(X) μ,D(X) Σ ,即 μ 恰好是
多维随机向量 X的均值向量, Σ 恰好是多维随机 向量 X 的协差阵。其中,
1
μ
2
,
p
11 12
Σ
21
22
p1 p2
1p
2
p
pp
20
三、多元正态分布的参数估计
若 X 的联合分布密度为 f (x1, x2 , , xp ),则 X(1) 的边缘 密度函数为:
f (x1, x2 , , xq )
f (x1, x2 ,
, xq , xq1,
, xp )dtq1
dt,p (2.3)
多维随机向量的独立性。若 p个随机变量
X1, X 2 ,, X p的联合分布密度等于各自边缘分布的 乘积,则称 X1, X 2 ,, X p是互相独立的。
1
x)(x( )
x)
n
(x1 x1)2
1
1 n
n
(x1 x1)(x 2 x2 )
1
n
(x 2 x2 )2
1
n
x 2
1
n
x
p
1
n
( x 1
x1)(x p
xp
多元统计
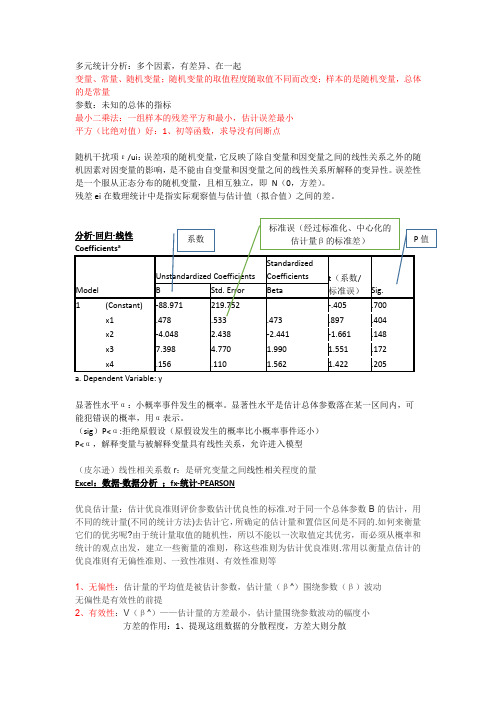
多元统计分析:多个因素,有差异、在一起变量、常量、随机变量;随机变量的取值程度随取值不同而改变;样本的是随机变量,总体的是常量参数:未知的总体的指标最小二乘法:一组样本的残差平方和最小,估计误差最小平方(比绝对值)好:1、初等函数,求导没有间断点随机干扰项ε/ui:误差项的随机变量,它反映了除自变量和因变量之间的线性关系之外的随机因素对因变量的影响,是不能由自变量和因变量之间的线性关系所解释的变异性。
误差性是一个服从正态分布的随机变量,且相互独立,即N(0,方差)。
残差ei在数理统计中是指实际观察值与估计值(拟合值)之间的差。
优良估计量:估计优良准则评价参数估计优良性的标准.对于同一个总体参数B的估计,用不同的统计量(不同的统计方法)去估计它,所确定的估计量和置信区间是不同的.如何来衡量它们的优劣呢?由于统计量取值的随机性,所以不能以一次取值定其优劣,而必须从概率和统计的观点出发,建立一些衡量的准则,称这些准则为估计优良准则.常用以衡量点估计的优良准则有无偏性准则、一致性准则、有效性准则等1、无偏性:估计量的平均值是被估计参数,估计量(β^)围绕参数(β)波动无偏性是有效性的前提2、有效性:V(β^)——估计量的方差最小,估计量围绕参数波动的幅度小方差的作用:1、提现这组数据的分散程度,方差大则分散3、样本容量越大越好为什么样本方差是除以n-1:自由度df:相互独立的变量个数标准化的好处:1、同一量纲2、不再有水平和分散程度的不同(均值0方差1)分析-描述统计-描述-将标准化得分另存为变量z标准化回归:线性回归中-选项-把在等式中包含常量的√去掉(随机)向量(x,y):把独立(随机)变量x、y放在一起形成一个整体行向量*列向量=一个数列向量*行向量=一个矩阵假设检验:假设的是总体,假设是具体的总检验:F统计量线性回归结果-方差分析表ANOVA有n个样本,i个解释变量,最小二乘法有n-(i+1)个方程,i+1是因为除了参数还有截距项。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
马拉松 (分)
137.72 128.3 135.9 129.95 146.62 133.13 139.95 130.15 134.03 133.53 131.35
⋮
一、欧氏距离
向量的各分量如果单位不全相同,则上述欧氏距离一
般就没有意义。即使单位全相同,但如果各分量的变异
性差异很大,则变异性大的分量在欧氏距离的平方和中
F x P X a
随机向量 X X1,X2,L,Xp 的分布函数:
F x 1 , x 2 , L , x p P X 1 x 1 , X 2 x 2 , L , X p x p
二、多元概率密度函数
一元的情形:
F (x )xftd t,
fx d F x
d x
多元的情形:
称协差阵)定义为:
Cov
X 1 ,Y1
Cov X1,Y2 L
Cov
X
,Y
Cov
X
2
,Y1
Cov X 2,Y2
L
M
M
Cov X p ,Y1 Cov X p ,Y2 L
Cov
X 1 ,Yq
Cov
X 2 ,Yq
M
Cov X p ,Yq
X1 E X1
E
M Y1 E Y1 ,L ,Yq E Yq
20.81 20.06 20.81 20.68 20.58 20.43 21.52 20.22 20.8 21.04 21.05
⋮
400米 (秒)
46.84 44.84 46.82 45.04 45.91 45.21 48.3 45.68 46.2 47.3 46.1
⋮
800米 (分)
1.81 1.74 1.79 1.73 1.8 1.73 1.8 1.76 1.79 1.81 1.82
平方欧氏距离为:
d2x,yx1y12x2y22Lxpyp2
xyxy
一、欧氏距离
X X1,X2,L,Xp 到总体π的平方欧氏距离定义为:
d2X,XμXμ
X112 X2 22 L
2
Xp p
平均大小 EX112 EX2 22 K
2
E Xp p
等于 VX1
VX2 K VXp
不适合直接使用欧氏距离的例子
即 VX EXEXXEX
V X1
Covx1,x2 L
Cov
X2,
X1
Vx2
L
M
M
Cov Xp, X1 Cov xp, x2 L
Cov
X1, Xp
Cov
X2, Xp
M
V Xp
V(X)亦记作Σ=(σij),其中σij=Cov(Xi,Xj)。
协差阵Σ既包含了X各分量的方差,也包含了每两个分 量之间的协方差。显然,Σ是一个对称矩阵。
n
m nm
C o v A iX i, B jY j A iC o vX i,Y j B j
i 1
j 1
i 1j 1
n m n m
推论 C ov X i, Y j C ovX i,Y j
i 1 j 1
i 1j 1
证明
n
m
CovXi,Yj
i1
j1
n
n m
设X是p维随机向量,由它的q(<p) 个分量组成的 向量X(1)的分布称为X的关于X(1)的边缘分布。
不妨设 X1 X1,L,Xq ,则对连续型的分布,有
f 1 ( x 1 , L ,x q ) L f ( x 1 , L ,x p ) d x q 1 L d x p
四、条件分布
R
21
M
1L M
p1 p 2 L
1p
ቤተ መጻሕፍቲ ባይዱ
2
p
M 1
R=(ρij)和Σ =(σij)之间有关系式:R=D−1ΣD−1
其中 D d ia g ( 1 1, 2 2,L , p p)。
R和Σ的相应元素之间的关系式为:
ij
ij ii jj
前述关系式即为:
1
11
0
R
M
0
477
V
(Y
)
AV
(X
)A/
126 256
126 40 91
256
91 219
.
三、相关矩阵
随机变量X和Y的相关系数定义为:
X,Y CovX,Y VXVY
X ( X 1 , X 2 , L , X p ) 和 Y ( Y 1 , Y 2 , L , Y q ) 的相关阵定
义为:
X1,Y1
阵分别为
5 4 1 2
72和12
9 3
253
令y1=2x1−x2+4x3,y2=x2−x3,y3=x1+3x2−2x3,试求y=(y1,y2,y3)′的
数学期望和协方差矩阵。
2 1 4 X1
Y
0 1
1 3
1 2
X2 X3
AX
,
E (Y ) AE ( X ) (40, 9, 15)/ ,
ki2VXi
i1
i1
证明
n
n
n
V ki Xi cov( ki Xi , ki Xi )
i1
i1
i1
nn
kikj cov Xi , X j
i1 j1
n
n
由独立性可得, ki2 cov Xi , Xi ki2V (xi )
j1
i1
例3 设随机向量 X(X1,X2,X3)/的数学期望和协方差矩
E X1q
E X2q
M
E Xpq
随机矩阵X的数学期望的性质
(1)设a为常数,则 E(aX)=aE(X)
(2)设A,B,C为常数矩阵,则 E(AXB+C)=AE(X)B+C
特别地,对于随机向量X,有 E(AX)=AE(X)
(3)设X1,X2,⋯,Xn为n个同阶的随机矩阵,则 E(X1+X2+⋯+ Xn)=E(X1)+E(X2)+⋯+E(Xn)
0L
1 L
22
M 0L
0
0
1211
12 22
L L
1MM p1
M
p2
L
pp
1
12pp
11
0
M
pp
M 0
0L
1 L
22
M 0L
0
0
M
1
pp
标准化变换
在数据处理时,常常因各变量的单位不完全相同而需要对 每个变量作标准化变换,最常用的标准化变换是令
Xi*Xiiii , i1,2,L,p
记 X *(X 1 *,X 2 *,L,X * p), 于是
一、数学期望(均值)
随机向量 X (X 1 ,X 2,L,X p)的数学期望
E X E X 1 ,E X 2 ,L ,E X p
记为μ=(μ1,μ2,⋯,μp)′。 随机矩阵X=(Xij)的数学期望
EX11
EX E Xij
EX21
M
E Xp1
EX12 L EX22 L
M
E Xp2 L
F(x1,L,xp)
L x1
xp
f(t1,L,tp)dt1Ldtp
p f(x1,L,xp)x1LxpF(x1,L,xp)
多元概率密度函数f (x1, ⋯,xp) : (1)f(x1,L,xp)0, 对 一 切 实 数 x1,L,xp;
(2) L f(x1,L,xp)dx1Ldxp1。
三、边缘分布
m
E Xi E Xi Yj E Yj
i1
i1 j1
j1
n
m
EXi E Xi
Yj E Yj
n
m
Cov Xi ,Yj
i1 j1
i1 j1
协差阵的性质
(5)设k1,k2, ⋯,kn是n个常数,X1,X2, ⋯,Xn是n个相互独 立的p维随机向量,则
V
n
n kiXi
一、欧氏距离
由于 E X i * 2 V X i * 1 ,i 1 ,2 , L ,p ,
故平方和 X 1 1 2 LX p p2 中各项的平均取值均
为1,从而各分量所起的平均作用都一样。 欧氏距离经变量的标准化之后能够消除各变量的
单位或方差差异的影响,但不能消除变量之间相关性 的影响,以致有时用欧氏距离显得不太合适。为此, 我们引入一个由印度著名统计学家马哈拉诺比斯 (Mahalanobis,1936年)提出的“马氏距离”的概念。
V A X b A V X A
当p=1时,上述等式就是我们熟知的如下等式:
V a X b a 2 V X
(3)设A和B为常数矩阵,则
C o v A X ,B Y A C o v X , Y B
例2 Σ0X的各分量间存在线性关系(依概率1)。
协差阵的性质
(4)设 A 1 ,A 2 ,L ,A n 和 B 1 ,B 2 ,L ,B m 为常数矩阵,则
附2 随机向量
§2.1 一元分布 §2.2 多元分布 §2.3 数字特征 §2.4 欧氏距离和马氏距离 §2.5 随机向量的变换 §2.6 特征函数(不讲)
§2.2 多元分布
一、多元概率分布 二、多元概率密度函数 三、边缘分布 四、条件分布 五、独立性
一、多元概率分布
随机向量:元素为随机变量的向量。 随机矩阵:元素为随机变量的矩阵。 随机变量X的分布函数:
f
x1 | x2
f2
x2
五、独立性
两个连续型随机向量的独立
fx ,y fX x g f Y y
