2016届山西省祁县中学高三5月月考数学(理) 试题 word版 含解析
【全国百强校】山西省祁县中学2016届高三5月月考理综物理试题(原卷版)
山西省祁县中学2016届高三5月月考理科综合物理试题二、选择题:本大题共8小题，每小题6分。
在每小题给出的四个选项中. 14~18题只有一项符合题目要求.19~21题有多项符合题目要求。
全部选对的得6分，选对但不全的得3分，有选错的得0分。
14．在物理学的研究及应用过程中涉及诸多的思想方法，如理想化、模型化、放大、极限思想，控制变量、猜想、假设、类比、比值法等等．以下关于所用思想方法的叙述不．正确的是 A ．在不需要考虑物体本身的大小和形状时，用质点来代替物体的方法是假设法B ．速度的定义式v ＝Δx Δt ，采用的是比值法；当Δt 趋近于0时，Δx Δt就可以表示物体在t 时刻的瞬时速度，该定义应用了极限思想C ．在探究电阻、电压和电流三者之间的关系时，先保持电压不变研究电阻与电流的关系，再保持电流不变研究电阻与电压的关系，该实验应用了控制变量法D ．如图示的三个实验装置，这三个实验都体现了放大的思想15．一物体做直线运动的v-t 图象如图甲所示，则图乙中能正确反映物体所受合力F 随时间变化情况的是16．如图所示，光滑轨道LMNPQMK 固定在水平地面上，轨道平面在竖直面内，MNPQM 是半径为R 的圆形轨道，轨道LM 与圆形轨道MNPQM 在M 点相切，轨道MK 与圆形轨道MNPQM 在M 点相切，b 点、P 点在同一水平面上，K 点位置比P 点低，b 点离地高度为2R ，a 点离地高度为2.5R ，若将一个质量为m 的小球从左侧轨道上不同位置由静止释放，关于小球的运动情况，以下说法中正确的是vt/s图甲 图乙A ．若将小球从LM 轨道上a 点由静止释放，小球一定不能沿轨道运动到K 点B ．若将小球从LM 轨道上b 点由静止释放，小球一定能沿轨道运动到K 点C ．若将小球从LM 轨道上a 、b 点之间任一位置由静止释放，小球一定能沿轨道运动到K 点D ．若将小球从LM 轨道上a 点以上任一位置由静止释放，小球沿轨道运动到K 点后做斜上抛运动，小球做斜上抛运动时距离地面的最大高度一定小于由静止释放时的高度17．如图所示，三个物体质量分别为m 1＝1.0kg 、m 2＝2.0kg 、m 3＝3.0kg ，已知斜面上表面光滑，斜面倾角θ＝30°，m 1和m 2之间的动摩擦因数μ＝0.8．不计绳和滑轮的质量和摩擦．初始时用外力使整个系统静止，当撤掉外力时，m 2将(g ＝10m/s 2，假设最大静摩擦力等于滑动摩擦力)A ．和m 1一起沿斜面下滑B ．和m 1一起沿斜面上滑C ．相对于m 1上滑D ．相对于m 1下滑18．电荷量相等的两点电荷在空间形成的电场有对称美．如图所示，真空中固定两个等量异种点电荷A 、B ，AB 连线中点为O .在A 、B 所形成的电场中，以O 点为圆心半径为R 的圆面垂直AB 连线，以O 为几何中心的边长为2R 的正方形平面垂直圆面且与AB 连线共面，两个平面边线交点分别为e 、f ，则下列说法正确的是A ．在a 、b 、c 、d 、e 、f 六点中找不到任何两个场强和电势均相同的点B ．将一电荷由e 点沿圆弧egf 移到f 点电场力始终不做功C ．将一电荷由a 点移到圆面内任意一点时电势能的变化量并不都相同D ．沿线段eOf 移动的电荷，它所受的电场力先减小后增大19. 如图所示，在开关S 闭合时，质量为m 的带电液滴处于静止状态，下列判断正确的是A ．保持S 闭合，将上极板稍向左平移，液滴将会向上运动bB ．保持S 闭合，将上极板稍向下平移，电流表中会有a→b 的电流C ．将S 断开，将上极板稍向左平移，液滴仍保持静止D ．将S 断开，将上极板稍向下平移，液滴仍保持静止20．如图所示，足够长的光滑导轨倾斜放置，其下端连接一个定值电阻R ，匀强磁场垂直于导轨所在平面，将ab 棒在导轨上无初速度释放，当ab 棒下滑到稳定状态时，速度为v ，电阻R 上消耗的功率为P 。
山西省祁县中学2016届高三数学5月月考试题 文
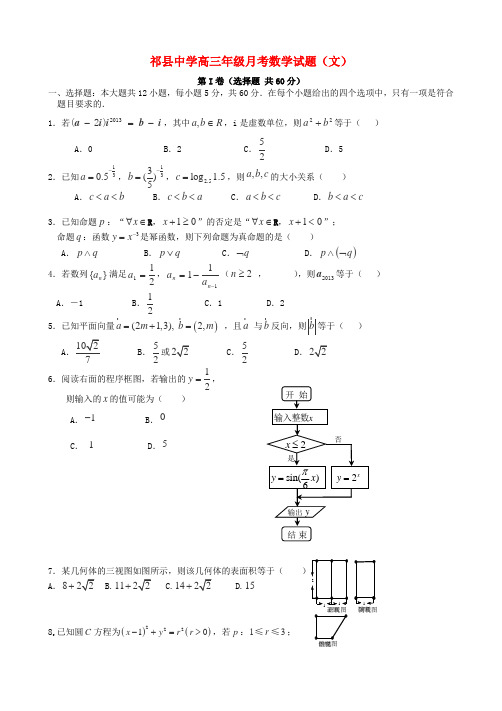
祁县中学高三年级月考数学试题（文）第I 卷（选择题 共60分）一、选择题：本大题共12小题，每小题5分，共60分．在每个小题给出的四个选项中，只有一项是符合题目要求的． 1．若i b ii a -=-2013)2(，其中R b a ∈,，i 是虚数单位，则22b a +等于（ ）A ．0B ．2C ．25D ．5 2．已知130.5a -=，133()5b -=， 2.5log 1.5c =，则,,a b c 的大小关系（ ）A ．c a b <<B ．c b a <<C ．a b c <<D ．b a c <<3．已知命题p ：“∈∀x R ，01≥+x ”的否定是“∈∀x R ，01<+x ”； 命题q ：函数3y x -=是幂函数，则下列命题为真命题的是（ ）A ．p q ∧B ．p q ∨C ．q ⌝D ．()p q ∧⌝4．若数列{}a n 满足a 112=，a a n n =--111（n ≥2 ， ），则2013a 等于（ ） A ．－1 B ．21C ．1D ．25．已知平面向量()21,3, (2,)a m b m =+= ，且 a 与b 反向，则b 等于（ ）AB ．52或 C ．52D． 6．阅读右面的程序框图，若输出的21=y ，则输入的x 的值可能为（ ）A ．1-B ．0C ． 1D ．57．某几何体的三视图如图所示，则该几何体的表面积等于（）A ．8+ B.11+14+158.已知圆C 方程为()()22210x y r r -+=>，若p ：13r ≤≤；1112正视图 侧视图俯视图q ：圆C 上至多有3个点到直线+30x =的距离为1，则p 是q 的（ ）A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件9．已知函数()33f x x x =-，若ABC ∆中，角C 是钝角，那么（ ）A ．()()sin cos f A fB > B ．()()sin cos f A f B <C ．()()sin sin f A f B >D ．()()sin sin f A f B >（小于）10．已知三棱锥ABC P -，在底面ABC ∆中，060A ∠=，BC =，ABC PA 面⊥，PA =，则此三棱锥的外接球的表面积为（ ）A ．163πB. C.323πD. 16π 11. 设函数()f x 在R 上可导，其导函数为()f x '，且函数()f x 在2x =-处取得极小值，则函数()y xf x '=的图象可能是（ ）（A ） （B ） （C ） （D ）12.已知函数()2()e x f x x ax b =++，当1b <时，函数()f x 在(),2-∞-，()1,+∞上均为增函数，则2a ba +-的取值范围是（ ）A ．22,3⎛⎤- ⎥⎝⎦B ．1,23⎡⎫-⎪⎢⎣⎭C ．2,3⎛⎤-∞ ⎥⎝⎦D ．2,23⎡⎤-⎢⎥⎣⎦第Ⅱ卷（非选择题 共90分）二、填空题：本大题共4个小题，每小题5分，共20分13. 函数()log (2)a f x x =-必过定点 。
山西省祁县中学高二数学4月月考试题 理
山西省祁县中学2017-2018学年高二数学4月月考试题 理一、选择题（本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的）1.复数2+3i 的共轭复数是（ ）A. -2+3iB. 2-3iC. -2-3iD. 3-2i 2.下列函数中，x ＝0是其极值点的函数是( )A ．f(x)＝－cosxB ．f(x)＝－x 3C ．f(x)＝sinx －xD ．f(x)＝1x3.下面使用类比推理，得到的结论正确的是( ） A.直线a,b,c,若a//b,b//c,则a//c.类比推出:向量,,a b c ，若//,//a b b c ，则//a c . B.同一平面内,直线a,b,c,若a⊥c,b⊥c,则a//b. 类比推出:空间中,直线a,b,c,若a⊥c,b⊥c,则a//b. C.以点(0,0)为圆心,r 为半径的圆的方程为222x y r +=.类比推出:以点(0,0,0)为球心,r 为半径的球面的方程为2222x y z r ++=. D.实数,a b ,若方程20x ax b ++=有实数根,则24a b ≥.类比推出:复数,a b ,若方程20x ax b ++=有实数根,则24a b ≥.4.已知函数y ＝ax 2＋bx ＋c ，其中a 、b 、c ∈{0,1,2,3,4}，则不同的二次函数的个数共有( ) A ．125个 B ．60个 C ．100个 D ．48个5.下面是一段演绎推理：大前提：如果直线平行于平面，则这条直线平行于平面内的所有直线； 小前提：已知直线b ∥平面α，直线a ⊂平面α； 结论：所以直线b ∥直线a. 在这个推理中( )A ．大前提正确，结论错误B ．大前提错误，结论错误C ．大、小前提正确，只有结论错误D ．小前提与结论都是错误的6.如果曲线()y f x =在点00(,())x f x处的切线方程为ln 30x y +=,那么（ ） A. 0()0f x '< B. 0()0f x '> C.0()0f x '= D. ()f x '在0x x =处不存在 7.已知函数()f x 的导函数()f x '的图象如右图所示，那么函数()f x 的图象最有可能的是( )8.由直线12x =，2x =，曲线1y x =及x 轴所围成的图形的面积是（ ）A ．174B ．154C ．1ln 22D ．2ln 29.用反证法证明数学命题时，首先应该做出与命题结论相反的假设，否定“自然数,,a b c 中恰有一个偶数”时正确的反设为 ( ) A. 自然数,,a b c 都是奇数B. 自然数,,a b c 都是偶数C. 自然数,,a b c 至少有两个偶数或都是奇数D. 自然数,,a b c 至少有两个偶数 10. 若关于x 的方程x 3－3x ＋m ＝0在[0,2]上有根，则实数m 的取值范围是( ) A ．[－2,0] B ．[0,2] C ．[－2,2] D ．(－∞，－2)∪(2，＋∞)11.若存在过点(1,0)的直线与曲线3y x =和21594y ax x =+-都相切，则a 等于（ ） A ．74-或25-64 B ．1-或25-64 C ．74-或7 D ．1-或21412. 以圆x 2＋y 2－2x －2y －1＝0内横坐标与纵坐标均为整数的点为顶点的三角形个数为( )A ．84B ．78C ．81D ．76 二、填空题（本大题共4小题，每小题5分）13.若复数1(1)z m m i =++-为纯虚数，则实数m =____________. 14.要在如图所示的花圃中的5个区域中种入4种颜色不同的花， 要求相邻区域不同色，有________种不同的种法(用数字作答)．15.0cos()cos66limx x xππ∆→+∆-∆的值为 ___ . 16.已知函数y ＝f （x ）是定义在R 上的奇函数，且当x∈（－∞，0）时不等式f （x ）＋xf′（x ）<0成立，若a ＝30.3·f（30.3），b ＝(log π3）)3(log π⋅f ， c ＝(log 391)·f (log 391).则a ，b ，c 的大小关系是________. 三、解答题（本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤） 17.（本小题满分10分） 已知3211()(4),xf x t dt t =-⎰求)()1(i f i f ⋅-的值（其中i 为虚数单位）18.（本小题满分12分）已知二次函数2()3f x ax bx =+-在1x =处取得极值，且在(0,3)-点处的切线与直线20x y +=平行．（1）求()f x 的解析式； （2）求函数()()4g x xf x x =+的单调递增区间．19.（本小题满分12分）从1到9的九个数字中取三个偶数四个奇数，试问： （1）能组成多少个没有重复数字的七位数？（2）在（1）中的七位数中三个偶数排在一起的有几个？（3）在（1）中的七位数中，偶数排在一起、奇数也排在一起的有几个？ （4）在（1）中任意两偶然都不相邻的七位数有几个？ （答题要求：先列式，后计算 , 结果用具体数字表示．）20.（本小题满分12分） 已知:当*n N ∈时，有1111111,2342121232n n S T n n n n n n=-+-++-=+++-+++；（1）求1212,,,;S S T T数学（理）试题共4页 第3页（2）猜想n S 与n T 的大小关系，并用数学归纳法证明.21.（本小题满分12分） （1）（用综合法证明）已知△ABC 的内角A 、B 、C 所对的边分别为a ，b ，c ，且A 、B 、C 成等差数列，a ，b ，c 成等比数列，证明：△ABC 为等边三角形。
山西省晋中市祁县中学高三数学理月考试卷含解析
山西省晋中市祁县中学高三数学理月考试卷含解析一、选择题：本大题共10小题，每小题5分，共50分。
在每小题给出的四个选项中，只有是一个符合题目要求的1. 下列函数是偶函数的是（）A．B．C．D．参考答案：A2. 设平面区域D是由双曲线y2﹣=1的两条渐近线和抛物线y2=﹣8x的准线所围成的三角形区域（含边界），若点（x，y）∈D，则的取值范围是（）A．[﹣1，] B．[﹣1，1] C．[0，] D．[0，]参考答案：B考点：双曲线的简单性质．专题：综合题；圆锥曲线的定义、性质与方程．分析：先求出双曲线的两条渐近线为，抛物线y2=﹣8x的准线为x=2，结合图象可得在点B（2，﹣1）时，=0，在点O（0，0）时，=1，由此求得目标函数的取值范围．解答：解：双曲线y2﹣=1的两条渐近线为y=，抛物线y2=﹣8x的准线为x=2．故可行域即图中阴影部分，（含边界）．目标函数z==2?﹣1中的表示（x，y）与（﹣1，﹣1）连线的斜率，故在点B（2，﹣1）时，=0，在点O（0，0）时，=1，∴2?﹣1∈[﹣1，1]故选：B．点评：本题主要考查抛物线、双曲线的标准方程，以及简单性质，简单的线性规划问题，属于中档题．3. 设函数在点处的切线方程为，则曲线处切线的斜率为（）A. 4B.C. 2D.参考答案：A略4. 等比数列{a n}的前n项和为S n，已知a2a3=2a1，且a4与2a7的等差中项为，则S5=（）A．29 B．31 C．33 D．36参考答案：B【考点】等比数列的性质．【分析】由题意可得a12q3=2a1，①a1q3+2a1q6=，②，联立①②可解得a1=16，q=，代入求和公式计算可得．【解答】解：设等比数列{a n}的公比为q，∵a2a3=2a1，∴a12q3=2a1，①∵a4与2a7的等差中项为，∴a4+2a7=，即a1q3+2a1q6=，②联立①②可解得a1=16，q=，∴S5==31故选：B【点评】本题考查等比数列和等差数列的综合应用，求出数列的首项和公比是解决问题的关键，属基础题．5. 已知抛物线C：，过其焦点F的直线与C交于A、B两点，O是坐标原点，记的面积为S，且满足，则p=（）A. B. 1 C. D. 2参考答案：D【分析】结合抛物线的定义，计算出三角形的面积，由此列方程，解方程求得的值.【详解】设，，则，根据抛物线的定义可知.依题意，则，∴，故选：D.【点睛】本小题主要考查抛物线的定义，考查与抛物线有关的三角形面积的计算，考查方程的思想，属于基础题.6. 已知不等式ax2﹣5x+b＞0的解集为{x|x＜﹣或x＞}，则不等式bx2﹣5x+a＞0的解集为（）A．{x|﹣＜x＜} B．{x|x＜﹣或x＞} C．{x|﹣3＜x＜2} D．{x|x＜﹣3或x＞2}参考答案：C【考点】一元二次不等式的解法．【专题】不等式的解法及应用．【分析】根据所给的一元二次不等式的解集，写出对应的一元二次方程的解，根据根与系数的关系得到不等式的系数的值，解出一元二次不等式得到解集．【解答】解：因为ax2﹣5x+b＞0的解集为{x|x＜﹣或x＞}，∴ax2﹣5x+b=0的解是x=﹣，x=∴=，=解得a=30，b=﹣5．则不等式bx2﹣5x+a＞0变为﹣5x2﹣5x+30＞0，∴x2+x﹣6＜0，解得|﹣3＜x＜2故选C【点评】考查学生理解一元二次不等式解集求法的能力，会解一元二次不等式的能力．7. O为坐标原点，F为抛物线C：y2=4x的焦点，P为C上一点，若|PF|=4，则△POF 的面积为（）A．2 B．2C．2D．4参考答案：C【考点】抛物线的简单性质．【分析】根据抛物线方程，算出焦点F坐标为（）．设P（m，n），由抛物线的定义结合|PF|=4，算出m=3，从而得到n=，得到△POF的边OF上的高等于2，最后根据三角形面积公式即可算出△POF的面积．【解答】解：∵抛物线C的方程为y2=4x∴2p=4，可得=，得焦点F（）设P（m，n）根据抛物线的定义，得|PF|=m+=4，即m+=4，解得m=3∵点P在抛物线C上，得n2=4×3=24∴n==∵|OF|=∴△POF的面积为S=|OF|×|n|==2故选：C8.条件，条件，则是的（A）充分不必要条件（B）必要不充分条件（C）充要条件（D）既不充分也不必要条件参考答案：答案：A9. 已知函数，对任意存在使，则的最小值为（）A. B. C. D.参考答案：D10. 已知一个几何体是由上下两部分组成的合体，其三视图如图，若图中圆的半径为1，等腰三角形的腰长为，则该几何体的体积是（）A．B．2πC．D．参考答案：A【考点】由三视图求面积、体积．【分析】由三视图知，此组合体上部是一个圆锥，下部是一个半球，半球体积易求，欲求圆锥体积需先求圆锥的高，再由公式求体积，最后再想加求出组合体的体积．【解答】解：这个几何体上部为一圆锥，下部是一个半球，由于半球的半径为1，故其体积为π×13=，圆锥的高为=2，故此圆锥的体积为×2×π×12=．∴此几何体的体积是V==．故选：A．二、填空题:本大题共7小题,每小题4分,共28分11. 定义在R上的偶函数满足：上是增函数，给出下列判断：①是周期函数；②的图像关于直线x=1对称；③在[0，1]上是增函数；④在[1，2]上是减函数；⑤其中正确的命题是。
2016届山西省祁县中学高三10月月考数学(理)试题word版含答案
2016届山西省祁县中学高三10月月考数学（理）试题一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1.“p 或q 是假命题”是“非p 为真命题”的（ ） A ．充分而不必要条件 B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件2.已知集合⎭⎬⎫⎩⎨⎧≥--=031x x x A ，⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧+-==)4(log 21x y x B ，则=B A C R )(（ ） A. φ B ．{}3 C ．{}43<≤x x D ．{}41<<x x3.函数f(x)的图象向右平移一个单位长度，所得图象与x y e =关于y 轴对称，则f(x)=（ ）A.1+x e B. 1-x e C. 1+-x e D. 1--x e4.若存在正数x 使2()1x x a -<成立，则a 的取值范围是（ ）A.(,)-∞+∞ B ．(2,)-+∞ C. (0,)+∞ D ．(1,)-+∞ 5.由曲线1=xy 及直线2,==y x y 围成的平面图形的面积是（ ）A.87B. 2ln 23-C.2ln 23+D.8256.已知函数1)391ln()(2+-+=x x x f ，则=+)21(lg )2(lg f f （ ） A ．1- B ．0 C ．1 D ．27.函数ππln cos 22y x x ⎛⎫=-<< ⎪⎝⎭的图象是（ ）xx8.若函数32)(2++-=x x x f ，则)(x f 的单调递增区间是（ ）A. []1,1- B ．)1,(-∞ C. []3,1 D. ),1(+∞9．已知函数)3(log )(22a ax x x f +-=在区间[)+∞,2上是增函数，则实数a 的取值范围是（ ）A. (]4，∞- B ．(],44- C. (],24- D ． (][)∞+⋃-∞-，，24 10.已知函数)(ln )(ax x x x f -=有两个极值点，则实数a 的取值范围是（ ）A ．)0,(-∞B ．)21,0(C ． )1,0(D ．),0(+∞11．设函数3y x =与22xy -=的图象的交点为00()x y ，，则0x 所在的区间是（ ） A ．(01)， B ．(12)，C ．(23)，D ．(34)，12. 设定义在R 上的函数)(x f 是最小正周期为π2的偶函数，)('x f 是)(x f 的导函数，当],0[π∈x 时，1)(0<<x f ；当),0(π∈x 且2π≠x 时，0)(')2(>-x f x π，则函数x x f y sin )(-=在]2,2[ππ-∈x 上的零点个数为（ ）A .2B .4 C.5 D. 8二、填空题：本大题共4小题,每小题5分,共20分.将答案填在答题卡中的横线上.13.设ax x f x ++=)110lg()(是偶函数，x x bx g 24)(-=是奇函数，那么b a +的值是_______14．函数()f x 对于任意实数x 满足条件()()12f x f x +=，若()15,f =-则()()5f f =_______ . 15.设曲线*)(1N n x y n ∈=+在点)1,1(处的切线与x 轴的交点的横坐标为n x ，令n n x a lg =，则9921a a a +++ 的值为_______ .16.已知，给出以下四个命题：（1）若，则；（2）直线是函数图象的一条对称轴；（3）在区间上函数是增函数；（4）函数的图象可由的图象向右平移个单位而得到.其中正确命题的序号为_______ .三、解答题：本大题共6小题,共70分. 解答应写出文字说明、证明过程或演算步骤. 17．（本大题满分10分）已知锐角ABC ∆中，内角C B A 、、的对应边分别为c b a 、、，且C b c B c b A a s i n )2(s i n )2(s i n2-+-= （1）求角A 的大小；（2）求C B cos cos 2+的取值范围 18．（本大题满分12分）若函数431)(23+-+=bx ax x x f 在2-=x 和1=x 处取的极值. （1）求函数()f x 的解析式；（2）讨论方程()f x k =实数解的个数．19. （本大题满分12分）已知是定义在上的偶函数，且时，．（1）求，；（2）求函数的表达式；（3）若，求的取值范围．20.（本小题满分12分）已知集合{}⎭⎬⎫⎩⎨⎧<+--=<+--=0)1(2,0)]13()[2(2a x ax x B a x x x A (1)当B A a 时，求2=; (2)求使A B ⊆的实数a 的取值范围。
高三月考数学试卷含解析
一、选择题（每题5分，共50分）1. 已知函数$f(x) = x^3 - 3x^2 + 4$，则$f(x)$的对称中心为（）。
A. $(0, 4)$B. $(1, 2)$C. $(2, 0)$D. $(3, 1)$2. 在等差数列$\{a_n\}$中，$a_1 + a_5 = 10$，$a_3 + a_4 = 12$，则$a_1$的值为（）。
A. 1B. 2C. 3D. 43. 已知圆$x^2 + y^2 - 4x - 6y + 9 = 0$的半径为（）。
A. 1B. 2C. 3D. 44. 函数$y = \log_2(x - 1)$的图象与直线$y = 3x - 1$的交点个数为（）。
A. 1B. 2C. 3D. 45. 若复数$z = a + bi$（$a, b \in \mathbb{R}$）满足$|z - 3i| = |z + 2|$，则$z$在复平面内的轨迹是（）。
B. 圆C. 直线D. 双曲线6. 在三角形ABC中，$AB = 4$，$AC = 6$，$BC = 8$，则$\cos A$的值为（）。
A. $\frac{1}{4}$B. $\frac{1}{2}$C. $\frac{3}{4}$D. $\frac{5}{8}$7. 已知函数$f(x) = ax^2 + bx + c$（$a \neq 0$），若$f(-1) = 0$，$f(1) = 0$，则$f(0)$的值为（）。
A. $-a$B. $-b$C. $-c$D. $a$8. 若$|x - 1| + |x + 2| = 3$，则$x$的取值范围是（）。
A. $-2 \leq x \leq 1$B. $-2 < x < 1$C. $x \leq -2$ 或 $x \geq 1$D. $x > -2$ 且 $x < 1$9. 已知数列$\{a_n\}$的前$n$项和为$S_n$，若$S_n = 3n^2 - 2n$，则$a_5$的值为（）。
山西省祁县中学高三月月考数学理试题扫描含答案
祁县中学2019年高三年级8月月考数学（理）答案一、选择题CACBD CDBBC BA二、填空题13．9 14．20x y --= 15．97- 16．12,33⎡⎤⎢⎥⎣⎦三、解答题17. 解：（1）由余弦定理22212cos 942327,2a b c bc A a =+-=+-⨯⨯⨯== 由正弦定理,sin sin a c A C=得sin 7C = （2）由已知得：1cos 1cos sin sin 3sin 22B A A B C ++⨯+⨯= sin sin cos sin sin cos 6sin A A B B B A C +++=sin sin sin()6sin ,sin sin 5sin A B A B C A B C +++=+=所以510a b c +==------① 又125sin sin ,22S ab C C ==所以25ab =------② 由①②解得5a b ==18.解：1cos(2)13() 1.)cos()2662x f x x x πωππωω+-=+---（）1)cos(2)323x x ππωω-+-=sin(2)36x ππω-+ sin(2)6x πω=-又()1f α=-，()0f β=，且αβ-的最小值为4π，则44T π=，∴最小周期22T ππω==， 则=1ω，()sin(2)6f x x π∴=-， （2） 50,22666x x ππππ≤≤∴-≤-≤Q 令2662x πππ-≤-≤得03x π≤≤， 令52266x πππ≤-≤得32x ππ≤≤， ()f x ∴的增区间为03π⎡⎤⎢⎥⎣⎦，，减区间为32ππ⎡⎤⎢⎥⎣⎦，()f x Q 在区间03π⎡⎤⎢⎥⎣⎦，上单调递增，在区间上32ππ⎡⎤⎢⎥⎣⎦，上单调递减， 又11(0),()222f f π=-=Q ， min 1()(0)2f x f ∴==-， max ()()13f x f π== 19.解：函数在区间上与x 轴有两个不同的交点， 必须，即，解得．所以当时，函数在区间上与x 轴有两个不同的交点； 由题意可得，因为，所以， 所以函数是单调递减的，要使在区间上有最小值，必须使在上单调递增或为常数，即，解得， 所以当时，函数使在区间上有最小值．若是真命题，则p 是假命题且q 是真命题，所以，解得，或，故实数a 的取值范围为：，22．解：(1) ()f x 的定义域为()0,+∞，()233(2)122()1x ax x f x a x x x ---⎛⎫'=-+= ⎪⎝⎭. ………………………………………1分 (i)当0a ≤时，210ax -<恒成立，21.()0,2x ∈时，'()0f x >，()f x 在()0,2上单调递增；()2,x ∈+∞时，'()0f x <，()f x 在()2,+∞上单调递减； ……………………2分 (ii) 当0a >时，由()0f x '=得，1232,x x x ===（舍去）， ①当12x x =，即14a =时，()0f x '≥恒成立，()f x 在(0,)+∞上单调递增；……3分 ②当12x x >，即14a >时， x⎛∈ ⎝或()2,x ∈+∞时，()0f x '>恒成立，()f x 在⎛ ⎝，()2,+∞单调递增；x⎫∈⎪⎭时，()0f x '<恒成立，()f x 在⎫⎪⎭上单调递减；……………4分 ③当12x x <即104a <<时， x⎫∈+∞⎪⎭或()0,2x ∈时，()0f x '>恒成立，()f x 在(0,2),⎫+∞⎪⎭单调递增；x⎛∈ ⎝时，()0f x '<恒成立，()f x 在⎛ ⎝上单调递减；……………5分 综上，当0a ≤时，()f x 单调递增区间为()0,2，单调递减区间为()2,+∞； 当14a =时，()f x 单调递增区间为()0,+∞，无单调递减区间； 当14a >时，()f x 单调递增区间为⎛ ⎝，()2,+∞，单调递减区间为⎫⎪⎭； 当104a <<时，()f x 单调递增区间为(0,2),⎫+∞⎪⎭，单调递减区间为⎛ ⎝． …………………………………………………6分 (2)由(1)知，当0a <时，()f x 单调递增区间为(0,2)，单调递减区间为(2,)+∞，又因为()10f a =<， …………………………………7分 取01max{,5}x a =-，令1()2ln f x x x =-，21()f x x =，则12'()10f x x=->在(2,)+∞成立，故1()2ln f x x x =-单调递增，10()52ln 512(2ln 5)1f x ≥-=+->， 0002220000011111()(2ln )0f x a x x a x x x x x =-+-≤+-≤-<， （注：此处若写“当x →+∞时，()f x →-∞”也给分）所以()f x 有两个零点等价于1(2)(22ln 2)04f a =-+>，得188ln 2a >--， 所以1088ln 2a >>--．……………………………………………………………8分 当0a =时，21()x f x x -=，只有一个零点，不符合题意； 当14a =时，()f x 在(0,)+∞单调递增，至多只有一个零点，不符合题意；………9分 当0a >且14a ≠时，()f x 有两个极值， 1(2)(22ln 2)04f a =-+>，ln f a a a =+-，记()ln g x x x x =-， …………………………………10分'()(1ln )1ln g x x x =+-=+，令()ln h x x =+，则()3221122h x x x x '=-+=. 当14x >时，()0h x '>，'()g x 在1,4⎛⎫+∞ ⎪⎝⎭单调递增； 当104x <<时，()0h x '<，'()g x 在10,4⎛⎫ ⎪⎝⎭单调递减． 故1()22ln 204g x g ⎛⎫''>=-> ⎪⎝⎭，()g x 在(0,)+∞单调递增．0x →时，()0g x →，故ln 0f a a a =+->．……………………11分又1(2)(22ln2)04f a=-+>，由(1)知，()f x至多只有一个零点，不符合题意．综上，实数a的取值范围为1,088ln2⎛⎫-⎪-⎝⎭. ……………………………………12分。
山西省祁县中学高三数学5月月考试题 理
2016年山西省祁县中学校高三月考数学试题（理科）一.单选题（每小题5分，共12小题，总分60分）1.已知i 是虚数单位,则2016i = ( ) A.1B.iC.i -D.-12.已知集合{}{}21,1A x y x B y y x ==+==+，则=B A I （ ）A 、∅B 、[1,1]-C 、[1,)-+∞D 、[1,)+∞3．已知等比数列}{n a 中，11=a ，且43,2,24a a a 成等差数列，则432a a a ++等于 ( ) A ．1B ．4C ．14D ．154.“=0a ”是“函数1()sin f x x a x=-+为奇函数”的 ( ) A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件 5.某几何体的直观图如图所示,该几何体的正视图和侧视图可能正确的是( )6.直线１－+=k kx y 与椭圆14922=+y x 的位置关系为 （ ）A.相切B.相交C.相离D.不确定7.平面上有一组平行线且相邻平行线间的距离为3,把一枚半径为1的硬币任意平掷在这个平面中,则硬币不与任何一条平行线相碰的概率是( )A. B. C. D.8.如图，程序框图的输出结果为－18，那么判断框①表示的“条件”应该是（ ） A. ?10>i B ．?9>i C ．?8>i D ．?7>i9.设点o 在ABC ∆内部，且有230OA OB OC ++=u u u r u u u r u u u r r，则ABC ∆的面积与AOC ∆的面积的比为（ ） A. 2 B.32 C. 3 D.5310.矩形ABCD 中，4,3AB BC ==，沿AC 将矩形ABCD 折成 一个直二面角B AC D --，则四面体ABCD 的外接球的体积为（ ）A.12512π B.1259π C.1256π D.1253π 11.函数ln ||||x x y x =的图像可能是（ ） 12.数列{}n a 满足⎩⎨⎧<-+≥-=+,,2,,1t a a t t a t a a n n n n n 当11+<<t a t （其中2>t ）时有)(*N k a a n k n ∈=+，则k 的最小值为 （ ）A. 10B. 8C. 6D. 4 二.填空题（每小题5分，共4小题，总分20分） 13.设xdx n sin 420∫=π,则ｎ）－（x1x 2展开式中的常数项为 14.如图,正六边形ABCDEF 的两个顶点A,D 为双曲线的焦点,其余四个 顶点都在双曲线上,则该双曲线的离心率为 .15.记约束条件⎪⎩⎪⎨⎧+-≤>>n nx y y x 300）（*∈N n 所表示的平面区域内的整点个数为n a ，则A B D C y O x11- y Ox1 1- y O x11- y O x11-ABDC数列{}n a 的前n 项和=n s 16. 函数)2,0∈,cos sin 2cos sin )(π［x xx xx x f ++•=的最小值为三.解答题（17—21题每题12分，选做题10分，总分70分） 17.(本小题满分12分)如图，平面四边形ABCD 中，5AB =，22AD =，3CD =，30CBD ∠=o ，120BCD ∠=o ，求：（Ⅰ）ADB ∠；（Ⅱ）ADC ∆的面积S . 18.(本小题满分12分)如图,四棱锥P-ABCD 中,底面ABCD 为矩形,PA ⊥平面ABCD, E 为PD 的中点. (1)证明:PB ∥平面AEC.(2)设二面角D-AE-C 为60°3求三棱锥E-ACD 的体积. 19.(本小题满分12分)第31届夏季奥林匹克运动会将于2016年8月5日—21日在巴西里约热内卢举行.下表是近五届奥运会中国代表团和俄罗斯代表团获得的金牌数的统计数据（单位：枚）.第30届伦敦第29届北京 第28届雅典 第27届悉尼 第26届亚特兰大中国 38 51 32 28 16 俄罗斯2423273226（Ⅰ）根据表格中两组数据完成近五届奥运会两国代表团获得的金牌数的茎叶图，并通过茎叶图比较两国代表团获得的金牌数的平均值及分散程度（不要求计算出具体数值，给出结论即可）；（Ⅱ）甲、乙、丙三人竞猜今年中国代表团和俄罗斯代表团中的哪一个获得的金牌数多（假设两国代表团获得的金牌数不会相等），规定甲、乙、丙必须在两个代表团中选一个，已知甲、乙猜中国代表团的概率都为45，丙猜中国代表团的概率为35，三人各自猜哪个代表团的结果互不影响.现让甲、乙、丙各猜一次，设三人中猜中国代表团的人数为X ，求X 的分布列及数学期望EX .20.(本小题满分12分)已知抛物线2:2C y px =经过点(2,2)M ，C 在点M 处的切线交x 轴于点N ，直线1l 经过点N 且垂直于x 轴.（Ⅰ）求线段ON 的长；（Ⅱ）设不经过点M 和N 的动直线2:l x my b =+交C 于点A 和B ，交1l 于点E ，若直线MA 、ME 、MB 的斜率依次成等差数列，试问：2l 是否过定点？请说明理由. 21.(本小题满分12分)已知函数()xf x e =（ 2.71828e =⋅⋅⋅是自然对数的底数）,()ln(1)g x x =+. （1）若()()()F x f x g x =-，求()F x 的极值； （2）对任意0,x ≥证明：()(1)f x g x >+； （3）对任意0,x ≥都有成立，求实数a 的取值范围. 请考生在第22.23.24题中任选一题作答，若多做，则按所做的第一题计分，每题共10分．22.几何证明选讲如图，AB 是⊙O 的直径，C 、F 是⊙O 上的两点，OC ⊥AB ，过点F 作⊙O 的切线FD 交AB 的延长线于点D ．连接CF 交AB 于点E ． （1）求证：DE 2=DB •DA ； （2）若DB =2，DF =4，试求CE 的长．23.坐标系与参数方程已知曲线C 的极坐标方程为ρ=4cosθ，以极点为原点，极轴为x 轴正半轴建立平面直角坐标系，设直线l 的参数方程为（t 为参数）．（1）求曲线C 的直角坐标方程与直线l 的普通方程；（2）设曲线C 与直线l 相交于P 、Q 两点，以PQ 为一条边作曲线C 的内接矩形，求该矩形的面积．24.不等式选讲已知定义在R 上的函数()|1||2|f x x x =++-的最小值为a ． (1)求a 的值；(2)若,,p q r 是正实数，且满足p q r a ++=，求证：2223p q r ++≥．2016年山西省祁县中学校高三月考数学试题（理科）参考答案一.单选题（每小题5分，共12小题，总分60分）二. 填空题（每小题5分，共4小题，总分20分）13. 24 14. 115.2)1(3+n n 16. －２ 三.解答题（17—21题每题12分，选做题10分，总分70分） (17) 【解析】（Ⅰ）在BCD ∆中，由正弦定理得：sin 3sin2CD BD BCD CBD =⋅∠==∠， ……………2分在ABD ∆中，由余弦定理得：222cos 2AD BD AB ADB AD BD+-∠=⋅==………4分 所以45ADB ∠=o ……………6分 （Ⅱ）因为30CBD ∠=o ，120BCD ∠=o ，所以30CDB ∠=o 因为sin sin(4530)ADC ∠=+=o o ……………8分 所以1sin 2S AD CD ADC =⋅⋅∠12=⨯=……………12分18.解：(1)设AC的中点为G,连接EG.在三角形PBD中,中位线EG∥PB,且EG在平面AEC 上,所以PB∥平面AEC.(2)设CD=m,分别以AD,AB,AP为x,y,z轴建立坐标系,则12⎫⎪⎪⎝⎭所以ADu u u rAEu u u r=12⎫⎪⎪⎝⎭,ACu u u r=),0m.设平面ADE的法向量为1nu r=(x1,y1,z1),则1n AD⋅u r u u u r=0,1n AE⋅u r u u u r=0,解得一个1nu r=(0,1,0).同理设平面ACE的法向量为2nu u r=(x2,y2,z2),则2n AC⋅u u r u u u r=0,2n AE⋅u u r u u u r=0,解得一个2nu u r因为cos3π=|cos<12,n nu r u u r>|=1212n nn n⋅u r u u ru r u u r=12,解得m=32.设F为AD的中点,则PA∥EF,且PA=2EF=12,EF⊥面ACD,即为三棱锥E-ACD的高.所以V E-ACD=错误!未找到引用源。
山西省祁县中学2016届高三理综5月月考试题
2016年祁县中学高三年级月考理科综合本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分，其中第Ⅱ卷第33～40题为选考题，其它题为必考题。
考生作答时，将答案答在答题卡上，在本试卷上答题无效。
考试结束后，将本试卷和答题卡一并交回。
注意事项：1．答题前，考生务必先将自己的姓名、准考证号填写在答题卡上，认真核对条形码上的姓名、准考证号，并将条形码粘贴在答题卡的指定位置上。
2．选择题答案使用2B铅笔填涂,如需改动，用橡皮擦干净后，再选涂其他答案的标号；非选择题答案使用0.5毫米的黑色中性（签字）笔或碳素笔书写，字体工整、笔迹清楚。
3．请按照题号在各题的答题区域(黑色线框)内作答超出答题区域书写的答案无效。
4．保持卡面清洁，不折叠，不破损。
5．做选考题时，考生按照题目要求作答，并用2B铅笔在答题卡上把所选题目对应的题目涂黑。
可能用到的相对原子质量：H—1 C—12 N—14 O—16 S—32 Cu—64第Ⅰ卷一、选择题：本题共13小题，每小题6分，在每小题给出的四个选项中，只有一项是符合题目要求的。
1. 图中①～④表示的是生物体细胞内4种有机成分的结构。
下列有关说法正确的是A. ①～④存在于所有植物细胞中B. ②中也含有与a类似的结构C. 细胞中没有①就不能产生③D. 没有③或其类似物时，细胞仍能合成①2．如图所示，植物的气孔是由两个含有叶绿体的保卫细胞围绕成，当保卫细胞吸水后，气孔会开放，反之则关闭。
保卫细胞内的淀粉磷酸化酶在酸性条件下，主要催化葡萄糖转化成淀粉，而在碱性条件下，主要催化淀粉转化成葡萄糖。
光照、高K+环境均可以促进气孔的开放。
有关分析不正确的是（）A．黑暗条件下，蒸腾作用小，气孔更易开放B．光照促进细胞内CO2浓度下降，pH上升，利于淀粉的水解C．高钾环境促进气孔的开放，可能是细胞对K+主动运输的结果D．淀粉水解为葡萄糖有利于提高渗透压，使保卫细胞吸水3.某生物技术公司发明一种生物打印机，可利用患者自身细胞“打印”出“静脉”等器官，这为解决器官移植面临的供体不足、免疫排异等问题提供了美好前景。
山西高三高中数学月考试卷带答案解析
山西高三高中数学月考试卷班级:___________ 姓名：___________ 分数：___________一、选择题1.已知全集为R ，集合M={﹣1，0，1，5}，N={x|x 2﹣x ﹣2≥0}，则M∩∁R N=（ ） A ．{0，1} B ．{﹣1，0，1} C ．{0，1，5} D ．{﹣1，1}2.设是虚数单位，若复数是纯虚数，则（） A ．4B ．3C ．2D ．13.在等差数列{a n }中，a 1=2，公差为d ，则“d=4”是“a 1，a 2，a 3成等比数列”的（ ） A ．充分不必要条件 B ．必要不充分条件 C ．充要条件 D ．既不充分也不必要条件4.从1，2，3，4，5这5个数中一次性随机地取两个数，则所取两个数之和能被3整除的概率是（ ） A ．B ．C ．D ．5.已知双曲线C ：-=1（a ＞0，b ＞0）的右焦点F 和A （0，b ）的连线与C 的一条渐近线相交于点P ，且，则双曲线C 的离心率为（ ）A ．3B ．C ．4D ．26.若输入，执行如图所示的程序框图，则输出的结果为（）A ．8B ．7C ．6D ．57.已知将函数f （x ）=tan （ωx+ ）（2＜ω＜10）的图象向右平移个单位之后与f （x ）的图象重合，则ω=（ ） A ．9B ．6C ．4D ．88.已知四棱锥中，平面平面，其中为正方形，为等腰直角三角形，，则四棱锥外接球的表面积为（）A ．B ．C ．D ．9.已知f （x ）=2x ﹣2﹣x ，a= ，b=，c=log 2，则f （a ），f （b ），f （c ）的大小顺序为（ ） A ．f （b ）＜f （a ）＜f （c ） B ．f （c ）＜f （b ）＜f （a ） C ．f （c ）＜f （a ）＜f （b ）D ．f （b ）＜f （c ）＜f （a ）10.已知椭圆的离心率为，四个顶点构成的四边形的面积为12，直线与椭圆交于、两点，且线段的中点为，则直线的斜率为（ ）A ．B ．C ．D ．111.如图，网格纸上小正方形的边长为1，粗线画出的是由正方形切割而成的几何体的三视图，则该几何体的体积为（ ）A ．B ．C ．6D ．712.在各项均为正数的等比数列{a n }中，若2a 4+a 3﹣2a 2﹣a 1=8，则2a 5+a 4的最小值为（ ） A ．12B ．C ．D ．二、填空题1.若向量满足=2=2，||=2，则向量的夹角为__．2.设曲线f （x ）=e xsinx 在（0，0）处的切线与直线x+my+l=0平行，则m=__． 3.已知实数x ，y 满足不等式组，且目标函数之z="ax+by" （a ＞0，b ＞0）的最大值为2，则的最小值为__．4.已知函数f （x ）=|log 2x|，g （x ）= ，若方程f （x ）﹣g （x ）=1在[a ，+∞）上有三个实根，则正实数a 的取值范围为__．三、解答题1.在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，且b=，cosAsinB+（c ﹣sinA ）cos （A+C ）=0．（1）求角B 的大小； （2）若△ABC 的面积为，求sinA+sinC 的值．2.已知数列{a n }的前n 项和为S n ，对任意的正整数n ，都有S n =a n +n ﹣3成立．（Ⅰ）求证：{a n ﹣1}为等比数列；（Ⅱ）求数列{na n }的前n 项和T n ．3.为了了解某学校高二年级学生的物理成绩，从中抽取n 名学生的物理成绩（百分制）作为样本，按成绩分成 5组：[50，60），[60，70），[70，80），[80，90），[90，100]，频率分布直方图如图所示．成绩落在[70，80）中的人数为20．（Ⅰ）求a 和n 的值；（Ⅱ）根据样本估计总体的思想，估计该校高二学生物理成绩的平均数和中位数m ；（Ⅲ）成绩在80分以上（含80分）为优秀，样本中成绩落在[50，80）中的男、女生人数比为1：2，成绩落在[80，100]中的男、女生人数比为3：2，完成2×2列联表，并判断是否有95%的把握认为物理成绩优秀与性别有关．参考公式和数据：K 2=．P （K 2≥k ）0.50 0.05 0.025 0.0054.如图所示，在多面体中，是边长为2的等边三角形，为的中点，．（1）若平面平面，证明：； （2）求证：； （3）若，求点到平面的距离．5.如图所示，抛物线C ：x 2=2py （p ＞0），其焦点为F ，C 上的一点M （4，m ）满足|MF|=4． （1）求抛物线C 的标准方程；（2）过点E （﹣1，0）作不经过原点的两条直线EA ，EB 分别与抛物线C 和圆F ：x 2+（y ﹣2）2=4相切于点A ，B，试判断直线AB是否经过焦点F．6.设函数f（x）=lnx+ax2+x+1．（I）a=﹣2时，求函数f（x）的极值点；（Ⅱ）当a=0时，证明xe x≥f（x）在（0，+∞）上恒成立．山西高三高中数学月考试卷答案及解析一、选择题1.已知全集为R，集合M={﹣1，0，1，5}，N={x|x2﹣x﹣2≥0}，则M∩∁RN=（）A．{0，1}B．{﹣1，0，1}C．{0，1，5}D．{﹣1，1}【答案】A【解析】∵，∴，∴。
山西省晋中市祁县中学高三数学理月考试题含解析
山西省晋中市祁县中学高三数学理月考试题含解析一、选择题：本大题共10小题，每小题5分，共50分。
在每小题给出的四个选项中，只有是一个符合题目要求的1. 将函数y=sin（x+）图象上各点的横坐标缩短到原来的倍（纵坐标不变），再向右平移个单位，那么所得图象的一条对称轴方程为( )A．x=﹣B．x=﹣C．x=D．x=参考答案：B【考点】函数y=Asin（ωx+φ）的图象变换．【专题】三角函数的图像与性质．【分析】根据函数y=Asin（ωx+φ）的图象变换规律，余弦函数的图象的对称性，可得结论．【解答】解：将函数y=sin（x+）图象上各点的横坐标缩短到原来的倍（纵坐标不变），可得函数y=sin（2x+）的图象，再向右平移个单位，那么所得图象对应的函数解析式为y=sin[2（x﹣）+]=sin（2x﹣）=﹣cos2x，故最后所得函数的图象的一条对称轴方程为2x=kπ，即 x=，k∈z，结合所给的选项可得只有B满足条件，故选：B．【点评】本题主要考查函数y=Asin（ωx+φ）的图象变换规律，余弦函数的图象的对称性，属于中档题．2. 已知向量,，若与共线,则实数的值是（）A．B．C．D．参考答案：B3. 甲、乙两位同学约定周日上午在某电影院旁见面，并约定谁先到后必须等10分钟，若等待10分钟后另一人还没有来就离开．如果甲是8：30分到达的，假设乙在8点到9点内到达，且乙在8点到9点之间何时到达是等可能的，则他们见面的概率是A． B． C． D．参考答案：D4. 设为偶函数，对于任意的的数都有，已知，那么等于( ）A．2 B．-2 C．．8 D．-8参考答案：C5. 设全U={1，2，3，4，5}，A={1，2}，B={2，3，4}，则（?U A）∪B( )A．{3，4} B．{3，4，5} C．{2，3，4，5} D．{1，2，3，4}参考答案：C考点：并集及其运算；补集及其运算．专题：计算题．分析：根据并集、补集的意义直接求解即得．解答：解：∵U={1，2，3，4，5}，A={1，2}，∴C U A={3，4，5}，∴（C U A）∪B={2，3，4，5}，故选C．点评：本题考查集合的基本运算，较容易．6. 将函数的图象向左平移个单位，所得到的函数图象关于轴对称，则的一个可能取值为A． B． C．D．参考答案：B7. .已知，，且，则向量与的夹角为（）A. 60°B. 120°C. 30°D. 150°参考答案：D【分析】将两边平方，根据向量的夹角公式得到答案.【详解】，，即故答案选D【点睛】本题考查了向量的运算和夹角公式，意在考查学生的计算能力.8. 将边长为a的正方形ABCD沿对角线AC折起，使得BD=a，则三棱锥D-ABC的体积为A、B、C、D、参考答案：D 略9. 已知等差数列{a n}的前n项和为S n,S9=-18，S13=-52，{b n}为等比数列，且b5 =a5，b7=a7，则b15的值为A．64 B．128 C．-64 D．-128参考答案：C略10. 已知满足约束条件，则的最大值为（A）0 （B）5 （C） 3 （D）17参考答案：C二、填空题:本大题共7小题,每小题4分,共28分11. 复数.（为虚数单位）的虚部是参考答案：12. 如图所示，圆O的直径AB＝6，C为圆周上一点，BC＝3过C作圆的切线l，则点A直线l的距离AD=_____________________参考答案：略13. 如图所示，在平面直角坐标系内，四边形为正方形且点坐标为.抛物线的顶点在原点，关于轴对称，且过点.在正方形内随机取一点，则点在阴影区域内的概率为．参考答案：14. 已知数列{a n }满足,,若[x ]表示不超过x 的最大整数，则．参考答案：115. 已知函数，若对任意的，不等式恒成立，则实数的取值范围为 .参考答案：16. 在等比数列{a n}中，a1=，a4=4，则公比q=______________；a1+a2+…+a n=_________________.参考答案：；本题考查了等比数列的概念以及等比数列的求和，难度中等．由题意可知，可得，所以。
山西省晋中市祁县中学校2019-2020学年高二下学期6月月考数学(理)试卷 Word版含答案
姓名，年级：时间：数学（理）试题一、选择题(本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的)1．若集合}01|{≤≤-=x x A ，}0)1(log |{2≤-=x x B ，则=B AA 。
}11|{≤≤-x xB 。
}11|{≤<-x xC 。
}0{ D.}11|{<≤-x x2．设A={x ｜x 2+4x=0},B={x ｜x 2+2（a+1）x+a 2—1=0｝，其中x ∈R,若A ∩B=B ，则实数a 的取值范围是A ．a ≤-1B ．a ≥1C ．a<—1或a=±1D ．a>1或a=±13．给出下列命题,其中正确命题的个数是错误!用样本频率分布估计总体频率分布的过程中,总体容量越大，估计越精确;错误!对于两个变量之间的相关系数，越接近于1，相关程度越强； 错误!设随机变量，若，则错误!在残差图中，残差点比较均匀地落在水平区域中，说明选用的模型比较合适，这样的带状区域的宽度越宽,说明模型的拟合精度越高，回归方程的预报精度越高． A. 1B. 2C 。
3D. 44．ξ，η为随机变量，且η＝aξ＋b，若E(ξ）＝1.6，E(η）＝3。
4，则a,b可能的值为A．0。
5,1。
4 B．1，4 C．2，0。
2 D．1.6，3。
45．某同学参加学校篮球选修课的期末考试，老师规定每个同学罚篮20次,每罚进一球得5分，不进记0分，已知该同学罚球命中率为60%，则该同学得分的数学期望和方差分别为A。
60，24 B. 80，120 C。
80，24 D。
60，1206．从20名男同学和30名女同学中选4人去参加一个会议，规定:男女同学至少各1人参加，为了计算不同的选法种数，列出了下列三个算式,其中正确算式的个数是A。
1 B. 0 C。
3 D。
27．分配4名水暖工去3户不同的居民家里检查暖气管道要求4名水暖工都分配出去，且每户居民家都要有人去检查,那么分配的方案共有A。
山西高三高中数学月考试卷带答案解析
山西高三高中数学月考试卷班级:___________ 姓名：___________ 分数：___________一、选择题1.已知集合，或，则="( " )．A．或B．C．D．或2.函数的反函数为（）A．B．C．D．3.已知数列为等差数列,为的前项和,,则的值为( )A．B．C．D．644.设,则、、的大小关系为( )A．＞＞B．＞＞C．＞＞D．＞＞5.等于（）A．B．C．D．6.设,则的值为( )A．B．C．、中较小的数D．、中较大的数7.设a、b、c是互不相等的正数，则下列不等式中不恒成立的是A．B．C．D．8.三棱锥中,两两相互垂直，且，则三棱锥的外接球的半径为（）9.已知非零向量与满足且则为( )A．等边三角形B．直角三角形C．等腰非等边三角形D．三边均不相等的三角形10.如图，为正方体的中心，△在该正方体各个面上的射影可能是( ).A．（1）、（2）、B．（1）、（3）C．（1）、（4）D．（2）、（4）（3）、（4）11.有两排座位，前排6个座位，后排7个座位，现安排2人就座，规定这２人左右不相邻，那么不同的坐法种数是（）12.如图，过抛物线y2=2px(p>0)的焦点F的直线交抛物线于两点A、B，交其准线于C，若|BC|=2|BF|且|AF|=3，则此抛物线的方程为( )A．y2=x B．y2=9x C．y2=x D．y2=3x13.已知集合，或，则="( " )．A．或B．C．D．或14.函数的反函数为（）A．B．C．D．15.已知数列为等差数列,为的前项和,,则的值为( )A．B．C．D．6416.设,则、、的大小关系为( )A．＞＞B．＞＞C．＞＞D．＞＞17.等于（）A．B．C．D．18.设,则的值为( )A．B．C．、中较小的数D．、中较大的数19.设a、b、c是互不相等的正数，则下列不等式中不恒成立的是A．B．C．D．20.三棱锥中,两两相互垂直，且，则三棱锥的外接球的半径为（）21.已知非零向量与满足且则为( )A．等边三角形B．直角三角形C．等腰非等边三角形D．三边均不相等的三角形22.如图，为正方体的中心，△在该正方体各个面上的射影可能是( ).A．（1）、（2）、B．（1）、（3）C．（1）、（4）D．（2）、（4）（3）、（4）23.有两排座位，前排6个座位，后排7个座位，现安排2人就座，规定这２人左右不相邻，那么不同的坐法种数是（）24.如图，过抛物线y2=2px(p>0)的焦点F的直线交抛物线于两点A、B，交其准线于C，若|BC|=2|BF|且|AF|=3，则此抛物线的方程为( )A．y2=x B．y2=9x C．y2=x D．y2=3x二、填空题1.若，则=______.2.数列满足：，则的值为_________ .3.已知点P（x，y）的坐标（x,y）满足，过P的直线与圆交于两点，那么的最小值为______.4.设为坐标原点,△和△均为正三角形，点在抛物线上，点在抛物线上，则△和△的面积之比为 . 5.若，则=______. 6.数列满足：，则的值为_________ .7.已知点P （x ，y ）的坐标（x,y ）满足，过P 的直线与圆交于两点，那么的最小值为______.8.设为坐标原点,△和△均为正三角形，点在抛物线上，点在抛物线上，则△和△的面积之比为 .三、解答题1.（本小题满分10分）如图,平面四边形中,,三角形的面积为,,,求: (1)的长; (2)2.如图，在组合体中，是一个长方体，是一个四棱锥．，，点且．（Ⅰ）证明：；（Ⅱ）求面与面所成的角的正切值；（Ⅲ）若，当为何值时，．3.一个盒子装有六张卡片，上面分别写着如下六个定义域为R 的函数：f 1(x )=x ，f 2(x )=x 2，f 3(x )=x 3，f 4(x )=sin x ，f 5(x )=cos x ，f 6(x )=2．（1）现从盒子中任取两张卡片，将卡片上的函数相加得一个新函数，求所得函数是奇函数的概率；（2）现从盒子中进行逐一抽取卡片，且每次取出后均不放回，若取到一张记有偶函数的卡片则停止抽取,否则继续进行,求恰好抽取了3次卡片的概率．4.已知各项均为正数的数列满足：，且.(１)求证：数列是等比数列；（２）设，，求，并确定最小的正整数n ，使为整数. 5.设函数（其中）的图象在处的切线与直线平行.（1）求的值； （2）求函数在区间[0,1]的最小值； （3）若,,,且,试根据上述（1）、（2）的结论证明:.6.有如下结论：“圆上一点处的切线方程为”，类比也有结论：“椭圆处的切线方程为”，过椭圆C ：的右准线l 上任意一点M 引椭圆C 的两条切线，切点为 A 、B.（1）求证：直线AB 恒过一定点；（2）当点M 的纵坐标为1时，求△ABM 的面积.7.（本小题满分10分）如图,平面四边形中,,三角形的面积为,,,求: (1)的长; (2)8.如图，在组合体中，是一个长方体，是一个四棱锥．，，点且．（Ⅰ）证明：；（Ⅱ）求面与面所成的角的正切值；（Ⅲ）若，当为何值时，．9.一个盒子装有六张卡片，上面分别写着如下六个定义域为R 的函数：f 1(x )=x ，f 2(x )=x 2，f 3(x )=x 3，f 4(x )=sin x ，f 5(x )=cos x ，f 6(x )=2．（1）现从盒子中任取两张卡片，将卡片上的函数相加得一个新函数，求所得函数是奇函数的概率；（2）现从盒子中进行逐一抽取卡片，且每次取出后均不放回，若取到一张记有偶函数的卡片则停止抽取,否则继续进行,求恰好抽取了3次卡片的概率．10.已知各项均为正数的数列满足：，且.(１)求证：数列是等比数列；（２）设，，求，并确定最小的正整数n ，使为整数. 11.设函数（其中）的图象在处的切线与直线平行.（1）求的值； （2）求函数在区间[0,1]的最小值； （3）若,,,且,试根据上述（1）、（2）的结论证明:.12.有如下结论：“圆上一点处的切线方程为”，类比也有结论：“椭圆处的切线方程为”，过椭圆C ：的右准线l 上任意一点M 引椭圆C 的两条切线，切点为 A 、B. （1）求证：直线AB 恒过一定点；（2）当点M 的纵坐标为1时，求△ABM 的面积.山西高三高中数学月考试卷答案及解析一、选择题1.已知集合，或，则="( " )．A．或B．C．D．或【答案】A【解析】略2.函数的反函数为（）A．B．C．D．【答案】D【解析】略3.已知数列为等差数列,为的前项和,,则的值为( )A．B．C．D．64【答案】B【解析】略4.设,则、、的大小关系为( )A．＞＞B．＞＞C．＞＞D．＞＞【答案】B【解析】略5.等于（）A．B．C．D．【答案】A【解析】略6.设,则的值为( )A．B．C．、中较小的数D．、中较大的数【答案】D【解析】略7.设a、b、c是互不相等的正数，则下列不等式中不恒成立的是A．B．C．D．【答案】D【解析】略8.三棱锥中,两两相互垂直，且，则三棱锥的外接球的半径为（）【答案】C【解析】略9.已知非零向量与满足且则为( )A．等边三角形B．直角三角形C．等腰非等边三角形D．三边均不相等的三角形【答案】A【解析】略10.如图，为正方体的中心，△在该正方体各个面上的射影可能是( ).A．（1）、（2）、B．（1）、（3）C．（1）、（4）D．（2）、（4）（3）、（4）【答案】C【解析】略11.有两排座位，前排6个座位，后排7个座位，现安排2人就座，规定这２人左右不相邻，那么不同的坐法种数是（）【答案】D【解析】略12.如图，过抛物线y2=2px(p>0)的焦点F的直线交抛物线于两点A、B，交其准线于C，若|BC|=2|BF|且|AF|=3，则此抛物线的方程为( )A．y2=x B．y2=9x C．y2=x D．y2=3x【答案】D【解析】略13.已知集合，或，则="( " )．A．或B．C．D．或【答案】A【解析】略14.函数的反函数为（）A．B．C．D．【答案】D【解析】略15.已知数列为等差数列,为的前项和,,则的值为( )A．B．C．D．64【答案】B【解析】略16.设,则、、的大小关系为( )A．＞＞B．＞＞C．＞＞D．＞＞【答案】B【解析】略17.等于（）A．B．C．D．【答案】A【解析】略18.设,则的值为( )A．B．C．、中较小的数D．、中较大的数【答案】D【解析】略19.设a、b、c是互不相等的正数，则下列不等式中不恒成立的是A．B．C．D．【答案】D【解析】略20.三棱锥中,两两相互垂直，且，则三棱锥的外接球的半径为（）【答案】C【解析】略21.已知非零向量与满足且则为( )A．等边三角形B．直角三角形C．等腰非等边三角形D．三边均不相等的三角形【答案】A【解析】略22.如图，为正方体的中心，△在该正方体各个面上的射影可能是( ).A．（1）、（2）、B．（1）、（3）C．（1）、（4）D．（2）、（4）（3）、（4）【答案】C【解析】略23.有两排座位，前排6个座位，后排7个座位，现安排2人就座，规定这２人左右不相邻，那么不同的坐法种数是（）【答案】D【解析】略24.如图，过抛物线y2=2px(p>0)的焦点F的直线交抛物线于两点A、B，交其准线于C，若|BC|=2|BF|且|AF|=3，则此抛物线的方程为( )A．y2=x B．y2=9x C．y2=x D．y2=3x【答案】D【解析】略二、填空题1.若，则=______.【答案】【解析】略2.数列满足：，则的值为_________ .【答案】-3【解析】略3.已知点P（x，y）的坐标（x,y）满足，过P的直线与圆交于两点，那么的最小值为______.【答案】4【解析】略4.设为坐标原点,△和△均为正三角形，点在抛物线上，点在抛物线上，则△和△的面积之比为 .【答案】16:1【解析】略5.若，则=______.【答案】【解析】略6.数列满足：，则的值为_________ .【答案】-3【解析】略7.已知点P（x，y）的坐标（x,y）满足，过P的直线与圆交于两点，那么的最小值为______.【答案】4【解析】略8.设为坐标原点,△和△均为正三角形，点在抛物线上，点在抛物线上，则△和△的面积之比为 .【答案】16:1【解析】略三、解答题1.（本小题满分10分）如图,平面四边形中,,三角形的面积为,,,求: (1)的长; (2)【答案】（1）；（2）【解析】（１）由已知可得……3分由得……5分（２）由上可得，又，所以可得，……7分……10分2.如图，在组合体中，是一个长方体，是一个四棱锥．，，点且．（Ⅰ）证明：；（Ⅱ）求面与面所成的角的正切值；（Ⅲ）若，当为何值时，．【答案】（1）略（2）3（3）2 【解析】(Ⅰ)证明： 因为，，所以为等腰直角三角形，所以． ……1分 因为是一个长方体，所以，而,所以,所以． …3分因为垂直于平面内的两条相交直线和，由线面垂直的判定定理，可得．…4分(Ⅱ)解：过点在平面作于，取的中点F 连接…5分则所以就是所求二面角的平面角．……6分因为，，,所以． …8分 (Ⅲ)解：当时，． …9分当时，四边形是一个正方形，所以，而，所以，所以． …10分 而，与在同一个平面内，所以． …11分 而，所以，所以。
高考模拟试题_山西省祁县中学2016届高三10月月考数学(理)试题-推荐下载
数学理科试题
一、选择题：本大题共 12 小题，每小题 5 分，共 60 分．在每小题给出的四个选项中，只 有一项是符合题目要求的．
1.“ p 或 q 是假命题”是“非 p 为真命题”的（ ）
A．充分而不必要条件
C．充要条件
2.已知集合
A
x
x x
1 3
0
，
B
x
B．必要而不充分条件
D．既不充分也不必要条件
A. B．3 C． x 3 x 4 D． x 1 x 4
y
3.函数 f(x)的图象向右平移一个单位长度，所得图象与 y ex 关于 y 轴对称，则 f(x)=（
A． (,0)
B． (0, 1 ) 2
11．设函数 y x3 与 y 22x 的图象的交点为 (x0，y0 ) ，则 x0 所在的区间是（
A． (0， 1)
B． (1， 2)
12. 设定义在 R 上的函数 f (x) 是最小正周期为 2 的偶函数， f '(x) 是 f (x) 的导函数，
C. 1,3
9．已知函数 f (x) log2 (x 2 ax 3a) 在区间 2,上是增函数，则实数 a 的取值范围
是（
）
A. ，4 B． 4,4 C. 4,2 D． ， 4 2，
10.已知函数 f (x) x(ln x ax) 有两个极值点，则实数 a 的取值范围是（ ）
13.设
14．函数
f
(x)
_______
f
lg(10x
1)
高三数学月考试题及答案-晋中市祁县中学2016届高三5月月考(文)
山西省祁县中学2016届高三5月月考（文）第I 卷（选择题 共60分）一、选择题：本大题共12小题，每小题5分，共60分．在每个小题给出的四个选项中，只有一项是符合题目要求的．1．若2013(2i)i i a b -=-，其中R b a ∈,，i 是虚数单位，则22b a +等于（ ）A ．0B ．2C ．25D ．5 2．已知130.5a -=，133()5b -=， 2.5log 1.5c =，则,,a b c 的大小关系（ ）A ．B ．C ．D ．3．已知命题p ：“∈∀x R ，01≥+x ”的否定是“∈∀x R ，01<+x ”； 命题q ：函数3y x -=是幂函数，则下列命题为真命题的是（ ）A ．p q ∧B ．p q ∨C ．q ⌝D ．()p q ∧⌝ 4．若数列{}a n 满足a 112=，a a n n =--111（n ≥2且*n ∈N ），则2013a 等于（ ） A ．－1 B ．21C ．1D ．2 5．已知平面向量()21,3, (2,)a m b m =+= ，且 a 与b 反向，则b 等于（ ）A B ．52或 C ．52D ．6．阅读右面的程序框图，若输出的21=y ， 则输入的x 的值可能为（ ） A ．B ．C ．D ．7．某几何体的三视图如图所示，则该几何体的表面积等于（ ）A ．8+ B.11+C.14+D.158.已知圆C 方程为()()22210x y r r -+=>，若p ：13r ≤≤；q ：圆C 上至多有3个点到直线+30x =的距离为1，则p 是q 的（ ）A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件9．已知函数()33f x x x =-，若ABC ∆中，角C 是钝角，那么（ ）A ．()()sin cos f A fB > B ．()()sin cos f A f B <C ．()()sin sin f A f B >D ．()()sin sin f A f B >（小于）10．已知三棱锥，在底面中，，，，，则此三棱锥的外接球的表面积为（ ）A ．16π3 B. C.32π3D. 16π 11. 设函数()f x 在R 上可导，其导函数为()f x '，且函数()f x 在2x =-处取得极小值，则函数()y xf x '=的图象可能是（ ）（A ） （B ） （C ） （D ）12.已知函数()2()e x f x x ax b =++，当1b <时，函数()f x 在(),2-∞-，()1,+∞上均为增函数，则2a ba +-的取值范围是（ ） A ．22,3⎛⎤- ⎥⎝⎦ B ．1,23⎡⎫-⎪⎢⎣⎭ C ．2,3⎛⎤-∞ ⎥⎝⎦ D ．2,23⎡⎤-⎢⎥⎣⎦第Ⅱ卷（非选择题 共90分）二、填空题：本大题共4个小题，每小题5分，共20分 13. 函数()log (2)a f x x =-必过定点 .14设等比数列{}n a 的公比为q ，若n S ，1-n S ，1+n S 成等差数列，则5375a a a a ++等于.15.已知变量,x y 满足约束条件13,1,x y y z kx y x y +≥⎧⎪≤=+⎨⎪-≤⎩若的最大值为5，且k 为负整数，则k =____________.16.已知等边三角形ABC 的边长为34，N M ，分别为AC AB ，的中点，沿MN 将ABC ∆折成直二面角，则四棱锥MNCB A -的外接球的表面积为 .三、解答题：本大题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤． 17．（本小题满分12分）在△ABC 中，角A ，B ，C 所对的边分别为()()()(),,,2sin cos sin a b c f x x A x B C x =-++∈R ，函数()f x 的图象关于点π,06⎛⎫⎪⎝⎭对称. （I ）当π0,2x ⎛⎫∈ ⎪⎝⎭时，求()f x 的值域； （II ）若7a =且sin sin B C +=ABC 的面积.18．（本小题满分12分）十八届五中全会公报指出：努力促进人口均衡发展，坚持计划生育的基本国策，完善人口发展战略，全面实施一对夫妇可生育两个孩子的政策，提高生殖健康、妇幼保健、托幼等公共服务水平．为了解适龄公务员对放开生育二胎政策的态度，某部门随机调查了200位30到40岁的公务员，得到情况如下表：(1)是否有99%以上的把握认为“生二胎与性别有关”，并说明理由；(2)把以上频率当概率，若从社会上随机抽取甲、乙、丙3位30到40岁的男公务员，求这三人中至少有一人要生二胎的概率．附：19．（本小题满分12分）在四棱锥中，平面，是正三角形，与的交点恰好是中点，又，，点在线段上，且．（Ⅰ）求证：平面；（Ⅱ）求点C 到平面PBD 的距离.20．（本小题满分12分）已知函数()a R .(Ⅰ)若在区间上是单调函数，求实数的取值范围； (Ⅱ)函数，若使得成立，求实数的取值范围.21. （本题满分12分） 如图，椭圆x 2a 2＋y 2b 2＝1(a >b >0)的上、下顶点分别为A 、B ，已知点B 在直线l ：y ＝－1上，且 椭圆的离心率e ＝32.(Ⅰ)求椭圆的标准方程；(Ⅱ)设P 是椭圆上异于A 、B 的任意一点，PQ ⊥y 轴，Q 为垂足，M 为线段PQ 的中点 直线AM 交直线l 于点C ，N 为线段BC 的中点，求证：OM ⊥MN .选做题：考生在第22、23、24题中任选一道作答，并用2B 铅笔将答题卡上所选的题目对应的题号右侧方框涂黑，按所涂题号进行评分；多涂、多答，按所涂的首题进行评分. 22.（本小题满分10分）选修4-1：几何证明选讲如图，AF 是圆E 切线,F 是切点, 割线ABC BM 是圆E 的直径，EF 交AC 于D ，AC AB 31=，030=∠EBC ,2MC =. （1）求线段AF 的长； （2）求证：ED AD 3=.23.（本小题满分10分）选修4—4：极坐标与参数方程在直角坐标系xOy 中，以原点O 为极点，x 轴的正半轴为极轴，建立极坐标系.已知曲线1C ：4cos ,3sin ,x t y t =+⎧⎨=-+⎩ （t 为参数）， 2C ：6cos ,2sin ,x y θθ=⎧⎨=⎩（θ为参数）.（Ⅰ）化1C ，2C 的方程为普通方程，并说明它们分别表示什么曲线； （Ⅱ）若1C 上的点P 对应的参数为π2t =-，Q 为2C 上的动点，求线段PQ 的中点M到直线3:cos sin 8C ρθθ-=+ 距离的最小值.24. （本小题满分10分） 选修4—5：不等式选讲 已知关于x 的不等式|2|1m x --≥，其解集为[0,4]. （Ⅰ）求m 的值；（Ⅱ）若a ，b 均为正实数，且满足a b m +=，求22a b +的最小值.祁县中学高三年级月考答案第Ⅰ卷（选择题，共60分）一、选择题：二、填空题：13. （3,1）14. 4 15. -1 16. 5218.（本小题满分12分）解：（1）由于=＜6.635，4分17.故没有99%以上的把握认为“生二胎与性别有关”．6分（2）题意可得，一名男公务员要生二胎的概率为=，一名男公务员不生二胎的概率为=，8分记事件A:这三人中至少有一人要生二胎则12分19.（本小题满分12分）解：（1）在正三角形ABC中，在中，因为M为AC中点，，所以，，所以所以.………………3分在等腰直角三角形中，，所以，，.………………5分所以.又平面，平面，所以平面…………6分（2）方法一：.………………8分………………10分∴.………………12分方法二：C到平面P B D距离等于A到P B D距离，即A到PM距离d，∴20．（本小题满分12分）解：⑴2分当导函数的零点落在区间内时，函数在区间上就不是单调函数，所以实数的取值范围是：；6分（也可以转化为恒成立问题.酌情给分.）（还可以对方程的两根讨论，求得答案.酌情给分）⑵由题意知,不等式在区间上有解，即在区间上有解．7分当时，（不同时取等号），，在区间上有解．8分令，则9分单调递增，时，11分所以实数的取值范围是，…………12分（也可以构造函数，分类讨论.酌情给分）21．（本小题满分12分）解：(1)依题意，得b＝1.∵e＝ca＝32，a2－c2＝b2＝1，∴a2＝4.∴椭圆的标准方程为x 24＋y 2＝1. (2)证明：设P (x 0，y 0)，x 0≠0，则Q (0，y 0)，且x 204＋y 20＝1. ∵M 为线段PQ 中点，∴M (x 02，y 0)． 又A (0,1)，∴直线AM 的方程为y ＝y 0－x 0x ＋1.∵x 0≠0，∴y 0≠1，令y ＝－1，得C (x 01－y 0，－1)． 又B (0，－1)，N 为线段BC 的中点，∴N (x 0－y 0，－1)． ∴NM →＝(x 02－x 0－y 0，y 0＋1)．∴OM →·NM →＝x 02(x 02－x 0－y 0)＋y 0·(y 0＋1) ＝x 204－x 20－y 0＋y 20＋y 0＝(x 204＋y 20)－x 20－y 0＋y 0＝1－(1＋y 0)＋y 0＝0， ∴OM ⊥MN .选做题22.（本小题满分10分）解：（1）因为BM 是圆E 直径所以, 090=∠BCM ，又2MC =,030=∠EBC ， 所以32=BC ，…………………………………2分 又,31AC AB =可知321==BC AB ，所以33=AC 根据切割线定理得： 93332=⨯=⋅=AC AB AF ，即3=AF … …………………………………5分（2）过E 作BC EH ⊥于H ，则ADF EDH ∆∆～， 从而有AF EH AD ED =，………………………………………8分 又由题意知，BC CH 321==2=EB 所以1=EH ， 因此31=AD ED ，即ED AD 3= …………………………………10分 23.解:（1）221:(4)(3)1,C x y -++=， 222:1364x y C +=1C 为圆心是(4,3)-，半径是1的圆. ………………………………………3分 2C 为中心在坐标原点，焦点在x 轴上，长半轴长是6，短半轴长是2的椭圆.…………………………………………………………4分（2）当π2t =时，(4,4)P -，………………………………………………………5分 设(6cos ,2sin )Q θθ 则(23cos ,2sin )M θθ+-+，3C为直线(80x -+=，……………………………………7分 M 到3C的距离d3)6πθ+从而当cos()1,6πθ+=时，d 取得最小值3- ………………………………10分24.解：（1）不等式|2|1m x --≥可化为|2|1x m -≤-，∴121m x m -≤-≤-，即31m x m -≤≤+, ……………………………2分 ∵其解集为[0,4]，∴3014m m -=⎧⎨+=⎩ ，3m =. …………………………………5分 （2）由（1）3a b +=，∵ 222()2a b a b ab +=++222222()()2()a b a b a b ≤+++=+，∴ 2292a b +≥，∴当且仅当32a b ==时，22a b +取最小值为92.…………10分 （方法二：）∵ 222222()(11)(11)()9a b a b a b +⋅+≥⨯+⨯=+=，∴ 2292a b +≥，∴当且仅当32a b ==时，22a b +取最小值为92.……………10分 （方法三：）∵3a b +=，∴3b a =-， ∴222222399(3)2692()222a b a a a a a +=+-=-+=-+≥， ∴当且仅当32a b ==时，22a b +取最小值为92.………………………10分。
山西省祁县中学高三数学10月月考试题 文
祁县中学2015---2016学年高三10月月考数学（文科）试题一．选择题（本大题共有12个小题，每小题5分，共60分）1．已知集合P={x ∈N|1≤x ≤10},集合Q={x ∈R|06--2=x x },则P ∩Q 等于( )A.{2}B.{1，2}C. {2，3}D.{3} 2.若函数)2(),3,0[)1(xf x f 则的定义域为+的定义域为（ ）A ．[1，8]B ．[1,4)C ．[0,2)D ．[0，2]3. 函数3)(5-+=x x x f 的零点落在的区间是（ ）A ．[]1,0B ．[]2,1C ．[]3,2D ．[]4,34.已知10.20.7321.5, 1.3,()3a b c -===,则,,a b c 的大小为 ( )A.c a b <<B. c b a <<C. a b c <<D. a c b <<5．在R 的定义运算： ⎝⎛c a bc ad d b -=⎪⎪⎭⎫，若不等式 ⎝⎛+-11a x 12≥⎪⎪⎭⎫-x a 对任意实数x 恒成立，则实数a 的最大值为( )A ．21-B ．23- C ．21 D ．236. 下列判断错误．．的是（ ）A ．“22bm am <”是“a < b ”的充分不必要条件B ．命题“01,23≤--∈∀x x R x ”的否定是“ 01,23>--∈∃x x R x ”C ．若f (x)是定义在R 上的奇函数，且f (x+2)也为奇函数，则f (x)是以4为周期的周期函数.D ．若q p Λ为假命题, 则p, q 均为假命题7若把函数x x y 2sin -2cos 3=的图象向右平移0)(>m m 个单位长度后，所得到的图象关于y 轴对称，则m 的最小值是（ ）A ．π3 B ．12π C ．π6 D ．5π6 8.函数f(x)＝ln(4＋3x －x 2)的单调递减区间是( ) A.），（∞+23 B.），（23-∞ C.），（41- D. ），（423 9. 函数1ln --=x e y x的图象大致是（ ）10. 若定义在R 上的函数)(-)1()(x f x f x f y =+=满足满足，且当]1,1[-∈x 时，2)(x x f =，函数⎩⎨⎧≤>=1,21),1-(log )(3x x x x g x ，则函数)(-)()(x g x f x h =在区间]5,5[-内的零点的个数为（ ）A ．6 B. 7 C. 8 D. 911. 已知函数()f x 是定义在实数集R 上得不恒为零的偶函数，且对任意实数x 都有(1)(1)()xf x x f x +=+，则5()2f =（ ）A ．0 B.12C.1D.5212. 设()f x 是R 上的偶函数，对任意x R ∈，都有(2)(2),f x f x -=+且当[2,0]x ∈-时，1()()1,(2,6]2x f x =--若在区间内关于x 的方程()log (2)0(1)a f x x a -+=>恰有3个不同的实数根，则a 的取值范围是（ ）A ．（1，2）B ．(2,)+∞ C． D．二．填空题13.已知:()()110p x m x m -+--<；:1223q x <<，若q 是p 的充分不必要条件， 则实数m 的取值范围是___________________。
山西省祁县高三数学12月月考试题 理(扫描版)
山西省祁县2018届高三数学12月月考试题理（扫描版）祁县中学2017年高三年级12月月考数学（理）答案一、选择题BDCABC BCACBB二、填空题13.161-=y 14.Z k k k ∈++-],,[ππππ1251215.[-1,3] 16.52π三、解答题17.解：（1）的最大值为2． 要使取最大值，，故的集合为（2），即．化简得，只有．在中，由余弦定理，．由知，即，当时取最小值1．18.解：(1) 12n n a n +=⋅；(2) ()()131229n nn S ++-+=-.19.解：（1）由三视图可知，四棱锥P ABCD -中PA ⊥平面ABCD ，…………………………(1分)同时，222BC AD CD ===，四边形ABCD 为直角梯形．……………………………………(2分)过点A 作AG BC ⊥于G ，则1AG CD ==,1GC AD ==．∴AC ==AB ，∴222AC AB BC +=，故A C A B ⊥．……………………………………………………………(4分) ∵PA ⊥平面A B ,AC ⊂平面A B ,∴PA AC ⊥.…………………………………………(5分)∵PA AB A =，∴AC ⊥平面PAB ．……………………………………………………………(6分)（2）由三视图可知，四棱锥P ABCD -的正三角形侧面为面PBC ．………………………(7分)PBC ∆为正三角形，∴2PB BC ==．在Rt PAB ∆中，PA =以A 为原点，,,AG AD AP 分别为,,x y z 轴建立空间直角坐标系，有(1,1,0),(1,1,0)P B C -．……………………………………………………(8分) 由（Ⅰ）知(1,1,0)AC =是平面PAB 的一条法向量．……………………………………………(9分)向量(0,2,0),(1,1,BC PC ==，设平面PBC 的法向量为(,,)x y z =n ，由0,0,BC PC ⎧⋅=⎪⎨⋅=⎪⎩n n ，得n的一组解=n ．……(10分)设平面ABP 与正三角形侧面PBC 所成二面角为θ，则c o s 3AC AC θ⋅==n n．……………(12分)20.21.22.解（1）当0a >，0b =时，函数()f x 在区间()0,+∞上的零点的个数即方程2x e ax =根的个数．由22xxe e ax a x=⇒=， ………………………………(1分)令()()()()()223222x x xxe x e x e h x h x x x x --'=⇒==， …………………………(2分)则()h x 在()0,2上单调递减，这时()()()2,h x h ∈+∞；()h x 在()2,+∞上单调递增，这时()()()2,h x h ∈+∞．所以()2h 是()y h x =的极小值即最小值，即()224e h =所以函数()f x 在区间()0,+∞上零点的个数，讨论如下：当20,4e a ⎛⎫∈ ⎪⎝⎭时，有0个零点； …………………………(3分)当24e a =时，有1个零点； ………………………(4分)当2,4e a ⎛⎫∈+∞ ⎪⎝⎭时，有2个零点． ………………………(5分)（2）由已知()2xf x e ax ax =--，∴()2xf x e ax a '=--，1x ，2x 是函数()f x 的两个不同极值点（不妨设12x x <），∴0a >（若0a ≤时，()0f x '>，即()f x 是R 上的增函数，与已知矛盾），且()10f x '=，()20f x '=．∴1120xe ax a --=，2220xe ax a --=……………(6分)两式相减得：12122x x e e a x x -=-， ……………………………(7分)于是要证明()12ln 22x x a +<，即证明1212212x xx x e e e x x +-<-，两边同除以2xe ， 即证12122121x x x x e ex x ---<-，即证()12122121x x x xx x e e --->-，即证()121221210x x x x x x e e ----+>， 令12x x t -=， 0t <．即证不等式210t tte e -+>，当0t <时恒成立． ………(9分)设()21t t t te e ϕ=-+，∴()2221122tt t t t t t e t e e e e ϕ⎛⎫'=+⋅⋅-=+- ⎪⎝⎭2212t tt e e ⎡⎤⎛⎫=--+⎢⎥ ⎪⎝⎭⎣⎦．………(10分) 设()212t th t e =--，∴()221111222t th t e e ⎛⎫'=-=- ⎪⎝⎭，当0t <，()0h t '<，()h t 单调递减，所以()()00h t h >=，即2102t t e ⎛⎫-+> ⎪⎝⎭，∴()0t ϕ'<，∴()t ϕ在0t <时是减函数．∴()t ϕ在0t =处取得极小值()00ϕ=．∴()0t ϕ>，得证．∴()12ln 22x xa +<． ………………………(12分)。
山西高三高中数学月考试卷带答案解析
山西高三高中数学月考试卷班级:___________ 姓名：___________ 分数：___________一、选择题1.已知集合,集合,则等于（）A．B．C．D．2.已知复数满足，则=（）A．B．C．D．53.下列命题正确的个数为（）“都有”的否定是“使得”‚“”是“”成立的充分条件ƒ命题“若，则方程有实数根”的否命题A．0B．1C．2D．3 4.某几何体的三视图如图所示，则该三视图的体积为（）A．B．C．D．5.函数的图象大致是（）6.阅读下边的程序框图，运行相应的程序，当输入N=6时，输出的s=（）A．62B．64C．126D．1247.已知双曲线E:的右焦点为F，圆C：与双曲线的渐近线交于A，B，O三点（O为坐标原点）.若为等边三角形，则双曲线E的离心率为（）A．B．2C．D．38.向量满足,且,则的夹角的余弦值为（）A．0B．C．D．9.已知的展开式中没有常数项，则n不能是（）A．5B．6C．7D．810.不透明的袋子内装有相同的五个小球，分别标有1-5五个编号，现有放回的随机摸取三次，则摸出的三个小球的编号乘积能被10整除的概率为（）A．B．C．D．11.已知函数（>0）,若且在上有且仅有三个零点，则=（）A．B．2C．D．12.已知函数，若不等式<0对任意均成立，则的取值范围为（）A．B．C．D．二、填空题1.抛物线的准线方程为 .2.设函数是定义在上的奇函数，且对任意的,当时，，则= .3.已知满足约束条件，若恒成立，则实数的取值范围为 .4.已知ΔABC是斜三角形，角A，B，C所对的边分别为,若且，则ΔABC的面积为 .三、解答题1.已知数列的前项和，其中.（I）求的通项公式；（II）若，求的前项和.2.如图，菱形ABCD的中心为O,四边形ODEF为矩形，平面ODEF平面ABCD，DE=DA=DB=2（I）若G为DC的中点，求证：EG//平面BCF;（II）若,求二面角的余弦值.3.甲、乙两人组成“火星队”参加投篮游戏，每轮游戏中甲、乙各投一次，如果两人都投中，则“火星队”得4分；如果只有一人投中，则“火星队”得2分；如果两人都没投中，则“火星队”得0分.已知甲每次投中的概率为，乙每次投中的概率为；每轮游戏中甲、乙投中与否互不影响，假设“火星队”参加两轮游戏，求：（I）“火星队”至少投中3个球的概率；（II）“火星队”两轮游戏得分之和X的分布列和数学期望EX.4.已知椭圆C:的左焦点为F,为椭圆上一点,AF交y轴于点M,且M为AF的中点.（I）求椭圆C的方程；（II）直线与椭圆C有且只有一个公共点A，平行于OA的直线交于P,交椭圆C于不同的两点D,E，问是否存在常数，使得，若存在，求出的值，若不存在，请说明理由.5.已知函数.（I）若函数在内单调递减，求实数的取值范围；（II）当时，关于的方程在上恰有两个不相等的实数根，求实数的取值范围.6.如图，已知为圆的直径，是圆上的两个点，是劣弧的中点,于,交于，交于.（I）求证：（II）求证：.7.在直角坐标系中，直线的参数方程为，以坐标原点为极点，轴的正半轴为极轴，建立极坐标系，曲线的极坐标方程为.（I）写出直线的普通方程和曲线的直角坐标方程；（II）直线与曲线交于两点，求.8.已知函数（I）求不等式的解集；（II）若对于任意的实数恒有成立，求实数a的取值范围.山西高三高中数学月考试卷答案及解析一、选择题1.已知集合,集合,则等于（）A．B．C．D．【答案】C【解析】,所以，选C.【考点】集合运算【方法点睛】1.用描述法表示集合，首先要弄清集合中代表元素的含义，再看元素的限制条件，明确集合类型，是数集、点集还是其他的集合．2．求集合的交、并、补时，一般先化简集合，再由交、并、补的定义求解．3．在进行集合的运算时要尽可能地借助Venn图和数轴使抽象问题直观化．一般地，集合元素离散时用Venn图表示；集合元素连续时用数轴表示，用数轴表示时要注意端点值的取舍．2.已知复数满足，则=（）A．B．C．D．5【答案】D【解析】选D.【考点】复数的模【名师点睛】本题重点考查复数的基本运算和复数的概念，属于基本题.首先对于复数的四则运算，要切实掌握其运算技巧和常规思路，如.其次要熟悉复数相关基本概念，如复数的实部为、虚部为、模为、对应点为、共轭为3.下列命题正确的个数为（）“都有”的否定是“使得”‚“”是“”成立的充分条件ƒ命题“若，则方程有实数根”的否命题A．0B．1C．2D．3【答案】B【解析】“都有”的否定是“使得”;“”是“”成立的必要条件；命题“若，则方程有实数根”的否命题为“若方程有实数根，则”，即或，因此 正确，选B.【考点】命题否定4.某几何体的三视图如图所示，则该三视图的体积为（）A．B．C．D．【答案】A【解析】几何体为一个半球内含一个圆锥，其体积为，选A.【考点】三视图【名师点睛】1.解答此类题目的关键是由多面体的三视图想象出空间几何体的形状并画出其直观图．2．三视图中“正侧一样高、正俯一样长、俯侧一样宽”，因此，可以根据三视图的形状及相关数据推断出原几何图形中的点、线、面之间的位置关系及相关数据．5.函数的图象大致是（）【答案】C【解析】为偶函数，所以不选A,当时，，所以不选B,当时，，所以不选D，因此选C.【考点】函数图像【思路点睛】（1）运用函数图象解决问题时，先要正确理解和把握函数图象本身的含义及其表示的内容，熟悉图象所能够表达的函数的性质.（2）在研究函数性质特别是单调性、最值、零点时，要注意用好其与图象的关系，结合图象研究.6.阅读下边的程序框图，运行相应的程序，当输入N=6时，输出的s=（）A．62B．64C．126D．124【答案】A【解析】第一次循环：，第二次循环：，第三次循环：，第四次循环：，第五次循环：，结束循环，输出，选A.【考点】循环结构流程图【名师点睛】算法与流程图的考查，侧重于对流程图循环结构的考查.先明晰算法及流程图的相关概念，包括选择结构、循环结构、伪代码，其次要重视循环起点条件、循环次数、循环终止条件，更要通过循环规律，明确流程图研究的数学问题，是求和还是求项.7.已知双曲线E:的右焦点为F，圆C：与双曲线的渐近线交于A，B，O三点（O为坐标原点）.若为等边三角形，则双曲线E的离心率为（）A．B．2C．D．3【答案】B【解析】由题意得选B.【考点】双曲线渐近线【方法点睛】解决椭圆和双曲线的离心率的求值及范围问题其关键就是确立一个关于a，b，c的方程或不等式，再根据a，b，c的关系消掉b得到a，c的关系式，建立关于a，b，c的方程或不等式，要充分利用椭圆和双曲线的几何性质、点的坐标的范围等.8.向量满足,且,则的夹角的余弦值为（）A．0B．C．D．【答案】B【解析】，，所以选B.【考点】向量夹角【方法点睛】平面向量数量积的类型及求法（1）求平面向量数量积有三种方法：一是夹角公式a·b＝|a||b|cos θ；二是坐标公式a·b＝x1x2＋y1y2；三是利用数量积的几何意义.（2）求较复杂的平面向量数量积的运算时，可先利用平面向量数量积的运算律或相关公式进行化简.9.已知的展开式中没有常数项，则n不能是（）A．5B．6C．7D．8【答案】D【解析】因为所以无解，因此选D.【考点】二项式定理【方法点睛】求二项展开式有关问题的常见类型及解题策略（1）求展开式中的特定项.可依据条件写出第r＋1项，再由特定项的特点求出r值即可.（2）已知展开式的某项，求特定项的系数.可由某项得出参数项，再由通项写出第r＋1项，由特定项得出r值，最后求出其参数.10.不透明的袋子内装有相同的五个小球，分别标有1-5五个编号，现有放回的随机摸取三次，则摸出的三个小球的编号乘积能被10整除的概率为（）A．B．C．D．【答案】A【解析】由题意5号，2号或4号至少摸出一次，即三种情况：一是5号摸出两次，2号或4号摸出一次；二是5号摸出一次，2号或4号摸出两次；三是5号摸出一次，2号或4号摸出一次，1号或3号摸出一次；，总共有，所求概率为，选A.【考点】古典概型概率【方法点睛】古典概型中基本事件数的探求方法（1）列举法.（2）树状图法：适合于较为复杂的问题中的基本事件的探求.对于基本事件有“有序”与“无序”区别的题目，常采用树状图法.（3）列表法：适用于多元素基本事件的求解问题，通过列表把复杂的题目简单化、抽象的题目具体化.（4）排列组合法：适用于限制条件较多且元素数目较多的题目.11.已知函数（>0）,若且在上有且仅有三个零点，则=（）A．B．2C．D．【答案】D【解析】或，即或因为函数在上有且仅有三个零点，所以,因此，选D.【考点】三角函数解析式【方法点睛】已知函数y＝Asin（ωx＋φ）＋B（A＞0，ω＞0）的图象求解析式（1）（2）由函数的周期T求ω，（3）利用“五点法”中相对应的特殊点求φ.12.已知函数，若不等式<0对任意均成立，则的取值范围为（）A．B．C．D．【答案】A【解析】因为，且单调递增，所以函数为R上单调递增的奇函数，从而又，当且仅当时取等号，所以的取值范围为，选A.【考点】函数性质【思路点睛】函数单调性的常见的命题角度有：1求函数的值域或最值；2比较两个函数值或两个自变量的大小；3解函数不等式：首先根据函数的性质把不等式转化为f（g（x））>f（h（x））的形式，然后根据函数的单调性去掉“f”，转化为具体的不等式（组），此时要注意g（x）与h（x）的取值应在外层函数的定义域内；4求参数的取值范围或值.二、填空题1.抛物线的准线方程为 .【答案】【解析】，所以准线方程为【考点】抛物线准线方程2.设函数是定义在上的奇函数，且对任意的,当时，，则= .【答案】-2【解析】，即周期为4，因此【考点】函数性质3.已知满足约束条件，若恒成立，则实数的取值范围为 .【答案】【解析】可行域为一个三角形ABC及其内部，其中，直线过点B时取最大值6，而恒成立等价于【考点】线性规划【易错点睛】线性规划的实质是把代数问题几何化，即数形结合的思想.需要注意的是：一，准确无误地作出可行域；二，画目标函数所对应的直线时，要注意与约束条件中的直线的斜率进行比较，避免出错；三，一般情况下，目标函数的最大或最小值会在可行域的端点或边界上取得.4.已知ΔABC是斜三角形，角A，B，C所对的边分别为,若且，则ΔABC的面积为 .【答案】【解析】有正弦定理得，,由余弦定理得，所以ΔABC的面积为【考点】解三角形【方法点睛】解三角形问题，多为边和角的求值问题，这就需要根据正、余弦定理结合已知条件灵活转化边和角之间的关系，从而达到解决问题的目的.其基本步骤是：第一步：定条件即确定三角形中的已知和所求，在图形中标出来，然后确定转化的方向.第二步：定工具即根据条件和所求合理选择转化的工具，实施边角之间的互化.第三步：求结果.三、解答题1.已知数列的前项和，其中.（I）求的通项公式；（II）若，求的前项和.【答案】（I）（II）【解析】（I）由求，注意分类讨论：当时,，解得；当时,，即，因此数列是以为首项，为公比的等比数列，最后由等比数列通项公式得（II）由于为等差乘等比型，因此求和要用错位相减法：即求，注意作差时项的符号变化，求和时项数的确定试题解析：（I）当时,,解得；当时，化简整理得因此，数列是以为首项，为公比的等比数列.从而，（II）由（I）可得，【考点】由求，错位相减法求和【方法点睛】给出Sn 与an的递推关系求an，常用思路是：一是利用Sn－Sn－1＝an（n≥2）转化为an的递推关系，再求其通项公式；二是转化为Sn 的递推关系，先求出Sn与n之间的关系，再求an.应用关系式时，一定要注意分n＝1，n≥2两种情况，在求出结果后，看看这两种情况能否整合在一起.2.如图，菱形ABCD的中心为O,四边形ODEF为矩形，平面ODEF平面ABCD，DE=DA=DB=2（I）若G为DC的中点，求证：EG//平面BCF;（II）若,求二面角的余弦值.【答案】（I）详见解析（II）【解析】（I）证明线面平行，一般利用线面平行判定定理，即从线线平行出发给予证明，而线线平行的寻找与论证，往往利用平几知识，如本题利用三角形中位线性质及平行四边形性质，取BC中点M，则GM//EF,GM=EF,所以四边形EFMG为平行四边形，即EG//FM,本题也可从面面平行出发证线面平行，即先证平面EOG//平面FBC，这可从两组线线平行出发，得两组线面平行，再得面面平行（II）利用空间向量求二面角，首先利用垂直关系建立恰当的空间直角坐标系，设立各点坐标，利用方程组解两个平面的法向量，利用向量数量积求夹角，最后根据向量夹角与二面角之间关系得结果试题解析：解:（1）证明：连接OE,OG,由条件G为中点∴OG//BC又EF//OBEF=OB∴四边形EFBO为平行四边形∴EO//FB，平面EOG//平面FBC∴EG//平面BCFABCD为菱形，所以OB OC ，又平面ODEF平面ABCD，四边形ODEF为矩形所以OF平面ABCD可建立如图的空间直角坐标系，设O（0，0，0），B（1，0，0），C（0，，0），E（-1,0,2）F（0，0，2），H（，，0），D（-1，0，0），设是面DEG的一个法向量，则即，取.同理取平面OEH的一个法向量是所以,∴二面角D—EH—O的余弦值为.【考点】线面平行判定定理，利用空间向量求二面角【思想点睛】垂直、平行关系证明中应用转化与化归思想的常见类型.（1）证明线面、面面平行，需转化为证明线线平行.（2）证明线面垂直，需转化为证明线线垂直.（3）证明线线垂直，需转化为证明线面垂直.3.甲、乙两人组成“火星队”参加投篮游戏，每轮游戏中甲、乙各投一次，如果两人都投中，则“火星队”得4分；如果只有一人投中，则“火星队”得2分；如果两人都没投中，则“火星队”得0分.已知甲每次投中的概率为，乙每次投中的概率为；每轮游戏中甲、乙投中与否互不影响，假设“火星队”参加两轮游戏，求：（I ）“火星队”至少投中3个球的概率；（II ）“火星队”两轮游戏得分之和X 的分布列和数学期望EX. 【答案】（I ）（II ）【解析】（I ）“火星队”至少投中3个球包括：甲投中两次乙投中一次，甲投中一次乙投中两次，甲投中两次乙投中两次，其概率对应为，根据概率加法得（II ）先确定随机变量取法：0，2,4，6，8，再分别求对应概率，列表可得概率分布列，最后根据公式求数学期望试题解析：解：（Ⅰ）设事件为“甲第次投中”,事件为“乙第次投中”由事件的独立性和互斥性答：“星队”至少投中3个球的概率为（Ⅱ）X 的所有可能的取值为0，2,4，6，8，,,∴X 的分布列为【考点】互斥事件概率，概率分布与数学期望【方法点睛】求解离散型随机变量的数学期望的一般步骤为：第一步是“判断取值”，即判断随机变量的所有可能取值，以及取每个值所表示的意义；第二步是“探求概率”，即利用排列组合、枚举法、概率公式（常见的有古典概型公式、几何概型公式、互斥事件的概率和公式、独立事件的概率积公式，以及对立事件的概率公式等），求出随机变量取每个值时的概率；第三步是“写分布列”，即按规范形式写出分布列，并注意用分布列的性质检验所求的分布列或某事件的概率是否正确；第四步是“求期望值”，一般利用离散型随机变量的数学期望的定义求期望的值，对于有些实际问题中的随机变量，如果能够断定它服从某常见的典型分布（如二项分布X ～B （n ，p ）），则此随机变量的期望可直接利用这种典型分布的期望公式（E （X ）＝np ）求得.因此，应熟记常见的典型分布的期望公式，可加快解题速度.4.已知椭圆C:的左焦点为F,为椭圆上一点,AF 交y 轴于点M,且M 为AF 的中点.（I ）求椭圆C 的方程；（II ）直线与椭圆C 有且只有一个公共点A ，平行于OA 的直线交于P,交椭圆C 于不同的两点D,E ，问是否存在常数，使得，若存在，求出的值，若不存在，请说明理由.【答案】（I）（II）【解析】（I）由几何意义得，所以再根据点在椭圆上得，解得（II）本题实质确定是否为定值，先确定切线的方程为，设直线DE的方程为，解出P点坐标,利用两点距离公式求出，再根据弦长公式求，最后求比值得试题解析：解:（Ⅰ）设椭圆的右焦点是，在中，所以椭圆的方程为（Ⅱ）设直线DE的方程为，解方程组消去得到若则，其中又直线的方程为,直线DE的方程为，所以P点坐标,所以存在常数使得【考点】椭圆标准方程，直线与椭圆位置关系【方法点睛】有关圆锥曲线弦长问题的求解方法涉及弦长的问题中，应熟练地利用根与系数关系，设而不求法计算弦长；涉及垂直关系时也往往利用根与系数关系、设而不求法简化运算；涉及过焦点的弦的问题，可考虑用圆锥曲线的定义求解。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2016届山西省祁县中学高三5月月考数学（理）试题
数学试题（理科）
一.单选题（每小题5分，共12小题，总分60分）
1.已知i 是虚数单位,则2016i = ( ) A.1
B.i
C.i -
D.-1
2.=B A （ ）
A 、∅
B 、[1,1]-
C 、[1,)-+∞
D 、[1,)+∞
3．已知等比数列}{n a 中，11=a ，且43,2,24a a a 成等差数列，则432a a a ++等于 ( ) A ．1
B ．4
C ．14
D ．15
4.“=0a ”是“函数1
()sin f x x a x
=-
+为奇函数”的 ( ) A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件 5.某几何体的直观图如图所示,该几何体的正视图和侧视图可能正确的是( )
6.直线１－+=k kx y 与椭圆14
92
2=+y x 的位置关系为 （ ）
A.相切
B.相交
C.相离
D.不确定 7.平面上有一组平行线且相邻平行线间的距离为3,把一枚半径为1的任意平掷在
这个平面中,则硬币不与任何一条平行线相碰的概率是( )
A.
B.
C.
D.
8.如图，程序框图的输出结果为－18，那么判断框①表示的“条件”应该是（ ） A. ?10>i B ．?9>i C ．?8>i D ．?7>i
9.设点o 在ABC ∆内部，且有230OA OB OC ++=
，则ABC ∆的
面积与AOC ∆的面积的比为（ ）
A
B
D
C
A. 2
C. 3
10.矩形ABCD 中，4,3AB BC ==，沿AC 将矩形ABCD 折成 一个直二面角B AC D --，则四面体ABCD 的外接球的体积为（ ）
A.
12512π B.1259π C.1256π D.1253
π 11.函数ln ||
|
x x y x =的图像可能是（ ）
12.数列
{}n a 满足⎩⎨
⎧<-+≥-=+,
,2,
,1
t a a t t a t a a n
n n n n 当11+<<t a t （其中2>t ）时有)(*N k a a n k n ∈=+，则k 的最小值为 （ ）
A. 10
B. 8
C. 6
D. 4 二.填空题（每小题5分，共4小题，总分20分）
13.设xdx n sin 420
∫
=
π,则
ｎ
）－（x
1
x 2展开式中的常数项为 14.如图,正六边形ABCDEF 的两个顶点A,D 为双曲线的焦点,其余四个 顶点都在双曲线上,则该双曲线的离心率为 .
15.记约束条件⎪⎩
⎪
⎨⎧+-≤>>n nx y y x 300）（*∈N n 所表示的平面区域内的整点个数为n a ，则
数列{}
n a 的前n 项和=n s 16. 函数)2,0∈,cos sin 2cos sin )(π［x x
x x
x x f ++•=
的最小值为
三.解答题（17—21题每题12分，选做题10分，总分70分） 17.(本小题满分12分)
如图，平面四边形ABCD 中，AB =AD =
CD =，30CBD ∠= ，120BCD ∠= ，求：
（Ⅰ）ADB ∠；
（Ⅱ）ADC ∆的面积S . 18.(本小题满分12分)
如图,四棱锥P-ABCD 中,底面ABCD 为矩形,PA ⊥平面ABCD,
y y y y
E 为PD 的中点. (1)证明:PB ∥平面AEC.
(2)设二面角D-AE-C 为60°求三棱锥E-ACD 的体积. 19.(本小题满分12分)
第31届夏季奥林匹克运动会将于2016年8月5日—21日在巴西里约热内卢举行.下表是近五届奥运会中国代表团和俄罗斯代表团获得的金牌数的统计数据（单位：枚）.
（Ⅰ）根据表格中两组数据完成近五届奥运会两国代表团获得的金牌数的茎叶图，并通过茎叶图比较两国代表团获得的金牌数的平均值及分散程度（不要求计算出具体数值，给出结论即可）；
（Ⅱ）甲、乙、丙三人竞猜今年中国代表团和俄罗斯代表团中的哪一个获得的金牌数多（假设两国代表团获得的金牌数不会相等），规定甲、乙、丙必须在两个代表团中选一个，已知甲、乙猜中国代表团的概率都为
45，丙猜中国代表团的概率为3
5
，三人各自猜哪个代表团的结果互不影响.现让甲、乙、丙各猜一次，设三人中猜中国代表团的人数为X ，求X 的分布列及数学期望EX .
20.(本小题满分12分)
已知抛物线2
:2C y px =经过点(2,2)M ，C 在点M 处的切线交x 轴于点N ，直线1l 经过点N 且垂直于
x 轴.
（Ⅰ）求线段ON 的长；
（Ⅱ）设不经过点M 和N 的动直线2:l x my b =+交C 于点A 和B ，交1l 于点E ，若直线MA 、ME 、MB 的斜率依次成等差数列，试问：2l 是否过定点？请说明理由. 21.(本小题满分12分)
已知函数()x
f x e =（ 2.71828e =⋅⋅⋅是自然对数的底数）,()ln(1)
g x x =+. （1）若()()()F x f x g x =-，求()F x 的极值； （2）对任意0,x ≥证明：()(1)f x g x >+；
（3）对任意0,x ≥都有成立，求实数a 的取值范围. 请考生在第22.23.24题中任选一题作答，若多做，则按所做的第一题计分，每题共10分． 22.几何证明选讲
如图，AB 是⊙O 的直径，C 、F 是⊙O 上的两点， OC ⊥AB ，过点F 作⊙O 的切线FD 交AB 的延长线于 点D ．连接CF 交AB 于点E ． （1）求证：DE 2=DB •DA ； （2）若DB =2，DF =4，试求CE 的长．
23.坐标系与参数方程
已知曲线C 的极坐标方程为ρ=4cos θ，以极点为原点，极轴为x 轴正半轴建立平面直角坐标系，设直线l 的
参数方程为（t 为参数）．
（1）求曲线C 的直角坐标方程与直线l 的普通方程；
（2）设曲线C 与直线l 相交于P 、Q 两点，以PQ 为一条边作曲线C 的内接矩形，求该矩形的面积．
24.不等式选讲
已知定义在R 上的函数()|1||2|f x x x =++-的最小值为a ． (1)求a 的值；
(2)若,,p q r 是正实数，且满足p q r a ++=，求证：222
3p q r ++≥．
2016年山西省祁县中学校高三月考 数学试题（理科）参考答案
二. 填空题（每小题5分，共4小题，总分20分）
13. 24 14.
115.
2
)
1(3+n n 16. －２ 三.解答题（17—21题每题12分，选做题10分，总分70分） (17) 【解析】（Ⅰ）在BCD ∆中，由正弦定理得：
sin 3sin CD BD BCD CBD =
⋅∠==∠， ……………2分
在ABD ∆中，由余弦定理得：
222
cos 2AD BD AB ADB AD BD
+-∠=
⋅
==
………4分 所以45ADB ∠= ……………6分 （Ⅱ）因为30CBD ∠= ，120BCD ∠= ，所以30CDB ∠=
因为sin sin(4530)ADC ∠=+= ……………8分 所以1
sin 2
S AD CD ADC =
⋅⋅∠
12=
⨯=
……………12分 18.解：(1)设AC 的中点为G,连接EG.在三角形PBD 中,中位线EG ∥PB,且EG 在平面AEC 上,所以PB ∥平面
AEC.
(2)设CD=m,分别以AD,AB,AP 为x,y,z 轴建立坐标系,则
12⎫
⎪⎪⎝
⎭
所以AD
AE
=12⎫
⎪⎪⎝⎭
,
AC
=)
,0m .
设平面ADE 的法向量为1n =(x 1,y 1,z 1),则1n AD ⋅ =0, 1n AE ⋅
=0,。