最新北师大版九年级数学下册1.1锐角三角函数公开课优质PPT课件(1)
合集下载
2019春九年级下册北师大版数学课件：1.1.锐角三角函数(1)(共15张PPT)
反本节课从梯子的倾斜程度谈起,通过探索直 角三角形中边角关系,得出了直角三角形中的锐角确 定后,它的对边比与邻边的比也随之确定,在直角三 角形中定义了正切的概念,接着,了解了坡面的倾斜 程度与正切的关系.
北师版·九年级数学·下册
1. 锐角三角函数
第一课时
1.经历探索直角三角形中某锐角确定后其对边与邻 边的比值也随之确定的过程,理解正切的意义. 2.能够用表示直角三角形中两边的比,表示生活中物 体的倾斜程度,并能够用正切进行简单的计算.
重点：理解锐角三角函数正切的意义,用正切表示倾 斜程度、坡度. 难点：从现实情境中理解正切的意义.
5
例2：在Rt△ABC中,∠C=90°,AC=4,BC=3,求tanA 和tanB.
解： tan A
BC 3 , AC 4
AC 4 tan B . BC 3
D
C
C
解： (1) tan A
a 7 , b 24
b 24 tan B . a 7
(2) b c2 a2 52 32 4, a 3 b 4 tan A , tan B . b 4 a 3 7 a 42 a 3 14, (3) tan A , a 6 b 3 3 b 7 1 6 14 S ABC ab 42 . 2 2
阅读课本内容，了解本节主要内容.
对边
A的对边 A的邻边
邻边
随之变化
陡
AC
BC 陡
h l
在直角三角形中,知道一边和一个锐角,你能求出其 它的边和角吗？猜一猜,这座古塔有多高？那你能运用所 学的数学知识测出这座古塔的高吗？
1
2
A
B
新北师大版九年级数学下册《三角函数的计算》优质ppt教学课件
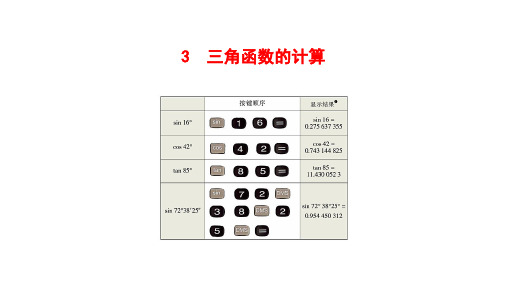
上表的显示结果是以“度”为单位的，再按 ˚ ′ ″ 键即可显示 以“度、分、秒”为单位的结果.
根据上述方法你能求出问题1中∠A的大小吗？
sin A = 1 = 0.25. 按键顺序和显示结果为
4
SHIFT sin 0 · 2 5 = 14.477 512 19°
再按 ° ′ ″ 键可显示14˚28′39″，所以∠A=14˚28′39″.
正弦值随着角度的增大（或减小）而增大（或减小）； 余弦值随着角度的增大（或减小）而减小（或增大）； 正切值随着角度的增大（或减小）而增大（或减小）.
知识点1 利用计算器求锐角三角函数值
1.如图,在△ABC中,∠ACB=90°,∠ABC=26°,BC=5.若用科学计算器 求边AC的长,则下列按键顺序正确的是( D )
D 39°
E
45°
C
A
【解析】（1）由题意，AC＝AB＝610 米.
（2）DE＝AC＝610米，
在Rt△BDE中，tan∠BDE＝ BE ，
DE
故BE＝DEtan39°． 因为CD＝AE，
所以CD＝AB－DE·tan 39°
＝610－610×tan 39°≈116（米）. 答：大楼的高度CD约为116 米．
B．sin65°54′-sin35°54′=sin30°
C．2sin15°30′=sin31°
D．sin72°18′-sin12°18′=sin47°42′
•2. 已知sin α＝1 ，求α，若用科学计算器计算且结果以“度、分、秒
2
”为单位，最后按键(D )
•A．AC/ON
B. SHIFT
C．MODE
(4)sin18°＋cos55°－tan59°≈－0.7817.
1.1锐角的三角函数第1课时正切与坡度课件(共33张PPT)北师大版九年级数学下册
在图中，梯子的倾斜程度与 tanA 有关系吗？
梯子的倾斜程度与tanA有关系吗？
tanA的值越大， 梯子越陡.
A
B1 B2
C2
C1
归纳总结
在 Rt△ABC 中，如果锐角 A 确定，那么 ∠A
的对边与邻边的比便随之确定，这个比叫做 ∠A
的正切，记作 tanA，即 tanA =
∠A的对边 ∠A的邻边
1.5
D
C
4
2. 如图，某人从山脚下的点A走了200m后到达山顶的点B. 已知点B到山脚的垂直距离为55m，求山坡的坡度. (结果精确到0.001m)
B
A
C
解 tan A BC = 55 ≈0.286. AC 2002 552
1. 在 Rt△ABC中，∠C= 90°，AC=5，AB= 13，求tan A 和tan B.
(2)
B1C1 AC1
和
B2C2 AC2
有什么关系？B1C1 B2C2
AC1 AC2
B3
B2
B1
(3) 如果改变 B2 在梯子上的位置. A C3 C2 C1
(如 B3C3 )呢？Rt△AB1C1∽Rt△AB2C2∽ Rt△AB3C3
议一议
B1C1 B2C2 B3C3 AC1 AC2 AC3
相似三角形的 对应边成比例
E
A 6m
4m
2m
B
CF 3m D
问题2 ：在下图中，梯子 AB 和 EF 哪个更陡？ 你是怎样判断的？
当铅直高度与水平宽度的比越大，梯子越陡.
倾斜角越大，梯子越陡.
A
E
总结：铅直高度与水平宽度
的比和倾斜角的大小都可用
4m
3.5 m
北师大版本九年级下册锐角三角函数精品课件PPT
老师寄语： 同学们，用你们的智慧发现数学；
用你们的聪明让数学服务生活！
再见
北师大版本九年级下册 1.1 锐角三角函数（第2课时）
1、在困境中时刻把握好的机遇的才能 。我在 想，假 如这个 打算是 我往履 行那结 果必定 失败， 由于我 在作决 策以前 会把患 上失的 因素斟 酌患上 太多。
2、人物作为支撑影片的基本骨架，在 影片中 发挥着 不可替 代的作 用，也 是影片 的灵魂 ，阿甘 是影片 中的主 人公， 是支撑 起整个 故事的 重要人 物，也 是给人 最大启 示的人 物。
如图,梯子的倾 斜程度与sinA和 cosA有关吗?
结论:梯子的倾斜程度与sinA和cosA有关: sinA越大,梯子越陡;cosA越小,梯子越陡.
北师大版本九年级下册 1.1 锐角三角函数（第2课时）
北师大版本九年级下册 1.1 锐角三角函数（第2课时）
例题
C
例1：如图:在Rt△ABC中,∠B=900,AC=200,
sin B .
C
┌
A
DB
北师大版本九年级下册 1.1 锐角三角函数（第2课时）
北师大版本九年级下册 1.1 锐角三角函数ABC中,AB=AC=5,BC=6. 5
求: sinB,cosB,tanB.
B
5 C
D
2.在Rt△ABC中,∠C=900,BC=20,sin A 4 .
若ＡC=5,CD=3,求sinB的值. A
C DB
北师大版本九年级下册 1.1 锐角三角函数（第2课时）
转化等角
北师大版本九年级下册 1.1 锐角三角函数（第2课时）
随堂小练
1.判断: 如图 (1) sinA= BC （
AB
(2) sinB= B C （
用你们的聪明让数学服务生活！
再见
北师大版本九年级下册 1.1 锐角三角函数（第2课时）
1、在困境中时刻把握好的机遇的才能 。我在 想，假 如这个 打算是 我往履 行那结 果必定 失败， 由于我 在作决 策以前 会把患 上失的 因素斟 酌患上 太多。
2、人物作为支撑影片的基本骨架，在 影片中 发挥着 不可替 代的作 用，也 是影片 的灵魂 ，阿甘 是影片 中的主 人公， 是支撑 起整个 故事的 重要人 物，也 是给人 最大启 示的人 物。
如图,梯子的倾 斜程度与sinA和 cosA有关吗?
结论:梯子的倾斜程度与sinA和cosA有关: sinA越大,梯子越陡;cosA越小,梯子越陡.
北师大版本九年级下册 1.1 锐角三角函数（第2课时）
北师大版本九年级下册 1.1 锐角三角函数（第2课时）
例题
C
例1：如图:在Rt△ABC中,∠B=900,AC=200,
sin B .
C
┌
A
DB
北师大版本九年级下册 1.1 锐角三角函数（第2课时）
北师大版本九年级下册 1.1 锐角三角函数ABC中,AB=AC=5,BC=6. 5
求: sinB,cosB,tanB.
B
5 C
D
2.在Rt△ABC中,∠C=900,BC=20,sin A 4 .
若ＡC=5,CD=3,求sinB的值. A
C DB
北师大版本九年级下册 1.1 锐角三角函数（第2课时）
转化等角
北师大版本九年级下册 1.1 锐角三角函数（第2课时）
随堂小练
1.判断: 如图 (1) sinA= BC （
AB
(2) sinB= B C （
北师大版数学九年级下 1.1锐角三角函数(第2课时) 教学课件(共21张PPT)
A.扩大100倍 B.缩小100倍
B
C.不变 D.不能确定
4.已知∠A,∠B为锐角
A
┌ C
(1)若∠A=∠B,则sin A = sin B;
(2)若sin A=sin B,则∠A = ∠B.
随堂训练
5.如图, ∠C=90°，CD⊥AB.
sin B= ((—CB—CD))= ((—AA—CB)) = ((—AADC—)) .
A
3 4┌
C
tan A BC 3 . AC 4
老师提示: 求锐角三角函数时,勾股定理的运用是很重要的.
课堂小结
锐角三角函数定义:
tanA
A的对边 A的邻边
=
sinA=
A的对边 斜边
cosA=
A的邻边 斜边
B 斜边
∠A的对边 ┌ A ∠A的邻边 C
请思考:在Rt△ABC中, sinA和cosB有什么关系?
记作cosA,即 cosA= A的邻边
B
A的斜边 斜边
锐角A的正弦、余弦、正切都
∠A的对边
是∠A的三角函数.
┌ A ∠A的邻边 C
知识讲解
• 定义中应该注意的几个问题:
1.sinA,cosA,tanA是在直角三角形中定义的,∠A是锐角 (注意数形结合,构造直角三角形).
2.sinA,cosA,tanA各是一个完整的符号,分别表示∠A的 正弦、余弦和正切,记号中习惯省去“∠”；
谢谢观赏
You made my day!
解:在Rt△ABC中,
sin A BC BC 0.6, AC 200
BC 2000.6 120.
分析: 根据锐角的正弦等于对边比斜边建立方程即可。
小组活动：请你求出cosA,tanA,sinC,cosC和tanC的值.
北师大版九年级数学下册锐角三角函数精品课件PPT1
B
∠A的对边 ┌ C
3.只有不断的思考,才会有新的发现;只有 量的变化,才会有质的进步.
北 师 大 版 九 年 级数 学下册 1 .1 锐 角 三 角函数 课 件
▪
1、在困境中时刻把握好的机遇的才能 。我在 想，假 如这个 打算是 我往履 行那结 果必定 失败， 由于我 在作决 策以前 会把患 上失的 因素斟 酌患上 太多。
1、再Rt△ＡＣＢ，Rt△ＤＥＦ中，∠Ｂ＝300， ∠Ｄ＝450， ∠Ｃ＝900，∠Ｆ＝ 900，
若ＡＢ＝ＤＥ＝２，
（１）求∠Ｂ的对边与斜边的比值；
（２）求∠Ａ的对边与斜边的比值；
（３）求∠Ｄ的对边与斜边的比值．
Ａ
Ｄ
北 师 大 版 九 年 级数 学下册 1 .1 锐 角 三 角函数 课 件
Ｃ
ＢＦ
Ｅ
例 北师大版 九年级数学下册 1.1 锐角三角函数 课件
那么
B与C
B 有' C 什' 么关系．你能解释一下吗？
AB
A'B '
B' B
A
C
A'
C'
在图中，由于∠C＝∠C'＝90°，∠A＝∠A'＝α，所以 Rt△ABC∽Rt△A'B'C'
BC AB BC B'C' B'C' A' B' AB A' B'
这就是说，在直角三角形中，当锐角A的度数一定时，不管三角 形的大小如何，∠A的对边与斜边的比也是一个固定值．并且直角 三角形中一个锐角的度数越大，它的对边与斜边的比值越大
北 师 大 版 九 年 级数 学下册 1 .1 锐 角 三 角函数 课 件
北师大版九年级数学下册锐角三角函数精品课件PPT
北师大版九年级数学下册 1.1.2锐角三角函数（第2课时）
•
1、在困境中时刻把握好的机遇的才能 。我在 想，假 如这个 打算是 我往履 行那结 果必定 失败， 由于我 在作决 策以前 会把患 上失的 因素斟 酌患上 太多。
•
2、人物作为支撑影片的基本骨架，在 影片中 发挥着 不可替 代的作 用，也 是影片 的灵魂 ，阿甘 是影片 中的主 人公， 是支撑 起整个 故事的 重要人 物，也 是给人 最大启 示的人 物。
感谢观看，欢迎指导！
[环节四] 一个锐角的正弦与它余角的余弦的关系
北师大版九年级数学下册 1.1.2锐角三角函数（第2课时）
北师大版九年级数学下册 1.1.2锐角三角函数（第2课时）
sinA cosA
90°
cosC sinC
“一个锐角的正弦等于它余角的余弦”“一个 锐角的余弦等于它余角的正弦”
北师大版九年级数学下册 1.1.2锐角三角函数（第2课时）
从而发现了什么？
这是一个变化的过程.对边与斜边的比值、邻边与 斜边的比值都随着倾斜角的改变而改变，同时，如果给 定一个倾斜角的值，它的对边与斜边的比值，邻边与斜 边的比值是唯一确定的.这是一种函数关系。
北师大版九年级数学下册 1.1.2锐角三角函数（第2课时）
北师大版九年级数学下册 1.1.2锐角三角函数（第2课时） 北师大版九年级数学下册 1.1.2锐角三角函数（第2课时）
2、如图，在△ABC中，AD是BC边上的高， tanB=cos∠DAC （1）求证：AC=BD （2）若SinC=，BC=9，求AD。
北师大版九年级数学下册 1.1.2锐角三角函数（第2课时）
北师大版九年级数学下册 1.1.2锐角三角函数（第2课时）
3、如图，菱形ABCD中，AE⊥BC于E点，EC=1， sinB=5 /13 ，求四边形ABCD的周长和面积。
•
1、在困境中时刻把握好的机遇的才能 。我在 想，假 如这个 打算是 我往履 行那结 果必定 失败， 由于我 在作决 策以前 会把患 上失的 因素斟 酌患上 太多。
•
2、人物作为支撑影片的基本骨架，在 影片中 发挥着 不可替 代的作 用，也 是影片 的灵魂 ，阿甘 是影片 中的主 人公， 是支撑 起整个 故事的 重要人 物，也 是给人 最大启 示的人 物。
感谢观看，欢迎指导！
[环节四] 一个锐角的正弦与它余角的余弦的关系
北师大版九年级数学下册 1.1.2锐角三角函数（第2课时）
北师大版九年级数学下册 1.1.2锐角三角函数（第2课时）
sinA cosA
90°
cosC sinC
“一个锐角的正弦等于它余角的余弦”“一个 锐角的余弦等于它余角的正弦”
北师大版九年级数学下册 1.1.2锐角三角函数（第2课时）
从而发现了什么？
这是一个变化的过程.对边与斜边的比值、邻边与 斜边的比值都随着倾斜角的改变而改变，同时，如果给 定一个倾斜角的值，它的对边与斜边的比值，邻边与斜 边的比值是唯一确定的.这是一种函数关系。
北师大版九年级数学下册 1.1.2锐角三角函数（第2课时）
北师大版九年级数学下册 1.1.2锐角三角函数（第2课时） 北师大版九年级数学下册 1.1.2锐角三角函数（第2课时）
2、如图，在△ABC中，AD是BC边上的高， tanB=cos∠DAC （1）求证：AC=BD （2）若SinC=，BC=9，求AD。
北师大版九年级数学下册 1.1.2锐角三角函数（第2课时）
北师大版九年级数学下册 1.1.2锐角三角函数（第2课时）
3、如图，菱形ABCD中，AE⊥BC于E点，EC=1， sinB=5 /13 ，求四边形ABCD的周长和面积。
北师大版九年级数学下册第一章 《30度,45度,60度角的三角函数值 》优课件
450 ┌
300
600 ┌
w请与同伴交流你是怎么想的?又是怎么做的?
做一做P10 3
知识在于积累
w(5)sin450,sin600等于多少? w(6)cos450,cos600等于多少?
学.科.网
w(7)tan450,tan600等于多少?
驶向胜利 的彼岸
300 450
450 ┌ 600 ┌
做一做P11 4
九年级数学(下)第一章
直角三角形的边角关系
zxxkw
第二节 30°45°60°角的三角函数
学.科.网
回顾与思考1
锐角三角函数定义
驶向胜利 的彼岸
w直角三角形中边与角的关系:锐角三角函数.
w在直角三角形中,若一个锐角确定,那么这个角的对边,
邻边和斜边之间的比值也随之确定.
sin A a , cos A b ,
w例2 如图:一个小孩荡秋千,秋千链子的长度
为2.5m,当秋zxxkw千向两边摆动时,摆角恰好为600,
且两边摆动的角度相同,求它摆至最高位置时与
其摆至最低位置时的高度之差(结果精确到
0.01m). w解:如图,根据题意可知,
∠AOD 1600 300, OD=2.5m,
O
2
cos300
OC,
O C OcO D o D 30 s0 2.532.16 (m )5.
c
c
B
sin B b , cosB a ,
c
c
c a
┌
sinA和cosB,有什么关系?
A
b
C
sinA=cosB,
想一想P10 2
本领大不大
悟心来当家
驶向胜利 的彼岸