2018届人教B版(理) 平面向量的概念与线性运算 单元测试
人教B版(理科数学) 平面向量名师精编单元测试

点睛:求两个向量的数量积有三种方法:利用定义;利用向量的坐标运算;利用数量积的几何意义.具体应用时可根据已知条件的特征来选择,同学时要注意数量积运算律的应用.
3.【2018年理新课标I卷】设抛物线C:y2=4的焦点为F,过点(–2,0)且斜率为 的直线与C交于M,N两点,则 =
由 得 因此 的最小值为圆心 到直线 的距离 减去半径1,为 选A.
点睛:以向量为载体求相关变量的取值范围,是向量与函数、不等式、三角函数、曲线方程等相结合的一类综合问题.通过向量的坐标运算,将问题转化为解方程、解不等式、求函数值域或直线与曲线的位置关系,是解决这类问题的一般方法.
2.【2018年理数天津卷】如图,在平面四边形ABCD中, , , , .若点E为边CD上的动点,则 的最小值为
(2)用向量基本定理解决问题的一般思路是:先选择一组基底,并运用该基底将条件和结论表示成向量的形式,再通过向量的运算来解决.
2.【2017北京,理6】设m,n为非零向量,则“存在负数 ,使得 ”是“ ”的
(A)充分而不必要条件(B)必要而不充分条件
(C)充分必要条件(D)既不充分也不必要条件
【答案】A
详解:由题可得 , , ,即 ,故答案为
点睛:本题主要考查向量的坐标运算,以及两向量共线的坐标关系,属于基础题。
2017年高考全景展示
1.【2017课标3,理12】在矩形ABCD中,AB=1,AD=2,动点P在以点C为圆心且与BD相切的圆上.若 = + ,则 + 的最大值为
A.3B.2 C. D.2
4.【2018年理新课标I卷】在△ 中, 为 边上的中线, 为 的中点,则
A. B. C. D.
最新-2018高三数学总复习 5-1平面向量的概念与线性运
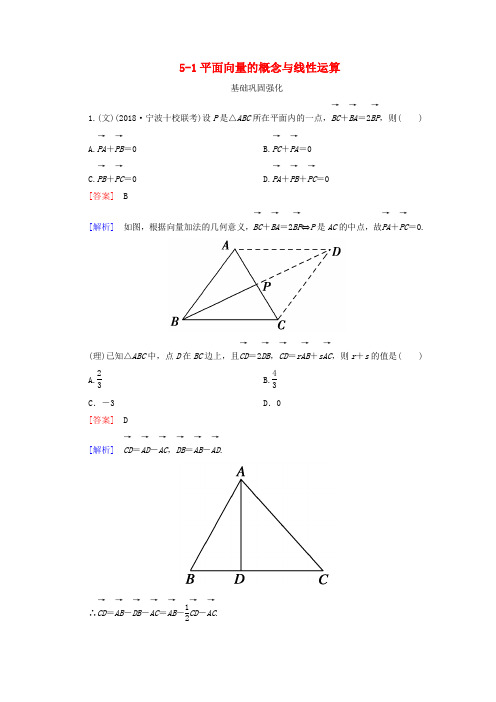
5-1平面向量的概念与线性运算基础巩固强化1.(文)(2018·宁波十校联考)设P 是△ABC 所在平面内的一点,BC →+BA →=2BP →,则( )A.PA →+PB →=0 B.PC →+PA →=0 C.PB →+PC →=0 D.PA →+PB →+PC →=0[答案] B[解析] 如图,根据向量加法的几何意义,BC →+BA →=2BP →⇔P 是AC 的中点,故PA →+PC →=0.(理)已知△ABC 中,点D 在BC 边上,且CD →=2DB →,CD →=rAB →+sAC →,则r +s 的值是( )A.23B.43 C .-3 D .0[答案] D[解析] CD →=AD →-AC →,DB →=AB →-AD →.∴CD →=AB →-DB →-AC →=AB →-12CD →-AC →.∴32CD →=AB →-AC →, ∴CD →=23AB →-23AC →.又CD →=rAB →+sAC →,∴r =23,s =-23,∴r +s =0.2.(2018·四川理,7)设a 、b 都是非零向量,下列四个条件中,使a |a |=b|b |成立的充分条件是( )A .a =-bB .a ∥bC .a =2bD .a ∥b 且|a |=|b |[答案] C[解析] 本小题考查共线向量、单位向量、向量的模等基本概念. 因a |a |表示与a 同向的单位向量,b |b |表示与b 同向的单位向量,要使a |a |=b|b |成立,则必须a 与b 同向共线,所以由a =2b 可得出a|a |=b|b |.[点评] a =-b 时,a 与b 方向相反;a ∥b 时,a 与b 方向相同或相反.因此A 、B 、D 都不能推出a |a |=b|b |.3.已知向量a =(1,3),b =(3,n ),若2a -b 与b 共线,则实数n 的值是( ) A .3+2 3 B .9 C .6 D .3-2 3[答案] B[解析] 2a -b =(-1,6-n ),∵2a -b 与b 共线,∴-1×n -(6-n )×3=0, ∴n =9.4.设平面内有四边形ABCD 和点O ,若OA →=a ,OB →=b ,OC →=c ,OD →=d ,且a +c =b +d ,则四边形ABCD 为( )A .菱形B .梯形C .矩形D .平行四边形 [答案] D[解析] 解法一:设AC 的中点为G ,则OB →+OD →=b +d =a +c =OA →+OC →=2OG →,∴G 为BD 的中点,∴四边形ABCD 的两对角线互相平分,∴四边形ABCD 为平行四边形.解法二:AB →=OB →-OA →=b -a , CD →=OD →-OC →=d -c =-(b -a )=-AB →,∴AB 綊CD ,∴四边形ABCD 为平行四边形.5.设OA →=e 1,OB →=e 2,若e 1与e 2不共线,且点P 在线段AB 上,|APPB |=4,如图所示,则OP →=( )A.15e 1-25e 2B.25e 1+15e 2C.15e 1+45e 2D.25e 1-15e 2 [答案] C[解析] AP →=4PB →,∴AB →=AP →+PB →=5PB →, OP →=OB →+BP →=OB →-15AB →=OB →-15(OB →-OA →)=45OB →+15OA →=15e 1+45e 2.6.P 是△ABC 内的一点,AP →=13(AB →+AC →),则△ABC 的面积与△ABP 的面积之比为( )A .2B .3 C.32 D .6[答案] B[解析] 由AP →=13(AB →+AC →),得3AP →=AB →+AC →,∴PB →+PC →+PA →=0,∴P 是△ABC 的重心. ∴△ABC 的面积与△ABP 的面积之比为3.7.(2018·福建省惠安三中模拟)已知向量a =(2x +1,4),b =(2-x,3),若a ∥b ,则实数x 的值等于________.[答案] 12[解析] ∵a ∥b ,∴3(2x +1)-4(2-x )=0,∴x =12.8.已知点A (2,3),C (0,1),且AB →=-2BC →,则点B 的坐标为________.[答案] (-2,-1)[解析] 设点B 的坐标为(x ,y ),则有AB →=(x -2,y -3),BC →=(-x,1-y ),因为AB →=-2BC →,所以⎩⎪⎨⎪⎧x -2=2x ,y -3=--y ,解得x =-2,y =-1.9.(2018·东北三省四市联考)在△ABC 中,AB =2AC =2,AB →·AC →=-1,若AO →=x 1AB →+x 2AC →(O 是△ABC 的外心),则x 1+x 2的值为________.[答案]136[解析] O 为△ABC 的外心,AO →=x 1AB →+x 2AC →,AO →·AB →=x 1AB →·AB →+x 2AC →·AB →,由向量数量积的几何意义,AO →·AB →=12|AB →|2=2,∴4x 1-x 2=2,①又AO →·AC →=x 1AB →·AC →+x 2AC →·AC →,∴-x 1+x 2=12,②联立①②,解得x 1=56,x 2=43,∴x 1+x 2=136.10.设两个非零向量a 与b 不共线,(1)若AB →=a +b ,BC →=2a +8b ,CD →=3(a -b ).求证:A 、B 、D 三点共线; (2)试确定实数k ,使k a +b 和a +k b 共线.[解析] (1)证明:∵AB →=a +b ,BC →=2a +8b ,CD →=3(a -b ), ∴BD →=BC →+CD →=2a +8b +3(a -b )=5(a +b )=5AB →. ∴AB →、BD →共线,又它们有公共点B ,∴A 、B 、D 三点共线. (2)解:∵k a +b 与a +k b 共线, ∴存在实数λ,使k a +b =λ(a +k b ), ∴(k -λ)a =(λk -1)b .∵a 、b 是不共线的两个非零向量,∴k -λ=λk -1=0,∴k 2-1=0.∴k =±1.能力拓展提升11.(2018·珠海调研)已知△ABC 及其平面内点M 满足MA →+MB →+MC →=0,若存在实数m 使得AB →+AC →=mAM →成立,则m 等于( )A .2B .3C .4D .5 [答案] B[解析] 解法1:由已知条件MB →+MC →=-MA →.如图,延长AM 交BC 于D 点,则D 为BC 的中点.延长BM 交AC 于E ,延长CM 交AB 于F ,则E 、F 分别为AC 、AB 的中点,即M 为△ABC 的重心.AM →=23AD →=13(AB →+AC →),即AB →+AC →=3AM →,则m =3.解法2:∵AB →+AC →=MB →-MA →+MC →-MA →=MB →+MC →-2MA →=mAM →,∴MB →+MC →=(m -2)AM →, ∵MA →+MB →+MC →=0,∴(m -2)AM →=AM →,∴m =3.12.如图,在△ABC 中,AD =DB ,AE =EC ,CD 与BE 交于F ,设AB →=a ,AC →=b ,AF →=x a +y b ,则(x ,y )为( )A .(12,12)B .(23,23)C .(13,13)D .(23,12)[答案] C[解析] 解法1:令BF →=λBE →,由题可知:AF →=AB →+BF →=AB →+λBE →=AB →+λ(12AC →-AB →)=(1-λ)AB →+12λAC →;同理,令CF →=μCD →,则AF →=AC →+CF →=AC →+μCD →=AC →+μ(12AB →-AC →)=12μAB→+(1-μ)·AC →,平面向量基本定理知对应系数相等,可得⎩⎪⎨⎪⎧1-λ=12μ,12λ=1-μ,解得⎩⎪⎨⎪⎧λ=23,μ=23.所以AF →=13AB →+13AC →,故选C.解法2:设CF →=λCD →,∵E 、D 分别为AC 、AB 的中点, ∴BE →=BA →+AE →=-a +12b ,BF →=BC →+CF →=(b -a )+λ(12a -b )=⎝ ⎛⎭⎪⎫12λ-1a +(1-λ)b , ∵BE →与BF →共线,a 、b 不共线, ∴12λ-1-1=1-λ12,∴λ=23,∴AF →=AC →+CF →=b +23CD →=b +23⎝ ⎛⎭⎪⎫12a -b =13a +13b ,故x =13,y =13. 13.在△ABC 中,已知D 是AB 边上一点,若AD →=2DB →,CD →=13CA →+λCB →,则λ=________.[答案] 23[解析]由图知CD →=CA →+AD →,①CD →=CB →+BD →,②且AD →+2BD →=0.①+②×2得:3CD →=CA →+2CB →, ∴CD →=13CA →+23CB →,∴λ=23.14.(2018·吉林省延吉市质检)已知:|OA →|=1,|OB →|=3,OA →·OB →=0,点C 在∠AOB 内,且∠AOC =30°,设OC →=mOA →+nOB →(m ,n ∈R +),则mn=________.[答案] 3[解析] 设mOA →=OF →,nOB →=OE →,则OC →=OF →+OE →,∵∠AOC =30°,∴|OC →|·cos30°=|OF →|=m |OA →|=m , |OC →|·sin30°=|OE →|=n |OB →|=3n ,两式相除得:m3n=|OC →|cos30°|OC →|sin30°=1tan30°=3,∴mn =3.15.已知向量OA →=(3,-4),OB →=(6,-3),OC →=(5-m ,-3-m ). (1)若A 、B 、C 三点共线,求实数m 的值; (2)若∠ABC 为锐角,求实数m 的取值范围.[解析] (1)已知向量OA →=(3,-4),OB →=(6,-3),OC →=(5-m ,-(3+m )). ∴AB →=(3,1),AC →=(2-m,1-m ), ∵A 、B 、C 三点共线,∴AB →与AC →共线,∴3(1-m )=2-m ,∴m =12.(2)由题设知BA →=(-3,-1),BC →=(-1-m ,-m )∵∠ABC 为锐角,∴BA →·BC →=3+3m +m >0⇒m >-34又由(1)可知,当m =12时,∠ABC =0°故m ∈⎝ ⎛⎭⎪⎫-34,12∪⎝ ⎛⎭⎪⎫12,+∞. 16.(文)已知a =(2x -y +1,x +y -2),b =(2,-2), (1)当x 、y 为何值时,a 与b 共线?(2)是否存在实数x 、y ,使得a ⊥b ,且|a |=|b |?若存在,求出xy 的值;若不存在,说明理由.[解析] (1)∵a 与b 共线, ∴存在非零实数λ使得a =λb ,∴⎩⎪⎨⎪⎧2x -y +1=2λ,x +y -2=-2λ,⇒⎩⎪⎨⎪⎧x =13,y ∈R .(2)由a ⊥b ⇒(2x -y +1)×2+(x +y -2)×(-2)=0⇒x -2y +3=0.① 由|a |=|b |⇒(2x -y +1)2+(x +y -2)2=8.②由①②解得⎩⎪⎨⎪⎧x =-1,y =1,或⎩⎪⎨⎪⎧x =53,y =73.∴xy =-1或xy =359.(理)已知点O (0,0)、A (1,2)、B (4,5),向量OP →=OA →+tAB →.(1)t 为何值时,点P 在x 轴上? (2)t 为何值时,点P 在第二象限?(3)四边形ABPO 能否为平行四边形?若能,求出t 的值;若不能,说明理由. (4)求点P 的轨迹方程.[解析] ∵OP →=OA →+tAB →=(1,2)+t (3,3) =(1+3t,2+3t ),∴P (1+3t,2+3t ). (1)∵P 在x 轴上,∴2+3t =0即t =-23.(2)由题意得⎩⎪⎨⎪⎧1+3t <0,2+3t >0.∴-23<t <-13.(3)∵AB →=(3,3),OP →=(1+3t,2+3t ). 若四边形ABPO 为平行四边形,则AB →=OP →,∴⎩⎪⎨⎪⎧1+3t =3,2+3t =3.而上述方程组无解,∴四边形ABPO 不可能为平行四边形.(4)∵OP →=(1+3t,2+3t ), 设OP →=(x ,y ),则⎩⎪⎨⎪⎧x =1+3t ,y =2+3t .∴x -y +1=0为所求点P 的轨迹方程.1.在四边形ABCD 中,AB →=a +2b ,BC →=-4a -b ,CD →=-5a -3b ,其中a 、b 不共线,则四边形ABCD 为( )A .梯形B .平行四边形C .菱形D .矩形[答案] A[解析] 由已知得AD →=AB →+BC →+CD →=-8a -2b ,故AD →=2BC →,由共线向量知识知AD ∥BC ,且|AD |=2|BC |,故四边形ABCD 为梯形,所以选A.2.已知|a |=3,|b |=1,且a 与b 同向共线,则a ·b 的值是( ) A .-3 B .0 C .3 D .-3或3 [答案] C[解析] ∵a 与b 同向共线,∴a ·b =|a |·|b |cos0=3,选C.3.已知O 是平面上一定点,A 、B 、C 是平面上不共线的三点,动点P 满足OP →=OA →+λ(AB→+AC →),λ∈[0,+∞),则点P 的轨迹一定通过△ABC 的( )A .外心B .垂心C .内心D .重心[答案] D[解析] 设AB →+AC →=AD →,则可知四边形BACD 是平行四边形,而AP →=λAD →表明A 、P 、D 三点共线.又D 在边BC 的中线所在直线上,于是点P 的轨迹一定通过△ABC 的重心.4.(2018·洛阳部分重点中学检测)如图所示,已知点G 是△ABC 的重心,过G 作直线与AB ,AC 两边分别交于M ,N 两点,且AM →=xAB →,AN →=yAC →,则x ·yx +y的值为( )A .3B.13C .2D.12[分析] 由M 、N 、G 三点共线知,存在实数λ、μ使AG →=λAM →+μAN →,结合条件AM →=xAB →,AN →=yAC →,可将AG →用AB →,AC →表示,又G 为△ABC 的重心,AG →用AB →,AC →表示的表示式唯一,可求得x ,y 的关系式.[答案] B[解析] 法1:由点G 是△ABC 的重心,知GA →+GB →+GC →=0,得-AG →+(AB →-AG →)+(AC →-AG →)=0,则AG →=13(AB →+AC →).又M 、N 、G 三点共线(A 不在直线MN 上),于是存在λ,μ∈R ,使得AG →=λAM →+μAN →(且λ+μ=1),则AG →=λx AB →+μy AC →=13(AB →+AC →),所以⎩⎪⎨⎪⎧λ+μ=1,λx =μy =13,于是得1x +1y =3,所以x ·y x +y =11x +1y=13.法2:特殊化法,利用等边三角形,过重心作平行于底边BC 的直线,易得x ·y x +y =13. 5.(2018·豫南四校调研考试)已知△ABD 是等边三角形,且AB →+12AD →=AC →,|CD →|=3,那么四边形ABCD 的面积为( )A.32B.332C .3 3 D.932[答案] B [解析]如图,由条件知,CD →=AD →-AC →=12AD →-AB →,∴CD →2=(12AD →-AB →)2,∴3=14AD →2+AB →2-AD →·AB →,∵|AD →|=|AB →|,∴54|AD →|2-|AD →|·|AB →|cos60°=3,解之得|AD →|=2.又BC →=AC →-AB →=12AD →,∴|BC →|=12|AD →|=1,∴|BC →|2+|CD →|2=|BD →|2,∴BC ⊥CD .∴S 四边形ABCD =S △ABD +S △BCD =12×22×sin60°+12×1×3=332,故选B.6.非零向量a =(sin θ,2),b =(cos θ,1),若a 与b 共线,则tan ⎝ ⎛⎭⎪⎫θ-π4=________.[答案] 13[解析] ∵非零向量a 、b 共线,∴存在实数λ,使a =λb ,即(sin θ,2)=λ(cos θ,1),∴λ=2,sin θ=2cos θ,∴tan θ=2,∴tan(θ-π4)=tan θ-11+tan θ=13.。
2018版高考数学(理)一轮复习题库:第五章第1讲平面向量的概念及其线性运算含解析

第1讲平面向量的概念及其线性运算一、选择题1。
已知两个非零向量a,b满足|a+b|=|a-b|,则下面结论正确的是()A.a∥bB.a⊥bC。
{0,1,3} D。
a+b=a-b答案B 2.对于非零向量a,b,“a+b=0”是“a∥b”的().A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件解析若a+b=0,则a=-b。
∴a∥b;若a∥b,则a=λb,a+b=0不一定成立.答案A3.已知O是△ABC所在平面内一点,D为BC边的中点,且2错误!+错误!+错误!=0,那么( ).A。
错误!=错误! B.错误!=2错误!C.错误!=3错误!D.2错误!=错误!解析由2错误!+错误!+错误!=0可知,O是底边BC上的中线AD的中点,故错误!=错误!。
答案A4.设A1,A2,A3,A4是平面直角坐标系中两两不同的四点,若错误!=λ错误!(λ∈R),错误!=μ错误!(μ∈R),且错误!+错误!=2,则称A3,A4调和分割A1,A2。
已知平面上的点C,D调和分割点A,B,则下列说法正确的是( ).A.C可能是线段AB的中点B.D可能是线段AB的中点C.C、D可能同时在线段AB上D.C、D不可能同时在线段AB的延长线上解析若A成立,则λ=错误!,而错误!=0,不可能;同理B也不可能;若C成立,则0<λ<1,且0<μ<1,错误!+错误!>2,与已知矛盾;若C,D同时在线段AB的延长线上时,λ>1,且μ>1,错误!+错误!<2,与已知矛盾,故C,D不可能同时在线段AB的延长线上,故D正确.答案D5.已知A,B,C是平面上不共线的三点,O是△ABC的重心,动点P满足错误!=错误!错误!,则点P一定为三角形ABC的().A.AB边中线的中点B.AB边中线的三等分点(非重心)C.重心D.AB边的中点解析设AB的中点为M,则错误!错误!+错误!错误!=错误!,∴错误!=错误!(错误!+2错误!)=错误!错误!+错误!错误!,即3错误!=错误!+2错误!,也就是错误!=2错误!,∴P,M,C三点共线,且P是CM上靠近C点的一个三等分点.答案B6.在四边形ABCD中,错误!=a+2b,错误!=-4a-b,错误!=-5a-3b,则四边形ABCD的形状是( ).A.矩形B.平行四边形C.梯形D.以上都不对解析由已知错误!=错误!+错误!+错误!=-8a-2b=2(-4a-b)=2错误!.∴错误!∥错误!,又错误!与错误!不平行,∴四边形ABCD是梯形.答案C二、填空题7.设a,b是两个不共线向量,错误!=2a+p b,错误!=a+b,错误!=a-2b,若A,B,D三点共线,则实数p的值为________.解析∵错误!=错误!+错误!=2a-b,又A,B,D三点共线,∴存在实数λ,使错误!=λ错误!。
2018《单元滚动检测卷》高考数学(理)(人教B版全国通用)单元滚动检测五 平面向量含解析

单元滚动检测五平面向量考生注意:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共4页.2.答卷前,考生务必用蓝、黑色字迹的钢笔或圆珠笔将自己的姓名、班级、学号填写在相应位置上.3.本次考试时间120分钟,满分150分.4.请在密封线内作答,保持试卷清洁完整.第Ⅰ卷(选择题共60分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.如图所示,四边形ABCD是梯形,AD∥BC,则错误!+错误!+错误!等于( )A.错误!B。
错误!C。
错误!D。
错误!2.设D为△ABC所在平面内一点,错误!=3错误!,则()A.错误!=-错误!错误!+错误!错误!B.错误!=错误!错误!+错误!错误!C。
错误!=错误!错误!-错误!错误! D.错误!=错误!错误!-错误!错误!3.已知点A(1,3),B(4,-1),则与向量错误!方向相反的单位向量是( )A.(-错误!,错误!) B.(-错误!,错误!)C.(错误!,-错误!)D.(错误!,-错误!)4.平面向量a与b的夹角为60°,a=(2,0),|b|=1,则|a+2b|等于( )A.错误!B.2错误!C.4 D.125.已知|错误!|=1,|错误!|=2,错误!·错误!=0,点D在∠CAB内,且∠DAB =30°,设错误!=λ错误!+μ错误!(λ,μ∈R),则错误!等于()A.3 B。
错误! C.错误!D.2错误!6.设O,A,B为平面上三点,且P在直线AB上,错误!=m错误!+n错误!,则m+n等于( )A.0 B.-1 C.1 D.不能确定7.△ABC的内角A,B,C所对边长分别是a,b,c,设向量n=(错误!a +c,sin B-sin A),m=(a+b,sin C),若m∥n,则角B的大小为( ) A。
错误!B。
错误!C。
错误! D.错误!8。
如图所示,△ABC中,∠ACB=90°,且AC=BC=4,点M满足错误!=3错误!,则错误!·错误!等于( )A.2 B.3C.4 D.69.已知向量a=(3,-2),b=(x,y-1),且a∥b,若x,y均为正数,则错误!+错误!的最小值是()A.错误!B。
新教材 人教B版高中数学必修第二册 6.1 平面向量及其线性运算 习题课件(精选配套习题,含解析)

6.1.1 向量的概念 6.1.2 向量的加法 P24 6.1.3 向量的减法 P43 6.1.4 数乘向量 P62 6.1.5 向量的线性运算 P83
——基础巩固—— 一、选择题(每小题 5 分,共 30 分) 1.下列说法正确的个数是( A ) ①温度、速度、位移、功这些物理量都是向量;②零向量没有方 向;③向量的模一定是正数;④非零向量的单位向量是唯一的. A.0 B.1 C.2 D.3 解析:①错误.只有速度、位移是向量.②错误.零向量有方向, 它的方向是不确定的.③错误.|0|=0.④错误.非零向量 a 的单位向 量有两个,一个与 a 同向,一个与 a 反向.
3.在矩形 ABCD 中,|A→B|=4,|B→C|=2,则向量A→B+A→D+A→C的 长度等于( B )
A.2 5 B.4 5 C.12 D.6
解析:根据平行四边形法则得A→B+A→D=A→C,所以A→B+A→D+A→C= 2A→C,所以向量A→B+A→D+A→C的长度等于 2|A→C|=2 42+22=4 5.
(1)D→G+E→A+C→B; (2)E→G+C→G+D→A+E→B.
解:(1)D→G+E→A+C→B=G→C+B→E+C→B=G→C+C→B+B→E=G→B+B→E= →
(2)E→G+C→G+D→A+E→B=E→G+G→D+D→A+A→E=E→D+D→A+A→E=E→A+ A→E=0.
11.(15 分)一艘船以 5 km/h 的速度向垂直于对岸方向行驶,航船 实际航行方向与水流方向成 30°角,求水流速度和船实际速度.
解析:(1)当 a+b=0 时,命题不成立,为假命题;(2)为真命题; (3)当 A,B,C 三点共线时,也可以有A→B+B→C+C→A=0,为假命题; (4)当 a,b 共线时,若 a,b 同向,则|a+b|=|a|+|b|;若 a,b 反向, 则|a+b|=||a|-|b||;当 a,b 不共线时,||a|-|b||<|a+b|<|a|+|b|,为假 命题.
第38题+平面向量的线性运算及平面向量的共线问题-2018精品之高中数学(理)黄金100题系列+Word版含解析

第38题 平面向量的线性运算及平面向量的共线问题I .题源探究·黄金母题【例1】如图,已知四边形ABCD 是等腰梯形,,E F 分别是,AD BC 的中点,,M N 是线段EF 上的两个点,且EM MN NF ==,下底是上底的2倍,若AB a =,BC b =,求AM .【解析】1122AD AB BC CD a b a a b =++=+-=+, ∴111242AE AD a b ==+. 又1113()()2224EF AB DC a a a =+=+=,∴1134EM EF a ==,所以1111()()4242AM AE EM a b a a b =+=++=+II .考场精彩·真题回放【例2】【2017课标1理13】已知向量a ,b 的夹角为60°,|a |=2,|b |=1,则| a +2 b |= .【答案】【解析】分析:222|2|||44||a b a a b b +=+⋅+4421cos60412=+⨯⨯⨯+=所以|2|12a b +==秒杀解析:利用如下图形,可以判断出2a b+的模长是以2为边长的菱形对角线的长度,则为【名师点睛】平面向量中涉及到有关模长的问题,用到的通法是将模长进行平方,利用向量数量积的知识进行解答,很快就能得出答案;另外,向量是一个工具型的知识,具备代数和几何特征,在做这类问题时可以使用数形结合的思想,会加快解题速度.【例3】【2015全国新课标Ⅰ卷】设D 为ABC ∆所在平面内一点3BC CD =,则( )A .1433AD AB AC =-+ B .1433AD AB AC =-C .4133AD AB AC =+ D .4133AD AB AC =-【答案】A【解析】由题知13AD AC CD AC BC =+=+=1()3AC AC AB +-=1433AB AC -+,故选A . 【例4】【2015高考新课标2理13】设向量a ,b 不平行,向量a b λ+与2a b +平行,则实数λ=_________.【答案】12【解析】因为向量a b λ+与2a b +平行,所以2a b k a b λ+=+(),则12,k k λ=⎧⎨=⎩,所以12λ=.【名师点睛】本题考查向量共线,明确平面向量共线定理,利用待定系数法得参数的关系是解题关键,属于基础题.【例5】【2015北京高考卷】在ABC △中,点M ,N 满足2AM MC =,BN NC =.若M N x A B y A =+,则x =______;y =_______.【答案】11,26- 【解析】由题意知无论,AB AC 的位置关系如何,对结果 都没有任何变化,即结论唯一,不妨设AC AB ⊥,4,3AB AC ==,因此以以A 为原点,AB 为x 轴,AC 为y 轴,建立直角坐标系,3(0,0),(0,2),(0,3),(4,0),(2,)2A M CB N ,1(2,),(4,0),(0,3)2MN AB AC =-==,则1(2,)(4,0)(0,3)2x y -=+,42x =,132y =-,所以11,26x y ==-.【例6】【2014福建8】设M 为平行四边形ABCD 对角线的交点,O 为平行四边形ABCD 所在平面内任意一点,则OA OB OC OD +++等于 ( )..2.3.4A OMB OMC OMD OM【答案】D【解析】由已知得,111,,,222OA OM CA OB OM DB OC OM AC =+=+=+1,2OD OM BD =+而,,CA AC DB BD =-=-所以4OA OB OC OD OM +++=,选D .【名师点睛】本题主要考查向量的加法法则与减法法则及几何意义.解决此类问题时经常出现的错误有:忽视向量的起点与终点,导致加法与减法混淆,对此,要注意三角形法则与平行四边形法则适用的条件.【例7】【2015高考广东卷】设a 是已知的平面向量且0a ≠,关于向量a 的分解,有如下四个命题: ①给定向量b ,总存在向量c ,使=+a b c ; ②给定向量b 和c ,总存在实数λ和μ,使λμ=+a b c ;③给定单位向量b 和正数μ,总存在单位向量c 和实数λ,使λμ=+a b c ;④给定正数λ和μ,总存在单位向量b 和单位向量c ,使λμ=+a b c .上述命题中的向量b ,c 和a 在同一平面内且两两不共线,则真命题的个数是( ) A .1 B .2 C .3 D .4 【答案】B【解析】利用向量加法的三角形法则,易知①是对的;利用平面向量的基本定理,易知②是对的;以a 的终点作长度为μ的圆,这个圆必须和向量b λ有交点,这个不一定能满足,③是错的;利用向量加法的三角形法则,结合三角形两边的和大于第三边,即必须b c a λμλμ+=+≥,所以④是假命题.综上,选B .【例8】【2015高考山东理4】已知菱形ABCD 的边长为a ,60ABC ∠= ,则BD CD ⋅=( )(A )232a - (B )234a - (C )234a 错误!未找到引用源。
2018全国卷高考复习平面向量(知识总结+题型)
第一部分平面向量的概念及线性运算向量a( a z 0)与b共线的充要条件是存在唯一一个实数入,使得bi a.【基础练习】1. 判断正误(在括号内打或“X”)⑴零向量与任意向量平行.()(2)若a// b, b// c,贝U a// c.()⑶向量云B与向量6D是共线向量,贝y A B, C, D四点在一条直线上.()(4)当两个非零向量a, b共线时,一定有b=入a,反之成立.()⑸在厶ABC中, D是BC中点,则A D= 2(心A B.()2. 给出下列命题:①零向量的长度为零,方向是任意的;②若③向量ABW BA相等.则所有正确命题的序号是()A.①B.③C.①③D.①②3.(2017•枣庄模拟)设D ABC所在平面内一点,K D= —4A C若目C= X D C X€ R), 则X =()A.2B.3C. —2D. —34.(2015 •全国n卷)设向量a, b不平行,向量入a+ b与a+ 2b平行,则实数X =5.(必修4P92A12改编)已知?ABCD勺对角线AC和BD相交于Q且OA= a,O B= b,则张 _____ BC= ______ (用a, b 表示).1 26.(2017 •嘉兴七校联考)设D, E分别是△ ABC的边AB BC上的点,AD= -AB BE=§BC若DE= 入l AB+ 入2AC 入 1 , 入2为实数),贝V 入 1 = _____________ , 入2= _______________ .考点一平面向量的概念【例1】下列命题中,不正确的是 _________ (填序号).①若I a| = |b| ,则a= b;②若A, B, C, D是不共线的四点,贝厂’AB=承”是“四边形ABCD为平行四边形”的充要条件;③若a= b, b= c,贝V a= c.【训练1】下列命题中,正确的是 _________ (填序号).①有向线段就是向量,向量就是有向线段;②向量a与向量b平行,则a与b的方向相同或相反;③两个向量不能比较大小,但它们的模能比较大小解析①不正确,向量可以用有向线段表示,但向量不是有向线段,有向线段也不是向量;②不正确,若a与b中有一个为零向量,零向量的方向是不确定的,故两向量方向不一定相同或相反;a, b都是单位向量,则a= b;考点三共线向量定理及其应用【例3】 设两个非零向量a 与b 不共线.(1)若 AB= a + b , BC= 2a + 8b , CD= 3( a — b ).求证:A, B , ⑵ 试确定实数k ,使ka + b 和a + kb 共线.【训练 3】已知向量 AB= a + 3b , BC= 5a + 3b , CD=- 3a + 3b ,则( )A.AB, C 三点共线 B.A, B, D 三点共线 C.A, C D 三点共线D.B, C, D 三点共线第二部分平面向量基本定理与坐标表示1. 平面向量的基本定理如果e 1, e 2是同一平面内的两个不共线向量,那么对于这一平面内的任意向量 对实数入1,入2,使a =入e+入2e 2.其中,不共线的向量 e 1, e 2叫做表示这一平面内所有向量的一组基底.2. 平面向量的正交分解 把一个向量分解为两个互相垂直的向量,叫做把向量正交分解3. 平面向量的坐标运算(1) 向量加法、减法、数乘向量及向量的模 设 a =(X 1, y” , b = (X 2, y 2),贝U③正确,向量既有大小,又有方向,不能比较大小;向量的模均为实数,可以比较大小 答案③考点二平面向量的线性运算1【例2】(2017 •潍坊模拟)在厶ABC 中, P , Q 分别是AB BC 的三等分点,且 AP= 3AB BQ= 13BC 若AB= a , AC= b ,则 PQ=( )311 A ・3a +3b 1 1B. — 3a +3b 1 1 C.J a -3b1 1 D. - 3a — 3b【训练2】(1)如图,正方形 ABCDK 点 E 是DC 的中点, 靠近B 点的三等分点,那么 EF 等于(A .^AB ^2D 三点共线;a ,有且只有-点F 是BC 的一个A BC.a+ b= (x i + X2, y土y) , a—b= (x i—X2, y i—y2), X a=(入x i, hy , | a| = :x1+y?.(2) 向量坐标的求法①若向量的起点是坐标原点,则终点坐标即为向量的坐标②设A(x i,y i),B(x?,y?),则AB= (x? —X i,y?—y i),| AB = : (x?—X i)?+( y? —y i) 24. 平面向量共线的坐标表示设a= (x i, y i) , b= (x?, y?),贝y a// b? x i y? —x?y i = o.【基础练习】i.(?0i7 •东阳月考)已知向量a= (2 , 4) , b= ( —1 , 1),则2a+ b 等于()A.(5 , 7)B.(5 , 9)C.(3 ,7)D.(3 , 9)2.(20i5 -全国I卷)已知点A(0 , i), B(3 , 2),向量AC= ( —4, —3),则向量BC=( )A.( —7,—4)B.(7 ,4)C.( —1,4)D.(i ,4)3.(20i6 -全国n卷)已知向量a= (m4) , b= (3 , —2),且a / b,则m=4.(必修4Pi0iA3改编)已知?ABCD勺顶点A—i, —2),耳3 , —i) , C(5 , 6),则顶点D的坐标为考点一平面向量基本定理及其应用【例1】(2014 •全国I卷)设D, E, F分别为△ ABC的三边BC CA AB的中点,贝U EB+ F C= ( )A.ADB.[A DC.1B CD. BC >4【训练1】如图,已知AB= a , AC= b , BD= 3DC用a , b表示AD则AD= __ .a DC"考点二平面向量的坐标运算【例2】(1)已知向量a = (5 , 2) , b= ( —4, —3) , c= (x , y),若3a—2b+ c = 0,则c =( ) A.( —23 , —12) B.(23 , 12)C.(7 , 0)D.( —7 , 0)【训练2】(1)已知点A— 1 , 5)和向量a= (2, 3),若AB= 3a ,则点B的坐标为()A.(7 , 4)B.(7 , 14)C.(5 , 4)D.(5 , 14)⑵(2015 •江苏卷)已知向量a= (2 , 1), b= (1 , —2).若na+ nb= (9 , —8)( m n € R),则m—n的值为_________ .考点三平面向量共线的坐标表示【例3】(1)已知平面向量a= (1 , 2), b= ( — 2 , m,且a / b,贝U 2a+ 3b= ___________(2)(必修4P101练习7改编)已知A (2 , 3) , B (4 , — 3),点P 在线段AB 的延长线上,且| AFf =|| Bp ,则点P 的坐标为 ____________单位向量是()⑵若三点A (1 , - 5),政a , — 2) , q — 2, - 1)共线,则实数a 的值为 _____________ .第三部分 平面向量的数量积及其应用1. 平面向量数量积的有关概念⑴ 向量的夹角:已知两个非零向量a 和b ,记O A a , O B- b ,则/ AOB- 0 (0 ° < 0 < 180°)叫做向量a 与b 的夹角.⑵ 数量积的定义:已知两个非零向量a 与b ,它们的夹角为 0,则数量| a || b |cos 0叫做a 与b 的数量积(或内积),记作a • b ,即a • b = | a || b |cos ___ 0,规定零向量与任一向量的数量积为0,即0 • a = 0.⑶数量积几何意义:数量积a • b 等于a 的长度| a |与b 在a 的方向上的投影| b |cos 0的乘积. 2. 平面向量数量积的性质及其坐标表示设向量a = (x i , y i ), b = (X 2, y 2), 0为向量a , b 的夹角.⑴ 数量积:a • b = | a || b |cos 0 = X 1X 2+ y i y 2.(2) 模:| a | = , a • a = , x i + y i . 亠宀 a • bX 1X 2+ y i y 2(3) 夹角:C0S 0= 1 冲=——2222.丨 a ll b | 寸x i + y i •寸X 2 + y 2⑷ 两非零向量 a 丄b 的充要条件:a • b = 0? X 1X 2+ y i y 2= 0.(5)| a • b | <| a || b |(当且仅当 a // b 时等号成立)? | X 1X 2+ yyl w 寸x ;+ y : • p x 2+ y 2. 3. 平面向量数量积的运算律:(1) a - b = b • a (交换律).(2)入a • b = X (a • b ) = a •(入b )(结合律).(3)( a + b ) - c = a - c + b - c (分配律). 【基础练习】1. (2015 •全国 n 卷)向量 a = (1 , — 1), b = ( — 1, 2),则(2a + b ) - a 等于( )A. — 1B.0C.1D.22. (2017 •湖州模拟)已知向量a , b ,其中|a | = 3, | b | = 2,且(a — b )丄a ,则向量a 和b 的 夹角是 ________ .2 n3. (2016 •石家庄模拟)已知平面向量a , b 的夹角为, |a | = 2,|b | = 1,则| a + b | = ________ .【训练3】 (1)(2017 •浙江三市十二校联考)已知点A (1 , 3) , B (4 , — 1),则与AB 同方向的3-4-- D4 - 53 - 5-3 - 5 -4 -4 - 5-3 - 5A35. (必修4P104例1改编)已知I a| = 5, | b| = 4, a与b的夹角0 = 120°,则向量b在向量a方向上的投影为 _________ .6. _______________________________________ (2017 •瑞安一中检测)已知a , b , c 是同一平面内的三个向量,其中 a = (1 , 2) , |b | = 1, 且a + b 与a — 2b 垂直,则向量 a • b =; a 与b 的夹角0的余弦值为 ________________________________ .【考点突破】考点一平面向量的数量积及在平面几何中的应用(用已知表示未知) 【例1】(1)(2015 •四川卷)设四边形ABCD 为平行四边形, 足B M= 3^C 6N = 2hf c 则 AM ・ NM 等于( ) A.20B. 15C.9D.6⑵(2016 •天津卷)已知△ ABC 是边长为1的等边三角形,点连接DE 并延长到点F ,使得DE= 2EF,则AF • BC 的值为(【训练1】(1)(2017 •义乌市调研)在Rt △ ABC 中 , / A = 90° , AB= AC= 2,点D 为AC 的中 点,点E 满足1BE= 3B C 则尺E ・E3D= _____⑵(2017 •宁波质检)已有正方形 ABC 啲边长为1,点E 是AB 边上的动点,贝U 0E- CB 勺值为 ________ ; 6E - [5C 的最大值为 ______ . 考点二平面向量的夹角与垂直【例2】(1)(2016 •全国n 卷)已知向量a = (1 , m ) , b = (3 , — 2),且(a + b )丄b ,则 作( )A. — 8B. — 6C.6D.8⑵ 若向量a = (k , 3), b = (1 , 4), c = (2, 1),已知2a — 3b 与c 的夹角为钝角,贝U k 的取值 范围是_______________ .【训练2】(1)(2016 •全国川卷)已知向量BA= 1 ,右3 , BC= , 2 ,则/ ABC=()A.30 °B.45 °C.60°D.120°2 2 2(2)(2016 •全国I 卷)设向量 a = (m 1) , b = (1 , 2),且 |a + b | = | a | + | b | ,贝 Um ^ .考点三平面向量的模及其应用n【例3】(2017 •云南统一检测)已知平面向量a 与b 的夹角等于—,若|a | = 2 , | b | = 3,则 |2a — 3b | =()| AB = 6, |AD | = 4,若点 M N 满D, E 分别是边AB BC 的中点,11A . —8B.81。
2018年高考数学文一轮复习文档:第四章 平面向量 第1
第1讲平面向量的概念及线性运算1.向量的有关概念(1)向量:既有大小又有方向的量叫做向量,向量的大小叫做向量的模. (2)零向量:长度为0的向量,其方向是任意的. (3)单位向量:长度等于1个单位的向量.(4)平行向量:方向相同或相反的非零向量,又叫共线向量,规定:0与任一向量共线. (5)相等向量:长度相等且方向相同的向量. (6)相反向量:长度相等且方向相反的向量. 2.向量的线性运算3.两个向量共线定理向量b 与非零向量a 共线的充要条件是有且只有一个实数λ,使得b =λa .1.辨明两个易误点(1)作两个向量的差时,首先将两向量的起点平移到同一点,要注意差向量的方向是由减向量的终点指向被减向量的终点.(2)在向量共线的重要条件中易忽视“a ≠0”,否则λ可能不存在,也可能有无数个. 2.三点共线的等价关系A ,P ,B 三点共线⇔AP →=λAB →(λ≠0)⇔OP →=(1-t )²OA →+tOB →(O 为平面内异于A ,P ,B的任一点,t ∈R )⇔OP →=xOA →+yOB →(O 为平面内异于A ,P ,B 的任一点,x ∈R ,y ∈R ,x +y =1).1.教材习题改编 如图,D ,E ,F 分别是△ABC 各边的中点,则下列结论错误的是( )A .EF →=CD →B .AB →与DE →共线 C .BD →与CD →是相反向量 D .AE →=12|AC →|D 根据向量的概念可知选D.2.教材习题改编 下列结论正确的是( ) A .若|a |=0,则a =0B .若a ,b 是两个单位向量,则a =bC .若a =b ,b =c ,则a =cD .若AB =AC ,则AB →=AC →C 根据向量的概念可知选C.3.教材习题改编 如图,▱ABCD 的对角线交于M ,若AB →=a ,AD →=b ,用a ,b 表示MD →为( )A .12a +12b B .12a -12b C .-12a -12bD .-12a +12bD MD →=12BD →=12(b -a )=-12a +12b ,故选D.4.教材习题改编 已知a ,b 是非零向量,命题p :a =b ,命题q :|a +b |=|a |+|b |,则p 是q 的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件A 若a =b ,则|a +b |=|2a |=2|a |,|a |+|b |=|a |+|a |=2|a |即p ⇒q , 若|a +b |=|a |+|b |,由加法的运算知a 与b 同向共线,即a =λb 且λ>0,故q ⇒/p . 所以p 是q 的充分不必要条件,故选A.5.教材习题改编 向量e 1与e 2不共线,若a =e 1-e 2与b =-2e 1+λe 2共线,则λ的值为________.因为e 1与e 2不共线,且a =e 1-e 2与b =-2e 1+λe 2共线,所以存在μ∈R ,使e 1-e 2=μ(-2e 1+λe 2)=-2μe 1+μλe 2,得⎩⎪⎨⎪⎧1=-2μ-1=μλ,所以λ=2. 2平面向量的有关概念给出下列命题:①有向线段就是向量,向量就是有向线段;②向量a 与向量b 平行,则a 与b 的方向相同或相反; ③向量AB →与向量CD →共线,则A 、B 、C 、D 四点共线; ④如果a ∥b ,b ∥c ,那么a ∥c . 其中正确命题的个数为( ) A .1 B .2 C .3D .0【解析】 ①不正确,向量可以用有向线段表示,但向量不是有向线段,有向线段也不是向量;②不正确,若a 与b 中有一个为零向量,零向量的方向是不确定的,故两向量方向不一定相同或相反;③不正确,共线向量所在的直线可以重合,也可以平行; ④不正确,如果b =0时,则a 与c 不一定平行. 【答案】 D对于向量的概念的三点注意(1)向量的两个特征:有大小和方向,向量既可以用有向线段和字母表示,也可以用坐标表示;(2)相等向量不仅模相等,而且方向也相同,所以相等向量一定是平行向量,而平行向量则未必是相等向量;(3)向量与数量不同,数量可以比较大小,向量则不能,但向量的模是非负实数,故可以比较大小.1.判断下列四个命题:①若a ∥b ,则a =b ;②若|a |=|b |,则a =b ;③若|a |=|b |,则a ∥b ;④若a =b ,则|a |=|b |.其中正确的个数是( )A .1B .2C .3D .4A 只有④正确.2.设a 0为单位向量,①若a 为平面内的某个向量,则a =|a |a 0;②若a 与a 0平行,则a =|a |a 0;③若a 与a 0平行且|a |=1,则a =a 0.上述命题中,假命题的个数是( )A .0B .1C .2D .3D 向量是既有大小又有方向的量,a 与|a |a 0的模相同,但方向不一定相同,故①是假命题;若a 与a 0平行,则a 与a 0的方向有两种情况:一是同向,二是反向,反向时a =-|a |a 0,故②③也是假命题.综上所述,假命题的个数是3.平面向量的线性运算(高频考点)平面向量的线性运算包括向量的加、减及数乘运算,是高考考查向量的热点.常以选择题、填空题的形式出现.高考对平面向量的线性运算的考查主要有以下三个命题角度: (1)求已知向量的和; (2)用已知向量表示未知向量; (3)求参数的值.(1)(2015²高考全国卷Ⅰ)设D 为△ABC 所在平面内一点,BC →=3CD →,则( ) A .AD →=-13AB →+43AC →B .AD →=13AB →-43AC →C .AD →=43AB →+13AC →D .AD →=43AB →-13AC →(2)(2015²高考北京卷)在△ABC 中,点M ,N 满足AM →=2MC →,BN →=NC →.若MN →=xAB →+yAC →,则x =________;y =________.【解析】 (1)AD →=AC →+CD →=AC →+13BC →=AC →+13(AC →-AB →)=43AC →-13AB →=-13AB →+43AC →.(2)因为 AM →=2MC →,所以AM →=23AC →.因为 BN →=NC →,所以AN →=12(AB →+AC →),所以MN →=AN →-AM →=12(AB →+AC →)-23AC →=12AB →-16AC →. 又MN →=xAB →+yAC →,所以x =12,y =-16.【答案】 (1)A (2)12 -16向量线性运算的解题策略(1)向量的加减常用的法则是平行四边形法则和三角形法则,一般共起点的向量求和用平行四边形法则,求差用三角形法则,求首尾相连向量的和用三角形法则.(2)找出图形中的相等向量、共线向量,将所求向量与已知向量转化到同一个平行四边形或三角形中求解.角度一 求已知向量的和1.设D ,E ,F 分别为△ABC 的三边BC ,CA ,AB 的中点,则EB →+FC →=( ) A .AD →B .12AD →C .BC →D .12BC → A EB →+FC →=12(AB →+CB →)+12(AC →+BC →)=12(AB →+AC →)=AD →,故选A.角度二 用已知向量表示未知向量2.(2017²龙岩模拟) 如图所示,下列结论正确的是( )①PQ →=32a +32b ;②PT →=32a -b ;③PS →=32a -12b ;④PR →=32a +b .A .①②B .③④C .①③D .②④C ①根据向量的加法法则,得PQ →=32a +32b ,故①正确;②根据向量的减法法则,得PT →=32a -32b ,故②错误;③PS →=PQ →+QS →=32a +32b -2b =32a -12b ,故③正确;④PR →=PQ →+QR →=32a +32b -b =32a +12b ,故④错误.故选C.角度三 求参数的值3.在△ABC 中,已知D 是AB 边上一点,若AD →=2DB →,CD →=13CA →+λCB →,则λ等于( )A .23B .13C .-13D .-23A 如图所示,过点D 分别作AC ,BC 的平行线,分别交BC ,AC 于点F ,E , 所以CD →=CE →+CF →.因为AD →=2DB →,所以CE →=13CA →,CF →=23CB →,故CD →=13CA →+23CB →,所以λ=23.平面向量共线定理的应用已知非零向量e 1,e 2不共线.(1)如果AB →=e 1+e 2,BC →=2e 1+8e 2,CD →=3(e 1-e 2), 求证:A 、B 、D 三点共线;(2)欲使k e 1+e 2和e 1+k e 2共线,试确定实数k 的值. 【解】 (1)证明:因为AB →=e 1+e 2, BD →=BC →+CD →=2e 1+8e 2+3e 1-3e 2=5(e 1+e 2)=5AB →, 所以AB →与BD →共线, 且有公共点B ,所以A 、B 、D 三点共线. (2)因为k e 1+e 2与e 1+k e 2共线, 所以存在λ,使k e 1+e 2=λ(e 1+k e 2), 则(k -λ)e 1=(λk -1)e 2. 由于e 1与e 2不共线,只能有⎩⎪⎨⎪⎧k -λ=0,λk -1=0,所以k =±1.1.已知a ,b 是不共线的向量,AB →=λa +b ,AC →=a +μb ,λ,μ∈R ,则A ,B ,C 三点共线的充要条件为( )A .λ+μ=2B .λ-μ=1C .λμ=-1D .λμ=1D 因为A 、B 、C 三点共线,所以AB →∥AC →,设AB →=mAC →(m ≠0),所以⎩⎪⎨⎪⎧λ=m ,1=m μ,所以λμ=1,故选D.2.已知a ,b 是两个不共线的非零向量,且a 与b 起点相同,若a ,t b ,13(a +b )三向量的终点在同一直线上,则t =________.因为a ,t b ,13(a +b )三向量的终点在同一条直线上,且a 与b 起点相同.所以a -t b 与a -13(a +b )共线.即a -t b 与23a -13b 共线.所以存在实数λ,使a -t b =λ⎝ ⎛⎭⎪⎫23a -13b ,所以⎩⎪⎨⎪⎧1=23λ,t =13λ,解得λ=32,t =12,即t =12时,a ,t b ,13(a +b )三向量的终点在同一条直线上.12, )1. 如图所示,D 是△ABC 的边AB 的中点,则向量CD →=( )A .-BC →+12BA →B .-BC →+12AB →C .BC →-12BA →D .BC →+12BA →A 因为CD →=CB →+BD →,CB →=-BC →,BD →=12BA →,所以CD →=-BC →+12BA →.2.在四边形ABCD 中,AB →=a +2b ,BC →=-4a -b ,CD →=-5a -3b ,则四边形ABCD 的形状是( )A .矩形B .平行四边形C .梯形D .以上都不对C 由已知,得AD →=AB →+BC →+CD →=-8a -2b =2(-4a -b )=2BC →,故AD →∥BC →.又因为AB →与CD →不平行,所以四边形ABCD 是梯形.3.设D ,E ,F 分别是△ABC 的三边BC ,CA ,AB 上的点,且DC →=2BD →,CE →=2EA →,AF →=2FB →,则AD →+BE →+CF →与BC →( )A .反向平行B .同向平行C .互相垂直D .既不平行也不垂直A 由题意得AD →=AB →+BD →=AB →+13BC →,BE →=BA →+AE →=BA →+13AC →, CF →=CB →+BF →=CB →+13BA →,因此AD →+BE →+CF →=CB →+13(BC →+AC →-AB →)=CB →+23BC →=-13BC →,故AD →+BE →+CF →与BC →反向平行.4.已知向量a ,b ,c 中任意两个都不共线,但a +b 与c 共线,且b +c 与a 共线,则向量a +b +c =( )A .aB .bC .cD .0D 依题意,设a +b =m c ,b +c =n a ,则有(a +b )-(b +c )=m c -n a ,即a -c =m c -n a .又a 与c 不共线,于是有m =-1,n =-1,a +b =-c ,a +b +c =0.5.已知P 是△ABC 内的一点,AP →=13(AB →+AC →),则△ABC 的面积与△ABP 的面积之比为( )A .2B .3C .32D .6B 由AP →=13(AB →+AC →),得3AP →=AB →+AC →,AP →+(AP →-AB →)+(AP →-AC →)=0.所以PB →+PC →+PA →=0,P 是△ABC 的重心.所以△ABC 的面积与△ABP 的面积之比为3.6.如图,已知AB 是圆O 的直径,点C ,D 是半圆弧的两个三等分点,AB →=a ,AC →=b ,则AD →=( )A .a -12bB .12a -b C .a +12bD .12a +b D 连接CD ,由点C ,D 是半圆弧的三等分点,得CD ∥AB 且CD →=12AB →=12a ,所以AD →=AC →+CD →=b +12a .7.(2017²唐山统考)已知a 与-b 是两个不共线向量,且向量a +λb 与-(b -3a )共线,则λ的值为________.因为a +λb 与-(b -3a )共线,所以存在实数μ,使a +λb =μ(3a -b ), 即⎩⎪⎨⎪⎧1=3μ,λ=-μ,所以⎩⎪⎨⎪⎧μ=13,λ=-13. -138.已知D ,E ,F 分别为△ABC 的边BC ,CA ,AB 的中点,且BC →=a ,CA →=b ,给出下列命题:①AD →=12a -b ;②BE →=a +12b ;③CF →=-12a +12b ;④AD →+BE →+CF →=0.其中正确命题的个数为________.BC →=a ,CA →=b ,AD →=12CB →+AC →=-12a -b ,故①错;BE →=BC →+12CA →=a +12b ,故②正确;CF →=12(CB →+CA →)=12(-a +b )=-12a +12b ,故③正确;所以AD →+BE →+CF →=-b -12a +a +12b +12b -12a =0.所以正确命题为②③④. 39.若|AB →|=|AC →|=|AB →-AC →|=2,则|AB →+AC →|=________.因为|AB →|=|AC →|=|AB →-AC →|=2,所以△ABC 是边长为2的正三角形,所以|AB →+AC →|为△ABC 的边BC 上的高的2倍,所以|AB →+AC →|=2 3.2 310.在直角梯形ABCD 中,∠A =90°,∠B =30°,AB =23,BC =2,点E 在线段CD 上,若AE →=AD →+μAB →,则μ的取值范围是________.由题意可求得AD =1,CD =3, 所以AB →=2DC →.因为点E 在线段CD 上, 所以DE →=λDC →(0≤λ≤1). 因为AE →=AD →+DE →,又AE →=AD →+μAB →=AD →+2μDC →=AD →+2μλDE →,所以2μλ=1,即μ=λ2.因为0≤λ≤1,所以0≤μ≤12.⎣⎢⎡⎦⎥⎤0,12 11. 如图,以向量OA →=a ,OB →=b 为邻边作▱OADB ,BM →=13BC →,CN →=13CD →,用a ,b 表示OM →,ON →,MN →.因为BA →=OA →-OB →=a -b ,BM →=16BA →=16a -16b ,所以OM →=OB →+BM →=16a +56b .因为OD →=a +b ,所以ON →=OC →+13CD →=12OD →+16OD →=23OD →=23a +23b ,所以MN →=ON →-OM →=23a +23b -16a -56b =12a-16b . 综上,OM →=16a +56b ,ON →=23a +23b ,MN →=12a -16b .12.设M 是△ABC 所在平面上的一点,且MB →+32MA →+32MC →=0,D 是AC 的中点,则|MD →||BM →|的值为( )A .13B .12C .1D .2A 因为D 是AC 的中点,延长MD 至E ,使得DE =MD ,所以四边形MAEC 为平行四边形,所以MD →=12ME →=12(MA →+MC →).因为MB →+32MA →+32MC →=0,所以MB →=-32(MA →+MC →)=-3MD →,所以|MD →||BM →|=|MD →||3MD →|=13,故选A . 13. 在平行四边形ABCD 中,E ,F 分别是BC ,CD 的中点,DE 交AF 于H ,记AB →,BC →分别为a ,b ,则AH →=( )A .25a -45bB .25a +45bC .-25a +45bD .-25a -45bB 如图,过点F 作BC 的平行线交DE 于G ,则G 是DE 的中点,且GF →=12EC →=14BC →,所以GF →=14AD →,则△AHD ∽△FHG ,从而HF →=14AH →,所以AH →=45AF →,AF →=AD →+DF →=b +12a ,所以AH →=45(b +12a )=25a +45b ,故选B.14.已知点G 是△ABC 的重心,过G 作一条直线与AB ,AC 两边分别交于M ,N 两点,且AM →=xAB →,AN →=yAC →,求xy x +y的值.法一:由已知得M ,G ,N 三点共线,所以AG →=λAM →+(1-λ)AN →=λxAB →+(1-λ)yAC →,因为点G 是△ABC 的重心,所以AG →=23³12(AB →+AC →)=13(AB →+AC →),所以⎩⎪⎨⎪⎧λx =13(1-λ)y =13,即⎩⎪⎨⎪⎧λ=13x 1-λ=13y,得13x +13y =1, 即1x +1y =3,通分变形得,x +y xy =3,所以xy x +y =13. 法二:利用等边三角形,过重心作平行于底边BC 的直线,易得x =23,y =23,所以xy x +y =13. 15. 如图,在△ABC 中,D ,F 分别是BC ,AC 的中点,AE →=23AD →,AB →=a ,AC →=b .(1)用a ,b 表示向量AD →,AE →,AF →,BE →,BF →; (2)求证:B ,E ,F 三点共线.(1)延长AD 到G ,使AD →=12AG →,连接BG ,CG ,得到平行四边形ABGC , 所以AG →=a +b , AD →=12AG →=12(a +b ), AE →=23AD →=13(a +b ), AF →=12AC →=12b ,BE →=AE →-AB →=13(a +b )-a =13(b -2a ), BF →=AF →-AB →=12b -a =12(b -2a ).(2)证明:由(1)可知BE →=23BF →,又因为BE →,BF →有公共点B ,所以B ,E ,F 三点共线.。
2018课标版文数一轮(5)第五章-平面向量(含答案)1-第一节 平面向量的概念及其线性运算
第一节平面向量的概念及其线性运算A组基础题组1.已知O,A,B是同一平面内的三个点,直线AB上有一点C满足2AC+CB=0,则OC=()A.2OA-OBB.-OA+2OBC.23OA-13OB D.-13OA+23OB2.(2016甘肃兰州模拟)如图所示,下列结论中正确的是()①PQ=32a+32b;②PT=32a-b;③PS=32a-12b;④PR=32a+b.A.①②B.③④C.①③D.②④3.已知向量a,b不共线,c=ka+b(k∈R),d=a-b.如果c∥d,那么()A.k=1且c与d同向B.k=1且c与d反向C.k=-1且c与d同向D.k=-1且c与d反向4.在四边形ABCD中,AB=a+2b,BC=-4a-b,CD=-5a-3b,则四边形ABCD的形状是()A.矩形B.平行四边形C.梯形D.以上都不对5.在平行四边形ABCD中,点E是AD的中点,BE与AC相交于点F,若EF=m AB+n AD(m,n∈R),则mn的值为()A.-12B.-2 C.2 D.126.已知D,E,F分别为△ABC的边BC,CA,AB的中点,且BC=a,CA=b,给出下列命题:①AD=12a-b;②BE=a+12b;③CF=-12a+12b;④AD+BE+CF=0.其中正确命题的个数为.7.若|AB|=|AC|=|AB-AC|=2,则|AB+AC|=.8.已知G为△ABC的重心,令AB=a,AC=b,过点G的一条直线分别交AB,AC于P,Q两点,且AP=ma,AQ=nb,则1m +1n=.9.如图,以向量OA=a,OB=b为邻边作▱OADB,BM=13BC,CN=13CD,用a,b表示OM,ON,MN.10.已知a,b不共线,OA=a,OB=b,OC=c,OD=d,OE=e,设t∈R,如果3a=c,2b=d,e=t(a+b),是否存在实数t,使C,D,E三点在同一条直线上?若存在,求出实数t的值;若不存在,请说明理由.B组提升题组11.已知点O为△ABC外接圆的圆心,且OA+OB+CO=0,则△ABC的内角A等于()A.30°B.45°C.60°D.90°12.已知:如图,|OA|=|OB|=1,OA与OB的夹角为120°,OC与OA的夹角为30°,若OC=λOA+μOB(λ、μ∈R),则λμ等于()A.32B.233C.12D.213.若点M是△ABC所在平面内的一点,且满足5AM=AB+3AC,则△ABM与△ABC的面积的比值为()A.15B.25C.35D.4514.(2016内蒙古包头九中期中)如图,在△ABC中,AH⊥BC于H,M为AH的中点,若AM=λAB+μAC,则λ+μ=.15.如图所示,在△ABC中,D,F分别是BC,AC的中点,AE=23AD,AB=a,AC=b.(1)用a,b表示向量AD,AE,AF,BE,BF;(2)求证:B,E,F三点共线.16.已知P为△ABC内一点,且3AP+4BP+5CP=0,延长AP交BC于点D,若AB=a,AC=b,用a、b表示向量AP、AD.答案全解全析A组基础题组1.A依题意,得OC=OB+BC=OB+2AC=OB+2(OC-OA),所以OC=2OA-OB,故选A.2.C①根据向量的加法法则,得PQ=32a+32b,故①正确;②根据向量的减法法则,得PT=32a-32b,故②错误;③PS=PQ+QS=32a+32b-2b=32a-12b,故③正确;④PR=PQ+QR=32a+32b-b=32a+12b,故④错误.故选C.3.D∵c∥d,∴c=λd(λ∈R),即ka+b=λ(a-b),∴k=λ,λ=-1.∴k=-1,则c=b-a,故c与d反向.4.C由已知,得AD=AB+BC+CD=-8a-2b=2(-4a-b)=2BC,故AD∥BC.又因为AB与CD不平行,所以四边形ABCD是梯形.5.B易知AEBC =EFFB=12,∴EF=13EB,∴EF=13EB=13(EA+AB)=1312DA+AB=1 6DA+13AB=13AB-16AD,∴m=13,n=-16,∴mn=-2.6.答案 3解析BC=a,CA=b,AD=12CB+AC=-12a-b,故①错;BE=BC+12CA=a+12b,故②正确;CF=12(CB+CA)=12(-a+b)=-12a+12b,故③正确;∴AD+BE+CF=-b-12a+a+12b+12b-12a=0,故④正确.∴正确命题为②③④.7.答案23解析∵|AB|=|AC|=|AB-AC|=2,∴△ABC是边长为2的正三角形,∴|AB+AC|为△ABC的边BC上的高的2倍,∴|AB+AC|=2 8.答案 3解析连接AG并延长交BC于点E,如图所示,由重心的性质可知AG=23AE=23×12(AB+AC)=13(AB+AC),又AB=1mAP,AC=1nAQ,所以AG=131mAP+1nAQ=13mAP+13nAQ.因为G,P,Q三点共线,所以13m +13n=1,即1m +1n=3.9.解析∵BA=OA-OB=a-b,∴BM=13BC=16BA=16a-16b,∴OM=OB+BM=16a+56b.∵OD=a+b,∴ON=OC+13CD=12OD+16OD=23OD=23a+23b,∴MN=ON-OM=23a+23b-16a-56b=12a-16b.综上,OM=16a+56b,ON=23a+23b,MN=12a-16b.10.解析存在.理由:由题设知,CD=d-c=2b-3a,CE=e-c=(t-3)a+tb,C,D,E三点在同一条直线上的充要条件是存在实数k,使得CE=k CD,即(t-3)a+tb=-3ka+2kb,整理得(t-3+3k)a=(2k-t)b.因为a,b不共线,所以有t-3+3k=0, t-2k=0,解得t=65.故存在实数t=65,使C,D,E三点在同一条直线上.B组提升题组11.A由OA+OB+CO=0得,OA+OB=OC,由O为△ABC外接圆的圆心,结合向量加法的几何意义知,四边形OACB为菱形,且∠CAO=60°,故∠BAC=30°.12.D过C作OB的平行线交OA的延长线于D.由题意可知,∠COD=30°,∠OCD=90°,∴OD=2CD,又由题意知OD=λOA,DC=μOB,∴λ|OA|=2μ|OB|,即λ=2μ,故λμ=2.13.C设AB的中点为D,连接MD,MC,由5AM=AB+3AC,得5AM=2AD+3AC,故C,M,D三点共线,且5DM=3DC,即在△ABM与△ABC中,边AB上的高的比值为35,所以△ABM与△ABC的面积的比值为35.14.答案12解析设BH=x CB,∵AM=12(AB+BH)=12[AB+x(AB-AC)]=12[(1+x)AB-x AC],且AM=λAB+μAC,∴1+x=2λ,-x=2μ,∴λ+μ=12.15.解析(1)延长AD到G,使AD=12AG,连接BG,CG,得到平行四边形ABGC,所以AG=a+b.AD=12AG=12(a+b),AE=23AD=13(a+b),AF=12AC=12b,BE=AE-AB=13(a+b)-a=13(b-2a),BF=AF-AB=12b-a=12(b-2a).(2)证明:由(1)可知BE=23BF, 又因为BE,BF有公共点B,所以B,E,F三点共线.16.解析∵BP=AP-AB=AP-a,CP=AP-AC=AP-b,3AP+4BP+5CP=0, ∴3AP+4(AP-a)+5(AP-b)=0,∴AP=13a+512b.设AD=t AP(t∈R),则AD=13ta+512tb.①又设BD=k BC(k∈R),由BC=AC-AB=b-a,得BD=k(b-a). 而AD=AB+BD=a+BD.∴AD=a+k(b-a)=(1-k)a+kb.②由①②得13t=1-k,512t=k,解得t=43.代入①得AD=49a+59b.∴AP=13a+512b,AD=49a+59b.。
2018课标版理数一轮(5)第五章-平面向量(含答案)1 第一节 平面向量的概念及其线性运算
1 4
栏目索引
5.已知a与b是两个不共线向量,且向量a+λb与-(b-3a)共线,则λ= . 答案 - 解析 由题意知存在k∈R,使得a+λb=k[-(b-3a)],
1 k , λ k , 3 所以 解得 1 3 k , λ 1 . 3
k λ, 所以k=±1. k λ 1,
所以存在实数λ,使ka+b=λ(a+kb)(λ<0), 所以
又λ<0,k=λ,所以k=-1. 故当k=-1时,两向量反向共线.
(4)已知a,b是两个非零向量,当a,b共线时,一定有b=λa(λ为常数),反之也 成立. (√)
栏目索引
1.下列说法正确的是 (
)
AB ∥ AB 所在的直线平行于 CD 就是 CD 所在的直线 A.
B.长度相等的向量叫相等向量 C.零向量长度等于0 D.共线向量是在同一条直线上的向量
)
OA +2 B.- OB
1 2 OA + OB D.- 3 3 OC = OC - OC =2 OA ),∴ OA OB + OB +2 OB +2( BC = AC = 解法一:
OA - A.2 OB
3.共线向量定理 向量a(a≠0)与b共线的充要条件是存在唯一一个实数λ,使得 b=λa .
判断下列结论的正误.(正确的打“√”,错误的打“×”)
(1)向量不能比较大小,但向量的模可以比较大小. (√)
(2) BA = OA - OB . (√)
AB 与向量 (3)向量 CD 是共线向量,则A,B,C,D四点在一条直线上. (×)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一节平面向量的概念与线性运算
[基础达标]
一、选择题(每小题5分,共30分)
1a,b是两个不共线的向量,若3a-b与a+λb共线,则实数λ=()
A.-
B.
C.-
D.
1.A【解析】由3a-b与a+λb共线,可设3a-b=k(a+λb),则解得λ=-.
2m,n的夹角为,且|m|=,|n|=2,在三角形ABC
中,=2m+2n,=2m-6n,D为BC边的中点,则||=() A.2 B.4 C.6 D.8
2.A【解析】)=(2m+2n+2m-6n)=2m-2n,故||2=(2m-2n)2=4m2-8m·n+4n2=12-8××2×+16=4,即得||=2.
3ABCD的边长为a,∠ABC=60°,则=()
A.-a2
B.-a2
C.a2
D.a2
3.D【解析】由题意可得a2,则
=()·=||2+a2.
4.设a,b是非零向量,下列四个条件中,一定能使=0成立的是()
A.a=-b
B.a∥b
C.a=2b
D.a⊥b
4.A【解析】=0,即=-,则a=-·b,故向量a与向量b共线且方向相反.
5O,A,B不在同一条直线上,点P为该平面上一点,且,则()
A.点P在线段AB上
B.点P在线段AB的反向延长线上
C.点P在线段AB的延长线上
D.点P不在直线AB上
5.B【解析】)=,即
,所以点P在线段AB的反向延长线上.
6.O是平面上一定点,A,B,C是该平面上不共线的三个点,一动点P满足:
+λ(),λ∈(0,+∞),则直线AP一定通过△ABC的() A.外心 B.内心 C.重心 D.垂心
6.C【解析】如图,取BC中点 D.∵+λ(),
=λ(),即=2λ,∴A,P,D三点共线,∴AP一定通过△ABC的重心.
二、填空题(每小题5分,共10分)
7.已知O为△ABC内一点,且+2=0,则△AOC与△ABC的面积之比是.
7.1∶2【解析】如图所示,取AC中点D,∴=2,∴,∴O为BD的中点,∴△AOC与△ABC的面积之比为两者高之比.
8.设D,E分别是△ABC的边AB,BC上的点,AD=AB,BE=BC.若=λ1+λ2 (λ1,λ2为实数),则λ1+λ2的值为.
8.【解析】由于
)=-
=λ1+λ2,则λ1=-,λ2=,故λ1+λ2=.
[高考冲关]
1.(5分O,P,Q,E,F,G,H,则=
()
A. B. C. D.
1.D【解析】在方格纸上作出,如图所示,则容易看出.
2.(5分ABCD为平行四边形,||=6,||=4.若点
M,N满足=3=2,则=()
A.20
B.15
C.9
D.6
2.C【解析】
=()·()=()·()=
×62-×42=9.
3.(5分△ABC中,过中线AD中点E任作一直线
分别交边AB,AC于M,N两点,设=x=y(x,y≠0),则4x+y的最小值是.
3.【解析】由题可知,所以,因
此,由于M ,E ,N 三点共线,所以=1(x>0,y>0),而
4x+y=(4x+y )·=1++1=,当且仅当y=2x ,即x=,y=时,
等号成立,即4x+y 的最小值为.
4.(10分)如图所示,已知点G 是△ABO 的重心.
(1)求
;
(2)若PQ 过△ABO 的重心G ,且=a , =b , =m a , =n b ,试探究是
否为定值,如果是,写出推理过程并求出定值,如果不是说明理由.
4.【解析】(1)如图所示,延长OG 交AB 于M 点,
则M 是AB 的中点.
∴=2.
∵G 是△ABO 的重心, ∴
=-2
.
∴=0.
(2)∵M 是AB 边的中点,
∴)= (a+b ).
又∵G是△ABO的重心,
∴(a+b).
∴(a+b)-m a=a+b.而=n b-m a,
∵P,G,Q三点共线,
∴有且只有一个实数λ,使得=λ.
∴a+b=λn b-λm a.
∴a+b=0.
∵a与b不共线,∴
消去λ,得=3,
即为定值3.。
