矩阵的线性变换
矩阵的变换和应用

矩阵的变换和应用矩阵是线性代数中重要的概念之一,它具有广泛的应用范围。
在数学、工程、科学等领域,矩阵用于描述和处理各种数据和问题。
本文将重点介绍矩阵的变换和应用,包括线性变换、旋转变换、缩放变换和平移变换等。
一、线性变换矩阵的线性变换是矩阵在向量空间中的应用之一。
线性变换是指将一个向量或一个向量组通过矩阵的相乘操作进行转换的过程。
在二维空间中,线性变换可以表示为如下形式:\[\begin{pmatrix}x' \\y'\end{pmatrix}=\begin{pmatrix}a &b \\c & d\end{pmatrix}\begin{pmatrix}x \\y\end{pmatrix}\]其中,矩阵的第一行表示了原始向量在x轴上的线性变换,第二行表示了原始向量在y轴上的线性变换。
通过对矩阵进行相乘运算,可以得到经过线性变换后的新向量坐标。
二、旋转变换旋转变换是矩阵在几何学中的重要应用之一。
通过矩阵的乘法运算,可以将一个向量绕着原点进行旋转。
在二维空间中,旋转变换可以表示为如下形式:\[\begin{pmatrix}x' \\y'\end{pmatrix}=\begin{pmatrix}\cos\theta & -\sin\theta \\\sin\theta & \cos\theta\end{pmatrix}\begin{pmatrix}x \\y\end{pmatrix}\]其中,θ表示旋转的角度。
通过对原始向量和旋转矩阵进行相乘运算,可以得到经过旋转变换后的新向量坐标。
三、缩放变换缩放变换是矩阵在图形学和几何学中的常见应用之一。
通过矩阵的乘法运算,可以将一个向量在x轴和y轴上进行不同比例的缩放。
在二维空间中,缩放变换可以表示为如下形式:\[\begin{pmatrix}x' \\y'\end{pmatrix}=s_x & 0 \\0 & s_y\end{pmatrix}\begin{pmatrix}x \\y\end{pmatrix}\]其中,s_x表示x轴的缩放比例,s_y表示y轴的缩放比例。
7.3 线性变换的矩阵

第七章 线性变换 学习单元3: 线性变换的矩阵_________________________________________________________● 导学 学习目标:理解线性变换在一个基下的矩阵的概念;会计算线性变换在一个基下的矩阵;理解线性变换在不同基下的矩阵的相似关系;掌握矩阵等价与矩阵相似的区别与联系。
学习建议:线性变换在一个基下的矩阵建立了线性变换与矩阵的对应关系,类似于平面上点与坐标的对应关系,有了这种对应关系,可以让线性变换问题与矩阵问题互相转化。
建议大家多看书,认真理解概念与结论。
重点难点:重点:深刻理解线性变换在一个基下的矩阵。
难点:理解线性变换在两个不同基下的矩阵的相似关系。
_________________________________________________________● 学习内容 一、线性变换的确定设V 为P 上n 维线性空间,1,,n εεL 为V 的一个基,对任何11,n n V x x ξξεε∈=++L ,()A L V ∈,则11()()()n n A x A x A ξεε=++L 。
即只要知道了1(),()n A A εεL ,则()A ξ也就确定了。
命题1 设1,,n εεL 为线性空间V 的一个基,,()A B L V ∈,则A = B 当且仅当()(),1,2,,i i A B i n εε==L 。
命题2 设1,,n εεL 为线性空间V 的一个基,1,,n ααL 为V 中一个向量组,则存在()A L V ∈,使(),1,2,,i i A i n εα==L 。
定理 设1,,n εεL 为V 的一个基,1,,n ααL 为V 中任意n 个向量,则存在唯一的()A L V ∈,使(),1,2,,i i A i n εα==L 。
例 设V 为P 上n 维线性空间,()A L V ∈,A 不可逆,证明存在V 的非零线性变换B ,使得BA = 0。
初中数学知识点矩阵的线性变换与应用

初中数学知识点矩阵的线性变换与应用初中数学知识点:矩阵的线性变换与应用矩阵的线性变换是初中数学中的一个重要知识点,它广泛应用于代数、几何和物理等领域。
本文将介绍矩阵的线性变换的概念、线性变换的性质以及矩阵在几何变换中的应用。
一、矩阵的线性变换的概念矩阵的线性变换是指通过矩阵对向量进行操作,从而实现对向量的变换。
在数学中,矩阵可以表示为一个二维数组,通过对矩阵进行乘法运算,可以实现对向量的伸缩、旋转和平移等操作。
二、线性变换的性质线性变换具有以下几个重要的性质:1. 保持零向量不变:对于任意矩阵A,有A*0=0,即矩阵A对零向量的线性变换结果仍为零向量。
2. 直线映射为直线:线性变换保持直线的性质,即直线经过线性变换后仍为直线。
3. 原点不变性:线性变换保持原点的位置不变,即原点经过线性变换后仍为原点。
4. 共线性保持性:线性变换保持向量共线的性质,即两个向量共线,则它们经过线性变换后仍共线。
三、矩阵在几何变换中的应用1. 平移变换:矩阵的平移变换可以实现对向量的平移操作。
通过向量的平移变换,我们可以描述物体在空间中的位置变化。
2. 旋转变换:矩阵的旋转变换可以实现对向量的旋转操作。
通过向量的旋转变换,我们可以描述物体在空间中的旋转变化。
3. 缩放变换:矩阵的缩放变换可以实现对向量的伸缩操作。
通过向量的缩放变换,我们可以描述物体在空间中的大小变化。
4. 剪切变换:矩阵的剪切变换可以实现对向量的剪切操作。
通过向量的剪切变换,我们可以描述物体在空间中的形状变化。
矩阵的线性变换在几何变换中具有广泛的应用,例如在计算机图形学中,矩阵的线性变换可以实现对图像的变换和渲染。
同时,在物理学中,矩阵的线性变换也被广泛应用于描述物体运动和力学变化。
总结:矩阵的线性变换是初中数学中的一个重要知识点,它是代数、几何和物理等领域中不可或缺的工具。
通过矩阵的线性变换,我们可以实现对向量的伸缩、旋转和平移等操作,同时在几何变换中具有广泛的应用。
线性变换的矩阵表示

线性变换的矩阵表示线性变换是数学中的重要概念,它在许多领域都有广泛应用。
线性变换可以通过矩阵表示,这种表示形式方便计算和讨论线性变换的性质。
本文将介绍线性变换的矩阵表示以及相关概念和性质。
1. 线性变换的定义线性变换是指满足以下两个条件的映射:(1) 对于任意向量u和v以及实数a和b,线性变换T满足T(a*u +b*v) = a*T(u) + b*T(v)。
(2) 线性变换T对于向量的加法和数乘运算封闭,即T(u + v) = T(u) + T(v),T(k*u) = k*T(u)(k为实数)。
2. 矩阵表示的意义线性变换的矩阵表示可以将线性变换转化为矩阵的乘法运算,从而方便计算和分析线性变换的性质。
对于任意线性变换T,可以找到一个矩阵A,使得对于任意向量u,有T(u) = A*u。
矩阵A被称为线性变换T的矩阵表示。
3. 线性变换的矩阵表示方法线性变换的矩阵表示可以通过以下步骤得到:(1) 选择标准基下的基向量,分别记作e1, e2, ..., en。
(2) 对于每个基向量ei,计算线性变换T(ei)的坐标表示,得到矩阵A的第i列。
(3) 将所有计算得到的列向量排列起来,得到矩阵A。
4. 矩阵表示的性质线性变换的矩阵表示具有以下性质:(1) 线性变换的合成对应于矩阵的乘法。
对于线性变换T1和T2,它们的矩阵表示分别为A和B,则它们的合成线性变换对应的矩阵表示为A*B。
(2) 线性变换的逆对应于矩阵的逆。
若线性变换T存在逆变换,它们的矩阵表示分别为A和A^-1,则逆变换对应的矩阵表示为A^-1。
(3) 线性变换的像空间和核空间可以通过矩阵表示进行刻画。
像空间对应于矩阵的列空间,而核空间对应于矩阵的零空间。
5. 矩阵表示的例子考虑一个二维平面上的旋转变换,将向量绕原点逆时针旋转θ度。
选择标准基下的基向量为e1 = (1, 0)和e2 = (0, 1)。
对于基向量e1,旋转变换后的坐标表示为cosθ*e1 - sinθ*e2。
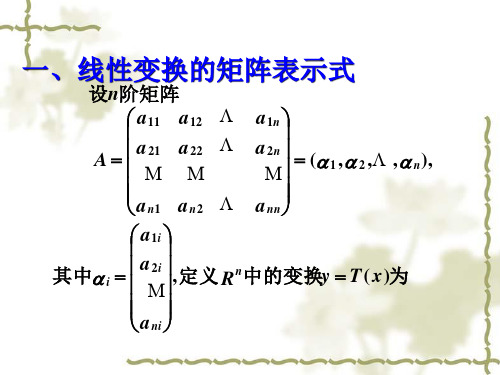
线性变换的矩阵表示式
0 1 0 0 0 2 A 0 0 0 0 0 0
0 0
n 1
0
例3 在 R3中,T表示将向量投影到xOy平面的线性
变换,即
(1)取基为Ti(,xji,
k,
yj zk) xi 求T的矩阵;
yj ,
(2)取基为
i ,
j,
i
j
k,
求T的矩阵.
解 即
Ti i ,
(1)
TTkj
j, 0,
1
T (i , j , k ) (i , j , k ) 0
0 1
0 0.
0 0ቤተ መጻሕፍቲ ባይዱ0
T i ,
(2)
T T
j ,
i j
,
即
1 0 1
T ( , , ) ( , , ) 0 1 1.
0 0 0
此例表明:同一个线性变换在不同的基下一般 有不同的矩阵.
i 1
i 1
x1
(T ( 1),T (
2),
,T (
n))
x2
xn
x1
( 1 , 2 , , n)A x2 ,
xn
即
T ( 1 , 2 ,
,
n)
x1 x2
( 1 , 2 ,
,
n) A
x1 x2 .
x
n
xn
上式唯一地确定了一个变换T ,并且所确定的 变换T是以A为矩阵的线性变换.
x
n
xn
可知 : 在基 1 , 2 , , n下,
的坐标为
x1
x2 ;
xn
T ( )的坐标为
x1
T ( ) A x2 .
矩阵的线性变换和过渡矩阵

矩阵的线性变换和过渡矩阵矩阵在数学中有着重要的作用,特别是在线性代数方面。
本文将讨论矩阵的线性变换以及过渡矩阵,这些概念是理解矩阵运算的重要组成部分。
矩阵的线性变换是指在矩阵乘法的基础上对向量进行变换。
线性变换将向量映射到了另一个向量,可以将其看作是对向量空间的一种操作。
对于一个$m \times n$的矩阵$A$,它可以被用来进行线性变换。
将$A$作为一个线性变换矩阵来看待,它将一个$n$维的向量$x$映射到一个$m$维的向量$y$。
向量$y$可以表示为$y=Ax$,这个公式也可以被称为线性变换的表达式。
线性变换的一个重要性质是它满足线性性。
也就是说,对于同一向量空间中的任意两个向量$x$和$y$以及任意两个标量$a$和$b$,都有:$T(ax+by) = aT(x) + bT(y)$其中$T$表示线性变换,也就是矩阵$A$。
现在考虑如何进行线性变换的组合。
如果有两个线性变换$T_1$和$T_2$,分别由矩阵$A_1$和$A_2$表示,可以进行组合成一个总的线性变换$T_3$,表示为$T_3=T_2 \circ T_1$。
组合后的线性变换的矩阵是由两个原始变换矩阵相乘的结果。
也就是说,$A_3=A_2A_1$。
过渡矩阵是在同一个向量空间内,由一个基向量组转化为另一个基向量组的矩阵。
它的作用是将一个向量在原来的基向量组下的坐标,转化为在新基向量组下的坐标。
因此,过渡矩阵可以被用来描述向量在不同基向量组下的表示。
当我们在同一个向量空间内考虑两个不同的基向量组时,过渡矩阵$P$的作用就体现出来了。
如果向量$v$在旧的基向量组下的坐标表示为$x$,在新的基向量组下的坐标表示为$y$,那么:$y=Px$过渡矩阵的逆可以被用来完成从新基向量组回到旧基向量组的变换。
也就是说,如果向量$v$在新的基向量组下的坐标表示为$y$,在旧的基向量组下的坐标表示为$x$,那么:$x=P^{-1}y$过渡矩阵可以被用来解决许多问题。
线性变换的矩阵表示线性变换与矩阵的关系与计算
线性变换的矩阵表示线性变换与矩阵的关系与计算线性变换的矩阵表示——线性变换与矩阵的关系与计算在数学中,线性变换是一类重要的变换,具有广泛的应用背景。
线性变换可以通过矩阵来表示,这为我们在计算和理解线性变换提供了便利。
本文将介绍线性变换与矩阵的关系,以及如何进行线性变换的矩阵计算。
一、线性变换与矩阵的关系线性变换是指保持直线性质和原点不动的变换。
对于一个n维向量空间V中的向量x,若存在一个线性变换T,将向量x映射为向量y,即y=T(x),则称T为从V到V的一个线性变换。
线性变换可以通过矩阵的乘法运算来表示。
设V是n维向量空间,取V中的一组基{v1,v2,...,vn},在这组基下,对于向量x和y,若y=T(x),则存在一个n×n的矩阵A,使得y=Ax。
这个矩阵A就是线性变换T对应的矩阵表示。
矩阵表示的好处在于,通过矩阵的乘法运算,我们可以将线性变换转化为矩阵的计算,从而简化问题的求解过程。
二、线性变换的矩阵表示对于线性变换T,我们希望找到它对应的矩阵表示A。
假设V是n 维向量空间,取V中的一组基{v1,v2,...,vn}。
根据线性变换的定义,对于向量vi,有T(vi)=wi,我们可以将T(vi)表示为基向量w1,w2,...,wn的线性组合。
设T(vi)=w1i+w2i+...+wni,其中wi是基向量wi的系数。
我们可以将系数wi构成一个列向量Wi,将基向量构成一个矩阵W。
则有W=[w1,w2,...,wn],Wi=AW,其中A是线性变换T对应的矩阵表示。
求解矩阵A的方法有很多种,最常用的方法是利用线性变换T在基向量上的作用。
将基向量vi映射为向量wi,我们可以在基向量的基础上用线性组合的方式得到wi。
将所有的基向量和对应的映射向量展开,我们可以得到矩阵A的表达式。
三、线性变换的矩阵计算在得到线性变换的矩阵表示后,我们可以利用矩阵的乘法运算对线性变换进行计算。
设矩阵A对应线性变换T,向量x对应向量y,即y=Ax。
矩阵中的线性变换与运算
应用:在向量空间中,转置矩 阵可以用来表示向量坐标的变 换
举例:对于矩阵A,其转置矩 阵记为A^T
线性变换的矩阵表 示
线性变换的定义:将向量空间中的 向量通过线性组合进行变换
线性变换的性质:线性变换具有加 法、数乘和结合律等性质
添加标题
添加标题
添加标题
添加标题
矩阵表示:线性变换可以用矩阵表 示,矩阵的每一列对应一个基向量
定义:两个线性变换的乘法是指将第一个线性变换的结果作为第二个线性变换的输入
性质:乘法满足结合律和单位元存在性,即(AB)C=A(BC),存在单位元E使得EA=AE=A
矩阵表示:两个线性变换的乘法可以通过矩阵相乘来表示,即线性变换A和B的乘积可以通过 矩阵A和B相乘得到
应用:线性变换的乘法在矩阵计算、微分学、积分学等领域有着广泛的应用
线性变换的逆:定义和性质
逆矩阵的求解方法
添加标题
添加标题
逆矩阵的定义和性质
添加标题
添加标题
逆矩阵的应用
矩阵的分解与特征 值
定义:将矩阵 分解为几个简 单的矩阵的乘
积
分类:行阶梯 形、列阶梯形、
三角形
计算方法:高 斯消元法、LU
分解等
应用:求解线 性方程组、计
算行列式等
定义:特征值是线 性变换在特征向量 上的表现,是矩阵 的一个重要属性。
矩阵中的线性变换与 运算
汇报人:XX
目录
添加目录标题
矩阵与线性变换 的基本概念
矩阵的运算
线性变换的矩阵 表示
线性变换的运算
矩阵的分解与特 征值
添加章节标题
矩阵与线性变换的 基本概念
矩阵是一个由数字组成的矩形阵列 矩阵的行数和列数可以不同 矩阵的加法、减法和数乘满足结合律和交换律 矩阵的乘法不满足结合律和交换律
矩阵与线性变换
矩阵与线性变换在线性代数中,矩阵与线性变换是密切相关的概念。
矩阵是一种有序矩形数表,而线性变换是一种保持向量加法和数乘的运算的函数。
本文将就矩阵与线性变换的概念、性质以及二者之间的关系进行探讨。
一、矩阵的定义和性质矩阵是数学中一种重要的代数结构,对于描述线性变换起到关键作用。
它是按照矩形的形式排列的一组数。
在定义方面,一个矩阵可以表示为m行n列的一个矩形数表,记作A=[a_{ij}],其中1 ≤ i ≤ m,1 ≤ j ≤ n。
其中,a_{ij}表示矩阵A中第i行第j列的元素。
矩阵的性质有以下几点:1. 矩阵的行数和列数分别称为矩阵的行数和列数。
对于一个m行n列的矩阵,可以记作A_{m×n}。
2. 矩阵A中的元素可以是实数或者复数。
根据元素的性质,可以将矩阵分为实矩阵和复矩阵。
3. 矩阵的转置是指行和列进行对换,记作A^T。
矩阵的转置可以通过矩阵的行与列进行对换得到。
4. 矩阵的加法和数乘是指对矩阵中的每个元素进行相应的操作得到一个新的矩阵。
二、线性变换的定义和性质线性变换是线性代数中一个重要的概念,用于描述一个向量空间内的向量的变换规则。
其基本思想是保持向量加法和数乘的运算。
在线性代数中,一个线性变换可以定义为一个函数T,将向量空间V的向量映射到另一个向量空间W的向量。
线性变换的性质有以下几点:1. 线性变换必须满足保持向量加法的运算规则,即对于向量v和u,T(v+u) = T(v) + T(u)。
2. 线性变换必须满足保持数乘的运算规则,即对于向量v和标量c,T(cv) = cT(v)。
3. 对于线性变换T,它的核是指所有使得T(v) = 0的向量v的集合。
核是向量空间的一个子空间。
4. 对于线性变换T,它的值域是指所有T(v)的向量v的集合。
值域是向量空间的一个子空间。
三、矩阵与线性变换的关系矩阵与线性变换之间存在着密切的联系。
具体而言,对于一个 m 行n 列的矩阵 A,可以定义一个线性变换 T_A,该线性变换将一个 n 维向量空间 V 的向量映射到一个 m 维向量空间 W 的向量。
矩阵与线性变换的性质与求解方法
矩阵与线性变换的性质与求解方法线性变换是线性代数中的重要概念,而矩阵则是线性变换的一个重要工具。
矩阵与线性变换之间有着密切的联系,矩阵可以描述线性变换的性质和求解方法。
本文将主要探讨矩阵与线性变换的性质以及求解方法。
1. 线性变换的定义与性质在开始讨论矩阵与线性变换的关系之前,我们先了解一下线性变换的定义和性质。
线性变换是指在向量空间中,保持加法和数乘运算的函数。
具体而言,对于向量空间V中的两个向量u和v 以及一个标量c,线性变换T应满足以下两个性质:(1)T(u + v) = T(u) + T(v) (加法性质)(2)T(cu) = cT(u) (数乘性质)2. 矩阵与线性变换的关系矩阵可以用来表示线性变换,这一点是线性代数的一项重要概念。
假设我们有一个线性变换T,将向量空间V中的向量映射到向量空间W中的向量,可以用以下形式表示:T(x) = Ax其中,x是向量空间V中的一个向量,A是一个矩阵,T(x)是线性变换T作用在向量x上的结果。
3. 线性变换的矩阵表示当线性变换T被表示为矩阵A时,我们可以通过矩阵与向量的乘法来计算线性变换作用于向量上的结果。
具体而言,对于线性变换T(x) = Ax,将向量x表示为列向量[x1, x2, ..., xn],矩阵A为一个m×n的矩阵,则可以用以下形式计算线性变换的结果:T(x) = Ax = [a1_1 x1 + a1_2 x2 + ... + a1_n xn, a2_1 x1 + a2_2 x2 + ... + a2_n xn, ..., am_1 x1 + am_2 x2 + ... + am_n xn]4. 线性变换的求解方法在实际问题中,我们需要求解线性变换作用于给定向量上的结果。
有两种常见的求解方法:矩阵乘法和矩阵求逆。
(1)矩阵乘法:如果我们已知线性变换T的矩阵表示A和向量x,我们可以通过矩阵乘法来计算线性变换的结果T(x)。
将向量x表示为列向量[x1, x2, ..., xn],矩阵A为一个m×n的矩阵,则可以用以下形式计算线性变换的结果:T(x) = Ax(2)矩阵求逆:如果我们已知线性变换T的矩阵表示A和线性变换的结果T(x),我们可以通过求解方程组Ax = T(x)来求解向量x。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
矩阵的线性变换
1 矩阵的线性变换
矩阵的线性变换是一种数学方法,它可以用来描述图像、物体等
的变换方式。
由于可以有效地描述物体变换过程,矩阵的线性变换得
到了许多研究者的青睐。
2 矩阵的具体定义
矩阵是一种数据结构,用以表示一类对象以及其属性之间的关系。
它由一个矩形结构组成,由行列交叉形成。
一个矩阵可以表达一个或
多个函数的变换过程,其结构具有一定的稳定性,不同行列的元素的
变化规律都是一致的。
3 矩阵的线性变换
矩阵的线性变换是一种基于矩阵的变换方法,它可以有效地描述
几何中物体的变换过程。
矩阵的线性变换可以将几何中物体变换为目
标状态,并可以将通过变换可以获得几何曲线、平面、曲面等的直观
表示。
4 应用
矩阵的线性变换的应用非常广泛,可以用于描述世界上任何物体
的变换。
它是绘图学、图像处理、机器学习等领域的重要组成。
例如,矩阵的线性变换可用于描述图像的缩放、旋转、平移等变换,从而实
现图像分析与处理。
此外,还可以用于运动跟踪、物体识别、机器人控制等场景。
5 总结
矩阵的线性变换是一种数学方法,具有建模灵活性和简单性的特点。
它可以有效解决几何形状的变换问题,广泛应用于计算机视觉、图像处理、机器学习等领域中。
未来,矩阵的线性变换将在计算机科学等更广阔的领域中发挥重要作用。
