中考数学试题分类46 综合型问题
2024年中考数学复习:综合与实践专项练习

综合与实践专项练习类型1 实践操作型试题1.(2022江苏宿迁)如图,在网格中,每个小正方形的边长均为1,每个小正方形的顶点称为格点,点A、B、C、D、M 均为格点.【操作探究】在数学活动课上,佳佳同学在如图①的网格中,用无刻度的直尺画了两条互相垂直的线段AB、CD,相交于点P,并给出部分说理过程.请你补充完整......:解:在网格中取格点E,构建两个直角三角形,分别是△ABC 和△CDE.在Rt△ABC中, tan∠BAC=BCAC =12,在Rt△CDE 中, ,所以tan∠BAC=tan∠DCE.所以∠BAC=∠DCE.因为∠ACP+∠DCE=∠ACB=90°,所以∠ACP+∠BAC=90°.所以∠APC=90°,即AB⊥CD.【拓展应用】(1)图②是以格点O 为圆心,AB 为直径的圆,请你只用无刻度的直尺........,在BM 上找出一点P,使PM=AM,写出作法,并给出证明;(2)图③是以格点O为圆心的圆,请你只用无刻度的直尺........,在弦AB 上找出一点P,使AM²=AP⋅AB,写出作法,不用证明.2.(2022 黑龙江齐齐哈尔)综合与实践数学是以数量关系和空间形式为主要研究对象的科学.数学实践活动有利于我们在图形运动变化的过程中去发现其中的位置关系和数量关系,让我们在学习与探索中发现数学的美,体会数学实践活动带给我们的乐趣.转一转:如图①,在矩形ABCD 中,点E、F、G分别为边BC、AB、AD 的中点,连接EF、DF,H 为DF 的中点,连接GH.将△BEF绕点B 旋转,线段DF、GH 和CE 的位置和长度也随之变化.当△BEF绕点B顺时针旋转90°时,请解决下列问题:(1)图②中,AB=BC,此时点E落在AB的延长线上,点F 落在线段BC上,连接AF,猜想GH 与CE 之间的数量关系,并证明你的猜想;(2)图③中,AB=2,BC=3,则GHCE =¯;(3)当AB=m,BC=n时, GHCE =¯;剪一剪、折一折:(4)在(2)的条件下,连接图③中矩形的对角线AC,并沿对角线AC剪开,得△ABC(如图④).点M、N分别在AC、BC上,连接MN,将△CMN沿MN 翻折,使点C 的对应点P 落在AB 的延长线上,若PM 平分∠APN,,则CM的长为.类型2 探究迁移型试题3.(2022 山东泰安)问题探究(1) 在△ABC 中,BD,CE 分别是∠ABC 与∠BCA的平分线.①若∠A=60°,AB=AC,如图1,试证明:BC=CD+BE;②将①中的条件“AB=AC”去掉,其他条件不变,如图2,问①中的结论是否成立?并说明理由;迁移运用(2)若四边形ABCD 是圆的内接四边形,且∠ACB=2∠ACD,∠CAD=2∠CAB,如图3,试探究线段AD,BC,AC 之间的等量关系,并证明.4.(2022 甘肃武威)已知正方形ABCD,E为对角线AC上一点.【建立模型】如图1,连接BE,DE.求证:BE=DE;【模型应用】如图2,F 是DE 延长线上一点,FB⊥BE,EF交AB 于点G,连接AF.(1)判断△FBG的形状并说明理由;(2)若G为AB 的中点,且AB=4,求AF的长;【模型迁移】如图3,F 是DE 延长线上一点,FB⊥BE,EF 交AB 于点G,BE=BF.求证:GE= (√2−1)DE.类型3 综合应用型试题5.(2022山东潍坊)为落实“双减”政策,老师布置了一项这样的课后作业:二次函数的图象经过点(-1,-1),且不经过第一象限,写出满足这些条件的一个函数表达式.【观察发现】请完成作业,并在直角坐标系中画出大致图象;【思考交流】小亮说:“满足条件的函数图象的对称轴一定在y轴的左侧.”小莹说:“满足条件的函数图象一定在x轴的下方.”你认同他们的说法吗?若不认同,请举例说明;【概括表达】小博士认为这个作业的答案太多,老师不方便批阅,于是探究了二次函数y=ax²+bx+c的图象与系数a,b,c 的关系,得出了提高老师作业批阅效率的方法.请你探究这个方法,写出探究过程.6.(2022湖南湘潭)在△ABC中,∠BAC=90°,AB=AC,直线l经过点A,过点B、C分别作l的垂线,垂足分别为点D、E.(1)特例体验:如图①,若直线l∥BC,AB=AC =√2,,分别求出线段BD、CE 和DE 的长;(2)规律探究:(i)如图②,若直线l从图①状态开始绕点A 旋转α(0°<α<45°),请探究线段BD、CE和DE 的数量关系并说明理由;(ii)如图③,若直线l从图①状态开始绕点A顺时针旋转α(45°<α<90°),与线段BC相交于点H,请再探究线段BD、CE 和DE的数量关系并说明理由;(3)尝试应用:在图③中,延长线段BD交线段AC于点F,若CE=3,DE=1,求S△BFC-。
中考数学-专题-综合型问题45页文档

56、书不仅是生活,而且是现在、过 去和未 来文化 生活的 源泉。 ——库 法耶夫 57、生命不可能有两次,但许多人连一 次也不 善于度 过。— —吕凯 特 58、问渠哪得清如许,为有源头活水来 。—— 朱熹 59、我的努力求学没有得到别的好处, 只不过 是愈来 愈发觉 自己的 无知。 ——笛 卡儿
拉
60、生活的道路一旦选定,就要勇敢地 走到底 ,决不 回头。 ——左ຫໍສະໝຸດ 中考数学-专题-综合型问题
36、“不可能”这个字(法语是一个字 ),只 在愚人 的字典 中找得 到。--拿 破仑。 37、不要生气要争气,不要看破要突 破,不 要嫉妒 要欣赏 ,不要 托延要 积极, 不要心 动要行 动。 38、勤奋,机会,乐观是成功的三要 素。(注 意:传 统观念 认为勤 奋和机 会是成 功的要 素,但 是经过 统计学 和成功 人士的 分析得 出,乐 观是成 功的第 三要素 。
中考数学真题分类汇编(150套)专题四十六 综合型问题
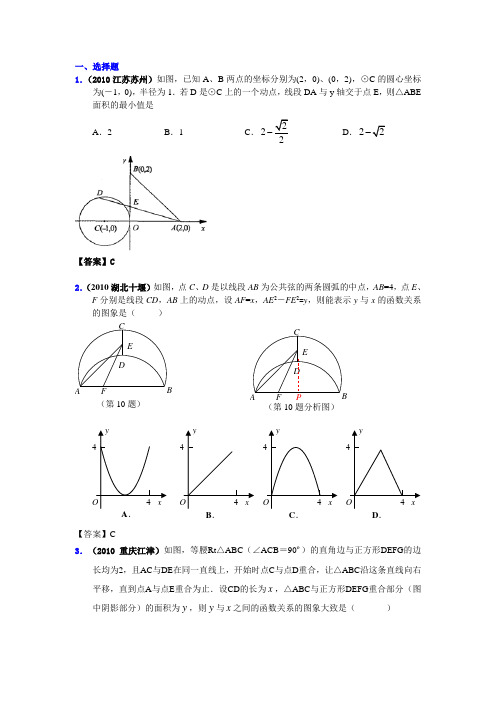
一、选择题 1.(2010江苏苏州)如图,已知A 、B 两点的坐标分别为(2,0)、(0,2),⊙C 的圆心坐标为(-1,0),半径为1.若D 是⊙C 上的一个动点,线段DA 与y 轴交于点E ,则△ABE 面积的最小值是 A .2 B .1 C.22-D.2【答案】C 2.(2010湖北十堰)如图,点C 、D 是以线段AB 为公共弦的两条圆弧的中点,AB =4,点E 、F 分别是线段CD ,AB 上的动点,设AF =x ,AE 2-FE 2=y ,则能表示y 与x 的函数关系的图象是( )【答案】C3.(2010 重庆江津)如图,等腰Rt △ABC (∠ACB =90º)的直角边与正方形DEFG 的边长均为2,且AC 与DE 在同一直线上,开始时点C 与点D 重合,让△ABC 沿这条直线向右平移,直到点A 与点E 重合为止.设CD 的长为x ,△ABC 与正方形DEFG 重合部分(图中阴影部分)的面积为y ,则y 与x 之间的函数关系的图象大致是( )(第10题) CDE FAB(第10题分析图) CDEF AB P【答案】A 二、填空题1.(2010浙江宁波) 如图,已知⊙P 的半径为2,圆心P 在抛物线2112y x =-上运动,当⊙P 与x 轴相切时,圆心P 的坐标为 ▲ .【答案】)2,6(或)2,6(-(对一个得2分)三、解答题1.(2010安徽芜湖)(本小题满分14分)如图,在平面直角坐标系中放置一矩形ABCO ,其顶点为A (0,1)、B (-33,1)、C (-33,0)、O (0,0).将此矩形沿着过E (-3,1)、F (-433,0)的直线EF 向右下方翻折,B 、C 的对应点分别为B ′、C ′.(1)求折痕所在直线EF 的解析式;(2)一抛物线经过B 、E 、B ′三点,求此二次函数解析式;(3)能否在直线EF 上求一点P ,使得△PBC 周长最小?如能,求出点P 的坐标;若不能,说明理由.【答案】2.(2010广东广州,24,14分)如图,⊙O 的半径为1,点P 是⊙O 上一点,弦AB 垂直平分线段OP ,点D 是APB 上任一点(与端点A 、B 不重合),DE ⊥AB 于点E ,以点D 为圆心、DE 长为半径作⊙D ,分别过点A 、B 作⊙D 的切线,两条切线相交于点C .(1)求弦AB 的长;(2)判断∠ACB 是否为定值,若是,求出∠ACB 的大小;否则,请说明理由;(3)记△ABC 的面积为S ,若2SDE =ABC 的周长.【答案】解:(1)连接OA ,取OP 与AB 的交点为F ,则有OA =1.∵弦AB 垂直平分线段OP ,∴OF =12OP =12,AF =BF . CP DOBAEF CPD OBAEH G在Rt △OAF 中,∵AF,∴AB =2AF(2)∠ACB 是定值.理由:由(1)易知,∠AOB =120°, 因为点D 为△ABC 的内心,所以,连结AD 、BD ,则∠CAB =2∠DAE ,∠CBA =2∠DBA ,因为∠DAE +∠DBA =12∠AOB =60°,所以∠CAB +∠CBA =120°,所以∠ACB =60°; (3)记△ABC 的周长为l ,取AC ,BC 与⊙D 的切点分别为G ,H ,连接DG ,DC ,DH ,则有DG =DH =DE ,DG ⊥AC ,DH ⊥BC .∴ABD ACD BCD S S S S ∆∆∆=++=12AB •DE +12BC •DH +12AC •DG =12(AB +BC +AC ) •DE =12l •DE . ∵2S DE =212l DEDE =l =∵CG ,CH 是⊙D 的切线,∴∠GCD =12∠ACB =30°, ∴在Rt △CGD 中,CG =tan30DG,∴CH =CG.又由切线长定理可知AG =AE ,BH =BE ,∴l =AB +BC +AC ==,解得DE =13,∴△ABC. 3.(2010江苏南京)(8分)如图,正方形ABCD 的边长是2,M 是AD 的中点,点E 从点A 出发,沿AB 运动到点B 停止,连接EM 并延长交射线CD 于点F ,过M 作EF 的垂线交射线BC 于点G ,连结EG 、FG 。
中考数学模拟分类汇编46 综合型问题

中考数学模拟分类汇编46 综合型问题一、选择题1. (2011年北京四中中考全真模拟15)2001年7月13日,北京市获得了第29届运动会的主办权,这一天是星期五,那么第29届奥运会在北京市举办的那一年的7月13日是星期( )A.1B. 3C. 5D. 日 答案:D1、(2011年浙江杭州二模)如图,在矩形ABCD 中,BC=8,AB=6,经过点B 和点D 的两个动圆均与AC 相切,且与AB 、BC 、AD 、DC 分别交于点G 、H 、E 、F ,则EF+GH 的最小值是( ) A .6 B .8 C .9.6 D .10答案:C2、(2011年浙江杭州七模)下列命题:①同位角相等;②如果009045<α<,那么α>αcos sin ;③若关于x 的方程223=+-x mx 的解是负数,则m 的取值范围为m <-4;④相等的圆周角所对的弧相等.其中假.命题..有( ) A .1个 B .2个 C .3个 D .4个答案:C二、填空题1. (2011年北京四中中考全真模拟15)从甲站到乙站有两种走法。
从乙站到丙站有三种走法。
从乙站到丙站有______种走法。
A. 4B. 5C. 6D.7 答案:C2. (2011年北京四中中考全真模拟15)一个窗户被装饰布档住一部分,其中窗户的长与宽之间比为3:2装饰布由一个半圆和两个四分之一圆组成,圆的直径都是2n,这个窗口未被A G BH CFDE第1题遮挡部分的面积为__________。
答案:2 23216nnπ-3. (2011年北京四中中考全真模拟16)如图所示,图中共有条线段,共有个长方形。
答案:18,9.4. (2011年北京四中中考全真模拟17)如图,要给这个长、宽、高分别为x、y、z的箱子打包,其打包方式如右图所示,则打包带的长至少要_________ (单位:mm)(用含x、y、z的代数式表示)答案:2x+4y+6z1、(2011年浙江杭州八模)已知正整数a满足不等式组232-≤+≥axax(x为未知数)无解,则函数41)3(2---=xxay图象与x轴的坐标为答案:11(,0)(,0)24-三、解答题1、(2011年江苏盐都中考模拟)(本题12分)已知:如图,在平面直角坐标系中,四边形ABCO是菱形,且∠AOC=60°,点B的坐标是(0,83),点P从点C开始以每秒1个单位长度的速度在线段CB上向点B移动,同时,点Q从点O开始以每秒a(1≤a≤3)个单位长度的速度沿射线OA方向移动,设t(0<t≤8)秒后,直线PQ交OB于点D.(1)求∠AOB的度数及线段OA的长(2)求经过A、B、C三点的抛物线的解析式;(3)当a=3,OD=334时,求t的值及此时直线PQ的解析式;(4)当a为何值时,以O、Q、D为顶点的三角形与△OAB相似?当a为何值时,以O、Q、D为顶点的三角形与△OAB不相似?请给出你的结论,并加以说明.解:(1)∠AOB=30°,OA=8;(2分)(2)38432+-=xy;(2分)(3)当a=3时,CP=t, OQ=3t,OD=334,∴PB=8-t,BD=833203343=-由△OQD∽△BPD得ODBDOQBP=,即334332038=-tt,∴t=21。
中考数学综合型问题专题训练.docx

中考数学综合型问题专题训练•综合型问题(时间:40分钟)【代数型综合题】特征:指以代数知识为主的或以代数变形技巧为主的一类综合题。
涉及知识:主要包括方程、函数、不等式等内容。
解题策略:用到的数学思想方法有化归思想、分类思想、数形结合思想及代入法、待定系数法、配方法等。
注意:⑴重视归纳整理教材中的基础知识、基本技能、基本方法;⑵重视各知识点之间的联系和数学思想方法、解题技巧的灵活运用;⑶重视知识间的横向联系。
【几何型综合题】特征:指以几何知识为主或者以几何变换为主的一类综合题。
涉及知识:主要包括几何的定义、公理、定理、几何变换等内容。
解题策略:解决几何型综合题的关键是把代数知识与几何图形的性质以及计算与证明有机融合起来,进行分析、推理,从而达到解决问题的目的。
注意:⑴要有较强的理解能力、分析能力、解决问题的能力;⑵对数学知识、数学方法有较强的驾驭能力, 并有较强的创新意识和创新能力。
【代数和几何型综合题】特征:指以代数知识与几何知识综合运用的一类综合题。
涉及知识:代数与几何综合题主要以函数与方程、二角形、四边形等相关知识为主的综合。
解题策略:几何图形的形象直观,代数方法具有一般性,解题过程的可操作性强,因此数形结合思想是数学中重要的思想方法。
注意:数形结合就是根据数学问题的题设和结论之间的内在联系,既分析其数量关系,又揭示其几何意义,使数量关系和几何图形巧妙地结合起来,并充分地利用这种结合,探求解决问题的思路,使问题得以解决的思考方法。
一、选择题:(6'x3 = 18‘)1、在平面直角坐标系中,先将抛物线y=J+x—2关于x 轴作轴对称变换,再将所得的抛物线关于y轴作轴对称变换,那么经两次变换后所得的新抛物线的解析式为()A、y = - x~—x+2B、y= - x~~\~x—2C、y = - x'+x+2D、y=x~+x+22^已知函数y=3—(x~m)(x—n),并且a、b是方程3—(x~m)(x~n)=0的两个根,则实数m、n、a、b的大小关系可能是()A、m<a<b<nB、C、a<m<b<nD、a<m<n<b3、如图,在ABCD中,分别以A3、AD为边向外作等边AABE, AADF,延长CB交AE于点G,点G 在点A、E 之间,连接CE、CF、EF,则以下四个结论_定正确的是()①左CDF^AEBC;②Z CDF= ZEAF; A ---------------- --③△ECF是等边三角形;\\ //④、CG侦E。
人教版中考数学专题总复习《综合型问题》练习题及答案精品教学课件PPT

(1)求抛物线的解析式; (2)若点 D 在抛物线上,点 E 在抛物线的对称轴上, 且以 A,O,D,E 为顶点的四边形是平行四边形,求 点 D 的坐标; (3)P 是抛物线上第二象限内的动点,过点 P 作 PM⊥x 轴,垂足为 M,是否存在点 P 使得以点 P,M, A 为顶点的三角形与△BOC 相似?若存在,求出点 P 的坐标;若不存在,请说明理由.
解:(1)设所求方程的根为 y,则 y=-x,所以 x= -y.
把 x=-y 代入已知方程 x2+x-2=0,得(-y)2+ (-y)-2=0.
化简,得 y2-y-2=0.
(2)设所求方程的根为 y,则 y=1x,所以 x=1y. 把 x=1y代入方程 ax2+bx+c=0,得 a(1y)2+b·1y+c=0, 去分母,得 a+by+cy2=0. 若 c=0,则有 ax2+bx=0,于是方程 ax2+bx+c =0 有一个根为 0,不符合题意, ∴c≠0,故所求方程为 cy2+by+a=0(c≠0).
2.解图表信息题关键是“识图”和“用图”.解 题时,要求通过认真阅读、观察和分析图象、图形、 表格来获取信息,根据信息中数据或图形的特征,找 出数量关系或弄清函数的对应关系,研究图形的性质, 进行推理、论证、计算,从而解决实际问题.图表信 息问题往往出现在“方程(组)、不等式(组)、函数、统 计与概率”等知识应用题中,审题时注意把握图表中 的信息.
18分2020德阳为了了解学生对体育活动的喜爱情况某校对参加足球篮球乒乓球羽毛球这四个课外活动小组的人员分布情况进行抽样调查并根据收集的数据绘制了下面两幅不完整的统计图请根据图中提供的信息解答下面的问题
综合型问题
人教版中考数学专题复习
1.阅读理解型问题一般篇幅较长,涉及内容丰富, 构思新颖别致.这类问题一般分两部分:一是阅读材 料,二是考查内容.它要求根据阅读获取的信息回答 问题.提供的阅读材料主要包括:一个新的数学概念 的形成和应用过程,或一个新的数学公式的推导与应 用,或提供新闻背景材料.
全国中考数学试卷分类汇编专题综合性问题

AB
AC折叠,点
A. 1
B.
3
C .2
2
D.
2
3
3
2
【答案】 A
【解析】:∵矩形沿直线 AC折叠,点 B 落在点 E 处,
∴∠ BAC=∠ EAC,AE=AB=C,D
∵矩形 ABCD的对边 AB∥ CD,
∴∠ DAC=∠ BAC,
∴∠ EAC=∠ DAC,
设 AE与 CD相交于 F,则 AF=CF,
又∵ BE1=AB-AE1=10-3x,△ E1FA1∽△ E1BF,∴ E1F:A1E1 =BE1 : E1F ,∴ E1F2
= A1E1?BE1,
过 A 作 AB PP ' ,则 AB OA sin 45 3 2 3 2 22
∴阴影部分 PAA ' P ' 的面积为 S
PP ' AB
32 42
12
④若∠ MON =45°, MN =2,则点 C 的坐标为( 0, 2 1).其中正确结论的个数
是(
)
y
N
C
B
M
OD
A
x
(第 12 题图)
A. 1 【答案】 C
B.2
C.3
D.4
【解析】①由图可知,点 M 的坐标为( OA , AM ),点 N 的坐标为( CN, OC),
∴ OA·AM=OC·CN=k,又∵ OA =OC ,∴ AM=CN ,∴△ OCN ≌△ OAM ,故①正确;
∴ AD 4x 1 AB 8x 2
故选 A.
【方法指导】 本题考查了矩形的性质,平行线的性质,等角对等边的性质,相似三角
形的判定与性质,勾股定理的应用,综合性较强,但难度不大,熟记各性质是解题的
2021年全国各地中考数学试卷解析版分类汇编综合性问题

综合性问题一、选择题1. (2014•年山东东营,第10题3分)如图,四边形ABCD为菱形,AB=BD,点B、C、D、G 四个点在同一个圆⊙O上,连接BG并延长交AD于点F,连接DG并延长交AB于点E,BD 与CG交于点H,连接FH,下列结论:①AE=DF;②FH∥AB;③△DGH∽△BGE;④当CG为⊙O的直径时,DF=AF.其中正确结论的个数是()A. 1 B. 2 C. 3 D. 4考点:圆的综合题.分析:①由四边形ABCD是菱形,AB=BD,得出△ABD和△BCD是等边三角形,再由B、C、D、G四个点在同一个圆上,得出∠ADE=∠DBF,由△ADE≌△DBF,得出AE=DF,②利用内错角相等∠FBA=∠HFB,求证FH∥AB,③利用∠DGH=∠EGB和∠EDB=∠FBA,求证△DGH∽△BGE,④利用CG为⊙O的直径及B、C、D、G四个点共圆,求出∠ABF=120°﹣90°=30°,在RT△AFB 中求出AF=AB在RT△DFB中求出FD=BD,再求得DF=AF.解答:解:①∵四边形ABCD是菱形,∴AB=BC=DC=AD,又∵AB=BD,∴△ABD和△BCD是等边三角形,∴∠A=∠ABD=∠DBC=∠BCD=∠CDB=∠BDA=60°,又∵B、C、D、G四个点在同一个圆上,∴∠DCH=∠DBF,∠GDH=∠BCH,∴∠ADE=∠ADB﹣∠GDH=60°﹣∠EDB,∠DCH=∠BCD﹣∠BCH=60°﹣∠BCH,∴∠ADE=∠DCH,∴∠ADE=∠DBF,在△ADE和△DBF中,∴△ADE≌△DBF(ASA)∴AE=DF故①正确,②由①中证得∠ADE=∠DBF,∴∠EDB=∠FBA,∵B、C、D、G四个点在同一个圆上,∠BDC=60°,∠DBC=60°,∴∠BGC=∠BDC=60°,∠DGC=∠DBC=60°,∴∠BGE=180°﹣∠BGC﹣∠DGC=180°﹣60°﹣60°=60°,∴FGD=60°,∴FGH=120°,又∵∠ADB=60°,∴F、G、H、D四个点在同一个圆上,∴∠EDB=∠HFB,∴∠FBA=∠HFB,∴FH∥AB,故②正确,③∵B、C、D、G四个点在同一个圆上,∠DBC=60°,∴∠DGH=∠DBC=60°,∵∠EGB=60°,∴∠DGH=∠EGB,由①中证得∠ADE=∠DBF,∴∠EDB=∠FBA,∴△DGH∽△BGE,故③正确,④如下图∵CG为⊙O的直径,点B、C、D、G四个点在同一个圆⊙O上,∴∠GBC=∠GDC=90°,∴∠ABF=120°﹣90°=30°,∵∠A=60°,∴∠AFB=90°∴AF=AB,又∵∠DBF=60°﹣30°=30°,∠ADB=60°,∴∠DFB=90°,∴FD=BD,∵AB=BD,∴DF=AF,故④正确,故选:D.点评:此题综合考查了圆及菱形的性质,等边三角形的判定与性质,全等三角形的判定和性质,运用四点共圆找出相等的角是解题的关键.解题时注意各知识点的融会贯通.2. (2014•甘肃白银、临夏,第10题3分)如图,边长为1的正方形ABCD中,点E在CB延长线上,连接ED交AB于点F,AF=x(0.2≤x≤0.8),EC=y.则在下面函数图象中,大致能反映y与x之闻函数关系的是()A.B.C.D.考点:动点问题的函数图象.分析:通过相似三角形△EFB∽△EDC 的对应边成比例列出比例式=,从而得到y 与x之间函数关系式,从而推知该函数图象.解答:解:根据题意知,BF=1﹣x,BE=y﹣1,且△EFB∽△EDC,则=,即=,所以y =(0.2≤x≤0.8),该函数图象是位于第一象限的双曲线的一部分.A、D的图象都是直线的一部分,B的图象是抛物线的一部分,C的图象是双曲线的一部分.故选C.点评:本题考查了动点问题的函数图象.解题时,注意自变量x的取值范围.3.(2014•甘肃兰州,第15题4分)如图,在平面直角坐标系中,四边形OBCD是边长为4的正方形,平行于对角线BD的直线l从O出发,沿x轴正方向以每秒1个单位长度的速度运动,运动到直线l与正方形没有交点为止.设直线l扫过正方形OBCD的面积为S,直线l 运动的时间为t(秒),下列能反映S与t之间函数关系的图象是()A.B.C.D.考点:动点问题的函数图象.分析:根据三角形的面积即可求出S与t的函数关系式,根据函数关系式选择图象.解答:解:①当0≤t≤4时,S=×t×t=t2,即S=t2.该函数图象是开口向上的抛物线的一部分.故B、C错误;②当4<t≤8时,S=16﹣×(t﹣4)×(t﹣4)=t2,即S=﹣t2+4t+8.该函数图象是开口向下的抛物线的一部分.故A错误.故选:D.点评:本题考查了动点问题的函数图象.本题以动态的形式考查了分类讨论的思想,函数的知识和等腰直角三角形,具有很强的综合性.三、解答题1. (2014•上海,第25题14分)如图1,已知在平行四边形ABCD中,AB=5,BC=8,cosB=45,点P是边BC上的动点,以CP为半径的圆C与边AD交于点E、F(点F在点E的右侧),射线CE与射线BA交于点G.(1)当圆C 经过点A 时,求CP 的长;(2)联结AP ,当AP ∥CG 时,求弦EF 的长;(3)当△AGE 是等腰三角形时,求圆C 的半径长.考点:圆的综合题分析: (1)当点A 在⊙C 上时,点E 和点A 重合,过点A 作AH ⊥BC 于H ,直接利用勾股定理求出AC 进而得出答案;(2)首先得出四边形APCE 是菱形,进而得出CM 的长,进而利用锐角三角函数关系得出CP 以及EF 的长;(3)当∠AEG =∠B 时,A 、E 、G 重合,只能∠AGE =∠AEG ,利用AD ∥BC ,得出△GAE ∽△GBC ,进而求出即可.解答: 解:(1)如图1,设⊙O 的半径为r ,当点A 在⊙C 上时,点E 和点A 重合,过点A 作AH ⊥BC 于H ,∴BH =AB •cosB =4,∴AH =3,CH =4,∴AC ==5,∴此时CP =r =5;(2)如图2,若AP ∥CE ,APCE 为平行四边形,∵CE =CP ,∴四边形APCE 是菱形,连接AC 、EP ,则AC ⊥EP ,∴AM =CM =,由(1)知,AB =AC ,则∠ACB =∠B ,∴CP =CE ==,∴EF =2=;(3)如图3:过点C 作CN ⊥AD 于点N ,∵cosB =45, ∴∠B <45°,∵∠BCG <90°,∴∠BGC >45°,∵∠AEG =∠BCG ≥∠ACB =∠B ,∴当∠AEG =∠B 时,A 、E 、G 重合,∴只能∠AGE =∠AEG ,∵AD ∥BC ,∴△GAE ∽△GBC ,∴=,即=,解得:AE =3,EN =AN ﹣AE =1,∴CE ===.点评: 此题主要考查了相似三角形的判定与性质以及勾股定理以及锐角三角函数关系等知识,利用分类讨论得出△AGE 是等腰三角形时只能∠AGE =∠AEG 进而求出是解题关键.2. (2014•四川巴中,第31题12分)如图,在平面直角坐标系xOy 中,抛物线y =ax 2+bx ﹣4与x 轴交于点A (﹣2,0)和点B ,与y 轴交于点C ,直线x =1是该抛物线的对称轴.(1)求抛物线的解析式;(2)若两动点M,H分别从点A,B以每秒1个单位长度的速度沿x轴同时出发相向而行,当点M到达原点时,点H立刻掉头并以每秒个单位长度的速度向点B方向移动,当点M到达抛物线的对称轴时,两点停止运动,经过点M的直线l⊥x轴,交AC或BC 于点P,设点M的运动时间为t秒(t>0).求点M的运动时间t与△APH的面积S的函数关系式,并求出S的最大值.考点:二次函数综合题.分析:(1)根据抛物线y=ax2+bx﹣4与x轴交于点A(﹣2,0),直线x=1是该抛物线的对称轴,得到方程组,解方程组即可求出抛物线的解析式;(2)由于点M到达抛物线的对称轴时需要3秒,所以t≤3,又当点M到达原点时需要2秒,且此时点H立刻掉头,所以可分两种情况进行讨论:①当0<t≤2时,由△AMP∽△AOC,得出比例式,求出PM,AH,根据三角形的面积公式求出即可;②当2<t≤3时,过点P作PM⊥x轴于M,PF⊥y轴于点F,表示出三角形APH的面积,利用配方法求出最值即可.解答:(1)∵抛物线y=ax2+bx﹣4与x轴交于点A(﹣2,0),直线x=1是该抛物线的对称轴,∴,解得:,∴抛物线的解析式是:y=x2﹣x﹣4,(2)分两种情况:①当0<t≤2时,∵PM∥OC,∴△AMP∽△AOC,∴=,即=,∴PM=2t.解方程x2﹣x﹣4=0,得x1=﹣2,x2=4,∵A(﹣2,0),∴B(4,0),∴AB=4﹣(﹣2)=6.∵AH=AB﹣BH=6﹣t,∴S=PM•AH=×2t(6﹣t)=﹣t2+6t=﹣(t﹣3)2+9,当t=2时S的最大值为8;②当2<t≤3时,过点P作PM⊥x轴于M,作PF⊥y轴于点F,则△COB∽△CFP,又∵CO=OB,∴FP=FC=t﹣2,PM=4﹣(t﹣2)=6﹣t,AH=4+(t﹣2)=t+1,∴S=PM•AH=(6﹣t)(t+1)=﹣t2+4t+3=﹣(t﹣)2+,当t=时,S最大值为.综上所述,点M的运动时间t与△APQ面积S的函数关系式是S=,S的最大值为.点评:本题是二次函数的综合题型,其中涉及到运用待定系数法求二次函数的解析式,三角形的面积,二次函数的最值等知识,综合性较强,难度适中.运用数形结合、分类讨论及方程思想是解题的关键.3. (2014•山东威海,第25题12分)如图,已知抛物线y=ax2+bx+c(a≠0)经过A(﹣1,0),B(4,0),C(0,2)三点.(1)求这条抛物线的解析式;(2)E为抛物线上一动点,是否存在点E使以A、B、E为顶点的三角形与△COB相似?若存在,试求出点E的坐标;若不存在,请说明理由;(3)若将直线BC平移,使其经过点A,且与抛物线相交于点D,连接BD,试求出∠BDA的度数.考点:二次函数综合题分析:(1)本题需先根据已知条件,过C点,设出该抛物线的解析式为y=ax2+bx+2,再根据过A,B两点,即可得出结果;(2)由图象可知,以A、B为直角顶点的△ABE不存在,所以△ABE只可能是以点E为直角顶点的三角形.由相似关系求出点E的坐标;(3)如图2,连结AC,作DE⊥x轴于点E,作BF⊥AD于点F,由BC∥AD设BC的解析式为y=kx+b,设AD的解析式为y=kx+n,由待定系数法求出一次函数的解析式,就可以求出D坐标,由勾股定理就可以求出BD的值,由勾股定理的逆定理就可以得出∠ACB=90°,由平行线的性质就可以得出∠CAD=90°,就可以得出四边形ACBF是矩形,就可以得出BF的值,由勾股定理求出DF的值,而得出DF=BF而得出结论.解答:解:(1)∵该抛物线过点C(0,2),∴可设该抛物线的解析式为y=ax2+bx+2.将A(﹣1,0),B(4,0)代入,得,解得,∴抛物线的解析式为:y=﹣x2+x+2.(2)存在.由图象可知,以A、B为直角顶点的△ABE不存在,所以△ABE只可能是以点E 为直角顶点的三角形.在Rt△BOC中,OC=2,OB=4,∴BC==.在Rt△BOC中,设BC边上的高为h,则×h=×2×4,∴h=.∵△BEA∽△COB,设E点坐标为(x,y),∴=,∴y=±2将y=2代入抛物线y=﹣x2+x+2,得x1=0,x2=3.当y=﹣2时,不合题意舍去.∴E点坐标为(0,2),(3,2).(3)如图2,连结AC,作DE⊥x轴于点E,作BF⊥AD于点F,∴∠BED=∠BFD=∠AFB=90°.设BC的解析式为y=kx+b,由图象,得,∴,y BC=﹣x+2.由BC∥AD,设AD的解析式为y=﹣x+n,由图象,得0=﹣×(﹣1)+n∴n=﹣,y AD=﹣x﹣.∴﹣x2+x+2=﹣x﹣,解得:x1=﹣1,x2=5∴D(﹣1,0)与A重合,舍去,D(5,﹣3).∵DE⊥x轴,∴DE=3,OE=5.由勾股定理,得BD=.∵A(﹣1,0),B(4,0),C(0,2),∴OA=1,OB=4,OC=2.∴AB=5在Rt△AOC中,Rt△BOC中,由勾股定理,得AC=,BC=2,∴AC2=5,BC2=20,AB2=25,∴AC2+BC2=AB2∴△ACB是直角三角形,∴∠ACB=90°.∵BC∥AD,∴∠CAF+∠ACB=180°,∴∠CAF=90°.∴∠CAF=∠ACB=∠AFB=90°,∴四边形ACBF是矩形,∴AC=BF=,在Rt△BFD中,由勾股定理,得DF=,∴DF=BF,∴∠ADB=45°.点评:本题考查了运用待定系数法求二次函数解析式和一次函数的解析式的运用,相似三角形的性质的运用,勾股定理的运用,矩形的判定及性质的运用,等腰直角三角形的性质的运用,解答时求出函数的解析式是关键.4. (2014•山东枣庄,第25题10分)如图,在平面直角坐标系中,二次函数y=x2﹣2x﹣3的图象与x轴交于A、B两点,与y轴交于点C,连接BC,点D为抛物线的顶点,点P是第四象限的抛物线上的一个动点(不与点D重合).(1)求∠OBC的度数;(2)连接CD、BD、DP,延长DP交x轴正半轴于点E,且S△OCE=S四边形OCDB,求此时P点的坐标;(3)过点P作PF⊥x轴交BC于点F,求线段PF长度的最大值.考点:二次函数综合题分析:(1)由抛物线已知,则可求三角形OBC的各个顶点,易知三角形形状及内角.(2)因为抛物线已固定,则S四边形OCDB固定,对于坐标系中的不规则图形常用分割求和、填补求差等方法求面积,本图形过顶点作x轴的垂线及可将其分为直角梯形及直角三角形,面积易得.由此可得E点坐标,进而可求ED直线方程,与抛物线解析式联立求解即得P点坐标.(3)PF的长度即为y F﹣y P.由P、F的横坐标相同,则可直接利用解析式作差.由所得函数为二次函数,则可用二次函数性质讨论最值,解法常规.解答:解:(1)∵y=x2﹣2x﹣3=(x﹣3)(x+2),∴由题意得,A(﹣1,0),B(3,0),C(0,﹣3),D(1,﹣4).在Rt△OBC中,∵OC=OB=3,∴△OBC为等腰直角三角形,∴∠OBC=45°.(2)如图1,过点D作DH⊥x轴于H,此时S四边形OCDB=S梯形OCDH+S△HBD,∵OH=1,OC=3,HD=4,HB=2,∴S梯形OCDH=•(OC+HD)•OH=,S△HBD=•HD•HB=4,∴S四边形OCDB=.∴S△OCE=S四边形OCDB==,∴OE=5,∴E(5,0).设l DE:y=kx+b,∵D(1,﹣4),E(5,0),∴,解得,∴l DE:y=x﹣5.∵DE交抛物线于P,设P(x,y),∴x2﹣2x﹣3=x﹣5,解得x=2 或x=1(D点,舍去),∴x P=2,代入l DE:y=x﹣5,∴P(2,﹣3).(3)如图2,设l BC:y=kx+b,∵B(3,0),C(0,﹣3),∴,解得,∴l BC:y=x﹣3.∵F在BC上,∴y F=x F﹣3,∵P在抛物线上,∴y P=x P2﹣2x P﹣3,∴线段PF长度=y F﹣y P=x F﹣3﹣(x P2﹣2x P﹣3),∵x P=x F,∴线段PF长度=﹣x P2+3x P=﹣(x P﹣)2+,(1<x P≤3),∴当x P =时,线段PF 长度最大为.点评:本题考查了抛物线图象性质、已知两点求直线解析式、直角三角形性质及二次函数最值等基础知识点,题目难度适中,适合学生加强练习.5. (2014•山东潍坊,第22题12分)如图1,在正方形ABCD 中,E 、F 分别为BC 、CD 的中点,连接AE 、BF ,交点为G . (1)求证:AE ⊥BF ;(2)将△BCF 沿BF 对折,得到△BPF (如图2),延长FP 交BA 的延长线于点Q ,求sin ∠BQP 的值;(3)将△ABE 绕点A 逆时针方向旋转,使边AB 正好落在AE 上,得到△AHM (如图3),若AM 和BF 相交于点N ,当正方形ABCD 的面积为4时,求四边形GHMN 的面积.考点:相似三角形的判定与性质;全等三角形的判定与性质;正方形的性质;解直角三角形. 分析:(1)由四边形ABCD 是正方形,可得∠ABE =∠BCF =90°,AB =BC ,又由BE =CF ,即可证得△ABE ≌△BCF ,可得∠BAE =∠CBF ,由∠ABF +∠CBF =900可得∠ABF +∠BAE =900,即AE ⊥BF ;(2)由△BCF ≌△BPF , 可得CF =PF ,BC =BP ,∠BFE =∠BFP ,由CD ∥AB 得∠BFC =∠ABF ,从而QB =QF ,设PF 为x ,则BP 为2x ,在Rt △QBF 中可求 QB 为25x ,即可求得答案; (3)由2)(AMAN AHM AGN =∆∆可求出△AGN 的面积,进一步可求出四边形GHMN 的面积.解答:(1)证明:∵E 、F 分别是正方形ABCD 边BC 、CD 的中点,∴CF =BE , ∴Rt △ABE ≌Rt △BCF∴∠BAE =∠CBF又∵∠BAE +∠BEA =900,∴∠CBF +∠BEA =900, ∴∠BGE =900, ∴AE ⊥BF(2)根据题意得:FP =FC ,∠PFB =∠BFC ,∠FPB =900,∵CD ∥AB , ∴∠CFB =∠ABF ,∴∠ABF =∠PF B .∴QF =QB 令PF =k (k >O ),则PB =2k ,在Rt △BPQ 中,设QB =x , ∴x 2=(x -k )2+4k 2, ∴x =25k ,∴sin ∠BQP =54252==k k QP BP (3)由题意得:∠BAE =∠EAM ,又AE ⊥BF , ∴AN =AB =2, ∵ ∠AHM =900, ∴GN //HM , ∴2)(AM AN AHM AGN =∆∆ ∴54)52(12==ΛAGN∴ 四边形GHMN =SΔAHM - SΔAGN =1一54= 54 答:四边形GHMN 的面积是54. 点评:此题考查了相似三角形的判定与性质、正方形的性质、全等三角形的判定与性质以及三角函数等知识.此题综合性较强,难度较大,注意掌握旋转前后图形的对应关系,注意数形结合思想的应用.6. (2014•山东潍坊,第24题13分)如图,抛物线y =ax 2+bx +c (a ≠O )与y 轴交于点C (O ,4),与x 轴交于点A 和点B ,其中点A 的坐标为(-2,0),抛物线的对称轴x =1与抛物线交于点D ,与直线BC 交于点E . (1)求抛物线的解析式;(2)若点F 是直线BC 上方的抛物线上的一个动点,是否存在点F 使四边形ABFC 的面积为17,若存在,求出点F 的坐标;若不存在,请说明理由;(3)平行于DE 的一条动直线Z 与直线BC 相交于点P ,与抛物线相交于点Q ,若以D 、E 、P 、Q 为顶点的四边形是平行四边形,求点P 的坐标。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第46章 综合型问题一、选择题1. (2011 浙江湖州,10,3)如图,已知A 、B 是反比例面数k y x= (k >0,x >0)图象上的两点,BC ∥x 轴,交y 轴于点C .动点P 从坐标原点O 出发,沿O→A→B→C (图中“→”所示路线)匀速运动,终点为C .过P 作PM ∥x 轴,PN ∥y 轴,垂足分别为M 、N .设四边形0MPN 的面积为S ,P 点运动时间为t ,则S 关于t 的函数图象大致为【答案】A2. (2011台湾全区,19)坐标平面上,二次函数362+-=x x y 的图形与下列哪一个方程式的图形没有交点?A . x =50B . x =-50C . y =50D . y =-50【答案】D3. (2011广东株洲,8,3分)某广场有一喷水池,水从地面喷出,如图,以水平地面为x 轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线y=-x 2+4(单位:米)的一部分,则水喷出的最大高度是( )A .4米B .3米C .2米D .1米【答案】D4. (2011山东聊城,12,3分)某公园草坪的防护栏是由100段形状相同的抛物线组成的.为了牢固起见,每段护栏需要间距0.4m 加设一根不锈钢的支柱,防护栏的最高点距底部0.5m (如图),则这条防护栏需要不锈钢支柱的总长度至少为( )A .50mB .100mC .160mD .200m【答案】C5. (2011河北,8,3分)一小球被抛出后,距离地面的高度h (米)和飞行时间t (秒)满足下列函数关系式:61t 5h 2+--=)(,则小球距离地面的最大高度是( )A .1米B .5米C .6米D .7米【答案】C二、填空题 1. (2011湖南怀化,16,3分)出售某种手工艺品,若每个获利x 元,一天可售出(8-x )个,则当x=________元时,一天出售该种手工艺品的总利润y 最大.【答案】42. (2011江苏扬州,17,3分)如图,已知函数xy 3-=与bx ax y +=2(a>0,b>0)的图象交于点P ,点P 的纵坐标为1,则关于x 的方程bx ax +2x3+=0的解为【答案】-3三、解答题1. (2011山东滨州,25,12分)如图,某广场设计的一建筑物造型的纵截面是抛物线的一部分,抛物线的顶点O 落在水平面上,对称轴是水平线OC 。
点A 、B 在抛物线造型上,且点A 到水平面的距离AC =4O 米,点B 到水平面距离为2米,OC =8米。
(1) 请建立适当的直角坐标系,求抛物线的函数解析式;(2) 为了安全美观,现需在水平线OC 上找一点P ,用质地、规格已确定的圆形钢管制作两根支柱P A 、PB 对抛物线造型进行支撑加固,那么怎样才能找到两根支柱用料最省(支柱与地面、造型对接方式的用料多少问题暂不考虑)时的点P ?(无需证明)(3) 为了施工方便,现需计算出点O 、P 之间的距离,那么两根支柱用料最省时点O 、P 之间的距离是多少?(请写出求解过程)【答案】解:(1)以点O 为原点、射线OC 为y 轴的正半轴建立直角坐标系………………1分 设抛物线的函数解析式为2y ax =,………………2分由题意知点A 的坐标为(4,8)。
且点A 在抛物线上,………………3分所以8=a×24,解得a=12,故所求抛物线的函数解析式为212y x =………………4分 (2)找法:延长AC,交建筑物造型所在抛物线于点D, ………………5分则点A 、D 关于OC 对称。
连接BD 交OC 于点P ,则点P 即为所求。
………………6分(3)由题意知点B 的横坐标为2,且点B 在抛物线上,所以点B 的坐标为(2,2)………………7分又知点A 的坐标为(4,8),所以点D 的坐标为(-4,8) (8)设直线BD 的函数解析式为 y=kx+b , (9)则有2248k b k b +=⎧⎨-+=⎩………………10 解得k=-1,b=4.故直线BD 的函数解析式为 y=-x+4, (11)把x=0代入 y=-x+4,得点P 的坐标为(0,4)两根支柱用料最省时,点O 、P 之间的距离是4米。
(12)2. (2011四川重庆,25,10分)某企业为重庆计算机产业基地提供电脑配件.受美元走低的影响,从去年1至9月,该配件的原材料价格一路攀升,每件配件的原材料价格y1(元)与月份x(1≤x≤9,且x取整数)之间的函数关系如下表:随着国家调控措施的出台,原材料价格的涨势趋缓,10至12月每件配件的原材料价格y2(元)与月份x(10≤x≤12,且x取整数)之间存在如图所示的变化趋势:(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识,直接写出y1与x之间的函数关系式,根据如图所示的变化趋势,直接写出y2与x之间满足的一次函数关系式;(2)若去年该配件每件的售价为1000元,生产每件配件的人力成本为50元,其它成本30元,该配件在1至9月的销售量p1(万件)与月份x满足关系式p1=0.1x+1.1(1≤x≤9,且x 取整数),10至12月的销售量p2(万件)p2=-0.1x+2.9(10≤x≤12,且x取整数).求去年哪个月销售该配件的利润最大,并求出这个最大利润;(3)今年1至5月,每件配件的原材料价格均比去年12月上涨60元,人力成本比去年增加20%,其它成本没有变化,该企业将每件配件的售价在去年的基础上提高a%,与此同时每月销售量均在去年12月的基础上减少0.1 a%.这样,在保证每月上万件配件销量的前提下,完成1至5月的总利润1700万元的任务,请你参考以下数据,估算出a的整数值.(参考数据:992=9801,982=9604,972=9409,962=9216,952=9025)【答案】(1)y1 与x之间的函数关系式为y1=20x+540,y2与x之间满足的一次函数关系式为y2=10x+630.(2)去年1至9月时,销售该配件的利润w=p1(1000-50-30-y1)=(0.1x+1.1)(1000−50−30−20x−540)=(0.1x+1.1)(380−20x)=-2x2+160x+418=-2( x -4)2+450,(1≤x≤9,且x 取整数)∥-2<0,1≤x≤9,∥当x =4时,w 最大=450(万元);去年10至12月时,销售该配件的利润w = p2(1000-50-30-y2)=(-0.1x +2.9)(1000-50-30-10x -630)=(-0.1x +2.9)(290-10x)=( x -29)2,(10≤x≤12,且x 取整数),当10≤x≤12时,∥x <29,∥自变量x 增大,函数值w 减小,∥当x =10时,w 最大=361(万元),∥450>361,∥去年4月销售该配件的利润最大,最大利润为450万元.(3)去年12月份销售量为:-0.1×12+0.9=1.7(万件),今年原材料的价格为:750+60=810(元),今年人力成本为:50×(1+20﹪)=60(元),由题意,得5×[1000(1+a ﹪)-810-60-30]×1.7(1-0.1a ﹪)=1700,设t= a ﹪,整理,得10t2-99t+10=0,解得t=99±940120,∥972=9409,962=9216,而9401更接近9409.∥9401=97.∥t1≈0.1或t2≈9.8,∥a1≈10或a2≈980.∥1.7(1-0.1a ﹪)≥1,∥a2≈980舍去,∥a≈10.答:a 的整数值为10.3. (2011山东潍坊,22,10分)2011年上半年,某种农产品受不良炒作的影响,价格一路上扬,8月初国家实施调控措施后,该农产品的价格开始回落.其中,1月份至7月份,该农产品的月平均价格y 元/千克与月份x 呈一次函数关系;7月份至12月份,月平均价格元/千克与月份x 呈二次函数关系.已知1月、7月、9月和12月这四个月的月平均价格分别为8元/千克、26元/千克、14元/千克、11元/千克.(1)分别求出当1≤x ≤7和7≤x ≤12时,y 关于x 的函数关系式;(2)2011年的12个月中,这种农产品的月平均价格哪个月最低?最低为多少?(3)若以12个月份的月平均价格的平均数为年平均价格,月平均价格高于年平均价格的月份有哪些?【解】(1)当17x ≤≤时,设y kx m =+,将点(1,8)、(7,26)分别代入y kx m =+,得8,726.k m k m +=⎧⎨+=⎩解之,得5,3.m k =⎧⎨=⎩ ∥函数解析式为35y x =+.当712x ≤≤时,设2y ax bx c =++,将(7,26)、(9,14)、(12,11)分别代入2y ax bx c =++,得: 49726,81914,1441211.a b c a b c a b c ++=⎧⎪++=⎨⎪++=⎩解之,得1,22,131.a b c =⎧⎪=-⎨⎪=⎩∥函数解析式为222131y x x =-+.(2)当17x ≤≤时,函数35y x =+中y 随x 的增大而增大,∥当1x =最小值时,3158y =⨯+=最小值.当712x ≤≤时,()22221311110y x x x =-+=-+,∥当11x =时,10y =最小值.所以,该农产品平均价格最低的是1月,最低为8元/千克.(3)∥1至7月份的月平均价格呈一次函数,∥4x =时的月平均价格17是前7个月的平均值.将8x =,10x =和11x =分别代入222131y x x =-+,得19y =,11y =和10y =. ∥后5个月的月平均价格分别为19,14,11,10,11.∥年平均价格为17719141110114615.3123y ⨯+++++==≈(元/千克). 当3x =时,1415.3y =<,∥4,5,6,7,8这五个月的月平均价格高于年平均价格.4. (2011四川成都,26,8分)某学校要在围墙旁建一个长方形的中药材种植实习苗圃,苗圃的一边靠围墙(墙的长度不限),另三边用木栏围成,建成的苗圃为如图所示的长方形ABCD .已知木栏总长为120米,设A B 边的长为x 米,长方形ABCD 的面积为S 平方米.(1)求S 与x 之间的函数关系式(不要求写出自变量x 的取值范围).当x 为何值时,S 取得最值(请指出是最大值还是最小值)?并求出这个最值;(2)学校计划将苗圃内药材种植区域设计为如图所示的两个相外切的等圆,其圆心分别为1O 和2O ,且1O 到AB 、BC 、AD 的距离与2O 到CD 、BC 、AD 的距离都相等,并要求在苗圃内药材种植区域外四周至少要留够0.5米宽的平直路面,以方便同学们参观学习.当(l)中S 取得最大值时,请问这个设计是否可行?若可行,求出圆的半径;若不可行,请说明理由. 【答案】(1)1800)30(2)2120(2+--=-=x x x S ,当30=x 时,S 取最大值为1800.(2)如图所示,过1O 、2O 分别作到AB 、BC 、AD 和CD 、BC 、AD 的垂直,垂足如图,根据题意可知,I O H O G O J O F O E O 222111=====;当S 取最大值时,AB =CD =30,BC =60, 所以1521O O O O 2211=====AB I G J F , ∥15O O 21==H E ,∥301515602121=--=--=H O E O EH O O ,∥两个等圆的半径为15,左右能够留0.5米的平直路面,而AD 和BC 与两圆相切,不能留0.5米的平直路面.6. (2011江苏无锡,25,10分)(本题满分10分)张经理到老王的果园里一次性采购一种水果,他俩商定:张经理的采购价y (元/吨)与采购量x (吨)之间函数关系的图象如图中的折线段ABC 所示(不包含端点A ,但包含端点C )。
